Калькулятор алгебры логики онлайн: Математическая логика · oнлайн с подробным объяснением

Калькулятор настольный Casio JW-200SC-BU, премиум

Премиальный настольный калькулятор Casio JW-200SC-BU будет каждый день радовать вас своим дизайном и удобством использования.

Эта модель специально создавалась для бухгалтеров и экономистов. Она имеет функции расчета налогов, конвертер валют, подсчета итоговой суммы и др. Промежуточные значения при расчетах можно сохранять в память. Крупные кнопки с эргономичным дизайном приятно нажимать, а надписи на них не сотрутся даже после многих лет использования. На калькуляторе Casio JW-200SC-BU установлена логика расчета процентов Profit Margin. С помощью логики CASIO можно выполнять на две операции больше, чем при помощи стандартной логики при расчете процентов.

Модель имеет стильный металлический корпус голубого цвета. Источника питания два — солнечные элементы и батарейка типа LR-44. Калькулятор самостоятельно выключается при простое, поэтому менять батарейку придется очень редко.

Покупайте эксклюзивный настольный калькулятор Casio JW-200SC-BU по выгодной цене с доставкой по всей России и гарантией 24 месяца в нашем интернет-магазине!

Расчет процентов Profit Margin: логика CASIO

Процент

Определите число, составляющее 5% от числа 200.

200 х 5 % = 10

Увеличение

Увеличьте число 100 на 5%.

100 х 5 % + = 105

Скидка

Уменьшите число 100 на 5%.

100 х 5 % — = 96

Отношение

Сколько процентов составляет число 30 от числа 60. Найдите процентное соотношение.

30 ÷ 60 % = 50

Наценка

От какого числа нужно отнять 20%, чтобы получить число 100.

100 ÷ 20 % = 125

Например, Вы закупили товар и планируете в скором времени объявить на него 20% скидку, но не можете опустить цену ниже 100. Если Вы просто прибавите 20% к числу 100 (получится 120), а затем сделаете скидку 20%, то опуститесь ниже минимальной цены (получится 96). Если воспользоваться функцией «Наценка», то получится искомое число — 125.

Процентное изменение

На сколько процентов нужно увеличить число 10, чтобы получить число 12.

12 — 10 % = 20

Например, Вы хотите сделать размер торговой наценки такой, чтобы розничная цена была равна 12, закупая по оптовой цене 10. Эта функция поможет найти размер процента торговой наценки.

Технические характеристики калькулятора

Тип: настольный дизайнерский калькулятор

12-разрядный

Цвет: голубой

Угол наклона дисплея: регулируемый

Материал лицевой панели: металл

Поверхность кнопок: пластик

Двойное питание: батарея + солн.питание

Тип батареи: LR-44 x 1 шт.

Автоматическое отключение питания: Есть

Разделитель групп разрядов: по 3 цифры

Размеры 107 х 178,5 х 26,1мм

Вес: 170 г

Функции калькулятора

Независимая память M+, M-, MR, MC

Клавиши нуля: 0, 00

Кнопка [%]: Есть. Логика расчета процентов Profit Margin

Корень квадратный: Есть

Кнопка обратной дроби [RV]: нет

Смена знаков [+/-]: Есть

Коррекция ввода [→]: Есть

Конвертер валют [LOCAL]: Есть

Расчет налогов [+TAX] [-TAX]: Есть

Расчет прибыли [COST] [SELL] [MARGIN]: нет

Функция расчета наценки и скидки [MU]: нет

Итоговая сумма [GT]: Есть

Функция проверки и коррекции [CHECK] [CORRECT]: нет

Округление: обычное 5/4, с уменьшением

Выбор режима десятичной точки: Есть (ADD2, 0, 1, 2, 3, 4, F)

Добавить комментарий

Уведомлять меня о новых комментариях по E-mail

Наши покупатели уже неоднократно заказывали этот калькулятор и делились с нами информацией, зачем он им необходим, планируют ли они использовать его для учебы или работы.

Прочитайте комментарии — и, возможно, вы откроете для себя новые варианты использования калькулятора:

• Росбанк

Записей не найдено.

Шпаргалки по ТДУ(11-15)

11)Логический базис

Лог.базис – полная система функций алгебры логики (Совокупность логических элементов И, ИЛИ, НЕ, с помощью которых можно воспроизвести и реализовать любую ФАЛ) Фун-ции Пирса и Шеффера являются логическими базисами.  – функция И-НЕ (базис Шеффера)  – функция ИЛИ-НЕ (базис Пирса) ИЛИ – НЕ, функция Пирса И – НЕ, функция Шеффера

12)Нормальные формы ФАЛ: ДСНФ и ДНФ ФАЛ удобно представить в некоторой исходной форме, которую называют нормальной. Затем, данную форму можно преобразовать, чтобы она соответствовала наиболее простой схеме.

1.ДНФ Дизъюнктивная нормальная форма (ДНФ) — представляет собой логическую сумму отдельных логических произведений аргументов взятых с инверсией или без нее (дизъюнкция элементарных конъюкций). Примером ДНФ является выражение:

где f – логическая функция; X1,X2,X3 — аргументы 2. ДСНФ

Дизъюнктивной совершенной нормальной формой (ДСНФ) называется ДНФ, содержащая в каждом из складываемых произведений все без исключения аргументы. ДСНФ представляет собой дизъюнкцию специально вводимых функций (минтермов), которые принимают значения LOG1 на тех же наборах, что и исходная функция Для представления ФАЛ в ДСНФ, необходимо выписать все наборы входных переменных, где LOG и поставить знаки отрицания над переменными, которые равны 0 Пример ДСНФ:

Последовательность представления в ДНФ: 1) На основании тождественных преобразований , ДСНФ выражают в основном базисе. 2) Применяя дистрибутивный закон конъюнкции относительно дизъюнкции, все конъюнкции приводят к элементарным 3) Для перехода от ДНФ к ДСНФ, каждый из членов логического выражения, в которых представлены не все переменные, следует добавить выражение вида

13) Нормальные формы ФАЛ: КСНФ и КНФ.

ФАЛ удобно представить в некоторой исходной форме, которую называют нормальной. Затем, данную форму можно преобразовать, чтобы она соответствовала наиболее простой схеме. 1. КНФ Конъюнктивная нормальная форма (КНФ) представляет собой логическое произведение отдельных логических сумм аргументов с инверсией или без нее. Примером КНФ является следующее выражение: где f – логическая функция; x1,x2,x3 – аргументы 2. КСНФ Конъюнктивной совершенной нормальной формой (КСНФ) называется КНФ содержащая в каждой из перемножаемых сумм все без исключения аргументы. КСНФ представляет собой конъюнкцию специально вводимых функцию-макстермов, которые равны

LOG0 там же, где и исходная функция. пример КСНФ: Для представления ФАЛ в КСНФ необходимо выписать все наборы переменных, где функция равна LOG0 и поставить знаки отрицания над 1. Последовательность представления КНФ: 1) КСНФ, выражается в основном базисе 2) Применяя дистрибутивный закон дизъюнкции приводятся к элементарным 3) Для перехода от КНФ к КСНФ каждому из членов, которые не содержат всех элементов, добавить слагаемое типа

14) Минимизация ФАЛ методом карт Карно Задачи минимизации ФАЛ – нахождение формы функции, содержащее мин. число входных элементов о операций м.у. ними. Карты Карно представляют собой визуальный метод, который дает возможность определять члены логического выражения, к которым можно применить закон склеивания Каждая клетка карты Карно соответствует минтерму и обозначается единицей для тех минтермов, которые присутствуют в исходной функции. Например, пусть требуется минимизировать логическую функцию, заданную таблицей истинности:

Карта Карно в этом случае будет иметь вид: На карте выделен контур, который не пересекает границу изменения только одной переменной и, следовательно, минимальная формула для данной функции будет иметь вид: f = x₂. Алгоритм минимизации: 1) Проставить единицы в те клетки карты Карно, которые соответствуют членам заданного выражения ДСНФ 2)Объединяем смежные клетки, содержащие единицы так, чтобы область содержала клеток, при этом, крайние клетки считаются смежными В области не должно быть 0, она не должна быть как можно больше; число областей как можно меньше; области могут пересекаться.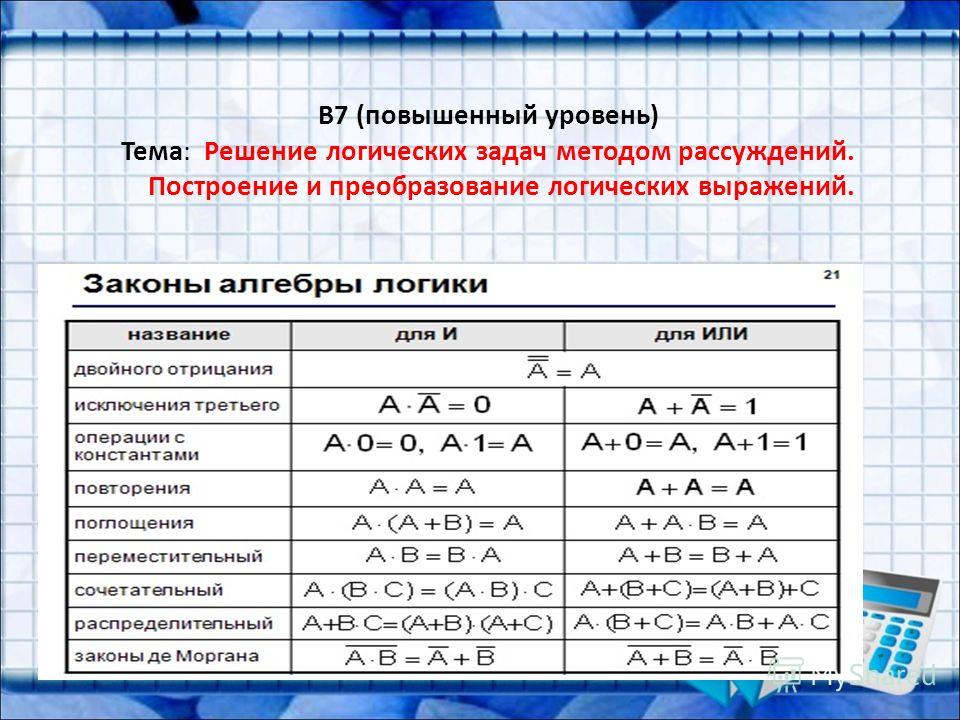 3)Смотрим первую область — какие переменные не меняются. Если неменяющаяся переменная не равна 0, то ставим над ней знак инверсии Пример: Для получения функции в форме КНФ, замкнутыми областями обхватываются клетки с 0 значениями. При записи членов берутся инверсные значения переменных с неизменным значением пределов областей.

15)Минимизация ФАЛ методом Квайна-Мак-Класки. Метод основывается на задании минтермов в виде условных чисел, называемых номерами. Каждому минтерму присваивают определенный индекс, под которым понимается число единиц в двоичном представлении номера минтерма. Алгоритм: 1) Разделить двоичные векторы области единиц логической функции на секции в соответствии с их индексами. Индекс двоичного вектора = число единиц, входящих в состав этого вектора. 2) Составить таблицу интервалов, используя правило склеивания. Склеивать между собой только те двоичные векторы, которые отличаются друг от друга только в одной координате (ближайшие векторы).

Склеивание происходит по этой координате. Ближайшие векторы могут находится только в соседних секциях таблицы. 3) В конце первого этапа получают все простые импликанты логической функции. 4) Полученное множество простых импликант минимизируют, т.е. выбирают минимальное количество простых импликант, которое позволяет покрыть всю область единиц логической функции. Пример: Пример: f={0,1,3,4,7,9,11,15}

X1	X2	X3	X4	f
0	0	0	0	1
0	0	0	1	1
0	0	1	0	0
0	0	1	1	1
0	1	0	0	0
0	1	0	1	1
0	1	1	0	1
0	1	1	1	1
1	0	0	0	0
1	0	0	1	1
1	0	1	0	0
1	0	1	1	1
1	1	0	0	0
1	1	0	1	0

Калькулятор упрощения логической алгебры

Калькулятор упрощения логических выражений

Программа предназначена для получения таблиц истинности логических функций с количеством переменных от одной до пяти.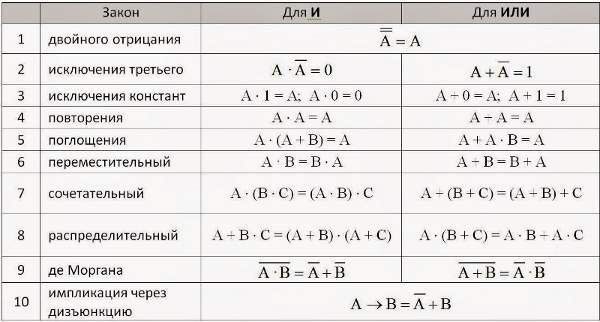 Логическая (булева) функция от n переменных y = f(x1, x2, …, xn) — это функция со всеми переменными, причем сама функция может принимать только два значения: 0 и 1.

А Б С Д

0 1

· + ¬

⊕ ⇒ ⇔

↓ |

( )

Вперёд!

Решение для перехода

Основные функции логики

Переменные, которые могут принимать только два значения 0 и 1, называются логическими переменными (или просто переменными). Обратите внимание, что логическая переменная x может подразумевать под номером 0 некоторое утверждение, которое является ложным, и под номером 1 какое-то утверждение, которое является истинным.

Из определения логической функции следует, что функция n переменных есть отображение Bn в B, которое может быть определено непосредственно таблицей, называемой таблицей истинности этой функции.

Основные функции логики — это функции двух переменных z = f(x,y).

Число этих функций 24 = 16. Перенумеруем их и расположим в естественном порядке.

Рассмотрим эти функции подробнее. Два из них f0 = 0 и f15 = 1 являются константами. Функции f3, f5, f10 и f12 по существу являются функциями одной переменной.

Наиболее важные функции двух переменных имеют специальные имена и обозначения.

1) f1 – соединение (функция И)
Обратите внимание, что конъюнкция на самом деле является обычным умножением (нулей и единиц). Эта функция обозначается x&y;

2) f7 есть дизъюнкция (или функция). Обозначается V.

3) f13 — импликация (следующая). Обозначается ->.
Это очень важная функция, особенно в логике. Его можно рассматривать так: если x = 0 (т.е. x «ложно»), то из этого факта можно вывести и «ложно» и «истинно» (и это будет правильно), если y = 1 (т.е. y «истинно»), то истина выводится как из «ложного», так и из «истинного», и это тоже правильно. Только вывод «из истины ложно» неверен. Обратите внимание, что любая теорема фактически всегда содержит эту логическую функцию;

4) f6 – сложение по модулю 2. Обозначается знаком «+» или знаком «+» в кружке.

5) f9 эквивалентность или подобие. Это f9 = 1 тогда и только тогда, когда x = y. Обозначается x ~ y.

6) f14 — черточка Шеффера. Эту функцию иногда называют «не и» (поскольку она равна отрицанию союза). Обозначается x|y.

7) f8 — стрелка Пирса (иногда эту функцию называют штрихом Лукасевича).

Остальные три функции (f2 , f4 и f11) не имеют специального обозначения.

Обратите внимание, что в логике часто рассматриваются функции из функций, т. е. суперпозиции вышеуказанных функций. При этом последовательность действий указывается (как обычно) в скобках.

Руководство пользователя

1. Все введенные пользователем символы будут отображаться на калькуляторе
2. Помимо символьных операндов, представленных в интерфейсе приложения, также возможен ввод с клавиатуры
3. функция, последние введенные символы можно удалить, нажав клавишу Backspace
4. Приложение поддерживает автоматическую проверку правильности введенных значений. То есть в случае ошибки символ на дисплее не появится, а наоборот, будет вибрировать, давая понять пользователю, что допущена ошибка
5. После того, как вы закончите ввод пользовательского выражения, необходимо нажать кнопку кнопка подтверждения для отображения таблицы истинности
6. Если расчетных значений слишком много, таблицу можно прокрутить вниз, чтобы просмотреть оставшиеся параметры
7. Вверху в качестве подсказки отображается выражение, введенное пользователем
8. Чтобы вернуться на главную страницу, нажмите в любом месте таблицы

Калькулятор булевой алгебры | Булева алгебра и решатель выражений

Булева алгебра — это раздел математики, который занимается операциями над логическими значениями и включает двоичные переменные. Используйте наш калькулятор булевой алгебры для решения выражений. Нажмите ниже, чтобы использовать его прямо сейчас.

Выражение

Введите выражение

Результат

Введите числа слева и нажмите кнопку «Рассчитать», чтобы получить здесь результат

Что такое булева алгебра?

Булева алгебра — это раздел алгебры, в котором значения истинности, «истина» и «ложь» используются в качестве значений переменных. Значение истинности «истина» обозначается 1, а значение истины «ложь» обозначается «0».

Таблица истинности  

Таблица истинности — это таблица, которая дает все возможные значения логических переменных и комбинации переменных. Можно преобразовать логическое уравнение в таблицу истинности. Другими словами, таблица истинности — это математическая таблица, в которой перечислены выходные данные конкретной цифровой логической схемы для всех возможных комбинаций ее входов. Эти таблицы истинности можно использовать для вывода логического выражения для данной цифровой схемы, и они широко используются в булевой алгебре.

Как формируется таблица истинности?

Ниже приведены характеристики таблицы истинности, которые позволяют ее формирование: 

1. В таблице истинности есть один столбец для каждой входной переменной (обычно представляемой как A и B, x и y или P и Q) и один последний столбец, показывающий все возможные результаты логической операции, которую представляет таблица (например, A AND B).
2. Каждая строка таблицы истинности содержит одну возможную конфигурацию входных переменных (например, A = true [1] B = false [0]) и результат операции для этих значений (продолжая пример, A AND B=ложь [0]).

Важные операции в булевой алгебре

Есть три важные операции в булевой алгебре, а также

1. Соединение
2. Diesjunction

9

Artancom Artancom Artancom Artancom Artancom
949494949494994
94494949494
94494949494














9004. 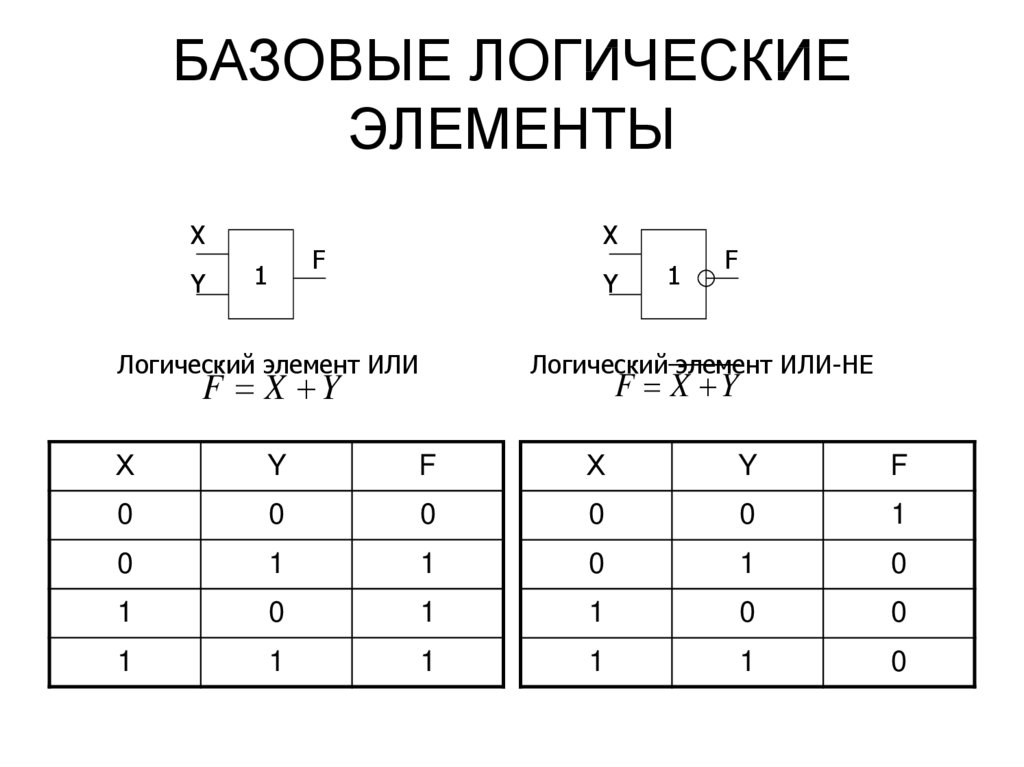Символ » . “ используется для представления соединения между двумя переменными A и B. Эта операция возвращает истинное значение, только если оба входных операнда истинны. Ниже приведена таблица истинности для соединения или операции И между двумя переменными A и B — 

A	B	A AND B
1	1	1
1	0	0
0	1	0
0	0	0

Операция дизъюнкции

. Символ «+» используется для обозначения дизъюнкции между двумя переменными A и B. Эта операция возвращает истинное значение, даже если один из входных операндов истинен. Ниже приведена таблица истинности для дизъюнкции или операции ИЛИ между двумя переменными A и B –

A	B	A OR B
1	1	1
1	0	1
0	1	1
0	0	0

Операция отрицания также известна как отрицание НЕ

. Символ « » или «-» используется для представления отрицания или НЕ переменной A. Это означает, что отрицание A представлено A’. Эта операция возвращает ложное значение, если входное значение истинно, и истинное значение, если входное значение ложно. Ниже приведена таблица истинности для операции отрицания или НЕ для переменной A – 9.0005

A	A’
1	0
0	1

Laws of Boolean algebra

Below are some of the important laws булевой алгебры –

Коммутативный закон

Согласно этому закону –

1. A + B = B + A
2. A . Б = Б . A

Ассоциативный закон

Согласно этому закону –  ​​

1. А + (В + С) = (А + В) + С
2. А. ( Б . С ) знак равно ( А . Б ) . C

Распределительный закон

Согласно этому закону –  ​​

1. A . ( B + C ) знак равно ( A. B ) + ( A . C )
2. A + ( B . C ) знак равно ( A + B ) . ( A . C )

Закон о личности

Согласно этому закону –

1. A + 0 = A
2. A . 1 = A

Закон идемпотента

Согласно этому закону –  ​​

1. А + А = А
2. А . A = A

Закон Де Моргана

Согласно этому закону –  ​​

1. (A . B ) ‘= A’ + B’
2. (A + B) ‘= A’ . B’

Логические выражения и как их решать?

Логическое выражение, результатом которого является логическое значение, будь то True или False, является логическим выражением. Давайте разберемся на примере.

Предположим, у нас есть логическое выражение A + B’

Как мы будем его решать? Подготовим для него таблицу истинности. We will have,

A	B	B’	A + B’
1	0	1	1
1	1	0	1
0	0	1	1
0	1	0	0

Обратите внимание, что в приведенной выше таблице мы сначала вычислили значение B’ при выполнении операции НЕ. После этого мы выполнили операцию ИЛИ между A и B’, чтобы получить желаемый результат для A + B’.

Как использовать калькулятор булевой алгебры для решения логических выражений?

Чтобы найти значение логического выражения с помощью калькулятора булевой алгебры, необходимо выполнить следующие шаги – 

Шаг 1  – Первым шагом является ввод выражения в разделе «Введите выражение» калькулятора булевой алгебры. Возьмем пример. Предположим, мы хотим решить логическое выражение A + B + C. Для этого мы введем это выражение в раздел «Введите выражение» калькулятора булевой алгебры. Ниже показано, как следует вводить выражение:

. Шаг 2. . После того, как мы ввели выражение, следующим шагом будет получение результата. Для этого нам просто нужно нажать на кнопку расчета. Как только мы это сделаем, мы получим результат в правой части выражения, которое мы ввели на предыдущем шаге. Ниже приведен снимок того, как будет отображаться результат – 

Теперь давайте сравним этот результат с тем, который мы получили бы, используя булевы законы.