Вычисления определенного интеграла Формула Ньютона – Лейбница
Теорема 2. Если функция непрерывна на отрезке и — какая-либо ее первообразная на этом отрезке, то имеет место формула:
.
Равенство называется формулой Ньютона-Лейбница. Используя краткое обозначение , эту формулу можно записать в виде
. (3)
Таким образом, вычисление определенного интеграла от непрерывной функции сводится к отысканию ее первообразной, то есть, по существу, неопределенного интеграла.
Нахождение определенных интегралов с помощью формулы Ньютона-Лейбница осуществляется в два этапа:
На первом этапе находят некоторую первообразную для подынтегральной функции ;
На втором этапе находится разность значений этой первообразной на концах отрезка .
Решение: Для подынтегральной функции произвольная первообразная имеет вид . Так как в формуле Ньютона-Лейбница можно использовать любую первообразную, то для вычисления интеграла возьмем первообразную, имеющую наиболее простой вид: . Тогда .
Пример 2. Вычислить интеграл .
Решение: По формуле Ньютона-Лейбница имеем:
.
Пример 3. Найдем интеграл . Поскольку , то по формуле Ньютона-Лейбница получаем .
Пример 4. Площадь криволинейной трапеции, ограниченной графиком функции , осью и прямыми и , равна .
Теорема 3. Пусть функция непрерывна на отрезке .
Если:
1) функция и ее производная непрерывны при ;
2) множеством значений функции при является отрезок ;
3) , , то справедлива формула
.
(4)
Формула (3) называется формулой замены переменной в определенном интеграле.
Заметим, что:
При вычислении определенного интеграла методом подстановки, использование замены переменной позволяет упростить исходный интеграл, приблизив его к табличному. При этом нет необходимости возвращаться к исходной переменной интегрирования – достаточно лишь найти новые пределы интегрирования и (для этого надо решить относительно переменной t уравнения и )).
Часто вместо подстановки используют подстановку . В этом случае нахождение новых пределов интегрирования по переменной t упрощается: , .
Не следует забывать менять пределы интегрирования при замене переменных.
Пример 5. Вычислить интеграл
Решение: Введем новую переменную по формуле
.
Определим и
.
Возведя в квадрат обе части равенства
,
получим
,
откуда
,
.
Находим новые пределы интегрирования.
Для этого в формулу
подставим старые пределы и
.
Получим:
,
откуда и, следовательно,
;
,
откуда и, следовательно,
.
Таким образом:
.
Пример 6. Вычислить интеграл .
Решение: Воспользуемся универсальной тригонометрической подстановкой. Положим , откуда , . Найдем новые пределы интегрирования: если , то ; если , то . Значит, . Следовательно:
.
Пример 7. Вычислить интеграл .
Решение: Положим , тогда , откуда . Находим новые пределы интегрирования: ; . Имеем: . Следовательно:
.
Формула ньютона лейбница сообщение. Определённый интеграл и методы его вычисления
Пусть на некотором отрезке оси Ох задана некоторая непрерывная функция f.
Положим, что эта функция не меняет своего знака на всем отрезке.
Если f есть непрерывная и неотрицательная на некотором отрезке функция, а F есть её некоторая первообразная на этом отрезке, тогда площадь криволинейной трапеции S равна приращению первообразной на данном отрезке .
Эту теорему можно записать следующей формулой:
S = F(b) — F(a)
Интеграл функции f(x) от а до b будет равен S. Здесь и далее, для обозначения определенного интеграла от некоторой функции f(x), с пределами интегрирования от a до b, будем использовать следующую запись (a;b)∫f(x). Ниже представлен пример как это будет выглядеть.
Формула Ньютона-Лейбница
Значит, мы можем приравнять между собой эти два результата. Получим: (a;b)∫f(x)dx = F(b) — F(a), при условии, что F есть первообразная для функции f на . Эта формула имеет название формулы Ньютона — Лейбница . Она будет верна для любой непрерывной на отрезке функции f.
Формула Ньютона-Лейбница применяется для вычисления интегралов.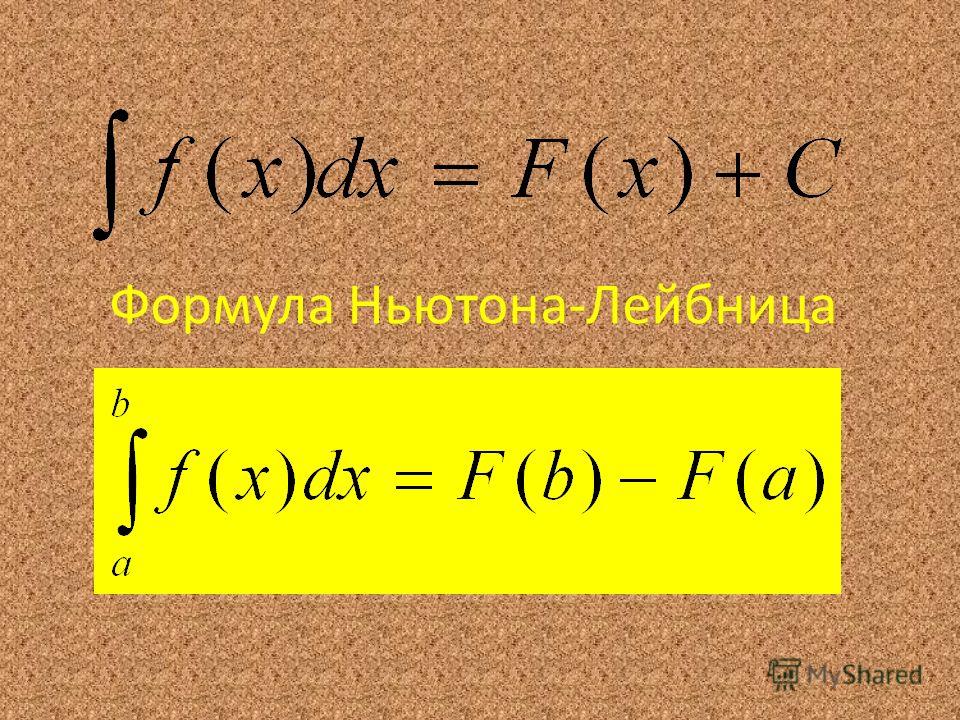
Рассмотрим несколько примеров:
Пример 1 : вычислить интеграл. Находим первообразную для подынтегральной функции x 2 . Одной из первообразных будет являться функция (x 3)/3.
Теперь используем формулу Ньютона — Лейбница:
(-1;2)∫x 2 dx = (2 3)/3 — ((-1) 3)/3 = 3
Ответ: (-1;2)∫x 2 dx = 3.
Пример 2 : вычислить интеграл (0;pi)∫sin(x)dx.
Находим первообразную для подынтегральной функции sin(x). Одной из первообразных будет являться функция -cos(x). Воспользуемся формулой Ньютона-Лейбница:
(0;pi)∫cos(x)dx = -cos(pi) + cos(0) = 2.
Ответ: (0;pi)∫sin(x)dx=2
Иногда для простоты и удобства записи приращение функции F на отрезке (F(b)-F(a)) записывают следующим образом:
Используя такое обозначение для приращения, формулу Ньютона-Лейбница можно переписать в следующем виде:
Как уже отмечалось выше, это лишь сокращение для простоты записи, больше ни на что эта запись не влияет. Эта запись и формула (a;b)∫f(x)dx = F(b) — F(a) будут эквивалентны.
Формула Ньютона — Лейбница
Основная теорема анализа или формула Ньютона — Лейбница даёт соотношение между двумя операциями: взятием определенного интеграла и вычислением первообразной
Формулировка
Рассмотрим интеграл от функции y = f (x ) в пределах от постоянного числа a до числа x , которое будем считать переменным. Запишем интеграл в следующем виде:
Данный вид интеграла называется интегралом с переменным верхним пределом. Используя теорему о среднем в определённом интеграле , легко показать что данная функция непрерывная и дифференцируемая. А также производная от данной функции в точке x равна самой интегрируемой функции. От сюда следует, что любая непрерывная функция имеет первообразную в виде квадратуры: . А так как класс первообразных функций функции f отличается на константу, легко показать, что: определенный интеграл от функции f на равен разности значений первообразных в точках b и а
Wikimedia Foundation
.
2010
.
- Формула Полной Вероятности
- Формула Релея — Джинса
Смотреть что такое «Формула Ньютона — Лейбница» в других словарях:
Формула Ньютона-Лейбница — Основная теорема анализа или формула Ньютона Лейбница даёт соотношение между двумя операциями: взятием определенного интеграла и вычислением первообразной Формулировка Рассмотрим интеграл от функции y = f(x) в пределах от постоянного числа a до… … Википедия
Формула конечных приращений — У этого термина существуют и другие значения, см. Теорема Лагранжа. Формула конечных приращений или теорема Лагранжа о среднем значении утверждает, что если функция непрерывна на отрезке и … Википедия
Формула Стокса — Теорема Стокса одна из основных теорем дифференциальной геометрии и математического анализа об интегрировании дифференциальных форм, которая обобщает несколько теорем анализа. Названа в честь Дж. Г. Стокса. Содержание 1 Общая формулировка 2… … Википедия
НЬЮТОНА — ЛЕЙБНИЦА ФОРМУЛА — формула, выражающая значение определенного интеграла от заданной функции f по отрезку в виде разности значений на концах отрезка любой первообразной Fэтой функции Названа именами И.
НЬЮТОНА-ЛЕЙБНИЦА ФОРМУЛА — основная формула интегрального исчисления. Выражает связь между определенным интегралом от функции f(x) и какой либо ее первообразной F(x) … Большой Энциклопедический словарь
Формула Лейбница — У этого термина существуют и другие значения, см. Список объектов, названных в честь Лейбница. У этого термина существуют и другие значения, см. Формула Лейбница (значения). Формулой Лейбница в интегральном исчислении называется правило… … Википедия
Ньютона-Лейбница формула — Ньютона Лейбница формула, основная формула интегрального исчисления. Выражает связь между определённым интегралом от функции f(х) и какой либо её первообразной F(х). . * * * НЬЮТОНА ЛЕЙБНИЦА ФОРМУЛА НЬЮТОНА ЛЕЙБНИЦА ФОРМУЛА, основная формула… … Энциклопедический словарь
Формула прямоугольников
Формула трапеций
— Определённый интеграл как площадь фигуры Численное интегрирование (историческое название: квадратура) вычисление значения определённого интеграла (как правило, приближённое), основанное на том, что величина интеграла численно равна площади… … ВикипедияТеорема Ньютона — Формула Ньютона Лейбница или основная теорема анализа даёт соотношение между двумя операциями: взятием определенного интеграла и вычислением первообразной.
Если непрерывна на отрезке и ее любая первообразная на этом отрезке, то имеет … Википедия
Определённым интегралом от непрерывной функции f (x ) на конечном отрезке [a , b ] (где ) называется приращение какой-нибудь её первообразной на этом отрезке. (Вообще, понимание заметно облегчится, если повторить тему неопределённого интеграла) При этом употребляется запись
Как видно на графиках внизу (приращение первообразной функции обозначено ),
Числа a и b называются соответственно нижним и верхним пределами интегрирования, а отрезок [a , b ] – отрезком интегрирования.
Таким образом, если F (x ) – какая-нибудь первообразная функция для f (x ), то, согласно определению,
(38)
Равенство (38) называется формулой Ньютона-Лейбница .
Разность F (b ) – F (a ) кратко записывают так:
Поэтому формулу Ньютона-Лейбница будем записывать и так:
(39)
Докажем, что определённый интеграл не зависит от того, какая первообразная подынтегральной функции взята при его вычислении. Пусть F (x ) и Ф(х ) – произвольные первообразные подынтегральной функции. Так как это первообразные одной и той же функции, то они отличаются на постоянное слагаемое: Ф(х ) = F (x ) + C . Поэтому
Тем самым установлено, что на отрезке [a , b ] приращения всех первообразных функции f (x ) совпадают.
Таким образом, для вычисления
определённого интеграла необходимо найти любую первообразную подынтегральной
функции, т.е. сначала следует найти неопределённый интеграл. Постоянная С из последующих вычислений исключается. Затем применяется формула Ньютона-Лейбница:
в первообразную функцию подставляется значение верхнего предела b , далее — значение
нижнего предела a и вычисляется разность F(b) — F(a) .
Полученное число и будет
определённым интегралом.
.
При a = b по определению принимается
Пример 1.
Решение. Сначала найдём неопределённый интеграл:
Применяя формулу Ньютона-Лейбница к первообразной
(при С = 0), получим
Однако при вычислении определённого интеграла лучше не находить отдельно первообразную, а сразу записывать интеграл в виде (39).
Пример 2. Вычислить определённый интеграл
Решение. Используя формулу
Свойства определённого интеграла
Теорема 2. Величина определённого интеграла не зависит от обозначения переменной интегрирования , т.е.
(40)
Пусть F (x ) – первообразная для f (x ). Для f (t ) первообразной служит та же функция F (t ), в которой лишь иначе обозначена независимая переменная. Следовательно,
На основании формулы (39) последнее равенство означает равенство интегралов
Теорема 3.
Постоянный множитель можно выносить за знак определённого интеграла , т.е.
(41)
Теорема 4. Определённый интеграл от алгебраической суммы конечного числа функций равен алгебраической сумме определённых интегралов от этих функций , т.е.
(42)
Теорема 5. Если отрезок интегрирования разбит на части, то определённый интеграл по всему отрезку равен сумме определённых интегралов по его частям , т.е. если
(43)
Теорема 6. При перестановке пределов интегрирования абсолютная величина определённого интеграла не меняется, а изменяется лишь его знак , т.е.
(44)
Теорема 7 (теорема о среднем). Определённый интеграл равен произведению длины отрезка интегрирования на значение подынтегральной функции в некоторой точке внутри его , т.е.
(45)
Теорема 8. Если верхний предел интегрирования больше нижнего и подынтегральная функция неотрицательна (положительна), то и определённый интеграл неотрицателен (положителен), т.
е. если
Теорема 9. Если верхний предел интегрирования больше нижнего и функции и непрерывны, то неравенство
можно почленно интегрировать , т.е.
(46)
Свойства определённого интеграла позволяют упрощать непосредственное вычисление интегралов.
Пример 5. Вычислить определённый интеграл
Используя теоремы 4 и 3, а при нахождении первообразных – табличные интегралы (7) и (6), получим
Определённый интеграл с переменным верхним пределом
Пусть f (x ) – непрерывная на отрезке [a , b ] функция, а F (x ) – её первообразная. Рассмотрим определённый интеграл
(47)
а через t обозначена переменная интегрирования, чтобы не путать её с верхней границей. При изменении х меняется и опредёленный интеграл (47), т.е. он является функцией верхнего предела интегрирования х , которую обозначим через Ф (х ), т.е.
(48)
Докажем, что функция Ф (х ) является первообразной для f (x ) = f (t ). Действительно, дифференцируя Ф (х ), получим
так как F (x ) – первообразная для f (x ), а F (a ) – постояная величина.
Функция Ф (х ) – одна из бесконечного множества первообразных для f (x ), а именно та, которая при x = a обращается в нуль. Это утверждение получается, если в равенстве (48) положить x = a и воспользоваться теоремой 1 предыдущего параграфа.
Вычисление определённых интегралов методом интегрирования по частям и методом замены переменной
где, по определению, F (x ) – первообразная для f (x ). Если в подынтегральном выражении произвести замену переменной
то в соответствии с формулой (16) можно записать
В этом выражении
первообразная функция для
В самом деле, её производная, согласно правилу дифференцирования сложной функции , равна
Пусть α и β – значения переменной t , при которых функция
принимает соответственно значения a и b , т.
е.
Но, согласно формуле Ньютона-Лейбница, разность F (b ) – F (a ) есть
Ньютон Лейбниц – это немецкий философ, который родился 1 июля 1646года. Помимо философии, его увлекли точные науки. Он отметился в логике, математике, механике, физике, истории, дипломатии, механике. Так же Ньютона принято считать и изобретателем, а так же языковедом. Он был основателем и первый смог возглавить Академию наук в Берлине. Лейбниц занял почетное место во Французской Академии наук, как иностранный член.
Самыми основными научными достижениями Лейбница считают:
Создание математического анализа. Исчисление дифференциальное и интегральное, которое он основал на бесконечных малых.
С его помощью была заложена основа математической логики.
Наука комбинаторика.
Двоичная система счисления с цифрами 0 и 1. Теперь на них основана вся современная техника.
Для психологии был очень важный вклад, как понятие бессознательных малых перцепций. Помимо этого, появилось учение о бессознательной психической жизни.
Выявил закон сохранения энергии и ввел понятие живой силы.
Ньютона считают завершителем философии 17века. Он стал родоначальником новой системы и дал ей название – монадология. Помимо достижений в философии, ему удалось выявить учения об синтезе и анализе. Лейбниц дал ему формулировку в виде закона достаточного основания. Как он отмечал, все это не отталкивалось только от мышления и логики, а еще и от бытия и онтологии. Философу можно присвоить авторство современной формулировки закона тождества. Именно он вывел в мир понимание термина «модель».
В своих работах, Лейбниц писал о разнообразии возможностей машинного моделирования в человеческом мозгу. Как оказалось, у него есть большое количество функций. Именно данный ученый впервые выставил миру идею о том, что одни виды энергии могут переходить в другие. Эти исследования внесли большой вклад в физику. Конечно, самым важным и известным трудом его жизни была формула. Ее так и назвали формула Ньютона Лейбница.
Формула Ньютона Лейбница
Пусть на некотором отрезке оси Ох задана некоторая непрерывная функция f.
Положим, что эта функция не меняет своего знака на всем отрезке.
Если f есть непрерывная и неотрицательная на некотором отрезке функция, а F есть её некоторая первообразная на этом отрезке, тогда площадь криволинейной трапеции S равна приращению первообразной на данном отрезке .
Эту теорему можно записать следующей формулой:
S = F(b) – F(a)
Интеграл функции f(x) от а до b будет равен S. Здесь и далее, для обозначения определенного интеграла от некоторой функции f(x), с пределами интегрирования от a до b, будем использовать следующую запись (a;b)∫f(x). Ниже представлен пример как это будет выглядеть.
Значит, мы можем приравнять между собой эти два результата. Получим: (a;b)∫f(x)dx = F(b) — F(a), при условии, что F есть первообразная для функции f на . Эта формула имеет название формулы Ньютона – Лейбница. Она будет верна для любой непрерывной на отрезке функции f.
Формула Ньютона-Лейбница применяется для вычисления интегралов. Рассмотрим несколько примеров:
Пример 1: вычислить интеграл.
Находим первообразную для подынтегральной функции x2. Одной из первообразных будет являться функция (x3)/3.
Теперь используем формулу Ньютона – Лейбница:
(-1;2)∫x2dx = (23)/3 – ((-1)3)/3 = 3
Ответ: (-1;2)∫x2dx = 3.
Пример 2: вычислить интеграл (0;pi)∫sin(x)dx.
Находим первообразную для подынтегральной функции sin(x). Одной из первообразных будет являться функция –cos(x). Воспользуемся формулой Ньютона-Лейбница:
(0;pi)∫cos(x)dx = -cos(pi) + cos(0) = 2.
Ответ: (0;pi)∫sin(x)dx=2
Иногда для простоты и удобства записи приращение функции F на отрезке (F(b)-F(a)) записывают следующим образом:
Используя такое обозначение для приращения, формулу Ньютона-Лейбница можно переписать в следующем виде:
Как уже отмечалось выше, это лишь сокращение для простоты записи, больше ни на что эта запись не влияет. Эта запись и формула (a;b)∫f(x)dx = F(b) — F(a) будут эквивалентны.
Данной формулой до сих пор пользуется большое количество ученых и вычислителей.
С ее помощью Лейбниц внес развитие во многие науки.
Решение прикладных задач сводится к вычислению интеграла, но не всегда это возможно сделать точно. Иногда необходимо знать значение определенного интеграла с некоторой степенью точности, к примеру, до тысячной.
Существуют задачи, когда следовало бы найти приближенное значение определенного интеграла с необходимой точностью, тогда применяют численное интегрирование такое, как метод Симпосна, трапеций, прямоугольников. Не все случаи позволяют вычислить его с определенной точностью.
Данная статья рассматривает применение формулы Ньютона-Лейбница. Это необходимо для точного вычисления определенного интеграла. Будут приведены подробные примеры, рассмотрены замены переменной в определенном интеграле и найдем значения определенного интеграла при интегрировании по частям.
Yandex.RTB R-A-339285-1
Формула Ньютона-Лейбница
Определение 1
Когда функция y = y (x) является непрерывной из отрезка [ a ; b ] ,а F (x) является одной из первообразных функции этого отрезка, тогда формула Ньютона-Лейбница считается справедливой.
Запишем ее так ∫ a b f (x) d x = F (b) — F (a) .
Данную формулу считают основной формулой интегрального исчисления.
Чтобы произвести доказательство этой формулы, необходимо использовать понятие интеграла с имеющимся переменным верхним пределом.
Когда функция y = f (x) непрерывна из отрезка [ a ; b ] , тогда значение аргумента x ∈ a ; b , а интеграл имеет вид ∫ a x f (t) d t и считается функцией верхнего предела. Необходимо принять обозначение функции примет вид ∫ a x f (t) d t = Φ (x) , она является непрерывной, причем для нее справедливо неравенство вида ∫ a x f (t) d t » = Φ » (x) = f (x) .
Зафиксируем, что приращении функции Φ (x) соответствует приращению аргумента ∆ x , необходимо воспользоваться пятым основным свойством определенного интеграла и получим
Φ (x + ∆ x) — Φ x = ∫ a x + ∆ x f (t) d t — ∫ a x f (t) d t = = ∫ a x + ∆ x f (t) d t = f (c) · x + ∆ x — x = f (c) · ∆ x
где значение c ∈ x ; x + ∆ x .
Зафиксируем равенство в виде Φ (x + ∆ x) — Φ (x) ∆ x = f (c) .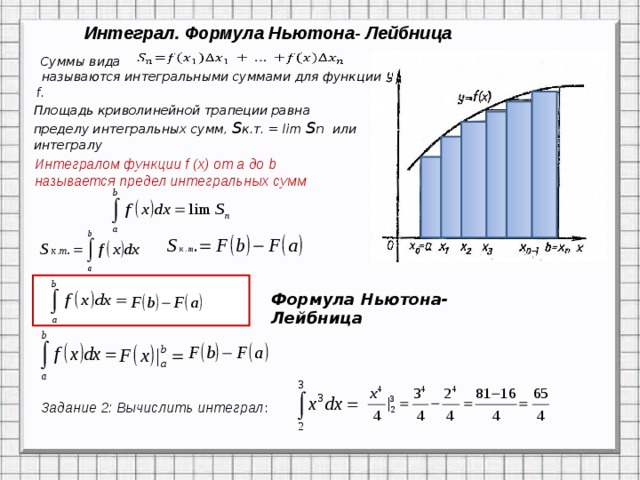
По определению производной функции необходимо переходить к пределу при ∆ x → 0 , тогда получаем формулу вида Φ » (x) = f (x) . Получаем, что Φ (x) является одной из первообразных для функции вида y = f (x) , расположенной на [ a ; b ] . Иначе выражение можно записать
F (x) = Φ (x) + C = ∫ a x f (t) d t + C , где значение C является постоянной.
Произведем вычисление F (a) с использованием первого свойства определенного интеграла. Тогда получаем, что
F (a) = Φ (a) + C = ∫ a a f (t) d t + C = 0 + C = C , отсюда получаем, что C = F (a) . Результат применим при вычислении F (b) и получим:
F (b) = Φ (b) + C = ∫ a b f (t) d t + C = ∫ a b f (t) d t + F (a) , иначе говоря, F (b) = ∫ a b f (t) d t + F (a) . Равенство доказывает формулу Ньютона-Лейбница ∫ a b f (x) d x + F (b) — F (a) .
Приращение функции принимаем как F x a b = F (b) — F (a) . С помощью обозначения формулу Ньютона-Лейбница принимает вид ∫ a b f (x) d x = F x a b = F (b) — F (a) .
Чтобы применить формулу, обязательно необходимо знать одну из первообразных y = F (x) подынтегральной функции y = f (x) из отрезка [ a ; b ] , произвести вычисление приращения первообразной из этого отрезка.
Рассмотрим несколько примером вычисления, используя формулу Ньютона-Лейбница.
Пример 1
Произвести вычисление определенного интеграла ∫ 1 3 x 2 d x по формуле Ньютона-Лейбница.
Решение
Рассмотрим, что подынтегральная функция вида y = x 2 является непрерывной из отрезка [ 1 ; 3 ] , тогда и интегрируема на этом отрезке. По таблице неопределенных интегралов видим, что функция y = x 2 имеет множество первообразных для всех действительных значений x , значит, x ∈ 1 ; 3 запишется как F (x) = ∫ x 2 d x = x 3 3 + C . Необходимо взять первообразную с С = 0 , тогда получаем, что F (x) = x 3 3 .
Воспользуемся формулой Ньютона-Лейбница и получим, что вычисление определенного интеграла примет вид ∫ 1 3 x 2 d x = x 3 3 1 3 = 3 3 3 — 1 3 3 = 26 3 .
Ответ: ∫ 1 3 x 2 d x = 26 3
Пример 2
Произвести вычисление определенного интеграла ∫ — 1 2 x · e x 2 + 1 d x по формуле Ньютона-Лейбница.
Решение
Заданная функция непрерывна из отрезка [ — 1 ; 2 ] , значит, на нем интегрируема.
Необходимо найти значение неопределенного интеграла ∫ x · e x 2 + 1 d x при помощи метода подведения под знак дифференциала, тогда получаем ∫ x · e x 2 + 1 d x = 1 2 ∫ e x 2 + 1 d (x 2 + 1) = 1 2 e x 2 + 1 + C .
Отсюда имеем множество первообразных функции y = x · e x 2 + 1 , которые действительны для всех x , x ∈ — 1 ; 2 .
Необходимо взять первообразную при С = 0 и применить формулу Ньютона-Лейбница. Тогда получим выражение вида
∫ — 1 2 x · e x 2 + 1 d x = 1 2 e x 2 + 1 — 1 2 = = 1 2 e 2 2 + 1 — 1 2 e (- 1) 2 + 1 = 1 2 e (- 1) 2 + 1 = 1 2 e 2 (e 3 — 1)
Ответ: ∫ — 1 2 x · e x 2 + 1 d x = 1 2 e 2 (e 3 — 1)
Пример 3
Произвести вычисление интегралов ∫ — 4 — 1 2 4 x 3 + 2 x 2 d x и ∫ — 1 1 4 x 3 + 2 x 2 d x .
Решение
Отрезок — 4 ; — 1 2 говорит о том, что функция, находящаяся под знаком интеграла, является непрерывной, значит, она интегрируема. Отсюда найдем множество первообразных функции y = 4 x 3 + 2 x 2 . Получаем, что
∫ 4 x 3 + 2 x 2 d x = 4 ∫ x d x + 2 ∫ x — 2 d x = 2 x 2 — 2 x + C
Необходимо взять первообразную F (x) = 2 x 2 — 2 x , тогда, применив формулу Ньютона-Лейбница, получаем интеграл, который вычисляем:
∫ — 4 — 1 2 4 x 3 + 2 x 2 d x = 2 x 2 — 2 x — 4 — 1 2 = 2 — 1 2 2 — 2 — 1 2 — 2 — 4 2 — 2 — 4 = 1 2 + 4 — 32 — 1 2 = — 28
Производим переход к вычислению второго интеграла.
Из отрезка [ — 1 ; 1 ] имеем, что подынтегральная функция считается неограниченной, потому как lim x → 0 4 x 3 + 2 x 2 = + ∞ , тогда отсюда следует, что необходимым условием интегрируемости из отрезка. Тогда F (x) = 2 x 2 — 2 x не является первообразной для y = 4 x 3 + 2 x 2 из отрезка [ — 1 ; 1 ] , так как точка O принадлежит отрезку, но не входит в область определения. Значит, что имеется определенный интеграл Римана и Ньютона-Лейбница для функции y = 4 x 3 + 2 x 2 из отрезка [ — 1 ; 1 ] .
Ответ: ∫ — 4 — 1 2 4 x 3 + 2 x 2 d x = — 28 , имеется определенный интеграл Римана и Ньютона-Лейбница для функции y = 4 x 3 + 2 x 2 из отрезка [ — 1 ; 1 ] .
Перед использованием формулы Ньютона-Лейбница нужно точно знать о существовании определенного интеграла.
Замена переменной в определенном интеграле
Когда функция y = f (x) является определенной и непрерывной из отрезка [ a ; b ] , тогда имеющееся множество [ a ; b ] считается областью значений функции x = g (z) , определенной на отрезке α ; β с имеющейся непрерывной производной, где g (α) = a и g β = b , отсюда получаем, что ∫ a b f (x) d x = ∫ α β f (g (z)) · g » (z) d z .
Данную формулу применяют тогда, когда нужно вычислять интеграл ∫ a b f (x) d x , где неопределенный интеграл имеет вид ∫ f (x) d x , вычисляем при помощи метода подстановки.
Пример 4
Произвести вычисление определенного интеграла вида ∫ 9 18 1 x 2 x — 9 d x .
Решение
Подынтегральная функция считается непрерывной на отрезке интегрирования, значит определенный интеграл имеет место на существование. Дадим обозначение, что 2 x — 9 = z ⇒ x = g (z) = z 2 + 9 2 . Значение х = 9 , значит, что z = 2 · 9 — 9 = 9 = 3 , а при х = 18 получаем, что z = 2 · 18 — 9 = 27 = 3 3 , тогда g α = g (3) = 9 , g β = g 3 3 = 18 . При подстановке полученных значений в формулу ∫ a b f (x) d x = ∫ α β f (g (z)) · g » (z) d z получаем, что
∫ 9 18 1 x 2 x — 9 d x = ∫ 3 3 3 1 z 2 + 9 2 · z · z 2 + 9 2 » d z = = ∫ 3 3 3 1 z 2 + 9 2 · z · z d z = ∫ 3 3 3 2 z 2 + 9 d z
По таблице неопределенных интегралов имеем, что одна из первообразных функции 2 z 2 + 9 принимает значение 2 3 a r c t g z 3 .
Тогда при применении формулы Ньютона-Лейбница получаем, что
∫ 3 3 3 2 z 2 + 9 d z = 2 3 a r c t g z 3 3 3 3 = 2 3 a r c t g 3 3 3 — 2 3 a r c t g 3 3 = 2 3 a r c t g 3 — a r c t g 1 = 2 3 π 3 — π 4 = π 18
Нахождение можно было производить, не используя формулу ∫ a b f (x) d x = ∫ α β f (g (z)) · g » (z) d z .
Если при методе замены использовать интеграл вида ∫ 1 x 2 x — 9 d x , то можно прийти к результату ∫ 1 x 2 x — 9 d x = 2 3 a r c t g 2 x — 9 3 + C .
Отсюда произведем вычисления по формуле Ньютона-Лейбница и вычислим определенный интеграл. Получаем, что
∫ 9 18 2 z 2 + 9 d z = 2 3 a r c t g z 3 9 18 = = 2 3 a r c t g 2 · 18 — 9 3 — a r c t g 2 · 9 — 9 3 = = 2 3 a r c t g 3 — a r c t g 1 = 2 3 π 3 — π 4 = π 18
Результаты совпали.
Ответ: ∫ 9 18 2 x 2 x — 9 d x = π 18
Интегрирование по частям при вычислении определенного интеграла
Если на отрезке [ a ; b ] определены и непрерывны функции u (x) и v (x) , тогда их производные первого порядка v » (x) · u (x) являются интегрируемыми, таким образом из этого отрезка для интегрируемой функции u » (x) · v (x) равенство ∫ a b v » (x) · u (x) d x = (u (x) · v (x)) a b — ∫ a b u » (x) · v (x) d x справедливо.
Формулу можно использовать тогда, необходимо вычислять интеграл ∫ a b f (x) d x , причем ∫ f (x) d x необходимо было искать его при помощи интегрирования по частям.
Пример 5
Произвести вычисление определенного интеграла ∫ — π 2 3 π 2 x · sin x 3 + π 6 d x .
Решение
Функция x · sin x 3 + π 6 интегрируема на отрезке — π 2 ; 3 π 2 , значит она непрерывна.
Пусть u (x) = х, тогда d (v (x)) = v » (x) d x = sin x 3 + π 6 d x , причем d (u (x)) = u » (x) d x = d x , а v (x) = — 3 cos π 3 + π 6 . Из формулы ∫ a b v » (x) · u (x) d x = (u (x) · v (x)) a b — ∫ a b u » (x) · v (x) d x получим, что
∫ — π 2 3 π 2 x · sin x 3 + π 6 d x = — 3 x · cos x 3 + π 6 — π 2 3 π 2 — ∫ — π 2 3 π 2 — 3 cos x 3 + π 6 d x = = — 3 · 3 π 2 · cos π 2 + π 6 — — 3 · — π 2 · cos — π 6 + π 6 + 9 sin x 3 + π 6 — π 2 3 π 2 = 9 π 4 — 3 π 2 + 9 sin π 2 + π 6 — sin — π 6 + π 6 = 9 π 4 — 3 π 2 + 9 3 2 = 3 π 4 + 9 3 2
Решение примера можно выполнить другим образом.
Найти множество первообразных функции x · sin x 3 + π 6 при помощи интегрирования по частям с применением формулы Ньютона-Лейбница:
∫ x · sin x x 3 + π 6 d x = u = x , d v = sin x 3 + π 6 d x ⇒ d u = d x , v = — 3 cos x 3 + π 6 = = — 3 cos x 3 + π 6 + 3 ∫ cos x 3 + π 6 d x = = — 3 x cos x 3 + π 6 + 9 sin x 3 + π 6 + C ⇒ ∫ — π 2 3 π 2 x · sin x 3 + π 6 d x = — 3 cos x 3 + π 6 + 9 sincos x 3 + π 6 — — — 3 · — π 2 · cos — π 6 + π 6 + 9 sin — π 6 + π 6 = = 9 π 4 + 9 3 2 — 3 π 2 — 0 = 3 π 4 + 9 3 2
Ответ: ∫ x · sin x x 3 + π 6 d x = 3 π 4 + 9 3 2
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
t\sin\left(x-t\right)dt$спросил
Изменено 1 год, 2 месяца назад
Просмотрено 234 раза
$\begingroup$
Как в этом случае применить формулу Ньютона-Лейбница для нахождения $f'(x)$? $f\left(x\right)=\displaystyle\int_0^xe^t\sin\left(xt\right)dt$ 9{-t}\sin\left(t\right)dt$, который можно рассчитать с помощью правила произведения и который на самом деле не равен $0$
Итак, мой вопрос: что я делаю неправильно в случае $1$? Есть ли какое-то стандартное правило или требование теоремы Ньютона-Лейбница, которое я упустил?
- интегрирование
- определенные интегралы
$\endgroup$
4
$\begingroup$
9t\sin(v-t)\;dt,\quad f(x) = x,\quad g(x) = x .
$$
$\endgroup$
$\begingroup$
Вы не можете применить Ньютона-Лейбница в случае I. Начиная с ответа GEdgar, вы можете найти интеграл по частям, как это сделал GEdgar, а затем взять тот, у которого $\frac{d}{dx}$ находится слева, чтобы есть $f'(x)$, так как это трюк. Вы можете продолжить оттуда, чтобы найти ваше приближение. Суть Ньютона-Лейбница состоит в том, чтобы найти аппроксимацию нулей функции $f(x)=0$, поэтому $b=a-(\frac{f(a)}{f'(a)})$ начинает приближаться к этому нулю, начиная с $a$, но я не вижу, чтобы в вашем вопросе было указано $a$.
В общем,
$$x_x=x_{n-1}-\frac{f(x_{n-1})}{f'(x_{n-1})}.$$ Много время $b$ или $x_n$ является лучшим приближением, чем $a$ или $x_{n-1}$.
$\endgroup$
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя адрес электронной почты и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
Исчисление— формула Ньютона Лейбница
спросил
Изменено 4 года, 5 месяцев назад
Просмотрено 506 раз
$\begingroup$
$$\int_{-3}^5 f(x)\,dx$$ 92}$.