Найти высоты параллелограмма и угол между ними
Высота — перпендикуляр исходящий из вершины угла на противоположенную сторону
a, b — стороны параллелограмма
Hb — высота на сторону b
Ha — высота на сторону a
α, β — углы параллелограмма
Формулы длины высоты параллелограмма, через сторону и угол, ( Hb, Ha):
Острый угол пересечения высот, равен острому углу параллелограмма.
Тупой угол пересечения высот, равен тупому углу параллелограмма.
Формулы площади параллелограмма
Формула периметра параллелограмма
Все формулы по геометрии
- Подробности
- Автор: Administrator
www-formula.ru
Площадь параллелограмма
Площадь параллелограмма можно рассчитать тремя способами. В первом способе нужно знать длину стороны и высоту проведенную к этой стороне, во втором способе нужно знать две стороны и угол между ними, в третьем нужно знать длины диагоналей и угол пересечения этих диагоналей.
По стороне и высоте
В первом способе достаточно знать длину стороны (a) и высоту проведенную к ней (h). Формула:
Пример:
Например сторона a равна 8см, высота h равна 4см, площадь параллелограмма равна см2
По сторонам и углу
Во втором способе нужно знать стороны a и b и угол α между ними. Формула
Пример:
Например сторона a равна 5см, сторона b равна 9см, угол α равен 60° (sin(60°) равен примерно 0.87), площадь параллелограмма равна см2
По диагоналям и углу пересечения
В третьем способе нужно знать длины диагоналей AC и BD и угол ∠AOB. Формула
Пример:
Например диагональ AC равна 7см, диагональ BD равна 5см, угол ∠AOB равен 60° (sin(60°) равен примерно 0.87), площадь параллелограмма равна см2
expange.ru
Площадь параллелограмма через угол между высотами
Как найти площадь параллелограмма через стороны и угол между высотами?
Задача.
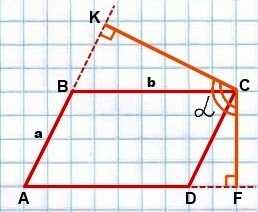
Стороны параллелограмма равны a и b, угол между высотами — α. Найти площадь параллелограмма.
Решение:
Площадь параллелограмма ABCD равна произведению длин сторон на синус угла между ними:
I. Угол между высотами, проведенными из вершины тупого угла параллелограмма, равен острому углу параллелограмма:
Следовательно,
и
II. Угол между высотами, проведенными из вершины острого угла параллелограмма, равен тупому углу параллелограмма:
Отсюда,
(как внутрениие односторонние углы при параллельных прямых AD и BC и секущей AB).
Так как
Ответ: a∙b∙sin α.
Таким образом, площадь параллелограмма равна произведению его сторон на синус угла между высотами.
В следующий раз рассмотрим, как найти площадь параллелограмма через высоты и образованный этими угол.
Как найти высоту параллелограмма?
Параллелограмм — это четырехугольник с противолежащими и попарно параллельными друг другу сторонами.
Высота параллелограмма — это линия, перпендикулярная одной из сторон параллелограмма и соединяющая эту сторону с противолежащим углом.
Для того чтобы узнать, как найти длину высоты параллелограмма, обратимся к формулам. Высота чаще всего обозначается буквой h.
Способ нахождения высоты зависит от известных нам величин в задании. Рассмотрим разные способы на конкретных примерах.
Пример 1
Даны площадь (S) и длина основания (a).
Пример: Площадь параллелограмма равна 100 см2, основание, к которому проведена высота, равно 20 см. Найдите высоту.
- h= 100/20 =5
- Ответ: 5 см
Пример 2
Даны длина прилежащей к высоте стороны параллелограмма (b) и угол, противоположный самой высоте (a).
- Формула: h = b* sin a
Пример: Обозначим наш параллелограмм буквами ABCD, высота BE проходит из угла ABC к стороне AD. Длина стороны AB равна 20 см, угол BAD равен 30 градусов. Найдите высоту.
Решение:
- h = 20 * sin 30° = 20 * 0,5 = 10
Ответ: 10 см
Пример 3
Даны длина стороны параллелограмма, прилегающая к высоте (n) и длина отсекаемой от основания части стороны (m).
Формула:
- h = корень из (n2 — m2)
Пример: в параллелограмме ABCD высота BE проходит из угла ABC к стороне AD. Длина AB равна 5 см, длина АЕ равна 3 см. Найдите высоту.
Решение:
- h = корень из (AD2 — AB2)
- h = корень из (52-32) = 4
- Ответ: 4 см
Пример 4
Даны длина диагонали, выходящей из того же угла, что и высота (d), и длина отсекаемой от основания части стороны (m).
Формула:
- h= корень из (d
Пример: в параллелограмме ABCD высота BE проходит из угла ABC к стороне AD. Диагональ BD равна 5 см, длина ED = 4 см.
- h = корень из (BD2 — ED2)
- h= корень из (52 — 42) = 3
- Ответ: 3 см
Если в задании требуется найти большую высоту параллелограмма, то необходимо посчитать длины обеих высо
elhow.ru