Формула объема детали: Расчет объема детали — онлайн калькулятор

Расчет обЪема и веса детали

На рисунке 1 приведена схема разбивки детали на элементарные объемы. Объем детали будет равен алгебраической сумме элементарных объемов.

Рисунок 1 – Схема разбивки детали на элементарные объемы

Рассмотрим элемент, объем которого мы можем найти по формуле (1)

V_Ι = V₁-V_А-V_В— V_С-V_Д-V_Е-V_Ж V_З , (1)

где объем V₁ — объем полого цилиндра:

V_{пол. цил.} = 0,785 ∙ h ∙ (D² – d²), (2)

V₁=0,785∙ 34 ∙ (192,776² – 97²)=740743,22 мм³

объем V_А – объем четверти тора:

V_А=2,47r²

(D-0,848r), (3)

V_А=2,47∙10²((97+20)-0,848∙10)=26804,44мм³

объем V_В — объем четверти тора:

V_В=2,47r²(D+0,848r), (4)

V_В=2,47∙10²((172-20)+0,848∙10)=39638,56мм³

объем V_С – объем полового цилиндра, находим по формуле (2)

V_С=0,785∙10²(152²-117²)= 73907,75 мм³

объем V_Д – объем восьми отверстий, имеющих форму цилиндра:

V_цил. = 0,785∙h∙D², (5)

V_Д=8∙0,785∙7∙9²=3560,76 мм³

объем V_Е – объем восьми отверстий, имеющих форму усеченного конуса:

V_Е= H(D²+Dd+d²), (6)

V_Е = ∙3(15²+15∙9+9²)=2769,48мм³

объем V_ж— объем полового цилиндра, находим по формуле (2)

V_ж=0,785∙14(175²+113²) = 6237,44 мм³

объем V_з – объем четверти тора, находится по формуле (4)

V_з = 19596,58 мм³

V_Ι = 378228,20 мм³

Рассмотрим второй элемент, объем которого мы можем найти по формуле (6)

V_ΙΙ = V₂-V_К-V_{И ,} (7)

где объем V₂— объем цилиндра, находим по формуле (5)

V₂ = 0,785∙97²∙56=413619,64 мм³

объем V_К— объем цилиндра, находим по формуле (5)

V_К = 0,785∙77²∙56=260638,84 мм

3

объем V_И— объем двух конических кольца:

V_И = 0,524(3D-2d)dH , (8)

V_И = 2∙0,524(3∙97-2∙3,5)3,5∙11=11458,83 мм³

V_ΙΙ=141521,97 мм³

Рассмотрим третий элемент объем, которого V_ΙΙΙ – это объем зубьев колеса, и он равен объему полого цилиндра (формула (2)), умноженному на коэффициент, равный 0,55:

V_ΙΙΙ =∙0,55 0,785∙34(210,78² – 192,78²) = 106655,70мм³, (9)

Складывая объемы трех этих элементов найденные по формулам (1), (7), (9) получим объем всей детали:

V_Д = V_Ι+V_ΙΙ+V_ΙΙΙ , (10)

где V_Д— объем детали;

V_Ι ,V_ΙΙ,V_ΙΙΙ – объемы, получаемые по формулам (1,7,9).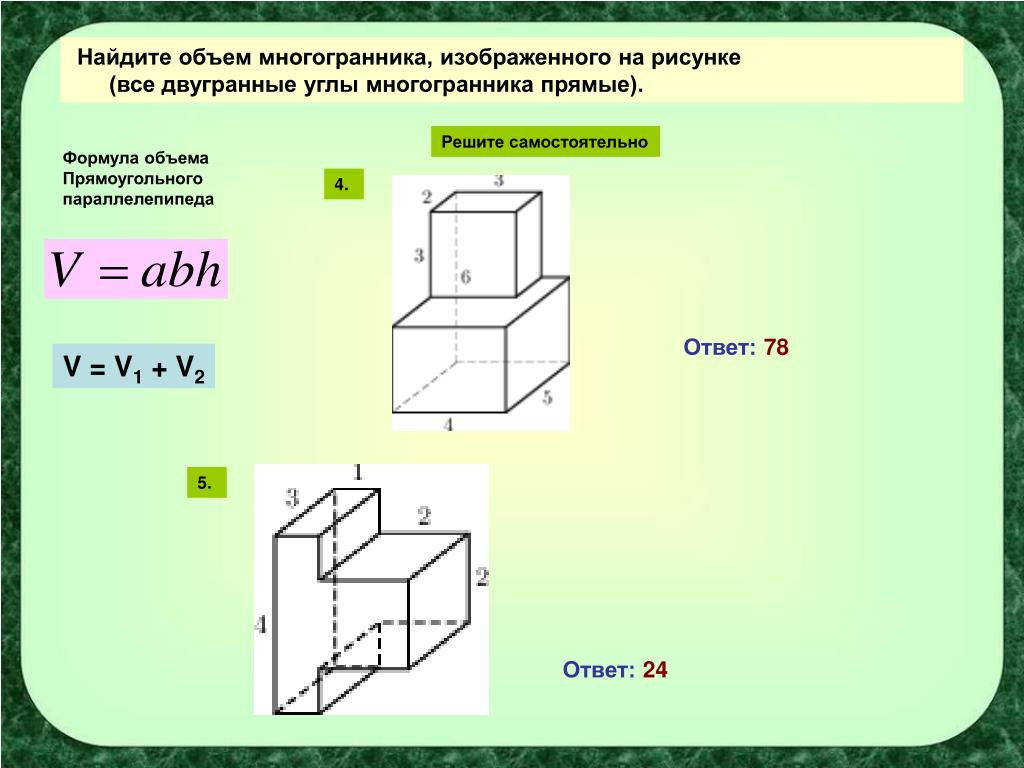

V_Д= 626405,87 мм³ = 626,406 см³

Теперь, зная объем детали, найдем массу детали по формуле (11):

М_Д = V_Д ∙ ρ, (11)

где ρ — плотность материала, =7,8г/см³.

М_Д = 626,406 ∙ 7,8 = 4917,29 г

Расчет ведем по ГОСТ 7505-89.

Группа стали назначается, исходя из среднего массового содержания углерода или легирующих элементов. Материал – Cталь 20ХН3А ГОСТ 4543-71, суммарная массовая доля легирующих элементов 4%, а значит группа стали М2.

Степень сложности определяется путем вычисления следующего

отношения (11):

С_i = , (12)

где V_ПОК – объем поковки;

V_Ф — объем геометрической фигуры, в которую вписывается форма детали (рисунок 2).

Рисунок 2 – Геометрическая фигура, в которую вписывается форма детали

Для данной детали описанной фигурой будет являться цилиндр, размеры которого увеличены на 1,05. Найдем объем этого цилиндра по формуле (2):

V_Ф = 0,785 ∙ 58,8 ∙ 221,32² = 2260936,19 (мм³).

Объем поковки на данном этапе находится по формуле (13):

V_ПОК = V_Д ∙ К_Р, (13)

где К_Р – расчетный коэффициент, К

Р = 1,7.

V_ПОК =626405,87 ∙ 1,7 = 1064889,97 (мм³).

С_i = = 0,47.

По расчету получаем степень сложности поковки С₂.

Класс точности поковки устанавливается в зависимости от технологического процесса и оборудования для ее изготовления, а также исходя из предъявляемых требований к точности размеров поковки.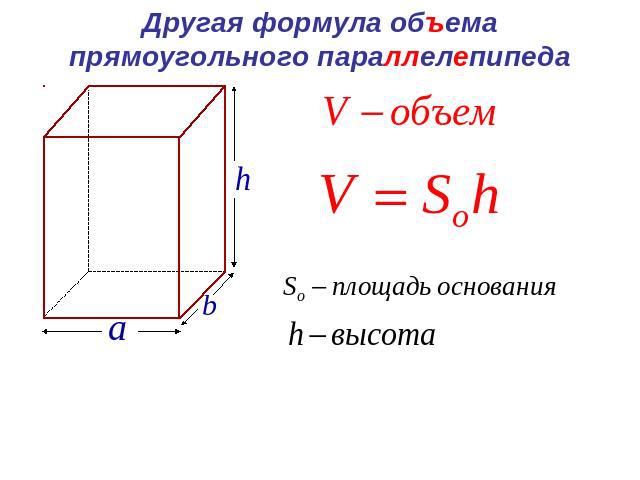 Согласно ГОСТ 7505-89 выбираем 4-й класс точности – Т4.

Массу поковки найдем по формуле, аналогичной формуле (11):

М_ПОК = 1064,889 ∙ 7,8 = 8306,1 г

Исходный индекс для последующего назначения основных припусков, допусков и допускаемых отклонений определяется в зависимости от массы, марки стали, степени сложности и класса точности поковки по ГОСТ 7505-89. В данном случае исходный индекс 14.

В цилиндрический сосуд налили

Друзья! В заданиях ЕГЭ по математике встречаются задачи, в которых речь идёт о погружении детали в жидкость или о переливании жидкости из одного сосуда в другой. Вопросы в условии связаны с нахождением объёма погружаемого в жидкость тела или с нахождением какого-либо параметра сосуда. Форма сосуда может быть различной: цилиндр, призма.

Что необходимо понимать? Если жидкость залита в цилиндрический сосуд, то она принимает форму цилиндра. Если она залита в имеющий форму призмы, то соответственно принимает форму призмы. Это означает, что формулы для объёмов цилиндра и призмы работают и для объёмов жидкостей помещённых в такие сосуды.

Формула объёма цилиндра (и призмы):

Если жидкость переливается в аналогичный сосуд с меньшим основанием, уровень (высота) жидкости увеличивается; если в сосуд с большим основанием, то уровень жидкости уменьшается.

Рекомендации!

В задачах на погружение детали в жидкость следует найти объём полученный после её погружения, далее найти разность объёмов до и после (если данные в условии это позволяют). Можно такие задачи решать и другим способом, используя закон Архимеда. Примеры рассмотрены ниже.

В задачах, где идёт речь о переливании жидкости в другой сосуд (с уменьшенной или увеличенной площадью основания) помните о том, что сам объём жидкости остаётся неизменным. Вы можете выразить его через площадь основания и высоту (S₁ и H₁) одного сосуда и площадь основания и высоту (S₂ и H₂) другого сосуда, далее полученные выражения приравнять.

При дальнейших преобразованиях получите отношение соответствующих величин – либо площадей оснований, их рёбер, либо высот. Пример такой задачи рассмотрен ниже в статье.

В цилиндрический сосуд налили 5000 см³ воды. Уровень жидкости оказался равным 40 см. В воду полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на 15 см. Чему равен объем детали? Ответ выразите в см³.

Мы знаем, что объём цилиндра равна произведению площади основания на высоту:

В жидкость погружаем деталь. Её уровень поднимается. Для того, чтобы вычислить объём детали необходимо из полученного объёма (полученного после погружения детали) вычесть объём жидкости, который был изначально.

Высота это есть уровень жидкости.

Итак, из имеющихся данных можем найти площадь основания:

Основание цилиндра у нас величина неизменная, но изменилась высота жидкости (при погружении детали) на 15 сантиметров, то есть она стала  

40 +15 = 55 см.

Найдём полученный объём:

Теперь можем вычислить объём детали:  6875 – 5000 = 1875 см³

Можно решать подобные задачи более рациональным способом.

По закону Архимеда объем детали равен объему вытесненной ею жидкости. Объем вытесненной жидкости равен 15/40  исходного объема:

Ответ: 1875

Решить самостоятельно:

Посмотреть решение

В сосуд, имеющий форму правильной треугольной призмы, налили 2500 см³ воды и полностью в нее погрузили деталь. При этом уровень жидкости в сосуде поднялся с отметки 20 см до отметки 24 см. Чему равен объем детали? Ответ выразите в см³.

Принцип решения тот же самый, что и в предыдущей задаче.

Мы знаем, что объём призмы равен произведению площади основания на высоту:

В жидкость погружаем деталь. Её уровень поднимается. Для того, чтобы вычислить объём детали необходимо из полученного объёма (полученного после погружения детали) вычесть объём жидкости, который был изначально.

Из имеющихся данных можем найти площадь основания призмы:

Основание призмы  не изменилось, но изменилась высота жидкости (при погружении детали)  она стала 24см.

Найдём полученный объём:

Теперь можем вычислить объём детали:  3000 – 2500 = 500 см³

Второй способ:

По закону Архимеда объем детали равен объему вытесненной ею жидкости. Объем вытесненной жидкости равен 4/20  исходного объема:

Ответ: 500

Решить самостоятельно:

Посмотреть решение

В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает 250 см. На какой высоте будет находиться уровень воды, если ее перелить в другой такой же сосуд, у которого сторона основания в 5 раз больше, чем у первого? Ответ выразите в см.

В подобных задачах с переливаниями жидкости следует помнить, что объём её остаётся прежним (он не изменен – куда бы её не перелили).

Объем жидкости в данном случае это объём правильной  треугольной призмы  (в её основании лежит правильный треугольник).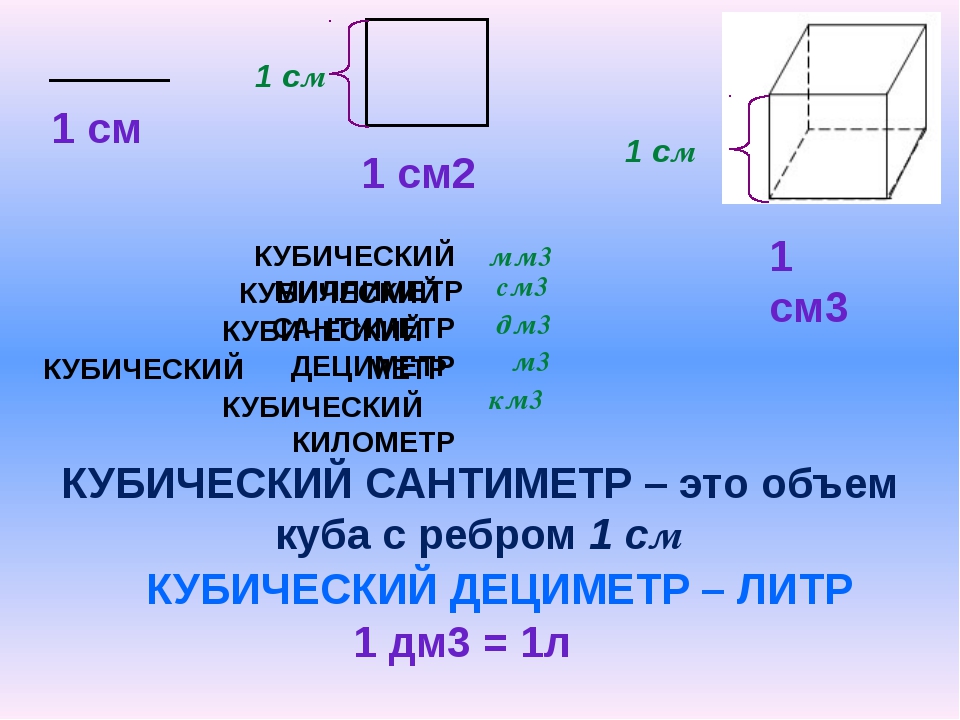 Он равен произведению  площади основания призмы на высоту:

Суть дальнейших действий сводится к тому, что мы можем выразить объёмы жидкостей в двух призмах: первой и второй (основание которой в 4 раза больше), а затем приравнять полученные выражения, в итоге после преобразований получим отношение двух высот.

Естественно, что высота жидкости уменьшится, если увеличить площадь основания.

Обозначим исходную высоту жидкости Н₁, полученную после переливания Н₂.

Найдём площадь основания призмы, обозначив его сторону как а. Площадь правильного треугольника равна:

Таким образом, объём залитой жидкости  в первую призму равен:

Площадь основания второй призмы равна:

Объём залитой жидкости  во вторую призму равен:

Найдём отношение высот:

Таким образом, при том же объёме жидкости её высота уменьшится в 25 раз и будет равна 10.

Или можно сказать так:

При увеличении стороны основания а в 5 раз уровень воды уменьшится в 25 раз.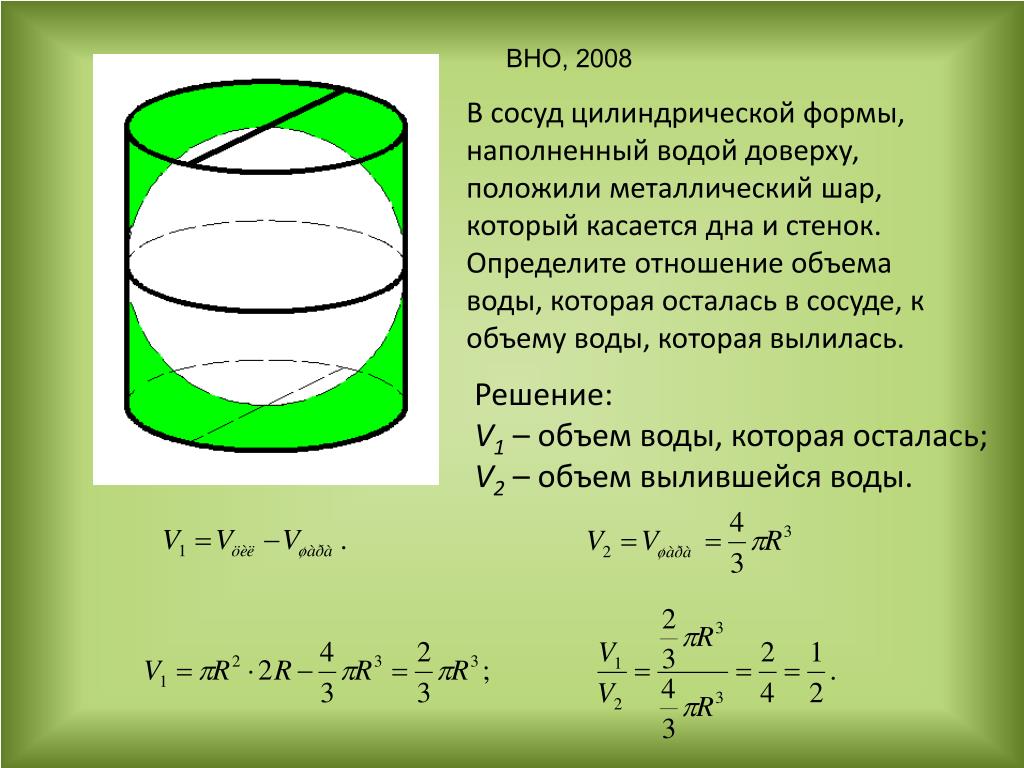

Ответ: 10

Решить самостоятельно:

Посмотреть решение

В цилиндрический сосуд, в котором находится 14 литров воды, опущена деталь. При этом уровень жидкости в сосуде поднялся в 1,1 раза. Чему равен объем детали? Ответ выразите в литрах.

Объём цилиндра равна произведению площади его основания на высоту:

Жидкость в сосуде имеет цилиндрическую объёмную форму.

Уровень жидкости поднялся в 1,1 раза – означает, что высота цилиндра увеличилась в 1,1 раза. Исходя из формулы объёма цилиндра понятно, что при увеличении высоты в 1,1 раза влечёт за собой увеличение объёма также в 1,1 раза (так как зависимость величин  прямопропорциона).

Это означает, что после погружения детали объём будет равен 14∙1,1 = 15,4 литра.

Таким образом, объём детали будет равен: 15,4 – 14 = 1.4 литра.

Ответ: 1,4

Решить самостоятельно:

Посмотреть решение

Если ход решения сразу не увидели, ставьте вопрос – что можно найти исходя из условия?

Например, если дан начальный объём и высота жидкости (в сосуде формы призмы или цилиндра), то мы можем найти площадь основания.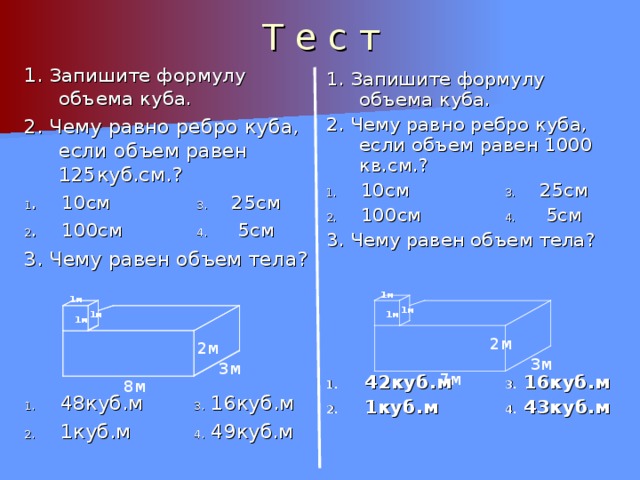 Затем, зная площадь основания и высоту жидкости после погружения детали мы можем найти объём.

Далее вычислить разницу между объёмами не составит труда  (это относится к первым двум задачам). В последней задаче для решения требуется немного логики.

В задачах по стереометрии на ЕГЭ есть много таких, где требуется найти изменение объёма или площади поверхности (шара, призмы, куба, пирамиды, конуса), при изменении одного из линейных размеров, имеются задачи и обратные им.

В данной рубрике мы рассмотрим такие задачи, не пропустите!

На десерт видео,  отдохнём от математики.

Успехов вам!

С уважением, Александр.

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

Объем частичного конуса – формула, определение, примеры

Чтобы понять понятие объема частичного конуса, мы должны сначала понять форму конуса и то, как из него формируется частичный конус. Конус представляет собой трехмерную геометрическую фигуру. Он имеет вершину и круглое основание. Вершину также называют вершиной конуса. Конус образован набором отрезков или линий, соединяющих общую точку, то есть вершину, со всеми точками основания, лежащего в плоскости, не содержащей вершины. В общем, мы используем «правильный круговой» конус, что означает, что ось конуса проходит через центр основания под прямым углом к ​​его плоскости. Когда прямой круглый конус разрезается вдоль его поперечного сечения, получается меньший правильный круглый конус и частичный конус.
Теперь, когда мы знаем, как формируется частичный конус, давайте воспользуемся этим, чтобы найти объем частичного конуса и какова его формула?

1.	Что такое неполный конус?
2.	Как найти объем конуса?
3.	Как найти объем частичного конуса?
4.	Вывод формулы объема частичного конуса
5.	Часто задаваемые вопросы об объеме частичного конуса

Что такое неполный конус?

Прямой круглый конус имеет вершину и круглое основание так, что ось конуса проходит через вершину и центр основания под прямым углом. Частичный конус имеет две круглые грани, и ось частичного конуса проходит через центры под прямым углом к ​​обеим круговым граням. Частичный конус не имеет вершины. Частичный конус также известен как усеченный конус.

Как найти объем конуса?

Объем конуса определяется как количество кубических единиц, занимаемых конусом. Следовательно, единицей измерения объема являются «кубические единицы». Например, это может быть выражено как m

3 , cm ³ , in ³ и т. д. в зависимости от заданных единиц. Давайте посмотрим, как мы найдем объем конуса.

Если цилиндр вписан в конус так, что основание и высота конуса и цилиндра одинаковы, то объем цилиндра и объем конуса сравниваются следующим образом:

Объем конуса = 1/3 × объем цилиндра

или Объем конуса = 1/3 × площадь основания × высота

Поскольку основание и радиус конуса и цилиндра одинаковы . Также, поскольку основание конуса представляет собой круг, следовательно, радиус основания = πr ²

или Объем конуса = 1/3 × πr ² × h

Как найти объем частичного конуса?

Объем частичного конуса получается из объема целого конуса на основе идеи о том, как частичный конус формируется из целого конуса.

Так как весь конус нарезается, чтобы получить частичный конус и маленький конус.

Следовательно, объем частичного конуса = объем всего конуса — объем малого конуса

или объем частичного конуса = 1/3 × радиус основания всего конуса × высота всего конуса — 1/ 3 × радиус основания малого конуса × высота малого конуса

Вывод формулы объема неполного конуса

Теперь выведем формулу объема неполного конуса на основе полученного результата.

Теперь для всего конуса:

Высота = единицы ‘H’

Радиус основания = единицы ‘R’

Для малого конуса:

Высота = единицы ‘H — h’

Радиус основания = единицы ‘r’

Объем частичного конуса = объем всего конуса — объем малого конуса

или объем частичного конуса = 1/3 × радиус основания всего конуса × высота всего конуса — 1/3 × радиус основания малого конуса × Высота малого конуса

= 1/3 × πR

2 × H — 1/3 × πr ² × (H — h)

= 1/3 × π × (R ² × H — r ² × (H — h))

= 1/3 × π(R ² H — r ² H + r ² h)

= 1/3 × π(H(R ² — r ² ) + r ² h)

Так как высота отношения целого конуса и высота малого конуса равна H:(H — h) = R:r, следовательно, отношение высоты всего конуса к высоте частичного конуса равно H:h = R:(R — r)

Н/ч = R/(R — r)

Умножая h с обеих сторон,

H = Rh/(R — r)

Подставляя это значение H в приведенное выше уравнение, мы получаем:

Объем частичного конуса, V = 1/3 × π( H(R ² — r ² ) + r ² h)
⇒ V = 1/3 × π[(Rh/(R — r)) × (R ² — r ² ) + r ² h]
⇒ V = 1/3 × π[(Rh/(R — r)) × (R — r)(R + r) + r ² ч]
⇒ V = 1/3 × π(Rh(R + r) + r ² ч)
⇒ V = 1/3 × π(R ² з + рр + р ² з)
⇒ V = 1/3 × π × h × (R ² + Rr + r ² )
⇒ V = 1/3 × πh(R ² + Rr + r ² )

Давайте теперь посмотрим на несколько решенных примеров объема частичного конуса для лучшего понимания.

 

Примеры объема частичного конуса

1. Пример 1: Основание и верхний радиус частичного конуса составляют 3 мм и 6 мм соответственно. Найдите объем частичного конуса, если высота 100 мм. (Используйте π = 3,14)

   Решение:

   Дано,

   Высота частичного конуса, h = 100 мм

   Радиус верха, r = 3 мм

   Радиус дна, R = 6 мм

   Объем частичный конус, V = 1/3 × πh(R ² + Rr + r ² )

   или V = 1/3 × 3,14 × 100 × (6 ² + 6 × 3 + 3 ²

   ⇒ V = 1/3 × 314 × 63

   ⇒ V = 314 × 21

   ⇒ V = 6,594 мм ³

   Ответ: Объем частичного конуса 6594 мм ³

2. Пример 2: Джеймс собирается наполнить шоколадным сиропом шесть конусов из печенья. Каждый конус имеет высоту 24 см и высоту наклона 25 см, найдите общее количество требуемого шоколадного сиропа.

   Раствор:

   Дано,

   Высота конуса, H = 24 см

   Наклонная высота конуса, L = 25 см

   Давайте найдем базовый радиус ‘r’ из конуса первого:

   L ² = R ² + H ²

   ⇒ R ² = L ² — H ²

   = L ² — H ²
   ⇒ R ² = 25 ² — 24 ²

   ⇒ R ² = 625 — 576 = 49

   ⇒ R = 7 см

   2 шоколадного сиропа πR

   ² × H

   Объем шоколадного сиропа в шести конусах = 6 × 1/3 × πR ² × В

   = 2 × (22/7) × 7 ² × 24

   = 2 × 22 × 7 × 24

   = 7392 см ³

перейти к слайдуперейти к слайду

Разбивайте сложные концепции с помощью простых визуальных средств.

Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.

Запись на бесплатный пробный урок

Практические вопросы по объему частичного конуса

 

перейти к слайдуперейти к слайду

Часто задаваемые вопросы об объеме частичного конуса

Какова формула объема частичного конуса?

Формула для расчета объема частичного конуса представлена ​​в виде: Объем частичного конуса, V = 1/3 × πh(R ² + Rr + r ² ), где ‘r’ и ‘ R’ — радиусы основания, такие, что R > r, а «h» — высота усеченного конуса.

Какие единицы используются при нахождении объема частичного конуса?

Единицей объема является «кубическая единица». Например, это может быть выражено как m ³ , cm ³ , in ³ и т. д. в зависимости от заданных единиц.

Как найти объем неполного конуса?

Объем частичного конуса можно рассчитать по формуле: Объем частичного конуса = объем всего конуса — объем маленького конуса

Какова формула объема конуса?

Формула для расчета объема конуса выглядит следующим образом: Объем конуса = 1/3 × πr ² × h, где r — радиус, а h — высота конуса.

Как отличить конус от частичного конуса?

Конус имеет круглое основание и вершину, тогда как неполный конус имеет две торцевые круглые грани.

Как формируется неполный конус?

Частичный конус образуется, когда целый конус разрезается по горизонтали, чтобы получить малый конус и неполный конус.

Скачать БЕСПЛАТНЫЕ учебные материалы

Рабочий лист

геометрия — Почему объем конуса составляет одну треть объема цилиндра?

Вот вывод объема конуса без исчисления, принципа Кавальери, метода исчерпывания или любых других бесконечно малых аргументов.

[ Редактировать В этом аргументе есть ошибка, см. ниже]

[ Редактировать 2 Ошибка была исправлена ​​путем рассмотрения отношения объема конуса к его описанию цилиндра при различных масштабах]

Мы можем разделить конус по горизонтали на две части, так что верхняя часть образует другой конус с меньшим основанием, а нижняя часть уже не конус, а объект, называемый «усеченной пирамидой».

Для конуса с радиусом основания $r$ и высотой $h$ мы можем использовать параметр $b$ с $0 \lt b \lt 1$, чтобы определить высоту усеченного конуса как $b h$. Поскольку весь конус и верхний конус образуют в вертикальном сечении подобные треугольники, верхний конус высотой $(1-b)h$ будет иметь радиус основания $(1-b)r$.

Объем усеченного конуса будет равен объему исходного конуса за вычетом объема верхнего конуса. Мы еще не знаем, какой вид примет функция, представляющая объем конуса, поэтому пока мы просто напишем $V_{cone} = V_{cone}(r,h)$, чтобы напомнить себе, что это будет некоторое функция высоты и радиуса основания. Таким образом, объем усеченного конуса $$V_{усеченный конус} = V_{конус}(r,h) — V_{конус}((1 — b)r, (1 — b)h)$$ 92)}{\pi} \lt 1$$

Это должно выполняться для всех $0 \lt b \lt 1$.

В этот момент мы могли бы использовать знакомый аргумент о пределах — в частности, когда $b$ приближается к нулю, нижняя граница приближается к верхней границе $1$, так что $\frac{Q 3}{\pi} = 1$ или $Q = \frac{\pi}{3}$.

Однако можно найти значение $Q$ и другим способом, не требующим предельного процесса.

Прежде всего заметим, что значение $Q$ ограничено геометрией задачи $0 \lt Q \lt \pi$, поскольку конус должен иметь некоторый объем, и этот объем должен быть меньше объема цилиндр радиусом $r$ и высотой $h$. Мы собираемся показать, что для всех значений $Q$ в этом диапазоне, за одним исключением, существует выбор $b$ с $0 \lt b \lt 1$, который приводит к тому, что приведенное выше неравенство не выполняется. В духе Шерлока Холмса: «…когда вы исключили невозможное, все, что останется, каким бы невероятным [или, в нашем случае, ожидаемым] оно ни было, должно быть правдой». 92) $. Тогда для $0 \lt \alpha \lt 1$ мы имеем $0 \lt Q \lt \pi/3$, и приведенное выше уравнение снова сводится к $b=1-\alpha$, так что $0 \lt b \lt 1$.

Следовательно, по геометрии задачи имеем $0 \lt Q \lt \pi$, но всякий раз, когда $0 \lt Q \lt \frac{\pi}{3}$ или $\frac{\pi}{3} \lt Q \lt \pi$ существует хотя бы одно значение $b$ с $0 \lt b \lt 1$, для которого неравенство не выполняется.