Теорема Вариньона
Выпуклый четырехугольник, вершинами которого являются середины сторон произвольного четырехугольника, является параллелограммом.
Доказательство*
С доказательством данной теоремы рекомендуется ознакомиться после изучения темы “Средняя линия треугольника”.
Проведем диагонали четырехугольника \(ABCD\). Рассмотрим \(\triangle ABC\): \(MN\) – средняя линия этого треугольника, следовательно, \(MN\parallel AC\).
Рассмотрим \(\triangle ADC\): \(PK\) – средняя линия этого треугольника, следовательно, \(PK\parallel AC\).
Таким образом, \(MN\parallel AC\parallel PK\).
Аналогичным образом доказывается, что \(MP\parallel BD\parallel NK\).
Следовательно, по определению \(MNKP\) – параллелограмм. 2\)
2\)
Замечание
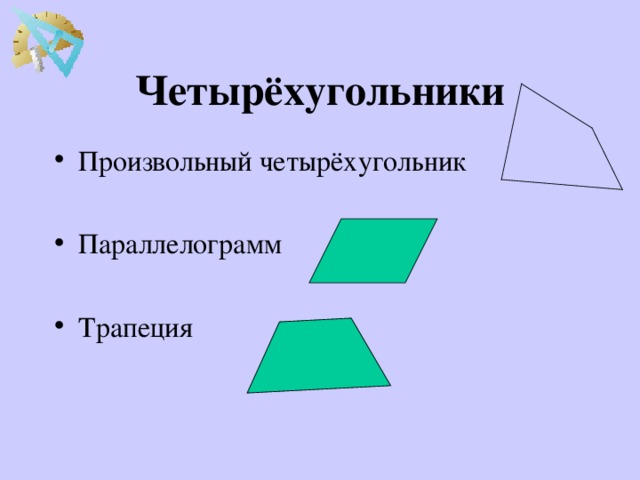
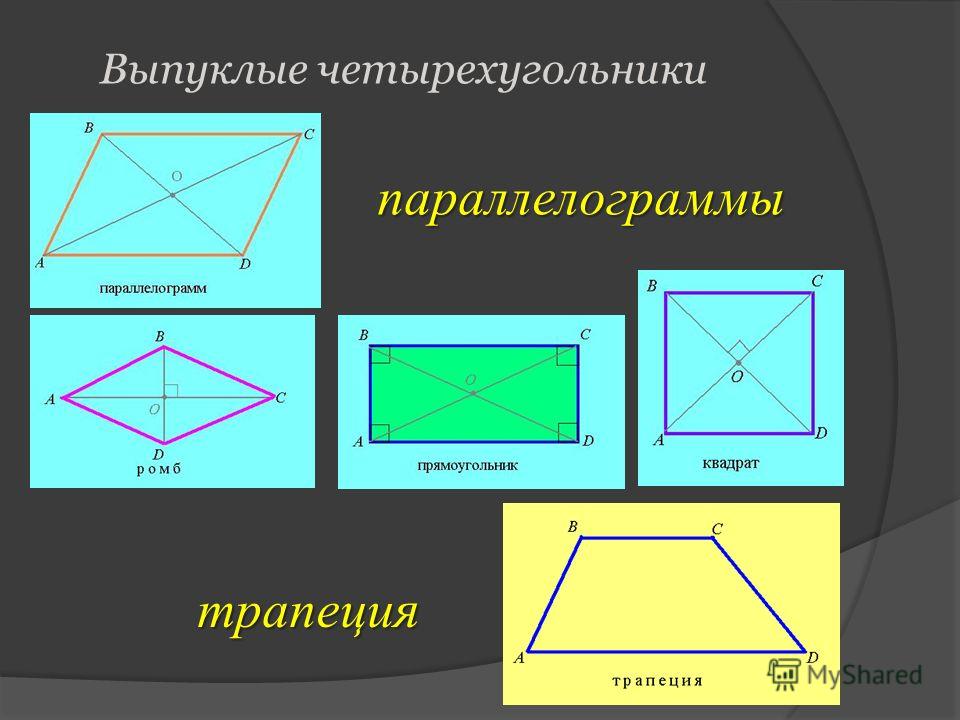
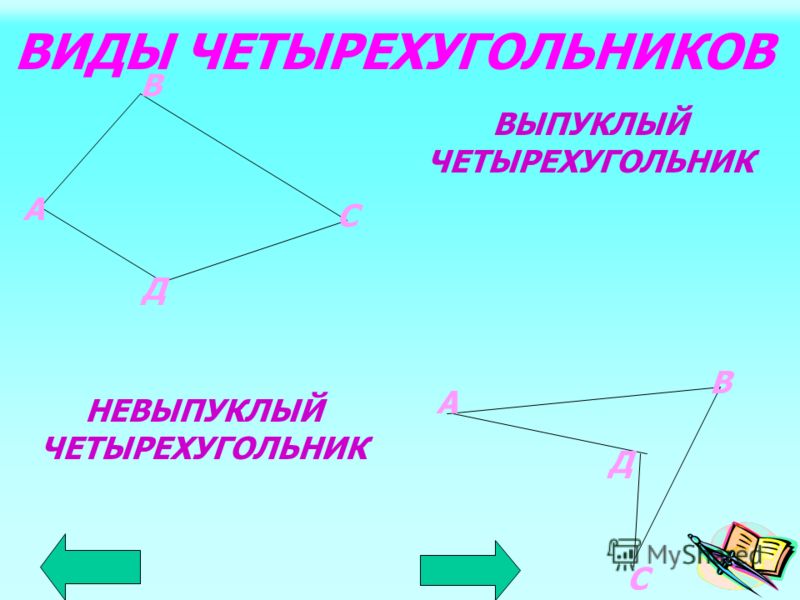
Все известные четырехугольники, изучаемые в школьной программе, подчиняются следующей схеме:
Таким образом, любой четырехугольник из этой схемы обладает свойствами всех предыдущих четырехугольников, из которых он следует.
Например, прямоугольник обладает свойствами параллелограмма и произвольного выпуклого четырехугольника; квадрат обладает свойствами прямоугольника, параллелограмма, выпуклого четырехугольника.
Помогите решить / разобраться (М)
Сообщения без ответов | Активные темы | Избранное
Правила форума
Посмотреть правила форума
| Don-Don |
| ||
04/03/14 |
| ||
| |||
| alcoholist |
| |||
22/01/11 |
| |||
| ||||
| Don-Don |
| ||
04/03/14 |
| ||
| |||
| alcoholist |
| ||
22/01/11 | |||
| |||
| Don-Don |
| ||
04/03/14 |
| ||
| |||
| Lia |
| ||
20/03/14 |
| ||
| |||
| Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию |
| Страница 1 из 1 | [ Сообщений: 6 ] |
Модераторы: Модераторы Математики, Супермодераторы
Кто сейчас на конференции |
Сейчас этот форум просматривают: нет зарегистрированных пользователей |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
| Найти: |
геометрия — Угол диагонали выпуклого четырехугольника.
Спросил
Изменено 6 лет, 10 месяцев назад
Просмотрено 1к раз
$\begingroup$
Учитывая выпуклый четырехугольник, в котором мы знаем углы углов и одной диагонали, мы можем найти угол второй диагонали?
Я попытался использовать тот факт, что $\alpha+\beta+\gamma+\delta=2\pi$ и $\phi+\beta+\phi’=\pi=\theta+\gamma+\theta’$, где $\theta’$ — это угол, противоположный $\theta$, а $\phi’$ — угол, противоположный $\phi$ (при гипотенузе). Но какие бы манипуляции я ни производил с этой точки, $\phi$ и $\phi’$ всегда присутствуют в моих уравнениях (например, $\phi=\alpha+\beta+\gamma-\pi-\phi’$).
Я также пытался использовать тригонометрию. Я использовал закон синусов, исключил ребра треугольников и получил следующее уравнение: $$\frac{\sin\theta’\sin\alpha}{\sin\gamma\sin(\beta-\theta)} =\ frac{\sin\phi\sin\delta}{\sin\beta\sin(\gamma-\phi’)}$$
Я пытаюсь упростить его, используя тригонометрические тождества, но что-то не могу найти.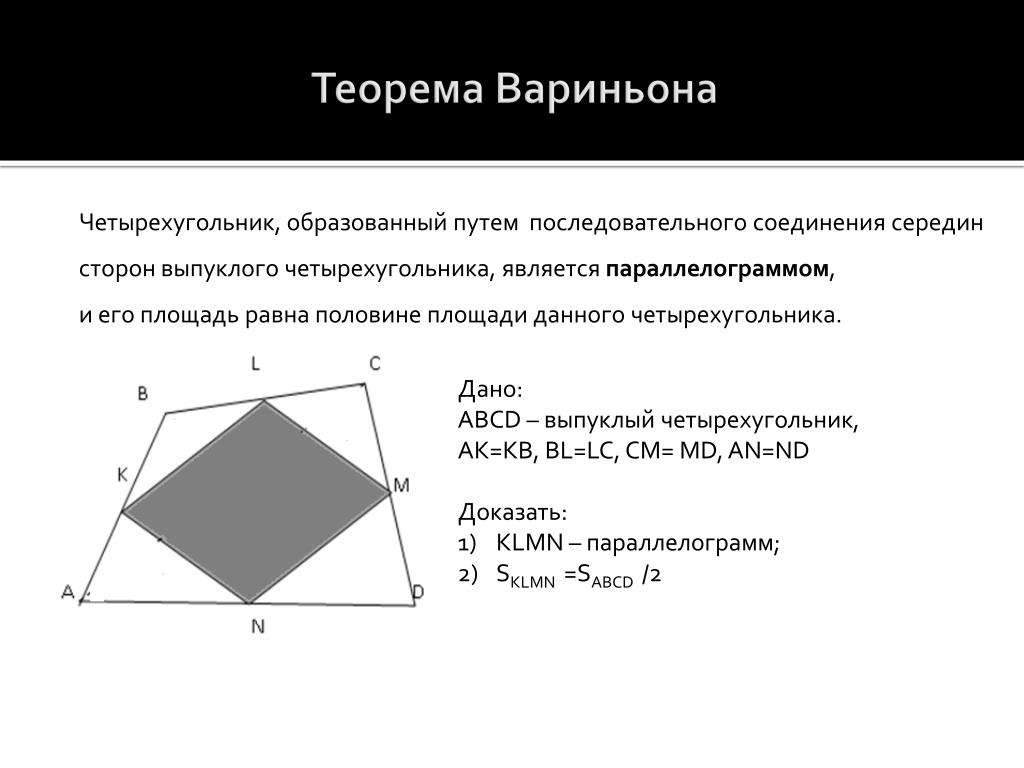
Я уверен, что я упускаю что-то очень простое…
- геометрия
$\endgroup$
1
$\begingroup$
Я нашел решение. Я хотел бы знать, есть ли лучшее/более простое решение.
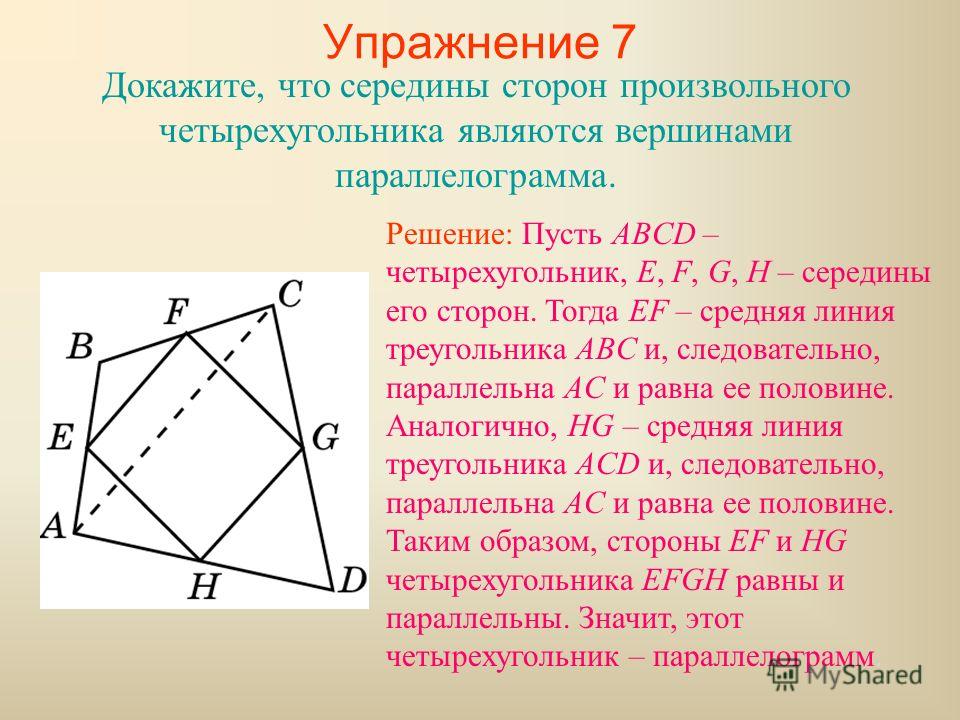
Вот картинка, на которой я добавил имена в некоторых сегментах линий.
Предположим, нам известны $\alpha, \beta, \gamma, \delta$ и $\phi$, и мы хотим найти $\theta$.
Используя закон синусов, мы имеем: $$\frac{\sin\phi}{X}=\frac{\sin\beta}{N}, \quad\frac{\sin\theta}{Y}=\frac{\sin\gamma}{M }, \ quad \ frac {\ sin (\ pi- \ theta- \ gamma)} {X} = \ frac {\ sin \ gamma} {M}, \ quad \ frac {\ sin (\ alpha- \ phi) }{Y}=\frac{\sin\delta}{N}$$ 9{-1}\left(\frac{\sin\delta\sin\phi}{\sin(\alpha-\phi)\sin\beta\sin\gamma}-\cot\gamma\right)$$
$\endgroup$
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
геометрия — Вписывание ромба в выпуклый четырехугольник
Ниже приводится доказательство конструктивности , в котором отсутствуют некоторые стандартные детали, в основном тот факт, что арифметические операции и извлечение квадратного корня можно выполнять с помощью линейки и циркуля.
В принципе, можно использовать доказательство, чтобы дать инструкции о том, как выполнять построение. Однако получаемая конструкция имеет мало реального геометрического содержания. Здесь, несомненно, изящная геометрическая конструкция. Но у используемого ниже алгебраического подхода есть приятная черта — он по существу автоматический. Если у человека есть определенный фон, взгляд на задачу показывает, что вписанный ромб можно построить.
Дан выпуклый четырехугольник $ABCD$, вершины которого идут, скажем, против часовой стрелки. Пусть $P$, $Q$, $R$, $S$ — точки на отрезках $AB$, $BC$, $CD$ и $DA$.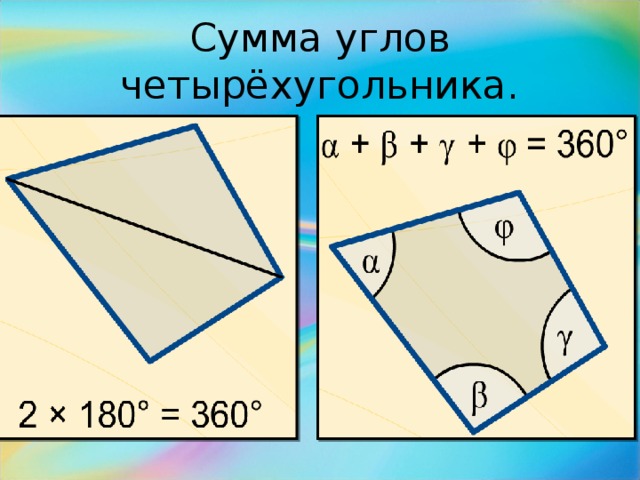
Лемма: Предположим, что $AP:BP=AS:DS$ и $CR:DR=CQ:BQ$. Тогда прямые $PS$ и $RQ$ параллельны.
Доказательство: Они оба параллельны $BD$.
Следствие: Если $AP:BP=AS:DS$ и $BP:BQ=DR:CR$, то $PQRS$ — параллелограмм.
В частности (неуместно здесь, но мило), если $P$, $Q$, $R$ и $S$ являются биссектрисами сторон, на которых они лежат, то получается неожиданный результат, что $PQRS$ является параллелограммом .
Небольшая игра покажет, что если мы выберем $P,Q,R,S$, как в следствии, но с малым $AP$, то $PS$ будет меньше, чем $PQ$. И если мы выберем $P$ так, чтобы $BP$ было мало, то $PS$ будет больше, чем $PQ$. Так что правильный выбор где-то посередине, мы получаем $PS=PQ$ и, следовательно, ромб.
Оставим классическую геометрию. Выберите систему координат с $A$ в начале координат и с $B$, скажем, в $(1,0)$. (Это не имеет значения.) Тогда точки $C$ и $D$ имеют «известные» координаты, а все линии нашего четырехугольника имеют известные линейные уравнения с коэффициентами, которые можно построить из заданных точек.