Гидростатика — Физика — Теория, тесты, формулы и задачи
Оглавление:
- Основные теоретические сведения
- Давление. Закон Паскаля. Гидростатическое давление
- Сообщающиеся сосуды
- Гидравлический пресс
- Закон Архимеда. Вес тела в жидкости
- Плавание тел
Давление. Закон Паскаля. Гидростатическое давление
К оглавлению…
Основным отличием жидкостей от твердых (упругих) тел является способность легко изменять свою форму. Части жидкости могут свободно сдвигаться, перемещаясь друг относительно друга. Поэтому жидкость принимает форму сосуда, в который она налита. В жидкость, как и в газообразную среду, можно погружать твердые тела. В отличие от газов жидкости практически несжимаемы. На тело, погруженное в жидкость или газ, действуют силы, распределенные по поверхности тела. Для описания таких распределенных сил в гидростатике вводится новая физическая величина – давление.
Давление определяется как отношение модуля силы F, действующей перпендикулярно поверхности, к площади S этой поверхности:
Если же сила направлена под некоторым углом к перпендикуляру к площадке, то создаваемое этой силой давление находится по формуле:
В системе СИ давление измеряется в паскалях (Па): 1 Па = 1 Н/м2. Часто используются внесистемные единицы: нормальное атмосферное давление (атм) и давление одного миллиметра ртутного столба (мм.рт.ст.):
1 атм = 101325 Па = 760 мм.рт.ст.
Закон Паскаля: давление, оказываемое на жидкость (или, к слову, газ), передается в любую точку этой жидкости без изменений и во всех направлениях.
Давление жидкости на дно или боковые стенки сосуда зависит от высоты столба жидкости над той точкой в которой измеряется давление. Гидростатическое давление столба жидкости рассчитывается по формуле:
Обратите внимание, что оказываемое давление никоим образом не зависит от формы сосуда, а зависит только от рода жидкости (т.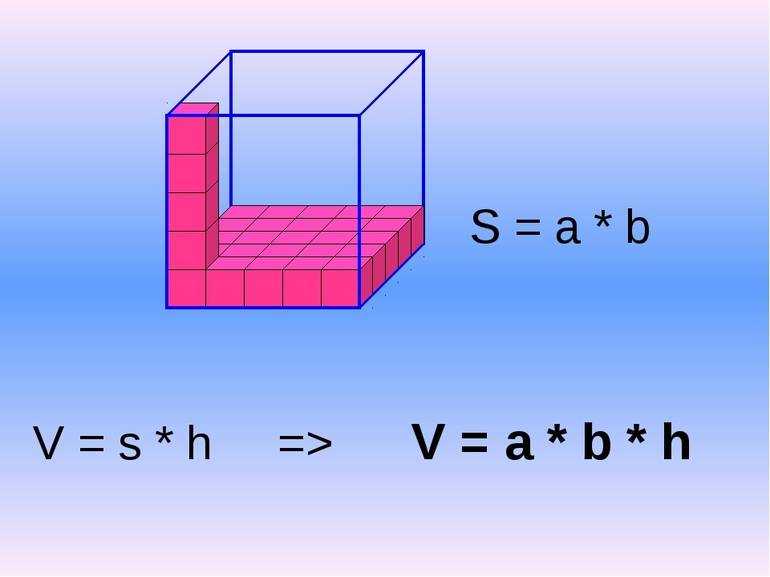 е. её плотности) и от высоты столба этой жидкости. Такое же давление на глубине h в соответствии с законом Паскаля жидкость оказывает и на боковые стенки сосуда.
е. её плотности) и от высоты столба этой жидкости. Такое же давление на глубине h в соответствии с законом Паскаля жидкость оказывает и на боковые стенки сосуда.
Итак, если в задаче по гидростатике идет речь о давлении столба жидкости на боковую грань в некоторой конкретной точке, то такое давление находится по предыдущей формуле, где h – расстояние от этой точки до поверхности жидкости. Но иногда в задачах по гидростатике необходимо рассчитать среднее давление на всю боковую поверхность сосуда. В таком случае применим формулу:
В этом случае, h – это общая высота столба жидкости в сосуде.
Если жидкость находится в цилиндре под поршнем, то действуя на поршень некоторой внешней силой F, можно создавать в жидкости дополнительное давление p0 = F/S, где: S – площадь поршня. Таким образом, полное давление в жидкости на глубине h можно записать в виде:
Если поршень убрать, то давление на поверхность жидкости будет равно атмосферному давлению. Если мы погружаемся в воду, то давление на некоторой глубине тоже будет состоять из двух давлений – давления атмосферы и давления столба воды (которое определяется глубиной погружения).
Если мы погружаемся в воду, то давление на некоторой глубине тоже будет состоять из двух давлений – давления атмосферы и давления столба воды (которое определяется глубиной погружения).
Сообщающиеся сосуды
К оглавлению…
Сообщающимися называют сосуды, имеющие между собой канал, заполненный жидкостью. Наблюдения показывают, что в сообщающихся сосудах любой формы однородная жидкость всегда устанавливается на одном уровне. задачи на сообщающиеся сосуды очень распространены в гидростатике.
Иначе ведут себя разнородные жидкости даже в одинаковых по форме и размерам сообщающихся сосудах. Дело в том, что в сообщающихся сосудах должно устанавливаться одинаковое давление на одной и той же высоте во всех частях сосуда. Но если жидкости различные, то и высота столбов этих жидкостей должна быть различной, чтобы создать одинаковое давление. Поэтому, разнородные жидкости в сообщающихся сосудах могут и не устанавливаться на одном уровне.
Алгоритм решения задач по гидростатике на сообщающиеся сосуды:
- Сделать рисунок.

- Выбрать горизонтальный уровень, ниже которого во всех сосудах находится одинаковая жидкость. Если такого уровня нет, то, естественно, за нулевой уровень выбираем дно сосудов.
- Записать давления относительно этого уровня во всех сосудах и приравнять.
- При необходимости использовать свойство несжимаемости жидкости (объем жидкости, вытекающей из одного сосуда, равен объему жидкости, втекающей в другой сосуд).
- Решить математически полученную систему уравнений.
Гидравлический пресс
К оглавлению…
Если оба вертикально расположенных цилиндра сообщающихся сосудов закрыть поршнями, то с помощью внешних сил, приложенных к поршням, в жидкости можно создать большое давление p, во много раз превышающее гидростатическое давление ρgh в любой точке системы. Тогда можно считать, что во всей системе устанавливается одинаковое давление p (согласно закону Паскаля). Если поршни имеют разные площади S1 и S2, то на них со стороны жидкости действуют разные силы F1 = pS1 и F2 = pS2. Такие же по модулю, но противоположно направленные внешние силы должны быть приложены к поршням для удержания системы в равновесии. Таким образом, для гидравлического пресса имеем формулу:
Такие же по модулю, но противоположно направленные внешние силы должны быть приложены к поршням для удержания системы в равновесии. Таким образом, для гидравлического пресса имеем формулу:
Это соотношение вытекает из равенства давлений и выполняется только в идеальном гидравлическом прессе, т.е. таком в котором нет трения. Если S2 >> S1, то и F2 >> F1. Устройства в которых выполняются эти условия называют гидравлическими прессами (машинами, домкратами). Они позволяют получить значительный выигрыш в силе. Если поршень в узком цилиндре переместить вниз под действием внешней силы F1 на расстояние h1, то поршень в широком цилиндре переместится на расстояние h2, которое может быть найдено из соотношения:
Данное соотношение вытекает из равенства объемов и выполняется в любом гидравлическом прессе. Это выражение получается потому, что при перемещении поршня перемещаются одинаковые объемы жидкости, то есть сколько жидкости ушло из одного цилиндра столько же пришло во второй, или V1 = V2. Таким образом, выигрыш в силе обязательно сопровождается таким же проигрышем в расстоянии. При этом произведение силы на расстояние остается неизменным:
Это выражение получается потому, что при перемещении поршня перемещаются одинаковые объемы жидкости, то есть сколько жидкости ушло из одного цилиндра столько же пришло во второй, или V1 = V2. Таким образом, выигрыш в силе обязательно сопровождается таким же проигрышем в расстоянии. При этом произведение силы на расстояние остается неизменным:
Последняя формула вытекает из равенства работ и выполняется только для идеальных машин, в которых не действуют силы трения. Таким образом, в гидравлическом прессе всё происходит в полном соответствии с «золотым правилом механики»: во сколько раз мы выигрываем в силе, во столько же раз мы проигрываем в расстоянии. При этом ни одна машина не может дать выигрыша в работе.
Так как гидравлический пресс является механизмом, то его работу можно характеризовать КПД (коэффициентом полезного действия). КПД гидравлического пресса в задачах по гидростатике рассчитывается по следующей формуле:
где: Апол = F2h2 – полезная работа (работа по подъему груза), Азатр = F1h1 – затраченная работа. В большинстве задач КПД гидравлического пресса принимают за 100%. КПД рассчитывается в том случае, если речь идет о неидеальном гидравлическом прессе.
В большинстве задач КПД гидравлического пресса принимают за 100%. КПД рассчитывается в том случае, если речь идет о неидеальном гидравлическом прессе.
Еще раз подчеркнем, что для неидеального гидравлического пресса выполняется только соотношение, вытекающее из равенства объемов вытесненной жидкости, а также для таких прессов рассчитывается КПД. Остальные соотношения из этого раздела выполняются только для идеального гидравлического пресса.
Закон Архимеда. Вес тела в жидкости
К оглавлению…
Из–за разности давлений в жидкости на разных уровнях возникает выталкивающая или Архимедова сила, которая вычисляется по формуле:
где: V – объем вытесненной телом жидкости, или же объем погружённой в жидкость части тела, ρ – плотность жидкости в которую погружено тело, и следовательно, ρV – масса вытесненной жидкости.
Архимедова сила, действующая на погруженное в жидкость (или газ) тело, равна весу жидкости (или газа), вытесненной телом.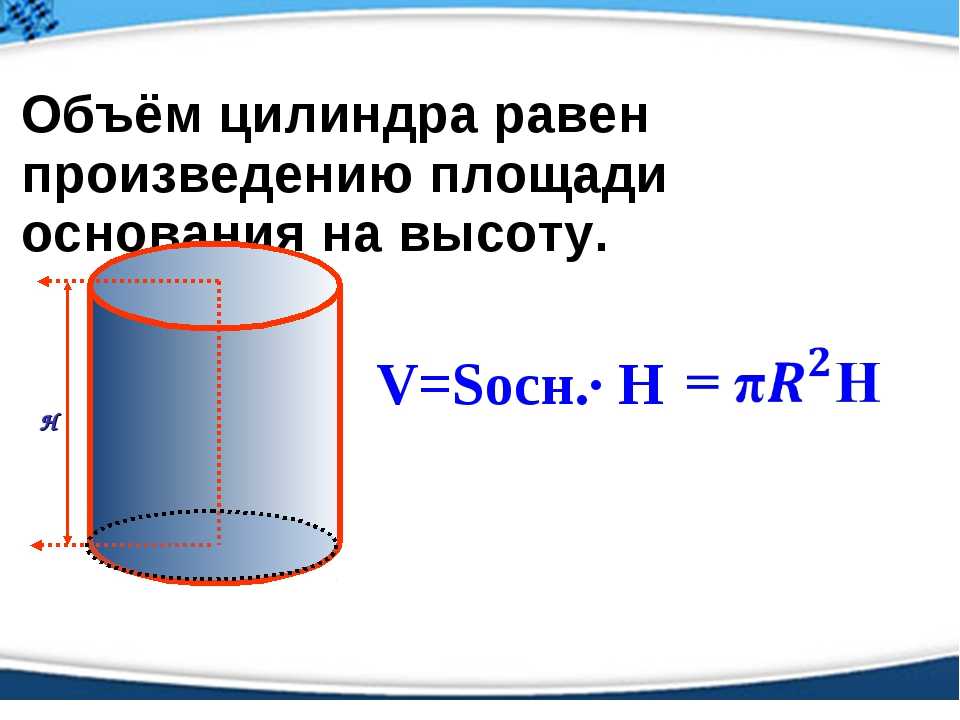 Это утверждение, называемое законом Архимеда, справедливо для тел любой формы.
Это утверждение, называемое законом Архимеда, справедливо для тел любой формы.
При этом вес тела (т.е. сила с которой тело действует на опору или подвес) погруженного в жидкость уменьшается. Если принять, что вес покоящегося тела в воздухе равен mg, а именно так мы и будем поступать в большинстве задач (хотя вообще говоря на тело в воздухе также действует очень маленькая сила Архимеда со стороны атмосферы, ведь тело погружено в газ из атмосферы), то для веса тела в жидкости можно легко вывести следующую важную формулу:
Эта формула может быть использована при решении большого количества задач. Ее можно запомнить. При помощи закона Архимеда осуществляется не только мореплавание, но и воздухоплавание. Из закона Архимеда вытекает, что если средняя плотность тела ρт больше плотности жидкости (или газа) ρ (или по–другому mg > FA), тело будет опускаться на дно. Если же ρт < ρ (или по–другому mg < FA), тело будет плавать на поверхности жидкости. Объем погруженной части тела будет таков, что вес вытесненной жидкости равен весу тела. Для подъема воздушного шара в воздухе его вес должен быть меньше веса вытесненного воздуха. Поэтому воздушные шары заполняют легкими газами (водородом, гелием) или нагретым воздухом.
Объем погруженной части тела будет таков, что вес вытесненной жидкости равен весу тела. Для подъема воздушного шара в воздухе его вес должен быть меньше веса вытесненного воздуха. Поэтому воздушные шары заполняют легкими газами (водородом, гелием) или нагретым воздухом.
Плавание тел
К оглавлению…
Если тело находится на поверхности жидкости (плавает), то на него действует всего две силы (Архимеда вверх и тяжести вниз), которые уравновешивают друг друга. Если тело погружено только в одну жидкость, то записав второй закон Ньютона для такого случая и выполнив простые математические операции можем получить следующее выражение связывающее объемы и плотности:
где: Vпогр – объем погруженной части тела, V – полный объем тела. При помощи этого соотношения легко решается большинство задач на плавание тел.
Формула закона Архимеда в физике
Формула закона Архимеда в физикеОпределение и формула закона Архимеда
Силу, которая действует на тело, находящееся в жидкости или газе называют выталкивающей силой.
Силу давления воды на верхнюю поверхность цилиндра вычислим как:
\[F_1={\rho }_ggh_1S\ \left(2\right).\]
Над нижней поверхностью тела высота столба жидкости равна $h_2$, значит, сила давления воды на нее составляет величину:
\[F_2={\rho }_ggh_2S\ \left(3\right).\]
Очевидно, что $F_2>F_1$. Разница между силами $F_2и{\ F}_1$ составляет силу выталкивания:
\[F_A=F_2-F_1={\rho }_ggS\ \left(h_2-h_1\right)={\rho }_ggSH={\rho }_ggV\ .\]
Мы получили, что сила Архимеда равна:
\[F_A={\rho }_gVg\ \left(4\right).\]
Выражение (4) можно назвать формулой закона Архимеда. Если тело частично погружено в жидкость, то V — часть тела, находящаяся в жидкости. Сила Архимеда оказывает свое действие на тела не только в жидкостях, но и газах, там, где существует гиростатическое давление.
Если обозначить массу жидкости, которая занимает объем, равный объему тела как $m_g={\rho }_gV$, то выражение (4) преобразуем к виду:
\[F_A=m_gg=P_g\ \left(5\right),\]
где $P_g$ — вес жидкости, которая занимает объем, равный объему тела находящийся в ней.
Закон Архимеда в современной формулировке: На любое тело, которое погружено в жидкость (газ), находящуюся в состоянии равновесия, действует со стороны жидкости (газа) сила выталкивания, равная произведению плотности вещества в котором находится тело, на ускорение свободного падения и на объем погруженной части тела.
Если погрузить в жидкость тело, то величина силы Архимеда не зависит от положения тела в жидкости. Сила выталкивания не зависит от вещества, из которого сделано, погруженное в жидкость тело, ни от глубины погружения тела (при полном погружении тела).
Из-за выталкивающей силы вес каждого тела в жидкости меньше, чем в воздухе. Уменьшение веса тела произойдет, если перенести тело из вакуума в любой газ. Если вес тела в вакууме равен $P$, то его вес в жидкости или газе равен:
\[P’=P-F_A\left(6\right).\]
Примеры задач на закона Архимеда
Пример 1
Задание. Чему равен объем тела, полностью погруженного в воду, если на него действует сила Архимеда, равная 100 Н?
Решение. 3$
3$
Пример 2
Задание. Чему равна плотность жидкости, в которую погружают тело, если его вес в воде составляет $P$, а в неизвестной жидкости $P_1$? Масса данного тела $m,\ $плотность воды ${\rho }_v$.
Решение. Сделаем рисунок.
Из закона Архимеда мы знаем, что тело теряет в своем весе величину, равную модулю силы Архимеда, то есть:
\[mg-P_1=F_A\left(2.1\right),\]
где $P=mg$ — вес тела в воздухе.
Сила Архимеда равна:
\[F_A={\rho }_gVg\ \left(2.2\right).\]
Значит, изменения веса тела при погружении его в воду запишем как:
\[mg-P_1={\rho }_{g1}Vg\left(2.3\right).\]
При погружении того же тела в неизвестную жидкость получим:
\[mg-P_2={\rho }_{g2}Vg\left(2.4\right).\]
Из формулы (2.4) выразим плотность жидкости:
\[{\rho }_{g2}=\frac{mg-P_2}{gV}\left(2. 5\right).\]
5\right).\]
Нам следует найти объем тела, мы его выразим из (2.3), получим:
\[V=\frac{mg-P_1}{g{\rho }_{g1}}\left(2.6\right).\]
Подставим результат (2.6)в выражение для плотности неизвестной жидкости (2.5):
\[{\rho }_{g2}={\rho }_{g1}\cdot \frac{mg-P_2}{mg-P_1}=\frac{mg-P_2}{mg-P_1}{\rho }_v.\]
Ответ. ${\rho }_{g2}=\frac{mg-P_2}{mg-P_1}{\rho }_v$
Читать дальше: формула коэффициента полезного действия.
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Объем вытесненной жидкости Калькулятор | Вычислить Объем вытесненной жидкости
✖Вес вытесненной жидкости – это вес жидкости, вытесненной погруженным в нее телом.ⓘ Вес вытесненной жидкости [W’] | Ассарий (Библейская Roman)Масс-атомная единицаАттограммаЭвердюпуа драмБекан (Библейский иврит)КаратсантиграммДалтонДекаграммДециграммDenarius (Библейская Roman)Didrachma (Библейский греческий)Драхма (Библейский греческий)Масса электрона (Rest)ExagramFemtogramГаммаGerah (Библейский иврит)ГигаграммГигатонназернаграммГектограммЦентнер (Великобритания)Центнер (США)Масса ЮпитераКилограммКилограмм-сила в квадрате в секунду на метркилофунтКилотонна (метрическая)ЛЕПТОН (Библейская Roman)Масса ДейтронаМасса ЗемлиМасса нейтонаМасса протонаМасса СолнцамегаграммМегатоннамикрограммМиллиграммMina (Библейский греческий)Mina (Библейский иврит)масса мюонананограммунцияПеннивейтPetagramпикограммамасса ПланкафунтФунт (Troy или фармацевтическое)паундальФунт-сила в квадрате в секунду на футQuadrans (Библейская Roman)Четверть (Великобритания)Четверть (США)Quintal (метрическая система)Скрупл (аптекарь)Шекель (Библейский иврит)тихоходСолнечная массаСтоун (Великобритания)Камень (США)Талант (Библейский греческий)Талант (Библейский иврит)ТераграммаТетрадрахма (Библейский греческий)Тон (анализ) (Великобритания)Тон (анализ) (США)Тон (длинный)Тон (метрической размерности)Тон (короткометражный)Тонна | +10% -10% | |
✖Плотность вытесненной жидкости – это плотность жидкости, вытесняемой погруженным в нее телом. | сантиграмм / литрдециграмм/ литрдекаграмм / литрПлотность Землифемтограмм/ литрЗерно на кубический футЗерно на галлон (Великобритания)Зерно на галлон (США)Грамм на кубический сантиметрГрамм на кубический метрГрамм на кубический миллиметрграмм / литрГрамм на миллилитргектограмм / литрКилограмм на кубический сантиметрКилограмм на кубический дециметрКилограмм на кубический метркилограмм/ литрмегаграмм / литрмикрограмм / литрМиллиграмм на кубический сантиметрМиллиграмм на кубический метрМиллиграмм на кубический миллиметрмиллиграмм / литрнанограмм / литрУнция на кубический футУнция на кубический дюймУнция на галлон (Великобритания)Унция на галлон (США)пикограмм / литрПланковская плотностьФунт на кубический футФунт на кубический дюймФунт на кубический ярдФунт на галлон (Великобритания)Фунт на галлон (США)Слаг на кубический футСлаг на кубический дюймСлаг на кубический ярдТонна (длинная) на кубический ярдТонна (короткая) на кубический ярд | +10% -10% |
|
✖Объем жидкости, вытесненной телом, равен объему жидкости, занимаемому частично погруженным в жидкость телом. |
Акр-футАкр-фут (исследование США)Акко-дюймовыйБочка (масло)Бочка (UK)Ствол (США)Ванна (библейский)Совет для ногКабина (библейский)СантилитрКентум кубический футКор (библейский)шнурКубический Ангстремкубический сантиметркубический дециметркубический футкубический дюймКилометры CubicКубический метрКубический Mileкубический миллиметркубический ярдКубок (метрический)Кубок (Великобритания)Кубок (США)ДекалитрДецилитрДестистерДекастерДесертная ложка (Великобритания)Десертная ложка (США)драхмаКапляFemtoliterЖидкость Унция (Великобритания)Жидкость Унция (США)Галлон (Великобритания)Галлона (США)гигалитрГилл (Великобритания)Гилл (США)ГектолитрHin (библейский)хогсхедГомер (библейский)Сто кубический футкилолитрЛитрLog (библейский)мегалитрМикролитрМиллилитрMinim (Великобритания)Minim (Великобритания)Minim (США)нанолитрPetaliterпиколитрПинта (Великобритания)Пинта (США)Quart (Великобритания)Quart (США)StereСтоловая ложка (метрическая)Столовая ложка (Великобритания)Столовая ложка (США)Таза (испанский)Чайная ложка (метрическая)Чайная ложка (Великобритания)Чайная ложка (США)тералитрTon РегистрацияТунОбъем Земли |
⎘ копия |
👎
Формула
сбросить
👍
Объем вытесненной жидкости Решение
ШАГ 0: Сводка предварительного расчета
ШАГ 1. Преобразование входов в базовый блок
Преобразование входов в базовый блок
Вес вытесненной жидкости: 32.5 Килограмм —> 32.5 Килограмм Конверсия не требуется
Плотность вытесняемой жидкости: 997 Килограмм на кубический метр —> 997 Килограмм на кубический метр Конверсия не требуется
ШАГ 2: Оцените формулу
ШАГ 3: Преобразуйте результат в единицу вывода
0.0325977933801404 Кубический метр —> Конверсия не требуется
< 10+ Плавучесть Калькуляторы
Метацентрическая высота в экспериментальном методе
Метацентрическая высота плавающего тела = ((Подвижный вес на плавучем судне*Расстояние, пройденное грузом на судне)/(Вес плавучего судна*tan(Угол пятки))) Идти
Угол крена для метацентрической высоты в экспериментальном методе
Угол пятки = atan((Подвижный вес на плавучем судне*Расстояние, пройденное грузом на судне)/(Вес плавучего судна*Метацентрическая высота плавающего тела)) Идти
Подвижный груз для метацентрической высоты в экспериментальном методе
Подвижный вес на плавучем судне = (Метацентрическая высота плавающего тела*Вес плавучего судна*tan(Угол пятки))/(Расстояние, пройденное грузом на судне) Идти
Период колебания корабля
Время Период колебаний плавающего тела = (2*pi)*(sqrt((Радиус вращения плавающего тела^2)/(Метацентрическая высота плавающего тела*[g]))) Идти
Радиус вращения для метацентрической высоты и периода колебаний
Радиус вращения плавающего тела = ((Время Период колебаний плавающего тела)*sqrt(Метацентрическая высота плавающего тела*[g]))/(2*pi) Идти
Объем тела в жидкости для метацентрической высоты и ГК
Объем тела, погруженного в воду = Момент инерции планирующего плавающего тела/(Метацентрическая высота плавающего тела+Расстояние центра тяжести от центра плавучести) Идти
Метацентрическая высота для периода колебаний и радиуса вращения
Метацентрическая высота плавающего тела = (4*(pi^2)*(Радиус вращения плавающего тела^2))/((Время Период колебаний плавающего тела^2)*[g]) Идти
Объем вытесненной жидкости
Объем жидкости, вытесненной телом = (Вес вытесненной жидкости)/(Плотность вытесняемой жидкости) Идти
Принцип Архимеда
Принцип Архимеда = Плотность*Ускорение силы тяжести*Скорость Идти
Центр плавучести
Центр плавучести плавучего тела = (Глубина погружения объекта в воду)/2 Идти
Объем вытесненной жидкости формула
Объем жидкости, вытесненной телом = (Вес вытесненной жидкости)/(Плотность вытесняемой жидкости)
V = (W’)/(ρdisplaced)
Какой объем вытесняемой жидкости?
Объем вытесненной жидкости эквивалентен объему объекта, полностью погруженного в жидкость, или той части объема под поверхностью для объекта, частично погруженного в жидкость.
Каково соотношение объема вытесняемой жидкости с плавучестью?
Когда тело погружено в жидкость, жидкость оказывает на тело восходящую силу. Эта направленная вверх сила равна весу жидкости, вытесняемой телом.
Share
Copied!
14.1 Жидкости, плотность и давление
Цели обучения
К концу этого раздела вы сможете:
- Называть различные фазы материи
- Описать характеристики фаз материи на молекулярном или атомарном уровне
- Различать сжимаемые и несжимаемые материалы
- Определение плотности и связанных с ней единиц СИ
- Сравните и сопоставьте плотности различных веществ
- Определить давление и связанные с ним единицы СИ
- Объясните взаимосвязь между давлением и силой
- Расчет силы по давлению и площади
Вещество чаще всего существует в виде твердого тела, жидкости или газа; эти состояния известны как три общие фазы материи. В этом разделе мы подробно рассмотрим каждый из этих этапов.
В этом разделе мы подробно рассмотрим каждый из этих этапов.
Характеристики твердых тел
Твердые тела твердые, имеют определенную форму и определенный объем. Атомы или молекулы в твердом теле находятся в непосредственной близости друг от друга, и между этими молекулами существует значительная сила. Твердые тела примут форму, определяемую характером этих сил между молекулами. Хотя настоящие твердые тела не являются несжимаемыми, тем не менее для изменения формы твердого тела требуется большая сила. В некоторых случаях сила между молекулами может заставить молекулы организоваться в решетку, как показано на (Рисунок). Структура этой трехмерной решетки представлена в виде молекул, соединенных жесткими связями (смоделированными как жесткие пружины), что дает ограниченную свободу движения. Даже большая сила вызывает лишь небольшие смещения атомов или молекул решетки, и твердое тело сохраняет свою форму. Твердые тела также сопротивляются силам сдвига. (Сдвиговые силы — это силы, действующие по касательной к поверхности, как описано в статье «Статическое равновесие и упругость». )
)
Характеристики жидкостей
Жидкости и газы считаются жидкостями , потому что они поддаются силам сдвига, тогда как твердые тела сопротивляются им. Подобно твердым телам, молекулы жидкости связаны с соседними молекулами, но таких связей гораздо меньше. Молекулы в жидкости не зафиксированы на месте и могут двигаться относительно друг друга. Расстояние между молекулами аналогично расстоянию в твердом теле, поэтому жидкости имеют определенные объемы, но форма жидкости меняется в зависимости от формы ее сосуда. Газы не связаны с соседними атомами и могут иметь большие расстояния между молекулами. Газы не имеют ни определенной формы, ни определенных объемов, так как их молекулы движутся, чтобы заполнить сосуд, в котором они находятся ((рисунок)).
Рис. 14.2 (а) Атомы в твердом теле всегда находятся в тесном контакте с соседними атомами и удерживаются на месте силами, представленными здесь пружинами. б) Атомы в жидкости также находятся в тесном контакте, но могут скользить друг по другу. Силы между атомами сильно сопротивляются попыткам сжатия атомов. в) Атомы в газе свободно перемещаются и разделены большими расстояниями. Газ необходимо держать в закрытом контейнере, чтобы предотвратить его свободное расширение и утечку.
Силы между атомами сильно сопротивляются попыткам сжатия атомов. в) Атомы в газе свободно перемещаются и разделены большими расстояниями. Газ необходимо держать в закрытом контейнере, чтобы предотвратить его свободное расширение и утечку.
Жидкости легко деформируются при воздействии нагрузки и не возвращают свою первоначальную форму после прекращения действия силы. Это происходит потому, что атомы или молекулы в жидкости могут свободно скользить и менять соседей. То есть жидкости текут (поэтому они являются типом жидкости), а молекулы удерживаются вместе за счет взаимного притяжения. Когда жидкость помещается в контейнер без крышки, она остается в контейнере. Поскольку атомы плотно упакованы, жидкости, как и твердые тела, сопротивляются сжатию; для изменения объема жидкости необходима чрезвычайно большая сила.
Напротив, атомы в газах разделены большими расстояниями, и поэтому силы между атомами в газе очень слабы, за исключением случаев, когда атомы сталкиваются друг с другом. Это делает газы относительно легко сжимаемыми и позволяет им течь (что делает их жидкостями). При помещении в открытый контейнер газы, в отличие от жидкостей, будут выходить наружу.
Это делает газы относительно легко сжимаемыми и позволяет им течь (что делает их жидкостями). При помещении в открытый контейнер газы, в отличие от жидкостей, будут выходить наружу.
В этой главе мы обычно называем газы и жидкости просто жидкостями, проводя различие между ними только тогда, когда они ведут себя по-разному. Существует еще одна фаза вещества — плазма, существующая при очень высоких температурах. При высоких температурах молекулы могут диссоциировать на атомы, а атомы диссоциировать на электроны (с отрицательными зарядами) и протоны (с положительными зарядами), образуя плазму. Плазма не будет подробно обсуждаться в этой главе, потому что плазма имеет очень отличные свойства от трех других распространенных фаз материи, обсуждаемых в этой главе, из-за сильных электрических сил между зарядами.
Плотность
Предположим, что брусок латуни и брусок дерева имеют одинаковую массу. Если оба блока бросить в резервуар с водой, почему дерево всплывет, а латунь утонет ((Рисунок))? Это происходит потому, что латунь имеет большую плотность, чем вода, а древесина имеет меньшую плотность, чем вода.
Рисунок 14.3 (a) Блок из латуни и блок из дерева имеют одинаковый вес и массу, но блок из дерева имеет гораздо больший объем. (b) При помещении в аквариум, наполненный водой, латунный куб тонет, а деревянный брусок всплывает. (Деревянный брусок на обеих картинках один и тот же; он был перевернут на бок, чтобы поместиться на шкале.)
Плотность является важной характеристикой веществ. Это имеет решающее значение, например, при определении того, тонет ли объект в жидкости или плавает.
Плотность
Средняя плотность вещества или объекта определяется как его масса на единицу объема,
[латекс] \rho =\frac{m}{V} [/латекс]
где греческая буква [латекс ] \rho [/latex] (rho) — символ плотности, m — масса, V — объем.
9{3} [/латекс] Как вы можете видеть, изучив (Рисунок), плотность объекта может помочь определить его состав. Плотность золота, например, примерно в 2,5 раза больше плотности железа, что примерно в 2,5 раза больше плотности алюминия. Плотность также раскрывает кое-что о фазе материи и ее подструктуре. Обратите внимание, что плотности жидкостей и твердых тел примерно сопоставимы, что согласуется с тем фактом, что их атомы находятся в тесном контакте. Плотность газов намного меньше, чем у жидкостей и твердых тел, потому что атомы в газах разделены большим количеством пустого пространства. Газы показаны для стандартной температуры [латекс] 0,0\text{°}\текст{C} [/латекс] и стандартного давления 101,3 кПа, при этом наблюдается сильная зависимость плотности от температуры и давления. Отображаемые плотности твердых и жидких веществ даны для стандартной температуры [латекс] 0,0\text{°}\text{C} [/латекс], а плотности твердых и жидких веществ зависят от температуры. Плотность твердых и жидких тел обычно увеличивается с понижением температуры.
Плотность золота, например, примерно в 2,5 раза больше плотности железа, что примерно в 2,5 раза больше плотности алюминия. Плотность также раскрывает кое-что о фазе материи и ее подструктуре. Обратите внимание, что плотности жидкостей и твердых тел примерно сопоставимы, что согласуется с тем фактом, что их атомы находятся в тесном контакте. Плотность газов намного меньше, чем у жидкостей и твердых тел, потому что атомы в газах разделены большим количеством пустого пространства. Газы показаны для стандартной температуры [латекс] 0,0\text{°}\текст{C} [/латекс] и стандартного давления 101,3 кПа, при этом наблюдается сильная зависимость плотности от температуры и давления. Отображаемые плотности твердых и жидких веществ даны для стандартной температуры [латекс] 0,0\text{°}\text{C} [/латекс], а плотности твердых и жидких веществ зависят от температуры. Плотность твердых и жидких тел обычно увеличивается с понижением температуры.
(рисунок) показывает плотность воды в различных фазах и температуру. {3}) [/латекс] 9{3} [/латекс]
{3}) [/латекс] 9{3} [/латекс]
Плотность вещества не обязательно постоянна по всему объему вещества. Если плотность вещества постоянна во всем веществе, говорят, что это однородное вещество . Твердый железный брусок является примером однородного вещества. Плотность постоянна на всем протяжении, а плотность любого образца вещества равна его средней плотности. Если бы плотность вещества не была постоянной, то говорят, что вещество находится в состоянии гетерогенное вещество . Кусок швейцарского сыра является примером гетерогенного материала, содержащего как твердый сыр, так и пустоты, заполненные газом. Плотность в определенном месте в неоднородном материале называется локальной плотностью и определяется как функция местоположения [латекс] \rho =\rho (x,y,z) [/латекс] ((Рисунок)) .
Рисунок 14.4 Плотность гетерогенной смеси может варьироваться. Локальная плотность в точке получается делением массы на объем в малом объеме вокруг данной точки.
Локальная плотность может быть получена с помощью процесса ограничения, основанного на средней плотности в небольшом объеме вокруг рассматриваемой точки, принимая предел, когда размер объема приближается к нулю,
[латекс] \rho =\underset{ \text{Δ}V\to 0}{\text{lim}}\frac{\text{Δ}m}{\text{Δ}V} [/latex]
, где [латекс] \ро [/латекс ] — плотность, м — масса, V — объем.
Поскольку газы могут свободно расширяться и сжиматься, плотность газов значительно зависит от температуры, тогда как плотность жидкостей зависит от температуры незначительно. Поэтому плотности жидкостей часто считают постоянными, при этом плотность равна средней плотности. 9{3}[/latex]), но его удельный вес равен 2,7 независимо от единицы плотности. Удельный вес — особенно полезная величина в отношении плавучести, которую мы обсудим позже в этой главе.
Давление
Вы, несомненно, слышали слово «давление», используемое по отношению к крови (высокое или низкое кровяное давление) и по отношению к погоде (погодные системы высокого и низкого давления). {2}. [/latex] Вот почему острая игла способна проткнуть кожу при приложении небольшого усилия, но приложение такого же усилия пальцем не прокалывает кожу ((Рисунок)).
{2}. [/latex] Вот почему острая игла способна проткнуть кожу при приложении небольшого усилия, но приложение такого же усилия пальцем не прокалывает кожу ((Рисунок)).
Рисунок 14.5 (a) Человек, которого тыкают пальцем, может вызвать раздражение, но сила не имеет длительного эффекта. (b) Напротив, той же силы, приложенной к участку размером с острый конец иглы, достаточно, чтобы сломать кожу.
Обратите внимание, что хотя сила является вектором, давление является скаляром. Давление является скалярной величиной, поскольку по определению оно пропорционально величине силы, действующей перпендикулярно площади поверхности. Единицей давления в СИ является 9.{2}. [/latex]
Несколько других единиц используются для давления, которые мы обсудим позже в этой главе.
Изменение давления с глубиной в жидкости с постоянной плотностью
Давление определяется для всех состояний вещества, но оно особенно важно при обсуждении жидкостей. Важной характеристикой жидкостей является отсутствие значительного сопротивления компоненту силы, приложенной параллельно поверхности жидкости. Молекулы жидкости просто текут, приспосабливаясь к горизонтальной силе. Сила, приложенная перпендикулярно поверхности, сжимает или расширяет жидкость. Если вы попытаетесь сжать жидкость, вы обнаружите, что в каждой точке внутри жидкости в направлении наружу возникает сила реакции, уравновешивающая силу, действующую на молекулы на границе.
Молекулы жидкости просто текут, приспосабливаясь к горизонтальной силе. Сила, приложенная перпендикулярно поверхности, сжимает или расширяет жидкость. Если вы попытаетесь сжать жидкость, вы обнаружите, что в каждой точке внутри жидкости в направлении наружу возникает сила реакции, уравновешивающая силу, действующую на молекулы на границе.
Рассмотрим жидкость постоянной плотности, как показано на (Рисунок). Давление на дне контейнера обусловлено давлением атмосферы [латекс] ({p}_{0}) [/латекс] плюс давление из-за веса жидкости. Давление жидкости равно весу жидкости, деленному на площадь. Вес жидкости равен произведению ее массы на ускорение свободного падения.
Рисунок 14.6 Дно этого контейнера выдерживает весь вес жидкости в нем. Вертикальные стороны не могут воздействовать на жидкость восходящей силой (поскольку она не может противостоять сдвигающей силе), поэтому дно должно поддерживать все это.
Поскольку плотность постоянна, вес можно рассчитать, используя плотность:
[латекс] w=mg=\rho Vg=\rho Ahg. [/latex]
[/latex]
Таким образом, давление на дне контейнера равно атмосферному давлению, добавленному к весу жидкости, деленному на площадь:
[латекс] p={p}_{0}+\frac{ \rho Ahg}{A}={p}_{0}+\rho hg. [/latex]
Это уравнение годится только для давления на глубине для жидкости постоянной плотности.
Давление на глубине для жидкости постоянной плотности
Давление на глубине в жидкости постоянной плотности равно атмосферному давлению плюс давление, обусловленное весом жидкости, или
[латекс] p={p}_{0}+\rho hg, [/latex]
Где p — давление на определенной глубине, [latex] {p}_{0} [/latex] — атмосферное давление, [latex] \rho [/latex] — плотность жидкости, г — ускорение свободного падения, ч — глубина.
Рисунок 14.7 Плотина «Три ущелья», воздвигнутая на реке Янцзы в центральном Китае в 2008 г., создала массивное водохранилище, в котором было перемещено более миллиона человек. (кредит: «Le Grand Portage»/Flickr)
Пример
Какую силу должна выдерживать плотина?
Рассмотрим давление и силу, действующие на плотину, удерживающую резервуар с водой ((Рисунок)). Предположим, что ширина плотины составляет 500 м, а глубина воды у плотины составляет 80,0 м, как показано ниже. а) Каково среднее давление воды на плотину? б) Рассчитайте силу, действующую на плотину.
Предположим, что ширина плотины составляет 500 м, а глубина воды у плотины составляет 80,0 м, как показано ниже. а) Каково среднее давление воды на плотину? б) Рассчитайте силу, действующую на плотину.
Среднее давление p из-за веса воды является давлением на средней глубине h 40,0 м, так как давление увеличивается линейно с глубиной. Сила, действующая на плотину со стороны воды, равна среднему давлению, умноженному на площадь контакта, [латекс] F=pA. [/latex]
раствор
- Среднее давление из-за веса жидкости
[латекс] p=h\rho g. [/латекс]
Ввод плотности воды из (Рисунок) и получение 9{13}\text{N} [/latex] вес воды в резервуаре. На самом деле это всего лишь 0,0800% веса.
Проверьте свое понимание
Если водохранилище на (рис.) покрывает площадь в два раза больше, но остается на той же глубине, нужно ли перепроектировать плотину?
Показать решение
Давление в статической жидкости в однородном гравитационном поле
Статическая жидкость — это жидкость, которая не находится в движении.
 В любой точке статической жидкости давление со всех сторон должно быть одинаковым, иначе жидкость в этой точке будет реагировать на результирующую силу и ускоряться.
В любой точке статической жидкости давление со всех сторон должно быть одинаковым, иначе жидкость в этой точке будет реагировать на результирующую силу и ускоряться.Давление в любой точке статической жидкости зависит только от глубины в этой точке. Как обсуждалось, давление в жидкости вблизи Земли меняется с глубиной из-за веса жидкости над определенным уровнем. В приведенных выше примерах мы предполагали, что плотность постоянна, а средняя плотность жидкости является хорошим представлением плотности. Это разумное приближение для таких жидкостей, как вода, где требуются большие силы для сжатия жидкости или изменения объема. В плавательном бассейне, например, плотность приблизительно постоянна, и вода на дне очень мало сжимается под весом воды наверху. Однако путешествие в атмосферу — это совсем другая ситуация. Плотность воздуха начинает значительно меняться уже на небольшом расстоянии от поверхности Земли.
Чтобы вывести формулу для изменения давления с глубиной в резервуаре, содержащем жидкость с плотностью ρ на поверхности Земли, мы должны начать с предположения, что плотность жидкости непостоянна.
 Жидкость, расположенная на более глубоких уровнях, подвергается большей силе, чем жидкость, расположенная ближе к поверхности, из-за веса жидкости над ней. Следовательно, давление, рассчитанное на заданной глубине, отличается от давления, рассчитанного с использованием постоянной плотности.
Жидкость, расположенная на более глубоких уровнях, подвергается большей силе, чем жидкость, расположенная ближе к поверхности, из-за веса жидкости над ней. Следовательно, давление, рассчитанное на заданной глубине, отличается от давления, рассчитанного с использованием постоянной плотности.Представьте себе тонкий элемент жидкости на глубине ч , как показано на (рис.). Пусть элемент имеет площадь поперечного сечения A и высоту [латекс] \text{Δ}y [/латекс]. Силы, действующие на элемент, обусловлены давлением p ( y ) над ним и [латексом] p(y+\text{Δ}y) [/latex] под ним. Вес самого элемента также показан на диаграмме свободного тела.
Рисунок 14.8 Силы, действующие на элемент массы внутри жидкости. Вес самого элемента показан на диаграмме свободного тела.
Поскольку элемент жидкости между y и [латекс] y+\text{Δ}y [/латекс] не ускоряется, силы уравновешены. Используя декартову ось y , ориентированную вверх, мы находим следующее уравнение для y -компоненты:
[латекс] p(y+\text{Δ}y)A-p(y)A-g\text{Δ}m =0(\text{Δ}y>0).
 [/latex]
[/latex]Обратите внимание, что если элемент имеет ненулевую y -компоненту ускорения, правая часть не будет равна нулю, а вместо этого будет массой, умноженной на г -ускорение. Массу элемента можно записать через плотность жидкости и объем элементов:
[латекс] \text{Δ}m=|\rho A\text{Δ}y|=\text{ −}\rho A\text{Δ}y\text{ }(\text{Δ}y>0). [/latex]
Подставляя это выражение для [латекс] \текст{Δ}m [/латекс] в (Рисунок) и затем разделив обе части на [латекс] А\текст{Δ}у [/латекс], мы находим
[латекс] \frac{p(y+\text{Δ}y)-p(y)}{\text{Δ}y}=\text{-}\rho g. [/latex]
Беря предел бесконечно малому элементу [латекс] \text{Δ}y\к 0 [/latex], мы получаем следующее дифференциальное уравнение, которое дает изменение давления в жидкости:
[латекс] \frac{dp}{dy}=\text{−}\rho g. [/latex]
Это уравнение говорит нам, что скорость изменения давления в жидкости пропорциональна плотности жидкости. Решение этого уравнения зависит от того, постоянна плотность ρ или изменяется с глубиной; то есть функция ρ ( y ).

Если диапазон анализируемых глубин не слишком велик, плотность можно считать постоянной. Но если диапазон глубин достаточно велик для заметного изменения плотности, как, например, в случае с атмосферой, плотность существенно меняется с глубиной. В этом случае мы не можем использовать приближение постоянной плотности.
Давление в жидкости с постоянной плотностью
Используем (Рисунок) для получения формулы давления на глубине ч от поверхности в резервуаре с жидкостью типа воды, где плотность жидкости можно считать постоянным.
Нам нужно проинтегрировать (Рисунок) от [латекс] y=0, [/латекс], где давление равно атмосферному давлению [латекс] ({p}_{0}), [/латекс] до [латекс] y=\text{−}h, [/latex] y -координата глубины: 9{\ text {−} h} \ rho gdy \ hfill \\ \ hfill p- {p} _ {0} & = \ hfill & \ rho gh \ hfill \\ \ hfill p & = \ hfill & {p} _ { 0}+\rho gh.\hfill \end{array} [/latex]
Следовательно, давление на глубине жидкости на поверхности Земли равно атмосферному давлению плюс ρgh , если плотность жидкости постоянной по высоте, как мы нашли ранее.

Обратите внимание, что давление в жидкости зависит только от глубины от поверхности, а не от формы сосуда. Таким образом, в сосуде, где жидкость может свободно перемещаться в различных частях, жидкость остается на одном уровне во всех частях, независимо от формы, как показано на (рис.).
Рисунок 14.9 Если жидкость может свободно течь между частями сосуда, она поднимается на одинаковую высоту в каждой части. В изображенном контейнере давление на дне каждой колонны одинаково; если бы это было не то же самое, жидкость текла бы до тех пор, пока давления не сравнялись бы.
Изменение атмосферного давления с высотой
Изменение атмосферного давления с высотой представляет особый интерес. Предполагая, что температура воздуха постоянна и что закон термодинамики идеального газа описывает атмосферу в хорошем приближении, мы можем найти изменение атмосферного давления с высотой, когда температура постоянна. (Мы обсудим закон идеального газа в одной из последующих глав, но мы предполагаем, что вы знакомы с ним из средней школы и химии.
 {-23}\text{J/K } [/латекс].
{-23}\text{J/K } [/латекс].Возможно, вы встречали закон идеального газа в форме [латекс] pV=nRT [/латекс], где n — число молей, а R — газовая постоянная. Здесь тот же закон записан в другой форме, с использованием плотности [латекс] \ро [/латекс] вместо объема V . Следовательно, если давление p меняется с высотой, то и плотность [латекс] \rho . [/latex] Используя плотность из закона идеального газа, скорость изменения давления с высотой определяется как
[латекс] \frac{dp}{dy}=\text{−}p(\frac{mg}{{k}_{\text{B}}T}), [/latex]
, где константа количества собраны в скобках. Заменив эти константы одним символом [latex] \alpha , [/latex], уравнение выглядит намного проще:
[latex] \begin{array}{ccc}\hfill \frac{dp}{dy}& =\hfill & \text{-}\alpha p\hfill \\ \hfill \frac{dp}{p}& =\hfill & \text{-}\alpha dy\hfill \\ \hfill \underset{{p}_{ 0}}{\overset{p(y)}{\int }}\frac{dp}{p}& =\hfill & \underset{0}{\overset{y}{\int }}\text{− }\alpha dy\hfill \\ \hfill {[\text{ln}(p)]}_{{p}_{0}}^{p(y)}& =\hfill & {[\text{− }\alpha y]}_{0}^{y}\hfill \\ \hfill \text{ln}(p)-\text{ln}({p}_{0})& =\hfill & \text {−}\alpha y\hfill \\ \hfill \text{ln}(\frac{p}{{p}_{0}})& =\hfill & \text{−}\alpha y\hfill \end {массив} [/латекс]
Это дает решение
[латекс] p(y)={p}_{0}\text{exp}(\text{−}\alpha y).
 [/latex]
[/latex]Таким образом, атмосферное давление падает экспоненциально с высотой, поскольку ось y направлена вверх от земли, а y имеет положительные значения в атмосфере над уровнем моря. Давление падает в [латекс] \frac{1}{e} [/latex], когда высота равна [латекс] \frac{1}{\alpha }, [/latex], что дает нам физическую интерпретацию для [латекс] \альфа [/латекс]: Константа [латекс] \фрак{1}{\альфа } [/латекс] — это шкала длины, которая характеризует изменение давления с высотой и часто упоминается как высота шкалы давления. 9{-23}\,\text{J/K}\,×\,\text{300 K}}=\frac{1}{8800\,\text{m}}. [/latex]
Таким образом, на каждые 8800 метров атмосферное давление падает в 1/ e раз, или примерно на одну треть своего значения. Это дает нам лишь грубую оценку реальной ситуации, поскольку мы предполагали и постоянную температуру, и постоянную g на столь больших расстояниях от Земли, и ни одно из этих утверждений в действительности не верно.
Направление давления в жидкости
Давление жидкости не имеет направления, поскольку является скалярной величиной, тогда как силы давления имеют четко определенные направления: они всегда действуют перпендикулярно любой поверхности.
 Причина в том, что жидкости не могут противостоять силам сдвига или оказывать на них силы сдвига. Таким образом, в статической жидкости, заключенной в резервуар, сила, действующая на стенки резервуара, действует перпендикулярно внутренней поверхности. Точно так же давление оказывается перпендикулярно поверхностям любого объекта в жидкости. (Рисунок) иллюстрирует давление, оказываемое воздухом на стенки шины и водой на тело пловца.
Причина в том, что жидкости не могут противостоять силам сдвига или оказывать на них силы сдвига. Таким образом, в статической жидкости, заключенной в резервуар, сила, действующая на стенки резервуара, действует перпендикулярно внутренней поверхности. Точно так же давление оказывается перпендикулярно поверхностям любого объекта в жидкости. (Рисунок) иллюстрирует давление, оказываемое воздухом на стенки шины и водой на тело пловца.Рисунок 14.10 (a) Давление внутри этой шины действует перпендикулярно ко всем поверхностям, с которыми она контактирует. Стрелки представляют направления и величины сил, действующих в различных точках. (b) Давление оказывается перпендикулярно всем сторонам этого пловца, так как вода потекла бы в пространство, которое он занимает, если бы его там не было. Стрелки представляют направления и величины сил, действующих на пловца в различных точках. Обратите внимание, что силы внизу больше из-за большей глубины, что дает сеть вверх или выталкивающую силу.
 Суммарная вертикальная сила, действующая на пловца, равна сумме выталкивающей силы и веса пловца. 9{2} [/латекс].
Суммарная вертикальная сила, действующая на пловца, равна сумме выталкивающей силы и веса пловца. 9{2} [/латекс]. - Давление от веса жидкости постоянной плотности определяется как [латекс] p=\rho \,gh [/латекс], где p — давление, h — глубина жидкости, [латекс ]\rho[/latex] — это плотность жидкости, а g — это ускорение свободного падения.
- плотность
- масса на единицу объема вещества или предмета
- жидкости
- жидкости и газы; жидкость — это состояние вещества, которое поддается сдвиговым силам 90 825
- давление
- сила на единицу площади, приложенная перпендикулярно площади, на которую действует сила 908:25
- удельный вес
- отношение плотности объекта к жидкости (обычно воде)
- Называть различные фазы материи
- Описать характеристики фаз вещества на молекулярном или атомарном уровне
- Различать сжимаемые и несжимаемые материалы
- Определение плотности и связанных с ней единиц СИ
- Сравните и сопоставьте плотности различных веществ
- Определение давления и связанных с ним единиц СИ
- Объясните взаимосвязь между давлением и силой
- Расчет силы по давлению и площади
- Среднее давление из-за веса жидкости составляет
[латекс]р=ч\ро г.[/латекс]
Ввод плотности воды из рисунка и получение 9{13}\text{N}[/latex] вес воды в резервуаре. На самом деле это всего лишь 0,0800% веса.
Проверьте свое понимание
Если бы водохранилище на рисунке занимало вдвое большую площадь, но сохраняло бы ту же глубину, нужно ли было бы перепроектировать плотину?
Показать решениеДавление, найденное в части (а) примера, полностью не зависит от ширины и длины озера; он зависит только от его средней глубины у плотины.
 Таким образом, сила зависит только от средней глубины воды и размеров плотины, а не от горизонтальной протяженности водохранилища. На диаграмме обратите внимание, что толщина плотины увеличивается с глубиной, чтобы уравновесить возрастающую силу из-за увеличивающегося давления.
Таким образом, сила зависит только от средней глубины воды и размеров плотины, а не от горизонтальной протяженности водохранилища. На диаграмме обратите внимание, что толщина плотины увеличивается с глубиной, чтобы уравновесить возрастающую силу из-за увеличивающегося давления.Давление в статической жидкости в однородном гравитационном поле
А статическая жидкость — это жидкость, которая не находится в движении. В любой точке статической жидкости давление со всех сторон должно быть одинаковым, иначе жидкость в этой точке будет реагировать на результирующую силу и ускоряться.
Давление в любой точке статической жидкости зависит только от глубины в этой точке. Как обсуждалось, давление в жидкости вблизи Земли меняется с глубиной из-за веса жидкости над определенным уровнем. В приведенных выше примерах мы предполагали, что плотность постоянна, а средняя плотность жидкости является хорошим представлением плотности. Это разумное приближение для таких жидкостей, как вода, где требуются большие силы для сжатия жидкости или изменения объема.
 В плавательном бассейне, например, плотность приблизительно постоянна, и вода на дне очень мало сжимается под весом воды наверху. Однако путешествие в атмосферу — это совсем другая ситуация. Плотность воздуха начинает значительно меняться уже на небольшом расстоянии от поверхности Земли.
В плавательном бассейне, например, плотность приблизительно постоянна, и вода на дне очень мало сжимается под весом воды наверху. Однако путешествие в атмосферу — это совсем другая ситуация. Плотность воздуха начинает значительно меняться уже на небольшом расстоянии от поверхности Земли.Чтобы вывести формулу для изменения давления с глубиной в резервуаре, содержащем жидкость с плотностью ρ на поверхности Земли, мы должны начать с предположения, что плотность жидкости непостоянна. Жидкость, расположенная на более глубоких уровнях, подвергается большей силе, чем жидкость, расположенная ближе к поверхности, из-за веса жидкости над ней. Следовательно, давление, рассчитанное на заданной глубине, отличается от давления, рассчитанного с использованием постоянной плотности.
Представьте себе тонкий элемент жидкости на глубине h , как показано на рис. Пусть элемент имеет площадь поперечного сечения A и высоту [латекс]\Delta y[/латекс]. Силы, действующие на элемент, обусловлены давлением p ( y ) над ним и [латекс]р(у+\Дельта у)[/латекс] под ним.
Рисунок 14.8 Силы, действующие на элемент массы внутри жидкости. Вес самого элемента показан на диаграмме свободного тела. Вес самого элемента также показан на диаграмме свободного тела.
Вес самого элемента также показан на диаграмме свободного тела.Так как элемент жидкости между и и [латекс]у+\Дельта у[/латекс] не ускоряется, силы уравновешены. Используя декартову ось y , ориентированную вверх, мы находим следующее уравнение для y -компоненты: \gt 0).[/latex]
Обратите внимание, что если элемент имеет ненулевую y -компоненту ускорения, правая часть не будет равна нулю, а вместо этого будет массой, умноженной на y — ускорение. Массу элемента можно записать через плотность жидкости и объем элементов:
[латекс]\Delta m=|\rho A\Delta y|=\text{−}\rho A\Delta y\text{ }(\Delta y \gt 0).[/latex]
Помещение этого выражение для [латекс]\Delta m[/latex] на рисунке, а затем разделив обе части на [latex]A\Delta y[/latex], находим
[latex]\frac{p(y+\Delta y)- p(y)}{\Delta y}=\text{−}\rho g.
 [/latex]
[/latex]Беря предел бесконечно малому элементу [latex]\Delta y\ за 0[/latex], мы получаем следующее дифференциальное уравнение, которое дает изменение давления в жидкости:
[латекс]\frac{dp}{dy}=\text{−}\rho g.[/latex]
Это уравнение говорит нам, что скорость изменения давления в жидкости пропорциональна плотности жидкость. Решение этого уравнения зависит от того, постоянна плотность ρ или изменяется с глубиной; то есть функция ρ ( y ).
Если диапазон анализируемых глубин не слишком велик, плотность можно считать постоянной. Но если диапазон глубин достаточно велик для заметного изменения плотности, как, например, в случае с атмосферой, плотность существенно меняется с глубиной. В этом случае мы не можем использовать приближение постоянной плотности.
Давление в жидкости с постоянной плотностью
Давайте воспользуемся рисунком, чтобы вывести формулу давления на глубине ч от поверхности в резервуаре с жидкостью, такой как вода, где плотность жидкости может быть принято постоянным.
 {\text{−}h}\rho gdy\hfill \\ \hfill p-{p}_{0}& =\hfill & \rho gh\hfill \\ \hfill p& =\hfill & {p}_{0}+\rho gh.\hfill \end{массив}[/latex]
{\text{−}h}\rho gdy\hfill \\ \hfill p-{p}_{0}& =\hfill & \rho gh\hfill \\ \hfill p& =\hfill & {p}_{0}+\rho gh.\hfill \end{массив}[/latex]Следовательно, давление на глубине жидкости на поверхности Земли равно атмосферному давлению плюс ρgh , если плотность жидкости постоянна по высоте, как мы нашли ранее.
Обратите внимание, что давление в жидкости зависит только от глубины от поверхности, а не от формы сосуда. Таким образом, в сосуде, где жидкость может свободно перемещаться в различных частях, жидкость остается на одном уровне в каждой части, независимо от формы, как показано на рисунке.
Рисунок 14.9 Если жидкость может свободно течь между частями сосуда, она поднимается на одинаковую высоту в каждой части. В изображенном контейнере давление на дне каждой колонны одинаково; если бы это было не то же самое, жидкость текла бы до тех пор, пока давления не сравнялись бы.Изменение атмосферного давления с высотой
Изменение атмосферного давления с высотой представляет особый интерес.
 {-23}\text{J/K}[/ латекс].
{-23}\text{J/K}[/ латекс].Возможно, вы встречали закон идеального газа в форме [латекс]pV=nRT[/латекс], где n — количество молей, а R — газовая постоянная. Здесь тот же закон записан в другой форме, с использованием плотности [латекс]\ро[/латекс] вместо объема V . Следовательно, если давление p изменяется с высотой, то и плотность [латекс]\ро .[/латекс] Используя плотность из закона идеального газа, скорость изменения давления с высотой определяется как
[латекс]\frac{dp}{dy}=\text{−}p(\frac{mg}{{k}_{\text{B}}T}),[/latex]
, где константа количества собраны в скобках. Заменив эти константы одним символом [latex]\alpha ,[/latex], уравнение выглядит намного проще:
[latex]\begin{array}{ccc}\hfill \frac{dp}{dy}& =\hfill & \text{-}\alpha p\hfill \\ \hfill \frac{dp}{p}& =\hfill & \text{-}\alpha dy\hfill \\ \hfill \underset{{p}_{ 0}}{\overset{p(y)}{\int }}\frac{dp}{p}& =\hfill & \underset{0}{\overset{y}{\int }}\text{− }\alpha dy\hfill \\ \hfill {[\text{ln}(p)]}_{{p}_{0}}^{p(y)}& =\hfill & {[\text{− }\alpha y]}_{0}^{y}\hfill \\ \hfill \text{ln}(p)-\text{ln}({p}_{0})& =\hfill & \text {−}\alpha y\hfill \\ \hfill \text{ln}(\frac{p}{{p}_{0}})& =\hfill & \text{−}\alpha y\hfill \end {массив}[/латекс]
Это дает решение
[латекс]p(y)={p}_{0}\text{exp}(\text{−}\alpha y).
 [/latex]
[/latex]Таким образом, атмосферное давление падает экспоненциально с высотой, поскольку ось y направлена вверх от земли, а y имеет положительные значения в атмосфере над уровнем моря. Давление падает в [латекс]\фрак{1}{е}[/латекс], когда высота равна [латекс]\фрак{1}{\альфа},[/латекс], что дает нам физическую интерпретацию для [латекс]\альфа[/латекс]: Константа [латекс]\фрак{1}{\альфа }[/латекс] — это шкала длины, которая характеризует изменение давления в зависимости от высоты и часто называется высотой шкалы давления. 9{-23}\,\text{J/K}\times \text{300 K}}=\frac{1}{8800\,\text{m}}.[/latex]
Следовательно, на каждые 8800 м давление воздуха падает в 1/ e раз, или примерно на треть своего значения. Это дает нам лишь грубую оценку реальной ситуации, поскольку мы предполагали и постоянную температуру, и постоянную g на столь больших расстояниях от Земли, и ни одно из этих утверждений в действительности не верно.
Направление давления в жидкости
Давление жидкости не имеет направления, поскольку является скалярной величиной, тогда как силы давления имеют четко определенные направления: они всегда действуют перпендикулярно любой поверхности.
Рисунок 14.10 (a) Давление внутри этой шины действует перпендикулярно ко всем поверхностям, с которыми она контактирует. Стрелки представляют направления и величины сил, действующих в различных точках. (b) Давление оказывается перпендикулярно всем сторонам этого пловца, так как вода потекла бы в пространство, которое он занимает, если бы его там не было. Стрелки представляют направления и величины сил, действующих на пловца в различных точках. Обратите внимание, что силы внизу больше из-за большей глубины, что дает сеть вверх или выталкивающую силу. Причина в том, что жидкости не могут противостоять силам сдвига или оказывать на них силы сдвига. Таким образом, в статической жидкости, заключенной в резервуар, сила, действующая на стенки резервуара, действует перпендикулярно внутренней поверхности. Точно так же давление оказывается перпендикулярно поверхностям любого объекта в жидкости. На рисунке показано давление воздуха на стенки покрышки и воды на тело пловца.
Причина в том, что жидкости не могут противостоять силам сдвига или оказывать на них силы сдвига. Таким образом, в статической жидкости, заключенной в резервуар, сила, действующая на стенки резервуара, действует перпендикулярно внутренней поверхности. Точно так же давление оказывается перпендикулярно поверхностям любого объекта в жидкости. На рисунке показано давление воздуха на стенки покрышки и воды на тело пловца. Суммарная вертикальная сила, действующая на пловца, равна сумме выталкивающей силы и веса пловца.
9{2}[/латекс].
Суммарная вертикальная сила, действующая на пловца, равна сумме выталкивающей силы и веса пловца.
9{2}[/латекс]. - Давление от веса жидкости постоянной плотности определяется как [латекс]p=\rho \,gh[/латекс], где p — давление, h — глубина жидкости, [латекс ]\rho[/latex] — плотность жидкости, а g — ускорение свободного падения.
- плотность
- масса на единицу объема вещества или предмета
- жидкости
- жидкости и газы; жидкость — это состояние вещества, которое поддается сдвиговым силам 90 825
- давление
- сила на единицу площади, приложенная перпендикулярно площади, на которую действует сила 908:25
- удельный вес
- отношение плотности объекта к жидкости (обычно воде)
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 1571
- OpenStax
- OpenStax
- Рассчитать скорость потока.
- Определить единицы объема.
- Опишите несжимаемые жидкости.
- Объясните следствия уравнения неразрывности.
Концептуальные вопросы
Какие из следующих веществ являются жидкостями при комнатной температуре и атмосферном давлении: воздух, ртуть, вода, стекло?
Показать решение
Почему газы легче сжимать, чем жидкости и твердые тела?
Объясните, как плотность воздуха зависит от высоты.
Показать решение
На изображении показан стакан ледяной воды, наполненный до краев. Будет ли вода переливаться через край, когда лед растает? Поясните свой ответ.
Как давление связано с остротой ножа и его режущей способностью?
Показать решение
Почему сила, приложенная неподвижной жидкостью к поверхности, всегда перпендикулярна поверхности?
Представьте себе, что в отдаленном месте недалеко от Северного полюса в озере плавает кусок льда. Рядом с озером на суше сидит ледник такого же объема, как и плавучий лед. Если оба куска льда должны растаять из-за повышения глобальной температуры, и весь растаявший лед попадет в озеро, какой из них вызовет наибольшее повышение уровня озера? Объяснять.
Рядом с озером на суше сидит ледник такого же объема, как и плавучий лед. Если оба куска льда должны растаять из-за повышения глобальной температуры, и весь растаявший лед попадет в озеро, какой из них вызовет наибольшее повышение уровня озера? Объяснять.
Показать решение
В балете танец на пуантах (на кончиках пальцев ног) намного тяжелее для пальцев ног, чем обычный танец или ходьба. Объясните почему, с точки зрения давления.
Атмосферное давление оказывает большую силу (равную весу атмосферы над вашим телом — около 10 тонн) на верхнюю часть тела, когда вы лежите на пляже и принимаете солнечные ванны. Почему ты можешь встать?
Показать решение
Почему атмосферное давление уменьшается с высотой быстрее, чем линейно?
На изображении показано, как мешки с песком, размещенные вокруг протечки за пределами речной дамбы, могут эффективно остановить поток воды под дамбой. Объясните, как небольшое количество воды внутри столба мешков с песком может уравновесить гораздо больший объем воды за дамбой.
Объясните, как небольшое количество воды внутри столба мешков с песком может уравновесить гораздо больший объем воды за дамбой.
Показать решение
Действует ли на плотину результирующая сила атмосферного давления? Поясните свой ответ.
Влияет ли атмосферное давление на давление газа в жестком резервуаре? На игрушечном воздушном шаре? Когда вообще атмосферное давление не влияет на полное давление в жидкости?
Показать решение
Крепкую винную бутылку можно разбить, забив пробку кулаком, но пробка должна прижиматься непосредственно к жидкости, наполняющей бутылку — между пробкой и жидкостью не может быть воздуха. Объясните, почему бутылка разбивается только в том случае, если между пробкой и жидкостью нет воздуха.
Проблемы
Золото продается тройскими унциями (31,103 г). Каков объем 1 тройской унции чистого золота?
Показать решение
Ртуть обычно поставляется в колбах по 34,5 кг (около 76 фунтов). Каков объем в литрах такого количества ртути?
Каков объем в литрах такого количества ртути?
Какова масса глубоко вдохнутого воздуха объемом 2,00 л? Обсудите влияние такого дыхания на объем и плотность вашего тела.
Показать решение
Простой метод определения плотности объекта состоит в измерении его массы и затем измерении его объема путем погружения его в мерный цилиндр. Какова плотность камня массой 240 г, который вытесняет [латекс] 89?{3} [/latex] воды? (Обратите внимание, что точность и практическое применение этого метода более ограничены, чем множество других, основанных на законе Архимеда.)
Предположим, у вас есть кофейная кружка с круглым поперечным сечением и вертикальными сторонами (равномерный радиус). Каков его внутренний радиус, если он вмещает 375 г кофе при глубине заполнения 7,50 см? Предположим, что плотность кофе равна плотности воды.
Показать решение
Прямоугольный бензобак вмещает 50,0 кг бензина при полном наполнении. Какова глубина резервуара, если его ширина 0,500 м на 0,900 м? (b) Обсудите, имеет ли этот бензобак достаточный объем для легкового автомобиля.
Какова глубина резервуара, если его ширина 0,500 м на 0,900 м? (b) Обсудите, имеет ли этот бензобак достаточный объем для легкового автомобиля.
Компактор для мусора может сжимать его содержимое в 0,350 раз больше его первоначального объема. Если пренебречь массой вытесненного воздуха, во сколько раз увеличится плотность мусора?
Показать решение
Полная стальная канистра для бензина массой 2,50 кг вмещает 20,0 л бензина. Какова средняя плотность полного газового баллона с учетом объема, занимаемого как сталью, так и бензином?
Какова плотность 18-каратного золота, состоящего из 18 частей золота, 5 частей серебра и 1 части меди? (Эти значения являются массовыми, а не объемными частями.) Предположим, что это простая смесь, имеющая среднюю плотность, равную взвешенным плотностям ее компонентов.
Показать решение
Кончик гвоздя оказывает огромное давление при ударе молотком, потому что он оказывает большую силу на небольшую площадь. {9{2}\text{?} [/latex] (Такое высокое давление возможно, потому что молоток, ударяющий по гвоздю, останавливается на таком коротком расстоянии.)
{9{2}\text{?} [/latex] (Такое высокое давление возможно, потому что молоток, ударяющий по гвоздю, останавливается на таком коротком расстоянии.)
Стеклянная трубка содержит ртуть. Какой должна быть высота столбика ртути, создающего давление, равное 1,00 атм?
Показать решение
Самые большие глубины океана на Земле находятся в Марианской впадине недалеко от Филиппин. Рассчитайте давление океана на дно этой впадины, учитывая ее глубину 11,0 км и плотность морской воды на всем протяжении. 9{3}. [/latex] (a) Определите чистую силу, действующую на плотину. б) Почему толщина плотины увеличивается с глубиной?
Показать решение
Глоссарий
14.
 1 Жидкости, плотность и давление – University Physics Volume 1
1 Жидкости, плотность и давление – University Physics Volume 114 Гидромеханика
Цели обучения
К концу этого раздела вы сможете:
Материя чаще всего существует в твердом, жидком или газообразном состоянии; эти состояния известны как три общие фазы материи. В этом разделе мы подробно рассмотрим каждый из этих этапов.
Характеристики твердых тел
Твердые тела твердые, имеют определенную форму и определенный объем. Атомы или молекулы в твердом теле находятся в непосредственной близости друг от друга, и между этими молекулами существует значительная сила. Твердые тела примут форму, определяемую характером этих сил между молекулами. Хотя настоящие твердые тела не являются несжимаемыми, тем не менее для изменения формы твердого тела требуется большая сила. В некоторых случаях сила между молекулами может заставить молекулы организоваться в решетку, как показано на рисунке. Структура этой трехмерной решетки представлена в виде молекул, соединенных жесткими связями (смоделированными как жесткие пружины), что дает ограниченную свободу движения. Даже большая сила вызывает лишь небольшие смещения атомов или молекул решетки, и твердое тело сохраняет свою форму. Твердые тела также сопротивляются силам сдвига. (Сдвиговые силы — это силы, действующие по касательной к поверхности, как описано в статье «Статическое равновесие и упругость».)
Твердые тела примут форму, определяемую характером этих сил между молекулами. Хотя настоящие твердые тела не являются несжимаемыми, тем не менее для изменения формы твердого тела требуется большая сила. В некоторых случаях сила между молекулами может заставить молекулы организоваться в решетку, как показано на рисунке. Структура этой трехмерной решетки представлена в виде молекул, соединенных жесткими связями (смоделированными как жесткие пружины), что дает ограниченную свободу движения. Даже большая сила вызывает лишь небольшие смещения атомов или молекул решетки, и твердое тело сохраняет свою форму. Твердые тела также сопротивляются силам сдвига. (Сдвиговые силы — это силы, действующие по касательной к поверхности, как описано в статье «Статическое равновесие и упругость».)
Характеристики жидкостей
Жидкости и газы считаются жидкостями , потому что они поддаются силам сдвига, тогда как твердые тела сопротивляются им. Подобно твердым телам, молекулы жидкости связаны с соседними молекулами, но таких связей гораздо меньше. Молекулы в жидкости не зафиксированы на месте и могут двигаться относительно друг друга. Расстояние между молекулами аналогично расстоянию в твердом теле, поэтому жидкости имеют определенные объемы, но форма жидкости меняется в зависимости от формы ее сосуда. Газы не связаны с соседними атомами и могут иметь большие расстояния между молекулами. Газы не имеют ни определенной формы, ни определенных объемов, поскольку их молекулы движутся, чтобы заполнить сосуд, в котором они находятся (рис.).
Молекулы в жидкости не зафиксированы на месте и могут двигаться относительно друг друга. Расстояние между молекулами аналогично расстоянию в твердом теле, поэтому жидкости имеют определенные объемы, но форма жидкости меняется в зависимости от формы ее сосуда. Газы не связаны с соседними атомами и могут иметь большие расстояния между молекулами. Газы не имеют ни определенной формы, ни определенных объемов, поскольку их молекулы движутся, чтобы заполнить сосуд, в котором они находятся (рис.).

Жидкости легко деформируются при воздействии нагрузки и не возвращаются к своей первоначальной форме после прекращения действия силы. Это происходит потому, что атомы или молекулы в жидкости могут свободно скользить и менять соседей. То есть жидкости текут (поэтому они являются типом жидкости), а молекулы удерживаются вместе за счет взаимного притяжения. Когда жидкость помещается в контейнер без крышки, она остается в контейнере. Поскольку атомы плотно упакованы, жидкости, как и твердые тела, сопротивляются сжатию; для изменения объема жидкости необходима чрезвычайно большая сила.
Напротив, атомы в газах разделены большими расстояниями, и поэтому силы между атомами в газе очень слабы, за исключением случаев, когда атомы сталкиваются друг с другом. Это делает газы относительно легко сжимаемыми и позволяет им течь (что делает их жидкостями). При помещении в открытый контейнер газы, в отличие от жидкостей, будут выходить наружу.
В этой главе мы обычно называем газы и жидкости просто жидкостями, проводя различие между ними только тогда, когда они ведут себя по-разному. Существует еще одна фаза вещества — плазма, существующая при очень высоких температурах. При высоких температурах молекулы могут диссоциировать на атомы, а атомы диссоциировать на электроны (с отрицательными зарядами) и протоны (с положительными зарядами), образуя плазму. Плазма не будет подробно обсуждаться в этой главе, потому что плазма имеет очень отличные свойства от трех других распространенных фаз материи, обсуждаемых в этой главе, из-за сильных электрических сил между зарядами.
Существует еще одна фаза вещества — плазма, существующая при очень высоких температурах. При высоких температурах молекулы могут диссоциировать на атомы, а атомы диссоциировать на электроны (с отрицательными зарядами) и протоны (с положительными зарядами), образуя плазму. Плазма не будет подробно обсуждаться в этой главе, потому что плазма имеет очень отличные свойства от трех других распространенных фаз материи, обсуждаемых в этой главе, из-за сильных электрических сил между зарядами.
Плотность
Предположим, что брусок из латуни и брусок дерева имеют одинаковую массу. Если оба бруска бросить в резервуар с водой, почему дерево всплывет, а латунь утонет (рисунок)? Это происходит потому, что латунь имеет большую плотность, чем вода, а древесина имеет меньшую плотность, чем вода.
Рисунок 14.3 (a) Блок из латуни и блок из дерева имеют одинаковый вес и массу, но блок из дерева имеет гораздо больший объем. (b) При помещении в аквариум, наполненный водой, латунный куб тонет, а деревянный брусок всплывает. \circ\text{C}[/латекс], а плотности твердых и жидких веществ зависят от температуры. Плотность твердых и жидких тел обычно увеличивается с понижением температуры. 9{3}[/латекс]
\circ\text{C}[/латекс], а плотности твердых и жидких веществ зависят от температуры. Плотность твердых и жидких тел обычно увеличивается с понижением температуры. 9{3}[/латекс] Плотность вещества не обязательно постоянна по всему объему вещества. Если плотность вещества постоянна во всем веществе, говорят, что это однородное вещество . Твердый железный брусок является примером однородного вещества. Плотность постоянна на всем протяжении, а плотность любого образца вещества равна его средней плотности. Если бы плотность вещества не была постоянной, то говорят, что вещество находится в состоянии гетерогенное вещество . Кусок швейцарского сыра является примером гетерогенного материала, содержащего как твердый сыр, так и пустоты, заполненные газом. Плотность в определенном месте в неоднородном материале называется локальной плотностью и определяется как функция местоположения [латекс]\rho =\rho (x,y,z)[/латекс] (рисунок).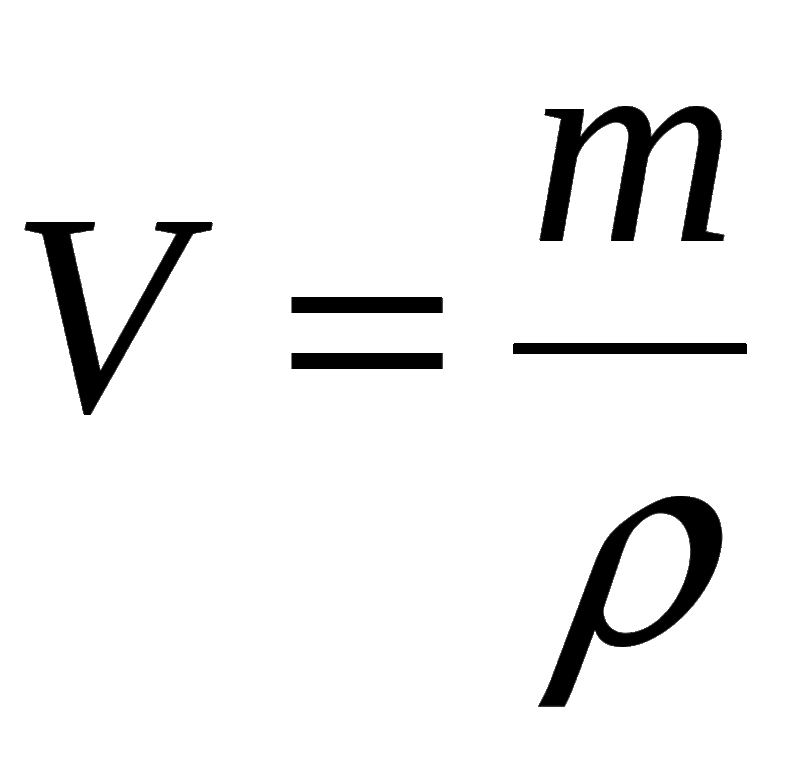
Локальная плотность может быть получена с помощью процесса ограничения, основанного на средней плотности в небольшом объеме вокруг рассматриваемой точки, принимая предел, когда размер объема приближается к нулю,
[латекс]\rho =\underset{\ Delta V\to 0}{\text{lim}}\frac{\Delta m}{\Delta V}[/latex]
, где [latex]\rho[/latex] — плотность, м — масса, а V – объем.
Поскольку газы могут свободно расширяться и сжиматься, плотность газов значительно зависит от температуры, тогда как плотность жидкостей зависит от температуры незначительно. Поэтому плотности жидкостей часто считают постоянными, при этом плотность равна средней плотности. 9{3}[/latex]), но его удельный вес составляет 2,7, независимо от единицы плотности. Удельный вес — особенно полезная величина в отношении плавучести, которую мы обсудим позже в этой главе.
Давление
Вы, несомненно, слышали слово «давление», используемое по отношению к крови (высокое или низкое кровяное давление) и по отношению к погоде (погодные системы высокого и низкого давления). Это только два из многих примеров давления в жидкостях. (Вспомните, что мы ввели понятие давления в книге «Статическое равновесие и упругость» в контексте объемного напряжения и деформации.)
Давление
Давление ( p ) определяется как нормальная сила F на единицу площади A , на которую действует сила, или [латекс]p=\frac{F}{A}. [/latex]
Чтобы определить давление в конкретной точке, давление определяется как сила dF , действующая на бесконечно малый элемент площадью dA , содержащий точку, в результате чего [латекс]p=\ frac{dF}{dA}[/latex].
Действие данной силы может существенно различаться в зависимости от площади, на которую она воздействует. Например, сила, приложенная к площади [латекс]1\,{\text{мм}}^{2}[/латекс], оказывает давление в 100 раз больше, чем та же сила, приложенная к площади [латекс]. {2}.[/latex] Вот почему острая игла способна проткнуть кожу при приложении небольшого усилия, а приложение такого же усилия пальцем — нет. проколоть кожу (рис.).
{2}.[/latex] Вот почему острая игла способна проткнуть кожу при приложении небольшого усилия, а приложение такого же усилия пальцем — нет. проколоть кожу (рис.).
Обратите внимание, что хотя сила является вектором, давление является скаляром. Давление является скалярной величиной, поскольку по определению оно пропорционально величине силы, действующей перпендикулярно площади поверхности. Единицей давления в СИ является паскалей 9.{2}.[/latex]
Несколько других единиц используются для давления, которые мы обсудим позже в этой главе.
Изменение давления с глубиной в жидкости с постоянной плотностью
Давление определяется для всех состояний вещества, но оно особенно важно при обсуждении жидкостей. Важной характеристикой жидкостей является отсутствие значительного сопротивления компоненту силы, приложенной параллельно поверхности жидкости. Молекулы жидкости просто текут, приспосабливаясь к горизонтальной силе. Сила, приложенная перпендикулярно поверхности, сжимает или расширяет жидкость. Если вы попытаетесь сжать жидкость, вы обнаружите, что в каждой точке внутри жидкости в направлении наружу возникает сила реакции, уравновешивающая силу, действующую на молекулы на границе.
Молекулы жидкости просто текут, приспосабливаясь к горизонтальной силе. Сила, приложенная перпендикулярно поверхности, сжимает или расширяет жидкость. Если вы попытаетесь сжать жидкость, вы обнаружите, что в каждой точке внутри жидкости в направлении наружу возникает сила реакции, уравновешивающая силу, действующую на молекулы на границе.
Рассмотрим жидкость постоянной плотности, как показано на рисунке. Давление на дне контейнера обусловлено давлением атмосферы [латекс]({p}_{0})[/латекс] плюс давление, обусловленное весом жидкости. Давление жидкости равно весу жидкости, деленному на площадь. Вес жидкости равен произведению ее массы на ускорение свободного падения.
Рисунок 14.6 Дно этого контейнера выдерживает весь вес жидкости в нем. Вертикальные стороны не могут воздействовать на жидкость восходящей силой (поскольку она не может противостоять сдвигающей силе), поэтому дно должно поддерживать все это.Поскольку плотность постоянна, вес можно рассчитать, используя плотность:
[латекс]w=mg=\rho Vg=\rho Ahg. [/latex]
[/latex]
Таким образом, давление на дне сосуда равно к атмосферному давлению, добавленному к весу жидкости, деленному на площадь:
[латекс]p={p}_{0}+\frac{\rho Ahg}{A}={p}_{0}+\ rho hg.[/latex]
Это уравнение годится только для давления на глубине для жидкости с постоянной плотностью.
Давление на глубине для жидкости постоянной плотности
Давление на глубине в жидкости постоянной плотности равно атмосферному давлению плюс давление, обусловленное весом жидкости, или
[латекс]p={p}_{0}+\rho hg,[/latex]
Где p — давление на определенной глубине, [latex]{p}_{0}[/latex] — атмосферное давление, [latex]\rho[/latex] — плотность жидкости, г — ускорение свободного падения, ч — глубина.
Рисунок 14.7 Плотина «Три ущелья», воздвигнутая на реке Янцзы в центральном Китае в 2008 году, создала массивное водохранилище, в котором было перемещено более миллиона человек. (кредит: «Le Grand Portage»/Flickr)Пример
Какую силу должна выдерживать плотина?
Рассмотрим давление и силу, действующую на плотину, удерживающую резервуар с водой (рис. ). Предположим, что ширина плотины составляет 500 м, а глубина воды у плотины составляет 80,0 м, как показано ниже. а) Каково среднее давление воды на плотину? б) Рассчитайте силу, действующую на плотину.
). Предположим, что ширина плотины составляет 500 м, а глубина воды у плотины составляет 80,0 м, как показано ниже. а) Каково среднее давление воды на плотину? б) Рассчитайте силу, действующую на плотину.
Среднее давление p из-за веса воды является давлением на средней глубине h 40,0 м, так как давление увеличивается линейно с глубиной. Сила, действующая на плотину со стороны воды, равна среднему давлению, умноженному на площадь контакта, [латекс]F=pA.[/латекс]
раствор
Концептуальные вопросы
Какие из следующих веществ являются жидкостями при комнатной температуре и атмосферном давлении: воздух, ртуть, вода, стекло?
Показать решение Ртуть и вода жидкие при комнатной температуре и атмосферном давлении. Воздух – это газ при комнатной температуре и атмосферном давлении. Стекло представляет собой аморфный твердый (некристаллический) материал при комнатной температуре и атмосферном давлении. Одно время считалось, что стекло течет, но течет очень медленно. Эта теория возникла из наблюдения, что старые стеклянные плоскости были толще внизу. В настоящее время считается маловероятным, что эта теория точна.
Почему газы легче сжимать, чем жидкости и твердые тела?
Объясните, как плотность воздуха зависит от высоты.
Показать решениеПлотность воздуха уменьшается с высотой. Для столба воздуха постоянной температуры плотность экспоненциально убывает с высотой. Это справедливое приближение, но поскольку температура меняется с высотой, это всего лишь приближение.
На изображении изображен стакан с ледяной водой, наполненный до краев. Будет ли вода переливаться через край, когда лед растает? Поясните свой ответ.
Как давление связано с остротой ножа и его режущей способностью?
Показать решениеДавление равно силе, деленной на площадь. Если нож острый, сила, приложенная к режущей поверхности, делится на меньшую площадь, чем такая же сила, прикладываемая тупым ножом. Это означает, что давление на более острый нож будет больше, что повысит его режущую способность.
Почему сила, приложенная неподвижной жидкостью к поверхности, всегда перпендикулярна поверхности?
Представьте себе, что в отдаленном месте недалеко от Северного полюса в озере плавает кусок льда.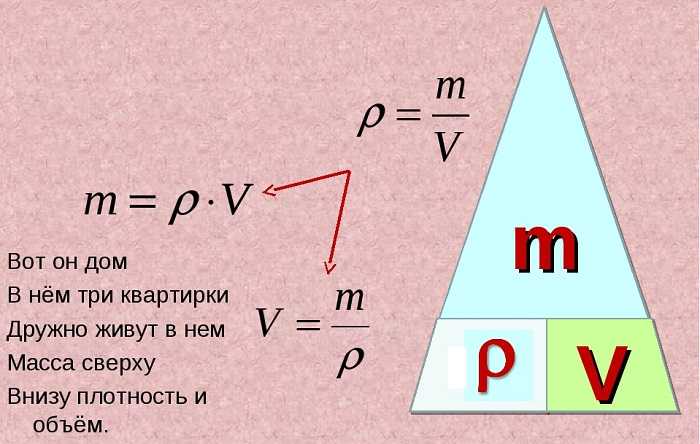 Рядом с озером на суше сидит ледник такого же объема, как и плавучий лед. Если оба куска льда должны растаять из-за повышения глобальной температуры, и весь растаявший лед попадет в озеро, какой из них вызовет наибольшее повышение уровня озера? Объяснять.
Рядом с озером на суше сидит ледник такого же объема, как и плавучий лед. Если оба куска льда должны растаять из-за повышения глобальной температуры, и весь растаявший лед попадет в озеро, какой из них вызовет наибольшее повышение уровня озера? Объяснять.
Если бы два куска льда имели одинаковый объем, они произвели бы одинаковый объем воды. Однако ледник вызвал бы наибольший подъем уровня озера, потому что часть плавающего куска льда уже погружена в озеро и, таким образом, уже влияет на его уровень.
В балете танец на пуантах (на кончиках пальцев ног) намного тяжелее для пальцев ног, чем обычный танец или ходьба. Объясните почему, с точки зрения давления.
Атмосферное давление оказывает большую силу (равную весу атмосферы над вашим телом — около 10 тонн) на верхнюю часть тела, когда вы лежите на пляже и принимаете солнечные ванны. Почему ты можешь встать?
Показать решение Давление воздействует на все ваше тело, если вы не находитесь в вакууме.
Почему атмосферное давление уменьшается с высотой быстрее, чем линейно?
На изображении показано, как мешки с песком, размещенные вокруг протечки за пределами речной дамбы, могут эффективно остановить поток воды под дамбой. Объясните, как небольшое количество воды внутри столба мешков с песком может уравновесить гораздо больший объем воды за дамбой.
Показать решениеИз-за того, что уровень реки очень высок, она начала просачиваться под дамбу. Мешки с песком помещаются вокруг места утечки, и удерживаемая ими вода поднимается до тех пор, пока не достигнет уровня реки, после чего вода в этом месте перестает подниматься. Мешки с песком будут поглощать воду до тех пор, пока уровень воды не достигнет уровня воды в дамбе.
Есть ли результирующая сила на плотине из-за атмосферного давления? Поясните свой ответ.
Влияет ли атмосферное давление на давление газа в жестком резервуаре? На игрушечном воздушном шаре? Когда вообще атмосферное давление не влияет на полное давление в жидкости?
Показать решение Атмосферное давление не влияет на давление газа в жестком резервуаре, но влияет на давление внутри воздушного шара.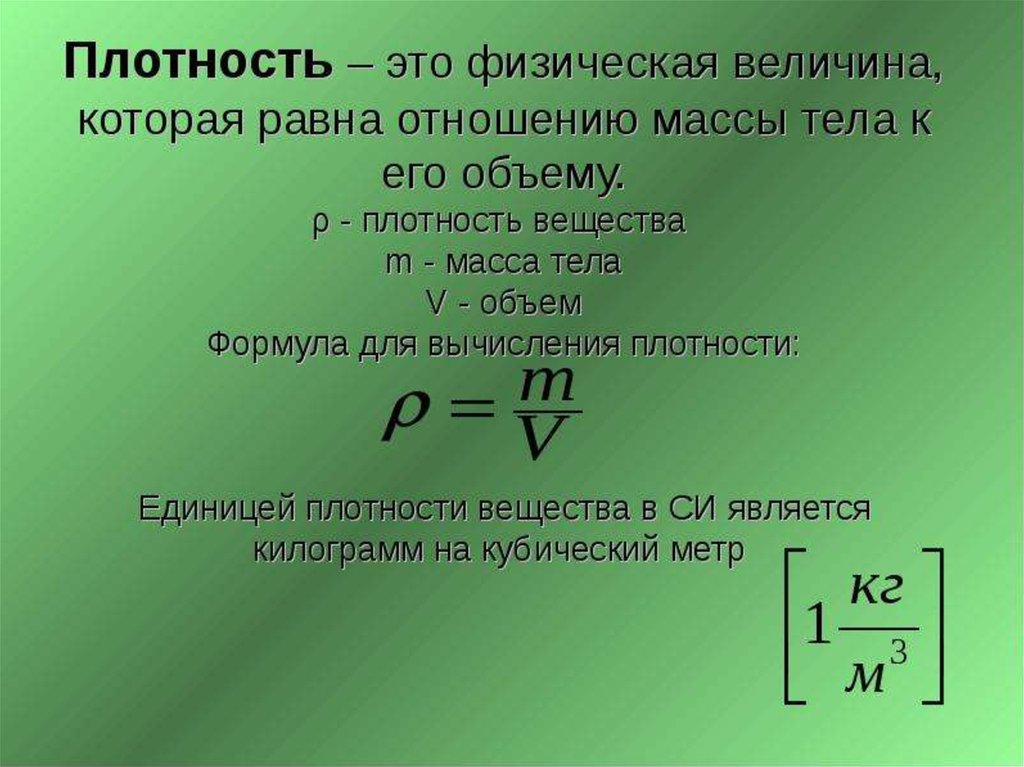 Обычно атмосферное давление влияет на давление жидкости, если только жидкость не заключена в жесткий контейнер.
Обычно атмосферное давление влияет на давление жидкости, если только жидкость не заключена в жесткий контейнер.
Крепкую винную бутылку можно разбить, забив пробку кулаком, но пробка должна прижиматься непосредственно к жидкости, наполняющей бутылку — между пробкой и жидкостью не может быть воздуха. Объясните, почему бутылка разбивается только в том случае, если между пробкой и жидкостью нет воздуха. 9{3}[/латекс]
Ртуть обычно поставляется в колбах по 34,5 кг (около 76 фунтов). Каков объем в литрах такого количества ртути?
Какова масса глубоко вдохнутого воздуха объемом 2,00 л? Обсудите влияние такого дыхания на объем и плотность вашего тела.
Show Solution Масса 2,58 г. Объем вашего тела увеличивается на объем вдыхаемого воздуха. Средняя плотность вашего тела уменьшается, когда вы делаете глубокий вдох, потому что плотность воздуха значительно меньше, чем средняя плотность тела. 9{3}[/latex] воды? (Обратите внимание, что точность и практическое применение этого метода более ограничены, чем множество других, основанных на законе Архимеда. )
)
Предположим, у вас есть кофейная кружка с круглым поперечным сечением и вертикальными сторонами (равномерный радиус). Каков его внутренний радиус, если он вмещает 375 г кофе при глубине заполнения 7,50 см? Предположим, что плотность кофе равна плотности воды.
Show Solution3,99 см
Полный прямоугольный бензобак вмещает 50,0 кг бензина. Какова глубина резервуара, если его ширина 0,500 м на 0,900 м? (b) Обсудите, имеет ли этот бензобак достаточный объем для легкового автомобиля.
Компактор для мусора может сжимать его содержимое в 0,350 раз больше его первоначального объема. Если пренебречь массой вытесненного воздуха, во сколько раз увеличится плотность мусора?
Show SolutionВ 2,86 раза плотнее
Полная стальная канистра для бензина массой 2,50 кг вмещает 20,0 л бензина. Какова средняя плотность полного газового баллона с учетом объема, занимаемого как сталью, так и бензином? 9{2}\text{?}[/latex] (Это высокое давление возможно потому, что молоток, ударяющий по гвоздю, останавливается на таком коротком расстоянии. )
)
Стеклянная трубка содержит ртуть. Какой должна быть высота столбика ртути, создающего давление, равное 1,00 атм?
Показать раствор[латекс]0,760\,\текст{м}=76,0\,\текст{см}=760\,\текст{мм}[/латекс]
Самые большие глубины океана на Земле находятся в Марианской впадине недалеко от Филиппин. Рассчитайте давление океана на дно этой впадины, учитывая ее глубину 11,0 км и плотность морской воды на всем протяжении. 9{6}\text{N}[/латекс]; б. Давление увеличивается по мере увеличения глубины, поэтому плотина должна быть толще по направлению к дну, чтобы выдерживать большее давление.
Глоссарий
12.
 1: Расход и его связь со скоростью
1: Расход и его связь со скоростьюЦели обучения
К концу этого раздела вы сможете:
Скорость потока \(Q\) определяется как объем жидкости, проходящей через некоторое место через область в течение определенного периода времени, как показано на рисунке \(\PageIndex{1}\). В символах это можно записать как 93 \, см\)). В этом тексте мы будем использовать любые метрические единицы, наиболее удобные для данной ситуации.
В этом тексте мы будем использовать любые метрические единицы, наиболее удобные для данной ситуации.
Пример \(\PageIndex{1}\): расчет объема по скорости кровотока: сердце перекачивает много крови за всю жизнь
Сколько кубометров крови перекачивает сердце за 75 лет жизни, если предположить, что средняя скорость кровотока составляет 5,00 л/мин?
Стратегия
Время и расход \(Q\) заданы, поэтому объем \(V\) можно рассчитать из определения расхода.
Решение
Решение \(Q = V/t\) для объема дает
\[V = Qt. \nonumber \]
Подстановка известных значений дает
\[\begin{align*}V &= \left(\dfrac{5. 3 \end{align*}\]
3 \end{align*}\]
Обсуждение
Это количество составляет около 200 000 тонн крови. Для сравнения, это значение примерно в 200 раз превышает объем воды, содержащейся в 50-метровом плавательном бассейне с 6 дорожками.
Расход и скорость являются связанными, но совершенно разными физическими величинами. Чтобы прояснить различие, подумайте о скорости течения реки. Чем больше скорость воды, тем больше расход реки. Но скорость течения также зависит от размера реки. Быстрый горный поток несет гораздо меньше воды, чем, например, река Амазонка в Бразилии. Точное соотношение между расходом \(Q\) и скоростью \(\overline{v}\) составляет
\[Q = A \overline{v},\]
, где \(A\) — площадь поперечного сечения, а \( \overline{v}\) — средняя скорость. Это уравнение кажется достаточно логичным. Соотношение говорит нам, что скорость потока прямо пропорциональна как величине средней скорости (далее называемой скоростью), так и размеру реки, трубы или другого водовода. Чем больше трубопровод, тем больше его площадь поперечного сечения. На рисунке \(\PageIndex{1}\) показано, как получается это отношение. Заштрихованный цилиндр имеет объем
Чем больше трубопровод, тем больше его площадь поперечного сечения. На рисунке \(\PageIndex{1}\) показано, как получается это отношение. Заштрихованный цилиндр имеет объем
\[V = Ad,\]
, который проходит через точку \(P\) за время \(t\). Разделив обе части этого соотношения на \(t\), мы получим
.\[\dfrac{V}{t} = \dfrac{Ad}{t}.\]
Заметим, что \(Q = V\t\), а средняя скорость равна \(\overline{v} = d/t\). Таким образом, уравнение принимает вид \(Q = A\overline{v}\).
На рисунке \(\PageIndex{2}\) показана несжимаемая жидкость, текущая по трубе с уменьшающимся радиусом. Поскольку жидкость несжимаема, через любую точку трубки за заданное время должно пройти одинаковое количество жидкости, чтобы обеспечить непрерывность потока. В этом случае, поскольку площадь поперечного сечения трубы уменьшается, скорость обязательно должна увеличиваться. Эту логику можно расширить, чтобы сказать, что скорость потока должна быть одинаковой во всех точках трубы. В частности, для пунктов 1 и 2,
В частности, для пунктов 1 и 2,
\[Q_1 = Q_2\]
\[A_1\overline{v}_1 = A_2\overline{v}_2\]
Это называется уравнением неразрывности и справедливо для любой несжимаемой жидкости. Следствия уравнения неразрывности можно наблюдать, когда вода течет из шланга в узкую форсунку: она выходит с большой скоростью — в этом назначение форсунки. И наоборот, когда река впадает в один конец водохранилища, вода значительно замедляется и, возможно, снова набирает скорость, когда выходит из другого конца водохранилища. Другими словами, скорость увеличивается, когда площадь поперечного сечения уменьшается, и скорость уменьшается, когда площадь поперечного сечения увеличивается.
Рисунок \(\PageIndex{2}\): Когда трубка сужается, тот же объем занимает большую длину. Чтобы один и тот же объем прошел точки 1 и 2 за заданное время, скорость должна быть больше в точке 2. Процесс точно обратим. Если жидкость течет в противоположном направлении, ее скорость будет уменьшаться при расширении трубы. (Обратите внимание, что относительные объемы двух цилиндров и соответствующие стрелки вектора скорости нарисованы не в масштабе.)
(Обратите внимание, что относительные объемы двух цилиндров и соответствующие стрелки вектора скорости нарисованы не в масштабе.)Поскольку жидкости практически несжимаемы, уравнение неразрывности справедливо для всех жидкостей. Однако газы сжимаемы, поэтому уравнение следует применять с осторожностью к газам, если они подвергаются сжатию или расширению.
Пример \(\PageIndex{2}\): Расчет скорости жидкости: скорость увеличивается при сужении трубы
Насадка с радиусом 0,250 см прикреплена к садовому шлангу с радиусом 0,900 см. Скорость потока через шланг и сопло составляет 0,500 л/с. Рассчитайте скорость воды (а) в шланге и (б) в насадке.
Стратегия
Мы можем использовать соотношение между расходом и скоростью, чтобы найти обе скорости. Мы будем использовать нижний индекс 1 для шланга и 2 для насадки. 92} 1,96 \, м/с = 25,5 \, м/с. \номер \]
Обсуждение
Скорость 1,96 м/с подходит для воды, вытекающей из шланга без насадки. Форсунка создает значительно более быстрый поток, просто сужая поток в более узкую трубку.
Форсунка создает значительно более быстрый поток, просто сужая поток в более узкую трубку.
Решение последней части примера показывает, что скорость обратно пропорциональна квадрату радиуса трубы, что приводит к большим эффектам при изменении радиуса. Мы можем задуть свечу на довольно большом расстоянии, например, сжав губы, тогда как задувание свечи с широко открытым ртом совершенно неэффективно.
Во многих ситуациях, в том числе в сердечно-сосудистой системе, происходит разветвление потока. Кровь перекачивается из сердца в артерии, которые подразделяются на более мелкие артерии (артериолы), которые разветвляются на очень тонкие сосуды, называемые капиллярами. В этой ситуации сохраняется непрерывность потока, но сохраняется сумма расходов в каждой из ветвей на любом участке вдоль трубы. Уравнение неразрывности в более общем виде принимает вид
\[n_1A_1\overline{v}_1 = n_2A_2\overline{v}_2,\]
, где \(n_1\) и \(n_2\) — количество ответвлений на каждом из участков вдоль трубы.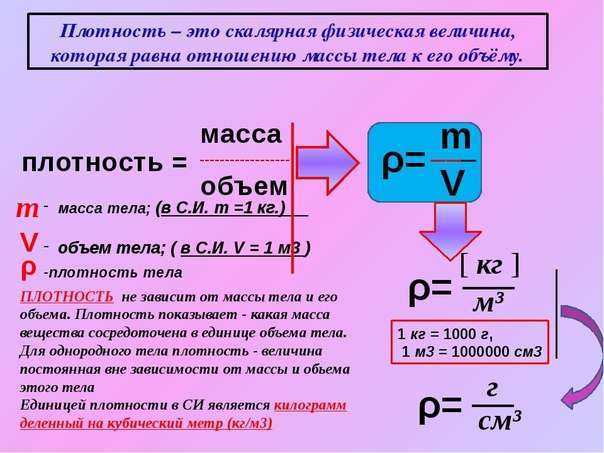
Пример \(\PageIndex{3}\): расчет скорости кровотока и диаметра сосуда: разветвления в сердечно-сосудистой системе
Аорта является основным кровеносным сосудом, по которому кровь покидает сердце, чтобы циркулировать по всему телу. а) Рассчитайте среднюю скорость движения крови в аорте при скорости потока 5,0 л/мин. Аорта имеет радиус 10 мм. (б) Кровь также течет через более мелкие кровеносные сосуды, известные как капилляры. При скорости кровотока в аорте 5,0 л/мин скорость крови в капиллярах составляет около 0,33 мм/с. Учитывая, что средний диаметр капилляра равен \(8,0 \, \мкм\), рассчитайте количество капилляров в системе кровообращения. 92} \\[5pt] &= 0,27 \, м/с. \end{align*}\]
Решение для (b)
Использование \(n_1A_1\overline{v}_1 = n_2A_2\overline{v}_1\), присвоение индекса 1 аорте и 2 индексу капилляры, и решение для \(n_2\) (количество капилляров) дает \(n_2 = \frac{n_1A_1\overline{v}_1}{A-2\overline{v}_2}.\) Преобразование всех величин в единицах метров и секунд и подстановка в приведенное выше уравнение дает
\[\begin{align*} n_2 &= \dfrac{(1)(\pi)(10 \times 10^{-3} m)^2 (0,27 \, м/с)}{(\pi)(4,0 \times 10^{-6} м)(0,33 \times 10^{-3} м/с)} \\[5pt] &= 5,0 \ раз 10^9\, капилляры.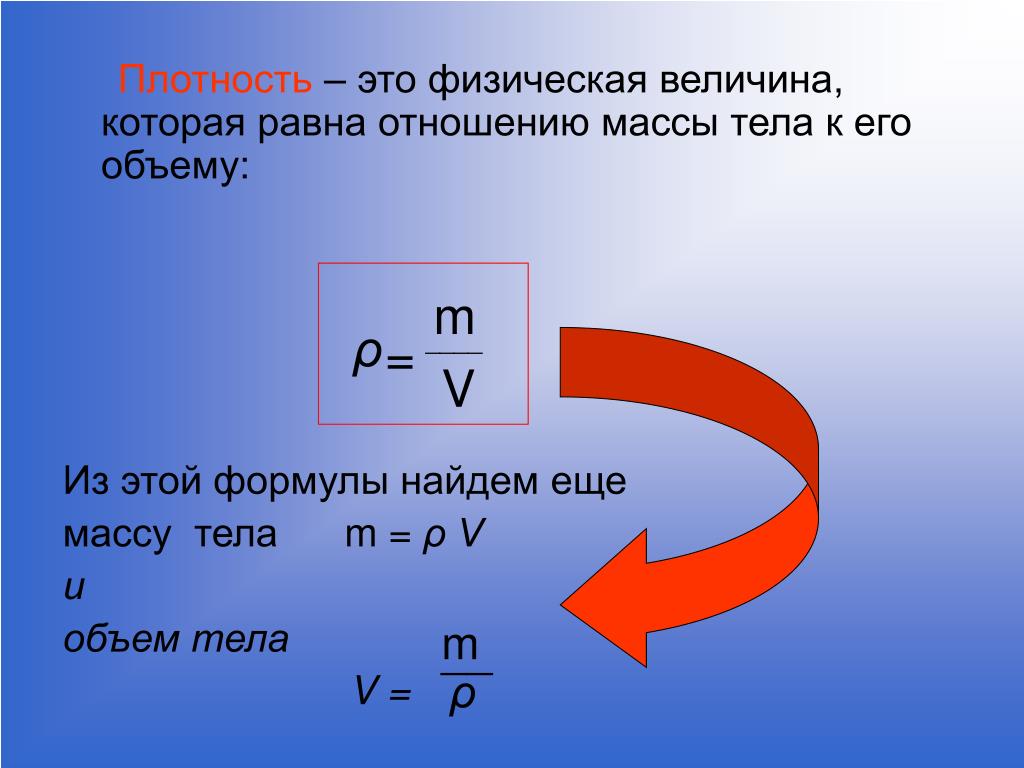



 ⓘ Объем вытесненной жидкости [V]
ⓘ Объем вытесненной жидкости [V]
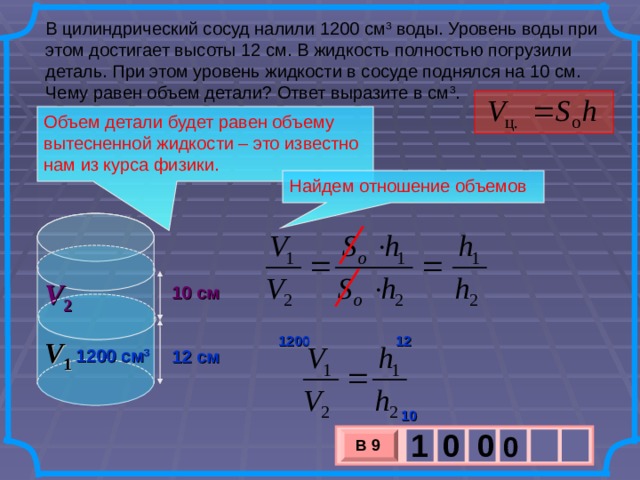 В любой точке статической жидкости давление со всех сторон должно быть одинаковым, иначе жидкость в этой точке будет реагировать на результирующую силу и ускоряться.
В любой точке статической жидкости давление со всех сторон должно быть одинаковым, иначе жидкость в этой точке будет реагировать на результирующую силу и ускоряться. Жидкость, расположенная на более глубоких уровнях, подвергается большей силе, чем жидкость, расположенная ближе к поверхности, из-за веса жидкости над ней. Следовательно, давление, рассчитанное на заданной глубине, отличается от давления, рассчитанного с использованием постоянной плотности.
Жидкость, расположенная на более глубоких уровнях, подвергается большей силе, чем жидкость, расположенная ближе к поверхности, из-за веса жидкости над ней. Следовательно, давление, рассчитанное на заданной глубине, отличается от давления, рассчитанного с использованием постоянной плотности. [/latex]
[/latex]

 {-23}\text{J/K } [/латекс].
{-23}\text{J/K } [/латекс]. [/latex]
[/latex] Причина в том, что жидкости не могут противостоять силам сдвига или оказывать на них силы сдвига. Таким образом, в статической жидкости, заключенной в резервуар, сила, действующая на стенки резервуара, действует перпендикулярно внутренней поверхности. Точно так же давление оказывается перпендикулярно поверхностям любого объекта в жидкости. (Рисунок) иллюстрирует давление, оказываемое воздухом на стенки шины и водой на тело пловца.
Причина в том, что жидкости не могут противостоять силам сдвига или оказывать на них силы сдвига. Таким образом, в статической жидкости, заключенной в резервуар, сила, действующая на стенки резервуара, действует перпендикулярно внутренней поверхности. Точно так же давление оказывается перпендикулярно поверхностям любого объекта в жидкости. (Рисунок) иллюстрирует давление, оказываемое воздухом на стенки шины и водой на тело пловца. Суммарная вертикальная сила, действующая на пловца, равна сумме выталкивающей силы и веса пловца. 9{2} [/латекс].
Суммарная вертикальная сила, действующая на пловца, равна сумме выталкивающей силы и веса пловца. 9{2} [/латекс]. Таким образом, сила зависит только от средней глубины воды и размеров плотины, а не от горизонтальной протяженности водохранилища. На диаграмме обратите внимание, что толщина плотины увеличивается с глубиной, чтобы уравновесить возрастающую силу из-за увеличивающегося давления.
Таким образом, сила зависит только от средней глубины воды и размеров плотины, а не от горизонтальной протяженности водохранилища. На диаграмме обратите внимание, что толщина плотины увеличивается с глубиной, чтобы уравновесить возрастающую силу из-за увеличивающегося давления.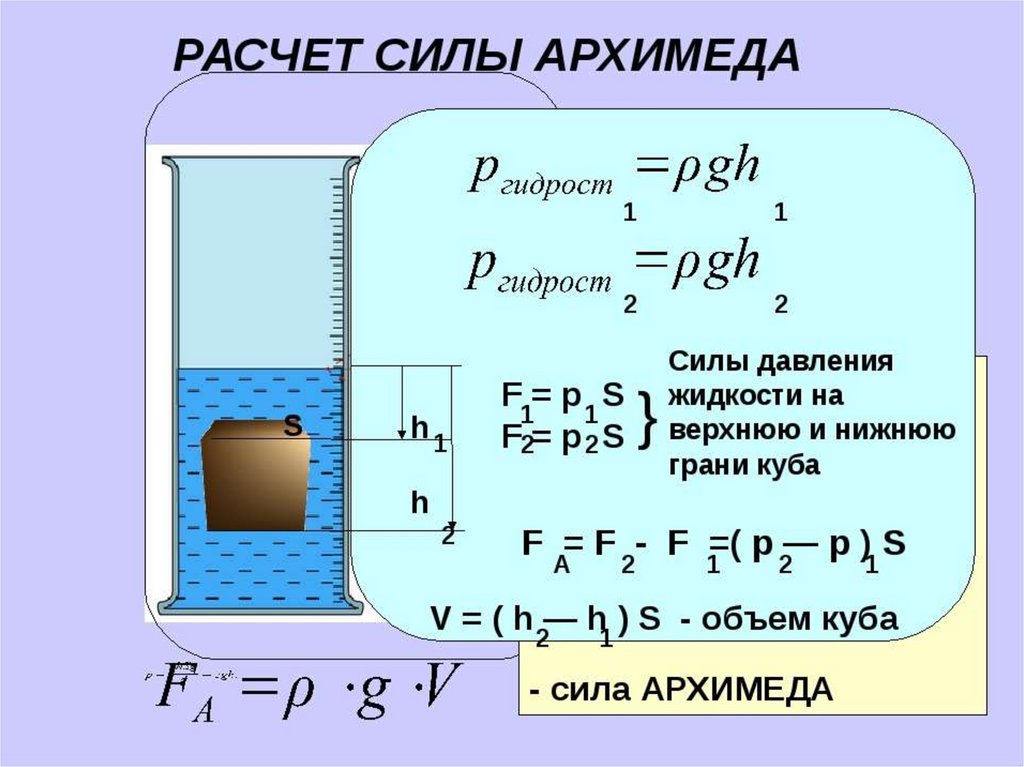 В плавательном бассейне, например, плотность приблизительно постоянна, и вода на дне очень мало сжимается под весом воды наверху. Однако путешествие в атмосферу — это совсем другая ситуация. Плотность воздуха начинает значительно меняться уже на небольшом расстоянии от поверхности Земли.
В плавательном бассейне, например, плотность приблизительно постоянна, и вода на дне очень мало сжимается под весом воды наверху. Однако путешествие в атмосферу — это совсем другая ситуация. Плотность воздуха начинает значительно меняться уже на небольшом расстоянии от поверхности Земли. Вес самого элемента также показан на диаграмме свободного тела.
Вес самого элемента также показан на диаграмме свободного тела. [/latex]
[/latex] {\text{−}h}\rho gdy\hfill \\ \hfill p-{p}_{0}& =\hfill & \rho gh\hfill \\ \hfill p& =\hfill & {p}_{0}+\rho gh.\hfill \end{массив}[/latex]
{\text{−}h}\rho gdy\hfill \\ \hfill p-{p}_{0}& =\hfill & \rho gh\hfill \\ \hfill p& =\hfill & {p}_{0}+\rho gh.\hfill \end{массив}[/latex] {-23}\text{J/K}[/ латекс].
{-23}\text{J/K}[/ латекс]. [/latex]
[/latex]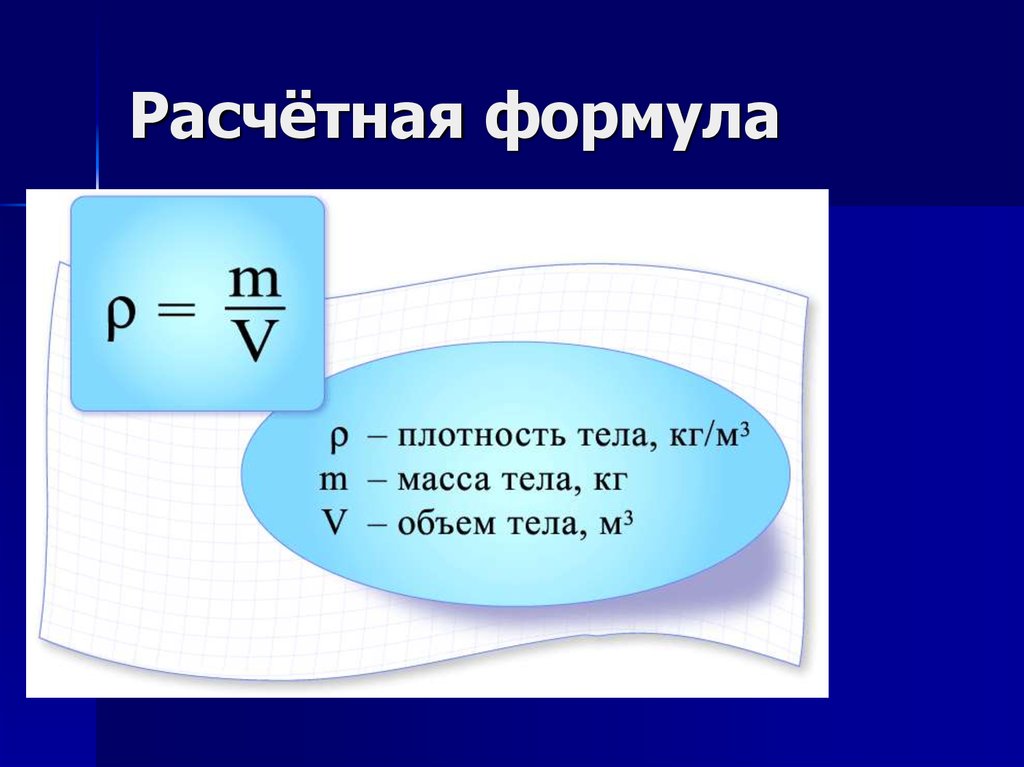 Причина в том, что жидкости не могут противостоять силам сдвига или оказывать на них силы сдвига. Таким образом, в статической жидкости, заключенной в резервуар, сила, действующая на стенки резервуара, действует перпендикулярно внутренней поверхности. Точно так же давление оказывается перпендикулярно поверхностям любого объекта в жидкости. На рисунке показано давление воздуха на стенки покрышки и воды на тело пловца.
Причина в том, что жидкости не могут противостоять силам сдвига или оказывать на них силы сдвига. Таким образом, в статической жидкости, заключенной в резервуар, сила, действующая на стенки резервуара, действует перпендикулярно внутренней поверхности. Точно так же давление оказывается перпендикулярно поверхностям любого объекта в жидкости. На рисунке показано давление воздуха на стенки покрышки и воды на тело пловца.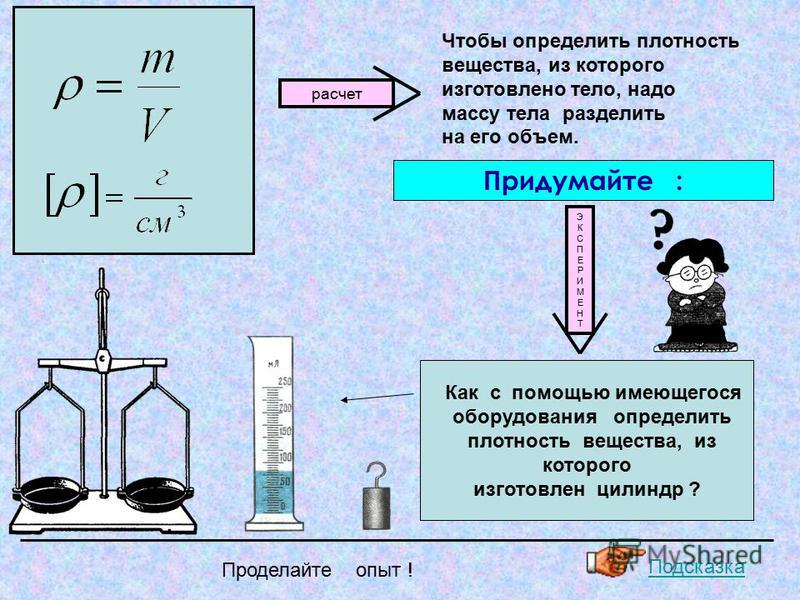 Суммарная вертикальная сила, действующая на пловца, равна сумме выталкивающей силы и веса пловца.
9{2}[/латекс].
Суммарная вертикальная сила, действующая на пловца, равна сумме выталкивающей силы и веса пловца.
9{2}[/латекс].