11 класс презентация, доклад, проект
• Решение задач на сложение
и умножение вероятностей
Теорема
Два события называются несовместными, если они не могут появиться одновременно в одном и том же испытании.
Вероятность появления хотя бы одного из двух несовместных событий, равна сумме вероятностей этих событий.
Р = Р(А) +Р(В)
На экзамене по геометрии школьнику достается один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос на тему «Вписанная окружность», равна 0,2. Вероятность того, что это вопрос на тему «Параллелограмм», равна 0,15. Вопросов, относящихся одновременно к этим двум темам, нет. Найдите вероятность того, что школьнику на экзамене достанется вопрос по одной из этих тем.
События «вопрос о вписанной окружности» и «вопрос о параллелограмме» — несовместные, поэтому вероятность выбрать один из них равна сумме вероятностей:
Теорема
События называются независимыми, если наступление одного из них не влияет на вероятность наступления другого события.
Если событие С означает совместное наступление двух независимых событий А и В, то вероятность события С равна произведению вероятностей событий А и В
Р(С) = Р(А) · Р(В)
Биатлонист стреляет по мишеням. Вероятность попасть в мишень при одном выстреле равна 0,8. Найдите вероятность того, что биатлонист поразит все пять мишеней.
Всего 5 выстрелов, вероятность попадания при одном выстреле равна 0,8, поэтому вероятность попадания всех пяти равна 0,8*0,8*0,8*0,8*0,8
=0,32768.
В одной вазе 12 конфет, 4 из которых шоколадные, а в другой вазе 8 конфет, 6 из которых шоколадные. Из каждой вазы взяли по одной конфете. Какова вероятность того, что обе конфеты шоколадные?
1) 4/12 вероятность того, что взята шоколадная конфета из первой вазы;
2) 6/8 вероятность того, что взята шоколадная конфета из второй вазы;
3) Р = 4/12 · 6/8 = ¼ = 0,25
Ответ: 0,25
Ответ: 0,07
Вероятность попадания в мишень равна 0,7;
вероятность промаха равна 1 – 0,7 = 0,3.
Т. к. результаты выстрелов – независимые события, вероятность того, что биатлонист четыре раза попал в мишень, а один раз промахнулся, равна:
Ответ: 0,07
Задачи на сложение и умножение вероятностей
Р= 0,7 ∙ 0,7 ∙ 0,7 ∙ 0,7 ∙ 0,3 ≈ 0,07
Ответ: 0,999
Ответ: 0,999
Тогда Р(А)= 1 — 0,001 = 0,999
.●
Ответ: 0,657
Ответ: 0,657
.
30. В классе 21 ученик, среди них 2 друга – Тоша и Гоша. На уроке физкультуры класс случайным образом разбивают на 3 равные группы . Найдите вероятность того, что Тоша и Гоша попали в одну группу.
Ответ: 0,3
Ответ: 0,3
31.
В классе 28 учащихся, среди них Наташа и Владик — брат и сестра. Для проведения медосмотра класс случайным образом разбивают на 2 равные группы. Найти вероятность того, что Владик и Наташа попали в разные группы.
Стрелок 4 раза стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,7. Найдите вероятность того, что стрелок первый раз попал в мишень, а последние 3 раза промахнулся.
Решение.
Так как вероятность попасть в мишень при одном выстреле равна 0,7, то вероятность попадания при первом выстреле равна P1(A) = 0,7, тогда вероятность того, что, стреляя , стрелок промахнулся, равна P2 = 1 — 0,7 = 0,3.
Вероятность того, что стрелок первый раз попал в мишень, а последние 3 раза промахнулся. P(B)= P1(A)∙ P2∙ P3∙ P4 = 0,7∙0,3∙0,3∙0.3 = 0,0189
Ответ: 0,0189.
15. В первой корзине лежат 2 яблока и 3 груши, а во второй – 3 яблока и 1 груша.
Решение:
Событие А: яблоко из первой корзины И
яблоко из второй корзины.
Тогда вероятность достать яблоко из первой корзины p1 = 2/5 = 0,4; из второй корзины p2 = 3/4 = 0,75.
А значит вероятность события А равна:
P(A) = 0,4 ∙ 0,75; P(A) = 0,3.
16. Стрелок стреляет по мишени один раз. В случае промаха стрелок делает второй выстрел по той же мишени. Вероятность попасть в мишень при одном выстреле равна 0,7. Найдите вероятность того, что мишень будет поражена (либо первым, либо вторым выстрелом).
Решение:
Событие А: попал ИЛИ не попал И попал.
Вероятность того, что стрелок не попадет, равна 1-0,7=0,3
Тогда вероятность события А равна:
P(A) = 0,7 + 0,3 ∙ 0,7;
P(A) = 0,91.
»
17. В реке водятся пескари и караси.
Утром после дождя при однократном закидывании удочки с вероятностью 0,2 попадается пескарь, и с вероятностью 0,1 — карась. Какова вероятность, что один раз забросив удочку, рыбак ничего не поймает?
Решение:
Событие А: поймает карася ИЛИ пескаря.
Значит P(A) = 0,2 + 0,1 = 0,3.
Событие В: ничего не поймает.
Значит, P(В) = 1 — 0,3 = 0,7.
0,657
27. Биатлонист пять раз стреляет по мишеням. Вероятность
попадания в мишень при одном выстреле равна 0,7. Найдите вероятность
того, что биатлонист первые четыре раза попал в мишени, а последний
раз промахнулся. Результат округлите до сотых.
0,07
Задачи на сложение и умножение вероятностей
28. В магазине стоят три платежных автомата. Каждый из них
того, что хотя бы один автомат исправен.
0,999
29. В интернет-магазине три телефонных оператора.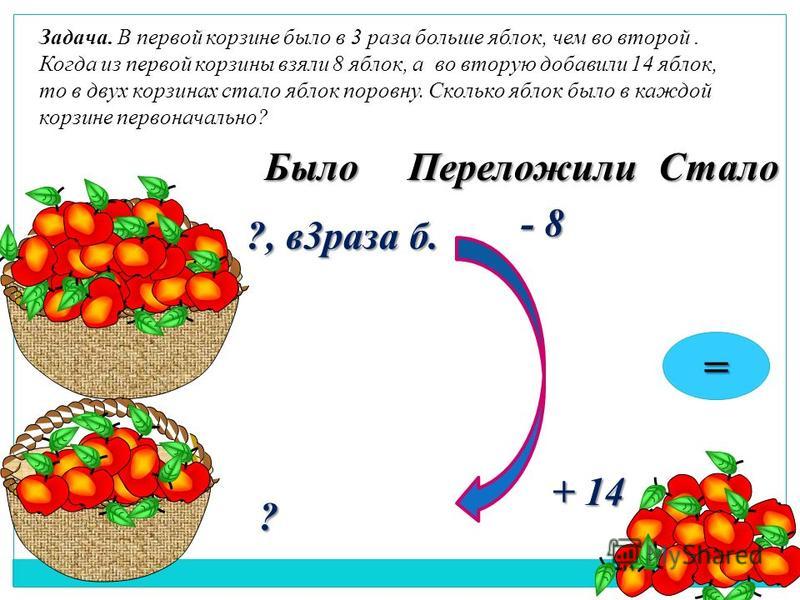
В случайный
момент оператор занят разговором с клиентом с вероятностью 0,7
независимо от других. Клиент звонит в магазин. Найдите вероятность
того, что хотя бы один оператор не занят.
30. В классе 21 ученик, среди них 2 друга – Тоша и Гоша. На уроке физкультуры класс случайным образом разбивают на 3 равные группы. Найдите вероятность того, что Тоша и Гоша попали в одну группу.
0,3
32. В группе иностранных туристов 51 человек. Среди них два испанца. Для посещения музея группу делят на две подгруппы – 25 и 26 человек – случайным образом. Найти вероятность того, что оба испанца окажутся в одной подгруппе.
31. В классе 28 учащихся, среди них Наташа и Владик — брат и сестра. Для проведения медосмотра класс случайным образом разбивают на 2 равные группы. Найти вероятность того, что Владик и Наташа попали в разные группы
Теория вероятностей. Нахождение вероятности поражения цели при трех выстрелах
Математика \ Математика
Страницы работы
2 страницы (Word-файл)
Посмотреть все страницы
Скачать файл
Содержание работы
Математика.
Теорвер. Задача 2
Вероятность попадания в цель при первом выстреле 0.3, при втором 0.4, при третьем 0.8. Вероятность поражения цели при одном попадании 0.6, при двух 0.7, при трех 0.9. Найти вероятность поражения цели при трех выстрелах.
Ответ 0.6176
Вероятность попадания в цель при первом выстреле 0.3, при втором 0.4, при третьем 0.6. Вероятность поражения цели при одном попадании 0.2, при двух 0.3, при трех 0.6. Найти вероятность поражения цели при трех выстрелах.
Ответ 0.2276
Вероятность попадания в цель при первом выстреле 0.4, при втором 0.5, при третьем 0.7. Вероятность поражения цели при одном попадании 0.5, при двух 0.6, при трех 0.9. Найти вероятность поражения цели при трех выстрелах.
Ответ 0.552
В первой корзине 2 персика и 4 яблока, во второй — 8 персиков и 3 яблока. Из первой корзины во вторую наудачу переложили 5 фруктов. Какова вероятность случайным образом достать персик и второй корзины?
Ответ 0.604166
Вероятность попадания в цель
при первом выстреле 0.
2, при втором 0.6, при третьем 0.9. Вероятность поражения
цели при одном попадании 0.2, при двух 0.3, при трех 0.8. Найти вероятность
поражения цели при трех выстрелах.
Ответ 0.3098
В первой корзине 2 яблока и 6 лимонов, во второй — 8 яблок и 3 лимона. Из первой корзины во вторую наудачу переложили 7 фруктов. Какова вероятность случайным образом достать яблоко и второй корзины?
Ответ 0.542
Вероятность попадания в цель при первом выстреле 0.3, при втором 0.5, при третьем 0.8. Вероятность поражения цели при одном попадании 0.3, при двух 0.4, при трех 0.9. Найти вероятность поражения цели при трех выстрелах.
Ответ 0.394
В первой корзине 8 апельсинов и 4 персика, во второй — 5 апельсинов и 7 персиков. Из первой корзины во вторую наудачу переложили 11 фруктов. Какова вероятность случайным образом достать персик и второй корзины?
Ответ 0.463
В первой корзине 6 яблок и 7
персиков, во второй — 8 яблок и 2 персика. Из первой корзины во вторую наудачу
переложили 12 фруктов.
Какова вероятность случайным образом достать персик и
второй корзины?
Ответ 0.38461
В первой корзине 4 апельсинов и 5 яблок, во второй — 8 апельсинов и 6 яблок. Из первой корзины во вторую наудачу переложили 8 фруктов. Какова вероятность случайным образом достать персик и второй корзины?
Ответ 0.474747
Вероятность попадания в цель при первом выстреле 0.3, при втором 0.7, при третьем 0.9. Вероятность поражения цели при одном попадании 0.1, при двух 0.2, при трех 0.8. Найти вероятность поражения цели при трех выстрелах.
Ответ 0.2845
В первой корзине 7 персиков и 6 груш, во второй — 4 персика и 8 груш. Из первой корзины во вторую наудачу переложили 12 фруктов. Какова вероятность случайным образом достать грушу и второй корзины?
Ответ 0.5641
Из последовательности 37,38,39,…,93 наудачу выбираются два разных числа. Найти вероятность того что одно из них больше 70, а другое меньше 70.
Ответ 0.475
В первой корзине 5 лимонов и
8 груш, во второй — 3 лимона и 7 груш.
Из первой корзины во вторую наудачу
переложили 12 фруктов. Какова вероятность случайным образом достать грушу и
второй корзины?
Ответ 0.653
В первой корзине 3 апельсина и 9 груш, во второй — 5 апельсинов и 8 груш. Из первой корзины во вторую наудачу переложили 11 фруктов. Какова вероятность случайным образом достать апельсин и второй корзины?
Ответ 0.3229
В первой корзине 3 персика и 4 груши, во второй — 5 персиков и 2 груши. Из первой корзины во вторую наудачу переложили 6 фруктов. Какова вероятность случайным образом достать персик и второй корзины?
Ответ 0.58
В первой корзине 6 персиков и 2 груши, во второй — 7 персиков и 5 груш. Из первой корзины во вторую наудачу переложили 7 фруктов. Какова вероятность случайным образом достать персик и второй корзины?
Ответ 0.645
Вероятность попадания в цель
при первом выстреле 0.2, при втором 0.4, при третьем 0.7. Вероятность поражения
цели при одном попадании 0.2, при двух 0.3, при трех 0.4. Найти вероятность
поражения цели при трех выстрелах.
Ответ 0.2156
В первой корзине 4 апельсинов и 2 яблока, во второй — 8 апельсинов и 5 яблок. Из первой корзины во вторую наудачу переложили 5 фруктов. Какова вероятность случайным образом достать апельсин и второй корзины?
Ответ 0.6296
В первой корзине 6 апельсина и 4 груши, во второй — 3 апельсина и 5 груш. Из первой корзины во вторую наудачу переложили 9 фруктов. Какова вероятность случайным образом достать грушу и второй корзины?
Ответ 0.506
Вероятность попадания в цель при первом выстреле 0.4, при втором 0.5, при третьем 0.7. Вероятность поражения цели при одном попадании 0.5, при двух 0.6, при трех 0.9. Найти вероятность поражения цели при трех выстрелах.
Ответ 0.552
Вероятность попадания в цель при первом выстреле 0.5 при втором 0.7, при третьем 0.8. Вероятность поражения цели при одном попадании 0.3, при двух 0.6, при трех 0.9. Найти вероятность поражения цели при трех выстрелах.
Ответ 0.6
В первой корзине 5 лимонов и
8 груш, во второй — 3 лимона и 7 груш.
Из первой корзины во вторую наудачу
переложили 12 фруктов. Какова вероятность случайным образом достать грушу и
второй корзины?
Ответ 0.65384
Вероятность попадания в цель при первом выстреле 0.5, при втором 0.6, при третьем 0.8. Вероятность поражения цели при одном попадании 0.3, при двух 0.4, при трех 0.5. Найти вероятность поражения цели при трех выстрелах.
Ответ 0.382
Похожие материалы
Информация о работе
Скачать файл
Выбери свой ВУЗ
- АлтГТУ 419
- АлтГУ 113
- АмПГУ 296
- АГТУ 267
- БИТТУ 794
- БГТУ «Военмех» 1191
- БГМУ 172
- БГТУ 603
- БГУ 155
- БГУИР 391
- БелГУТ 4908
- БГЭУ 963
- БНТУ 1070
- БТЭУ ПК 689
- БрГУ 179
- ВНТУ 120
- ВГУЭС 426
- ВлГУ 645
- ВМедА 611
- ВолгГТУ 235
- ВНУ им.
Даля 166 - ВЗФЭИ 245
- ВятГСХА 101
- ВятГГУ 139
- ВятГУ 559
- ГГДСК 171
- ГомГМК 501
- ГГМУ 1966
- ГГТУ им. Сухого 4467
- ГГУ им. Скорины 1590
- ГМА им. Макарова 299
- ДГПУ 159
- ДальГАУ 279
- ДВГГУ 134
- ДВГМУ 408
- ДВГТУ 936
- ДВГУПС 305
- ДВФУ 949
- ДонГТУ 498
- ДИТМ МНТУ 109
- ИвГМА 488
- ИГХТУ 131
- ИжГТУ 145
- КемГППК 171
- КемГУ 508
- КГМТУ 270
- КировАТ 147
- КГКСЭП 407
- КГТА им. Дегтярева 174
- КнАГТУ 2910
- КрасГАУ 345
- КрасГМУ 629
- КГПУ им. Астафьева 133
- КГТУ (СФУ) 567
- КГТЭИ (СФУ) 112
- КПК №2 177
- КубГТУ 138
- КубГУ 109
- КузГПА 182
- КузГТУ 789
- МГТУ им. Носова 369
- МГЭУ им. Сахарова 232
- МГЭК 249
- МГПУ 165
- МАИ 144
- МАДИ 151
- МГИУ 1179
- МГОУ 121
- МГСУ 331
- МГУ 273
- МГУКИ 101
- МГУПИ 225
- МГУПС (МИИТ) 637
- МГУТУ 122
- МТУСИ 179
- ХАИ 656
- ТПУ 455
- НИУ МЭИ 640
- НМСУ «Горный» 1701
- ХПИ 1534
- НТУУ «КПИ» 213
- НУК им. Макарова 543
- НВ 1001
- НГАВТ 362
- НГАУ 411
- НГАСУ 817
- НГМУ 665
- НГПУ 214
- НГТУ 4610
- НГУ 1993
- НГУЭУ 499
- НИИ 201
- ОмГТУ 302
- ОмГУПС 230
- СПбПК №4 115
- ПГУПС 2489
- ПГПУ им. Короленко 296
- ПНТУ им. Кондратюка 120
- РАНХиГС 190
- РОАТ МИИТ 608
- РТА 245
- РГГМУ 117
- РГПУ им. Герцена 123
- РГППУ 142
- РГСУ 162
- «МАТИ» — РГТУ 121
- РГУНиГ 260
- РЭУ им. Плеханова 123
- РГАТУ им. Соловьёва 219
- РязГМУ 125
- РГРТУ 666
- СамГТУ 131
- СПбГАСУ 315
- ИНЖЭКОН 328
- СПбГИПСР 136
- СПбГЛТУ им. Кирова 227
- СПбГМТУ 143
- СПбГПМУ 146
- СПбГПУ 1599
- СПбГТИ (ТУ) 293
- СПбГТУРП 236
- СПбГУ 578
- ГУАП 524
- СПбГУНиПТ 291
- СПбГУПТД 438
- СПбГУСЭ 226
- СПбГУТ 194
- СПГУТД 151
- СПбГУЭФ 145
- СПбГЭТУ «ЛЭТИ» 379
- ПИМаш 247
- НИУ ИТМО 531
- СГТУ им. Гагарина 114
- СахГУ 278
- СЗТУ 484
- СибАГС 249
- СибГАУ 462
- СибГИУ 1654
- СибГТУ 946
- СГУПС 1473
- СибГУТИ 2083
- СибУПК 377
- СФУ 2424
- СНАУ 567
- СумГУ 768
- ТРТУ 149
- ТОГУ 551
- ТГЭУ 325
- ТГУ (Томск) 276
- ТГПУ 181
- ТулГУ 553
- УкрГАЖТ 234
- УлГТУ 536
- УИПКПРО 123
- УрГПУ 195
- УГТУ-УПИ 758
- УГНТУ 570
- УГТУ 134
- ХГАЭП 138
- ХГАФК 110
- ХНАГХ 407
- ХНУВД 512
- ХНУ им. Каразина 305
- ХНУРЭ 325
- ХНЭУ 495
- ЦПУ 157
- ЧитГУ 220
- ЮУрГУ 309
Даля 166
Дегтярева 174
Макарова 543
Герцена 123
Гагарина 114
Каразина 305Карта сайта
Главная Обучение Библиотека Карта сайта
|
Персиановский)
2.014.01комбинаторика — Распределение 20 яблок по 3 корзинам
Задавать вопрос
Спросил
Изменено 1 год, 2 месяца назад
Просмотрено 150 раз
$\begingroup$
Я составил сводку возможных способов распределения 20 яблок по 3 корзинам.
Мне интересно, верны ли мои решения? Я знаю, что пара может ошибаться, так как я не использовал принцип исключения включения: 9{20}$$
- Корзина $1 (B_1)$ $\leq$ 5:
- Неотличимые яблоки:
$$x1′ + x2′ + x3′ = 14 => \dbinom{22}{20} — \dbinom{16}{14}$$ Вопрос здесь: предположим, что B1 <= 1, B2 <= 1, B3 <= 1 Я также получил: $x1' + x2' + x3' = 14$ => $\dbinom{22}{20} — \dbinom{16}{14}$ То же, что просто B1 <= 5? Но разве это не должно быть $\dbinom{20}{3}$ ? от точки зрения корзины Или $3*2*1=3!$ от pov яблок? Я думал, что это сведется к биномиальной теореме n выбирает k, поскольку неупорядочено с заменой, но ограничено значением меньше или равным 1. Я попытался привести пример выбора 3 объектов из 5 объектов, используя x1 + x2 + x3 + x4 + x5 = 3 и применить ограничение <= 1, я получил отрицательный результат на RHS. И это уж точно не равно $\dbinom{5}{3}$ ?! 9{15}$$
- В1 <= 5, В2 <= 3:
Неотличимые яблоки:
$$x1′ + x2′ + x3′ = 10 => \dbinom{22}{20} — \dbinom{12}{10}$$
Отличительные яблоки:
Декартово произведение множеств: |{0,1,2,3,4,5}$\times${0,1,2,3}| = 24
$$\dbinom{20}{0}\dbinom{20}{0} + \dbinom{20}{0}\dbinom{20}{1} + \dbinom{20}{0} \dbinom{20} {2} .
.. + \dbinom{20}{1} \dbinom{19}{0} + \dbinom{20}{1}\dbinom{19{12}$$Я надеюсь, что яблоки 4 и 6 будут различимы. Мне не нужно выполнять расчет для каждой перестановки, достаточно выполнить один расчет, как указано выше. Что происходит, когда и яблоки, и корзины становятся неразличимыми? и корзина становится неразличимой, а яблоко различимым?
- комбинаторика
- перестановки
- включение-исключение
- шары в корзинах
$\endgroup$
8
$\begingroup$
На мой первый взгляд, у вас проблемы с различимыми яблоками и различимыми корзинами в вопросе $4$ и $6$.
Наиболее подходящим способом преобразования различимых объектов в различимые прямоугольники являются экспоненциальные производящие функции, они предотвращают пересчет.
Давайте сначала проверим четвертый вопрос, мы видим, что вы делаете пересчет, когда яблоки различимы.
7}{7!}+…$$ 93}{3!}+…\bigg) $$$\endgroup$
3
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.Ответы на набор 1 (сложение и вычитание)
Поиск на моем сайте:
Ответ на каждую задачу можно решить разными способами. Изучите методы и найдите тот, который больше всего подходит вашему ребенку. Вы также можете комбинировать методы.
Вопрос 1
У Сьюзен есть 3 черничных кекса и 4 шоколадных печенья. Сколько всего кексов и печенья у Сьюзан?
Ответ: 7
Написать заявление
3 + 4 = 7
Рисование картинок
Нарисуйте количество кексов и печенья. Посчитай их.
Номер Строка
- Начните с номера маффинов.
- Подсчитайте шаги, соответствующие количеству файлов cookie.
- Число, которое вы получите (7), является ответом.
Чертежные модели
- Нарисуйте 2 прямоугольника для представления чисел.
- Меньшее число должно быть в меньшем прямоугольнике.
- Нарисуйте прямоугольники рядом.
- Нарисуйте фигурную скобку ‘{‘ (скобку) над обоими прямоугольниками, чтобы указать сумму или итог.
Содержание
Вопрос 2
У меня есть карандаши. Я дал своему младшему брату 2 своих карандаша. У меня осталось 4 карандаша. Сколько карандашей было у меня сначала?
Ответ: 6
Написать заявление
Чтобы сначала найти количество карандашей, представьте, что мы забираем 2 карандаша обратно у младшего брата и прибавляем к количеству оставшихся карандашей:
4 + 2 = 6Рисование картинок
- Нарисуйте оставшееся количество карандашей.
- Добавьте количество розданных карандашей.
- Пересчитай все карандаши.
Число Строка
Начнем с оставшихся 4 карандашей.
- Нарисуйте числовую прямую с цифрами 1, 2, 3, 4.
- Поставьте точку над цифрой 4. Помните, что мы достигли этого числа, вернувшись на 2 шага назад.
- Добавьте еще 2 числа после 4. Это число, с которого мы начали.
4 + 2 = 6
Модели для рисования
- Нарисуйте прямоугольник, чтобы обозначить количество оставшихся карандашей.
- Добавьте еще один прямоугольник сбоку, чтобы обозначить 2 розданных карандаша.
- Сначала нарисуйте ‘{‘ над обоими прямоугольниками, чтобы обозначить количество карандашей.
4 + 2 = 6
Содержание
Вопрос 3
У Салли 8 книг. У Джона на 3 книги больше, чем у Салли. Сколько всего книг у обоих детей?
Ответ: 19
Написание заявлений
Этот вопрос состоит из нескольких шагов. Желательно писать заявления, чтобы отслеживать нашу работу.
Книги Салли: 8
Книги Джона: 8 + 3 = 11
Allogether: 8 + 11 = 19
(оба)Рисунок
мы нарисуем 8 книг.
У Джона на 3 книги больше, чем у Салли. Нарисуйте столько же книг, сколько Салли, затем нарисуйте еще 3 книги.
Теперь посчитайте все книги.
Модели для рисования
- Нарисуйте прямоугольник для Салли. Напишите в нем цифру 8.
- Нарисуйте прямоугольник того же размера для Джона, затем добавьте еще 3 прямоугольника.
- Нарисуйте ‘}’ в местах, показанных ниже.
Начиная с модели:
Книги Салли: 8
Книги Джона: 8 + 3 = 11
Итого = 8 + 11
= 19Содержание
Вопрос 4
Книга стоит 12 долларов. Игрушечная машинка на 7 долларов дешевле книги. Сколько денег мне нужно, чтобы купить книгу и игрушечную машинку?
Ответ: $17
Написание заявлений
Этот вопрос состоит из нескольких шагов. Желательно писать заявления, чтобы отслеживать нашу работу. Нам не нужно писать знак $ в нашей работе.
Книга: 12
Той CAR: 12 — 7 = 5
Ally: 12 + 5 = 17
(оба)Рисование. рисовать картинки, поэтому вместо этого мы используем метки.
- Нарисуйте 12 баллов за книгу.
- Нарисуйте на 7 очков меньше, чем машинка.
- Теперь посчитайте все отметки.
Чертежные модели
- Нарисуйте прямоугольник для книги. Разрежьте прямоугольник на 2 части.
- Напишите цифру 7 во второй части. Напишите число 12 над прямоугольником.
- Нарисуйте еще один прямоугольник для игрушечной машинки. Размер этого прямоугольника должен быть такого же размера, как и первая часть книги.
Из модели видно, что:
Книга: 12
Игрушечная машинка: 12 — 7 = 5
Итого = 12 + 5
1 9 7 8 902 903
Содержание
Вопрос 5
Микки на 4 года моложе Тома. Их общий возраст составляет 18 лет.
Сколько лет Микки?Ответ: 7
Рисование моделей / Составьте список
Сначала мы рисуем модели. Поскольку Микки младше Тома на 4 года, разница в их возрасте составляет 4 года.
Теперь перечислим комбинации пар чисел, которые в сумме составляют 18. (Нам не нужно составлять полный список.)
- 8 + 10
- 9 + 9
- 10 + 8
- 11 + 7
- 12 + 6
Теперь найдем разницу между перечисленными числами. Пара, которую мы хотим, должна иметь разницу 4.
Разница- 8 + 10 10 — 8 = 2
- 9 + 9 9 — 9 = 0
- 10 + 8 10 — 8 = 2
- 11 + 7 11 — 7 = 4 …. Эврика!!
- 12 + 6
Поскольку Микки моложе, его возраст равен меньшему числу, равному 7.
Вопрос 6
Сэм купил фруктов. Яблок на 5 больше, чем апельсинов. Грушей на 7 меньше, чем яблок. Если есть 6 груш, сколько всего фруктов купил Сэм?
Ответ: 27
Написание заявлений
Этот вопрос сложный, поэтому мы должны решать его по частям.
Начнем с числа, которое мы знаем, это количество груш.Груши: 6
Яблоки: Поскольку груш меньше, чем яблок, количество яблок должно быть больше, чем количество груш.
6 + 7 = 13
Апельсины: Поскольку яблок больше, чем апельсинов, количество апельсинов должно быть меньше, чем количество яблок.
13 — 5 = 8Всего: 6 + 13 + 8 = 27
Начертите метки
- 9006 для рисования копий.
- Груш меньше, чем яблок, поэтому нарисуйте для яблок на 7 отметок больше, чем для груш.
- Яблок больше, чем апельсинов, поэтому нарисуйте для апельсинов на 5 меток меньше, чем для яблок.
- Нарисуйте груши.
- Нарисуй яблоки. Разделите его на 3 части, как показано на рисунке. Одну часть для сравнения с грушами и одну часть для сравнения с апельсинами.
- Нарисуй апельсины.
.. + \dbinom{20}{1} \dbinom{19}{0} + \dbinom{20}{1}\dbinom{19{12}$$
7}{7!}+…$$ 93}{3!}+…\bigg) $$
Помните, что мы достигли этого числа, вернувшись на 2 шага назад. 
Сколько лет Микки?
Начнем с числа, которое мы знаем, это количество груш.Now do the working:
Pears: 6
Apples: 6 + 7 = 13
Oranges: 13 — 5 = 8
Total: 6 + 13 + 8 = 27
Модели для рисования
Одну часть для сравнения с грушами и одну часть для сравнения с апельсинами.Работать:
Груши: 6
Яблоки: 6 + 7 = 13
апельсины: 13 — 5 = 8
Всего: 6 + 13 + 8 = 27
Таблица. есть какие-либо вопросы или комментарии по этим пояснениям.
Нажмите здесь, чтобы связаться с нами.
8 Выдающаяся польза яблок для здоровья
Снова наступило то время года: сезон сбора яблок. И есть ряд веских причин, почему вы захотите наполнить корзину.
Яблоки вкусны не только сами по себе или при добавлении в блюда, но и очень полезны для здоровья. «Яблоки были связаны с многочисленными преимуществами для здоровья, включая улучшение здоровья кишечника и снижение риска инсульта, высокого кровяного давления, диабета, сердечных заболеваний, ожирения и некоторых видов рака», — говорит Джессика Левинсон, RDN, кулинарный эксперт по питанию в Вестчестере, Нью-Йорк.
Йорк.
По данным Министерства сельского хозяйства США, яблоко среднего размера является хорошим источником клетчатки: оно содержит 4,8 грамма питательных веществ. Это же яблоко также является хорошим источником витамина С, предлагая 90,2 миллиграмма вместе с небольшим количеством других витаминов и минералов.
Сара Голд Анзловар, RDN, бостонская владелица Sarah Gold Nutrition, предлагает добавлять фрукты в салаты или жареный сыр, делать запеченные яблоки в качестве полезного десерта или готовить тушеную курицу с яблоками в мультиварке. для легкого обеда или ужина.
«Все яблоки полезны, хотя содержание питательных веществ и антиоксидантов в разных яблоках немного различается — лучше всего есть те сорта, которые вам нравятся», — говорит Анзловар.
Вот почему еще фраза «одно яблоко в день помогает не ходить к врачу» может быть правдой.
7 Впечатляющая польза яблок для здоровья
1. Яблоки могут снизить высокий уровень холестерина и кровяное давление Насладитесь сочным яблоком, и вы поможете сохранить свое здоровье.
«Исследования связывают потребление яблок со снижением риска сердечно-сосудистых заболеваний, что может быть связано с тем, что растворимая клетчатка, содержащаяся в яблоках, снижает уровень холестерина», — говорит Анзловар.
Растворимая клетчатка растворяется в воде, образуя гелеобразный материал, согласно данным клиники Майо.
По данным Университета Иллинойса, растворимая клетчатка помогает предотвратить накопление холестерина в выстилке стенок кровеносных сосудов, тем самым снижая заболеваемость атеросклерозом (ограниченным кровотоком в артериях из-за накопления бляшек) и сердечными заболеваниями. Это также может помочь снизить уровень артериального давления: в одном из предыдущих обзоров было обнаружено, что более высокое потребление растворимой клетчатки связано со снижением риска сердечно-сосудистых заболеваний.
Предыдущие исследования показывают, что регулярное употребление яблок (или груш) снижает риск инсульта на 52 процента. Кроме того, исследование, опубликованное в феврале 2020 года в Американском журнале клинического питания , показало, что употребление двух яблок в день помогло участникам исследования снизить уровень холестерина ЛПНП («плохого») и триглицеридов.
Вы, вероятно, слышали, что клетчатка полезна для пищеварения, и это правда! По данным Гарвардского Т.Х. Chan of Public Health, оба типа клетчатки (растворимая и нерастворимая, что означает, что она не может быть поглощена водой) важны для пищеварения. И вам повезло — в яблоках есть оба типа, по данным Университета Иллинойса.
Растворимая клетчатка помогает замедлить пищеварение, позволяя вам чувствовать себя сытым, а также замедляет усвоение глюкозы, что помогает контролировать уровень сахара в крови. Между тем, согласно Гарварду, нерастворимая клетчатка может помочь продвижению пищи по вашему организму и помочь при запорах и регулярности.
Обязательно ешьте кожуру яблока, которая содержит большую часть нерастворимой клетчатки яблока, по данным Университета Иллинойса.
3. Яблоки могут поддерживать здоровую иммунную систему Кто не хочет, чтобы осенью укрепилась иммунная система? Яблоки могут быть важным инструментом в вашем наборе инструментов для поддержки иммунитета.
Согласно прошлым исследованиям на животных, диета, богатая растворимой клетчаткой, помогла преобразовать иммунные клетки, которые были провоспалительными, в противовоспалительные и поддерживающие иммунитет. Другое исследование на животных, опубликованное в мае 2018 года в журнале Immunity , показало, что диета с высоким содержанием пищевых волокон помогает защитить мышей от гриппа. (Однако неясно, будут ли эти эффекты проявляться у людей.)
Тем не менее, есть основания полагать, что яблоки могут укреплять иммунитет, отчасти потому, что они содержат иммуностимулирующий витамин С. Один прошлый большой обзор показал, что регулярное потребление витамина C играет много ролей, помогая функционированию иммунной системы. Например, согласно прошлым исследованиям, он может помочь укрепить эпителиальный (тип ткани) барьер против патогенов и защитить от окислительного стресса окружающей среды, такого как загрязнение и радиация.
4. Яблоки полезны при диабете Если у вас диабет 2 типа, рассмотрите возможность включения яблок в свой рацион.
Конечно, это фрукты, но это распространенное заблуждение, что людям с диабетом нельзя есть фрукты.
В этом случае растворимая клетчатка яблок может помочь замедлить всасывание сахара в кровоток и улучшить уровень сахара в крови, отмечает клиника Майо. Кроме того, согласно Майо, здоровая диета, включающая нерастворимую клетчатку, в первую очередь может снизить вероятность развития диабета 2 типа.
Кроме того, исследование людей с диабетом 2 типа, опубликованное в августе 2016 года в Experimental and Therapeutic Medicine , показало, что регулярное потребление растворимой клетчатки помогает снизить резистентность к инсулину и улучшить уровень сахара и триглицеридов в крови.
5. Антиоксиданты в яблоках могут играть роль в профилактике рака Хотя не существует надежного способа предотвратить рак, яблоки могут помочь в борьбе с этими заболеваниями. «Яблоки могут снизить риск некоторых видов рака, что, по мнению исследователей, связано с антиоксидантами, содержащимися в яблоках», — говорит Анзловар.
Прошлые исследования показывают, что яблоки богаты антиоксидантами, а лабораторные исследования показали, что эти антиоксиданты ограничивают рост раковых клеток.
Обзор, опубликованный в октябре 2016 года в Public Health Nutrition , показал, что регулярное употребление яблок связано со снижением риска некоторых видов рака, в том числе колоректального рака, рака полости рта, пищевода и молочной железы.
Клетчатка в яблоках может способствовать предотвращению рака. Исследование, опубликованное в марте 2016 года в журнале Pediatrics , показало, что женщины, которые ели больше продуктов с высоким содержанием клетчатки в подростковом и юношеском возрасте (особенно много фруктов и овощей), имели более низкий риск рака молочной железы в более позднем возрасте.
Другое исследование, опубликованное в январе 2019 года в журнале The Lancet , показало, что диета с высоким содержанием пищевых волокон может помочь защитить от колоректального рака и рака молочной железы, а также от диабета 2 типа и сердечно-сосудистых заболеваний.
Диета, богатая фруктами (и овощами), может помочь вам поддерживать здоровый вес или сбросить килограммы, согласно данным Центров по контролю и профилактике заболеваний.
Поскольку яблоки богаты пищевыми волокнами, они занимают первое место в этом списке. «Клетчатка замедляет пищеварение и повышает уровень сахара в крови, сохраняя чувство сытости и снижая вероятность переедания», — говорит Левинсон.
Согласно исследованию The Lancet , люди, которые ели больше клетчатки, имели значительно меньшую массу тела. Предыдущие исследования показывают, что женщины с избыточным весом, которые съедали по три яблока в день, потеряли 1,22 кг (2,7 фунта) за 12 недель.
В яблоке среднего размера всего 95 калорий, поэтому этот фрукт нужно держать под рукой, когда возникает тяга к сладкому.
7. Яблоки могут помочь предотвратить болезнь Альцгеймера Пора начать есть больше яблок и других продуктов, богатых флавоноидами, таких как ягоды и чай.
Исследование, опубликованное в августе 2020 года в Американском журнале клинического питания , показало, что взрослые в возрасте 50 лет и старше, которые включали в свой рацион лишь небольшое количество продуктов, богатых флавоноидами, таких как ягоды, яблоки и чай, были в 2-4 раза больше. вероятность развития болезни Альцгеймера и родственных типов деменции в течение 20 лет по сравнению с людьми, которые ели больше продуктов, богатых флавоноидами.
Кроме того, обзор, опубликованный в январе 2020 года в журнале Biomolecules , показал, что кверцетин, флавоноид, содержащийся в яблоках, защищает нейроны от окислительного повреждения, а также обладает другими свойствами против болезни Альцгеймера. Но исследователи говорят, что необходимо провести дополнительные исследования за пределами лабораторных условий.
8. Яблоки могут помочь сохранить ваш кишечник здоровым Здоровье кишечника — очень модная тема в наши дни, и оказывается, что употребление яблок может быть одним из способов сделать одолжение вашей пищеварительной системе.
Яблоки содержат тип крахмала, называемый пектином, который является пребиотиком. По данным клиники Кливленда, пребиотики важны, потому что они помогают питать «хорошие» бактерии в вашем кишечнике; они также повышают иммунную функцию, стимулируют выработку гормонов и помогают вашему организму усваивать определенные минералы (например, кальций и фосфор), помимо других преимуществ.
Яблоки также содержат бактерии, которые могут быть полезны для вашего кишечника, как показало одно исследование, опубликованное в июле 2019 года в журнале Frontiers in Microbiology 9.0583 . Тем не менее, исследователи отметили, что свежесобранные органические яблоки имеют более разнообразную и отчетливую колонию бактерий по сравнению с яблоками, выращенными традиционным способом, купленными в магазине. !
Поздний прием пищи увеличивает чувство голода и снижает количество сожженных калорий
Люди, которые пропускают завтрак и съедают поздний ужин, испытывают более сильную тягу к еде и сжигают меньше энергии в течение дня, как показало новое исследование.
от Lisa Rapaport