Онлайн решение уравнений с дискриминантом: Дискриминант онлайн

Квадратное уравнение

Квадратное уравнение

Квадратное уравнение

— это уравнение вида

a x² + b x + c = 0,

где a не равно 0.

• Геометрический смысл

• Вывод формулы для решения квадратного уравнения

• Дискриминант квадратного уравнения

• Теорема Виета

• Разложение квадратного уравнения на множители

• Примеры решения квадратных уравнений

Геометрический смысл

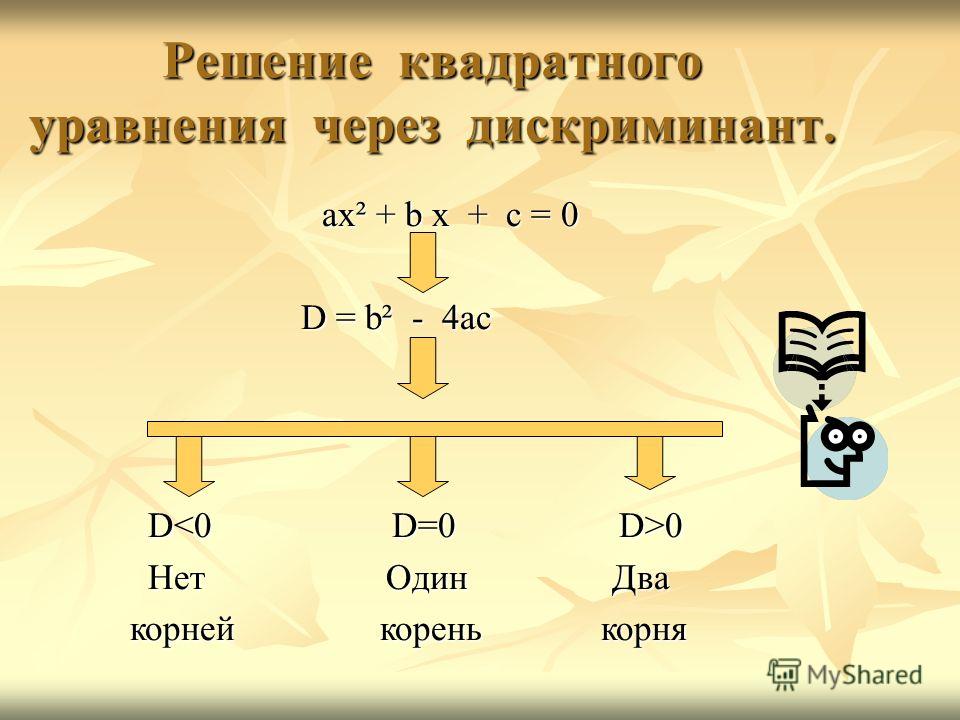
Графиком квадратичной функции является парабола. Решениями (корнями) квадратного уравнения называют точки пересечения параболы с осью абсцисс. Если парабола, описываемая квадратичной функцией, не пересекается с осью абсцисс, уравнение не имеет вещественных корней. Если парабола пересекается с осью абсцисс в одной точке (вершине параболы), уравнение имеет один вещественный корень (также говорят, что уравнение имеет два совпадающих корня). Если парабола пересекает ось абсцисс в двух точках, уравнение имеет два вещественных корня.

Если коэффициент a положительный, ветви параболы направлены вверх, если отрицательный — ветви параболы направлены вниз. Если коэффициент b положительный, то вершина параболы лежит в левой полуплоскости, если отрицательный — в правой полуплоскости.

Вывод формулы для решения квадратного уравнения

Формулу для решения квадратного уравнения

a x² + b x + c = 0

можно получить так:

• перенесем c в правую частьa x² + b x = — c
• умножим уравнение на 4a(2a x)² + 4a b x = — 4a c
• добавим b² к обоим частям(2a x)² + 4a b x + b² = b² — 4a c
• в левой части выделим полный квадрат(2a x + b)² = b² — 4a c
• извлечем квадратный корень2a x + b = ± √b
  2 — 4a c
• перенесем b в правую часть2a x = — b ± √b² — 4a c
• разделим уравнение на 2a

  x =	-b ± √b2 — 4a c
  	2 a

Дискриминант квадратного уравнения

Дискриминантом

квадратного уравнения называют число равное

D = b² − 4ac

Квадратное уравнение с вещественными коэффициентами может иметь от 0 до 2 вещественных корней в зависимости от значения дискриминанта:

• при D > 0 корней два, и они вычисляются по формуле

  x1,2 =	-b ± √D
  	2 a

• при D = 0 корень один (два равных или совпадающих корня), кратности 2:

  x =	-b
  	2 a

• при Dx_1,2 =  -b ± i√-D 2 a

Теорема Виета

Приведенным квадратным уравнением

называется уравнение, в котором коэффициент при x² равен единице. Такое уравнение может быть получено делением всего выражения на коэффициент a:

x² + px + q = 0,

где p = 

ba

, q = 

ca

Сумма корней приведённого квадратного уравнения

x² + px + q = 0

равна коэффициенту p, взятому с обратным знаком, а произведение корней равно свободному члену q:
      x

1 + x₂ = -p,      x₁x₂ = q.

Разложение квадратного уравнения на множители

Если известны оба корня квадратного уравнения, его можно разложить по формуле

ax² + bx + c = a(x — x₁)(x — x₂)

Примеры решения квадратных уравнений

Например. Найти корни квадратного уравнения: 2x² + 5x + 3 = 0
D = 5² — 4·3·2 = 25 — 24 = 1

x1 =  —5 + √1  = -1, 2·2

x2 =  —5 — √1  = -1 1 2·2 2

Упражнения. Квадратные уравнения.

Тесты по теме «Квадратные уравнения» онлайн

• Неполные квадратные уравнения. Уравнение x2 =a.

  20.12.2020 208 0

  Тест предназначен для учащихся средней школы  для проверки уровня знаний по  теме «Уравнение  x2 =a».

• Нахождение корней квадратных уравнений (полных и неполных)

  18.12.2020 5650 0

  Тест содержит 15 заданий на нахождение корней квадратных уравнений. Задания в тест выбираются случайным образом из общей базы заданий (50 полных уравнений и 50 неполных). Критерии: «3» 50-69%, «4» 70-90%, «5» 91-100%. Оценка выставляется сразу после прохождения теста.  

• Квадратные и биквадратные уравнения

  16.04.2020 2087 0

  Тест для проверки умения решать квадратные и биквадратные уравнения, раскладывать квадратный трёхчлен на множители. Составлен по учебнику «Алгебра 8 класс» Мерзляк А.Г. и др. Задания с вводом числа и выбором из предложенных. Уровень сложности средний.

• Входной тест Алгебра 9

  24.07.2020 451 0

  Тест по Алгебре 9 класса направленный на выявление остаточных знаний учащихся.По времени не ограничен. Не торопитесь.

• Контрольный тест «Квадратные уравнения»

  05. 09.2020 1324 0

  Итоговый проверочный тест на закрепление темы «Решение квадратных уравнений». Состоит из 9 вопросов. За каждый правильный ответ ученик набирает 1 балл. В основном включает в себя задания с вводом нужного ответа.

• Дискриминант квадратного уравнения

  13.12.2020 3208 0

  В тест включено 11 заданий по теме «Дискриминант квадратного уравнения». Критерии: «3» от 50 до 69%, «4» от 70 до 90%, «5» от 91 до 100%. Оценка выставляется сразу после прохождения теста. 

• Квадратные уравнения (основные понятия)

  30.03.2020 532 0

  Данный текст ориентирован на проверку знаний по темам «Понятие квадратного уравнения» и «Неполные квадратные уравнения»

• Неполные квадратные уравнения

  17. 08.2020 2420 0

  Проверочный тест на закрепление темы «Неполные квадратные уравнения». Состоит из 7 вопросов. За каждый правильный ответ ученик набирает 1 балл. Включает в себя задания с выбором правильного ответа и с вводом нужного ответа.

• Тест по алгебре

  30.08.2019 1687

  В данном тесте содержится 20 вопросов по алгебре за 8 класс. Тест содержит вопросы по следующим темам: — Квадратные уравнения — Неравенства

• Алгебра. 7 класс. Квадратные уравнения

  21.04.2022 171 0

  Тест проверяет начальные знания о квадратных уравнениях и о дискриминанте

• Решение квадратных уравнений

  01. 11.2018 691 0

  Тест для учащихся 8 класса и старше. Контактные данные нужны только для отправки моих комментариев (ссылка на страницу VK,  электронная почта, WA). Если ответом к вопросу является дробное выражение — в ответе нужно указать десятичную дробь. Тест полезен в качестве проверки знаний при подготовке к экзаменам. Время прохождения ограничено — 30 минут. 

• ОУД.03 Математика. Рациональные, иррациональные, показательные и тригонометрические уравнения.

  04.06.2020 455 0

  Перед Вами тренировочный тест, проверяющий усвоение небольшой, логически завершенной части темы «Уравнения и неравенства». Содержание и уровень сложности включенных в него заданий, в основном, отвечают обязательным требованиям к математической подготовке студентов, обучающихся по специальностям технического профиля.

• Решите уравнение и выберите вариант ответа

  05.12.2020 127 0

  Тренировочный тест по теме «Решение простых тригонометрических уравнений». Предназначен учащимся 10-11 классов. 

• Теорема Виета

  13.11.2019 3569 0

  Использовать навыки нахождения корней уравнения с помощью теоремы Виета.  Первые уравнения с парамером в квадратном уравнении.

• Решение квадратных уравнений

  22. 12.2019 2257 0

  Тест предназначен для учащихся 8 класса после изучения темы «Квадратные уравнения»

• Формулы корней квадратного уравнения

  31.03.2020 2366 0

  Тест по теме «Формулы корней квадратного уравнения». В тесте 9 вопросов.

• Тест по математике

  15.04.2020 8 0

  Данный тест содержит 10 вопросов по дисциплине математика по теме «свойства функции» . Содержит задания на выбор одного правильного ответа, задания множественного выбора, задания на установление соответствия, задания на установление последовательности, задания открытой формы

• Квадратное уравнение.

  Теорема Виета

  07.05.2020 102 0

  Данный тест — контроль знаний по теме «Квадратное уравнение. Теорема Виета»

• Квадратное уравнение. Квадратный трехчлен

  13.05.2020 142 0

  За выполнение тестовых заданий вы сможете получить только 6 баллов, остальная часть оценки за контрольную работу — задания с развернутыми решениями

• Тест по модулю 2

  20.08.2020 10 0

  Привет, ребята! Пришло время показать свои знания на практике.  

• Теорема Виета

  05.09.2020 938 0

  Проверочный тест на закрепление темы «Теорема Виета». Состоит из 6 вопросов. За каждый правильный ответ ученик набирает 1 балл. Включает в себя задания с выбором правильного ответа, с вводом нужного ответа, в установлении соответствий.

• Квадратные уравнения

  14.11.2020 791 0

  Контрольный тест по теме «Квадратные уравнения» для 8 класса. Основная цель теста- проверка понимания и знания темы.

• Дискриминант квадратного уравнения

  28. 11.2020 37 0

  Проверим умеешь ли ты вычислять  дискриминант? Для выполнения заданий вам нужно сначала решить в тетради, затем написать ваш ответ в поле для ответа.

• Квадратные уравнения. Основные понятия.

  13.12.2020 1512 0

  Данный тест предназначен для тренировки и закрепления понятий «вид квадратного уравнения», «коэффициенты квадратного уравнения», «алгоритм решения полного квадратного уравнения». В тесте 10 заданий. Критерии: «3» от 50 до 69%, «4» от 70 до 90%, «5» от 91 до 100%. Оценка выставляется сразу после прохождения теста. 

• Нахождение корней квадратных уравнений (неполных)

  18. 12.2020 440 0

  Тест содержит 20 заданий на нахождение корней полных и неполных квадратных уравнений. Задания в тест выбираются случайным образом из общей базы заданий (50 уравнений). Критерии: «3» 50-69%, «4» 70-90%, «5» 91-100%. Оценка выставляется сразу после прохождения теста 

• Квадратные уравнения. Основные понятия.

  21.12.2020 41 0

  Тест предназначен для учащихся средней школы  для проверки уровня знаний по  теме «Неполные квадратные уравнения. Основные понятия»

• Квадратные уравнения, коэффициенты, дискриминант.

  24. 12.2020 58 0

  Тест предназначен для обучающихся средней школы  для проверки уровня знаний по  теме «Квадратные уравнения. Основнпые понятия». В тесте представлены вопросы на определение коэффициентов квадратного уравнения, применение формулы дискриминанта для определения количества корней квадратного уравнения.

• Неполные квадратные уравнения.

  20.02.2021 24 0

  Проверочная работа по теме «Неполные квадратные уравнения» предназначена для проверки знаний по указанной теме. Работа составлена на основе прототипов заданий ОГЭ по математике.

• Решение полных квадратных уравнений.

  

  20.02.2021 36 0

  Проверочная работа по теме «Решение полных квадратных уравнений» предназначена для проверки знаний по указанной теме. Работа составлена на основе прототипов заданий ОГЭ по математике.

• Квадратные уравнения

  14.03.2021 193 0

  Этот тест предназначен для учеников 8 класса, изучающих тему Квадратные уравнения и может быть использован на уроках обощения или при подготовке к контрольной работе

• Квадратные уравнения

  05.04.2021 65 0

  тест по подготовке к ГИА по теме «Квадратные уравнения»

• Теория по теме «Квадратные уравнения»

  15. 07.2021 29 0

  Опрос по теме «Зависимость количества корней квадратного уравнения от знака дискриминаната»

• Квадратные уравнения

  09.11.2021 10 0

  Тест разработан для текущего тестирования для 8 класса по теме: «Квадратные уравнения» Тест по теме «Квадратные уравнения. Основные понятия» Данный тест предназначен для тренировки и закрепления понятий «вид квадратного уравнения», «коэффициенты квадратного уравнения», «алгоритм решения полного квадратного уравнения». Тест состоит из 10 вопросов.Оценка выставляется сразу после прохождения теста. В заданиях с 1 по 8 выберите один ответ    из предложенных вариантов ответов. В заданиях 9 и 10 запишите  ответ. Удачи!

• ЕГЭ 2023 — Задание- Решить рациональные уравнения и выражения

  09. 11.2021 5 0

   ЕГЭ 2023 — Задание-  Рациональные уравнения и выражения

• Целое уравнение и его корни. 9 класс

  23.11.2021 243 0

  Тест по теме «Целое уравнение и его корни», 9 класс. Квадратное уравнение, кубическое, биквадратное и т.д.

• Теорема Виета

  09.02.2022 233 0

  Тест по алгебре для обучающихся в 8 классе по теме «Теорема Виета»

Формула дискриминанта — правила и примеры вычисления корней квадратных уравнений

Существует несколько способов решений квадратного уравнения. Один из них — применение формулы дискриминанта. Помня общее выражение и алгоритм, вычислить корни степенного равенства второй степени не составит труда. Естественно, нужно хорошо знать арифметику, выполнение действий с дробями и сам принцип. При этом дискриминант — это не просто удобный параметр, используя который, можно найти решение. Это ещё и характеристика, имеющая объяснимый геометрический смысл.

Содержание

• Общие сведения
• Смысл дискриминанта
• Взаимосвязь параметра
• Типовые примеры
• Вычисления на онлайн-калькуляторе

Общие сведения

Решение квадратных уравнений — одно из ключевых моментов в математике. Ещё древние вавилоняне и греки пытались найти закономерности при решении таких равенств. Но первым, кто описал методы нахождения дополнением квадрата, был индийский философ Будхаяма. Именно он предложил записывать уравнения в виде: ax ² = c и ax ² + bx = c. В дальнейшем способы усовершенствовались. Так, Евклид предложил метод геометрического вычисления ответа.

Но наиболее значимым стало открытие Буля. Изучая формулы различных уравнений, он пришёл к выводу, что выражения почти всегда можно упростить, заменив переменные другим набором, содержащим новые неизвестные. При этом, найдя их, определить первоначальные уже не составляет труда.

Такой способ был применён и к квадратному уравнению. Благодаря ему стало возможным упростить квадратичную форму с двумя переменными, используя дискриминант. Это понятие тесно связано с многочленом, имеющим следующий вид: d (m) = a 0 *mⁿ + a 1 *m^n-1 + a 2 *m^n-2 + … + a n-1 *m + a n, где m — искомое неизвестное, a n, a n-1, a n-2, … a 1 и a 0 — числовые постоянные.

Термин «дискриминант» был придуман не математиками, но успешно стал ими использоваться при вычислении квадратичных функций. Произошёл он от латинского слова discriminans, что в дословном переводе означает «разделяющий». Важной величиной стало значение, придуманное Булем и имеющее вид b2 — 4ac. Учёный открыл, что после того как переменные линейно изменятся, дискриминант будет равняться первоначальному, умноженному на член, находимому из функции поведения неизвестных.

При решении равенств, содержащих формулу дискриминанта и его корней, используют формулу для быстрого определения количества возможных решений и их числового нахождения. Математически определение записывают следующим образом: p (x) = m + mx + ⋯ + mx, m ≠ 0, где: D (p) = m∏(m − m). То есть дискриминантом многочлена p (x) является сумма произведений корней на неизвестный коэффициент в основном поле их существования.

Смысл дискриминанта

Дискриминант — одно из эффективных решений квадратных выражений. С его помощью легко можно выявить, сколько корней имеет уравнение или установить, что их нет. Применять его можно как к полным квадратным равенствам, так и неполным. Но всё же во втором случае использовать дискриминант не нужно.

Эта тема изучается в седьмом и восьмом классе средней школы. Лучше понять смысл параметра поможет простой пример. Пусть имеется уравнение вида m² + 2m — 8 = 0. Не имея понятие о дискриминанте, решение уравнения сводится к приведению его к формуле квадрата суммы m² + 2m +1 — 1- 8 = 0. Добавление и вычитание единицы возможно, так как в итоге получается сложение с нулём.

Первые три члена представляют собой квадрат суммы, который можно свернуть по формуле сокращённого умножения до вида a² +2ab + b² = (a+b)². Отсюда, применительно к рассматриваемому примеру, получится: (m + 1)² — 1 — 8 = 0. После преобразований с переносом неизвестного в одну сторону (а известных — в другую) и раскрытием скобки получится равенство: (m + 1)² = 9. То есть возможными решениями будут m = 2 для (m + 1) = 3 и m = -4 для (m + 1) = -3.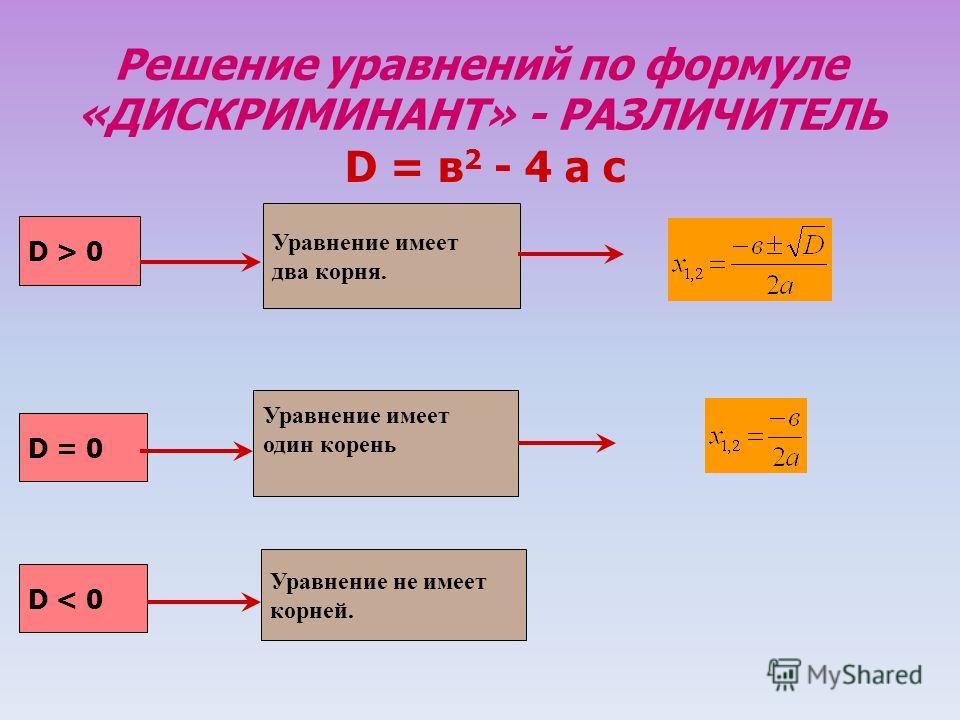

В общем виде все эти преобразования можно выполнить в следующей последовательности:

Уравнение am² + bm + c = 0 нужно переписать в приведённом виде, то есть разделить каждый член на первый коэффициент: m² + bm / a + c / a = 0.

Согласно формуле сокращённого умножения нужно добиться того, чтобы при неизвестном во втором члене стояло удвоенное произведение. Поэтому числитель и знаменатель нужно помножить на двойку: m² + 2bm / 2a + c / a = 0.

Полученное выражение стоит переписать в более наглядном виде m ² + 2 m * (b /2 a) + c / a = 0. Это равенство являлось бы приведённым к формуле сокращённого умножения, если бы в последнем члене был квадрат.

Ко второму члену следует прибавить и вычесть (b/2a)². В итоге получится m² + 2m * (b/2a) + (b/2a)² — (b/2a)² + c/a = 0.

Первые три слагаемые — это классическая формула квадрата суммы. Применив её, получится: (m + b/2a)² = (b/2a)² — c/a.

Затем нужно раскрыть скобки и привести к общему знаменателю. Получится конструкция вида (m + b/2a)² = b 2 -4 ac /4 a ².

Умножив на 4a² обе части. Выражение примет вид (2 am + b)² = b ² — 4 ac.

Многочлен b2 — 4ac было решено принять за дискриминант. Это выражение по сути и определяет возможность существования решений и количество корней. Выполнив его расчёт, фактически и находится ответ уравнения.

Взаимосвязь параметра

Объяснение дискриминанта имеет и графическое обоснование. Физически задача заключается в комплексном подходе установления взаимосвязи. Фактически это фиксирование нулей параболы уравнения, то есть точек, в которой она пересекает ось абсциссы. Знак при переменной в квадрате будет определять положение веток параболы. Они будут идти вверх при a > 0, и вниз, если a < 0.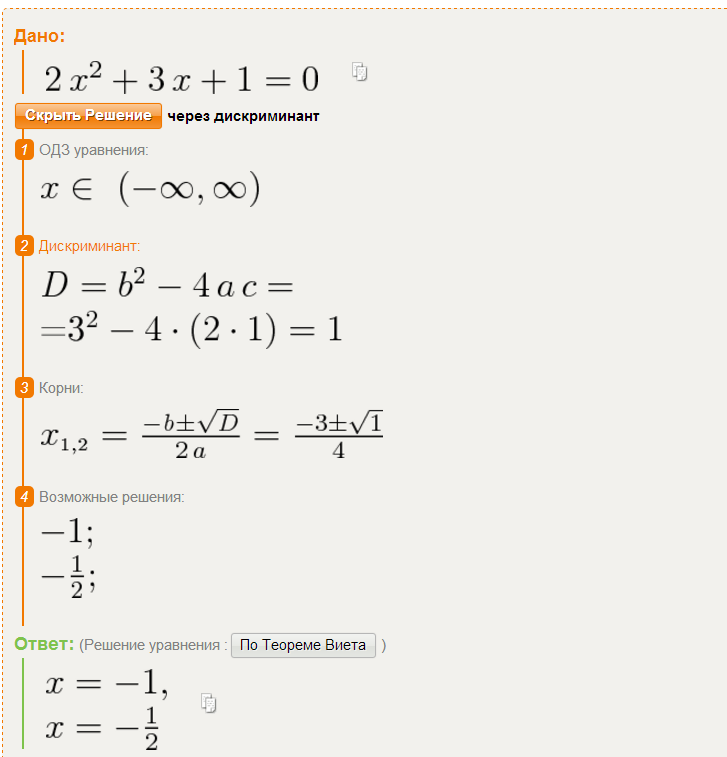

Исходя из этого, дискриминант равняется отношению суммы или разности числового коэффициента, стоящего возле неизвестного в первой степени с корнем квадратным из b ² — 4 ac к удвоенному произведению первого коэффициента в уравнениях x1 = (- b + √ b ² — 4 ac) / 2a; x2 = (- b — √ b ² — 4 ac) / 2a. Подкоренное выражение называют формулой сокращённого дискриминанта.

Дискриминант при нахождении корней уравнения может принимать три значения:

Отрицательное. В случае, когда он меньше нуля, точный квадрат должен равняться числу с минусом, чего не может быть из-за свойств квадратной степени. Поэтому при таком положении вещей решений или действительных корней у уравнения нет. График уравнения не пересекает ось абсциссы.

Равное нулю. Это состояние характеризуется уравнением вида: (2 am + b)² = 0. Так как квадрат числа может быть равен нулю, только если это число нулевое, то рассматриваемое уравнение можно переписать как m = — b / 2a. Это и есть упрощённая формула при дискриминанте, равному 0. На графике существует лишь одна точка пересечения с осью абсциссы.

Положительное. Это наиболее распространённый случай и самый тяжёлый для проведения расчётов. При нём из обеих частей уравнения теоремы (2 am + b) ² = b ² — 4 ac надо извлечь квадратный корень. В итоге получится 2am + b =± √D. Тут следует отметить следующее: минус возникает из-за того, что возводимое в квадрат число может быть как положительное, так и отрицательное. Например, 9² = 81 и -9² = 81. Из этого выражения можно выразить неизвестное. Оно будет равняться половинному значению m = (-b ± √D) / 2a. Парабола пересекает ось абсцисс в двух точках.

Последнее выражение является формулой корней квадратного уравнения. Именно с её помощью могут решаться равенства, в степени которых стоит двойка. Через дискриминант можно вычислять корни и уравнений больших порядков. Для этого используются приёмы понижения степени до квадратного. Но эти операции учащиеся начинают изучать на уроках в выпускном классе, когда проходят решение уравнений n-го порядка.

Типовые примеры

Даже зная правило поиска корней через дискриминант, научиться быстро вычислять корни уравнения не получится, если не практиковаться. Поэтому решение практических задач обязательно входит школьную в программу обучения:

Дано равенство 6x² — 13x +2 = 0. Нужно определить количество его корней, если они существуют, их числовые значения. В первую очередь нужно нарисовать таблицу, в которую выписаны все заданные коэффициенты. Так: a = 6; b = -13; c = 2. Эти значения нужно подставить в формулу дискриминанта и найти его: D = b² — 4ac = (-13)² — 4 * 6 *2 = 149 — 68 = 121. То есть D больше нуля. Значит, согласно правилу, уравнение будет иметь два корня. Теперь их нужно рассчитать: x1 = (13 + √126) / 2 * 6 = 2; x2 = (13 — √126) / 2 * 6 = 1/6. Задание решено.

Определить возможность решения уравнения 4m² — 2m — 3 = 2. Для приведения к удобному виду двойку нужно перенести влево. В итоге получится 4m² — 2m — 5 =0. Дискриминант равняется: D = 4 — 4 * 4 * (-5) = 4 + 80 = 84. Так как он больше нуля, то корней будет два. Тут сложность заключается в том, что нет целого числа, которое равнялось бы корню из √84. Однако, √84 = √4 * √21 = 2 √21. Используя формулы, получаем что m = (2 ± 2√21) / 2 * 4. Двойку можно вынести в числителе за скобки, получив тем самым удобную запись: m = (2 * (1 ±√21) / 2 * 4 = (1 ± √21) / 4. Это выражение и есть искомое решение.

Решить уравнение: x /3 — x² / 4 + 1 /6 = 3x / 2 — 4x² / 3. Для упрощения равенства нужно правую и левую сторону умножить на двенадцать: 12x / 3 — 12 * x² / 4 + 12 /6 = (3 * 12x) / 2 — (4 * 12x²) / 3. Получится 4 x — 3 x ² + 2 = 18 x — 16 x ². Члены нужно привести к стандарту: 4 x — 3 x ² + 2 — 18 x + 16 x ² = 13 x ² — 14 x + 2 = 0. Считаем дискриминант: D = (-14)² — 4 * 13 * 2 = 92. Он больше нуля, поэтому есть смысл искать корни: X = (14 ± √ 92) / 2 * 13 = (14 ± 2 √ 23) / 2 * 13 = 2 (7±√23) / 2 *13 = (7± √23) /13.

Таким образом, любое выражение нужно стремиться переписать так, чтобы оно приняло классический вид. Это может быть умножение или деление на какое-либо число, поиск общего знаменателя. А уже после нужно искать дискриминант, по виду которого можно определить, есть ли смысл в дальнейшем нахождении корней уравнения.

Вычисления на онлайн-калькуляторе

Поиск решений уравнения через дискриминант — довольно простая тема. Необходимо запомнить всего две формулы и свойства, зависящие от значения дискриминанта. Но на практике попадаются примеры содержащие интегралы, логарифмы, экспоненциальные функции. При этом всё это может быть записано в виде сложных дробей.

Решая задания самостоятельно, даже имея большой опыт и знания, есть вероятность допущения ошибки. Поэтому при вычислении сложных примеров стоит использовать онлайн-калькуляторы.

Из сервисов, предлагающих такие услуги, можно отметить:

• Math.semestr;
• Kontrolnaya-rabota;
• Onlinemschool;
• Wpcalc;
• Webmath.

Эти российские сайты. Их интерфейс интуитивно понятен. Для выполнения вычислений не нужно указывать персональные данные или платить за услуги. От пользователя лишь требуется записать в предложенную форму квадратное уравнение или даже матрицу, состоящую из них. Программа автоматически выполнит нужный расчёт и предоставит пошаговое решение. Кроме того, на сайтах решателей уравнений содержится в кратком виде теоретический материал и типовые примеры с подробным решением.

Даже ничего не понимающий в дискриминантах человек, воспользовавшись онлайн-калькулятором несколько раз, сможет восполнить пробелы в знаниях, самостоятельно научиться решать примеры, узнает, как правильно должен писаться дискриминант. Использование онлайн-сайтов для математических решений позволяет сэкономить время и получить точный результат.

Предыдущая

МатематикаТранспортир — как правильно пользоваться инструментом для построения и измерения углов?

Следующая

МатематикаКак решать пропорции — правила, методы и примеры вычислений

Калькулятор дискриминанта онлайн, пошаговое объяснение

В случае квадратных уравнений дискриминант обычно используется для определения характера корней. Хотя определить дискриминант для любого многочлена сложно, мы можем использовать формулы для получения дискриминанта квадратных и кубических уравнений.

Этот онлайн-калькулятор вычисляет дискриминант квадратного полинома, а также многочленов более высоких степеней.

В алгебре дискриминант полинома представляет собой полиномиальную функцию его коэффициентов, которая позволяет вывести некоторые свойства корней без их вычисления.

Вероятно, вы знакомы с дискриминантной формулой квадратного многочлена ax²+bx+c, которая равна b²-4ac, и используете ее для вычисления корней.

Дискриминант, с другой стороны, позволяет нам вывести некоторые корневые атрибуты, не вычисляя их. Он равен нулю в случае квадратного многочлена тогда и только тогда, когда он имеет двойной корень. Если многочлен имеет два действительных корня, он положителен; если корни комплексные, он отрицателен.

Дискриминант вычисляется с помощью калькулятора ниже, и вы можете прочитать больше о дискриминантах прямо под ним.

Узнайте больше о дискриминанте, включая его формулы, а также о связи между дискриминантом и природой корней.

Содержание

Что такое дискриминантный калькулятор?

Калькулятор дискриминанта — это бесплатное онлайн-приложение, которое вычисляет значение дискриминанта для предоставленных коэффициентов квадратного уравнения. Наш дискриминантный онлайн-калькулятор ускоряет и упрощает вычисления, отображая результат за доли секунды. Спасибо, что посетили наш дискриминантный калькулятор. Когда вам нужно быстро найти дискриминант полиномов от двух до пяти степеней, таких как квадратичные, кубические, четвертые или пятые полиномы, используйте его без зазрения совести. Нужно ли изучать дискриминант в математике? Или как выглядит математическая формула дискриминанта? Пожалуйста, прокрутите вниз!

Читайте также: Калькулятор двойных интегралов: определение, примеры

Дискриминант определяется математически, и в следующих разделах объясняется, как найти дискриминант многочлена.

Мы посвящаем целый раздел дискриминанту квадратного уравнения, потому что знаем, как часто они используются. Однако мы не останавливаемся на второй степени. Проходим весь путь до пятого.

Дискриминантный калькулятор шаг за шагом

Ниже описано, как использовать дискриминантный калькулятор:

Шаг 1: Заполните поля ввода значениями коэффициентов, такими как «a», «b» и «c».

Затем, шаг 2: Чтобы получить результат, нажмите кнопку «Решить».

Затем, шаг 3: В поле вывода будет представлено значение дискриминанта.

Определение калькулятора дискриминанта

В арифметике дискриминант полинома является функцией коэффициентов полинома. Это полезно для выяснения того, какие решения имеет полиномиальное уравнение, без необходимости их нахождения. Он различает решения уравнения (как равные и неравные, действительные и недействительные), поэтому название «дискриминант». Обычно он обозначается ∆ или D. Значением дискриминанта может быть любое действительное число (т. е. положительное, отрицательное или 0). 9{n(n-1)/2}] / A_n × Res_x (A, A’)

, где Res — первое производное A’ и результат A. Определитель матрицы Сильвестра A и A’ равен исход.

A равно ax²+bx+c в случае квадратичного многочлена, а A’ равно 2ax+b. Вы получите b²-4ac, если выпишете матрицу Сильвестра для этих двух многочленов и получите определитель.

Калькулятор дискриминанта с шагами

Дискриминант — это функция коэффициентов полиномиального уравнения, которая показывает природу корней данного уравнения. Для его обозначения используется символ ∆ (читается как ∆). Продолжайте читать, если вас беспокоит фраза «что вам говорит дискриминант».

Кроме того, используйте этот онлайн-калькулятор квадратичных формул, чтобы решить квадратную задачу, используя квадратичную формулу или метод полного квадрата.

Калькулятор дискриминанта Характер корней:

В квадратном уравнении:

Характер корней определяется дискриминантом квадратного уравнения.

• Корни действительны и иррациональны, если ∆ больше 0 и не является полным квадратом.
• Тогда корни эквивалентны и вещественны, если ∆ = 0,
• Тогда корни мнимые, если ∆ меньше нуля.
• Аналогично, корни разумны, если ∆ — полный квадрат.

В кубическом уравнении:

Характер корней определяется дискриминантом кубического уравнения.

• Все три корня действительны, если ∆ больше нуля.
• Если ∆ меньше 0, то один корень вещественный, а два других — комплексно-сопряженные.
• Два корня равны, если ∆ = 0.

В уравнении четвертой степени:

Характер корней определяется дискриминантом уравнения четвертой степени.

• Если ∆ больше 0, все четыре корня действительны.
• Два корня действительные и два корня сложные, если ∆ меньше 0.
• корни сопряжены
• Если ∆ = 0, два или более корня должны быть равны. Доступно шесть вариантов:
• Существует три уникальных действительных корня, один из которых двойной.
• Оба истинных корня двойные и раздельные.
• Имеются два отдельных действительных корня, один из которых имеет кратность три.
• Один из четырех действительных корней кратности четыре.
• Два комплексных корня и один действительный двойной корень
• Пара корней с двойными комплексами.

Калькулятор дискриминанта Количество корней:

В квадратном уравнении:

Количество корней в квадратном уравнении определяется дискриминантом уравнения.

• Корней квадратного уравнения два.

В кубическом уравнении:

Дискриминант кубического уравнения определяет количество корней в уравнении.

• Корни кубического уравнения равны трем.

В уравнении четвертой степени:

Дискриминант уравнения четвертой степени определяет количество корней в уравнении.

• Корней уравнения четвертой степени четыре.

Онлайн-калькулятор дискриминанта отображает характер корней в уравнениях четвертой степени, а также может использоваться для определения характера корней в кубических и квадратных уравнениях.

Калькулятор дискриминанта в терминах параболы

Форма параболы на графике определяется дискриминантом уравнения.

• Парабола не пересекает ось x координатной плоскости, если ∆ больше 0.
• Если ∆ меньше нуля, парабола дважды пересекает ось x координатной плоскости.
• Если ∆ = 0, парабола касается оси x координатной плоскости.

Свойства калькулятора дискриминанта

Мы можем вывести некоторые фундаментальные аспекты дискриминантов из арифметической формулы для дискриминантов, представленной в предыдущих разделах.

Предположим, что D(p) является дискриминантом p, как определено выше. Значения D(p) следующие:

Во-первых, D(p) всегда является действительным целым числом, так как p является вещественным полиномом.

Тогда D(p) = 0 тогда и только тогда, когда p имеет кратный корень.

Аналогично, D(p) больше 0 тогда и только тогда, когда количество недействительных корней p кратно четырем (включая ноль).

В частности, D(p) больше 0, если все корни вещественные и простые.

С точки зрения дискриминантной инвариантности имеем:

При трансляции D(p) инвариантно:

Если q(x) = p(x + a), то D(q) = D(p).

D(p) инвариантно (с точностью до масштаба) относительно гомотетии:

Если q(x) = p(a * x), то D(q) = aⁿ⁽ⁿ⁻¹⁾D(p).

Дискриминант Калькулятор формулы квадратного уравнения

Рассмотрим квадратичный полином ax² + bx + c. Формула для его дискриминанта:

b² – 4ac

Как мы все помним, квадратный корень из этого дискриминанта появляется в формуле для корней квадратного многочлена:

[-b ± √(b² – 4ac)] / (2a)

Мы можем вывести по знаку дискриминанта без вычисления корней:

D > 0, если многочлен имеет два различных действительных корня; D 0, если многочлен имеет пару сопряженных комплексных корней; и D = 0, если многочлен имеет двойной корень.

Кроме того, если коэффициенты a, b и c рациональны, то оба корня полинома рациональны тогда и только тогда, когда D является квадратом рационального числа.

D больше 0 относительно параболы в реальной плоскости тогда и только тогда, когда парабола не пересекает горизонтальную ось;

Если парабола касается горизонтальной оси в двух точках, D меньше 0; если парабола касается (касается) горизонтальной оси, то D равно 0.

Помните, что квадратные уравнения можно решить, заполнив квадрат!

Дискриминант Калькулятор полиномов высших степеней

Как мы показали, общий квадратичный дискриминант имеет только два члена. С другой стороны, дискриминант усложняется по мере увеличения степени многочлена:

• Общий кубический дискриминант состоит из пяти членов.
• С другой стороны, дискриминант квартики состоит из 16 членов.
• Тогда дискриминант квинтики, с другой стороны, имеет 59 слов.
• Тогда дискриминант секстанта содержит 246 слов.
• Точно так же дискриминант скептика, с другой стороны, имеет 1103 слова.

Эти числа формируют последовательность OEIS A007878. Там вы найдете еще несколько терминов.

Дискриминант Калькулятор кубического многочлена

Рассмотрим кубический многочлен ax³ + bx² + cx + d. Его дискриминантная формула выглядит так:

b²c² – 4ac³ – 4b³d – 27a²d² + 18abcd.

Имеем,

D больше 0, если в корнях три различных действительных числа.

Аналогично, D меньше 0, если имеется один действительный корень и два комплексно-сопряженных корня.

Тогда D = 0, если хотя бы два корня равны (один корень кратности 3 или два различных действительных корня, один из которых двукратный).

Дискриминант Калькулятор полинома четвертой степени

Рассмотрим многочлен четвертой степени ax⁴ + bx³ + cx² + dx + e. Формула для его дискриминантного чтения:

256A³E³ — 192A²BDE² — 128A²C²E² + 144A²CD²E — 27A²D⁴ + 144AB²CE² — 6AB²D²E — 80ABC²DE + 18ABCD³ + 16AC⁴E — 4AC²D — 27B⁴ED + 18Bâчены — 4B³ -4B³.

Если имеется четыре отдельных действительных корня или четыре различных недействительных корня, D больше 0. (две пары сопряженных комплексных корней).

Если имеются два отдельных действительных корня и два различных недействительных корня, D меньше 0. (одна пара сопряженных комплексных корней).

D = 0 тогда и только тогда, когда существуют два или более одинаковых корня. Доступно шесть вариантов:

• Три отдельных действительных корня, один из которых двойной.
• Два уникальных действительных корня, оба двойные.
• Тогда два уникальных действительных корня, один из которых имеет три кратности.
• Один действительный корень с четырьмя кратностями.
• Аналогично, один вещественный двойной корень и два невещественных комплексно-сопряженных корня.
• Тогда два двойных невещественных комплексно-сопряженных корня.

Дискриминант Калькулятор многочлена пятой степени

Мы не приводим формулу как есть, с 59 членами, каждое из которых является мономом восьми степеней от шести переменных.

Вам может быть интересно, как найти дискриминант пятичлена пятой степени.

К счастью, у нас есть дискриминантный калькулятор, который включает эту формулу. Когда вам нужно рассмотреть многочлен пятой степени, это инструмент для использования.

После этого используйте следующий набор правил, чтобы выяснить, каковы свойства вашего многочлена:

Если имеется пять уникальных действительных корней или один действительный корень и две пары недействительных комплексно-сопряженных корней, D больше 0.

Если существуют три уникальных действительных корня и одна пара недействительных комплексно-сопряженных корней, D меньше 0.

D = 0 тогда и только тогда, когда существуют два или более одинаковых корня. Есть четыре варианта:

• Шесть различных ситуаций только с подлинными корнями.
• Один вещественный корень кратности три и одна пара невещественных комплексно-сопряженных корней.
• Затем один действительный одиночный корень и одна пара невещественных комплексно-сопряженных двойных корней
• Аналогично, один действительный одиночный корень и одна пара невещественных комплексно сопряженных двойных корней

Стандартная форма калькулятора дискриминанта

Стандартная форма дискриминанта для квадратного уравнения ax² + bx + c = 0:

Дискриминант, D = b² – 4ac

Где

• а — коэффициент x².
• b — коэффициент при x.
• c — постоянный член.

Как пользоваться калькулятором дискриминанта

Чтобы использовать калькулятор дискриминанта, выполните следующие действия:

• Сначала выберите степень многочлена, которую вы хотите рассмотреть. Выбирайте полиномы со степенями от 2 до 5, такие как квадратичные (степень 2), кубические (степень 3), четвертые (степень 4) или пятые (степень 5) полиномы.
• Если вам нужно, например, найти дискриминант квадратного уравнения, используйте секунду в качестве степени.
• Введите все коэффициенты полинома, включая нулевые.
• Наслаждайтесь результатом, который сразу дает наш дискриминантный калькулятор!

Как найти дискриминант с помощью калькулятора дискриминанта?

Калькулятор дискриминанта подскажет, как шаг за шагом решать предложенные уравнения. Если вам нужно решить квадратные уравнения или полиномиальные уравнения более высокой степени, этот калькулятор может помочь! Следуйте этим вводам, чтобы получить дискриминант уравнений:

Входные данные:

Для начала выберите степень полинома, для которого вы хотите получить дискриминант, из выпадающего меню этого инструмента.

Затем для выбранного уравнения введите значения коэффициентов. (Введите значения на основе выбранной степени полинома)

Наконец, нажмите клавишу компьютера.

Выводы:

Калькулятор дискриминанта покажет следующее:

Затем дискриминант предоставленного уравнения.

Затем естественное состояние корней.

Завершите вычисление дискриминанта.

Дискриминант Калькулятор квадратного уравнения

Дискриминант квадратного уравнения

Дискриминант квадратного уравнения после ax²+bx+c=0 равен b²−4ac. Для дискриминанта используется обозначение Δ (дельта), поэтому мы имеем Δ=b²−4ac.

В калькуляторе есть функция, позволяющая вычислять дискриминант квадратных уравнений онлайн. Чтобы найти дискриминант уравнения, выполните следующие действия: 3x²+4x+3=0, введите дискриминант(3⋅x²+4⋅x+3=0;x), калькулятор выдаст результат -20.

Вычисление дискриминанта многочлена позволяет определить, сколько корней имеет квадратное уравнение:

Когда вычисление дискриминанта дает отрицательное значение, уравнение не имеет корня.

Однако, когда дискриминант равен нулю, уравнение имеет корень.

Когда дискриминант дает положительное число, уравнение имеет два уникальных корня.

Однако для поиска корней уравнения можно использовать решатель уравнений.

Примеры дискриминантного калькулятора

Пример 1

Найдите дискриминант следующего уравнения: √3×2 + 10x − 8√3 = 0. 0. Сравнивая это с ax² + bx + c = 0, мы получаем a = √3, b = 10 и c = -8√3.

Формула квадратичного дискриминанта:

D = b² – 4ac

= (10)2 – 4(√3)(-8√3)

= 100 + 96

= 196

Ответ: Дискриминант2 = 196.

Пример 2

Чему равен дискриминант квадратного уравнения 9z² − 6b²z − (a⁴ − b⁴) = 0.

Решение:

Сравнивая данное уравнение с ax² + bx + c = 0, получаем a = 9, b = — 6b², а c = – (a⁴ − b⁴). Его дискриминант:

D = b² – 4ac

= (-6b²)² – 4 (9) [-(a⁴ − b⁴)]

= 36b⁴ + 36a⁴ – 36b⁴

= 36a⁴

Ответ: Дискриминант данного квадратного уравнения есть 36a4.

Дискриминантный калькулятор Многопараметрический

Определите, имеют ли приведенные ниже квадратные уравнения два действительных корня, один действительный корень или не имеют действительных корней. (а) 3x² — 5x — 7 = 0 (б) 2x² + 3x + 3=0.

Решение:

(a) Сравнивая данное уравнение с ax² + bx + c = 0, мы получаем a = 3, b = -5 и c = -7. Его дискриминант равен

D = b² – 4ac

= (-5)2 – 4(3)(-7)

= 25 + 84

= 109

В результате у нас есть положительный дискриминант, и уравнение имеет два действительных корня.

(b) Сравнивая данное уравнение с ax² + bx + c = 0, мы получаем a = 2, b = 3 и c = 3. Его дискриминант равен

D = b² – 4ac

= (3 )² – 4(2)(3)

= 9 – 24

= -15

В результате получаем отрицательный дискриминант, и уравнение не имеет действительных корней.

Ответ: а) два действительных корня; б) действительных корней нет.

Дискриминантный калькулятор с k

Найдите значения k

Шаг 1 из 2: Запишите данное квадратное уравнение. Данное квадратное уравнение есть. kx² – 14x + 8 = 0,

Затем, шаг 2 :

Найдите значение k. Здесь дано, что один корень квадратного уравнения kx² – 14x + 8 = 0 равен 2. Итак, по заданному условию. Следовательно, требуемое значение k = 5.

Часто задаваемые вопросы о калькуляторе дискриминанта

Что такое дискриминант?

В математике дискриминант является функцией полиномиальных коэффициентов и определен для полиномов. Оно описывает характер корней или, другими словами, различает их. Дискриминант квадратного уравнения, например, используется для нахождения:

• Сколько на нем корней?
• Настоящие ли корни?

Что такое дискриминантная формула?

Различные многочлены имеют разные формулы дискриминанта:

ИЛИ D = b² – 4ac – дискриминант квадратного уравнения ax² + bx + c = 0.

D = b²c² – 4ac³ – 4b³d – 27a²d² + 18abcd – дискриминант кубическое уравнение ax³ + bx² + cx + d = 0.

Как вычислить дискриминант квадратного уравнения?

Чтобы найти дискриминант квадратного уравнения, сделайте следующее:

Сравните предыдущее уравнение с ax² + bx + c = 0, чтобы найти a, b и c.

Подставить значения D = b²- 4ac в дискриминантную формулу.

Что делать, если дискриминант = 0?

Если дискриминант квадратного уравнения ax² + bx + c = 0 равен 0 (т. е. если b² – 4ac = 0), то квадратная формула принимает вид x = -b/2a и, следовательно, квадратное уравнение имеет только один действительный корень .

Что говорит нам положительный дискриминант?

Если дискриминант квадратного уравнения ax² + bx + c = 0 положителен (т. е. b² – 4ac больше 0), квадратная формула принимает вид x = (-b ± √(положительное число)) / 2a, при этом только два действительных и различных корня.

Что говорит нам отрицательный дискриминант?

Если дискриминант квадратного уравнения ax² + bx + c = 0 отрицателен (т. е. b² – 4ac меньше 0), квадратичная формула принимает вид x = (-b ± √(отрицательное число)) / 2a, при этом всего два сложных и отдельных корня.

Какая формула для дискриминантов кубических уравнений?

Дискриминант кубического уравнения выражается через его коэффициенты и определяется формулой ax³ + bx² + cx + d = 0 или D = b²c² − 4ac³ − 4b³d − 27a²d² + 18abcd.

Когда дискриминант равен нулю, сколько чисел будет иметь решение квадратного уравнения?

Компонент квадратного корня квадратной формулы, b²-4ac, является дискриминантом или определителем квадратного уравнения. Решение должно быть единственным, если дискриминант равен нулю. Решение не существует, если дискриминант меньше нуля. Если оно больше нуля, возможны два реальных решения уравнения.

Какие существуют формы квадратного уравнения?

Квадратное уравнение можно записать тремя различными способами.

Вершинная форма является факторизованной формой.

В этой ситуации обычная форма квадратного уравнения — y = ax² + bx + c, а дискриминант квадратного уравнения — b²- 4ac. y = (axe + c) (bx + d) — факторизованная форма квадратного уравнения. y = a (x + b)² + c — вершинная версия квадратного уравнения.

Необходимо отметить номера a, b и c.

В чем смысл квадратных уравнений?

В нашей повседневной жизни квадратные уравнения используются для расчета площадей, определения прибыли продукта и расчета скорости объекта, среди прочего. В квадратном уравнении будет хотя бы одна переменная в квадрате, которая записывается как ax² + bx + c = 0, где x — переменная, a, b и c — константы, а a не равно нулю. Чтобы определить ответ на задачу, используйте дискриминантную квадратичную функцию.

Что означает дискриминант 0?

Если дискриминант равен 0, это означает, что у вас есть 0 под квадратным корнем в квадратной формуле. Квадратный корень из нуля равен 0. В этом случае плюс и минус квадратной формулы просто исчезают. Остается только один вариант.

Калькулятор квадратного уравнения с шагами

Рабочий пример, иллюстрирующий, как работает калькулятор решения:

Решатель квадратного уравнения с пошаговым решением

Квадратное уравнение в основном представляет собой математическое выражение с одной переменной и формой 92+bx+c, \neq0 — заданное квадратное уравнение. Вещественное число «k» называется нулем квадратного многочлена тогда и только тогда, когда p(k)=0.

Есть 3 классических способа нахождения корней или нулей квадратного уравнения, а именно.

• Графики
• Квадратичная формула
• Завершение квадратного метода
• Метод факторинга

Квадратное уравнение является уравнением степени 2. Это означает, что наибольшая степень неизвестного или переменной равна 2. Обычно квадратное уравнение имеет два решения. 92= ​​и, таким образом, x=\sqrt{c} .

Наш калькулятор поможет вам найти значение x независимо от характера вашего квадратного уравнения.

Более интересный случай, когда все константы a,b,c отличны от нуля. Решение такой задачи – дело нетривиальное. К счастью, у нас есть 3 классических метода, которые помогут вам решить такое уравнение. Наш бесплатный онлайн-калькулятор алгебры поможет вам найти решение любого квадратного уравнения.

Как вы видели из вышеизложенного, вычисления, включающие нахождение квадратного корня, означают, что вы можете получить результаты как с действительными, так и с мнимыми частями. Наш онлайн-калькулятор алгебры также поддерживает мнимые числа. Точно так же калькулятор также распечатает как действительную, так и мнимую части корней вашего полиномиального уравнения.

Решатель квадратных уравнений с шагами

Самое приятное в использовании нашего онлайн-калькулятора то, что он показывает вам все операции. Это единственный калькулятор алгебры, который показывает вам пошаговое решение. Наш решатель квадратного уравнения шаг за шагом покажет вам всю работу вместе с необходимым объяснением. Это действительно идеальный способ выучить алгебру. Калькулятор не только поможет вам найти значение x, но также покажет вам, как манипулировать и решать квадратные уравнения онлайн. Вы можете научиться решать квадратные уравнения онлайн, сначала попробовав решить уравнения самостоятельно, а затем сравнив свои результаты с результатами калькулятора.

Решатель квадратных уравнений с помощью факторинга: алгебра 2 калькулятор факторинга

Факторинг — это один из основных способов решения квадратного уравнения. 2-4AC. Отрицательный Дискриминант означает, что полином не может быть разложен на некоторые действительные коэффициенты h,k. 92 — 4ac}}{ 2a }

С помощью этой формулы вы можете найти корни любого квадратного уравнения, просто подставив значения a,b,c в правильное положение в формуле.

Формула утверждает, что любой многочлен второй степени может быть решен по формуле где a,b,c — константы в уравнении соответственно. С помощью этого калькулятора легко найти корни любого уравнения без забот. Просто введите свою математику в текстовую область и нажмите кнопку расчета, чтобы найти решение. 92=-1 . С другой стороны, действительное решение означает, что все корни являются действительными числами.

Автоматический решатель квадратных уравнений позволяет вам видеть все шаги и работу с корнями вашего многочлена.

завершение формулы квадрата с помощью этого калькулятора с шагами

Квадратное уравнение формы ax ²  + bx + c = 0 для x, где a \ne 0 можно решить, используя формулу квадрата с помощью этого калькулятора. Это онлайн-калькулятор, способный заполнить 92=0

В более поздней форме уравнение легко решить, просто взяв квадратные корни с обеих сторон выражения. Это сводит LHS к многочлену первой степени, который можно решить с помощью факторизации и упрощения.

Хорошие квадратные уравнения (факторизуемые уравнения) не всегда имеют место. На самом деле, большинство квадратичных уравнений нельзя разложить на полиномы первой степени. Тем не менее мы можем ввести в такие уравнения идеальные квадраты, просто добавив константу.

92-4ас). Константа полезна для определения характера решения квадратного уравнения еще до того, как мы займемся его решением. Если квадратное уравнение имеет положительный дискриминант, то оно имеет два корня. Если D=0, то возможно одно ненулевое решение. Наконец, если D отрицательно, уравнение будет иметь комплексные корни. Комплексный корень будет иметь как действительную, так и мнимую часть.

Калькулятор квадратичных формул воображаемый

Квадратное уравнение с отрицательным дискриминантом всегда будет иметь по крайней мере 1 комплексный корень. Этот калькулятор поможет вам решить квадратные уравнения, используя формулу полного квадрата, даже если корни являются комплексными числами. 92-\frac{19}{4}=0

Шаг 4. Извлеките квадратный корень из обеих частей уравнения и упростите

x-\frac{3}{2}=\pm \sqrt{\frac{19 }{4}}

Шаг 5. Решение

x=\frac{(3+\sqrt{19})}{2}   ИЛИ  x=\frac{(3-\sqrt{19})}{2}

Решение квадратного уравнения с помощью калькулятора факторинга

Обратите внимание, что в приведенном выше примере мы сначала делим на 2, чтобы привести выражение к уравнению стандартной формы. Со стандартным уравнением теперь можно применить процедуру полного квадрата для определения решения.

Допустимые математические символы и их использование
Если вы решите написать свои математические выражения, вот список допустимых математических символов и операторов.

Дискриминантный калькулятор

Содержание

Калькулятор дискриминанта — это онлайн-инструмент, который предоставляет значение дискриминанта для заданных коэффициентов в квадратном уравнении. Онлайн-калькулятор дискриминанта STUDYQUERIES делает вычисления быстрее и проще, отображая значение за доли секунды.

Как использовать дискриминантный калькулятор?

Чтобы использовать дискриминантный калькулятор, выполните следующие действия:

• Шаг 1: Введите значения коэффициентов, такие как «a», «b» и «c», в соответствующие поля
• Шаг 2: Теперь нажмите «Рассчитать», чтобы увидеть результат
• Шаг 3: Значение дискриминанта отображается в поле вывода

Дискриминантный калькулятор 92-4ac}}{2a}$$

Его можно найти, используя квадратичную формулу для нахождения дискриминантной функции. Он представлен как b²-4ac, а дискриминант может быть нулевым, положительным или отрицательным. Это указывает, будет ли решение отсутствовать, одно решение или два решения.

Калькулятор единичного круга

Калькулятор разложения на неполные дроби

Калькулятор трансформации

Калькулятор интегрирования деталей

Дискриминантный калькулятор

Обратите внимание на следующие характеристики формулы дискриминантной алгебры:

• Нулевой дискриминант указывает на то, что существуют повторяющиеся действительные решения квадратного уравнения;
• В случае отрицательного дискриминанта ни одно из решений не является действительным;
• Квадратное уравнение имеет два различных решения, которые являются действительными числами для положительного дискриминанта.

Следующее квадратное уравнение показывает учащимся, как определить дискриминант, показывая различные решения. 92-4ac <0$$

Здесь,

a, b, c = действительные числа

а ≠ 0

дискриминант = отрицательный

Если радикал отрицательный, значение под ним будет отрицательным. Не существует реальных решений для нахождения квадратного корня из отрицательного числа, потому что вы не можете использовать действительные числа. Однако можно использовать мнимые числа. Тогда у вас будет два сложных решения: одно путем добавления мнимого квадратного корня, а другое путем его вычитания. 92-4ac >0 \ as\ a\ perfect\ квадрат\ as\ well$$

Здесь,

a, b, c = действительные числа

а ≠ 0

дискриминант = положительный и полный квадрат

Следовательно, корни квадратного уравнения неравны, действительны и рациональны.

Что следует помнить при использовании квадратичной формулы

• Для получения решения абсолютно необходимо правильно составить уравнение. 2 − 4ac$$. Он определяет количество и тип решений, которые имеет квадратное уравнение. Если дискриминант положительный, то существует 2 действительных решения. Если он равен 0, существует 1 реальное повторяющееся решение. Если дискриминант отрицателен, есть 2 комплексных решения (но нет действительных решений). Дискриминант также может рассказать нам о поведении графика квадратичной функции.

  Калькулятор единичного круга

  Калькулятор разложения на неполные дроби

  Калькулятор трансформации

  Калькулятор интегрирования деталей

  Часто задаваемые вопросы

  Когда дискриминант равен нулю, сколько чисел будет иметь решение квадратного уравнения?

  Дискриминант или определитель квадратного уравнения является компонентом квадратного корня квадратной формулы, b²-4ac. Дискриминант должен быть равен нулю, чтобы было единственное решение. Если дискриминант меньше нуля, решение не может быть найдено. В том случае, если оно больше нуля, действительных решений уравнения может быть два.

  Какие существуют формы квадратного уравнения?

  Три основные формы квадратного уравнения –

  • Стандартная форма
  • Факторная форма
  • Вершинная форма.

  Стандартная форма квадратного уравнения представляется как y = ax² + bx + c, а дискриминант квадратного уравнения в этом случае равен b² − 4ac. Факторизованная форма квадратного уравнения представлена ​​​​как y = (ax + c) (bx + d). Вершинная форма квадратного уравнения представляется как y = a (x + b)² + c.

  Следует отметить, что числа a, b и c.

  Какое значение имеют квадратные уравнения?

  Квадратные уравнения используются в нашей повседневной жизни по-разному, включая расчет площадей, определение прибыли от продукта и расчет скорости объекта. В квадратном уравнении будет по крайней мере одна квадратичная переменная, представленная в виде ax² + bx + c = 0, где x — переменная, «a», «b», «c» — константы, а «a» — не константа.

  No related posts.