Решение неравенств с корнями: Иррациональные неравенства — подготовка к ЕГЭ по Математике

Решить неравенство с квадратным корнем. Иррациональные неравенства. Теория и примеры. Сбор и использование персональной информации

В данном уроке мы рассмотрим решение иррациональных неравенств, приведем различные примеры.

Тема: Уравнения и неравенства. Системы уравнений и неравенств

Урок: Иррациональные неравенства

При решении иррациональных неравенств довольно часто необходимо возводить обе части неравенства в некоторую степень, это довольно ответственная операция. Напомним особенности.

Обе части неравенства можно возвести в квадрат, если обе они неотрицательны, только тогда мы получаем из верного неравенства верное неравенство.

Обе части неравенства можно возвести куб в любом случае, если исходное неравенство было верным, то при возведении в куб мы получим верное неравенство.

Рассмотрим неравенство вида:

Подкоренное выражение должно быть неотрицательным. Функция может принимать любые значения, необходимо рассмотреть два случая.

В первом случае обе части неравенства неотрицательны, имеем право возвести в квадрат. Во втором случае правая часть отрицательна, и мы не имеем права возводить в квадрат. В таком случае необходимо смотреть на смысл неравенства: здесь положительное выражение (квадратный корень) больше отрицательного выражения, значит, неравенство выполняется всегда.

Итак, имеем следующую схему решения:

В первой системе мы не защищаем отдельно подкоренное выражение, т. к. при выполнении второго неравенства системы подкоренное выражение автоматически должно быть положительно.

Пример 1 — решить неравенство:

Согласно схеме, переходим к эквивалентной совокупности двух систем неравенств:

Проиллюстрируем:

Рис. 1 — иллюстрация решения примера 1

Как мы видим, при избавлении от иррациональности, например, при возведении в квадрат, получаем совокупность систем. Иногда эту сложную конструкцию можно упростить. В полученной совокупности мы имеем право упростить первую систему и получить эквивалентную совокупность:

В качестве самостоятельного упражнения необходимо доказать эквивалентность данных совокупностей.

Рассмотрим неравенство вида:

Аналогично предыдущему неравенству, рассматриваем два случая:

В первом случае обе части неравенства неотрицательны, имеем право возвести в квадрат. Во втором случае правая часть отрицательна, и мы не имеем права возводить в квадрат. В таком случае необходимо смотреть на смысл неравенства: здесь положительное выражение (квадратный корень) меньше отрицательного выражения, значит, неравенство противоречиво. Вторую систему рассматривать не нужно.

Имеем эквивалентную систему:

Иногда иррациональное неравенство можно решить графическим методом. Данный способ применим, когда соответствующие графики можно достаточно легко построить и найти их точки пересечения.

Пример 2 — решить неравенства графически:

а)

б)

Первое неравенство мы уже решали и знаем ответ.

Чтобы решить неравенства графически, нужно построить график функции, стоящей в левой части, и график функции, стоящей в правой части.

Рис. 2. Графики функций и

Для построения графика функции необходимо преобразовать параболу в параболу (зеркально отобразить относительно оси у), полученную кривую сместить на 7 единиц вправо. График подтверждает, что данная функция монотонно убывает на своей области определения.

График функции — это прямая, ее легко построить. Точка пересечения с осью у — (0;-1).

Первая функция монотонно убывает, вторая монотонно возрастает. Если уравнение имеет корень, то он единственный, по графику легко его угадать: .

Когда значение аргумента меньше корня, парабола находится выше прямой. Когда значение аргумента находится в пределах от трех до семи, прямая проходит выше параболы.

Имеем ответ:

Эффективным методом решения иррациональных неравенств является метод интервалов.

Пример 3 — решить неравенства методом интервалов:

а)

б)

согласно методу интервалов, необходимо временно отойти от неравенства. Для этого перенести в заданном неравенстве все в левую часть (получить справа ноль) и ввести функцию, равную левой части:

теперь необходимо изучить полученную функцию.

ОДЗ:

Данное уравнение мы уже решали графически, поэтому не останавливаемся на определении корня.

Теперь необходимо выделить интервалы знакопостоянства и определить знак функции на каждом интервале:

Рис. 3. Интервалы знакопостоянства к примеру 3

Напомним, что для определения знаков на интервале необходимо взять пробную точку и подставить ее в функцию, полученный знак функция будет сохранять на всем интервале.

Проверим значение в граничной точке:

Очевиден ответ:

Рассмотрим следующий тип неравенств:

Сначала запишем ОДЗ:

Корни существуют, они неотрицательны, обе части можем возвести в квадрат. Получаем:

Получили эквивалентную систему:

Полученную систему можно упростить. При выполнении второго и третьего неравенств первое истинно автоматически. Имеем::

Пример 4 — решить неравенство:

Действуем по схеме — получаем эквивалентную систему.

Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.

Сбор и использование персональной информации

Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.

От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.

Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.

Какую персональную информацию мы собираем:

• Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.

Как мы используем вашу персональную информацию:

• Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
• Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
• Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
• Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.

Раскрытие информации третьим лицам

Мы не раскрываем полученную от Вас информацию третьим лицам.

Исключения:

• В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
• В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.

Защита персональной информации

Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.

Соблюдение вашей конфиденциальности на уровне компании

Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.

Цели:

1. Общеобразовательная: систематизировать, обобщить, расширить знания и умения учащихся, связанные с применением методов решения неравенств.
2. Развивающая: развивать у учащихся умение слушать лекцию, конспективно записывая ее в тетрадь.
3. Воспитательная: формировать познавательную мотивацию к изучению математики.

Ход урока

I. Вводная беседа:

Мы с вами закончили тему “Решение иррациональных уравнений” и сегодня начинаем учиться решать иррациональные неравенства.

Сначала давайте вспомним, какие виды неравенств вы умеете решать и какими методами?

Ответ : Линейные, квадратные, рациональные, тригонометрические. Линейные решаем, исходя из свойств неравенств, тригонометрические сводим к простейшим тригонометрическим, решаемым с помощью тригонометрического круга, а остальные, в основном, методом интервалов.

Вопрос : На каком утверждении основан метод интервалов?

Ответ : На теореме, утверждающей, что непрерывная функция, не обращающаяся в ноль на некотором интервале, сохраняет свой знак на этом интервале.

II. Давайте рассмотрим иррациональное неравенство типа >

Вопрос : Можно ли применить для его решения метод интервалов?

Ответ : Да, так как функция y = – непрерывна на D(y).

Решаем такое неравенство методом интервалов .

Вывод: мы довольно легко решили данное иррациональное неравенство методом интервалов, фактически сведя его к решению иррационального уравнения.

Давайте попробуем решить этим методом другое неравенство.

3) f(x) непрерывна на D(f)

4) Нули функции:

• Долго искать D(f).
• Трудно вычислять контрольные точки.

Возникает вопрос: “Нет ли других способов решения этого неравенства?”.

Очевидно, есть, и сейчас мы с вами с ними познакомимся.

III. Итак, тема сегодняшнего урока: “Методы решения иррациональных неравенств”.

Урок будет проходить в виде лекции, так как в учебнике нет подробного разбора всех методов. Поэтому наша важная задача: составить подробный конспект этой лекции.

IV. О первом методе решения иррациональных неравенств мы с вами уже поговорили.

Это – метод интервалов , универсальный метод решения всех типов неравенств. Но он не всегда приводит к цели коротким и простым путем.

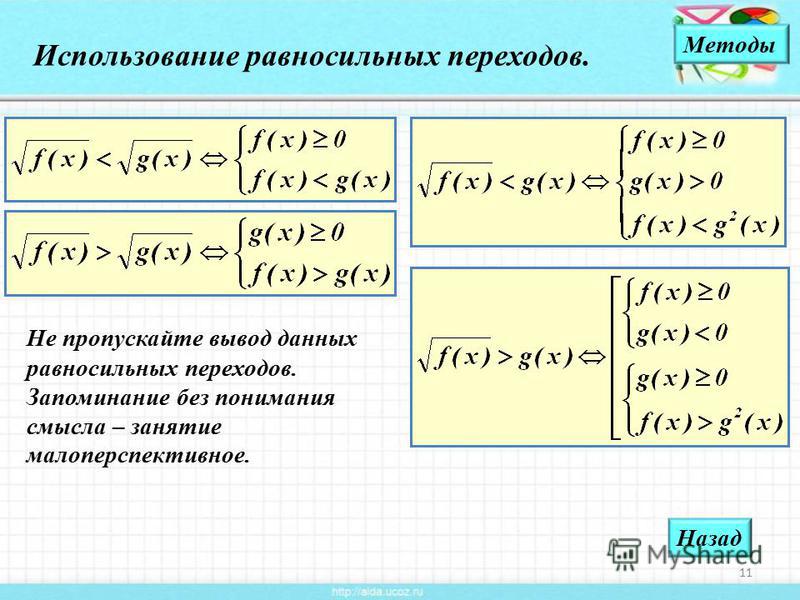
V. При решении иррациональных неравенств можно использовать те же идеи, что и при решении иррациональных уравнений, но так как простая проверка решений невозможна (ведь решениями неравенств являются чаще всего целые числовые промежутки), то необходимо использовать равносильность.

Приведем схемы решения основных типов иррациональных неравенств методом равносильных переходов от одного неравенства к системе неравенств.

2. Аналогично доказывается, что

Запишем эти схемы на опорной доске. Над доказательствами 3 и 4 типа подумайте дома, на следующем уроке мы их обсудим.

VI. Решим новым способом неравенство.

Исходное неравенство равносильно совокупности систем.

VII. И существует еще третий метод, часто помогающий решать сложные иррациональные неравенства. Мы с вами о нем уже говорили применительно к неравенствам с модулем. Это метод замены функций (замены множителей) . Напомню вам, что суть метода замены заключается в том, что разность значений монотонных функций можно заменить разностью значений их аргументов.

Рассмотрим иррациональное неравенство вида

то есть –

По теореме, если p(x) возрастает на некоторм промежутке, которому принадлежат a и b , причем a >b , то неравенства p(a) – p(b ) > 0 и a – b > 0 равносильны на D(p) , то есть

VIII. Решим методом замены множителей неравенство.

Значит, данное неравенство равносильно системе

Таким образом, мы увидели, что применение метода замены множителей для сведения решения неравенства к методу интервалов существенно сокращает объем работы.

IX. Теперь, когда мы разобрали три основных метода решения уравнений, давайте выполним самостоятельную работу с самопроверкой.

Нужно выполнить следующие номера (по учебнику А. М. Мордковича): 1790(а) – решить_ методом_ равносильныхпереходов,_ 1791(а) – решить методом замены множителей. Для решения иррациональных неравенств предлагается использовать способы, ранее разобранные при решении иррациональных уравнений:

• замена переменных;
• использование ОДЗ;
• использование свойств монотонности функций.

Завершением изучения темы является контрольная работа.

Анализ контрольной работы показывает:

• типичные ошибки слабых учащихся помимо арифметических и алгебраических – неверные равносильные переходы к системе неравенств;
• метод замены множителей успешно используется только сильными учащимися.

Цели:

1. Общеобразовательная: систематизировать, обобщить, расширить знания и умения учащихся, связанные с применением методов решения неравенств.
2. Развивающая: развивать у учащихся умение слушать лекцию, конспективно записывая ее в тетрадь.
3. Воспитательная: формировать познавательную мотивацию к изучению математики.

Ход урока

I. Вводная беседа:

Мы с вами закончили тему “Решение иррациональных уравнений” и сегодня начинаем учиться решать иррациональные неравенства.

Сначала давайте вспомним, какие виды неравенств вы умеете решать и какими методами?

Ответ : Линейные, квадратные, рациональные, тригонометрические. Линейные решаем, исходя из свойств неравенств, тригонометрические сводим к простейшим тригонометрическим, решаемым с помощью тригонометрического круга, а остальные, в основном, методом интервалов.

Вопрос : На каком утверждении основан метод интервалов?

Ответ : На теореме, утверждающей, что непрерывная функция, не обращающаяся в ноль на некотором интервале, сохраняет свой знак на этом интервале.

II. Давайте рассмотрим иррациональное неравенство типа >

Вопрос : Можно ли применить для его решения метод интервалов?

Ответ : Да, так как функция y = – непрерывна на D(y).

Решаем такое неравенство методом интервалов .

Вывод: мы довольно легко решили данное иррациональное неравенство методом интервалов, фактически сведя его к решению иррационального уравнения.

Давайте попробуем решить этим методом другое неравенство.

3) f(x) непрерывна на D(f)

4) Нули функции:

• Долго искать D(f).
• Трудно вычислять контрольные точки.

Возникает вопрос: “Нет ли других способов решения этого неравенства?”.

Очевидно, есть, и сейчас мы с вами с ними познакомимся.

III. Итак, тема сегодняшнего урока: “Методы решения иррациональных неравенств”.

Урок будет проходить в виде лекции, так как в учебнике нет подробного разбора всех методов. Поэтому наша важная задача: составить подробный конспект этой лекции.

IV. О первом методе решения иррациональных неравенств мы с вами уже поговорили.

Это – метод интервалов , универсальный метод решения всех типов неравенств. Но он не всегда приводит к цели коротким и простым путем.

V. При решении иррациональных неравенств можно использовать те же идеи, что и при решении иррациональных уравнений, но так как простая проверка решений невозможна (ведь решениями неравенств являются чаще всего целые числовые промежутки), то необходимо использовать равносильность.

Приведем схемы решения основных типов иррациональных неравенств методом равносильных переходов от одного неравенства к системе неравенств.

2. Аналогично доказывается, что

Запишем эти схемы на опорной доске. Над доказательствами 3 и 4 типа подумайте дома, на следующем уроке мы их обсудим.

VI. Решим новым способом неравенство.

Исходное неравенство равносильно совокупности систем.

VII. И существует еще третий метод, часто помогающий решать сложные иррациональные неравенства. Мы с вами о нем уже говорили применительно к неравенствам с модулем. Это метод замены функций (замены множителей) . Напомню вам, что суть метода замены заключается в том, что разность значений монотонных функций можно заменить разностью значений их аргументов.

Рассмотрим иррациональное неравенство вида

то есть –

По теореме, если p(x) возрастает на некоторм промежутке, которому принадлежат a и b , причем a >b , то неравенства p(a) – p(b ) > 0 и a – b > 0 равносильны на D(p) , то есть

VIII. Решим методом замены множителей неравенство.

Значит, данное неравенство равносильно системе

Таким образом, мы увидели, что применение метода замены множителей для сведения решения неравенства к методу интервалов существенно сокращает объем работы.

IX. Теперь, когда мы разобрали три основных метода решения уравнений, давайте выполним самостоятельную работу с самопроверкой.

Нужно выполнить следующие номера (по учебнику А. М. Мордковича): 1790(а) – решить_ методом_ равносильныхпереходов,_ 1791(а) – решить методом замены множителей.Для решения иррациональных неравенств предлагается использовать способы, ранее разобранные при решении иррациональных уравнений:

• замена переменных;
• использование ОДЗ;
• использование свойств монотонности функций.

Завершением изучения темы является контрольная работа.

Анализ контрольной работы показывает:

• типичные ошибки слабых учащихся помимо арифметических и алгебраических – неверные равносильные переходы к системе неравенств;
• метод замены множителей успешно используется только сильными учащимися.

Всякое неравенство, в состав которого входит функция, стоящая под корнем, называется иррациональным . Существует два типа таких неравенств:

В первом случае корень меньше функции g (x ), во втором — больше. Если g (x ) — константа , неравенство резко упрощается. Обратите внимание: внешне эти неравенства очень похожи, но схемы решения у них принципиально различаются.

Сегодня научимся решать иррациональные неравенства первого типа — они самые простые и понятные. Знак неравенства может быть строгим или нестрогим. Для них верно следующее утверждение:

Теорема. Всякое иррациональное неравенство вида

Равносильно системе неравенств:

Неслабо? Давайте рассмотрим, откуда берется такая система:

1. f (x ) ≤ g 2 (x ) — тут все понятно. Это исходное неравенство, возведенное в квадрат;
2. f (x ) ≥ 0 — это ОДЗ корня. Напомню: арифметический квадратный корень существует только из неотрицательного числа;
3. g (x ) ≥ 0 — это область значений корня. Возводя неравенство в квадрат, мы сжигаем минусы. В результате могут возникнуть лишние корни. Неравенство g (x ) ≥ 0 отсекает их.

Многие ученики «зацикливаются» на первом неравенстве системы: f (x ) ≤ g 2 (x ) — и напрочь забывают два других. Результат предсказуем: неправильное решение, потерянные баллы.

Поскольку иррациональные неравенства — достаточно сложная тема, разберем сразу 4 примера. От элементарных до действительно сложных. Все задачи взяты из вступительных экзаменов МГУ им. М. В. Ломоносова.

Примеры решения задач

Задача. Решите неравенство:

Перед нами классическое иррациональное неравенство : f (x ) = 2x + 3; g (x ) = 2 — константа. Имеем:

Из трех неравенств к концу решения осталось только два. Потому что неравенство 2 ≥ 0 выполняется всегда. Пересечем оставшиеся неравенства:

Итак, x ∈ [−1,5; 0,5]. Все точки закрашены, поскольку неравенства нестрогие .

Задача. Решите неравенство:

Применяем теорему:

Решаем первое неравенство. Для этого раскроем квадрат разности. Имеем:

2x 2 − 18x + 16 2x 2 − 18x + 16 x 2 − 10x x (x − 10) x ∈ (0; 10).

Теперь решим второе неравенство. Там тоже квадратный трехчлен :

2x 2 − 18x + 16 ≥ 0;
x 2 − 9x + 8 ≥ 0;
(x − 8)(x − 1) ≥ 0;
x ∈ (−∞; 1]∪∪∪∪}

4. Иррациональные уравнения и неравенства

§4. ИРРАЦИОНАЛЬНЫЕ УРАВНЕНИЯ И НЕРАВЕНСТВА

При решении иррациональных уравнений, как правило, применяют преобразование, связанное с возведением обеих частей уравнения в натуральную степень. Следует помнить, что при возведении обеих частей уравнения в нечетную сте- пень получается уравнение, равносильное исходному. Если же возводить обе части уравнения в четную степень, то, вообще говоря, получается уравнение, являющееся следствием исходного, т.е. такое, которое кроме корней исходного уравнения может содержать и другие (посторонние) корни. В этом случае необходимо проверить все найденные значения непосредственной подстановкой в исходное уравнение. Все корни четной степени следует считать арифмети- ческими: не имеет смысла при ; при и при .

Пример 1. Решить уравнение: . Решение. Возведем в квадрат обе части исходного уравнения: Возведя обе части последнего уравнения в квадрат, получим . Корни этого уравнения: . Проверим найденные значения: 1)при , следовательно, не является корнем исходного уравнения; 2) при . Поэтому – корень исходного уравнения. Ответ: – 1.

31

Применяется и другой путь решения иррациональных уравнений – переход к равносильным системам, в которых учитывается ОДЗ уравнения и требование неотрицатель-ности обеих частей уравнения, возводимых в четную степень. . Пример 2. Решить уравнение: .

Решение. Ответ: .

Важным методом решения иррациональных уравнений яв- ляется метод замены переменной.

Пример 3. Найти сумму корней уравнения: . (1)

Решение. Непосредственное возведение в квадрат обеих частей этого уравнения приводит к уравнению четвертой сте- пени относительно , решить которое довольно сложно. Ре- шение упрощается при использовании вспомогательного не- известного. Обозначим , где . Тогда , откуда . Уравнение (1) принимает вид: . Последнее

32

уравнение имеет корни . Так как не удовлетворяет условию , то ; . Это уравнение имеет корни . Проверкой убеждаемся, что оба значе- ния являются корнями исходного уравнения (1). .

Ответ: .

Иррациональные неравенства

Основной метод решения иррациональных неравенств заключается в том, что исходное неравенство сводится к равносильной ему системе или совокупности систем рациональных неравенств. При решении иррациональных неравенств следует найти ОДЗ неравенства, а затем обоснованно осуществлять равносильный переход на всей ОДЗ или ее частях.

Пример 4. Найти сумму целых решений неравенства . (2)

Решение. ОДЗ неравенства (2): т.е. . При и неравенство (2) выполняется; следовательно, эти значения являются его решениями. Пусть . Тогда и неравенство (2) равносильно неравенству

33

. Учитывая,

что , получаем . Итак, множество решений неравенства (2) имеет вид: . Сумма целых чисел из этого множества : .

Ответ: – 10.

Имеют место следующие соотношения ( ) : (3) . (4) (5) . (6) (7) . (8) Пример 5. Найти число целых решений неравенства .

Решение. Данное неравенство, согласно (7), равносильно совокупности двух систем

34 (9) Вторая система совокупности (9) равносильна системе:

Далее, так как то первая система совокупности (9) равносильна системе: . Множеством решений исходного неравенства является объединение множеств и , т. е. промежуток . Целые значения из этого множества: . Ответ: .

Пример 6. Найти сумму целых решений неравенства .

Решение. Обе части неравенства ( при ОДЗ ) неотрицательны, поэтому оно равносильно системе При имеем и ,

35

поэтому решением последней системы, а значит и исходного

неравенства, являются все числа из промежутка . Сумма целых решений неравенства: . Ответ: 15. ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ 1. Решить уравнение: а) ; (Ответ: 2 )

б) ; (Ответ: – 1 )

в) ; (Ответ: 4 )

г) ; (Ответ: 3 ) д) ; (Ответ: 3 )

е) ; (Ответ: 2 ) ж) ; (Ответ: 5 ) з) ; (Ответ: 7 ) и) ; (Ответ: – 15 ) й) .

(Ответ: )

2. Найти сумму корней уравнения: а) . (Ответ: 2,5 ) б) ; (Ответ: 8 )

в) ; (Ответ: –5 ) г) ; (Ответ: 3 )

д) ; (Ответ: 11 )

36

е) . (Ответ: 4 ) 3. Найти длину промежутка решений неравенства: а) ; (Ответ: 2 ) б) ; (Ответ: 5 ) в) . (Ответ: 9 )

4. Найти наименьшее целое значение , удовлетворяющее неравенству: а) . (Ответ: 3 ) б) . (Ответ: 2 ) в) . (Ответ: 4 ) г) . (Ответ: 3 ) д) . (Ответ: 2 )

5. Найти сумму целых решений неравенства: а) . (Ответ: 60 )

б) . (Ответ: – 18 )

в) . (Ответ: 5 )

г) . (Ответ: 7)

д) . (Ответ: – 9 ) 6. Решить неравенство: . (Ответ: )

37

Математика: Иррациональные уравнения и неравенства

6.

Иррациональные уравнения и неравенства

Комментарий. Сущность процесса решения уравнений можно описать следующим образом: исходное уравнение упрощается посредством определенных преобразований, т.е. выстраивается цепочка от исходного к некоторому итоговому уравнению, решение которого очевидно или способ (алгоритм) решения которого хорошо известен. При этом возможны три типа преобразований, три принципиально разные ситуации.

1. Применяемые в процессе решения преобразования таковы, что множества корней исходного и итогового уравнений совпадают; в этом случае исходное и итоговое уравнения называют равносильными; соответствующие преобразования также называют равносильными.

2. Применяемые в процессе решения преобразования таковы, что множество корней итогового уравнения «шире», чем множество корней исходного уравнения; в этом случае говорит, что в процессе решения применены неравносильные преобразования, которые могли привести к появлению посторонних корней.

3. Применяемые в процессе решения преобразования таковы, что множество корней итогового уравнения «уже», чем множество корней исходного уравнения; в этом случае говорят, что в процессе решения применены неравносильные преобразования, которые могли привести к потере корней.

Проиллюстрируем сказанное примерами.

Пример 6.1.

а) Дано уравнение:

Перепишем уравнение, разложив на множители знаменатели:

Умножим обе части уравнения на выражение x² + 4; это равносильное преобразование, т.к. x² + 4 ≠ 0 при любом значении х:

б) Дано уравнение:

Возведем обе его части в квадрат:

Так как , то получаем . Множество корней этого уравнения — все действительные числа. При этом простая проверка показывает, что отрицательное число не может быть корнем исходного уравнения. Таким образом, в процессе решения были применены неравносильные преобразования и появились посторонние корни. Действительно, возведение обоих частей уравнения в четную степень является равносильным преобразованием только в том случае, если обе части уравнения неотрицательны.

в) Дано уравнение: x² — 2х – 3 = 4х + 5 + x² .

Перепишем уравнение, разложив квадратные трехчлены на множители:

(х + 1)(х — 3) = (5 — х)(х + 1).

Разделим обе части уравнения на выражение х + 1 : х – 3 = 5 — х.

Последнее уравнение имеет единственный корень х = 4, в то время как исходное уравнение имеет два корня: x₁ = 4 и x₂ = -1. Таким образом, в процессе решения уравнения было применено неравносильное преобразование, которое привело к потере корней. Действительно, проводя деление на выражение х + 1, мы не потребовали, чтобы х + 1 ≠ 0.

Как видно из примеров неравносильные преобразования могут стать причиной неверного решения уравнения, привести к ошибке. Так может быть запретить неравносильные преобразования?! Можно запретить. Это один из возможных подходов. Он снимает проблему посторонних и потерянных корней, но приводит, как правило, к некоторому техническому усложнению процесса решения уравнения: появляются смешанные системы (уравнение и неравенство) и совокупности таких систем.

Так, уравнение из примера 6.1, б равносильно совокупности:

Уравнение x² — 2х – 3 = 4х + 5 — x² из примера 6.1, в равносильно совокупности

Рассмотренные совокупности решаются просто, но в более сложных случаях обязательное соблюдение условия равносильности преобразований может привести к серьезным техническим трудностям, сделать решение слишком ветвящимся и громоздким. Поэтому, не будем строго запрещать применение любых неравносильных преобразований. Все ли они одинаково опасны? Понятно, что более опасны неравносильные преобразования, приводящие к потере корней. В примере 6.1, в нам удалось легко понять причину потери корня и исправиться, но в большинстве случаев потерянные корни отыскать весьма трудно (заметим также, что малоопытный решающий, а абитуриент часто именно таков, может вовсе не заметить факта потери корня, и не будет пытаться его отыскать, хотя это, может быть, и получилось бы).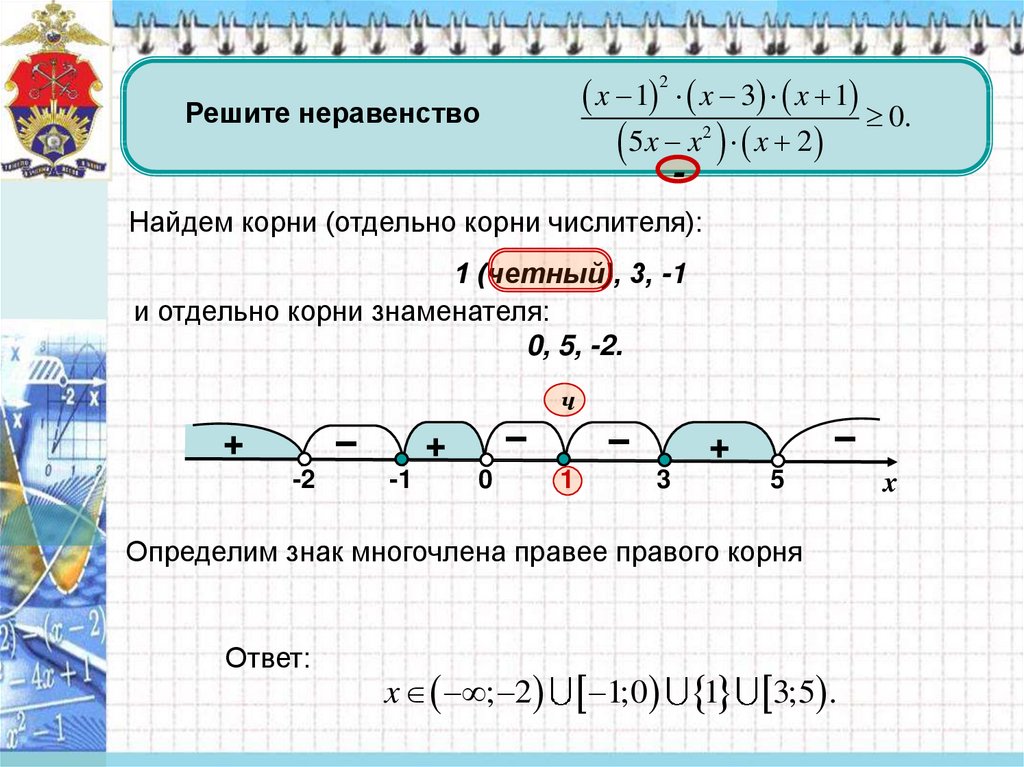

Итак, на не равносильные преобразования, приводящие к потере корней, мы накладываем строгий и категорический запрет. При решении уравнений, таким образом, мы не будем применять деление обеих частей уравнения на выражение, обращающееся в ноль в области определения уравнения, и не будем применять преобразования, приводящие к сужению области определения уравнения.

Что же касается, неравносильных преобразований, приводящих к появлению посторонних корней, то такие преобразования вполне допустимы. Но при этом, обязательным заключительным этапом решения должна быть проверка всех найденных в итоге корней. Заметим, что тактика проверки зависит непосредственно от класса уравнений (рациональные, иррациональные, логарифмические и т.д.), ибо в каждом случае свои причины появления посторонних корней. В этой связи, тактика проверки конечно должна быть гибкой, но можно пользоваться и универсальным приемом: подстановка всех корней итогового уравнения в исходное с последующим вычислением или «прикидкой».

Пример 6.2.

Решим уравнение:

Комментарий. При решении этого уравнения будем придерживаться стратегии, допускающей неравносильные преобразования при обязательной проверке корней. Решая уравнения вида, следует перед возведением в квадрат уединить один из корней, перенеся его в правую часть уравнения. Уединить можно любой из корней, и в большинстве случаев, все равно какой. Но иногда уединение определенного корня приводит к более простому решению, чем уединение других. Поэтому всегда следует анализировать ситуацию в указанном аспекте.

Решение

В нашем уравнение сумма коэффициентов при х в первом и третьем подкоренных выражениях равна коэффициенту при х во втором подкоренном выражении. Поэтому уединить целесообразно именно корень . Полученное после возведения в квадрат уравнение будет содержать х только под корнем. Если бы мы уединяли любой из других корней, то после возведения в квадрат получали бы уравнения, содержащие х и под корнем, и вне корня, что менее удобно для последующего решения.

Итак, имеем:

Комментарий. При решении иррационального уравнения мы осуществляем так называемую рационализацию уравнения, т.е. избавляемся от радикалов (корней). Но, избавляясь от корней, мы избавляемся и от ограничений на подкоренные выражения: Иными словами, происходит расширение области определения уравнения. Это причина появления посторонних корней. Поэтому все корни итогового уравнения, полученного в ходе решение, следует проверить на принадлежность области определения исходного уравнения. В нашем случае область определения исходного уравнения задается системой:

Решив эту систему, получаем область определения уравнения:

Очевидно, что  — посторонний корень, появившийся в процессе решения из-за применения неравносильных преобразований, приведших к расширению области определения уравнения, а x₂ = 0 —– принадлежит области определения уравнения и является его корнем (что легко проверить непосредственной подстановкой).

Ответ: х = 0.

Комментарий. Но единственная ли причина появления посторонних корней при решении иррациональных уравнений с радикалами четной степени — расширение области определения исходного уравнения? Не кроется ли в возведении обеих частей уравнения в четную степень еще одна, менее очевидная, но не менее опасная в смысле ошибки, причина появления посторонних корней?

Пример 6.3.

а) Решим уравнение:

При решении этого уравнения будем придерживаться стратегии, допускающей неравносильные преобразования, т.е. возведем обе части уравнения в квадрат, решим полученное рациональное уравнение и сделаем проверку корней.

Итак,

Проверим, удовлетворяют ли эти корни исходному уравнению.

Пусть х = -1, тогда левая часть исходного уравнения равна -6. Таким образом, х = -1 — посторонний для исходного уравнения корень, появившийся в процессе решения из-за применения неравносильных преобразований. Пусть теперь, х = 7. Тогда исходное уравнение превращается в верное числовое равенство. Исходное уравнение, таким образом, имеет единственный корень х = 7.

б) Решим теперь уравнение (его чрезвычайно, малое отличие от предыдущего уравнения очевидно).

Поступая так же, как в случае «а», получаем:

Итоговое уравнение имеет такие же корни, что и уравнение из случая «а». Проверим их подстановкой в исходное уравнение . Пусть х = -1, тогда исходное уравнение превращается в верное числовое равенство. Пусть, далее, х = 7. Тогда левая часть исходного уравнения равна -2. Таким образом, х = 7 — посторонний для исходного уравнения корень.

В процессе решения следствием уравнений «а», «б» является одно и тоже уравнение имеющее два корня: x₁ = -1 и x₂ = 7. Корень x₁ = -1 — есть корень уравнения «б», но посторонний для уравнения «а»; корень x₂  = 7 — наоборот, корень уравнения «а», посторонний для уравнения «б».

В каждом из случаев «а» и «б» корни, оказавшиеся посторонними, принадлежат области определения данного уравнения. Значит, расширение области определения исходного уравнения — не единственная причина появления посторонних корней. В чем же дело? Заметим, что и в случае «а», и в случае «б» при подстановке в исходное уравнение корень, оказывающийся посторонним, приводит к ситуации: левая и правая части уравнения равны по абсолютной величине, но противоположны по знаку. Это не случайно. Уравнение является следствием не только уравнения , но и следствием уравнения . Какие следует сделать из этого выводы?

Во-первых, поскольку появление посторонних корней при решении иррациональных уравнений, содержащих радикалы четной степени может быть и не связано с областью определения исходного уравнения, то и проверка корней не может осуществляться только по области определения, или условиям ее задающим.

Во-вторых, проверка корней иррационального уравнения, должна учитывать обе причины появления посторонних корней; универсальный прием, как уже говорилось, состоит в непосредственной подстановке в исходное уравнение, но могут быть реализованы и другие подходы.

1. Сначала отсечь те корни, которые не принадлежат области определения исходного уравнения, а оставшиеся проверить непосредственной подстановкой во все уравнения левая и правая части которых возводились в квадрат в процессе решения.

2. Опять же исключить все корни, не принадлежащие области определения, а затем проанализировать все случаи возведения в квадрат обеих частей уравнения, выделить те случаи, где было нарушено условие равносильности:

   Далее только в эти уравнения подставить корни итогового уравнения, принадлежащие области определения исходного уравнения.

3. Если решать иррациональные уравнения, применяя только равносильные преобразования, то в каждом случае возведения в квадрат следует предусматривать условие равносильности, сформулированное выше, и изначально следует зафиксировать условия, задающие область определения исходного уравнения.

Рассмотрим схемы равносильных преобразований для иррациональных уравнений основных видов.

I.

II.

III.

IV.

V.

VI.

Заметим, что важно, конечно, не выучить наизусть эти схемы, а понять их, уметь самостоятельно составлять схемы равносильности для других случаев.

Не надо думать, что в процессе решения иррационального уравнения обязательно появляются посторонние корни. Рассмотрим пример.

Пример 6.4.

Решим уравнение:

Решение

Возведя обе части уравнения в квадрат, получаем 1 + 3х = x² + 2х + 1, т.е. уравнение x² – х = 0. Его корни x₁ = 0 и x₂ = 1. Подставляя каждый из найденных корней в исходное уравнение, убеждаемся, что оба они являются его корнями.

Пример 6.5.

Решим уравнение:

Решение

Уединим радикалы:

Возведем обе части уравнения в квадрат (дважды):

Корни последнего уравнения:

Далее следует провести проверку корней. Область определения исходного уравнения задается условиями т.е. 1 ≤ x ≤ 3. Как нетрудно проверить, полагая приближенно равным 1,7, что оба корня x₁ и x₂ принадлежат области определения исходного уравнения. Значит, если среди x₁ и x₂ есть посторонний корень, то причина его появления связана с нарушением условия равносильного возведения обеих частей уравнения в квадрат. Ясно, также, что первое из проделанных в данном решении возведений в квадрат — равносильное преобразование, поэтому если и появились посторонние корни, то при возведении в квадрат обеих частей уравнения Непосредственной подстановкой именно в это уравнение проверим наши корни x₁ и x₂ .

Итак, пусть тогда:

Мы пришли к верному числовому равенству. Значит  — корень данного уравнения.

Пусть теперь

Тогда

Ясно, что левая часть уравнения отрицательна, а правая положительна. Поэтому  — посторонний корень.

Пример 6.6.

Решим уравнение:

Распределим радикалы следующим образом:

Возведем обе части уравнения в квадрат и приведем подобные слагаемые:

Возведем обе части полученного уравнения в квадрат, раскроем скобки и приведем подобные слагаемые:

Проведем проверку корней. Сразу замечаем, что корень не имеет смысла при x = -0,5. Поэтому единственный возможный корень исходного уравнения — это х = 2, удовлетворяющий всем условиям области определения. Поскольку, возводя обе части уравнения в квадрат, мы всякий раз соблюдали условие равносильности, то х = 2 — единственный корень исходного уравнения.

Пример 6.7.

Решим уравнение: .

При решении этого уравнения покажем применение метода введения новой переменной при решении иррациональных уравнений.

Возведем обе части уравнения в квадрат:

Пусть теперь , тогда уравнение можно переписать в виде:

.

Это уравнение имеет два корня: . Таким образом, следствием исходного уравнения является совокупность систем:

.

Решим первую систему совокупности.

Обозначим: и .

Тогда имеем:

Таким образом,

Корни этой совокупности систем:

Аналогично, решая вторую систему исходной совокупности, получаем:

.

Пример 6.8.

Решим уравнение:

Подкоренные выражения и представляют из себя полные квадраты:

Тогда:

Пусть , тогда уравнение можно переписать в виде:

Возведем обе части последнего уравнения в квадрат, затем воспользуемся тождеством и формулой разности квадратов:

Если у = 0, то , т.е. х = 1. Если у = 2, то , т.е. х = 5. Если у = 1, то , т.е. х = 2. Если у = -1, то уравнение не имеет корней.

Непосредственной подстановкой в исходное уравнение всех найденных значений х, приходим к выводу, что только х = 5 является корнем данного уравнения.

Рассмотрим далее примеры решения иррациональных уравнений с корнями степени, большей, чем вторая.

Пример 6.9.

Решим уравнение:

Перераспределим радикалы

Возведем обе части уравнения в третью степень:

Выражение в скобках, очевидно, есть — , т. е.:

Снова возведем обе части уравнения в третью степень:

Далее имеем:

В процессе решения, был применен прием, связан ный с заменой суммы на выражение , что могло привести к появлению посторонних корней (такой вывод позволяет сделать определенная искусственность этого приема). Поэтому проверим все найденные корни непосредственной подстановкой в исходное уравнение.

Если х = -2, то исходное уравнение обращается в верное числовое равенство.

Для подстановки значений возьмем приближенное значение: Тогда и .

Если х = -0,4, то:

Ясно, что это числовое равенство неверно, поскольку все три значения корней положительны, а сумма положительных чисел не может быть равна 0.

Если х = -2,6, то:

Ясно, что эта сумма не может быть равна 0, т.к. уже Заметим, что довольно часто, «прикидка» при проверки корней позволяет сделать необходимый вывод на определенном промежуточном этапе вычислений, и доводить их до явного числового равенства или неравенства совсем не обязательно (это снова к вопросу о гибкой тактике проверки корней).

Таким образом, х = -2 — единственный корень данного уравнения.

Ответ: -2.

Комментарий. Запишем в общем виде прием решения, рассмотренный в этом примере:

По аналогичной схеме решаются уравнения вида .

Большие трудности у абитуриентов вызывают иррациональные уравнения, содержащие радикалы разных степеней. Рассмотрим примеры.

Пример 6.10.

а) Решим уравнение: .

Это уравнение легко рационализируется возведением обеих его частей в шестую степень:

И далее:

Подстановкой выясняем, что только х = 2 является корнем данного уравнения.

б) Решим уравнение:

В этом случае возведение обеих частей уравнения в шестую степень уже нецелесообразно. Проведем замену переменных.

Пусть и тогда a + b = 1. Возведем в куб первое уравнение системы ,и в квадрат второе уравнение этой системы; затем почлено сложим полученные уравнения. В итоге получаем: a³ + b² = 1.

Таким образом, имеем систему уравнений:

Решая ее, получаем: т.е. совокупность систем:

В итоге Непосредственная подстановка в исходное уравнение показывает, что среди этих корней нет посторонних.

Комментарий. Заметим, что описанный в случае «б» прием является достаточно распространенным. Рассмотрим его применение при решении уравнений с радикалами высших степеней.

Пример 6.11.

Решим уравнение:

Пусть Тогда . Возведем в четвертую степень обе части каждого из уравнений системы , и почленно сложим полученные уравнения. В итоге получаем:

Таким образом, имеем систему уравнений:

Это симметрическая система уравнений, стандартно решающаяся заменой переменных a + b = y и ab = z.

Имеем корни: . Отсюда x₁ = 2, x₂ = 6. Проверка показывает, что это действительно корни данного уравнения.

Ответ: x₁ = 2, x₂ = 6.

Пример 6.12.

Решим уравнение:

Аналогично предыдущему примеру получаем симметрическую систему относительно переменных и :

Корни этой системы легко угадываются: Далее получаем корни исходного уравнения: x₁ = 1 и x₂ = 32.

Ответ: x₁ = 1, x₂ = 32.

Комментарий. Рассмотрим далее несколько примеров решения иррациональных неравенств. Все они, как мы уже обсуждали, решаются применением исключительно равносильных преобразований. Поэтому приведем схемы основных равносильных переходов (.

I.

II.

III.

IV.

V.

VI.

VII.

Комментарий. Представленные схемы принципиально не изменяются, если исходно рассматривать нестрогие неравенства.

Пример 6.13.

Решим неравенство:

Решение

Применим схему V:

Таким образом, решение неравенства:

Ответ: 

Пример 6. 14.

Решим неравенство:

Решение

Применим схему III:

Таким образом, решение неравенства:

Ответ: 

Пример 6.15.

Решим неравенство:

Решение

Перераспределим радикалы: и, воспользовавшись в качестве принципиального ориентира схемой I, получаем:

Таким образом, решение неравенства: [4, 5).

Ответ: [4, 5).

Пример 6.16.

Решим неравенство:

Решение

Преобразуем первую дробь, и будем решать неравенство, применяя метод введения новой переменной:

Таким образом, решение неравенства: (2, 8).

Ответ: (2, 8).

Пример 6.17.

Решим неравенство:

На этом примере мы также как и в предыдущем случае посмотрим особенности применения метода введения новой переменной при решении иррациональных неравенств.

Пусть , тогда Таким образом:

Итак, решение неравенства:

Ответ: 

Комментарий. Можно было решить это неравенство и без применения метода введения новой переменной, рассмотрев отдельно (в совокупности) случаи, задаваемые условиями х > 0 и x < 0. Приводим запись такого решения:

Результат, естественно не зависит от способа решения:

В заключение рассмотрим пример решения иррационального неравенства с двумя переменными (группа С).

Пример 6.18.

Решим неравенство:

Решение

Пусть , тогда неравенство можно записать в виде:

По известной нам схеме это неравенство равносильно системе:

Итак, условия должны выполняться одновременно, т.е. должна выполняться система:

Из нее следует, что т.е. Это означает, что y = 0.

Подставим найденное значение в исходное неравенство; получим неравенство, из которого следует, что x = 1.

Таким образом, решение данного неравенства: x = 1, y = 0.

Ответ: x = 1, y = 0

Решение неравенств с использованием квадратных корней (видео и практика)

TranscriptPractice

Привет и добро пожаловать в это видео на Решение неравенств с использованием квадратных корней .

При решении неравенств с квадратными корнями нам нужно выполнить два простых шага. Первый шаг — решить неравенство для x так же, как и любое другое неравенство. В этом шаге нет ничего особенного. Но второй шаг уникален для неравенств с четными корнями. Сегодня мы рассмотрим именно квадратные корни. Второй шаг — установить все, что находится под радикальным символом, больше или равное нулю, и решить для х снова. Мы делаем это, потому что у вас не может быть отрицательного значения x под квадратным корнем. Другими словами, вы не можете извлечь квадратный корень из отрицательного числа. Это даст нам два неравенства, которые мы затем объединим, чтобы составить составное неравенство, если знаки противоположны. Если знаки совпадают, используем более ограничительное неравенство.

Давайте рассмотрим несколько примеров, чтобы понять, о чем я говорю.

\(\sqrt{x+3}\)>\(4\)
 
Сначала мы хотим решить это неравенство для х нормально. Мы делаем это, следуя тем же шагам, как если бы решали уравнение, а не неравенство.

Начнем с возведения в квадрат обеих сторон.

\(x+3\)>\(16\)
 
И затем мы вычтем 3 с обеих сторон.

\(x\)>\(13\)
 
Это дает нам x больше 13.

Теперь пришло время для нашего специального шага. Мы хотим установить то, что находится под радикальным символом больше или равно 0, и решить для х снова.

Таким образом, x плюс 3 находится под подкоренным символом.

Итак, мы установим x плюс 3 больше или равно 0

\(x+3\)≥\(0\)
 
Итак, теперь мы собираемся вычесть 3 из обеих сторон.

\(x\)≥\(-3\)
 
Что дает нам x больше или равно отрицательному числу 3. один как наш окончательный ответ. \(x\)>\(13\) является более ограничительным, чем \(x\)≥\(-3\), потому что, согласно второму неравенству, 0 может быть включено, поскольку оно больше или равно -3, но это не совсем наш набор решений, потому что он не больше 13. Поэтому мы хотим рассматривать только значения x больше 13.

Давайте попробуем другой.

Найти x .

\(\sqrt{2x-5}+7\)  
Начнем с вычитания 7 с обеих сторон.

\(\sqrt{2x-5}\)  
Затем возводим обе стороны в квадрат.

\(2x-5\)  
Прибавьте 5 к обеим сторонам

\(2x\)  
И разделите на 2 с обеих сторон.

\(x\)  
Далее мы установим \(2x–5\) больше или равным 0 и снова найдем x .

\(2x-5\)≥\(0\)
 
Итак, мы собираемся добавить 5 к обеим сторонам.

\(2x\)≥\(5\)
 
И разделить на 2 с обеих сторон.

\(x\)≥\(\frac{5}{2}\)
 
В этом примере наши знаки неравенства обращены в противоположные стороны, поэтому мы хотим объединить их, чтобы получить сложное неравенство. Наш окончательный ответ: \(\frac{5}{2}\)≤\(x\)  
Давайте попробуем вместе еще один пример.
 
\(\sqrt{-3x+1}-9\)≥\(11\)
 
Найдите x обычным образом.

\(\sqrt{-3x+1}\)≥\(20\)
 
\(-3x+1\)≥\(400\)
 
\(-3x\)≥\(399\)

\(x\)≤\(-133\)
 
Затем решите так, чтобы то, что находится под радикалом, не было отрицательным.

\(-3x+1\)≥\(0\)
 
\(-3x\)≥\(-1\)
 
\(x\)≤\(\frac{1}{3}\ )
 
Так как знаки в одном направлении, мы выбираем более ограничительный случай в качестве нашего окончательного ответа: \(x\)≤\(-133\).

Прежде чем мы пойдем, я хочу решить еще одну задачу, но на этот раз попробуй ее сам. Как только я дам вам задачу, остановите видео и решите неравенство самостоятельно. Затем нажмите кнопку воспроизведения и посмотрите, совпадает ли ваш ответ с моим.

\(\sqrt{4x+4}+11\)  
Думаете, у вас получилось? Посмотрим!

Во-первых, мы хотим нормально решить наше неравенство.

\(\sqrt{4x+4}\)  
\(4x+4\)  
\(4x\)  
\(x\)  
Затем мы устанавливаем то, что под радикалом больше или равно 0, и решаем для x снова.

\(4x+4\)≥\(0\)
 
\(4x\)≥\(-4\)
 
\(x\)≥\(-1\)
 
Так как наши знаки находятся в противоположных направлениях, наше окончательное неравенство будет составным неравенством: \(-1\)≤\(x\)  
Помните, что мы не можем извлечь квадратный корень из отрицательного значения, поэтому мы помещаем выражение под радикалом, чтобы оно было больше или равно 0. Это верно для любого четного корня, такого как корень четвертой или восьмой степени. Однако вполне нормально брать нечетный корень из отрицательного значения. Например, кубический корень из -8 равен -2, потому что \(-2 \times -2 \times -2 = -8\).
 
Если вас попросят решить неравенство с другим четным корнем, выполните те же действия, что и здесь. Если это нечетный корень, вам не нужно беспокоиться о втором шаге, и вы можете остановиться после первоначального решения неравенства.
 
Надеюсь, это видео о решении неравенств с квадратными корнями было полезным. Спасибо за просмотр и удачной учебы!

Вопрос №1:

 
Решите это неравенство для x .
\(\sqrt{x-5}\)

\(x\)

\(x≥5\)

\(-5≤x\)

\(5≤x\)

Показать Ответ

Ответ:

При решении неравенства мы выполняем те же действия, что и при решении уравнения. Поскольку значение под радикалом не может быть равно нулю, мы должны добавить дополнительный шаг, установив то, что находится под радикалом, больше или равное нулю, и решить для 92\) \(x-5\) \(x\)  
\(x-5≥0\)
\(x≥5\)
 
Поскольку знаки противоположны, наш ответ будет составным неравенством \ (5≤x\)

Скрыть ответ

Вопрос №2:

 
Решите это неравенство для x .
\(\sqrt{3x+9}>12\)

\(x≥-3\)

\(x>45\)

\(-3≤x\)

\(3≤x \)

Показать Ответ

Ответ:

При решении неравенства используем те же действия, что и при решении уравнения. Поскольку у нас не может быть нуля под радикалом, у нас есть дополнительный шаг, чтобы гарантировать, что наш набор решений не включает никакого значения для 92\)
\(3x+9>144\)
\(3x>135\)
\(x>45\)

\(3x+9≥0\)
\(3x≥-9\)
\(x≥-3\)

Поскольку знаки расположены в одном направлении, мы выбираем более строгий ответ, то есть \(x>45\).

Скрыть ответ

Вопрос №3:

 
Решите это неравенство для x .
\(\sqrt{5x-1}-2\)

\(x≥\frac{1}{5}\)

\(x\)

\(-\frac{1}{5} ≤x\)

\(\frac{1}{5}≤x\) 92\) \(5x-1\) \(5x\) \(x\)  
\(5x-1≥0\)
\(5x≥1\)
\(x≥\frac{1}{5 }\)
 
Поскольку знаки противоположны, наш ответ будет в виде составного неравенства, которое будет \(\frac{1}{5}≤x\)

Скрыть ответ

Вопрос # 4:

 
Решите это неравенство для x .
\(\sqrt{6x+10}≥8\)

\(x≥-\frac{5}{3}\)

\(x≥9\)

\(-\frac{5} {3}≤x≤9\)

\(\frac{5}{3}≤x≤92\)
\(6x+10≥64\)
\(6x≥54\)
\(x≥9\)

\(6x+10≥0\)
\(6x≥-10\)
\(x≥-\frac{5}{3}\)

Поскольку знаки имеют одинаковое направление, мы выбираем ответ, который является более строгим и не включает ноль, то есть \(x≥9\).

Скрыть ответ

Вопрос №5:

 
Решите это неравенство для x .
\(\sqrt{7x+4}-5≥7\)

\(x≥-\frac{4}{7}\)

\(x≥20\)

\(-\frac{ 4}{7}≤x≤20\) 92=10$, затем $x=+\sqrt{10}$ и $x=-\sqrt{10}$

Но как мне применить это к неравенству, я бы получил $x>\sqrt{10 }$ и $x>-\sqrt{10}$

Но по какой-то причине это просто не имеет для меня смысла. Может ли кто-нибудь объяснить мне это математически, вместо того, чтобы просто запоминать подобные вещи?

• алгебра-предварительное исчисление
• неравенство
• радикалы

$\endgroup$

4

92 — 10 > 0$

$(x + \sqrt {10})(x — \sqrt {10}) > 0 $

$(x + \sqrt {10})$ и $(x — \sqrt {10})$ либо оба положительны, либо оба отрицательны.

Таким образом, когда они обе положительны и мы делим обе части на одно из условий:

$x + \sqrt {10} > 0$ и $x — \sqrt {10} > 0$

Это упрощается до . 10} < 0$ 92 - 10 < 0$

$(x — \sqrt{10})(x + \sqrt{10}) < 0$

Мы знаем, что один из членов $(x — \sqrt{10}) $ или $(x + \sqrt{10})$ отрицательно.

Поскольку $(x — \sqrt{10})$ всегда меньше, мы знаем, что это отрицательный член.

Таким образом, если мы разделим обе части на $(x — \sqrt{10})$, получим:

$x + \sqrt{10} > 0$

Это упрощается до:

$x > -\ sqrt{10}$

, когда мы разделим обе части на $(x + \sqrt{10})$, мы получим: 92} > \sqrt{10}$

$|x| > \sqrt{10}$

$ \оставил\{ \начать{массив}{л} x > \sqrt{10} &\mbox{, если $x \geq 0$}\\ -x>\sqrt{10} &\mbox{, если $x < 0$} \конец{массив} \Правильно. \ $

$ \оставил\{ \начать{массив}{л} x > \sqrt{10} &\mbox{, если $x \geq 0$}\\ x<-\sqrt{10} &\mbox{, если $x < 0$} \конец{массив} \Правильно. \ $

Следовательно, $x > \sqrt{10}$ или $x<-\sqrt{10}$

$\endgroup$

$\begingroup$

92$? Получится парабола. Теперь, для каких значений $x$ $y > 10$? Ответ: $x>\sqrt{10}$ и $x<\sqrt{10}$.

Вы можете увидеть подобный график здесь: http://www.wolframalpha.com/input/?i=x%5E2+%3D+10

$\endgroup$

$\begingroup$

Квадратное уравнение обычно имеет два решения (кроме x ² =0 и т. д.). Следовательно, такое квадратное неравенство имеет два множества решений, в данном случае одно положительное и одно отрицательное.

$\endgroup$

Твой ответ

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

Неравенство с квадратным корнем 9{\frac{1}{2}} > x $ выполняется. каков диапазон х?

Мой подход — я возвел обе стороны в квадрат и приступил к решению полученного квадратного уравнения, чтобы решить неравенство. Однако этот метод дает только -1 и 2 как корни квадратного числа. Но очевидно, что это не правильный ответ, так как это неравенство (с равенством) даже если x положить равным -2.

Что я делаю не так, почему я получаю неправильный интервал?

Как правильно решать неравенства такого рода?

• неравенство

$\endgroup$

2

$\begingroup$

ПОДСКАЗКА

Нельзя всегда возводить неравенства в квадрат.

Вы должны убедиться, что обе стороны положительны. И вы также должны убедиться, что подкоренное число положительное.

Однако в этом случае нетрудно доказать, что неравенство верно при $-2 \le x<0$, так что оно не имеет большого значения. Теперь вам просто нужно проверить $x \ge 0$. 9{\frac12},x\geq0$, поэтому:

Вы можете возвести в квадрат каждую сторону неравенства, не меняя знака.

Как вы заметили, решение квадратного уравнения дает вам $-1

Пересечение этого диапазона с $x\geq0$ дает вам $0\leq x<2$.

Итак, $\color\green{0\leq x<2}$ — еще одна часть решения.

---

Следовательно, комбинированное решение представляет собой объединение:

• $-2\leq x<0$
• $0\leq x<2$

Или просто $-2\leq x<2$.

$\endgroup$

$\begingroup$

Вы также можете подойти к этому, рассмотрев свойства кривых для функций $ \ y \ = \ x \ $ и $ \ y \ = \ \sqrt{x+2} \ $ . Функция квадратного корня дает только неотрицательные значения, а кривая $ \ y \ = \ \ \ sqrt {x + 2} \ $ — это кривая для $ \ y \ = \ \ \ sqrt {x} \ $, сдвинутая по горизонтали.