Формулы сокращенного умножения четвертой степени: Формулы сокращенного умножения

Формула сокращенного умножения четвертой степени. Формулы сокращенного умножения

Формула сокращенного умножения четвертой степени. Формулы сокращенного умножения

Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.

Сбор и использование персональной информации

Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.

От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.

Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.

Какую персональную информацию мы собираем:

• Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т. д.

Как мы используем вашу персональную информацию:

• Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
• Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
• Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
• Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.

Раскрытие информации третьим лицам

Мы не раскрываем полученную от Вас информацию третьим лицам.

Исключения:

• В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
• В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.

Защита персональной информации

Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.

Соблюдение вашей конфиденциальности на уровне компании

Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.

Для того что бы упростить алгебраические многочлены, существуют формулы сокращенного умножения . Их не так уж и много и они легко запоминаются, а запомнить их нужно. Обозначения которые используются в формулах, могут принимать любой вид (число или многочлен).

Первая формула сокращенного умножения называется разность квадратов . Она заключается в том что из квадрата одного числа отнимается квадрат второго числа равен величине разности данных чисел, а также их произведению.

а 2 — b 2 = (а — b)(a + b)

Разберем для наглядности:

22 2 — 4 2 = (22-4)(22+4)=18 * 26 = 468
9а 2 — 4b 2 c 2 = (3a — 2bc)(3a + 2bc)

Вторая формула о сумме квадратов . Звучит она как, сумма двух величин в квадрате равняется квадрату первой величины к ней прибавляется двойное произведение первой величины умноженное на вторую, к ним прибавляется квадрат второй величины.

(а + b) 2 = a 2 +2ab + b 2

Благодаря данной формуле, становится намного проще вычислять квадрат от большого числа, без использования вычислительной техники.

Так к примеру: квадрат от 112 будет равен
1) В начале разберем 112 на числа квадраты которых нам знакомы
112 = 100 + 12
2) Вписываем полученное в скобки возведенные в квадрат
112 2 = (100+12) 2
3) Применяя формулу, получаем:
112 2 = (100+12) 2 = 100 2 + 2 * 100 * 12 + 122 = 10000 + 2400+ 144 = 12544

Третья формула это квадрат разности . Которая гласит о том, что две вычитаемые друг друга величины в квадрате равняются, тому что, от первой величины в квадрате отнимаем двойное произведение первой величины умноженное на вторую, прибавляя к ним квадрат второй величины.

(а +b) 2 = а 2 — 2аb + b 2

где (а — b) 2 равняется (b — а) 2 . В доказательство чему, (а-b) 2 = а 2 -2аb+b 2 = b 2 -2аb + а 2 = (b-а) 2

Четвертая формула сокращенного умножения называется куб суммы . Которая звучит как: две слагаемые величины в кубе равны кубу 1 величины прибавляется тройное произведение 1 величины в квадрате умноженное на 2-ую величину, к ним прибавляется тройное произведение 1 величины умноженной на квадрат 2 величины, плюс вторая величина в кубе.

(а+b) 3 = а 3 + 3а 2 b + 3аb 2 + b 3

Пятая, как вы уже поняли называется куб разности . Которая находит разности между величинами, как от первого обозначения в кубе отнимаем тройное произведение первого обозначения в квадрате умноженное на второе, к ним прибавляется тройное произведение первого обозначения умноженной на квадрат второго обозначения, минус второе обозначение в кубе.

(а-b) 3 = а 3 — 3а 2 b + 3аb 2 — b 3

Шестая называется — сумма кубов . Сумма кубов равняется произведению двух слагаемых величин, умноженных на неполный квадрат разности, так как в середине нет удвоенного значения.

а 3 + b 3 = (а+b)(а 2 -аb+b 2)

По другому можно сказать сумму кубов можно назвать произведение в двух скобках.

Седьмая и заключительная, называется разность кубов (ее легко перепутать с формулой куба разности, но это разные вещи). Разность кубов равняется произведению от разности двух величин, умноженных на неполный квадрат суммы, так как в середине нет удвоенного значения.

а 3 — b 3 = (а-b)(а 2 +аb+b 2)

И так формул сокращенного умножения всего 7, они похожи друг на друга и легко запоминаются, единственно важно не путаться в знаках. Они так же рассчитаны на то, что их можно использовать в обратном порядке и в учебниках собрано довольно много таких заданий. Будьте внимательны и все у вас получится.

Если у вас появились вопросы по формулам, обязательно пишите их в комментариях. Будем рады ответить вам!

Если Вы находитесь в декретном отпуске, но хотите зарабатывать деньги. Просто перейдите по ссылке Интернет бизнес с Орифлейм . Там все очень подробно написано и показано. Будет интересно!

Формулы сокращенного выражения очень часто применяются на практике, так что их все желательно выучить наизусть. До этого момента нам будет служить верой и правдой , которую мы рекомендуем распечатать и все время держать перед глазами:

Первые четыре формулы из составленной таблицы формул сокращенного умножения позволяют возводить в квадрат и куб сумму или разность двух выражений. Пятая предназначена для краткого умножения разности и суммы двух выражений. А шестая и седьмая формулы используются для умножения суммы двух выражений a и b на их неполный квадрат разности (так называют выражение вида a 2 −a·b+b 2 ) и разности двух выражений a и b на неполный квадрат их суммы (a 2 +a·b+b 2 ) соответственно.

Стоит отдельно заметить, что каждое равенство в таблице представляет собой тождество . Этим объясняется, почему формулы сокращенного умножения еще называют тождествами сокращенного умножения.

При решении примеров, особенно в которых имеет место разложение многочлена на множители , ФСУ часто используют в виде с переставленными местами левыми и правыми частями:

Три последних тождества в таблице имеют свои названия. Формула a 2 −b 2 =(a−b)·(a+b) называется формулой разности квадратов , a 3 +b 3 =(a+b)·(a 2 −a·b+b 2 ) — формулой суммы кубов , а a 3 −b 3 =(a−b)·(a 2 +a·b+b 2 ) — формулой разности кубов . Обратите внимание, что соответствующим формулам с переставленными частями из предыдущей таблицы фсу мы никак не назвали.

Дополнительные формулы

В таблицу формул сокращенного умножения не помешает добавить еще несколько тождеств.

Сферы применения формул сокращенного умножения (фсу) и примеры

Основное предназначение формул сокращенного умножения (фсу) объясняется их названием, то есть, оно состоит в кратком умножении выражений. Однако сфера применения ФСУ намного шире, и не ограничивается кратким умножением. Перечислим основные направления.

Несомненно, центральное приложение формулы сокращенного умножения нашли в выполнении тождественных преобразований выражений . Наиболее часто эти формулы используются в процессе

упрощения выражений .

Пример.

Упростите выражение 9·y−(1+3·y) 2 .

Решение.

В данном выражении возведение в квадрат можно выполнить сокращенно, имеем 9·y−(1+3·y) 2 =9·y−(1 2 +2·1·3·y+(3·y) 2) . Остается лишь раскрыть скобки и привести подобные члены: 9·y−(1 2 +2·1·3·y+(3·y) 2)= 9·y−1−6·y−9·y 2 =3·y−1−9·y 2 .

В предыдущем уроке мы разобрались с разложением на множители. Освоили два способа: вынесение общего множителя за скобки и группировку. В этом уроке — следующий мощный способ: формулы сокращённого умножения . В краткой записи — ФСУ.

Формулы сокращённого умножения (квадрат суммы и разности, куб суммы и разности, разность квадратов, сумма и разность кубов) крайне необходимы во всех разделах математики. Они применяются в упрощении выражений, решении уравнений, умножении многочленов, сокращении дробей, решении интегралов и т.д. и т.п. Короче, есть все основания разобраться с ними. Понять откуда они берутся, зачем они нужны, как их запомнить и как применять.

Разбираемся?)

Откуда берутся формулы сокращённого умножения?

Равенства 6 и 7 записаны не очень привычно. Как бы наоборот. Это специально.) Любое равенство работает как слева направо, так и справа налево. В такой записи понятнее, откуда берутся ФСУ.

Они берутся из умножения.) Например:

(a+b) 2 =(a+b)(a+b)=a 2 +ab+ba+b 2 =a 2 +2ab+b 2

Вот и всё, никаких научных хитростей. Просто перемножаем скобки и приводим подобные. Так получаются все формулы сокращённого умножения. Сокращённое умножение — это потому, что в самих формулах нет перемножения скобок и приведения подобных. Сокращены.) Сразу дан результат.

ФСУ нужно знать наизусть. Без первых трёх можно не мечтать о тройке, без остальных — о четвёрке с пятёркой.

)

Зачем нужны формулы сокращённого умножения?

Есть две причины, выучить, даже зазубрить эти формулы. Первая — готовый ответ на автомате резко уменьшает количество ошибок. Но это не самая главная причина. А вот вторая…

Если Вам нравится этот сайт…

Кстати, у меня есть ещё парочка интересных сайтов для Вас.)

Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)

можно познакомиться с функциями и производными.

Формулы сокращенного умножения — презентация онлайн

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

1. Формулы сокращенного умножения.

Учитель математики МАОУ лицей №3
города Кропоткин Краснодарского края
Зозуля Елена Алексеевна

2. Кто ввел понятие о формулах сокращенного умножения?

Формулы сокращённого умножения многочленов —
часто встречающиеся случаи умножения
многочленов. Многие из них являются частным
случаем Бинома Ньютона.
Изучаются в средней школе в курсе алгебры.Бино́м
Нью́то́на — формула для разложения на отдельные
слагаемые целой неотрицательной степени суммы
двух переменных
Долгое время считалось, что для натуральных
показателей степени эту формулу, как и
треугольник, позволяющий находить
коэффициенты, изобрёл Блез Паскаль, описавший
её в XVII веке.
Однако историки науки обнаружили, что формула
была известна ещё китайскому математику Яну
Хуэю, жившему в XIII веке, а также исламским
математикам ат-Туси (XIII век) и ал-Каши (XV век).
Исаак Ньютон около 1676 года обобщил формулу
для произвольного показателя степени (дробного,
отрицательного и др.). Из биномиального
разложения Ньютон, а позднее и Эйлер,
выводили всю теорию бесконечных рядов.
Очень часто приведение многочлена к
стандартному виду можно осуществить
путём применения формул сокращённого
умножения . Все они доказываются
непосредственным раскрытием скобок и
приведением подобных слагаемых.
Формулы сокращённого умножения нужно
знать наизусть!!!

5. Формулы сокращенного умножения для квадратов:

(a b) a 2ab b
2
(a b) a 2ab b
2
2
2
2
2
a b (a b)( a b)
2
2
(a b c) a b c 2ab 2ac 2bc
2
2
2
2

6. Формулы сокращенного умножения для кубов:

(a b) 3 a 3 3a 2b 3ab 2 b 3
(a b) a 3a b 3ab b
3
3
2
2
3
a b (a b)( a ab b )
3
3
2
2
a 3 b 3 (a b)( a 2 ab b 2 )
(a b c) a b c 3a b 3a c
3
3
3
3
2
2
3ab 3ac 3b c 3bc 6abc
2
2
2
2

7.

Формулы сокращенного умножения для четвертой степени:(a b) a 4a b 6a b 4ab b
4
4
3
2 2
3
(a b) a 4a b 6a b 4ab b
4
4
3
2 2
3
4
4
a b (a b)(a b)(a b )
4
4
2
2
a b (a 2ab b )(a 2ab b )
4
4
2
2
2
2
a a b b (a ab b )(a ab b )
4
2 2
4
2
2
2
2

8. Формулы сокращенного умножения для n-ой степени:

a b (a b)(a
n
n
n 1
a
n 2
b a
n 3 2
b ..
. a 2b n 3 ab n 2 ab n 1 )
a b (a b)(a
n
n
2 n 3
. a b
a b
2n
2n
n 1
a
ab
n 2
n 2
b a
ab
n 3 2
n 1
b ..
)
(a b )( a b )
n
n
n
n

9. Задачи

1.Представить в виде
многочлена
(x 5)
2
2
Применяем формулу
квадрата разности и
получаем:
(x ) 2x
2 2
2
5 ( 5 ) x 2 5x 5
2
4
2
2. Представить в
виде многочлена :
( 3 x)( x 3)( x 3 )
2
Очевидно, что можно решить задачу открыв
первые две скобки, далее последующие
две. Но, если присмотреться, можно
заметить более простой путь к решению
задачи. А именно — занеся минус в первые
скобки и открыв крайние мы получим
квадрат разности, который легко
преобразуется в многочлен:
( 3 x)( x 2 3)( x 3 ) ( x 3 )( x 3 )( x 2 3) ( x 2 3)( x 2 3)
( x 3) x 6 x 9
2
2
4
2
3.Подставить вместо
многоточия одночлены
так, чтобы
выполнялось
равенство:
(15x …) … … 50 y
2
Согласно формуле сокращенного умножения
квадрата разницы найдем второй член в
равенстве слева. Его квадрат равен 50y, а,
значит, недостающий одночлен равен
50 y 2 25 y 5 2 y
Левая часть равенства определена, теперь
нам не составит труда заполнить остальные
многоточия. (15 х) 2 225 х 2 — первый одночлен
правой части
найден. Найдем и
второй:
2 15х 5 2 у 150х 2 у
(15х 5 2 у )
2
225х 150 х 2 у 50 у
2
4. Преобразуйте в
многочлен
выражение:
( х 6)( х 6 х 36) 2( х 3)( х 3)
2
( х 6)( х 6 х 36) 2( х 3)( х 3) ( х 216) 2( х 9)
2
3
2
х 216 2 х 18 х 2 х 234
3
2
3
2

18.

Список литературы: 1.Википедия
2.”Только факты” под
редакцией Ридерс Дайджест.
3. www.Grandars.ru

English     Русский Правила

Таблица формул сокращенного умножения. Формулы сокращённого умножения

Содержание

1. Список формул сокращенного умножения (ФСУ) в виде таблицы
2. Вывод формулы разности кубов
3. Основная задача формул сокращённого умножения
4. Квадрат суммы двух выражений
5. Квадрат разности двух выражений
6. Формулы для четвёртой степени
7. Как читаются формулы сокращенного умножения?
8. Квадрат суммы
9. Применить формулу сокращённого умножения самостоятельно, а затем посмотреть решение
10. Выделение полного квадрата
11. Применить формулу сокращённого умножения самостоятельно, а затем посмотреть решение
12. Дополнительные формулы
13. Куб суммы и куб разности
14. Примеры задач на применение формулы разности кубов
15. Как разложить на множители разность кубов
16. Неполный квадрат разности
17. Группа формул: сумма степеней
18. Разность степеней

Список формул сокращенного умножения (ФСУ) в виде таблицы

Формулы сокращенного умножения (фсу) изучаются на уроках алгебры в 7 классе после разговора про действия с многочленами и одночленами, при этом рассматриваются 7 основных формул. 3;

(a−b)·(a²+a·b+b²)=a³−b³.

Под буквами a и b понимаются числа, переменные, или, вообще, любые числовые и буквенные выражения.

Формулы сокращенного выражения очень часто применяются на практике, так что их все желательно выучить наизусть. До этого момента нам будет служить верой и правдой таблица формул сокращенного умножения, которую мы рекомендуем распечатать и все время держать перед глазами:

Первые четыре формулы из составленной таблицы формул сокращенного умножения позволяют возводить в квадрат и куб сумму или разность двух выражений. Пятая предназначена для краткого умножения разности и суммы двух выражений. А шестая и седьмая формулы используются для умножения суммы двух выражений a и b на их неполный квадрат разности (так называют выражение вида a²−a·b+b²) и разности двух выражений a и b на неполный квадрат их суммы (a²+a·b+b²) соответственно.

Стоит отдельно заметить, что каждое равенство в таблице представляет собой тождество. Этим объясняется, почему формулы сокращенного умножения еще называют тождествами сокращенного умножения.

При решении примеров, особенно в которых имеет место разложение многочлена на множители, ФСУ часто используют в виде с переставленными местами левыми и правыми частями:

Три последних тождества в таблице имеют свои названия. Формула a²−b²=(a−b)·(a+b) называется формулой разности квадратов, a³+b³=(a+b)·(a²−a·b+b²) – формулой суммы кубов, а a³−b³=(a−b)·(a²+a·b+b²) – формулой разности кубов. Обратите внимание, что соответствующим формулам с переставленными частями из предыдущей таблицы фсу мы никак не назвали.

Вывод формулы разности кубов

Для доказательства справедливости формулы разности кубов достаточно перемножить выражения раскрыв скобки:

(a – b)·(a² + ab + b²) =
= a³ + a²b + ab² – ba² – ab² – b³ = a³ – b³

Основная задача формул сокращённого умножения

Внимание!

Если вам нужна помощь с академической работой, то рекомендуем обратиться к профессионалам. Более 70 000 экспертов готовы помочь вам прямо сейчас.

Формулы сокращённого умножения (ФСУ) нужны для того, чтобы умножать и возводить в степень числа, выражения, в том числе многочлены. То есть, при помощи формул можно работать с числами значительно быстрее и проще. Таким образом можно из сложного уравнения сделать обычное, что упростит задачу.

Квадрат суммы двух выражений

Существует ряд случаев, когда умножение многочлена на многочлен можно значительно упростить. Таковым к примеру является случай (2x + 3y)².

Выражение (2x + 3y)² это перемножение двух многочленов, каждый из которых равен (2x + 3y)

(2x + 3y)² = (2x + 3y)(2x + 3y)

Получили умножение многочлена на многочлен. Выполним его:

(2x + 3y)² = (2x + 3y)(2x + 3y) = 4x² + 6xy + 6xy + 9y² = 4x² + 12xy + 9y²

То есть выражение (2x + 3y)² равно 4x² + 12xy + 9y²

(2x + 3y)² = 4x² + 12xy + 9y²

Решим аналогичный пример, который попроще:

(a + b)²

Выражение (a + b)² это перемножение двух многочленов, каждый из которых равен (a + b)

(a + b)² = (a + b)(a + b)

Выполним это умножение:

(a + b)² = (a + b)(a + b) = a² + ab + ab + b² = a² + 2ab + b²

То есть выражение (a + b)² равно a² + 2ab + b²

(a + b)² = a² + 2ab + b²

Оказывается, что случай (a + b)² можно распространить для любых a и b. Первый пример, который мы решили, а именно (2x + 3y)² можно решить с помощью тождества (a + b)² = a² + 2ab + b². Для этого нужно подставить вместо переменных a и b соответствующие члены из выражение (2x + 3y)². В данном случае переменной a соответствует член 2x, а переменной b соответствует член 3y

a = 2x

b = 3y

И далее можно воспользоваться тождеством (a + b)² = a² + 2ab + b², но вместо переменных a и b нужно подставлять выражения 2x и 3y соответственно:

(2x + 3y)² = (2x)² + 2 × 2x × 3y + (3y)² = 4x² + 12xy + 9y²

Как и в прошлый раз получили многочлен 4x² + 12xy + 9y². Решение обычно записывают покороче, выполняя в уме все элементарные преобразования:

(2x + 3y)² = 4x² + 12xy + 9y²

Тождество (a + b)² = a² + 2ab + b² называют формулой квадрата суммы двух выражений. Эту формулу можно прочитать так:

Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого выражения на второе плюс квадрат второго выражения.

Рассмотрим выражение (2 + 3)². Его можно вычислить двумя способами: выполнить сложение в скобках и возвести полученный результат в квадрат, либо воспользоваться формулой квадрата суммы двух выражений.

Первый способ:

(2 + 3)² = 5² = 25

Второй способ:

(2 + 3)² = 2² + 2 × 2 × 3 + 3² = 4 + 12 + 9 = 25

Пример 2. Преобразовать выражение (5a + 3)² в многочлен.

Воспользуемся формулой квадрата суммы двух выражений:

(a + b)² = a² + 2ab + b²

(5a + 3)² = (5a)² + 2 × 5a × 3 + 3² = 25a² + 30a + 9

Значит, (5a + 3)² = 25a² + 30a + 9.

Попробуем решить данный пример, не пользуясь формулой квадрата суммы. У нас должен получиться тот же результат:

(5a + 3)² = (5a + 3)(5a + 3) = 25a² + 15a + 15a + 9 = 25a² + 30a + 9

Формула квадрата суммы двух выражений имеет геометрический смысл. Мы помним, что для вычисления площади квадрата нужно возвести во вторую степень его сторону.

Например, площадь квадрата со стороной a будет равна a². Если увеличить сторону квадрата на b, то площадь будет равна (a + b)²

Рассмотрим следующий рисунок:

Представим, что сторону квадрата, изображённого на данном рисунке увеличили на b. У квадрата все стороны равны. Если его сторону увеличить на b, то остальные стороны тоже увеличатся на b

Получился новый квадрат, который больше предыдущего. Чтобы хорошо увидеть его, достроим отсутствующие стороны:

Чтобы вычислить площадь этого квадрата, можно по отдельности вычислить квадраты и прямоугольники, входящие в него, затем сложить полученные результаты.

Сначала можно вычислить квадрат со стороной a — его площадь будет равна a². Затем можно вычислить прямоугольники со сторонами a и b — они будут равны ab. Затем можно вычислить квадрат со стороной b

В результате получается следующая сумма площадей:

a² + ab + ab + b²

Сумму площадей одинаковых прямоугольников можно заменить на умножение 2ab, которое буквально будет означать «повторить два раза площадь прямоугольника ab». Алгебраически это получается путём приведения подобных слагаемых ab и ab. В результате получается выражение a² + 2ab + b², которое является правой частью формулы квадрата суммы двух выражений:

(a + b)² = a² + 2ab + b²

Квадрат разности двух выражений

Формула квадрата разности двух выражений выглядит следующим образом:

(a − b)² = a² − 2ab + b²

Эту формулу можно прочитать так:

Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого выражения на второе плюс квадрат второго выражения.

Формула квадрата разности двух выражений выводится таким же образом, как и формула квадрата суммы двух выражений. Выражение (a − b)² представляет собой произведение двух многочленов, каждый из которых равен (a − b)

(a − b)² = (a − b)(a − b)

Если выполнить это умножение, то получится многочлен a² − 2ab + b²

(a − b)² = (a − b)(a − b) = a² − ab − ab + b² = a² − 2ab + b²

Пример 1. Преобразовать выражение (7x − 5)² в многочлен.

Воспользуемся формулой квадрата разности двух выражений:

(a − b)² = a² − 2ab + b²

(7x − 5)² = (7x)² − 2 × 7x × 5 + 5² = 49x² − 70x + 25

Значит, (7x − 5)² = 49x² − 70x + 25.

Попробуем решить данный пример, не пользуясь формулой квадрата разности. У нас должен получиться тот же результат:

(7x − 5)² = (7x − 5)(7x − 5) = 49x² − 35x − 35x + 25 = 49x² − 70x + 25.

Формула квадрата разности двух выражений тоже имеет геометрический смысл. Если площадь квадрата со стороной a равна a², то площадь квадрата, сторона которого уменьшена на b, будет равна (a − b)²

Рассмотрим следующий рисунок:

Представим, что сторону квадрата, изображённого на данном рисунке уменьшили на b. У квадрата все стороны равны. Если одну сторону уменьшить на b, то остальные стороны тоже уменьшатся на b

Получился новый квадрат, который меньше предыдущего. На рисунке он выделен жёлтым. Сторона его равна a − b, поскольку старая сторона a уменьшилась на b. Чтобы вычислить площадь этого квадрата, можно из первоначальной площади квадрата a² вычесть площади прямоугольников, которые получились в процессе уменьшения сторон старого квадрата. Покажем эти прямоугольники:

Тогда можно написать следующее выражение: старая площадь a² минус площадь ab минус площадь (a − b)b

a² − ab − (a − b)b

Раскроем скобки в выражении (a − b)b

a² − ab − ab + b²

Приведем подобные слагаемые:

a² − 2ab + b²

В результате получается выражение a² − 2ab + b², которое является правой частью формулы квадрата разности двух выражений:

(a − b)² = a² − 2ab + b²

Формулы квадрата суммы и квадрата разности в общем называют формулами сокращённого умножения. Эти формулы позволяют значительно упростить и ускорить процесс перемножения многочленов.

Ранее мы говорили, что рассматривая член многочлена по отдельности, его нужно рассматривать вместе со знаком, который перед ним располагается.

Но применяя формулы сокращённого умножения, знак исходного многочлена не следует рассматривать в качестве знака самого этого члена.

Например, если дано выражение (5x − 2y)², и мы хотим воспользоваться формулой (a − b)² = a² − 2ab + b², то вместо b нужно подставлять 2y, а не −2y. Это особенность работы с формулами, которую не следует забывать.

(5x − 2y)²
a = 5x
b = 2y
(5x − 2y)² = (5x)² − 2 × 5x × 2y + (2y)² = 25x² − 20xy + 4y²

Если подставлять −2y, то это будет означать, что разность в скобках исходного выражения была заменена на сумму:

(5x − 2y)² = (5x + (−2y))²

и в таком случае нужно применять не формулу квадрата разности, а формулу квадрата суммы:

(5x + (−2y)²
a = 5x
b = −2y
(5x + (−2y))² = (5x)² + 2 × 5x × (−2y) + (−2y)² = 25x² − 20xy + 4y²

Исключением могут быть выражения вида (x − (−y))². В данном случае, применяя формулу (a − b)² = a² − 2ab + b² вместо b следует подставить (−y)

(x − (−y))² = x² − 2 × x × (−y) + (−y)² = x² + 2xy + y²

Но возводя в квадрат выражения вида x − (−y), удобнее будет заменять вычитание на сложение x + y. Тогда первоначальное выражение примет вид (x + y)² и можно будет воспользоваться формулой квадрата суммы, а не разности:

(x + y)² = x² + 2xy + y²

Формулы для четвёртой степени

(a + b)4 = a4 + 4a3b + 6a2b2 + 4ab3 + b4

(a – b)4 = a4 – 4a3b + 6a2b2 – 4ab3 + b4

a4 – b4 = (a – b)(a + b)(a2 + b2)

Как читаются формулы сокращенного умножения?

Чтобы рассказать решение примера, в котором были использованы формулы сокращенного умножения, нужно знать, как эти формулы читаются. Дадим соответствующие формулировки.

Сначала разберемся с принципом чтения формул сокращенного умножения. Это удобнее всего сделать, рассмотрев любую и них, например, первую формулу квадрата суммы вида (a+b)²=a²+2·a·b+b².

В левой ее части находится выражение (a+b)², которое представляет собой квадрат суммы двух выражений a и b, оно так и читается (отсюда понятно и название формулы). Дальше стоит знак равно, он и произносится как равно. В правой части формулы расположена сумма трех слагаемых a², 2·a·b и b². a² и b² – это квадраты первого и второго выражений соответственно, а 2·a·b читается как удвоенное произведение выражений a и b, слово «удвоенное» отвечает числовому коэффициенту 2. Осталось соединить все эти рассуждения в одно предложение, которое будет ответом на вопрос, как читается формула квадрата суммы.

Итак, квадрат суммы двух выражений a и b равен сумме квадрата первого выражения, удвоенного произведения первого и второго выражений и квадрата второго выражения.

Аналогично читаются и остальные фсу.

Так квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение этих выражений плюс квадрат второго выражения. Эта формулировка второй фсу вида (a−b)²=a²−2·a·b+b².

Дальше читаем формулу (a+b)³=a³+3·a²·b+3·a·b²+b³. Куб суммы двух выражений a и b равен сумме куба первого выражения, утроенного произведения квадрата первого выражения на второе, утроенного произведения первого выражения на квадрат второго и куба второго выражения.

Аналогично читается и формула куба разности (a−b)³=a³−3·a²·b+3·a·b²−b³. Куб разности двух выражений равен кубу первого выражения минус утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого на квадрат второго выражения минус куб второго выражения.

Переходим к чтению пятой по списку формулы сокращенного выражения (a−b)·(a+b)=a²−b². Произведение разности двух выражений и их суммы равно разности квадратов первого и второго выражений.

А для удобства чтения шестой и, последней, седьмой ФСУ используют термины «неполный квадрат суммы» и «неполный квадрат разности» выражений a и b, которыми называют выражения a²+a·b+b² и a²−a·b+b² соответственно. (В свою очередь выражения a²+2·a·b+b² и a²−2·a·b+b² называют полным квадратом суммы и разности соответственно.)

Итак, произведение суммы двух выражений на их неполный квадрат разности равно сумме кубов этих выражений. Так читается формула (a+b)·(a²−a·b+b²)=a³+b³. И произведение разности двух выражений на неполный квадрат их суммы равен разности кубов этих выражений, этому утверждению отвечает формула сокращенного умножения вида (a−b)·(a²+a·b+b²)=a³−b³.

Квадрат суммы

Формулой квадрата суммы называется равенство

(квадрат суммы двух чисел равен квадрату первого числа плюс удвоенное произведение первого числа на второе плюс квадрат второго числа).

Вместо a и b в эту формулу могут быть подставлены любые числа.

Формула квадрата суммы часто применяется для упрощения вычислений. Например,

.

С помощью формулы квадрата суммы многочлен можно разложить на множители, а именно, представить в виде произведения двух одинаковых множителей можно разложить на множители, а именно, представить в виде произведения двух одинаковых множителей .

Формула следует из правила умножения многчлена на многочлен:

Пример 1. Записать в виде многочлена выражение

.

Решение. По формуле квадрата суммы получаем

Пример 2. Записать в виде многочлена выражение

.

Решение. По формуле квадрата суммы получаем

Применить формулу сокращённого умножения самостоятельно, а затем посмотреть решение

Пример 3. Выяснить, является ли многочлен

квадратом какого-либо двучлена.

Правильное решение и ответ.

Пример 4. Разложить на множители

.

Правильное решение и ответ.

Выделение полного квадрата

Часто в многочлене второй степени содержится квадрат суммы или разности, но содержится в скрытом виде. Чтобы получить полный квадрат в явном виде, нужно преобразовать многочлен. Для этого, как правило, одно из слагаемых многочлена представляется в виде удвоенного произведения, а затем к многочлену прибавляется и из него вычитается одно и то же число.

Пример 7. Рассмотрим многочлен второй степени

.

Решение. Этот многочлен можно преобразовать следующим образом:

Здесь мы представили 5x в виде удвоенного произведения 5/2 на x, прибавили к многочлену и вычли из него одно и то же число , далее применили формулу квадрата суммы для двучлена , далее применили формулу квадрата суммы для двучлена .

Итак, мы доказали равенство

,

показывающее, что многочлен второй степени

равен полному квадрату плюс число плюс число .

Пример 8. Рассмотрим многочлен второй степени

.

Решение. Проведём над ним следующие преобразования:

.

Здесь мы представили 8x в виде удвоенного произведения x на 4, прибавили к многочлену и вычли из него одно и то же число 4², применили формулу квадрата разности для двучлена x − 4.

Итак, мы доказали равенство

,

показывающее, что многочлен второй степени

равен полному квадрату плюс число −16.

Применить формулу сокращённого умножения самостоятельно, а затем посмотреть решение

Пример 9. Выделить полный квадрат в многочлене второй степени

.

Правильное решение и ответ.

Дополнительные формулы

В таблицу формул сокращенного умножения не помешает добавить еще несколько тождеств.

Во-первых, полезной будет формула бинома Ньютона вида , где – биномиальные коэффициенты, стоящие в строке под номером n в треугольнике Паскаля. С ее помощью можно сокращенно возводить сумму двух выражений в любую натуральную степень. Кстати, ФСУ квадрата и куба суммы и разности являются частными случаями формулы бинома Ньютона при n=2 и n=3.

Во-вторых, полезной бывает формула возведения в квадрат суммы трех, четырех и большего количества слагаемых вида
(a₁+a₂+…+a_n)²=a₁²+a₂²+…+a_n−1²+a_n²+
+2·a₁·a₂+2·a₁·a₃+2·a₁·a₄+…+
+2·a₁·a_n−1+2·a₁·a_n+
+2·a₂·a₃+2·a₂·a₄+…+2·a₂·a_n−1+2·a₂·a_n+
+…+
+2·a_n−1·a_n.

Она читается так: квадрат суммы n слагаемых равен сумме квадратов всех этих слагаемых и удвоенных произведений всех возможных пар этих слагаемых. Для примера возведем в квадрат с использованием этой формулы сумму трех слагаемых a, b и c, имеем (a+b+c)²=a²+b²+c²+2·a·b+2·a·c+2·b·c. В частном случае при n=2 эта формула становится уже известной нам формулой квадрата суммы двух слагаемых.

И еще не помешает держать перед глазами формулу разности n-ых степеней двух слагаемых вида aⁿ−bⁿ=
=(a−b)·(aⁿ⁻¹+aⁿ⁻²·b+aⁿ⁻³·b²+…+a·bⁿ⁻²+bⁿ⁻¹), которую обычно представляют раздельно для четных и нечетных показателей. Для четных показателей 2·m она имеет вид a^2·m−b^2·m=
=(a²−b²)·(a^2·m−2+a^2·m−4·b²+a^2·m−6·b⁴+…+b^2·m−2), а для нечетных показателей 2·m+1 – вид a^2·m+1−b^2·m+1=
=(a−b)·(a^2·m+a^2·m−1·b+a^2·m−2·b²+…+b^2·m).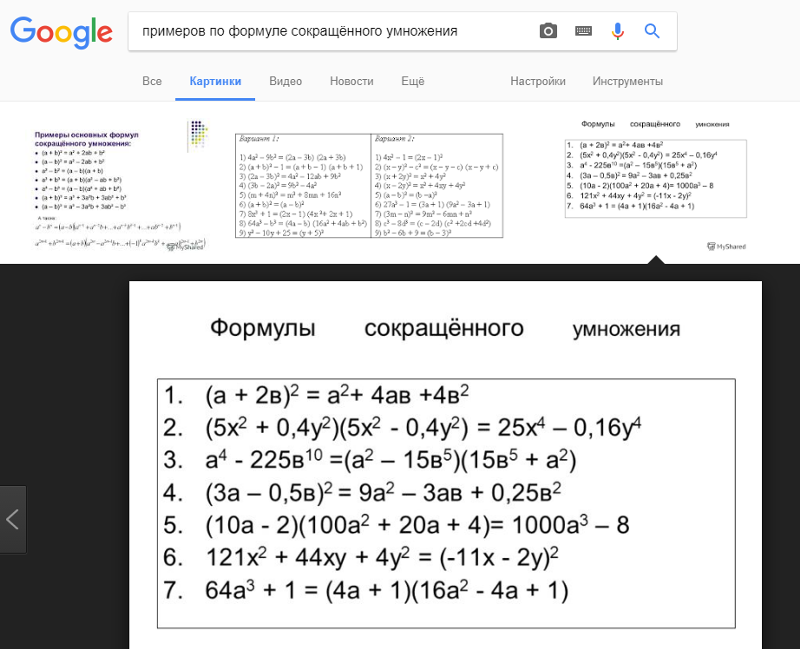 Частными случаями этой формулы являются формулы разность квадратов (при n=2), разность кубов (при n=3) и сумма кубов (при n=3 и если b заменить на −b).

Куб суммы и куб разности

Формулы куба суммы двух выражений и куба разности двух выражений выглядят следующим образом:

(a + b)³ = a³ + 3a²b + 3ab² + b³

(a − b)³ = a³ − 3a²b + 3ab² − b³

Формулу куба суммы двух выражений можно прочитать так:

Куб суммы двух выражений равен кубу первого выражения плюс утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго плюс куб второго выражения.

А формулу куба разности двух выражений можно прочитать так:

Куб разности двух выражений равен кубу первого выражения минус утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго минус куб второго выражения.

При решении задач желательно знать эти формулы наизусть. Если не запомнили — не беда! Их можно выводить самостоятельно. Мы это уже умеем.

Выведем формулу куба суммы самостоятельно:

(a + b)³

Выражение (a + b)³ представляет собой произведение из трёх многочленов, каждый из которых равен (a + b)

(a + b)³ = (a + b)(a + b)(a + b)

Но выражение (a + b)³ также может быть записано как (a + b)(a + b)²

(a + b)³ = (a + b)(a + b)²

При этом сомножитель (a + b)² является квадратом суммы двух выражений. Этот квадрат суммы равен выражению a² + 2ab + b².

Тогда (a + b)³ можно записать как (a + b)(a² + 2ab + b²).

(a + b)³ = (a + b)(a² + 2ab + b²)

А это есть умножение многочлена на многочлен. Выполним его:

(a + b)³ = (a + b)(a² + 2ab + b²) = a³ + 2a²b + ab² + a²b + 2ab² + b³ = a³ + 3a²b + 3ab² + b³

Аналогично можно вывести формулу куба разности двух выражений:

(a − b)³ = (a − b)(a² − 2ab + b²) = a³ − 2a²b + ab² − a²b + 2ab² − b³ = a³ − 3a²b + 3ab² − b³

Пример 1. Преобразуйте выражение (x + 1)³ в многочлен.

Воспользуемся формулой куба суммы двух выражений:

(a + b)³ = a³ + 3a²b + 3ab² + b³

(x + 1)³ = x³ + 3 × x² × 1 + 3 × x × 1² + 1³ = x³ + 3x² + 3x + 1

Попробуем решить данный пример, не используя формулу куба суммы двух выражений. У нас получится тот же результат, но решение станет длиннее:

(x + 1)³ = (x + 1)(x + 1)(x + 1) = (x + 1)(x² + 2x + 1) = x³ + 2x² + x + x² + 2x + 1 = x³ + 3x² + 3x + 1

Пример 2. Преобразовать выражение (6a² + 3b³)³ в многочлен.

Воспользуемся формулой куба суммы двух выражений:

(a + b)³ = a³ + 3a²b + 3ab² + b³

(6a² + 3b³)³= (6a²)³ + 3 × (6a²)² × 3b³ + 3 × 6a² × (3b³)² + (3b³)³ = 216a⁶ + 3 × 36a⁴ × 3b³ + 3 × 6a² × 9b⁶ + 27b⁹

Пример 3. Преобразовать выражение (n² − 3)³ в многочлен.

Воспользуемся формулой куба разности двух выражений:

(a − b) = a³ − 3a²b + 3ab² − b³

(n² − 3)³ = (n²)³ − 3 × (n²)² × 3 + 3 × n² × 3² − 3³ = n⁶ − 9n⁴ + 27n² − 27

Пример 4. Преобразовать выражение (2x² − x³)³ в многочлен.

Воспользуемся формулой куба разности двух выражений:

(a − b) = a³ − 3a²b + 3ab² − b³

(2x² − x³)³ = (2x²)³ − 3 × (2x²)² × x³ + 3 × 2x² × (x³)² − (x³)³ =
8x⁶ − 3 × 4x⁴ × x³ + 3 × 2x² × x⁶ − x⁹ =
8x⁶ − 12x⁷ + 6x⁸ − x⁹

Примеры задач на применение формулы разности кубов

Пример 1.

Разложить на множители x³ – 27.

Решение:

x³ – 27 = x³ – 3³ = (x – 3)·(x² + 3x + 9)

Пример 2.

Разложить на множители 8x³ – 27y⁶.

Решение:

8x³ – 27y⁶ = (2x)³ – (3y²)³ =
= (2x – 3y²)·(4x² + 6xy² + 9y⁴)

Пример 3.

Упростить выражение 27x³ – 13x – 1.

Решение:

Можно заметить, что для выражения в числителе можно применить формулу разности кубов

27x³ – 13x – 1= (3x – 1)·(9x² + 3x +1)3x – 1= 9x² + 3x +1

Как разложить на множители разность кубов

Рассмотрим пример. Необходимо разложить на множители разность кубов.

Обратим внимание, что «27а³» — это «(3а)³», значит, для формулы разности кубов вместо «a» мы используем «3a».

Используем формулу разности кубов. На месте «a³» у нас стоит «27a³», а на месте «b³», как и в формуле, стоит «b³».

Неполный квадрат разности

Выражение:

a² – 2ab + b²

Это квадрат разности, который также называется полным квадратом разности относительно выражения:

a² – ab + b²,

которое называется неполным квадратом разности. Неполный квадрат разности двух чисел равен квадрату первого числа, минус произведение первого числа на второе, плюс квадрат второго числа. Неполный квадрат разности отличается от полного только произведением чисел, которое не удваивается.

Группа формул: сумма степеней

Группа формул «Сумма степеней» составляет Таблицу 2. Эти формулы можно получить, выполняя вычисления в следующем порядке:

(x + y)2 = (x + y)(x + y) , (x + y)3 = (x + y)2(x + y) , (x + y)4 = (x + y)3(x + y)

Группу формул «сумма степеней» можно получить также с помощью треугольника Паскаля и с помощью бинома Ньютона, которым посвящены специальные разделы нашего справочника.

Таблица 2. – Сумма степеней

Название формулы	Формула
Квадрат (вторая степень) суммы	(x + y)2 = x2 + 2xy + y2
Куб (третья степень) суммы	(x + y)3 = x3 + 3x2y + 3xy2 + y3
Четвертая степень суммы	(x + y)4 = x4 + 4x3y + 6x2y2 + 4xy3 + y4
Пятая степень суммы	(x + y)5 = x5 + 5x4y + 10x3y2 + 10x2y3 + 5xy4 + y5
Шестая степень суммы	(x + y)6 = x6 + 6x5y + 15x4y2 + 20x3y3 + 15x2y4 + 6xy5 + y6

Общая формула для вычисления суммы

(x + y)ⁿ

с произвольным натуральным значением n рассматривается в разделе «Бином Ньютона» нашего справочника.

Разность степеней

Если в формулах из Таблицы 2 заменить y на – y , то мы получим группу формул «Разность степеней» (Таблица 3.):

Таблица 3. – Разность степеней

Название формулы	Формула
Квадрат (вторая степень) разности	(x – y)2 = x2 – 2xy + y2
Куб (третья степень) разности	(x – y)3 = x3 – 3x2y + 3xy2 – y3
Четвертая степеньразности	(x – y)4 = x4 – 4x3y + 6x2y2 – 4xy3 + y4
Пятая степень разности	(x – y)5 = x5 – 5x4y + 10x3y2 – 10x2y3 + 5xy4– y5
Шестая степень разности	(x – y)6 = x6 – 6x5y + 15x4y2 – 20x3y3 + 15x2y4 – 6xy5 + y6

Источники

• http://www. cleverstudents.ru/expressions/formulas_of_short_multiplication.html
• https://ru.onlinemschool.com/math/library/multiplication_formulas/dif33/
• https://NauchnieStati.ru/spravka/formuly-sokrashhjonnogo-umnozhenija/
• http://spacemath.xyz/formuly-sokrashhennogo-umnozheniya/
• https://ru.onlinemschool.com/math/formula/multiplication_formula/
• https://function-x.ru/formuly_sokrashchennogo_umnozhenija.html
• http://math-prosto.ru/?page=pages/how_to_use_formulas_of_abridged_multiplication/difference_of_cubes.php
• https://naobumium.info/algebra/formuly_sokr_umnojeniya.php
• http://www.studik.kiev.ua/ru/formuly-sokrashhennogo-umnozhenija/

Что такое BODMAS, BIDMAS и PEMDAS?

Если вам нужна PDF-версия этой страницы, просто нажмите Bodmas PDF

BODMAS объясняет «Порядок операций» в математике, а BIDMAS и PEMDAS делают то же самое, но используют немного разные слова. Если вышеизложенное звучит для вас как абракадабра, посмотрите наше короткое видео ниже, где Али объясняет, как все это работает.

Что такое аббревиатура?

Акроним — это слово, состоящее из начальных букв слов в фразе. Аббревиатуры могут произноситься как отдельные слова.

Подумайте о НАСА и часто задаваемых вопросах. Оба они произносятся так, как если бы они были самостоятельным словом. Тем не менее, НАСА означает N National A Aeronautics и S темп A администрация, а FAQ означает F часто A sked Q вопросы.

Аналогичным образом буквы в BODMAS, BIDMAS и PEMDAS обозначают слова.

BODMAS, BIDMAS и PEMDAS — это аббревиатуры для запоминания порядка операций в математике.

Что означают буквы в словах BODMAS, BIDMAS и PEMDAS?

В случае математических сокращений BODMAS, BIDMAS и PEMDAS все они означают одно и то же и служат одной и той же цели. Вот что означают буквы:

• Кронштейны
• Заказов
• Подразделение
• Умножение
• Дополнение
• Вычитание

• Скобки
• Индексы
• Подразделение
• Умножение
• Дополнение
• Вычитание

• Скобки
• Экспоненты
• Умножение
• Подразделение
• Дополнение
• Вычитание

Третья серия выше наиболее часто используется в США, в то время как британские школы почти всегда принимают серию 1 или серию 2 выше. Когда ваш ребенок впервые столкнется с одним из них, вам следует запомнить, какой именно, потому что в разных школах используются разные. Придерживаясь того же, который используется в вашей школе, вы, по крайней мере, избежите одного уровня сложности.

Что такое ордера, индексы и экспоненты?

Порядки, индексы и экспоненты — это маленькие надстрочные числа, которые представляют степени в математике.

Скобки, Деление, Умножение, Сложение и Вычитание — все это слова, с которыми мы знакомы, но что насчет второго элемента акронимов — Порядков, Индексов или Экспонентов? Это «числа половинного размера», которые часто встречаются в математических выражениях. В следующем примере 2 является индексом (единственное число множественного числа индексы ):

3 ² = 3 х 3

Что такое математические операции?

Математическая операция может рассматриваться как один из символов, который заставляет что-то происходить в математике. Знак умножения (х) означает, что нужно умножить два числа, а знак сложения (+) означает, что нужно сложить два числа. Это операций .

Каков правильный порядок операций в математике?

Правильный порядок действий в математике: B ракетки, O ряды, D провидение, M умножение, A сложение и S вычитание.

Если вы используете BIDMAS, замените O заказов на I индексов.

Весь смысл BIDMAS и BODMAS в том, чтобы помочь вам запомнить, какие операции выполнять в каком порядке. К сожалению, математика подсказывает, что это не порядок слева направо, как можно было бы ожидать: давайте рассмотрим типичный пример и посмотрим, получите ли вы правильный ответ:

2 + 3 х 4

Вы пришли к выводу, что ответ равен 20? Если да, то вы произвели вычисления слева направо и сказали, что 2 плюс 3 равно 5 , а затем умножить на 4, чтобы получить 20 . К сожалению, с математической точки зрения это неверно!

Если вы посмотрите на правила BIDMAS/BODMAS, вы увидите, что умножение предшествует сложению (две операции, с которыми мы имеем дело), ​​и поэтому вы должны были иметь дело с умножением ДО вы имели дело с Дополнением. Таким образом, правильная логика такова: 3 умножить на 4, получится 12 , а затем прибавить к 2, чтобы получить 14 . 14 это правильный ответ.

Я уже сбился со счета, сколько раз мне звонил родитель, который говорил: «Ты просто ошибаешься. Смотри, я сделал это на своем калькуляторе и набрал 2 + 3 x 4, и это всегда, но всегда дает мне ответ 20».

Среди многих тысяч вопросов на сайте Education Quizzes именно этот выпуск Порядка операций чаще всего вызывает вопросы у наших учителей, и когда кажется, что у родителей есть калькуляторы, неудивительно, почему!

Порядки, индексы и экспоненты — это маленькие надстрочные числа, которые представляют степени в математике.

Используются ли на экзамене 11-Plus BODMAS или BIDMAS?

Вообще говоря, нет. В это может потребоваться некоторое доверие, но на экзамене 11-Plus неправильный ответ часто помечается как правильный, а правильный ответ занижается! Это связано с тем, что некоторые авторитетные лица считают, что дети в возрасте до 11 лет не должны знать порядок операций, определенный BIDMAS / BODMAS, и поэтому они ожидают, что учащиеся ошибочно будут выполнять вычисления слева направо.

Во избежание возможности того, что кандидат 11-Plus может быть занижен за правильный ответ (!) обязательно уточните в своей школе, следует ли применять правила порядка действий в математических вопросах.

Каковы правила BODMAS или BIDMAS?

Чтобы увидеть, как правила BIDMAS (или BODMAS) применяются в более сложных сценариях, нам нужно проанализировать математическое выражение, содержащее все различные элементы. Если вы готовы, то давайте начнем!

2 x 20 ÷ 2 + (3+4) x 3 ² – 6 + 15

Этап 1

Разберитесь со скобами, чтобы получить:

2 х 20 ÷ 2 + 7 х 3 ² – 6 + 15

Этап 2

Сделка с индексами (если вы думаете о BIDMAS) или ордерах (если вы думаете о BODMAS), чтобы получить:

2 х 20 ÷ 2 + 7 х 9 – 6 + 15

Этап 3

Деление и умножение имеют одинаковый ранг, поэтому действуйте вместе слева направо, чтобы получить:

20 + 63 – 6 + 15

Этап 4

Сложение и вычитание имеют одинаковый ранг, поэтому действуйте вместе слева направо, чтобы получить:

92

СОВЕТ. Работайте поэтапно и не пытайтесь срезать путь.

Я надеюсь, что эта статья помогла вам понять, что такое BODMAS, BIDMAS и PEMDAS. Для более подробного ознакомления с порядком операций, а также с некоторыми интересными примерами, вы можете прочитать статью Wiki по адресу: Порядок операций, но не ожидайте, что отделаетесь без головной боли!

Итак, это объяснение BODMAS, BIDMAS и PEMDAS — есть ли что-нибудь еще, что вы хотели бы знать? Просмотрите наш Банк знаний, если у вас есть вопросы об образовании. У нас есть множество статей, наполненных информацией, советами и советами для родителей. Это ценное оружие в арсенале любого родителя!

Нечего бояться. Это проще, чем вы думали!

Excel 2013: сложные формулы

Урок 14: сложные формулы

/en/excel2013/simple-formulas/content/

Введение

Простая формула — это математическое выражение с одним оператором, например 7+9 . Сложная формула содержит более одного математического оператора, например 5+2*8 . Если в формуле более одной операции, порядок операций указывает Excel, какую операцию следует вычислить первой. Чтобы использовать Excel для расчета сложных формул, вам необходимо понять порядок операций

Дополнительно: Загрузите нашу практическую рабочую тетрадь. 92, например)

M Ultiplication и Division , в зависимости от того, что наступит первая

A DDITY и Подключение , что вы можете заказать в первой

A. PEMDAS или P аренда E извините M y D ухо A unt S союзник.

Щелкните стрелки в слайд-шоу ниже, чтобы узнать больше о том, как порядок операций используется для вычисления формул в Excel. 92=4.

Далее мы решим любое умножение и деление слева направо. Поскольку операция деления предшествует умножению, она вычисляется первой: 3/4=0,75.

Теперь решим оставшуюся операцию умножения: 0,75*4=3.

Далее мы вычислим любое сложение или вычитание, снова работая слева направо. Сначала идет сложение: 10+3=13.

Наконец, у нас осталась одна операция вычитания: 13-1=12.

Теперь у нас есть ответ: 12. Это точно такой же результат, который вы получите, если введете формулу в Excel.

Создание сложных формул

В приведенном ниже примере мы продемонстрируем, как Excel решает сложную формулу, используя порядок операций. Здесь мы хотим рассчитать стоимость налога с продаж для счета за питание. Для этого запишем нашу формулу как =(D2+D3)*0,075 в ячейке D4 . Эта формула суммирует цены наших товаров, а затем умножает это значение на налоговую ставку 7,5% (которая записывается как 0,075) для расчета стоимости налога с продаж.

Создание сложной формулы

Excel следует порядку операций и сначала складывает значения в круглых скобках: (44,85+39,90) = 84,75 $ . Затем это значение умножается на налоговую ставку: $84,75*0,075 . Результат покажет, что налог с продаж составляет $6,36 .

Заполненная формула и вычисленное значение

Особенно важно вводить сложные формулы с правильным порядком операций. В противном случае Excel не будет точно вычислять результаты. В нашем примере, если круглые скобки не включены, сначала вычисляется умножение, и результат неверен. Круглые скобки — лучший способ определить, какие вычисления будут выполняться в Excel первыми.

Результат неправильной формулы

Чтобы создать сложную формулу, используя порядок операций:

В нашем примере ниже мы будем использовать ссылок на ячейки вместе с числовыми значениями для создания сложной формулы, которая будет вычислять общая стоимость для счета за питание. Формула рассчитает стоимость каждого пункта меню, а затем сложит эти значения.

1. Выберите ячейку , которая будет содержать формулу. В нашем примере мы выберем ячейку C4 .

   Выбор ячейки C4

2. Введите формулу . В нашем примере мы введем =B2*C2+B3*C3 . Эта формула будет следовать порядку операций, сначала выполняя умножение: 2,29*20 = 45,80 и 3,49*35 = 122,15 . Затем он сложит эти значения вместе, чтобы вычислить общее количество: 45,80+122,15 .

   Создание сложной формулы

3. Дважды проверьте формулу на точность, затем нажмите Введите на клавиатуре. Формула вычислит и отобразит результат . В нашем примере результат показывает, что общая стоимость заказа составляет 167,95 $ .

   Завершенная формула и расчетное значение

Вы можете добавить круглых скобок к любому уравнению, чтобы его было легче читать. Хотя это не изменит результат формулы в этом примере, мы могли бы заключить операции умножения в круглые скобки, чтобы уточнить, что они будут вычисляться перед сложением.

Включение круглых скобок в формулу для ясности

Excel не всегда сообщит вам , если ваша формула содержит ошибку, поэтому вы должны проверить все свои формулы. Чтобы узнать, как это сделать, вы можете прочитать урок «Перепроверьте свои формулы» из нашего учебника по формулам Excel.

Вызов!

1. Откройте существующую книгу Excel. Если вы хотите, вы можете использовать нашу рабочую тетрадь.
2. Создайте сложную формулу, которая будет выполнять сложение перед умножением. Если вы используете пример, создайте формулу в ячейке D6 , которая сначала добавляет значений ячеек D3 , D4 и D5 , а затем умножает на 0,015 90. Подсказка: вам нужно подумать о порядке операций, чтобы это работало правильно.

Продолжать

Предыдущий: Простые формулы

Далее:Относительные и абсолютные ссылки на ячейки

/en/excel2013/relative-and-absolute-cell-references/content/

Формулы сокращенного умножения. Alldocube X1 — Технические характеристики Смартфоны имеют одну или несколько фронтальных камер разного дизайна

Формулы сокращенного умножения.

Изучение формул сокращенного умножения: квадрат суммы и квадрат разности двух выражений; разность квадратов двух выражений; куб суммы и куб разности двух выражений; сумма и разность кубов двух выражений.

Применение формул сокращенного умножения при решении примеров.

Для упрощения выражений, факторизации многочленов и приведения многочленов к стандартному виду используются формулы сокращенного умножения. Формулы сокращенного умножения нужно знать наизусть .

Пусть a, b R. Тогда:

1. Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого выражения на второе плюс квадрат второго выражения .

(a + b) 2 = a 2 + 2ab + b 2

2. Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого выражения на второе плюс квадрат второго выражения.

(a — b) 2 = a 2 — 2ab + b 2

3. Разность квадратов двух выражений равна произведению разности этих выражений на их сумму.

a 2 — b 2 = (a -b) (a + b)

4. Куб суммы двух выражений равен кубу первого выражения плюс утроенный квадрат первого выражения и второе плюс утроенное произведение первого выражения на квадрат второго плюс куб второго выражения.

(a + b) 3 = a 3 + 3a 2 b + 3ab 2 + b 3

5. Куб разности двух выражений равен кубу первого выражения минус утроенный квадрат первого выражения выражение, а второе плюс утроенное произведение первого выражения на квадрат второго минус куб второго выражения.

(a — b) 3 = a 3 — 3a 2 b + 3ab 2 — b 3

6. Сумма кубов двух выражений равна произведению суммы первого и второго выражений на неполный квадрат разности этих выражений.

a 3 + b 3 = (a + b) (a 2 — ab + b 2)

7. Разность кубов двух выражений равна произведению разности первого и второго выражений на неполный квадрат суммы этих выражений.

a 3 — b 3 = (a — b) (a 2 + ab + b 2)

Применение формул сокращенного умножения при решении примеров.

Пример 1.

Вычислить

а) Используя формулу квадрата суммы двух выражений, имеем

(40 + 1) 2 = 40 2 + 2 40 1 + 1 2 = 1600 + 80 + 1 = 1681

б) Используя формулу квадрата разности двух выражений, получаем

98 2 = (100 — 2) 2 = 100 2 — 2 100 2 + 2 2 = 10000 — 400 + 4 = 9604

получаем

Пример 3.

Упростим выражение

(x — y) 2 + (x + y) 2

Используем формулы квадрата суммы и квадрата разности двух выражений

(x — y) 2 + (x + y) 2 = x 2 — 2xy + y 2 + x 2 + 2xy + y 2 = 2x 2 + 2y 2

Формулы сокращенного умножения в одной таблице:

(a + b) 2 = a 2 + 2ab + b 2
(a — b) 2 = a 2 — 2ab + b 2
a 2 — b 2 = (a — b) (a + b)
(a + b) 3 = a 3 + 3a 2 b + 3ab 2 + b 3
(a — b) 3 = a 3 — 3a 2 b + 3ab 2 — b 3
a 3 + b 3 = (a + b) (a 2 — ab + b 2)
a 3 — b 3 = (a — b) (a 2 + ab + b 2)

Информация о марке, модели и альтернативных названиях конкретного устройства, если таковые имеются.

Дизайн

Информация о габаритах и ​​массе устройства, представленная в различных единицах измерения. Используемые материалы, предлагаемые цвета, сертификаты.

SIM-карта

SIM-карта используется в мобильных устройствах для хранения данных, удостоверяющих подлинность абонентов мобильной связи.

Мобильные сети

Мобильная сеть — это радиосистема, которая позволяет нескольким мобильным устройствам связываться друг с другом.

Мобильные технологии и скорости передачи данных

Связь между устройствами в мобильных сетях осуществляется с использованием технологий, обеспечивающих различные скорости передачи данных.

Операционная система

Операционная система — это системное программное обеспечение, которое контролирует и координирует работу аппаратных компонентов устройства.

SoC (система на кристалле)

Система на кристалле (SoC) объединяет все основные аппаратные компоненты мобильного устройства в один чип.

Встроенная память

Каждое мобильное устройство имеет встроенную (несъемную) фиксированную память.

Карты памяти

Карты памяти используются в мобильных устройствах для увеличения объема памяти для данных.

Экран

Экран мобильного устройства характеризуется технологией, разрешением, плотностью пикселей, длиной диагонали, глубиной цвета и т. д.

Датчики

Различные датчики выполняют различные количественные измерения и преобразуют физические показатели в сигналы, которые могут быть распознаны мобильным устройством.

Задняя камера

Основная камера мобильного устройства обычно располагается на его задней панели и может быть объединена с одной или несколькими дополнительными камерами.

Фронтальная камера

Смартфоны имеют одну или несколько фронтальных камер различной конструкции — выдвижная камера, поворотная камера, вырез или отверстие в дисплее, камера под дисплеем.

Аудио

Информация о типе динамиков и аудиотехнологиях, поддерживаемых устройством.

Радио

Радио мобильного устройства представляет собой встроенный FM-приемник.

Определение местоположения

Информация о технологиях навигации и позиционирования, поддерживаемых устройством.

Wi-Fi

Wi-Fi — это технология, обеспечивающая беспроводную связь для передачи данных на короткие расстояния между различными устройствами.

Bluetooth

Bluetooth — это стандарт безопасной беспроводной передачи данных между различными типами устройств на короткие расстояния.

USB

USB (универсальная последовательная шина) — это отраслевой стандарт, позволяющий различным электронным устройствам обмениваться данными.

Гнездо для наушников

Это аудиоразъем, который также называется аудиоразъемом. Наиболее широко используемый стандарт в мобильных устройствах — разъем для наушников 3,5 мм.

Подключение устройств

Информация о других важных технологиях подключения, поддерживаемых устройством.

Браузер

Веб-браузер — это программное приложение для доступа и просмотра информации в Интернете.

Форматы/кодеки видеофайлов

Мобильные устройства поддерживают различные форматы видеофайлов и кодеки, которые соответственно хранят и кодируют/декодируют цифровые видеоданные.

Аккумулятор

Аккумуляторы мобильных устройств различаются по емкости и технологии. Они обеспечивают электрический заряд, необходимый для их функции.

Математические выражения (формулы) сокращенное умножение (квадрат суммы и разности, куб суммы и разности, разность квадратов, сумма и разность кубов) чрезвычайно незаменимы во многих областях точных наук. Эти 7 символьных записей незаменимы при упрощении выражений, решении уравнений, умножении многочленов, сокращении дробей, решении интегралов и многом другом. А это значит, что будет очень полезно понять, как они получаются, для чего нужны, а главное, как их запомнить, а затем применить. Затем применяя формулы сокращенного умножения на практике, самое сложное будет посмотреть что такое Х и что у вас есть. Очевидно, что никаких ограничений для a и b нет, а значит это могут быть любые числовые или буквенные выражения.

И так они такие:

Первые х 2 — at 2 = (x — y) (x + y) .Для расчета разностных квадратов два выражения надо умножить на разности этих выражений на их суммы.

Второе (х + у) 2 = х 2 + 2ху + у 2 … Чтобы найти квадрат суммы двух выражений, нужно прибавить удвоенное к квадрату первого выражение произведение первого выражения на второе плюс квадрат второго выражения.

Третье (x — y) 2 = x 2 — 2xy + y 2 … Для вычисления квадрата разности нужно два выражения от квадрата первого выражения отнять удвоенное произведение первое выражение на второе плюс квадрат второго выражения.

Четвертый (x + y) 3 = x 3 + 3x 2 y + 3x 2 + y 3. Для вычисления кубических сумм два выражения нужно сложить с кубом первого выражение тройное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго плюс куб второго выражения.

Пятый (х — у) 3 = х 3 — 3х 2 у + 3х 2 — at 3 … Для вычисления куба разности двух выражений необходимо из куба первого выражения вычесть утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго минус куб второго выражения.

Шестое x 3 + at 3 = (x + y) (x 2 — xy + y 2) Чтобы вычислить сумму кубов двух выражений, нужно перемножить суммы первых а второе — неполным квадратом разности этих выражений.

Седьмая x 3 — at 3 = (x — y) (x 2 + xy + y 2) Для выполнения вычисления кубы разности два выражения, разница между первым и вторым выражением надо умножить на неполный квадрат суммы этих выражений.

Нетрудно запомнить, что все формулы применяются для выполнения расчетов и в обратном направлении (справа налево).

Существование этих закономерностей было обнаружено около 4 тысяч лет назад.

No related posts.