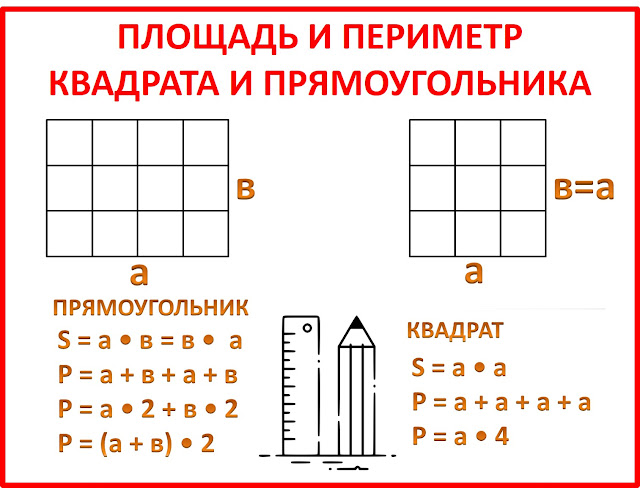
Конспект урока математики «Формулы периметра и площади прямоугольника» (3 класс) | План-конспект урока по математике (3 класс):
Дата: 14.02.2020 | ФИО учителя: Копотева Людмила Ильинична |
Школа: 104 | ФИ студента: Устинова Ульяна, 31 группа |
Класс: 3 «Б» | ФИО методиста: Серебренникова С.В. |
Кабинет: 206 | Подпись:______________ |
Конспект по математике
Тема: «Формулы периметра и площади прямоугольника»
Цели деятельности учителя: формирование у детей понятия формулы, умений записывать с помощью формул правила нахождения периметра, площади; умение выражать зависимость между величинами; совершенствование навыков решения составных уравнений и решения задач на нахождение площади прямоугольника и периметра.
Планируемые результаты:
Предметные:
Знать: единицы измерения площади, периметра, формулу нахождения периметра и площади прямоугольника; как устанавливать взаимосвязь между величинами площади и периметра прямоугольника.
Уметь: решать задачи на нахождение периметра и площади прямоугольника.
Личностные: принимать и осваивать социальную роль обучающегося; проявлять мотивы к учебной деятельности, навыки сотрудничества с взрослыми и сверстниками в разных социальных ситуациях; осознавать личностный смысл учения.
Тип урока: открытие нового знания
Оборудование: Л.Г. Петерсон, учебник «Математика», 3 класс, 2Ч. – Москва: «Ювента», 2012 – 96с., презентация.
Этап: | Время: | Деятельность учителя: | Деятельность учащихся: | УУД: |
Словесный метод: слово учителя | 1 мин | — Здравствуйте ребята! Меня зовут Ульяна Владимировна, и сегодня я проведу у вас урок математики. | Приветствуют учителя. | К: планирование учебного сотрудничества с учителем и сверстниками. |
Словесный метод: беседа | 4-5 мин | — Ребята, посмотрите на экран, как вы понимаете пословицу: «Краткость — сестра таланта»? — Математика — это точная наука. При решении различных примеров, уравнений, задач вы пользуетесь правилами, алгоритмами, памятками, которые используете в виде краткой записи. — Сегодня на уроке вы продолжите учиться использовать краткую запись в математике. — Что ожидает вас в пути во время открытий? — Какие шаги учебной деятельности вы выполняете, преодолевая трудности? — Итак, ребята, посмотрите на слайд. 12 • 3 + 8 • 3 30 + х = 60 х • 9 = 72 а = S : b а • b = S 4 • 16 — На какие группы можно разбить данные записи? — Назовите выражения. — Что общего в этих записях? — На какие группы их можно разбить? — Что такое уравнение? — Назовите уравнения. — Решите уравнения. (х = 8; х = 30.) | — Это рассказ самой важной и основной информации. — Мы столкнёмся с трудностями в учебной деятельности. — Сначала мы повторяем необходимое, потом будет задание на пробное действие. Мы постараемся его выполнить и, наверное, не получится. Мы подумаем, почему не получилось, поставим цель, составим план действий и, работая по плану, откроем новый способ. -Выражения, равенства. — 12 • 3+8 • 3; 4 • 16 -Это равенства, содержащие переменные. — Уравнения и не уравнения (формулы). — Равенство, содержащее переменную, значение которой нужно найти. — х • 9 = 72; 30 + х =60 Решают уравнения. | К: выражение своих мыслей с достаточной полнотой и точностью. |
Словесный метод: беседа Аналитико-синтетический: подводящий диалог Практический: решение задачи | 5 мин | — Что можно найти, используя данную запись: а • b = S? — Что можно найти, используя данную запись: а = S : b? — Данные равенства верны при любых значениях входящих в них букв. Их принято называть формулами. — Слово «формула» похоже на слово «форма», и это не случайно. Подобно тому, как формочка для песка помогает лепить из него пирожки, так и формулы помогают решать задачи, т.к. помогают вычислять значения одной из величин по известным значениям остальных величин.(Слайд) — Что же такое формула? Как вы понимаете? — Чем формулы отличаются от уравнений? — Для чего нужны формулы? -Посмотрите на слайд, перед вами задача. Вам нужно будет решить ее в тетради. Открываем тетрадь, отступаем 4 клетки от последней работы и на 5 строчке пишем сегодняшнее число. -Посмотрите на слайд, прочитайте задачу. Задача: Найдите площадь прямоугольника, если его периметр равен 16 см, а длина равна 6 см. -Попробуйте, решите данную задачу в тетрадь. — Итак, ребята, можете мне сказать, какое задание вы выполняли? -Кто-нибудь смог выполнить данную задачу? -Где возникло затруднение?
— Почему же возникло затруднение? — Кто-нибудь уже догадался, какова тема нашего сегодняшнего урока? | — Площадь прямоугольника. — Сторону прямоугольника.
Воспринимают информацию. — Выражение, с помощью которого можно решить пример. — В уравнениях буквы обозначают некоторые числа, а в формулах — значения величин; формулы верны для всех значений букв, а уравнения — только для корней. -Помогают при решении задач. Читают задачу. Выполняют задание. — Решали задачу на нахождение площади прямоугольника. — Нет. — При применении формулы площади, если не известна вторая сторона. — Потому что у нас нет нужной формулы для нахождения стороны прямоугольника по известному периметру. — Формулы периметра и площади прямоугольника. | П: прослушивание и восприятие художественного текста К: умение с достаточной полнотой выражать свои мысли |
Объяснительно-иллюстративный: беседа по формулам, презантация. Словесный: беседа Аналитико-синтетический: подводящий диалог Словесный: беседа Практический: Работа с задачей | 7-10 мин | — Верно, тема нашего сегодняшнего урока «Формулы периметра и площади треугольника». Кто может мне назвать цель нашего урока? — А чтобы построить формулу для нахождения стороны по периметру, какую формулу нужно хорошо знать? — Какова задача нашего урока? -Рисунок, какой геометрической фигуры поможет нам разобраться в данной теме? -Посмотрите внимательно на первую формулу. — Как вы прочитаете первую формулу? — Когда мы используем эту формулу? — А что помогут вычислить эти формулы? A = S:b b = S:a — Прочитайте их. — Что можно сказать о новых равенствах? — Теперь посмотрим, как связаны между собой периметр и стороны прямоугольника. Напомните, что такое периметр? — Какую формулу можно записать для периметра прямоугольника? — Любой из этих формул можно пользоваться для нахождения периметра. А какую из них удобнее использовать для решения задач? — Прочитайте последнюю формулу. — Опираясь на эту формулу, вы попробуете вывести формулу стороны прямоугольника по его периметру и второй стороне. С чего начнете? — Что вам напоминает эта запись? — Решите его.
— Теперь так же выведите формулу для нахождения ширины прямоугольника: b =Р : 2 -а — Прочитайте полученные формулы. — Что поможет вам проверить наши выводы? — Отройте учебник на странице 86. — Совпал ли ваш вывод с выводом учебника? -Давайте закрепим наши знания. Как найти площадь прямоугольника? — Какие единицы измерения площади вы знаете? — Как найти сторону прямоугольника? — Что означает формула периметра? — Какие единицы измерения периметра вы знаете? -Вернемся к задаче, которую мы не смогли решить в начале урока. -Сейчас вы сможете ее решить? — Что вам поможет? — Пользуясь, формулами площади и периметра найдите площадь прямоугольника, если его периметр равен 16см, а длина равна 6см. — Проверьте по подробному образцу: 1) 16 : 2 – 6 = 2 (см)- ширина. 2) 6 • 2 = 12(см2) Ответ: S = 12 см2 — Что вам позволяет новый способ? | — Построить формулу нахождения стороны по периметру. — Формулу нахождения периметра прямоугольника. — Построить формулу периметра и научиться, используя формулы, находить стороны прямоугольника. -Прямоугольник. — Площадь прямоугольника равна произведению длин его сторон. — Когда нужно найти площадь. — Длину стороны прямоугольника. — Длина стороны прямоугольника равна его площади, деленной на длину другой стороны. — В них длина и ширина выражены через площадь и длину другой стороны. — Сумма длин сторон фигуры. — Р = а + b + а + b или Р = а • 2 + b • 2 или Р = (а + b) • 2. — Последнюю, в ней всего 2 действия. — Периметр прямоугольника равен сумме его длины и ширины, умноженной на 2. -Выделим в формуле периметра прямоугольника одну из сторон, формулу, которой будем выводить, например, а. — Составное уравнение. (a + b) • 2 = P a + b = P : 2 a = P : 2 – b -Длина стороны прямоугольника равна разности половины периметра и длины другой его стороны. — Учебник Выполняют задание. — Да, мы сделали правильный вывод. — Чтобы найти площадь прямоугольника, надо длину умножить на ширину. — мм2, см2, дм2, м2 — Чтобы найти сторону прямоугольника, надо площадь разделить на другую сторону. — Периметр прямоугольника равен сумме его длины и ширины, умноженной на 2. — мм, см, дм, м -Да . — Формулы площади и периметра. Выполняют задание. Самопроверка. — Находить площадь, периметр, сторону по площади и периметру. | К: умение с достаточной полнотой выражать свои мысли П: определение основной и второстепенной информации. К: умение с достаточной полнотой выражать свои мысли К: умение с достаточной полнотой выражать свои мысли К: умение с достаточной полнотой выражать свои мысли П: осознание и произвольное построение речевого высказывания в письменной форме. |
Физминутка. | 1-2 мин | — Вы устали? Давайте встанем и разомнемся. Смотрите на экран и повторяйте движения. | Смотрят видеоролик и повторяют движения. | Л: комфортное ощущение в группе. |
Аналитико-синтетический: подводящий диалог Практический: Работа у доски, в парах | 5-7 мин | -Давайте перейдем к заданию 1, на стр. 86. Прочитайте задание. -Давайте решим вместе, одного ученика вызывает к доске, чтобы он решил один пример и так 3 примера. — Как найти площадь прямоугольника? 6 • 9 = 54 (м2) — площадь. -Как найти периметр прямоугольника? (6 + 9) • 2 = 30 (м) — периметр. б)58 дм и 70 дм. — Как найти площадь прямоугольника? 58 • 70 = 4060 (дм2) — площадь. -Как найти периметр прямоугольника? 58 • 2 + 70 • 2 = 116 + 140 = 256 (дм) — периметр. в)30 см и 80 см. — Как найти площадь прямоугольника? 30 • 80 = 2400 (см2) – площадь. -Как найти периметр прямоугольника? (30 + 80) • 2 = 220 (см) — периметр. -Следующее задание на стр. 87, номер 2. Вам предстоит выполнить в парах. Работа в парах. а)S = 4800 см2 b = S : а а = 60 см b = ? см b = 4800 : 60 = 80 (см) б)S = 1600 см2 а = 40 см b = ? см b = 1600: 40 = 40 (см)- данный прямоугольник — квадрат -Давайте сверимся с эталоном. (Слайд) | — Найди площадь и периметр прямоугольника со сторонами: а) 6 м и 9 м — Нужно умножить две стороны прямоугольника. -Чтобы найти периметр нужно сумму сторон умножить на 2. . — Нужно умножить две стороны прямоугольника. -Чтобы найти периметр нужно сумму сторон умножить на 2. — Нужно умножить две стороны прямоугольника. -Чтобы найти периметр нужно сумму сторон умножить на 2. Выполняют работу в парах. -Самопроверка. | П: определение основной и второстепенной информации. П: осознание и произвольное построение речевого высказывания в письменной форме. П: осознание и произвольное построение речевого высказывания в письменной форме. |
Практический: решение карточки. | 5-7 мин | — Сейчас каждый из вас получит карточку с заданием, вам нужно будет выполнить его самостоятельно (задание на стр. 87 номер 3) А) Напиши формулы периметра и площади квадрата со стороной а. Б) Найди периметр и площадь квадрата со стороной 30 см. В) Найди площадь квадрата, периметр которого равен 36 дм. -Все решили? Обменяйтесь листочками с соседом и проверьте с эталоном. Эталон для самопроверки. а) S = а • а Р = а + а + а + а или Р = а • 4 б) S = 30 • 30 = 900 (см2) Р = 30 • 4 = 120 (см) а = Р : 4 а = 36 : 4 = 9 (дм) S = 9 • 9 = 81 (дм2). — Оцените свою работу знаками «+» или «?» — У кого есть ошибки? Где вы допустили ошибку? — Над чем вам надо поработать, чтобы не допускать ошибок? — Не расстраивайтесь, у вас всё получится. -У кого ошибок нет? Хорошо. | Выполняют задание в карточке. Оценивают. Высказывают свое мнение. | Л: контроль и оценка процесса и результатов деятельности. |
Словесный: подводящий диалог. | 2 мин | — Какую цель вы перед собой ставили? — Достигли цели? Докажите. — Вспомним формулы. — Научились ли вы использовать новый способ? (Да.) | -Построить формулу нахождения стороны по периметру. — Мы узнали, что такое формула, вывели формулы площади и периметра, научились находить сторону по площади и периметру. -Да.
| К: выражение своих мыслей с достаточной полнотой и точностью. |
Частично-поисковый: самоанализ | 2-3 мин | — Вот и подошел к концу наш урок. -Давайте вспомним тему нашего урока. -Спасибо за урок, вы все хорошо работали. До свидание. | -Формулы периметра и площади прямоугольника. | Л: контроль и оценка процесса и результатов деятельности. |
Урок математики, 3-й класс. «Формулы периметра и площади прямоугольника»
Тема урока: формулы периметра и площади прямоугольника.
Тип урока: урок введения нового знания.
Цель урока: построение формулы
нахождения стороны прямоугольника по его
периметру и другой стороне.
Задачи:
1) сформировать представление о формуле, как о равенстве, устанавливающем взаимосвязь между величинами. Научить, в простейших случаях, выражать зависимость между величинами с помощью формул. Отрабатывать навыки устных и письменных вычислений.
2) Развивать способности анализировать, сравнивать, обобщать.
3) Воспитывать коммуникативные способности, культуру речи.
Оборудование: бланк с задачами
Ход урока
1. Самоопределение к деятельности.
Математика пришла,
Занимай свои места.
Найди для головы полезное занятье!
Чтоб от безделья не зевать,
Полезно “голову ломать”!
— Как понимаете фразеологический оборот “ломать голову”?
2.
 Актуализазия знаний.
Актуализазия знаний.
1) Что общего в записях?
2 · x = 480
Y – 56 = 64
A = S: b
d : 5=12
S = a · b
540 : z = 18
P = (a+b) · 2
(Это равенства, содержащие переменные.)
2) На какие группы их можно разделить?
(Уравнения и формулы.)
2 · x = 480 |
S = a · b |
Y – 56 = 64 |
a = S : b |
d : 5 = 12 |
P = (a+b) · 2 |
540 : z = 18 |
3) Что называют уравнением? (Равенство с
переменной, значение которой надо найти.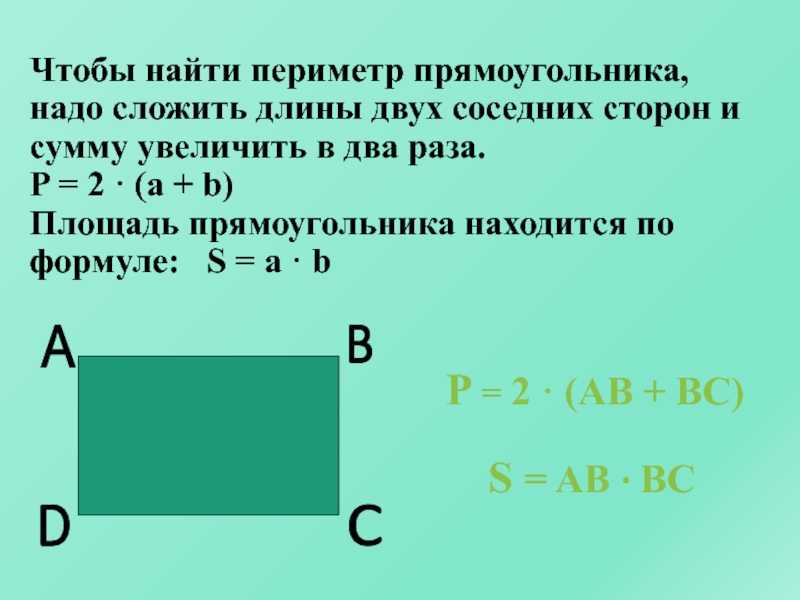 )
)
4) Найдите корни уравнений и запишите их через запятую в тетради.(240, 120, 60, 30.)
5) Что интересного вы заметили? (Все числа круглые, каждое следующее уменьшается в 2 раза.)
6) Какое число следующее? (15)
7) Запишите его, мысленно уберите запятые и прочитайте полученное число.(240 120 603 015.)
8) Посмотрите на равенства второго столбика. Что показывает первая формула? Вторая? А третья?
9) Чем отличаются формулы от уравнений? (В уравнениях буквы обозначают некоторые числа, а в формулах — значения величин; формулы верны для всех значений букв, а уравнения — только для корней)
10) Для чего нужны формулы?
11) На какое слово похоже слово “формула”? (Слово “формула” похоже на слово “форма”. Формочка для песка помогает лепить из него пирожки, а формулы помогают решать задачи, задавая форму связей между величинами)
12) Попробуйте сформулировать
определение формулы.
(Формула – это верное равенство, устанавливающее взаимосвязь между величинами)
3. Постановка учебной задачи.
— Используя данные формулы, решите задачи № 1, № 2, № 3 из бланка задач. Работать будете в парах.
Задачи
1) Найти площадь прямоугольника со сторонами 30 см и 80 см.
2) Найти сторону прямоугольника, площадь которого равна 1800 кв. см, а вторая сторона 20 см.
3) Ширина прямоугольника 8 см. Чему равна длина, если периметр равен 40 см?
4) Длина прямоугольника 3м, а ширина 2 дм. Чему равен периметр?
5) Ширина прямоугольника 6 см. Чему равна длина, если периметр равен 44 см?
6) Длина прямоугольника 5 см, а ширина на 10 мм короче. Чему равен его периметр?
Проверка решения.
— Какая формула помогла решить первую задачу? Вторую?(S = a · b), (a =S: b)
— Почему не смогли решить третью задачу? (Нужной формулы нет в списке изученных нами формул)
-Так чем же мы будем заниматься на уроке? (Мы будем выводить формулу нахождения стороны прямоугольника через периметр и другую сторону)
-Тема нашего урока: “Формулы периметра и площади прямоугольника”.
4. “Открытие” детьми нового знания.
1) С чего начнём? (Построим чертёж и введём обозначения)
Дети могут вывести формулу на основе логических рассуждений, опираясь на чертёж. Сумма длины и ширины – это половина периметра, а чтобы найти одну из сторон, из этой половины надо вычесть другую сторону: a = P: 2 — b
Второй способ.
2) Что напоминает эта формула: P= (a+b) · 2? (Уравнение)
3) Какое это уравнение? (Это составное уравнение)
4) Чем является сумма a и b?(Первым множителем)
5) Как найти неизвестный множитель?(a+b=P:2)
6) Что теперь у нас неизвестно? (Слагаемое)
7) Как найти неизвестное слагаемое? (a=P:2-b)
-Итак, мы вывели формулу нахождения
длины прямоугольника.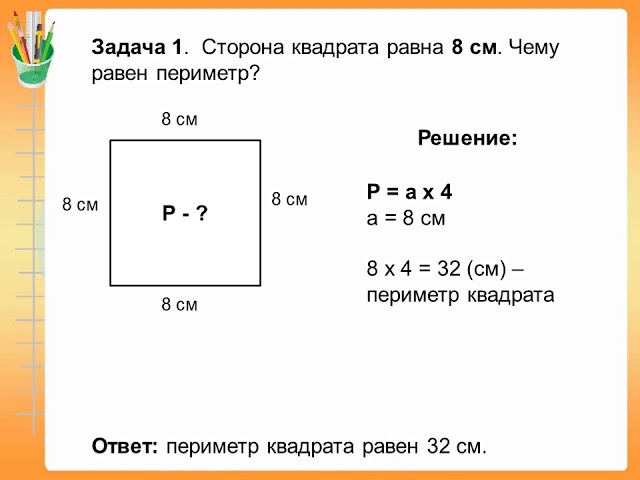 А как будет выглядеть
формула нахождения ширины прямоугольника?(b=P:2-a)
А как будет выглядеть
формула нахождения ширины прямоугольника?(b=P:2-a)
— Что же такое формула? (Формула – это верное равенство, устанавливающее взаимосвязь между величинами)
— Прочтите полученную формулу. (Длина стороны прямоугольника равна разности половины периметра и длины другой стороны)
— А теперь, используя новую формулу, давайте решим задачу, с которой вы не смогли справиться.
b=P: 2-a=40:2-8=12(см)
5. Физминутка.
Солнце заглянуло в класс
Отдыхать зовёт всех нас.
Раз, два, три, четыре, пять
Надо нам присесть и встать.
Руки вытянуть пошире,
Раз, два, три, четыре, пять
Наклониться – три-четыре,
И на месте поскакать.
На носок, потом на пятку,
Все мы делаем зарядку.
6. Первичное закрепление во внешней
речи.
1)Посмотрите на оставшиеся задачи. Какую из них мы сможем решить, используя вновь выведенную формулу? (№ 4)
b = P : 2 – a = 44 : 2- 6 = 16 (см)
— А есть ли другой способ решения этой задачи? (Подставим известные величины в формулу)
P= (a+b) · 2
44= (6+b) · 2
(6+b) · 2=44
6 + b = 44 : 2
6+b=22
b=22-6
b=16
Ответ: длина прямоугольника 16 см.
7. Самостоятельная работа с
самопроверкой по вариантам:
Работа по учебнику: Петерсон Л. Г. Математика. 3 класс. Часть 2. – М.: Издательство “Ювента”, 2005. – 96 с.: ил. : [1]
1 вариант № 4 (стр. 86)
86)
2 вариант № 6 (стр. 87)
На доске:
3 м =30 дм
Р=(30+2) · 2=64 (дм)
10 мм =1 см
5-1=4(см)
Р=(5+4) · 2=18(см)
8. Включение в систему знаний и
повторение.
Решение уравнений из № 7(а, е) с опорой на выведенный ранее алгоритм.
9. Рефлексия деятельности.
— Какова цель нашего урока?
— Достигли ли мы поставленной цели?
— Как оцениваете свою работу?
10. Домашнее задание.
— Выучить формулы из опорного конспекта в учебнике на стр. 86 и решить задачи из № 3, стр. 87.
Литература
1. Петерсон Л.Г. Математика. 3 класс.
Часть 2. – М.: Издательство “Ювента”, 2005. – 96 с.:
ил.
Петерсон Л.Г. Математика. 3 класс.
Часть 2. – М.: Издательство “Ювента”, 2005. – 96 с.:
ил.
Урок 22. площадь прямоугольника — Математика — 3 класс — Общие дети, г. Воронеж
Содержание
Урок 22. площадь прямоугольника — Математика — 3 класс
Математика, 3 класс
Урок №22. Площадь прямоугольника
Перечень вопросов, рассматриваемых в теме:
- Как вычислить площадь прямоугольника?
- В каких единицах измеряется площадь?
- Какими способами можно сравнить геометрические фигуры?
Глоссарий по теме:
Площадь – внутренняя часть любой плоской геометрической фигуры.
Квадрат – это прямоугольник, у которого все стороны равны.
Прямоугольник – это четырёхугольник, у которого все углы прямые.
Квадратный сантиметр – квадрат со стороной 1 сантиметр.
Основная и дополнительная литература по теме урока:
1. Моро М. И., Бантова М. А. и др. Математика 3 класс. Учебник для общеобразовательных организаций М.; Просвещение, 2017. – с. 60-61.
Учебник для общеобразовательных организаций М.; Просвещение, 2017. – с. 60-61.
2. Рудницкая В. Н. Тесты по математике:3 класс. М.: Издательство «Экзамен», 2016 с. 38-43.
3. Волкова Е. В. ВПР. Математика 3 класс Практикум по выполнению типовых заданий. ФГОС .М.: Издательство «Экзамен», 2018, с. 36-53.
Теоретический материал для самостоятельного изучения
Упоминание о первых геометрических фигурах встречается еще у древних египтян и древних шумеров. Учёными-археологами (они ищут разные исторические древности) был найден папирусный свиток (бумага древних египтян, изготавливаемая из растения папирус) с геометрическими задачами, в которых упоминались геометрические фигуры. И каждая из них называлась каким-то определенным словом. Одним определенным словом называлась фигура прямоугольник независимо от того какие стороны были у этого прямоугольника. А если у прямоугольника все стороны были одинаковые, то такой прямоугольник имел специальное название – квадрат.
И названия всем геометрическим фигурам дали тоже древнегреческие учёные.
Найдём площадь геометрической фигуры.
Чтобы найти площадь фигуры, надо узнать сколько раз в фигуре поместится квадрат со стороной 1 см. Площадь этой геометрической фигуры составляет 18 квадратов. Для удобства подсчёта количество квадратов можно воспользоваться знаниями таблицы умножения. По 6 взять 3 раза получится 18 квадратов.
Найдём площадь прямоугольника со сторонами 6 см и 3 см.
Для этого достаточно умножить длину на ширину. 6 ∙ 3 = 18 см2
Таким образом, формулируем вывод: чтобы найти площадь прямоугольника, надо длину умножить на ширину.
S = a ∙ b
S – площадь
a – длина
b – ширина
Задания тренировочного модуля:
1.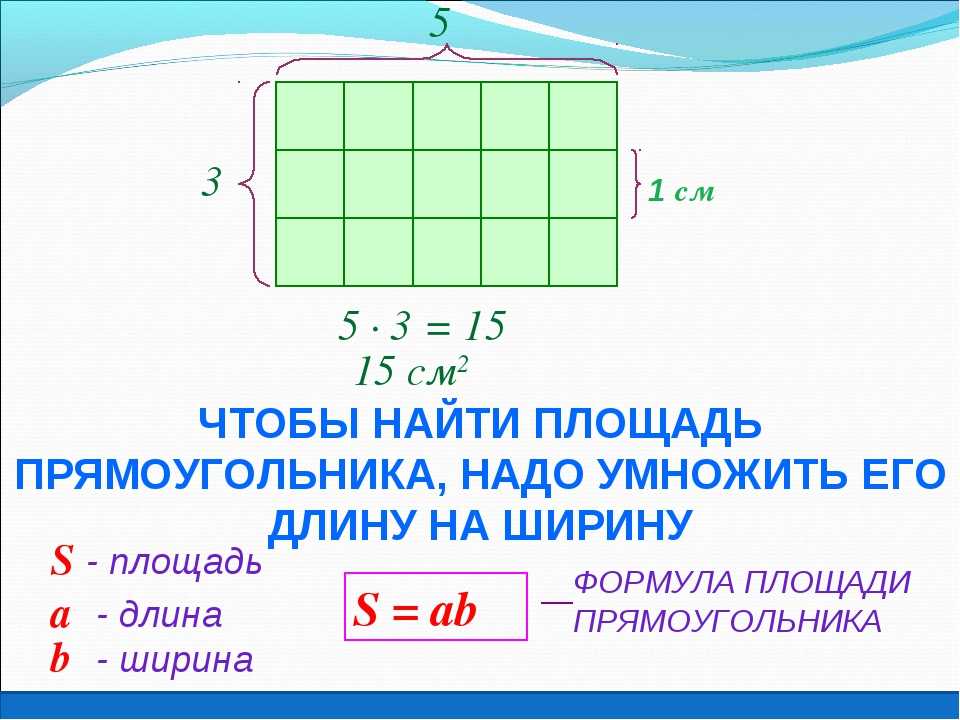 Заполните пропуски в таблице.
Заполните пропуски в таблице.
Правильный ответ:
2. Длина прямоугольника 8см, ширина 4 см. Чему равна площадь прямоугольника? Выделите правильный ответ.
12 см; 32 см; 24 см2; 32 см2; 24; 12 см2.
Правильный ответ:32см2.
| 1. |
Площадь квадрата
Сложность: лёгкое |
1 |
| 2. |
Площадь прямоугольника
Сложность: лёгкое |
1 |
| 3. |
Найди сторону прямоугольника, зная его площадь
Сложность: лёгкое |
1 |
4.
|
Найди площадь квадрата, зная его периметр
Сложность: среднее |
2 |
| 5. |
Найди периметр прямоугольника, зная его площадь
Сложность: среднее |
2 |
| 6. | У какой клумбы больше площадь? Сложность: среднее | |
| 7. |
Площадь незакрашенной части прямоугольника
Сложность: среднее |
2 |
| 8. |
Изменится ли периметр и площадь клумбы
Сложность: сложное |
3 |
9.
|
Площадь дорожки в саду
Сложность: сложное |
3 |
| 10. |
Сравни площади квадратов
Сложность: сложное |
3 |
3 класс, периметр и площадь прямоугольника
Дата публикации: .
Что такое прямоугольник и квадрат
Прямоугольник – это четырёхугольник, у которого все углы прямые. Значит, противоположные стороны равны друг другу.
Квадрат – это прямоугольник, у которого равны и стороны, и углы. Его называют правильным четырёхугольником.
Четырёхугольники, в том числе прямоугольники и квадраты, обозначаются 4 буквами – вершинами. Для обозначения вершин используют латинские буквы: A, B, C, D …
Пример.
Читается так: четырёхугольник ABCD; квадрат EFGH.
Что такое периметр прямоугольника? Формула расчета периметра
Периметр прямоугольника – это сумма длин всех сторон прямоугольника или сумма длины и ширины, умноженная на 2.
Периметр обозначается латинской буквой P. Так как периметр – это длина всех сторон прямоугольника, то он периметр записывается в единицах длины: мм, см, м, дм, км.
Например, периметр прямоугольника АВСD обозначается как PABCD, где А, В, С, D – это вершины прямоугольника.
Запишем формулу периметра четырехугольника ABCD:
PABCD = AB + BC + CD + AD = 2 * AB + 2 * BC = 2 * (AB + BC)
Пример.
Задан прямоугольник ABCD со сторонами: AB=СD=5 см и AD=BC=3 см.
Определим PABCD.
Решение:
1. Нарисуем прямоугольник ABCD с исходными данными.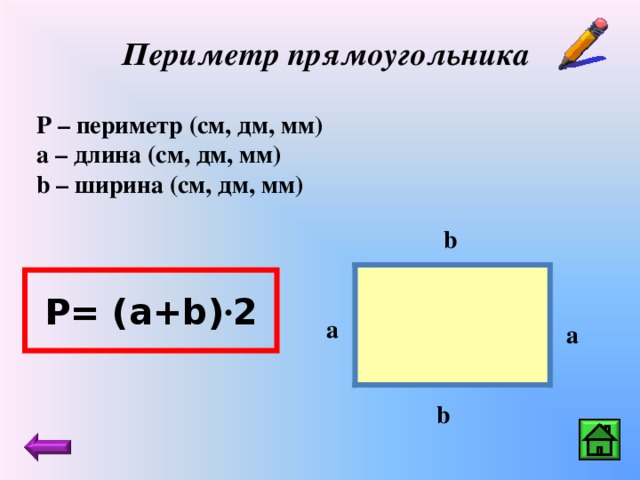
2. Напишем формулу для расчета периметра данного прямоугольника:
PABCD = 2 * (AB + BС)
3. Подставим в формулу наши данные:
PABCD = 2 * (5 см + 3 см) = 2 * 8 см = 16 см
Ответ: PABCD = 16 см.
Формула расчета периметра квадрата
У нас есть формула для определения периметра прямоугольника.
PABCD = 2 * (AB + BC)
Применим её для определения периметра квадрата. Учитывая, что все стороны квадрата равны, получаем:
PABCD= 4 * AB
Пример.
Задан квадрат ABCD со стороной, равной 6 см. Определим периметр квадрата.
Решение.
1. Нарисуем квадрат ABCD с исходными данными.
2. Вспомним формулу расчета периметра квадрата:
PABCD = 4 * AB
3. Подставим в формулу наши данные:
Подставим в формулу наши данные:
PABCD = 4 * 6 см = 24 см
Ответ: PABCD = 24 см.
Задачи на нахождение периметра прямоугольника
1. Измерь ширину и длину прямоугольников. Определи их периметр.
2. Нарисуй прямоугольник ABCD со сторонами 4 см и 6 см. Определи периметр прямоугольника.
3. Нарисуй квадрат СEOM со стороной 5 см. Определи периметр квадрата.
Где используется расчет периметра прямоугольника?
1. Задан участок земли, его нужно обнести забором. Какой длины будет забор?
В данной задаче необходимо точно рассчитать периметр участка, чтобы не купить лишний материал для постройки забора.
2. Родители решили сделать ремонт в детской комнате. Необходимо знать периметр комнаты и её площадь, чтобы правильно рассчитать количество обоев.
Определи длину и ширину комнаты, в которой ты живешь. Определи периметр своей комнаты.
Что такое площадь прямоугольника?
Площадь – это числовая характеристика фигуры.
Площадь измеряется квадратными единицами длины: см2, м2, дм2 и др. (сантиметр в квадрате, метр в квадрате, дециметр в квадрате и т.д.)
В вычислениях обозначается латинской буквой S.
Для определения площади прямоугольника необходимо длину прямоугольника умножить на его ширину.
Площадь прямоугольника вычисляется умножением длины АК на ширину КМ. Запишем это в виде формулы.
S AKMO = AK * KM
Пример.
Чему равна площадь прямоугольника AKMO, если его стороны равны 7 см и 2 см?
S AKMO= AK * KM = 7 см * 2 см = 14 см2.
Ответ: 14 см2.
Формула вычисления площади квадрата
Площадь квадрата можно определить, умножив сторону саму на себя.
Пример.
В данном примере площадь квадрата вычисляется умножением стороны АB на ширину BC, но так как они равны, получается умножение стороны AB на AB.
S AВСО = AB * BC = AB * AB
Пример.
Определи площадь квадрата AKMO со стороной 8 см.
S AKMО = AK * KM = 8 см * 8 см = 64 см2
Ответ: 64 см2.
Задачи на нахождение площади прямоугольника и квадрата
1.Задан прямоугольник со сторонами 20 мм и 60 мм. Вычисли его площадь. Запиши ответ в квадратных сантиметрах.
2. Был куплен дачный участок размером 20 м на 30 м. Определи площадь дачного участка, ответ запиши в квадратных сантиметрах.
Как найти площадь фигуры? Ответ на webmath.ru
Содержание:
Определения
Площадь является одним из основных математических понятий. Она характеризует как плоские, так и поверхностные геометрические объекты.
Определение
Площадью плоской замкнутой фигуры называется величина части плоскости, которая находится внутри указанной фигуры.
Единицей измерения площади плоской фигуры является квадрат со стороной, равной единице. Число, соответствующее площади некоторой фигуры, состоящей из частей, равно сумме чисел, соответствующих площадям этих частей. Измерение площадей треугольников и многоугольников основано на возможности построения равновеликих им прямоугольников.
Площадь произвольной ограниченной плоской фигуры определяется как общий предел площадей описанных и вписанных в нее многоугольников, наибольшие стороны которых по длине стремятся к нулю.
Если фигура имеет площадь, то она называется квадрируемой.
Формулы площади основных геометрических фигур
Площадь треугольника
Чтобы найти площадь треугольника, надо найти полупроизведение двух его сторон на синус угла между ними. {2}$$
Читать дальше: формула площади круга и примеры решений →
Площадь квадрата
Чтобы найти площадь квадрата, надо длину его стороны возвести в квадрат, то есть
Читать дальше: формула площади квадрата и примеры решений →
Площадь прямоугольника
Чтобы найти площадь прямоугольника, надо его длину умножить на ширину, то есть
Читать дальше: формула площади прямоугольника и примеры решений →
Площадь параллелограмма
Чтобы найти площадь параллелограмма, нужно найти произведение стороны $a$ параллелограмма на высоту , проведенную к этой стороне, то есть
Читать дальше: формулы площади параллелограмма и примеры решений →
Площадь трапеции
Чтобы найти площадь трапеции, нужно длину средней линии умножить на длину высоты , опущенной к основанию:
Читать дальше: формулы площади трапеции и примеры решений →
Площадь ромба
Чтобы найти площадь ромба, надо длину стороны умножить на длину высоты, проведенной к этой стороне:
Читать дальше: формулы площади ромба и примеры решений →
Площадь эллипса
Чтобы найти площадь эллипса, нужно найти произведение длин большой и малой полуосей этого эллипса на число $\pi$, то есть
Читать дальше: формула площади эллипса и примеры решений →
«Площади фигур».
 3-й класс
3-й классТип урока: урок комплексного применения знаний и умений
Цель урока: создавать условия для формирования умения решать задачи на нахождение площади фигур через совершенствование вычислительных навыков, знакомство со старинными мерами длины и площади, развитие логического мышления учащихся, кругозора, трудолюбия и аккуратности.
Задачи урока:
Образовательные:
- формировать целостный взгляд на мир средствами междисциплинарных связей на уроке; ориентировать на разнообразие способов решения задач и выбор наиболее рациональных из них; отрабатывать навыки решения задач с применением известных формул.
Развивающие:
- развивать творческую и мыслительную деятельность учащихся через решение геометрических заданий; формировать навыки самостоятельной и коллективной работы.
Воспитательные:
- прививать учащимся интерес к предмету через
решение задач; формировать умение ясно и четко
излагать свои мысли, правильно и рационально
решать геометрические задачи; воспитывать веру в
свои силы.

Методы: практический, частично-поисковый.
Организация пространства: работа фронтальная, групповая, индивидуальная, в парах (учащиеся располагаются за столами по 4 человека).
Оборудование: модели единиц площади (1см2, 1дм2, 1м2) на стенах класса, модели сложных фигур на листах А2, индивидуальные листы, презентация, листы А4, фломастеры.
Личностные УУД: осваивать новые виды деятельности, участвовать в творческом, созидательном процессе.
Регулятивные УУД: определять и формулировать цель на уроке с помощью учителя; планировать своё действие в соответствии с поставленной задачей; вносить необходимые коррективы в действие после его завершения на основе его оценки и учёта характера сделанных ошибок.
Коммуникативные УУД: развивать коммуникативные навыки работы в группе.
Познавательные УУД: ориентироваться в своей
системе знаний; понимать информацию,
представленную в схематичной, модельной форме; выбирать
наиболее эффективные способы решения задач в
зависимости от конкретных условий; самостоятельно
создавать способы решения проблем творческого и
поискового характера.
Планируемые результаты:
Метапредметные
- использовать знаково-символические средства представления информации для создания способов решения практических задач.
Предметные результаты
- Уметь вычислять площади простых и сложных фигур разными способами;
- Уметь использовать наглядные модели (план, чертеж, схема), отражающие отношения между предметами для решения задач;
- Овладеть основами пространственного воображения, измерения, наглядного представления периметра и площади фигур.
Ход урока
I. Организационный момент
Учитель:
— Чтобы спорилось нужное дело,
Чтобы в жизни не знать неудач,
В мир математики отправимся смело,
В мир примеров и разных задач.
А девизом нашего урока будут слова: (Хором.)Думать — коллективно!
Решать — оперативно!
Отвечать — доказательно!
Бороться — старательно!
И открытия нас ждут обязательно! (Слайд 2.)
II. Актуализация знаний учащихся
Учитель:
— Перед Вами древнерусская деревня. (Слайд 3.)
(Читает ученик.) Полторы тысячи лет прошло с тех пор, как на берегу реки на большой лесной равнине поселились славяне. Свое поселение они обнесли частоколом, высотой в целую сажень. Длина деревни достигала одной версты. В домах древних славян пол был углублен в землю почти на целый аршин. В углу находилась сложенная из камня печь - она обогревала дом, на ней же готовили еду. Вход в избу закрывала дверь толщиной в вершок.
— О каких величинах Вы услышали?
— Их использовали наши предки. Ребята познакомят с ними. (Слайды 4 — 9.) (Сообщения учащихся о старинных единицах длины и показ.)
1) Вершок – длина фаланги указательного пальца, мера длины, равная примерно 4-5 см.
2) Пядь — мера длины, равная расстоянию между
концами вытянутых пальцев – большого и
указательного.
3) Локоть – расстояние от концов пальцев до локтя согнутой руки.
4) При торговле с восточными народами стали применять аршин. В нем укладывается 16 вершков. Это примерно 71см. Первоначально “аршин” обозначал длину человеческого шага.
5) В Древней Руси применялись косая сажень – расстояние от пальцев левой ноги до конца пальцев поднятой правой руки; маховая сажень – расстояние между концами пальцев разведенных в стороны рук.
6) Для измерения больших расстояний на Руси использовали версту.
Учитель:
— Сегодня мы пользуемся современными терминами, обозначающими меры длины. Где могут встретиться “локти”, “аршины”, “пяди”?
— Часто в своей речи мы используем пословицы, но, не зная толкования слова “пядь”, вряд ли бы сумели мы разобраться в значении выражений “Семи пядей во лбу”, “На свой аршин мерит”.
III. Постановка цели и задач урока. Мотивация
учебной деятельности учащихся
Мотивация
учебной деятельности учащихся
Подготовка: участник № 1 складывает лист формата А4 так, чтобы он разделился на 8 частей.
Учитель:
— Участники, по очереди запишите современные единицы, которые используем на уроках математики. № 1, разрежьте лист на отдельные листочки. Разделите листочки на группы. Назовите их. (Единицы длины и единицы площади.)
| см | дм | м | мм |
| см2 | дм2 | м2 | км |
— № 2, переверните листочки с единицами площади, перемешайте и раздайте их участникам своей группы.
— № 1, 3, 4, посмотрите на листочек и выберите, к
какой модели сейчас отправитесь. (Участники №
1,3,4 групп получают листочки с записью единиц
площади и отправляются к выбранным моделям: 1см2,
1дм2, 1м2, представленных на
стенах класса. )
)
— Обсудите в группах, почему выбрали эту модель. Обсуждение и представление выбранной модели:
1) 1см2 — очень маленький, но играет важную роль в математике. Это квадрат со стороной 1см;
2) 1 дм2 — квадрат со стороной 1дм или 10см. В нем содержится 100 см2;
3) 1 м2 в 100 раз больше 1дм2 и в 10000 раз больше 1см2.
— Назовите одним словом. (Единицы площади.)
— Для измерения площади у русского народа были свои особые мерки: “копна”, “выть”, “соха”, “обжа”, “десятина”. От древних землемеров нам досталось только слово “площадь”.
— № 2, образуйте группу. Назовите ее. (Современные единицы длины.)
— Сформулируйте тему урока. Чему будем учиться?
— Еще 4-5 тысяч лет назад жители древнего города Вавилон умели определять площадь. Какая фигура служила эталоном при измерении площади?
— Квадрат, благодаря своим замечательным
свойствам. Знаете их? Выясните в группах. (Обсуждение
и обмен мнениями: 1) Равные стороны; 2) Прямые углы;
3) Совершенная форма; 4) Легко строить.)
Знаете их? Выясните в группах. (Обсуждение
и обмен мнениями: 1) Равные стороны; 2) Прямые углы;
3) Совершенная форма; 4) Легко строить.)
— В Древнем Китае мерой площади была другая фигура. Догадайтесь, какая.
— Почему на уроке по нахождению площади фигур присутствуют единицы длины?
IV. Первичное закрепление в знакомой ситуации
а) Типовые задания
Устный счет “Калькулятор площади”. (Слайд 10 .)
Решение задач и объединение учащихся в группы в зависимости от ответа.
1. Длина прямоугольника 6см, ширина 2см. Чему равна третья часть площади прямоугольника?
2. Площадь коридора 18м2. Вычислите ширину, если длина 9м.
3. Найдите площадь прямоугольника, ширина которого 2см, и она в 3 раза меньше его длины.
4. Площадь фундамента дома квадратной формы 64м2. Чему равна сторона фундамента?
5. Найдите площадь прямоугольника, одна сторона
которого 6см, другая – на 2см короче.
6. Во сколько раз площадь зала, равная 27м2, больше площади комнаты, равной 9м2?
Игра “Математическое лото”. (Слайд 11.)
Правила игры: 1 – придумать, 2 – решить, 3 – оценить.
Подготовка: участник № 3 складывает лист формата А4 так, чтобы он разделился на 8 частей. Получается таблица:
| a (длина) | ? | ||
| b (ширина) | ? | ||
| P (периметр) | ? | ? | |
| Ѕ (площадь) | ? | ? |
1. Составление задач. Передача листа-таблицы по
команде для решения другой группе (по часовой
стрелке).
Составление задач. Передача листа-таблицы по
команде для решения другой группе (по часовой
стрелке).
2. Решение задач (заполнение таблицы). Передача листа-таблицы по команде для проверки следующей группе.
3. Проверка и оценка решения.
б) конструктивные задания (в измененной ситуации)
Учитель:
— Внимание на экран! (Слайд 12.)
Запишите, какими способами Вы найдете площади этих фигур.
— По сигналу встаньте, найдите пару и расскажите о своих способах. Если у Вас есть этот способ, поставьте “+”, если нет, дополните свой список. Запись известных способов:
1) Пользуясь формулой;
2) Палеткой;
3) Дополнить до прямоугольника или квадрата;
4) Разбить на квадратные мерки;
5) Разделить на отдельные квадраты и прямоугольники и найти их площади;
6) Из площади большой фигуры вычесть площадь маленькой фигуры.
— Расскажите в группе по одному способу, начиная
с участника № 1. (Сбор информации, обмен
знаниями и дополнение списка ответов в паре при
перемещении по классу; обмен информацией в своей
группе.)
(Сбор информации, обмен
знаниями и дополнение списка ответов в паре при
перемещении по классу; обмен информацией в своей
группе.)
— Подчеркните нерациональные способы. Почему Вы считаете их нерациональными? Покажите рациональные способы.
V. Физкультминутка
Учащиеся делятся на группы, получают карточки (“татарский танец”, “русская плясовая”, “полька”, “марш”), исполняют танцевальные движения под музыку.
VI. Творческое применение и добывание знаний в новой ситуации
а) Вычисление площади сложной фигуры на листе формата А2, представление работы групп.
б) Индивидуальная работа с планом классной комнаты, проверка ответов с партнером по плечу. (Слайд 13.)
в) Практическая работа по измерению площади, занимаемой группой, высказывание ответов.
VII. Информация о домашнем задании, инструктаж
1) Решите разноуровневые задания на карточке (Приложение);
2) Найдите площадь одной из комнат Вашей
квартиры.
VIII. Итог урока
Учащиеся отвечают на вопросы:
- Что такое площадь?
- Как измерить площадь?
- Назовите единицы площади.
- По какой формуле находят площадь прямоугольника, квадрата?
- Какие площади у равных фигур?
- Какое свойство площади знаете?
- Людям каких профессий необходимо знание площади?
- Где Вы можете применить знания площади?
Проверка: зажигается звезда. (Слайд 14.)
Учитель:
— Послушайте притчу.
Шёл мудрец и встретил трех работников. “Что ты сегодня делал?” — спросил он каждого. Первый ответил: “Я целый день таскал ненавистные камни”. Второй ответил: “Я немного устал, но добросовестно выполнял свою работу”. Третий ответил: “Работа принесла мне радость и большое удовлетворение”.
— Кто из вас на уроке был первым работником,
вторым работником, третьим работником? Очень
хорошо, что работа на этом уроке принесла вам
радость, вы открыли новые знания.
— Что для Вас было новым?
Использованная литература.
1. Федеральный государственный образовательный стандарт начального общего образования. Москва, 2010 г.
2. Концепция духовно-нравственного развития и воспитания личности гражданина России.
3. Овчинникова М.В. Методика изучения темы “Величины” на уроках математики в начальных классах: Методические рекомендации для студентов факультета “Начальное обучение. Дошкольное воспитание”. Ялта: ЦОП “Надежда”, 2000.
4. Райкина Т.Н. Математика. 3 класс. В 2 ч. Саратов: Лицей, 2009.
5. Жильцова Т.В., Обухова А.А. Поурочные разработки по наглядной геометрии: 1-4 класс. М.: ВАКО, 2004.
|
Название этапа урока |
Содержание этапа |
Деятельность учителя |
Деятельность учащихся |
Формы работы |
Результат (формируемые УУД) |
|
I. |
Ребята, на каждом уроке вы стремитесь сделать для себя открытие, получить новые знания. Вот и сегодня мы постараемся углубить математические знания, узнать новое. С маленькой удачи начинается большой успех. Улыбнитесь и пожелайте друг другу удачи. В добрый путь за знаниями! |
Организует актуализацию требований к ученику со стороны учебной деятельности. |
Дети желают друг другу удачи.
|
Коллективная |
Личностные: самоопределение Регулятивные: целеполагание. Коммуникативные: планирование учебного сотрудничества с учителем и сверстниками. |
|
II . Актуализация знаний и фиксация затруднения в детальности.
|
Новые знания нам будет очень трудно осваивать без умения быстро и верно считать, поэтому, как всегда, начнем урок с устного счета: Устный счет. 1.Найдите в каждом ряду числа, которые не являются результатом табличного умножения. — 6,18,17,12, 41 24,30,16,11,28 2) Игра “ Кто быстрее” (дети друг другу задают примеры на умножение) 3)В городском сквере 2 ряда лип, по 8деревьев в каждом ряду и ещё 7 берёз. Сколько всего деревьев в сквере? 4)Какие фигуры изображены на доске? (треугольник, круг, прямоугольник, ромб, овал) — Среди данных фигур найдите прямоугольники. Докажите свой выбор. |
Создаёт условия для возникновения у учеников внутренней потребности включения в учебную деятельность.
Показывает фигуры, просит их назвать.
|
Дети устно отвечают на вопросы, показывают карточки с верным ответом; друг другу задают примеры на умножение
Называют номер фигуры и доказывают свой выбор.
|
Коллективная, индивидуальная |
Коммуникативные: планирование учебного сотрудничества с учителем и сверстниками. Познавательные: логические – анализ объектов с целью выделения признаков. |
|
III. Постановка учебной задачи (2 – 3 мин) |
Задача на нахождение площади. В группах предлагает посчитать площадь прямоугольника. (Раздают карточки с чертежом прямоугольника/7на3/ расчерченного на квадратные см)
— Проблема: как найти площадь, не расчерчивая каждый раз на квадратные сантиметры? — Сформулируйте тему урока. — Какую цель вы поставите для себя на сегодняшнем уроке?
|
Предлагает найти площадь прямоуголь ника посчитав квадраты. Предлагает сравнить свои ответы с эталоном (слайд) |
Подсчитывают квадратные сантиметры-21см.
Ответ детей: Сегодня мы научимся находить площадь прямоугольника и использовать знания при решении задач. |
Коллективная, групповая |
Регулятивные: целеполагание; Коммуникативные: постановка вопросов. Познавательные: самостоятельное выделение – формулирование познавательной цели. |
|
IV. Построение проекта выхода из затруднения (10 – 11 мин)
|
-Каким способом вы производили подсчёт квадратных см в прямоугольнике? — Какое математическое действие помогло вам узнать количество квадратных см в прямоугольнике?(умножение)
Что обозначает число 7? (длина) 3?(ширина). (7*3=21) Делают вывод: S = длину х ширину. — Откройте учебники, сравните свои выводы с эталоном (чтение правила на стр. 54) Сформулируйте вывод: как найти площадь? Сформулируйте вывод: как найти площадь? |
Предлагает сформулировать правило нахождения S.
Предлагает ещё раз сформулировать правило нахождения S
|
Находят площадь.
Формулировка правила. Проверка по эталону (слайд)
|
|
Коммуникативные: постановка вопросов; Познавательные: самостоятельное выделение – формулирование познавательной цели;
Регулятивные: планирование, прогнозирование; Познавательные: моделирование; Логические – решение проблемы, построение логической цепи рассуждений, доказательство;
Коммуникативные – инициативное сотрудничество в поиске и выборе информации. |
|
Физкультминутка.
|
«Мы чертёжники». -Начертите глазами луч (на стене найдите точку и отправьте луч далеко сквозь окно), кончиком носа — окружность, правой рукой- прямой угол, а левой- острый! Чертите аккуратно! Левой ногой — квадрат, а правой прямоугольник. Сформулируйте вывод: для чего необходимо выполнять физкультминутку? «Чтобы отдохнуть и расти здоровыми». |
Показывает движения, как образец. |
Дети выполняют соответствующие движения.
|
Индивидуальная |
Личностные: самоопределение |
|
V. Первичное закрепление во внешней речи (4 – 5 мин) |
Решение задачи по учебнику стр. Решим задачу: — Начертите в тетрадях прямоугольник длина которого 9см, а ширина — 2см. Найдите его площадь.( Выполняется задание с комментированием). — Какими еще могут быть длины сторон прямоугольника с такой площадью? (3 и 6) Сформулируйте вывод: как найти площадь?
|
Предлагает выполнить задания по учебнику.
Предлагает ещё раз сформулировать правило нахождения S
|
Решают типовые задания с проговариванием алгоритма вслух. Взаимопроверка в парах
Ребята делают предположения и обосновывают свои ответы. |
Парная, индивидуальная |
Регулятивные: контроль, оценка, коррекция; Познавательные: умение структуризировать знания, выбор наиболее эффективных способов решения задач; рефлексия способов и условий действия; Коммуникативные: управление поведением партнера – контроль, коррекция, оценка действий партнера. |
|
VI. Самостоятельная работа с самопроверкой (4 – 5 мин) |
Предлагаю вам побыть в роли строителей. Нам необходимо для классной комнаты закупить напольное покрытие.Выполнив необходимые измерения и пользуясь математическими знаниями узнайте, сколько квадратных метров покрытия вы закупите? (Дети работают в группах). |
Предлагает побыть в роли строителей. |
Самостоятельное решение в тетради. Проверка с эталона. (слайд) |
Групповая |
Регулятивные: контроль, коррекция, выделение и осознание того, что уже усвоено и что еще подлежит усвоению, осознание качества и уровня усвоения; Личностные: самоопределение. |
|
VII. Включение в систему знаний и повторение (4 – 5 мин)
|
Приготовьте веер с цифрами. Определите площадь фигур. Кто из ребят правильно выполнил задание? |
Координирует работу учащихся. |
Высказывают свое мнение, аргументируют. |
фронтальная |
Познавательные: анализировать и выделять существенную информацию из текста. |
|
VIII. Рефлексия деятельности (итог урока) (2 – 3 мин) |
— Какую цель мы ставили в начале урока, достигли мы ее? Расскажите по схеме, чему научились. Я знаю ….. Я запомнил…. Я смог …
|
Предлагает вопросы для рефлексии. |
Подводят итог своей работы на уроке, делают выводы. |
Индивидуальная |
Регулятивные: контроль, коррекция. Личностные: самоопределение. |
|
|
Домашнее задание. 1. стр.55, №4,6.
2.
|
Предлагает выбрать задания для домашней работы |
Обсуждение и запись задания в дневник.
|
Индивидуальная |
Регулятивные: коррекция. Личностные: самоопределение. |
Математика 3 класс Нахождение площади фигуры | План-конспект урока по математике (3 класс) по теме:
Урок математики 3 класс.
Тема: ПЛОЩАДЬ ПРЯМОУГОЛЬНИКА.
Тип урока: урок изучения нового и первичного закрепления новых знаний
Цели урока:
- Обеспечить усвоение детьми способа нахождения площади прямоугольника.
- Способствовать формированию ключевых компетентностей: познавательной, информационной, коммуникативной, развивающей.

Задачи урока:
Образовательные:
- Вывести правило вычисления площади прямоугольника.
- Актуализировать знания о признаках и свойствах геометрических фигур.
- Закреплять умение решать задачи на приведение к единице, записывая условие в таблицу.
- Способствовать совершенствованию вычислительных навыков.
Развивающие:
- Способствовать развитию основных операций мышления (сравнение, обобщение, умение делать выводы на основе полученной информации).
- Развитие умения анализировать и находить пути решения поднимаемой проблемы.
- Формирование основных компонентов УУД (умение ставить учебную задачу, обобщать, делать выводы)
Воспитательные:
- Содействовать повышению интереса к чтению книг.
- Формировать навыки самоанализа.
Технологии: игровая, информационно-компьютерная, развивающая, образовательная (выбор оптимальной модели обучения для данных конкретных условий).
Методы: словесные, наглядные, деятельностные, практические, (выполнение учащимися практических действий)
Оборудование:
- Презентация Рower Point.
- Вееры с цифрами 25 штук,
- Конверты (по 1 шт. на парту) 15 штук.
- Палетки 15 штук.
- Прямоугольник 2см х6см 15штук.
- Карточки – помогайки: 1 см2, Sпр.=а х в,
единицы длины, таблица умножения, порядок действий.
- Текст задачи 15 штук.
- Мартышка 1 штука.
- Корзина 1 штука.
- Бананы (жёлтые и зелёные) по 2 штуки 25 штук.
Ход урока.
- Организационный момент.
- Самоопределение.
- Поднимите руки те, кто из вас любит сказки?
Сегодня к нам на урок придут герои одной очень известной сказки. А чтобы узнать автора этой сказки — надо разгадать кроссворд.
- Устный счёт.
А) Отгадайте кроссворд.
Возьмите в руки вееры, показывайте только одни ответы:
- Сколько раз по 4 содержится в 12 (три)
- На сколько надо разделить 49, чтобы получить 7 ( на семь)
- 36 уменьши в 6 раз (шесть)
- 53 уменьши на 48 (пять)
- 4 увеличь в 2 раза (восемь)
- Кто автор этой сказки? (Григорий Остер)
- Кто догадался, как называется сказка?
(«38 попугаев»)
Б) Геометрический материал.
- Какого героя вы видите на экране? (Удава)
Он принёс вам следующее задание. Рассмотрите фигуры.
- Какая из данных фигур лишняя? (треугольник)
- Почему? (все остальные – четырехугольники)
- Теперь какая фигура лишняя? (№1 – не прямые углы),
- У какой из этих фигур все стороны равны? (квадрат)
- Как называется данная фигура? (прямоугольник)
- Какие свойства прямоугольника вы знаете? (4 угла, 4 стороны, углы прямые, противоположные стороны равны
В) Единицы измерения величин.
Какие единицы измерения длины вы знаете? (см, мм, дм, м)
Герои мультфильма решили поиграть. Чтобы узнать кому какой мяч достался, расставим величины в порядке возрастания. (мм, см, дм, м)
Г) Вырази. Герои сказки принесли для вас ещё интересное задание:
- Толщина кожи слона составляет 2 см 5 мм. Сколько это будет мм? (25мм)
- У некоторых обезьян хвост может быть длиннее их тела.
 Длина хвоста обезьяны 65 см. Сколько это дм и см? (6 дм 5 см)
Длина хвоста обезьяны 65 см. Сколько это дм и см? (6 дм 5 см) - Длина обычного удава в природе 3 м. Сколько это дм? (30 дм)
- Длина тела самых мелких попугайчиков не более 1 дм. Сколько это см? (10 см)
4. Подводящий диалог.
Д) Найди пару. Обезьяна, Попугай и Слонёнок не могут справиться с заданием. Давайте им поможем.
Рассмотрите фигуры.
- Что общего у этих фигур? (Фигуры разбиты на равные квадраты, эти фигуры прямоугольники)
- Какая из данных записей подходит к первому прямоугольнику?(3х4)
Фигура №1.
- Сколько квадратов в первом столбце?(3)
- Сколько квадратов в строке?(4)
- Сколько раз по 3 взяли? (4)
- Докажите. (3 квадрата в одном столбце и 4 квадрата в строке)
- Чему равно произведение? Покажите ответ на веерах.
- Что такое 12 в этом прямоугольнике? (количество одинаковых квадратов в прямоугольнике)
- Какая запись подходит ко второй фигуре? (2 х 3).
 Чему равно произведение? (6)
Чему равно произведение? (6)
- Какая запись подходит к третьей фигуре? (2 х 5). Чему равно произведение? (10)
- Если мы будем знать площадь каждого из этих квадратиков, что мы сможем узнать? (площадь прямоугольника)
- Кто догадался, какая тема сегодняшнего урока? («Нахождение площади прямоугольника»)
- Определение темы.
Сегодня мы должны научиться находить площадь прямоугольника удобным и быстрым способом.
- Зачем нам надо уметь находить площадь прямоугольника? (поклеить обои, покрасить пол, поклеить потолок).
- Какие единицы площади вы знаете? (см2)
- Что значит квадратный сантиметр? (площадь квадрата, сторона которого 1 см)
- Открытие новых знаний.
- Практическая работа в парах.
Откройте конверты, достаньте прямоугольник и палетку. ( Прямоугольник 2см на 6 см)
- Наложите палетку и посчитайте сколько квадратных см укладывается в прямоугольнике? (12 см2 )
- Сколько полос с квадратами в прямоугольнике? (2 полосы)
- Сколько квадратов в каждой полосе? (6)
- Как узнать сколько всего квадратов? (по 2 взяли 6 раз, т.
 е 2х6)
е 2х6) - Что такое 6 см в прямоугольнике? (длина)
- Что такое 2 см? (ширина)
- Как нашли площадь? (длину умножили на ширину)
Записываем в тетрадь. 1 ученик на доске.
№1.
6 х 2 = 12 (см2)
Ответ: 12 см2.
- А Слонёнок нашёл площадь этого прямоугольника вот так: по 2 взял 6 раз.
- Как вы думаете можно ли таким способом найти площадь прямоугольника?
- Какой вывод можно сделать? Как найти площадь? (длину умножить на ширину или ширину умножить на длину)
- Нахождение площади (формула)
Если длина прямоугольника а, ширина в.
- Как узнать площадь прямоугольника?
В математике принято площадь обозначать буквой S. И сегодня вы сами вывели формулу нахождения площади прямоугольника.
Давайте проверим. Откройте учебник с.54, прочитайте правило.
Для нахождения площади прямоугольника достаточно измерить его длину и ширину в см и полученные числа перемножить. Площадь прямоугольника будет выражена в квадратных см.
Площадь прямоугольника будет выражена в квадратных см.
Формулу записываем в тетрадь.
- Физ. минутка
Под музыку из мультфильма.
- Первичное закрепление материала.
№ 3 (1) Прочитайте задание. Начертите прямоугольник, длина которого 9 см, а ширина 2 см.
- Найдите площадь прямоугольника , пользуясь формулой.
- Запишите решение в тетрадь (один ученик диктует).
9 х 2 = 18 (см2)
Ответ: 18 см2.
А обезьяна нашла площадь по-другому. Прочитайте 2 х 9=18 (см2 )
- Как вы думаете, правильно ли она нашла площадь ?
- Решение задачи.
- Что больше всего любят есть обезьяны? (бананы). Обезьянка приготовила для вас задачу.
20 кг бананов разложили в 4 одинаковых ящика. Сколько потребуется таких ящиков, чтобы разложить 30кг бананов.
- Что известно в задаче? ( 20 кг бананов разложили в 4 одинаковых ящика)
- Что такое 20кг? (общая масса)
- Сколько было ящиков? (4)
- Что известно про ящики? (одинаковые)
- Нам известна масса 1 ящика? (нет)
- Что надо узнать в задаче? (сколько потребуется ящиков, чтобы разложить 30 кг бананов)
- Что такое 30 кг? (общая масса)
- Количество ящиков? (не знаем, но все ящики одинаковые)
- Каким действием найти массу одного ящика? (делением)
- Каким действием можно узнать количество ящиков, чтобы разложить 30 кг бананов? (делением)
Запишите решение самостоятельно.
Проверка с доской.
- Самостоятельная работа с. 73 №5
1в. – 1 строчка
2в. – 2 строчка
2 ученика за доской – потом проверяют.
- Поднимите руки, кто решил примеры без ошибок?
- Кто допустил ошибки?
- Итог урока.
- Что нового узнали на уроке? (как вычислить площадь прямоугольника)
- Как найти площадь прямоугольника? (надо длину умножить на ширину)
- Кто написал сказку «38 попугаев»? (Григорий Остер)
Он написал ещё много увлекательных книг: «Середина сосиски», «Книга о вкусной и здоровой пище людоеда», «Вредные советы и другие истории», которые я рекомендую вам прочитать.
- Домашнее задание
с. 55 № 4, 7. Правило с. 73 наизусть.
- Рефлексия.
Герои сказки прощаются с нами.
Кому было сегодня на уроке легко и интересно положите в корзину Обезьяны жёлтый банан, а кому было трудно – зелёный.
Урок окончен!
областей прямоугольников и квадратов — математика для 3-го класса
Как найти площадь прямоугольников и квадратов
Прямоугольники и квадраты — две наиболее распространенные формы.
Можете ли вы представить себе прямоугольник? 000
Вот несколько примеров прямоугольных объектов:
Можете ли вы думать о квадратных объектах?
Вот несколько квадратных объектов:
В этом уроке мы научимся находить область прямоугольников и квадратов.
Давайте рассмотрим
Площадь — это пространство, которое занимает форма или объект.
Посмотрите на эту фигуру.
Сколько квадратов покрывает этот зеленый прямоугольник?
Занимает 6 квадратов.
Его площадь составляет 6 квадратных единиц .
Мы используем единиц площади , чтобы точно знать, как измеряется форма.
Например, если каждый квадрат в приведенной выше сетке равен 1 квадратному метру, то площадь зеленого прямоугольника составляет 6 квадратных метров .
Совет: Мы можем записать 6 квадратных метров как 6 m² . Это читается как «6 квадратных метров » .
Обратите внимание на маленькую цифру 2, написанную в верхней правой части m. Это действительно важно.
Площадь прямоугольника
Чтобы узнать площадь прямоугольника, мы подсчитываем количество квадратов, которые он покрывает.
Другой способ — умножить на на длину сторон .
В прямоугольнике противоположных сторон равны .
Длина сторон, идущих от слева направо , называется шириной .
Длина сторон, идущих от сверху вниз , называется высотой или длиной .
Чтобы найти площадь прямоугольника , умножьте ширину на высоту.
ширина x высота = площадь
Давайте воспользуемся этой формулой, чтобы найти ширину зеленого прямоугольника.
Сначала , знайте ширину и высоту.
Ширина составляет 3 квадратных единицы, а высота составляет 2 квадратных единицы.
Теперь умножьте ширины на высоту.
3 x 2 = 6 квадратных единиц
✅ Если 1 квадратная единица равна 1 квадратному метру, то 6 квадратных единиц равны 6 квадратным метрам (6 м²).
Это тот же ответ, который мы получили, когда подсчитали каждый квадрат. 000
Площадь Квадрата
У квадрата 4 равные стороны.
Это означает, что длина сторон одинакова.
Чтобы найти площадь квадрата , умножьте на длину одной стороны на себя.
Какая площадь у этого квадрата?
Длина каждой стороны 3.
3 x 3 = 9 квадратных единиц
Площадь квадрата 9 кв.
✅ Если 1 квадратная единица равна 1 сантиметру, то 9 квадратных единиц равны 9 квадратному сантиметру (9 см²).
Отличная работа! 000
Без сетей
Если нет сеток с квадратами, чтобы помочь вам, вы все равно можете вычислить площадь фигуры.
Чтобы найти площадь прямоугольника , умножьте на :
длина ширины x длина высоты = площадь
Чтобы найти площадь квадрата , умножьте на :
длина любой стороны сама по себе
Попрактикуемся на примерах!
Найдите площадь этого прямоугольника:
Мы видим, что ширина 10 дюймов, а высота 6 дюймов.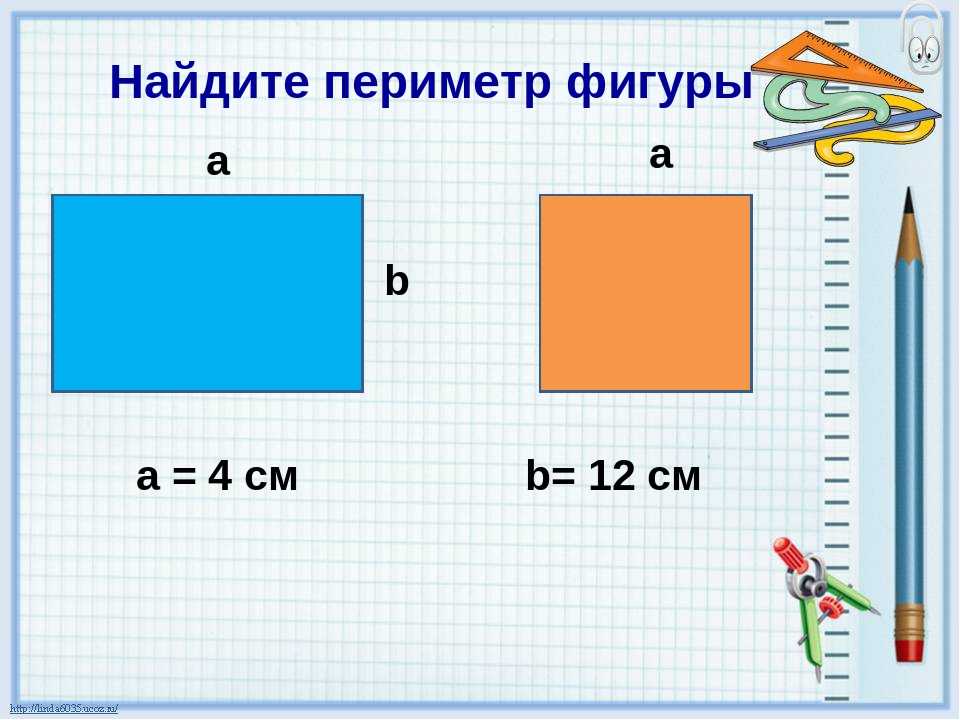
Мы умножаем этих двух чисел вместе.
10 x 6 = 60
✅ Площадь этого прямоугольника составляет 60 квадратных дюймов (или 60 кв. Дюймов) .
😃 Обязательно укажите после числа, указав единицу площади .
Какова площадь этого квадрата?
Длина одной стороны 4 фута.
Давайте умножим на себя.
4 фута x 4 фута = 16 квадратных футов
✅ Площадь этого квадрата составляет 16 квадратных футов или 16 футов².
Отличная работа! 000
Смотри и учись
youtube.com/embed/1dqAOKdJmRI&t=52s» frameborder=»0″/>Теперь попробуйте выполнить практические упражнения. 000
областей сложных фигур — математика для 3-го класса
Как найти область сложных фигур
На последних уроках вы научились определять площадь прямоугольников и квадратов.
В этом уроке вы узнаете, как найти площадь сложных фигур.
Сложные фигуры — это фигуры, которые не являются ни квадратами, ни прямоугольниками.
Их еще называют неправильными формами. 000
Площадь сложных фигур
Как узнать площадь этого парка?
Чтобы найти область сложной формы , начните с , разделив ее на меньшие, правильные формы , такие как квадрат и прямоугольник.
Как мы можем это разделить?
Вы поняли! Мы можем разделить эту фигуру на прямоугольник и квадрат. 000
👆 7 км и 2 км были вычеркнуты , потому что они больше не применяют к новым формам.
— Форма верха представляет собой прямоугольник . Ширина 2 км, длина 7 км.
— Форма основания представляет собой квадрат . Длина всех его сторон 5 км каждая.
👉 Давайте сначала найдем площадь прямоугольника .
2 x 7 = 14
Прямоугольник имеет площадь 14 км² (квадратных километров).
👉 Затем находим площадь квадрата.
5 x 5 = 25
Площадь квадрата составляет 25 км² (квадратных километров).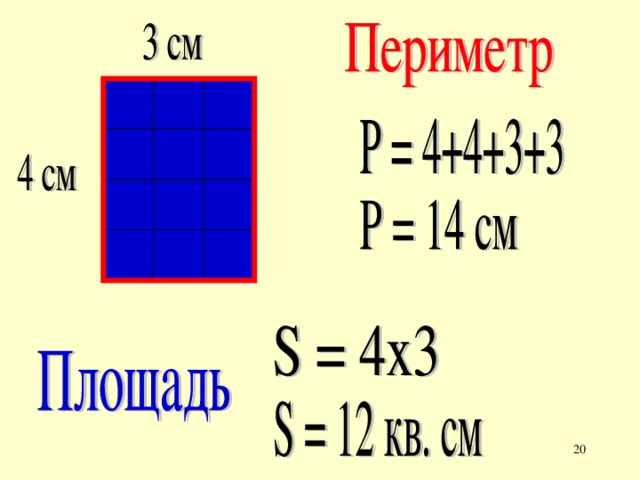
👉 Теперь мы складываем две области, , чтобы получить площадь всего парка.
14 + 25 = 39
✅ Площадь парка составляет 39 квадратных километров ( или 39 км²).
Пример 2: Площадь плавательного бассейна
Какова площадь этого бассейна? 000
Сначала , вам нужно выяснить, как разделить его на .
— Один из способов — разделить его на 3 прямоугольника.
— Другой способ — разделить его на 2 прямоугольника.
Какой способ сделать проще? 000
Да, второй! Потому что нам нужно иметь дело только с двумя формами.
Давайте найдем таким образом территорию бассейна. 000
000
Посмотрите на размеры двух прямоугольников:
Совет : Мы не знали длину длинной стороны второго прямоугольника, поэтому нам пришлось прибавить длины сторон, которые мы знали.
Чтобы найти площадь первого прямоугольника , умножьте 8 м на 9 м:
8 x 9 = 72 м²
Чтобы найти площадь второго прямоугольника , умножьте 16 м на 6 м:
6 x 16 = 96 м²
Теперь мы складываем две области вместе:
72 + 96 = 168 м²
✅ Площадь бассейна 168 квадратных метров ( или 168 м²).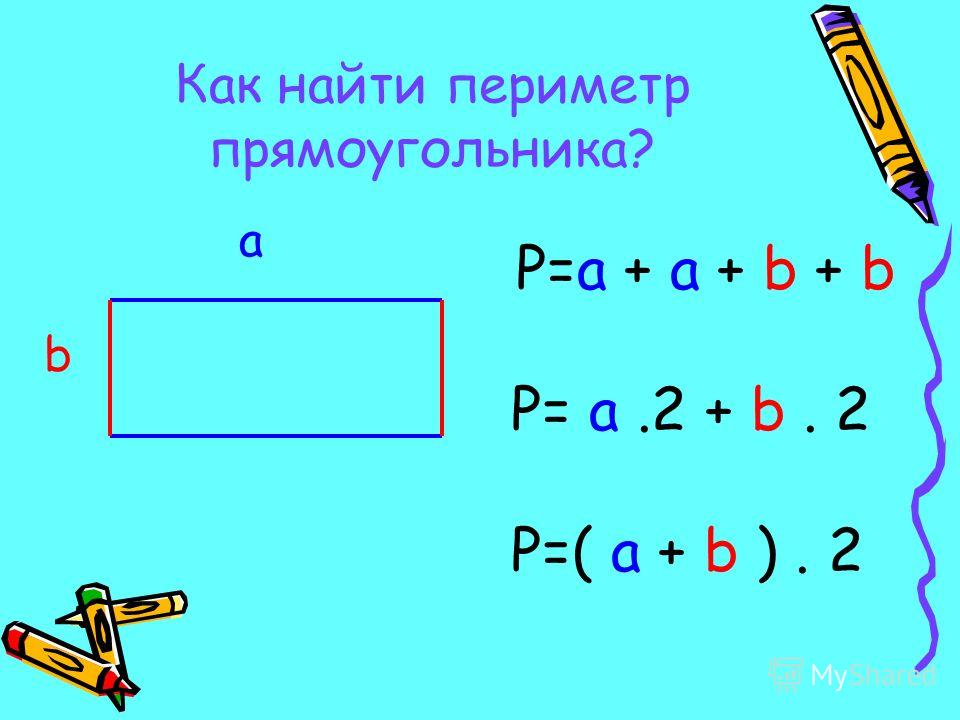
Смотри и учись
Теперь попробуйте выполнить практические упражнения. 000
Как рассчитать площадь | Помощь с математикой
Расчетная зона
Площадь измеряется в квадратах (или квадратных единицах).
Сколько квадратов в этом прямоугольнике?
Мы можем сосчитать квадраты или взять длину и ширину и использовать умножение. Прямоугольник выше имеет площадь 15 квадратных единиц.
Площадь прямоугольника = длина x ширина
Примеры расчета площади прямоугольника
Единицы измерения площади
Измеряем площадь квадратами. Мы используем квадраты разного размера в зависимости от того, насколько велика или мала площадь.
| Пример | Длина стороны квадратов | Блок |
| Размер ногтя на большом пальце | Миллиметр | мм 2 |
| Размер листка бумаги | Сантиметр | см 2 |
| Размер комнаты | Метр | м 2 |
| Размер города | Километр | км 2 |
| Не забывайте крошечный 2 |
Мы пишем размеры квадрата с помощью маленького 2 рядом с единицей. Мы пишем mm 2 , cm 2 , m 2 , km 2 , cm 2 Мы можем сказать «63 миллиметра в квадрате» или «63 квадратных миллиметра» |
Мы могли бы использовать маленькие квадраты для измерения больших площадей. Единственная проблема заключается в том, что нам придется использовать очень большие числа. Например, поле может быть измерено в 5 000 000 000 квадратных миллиметров, тогда как 5 000 квадратных метров было бы гораздо проще сказать, написать и визуализировать.
Вероятно, вы услышите больше единиц измерения площади; квадратные дюймы, квадратные футы, квадратные ярды, квадратные мили, акры, гектары — все это единицы, используемые для измерения площади.
Дополнительные примеры расчета площади
Площадь квадрата
Длина и ширина квадрата одинаковы, поэтому нам просто нужно умножить длину на длину.
| Площадь = длина x длина Площадь = 6 см x 6 см = 36 см 2 |
Площадь круга
Площадь круга = πr 2
, где r — радиус круга, а π — отношение длины окружности к ее диаметру.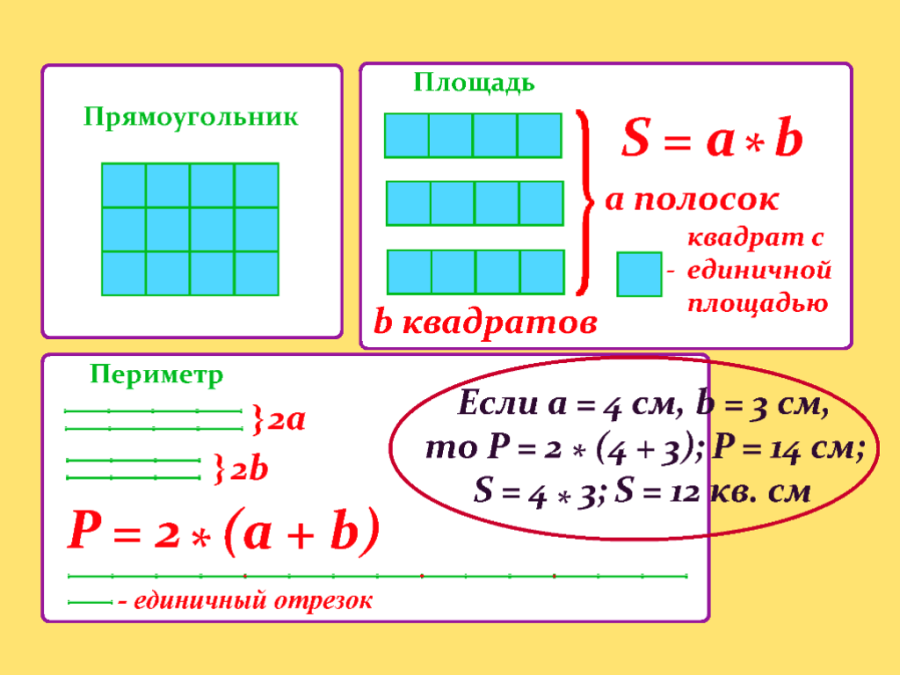
π (произносится как «пирог» и часто пишется как «пи») — бесконечная десятичная дробь с общим приближением 3,14159. Вы можете узнать больше о Pi здесь
Пример расчета площади круга
| Площадь = πr 2 Площадь = 3,14159 x (4 см) 2 Площадь = 3,14159 x 16 см 2 Площадь = 50,27 см 2 Ответ округлен до 2 десятичных знаков |
Объяснение формулы площади круга
Возьмите круг, разделите его на сектора одинакового размера и переставьте их, как показано ниже.Обратите внимание, как по мере уменьшения размеров секторов форма становится больше похожей на прямоугольник. Примечание. Нет предела тому, насколько маленькими могут быть эти секторы и насколько они могут напоминать прямоугольник при расположении.
Предполагая, что мы знаем, что длина окружности равна 2πr, мы можем добавить размеры к «прямоугольнику», как показано ниже. Используя формулу площади прямоугольника, площадь = ширина x высота, мы можем увидеть, как можно показать, что наш круг, переконфигурированный как прямоугольник, имеет площадь, которая приблизительно равна πr x r или πr 2
Перестановка секторов круга
Перестановка секторов круга — начинает выглядеть как прямоугольник
Площадь сложных форм
Во многих случаях для вычисления общей площади требуется вычисление нескольких площадей с последующим сложением, вычитанием или какой-либо другой комбинацией операций для поиска требуемой площади.
Примечание. В приведенных ниже примерах единицы измерения не показаны, а ответы и значение π (Пи) округлены до ближайшей сотой.
Пример: простые составные формы
Пример вычисления площади ниже относительно прост. Фигуру можно рассматривать как треугольник в сочетании с прямоугольником.
| Площадь треугольной части: ½ x основание x высота ½ x 9 x 4 = 18 Площадь прямоугольной части: Общая площадь = 18 + 54 = 72 |
В приведенном выше примере показано общее требование при работе с составными формами — поиск размеров, которые не показаны.Обучая своих детей, при необходимости помогайте им найти эти «недостающие» измерения. Ниже приведен еще один пример.
Определение размеров
| Каковы размеры маленькой прямоугольной детали? Ширина? 12-7-2 = 3 Высота? 8–6 = 2 |
Пример: вычитание одной площади из другой
В примере ниже фигура выглядит как прямоугольник с вырезанным треугольником.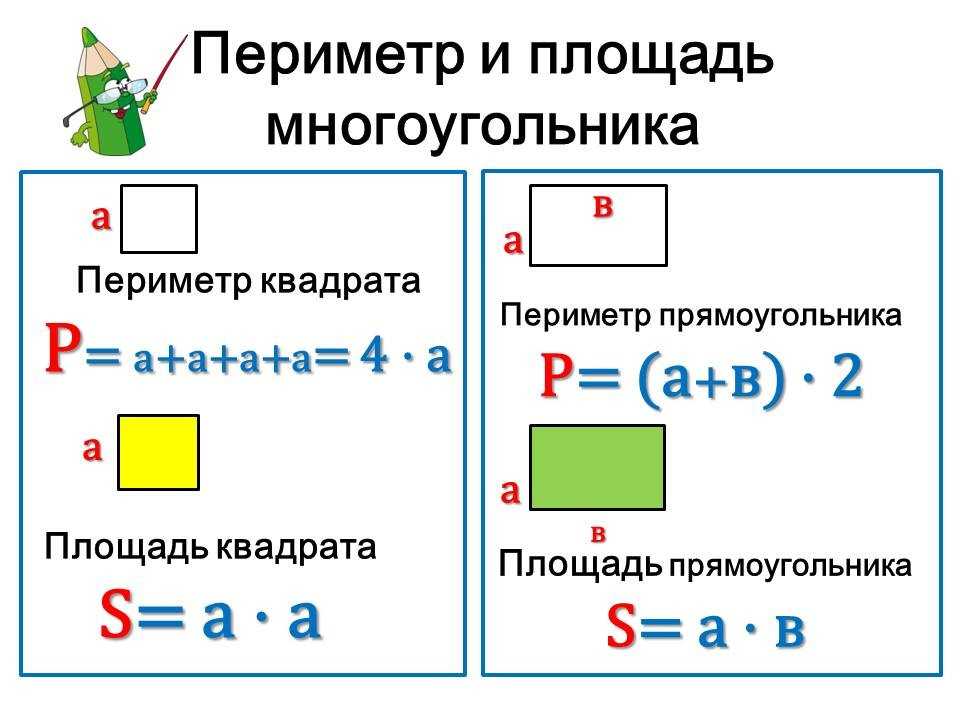
| Площадь прямоугольной части: ширина x высота 5 x 6 = 30 Площадь треугольной части: Общая площадь = 30 — 4,50 = 25,50 |
Пример: частичные области
Пример ниже аналогичен приведенному выше, хотя, поскольку у нас есть полукруг, нам нужно вычислить долю (половину) площади круга. Обратите внимание, что в этом примере показан диаметр, а не радиус.
| Площадь треугольной части: ½ x основание x высота ½ x 6 x 6 = 18 Площадь полукруглой части: Общая площадь = 18 — 3,53 = 14,47 |
Пример: Решения! Объединить? Вычтем
Обычно используется более одного способа вычисления окончательной площади. В приведенных ниже примерах фигуру можно рассматривать как два объединенных прямоугольника или как один большой прямоугольник с меньшим прямоугольником, «вырезанным» из правого верхнего угла.
В приведенных ниже примерах фигуру можно рассматривать как два объединенных прямоугольника или как один большой прямоугольник с меньшим прямоугольником, «вырезанным» из правого верхнего угла.
Рабочие листы расчета площади
Распечатайте приведенные ниже рабочие листы и используйте их для практики при обучении своих детей.
Здесь вы найдете другие распечатанные геометрические рабочие листы.
Рабочие листы
Добро пожаловать на страницу рабочих листов Math Salamanders Area.
На этой странице есть ссылки на все наши рабочие листы с областями, включая области прямоугольников, треугольников и четырехугольников.
Эти листы предназначены для детей от 3-х классов и старше.
Эта страница содержит ссылки на другие веб-страницы математики, где вы найдете ряд занятий и ресурсов.
Если вы не можете найти то, что ищете, попробуйте выполнить поиск на сайте с помощью окна поиска Google вверху каждой страницы.
На этой веб-странице вы найдете ссылки на все наши конкретные страницы рабочих листов.
У нас есть ряд различных рабочих листов по площади, включая область прямоугольников, прямоугольных треугольников и четырехугольников.
Существует также распечатываемая страница формул для определения площади различных 2-мерных фигур.
Попробуйте приложение, разработанное компанией PhET Interactive Simulations из Университета Колорадо.
Это отличный способ исследовать территорию и периметр в увлекательной и увлекательной форме.
Мы также создали несколько задач, которые можно использовать вместе с приложением.
На нашей странице поддержки для печати есть формулы для площади обычных 2-мерных фигур.
Листы здесь включают поиск области прямоугольников, а также области прямолинейных форм.
Прямолинейные фигуры — это фигуры, состоящие из нескольких прямоугольников.
У нас есть широкий выбор листов для учеников от 3-го класса и выше.
Листы здесь включают определение площади и периметров прямоугольников и прямолинейных форм.
Прямолинейные фигуры — это фигуры, состоящие из нескольких прямоугольников.
У нас есть некоторая поддержка, а также широкий выбор листов, подходящих для учащихся от 3-го класса и выше.
Существуют проблемы с площадью и периметром, а также проблемы с более длинной областью и периметром.
Этот раздел содержит рабочие листы по области для 5-го и 6-го классов.
Основное внимание уделяется вычислению площади прямоугольных треугольников.
Использование этих листов поможет вашему ребенку:
- умеют рассчитать площадь треугольника;
- выучите формулы для вычисления площади треугольников.
Этот раздел содержит рабочие листы по области для 5-го и 6-го классов.
Основное внимание уделяется вычислению площадей различных четырехугольников.
Использование этих листов поможет вашему ребенку:
- умеют вычислять площадь ряда четырехугольников.
- выучите формулы для вычисления площади определенных типов четырехугольника.

Узнайте, как рассчитать площадь круга, и ознакомьтесь с некоторыми рабочими примерами.
Существует ряд рабочих листов, которые помогут вам отработать этот навык, а также некоторые задачи со словами, чтобы увидеть, сможете ли вы применить его.
Взгляните на еще несколько наших рабочих листов, похожих на эти.
Вот наша подборка бесплатных распечатываемых листов периметра для 3-го и 4-го классов.
Все листы отсортированы от самого простого к самому сложному.
Использование этих листов поможет вашему ребенку:
- проработать периметр ряда прямоугольников;
- найдите периметр прямолинейной формы.
Все листы в этом разделе поддерживают тесты элементарной математики.
Вот наша подборка рабочих листов по геометрии для 4-го класса.
Использование этих листов поможет вам:
- классифицируют углы — острый, тупой, прямой, рефлекторный, прямой;
- классифицируют треугольники — острые, тупые, правые;
- измерять углы с помощью транспортира;
- знает, что углы в треугольнике составляют в сумме 180 °
- постройте и запишите координаты в первом квадранте.

Все листы в этом разделе поддерживают тесты по элементарной математике.
Вот наш ассортимент рабочих листов.
Использование этих листов поможет вашему ребенку:
- знать, что такое объем и как его найти;
- найти объем фигур, считая кубики;
- найти объем прямоугольной призмы;
- решение основных задач, связанных с объемом
Саламандры по математике надеются, что вам понравятся эти бесплатные распечатываемые рабочие листы по математике. и все другие наши математические игры и ресурсы.
Мы приветствуем любые комментарии о нашем сайте или рабочие листы в поле для комментариев Facebook внизу каждой страницы.
Что такое площадь? — Определение, факты и пример
Area Games
Area
Используйте единичные квадраты, чтобы понять концепцию площади и найти площадь для различных двухмерных форм.
охватывает Common Core Curriculum 3. MD.7Играть сейчасПосмотреть все игры по геометрии >>
MD.7Играть сейчасПосмотреть все игры по геометрии >>
Учитесь с полной программой обучения математике K-5
Что такое область? В геометрии площадь можно определить как пространство, занимаемое плоской формой или поверхностью объекта. Площадь фигуры — это количество единичных квадратов, покрывающих поверхность замкнутой фигуры. Площадь измеряется в квадратных единицах, таких как квадратные сантиметры, квадратные футы, квадратные дюймы и т. Д.
Площадь приведенных ниже квадратов со стороной 1 сантиметр каждый будет измеряться в квадратных сантиметрах (см²).
Здесь площадь фигур ниже будет измеряться в квадратных метрах (м²) и квадратных дюймах (дюйм²).
Слово «площадь» происходит от латинского «площадь», что означает «свободный участок ровной поверхности».Происхождение далее привело к неправильному получению площади как «определенного количества пространства, заключенного в пределах набора границ».
Мы часто находим площадь пола комнаты, чтобы определить размер покупаемого ковра. Покрытие пола плиткой, покрытие стен краской или обоями или строительство бассейна — другие примеры, где площадь вычисляется.
Обычные простые формы и многоугольники имеют свои собственные формулы для вычисления площади. Вот как вычисляется площадь обычных двухмерных или двумерных фигур:
| Двумерные геометрические формы: |
| Название формы: | Изображение формы: | Формула площади: |
| Круг | Площадь = πr², где r радиус. | |
| Треугольник | Площадь = bh, где b — основание, А h — высота. | |
| Квадрат | Площадь = l × l, где l — длина каждой стороны. | |
| Прямоугольник | Площадь = д × ш, где l длина и w — ширина. | |
| Параллелограмм | Площадь = b × h, где b — основание, и h — высота по перпендикуляру. | |
| Трапеция | Площадь = (a + b) h, , где a и b — длины параллельных сторон, и h — высота по перпендикуляру. |
В реальной жизни не каждую плоскую фигуру можно однозначно классифицировать как прямоугольник, квадрат или треугольник. Чтобы найти площадь составной фигуры, состоящей из более чем одной фигуры, нам нужно найти сумму площадей обеих или всех фигур, образующих составную фигуру.
Площадь внешней поверхности твердой или трехмерной формы называется площадью поверхности. Например, прямоугольная призма имеет 6 прямоугольных оснований и боковые грани. Итак, общая площадь поверхности — это сумма площадей всех 6 прямоугольников.
Интересные факты
|
Давайте споем!
Для посадки овощей в саду,
Найдите площадь поля — все внутри.
Умножьте его длину на ширину,
И вот формула площади, которую вы применили!
Давайте сделаем это!
Вместо того, чтобы раздавать своим детям рабочие листы по математике, вовлекайте их в проекты по благоустройству дома. Сообщите им о комнате, которую вы собираетесь покрасить. Попросите их подсчитать общую площадь стен, чтобы узнать, сколько требуется краски.
Обсудите, чем все стены в комнате могут отличаться друг от друга, и, таким образом, проведение общих измерений с последующим вычитанием площади двери, окон или книжных полок поможет в оценке необходимого количества краски.
Вы также можете попросить рассмотреть возможность определения общей площади подарка, который они упаковывают, чтобы определить необходимое количество оберточной бумаги.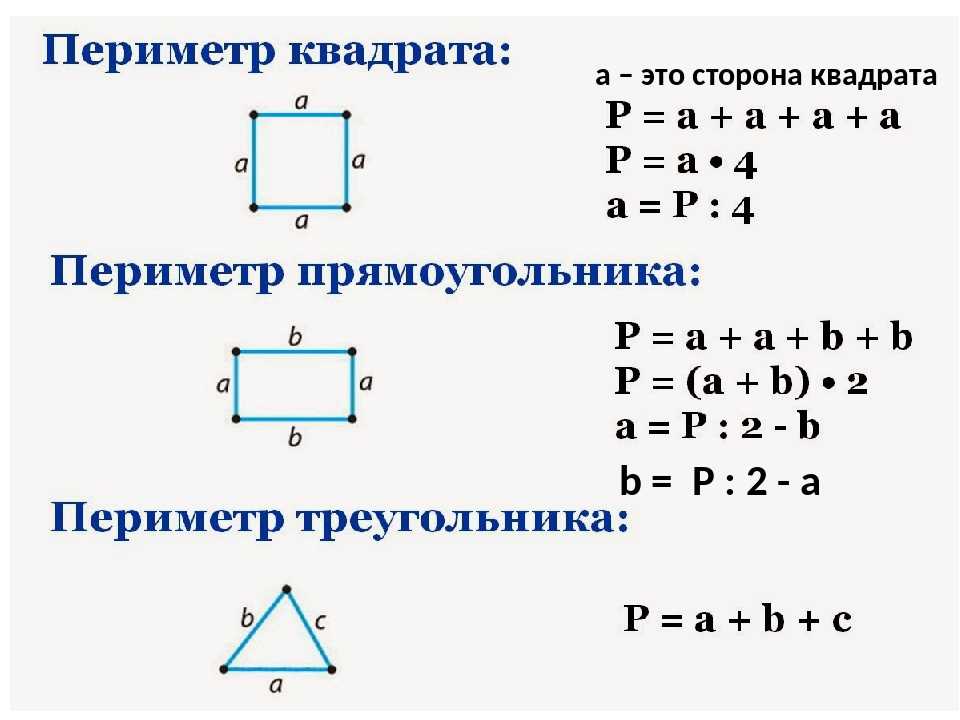
Сопутствующий математический словарь
Математика для 3-го класса — Блок 4: Область
Сводка по агрегату
В Блоке 4 учащиеся понимают площадь как объем двумерного пространства, занимаемого фигурой, и связывают это со своей работой с умножением в Блоках 2 и 3.
В младших классах учащиеся могут неформально сравнивать площадь, видя, какая из двух фигур занимает больше места. Во 2 классе учащиеся разделили прямоугольник на строки и столбцы квадратов одинакового размера и посчитали их общее количество, включая подсчет пропусков и повторное сложение, чтобы сделать это более эффективно (2.G.2, 2.OA .4).
Учащиеся начинают свою работу в этом модуле, развивая понимание площади как атрибута плоских фигур (3.MD.5) и измеряя ее, считая единичные квадраты (3.MD.6). После обширной работы по развитию пространственного структурирования студентов ученики подключают площадь к операции умножения длины и ширины фигуры (3.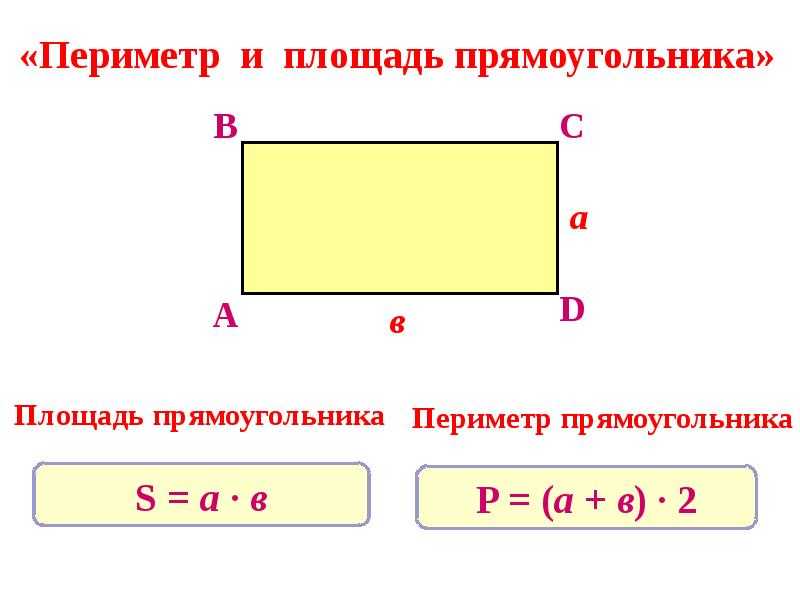 MD.7a, b). Наконец, учащиеся связывают меру площади как с умножением, так и с площадью, видя на конкретных примерах, что площадь прямоугольника с целочисленными длинами сторон $$ a $$ и $$ b + c $$ является суммой $$ a \ times b $$ и $$ a \ times c $$ (3.MD.7c) и, используя более общую идею, что площадь является аддитивной, найти площадь составных фигур (3.MD.7d). Таким образом, модуль служит способом связать темы и размышления между модулями, обеспечивая согласованность между работой с умножением и делением в модулях 2 и 3 (3.OA) с работой над областью в этом модуле (3.MD.C) .
MD.7a, b). Наконец, учащиеся связывают меру площади как с умножением, так и с площадью, видя на конкретных примерах, что площадь прямоугольника с целочисленными длинами сторон $$ a $$ и $$ b + c $$ является суммой $$ a \ times b $$ и $$ a \ times c $$ (3.MD.7c) и, используя более общую идею, что площадь является аддитивной, найти площадь составных фигур (3.MD.7d). Таким образом, модуль служит способом связать темы и размышления между модулями, обеспечивая согласованность между работой с умножением и делением в модулях 2 и 3 (3.OA) с работой над областью в этом модуле (3.MD.C) .
Студенты будут глубоко заниматься многими математическими практиками в этом модуле. Например, студенты «используют стратегии для поиска продуктов и коэффициентов, основанные на свойствах операций; например, чтобы найти [площадь прямоугольника путем умножения] $$ 4 \ times 7 $$, они могут распознать, что $$ 7 = 5 + 2 $$, и вычислить $$ 4 \ times 5 + 4 \ times 2 $$.Это пример видения и использования структуры (МР. 7). Такие процессы рассуждения сводятся к кратким аргументам, которые студенты могут построить и критиковать (MP.3) »(PARCC Model Content Frameworks for Mathetmatics, стр. 16). Кроме того, учащиеся используют физические плитки, линейки, чтобы связать длины сторон с физическими плитками, а позже в модуле — свойства самих операций, чтобы найти площадь прямоугольника (МР.5). Кроме того, «чтобы построить от пространственного структурирования к пониманию количества единиц площади как произведения количества единиц в строке и количества строк, студенты могут рисовать прямоугольные массивы квадратов и учиться определять количество квадратов в каждой строке с помощью все более изощренные стратегии, такие как пропуск числа в каждой строке и, в конечном итоге, умножение числа в каждой строке на количество строк (MP.8) »(GM Progression, стр. 17).
7). Такие процессы рассуждения сводятся к кратким аргументам, которые студенты могут построить и критиковать (MP.3) »(PARCC Model Content Frameworks for Mathetmatics, стр. 16). Кроме того, учащиеся используют физические плитки, линейки, чтобы связать длины сторон с физическими плитками, а позже в модуле — свойства самих операций, чтобы найти площадь прямоугольника (МР.5). Кроме того, «чтобы построить от пространственного структурирования к пониманию количества единиц площади как произведения количества единиц в строке и количества строк, студенты могут рисовать прямоугольные массивы квадратов и учиться определять количество квадратов в каждой строке с помощью все более изощренные стратегии, такие как пропуск числа в каждой строке и, в конечном итоге, умножение числа в каждой строке на количество строк (MP.8) »(GM Progression, стр. 17).
В будущих классах учащиеся будут полагаться на понимание площади для решения все более сложных задач, касающихся площади, периметра, площади поверхности и объема (4. MD.3, 5.MD.3–5, 6.G.1–4 ). Студенты также будут использовать это понимание вне своего изучения геометрии, например, в задачах многозначного умножения в 4 классе (4.NBT.5), умножении дробей в 5 классе (5.NF.4) и даже в задачах полиномиального умножения в алгебре. (A.APR.1) полагаются на модель площади.
MD.3, 5.MD.3–5, 6.G.1–4 ). Студенты также будут использовать это понимание вне своего изучения геометрии, например, в задачах многозначного умножения в 4 классе (4.NBT.5), умножении дробей в 5 классе (5.NF.4) и даже в задачах полиномиального умножения в алгебре. (A.APR.1) полагаются на модель площади.
Темп: 16 учебных дней (13 уроков, 2 гибких дня, 1 контрольный день)
Чтобы узнать, как изменить темп обучения на 2020-2021 учебный год в связи с закрытием школ, см. Наши Рекомендуемые корректировки объема и очередности для 3-го класса.
Что такое площадь?
Площадь — это размер поверхности!
Пример:
У всех этих фигур одинаковая площадь 9:
.
Это помогает представить , сколько краски покроет форму.
Площадь простых форм
Существуют специальные формулы для определенных форм:
Пример: Какова площадь этого прямоугольника?
Формула:
Площадь = ш × в
ш = ширина
в = высота
Ширина равна 5, а высота равна 3, поэтому мы знаем, что w = 5 и h = 3 :
Площадь = 5 × 3 = 15
Узнайте больше в Area of Plane Shapes.
Площадь по счету квадратов
Мы также можем нанести фигуру на сетку и подсчитать количество квадратов:
Прямоугольник имеет площадь 15
Пример: когда каждый квадрат равен 1 метр со стороны, тогда площадь будет 15 м 2 (15 квадратных метров)
Квадратный метр vs Квадратный метр
Базовая единица площади в метрической системе — квадратный метр , который представляет собой квадрат с 1 метром на каждой стороне:
1 квадратный метр
Будьте осторожны, говоря «квадратные метры», а не «квадратные метры»:
Существуют также «квадратные мм», «квадратные см» и т. Д., Подробнее см. В метрической зоне.
Приблизительная площадь по подсчету квадратов
Иногда квадраты не совсем соответствуют форме, но мы можем получить «приблизительный» ответ.
В одну сторону:
- больше чем половина квадрата считается как 1
- меньше чем половина квадрата считается как 0
Как это:
Этот пятиугольник имеет площадь примерно 17
Или мы можем сосчитать один квадрат, когда
областей складываются в .
Пример: Здесь область, отмеченная « 4 », кажется равной примерно 1 целому квадрату (также для « 8 »):
Этот круг имеет площадь примерно 14
Но лучше всего использовать формулу (когда это возможно):
Пример: круг имеет радиус 2,1 метра:
Формула:
Площадь = π × r 2
Где:
Радиус 2.1м , итого:
Площадь = 3,1416 … × (2,1 м) 2
= 3,1416 … × (2,1 м × 2,1 м)
= 13,854 … м 2
Итак, круг имеет площадь 13,85 квадратных метров (с точностью до 2 знаков после запятой)
Область сложных форм
Иногда мы можем разбить фигуру на две или более простые формы:
Пример: Какова площадь этой фигуры?
Разобьем область на две части:
Часть А представляет собой квадрат:
Площадь A = 2 = 20 м × 20 м = 400 м 2
Часть B представляет собой треугольник. При взгляде сбоку он имеет основание 20 м и высоту 14 м.
При взгляде сбоку он имеет основание 20 м и высоту 14 м.
Площадь B = ½b × h = ½ × 20 м × 14 м = 140 м 2
Итак, общая площадь:
Площадь = Площадь A + Площадь B
Площадь = 400 м 2 + 140 м 2
Площадь = 540м 2
Площадь путем сложения треугольников
Мы также можем разбить фигуру на треугольники:
Затем измерьте основание ( b ) и высоту ( h ) каждого треугольника:
Затем вычислите каждую площадь (используя Area = ½b × h) и сложите их все.
Тест: Площадь и периметр — Математика 3 класс
Тест: Площадь и периметр — Математика 3 классАнглийский язык
Астрономия
Белорусский язык
Биология
География
ИЗО
Информатика
История
Итальянский язык
Краеведение
Литература
Математика
Музыка
Немецкий язык
ОБЖ
Обществознание
Окружающий мир
ОРКСЭ
Русский язык
Технология
Физика
Физкультура
Химия
Черчение
Для учителей
Дошкольникам
VIP — доступ
- Предметы »
- Математика »
- 3 класс »
- Площадь и периметр
Площадь и периметр
Это тест-тренажёр. Если результат теста тебя не устраивает, его можно пройти снова!
Если результат теста тебя не устраивает, его можно пройти снова!
Математика 3 класс | Автор: Е.В.Федорова | ID: 11835 | Дата: 10.1.2020
+39 -43Помещать страницу в закладки могут только зарегистрированные пользователи
Зарегистрироваться
Вопрос №
1
Как найти площадь прямоугольника со сторонами 3 см и 8 см? Найди все правильные решения.
3 · 8 = 24 см
3 · 8 = 24 кв.см
(3+8) · 2= 22 кв.см
3 · 2+ 8 · 2= 22 кв.см
8 · 3 = 24 кв.см
Вопрос №
2
Как найти периметр прямоугольника со сторонами 3 см и 8 см?
3 + 8 · 2= 19 см
3 · 8 = 24 см
(3+8) · 2= 22 см
3 · 2 + 8 = 14см
Вопрос №
3
Как найти периметр квадрата со стороной 3 см ?
3 · 4 = 12 см
3 · 3 = 9 см
3 + 3 · 2 = 9 см
3 + 3= 6 см
Вопрос №
4
Как найти площадь квадрата со стороной 3 см ?
3 · 4= 12 кв. см
см
3 · 3 = 9 кв. см
(3 + 3) · 2 = 12 кв. см
3 · 2 + 3 · 2= 12 кв. см
Вопрос №
5
Площадь прямоугольника составляет 16 кв.см, ширина 2 см. С помощью вычислений мы нашли длину этого прямоугольника: 16 : 2 = 8 см. Какая формула помогла найти ширину прямоугольника?
S = a · b
S = a · 4
Р = (a +b) · 2
Вопрос №
6
Площадь прямоугольника составляет 12 кв.см, длина 6 см. Каким действием можно найти ширину этого прямоугольника?
12 — 6
12 : 6
12 : 2 — 6
(12 +6) · 2
Вопрос №
7
Чему равна ширина прямоугольника, площадь которого составляет 35 кв.см, а длина 7см?
28 см
5 см
7 см
21 см
Вопрос №
8
Чему равна длина прямоугольника, площадь которого составляет 7 кв. см, а ширина 1см?
см, а ширина 1см?
7см
6 см
5 см
2 см
Вопрос №
9
Чему равна сторона квадрата, площадь которого составляет 36 кв.см? Выбери формулу, которая поможет тебе решить эту задачу.
S = a : b
S = a · а
S = a · 4
S = a · 2 + b · 2
Вопрос №
10
Чему равна сторона квадрата, площадь которого составляет 36 кв.см?
9 см
6 см
13 см
72 см
Вопрос №
11
Чему равна сторона квадрата, площадь которого составляет 64 кв.см?
7 cм
8 см
9 см
16 см
Вопрос №
12
Периметр квадрата равен 20 см.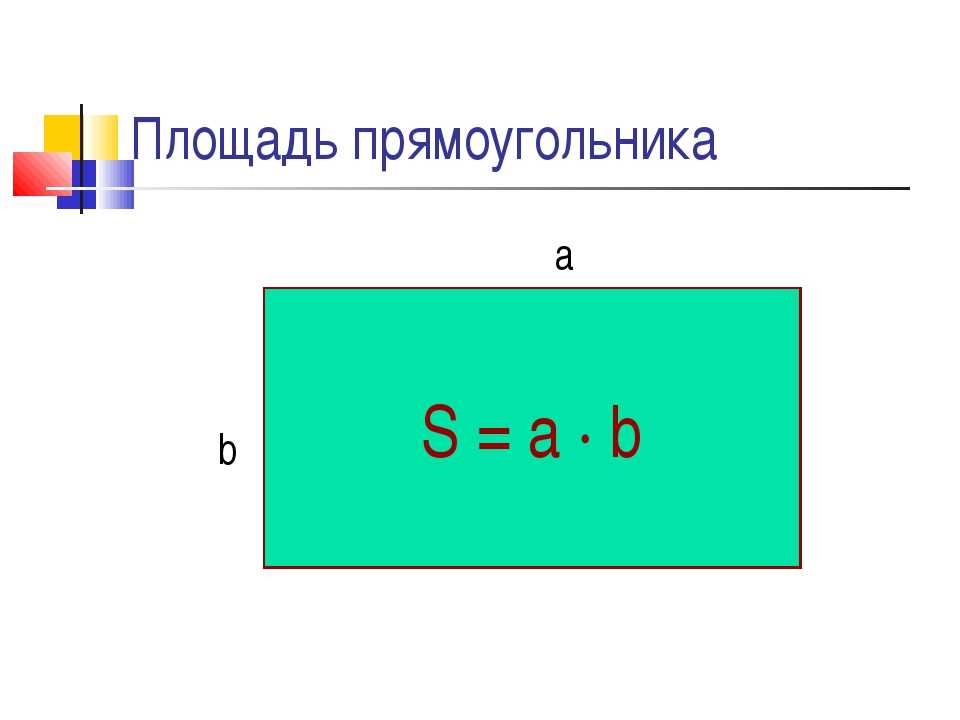 Чему равна сторона этого квадрата? Выбери формулу, которая поможет тебе найти сторону квадрата.
Чему равна сторона этого квадрата? Выбери формулу, которая поможет тебе найти сторону квадрата.
Р = a · а
Р = a · 2 + b
Р = a · 4
Вопрос №
13
Периметр квадрата равен 20 см. Чему равна сторона этого квадрата?
20 : 4 = 5 см
20 : 2 = 10 см
4 · 5 = 20 см
20 — 4 = 16 см
Вопрос №
14
Периметр квадрата равен 12 см. Чему равна сторона этого квадрата?
4 см
3 см
6 см
2см
Вопрос №
15
Периметр прямоугольника 20 см, ширина 4 см. Чему равна площадь этого прямоугольника? Выбери правильное решение.
P= (a + b) · 2 1) 20 : 2 = 10(см) — длина и ширина 2) 10 — 4= 6(см) — длина 3) 6 · 4 = 24 кв. см — площадь прямоугольника
см — площадь прямоугольника
S = a · b 1) 20 : 4 = 5(см) — длина 2) 5 · 4 = 20 кв.см — площадь прямоугольника
Вопрос №
16
Периметр прямоугольника 14 см, ширина 3 см. Чему равна площадь этого прямоугольника? Найди все правильные решения.
S = a · b 1) 14 · 3 = 42 кв.см — площадь прямоугольника
P= (a + b) · 2 1) 14 : 2 = 7(см) — длина и ширина 2) 7 — 3= 4(см) — длина 3) 3 · 4 = 12 кв.см — площадь прямоугольника
P= a · 2 + b · 2 1) 3 · 2 = 6(см) — две ширины 2) 14 — 6 = 8(см) — две длины 3)8 : 2 = 4(см) длина 4) 3 · 4 = 12 кв. см — площадь прямоугольника
Вопрос №
17
Площадь квадрата 25 кв.см. Чему равен его периметр? Выбери правильное решение.
1) 25 · 4 = 100 см — периметр квадрата
1) 5 · 5 = 25 (кв. см) — площадь квадрата
см) — площадь квадрата
1) 25 = 5 · 5 5(см) — сторона 2) 5 · 4 = 20 см — периметр квадрата
Вопрос №
18
Площадь квадрата 36 кв.см. Чему равен его периметр?
9 см
36 см
12 см
24 см
Вопрос №
19
Для какой задачи подходит такое решение:
1) 10 : 2 = 5 (см) — длина и ширина
2) 5 — 3 = 2(см) — ширина
3) 3 · 2 =6 (кв. см) — площадь
Стороны прямоугольника 10 см и 2 см. Чему равна его площадь?
Чему равна площадь прямоугольника, периметр которого равен 10 см,а длина 3 см?
Чему равна площадь прямоугольника, длина которого 10 см, а ширина на 5 см меньше?
Вопрос №
20
Для какой задачи подходит такое решение:
1) 6 : 3 = 2(см) — ширина
2) (2 + 3) · 2 = 10 (см)
Чему равен периметр квадрата со стороной 2см?
Чему равен периметр квадрата, площадь которого 6 кв. см?
см?
Чему равен периметр прямоугольника, площадь которого 6 кв.см и одна из сторон 3см?
Показать ответы
Получение сертификата
о прохождении теста
Доступно только зарегистрированным пользователям
© TestEdu.ru 2013-2022
E-mail администратора: [email protected]
Урок для 3 класса по теме: «Площадь прямоугольника и квадрата»
Утегенова Сауле Мараловна
учитель начальных классов
ОСШ № 17 г. Балхаш
Тема: Площадь прямоугольника и квадрата.
Цели: 1) систематизировать знания о прямоугольнике, квадрате и о нахождении площади и периметра данных фигур;
2) развивать логическое мышление, память, вычислительные навыки;
3) воспитывать чувство гордости своиму успеху, взаимопомощи, патриотические чувства.
Оборудование: слайды по теме, листы самоконтроля, карточки с заданиями, палетки, конверты с геометрическими фигурами, карточки–ответы консультантам, тесты – программа в компьютере.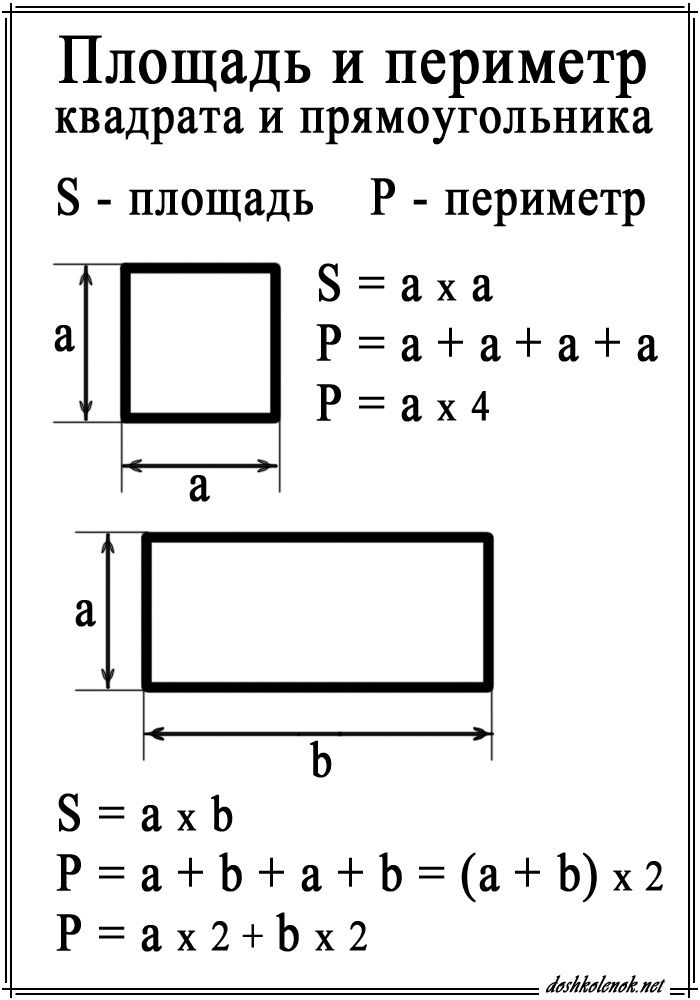
Ход урока
1. Психологический настрой.
Наш весёлый школьный звонок
Пригласил нас всех на урок.
Мы сегодня будем играть,
Загадки разгадывать, устно считать.
Площадь фигуры найдём,
Чуть – чуть отдохнём.
К задачам нашим решенье найдём.
Компьютер к работе, тоже для нас.
И всем мы желаем успехов сейчас!
2. Целеполагание.
По мониторингу прошлого урока учащиеся, набравшие большое кол-во баллов
им предоставляется право сегодня выполнять роль консультантов. По итогам прошлого урока многие из вас показали хорошие результаты. Я вам сегодня предлагаю поработать по карточкам с зад. сложного уровня. Тот кто испытал сложности в работе, вам предлагаю карточки простого уровня.
В листах самоконтроля будете как всегда выставлять кол – во баллов за каждое выполненное задание .В конце урока подведём итоги.
Каждое задание скрывает за собой буквы, в конце урока нам нужно собрать слово и узнать, какое же событие отметит наша страна в декабре месяце.
3. Математический диктант.( у доски 2 ученика) А
1) найдите частное чисел 25 и 5;
2) какое число разделить на 4, чтобы получить 6?
3) частное чисел 35 и 5, увеличить на 5;
4) найдите разность чисел 54 и 9;
5) на какое число надо разделить 32, чтобы получилось 8?
6) делимое 40, делитель 5. Чему равно частное чисел?
7) найдите делитель, если делимое 36, а частное 4;
8) множители 8 и 5. найдите произведение чисел.
9) во сколько раз 27 больше 9?
10) частное чисел 28 и 7, увеличить на 10.
Работа у доски
1 ученик Н 2 ученик В
… · 7 = 21 … : 6 = 3 5 · 8 * 6 · 5 9· 3 * 8 · 4
9 · … = 36 45 : … = 5 4 · 6 * 8 · 3 24 : 3 * 36 : 9
24 : … = 4 4 · …= 16 45 : 5 * 36 : 4 12 : 4 * 21 : 3
…· 7 = 35 …· 8 = 40 4 · 7 * 8 · 4 3 · 6 * 9 · 2
40 : …= 8 40 : …= 20 25 : 5 * 10 : 2 32 : 4 * 35 : 5
4. Решение выражений ( № 2) И
Карточка № 1 Карточка № 2
4 ·… = 32 9 · …= 27 70 – 8 · 2= 30 + 4 · 7=
45 : …= 5 28 : …= 7 26 + 24 : 4= 32 : 8+39=
8 · …= 24 5 · …= 20 50 – 5 · 4= 64 – 28 : 7 =
… : 6 = 3 7 · … = 35 45 : 5 + 36 = 40 : 8 + 24 =
5. Нахождение периметра прямоугольника. Е
Отступите вниз 2 клетки и поставьте точку. Отложите вниз 4 клетки и поставьте точку, вправо 8 клеток, вверх 4 клетки. Соедините точки. Какая фигура получилась? Обозначьте стороны прямоугольника.
Соедините точки. Какая фигура получилась? Обозначьте стороны прямоугольника.
Найдите периметр .
Р=(4+2)·2=12(см)
▲ — 8
6. Объяснение нового материала. ( Слайды на компьютере)
1) Какие фигуры лишние? Почему?
2) Тема нашего урока : Площадь прямоугольника и квадрата.
3) Дополните высказывание:
Прямоугольник это …………………, у которого все углы …………… .
4) Составьте формулу нахождения прямоугольника.
Длина – 6 см
Ширина – 3 см
S = 6 · 3 = 18 cm
S = a · b З
5) Правило:
Чтобы найти площадь прямоугольника, необходимо умножить длину на ширину, взятых в одинаковых единицах измерения.
Отгадайте загадку:
Он давно знакомый мой,
Каждый угол в нём прямой.
Все четыре стороны
Одинаковой длины.
Вам его представить рад .
Как зовут его? ( Квадрат)
6) Что такое квадрат?
Квадрат – это четырехугольник, у которого все стороны равны.
7) Составьте формулу нахождения квадрата.
Сторона квадрата 2 см.
Длина – а
А – 2 см
S = 2 · 2 = 4 ( cм²)
S = a · а C
8) Правило
Чтобы найти площадь квадрата, необходимо умножить длины сторон.
7. Закрепление нового материала
1) Дан прямоугольник со сторонами 5 см и 3 см. найдите площадь и периметр.
2) Квадрат со стороной 3 см. найдите площадь и периметр. И
Проверяют по компьютеру.
3) Найди ошибку.
Длина – 2 дм
Ширина – 5 см М
S = ? cm²
S = 5 · 3 = 15 (cm²)
Исправили ошибку : S = 20 ·5 = 100 (см²)
8. Физминутка ( муз.)
9. Решение примеров ( задание 5) О
Простой уровень Сложный уровень
А 450 : 5 = Ч 250 : 5 = А 40 · 6 – 30 · 3 = З 360 : 4 + 250 : 5 =
Д 80 · 5 = А 80 · 4 = Ч 240 : 3 + 8 ·3 = А 450 : 9 + 8 · 5=
А 40 · 3 = З 360 : 9 = А 250 : 5 + 4 · 5 = Д 240 : 6 + 9 · 5 =
Составить слово по схеме:
40, 90, 400, 320, 50, 120. 140, 150, 85, 70, 104, 90.
10. Решение задачи ( с. 83 , № 4) С
Что известно в задаче? Что нужно найти? Для чего прорывают каналы ?
Проверка ( слайд )
11. Работа с палеткой. ( тест 4 ученика на компьютере).Т
Работа с палеткой. ( тест 4 ученика на компьютере).Т
По течению принесло слово « палетка».
Алгоритм.
Наложить палетку на фигуру.
Сосчитать число а полных клеток.
Сосчитать число в клеток, входящих в фигуру частично.
Сосчитать приближённое значение площади
Предлагаю перейти с простого уровня на сложный.
Найдите площадь фигур по палетке.
( 4 ученика работают на компьютере с тестами) Ь
12. Подведение итогов.
Что нового вы узнали на уроке? Как найти площадь прямоугольника? Как найти площадь квадрата?
Какое слово получилось? С каким праздником связано это слово?
НЕЗАВИСИМОСТЬ
Подсчитайте с каким результатом мы подходим к этому событию.
Кто получил «5» , «4», «3», «2»?
Подсчитаем процент успеваемости.
Как найти площадь прямоугольника 3 класс
Названия геометрических фигур происходят от количества их сторон. Например, треугольник, четырехугольник, пятиугольник. Но есть фигуры, которые названы по другим признакам, например, прямоугольник, квадрат, ромб, трапеция. Все эти фигуры — четырехугольники, но отличаются друг от друга величиной углов и сторон.
Прямоугольник — четырехугольник с разными сторонами у которого все углы по 90о.
Квадрат — прямоугольник, у которого все углы по 90 градусов и стороны равные.
Такие отличия есть и у других фигур, например, треугольники подразделяются на прямоугольные, равносторонние, равнобедренные и разносторонние. Свойства фигуры зависят как от количества сторон, так и от других характеристик — величины углов и сторон. Только измерив все параметры, можно точно описать фигуру и определить, какими формулами и правилами пользоваться при вычислениях.
Что такое геометрическая фигура
Под этим термином понимают часть плоскости, ограниченной несколькими замкнутыми (соединенными) линиями. В результате соединения линий образуется отрезки, которые называются сторонами фигуры и точки соприкосновения, которые носят название вершин. У треугольника три стороны и три вершины, у четырехугольника — четыре стороны и четыре вершины.
В геометрии есть фигуры, которые выпадают из этого ряда. Это точка, прямая линия, отрезок, луч. Отличаются они от остальных фигур, тем, что не занимают никакой площади, это просто части линии.
Что такое площадь
Теперь рассмотрим еще одно понятие геометрии — площадь. Это часть плоскости, которая находится внутри многоугольника. Другими словами, все, что находится между сторонами фигуры и является ее площадью. Геометрия — часть математики, то есть, наука точная, которая стремится все измерить и описать цифрами. Не стала исключением и площадь. Часть плоскости, которая находится внутри фигуры, разбили на маленькие части с равными сторонами, идущими под прямым углом друг к другу. Такая фигура называется квадрат.
Такая фигура называется квадрат.
Квадрат — геометрическая фигура из четырех равных сторон и четырех прямых углов.
За единицу площади взяли квадрат, сторона которого равна единице длины (1 миллиметр, 1 метр, 1 сантиметр). Площадь, которую занимает квадрат со стороной 1 сантиметр назвали квадратный сантиметр (обозначает см2). Если квадрат построен из сторон в 1 м, то его площадь 1 м2. Найти площадь фигуры — значит определить, сколько таких квадратиков можно поместить внутри фигуры.
Расчет площади прямоугольника
Разберем простую задачу — как высчитать площадь прямоугольника? Можно решить ее двумя способами. Самый простой, но самый длинный и трудоемкий — нарисовать прямоугольник и с помощью карандаша и линейки разбить его на маленькие квадратики. Затем посчитать количество квадратиков и узнать, сколько их поместилось внутри.
Такой способ простой и доступный, если длина сторон прямоугольника — целое количество сантиметров или метров. А вот при их нецелом количестве, например стороны три с половиной и четыре с половиной сантиметра (3,5 см и 4,5 см), посчитать сложнее. Еще сложнее, если стороны, например 3см и 2 мм и 4 см и 7 мм. Рисовать придется миллиметровые квадратики, что довольно сложно и долго.
А вот при их нецелом количестве, например стороны три с половиной и четыре с половиной сантиметра (3,5 см и 4,5 см), посчитать сложнее. Еще сложнее, если стороны, например 3см и 2 мм и 4 см и 7 мм. Рисовать придется миллиметровые квадратики, что довольно сложно и долго.
Ученые древности, идя таким путем заметили интересную особенность, если посчитать квадраты внутри фигуры и сравнить их с результатом умножения длин сторон прямоугольника, то они окажутся одинаковыми. Проверив это на многих прямоугольниках и квадратах составили правило:
Площадь прямоугольника равна длине умноженной на ширину.
В учебниках можно найти и другую формулировку — площадь прямоугольника равна произведению соседних сторон, или еще иначе — площадь прямоугольника равна произведению основания на высоту. Суть этих утверждений одна и та же. Выражается она в формуле:
S=AB ∙BC.
Как уже говорилось, площадь измеряется в квадратных единицах — метрах, сантиметрах, дециметрах. Результат может быть как целым, так и дробным, например, 4 см2, 6 см2, или 4,6 см2 (4см2 и 6мм2).
Результат может быть как целым, так и дробным, например, 4 см2, 6 см2, или 4,6 см2 (4см2 и 6мм2).
Использование этой формулы — самый простой способ, как вычислить площадь прямоугольника с разными сторонами. Подходит он и для решения задачи вычисления квадрата (прямоугольника с равными сторонами). Для квадрата формула может выглядеть несколько иначе.
S=АВ2
Как она получалась? Начнем с основной формулы S=AB ∙BC. У квадрата АВ=ВС, отсюда S= АВ ∙ АВ = АВ2.
Периметр
Еще одна важная характеристика прямоугольника — периметр. Это сумма длин всех сторон. Периметр легко найти, измерив все стороны и сложив результаты. Но, как и в случае с площадью, лучше воспользоваться формулой. Сначала найдем периметр квадрата:
Р = АВ+ВС+СD+AD.
Но у квадрата все стороны одинаковые, значит, выражение можно записать иначе:
Р= АВ+АВ=АВ=АВ = 4 ∙ АВ, или 4АВ.
Для прямоугольника с разными сторонами периметр находится по такой же формуле:
Р = АВ+ВС+СD+AD.
Но здесь равны не все стороны, а только противоположные:
АВ= СD и ВС= AD
Перепишем начальную формулу по-другому:
Р= (АВ +СD) и (ВС + AD). Из равенства сторон получим Р=2АВ+2ВС + 2(АВ+ВС). Словами это будет звучать так:
Периметр прямоугольника равен сумме соседних сторон умноженной на два.
Как видно из приведенных утверждений, площадь и периметр прямоугольника можно вычислить двумя способами — непосредственным измерением и вычислением. Второй способ намного удобнее, особенно, если приходится находить площади и периметры реальных участков, например, площадки под строительство, дачного участка, комнаты.
Смотрите также другие геометрические фигуры:
Содержание
- Как найти площадь круга
- Площадь многоугольника
- Как найти площадь трапеции
- Признаки подобия треугольников
- Параллелепипед
- Шар и сфера, объем шара, площадь сферы, формулы
Связь между площадью и периметром — 3-й класс математики
Периметр и площадь — две разные вещи. Но они оба связаны с длиной прямоугольника (или высотой ) и шириной . Понимание этого может очень пригодиться в жизни.
Но они оба связаны с длиной прямоугольника (или высотой ) и шириной . Понимание этого может очень пригодиться в жизни.
Совет: этот урок довольно длинный. Сделайте все возможное, чтобы впитать его! 🤓
Давайте рассмотрим
Что такое периметр?
Периметр длина или расстояние вокруг форма или пространство.
К найдите периметр формы или пространства, просто добавьте длины всех сторон.
Будь то 3 стороны, 4 стороны, 5 сторон… или больше. Просто добавьте их все.
Что такое площадь?
Площадь — это пространство, занимаемое плоской фигурой.
Чтобы найти площадь прямоугольника, умножить его ширину на его высоту.
Два прямоугольника могут иметь одинаковый периметр, но разные площади.
Отличная работа! 🎊
Теперь давайте потренируемся решать задачи на площадь и периметр.
Пример 1: Тот же периметр, разная площадь
Фигуры ниже имеют одинаковый периметр , но разные площадь .
Какова площадь прямоугольника B?
👉 Начните , используя уже известную информацию.
У нас есть высота и ширина прямоугольника А. Мы можем использовать их, чтобы найти его периметр.
Мы делаем это с помощью , добавляя длину всех его сторон.
4 + 4 + 3 + 3 = 14 метра
Это означает, что периметра прямоугольника B 4 тоже 1 метр. Мы еще не можем вычислить площадь B, потому что длина одной стороны все еще отсутствует. Как найти недостающую сторону? 🤔 👉 Работаем той стороной, которую знаем. Мы знаем, что ширина 2 метра. Так как противоположны сторонам равно , мы удваиваем чтобы получить сумму двух сторон. Теперь вычтем полученную сумму из общего периметра. Это означает, что сумма из два неизвестно стороны 10 м. Мы делим на 2, чтобы получить длину каждой неизвестной стороны. 👍 Теперь мы знаем, что высота прямоугольника B равна 5 метров! Поскольку мы знаем высоту и ширину прямоугольника B, мы наконец можем найти его площадь. Это просто, мы просто умножаем : ✅ Область прямоугольника B составляет 10 квадрат метры (или 10 м² ). Прямоугольники ниже имеют одинаковую площадь , но разные периметр . 👉 Чтобы найти периметра прямоугольника, нам нужно знать его высоту и ширину. Мы знаем только ширину прямоугольника A — его высота отсутствует ! Как узнать его высоту? 🤔 Используя информацию, полученную из прямоугольника B. Мы знаем, что площади двух прямоугольников равны. Формула для область — высота x ширина. Используем это сейчас: Площадь прямоугольника B равна 30 дюймов². 👍 Это означает, что площадь прямоугольника А также равна 30 дюймов². 👉 Наш следующий шаг — найти недостающую сторону прямоугольника А. Мы делаем это, используя информацию, которая у нас уже есть. Мы знаем, что ширина прямоугольника А равна 3 дюймам, а его площадь равна 30 дюймов². Наша формула: Итак, давайте заполним нашу формулу числами: 😐
😐 2 + 2 = 4
14 — 4 = 10
 👍
👍 10 ÷ 2 = 5
2 x 5 = 10 м²

Пример 2: та же площадь, разный периметр
👆Что такое периметр Прямоугольник A ?
 Если мы вычислим площадь прямоугольника B, то мы уже знаем площадь прямоугольника A.
Если мы вычислим площадь прямоугольника B, то мы уже знаем площадь прямоугольника A. 5 x 6 = 30 дюйм²

H x W = площадь
H x 3 = 30
75 90 Вспомните, как решить уравнение Переменная? Это просто так. 😃
Наша переменная H (для высоты). Нам нужно добраться в одиночку с левой стороны.
Для этого нам нужно отменить умножение слева на , используя отдел .
Делим обе стороны на 3!
Помните, что то, что вы делаете на одной стороне, должно быть сделано и на другой стороне. Это сохранит уравнение сбалансированным .
Это сохранит уравнение сбалансированным .
H x 3 ÷ 3 = 30 ÷ 3
H = 10 дюймов
. Отсутствующая сторона составляет 10 дюймов .
Мы знаем, что это правильно, потому что когда мы умножьте на две стороны, чтобы получить его площадь, мы получим 30 дюймов². 👍 Это соответствует площади прямоугольника B!
👉 Теперь мы находим его периметр.
Это просто. Мы просто добавляем все стороны .
Помните, что противоположные стороны прямоугольника всегда равны.
Это означает, что мы удваиваем высоту, а также ширину.
3 + 3 + 10 + 10 = 26 дюймов
✅ периметр прямоугольника А равен 26 дюймов .
Отличная работа! А теперь попробуйте практические упражнения. 💪
Математика 3 класс | Формы и их периметр
Краткое содержание модуля
В модуле 5 учащиеся изучают концепции периметра и геометрии. Учащиеся постепенно формировали свое понимание геометрических понятий с детского сада, когда учащиеся учатся называть фигуры независимо от их размера и ориентации. Они также учатся различать плоские и твердые формы. В 1 классе понимание учащихся становится более тонким, поскольку они учатся различать определяющие и неопределяющие атрибуты, а также составлять и разбирать как плоские, так и объемные формы. Во 2 классе учащиеся рисуют и определяют фигуры с определенными атрибутами. Все это понимание готовит их к 3 классу, в котором учащиеся начинают свое путешествие по измерению этих атрибутов, включая площадь (рассматривается в Разделе 4) и периметр (изучается здесь), а также классификацию форм на основе атрибутов в одну или больше категорий.
В 1 классе понимание учащихся становится более тонким, поскольку они учатся различать определяющие и неопределяющие атрибуты, а также составлять и разбирать как плоские, так и объемные формы. Во 2 классе учащиеся рисуют и определяют фигуры с определенными атрибутами. Все это понимание готовит их к 3 классу, в котором учащиеся начинают свое путешествие по измерению этих атрибутов, включая площадь (рассматривается в Разделе 4) и периметр (изучается здесь), а также классификацию форм на основе атрибутов в одну или больше категорий.
Учащиеся начинают этот раздел с построения представлений 2-го класса о многоугольниках и их свойствах, особенно развивая и расширяя свои знания о четырехугольниках. Они исследуют атрибуты многоугольников и классифицируют примеры по различным категориям, затем исследуют атрибуты четырехугольников и классифицируют примеры по различным категориям (3.G.1). Учащиеся также рисуют многоугольники на основе их атрибутов. Затем учащиеся используют танграмы для составления и разложения фигур. В теме B учащиеся переходят к измерению атрибута этих многоугольников, а именно периметра. Они определяют периметр как границу двумерной формы и сравнивают периметры различных форм, используя конкретные единицы измерения. Затем находят периметр многоугольника, стороны которого отмечены метками единичной длины, а затем цифрами. Затем, после нахождения периметра путем измерения длины каждой стороны, они находят периметр, когда необходимо вывести некоторую информацию о длине сторон фигуры, например, когда прямоугольник имеет только одну длину и одну ширину. Затем учащиеся решают реальные и математические задачи, как с фигурой, так и без нее, включая периметры многоугольников (3.MD.8). Имея такое понимание периметра, они могут сравнить измерение площади и периметра прямоугольника в Теме C, видя, что прямоугольник с определенной площадью может иметь различные периметры и, наоборот, прямоугольник с определенным периметром может иметь множество областей, соединяющих дополнительный кластерный контент периметра с основным кластерным контентом области.
В теме B учащиеся переходят к измерению атрибута этих многоугольников, а именно периметра. Они определяют периметр как границу двумерной формы и сравнивают периметры различных форм, используя конкретные единицы измерения. Затем находят периметр многоугольника, стороны которого отмечены метками единичной длины, а затем цифрами. Затем, после нахождения периметра путем измерения длины каждой стороны, они находят периметр, когда необходимо вывести некоторую информацию о длине сторон фигуры, например, когда прямоугольник имеет только одну длину и одну ширину. Затем учащиеся решают реальные и математические задачи, как с фигурой, так и без нее, включая периметры многоугольников (3.MD.8). Имея такое понимание периметра, они могут сравнить измерение площади и периметра прямоугольника в Теме C, видя, что прямоугольник с определенной площадью может иметь различные периметры и, наоборот, прямоугольник с определенным периметром может иметь множество областей, соединяющих дополнительный кластерный контент периметра с основным кластерным контентом области. Затем учащиеся решают различные задачи на площадь и периметр.
Затем учащиеся решают различные задачи на площадь и периметр.
В этом разделе учащиеся рассуждают абстрактно и количественно, переводя числа и уравнения туда и обратно в контексте задач периметра (MP.2). Учащиеся также будут придумывать жизнеспособные аргументы и критиковать рассуждения других по мере того, как они развивают тонкое понимание разницы между площадью и периметром, а также когда они классифицируют формы в соответствии с их атрибутами и обосновывают свое обоснование (MP.3). Наконец, учащиеся будут использовать соответствующие инструменты стратегически, используя линейки для измерения длин сторон многоугольников, чтобы найти их периметр, а также использовать линейки и инструменты для определения прямых углов, чтобы найти атрибуты фигур для определения их классификации (MP.5).
Учащиеся будут глубже понимать эти идеи в будущих классах. В 4 классе учащиеся решают более сложные текстовые задачи на площадь и периметр (4.MD.3), а также классифицируют фигуры на основе наличия параллельных и перпендикулярных фигур (4. G.2), что очень связано с их изучение углов (4.МД.5—7). Начальная работа по категоризации в 3 классе достигает кульминации в 5 классе, где учащиеся имеют полное представление об иерархической природе классификации фигур (5.G.3). В средних и старших классах все более сложные задачи зависят от глубокого понимания учащимися атрибутов форм и способов их измерения, которые пронизывают весь этот раздел.
G.2), что очень связано с их изучение углов (4.МД.5—7). Начальная работа по категоризации в 3 классе достигает кульминации в 5 классе, где учащиеся имеют полное представление об иерархической природе классификации фигур (5.G.3). В средних и старших классах все более сложные задачи зависят от глубокого понимания учащимися атрибутов форм и способов их измерения, которые пронизывают весь этот раздел.
Темп: 17 учебных дней (15 уроков, 1 гибкий день, 1 контрольный день)
Fishtank Plus для математики
Разблокируйте функции, чтобы оптимизировать время подготовки, планировать увлекательные уроки и следить за успеваемостью учащихся.
Узнать больше
Оценка
Следующие оценки сопровождают Раздел 5.
Предварительная часть
Предложите учащимся пройти предварительную оценку и самооценку перед началом модуля. Используйте Руководство по анализу предварительной оценки, чтобы определить пробелы в фундаментальном понимании и наметить план ускорения обучения на протяжении всего модуля.
Промежуточный модуль
Предложите учащимся пройти промежуточную оценку после урока 8.
Послемодуль
Используйте приведенные ниже ресурсы для оценки усвоения учащимися содержания модуля и плана действий для будущих модулей.
Постмодальная оценка
Ключ к ответам после модульной оценки
Руководство по анализу послемодульной оценки
92F25A3F-8529-4314-9899-6EE68694E3D0Пост-юнит самооценка
Расширенный пакет оценивания
Используйте данные учащихся для управления планированием с помощью расширенного набора модульных оценок, помогающих оценить уровень владения учащимися базовыми навыками и понятиями, а также их прогресс в освоении содержания модуля.
Загрузка образца
Подготовка блока
Интеллектуальная подготовка
Рекомендации по подготовке к обучению этому разделу
A628D5C3-5B97-4E03-B1EC-5AD5C66D8950Интеллектуальная подготовка для всех разделов
- Прочтите и прокомментируйте разделы «Сводка модуля» и «Основные сведения» плана модуля.

- Выполните все целевые задачи и аннотируйте их с учетом «Сводки модуля» и «Основных моментов».
- Пройти итоговую оценку.
Основные понятия
Основные математические концепции, которые учащиеся поймут в этом модуле
A628D5C3-5B97-4E03-B1EC-5AD5C66D8950- «Периметр — это граница двумерной формы. Для многоугольника длина периметра равна сумме длин сторон» (GM Progression, стр. 16).
- Прямоугольники с одинаковым периметром не обязательно имеют одинаковую площадь. Прямоугольники с одинаковой площадью не обязательно имеют одинаковый периметр.
- Фигуры в разных категориях могут иметь общие атрибуты, определяющие более крупную категорию фигур высшего уровня. Например, категория фигур, называемых четырехугольниками, включает такие категории, как квадраты, прямоугольники, ромбы, параллелограммы и трапеции, поскольку все они являются замкнутыми фигурами с четырьмя сторонами.
Материалы
Материалы, изображения и инструменты, которые потребуются преподавателям и учащимся для этого занятия Дополнительная информация.
 Вы можете предоставить учащимся шаблон сетки квадратных дюймов, разрезанный на отдельные блоки, если у вас недостаточно плиток квадратного дюйма.
Вы можете предоставить учащимся шаблон сетки квадратных дюймов, разрезанный на отдельные блоки, если у вас недостаточно плиток квадратного дюйма.Запас слов
Термины и обозначения, которые учащиеся изучают или используют на уроке
A628D5C3-5B97-4E03-B1EC-5AD5C66D8950attribute
parallelogram
parallel
perimeter
polygon
quadrilateral
rhombus
right angle
Чтобы увидеть весь словарный запас для модуля 5, просмотрите наш глоссарий лексики для 3-го класса.
Модульная практика
Речевые задачи и упражнения на беглость речи
Получите доступ к ежедневным репетициям текстовых задач и нашим ориентированным на содержание упражнениям на беглость речи, созданным, чтобы помочь учащимся укрепить свои навыки применения и беглости речи.
Предварительный просмотр
Узнать больше
Карта урока
Тема A: Атрибуты двумерных фигур
Сравните и классифицируйте полигоны.
3.G.A.1
Сравните и классифицируйте четырехугольники.
3.G.A.1
Рисование фигур с указанными атрибутами.
3.G.A.1
Причина по составлению и разложению полигонов с помощью танграмов.
3.G.A.1
Тема B: Понимание периметра
Под периметром понимается граница вокруг двумерной формы. Сравните периметры различных форм.
3.МД.Д.8
Найдите периметр, измерив длины сторон в целых единицах.
3.МД.Д.8
Найдите периметр фигуры с отмеченными длинами всех сторон.
3.МД.Д.8
Найдите периметр многоугольников со сторонами одинаковой длины и прямоугольников, у которых отсутствуют некоторые длины сторон.
3.МД.Д.8
Решите текстовые задачи на нахождение периметра по длинам сторон.
3.МД.Д.8
Найдите длины сторон многоугольников со сторонами равной длины и прямоугольников, если известны периметр и другие длины сторон.
3.МД. Д.8
Д.8
Решите более сложные текстовые задачи, связанные с периметром, например, найдите недостающую длину стороны по заданному периметру и другим длинам сторон.
3.МД.Д.8
Тема C: Различие между площадью и периметром
Найдите прямоугольники с одинаковой площадью и разными периметрами.
3.МД.Д.8
Найдите прямоугольники с одинаковым периметром и разными площадями.
3.МД.Д.8
Решайте различные текстовые задачи на площадь и периметр.
3.МД.Д.8
Рассуждение о составлении и разложении многоугольников с помощью тетрамино.
3.G.A.1
Общие базовые стандарты
Ключ
Основной кластер
Вспомогательный кластер
Дополнительный кластер
Основные стандарты
Стандарты содержания, описанные в этом модуле
A628D5C3-5B97-4E03-B1EC-5AD5C66D8950Геометрия
3.Г.А.1 — Поймите, что фигуры в разных категориях (например, ромбы, прямоугольники и другие) могут иметь общие атрибуты (например, иметь четыре стороны) и что общие атрибуты могут определять более крупную категорию (например, четырехугольники).
 Распознайте ромбы, прямоугольники и квадраты как примеры четырехугольников и нарисуйте примеры четырехугольников, не принадлежащих ни к одной из этих подкатегорий.
Распознайте ромбы, прямоугольники и квадраты как примеры четырехугольников и нарисуйте примеры четырехугольников, не принадлежащих ни к одной из этих подкатегорий.
Измерения и данные
3.МД.Д.8 — Решать реальные и математические задачи, связанные с периметрами многоугольников, включая нахождение периметра по длинам сторон, нахождение неизвестной длины стороны и отображение прямоугольников с одинаковым периметром и разными площадями или с одинаковой площадью и разными периметрами.
Основополагающие стандарты
Стандарты, описанные в предыдущих модулях или классах, которые являются важной основой для текущего модуля
A628D5C3-5B97-4E03-B1EC-5AD5C66D8950Геометрия
2.Г.А.1
Измерения и данные
2.
 МД.А.1
МД.А.13.MD.C.5
3.MD.C.6
3.MD.C.7
Операции и алгебраическое мышление
3.OA.D.8
Будущие стандарты
Стандарты будущих классов или разделов, которые связаны с содержанием данного раздела
A628D5C3-5B97-4E03-B1EC-5AD5C66D8950Геометрия
4.Г.А.1
5.RUS3
Измерения и данные
4.МД.А.3
Стандарты математической практики
CCSS.MATH.PRACTICE.MP1 — Разбираться в проблемах и настойчиво решать их.
CCSS.
 MATH.PRACTICE.MP2
— Рассуждайте абстрактно и количественно.
MATH.PRACTICE.MP2
— Рассуждайте абстрактно и количественно.CCSS.MATH.PRACTICE.MP3 — Придумывайте жизнеспособные аргументы и критикуйте рассуждения других.
CCSS.MATH.PRACTICE.MP4 — Модель с математикой.
CCSS.MATH.PRACTICE.MP5 — Стратегически используйте соответствующие инструменты.
CCSS.MATH.PRACTICE.MP6 — Следите за точностью.
CCSS.MATH.PRACTICE.MP7 — Ищите и используйте структуру.
CCSS.MATH.PRACTICE.MP8 — Ищите и выражайте закономерность в повторяющихся рассуждениях.
Блок 4
Область
значок/стрелка/вправо/крупныйБлок 6
Дроби
Запрос Математика — прямоугольник 4 на 3
Процессы математических запросов: 90; определить параметры; исследовать. Концептуальная область исследования: Площадь и периметр; формулы.
В своем первом ответе на подсказку учащиеся задали некоторые из следующих вопросов:
Существуют ли другие прямоугольники площадью 12 квадратных единиц?
Какие еще фигуры могут иметь площадь 12 квадратных единиц?
Чем отличаются и одинаковы ли прямоугольники?
Сколько можно прямоугольников одинаковой площади?
У какого прямоугольника самый длинный периметр? … кратчайший?
Существует ли прямоугольник, площадь которого равна длине его периметра?
В этот момент может возникнуть дискуссия о том, является ли прямоугольник 4 на 3 «таким же» как прямоугольник с размерами 3 на 4. Принимая, что это не так, мы могли бы предположить, что количество прямоугольников с одинаковой площадью равно половине площади (при условии, что размеры — целые числа). Итак, есть шесть прямоугольников площадью 12 квадратных единиц и четыре прямоугольника площадью восемь. Однако, если площадь — простое число, их будет только два. Исследование может перерасти в рассмотрение множителей простых и составных чисел.
Итак, есть шесть прямоугольников площадью 12 квадратных единиц и четыре прямоугольника площадью восемь. Однако, если площадь — простое число, их будет только два. Исследование может перерасти в рассмотрение множителей простых и составных чисел.
Возможно, учитель предпочитает оставить длину периметра постоянной для начальной подсказки (см. ниже), когда могут возникнуть подобные вопросы:
Чем отличаются и одинаковы ли прямоугольники?
Сколько можно прямоугольников с одинаковым периметром?
У кого самая большая площадь? … наименьший?
Предположения, вытекающие из конкретных случаев, показанных в двух приведенных выше подсказках, можно объединить. Итак, рассматривая прямоугольник 4 на 3, есть шесть прямоугольников с площадью 12 квадратных единиц и шесть с периметром 14 единиц. Всегда ли так с каждым прямоугольником? Этот путь к исследованию может усилить различие между понятием площади и периметра.
Мэтью Бернстайн , учитель 5-6 класса государственной школы Фреда Варли (Маркхэм, Онтарио), сообщает об опросе, который его ученики провели в подсказке:
Даже сделав только Немного поработав над площадью и периметром, я почувствовал, что мои 5-е классы справятся с этим вопросом, поскольку учебная программа 4-го класса в Онтарио просит учащихся выяснить формулу площади прямоугольника. Когда я представил подсказку, было много отличных размышлений.
У студентов возникло любопытство, и они немедленно захотели узнать, есть ли другие прямоугольники с такой же площадью. Затем стали исследовать другие фигуры площадью 12 квадратных единиц, в том числе треугольники. Это в конечном итоге привело к тому, что одна группа использовала блоки шаблонов для независимого исследования формулы площади трапеции. В ходе опроса, который длился более двух дней, студенты многое узнали. Это позволило легко перейти к изучению формул параллелограмма и трапеции!
Первое изображение (вверху слева) показывает первоначальные ответы учащихся на подсказку. На других рисунках показаны листы планирования, которые использовали учащиеся, и примеры их запросов.
На других рисунках показаны листы планирования, которые использовали учащиеся, и примеры их запросов.
Мишель Коул , руководитель отдела обучения математике в Ормистон-Бушфилдской академии, Питерборо (Великобритания), дала подсказку своему семикласснику в качестве введения в концепции периметра и площади. Она сообщает, что ответы студентов были «вдохновляющими, удивительными и действительно превзошли все мои ожидания».
Студенты задавали вопросы по широкому кругу математических тем: периметр и площадь; симметрия, углы и другие свойства фигур; координаты; объем; и увеличение с коэффициентом масштабирования ½. Другие вопросы предлагали новые направления исследований:
Сколько прямоугольников (или квадратов) вы видите в каждой фигуре?
Сколько треугольников из одной точки вы можете найти?
Какие фигуры можно составить из каждой фигуры?
Какую часть сетки занимают фигуры?
Мишель описывает, как она подошла к расследованию:
Я экспериментировала с подсказками, которые в прошлом я немного структурировала. Это был первый раз, когда я просто дал им схему на бумаге формата А3 и сказал: «Какие вопросы мы можем задать?»
Это был первый раз, когда я просто дал им схему на бумаге формата А3 и сказал: «Какие вопросы мы можем задать?»
Учащиеся записали свои вопросы и идеи на бумаге формата А3.
Студенты немного неохотно излагали свои мысли на бумаге, но как только они поняли, что у них есть свобода действий, чтобы обдумать вопросы, которые мы затем обсудим, у них появилось множество разнообразных идей.
Когда мы обсуждали их идеи, мы также говорили о том, на какие вопросы мы могли бы ответить (например, что такое периметр? какова площадь?) по сравнению с вопросами, на которые мы не могли ответить (например, «где начало? почему они разного цвета?).
Затем мы сосредоточили задание на периметре и площади, а учащиеся исследовали периметр, когда они собирали более одной парты вместе.
Я использую «что такое же?» в чем отличие?» довольно регулярно подсказывайте в качестве стартового (вы можете видеть, что некоторые студенты использовали это как вопросы на своих листах). Именно это помогло повысить их устойчивость и заставило их мыслить в более широком контексте, чем самый очевидный.
Именно это помогло повысить их устойчивость и заставило их мыслить в более широком контексте, чем самый очевидный.
Амелия О’Брайен , преподаватель United World College Thailand на Пхукете, опробовала подсказку в своем классе 3. Она сообщает, что обнаружила, что метод исследования математики так же эффективен для младших школьников, как и для учащихся средней школы:
3-й класс опробовал подсказку, сначала используя программу визуального мышления Project Zero «вижу, думаю, удивляюсь» в качестве совместной группа, обмен и развитие идей друг друга. Сначала некоторые ученики могли «видеть» лицо (если добавить еще один прямоугольный глаз!), а другие могли «видеть» сходство с китайским иероглифом «вверх». «После того, как студентов попросили думать как математики, студенты сразу установили связи с массивами. Стоит отметить, что мы одновременно исследуем умножение и деление».
После моделирования ожиданий и обсуждения возможных способов распаковки и ответа на подсказку, включая начало предложения и предложения других способов, которыми мы могли бы представить подсказку, используя многомерный подход, мы продолжили наше мышление в малых группах.
Учащиеся определяли закономерности, экспериментировали с символами и цифрами, и им предлагалось задавать вопросы. Затем они выбирают интересующий их вопрос для изучения.
Поскольку вопросы-подсказки и связанные с ними вопросы по своей сути различаются, большинство учащихся выбрали соответствующий сложный вопрос, основываясь на своих собственных предварительных знаниях и понимании. Затем мы планировали, как будем проводить наши исследования, выбирая и связывая понятия, которые могли бы помочь сфокусировать наше мышление. Большинство учащихся решили поэкспериментировать, моделируя (используя кубики, фишки или бумагу с сеткой) или проводя исследования с использованием математических словарей и дискуссий.
Раньше я не использовал математические подсказки для таких юных учеников и не был уверен, как это поведет себя. При некотором дифференцированном моделировании быстрый и последующие опросы оказались такими же увлекательными и содержательными, как и использование этого подхода со старшими учениками!
Ученики 6-го класса Международной школы Луанды (Ангола) начали свои исследования в области измерения с рассмотрения подсказки прямоугольников. Пытаясь понять смысл подсказки, ученики задавали вопросы, связывая имеющиеся у них знания соответствующих математических понятий с подсказкой.
Пытаясь понять смысл подсказки, ученики задавали вопросы, связывая имеющиеся у них знания соответствующих математических понятий с подсказкой.
Класс продолжал проводить личные расследования, в ходе которых генерация еще большего количества вопросов открывала новые пути для исследования. Качество и глубина этого генеративного опроса свидетельствует о сложности процессов исследования, разработанных в классе.
На картинке показаны вопросы и наблюдения из Айн Кэрролл 7 класс. Сначала они сосредотачиваются на площади и периметре прямоугольников в подсказке, прежде чем учащиеся начнут задаваться вопросом, можно ли создать другие фигуры с такой же площадью. Один ученик размышляет о количестве прямоугольников, площадь которых в два раза больше, чем в подсказке. На двух других фотографиях показан вклад отдельных студентов в исследование.
Аманда Клан , учитель математики, работающий по принципу PYP, , опубликовала этот блог об использовании подсказки 4 на 3 в своем классе на своем веб-сайте Doing Maths .
Samia Henaine разместила диаграмму в Twitter с подписью: «Удалите три квадрата по единиц из прямоугольника 4 на 3 и посмотрите, что получится».
Подсказка порождает новые строки запроса с прямоугольником 4 на 3:
Что происходит с площадью прямоугольника?
Какие исключения дают самый длинный и самый короткий периметр?
Сколько различных периметров возможно при удалении трех квадратов?
Что произойдет, если убрать больше или меньше квадратов?
Можно ли создать такой же периметр, удалив два, три или четыре квадрата?
Что произойдет, если убрать квадрат из середины прямоугольника?
……………….
Самия — учитель математики, координатор PYP и ИКТ в средней школе Хуссам Эддин Харири в Сайде (Ливан). Дополнительные запросы см. на ее веб-сайте «Учителя математики как строители мостов» .
Дополнительные запросы см. на ее веб-сайте «Учителя математики как строители мостов» .
Май 2022
Запросы могут начинаться с самых простых подсказок. Марк Гринуэй (преподаватель продвинутых навыков в Великобритании) связался с Inquiry Maths по поводу разработки подсказок для учащихся с более низкими предыдущими достижениями. Он предложил использовать прямоугольник 4 на 3 в качестве подсказки. Потенциально это может привести к очень открытому расследованию, охватывающему ряд различных направлений. Однако такая подсказка, как прямоугольник 4 на 3, настолько знакома учащимся, что может не соответствовать первому критерию для 9.0003 создание подсказки : «Подсказка должна вызывать у учащихся любопытство и задавать вопросы типа «это не может быть правильным» или «я заметил…». Подсказки должны быть привлекательными и созреть для предположений или предположение».
Нет никакой гарантии, что, помимо описания очевидных особенностей прямоугольника, учащиеся смогут выделить ключевое понятие, на основе которого можно построить исследование. Например, учащийся может определить площадь как 12 квадратных единиц, но не сможет экстраполировать концепцию площади в качестве основы для исследования. Такой шаг требует использования хорошо развитых навыков исследования и особенно высокого уровня уверенности и творчества.
Например, учащийся может определить площадь как 12 квадратных единиц, но не сможет экстраполировать концепцию площади в качестве основы для исследования. Такой шаг требует использования хорошо развитых навыков исследования и особенно высокого уровня уверенности и творчества.
Если учащимся не хватает этих навыков, учителю необходимо уточнить запрос. Вмешательство учителя в этот момент уменьшает возможность работы учащихся над своими вопросами и утверждениями, что является ключевым мотивационным аспектом исследования. В подсказке лучше «предложить» ключевую концепцию, чтобы учащиеся могли обобщить ее на другие случаи для себя. Когда прямоугольник помещается в контекст ряда прямоугольников, имеющих одну и ту же характеристику (например, площадь), то первоначальный запрос может развиться на основе наблюдений учащихся.
После первой фазы учитель может выделить ограничение в подсказке и предложить учащимся изменить подсказку, оставив другую характеристику (например, периметр) прямоугольника 4 на 3 постоянной. Хотя предложение изменений в подсказке расширяет возможности учащихся, это остается высокоразвитым навыком. Студенты должны не только научиться быть творческими, они также должны научиться делать математически обоснованные предложения.
Хотя предложение изменений в подсказке расширяет возможности учащихся, это остается высокоразвитым навыком. Студенты должны не только научиться быть творческими, они также должны научиться делать математически обоснованные предложения.
Учитель может провести полностью открытый опрос, начав только с прямоугольника 4 на 3. Риск заключается в том, что под давлением необходимости «охватить» учебную программу расследование может пойти в одном из многих разных направлений.
В качестве альтернативы учитель может направить запрос в определенном направлении, предлагая подсказки, неотъемлемой частью которых является прямоугольник 4 на 3.
Действительно, учитель, который начинает серию вопросов с одного ключевого компонента, тем самым подчеркивает взаимосвязанный характер математики.
Две дополнительные подсказки связывают прямоугольник 4 на 3 с последовательностями и симметрией отражения.
Подробнее о различиях между различными типами опросов и о факторах, влияющих на принятие решения о выборе открытого, управляемого или структурированного опроса, см. Уровни изучения математики .
Уровни изучения математики .
Подсказка 1
Подсказка предлагает учащимся задавать вопросы и делать наблюдения по последовательностям : Сколько существует последовательностей, содержащих прямоугольник 4 на 3? Есть ли другой прямоугольник перед последовательностью в подсказке? Можете ли вы найти выражение (словесное или алгебраическое), описывающее площадь и периметр фигуры n ? Каковы правила от термина к термину или от позиции к термину для последовательностей?
Подсказка 2
Вторая альтернативная подсказка предлагает учащимся удалить квадраты для создания прямоугольных узоров с линиями симметрии . Сколько узоров можно создать с помощью одной или двух линий симметрии? Что делать, если вы удалите более двух квадратов? Почему нельзя делать выкройки с более чем двумя линиями симметрии? Какая форма вам понадобилась бы, если бы это было вашей целью?
Лист подсказок
PowerPoint
Могут ли они быть равны?
Возраст от 11 до 14 лет
Уровень задачи
У нас было множество решений этой задачи, так что молодцы все, кто ответил!
Дэвид, Ной, Феликс, Том, Эми и Лаура из Бристольской гимназии вместе работали над этой задачей. Дэвид говорит:
Дэвид говорит:
Мы обнаружили, что прямоугольник 6 на 3 работает, потому что 6+3+6+3=18 и 6×3=18, так что площадь и периметр равны.
Лора и Эми говорят:
Мы систематически работали над перечислением всех возможных прямоугольников, т.е. 1×1 1×2 1×3 1×4 … и решить, есть ли падежи с 1, 2 или 3
2×1 2×2 2×3 2×4…
3×1 3×2 3×3 3×4…
Мы заметили диагональный узор, в котором периметр становится меньше площади.
Мы все еще работаем над решением!
Молодцы Гурав из Индии, Радха из Стэнхоупа, Кирсти из колледжа да Винчи и Кейтлин из начальной школы Маршфилда, которые правильно нашли прямоугольники с одинаковой площадью и периметром, например 4×4 и 3×6.
Ханна из школы для девочек из Лестера сделала несколько хороших заметок о четных и нечетных числах:
Я понял, что по крайней мере одно из значений длины или ширины прямоугольника должно быть четным. Периметр всегда будет четным, потому что длина умножается на 2, что делает его четным, и прибавляется к ширине, которая была умножена на 2, что также делает его четным. Но если и длина, и ширина нечетны, то площадь будет нечетной, а это означает, что периметр не может быть таким же, как
область.
Но если и длина, и ширина нечетны, то площадь будет нечетной, а это означает, что периметр не может быть таким же, как
область.
Щелкните здесь, чтобы узнать, как Декстер из школы Уилсона использовал диаграммы для понимания различных прямоугольников и как он также использовал алгебру, чтобы найти примеры прямоугольников, у которых периметр равен площади.
Люси из Бельгии визуально заметила, что происходит с прямоугольниками с целым числом длин сторон:
Каждый квадрат по краям составляет одну единицу периметра, за исключением четырех угловых квадратов. Они составляют две единицы периметра, но только одну единицу площади. Это означает, что периметр на 4 больше, чем площадь, и в середине должны быть квадраты, которые будут учитываться только для площади, а не для периметра.
Бхавик из школы для мальчиков королевы Елизаветы также рассматривал прямоугольники с целым числом длин сторон и пришел к такому же выводу. Щелкните здесь, чтобы увидеть его очень четкое объяснение того, почему может быть только два таких прямоугольника, площадь которых равна периметру.
Натан из начальной школы Рашмора попытался использовать алгебру, которую продолжили Вики из Фарнборо-Хилл, Элиза и Жаклин из Колледжа Шевалье, Австралия, и Том. Вики заметила, что для прямоугольника x на y площадь равна периметру, если: $$ \begin{align*} xy &= 2x+2y \\ xy-2y &= 2x \\ y(x -2) &= 2х\\ у &= \frac {2x}{x-2} \end{align*} $$
Затем Нихарика посмотрела на возможные значения x и y из этого уравнения: $$ \begin{align*} y &= \frac {2x}{x-2} \text{ and } x ,y> 0 \\ \Rightarrow x-2 & > 0 \\ x&> 2 \end{align*} $$ Этих прямоугольников бесконечное множество.
Подстановка различных значений x и y и проверка правильности ответов — хороший навык решения задач — молодцы Кристоф и Мимас, которые сделали это. Также Шашанк из Индии нарисовал график возможных x и y значения:
Эстер прокомментировала это:
Хотя вы всегда можете подставить число в формулу, которую я использовал, $2x+2y=xy$, конечный результат не всегда является целым числом.
На самом деле единственными прямоугольниками с целыми длинами сторон являются прямоугольник 3×6 и квадрат 4×4.
Любые другие числа, подставленные в формулу как x , дадут десятичный вывод для y .
Например, если вы введете 5 как x , ваше значение для y будет 10/3.
Молодцы ученица 2BE мисс Джеррард из средней школы Перта, которая заметила некоторые интересные связи между площадью и периметром:
Мы все нашли 2 прямоугольника, которые сработали довольно быстро. Это были квадрат со сторонами 4 (A=P=16) и прямоугольник со сторонами 3 и 6 (A=P=18).
Затем мы решили попробовать использовать десятичные дроби, чтобы посмотреть, сможем ли мы найти что-нибудь еще, поскольку мы застряли. Один из нас обнаружил, что прямоугольник со сторонами 10 и 2,5 работает, так как он дает нам площадь и периметр 25.
После того, как мы нашли этот прямоугольник, кому-то еще в классе удалось обнаружить закономерность, связывающую числа. Начните с квадрата со сторонами 4 на 4.
Начните с квадрата со сторонами 4 на 4.
Затем посмотрите на прямоугольник со стороной 3 и шириной 6.
Разница между длинами 3 и 4 равна 1, разница между ширинами 4 и 6 равна 2
Чтобы перейти от 3 к следующей длине, нужно разделить разницу между 4 и 3 пополам и вычесть ее из 3, чтобы получить 2,5.
Чтобы перейти от 6 к следующей ширине, удвойте разницу между 4 и 6 и прибавьте ее к 6, чтобы получить 10.
Мы обнаружили, что если вы продолжите делить разницу длин пополам и вычитать это, а также удваивать ширину и прибавлять, вы можете найти гораздо больше прямоугольников с одинаковым периметром и площадью:
$4$ на $4$
$3$ на $6 $
$2\frac{1}{2}$ на $10$
$2\frac{1}{4}$ на $18$
$2\frac{1}{8}$ на $34$
..
Вы все молодцы.
Путь к пониманию площади и периметра
Измерение касается методов, которые мы используем для определения размера вещей. Каждый объект имеет различные атрибуты, которые можно измерить, такие как длина, площадь, объем или вес. 1 Длина, площадь и объем относятся к форме и протяженности объекта и могут называться «геометрическими» атрибутами. Вес, с другой стороны, относится к физическому строению тела.
1 Длина, площадь и объем относятся к форме и протяженности объекта и могут называться «геометрическими» атрибутами. Вес, с другой стороны, относится к физическому строению тела.
Измерения площади и периметра широко используются в повседневной жизни и могут быть проиллюстрированы различными практическими ситуациями, такими как измерение размера комнаты, говоря о ее площади, или сколько забора нужно поставить вокруг детской площадки.
Несмотря на то, что примеры площади и периметра присутствуют во многих ситуациях «реальной жизни», изучение этих понятий в рамках учебной программы по математике в начальной школе может быть запутанным или сложным для некоторых учащихся.
Когда обучение, как правило, сосредоточено на процедурном понимании и использовании формул, а не на концептуальных и реляционных знаниях, учащиеся учатся запоминать формулы для «решения» проблем без надлежащего понимания понятий. Некоторые учащиеся также путают понятия площади и периметра, потому что им трудно понять разницу между линейными (одномерными) единицами и квадратными (двумерными) единицами или они не могут связать свой повседневный опыт с площадью и периметром с тем, что они изучают на уроках. класс. 2
класс. 2
Тесная связь между измерением площади и другими математическими понятиями, такими как умножение, площадь поверхности и объем, делает площадь важным компонентом учебной программы по математике K–12, но без четкого понимания того, что означает площадь, учащиеся сталкиваются с трудностями в понимании родственные понятия. 3
Концептуальное понимание имеет решающее значение для понимания математических идей, а не просто отдельных фактов и формул. Благодаря концептуальному пониманию учащиеся также приобретают основы и способность переносить свои знания в новые ситуации, применять их в новых контекстах, устанавливать связи и рассуждать, поддерживая аргументы о незнакомых проблемах. 4 Целью этого раздела является развитие у моих учеников прочного концептуального понимания периметра и особенно площади. Действия, предлагаемые в этом разделе, позволяют учащимся построить свое понимание площади и периметра и оценить, чем они отличаются, с помощью манипуляций и классов.
Во время этого семинара «Площадь, периметр, объем и все такое» у меня была возможность поразмышлять о своей практике преподавания площади и периметра, а также о том, какие заблуждения чаще всего возникают у моих студентов при изучении этой конкретной темы.
Как правило, учащиеся сталкиваются с трудностями при связывании массивов умножения с площадью прямоугольной фигуры. Студенты часто путают понятия площади и периметра при переходе от использования манипулятивных средств к изобразительному представлению. Во многих случаях они предполагают, что прямоугольные фигуры с одинаковым периметром должны иметь одинаковую площадь, и наоборот.
Я также ознакомился с данными тестирования, доступными для группы учеников, которые были в моем 3-м классе в 2017 году, и сравнил их результаты в области геометрии и измерений. По окончании 3-го класса 7 % учащихся показали результаты ниже нормы, а 66 % учащихся — выше нормы. К концу 5 класса в 2019 г., та же группа студентов набрала на 24 % ниже стандарта и только на 27 % выше стандарта. 5 Несмотря на то, что этих конкретных результатов теста, вероятно, недостаточно, чтобы сделать твердый вывод о понимании моими учащимися площади и периметра, существует закономерность в том, как многие учащиеся решают задачи на площадь и периметр. Студенты сталкиваются с трудностями, чтобы связать массивы умножения с площадью прямоугольной фигуры. Студенты с ограниченным пониманием этих двух концепций могут не понять, что могут быть прямоугольники с одинаковой площадью, но разными периметрами, а также прямоугольники с одинаковым периметром, но разными площадями.
5 Несмотря на то, что этих конкретных результатов теста, вероятно, недостаточно, чтобы сделать твердый вывод о понимании моими учащимися площади и периметра, существует закономерность в том, как многие учащиеся решают задачи на площадь и периметр. Студенты сталкиваются с трудностями, чтобы связать массивы умножения с площадью прямоугольной фигуры. Студенты с ограниченным пониманием этих двух концепций могут не понять, что могут быть прямоугольники с одинаковой площадью, но разными периметрами, а также прямоугольники с одинаковым периметром, но разными площадями.
France Machaba в своем исследовании о неправильных представлениях о площади и периметре, опубликованном в 2016 году 6 , сослался на многочисленные исследования в области математического образования, в которых сообщалось, что понятия площади и периметра являются постоянным источником путаница для учащихся. В своем отчете Мачаба предположил, что это, возможно, связано с тем, что и площадь, и периметр включают измерения, или потому, что студентов учат формулам для обоих понятий примерно в одно и то же время, и они путаются из-за отсутствия концептуального понимания. Смешение этих двух понятий приводит к ошибочным представлениям.
Смешение этих двух понятий приводит к ошибочным представлениям.
Я заметил путаницу и непонимание в своем классе, но я не думаю, что площадь и периметр следует учить отдельно. Напротив, я думаю, что одновременное представление обеих концепций является мощной учебной стратегией, но таким образом, чтобы студенты могли понять контрастирующие различия между ними.
Во время нашего нынешнего семинара с доктором Хоу мы научились подходить к различию между площадью и периметром таким образом, чтобы обеспечить полное понимание и более глубокое знание содержания. В результате я планирую развивать свой модуль как последовательность преднамеренных действий, чтобы помочь моим ученикам развить правильное и прочное понимание взаимосвязи между площадью и периметром и использовать соответствующие методы для решения задач, связанных с площадью и периметром.
Я преподаю математику в 3-м классе Международной школы Зарроу в Талсе, Оклахома. Zarrow — это государственная специализированная школа, в которой проводится языковое погружение на испанском языке. В штат школы входят учителя и ассистенты учителей из разных испаноязычных стран, а также преподаватели-носители английского языка. Текущее количество учащихся составляет около 500 учеников от дошкольного до 5-го класса. 7 Школа принимает учащихся на основе электронной случайной лотереи по географическому квадранту для семей, проживающих в границах государственных школ Талсы, чтобы предоставить учащимся из всех районов Талсы равный доступ к программе. Этот процесс также предусматривает предпочтение братьев и сестер, чтобы поощрять участие семьи в школьном сообществе. Однако политика предпочтения братьев и сестер не является гарантией приема в школу, поскольку братья и сестры не участвуют в лотерее с новыми учениками, не являющимися братьями и сестрами. 8 Школа получает дополнительные средства через местный фонд Zarrow Foundation и школьную ассоциацию родителей и учителей (PTA). Вовлеченность родителей – одна из самых высоких в районе.
В штат школы входят учителя и ассистенты учителей из разных испаноязычных стран, а также преподаватели-носители английского языка. Текущее количество учащихся составляет около 500 учеников от дошкольного до 5-го класса. 7 Школа принимает учащихся на основе электронной случайной лотереи по географическому квадранту для семей, проживающих в границах государственных школ Талсы, чтобы предоставить учащимся из всех районов Талсы равный доступ к программе. Этот процесс также предусматривает предпочтение братьев и сестер, чтобы поощрять участие семьи в школьном сообществе. Однако политика предпочтения братьев и сестер не является гарантией приема в школу, поскольку братья и сестры не участвуют в лотерее с новыми учениками, не являющимися братьями и сестрами. 8 Школа получает дополнительные средства через местный фонд Zarrow Foundation и школьную ассоциацию родителей и учителей (PTA). Вовлеченность родителей – одна из самых высоких в районе.
На основании данных профиля школы, опубликованных нашим округом, этнический состав учащихся выглядит следующим образом:
Этническая принадлежность | Процент % |
Белый | 43,8 |
Латиноамериканец | 30,0 |
Многорасовый | 12,9 |
Афроамериканец | 6,3 |
Индеец | 5,4 |
Азиат/С. | 1,4 |
Около 30 % учащихся являются одаренными, 12 % изучают английский язык и 7 % являются учащимися с ограниченными возможностями. 56 % студентов — девушки, 46 % — юноши. 9 В каждом классе есть три класса. В каждом классе есть сертифицированный двуязычный преподаватель испанского и английского языков и ассистент учителя, говорящего на испанском языке. Обучение осуществляется автономно в классах от pre-K до 2 и и разделено по предметным областям в классах с 3-го по 5-й. Я преподаю математику в 3-м классе всем 3-классникам в Зарроу (72 ученика). Я провожу обучение в основном на испанском языке, используя Eureka Math, дополненную компьютерной программой на английском языке (Zearn). В дополнение к учителю математики в команду 3-го класса входят учитель словесности и учитель естественных наук/общественных наук, каждый из которых регулярно сотрудничает в рамках межпредметных блоков. Наша основная цель — предоставить возможности для развития навыков критического мышления учащихся независимо от способностей и стилей обучения. Все эти возможности также способствуют более органичному усвоению второго языка, поскольку учащиеся изучают и используют изучаемый язык (испанский) посредством экспериментов и открытий.
Все эти возможности также способствуют более органичному усвоению второго языка, поскольку учащиеся изучают и используют изучаемый язык (испанский) посредством экспериментов и открытий.
Я намерен преподавать этот модуль, чтобы обогатить академические знания моих учеников во время обучения математике в 3-м классе.
Целью этого модуля является углубление понимания учащимися периметра и площади, а также рассуждений о взаимосвязях и различиях между этими двумя понятиями. С этой целью учащиеся будут исследовать площадь и периметр с помощью манипуляций и конкретных представлений, чтобы развить концептуальное понимание концепций до использования формул.
Во время исследования учащиеся будут изучать фигуры, составленные из комбинаций единичных квадратов, и узнают, что изменение расположения единичных квадратов в этих фигурах без изменения площади может привести к изменению периметра. С помощью последовательности действий учащиеся экспериментально откроют площадь как квадратные единицы на (или внутри) прямоугольной фигуры, а не как единицы длины вокруг (периметр). Наконец, в ходе дополнительного задания учащимся будет предложено создать более одного устройства для данной области, чтобы найти максимально возможный периметр. Во время модуля учащиеся смогут исследовать, что происходит с периметром и площадью прямоугольной фигуры, когда фигура каким-либо образом изменяется путем удаления единичных квадратов. В частности, они обнаружат, что, хотя удаление квадратов уменьшает площадь, периметр может остаться прежним или даже увеличиться! Студенты смогут рисовать прямоугольники и другие прямолинейные фигуры и определять их площадь и периметр. Учащиеся смогут эффективно общаться с помощью рисунков и чисел, работать совместно в небольших группах и успешно применять свои знания о площади и периметре в реальной жизненной ситуации.
Наконец, в ходе дополнительного задания учащимся будет предложено создать более одного устройства для данной области, чтобы найти максимально возможный периметр. Во время модуля учащиеся смогут исследовать, что происходит с периметром и площадью прямоугольной фигуры, когда фигура каким-либо образом изменяется путем удаления единичных квадратов. В частности, они обнаружат, что, хотя удаление квадратов уменьшает площадь, периметр может остаться прежним или даже увеличиться! Студенты смогут рисовать прямоугольники и другие прямолинейные фигуры и определять их площадь и периметр. Учащиеся смогут эффективно общаться с помощью рисунков и чисел, работать совместно в небольших группах и успешно применять свои знания о площади и периметре в реальной жизненной ситуации.
Двуязычный словарь
Овладение академическим языком на испанском языке всегда является жизненно важной целью обучения, встроенной в преподавание конкретной предметной области в нашей школе погружения. По этой причине я хотел бы начать этот раздел с краткого двуязычного глоссария наиболее важных терминов, которые учащиеся должны знать, чтобы выражать свои идеи на испанском языке во время разработки этого модуля.
В моей преподавательской практике, когда я ввожу новую тему и появляются новые словарные слова, которые могут быть незнакомы моим ученикам (по крайней мере, в испанском языке), я представляю новое слово и объясняю определение. Часто учащиеся используют свои фоновые знания или взаимосвязь между английским словом и испанскими родственными словами, чтобы определить значение нового слова. В группе мы устанавливаем определение слова, подходящую иллюстрацию или пример, если это необходимо, и я создаю якорные диаграммы, которые остаются в классе, чтобы учащиеся могли обращаться к ним по мере необходимости. В то же время учащиеся записывают слово, определение и пример или иллюстрацию в свои математические журналы для будущих ссылок.
Английские термины | Испанские термины |
Район | Район |
Квадратная плитка | Бальдоса Куадрада |
Колонка | Колонны |
Площадь | Куадрадо |
Сетка | Куадрикула |
Уравнение | Эквасьон |
Ряд | Филас |
Боковой | Ладос |
Боковой | Боковой |
Длина | Долготы |
Массив | Матриз |
Модель | Модель |
Миллиметровая бумага/сетчатая бумага | Папель куадрикуладо |
Периметр | Периметро |
Аддитивное свойство | Propiedad aditiva |
Прямоугольник | Прямоугольный |
Квадратные единицы | Квадратный номер |
Линейные единицы | Линейные линии |
Важные определения: площадь и периметр
Несмотря на то, что существует множество доступных определений площади и периметра, я включил определения здесь, чтобы сохранить организацию и последовательность этого раздела.
Площадь двумерной фигуры определяется как количество пространства внутри границ фигуры. Это физическая величина, которая указывает количество квадратных единиц, занимаемых двумерным объектом.
Площадь двумерной поверхности измеряется путем нахождения общего количества единиц площади одинакового размера, необходимых для покрытия формы без зазоров или перекрытий. Когда эта фигура представляет собой прямоугольник с целым числом длин сторон, его легко разделить на квадраты равной площади.
Рис. 1. В показанном примере площадь квадрата составляет 12 квадратных единиц, поскольку для покрытия поверхности, заключенной в квадрат, необходимо 12 квадратных единиц.
Периметр определяется как мера длины границы, окружающей замкнутую геометрическую фигуру. Термин «периметр» происходит от греческих слов «пери» и «метр», которые означают «вокруг» и «мера». В геометрии он относится к непрерывной линии, образующей путь за пределами двумерной формы.
Как упоминалось ранее, основной целью этого модуля является выполнение заданий, позволяющих учащимся понять разницу между площадью и периметром. В результате учителя должны помнить о фундаментальных различиях между площадью и периметром, как указано ниже.
В результате учителя должны помнить о фундаментальных различиях между площадью и периметром, как указано ниже.
Площадь относится к измерению поверхности объекта, а периметр относится к контуру, окружающему замкнутую фигуру. Площадь представляет собой пространство, занимаемое объектом, а периметр представляет собой границу формы.
Измерение площади представляет собой два измерения и выражается в квадратных единицах, таких как квадратные километры, квадратные футы или квадратные дюймы. Периметр фигуры представляет одно измерение и измеряется в линейных единицах, таких как километры, дюймы или футы. 10
Последовательность учебной программы Eureka Math от умножения до площади. Где путаница?
Хонг и Ранналлс в 2019 году проанализировали три разные серии учебников, ориентированных на Common Core, и обнаружили, что эти популярные учебники имеют концептуальные ограничения при введении понятий площади и периметра в начальных классах, а также недостаточно возможностей для изучения этих понятий учащимися. Хотя учебники являются лишь одним из компонентов учебного процесса, во многих школьных округах для обучения требуется специальная учебная программа. В результате учителя должны понимать ограничения в учебной программе, чтобы заполнить пробелы, выполняя задания, которые способствуют рассуждениям и концептуальному пониманию. Авторы предлагают модифицировать существующие задания в учебниках/рабочих тетрадях как способ удовлетворения этой потребности. Изменяя задания, учителя могут работать в рамках учебных материалов, в то же время предоставляя учащимся возможности для развития концептуального понимания. 11
Хотя учебники являются лишь одним из компонентов учебного процесса, во многих школьных округах для обучения требуется специальная учебная программа. В результате учителя должны понимать ограничения в учебной программе, чтобы заполнить пробелы, выполняя задания, которые способствуют рассуждениям и концептуальному пониманию. Авторы предлагают модифицировать существующие задания в учебниках/рабочих тетрадях как способ удовлетворения этой потребности. Изменяя задания, учителя могут работать в рамках учебных материалов, в то же время предоставляя учащимся возможности для развития концептуального понимания. 11
Поскольку Eureka Math является «учебной программой, принятой округом» по математике, мои инструкции будут следовать последовательности и объему, предложенным в Eureka, но я изменю способ подачи материала, добавив новые знания и стратегии, чтобы устранить неправильные представления учащихся о различиях. между площадью и периметром. Я включу этот модуль в начало модуля 4 (Умножение и площадь).
В 3-м классе учащиеся начинают год с изучения фактов об умножении и свойств умножения (Эврика, модули 1 и 3). Затем они переходят от создания равных групп (равное количество объектов в каждой группе) к прямоугольным массивам и, наконец, к площадным моделям. Модуль 2 посвящен измерению времени, веса и емкости, и учащиеся знакомятся с метрическими и обычными системами измерения.
Рисунок №2. Эта последовательность показывает переход от прямоугольного массива к модели площади в классе 3 rd .
Равные группы элементов, а позже и сетка, представляющая эти элементы в строках и столбцах, представлены в модулях 1 и 3 для объяснения умножения и его свойств. В модуле 4, когда представлена концепция площади, элементы внутри сетки удаляются, и учащиеся будут считать отдельные квадраты, чтобы определить площадь прямоугольника. К концу модуля система сетки будет устранена, и учащиеся будут определять площадь прямоугольника путем умножения сторон.
Модули 1 и 3 курса Eureka Math предназначены для того, чтобы заложить основы понимания прямоугольных массивов для подготовки учащихся к изучению Модуля 4. В модулях 1 и 3 учащиеся переходят от группировки элементов к добавлению групп (повторное добавление), которые они использовали в 2 -й класс для организации элементов в строки и столбцы или массивы. В этих двух модулях они также изучают коммутативное свойство умножения, манипулируя массивами. Например, массив примера на рис. 2 может быть представлен в виде трех строк по 4 элемента в каждом, что в сумме дает 12 элементов, или в виде четырех рядов по 3 элемента в каждом с одинаковой суммой.
В модулях 1 и 3 учащиеся переходят от группировки элементов к добавлению групп (повторное добавление), которые они использовали в 2 -й класс для организации элементов в строки и столбцы или массивы. В этих двух модулях они также изучают коммутативное свойство умножения, манипулируя массивами. Например, массив примера на рис. 2 может быть представлен в виде трех строк по 4 элемента в каждом, что в сумме дает 12 элементов, или в виде четырех рядов по 3 элемента в каждом с одинаковой суммой.
В модуле 4 Eureka вводится понятие площади, но обсуждение ограничивается прямоугольными фигурами, и учащиеся начинают использовать сетки без элементов внутри. Хотя сетка с элементами внутри и пустая сетка являются графическими представлениями, пустая сетка, безусловно, требует более абстрактного понимания. Как правило, учащиеся не сталкиваются с какими-либо значительными трудностями при подсчете квадратов и определении того, что общее количество квадратов равно площади или поверхности внутри прямоугольника, как только понятие площади определено. Непонимание чаще возникает, когда мы убираем сетку и учащимся нужно найти площадь прямоугольных фигур, заданных единицами длины одной или двух сторон, как в последнем прямоугольнике на рисунке № 2. Ожидается, что на этом этапе модуля учащиеся смогут установить связь между подсчетом квадратов и умножением сторон для определения площади, а также с массивами умножения, которые они уже изучили, и смогут различать понятие периметра (поверхностно рассматривается в модуле) с использованием тех же длин сторон, которые они используют для вычисления площади.
Непонимание чаще возникает, когда мы убираем сетку и учащимся нужно найти площадь прямоугольных фигур, заданных единицами длины одной или двух сторон, как в последнем прямоугольнике на рисунке № 2. Ожидается, что на этом этапе модуля учащиеся смогут установить связь между подсчетом квадратов и умножением сторон для определения площади, а также с массивами умножения, которые они уже изучили, и смогут различать понятие периметра (поверхностно рассматривается в модуле) с использованием тех же длин сторон, которые они используют для вычисления площади.
В дополнение ко всему вышесказанному, по мере продолжения модуля 4 учащиеся должны составить или разложить объединенные прямоугольники, чтобы определить общую площадь, чтобы сделать вывод, что площадь является аддитивным свойством. Хотя Eureka Math включает в себя рабочие тетради для студентов с большим количеством практических задач, большинство задач не предназначены для того, чтобы студенты могли понять разницу между площадью и периметром или линейными и квадратными единицами, поскольку основное внимание уделяется большему количеству задач. повторение и отработка одного и того же навыка. Я думаю, что учащимся необходимо знакомиться с задачами, которые дают им больше возможностей исследовать площадь и периметр в одной и той же задаче, чтобы рассуждать о различиях между двумя концепциями. На мой взгляд, это должно произойти до того, как студентов попросят найти площадь прямоугольников или комбинированных прямоугольников без сетки. Не потому, что прямоугольники сложны, они прямолинейны, а именно из-за развития содержания, то, как оно представлено в учебной программе, создает путаницу и недопонимание.
повторение и отработка одного и того же навыка. Я думаю, что учащимся необходимо знакомиться с задачами, которые дают им больше возможностей исследовать площадь и периметр в одной и той же задаче, чтобы рассуждать о различиях между двумя концепциями. На мой взгляд, это должно произойти до того, как студентов попросят найти площадь прямоугольников или комбинированных прямоугольников без сетки. Не потому, что прямоугольники сложны, они прямолинейны, а именно из-за развития содержания, то, как оно представлено в учебной программе, создает путаницу и недопонимание.
Аухред и Митчелмор в 2000 году опубликовали исследование, состоящее в наблюдении и анализе 150 учеников с 1 по 4 классы, когда они решали задачи на основе массивов, чтобы определить различные стратегии, применяемые учащимися, и успех этих стратегий. 12 Обоснованием для этого исследования послужило соображение о том, что непонимание учащихся и плохая успеваемость при решении задач на площади связаны с тенденцией слишком рано вводить формулу площади в начальной школе. Авторы считают, что при запоминании учащимися формул без понимания понятий у них возникают трудности с обобщающими приемами. Они заметили, что, хотя учащиеся могли вычислить площадь прямоугольника, зная оба измерения, они не могли передать это понимание при нахождении площади квадрата, зная только длину одной стороны. Авторы также обнаружили, что учащиеся часто испытывают затруднения при переходе от физического покрытия прямоугольника единичными квадратами, действия, которое предполагает аддитивный процесс, к использованию формулы прямоугольника, которая является мультипликативной. Другие распространенные недоразумения включают путаницу с площадью и периметром, применение формулы для нахождения площади прямоугольника к плоским фигурам, отличным от прямоугольников, и использование линейных единиц вместо квадратных для измерения площади. Исследование рекомендует, чтобы учителя давали учащимся достаточно времени для понимания понятий площади и периметра без заучивания формул.
Авторы считают, что при запоминании учащимися формул без понимания понятий у них возникают трудности с обобщающими приемами. Они заметили, что, хотя учащиеся могли вычислить площадь прямоугольника, зная оба измерения, они не могли передать это понимание при нахождении площади квадрата, зная только длину одной стороны. Авторы также обнаружили, что учащиеся часто испытывают затруднения при переходе от физического покрытия прямоугольника единичными квадратами, действия, которое предполагает аддитивный процесс, к использованию формулы прямоугольника, которая является мультипликативной. Другие распространенные недоразумения включают путаницу с площадью и периметром, применение формулы для нахождения площади прямоугольника к плоским фигурам, отличным от прямоугольников, и использование линейных единиц вместо квадратных для измерения площади. Исследование рекомендует, чтобы учителя давали учащимся достаточно времени для понимания понятий площади и периметра без заучивания формул.
Я согласен с тем, что учащиеся начальных классов нуждаются в конкретных манипуляциях, чтобы понять математические понятия, прежде чем вводить формулы. Успех детей в понимании области и периметра связан с ресурсами, которые они используют при решении задач. Им нужны предметы (плитки, кирпичи, сложенная или разрезанная бумага), которые они могут подогнать, сложить, сопоставить и сосчитать, чтобы они могли работать над развитием концептуального понимания площади и периметра и их различий. Это мои рабочие предположения при создании этого модуля.
Успех детей в понимании области и периметра связан с ресурсами, которые они используют при решении задач. Им нужны предметы (плитки, кирпичи, сложенная или разрезанная бумага), которые они могут подогнать, сложить, сопоставить и сосчитать, чтобы они могли работать над развитием концептуального понимания площади и периметра и их различий. Это мои рабочие предположения при создании этого модуля.
Сенсорные пути
Последний проект, который учащиеся завершат в этом блоке, включает в себя разработку сенсорной дорожки, потому что наш школьный родительский комитет выделил средства на создание сенсорной тропы для наших учеников в Зарроу.
Сенсорные пути — это «пути активности или движения», которые помогают детям создавать нейронные пути или связи в мозгу, отвечающие за чувства. Высокоэнергетический характер упражнений, включенных в последовательность действий сенсорных путей, помогает детям выполнять сложные, многоэтапные задания.
Типичная сенсорная дорожка состоит из дорожки, на которой дети должны выполнять упражнения, специально предназначенные для развития моторики. Занятия требуют, чтобы дети прыгали, шагали и прыгали, чтобы заставить кровь качать кровь, что помогает детям сидеть неподвижно и сосредоточиться на более длительные периоды времени в классе. Сенсорные дорожки — это отличный «мозговой перерыв» в течение учебного дня или во время перемен в помещении. 13
Занятия требуют, чтобы дети прыгали, шагали и прыгали, чтобы заставить кровь качать кровь, что помогает детям сидеть неподвижно и сосредоточиться на более длительные периоды времени в классе. Сенсорные дорожки — это отличный «мозговой перерыв» в течение учебного дня или во время перемен в помещении. 13
Обычно эти сенсорные дорожки делаются из наклеек, которые можно приклеить к любой поверхности. В конце этого блока 3 9Ученики 1150 rd применят свои знания о площади и периметре, чтобы выбрать один из школьных коридоров, который может быть лучшим вариантом для построения нашего сенсорного пути. Чтобы выполнить это задание, учащиеся должны будут рассмотреть доступную площадь (окружающий прямоугольник) коридоров и расположение, обеспечивающее, возможно, самый большой периметр для безопасных занятий в помещении.
Принимая во внимание, что мои 3-классники должны иметь опыт, в котором они могут манипулировать пространством, которое они измеряют, чтобы построить глубокое понимание, мероприятия и стратегии обучения, предлагаемые в этом разделе, будут включать использование манипулятивных действий и «реального» опыта.
В центре внимания данного модуля — устранение неправильного понимания того, что прямоугольные фигуры с одинаковым периметром должны иметь одинаковую площадь и наоборот. Нередко учащиеся младших классов думают, что при уменьшении или увеличении площади фигуры периметр также будет уменьшаться или увеличиваться. Студенты не понимают, что может быть много прямоугольников с одинаковой площадью, но разными периметрами. Наоборот, если периметр в наборе прямоугольников одинаков, площадь этих прямоугольников не обязательно должна быть одинаковой. Например, прямоугольники со сторонами 2 на 4 и 1 на 8 имеют площадь 8 квадратных единиц, но их периметры равны 12 единицам и 18 единицам соответственно. Точно так же прямоугольники с одинаковым периметром могут иметь разную площадь. Например, прямоугольники 3 × 4 и 2 × 5 со сторонами 3 на 4 и 2 на 5 имеют периметр 14 единиц, но их площади равны 12 квадратных единиц и 10 квадратных единиц соответственно.
Выполняя задания в этом разделе, учащиеся смогут обобщать взаимосвязь между площадью и периметром. Например, для прямоугольника с целым числом длин сторон размеры являются факторами площади. Когда разница между размерами прямоугольника с заданной площадью наименьшая, у вас будет наименьший периметр. Когда разница между размерами прямоугольника с заданной площадью будет наибольшей, у вас будет самый большой периметр. При фиксированном периметре прямоугольник с наибольшей площадью будет иметь самые близкие друг к другу размеры (квадрат). При фиксированном периметре с целым числом длин сторон прямоугольник с наименьшей площадью будет иметь размеры, наиболее удаленные друг от друга. 14 Одна из длин сторон будет равна 1. Во время занятий в этом разделе, хотя учащиеся будут выкладывать прямоугольники различных размеров, чтобы определить площадь и периметр, и делать обобщения о взаимосвязях между площадью и периметром, основное внимание будет уделяться экспериментированию. с непрямоугольными фигурами, чтобы лучше понять различия между двумя понятиями.
Например, для прямоугольника с целым числом длин сторон размеры являются факторами площади. Когда разница между размерами прямоугольника с заданной площадью наименьшая, у вас будет наименьший периметр. Когда разница между размерами прямоугольника с заданной площадью будет наибольшей, у вас будет самый большой периметр. При фиксированном периметре прямоугольник с наибольшей площадью будет иметь самые близкие друг к другу размеры (квадрат). При фиксированном периметре с целым числом длин сторон прямоугольник с наименьшей площадью будет иметь размеры, наиболее удаленные друг от друга. 14 Одна из длин сторон будет равна 1. Во время занятий в этом разделе, хотя учащиеся будут выкладывать прямоугольники различных размеров, чтобы определить площадь и периметр, и делать обобщения о взаимосвязях между площадью и периметром, основное внимание будет уделяться экспериментированию. с непрямоугольными фигурами, чтобы лучше понять различия между двумя понятиями.
Начав с определенного прямоугольника, учащиеся изучат различные возможные формы, полученные путем исключения одного единичного квадрата за раз. Этот тип исследования будет генерировать множество вариантов для анализа и обобщения учащихся. Во всех случаях учащиеся сохранят свои новые расположения в пределах области исходного прямоугольника, также известного как «окружающий прямоугольник», следя за тем, чтобы учащиеся не удаляли всю строку или столбец исходного прямоугольного массива. Последовательность действий завершится опытом «реального мира», в котором учащиеся должны будут использовать школьные коридоры как «окружающие прямоугольники», чтобы упорядочить возможные варианты дизайна сенсорных путей.
Этот тип исследования будет генерировать множество вариантов для анализа и обобщения учащихся. Во всех случаях учащиеся сохранят свои новые расположения в пределах области исходного прямоугольника, также известного как «окружающий прямоугольник», следя за тем, чтобы учащиеся не удаляли всю строку или столбец исходного прямоугольного массива. Последовательность действий завершится опытом «реального мира», в котором учащиеся должны будут использовать школьные коридоры как «окружающие прямоугольники», чтобы упорядочить возможные варианты дизайна сенсорных путей.
Упражнения, включенные в этот раздел, потребуют использования плиток в качестве манипуляций, а также рисования на миллиметровой бумаге и записи результатов в диаграммы.
На рисунке ниже представлены некоторые примеры возможных расположений, которые учащиеся могут найти при манипулировании прямоугольниками путем исключения последующих единичных квадратов. На рисунке показаны не все возможные варианты.
Рисунок №3: Пример исключения единичного квадрата для различения площади и периметра. Здесь представлены не все возможные аранжировки. Поскольку количество возможных аранжировок будет довольно большим, я рекомендую ограничить эту деятельность небольшими прямоугольными массивами.
Здесь представлены не все возможные аранжировки. Поскольку количество возможных аранжировок будет довольно большим, я рекомендую ограничить эту деятельность небольшими прямоугольными массивами.
Образец таблицы, показанный ниже, может быть использован учащимися для записи своих результатов, поскольку они удаляют по одному квадрату за раз в пределах размеров исходного прямоугольника. Для каждого исключения потребуется диаграмма.
Рисунок № 4: Образец диаграммы для записи площади и периметра получившихся договоренностей во время деятельности по ликвидации отряда.
В этом разделе я хотел бы включить различные стратегии обучения, чтобы удовлетворить потребности и различные стили обучения моих учеников.
Несмотря на то, что Eureka Math на испанском языке будет являться основным ресурсом, определяющим объем и последовательность обучения математике, предлагаемые в этом разделе задания призваны помочь лучшему пониманию различий между площадью и периметром.
Упражнения будут преподаваться в виде последовательности мини-уроков с конкретными целями.
Основные стратегии обучения, которые я планирую реализовать, следующие:
Практическое обучение: учащиеся будут использовать конкретные модели или манипуляции (плитки с квадратами). Использование манипулятивных средств во время обучения математике помогает учащимся в процессе построения своих когнитивных моделей для представления абстрактных математических понятий. С помощью манипулятивных средств студенты общаются друг с другом и с учителями. Участвуя в занятиях с манипуляторами, учащиеся могут выражать свое мышление, приобретая уверенность в своих математических способностях. 15
Все занятия, включенные в этот модуль, будут включать практический компонент. От первого задания, в котором учащиеся должны использовать плитки для определения площади прямоугольников, до финального проекта, в котором им необходимо определить расположение с наилучшей «проходной периметром», чтобы спроектировать сенсорную дорожку, используя участки школьных коридоров как «окружающие прямоугольники».
Совместное обучение: во время выполнения заданий, предложенных в этом разделе, учащиеся будут иметь возможность работать с партнерами и в совместных группах. Они будут сотрудничать, чтобы найти решения, делиться своими методами и идеями, а также продвигать дискуссии и анализ. В ходе этого процесса я позабочусь о том, чтобы предоставить учащимся четкие инструкции и поддержку, чтобы они могли успешно перейти от работы с партнером к совместной работе в малых группах, обсуждениям и презентациям всего класса. Эта стратегия помогает учащимся поддерживать друг друга как учащихся, потому что позволяет продуктивно бороться. В результате учащиеся учатся на своих ошибках через объяснения своих сверстников и учителя. Когда учащиеся контролируют свое обучение, у них есть время опробовать идеи, послушать друг друга и завоевать доверие своих сверстников и всего класса. 16 Все мероприятия, предлагаемые в этом разделе, предназначены для работы учащихся в парах или небольших группах для развития сотрудничества и взаимного обучения.
Чтение-Рисование-Запись: Эта стратегия широко используется при решении задач в Eureka Math. Идея плана состоит в том, чтобы подойти к математическим задачам, нарисовав графическое представление данной информации, чтобы прояснить понимание учащимися проблемы. Эта стратегия подходит не только для «словных задач», но также полезна для приближения к вопросам области и периметра. Эта стратегия состоит из трех конкретных шагов:
- ПРОЧИТАТЬ: Учащиеся читают задачу или вопрос. Всегда полезно прочитать вопрос как минимум два раза и предоставить учащимся возможность объяснить свое понимание заданного вопроса.
- РИСОВАНИЕ: Учащиеся нарисуют картинку, соответствующую полученной информации. На этом этапе учащиеся должны проанализировать, что они могут извлечь из данных, представленных в задаче, и какую модель лучше всего использовать. Чтобы учащиеся могли выполнить этот шаг, они должны быть знакомы с различными графическими изображениями.
 Ожидается, что они познакомились с различными графическими моделями в математике, такими как стержневые модели, массивы, равные группы, группы одинакового размера, разбиения, мозаичные поверхности и т. д.
Ожидается, что они познакомились с различными графическими моделями в математике, такими как стержневые модели, массивы, равные группы, группы одинакового размера, разбиения, мозаичные поверхности и т. д. - НАПИСАТЬ: Учащиеся смогут делать выводы на основе рисунков в виде числового предложения, уравнения или утверждения.
При использовании подхода RDW учащиеся могут нарисовать модель того, что они читают, и рисунок поможет лучше понять проблему. Рисование модели помогает учащимся увидеть, какая операция или операции необходимы, какие закономерности могут возникнуть и какие модели работают, а какие нет. При использовании RDW студенты должны применять на практике несколько Стандартов математической практики, а в некоторых случаях и все. Некоторые из них включают в себя: разобраться в проблемах и настойчиво решать их, моделировать с помощью математики, стратегически использовать соответствующие инструменты, а также искать и использовать структуру. 17 Большинство заданий этого раздела требуют иллюстраций, чтобы учащиеся могли выразить свое мышление.
17 Большинство заданий этого раздела требуют иллюстраций, чтобы учащиеся могли выразить свое мышление.
Обучение на основе проектов: кульминационным моментом модуля является прикладной проект «реальной жизни», в котором учащиеся смогут интегрировать свое понимание из предыдущих занятий модуля. В этом проекте учащиеся смогут интегрировать практическое и совместное обучение через завершение проекта.
Обучение на основе проектов — это педагогический метод, основанный на идее Джона Дьюи об «обучении на практике». В этой образовательной стратегии учитель ставит цель и выступает в качестве посредника, обеспечивая поддержку и руководство, когда это необходимо. Студенты, работая в группах, создают продукт, чтобы представить полученные знания по определенной теме. Конечный продукт может включать в себя различные средства массовой информации, такие как письма, искусство, рисунки, трехмерные изображения, видео, фотографии или технологические презентации. В основе PBL лежит аутентичность или применение в реальной жизни, и он считается альтернативой бумажному запоминанию наизусть в классах под руководством учителя. Некоторые из преимуществ реализации стратегий обучения на основе проектов в классе включают в себя более глубокое понимание концепций, более широкую базу знаний, улучшенные коммуникативные и межличностные / социальные навыки, улучшенные лидерские качества, повышение креативности и улучшение навыков письма. 18
Некоторые из преимуществ реализации стратегий обучения на основе проектов в классе включают в себя более глубокое понимание концепций, более широкую базу знаний, улучшенные коммуникативные и межличностные / социальные навыки, улучшенные лидерские качества, повышение креативности и улучшение навыков письма. 18
Ниже предлагаются задания, которые помогут учащимся лучше понять разницу между площадью и периметром в 3-м классе и .
Важные соображения:
Прежде чем учащиеся приступят к выполнению заданий, важно определить, что такое «единица». В этом случае одна квадратная единица будет определена как одна квадратная плитка с длиной стороны 1 дюйм.
При укладке мозаики учитель будет направлять учащихся в процессе использования длины стороны плитки вокруг линейных фигур для определения периметра.
Позже, после того, как учащиеся освоят различия между площадью и периметром, было бы неплохо изучить аналогичные действия, включающие плитки разных размеров, чтобы сравнить единичные квадраты, состоящие из одного квадрата 2 и 1 см 2 .
Работа с единицами измерения разных размеров поможет учащимся лучше понять, что размер единицы, которую мы используем для измерения чего-либо, влияет на измерение. Другими словами, если мы измеряем одну и ту же величину разными единицами измерения, для выражения измерения потребуется больше меньшей единицы и меньше большей единицы.
Я начну тему с рассмотрения массивов умножения и того, как они связаны с площадью прямоугольных фигур. Важно обратиться к предыдущим блокам (модули 1 и 3 в Eureka Math), чтобы учащиеся могли применить свои базовые знания для изучения понятий площади и периметра.
Деятельность 1:
В качестве предварительного задания учащиеся должны установить связи между массивами умножения и площадью прямоугольных фигур. Студенты будут работать в партнерстве для этой деятельности.
Материалы:
- Набор карточек с прямоугольными матрицами, которые я приготовлю заранее и заламинирую.
- Карандаш или маркер
- Сетчатая бумага
Проезд:
Один учащийся будет держать карточку с прямоугольным массивом; другому учащемуся нужно написать факт умножения, соответствующий массиву, изображенному на карточке, нарисовать прямоугольник на миллиметровой бумаге, определить длину сторон, написать уравнение умножения и решение умножения внутри прямоугольника. Каждый партнер по очереди продолжает игру. По мере выполнения задания я буду задавать учащимся вопросы о связи между массивами умножения и прямоугольной областью.
Каждый партнер по очереди продолжает игру. По мере выполнения задания я буду задавать учащимся вопросы о связи между массивами умножения и прямоугольной областью.
Вариации этого задания могут включать в себя то, что один партнер показывает карточку с фактом умножения, а другой партнер рисует прямоугольный массив на сетке и решение внутри прямоугольника. Оба партнера могут продолжать до тех пор, пока у них не закончатся карты или они не заполнят сетку прямоугольниками. Чтобы сделать это упражнение как можно более динамичным, я выберу факты умножения, которые генерируют массивы разумных размеров, чтобы учащиеся могли рисовать их, не тратя слишком много времени. Важно иметь в виду, что цель этого занятия состоит в том, чтобы учащиеся установили связь между умножением и площадью, а не в том, чтобы учащиеся занимались рисованием больших массивов умножения.
После того, как все прямоугольники будут представлены, учащиеся должны определить периметр каждого прямоугольника, подсчитав единицы вокруг краев. Я буду вести беседу в классе с наводящими вопросами о взаимосвязи между площадью и периметром прямоугольных фигур.
Я буду вести беседу в классе с наводящими вопросами о взаимосвязи между площадью и периметром прямоугольных фигур.
Во время беседы в классе я буду подчеркивать разницу между квадратными и линейными единицами.
Рисунок №5: Пример действия №1.
Деятельность 2:
Это второе задание можно представить как продолжение предыдущего задания, чтобы подчеркнуть концепции, или как альтернативу первому. Если учащиеся находятся в классе с «Математическими центрами», у них может быть выбор заполнить один или другой. Цель работы — научить учащихся вычислять площадь и периметр прямоугольных фигур.
Материалы:
Каждой паре учащихся потребуется следующее:
- Пустая бумага с сеткой. Каждый квадрат на сетке будет представлять 1 единичный квадрат.
- Две игральные кости
- Маркеры или цветные карандаши
Проезд:
Учащиеся делят лист бумаги пополам и решают, какую половину будет использовать каждый из партнеров.
Каждый партнер бросает кубик, и тот, кто выкинет наибольшее число, начнет игру. Оба ученика будут использовать один и тот же лист сетки для своих рисунков, но каждый партнер начнет рисовать в противоположных углах листа.
Первый игрок бросает кости и рисует прямоугольник с длинами сторон, равными числам, выпавшим на костях. Например, если числа были 2 и 4, учащийся нарисует прямоугольник размером две единицы на четыре единицы. Затем учащийся напишет соответствующее уравнение умножения и запишет значение площади. Второй партнер повторит процедуру, создав прямоугольник на своей половине сетки.
Партнеры продолжают по очереди формировать прямоугольники. Прямоугольники должны касаться друг друга любой «свободной» стороной. Игра продолжается до тех пор, пока один из партнеров не сможет начертить прямоугольник с оставшимся пространством в пределах половины листа бумаги. Каждый партнер суммирует общую площадь своих прямоугольников. Ученик с наибольшей площадью становится победителем.
Это задание можно разнообразить, раздав каждому учащемуся кубики с номерами соответствующих уровней. На уровне класса учащиеся могут работать со стандартными кубиками от 1 до 6. Студенты, готовые к вызову, могут использовать многогранные кости. Студенты также могли вычислить площадь «свободного пространства» с каждой стороны. В дополнение к нахождению площади, которая является основной целью занятия, учащиеся определят общий периметр вокруг составных фигур на каждой стороне листа и будут сравнивать их площади и периметры. В качестве введения к следующему заданию весь класс сравнивает свои результаты, отмечая случаи, когда «сторона» с наибольшей площадью имеет и наибольший периметр или когда, наоборот, «сторона» с меньшей площадью имеет наибольший периметр. Эти результаты откроют дискуссию о взаимосвязи между площадью и периметром. Должны ли прямолинейные фигуры с одинаковой площадью иметь одинаковый периметр? Увеличивается ли периметр с площадью и наоборот? Я буду использовать результаты этого задания, чтобы помочь учащимся в процессе размышлений о возможных отношениях между площадью и периметром. Основываясь на заинтересованности учащихся, я даже предложу им найти периметр отдельных прямоугольников на каждой стороне листа, чтобы идентифицировать прямоугольники с одинаковой площадью, но с разными периметрами, и прямоугольники с одинаковым периметром, но разной площадью. Это упражнение заставит вас осознать разницу между площадью и периметром и поможет перейти к следующему упражнению.
Основываясь на заинтересованности учащихся, я даже предложу им найти периметр отдельных прямоугольников на каждой стороне листа, чтобы идентифицировать прямоугольники с одинаковой площадью, но с разными периметрами, и прямоугольники с одинаковым периметром, но разной площадью. Это упражнение заставит вас осознать разницу между площадью и периметром и поможет перейти к следующему упражнению.
Рисунок №6: На этом рисунке показан пример выполнения действия 2.
Деятельность 3:
Это упражнение, хотя и очень простое, служит для иллюстрации различных площадей прямоугольников с одинаковым периметром. Его можно добавить в качестве альтернативы для задания 2 или после него, чтобы акцентировать внимание на разработке концепции и понимании различий между площадью и периметром.
Материалы:
Каждой паре учащихся потребуется следующее:
- Пустая бумага с сеткой. Каждый квадрат на сетке будет представлять 1 единичный квадрат.
- Карандаши или маркеры
Проезд:
Учащиеся работают в парах. Каждой паре будет присвоено значение периметра, и задача будет заключаться в том, чтобы найти все возможные прямоугольники с целыми числами сторон для заданного периметра и найти площадь каждого из них.
Каждой паре будет присвоено значение периметра, и задача будет заключаться в том, чтобы найти все возможные прямоугольники с целыми числами сторон для заданного периметра и найти площадь каждого из них.
Учащиеся обсудят результаты, чтобы сделать вывод, что для заданного периметра площадь наименьшая, когда прямоугольник длинный и тонкий, и наибольшая, когда длина прямоугольника приближается к
возможно быть квадратом. Длинные тонкие прямоугольники могут иметь меньшую площадь, чем почти квадратные прямоугольники с таким же периметром.
Рисунок №7: На этом рисунке показан пример действия 3. Мы можем заметить, что самый длинный и самый тонкий прямоугольник со сторонами 1 на 8 единиц имеет наименьшую площадь. С другой стороны, прямоугольник со сторонами 4 на 5 единиц имеет наибольшую площадь в этой серии прямоугольников с таким же периметром.
Деятельность 4:
В этом упражнении учащиеся закрепят свое понимание различий между площадью и периметром. Исследовательский характер деятельности позволяет учащимся иметь дело с обоими понятиями одновременно, а не по отдельности. На мой взгляд, учащимся следует разрешить сравнивать площадь и периметр «бок о бок», чтобы получить лучшее концептуальное понимание. В целом, учебный материал, доступный в математике 3 -го класса , обширен по количеству упражнений, представленных учащимся для решения задач на площадь или периметр по отдельности, но они предлагают очень ограниченное количество примеров для учащихся, чтобы сравнить обе концепции в в то же время, и эти примеры часто ограничиваются прямоугольниками. В этом упражнении мы отойдем от простых прямоугольников, и учащиеся узнают, что происходит, когда они удаляют единичные квадраты по одному. Какие возможны договоренности, а также что происходит с площадью и периметром.
Исследовательский характер деятельности позволяет учащимся иметь дело с обоими понятиями одновременно, а не по отдельности. На мой взгляд, учащимся следует разрешить сравнивать площадь и периметр «бок о бок», чтобы получить лучшее концептуальное понимание. В целом, учебный материал, доступный в математике 3 -го класса , обширен по количеству упражнений, представленных учащимся для решения задач на площадь или периметр по отдельности, но они предлагают очень ограниченное количество примеров для учащихся, чтобы сравнить обе концепции в в то же время, и эти примеры часто ограничиваются прямоугольниками. В этом упражнении мы отойдем от простых прямоугольников, и учащиеся узнают, что происходит, когда они удаляют единичные квадраты по одному. Какие возможны договоренности, а также что происходит с площадью и периметром.
Для выполнения этого задания учащиеся должны работать в группах по три человека.
Материалы:
- Один лист ламинированной сетчатой бумаги (1 квадрат = 1 дюйм 2 )
- Пенопластовые или пластиковые плитки (1 в 2 ).
 Плитки должны быть того же размера, что и единичный квадрат на ламинированной сетчатой бумаге .
Плитки должны быть того же размера, что и единичный квадрат на ламинированной сетчатой бумаге . - Сетчатая бумага для рисования (½ или ¼ дюйма 2 )
- Карандаш и ластик
- Набор карт записи, аналогичный рисунку №4
- Камера для документов
- Smartboard
Это задание может идти в разных направлениях, я могу назначить один и тот же начальный прямоугольник всему классу, я могу назначить разные прямоугольники разным группам или я могу позволить учащимся выбрать свои начальные прямоугольники, помня, что размер будет ограничен размер ламинированной сетчатой бумаги и количество доступных плиток. Хотя лист бумаги для использования в классе имеет размеры 11 на 9 дюймов с «полезной» площадью приблизительно 10 на 7 дюймов, я предлагаю учащимся исследовать прямоугольники с меньшими размерами, такими как 3 на 4, 4 на 5, 6 на 4. и т. д., чтобы поддерживать управляемость занятиями в течение одного урока.
Проезд:
Учащиеся будут выбирать «работу» в своих группах. Один человек будет следить за укладкой плиток на ламинированную сетку и удалением их (по одной за раз) для создания различных аранжировок. Другой учащийся будет копировать (рисовать) каждое расположение на другом листе бумаги с сеткой, чтобы отслеживать все возможные расположения, удаляя плитки по одной. Третий учащийся будет отвечать за запись возможных аранжировок в таблицах, чтобы способствовать дальнейшему обсуждению в классе и выводам.
Один человек будет следить за укладкой плиток на ламинированную сетку и удалением их (по одной за раз) для создания различных аранжировок. Другой учащийся будет копировать (рисовать) каждое расположение на другом листе бумаги с сеткой, чтобы отслеживать все возможные расположения, удаляя плитки по одной. Третий учащийся будет отвечать за запись возможных аранжировок в таблицах, чтобы способствовать дальнейшему обсуждению в классе и выводам.
Я попрошу своих учеников соблюдать некоторые условия при удалении квадратов. Главный из них заключается в том, что оставшиеся в любой момент квадраты связаны друг с другом в том смысле, что с любого квадрата на любой другой можно перейти, пройдя через середины сторон (а не через углы). Кроме того, окружающий прямоугольник должен оставаться прежним и не уменьшаться. Вместе эти условия гарантируют, что в любой строке всегда есть один квадрат и один в любом столбце. Другими словами, они не могут удалить ни целую строку, ни весь столбец. Представленный ранее рисунок № 3 показывает пример этой активности прямоугольника 3 на 4.
Чтобы сделать это занятие как можно более эффективным по времени, я назначу один и тот же ограничивающий прямоугольник всему классу. После того, как каждая группа закончит свое исследование, они поделятся всеми найденными способами вычитания каждой единицы (-1 единица, -2 единицы, -3 единицы и т. д.) с остальным классом, чтобы убедиться, что у них есть все возможные варианты. комбинации. Другой альтернативой является назначение разных единиц вычитания для каждой небольшой группы учащихся. В результате каждая небольшая группа будет отвечать за поиск всех возможных комбинаций только для одного типа вычитания единиц. Например, группа 1 будет работать, исключая одну единицу, группа 2 — две единицы и так далее. После того, как этот шаг будет завершен, учащиеся проверят, нет ли недостающих механизмов для любого возможного исключения, и определят площадь и периметр для каждого полученного механизма.
Чтобы выполнить этот шаг эффективно, я предлагаю использовать бумагу с сеткой, документ-камеру и интерактивную доску. Учащиеся остаются в своих малых группах и по очереди рисуют одну композицию на бумаге с сеткой под документ-камерой, чтобы все могли видеть рисунок на интерактивной доске. Пока вся группа будет следить за ходом, остальные ученики будут следить за оставшимися возможными договоренностями. Каждый ученик, который подходит к документ-камере, будет рисовать новый, чтобы избежать повторений. Они будут последовательно рисовать картинку для каждого возможного уничтожения юнита.
Учащиеся остаются в своих малых группах и по очереди рисуют одну композицию на бумаге с сеткой под документ-камерой, чтобы все могли видеть рисунок на интерактивной доске. Пока вся группа будет следить за ходом, остальные ученики будут следить за оставшимися возможными договоренностями. Каждый ученик, который подходит к документ-камере, будет рисовать новый, чтобы избежать повторений. Они будут последовательно рисовать картинку для каждого возможного уничтожения юнита.
Затем учащиеся будут участвовать в беседах в небольших группах, чтобы обсудить свои выводы и сделать как можно больше обобщений о взаимосвязях между площадью и периметром для своих конкретных примеров. Я буду направлять обсуждение в классе с вопросами, чтобы поддержать процесс. Например, что происходит с площадью и периметром при удалении «углового квадрата»? Что произойдет с площадью и периметром, если удаленный квадрат окажется в другом месте? Что происходит, когда они начинают удалять два или более квадрата? Есть образец?. Цель наводящих вопросов должна заключаться в том, чтобы способствовать пониманию того, что площадь и периметр представляют собой разные концепции и типы измерений.
Цель наводящих вопросов должна заключаться в том, чтобы способствовать пониманию того, что площадь и периметр представляют собой разные концепции и типы измерений.
Деятельность 5:
Это кульминация деятельности этого подразделения. Я выбрал его, потому что он представляет проблему с приложением, связанную с нашей школьной жизнью в Зарроу. Как я объяснял ранее, наша школьная PTA будет спонсировать создание сенсорного пути, и я верю, что мои ученики будут чувствовать мотивацию, чтобы иметь возможность применять свои знания в «реальной» школьной ситуации. Я уже говорил со своим директором об этом мероприятии, и она очень благосклонно отнеслась к участию студентов.
Для этого задания учащиеся будут разделены на четыре группы. Каждая группа будет отвечать за один зал следующим образом:
Группа 1: Детский зал
Группа 2: Главный зал
Группа 3: 1 ст и 2 й сорта зал
Группа 4: Библиотечный зал
Я включил схему расположения школы, чтобы показать расположение залов, которые рассматривались для сенсорного пути.
Чтобы представить задание, я рассмотрю предыдущее обучение со всем классом, чтобы учащиеся поняли, что то, что мы собираемся сделать, похоже на предыдущее задание, которое они выполняли ранее, но теперь с прикладным компонентом.
Я также покажу пару видеороликов (их много в Интернете) о различных конструкциях сенсорных дорожек в школах, чтобы расширить базовые знания и способствовать обмену идеями между учащимися.
Материалы:
- Сетчатая бумага для рисования (½ или ¼ дюйма 2 )
- Карандаш и ластик
- Малярная лента
После того, как учащиеся разделятся на группы и каждой группе будет назначен свой зал, они приступят к измерению длины сторон залов. Размеры доступного пространства составят их «окружающие прямоугольники». В результате их проекты должны вписываться в площадь исходного прямоугольника для каждого зала. Учащиеся наклеивают малярную ленту, чтобы установить эти ограничения. В нашей школе все места общего пользования выложены плиткой. Итак, залы выложены плиткой, а размер плитки равен 1 футу. на 1 фут. Для этой деятельности 1 единица квадрата равна 1 футу 2 или 1 плитка.
Итак, залы выложены плиткой, а размер плитки равен 1 футу. на 1 фут. Для этой деятельности 1 единица квадрата равна 1 футу 2 или 1 плитка.
Когда команды определят доступную площадь, они вернутся в класс, чтобы начать работу над своим дизайном. Всем классом мы обсудим, какие ограничения приходится учитывать учащимся в этом проекте. Например, по этим плиткам будут ходить люди, поэтому дизайн должен позволять передвигаться с одной стороны зала на другую. Как и в предыдущих действиях, плитки в дизайне должны соединяться по бокам, а не по углам, а целые строки или столбцы не могут быть удалены.
Теперь учащиеся готовы начертить прямоугольник на бумаге с сеткой, а затем они начнут работать над возможным расположением или дизайном. Они будут действовать аналогично действию № 3, «удаляя» плитки из исходного прямоугольника, пока не определят, какое расположение предлагает наилучшую схему для ходьбы и движения. Учащиеся должны нарисовать свои варианты на бумаге с сеткой, как показано в примере на рисунке №3.
Исходя из количества учеников, которых я обычно посещаю в классе; в каждой группе будет около шести студентов. Это позволяет каждому студенту работать только с одним типом исключения. Например, один учащийся перепробует все возможные варианты исключения квадрата из 1 единицы; другой будет работать, исключая 2, и так далее. Тем не менее, я не буду накладывать это ограничение, потому что некоторые команды могут решить, что они хотят пропустить удаление 1 или даже 2 клеток и начать сразу с удаления трех плиток.
Хотя будет интересно посмотреть, как далеко учащиеся смогут упорствовать в процессе исключения единичных квадратов, основная цель этого задания не в том, чтобы найти все возможные комбинации, которые были бы огромными, потому что залы большие. Основная цель мероприятия состоит в том, чтобы учащиеся рассмотрели как можно больше вариантов для каждого зала, чтобы окончательно определить, какая комбинация площади, периметра и дизайна обеспечивает «наилучший» вариант пешеходной дорожки, которая потенциально будет использоваться для проектирования сенсорной дорожки. .
.
После того, как каждая команда будет удовлетворена своим выбором, учащиеся нарисуют рисунок на полу в коридоре малярным скотчем. Каждая команда будет иметь возможность объяснить свой дизайн и обоснование своего выбора.
Рисунок № 8: Диаграмма, представляющая международную начальную школу Зарроу и четыре области, которые потенциально могут быть использованы для построения нашего сенсорного пути.
Программа школьного тестирования в Оклахоме — Логин. https://oklahoma.measuredprogress.org/. Это веб-сайт Департамента образования Оклахомы, на котором можно найти информацию о результатах тестирования штата.
/@eurekamat. «Читай, рисуй, пиши: лучшая стратегия решения проблем». Середина. 05 мая 2015 г. https://medium.com/eureka-math/read-draw-write-a-better-strategy-for-solving-746300f5cdb8. Информация о стратегии решения проблем RDW.
Амидон, Джоэл, Энн Монро и Марк Ортвейн. «Стратегии планирования и обучения». Люмен. https://courses.lumenlearning.com/educationx92x1/chapter/project-based-learning/. Описание стратегий обучения на основе проектов.
Люмен. https://courses.lumenlearning.com/educationx92x1/chapter/project-based-learning/. Описание стратегий обучения на основе проектов.
Бекманн, Сибилла. Математика для учителей начальных классов с заданиями . МТМ, 2018.
«Стратегии совместного обучения». Национальный совет учителей математики.
https://www.nctm.org/Publications/Mathematics-Teaching-in-Middle-School/Blog/Cooperative-Learning-Strategies/. Эта книга является полезным ресурсом для учителей. Выбранная глава
описывает стратегии совместного обучения.
Хуан, Хсин-Мей Э. и Клаус Г. Витц. «Детские представления об измерении площади и
Их стратегии решения задач измерения площади». Журнал учебных программ и преподавания.
http://www.sciedu.ca/journal/index.php/jct/article/view/2041/1230. Кабинет детский
понимание взаимосвязи между умножением и площадью и различия между
площадь и периметр.
Мачаба, М. «Понятия площади и периметра: выводы и заблуждения учащихся 10 класса»
Учащиеся». Пифагор. https://pythagoras.org.za/index.php/pythagoras/article/view/304/476.
Анализ неверных представлений учащихся о площади и периметре.
Исследованиеориентировано на учащихся 10-х классов, но включает информацию, применимую к начальному уровню.
«Магнитные школы». Государственные школы Талсы. https://www.tulsaschools.org/parents-
учащиеся/зачисление/перевод/магнит-школы. Информация о приложении магнитной школы.
«Прочитайте «Сложение: помощь детям в изучении математики» на NAP.edu.» Национальные академии
Пресса: OpenBook. https://www.nap.edu/read/9822/chapter/1#xv. Интересное исследование о том, как
Реформы в сфере образования за последние годы изменили способ изучения математики учащимися.
С, Сурбхи. «Разница между площадью и периметром (со сравнительной таблицей)». Ключевые отличия.
01 сентября 2017 г. https://keydifferences.com/difference-between-area-and-perimeter.html.
Разработка концепции площади и периметра.
«Школьные анкеты». Государственные школы Талсы. https://www.tulsaschools.org/our-schools/school-
профилей. Профильная информация о Zarrow International
«Стандарты математической практики». стандарты математической практики | Общее ядро
Инициатива государственных стандартов. http://www.corestandards.org/Math/Practice/. Общее ядро
официальный сайт.
Уолтон и Тамела Рэндольф. «Альтернативные методы понимания формул площади». Иллинойс
Учитель математики. http://journal.ictm.org/index.php/imt/article/view/89. Эта статья
Эта статья
подчеркивает важность четкого концептуального понимания при обучении
математика вместо запоминания формул. В отчете также представлены идеи о мероприятиях для
.учащихся, чтобы получить концептуальное понимание.
«Зачем преподавать математику с помощью манипуляций?» Манипуляции в математике: зачем учить математику с
Манипуляторы | Расчетное время прибытия Hand2mind. https://www.hand2mind.com/resources/why-teach-math-with-
манипуляторы. Использование манипуляций в математике.
«Трудность «длина × ширина»: является ли квадрат единицей измерения?» Журнал
Математическое поведение. 11 апреля 2006 г.
https://www.sciencedirect.com/science/article/pii/S0732312306000125?via=ihub.
- Бекманн, Сибилла. Математика для учителей начальных классов с заданиями .
 Пирсон, 2018.
Пирсон, 2018. - https://www.open.edu/openlearncreate/pluginfile.php/134950/mod_resource/content/3/EM10_AIE_Final.pdf. (2019).
- Уолтон и Тамела Рэндольф. «Альтернативные методы понимания формул площади». Учитель математики из Иллинойса. http://journal.ictm.org/index.php/imt/article/view/89.
- «Прочитайте «Сложение: помощь детям в изучении математики» на NAP.edu». Издательство национальных академий: OpenBook. https://www.nap.edu/read/9822/chapter/1#xv
- «Программа школьного тестирования в Оклахоме — вход в систему». Программа школьного тестирования Оклахомы — Войти. https://oklahoma.measuredprogress.org/.
- Мачаба, М. «Понятия площади и периметра: взгляды и заблуждения учащихся 10 класса». Пифагор. https://pythagoras.org.za/index.php/pythagoras/article/view/304/476.
- «Школьные анкеты». Государственные школы Талсы. https://www.
 tulsaschools.org/our-schools/school-profiles.
tulsaschools.org/our-schools/school-profiles. - «Магнитные школы». Государственные школы Талсы. https://www.tulsaschools.org/parents-students/enrolltransfer/magnet-schools.
- г. «Школьные профили». Государственные школы Талсы. https://www.tulsaschools.org/our-schools/school-profiles.
- С, Сурбхи. «Разница между площадью и периметром (со сравнительной таблицей)». Ключевые отличия. 01 сентября 2017 г. https://keydifferences.com/difference-between-area-and-perimeter.html.
- Хонг Д. и Кристина Ранналлс. Ранналлс, «Заполнение пробелов». Обучение детей математике 25, вып. 5 (2019). doi: 10.5951/teachilmath.25.5.0274.
- Аутред, Линн Н. и Майкл С. Митчелмор. «Интуитивное понимание маленькими детьми прямоугольного измерения площади». Журнал исследований в области математического образования 31, вып. 2 (2000): 144-67. дои: 10.2307/749749.
- «Сенсорные пути! Что это, черт возьми, такое?» Fit и Fun Playscapes.
 04 апреля 2019 г. https://fitandfunplayscapes.com/sensory-paths-what-the-heck-are-those/.
04 апреля 2019 г. https://fitandfunplayscapes.com/sensory-paths-what-the-heck-are-those/. - Мачаба, М. «Понятия площади и периметра: взгляды и заблуждения учащихся 10 класса». Пифагор. https://pythagoras.org.za/index.php/pythagoras/article/view/304/476.
- 15. «Зачем учить математике с помощью манипуляций?» манипуляции в математике: зачем преподавать математику с помощью манипуляций | Расчетное время прибытия Hand2mind. https://www.hand2mind.com/resources/why-teach-math-with-manipulatives.
- «Стратегии совместного обучения». Национальный совет учителей математики. https://www.nctm.org/Publications/Mathematics-Teaching-in-Middle-School/Blog/Cooperative-Learning-Strategies/.
- /@eurekamat. «Читай, рисуй, пиши: лучшая стратегия решения — Eureka Math». Середина. 05 мая 2015 г. https://medium.com/eureka-math/read-draw-write-a-better-strategy-for-solving-746300f5cdb8.
- Амидон, Джоэл, Энн Монро и Марк Ортвейн.
 «Стратегии планирования и обучения». Люмен. https://courses.lumenlearning.com/educationx92x1/chapter/project-based-learning/.
«Стратегии планирования и обучения». Люмен. https://courses.lumenlearning.com/educationx92x1/chapter/project-based-learning/. - https://sde.ok.gov/sites/ok.gov.sde/files/OAS-Math-Final%20Version_3.pdf. (2019).
- «3 класс » Измерения и данные». 3 класс » Измерения и данные | Common Core State Standards Initiative.http://www.corestandards.org/Math/Content/3/MD/.
Академические стандарты, которые должен охватывать этот модуль, перечислены и описаны ниже.
Все стандарты относятся к математическому содержанию и математическим практикам для 3-го класса.
Поскольку Департамент образования штата Оклахома не принял Единые базовые государственные стандарты (CCSS), я включил в это приложение Стандарты штата Оклахома по геометрии и измерениям, которые относятся к этой единице, а также Единые базовые государственные стандарты и стандарты математической практики.
Академические стандарты Оклахомы по математике для 3-го класса.

Геометрия и измерения:
3.GM.2.1 Нахождение периметра многоугольника по целым числам длин сторон в реальных и математических ситуациях.
3.GM.2.2 Разработать и использовать формулы для определения площади прямоугольников. Обоснуйте, почему длина и ширина умножаются, чтобы найти площадь прямоугольника, разбив прямоугольник на одну единицу по одной единице квадратов и рассмотрев их как сгруппированные в строки и столбцы.
3.GM.2.8 Найдите площадь двумерной фигуры, подсчитав общее количество единичных квадратов одинакового размера, которые заполняют фигуру без пробелов и перекрытий.
Математические действия и процессы:
Развивайте глубокое и гибкое концептуальное понимание. Студенты продемонстрируют глубокое и гибкое концептуальное понимание математических понятий, операций и отношений, устанавливая математические и реальные связи.
Развивайте способность делать предположения, моделировать и обобщать. Студенты будут создавать, выявлять и расширять шаблоны в качестве стратегии решения и осмысления проблем.
Развивайте способность к математическому общению. Студенты будут обсуждать, писать, читать, интерпретировать и переводить идеи и концепции математически. 19
Единые базовые государственные стандарты по математике 3-й класс.
Геометрические измерения: понять понятия площади и соотнести площадь с умножением и сложением.
3.MD.C.5 Распознавать площадь как атрибут плоских фигур и понимать принципы измерения площади.
3.MD.C.6 Измерение площадей путем подсчета единичных квадратов.
3.MD.C.7 Связь с операциями умножения и сложения.
Геометрическое измерение: распознать периметр.
3.MD.D.8 Решать реальные и математические задачи, связанные с периметрами многоугольников, в том числе нахождение периметра по длинам сторон, нахождение неизвестной длины стороны и отображение прямоугольников с одинаковым периметром и разными площадями или с одинаковой площадью и разные периметры. 20
Стандарты математической практики:
CCSS. MATH.PRACTICE.MP2 Рассуждайте абстрактно и количественно.
MATH.PRACTICE.MP2 Рассуждайте абстрактно и количественно.
Подкованные в математике учащиеся понимают величины и их отношения в проблемных ситуациях. Количественное рассуждение влечет за собой привычки создавать последовательное представление проблемы; рассмотрение задействованных единиц; внимание к значению величин, знание и гибкое использование различных свойств операций и объектов.
CCSS.MATH.PRACTICE.MP4 Модель с математикой.
Учащиеся, хорошо разбирающиеся в математике, могут применять известные им математические знания для решения проблем, возникающих в повседневной жизни, обществе и на рабочем месте.
CCSS.MATH.PRACTICE.MP7 Ищите и используйте структуру.
Подкованные в математике учащиеся внимательно смотрят, чтобы различить шаблон или структуру.
Перейти к математике, 3 класс, ключ к ответу, Pdf Периметр и площадь – ключ к ответу, перейти к математике ученики. Основные понятия периметра и площади четко объясняются, чтобы учащиеся получали высокие оценки.
 Кроме того, углубленное знание главы 11 «Периметр и площадь» Go Math Class 3 Ключ к ответу упоминается с четким объяснением. Кроме того, Go Math Grade 3 Perimeter and Area очень удобна для учащихся, которые испытывают трудности и хотят дополнительно попрактиковаться в небольших группах. Каждая проблема решается и упоминается с подробным объяснением, чтобы помочь студентам во время их практики. Тест, домашняя работа, формирующая оценка или просто дополнительная практика, которую вы хотите решить, можно легко выполнить с помощью Ключа ответов Go Math для 3 класса Глава 11 Периметр и ключ ответа области.
Кроме того, углубленное знание главы 11 «Периметр и площадь» Go Math Class 3 Ключ к ответу упоминается с четким объяснением. Кроме того, Go Math Grade 3 Perimeter and Area очень удобна для учащихся, которые испытывают трудности и хотят дополнительно попрактиковаться в небольших группах. Каждая проблема решается и упоминается с подробным объяснением, чтобы помочь студентам во время их практики. Тест, домашняя работа, формирующая оценка или просто дополнительная практика, которую вы хотите решить, можно легко выполнить с помощью Ключа ответов Go Math для 3 класса Глава 11 Периметр и ключ ответа области.Для светлого будущего школьников необходимо обязательно следовать главе 11 «Периметр и площадь ответа на вопросы по математике 3 класса». Улучшите способность решать проблемы, используя ключ ответа HMH Go Math Grade 3.
Урок 1: Периметр модели
- Периметр модели — страница № 629
- Проверка урока по периметру модели — страница № 630
Урок 2: Поиск периметра
- Поиск периметра – Страница № 635
- Проверка урока «Найти периметр» — страница № 636
Урок 3: Поиск неизвестных длин сторон
- Поиск неизвестных длин сторон – № страницы 641
- Проверка урока «Найти неизвестные длины сторон» — страница № 642
Урок 4: Понимание области
- Понимание области – страница № 647
- Проверка урока «Понимание области» — страница № 648
Урок 5: Измерение площади
- Измерение площади — страница № 653
- Проверка урока «Измерение площади» — страница № 654
Урок 6: Использование площадных моделей
- Использование площадных моделей — страница № 659
- Проверка урока «Использование зональных моделей» — страница № 660
Контрольная точка в середине главы
- Контрольная точка в середине главы – № страницы 661
- Проверка урока в середине главы — страница № 662
Урок 7: Решение задач Площадь прямоугольников
- Решение задач Площадь прямоугольников – Страница № 667
- Решение задач Площадь прямоугольников Проверка урока – страница № 668
Урок 8: Площадь совмещенных прямоугольников
- Площадь совмещенных прямоугольников — страница № 673
- Площадь комбинированных прямоугольников Проверка урока — страница № 674
Урок 9: Тот же периметр, разные области
- Тот же периметр, разные области — страница № 679
- Один и тот же периметр, разные зоны Проверка урока — страница № 680
- Один и тот же периметр, разные области.
 Проверка урока 1 — Страница № 685
Проверка урока 1 — Страница № 685 - Один и тот же периметр, разные области Проверка урока 2 – Страница № 686
Обзор/Тест
- Обзор/Тест – Страница № 687
- Обзор/Тест — Страница № 688
- Обзор/Тест — Страница № 689
- Обзор/Тест — Страница № 690
- Обзор/Тест — Страница № 691
- Обзор/Тест — Страница № 692
Периметр модели – № страницы 629
Найдите периметр фигуры. Каждая единица равна 1 сантиметру.
Вопрос 1.
22 сантиметра
Ответ:
22 сантиметра
Пояснение:
Каждый квадрат сетки представляет собой квадрат размером 1 на 1 сантиметр. Итак, нам нужно сложить длины темных сегментов прямо над фигурой. Начинайте отсчет с клетки, где стоит 1. Этот параметр составляет 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22 сантиметра в длину. Итак, 22 сантиметра.
Вопрос 2.
__________ сантиметров
Ответ:
22 сантиметра
Объяснение:
Посмотрите на длину каждой стороны. Затем добавьте длину каждой стороны, чтобы получить периметр данной формы. Длины сторон равны 6 + 5 + 6 + 5 = 22 сантиметра.
Затем добавьте длину каждой стороны, чтобы получить периметр данной формы. Длины сторон равны 6 + 5 + 6 + 5 = 22 сантиметра.
Вопрос 3.
__________ сантиметров
Ответ:
26 сантиметров
Объяснение:
Учитывая, что каждая единица равна 1 сантиметру. Длины каждого ящика посчитайте от числа 1. Значит, этот параметр равен 26 сантиметров длиной . или 6 + 5 + 2 + 2 + 2 + 2 + 2 + 5 = 26,
Вопрос 4.
__________ сантиметров
Ответ:
30 сантиметров
Объяснение:
Посмотрите на длину каждой стороны. Затем добавьте длину каждой стороны, чтобы получить периметр данной формы. Длины сторон равны 2 + 3 + 3 + 3 + 2 + 5 + 7 + 5 = 30 сантиметров.
Решение проблем
Используйте чертеж для 5–6. Каждая единица равна 1 сантиметру.
Вопрос 5.
Чему равен периметр фигуры Патрика?
__________ сантиметров
Ответ:
20 сантиметров
Объяснение:
Периметр фигуры Патрика = 5 + 5 + 5 + 5 = 20 сантиметров.
Вопрос 6.
Насколько больше периметр фигуры Джиллиан, чем периметр фигуры Патрика?
__________ сантиметров
Ответ:
2 сантиметра
Объяснение:
Во-первых, периметр фигуры Джиллиан = 8 + 1 + 4 + 2 + 4 + 3 = 22 сантиметра.
Разница = 22 – 20 = 2 сантиметра.
Периметр фигуры Джиллиан на 2 сантиметра больше периметра фигуры Патрика.
Периметр модели – № страницы 630
Проверка урока
Вопрос 1.
Найдите периметр фигуры.
Каждая единица равна 1 сантиметру.
Опции:
а. 14 сантиметров
б. 16 сантиметров
в. 18 сантиметров
д. 20 сантиметров
Ответ:
d. 20 сантиметров
Объяснение:
Учитывая, что каждая единица равна 1 сантиметру. Подсчитайте длины каждого квадрата темных линий из числа 1. Значит, этот параметр равен 20 сантиметрам.
Вопрос 2.
Найдите периметр фигуры.
Каждая единица равна 1 сантиметру.
Опции:
а. 19 сантиметров
б. 26 сантиметров
в. 33 см
д. 55 сантиметров
Ответ:
b. 26 сантиметров
Пояснение:
Найдите длину каждой коробки и сложите их, чтобы найти периметр заданной формы. Периметр данной фигуры равен 8 + 4 + 3 + 1 + 4 + 4 + 1 + 1 = 26 сантиметров.
Обзор спирали
Вопрос 3.
В каком из них дроби перечислены в порядке от наименьшего к наибольшему?
\(\frac{2}{4}, \frac{2}{3}, \frac{2}{6}\)
Опции:
a. \(\frac{2}{3}, \frac{2}{4}, \frac{2}{6}\)
б. \(\frac{2}{6}, \frac{2}{4}, \frac{2}{3}\)
c. \(\frac{2}{4}, \frac{2}{3}, \frac{2}{6}\)
d. \(\frac{2}{3}, \frac{2}{6}, \frac{2}{4}\)
Ответ:
b. \(\frac{2}{6}, \frac{2}{4}, \frac{2}{3}\)
Объяснение:
Числитель данных множителей один и тот же. Итак, посмотрите на знаменатели, чтобы сравнить размер частей. Чем меньше знаменатель, тем больше дробь. В данной задаче 3 — меньший знаменатель по сравнению с 4 и 6. Тогда 4 — следующий меньший знаменатель. Итак, дроби в порядке от наименьшей к наибольшей: 2/6, 2/4, 2/3.
Тогда 4 — следующий меньший знаменатель. Итак, дроби в порядке от наименьшей к наибольшей: 2/6, 2/4, 2/3.
Вопрос 4.
Школа Кейси начинается в то время, которое показывают часы. Во сколько начинается школа Кейси?
Опции:
г. н.э. 6:40
б. 8:06
в. 8:30
д. 9:30
Ответ:
c. 8:30
Объяснение:
На рисунке часовая стрелка показывает цифру 8. Итак, мы говорим, что сейчас 8 часов. Минутная стрелка стоит на 6. Чтобы найти минуты, умножьте 6 х 5 = 30. Таким образом, получается 30 минут. Время 8 часов 30 минут.
Вопрос 5.
Майкл и Декс сравнивают полоски дробей. Какое утверждение НЕ верно?
Опции:
а. \(\frac{1}{2}<\frac{2}{2}\)
b. \(\frac{2}{3}>\frac{1}{3}\)
г. \(\frac{4}{8}<\frac{3}{8}\)
d. \(\frac{4}{6}>\frac{2}{6}\)
Ответ:
c. \(\frac{4}{8}<\frac{3}{8}\)
Объяснение:
Знаменатели данных дробей одинаковы. Итак, посмотрите на числители, чтобы сравнить числа.
1 < 2 верно.
2 > 1 верно.
4 < 3 неверно. Итак, 4/8 < 3/8 неверно.
Вопрос 6.
Эйден хочет найти массу шара для боулинга. Какую единицу он должен использовать?
Опции:
а. литер
б. дюйм
в. грамм
д. килограмм
Ответ:
d. килограмм
Объяснение:
Килограмм используется для нахождения массы шара для боулинга.
Найти периметр – № страницы 635
Используйте линейку, чтобы найти периметр. (Примечание: на мобильных устройствах, таких как смартфоны или планшеты, измерения будут неточными.)
Вопрос 1.
12 см
Ответ:
12 см
Объяснение:
Прибавьте длины измеренных сторон к периметру. 4 + 3 + 2 + 3 = 12 см.
Вопрос 2.
_________ сантиметров
Ответ:
13 сантиметров
Пояснение:
Измерьте сантиметровой линейкой длину каждой стороны.
Запишите и сложите длины сторон, измеренные с точностью до сантиметра.
5 см + 1 см + 1 см + 2 см + 4 см = 13 сантиметров.
Вопрос 3.
_________ дюймов
Ответ:
8 дюймов
Пояснение:
С помощью дюймовой линейки измерьте длину каждой стороны с точностью до дюйма.
Запишите и сложите длины сторон, измеренные с точностью до дюйма.
2 дюйма + 2 дюйма + 2 дюйма + 2 дюйма = 8 дюймов.
Вопрос 4.
_________ дюймов
Ответ:
6 дюймов
Объяснение:
Используйте дюймовую линейку для измерения длины каждой стороны.
Запишите и сложите длины сторон, измеренные с точностью до дюйма.
2 дюйма + 2 дюйма + 2 дюйма = 6 дюймов.
Решение задач
Нарисуйте картинку, чтобы решить 5–6.
Вопрос 5.
У Эвана есть квадратная наклейка со стороной 5 дюймов. Каков периметр наклейки?
_________ дюймов
Ответ:
20 дюймов
Объяснение:
Стороны квадрата равны. Каждая сторона имеет 5 дюймов. Итак, периметр наклейки 5 х 4 = 20 дюймов.
Итак, периметр наклейки 5 х 4 = 20 дюймов.
Вопрос 6.
Софи рисует фигуру, имеющую 6 сторон. Каждая сторона по 3 сантиметра. Чему равен периметр фигуры?
_________ сантиметров
Ответ:
18 сантиметров
Объяснение:
Периметр фигуры равен сумме всех сторон.
Учитывая, что Софи нарисовала фигуру, у которой 6 сторон по 3 сантиметра. Таким образом, периметр фигуры = 3 + 3 + 3 + 3 + 3 + 3 = 18 сантиметров. .
Вопрос 1.
Вырежьте этикетку размером с показанную форму. Каков периметр в дюймах этикетки Тая?
Опции:
а. 4 дюйма
б. 5 дюймов
в. 6 дюймов
д. 7 дюймов
Ответ:
c. 6 дюймов
Пояснение:
С помощью дюймовой линейки Тай может измерить длину каждой стороны заданной фигуры. Теперь найдите длины каждой стороны.
1 дюйм + 2 дюйма + 1 дюйм + 2 дюйма = 6 дюймов.
Вопрос 2.
Джулия нарисовала фигуру, показанную ниже. Чему равен периметр фигуры в дюймах?
Опции:
а. 2 дюйма
2 дюйма
б. 4 дюйма
г. 6 дюймов
д. 8 дюймов
Ответ:
d. 8 дюймов
Пояснение:
Джули может использовать дюймовую линейку, чтобы измерить длину каждой стороны фигуры. Теперь найдите длины каждой стороны. Каждая сторона имеет 2 дюйма. Итак, периметр фигуры равен 2 дюймам + 2 дюймам + 2 дюймам + 2 дюймам = 8 дюймов.
Обзор спирали
Вопрос 3.
Каков периметр фигуры ниже?
Опции:
а. 8 шт.
б. 10 единиц
г. 20 шт.
д. 22 шт.
Ответ:
c. 20 единиц
Объяснение:
На рисунке каждая единица равна 1 сантиметру. Длины каждого ящика посчитайте от числа 1. Значит, этот параметр равен 20 единицам длины.
Вопрос 4.
Винс приходит на урок игры на трубе после школы во время, показанное на часах. Во сколько Винс приходит на урок игры на трубе?
Опции:
а. 3:26 утра
б. 4:26 утра
с. 15:26
д. 16:26
Ответ:
c. 15:26
15:26
Пояснение:
Учитывая, что Винс приходит на урок игры на трубе после школы во время, показанное на часах. Как упоминается после школьного времени, сейчас полдень. Время после полудня и до полуночи записывается с помощью P.M. Часовая стрелка показывает цифру 3. Итак, ответ — 15:26.
Вопрос 5.
Маленький аквариум Мэтью вмещает 12 литров. Его большой аквариум вмещает 25 литров. Сколько еще литров вмещает его большой аквариум?
Опции:
а. 12 литров
б. 13 литров
в. 25 литров
д. 37 литров
Ответ:
b. 13 литров
Пояснение:
Чтобы получить больше литров, вычтите литры большого аквариума из литров маленького аквариума. Итак, большой аквариум на 25 литров — 12 литров = на 13 литров больше, чем маленький аквариум Мэтью.
Вопрос 6.
Сесила и Саша сравнивают полоски дробей. Какое утверждение является правильным?
Опции:
а. \(\frac{1}{2}<\frac{1}{3}\)
г. до н.э. \(\frac{1}{8}>\frac{1}{6}\)
c. \(\frac{1}{4}>\frac{1}{2}\)
\(\frac{1}{4}>\frac{1}{2}\)
d. \(\frac{1}{6}<\frac{1}{4}\)
Ответ:
d. \(\frac{1}{6}<\frac{1}{4}\)
Пояснение:
Сесила и Саша сравнивают полосы дробей. В данных дробях числители одинаковы. Итак, сравните знаменатели, чтобы найти наибольшую дробь. Чем меньше знаменатель, тем больше дробь.
2 < 3 неправильно.
8 > 6 неправильно.
4 > 2 неправильно.
6 < 4 верно.
Итак, 1/6 < 1/4 — правильный ответ.
Найти неизвестные длины сторон – № страницы 641
Найти неизвестные длины сторон.
Вопрос 1.
Периметр = 33 сантиметра
5 + 8 + 7 + 4 + x = 33
24 + x = 33
x = 9
x = ____ 9 _____ сантиметров
Ответ: Объяснение:
Если бы я знал длину x, я бы сложил все длины сторон, чтобы найти периметр. Дан периметр = 33 сантиметра.
Сложите длины данных сторон. 5 + 8 + 7 + 4 + х = 33.
24 + х = 33.
х = 33 – 24 = 9.
х = 9 сантиметров.
Вопрос 2.
Периметр = 14 футов
r = ____ футов
Ответ:
3 фута
Объяснение:
Дан периметр = 14 футов.
Сложите длины заданных сторон, чтобы найти r.
4 фута + 4 фута + r + r = 14 футов.
Если r = 1 -> 4 + 4 + 1 + 1 = 10 не равно 14.
Если r = 2 -> 4 + 4 + 2 + 2 = 12 не равно 14.
Если r = 3 -> 4 + 4 + 3 + 3 = 14 равно 14.
Итак, r = 3 фута.
Вопрос 3.
Периметр = 37 метров
s = ____ метров
Ответ:
11 метров
Объяснение:
Учитывая, что периметр = 37 метров.
Сложите длины заданных сторон, чтобы найти s.
8 + 11 + 5 + 2 + с = 37.
26 + с = 37.
с = 37 – 26 = 11.
с = 11 метров.
Вопрос 4.
Периметр = 92 дюйма
t = ____ дюймов
Ответ:
15 дюймов
Объяснение:
Учитывая, что периметр = 92 дюйма.
Сложите длины заданных сторон, чтобы найти t.
7 + 23 + 12 + 12 +23 + t = 92
77 + t = 92.
s = 92 – 77 = 15.
s = 15 дюймов.
Решение проблем
Вопрос 5.
У Стивена есть прямоугольный ковер с периметром 16 футов. Ширина коврика 5 футов. Какая длина коврика? ____ футов
Ответ:
3 фута
Объяснение:
Учитывая, что у Стивена есть прямоугольный ковер с периметром 16 футов. Прямоугольник имеет 4 стороны с двумя парами противоположных сторон, которые равны по длине.
Пусть длина будет x.
Если x = 1 фут -> 5 + x + 5 + x = 5 + 1 + 5 + 1 = 12 футов не равно 16.
Если x = 2 фута -> 5 + x + 5 + x = 5 + 2 + 5 + 2 = 14 футов не равно 16.
Если x = 3 фута -> 5 + x + 5 + x = 5 + 3 + 5 + 3 = 16 футов равно 16.
Итак, длина одеяла составляет 3 фута.
Вопрос 6.
У Керстин есть квадратная плитка. Периметр плитки 32 дюйма. Какова длина каждой стороны плитки?
____ дюймов
Ответ:
8 дюймов
Объяснение:
Четыре стороны квадрата равны по длине.
Итак, 4 x s = 32
4 x 8 = 32.
Итак, длина каждой стороны квадрата равна 8 дюймам.
Поиск неизвестных длин сторон – № страницы 642
Проверка урока
Вопрос 1.
Джесси надевает ленту на квадратную рамку. Он использует 24 дюйма ленты. Какова длина каждой стороны рамы? Вариантов:
г. н.э. 4 дюйма
б. 5 дюймов
в. 6 дюймов
д. 8 дюймов
Ответ:
c. 6 дюймов
Пояснение:
Джесси обвязывает лентой квадратную рамку. У квадрата четыре стороны, которые равны по длине.
Итак, 4 х k = 24 дюйма.
4 х 6 = 24 дюйма.
Каждая сторона рамы 6 дюймов.
Вопрос 2.
Давия рисует фигуру с 5 сторонами. Две стороны имеют длину 5 дюймов каждая. Две другие стороны имеют длину 4 дюйма каждая. Периметр формы составляет 27 дюймов. Какова длина пятой стороны?
Опции:
а. 9 дюймов
б. 13 дюймов
в. 14 дюймов
д. 18 дюймов
Ответ:
а. 9 дюймов
Объяснение:
. Из предоставленной информации Давия рисует фигуру с 5 сторонами.
Из предоставленной информации Давия рисует фигуру с 5 сторонами.
2 стороны = каждая 5 дюймов в длину.
2 стороны = длина 4 дюйма каждая.
Пусть другая сторона равна k.
Периметр фигуры = 5 + 5 + 4 + 4 + k = 27 дюймов.
18 + к = 27 дюймов.
к = 27 – 18 дюймов.
к = 9 дюймов.
Спиральный обзор
Вопрос 3.
Что из следующего представляет 7 + 7 + 7 + 7?
Опции:
а. 4 × 4
б. 4 × 7
в. 6 × 7
д. 7 × 7
Ответ:
b. 4 × 7
Объяснение:
7 + 7 + 7 + 7 = 28.
4 x 4 = 16 не равно 28.
4 x 7 = 28 равно 28.
7 + 7 + 7 + 7 = 4 × 7.
Вопрос 4.
Боб купил 3 набора моделей автомобилей. Он подарил Энн 4 машины. У Боба осталось 11 машин. Сколько моделей автомобилей было в каждом наборе?
Опции:
а. 18
б. 11
г. 7
д. 5
Ответ:
d. 5
Объяснение:
Если у Боба осталось 11 автомобилей после того, как он отдал 4 Энн, это означает, что всего у него было 15 автомобилей. Если всего у Боба было 15 машин, и эти 15 машин были разделены на 3 пачки, то в каждой пачке было 5 машин. Ответ: по 5 машин в каждой пачке.
Если всего у Боба было 15 машин, и эти 15 машин были разделены на 3 пачки, то в каждой пачке было 5 машин. Ответ: по 5 машин в каждой пачке.
Вопрос 5.
Рэнди смотрел на часы, когда начинал и заканчивал чтение. Как долго Рэнди читал?
Опции:
а. 55 минут
г. до н.э. 45 минут
в. 35 минут
д. 15 минут
Ответ:
b. 45 минут
Пояснение:
Рэнди начал читать в 4:10.
Рэнди закончил читать в 4:55.
Вычтите, чтобы найти время чтения Рэнди.
4:55 – 4:10 = 45 минут
Итак, Рэнди читал 45 минут.
Вопрос 6.
Какое утверждение представляет модель?
Опции:
а. \(\frac{4}{4}\) = 1
б. \(\frac{3}{4}\) = 1
c. \(\frac{2}{4}\) = 1
д. \(\frac{1}{4}\) = 1
Ответ:
а. \(\frac{4}{4}\) = 1
Пояснение:
Первое изображение представляет весь круг, разделенный на 4 равные части. Итак, каждая часть равна \(\frac{1}{4}\).
Вместе все 4 части представляют \(\frac{4}{4}\) или один полный круг.
Второе изображение представляет собой один полный круг.
\(\frac{4}{4}\) = 1.
Понять площадь – номер страницы 647
Подсчитайте, чтобы найти площадь фигуры.
Вопрос 1.
Площадь = 6 квадратных единиц
Ответ:
6 квадратных единиц
Объяснение:
Площадь — это мера количества единичных квадратов, необходимых для покрытия плоской поверхности. Единичный квадрат – это квадрат со стороной, равной 1 единице. Его площадь составляет 1 квадратную единицу (кв. ун). Подсчитайте количество квадратов, чтобы получить ответы. 1, 2, 3, 4, 5, 6.
Площадь = 6 квадратных единиц.
Вопрос 2.
Площадь = ______ квадратных единиц
Ответ:
4 квадратных единицы
Объяснение:
Подсчитайте количество квадратов, чтобы получить ответы. 1, 2, 3, 4.
Площадь = 4 квадратных единицы.
Вопрос 3.
Площадь = ______ квадратных единиц
Ответ:
5 квадратных единиц
Объяснение:
Подсчитайте количество квадратов, чтобы получить ответы. 1, 2, 3, 4, 5.
1, 2, 3, 4, 5.
Площадь = 5 квадратных единиц.
Вопрос 4.
Площадь = ______ квадратных единиц
Ответ:
7 квадратных единиц
Объяснение:
Подсчитайте количество квадратов, чтобы получить ответы. 1, 2, 3, 4, 5, 6, 7.
Площадь = 7 квадратных единиц.
Вопрос 5.
Площадь = ______ квадратных единиц
Ответ:
8 квадратных единиц
Объяснение:
Подсчитайте количество квадратов, чтобы получить ответы. 1, 2, 3, 4, 5, 6, 7, 8.
Площадь = 8 квадратных единиц.
Вопрос 6.
Площадь = ______ квадратных единиц
Ответ:
13 квадратных единиц
Объяснение:
Подсчитайте количество квадратов, чтобы получить ответы. 1, 2, 3, 4, 5, 6, 7, 8,9, 10, 11, 12, 13.
Площадь = 13 квадратных единиц.
Запишите площадь или периметр для каждой ситуации.
ВОПРОС 7.
Ковровое покрытие А. Пол
_________
Ответ:
Область
Вопрос 8.
FENCING A GARDEN
_________
Ответ:
2. Пеример
. схема для 9–10. Ответ: Объяснение: Вопрос 9. Ответ: Объяснение: Вопрос 10. Ответ: Объяснение: Проверка урока Вопрос 1. Ответ: Пояснение: Вопрос 2. Ответ: Пояснение: Spiral Review Вопрос 3. Ответ: Пояснение: Вопрос 4. Ответ: Пояснение: Вопрос 5. Ответ: Объяснение: Вопрос 6. Ответ: Пояснение: Подсчитайте, чтобы найти площадь фигуры. Вопрос 1. Ответ: Объяснение: Вопрос 2. Ответ: Объяснение: Вопрос 3. Ответ: Объяснение: Вопрос 4. Ответ: Объяснение: Решение проблем Алан красит свою палубу в серый цвет. Вопрос 5. Ответ: Пояснение: Вопрос 6. Ответ: Пояснение: Проверка урока Каждая единица площади на диаграмме равна 1 квадратному футу. Вопрос 1. Ответ: Объяснение: Вопрос 2. Ответ: Объяснение: Spiral Review Вопрос 3. Ответ: Объяснение: Вопрос 4. Ответ: Объяснение: Вопрос 5. Ответ: Объяснение: Вопрос 6. Ответ: Объяснение: Найдите площадь каждой фигуры. Каждая единица площади равна 1 квадратному футу. Вопрос 1. Ответ: Объяснение: Вопрос 2. _________ квадратных футов Найдите площадь каждой фигуры. Ответ: Объяснение: Вопрос 3. Ответ: Объяснение: Вопрос 4. Ответ: Объяснение: Вопрос 5. Ответ: Объяснение: Решение проблем Вопрос 6. Ответ: Объяснение: Вопрос 7. Ответ: Объяснение: Проверка урока Вопрос 1. Ответ: Пояснение: Вопрос 2. Ответ: Пояснение: Обзор спирали Вопрос 3. Ответ: Объяснение: Вопрос 4. Ответ: Объяснение: Вопрос 5. Ответ: Объяснение: Вопрос 6. Ответ: Объяснение: Словарь Выберите лучший термин из поля. Вопрос 1. Ответ: Вопрос 2. Ответ: Понятия и навыки Найдите периметр фигуры. Каждая единица равна 1 сантиметру. Вопрос 3. Ответ: Объяснение: Вопрос 4. Ответ: Объяснение: Найдите неизвестные длины сторон. Вопрос 5. Ответ: Объяснение: Вопрос 6. Ответ: Объяснение: Найдите площадь фигуры. Каждая единица площади равна 1 квадратному метру. Вопрос 7. Ответ: Объяснение: Вопрос 8. Ответ: Обзор: Вопрос 9. Ответ: Объяснение: Вопрос 10. Ответ: Объяснение: Вопрос 11. Ответ: Объяснение: Вопрос 12. Ответ: Объяснение: Ответ: Объяснение: Используйте информацию для 1–3. Художник делает прямоугольные фрески разных размеров. Ниже приведены доступные размеры. Каждая единица площади равна 1 квадратному метру. Вопрос 1. Вопрос 2. Ответ: Вопрос 3. Ответ: Вопрос 4. Ответ: Объяснение: Проверка урока Вопрос 1. Ответ: Объяснение: Вопрос 2. Ответ: Объяснение: Спиральный обзор Вопрос 3. Ответ: Пояснение: Вопрос 4. Ответ: Объяснение: Вопрос 5. Ответ: Объяснение: Вопрос 6. Ответ: Объяснение: Используйте Распределительное свойство, чтобы найти площадь. Вопрос 1. Ответ: Объяснение: ВОПРОС 2. Ответ: . 3 x 6 = 18. Нарисуйте линию, чтобы разделить фигуру на прямоугольники. Найдите площадь фигуры. Вопрос 3. Ответ: Объяснение: Вопрос 4. Ответ: Объяснение: 6 x 29 4 910; 2 x 8 = 16. Решение проблем Схема комнаты Фрэнка справа. Каждая единица площади равна 1 квадратному футу. Вопрос 5. Ответ: Вопрос 6. Ответ: Объяснение: Проверка урока Вопрос 1. Ответ: Объяснение: Вопрос 2. Ответ: Объяснение: Обзор спирали Вопрос 3. Ответ: Объяснение: Вопрос 4. Ответ: Объяснение: Вопрос 5. Ответ: Вопрос 6. Ответ: Объяснение: Найдите периметр и площадь. Вопрос 1. B: Периметр = ______ единиц; Ответ: Объяснение: Вопрос 2. B: Периметр = ______ единиц; Ответ: Объяснение: A: Периметр = 4 + 1 + 4 + 1 = 10 Решение проблем Вопрос 3. Ответ: Пояснение: Вопрос 4. Ответ: Пояснение: Вопрос 1. Ответ: Объяснение: Вопрос 2. Ответ: Объяснение: Обзор спирали Вопрос 3. Ответ: Объяснение: Вопрос 4. Ответ: Объяснение: Найдите периметр и площадь. Укажите, у какого прямоугольника периметр больше. Вопрос 1. B: Площадь = _______ квадратных единиц; Ответ: Объяснение: Вопрос 2. Вопрос 2. Ответ: Объяснение: Вопрос 3. Вопрос 3. Ответ: Объяснение: Решение проблем Используйте рисунки плиток для 4–5. Вопрос 4. Ответ: Объяснение: Вопрос 5. Ответ: Объяснение: Проверка урока Вопрос 1. Ответ: Объяснение: Вопрос 2. Ответ: Объяснение: Spiral Review Вопрос 3. Ответ: Объяснение: Вопрос 4. Ответ: Объяснение: Вопрос 5. Ответ: Объяснение: Вопрос 6. Ответ: Объяснение: Вопрос 1. Ответ: Объяснение: Вопрос 2. Ответ: Объяснение: Вопрос 3. Ответ: Объяснение: Вопрос 4. Ответ: Объяснение: Вопрос 5. Ответ: Объяснение: Вопрос 6. Длина стороны квадрата равна сантиметрам. Ответ: Объяснение: Вопрос 7. Объяснение: Вопрос 8. Ответ: Объяснение: Вопрос 9. Ответ: Объяснение: Вопрос 10. Ответ: Вопрос 11. Ответ: Объяснение: Вопрос 12. Первый сад = 8 x 6 = 48 футов. a. Площадь первого сада составляет 48 квадратных футов. Ответ: Вопрос 12. Ответ: Вопрос 12. Ответ: Объяснение: Вопрос 12. Ответ: Вопрос 13. Ответ: Объяснение: Вопрос 14. Ответ: Вопрос 14. Ответ: Объяснение: Вопрос 15. Ответ: Объяснение: Вопрос 16. Ответ: Объяснение: Перейти к математике 3 класс Ключ к ответу Глава 11 Периметр и площадь даны с ответами и пояснениями. Двигайтесь с каждым шагом решения процесса, чтобы легко решать свои проблемы.
12 квадратных единиц
Подсчитайте количество квадратов, чтобы получить ответы. 1, 2, 3, 4, 5, 6, 7, 8,9, 10, 11, 12.
Площадь = 12 квадратных единиц.
Роберто строит платформу для своей модели железной дороги. Какова площадь платформы?
Площадь = ______ квадратных единиц
12 квадратных единиц
Площадь платформы = Подсчитайте общее количество квадратов, чтобы получить ответы. 1, 2, 3, 4, 5, 6, 7, 8,9, 10, 11, 12.
Площадь = 12 квадратных единиц.
Робер поставит рамку по краям платформы. Сколько границы ему понадобится?
Граница = ______ единиц
16 единиц
Чтобы узнать края платформы, нам нужно вычислить периметр заданной формы. Итак, нам нужно сложить длины всех сторон. 2 + 4 + 3 + 2 + 1 + 1 + 2 + 1 = 16 единиц.
2 + 4 + 3 + 2 + 1 + 1 + 2 + 1 = 16 единиц. Область понимания – страница № 648
Джош использовал резиновые ленты, чтобы сделать фигуру, показанную ниже, на своей геоборде. Чему равна площадь фигуры?
Опции:
а. 3 квадратных блока
b. 4 квадратных блока
c. 5 квадратных единиц
d. 6 квадратных единиц
а. 3 квадрата
Если Джош использовал резиновые ленты, чтобы сделать фигуру, показанную ниже, на своей геоборде, он может разделить фигуру на 2 меньшие правильные фигуры.
Фигура 1, отмеченная как квадрат = 1 квадратная единица.
Фигура 2, отмеченная как прямоугольник = 2 квадрата.
Общая площадь = Форма 1 + Форма 2 = 1 + 2 = 3 квадратных единицы.
Вильма нарисовала фигуру, показанную ниже, на точечной бумаге. Какова площадь фигуры, которую она нарисовала?
Опции:
а. 4 квадратных блока
b. 5 квадратных единиц
5 квадратных единиц
c. 6 квадратных единиц
d. 7 квадратных единиц
б. 5 квадратных единиц
Вильма нарисовала фигуру, показанную ниже, на точечной бумаге.
Площадь фигуры = количество объединенных квадратных блоков = 1 + 1 + 1 + 1 + 1 = 5 квадратных единиц.
Леонардо знает, что до летних каникул осталось 42 дня. Сколько недель осталось до летних каникул Леонардо? (Подсказка: в неделе 7 дней.)
Опции:
a. 5 недель
б. 6 недель
c. 7 недель
д. 8 недель
b. 6 недель
Леонардо знает, что до летних каникул осталось 42 дня. В неделе 7 дней. Итак, разделив 42 на 7, Леонардо найдет летние каникулы в неделях. 42/7 = 6 недель.
Нэн разрезала бутерброд с подводной лодки на 4 равные части и съела одну часть. Какая дробь представляет часть бутерброда, которую съела Нэн?
Опции:
а. \(\frac{1}{4}\)
\(\frac{1}{4}\)
б. \(\frac{1}{3}\)
c. \(\frac{4}{4}\)
d. \(\frac{4}{1}\)
а. \(\frac{1}{4}\)
Нэн разрезала бутерброд на 4 равные части и съела одну часть. Итак, оставшихся частей 3. Доля сэндвича, который Нан съел = \(\frac{1}{4}\).
Ванда завтракает. В какое разумное время Ванда завтракает?
Опции:
а. 7:45 утра
б. 19:45
г. 14:15
д. 2:15 утра
а. 7:45 утра
Разумное время для завтрака Ванды — 7:45 утра. Потому что завтрак будет съеден утром, т.е.
У Дика есть 2 пакета собачьего корма. В каждом мешке 5 кг еды. Сколько всего килограммов еды у Дика?
Опции:
а. 3 килограмма
б. 5 килограммов
гр. 7 килограммов
d. 10 килограммов
d. 10 килограммов
У Дика всего 2 x 5 = 10 кг еды. Измерение площади – № страницы 653
 Каждая единица квадрата равна 1 квадратному сантиметру.
Каждая единица квадрата равна 1 квадратному сантиметру.
Площадь 14 квадратных сантиметров.
14 квадратных сантиметров
Количество единичных квадратов на данной фигуре равно 14. Значит, площадь фигуры = 14 квадратных сантиметров.
Площадь = ________ квадратных сантиметров
16 квадратных сантиметров
Площадь фигуры = 16 квадратных сантиметров.
Площадь = ________ квадратных сантиметров
11 квадратных сантиметров
Площадь фигуры = 11 квадратных сантиметров.
Площадь = ________ квадратных сантиметров
22 квадратных сантиметра
Площадь фигуры = 22 квадратных сантиметра. Используйте диаграмму справа для 5–6. Каждая единица площади равна 1 квадратному метру.
Используйте диаграмму справа для 5–6. Каждая единица площади равна 1 квадратному метру.
Какова часть колоды, которую Алан уже закрасил серым цветом?
_______ квадратных метров
16 квадратных метров
Площадь колоды, которую Алан уже покрасил в серый цвет, составляет 16 квадратных метров.
Какова площадь колоды, которую Алану осталось закрасить?
_______ квадратных метров
19 квадратных метров
Площадь колоды, которую Алану осталось покрасить, составляет 19 квадратных метров. Измерение площади – № страницы 654
Сколько квадратных футов заштриховано?
Опции:
а. 19 квадратных футов
б. 21 кв. фут
c. 23 квадратных фута
д. 25 квадратных футов
25 квадратных футов
c. 23 квадратных фута
Какая площадь НЕ была заштрихована?
Опции:
а. 19 квадратных футов
б. 21 кв. фут
c. 23 квадратных фута
д. 25 квадратных футов
а. 19 квадратных футов
Соня покупает 6 упаковок булочек. В каждой упаковке 6 рулонов. Сколько булочек покупает Соня?
Опции:
а. 42
б. 36
г. 24
д. 12
б. 36
6 x 6 = 36. Соня покупает 36 рулонов.
Чарли смешал 6 литров сока с 2 литрами содовой, чтобы сделать фруктовый пунш. Сколько литров фруктового пунша приготовил Чарли?
Опции:
а. 3 литра
б. 4 литра
в. 8 литров
д. 12 литров
c. 8 литров
6 + 2 = 8 литров. Чарли может приготовить 8 литров фруктового пунша.
На каком рисунке \(\frac{2}{3}\) заштрихован круг?
Опции:
а.
б.
с.
д.
d.
Вариант d — правильный ответ. 2/3 означает, что весь круг состоит из 3 частей. 2 части заштрихованы.
Используйте модели, чтобы назвать дробь, эквивалентную \(\frac{1}{2}\).
Опции:
а. \(\frac{2}{1}\)
б. \(\frac{2}{2}\)
c. \(\frac{2}{4}\)
d. \(\frac{4}{4}\)
c. \(\frac{2}{4}\)
\(\frac{2}{4}\) = \(\frac{1}{2}\). Таким образом, ответ: \(\frac{2}{4}\) Используйте модели площадей – № страницы 659
24 квадратных фута
Есть 3 ряда по 8 квадратов.
3 x 8 = 24.
Каждая единица площади равна 1 квадратному метру.
16 квадратных футов
Имеется 4 ряда по 4 единичных квадрата.
4 х 4 = 16 квадратных футов.
_________ квадратных метров
12 квадратных метров
Есть 2 ряда по 6 квадратов.
2 х 6 = 12 квадратных метров.
_________ квадратных метров
24 квадратных метра
Имеется 4 ряда по 6 единиц квадратов.
4 х 6 = 24 квадратных метра.
_________ квадратных метров
15 квадратных метров
Имеется 5 рядов по 3 квадрата.
5 х 3 = 15 квадратных метров.
Лэндон сделал коврик для прихожей. Каждая единица площади равна 1 квадратному футу. Какова площадь коврика?
_________ квадратных футов
20 квадратных футов
Подсчитайте количество квадратных коробок = 20 квадратных футов. Или есть 2 ряда по 10 квадратов.
Или есть 2 ряда по 10 квадратов.
2 х 10 = 20 квадратных футов.
Ева делает рамку в верхней части рамки. Каждая единица квадрата равна 1 квадратному дюйму. Какова площадь границы?
_________ квадратных футов
8 квадратных футов
Подсчитайте количество квадратных коробок = 20 квадратных футов. Или есть 1 ряд из 8 единичных квадратов.
1 x 8 = 8 квадратных футов. Использование моделей – страница № 660
Пол у входа в офис выложен плиткой. Каждая квадратная плитка равна 1 квадратному метру. Какова площадь пола?
Опции:
а. 8 квадратных метров
г. до н.э. 9 кв.м.
гр. 10 квадратных метров
р. 12 квадратных метров
b. 9 квадратных метров
Имеется 9 квадратных коробок. Итак, площадь пола = 9 квадратных метров.
Мисс Бернс покупает новый ковер. Каждая единица площади равна 1 квадратному футу. Какова площадь коврика?
Каждая единица площади равна 1 квадратному футу. Какова площадь коврика?
Опции:
а. 5 квадратных футов
б. 7 квадратных футов
c. 10 квадратных футов
д. 12 квадратных футов
г. 10 квадратных футов
Площадь ковра = 10 квадратных футов.
Энн и Билл сравнивают полоски дробей. Какое утверждение является правильным?
Опции:
а. \(\frac{3}{8}>\frac{5}{8}\)
б. \(\frac{3}{4}<\frac{1}{4}\)
c. \(\frac{3}{6}>\frac{4}{6}\)
d. \(\frac{1}{3}<\frac{2}{3}\)
d. \(\frac{1}{3}<\frac{2}{3}\)
Знаменатели данных дробей совпадают. Итак, сравните числители, чтобы найти правильный ответ.
3 > 5 неправильно.
3 < 1 неправильно.
3 > 4 неправильно.
1 < 2 верно.
Ответ \(\frac{1}{3}<\frac{2}{3}\).
Клэр купила 6 пачек бейсбольных карточек. В каждой колоде было одинаковое количество карт. Если Клэр купила всего 48 бейсбольных карточек, сколько карточек было в каждой пачке?
В каждой колоде было одинаковое количество карт. Если Клэр купила всего 48 бейсбольных карточек, сколько карточек было в каждой пачке?
Опции:
а. 54
б. 42
в. 8
д. 6
c. 8
6 x k = 48. Таким образом, k = 48/6 = 8.
В каждой колоде было 8 карт.
Остин ушел в школу в 7:35 утра. Он пришел в школу через 15 минут. Во сколько Остин пришел в школу?
Опции:
а. 7:40 утра
б. 7:50 утра
с. 7:55 утра
д. 8:00 УТРА.
b. 7:50 утра
7:35 утра. + 15 минут = 7:50
Комната Вятта представляет собой прямоугольник с периметром 40 футов. Ширина комнаты 8 футов. Какова длина комнаты?
Опции:
а. 5 футов
б. 12 футов
в. 16 футов
д. 32 фута
б. 12 футов
Периметр прямоугольника = 40 футов.
Ширина комнаты 8 футов.
8 + k + 8 + k = 40.
Если k = 10 -> 8 + 10 + 8 + 10 = 36.
Если k = 11 -> 8 + 11 + 8 + 11 = 38.
Если k = 12 -> 8 + 12 + 8 + 12 = 40.
Итак, длина комнаты = 12 футов. Контрольная точка середины главы – № страницы 661
Расстояние вокруг фигуры _____________ .
_____________
Периметр
Мерой количества единичных квадратов, необходимых для покрытия фигуры без пропусков и перекрытий, является ___________ .
_____________
Площадь
_______ сантиметров
16 сантиметров
5 + 2 + 2 + 1 + 2 + 1 + 1 + 2 = 16 сантиметров.
_______ сантиметров
14 см
4 + 3 + 4 + 3 = 14 см.
Периметр = 33 сантиметра
г = ______ сантиметров
3 сантиметра
Учитывая, что периметр = 33 сантиметра.
10 + 6 + 10 + г + 4 = 33 сантиметра.
30 + г = 33 сантиметра.
г= 33 – 30 сантиметров.
г = 3 сантиметра.
Периметр = 32 фута
k = ______ футов
4 фута
Периметр = 32 фута.
12 футов + k + 12 футов + k = 32 фута.
Если k = 1, то 12 + 1 + 12 + 1 = 26 футов не равно 32 футам.
Если k = 2, то 12 + 2 + 12 + 2 = 28 футов не равно 32 футам.
Если k = 3, то 12 + 3 + 12 + 3 = 30 футов не равно 32 футам.
Если k = 4, то 12 + 4 + 12 + 4 = 32 фута равно 32 футам.
Итак, k = 4 фута.
______ квадратные метры
14 квадратных метров
______ квадратные метры
30 квадратных метров
9 10 10 10 10 1010 29 910 29 910 10 10 10 1010 29 10 1010 29 10 101029 910 29 10 1010 29 10 10 1010 299 10 1010 29 10 1010 29 910 29 910 29. Контрольная точка середины главы – страница № 662
Рамона делает крышку для своей прямоугольной шкатулки для драгоценностей. Шкатулка для драгоценностей имеет длину сторон 6 сантиметров и 4 сантиметра. Какова площадь крышки, которую делает Рамона?
______ квадратных метров
24 квадратных метра.
Площадь крышки = 4 см x 6 см = 24 см.
Рамона делает крышку 24 см для своей прямоугольной шкатулки.
Эдриен украшает квадратную рамку для картины. Она приклеила 36-дюймовую ленту по краю рамки. Какова длина каждой стороны рамки картины?
a = ______ дюймов
9 дюймов
=Квадрат имеет одинаковую длину.
Длина каждой стороны 4 х а = 36 дюймов.
а = 36/4 = 9 дюймов.
Марго подметет комнату. Схема пола, который ей нужно подмести, показана справа. Какова площадь пола?
______ квадратных единиц
27 квадратных единиц
27 квадратных единиц
Джефф делает плакат для автомойки для Campout Club. Чему равен периметр плаката?
______ футов
8 футов
Периметр = 3 + 1 + 3 + 1 = 8 футов. дюймы. Чему равен периметр прямоугольника? Чему равна площадь прямоугольника?
Периметр ______ дюймов
Площадь = ______ квадратных дюймов
Периметр = 36 дюймов.
Площадь = 80 квадратных дюймов.
Периметр прямоугольника = 8 + 10 + 8 + 10 = 36,
Площадь = 10 х 8 = 80 квадратных дюймов. Решение задач Площадь прямоугольников – № страницы 667

Заполните таблицу, чтобы найти площадь каждой фрески. Фреска Длина (в метрах) Ширина (в метрах) Площадь (в квадратных метрах) А 2 1 2 Б 2 2 4 С 2 __4_______ __8_______ Д 2 ____8_____ ___16______
Найдите и опишите закономерность изменения длины и ширины фресок от A до D.
Введите ниже:
_____________
Для каждой фрески ширина удваивается, а длина остается прежней.
Как меняются площади фресок при изменении ширины?
Введите ниже:
_____________
Для каждой фрески площадь удваивается.
Дэн построил настил длиной 5 футов и шириной 5 футов. Он построил еще одну колоду длиной 5 футов и шириной 7 футов. Он построил третью палубу длиной 5 футов и 9ноги в ширину. Как меняются площади?
Введите ниже:
_____________
Площадь каждой палубы увеличивается на 10 квадратных футов.
Площадь 1-й палубы = 5 x 5 = 25 футов.
Площадь второй палубы = 5 x 7 = 35 футов.
Площадь 3-й палубы = 5 x 9 = 45 футов.
Площадь каждой палубы увеличена на 10 квадратных футов. Решение задач Площадь прямоугольников – № страницы 668
Лорен нарисовала рисунки ниже. Каждая единица квадрата равна 1 квадратному сантиметру. Если шаблон продолжится, какова будет площадь четвертой фигуры?
Опции:
а. 10 квадратных сантиметров
б. 12 квадратных сантиметров
c. 14 квадратных сантиметров
д. 16 квадратных сантиметров
б. 12 квадратных сантиметров
12 квадратных сантиметров
4 x 3 = 12 см. Площадь четвертой фигуры равна 12 квадратных сантиметров.
Генри построил сад шириной 3 фута и длиной 3 фута. Он также построил сад шириной 3 фута и длиной 6 футов, а также сад шириной 3 фута и длиной 9 футов.ноги длинные. Как меняются площади?
Опции:
а. Площади не меняются.
б. Площади удваиваются.
с. Площадь увеличилась на 3 кв.
д. Площадь увеличилась на 9 кв.
d. Площадь увеличилась на 9 кв.
1-й сад = 3 x 3 = 9 футов.
2-й сад = 3 х 6 = 18 футов.
3-й сад = 3 х 9 = 27 футов.
Площадь увеличивается на 9 квадратных футов.
Джо, Джим и Джек делят 27 футбольных карточек поровну. Сколько карточек получил каждый мальчик?
Опции:
а. 7
б. 8
г. 9
д. 10
c. 9
x + x + x = 27.
3x = 27.
x = 27/3 = 9.
Каждый мальчик получает по 9 футбольных карточек.
Нита использует \(\frac{1}{3}\) коробки с 12 яйцами. Сколько яиц она использует?
Опции:
а. 3
б. 4
г. 6
д. 9
b. 4
\(\frac{1}{3}\) коробки с 12 яйцами = \(\frac{1}{3}\) x 12 = 4.
Нита использует 4 яйца.
Бренда сделала 8 ожерелий. Каждое ожерелье состоит из 10 больших бусин. Сколько больших бусин использовала Бренда, чтобы сделать ожерелья?
Опции:
а. 80
б. 85
г. 90
д. 100
а. 80
8 x 10 = 80 бусин.
Бренда использует 80 бусин, чтобы сделать ожерелья
Нил укладывает плитку на пол на кухне. Каждая квадратная плитка равна 1 квадратному футу. Нил использует 6 рядов плиток по 9 плиток в каждом ряду. Какова площадь пола?
Опции:
а. 15 квадратных футов
б. 52 квадратных фута
52 квадратных фута
c. 54 квадратных фута
д. 57 квадратных футов
c. 54 квадратных фута
Площадь пола = 6 x 9 = 54 квадратных фута. Площадь объединенных прямоугольников – № страницы 673
Покажите свои уравнения умножения и сложения.
28 квадратных единиц
______ Квадратные единицы
27 квадратных единиц
9 + 18 = 27
27 квадратных единиц.
Введите ниже:
_____________
31 квадратная единица
5 x 5 = 25; 2 x 3 = 6
25 + 6 = 31
31 квадратная единица
Введите ниже:
_____________
32 квадратных единицы
16 + 16 = 32.
32 квадрата
Нарисуйте линию, чтобы разделить форму комнаты Фрэнка на прямоугольники.
Какова общая площадь комнаты Фрэнка?
_______ квадратных футов
75 квадратных футов
6 x 5 = 30; 5 x 9 = 45
30 + 45 = 75.
75 квадратных футов Площадь объединенных прямоугольников – № страницы 674
На схеме показан задний двор Бена. Каждая единица площади равна 1 квадратному ярду. Какова площадь заднего двора Бена?
Опции:
а. 12 квадратных метров
б. 16 квадратных метров
16 квадратных метров
c. 18 квадратных метров
д. 24 квадратных ярда
b. 16 квадратных ярдов
6 x 3 = 18 квадратных ярдов
На рисунке показана комната в художественной галерее. Каждая единица площади равна 1 квадратному метру. Какова площадь комнаты?
Опции:
г. н.э. 24 квадратных метра
б. 30 квадратных метров
c. 36 кв.м.
р. 40 квадратных метров
b. 30 квадратных метров
3 x 5 = 15; 3 x 5 = 15
15 + 15 = 30 квадратных метров
Наоми нужно решить 28 ÷ 7 = ■. Какой связанный факт умножения она может использовать, чтобы найти неизвестное число?
Опции:
а. 3 × 7 = 21
б. 4 × 7 = 28
в. 5 × 7 = 35
г. 6 × 7 = 42
b. 4 × 7 = 28
28 ÷ 7 = 4. Итак, ответ 4 x 7 = 28.
Карен нарисовала треугольник со сторонами 3 сантиметра, 4 сантиметра и 5 сантиметров. Чему равен периметр треугольника?
Опции:
а. 7 сантиметров
б. 9 сантиметров
в. 11 сантиметров
д. 12 сантиметров
d. 12 сантиметров
Периметр = 3 сантиметра + 4 сантиметра + 5 сантиметров = 12 сантиметров.
Прямоугольник разделен на равные части. Как называются равные части?
Опции:
а. половина
б. третий
c. четвертый
д. шестой
c. четвертый
Используйте дюймовую линейку. Какова длина этого отрезка с точностью до полдюйма?
Опции:
а. 1
б. 1 \(\frac{1}{2}\)
c. 2
д. 2 \(\frac{1}{2}\)
c. 2
Отрезок = 2 дюйма. Тот же периметр, разные площади — № страницы 679
Укажите, какой прямоугольник имеет большую площадь.
A: Периметр = 12 ;
Площадь = 9 квадратных единиц
Площадь = ______ квадратных единиц;
Прямоугольник ______ имеет большую площадь.
Прямоугольник A имеет большую площадь.
A: Периметр = 12 ;
Площадь = 9 квадратных единиц
B: Периметр = 2 + 4 + 2 + 4 = 12
Площадь = 2 x 4 = 8 квадратных единиц
Прямоугольник A имеет большую площадь.
A: периметр = ______ единиц;
Площадь = ______ квадратных единиц;
Площадь = ______ квадратных единиц;
Прямоугольник ______ имеет большую площадь.
Прямоугольник A имеет большую площадь.
Площадь = 4 x 1 = 4 квадратных единицы
B: Периметр = 3 + 2 + 3 + 2 = 10
Площадь = 3 x 2 = 6 квадратных единиц
Прямоугольник B имеет большую площадь.
Спальни Тары и Джоди имеют форму прямоугольника. Спальня Тары 9 футов в длину и 8 футов в ширину. Спальня Джоди имеет 7 футов в длину и 10 футов в ширину. Чья спальня имеет большую площадь? Объяснять. Спальня
_________ больше.
Спальня Тары имеет большую площадь, чем спальня Джоди.
Площадь спальни Тары = 9 x 8 = 72 фута.
Площадь спальни Джоди = 7 х 10 = 70 футов.
72 фута > 70 футов.
Спальня Тары имеет большую площадь, чем спальня Джоди.
Г-ну Санчесу нужно оградить прямоугольный сад длиной 16 футов. Он хочет, чтобы сад имел максимально возможную площадь. Какой длины должны быть стороны сада?
Ширина: ______ Длина: ______ футов в длину
Все четыре стороны должны быть 4 фута в длину.
У мистера Санчеса есть 16-футовая ограда для прямоугольного сада.
Периметр = 1 + 7 + 1 + 7 = 16 футов. Площадь = 1 х 7 = 7 футов.
Площадь = 1 х 7 = 7 футов.
Периметр = 2 + 6 + 2 + 6 = 16 футов. Площадь = 2 х 6 = 12 футов.
Периметр = 3 + 5 + 3 + 5 = 16 футов. Площадь = 3 х 5 = 15 футов.
периметр = 4 + 4 + 4 + 4 = 16 футов. Площадь = 4 х 4 = 16 футов.
Площадь максимальна, когда все четыре стороны имеют длину 4 фута. Тот же периметр, разные области – № страницы 680
Какая фигура имеет периметр 12 единиц и площадь 8 квадратных единиц?
Опции:
а.
б.
с.
д.
b
Периметр = 2 + 4 + 2 + 4 = 12 единиц.
Площадь = 2 x 4 = 8 квадратных единиц
Все четыре прямоугольника ниже имеют одинаковый периметр. Какой прямоугольник имеет наибольшую площадь?
Опции:
а.
б.
с.
д.
d
а. Площадь = 2 х 10 = 20,
б. Площадь = 3 х 9 = 27,
ц. Площадь = 4 х 8 = 32,
д. Площадь = 5 x 7 = 35.
Площадь = 5 x 7 = 35.
d имеет наибольшую площадь.
Керри накрывает стол с 8 рядами квадратных плиток. В каждом ряду по 7 плиток. Какую площадь покрывает Керри в квадратных единицах?
Опции:
а. 15 квадратных единиц
b. 35 квадратных единиц
c. 42 квадратных блока
d. 56 квадратных единиц
d. 56 квадратных единиц
Площадь = 8 x 7 = 56.
Керри занимает площадь 56 квадратных единиц.
У фон есть прямоугольная мастерская с периметром 26 футов. Длина рабочего помещения 6 футов. Какова ширина рабочей комнаты Вон?
Опции:
а. 7 футов
б. 13 футов
в. 20 футов
д. 26 футов
а. 7 футов
Периметр = 26 футов.
Длина = 6 футов.
У данного Фона прямоугольная рабочая комната. Итак, у прямоугольника две длины и две ширины равны.
Периметр прямоугольника = Длина + Ширина + Длина + Ширина = 6 + Ш + 6 + Ш = 26 футов.
12 + 2 Вт = 26 футов.
2 Вт = 26 – 12 = 14.
Вт = 14/2 = 7 футов. Тот же периметр, разные площади – № страницы 685
A: Площадь = 8 квадратных единиц;
Периметр = 18 единиц;
Периметр = _______ единиц;
Периметр прямоугольника _______ больше.
Периметр прямоугольника A больше
A: Площадь = 8 квадратных единиц;
Периметр = 18 единиц;
B: Площадь = ___8____ квадратных единиц;
Периметр = ____12___ единиц;
Периметр прямоугольника ___A____ больше.
A: Площадь = _______ квадратных единиц;
Периметр = _______ единиц;
B: Площадь = _______ квадратных единиц;
Периметр = _______ единиц;
Периметр прямоугольника _______ больше.
Периметр прямоугольника B больше
A: Площадь = 12 квадратных единиц;
Периметр = 14 единиц;
B: Площадь = ___12____ квадратных единиц;
Периметр = ____16___ единиц;
Периметр прямоугольника ___B____ больше.
A: Площадь = _______ квадратных единиц;
Периметр = _______ единиц;
B: Площадь = _______ квадратных единиц;
Периметр = _______ единиц;
Периметр прямоугольника _______ больше.
Периметр прямоугольника B больше
A: Площадь = 16 квадратных единиц;
Периметр = 16 единиц;
B: Площадь = ___16____ квадратных единиц;
Периметр = ____20___ единиц;
Периметр прямоугольника ___B____ больше.
Сравните площади схемы A и схемы B.
Площадь схемы A ________ Площадь схемы B
Площади прямоугольника A и прямоугольника B равны.
A: Площадь = 20 квадратных единиц;
B: Площадь = ___20____ квадратных единиц;
Сравните периметры. У какой конструкции периметр больше?
Периметр A ________ Периметр B
Периметр A Больше периметра B
A: Периметр = 24 единицы ;
B: Периметр = ____18___ единиц; Тот же периметр, разные площади – № страницы 686
Джейк нарисовал два прямоугольника. Какое из утверждений верно?
Опции:
а. Периметры одинаковые.
б. Площадь А больше.
г. Периметр А больше.
д. Периметр B больше
d. Периметр B больше
A: Площадь = 6 квадратных единиц;
Периметр = 10 единиц;
B: Площадь = ___6____ квадратных единиц;
Периметр = ____14___ единиц;
Периметр B больше.
Алиса нарисовала два прямоугольника. Какое из утверждений верно?
Опции:
а. Периметр B больше.
б. Периметр А больше.
г. Площадь В больше.
д. Периметры одинаковые.
b. Периметр А больше.
A: Площадь = 18 квадратных единиц;
Периметр = 22 единицы;
B: Площадь = ___18____ квадратных единиц;
Периметр = ____18___ единиц;
Периметр A больше.
Машу попросили найти значение 8 – 3 x 2. Она написала неверный ответ. Какой правильный ответ?
Опции:
а. 22
б. 10
г. 4
д. 2
d. 2
8 – (3 x 2) = 8 – 6 = 2
Какая дробь обозначает точку на числовой прямой?
Опции:
а. \(\frac{1}{4}\)
б. \(\frac{2}{3}\)
c. \(\frac{3}{4}\)
d. \(\frac{3}{1}\)
c. \(\frac{3}{4}\)
Из данного рисунка мы можем записать имя дроби в точке на числовой прямой = \(\frac{3}{4}\)
Кайл нарисовал три отрезка такой длины: \(\frac{2}{4}\) дюйм, \(\frac{2}{3}\) дюйм и \(\frac{2) {6}\) дюйм. В каком списке дроби упорядочиваются от наименьшей к наибольшей?
Опции:
а. \(\frac{2}{6}, \frac{2}{4}, \frac{2}{3}\)
б. \(\frac{2}{3}, \frac{2}{4}, \frac{2}{6}\)
c. \(\frac{2}{4}, \frac{2}{3}, \frac{2}{6}\)
d. \(\frac{2}{6}, \frac{2}{3}, \frac{2}{4}\)
c. \(\frac{3}{4}\)
Даны дроби: \(\frac{2}{4}\) дюйм, \(\frac{2}{3}\) дюйм и \(\frac{2}{6}\) дюйм.
Все дроби имеют одинаковый числитель. Знаменатели должны сравнить, чтобы найти ответ. Меньший знаменатель представляет большее число. Итак, \(\frac{2}{6}, \frac{2}{4}, \frac{2}{3}\) — это ответ.
В понедельник выпало \(\frac{3}{8}\) дюймов снега. Во вторник выпало \(\frac{5}{8}\) дюймов снега. Какое утверждение правильно сравнивает количество снега?
Опции:
а. \(\frac{3}{8}=\frac{5}{8}\)
б. \(\frac{3}{8}<\frac{5}{8}\)
c. \(\frac{5}{8}<\frac{3}{8}\)
\(\frac{5}{8}<\frac{3}{8}\)
d. \(\frac{3}{8}>\frac{5}{8}\)
б. \(\frac{3}{8}<\frac{5}{8}\)
Даны дроби: \(\frac{3}{8}\) и \(\frac{5}{) 8}\).
Знаменатели у данных дробей равны. Итак, сравните числители, чтобы найти правильное уравнение.
3 < 5. Итак, \(\frac{3}{8}<\frac{5}{8}\) — правильный ответ. Обзор/Тест – Страница № 687
Найдите периметр каждой фигуры на сетке. Определите фигуру, периметр которой равен 14 единицам. Отметьте все подходящие варианты.
Опции:
а.
б.
с.
д.
a и c имеют периметр 14 единиц.
а. Периметр А = 14 единиц.
б. Периметр B = 16 единиц.
с. Периметр С = 14 единиц.
д. Периметр D = 16 единиц
Ким хочет обрезать рисунок, который она нарисовала. Сколько сантиметров обрезки нужно Киму по периметру картины?
_________ сантиметров
24 сантиметра
Периметр = 6 + 6 + 6 + 6 = 24 сантиметра.
София нарисовала этот прямоугольник на точечной бумаге. Чему равна площадь прямоугольника?
_________ квадратных единиц
8 квадратных единиц
8 квадратных единиц Обзор/Тест – Страница № 688
На рисунке показан план Сета на заднем дворе. Каждая единица площади равна 1 квадратному футу.
Какие уравнения может использовать Сет, чтобы найти площадь форта?
Отметьте все подходящие варианты.
Опции:
а. 4 + 4 + 4 + 4 = 16
б. 7 + 4 + 7 + 4 = 22
с. 7 + 7 + 7 + 7 = 28
д. 4 × 4 = 16
э. 7 × 7 = 49
ф. 4 × 7 = 28
b и f верны.
Площадь = 4 × 7 = 28
Периметр = 7 + 4 + 7 + 4 = 22.
Площадь какого прямоугольника равна количеству квадратных единиц его периметр?
Опции:
а.
б.
с.
д.
B прямоугольник имеет количество квадратных единиц площади, равное количеству единиц его периметра
a. Площадь = 1 х 7 = 7 единиц.
Площадь = 1 х 7 = 7 единиц.
Периметр = 1 + 7 + 1 + 7 = 16 единиц.
б. а. Площадь = 4 х 4 = 16 единиц.
Периметр = 4 + 4 + 4 + 4 = 16 единиц.
с. а. Площадь = 2 х 6 = 12 единиц.
Периметр = 2 + 6 + 2 + 6 = 16 единиц.
д. а. Площадь = 3 х 5 = 7 единиц.
Периметр = 3 + 5 + 3 + 5 = 16 единиц.
Ванесса рисует квадрат с помощью линейки. Периметр квадрата равен 12 сантиметрам. Выберите число, чтобы закончить предложение.
_________ сантиметров
3 сантиметра
Периметр = s + s + s + s = 12 сантиметров.
4s = 12 сантиметров.
с = 3 сантиметра. Повторение/Тест – Страница № 689
Томас нарисовал два прямоугольника на бумаге с сеткой.
Обведите слова, которые делают предложение верным.
Прямоугольник A имеет площадь, равную площади прямоугольника B, и периметр, равный периметру прямоугольника B. Прямоугольник B.
Прямоугольник B.
Периметр меньше периметра прямоугольника B.
A: Площадь = 3 x 4 = 12 единиц.
Периметр = 3 + 4 + 3 + 4 = 14 единиц.
B: Площадь = 2 x 6 = 12 единиц.
Периметр = 2 + 6 + 2 + 6 = 16 единиц.
Юдзи нарисовал эту фигуру на бумаге с сеткой. Чему равен периметр фигуры?
________ единиц
18 единиц
Какова площадь изображенной фигуры? Каждая единица площади равна 1 квадратному метру.
________ квадратных метров
13 квадратных метров Обзор/Тест – Страница № 690
Шон нарисовал прямоугольник шириной 2 единицы и длиной 6 единиц. Нарисуйте другой прямоугольник с таким же периметром, но другой площадью.
Введите ниже:
_____________
Площадь = 2 x 6 = 12 квадратных единиц.
Площадь = 4 x 4 = 16 квадратных единиц.
Миссис Риос обклеила комнату, показанную ниже, окантовкой обоев. Она использовала 72 фута границы обоев. Чему равна неизвестная длина стороны? Показать свою работу.
a = ________ футов
16 футов
20 + a + 6 + 8 + 14 + 8 = 72 фута.
а + 56 = 72 фута.
а = 72 – 56 футов.
а = 16 футов.
Во дворе Элизабет есть два сада. Первый сад имеет длину 8 футов и ширину 6 футов. Второй сад составляет половину длины первого сада. Площадь второго сада в два раза больше площади первого сада. Для чисел 12a–12d выберите True или False.
Длина второго сада = половина длины первого сада = 4 фута.
Площадь второго сада = Удвоенная площадь первого сада = 2 x 48 = 96.
Ширина второго сада = 4 x s = 96.
s = 96/4 = 24
я. Правда
ii. Ложь
i. Правда
Правда
b. Площадь второго сада составляет 24 квадратных метра.
я. Правда
ii. Неверно
ii. Ложь
c. Ширина второго сада 12 футов.
я. Правда
ii. Неверно
ii. Ложь
d. Ширина второго сада составляет 24 фута.
я. Правда
ii. Ложь
i. Правда Обзор/Тест – Страница № 691
Маркус купил несколько открыток. Каждая открытка имела периметр 16 дюймов. Какая могла быть одна из открыток, купленных Маркусом? Отметьте все подходящие варианты.
Опции:
а.
б.
с.
д.
варианты a и d верны.
3 + 5 + 3 + 5 = 16 дюймов
4 + 6 + 4 + 6 = 20 дюймов.
5 + 10 + 5 + 10 = 30 дюймов.
4 + 4 + 4 + 4 = 16 дюймов.
Энтони хочет сделать две разные прямоугольные клумбы, каждая площадью 24 квадратных фута. Вокруг каждой клумбы он соорудит деревянный каркас. Боковые клумбы будут иметь целые числа.
Вокруг каждой клумбы он соорудит деревянный каркас. Боковые клумбы будут иметь целые числа.
Часть A
Каждая единица измерения в приведенной ниже сетке равна 1 квадратному футу. Нарисуйте две возможные клумбы. Обозначьте каждую буквой.
Введите ниже:
__________
Часть B
Какая из клумб возьмет больше дерева на каркас?
Объясни, откуда ты знаешь.
Введите ниже:
__________
Периметр A больше периметра B.
Площадь = 24.
3 x 8 = 24; 4 х 6 = 24,
А Периметр = 8 + 3 + 8 + 3 = 22 фута.
B Периметр = 4 + 6 + 4 + 6 = 20 футов.
Периметр A больше периметра B. Обзор/Тест – Страница № 692
Кейша рисует набросок своей гостиной на бумаге с сеткой. Каждая единица площади равна 1 квадратному метру. Напишите и решите уравнение умножения, с помощью которого можно найти площадь гостиной в квадратных метрах.
Введите ниже:
__________
40 метров.
4 х 10 = 40 м.
Мистер Викс проектирует дома. Он использует бумагу с сеткой, чтобы спланировать новый дизайн дома. Кухня будет иметь площадь от 70 квадратных футов до 85 квадратных футов. Кладовая будет иметь площадь от 4 квадратных футов до 15 квадратных футов. Нарисуйте и подпишите схему, чтобы показать, что мог спроектировать мистер Уикс. Объясните, как найти общую площадь.
Введите ниже:
__________
78 квадратных футов
Площадь кухни = 8 x 9= 72 квадратных фута. (70 < 72 < 85)
Площадь кладовой = 3 x 2 = 6 квадратных футов. (4 < 6 < 15)
Общая площадь кухни и кладовой = 72 + 6 = 78 квадратных футов. Заключение


 Рада всех видеть, садитесь.
Рада всех видеть, садитесь.
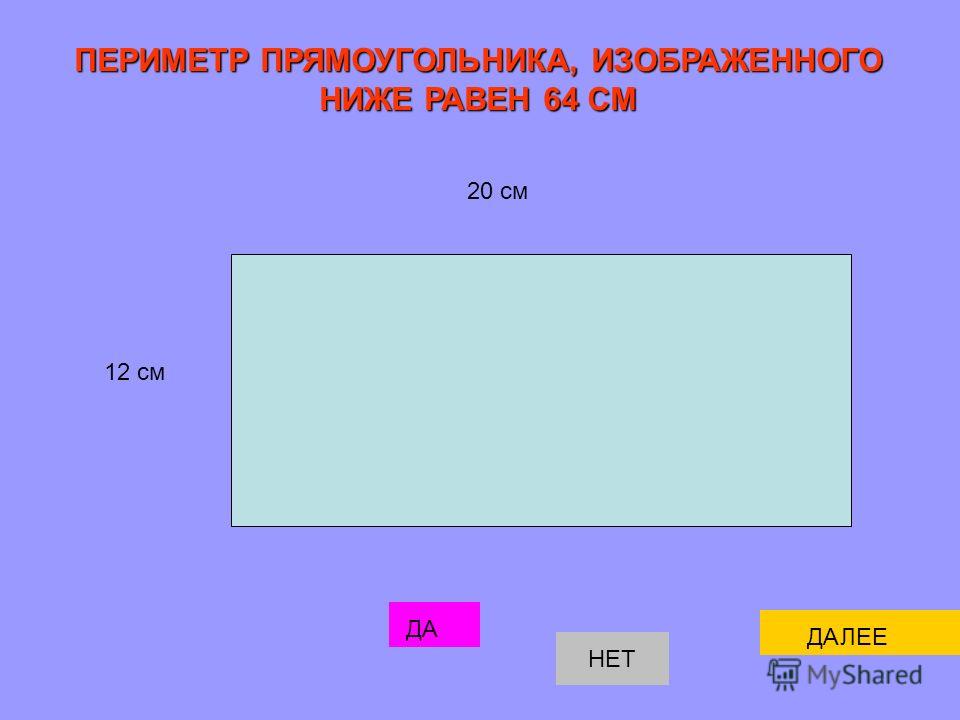
 (14 февраля)
(14 февраля)
 S = a • b
S = a • b Перед вами таблица с правилами, прочитайте правила.
Перед вами таблица с правилами, прочитайте правила.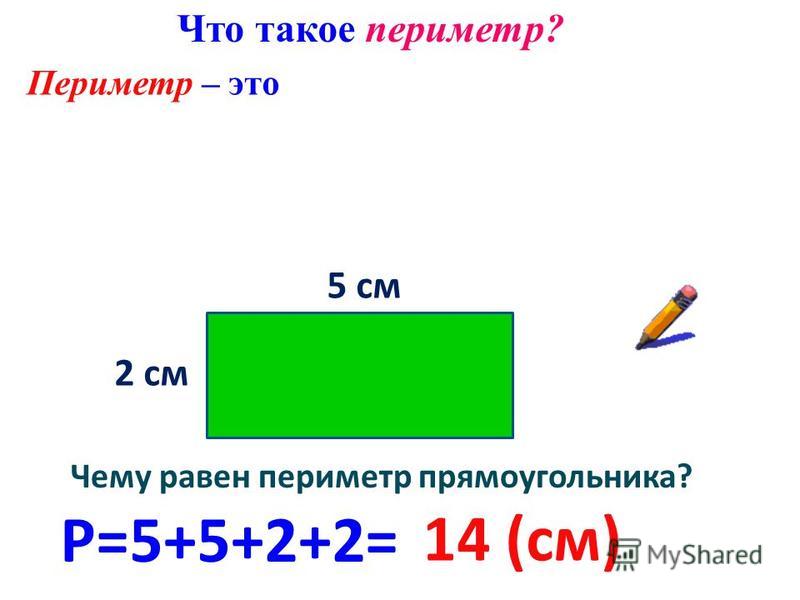




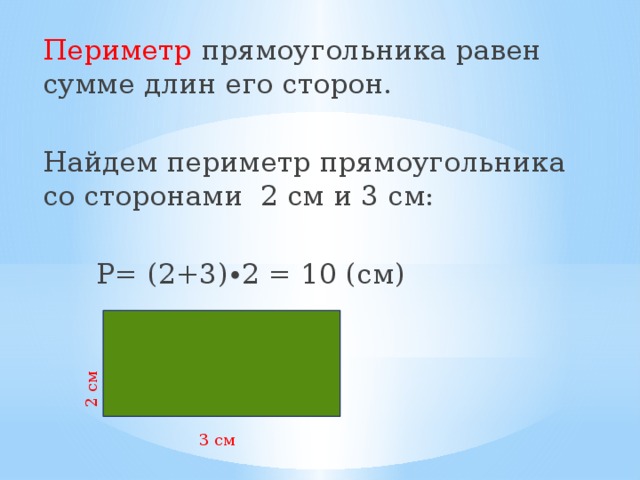

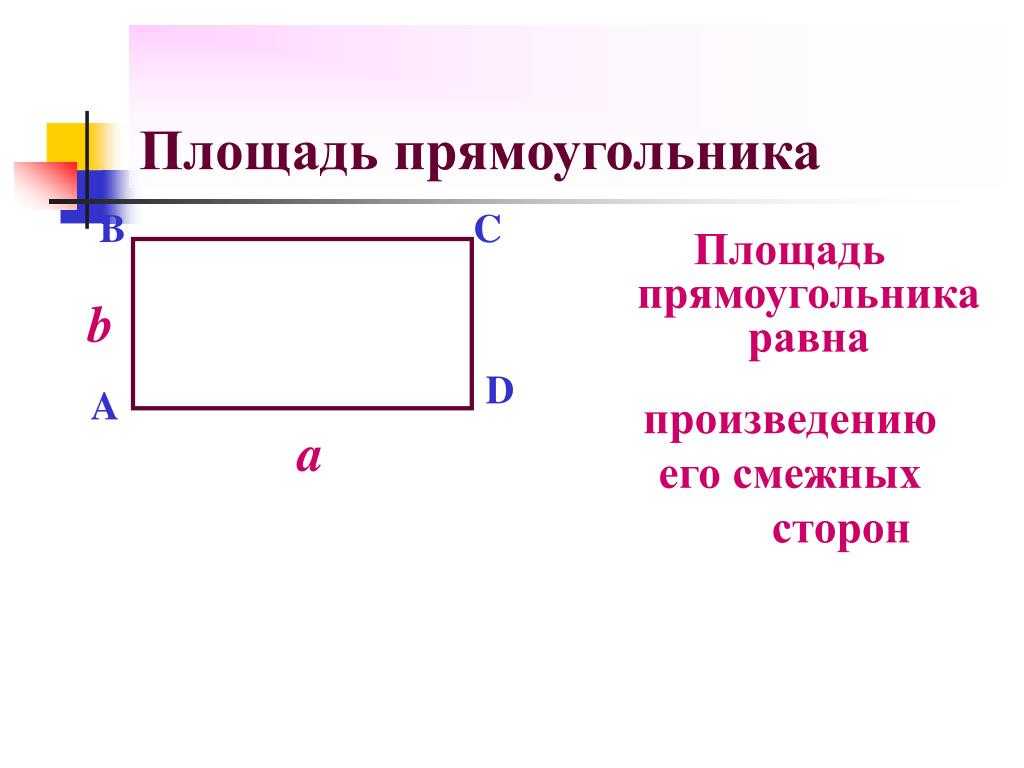

 )
) Самоопределение к деятельности (1 – 2 мин)
Самоопределение к деятельности (1 – 2 мин)
 (5-6 мин.)
(5-6 мин.)



 Каким образом получите искомое вами число -21?
Каким образом получите искомое вами число -21?


 55 № 3
55 № 3
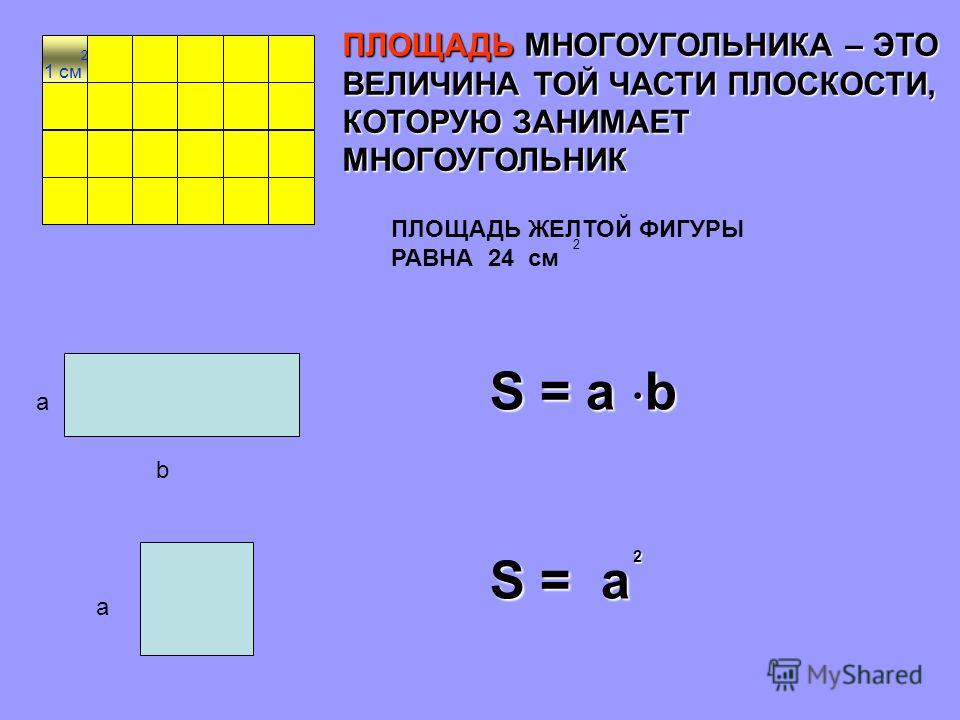


 Творческое задание. Придумать задачу на нахождение площади прямоугольника для своего друга.
Творческое задание. Придумать задачу на нахождение площади прямоугольника для своего друга.
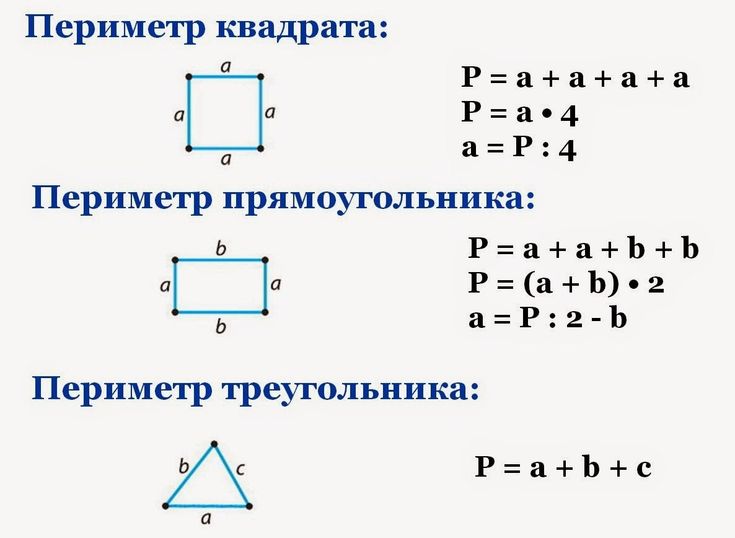
 Длина хвоста обезьяны 65 см. Сколько это дм и см? (6 дм 5 см)
Длина хвоста обезьяны 65 см. Сколько это дм и см? (6 дм 5 см) Чему равно произведение? (6)
Чему равно произведение? (6) е 2х6)
е 2х6)