Формула периметра квадрата и прямоугольника: Периметр прямоугольника, квадрата и ромба

alexxlab / / Разное

§ Периметр. Как найти периметр прямоугольника, квадрата и треугольника

Похоже, вы используете блокировщик рекламы. Наш сайт существует и развивается только за счет дохода от рекламы.

Пожалуйста, добавьте нас в исключения блокировщика.

Скрыть меню

На главную страницу

Войти при помощи

Темы уроков

Начальная школа

  • Геометрия: начальная школа
  • Действия в столбик
  • Деление с остатком
  • Законы арифметики
  • Периметр
  • Порядок действий
  • Разряды и классы. Разрядные слагаемые
  • Счет в пределах 10 и 20

Математика 5 класс

  • Взаимно обратные числа и дроби
  • Десятичные дроби
  • Натуральные числа
  • Нахождение НОД и НОК
  • Обыкновенные дроби
  • Округление чисел
  • Перевод обыкновенной дроби в десятичную
  • Площадь
  • Проценты
  • Свойства сложения, вычитания, умножения и деления
  • Среднее арифметическое
  • Упрощение выражений
  • Уравнения 5 класс
  • Числовые и буквенные выражения

Математика 6 класс

  • Масштаб
  • Модуль числа
  • Окружность. Площадь круга
  • Отношение чисел
  • Отрицательные и положительные числа
  • Периодическая дробь
  • Признаки делимости
  • Пропорции
  • Рациональные числа
  • Система координат
  • Целые числа

Алгебра 7 класс

  • Алгебраические дроби
  • Как применять формулы сокращённого умножения
  • Многочлены
  • Одночлены
  • Системы уравнений
  • Степени
  • Уравнения
  • Формулы сокращённого умножения
  • Функция в математике

Геометрия 7 класс

  • Точка, прямая и отрезок
  • Что такое аксиома и теорема

Алгебра 8 класс

  • Квадратичная функция. Парабола
  • Квадратные неравенства
  • Квадратные уравнения
  • Квадратный корень
  • Неравенства
  • Системы неравенств
  • Стандартный вид числа
  • Теорема Виета

Алгебра 9 класс

  • Возрастание и убывание функции
  • Нули функции
  • Область определения функции
  • Отрицательная степень
  • Среднее
    геометрическое

Алгебра 10 класс

  • Иррациональные числа

Алгебра 11 класс

  • Факториал

Чтобы что-то получить, надо что-нибудь вложить.

Народная мудрость

на главную

Введите тему

Русский язык Поддержать сайт

Запомните!

Периметр — это сумма длин всех сторон многоугольника.

Иногда для вычисления периметра геометрических фигур используются специальные формулы, в которых периметр обозначается заглавной латинской буквой «P».

Периметр измеряется в единицах длины: мм, см, м, км и т.д.

При нахождении периметра мы рекомендуем писать название фигуры маленькими буквами под знаком «P», чтобы не забывать чей периметр вы находите.

Запомните!

Периметр прямоугольника — это сумма длины и ширины, умноженная на «2».

P = (a + b) · 2

, где «a» — длина прямоугольника, «b» — ширина прямоугольника.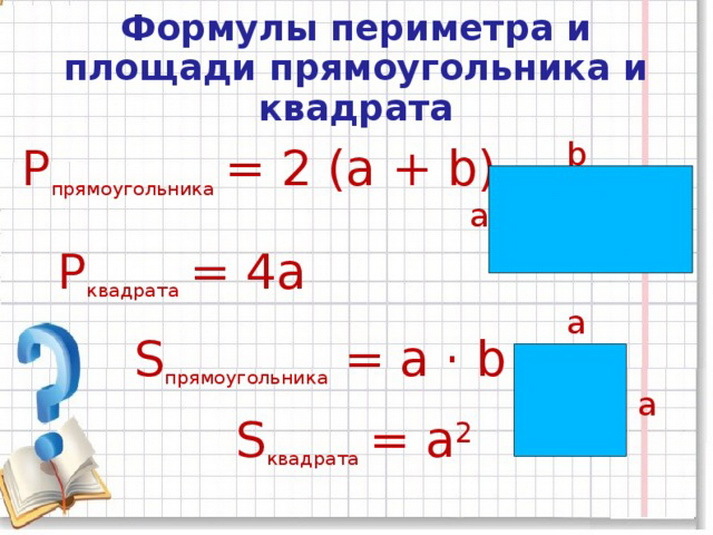

Стороны прямоугольника, которые лежат друг против друга (противолежащие), мы называем длиной и шириной.

AB = 3 см, BC = 7 см

PABCD = (AB + BC) · 2
PABCD = (7 + 3) · 2 = 10 · 2 = 20 (см)

Запомните!

Периметр квадрата — это длина стороны квадрата, умноженная на «4».

P = a · 4

, где a — длина стороны квадрата.

KE = 7 см

PEKFM = 4 · KE
PEKFM = 4 · 7 = 28 (см)

Периметр любого многоугольника (в том числе и периметр треугольника

) рассчитывается по определению периметра. Для этого надо просто сложить длины всех сторон многоугольника.

PABCDE = AB + BC + CD + DE + EA = 3 + 4 + 3 + 2 + 2 = 14 (см)

Формулы периметра и программы для расчета периметра

Содержание:

  • Формула периметра круга (длины окружности):
  • Формула периметра треугольника:
  • Формула периметра прямоугольника:
  • Формулы периметра квадрата:
  • Формула периметра трапеции:
  • Формула периметра параллелограмма:
  • Формула периметра ромба:

Периметр геометрической фигуры — суммарная длина границ плоской геометрической фигуры. Периметр имеет ту же размерность величин, что и длина.


Формула периметра круга (длины окружности):

1) Периметр круга равен произведению радиуса на два пи (3.1415).

P — Периметр круга (длина окружности)

π — число пи (3.1415)

r — радиус круга (окружности)

См. также: Программа для расчета периметра круга (длины окружности).


Формула периметра треугольника:

1) Периметр треугольника равен сумме 3-ех его сторон (a, b, c).

P — периметр треугольника

a, b, c — длины сторон треугольника

См. также: Программа для расчета периметра треугольника.

Формула периметра прямоугольника:

1) Периметр прямоугольника равен удвоенной сумме 2-х его смежных сторон (a, b).

P — периметр прямоугольника

a — длина 1-ой стороны прямоугольника

b — длина 2-ой стороны прямоугольника

См.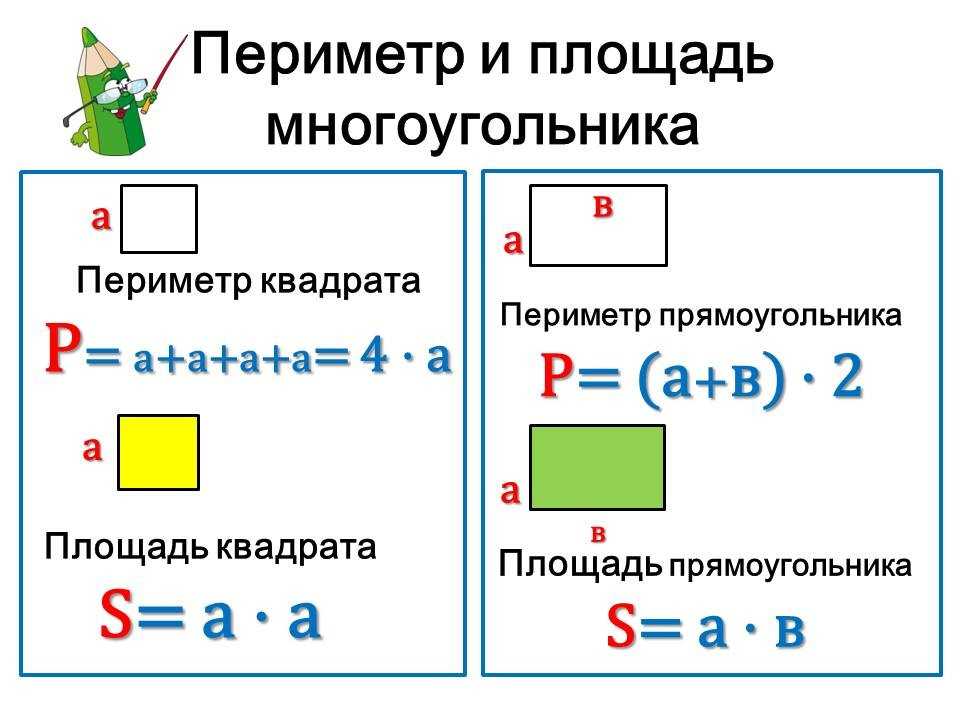 также: Программа для расчета периметра прямоугольника.


Формулы периметра квадрата:

1) Периметр квадрата равен сумме 4-х длин его сторон или произведению длины любой его стороны на четыре (так как у квадрат длины всех сторон равны).

2) Периметр квадрата равен произведению длины его диагонали на два корня из двух.

P — периметр квадрата

a — длина стороны квадрата

d — длина диагонали квадрата

См. также: Программа для расчета периметра квадрата.


Формула периметра трапеции:

1) Периметр трапеции равен сумме 4-х её сторон (a, b, c, d).

P — периметр трапеции

a, c — длины оснований трапеции

b, d — длины боковых сторон трапеции

См. также: Программа для расчета периметра трапеции.

Формула периметра параллелограмма:

1) Периметр параллелограмма равен удвоенной сумме 2-х его смежных сторон (a, b).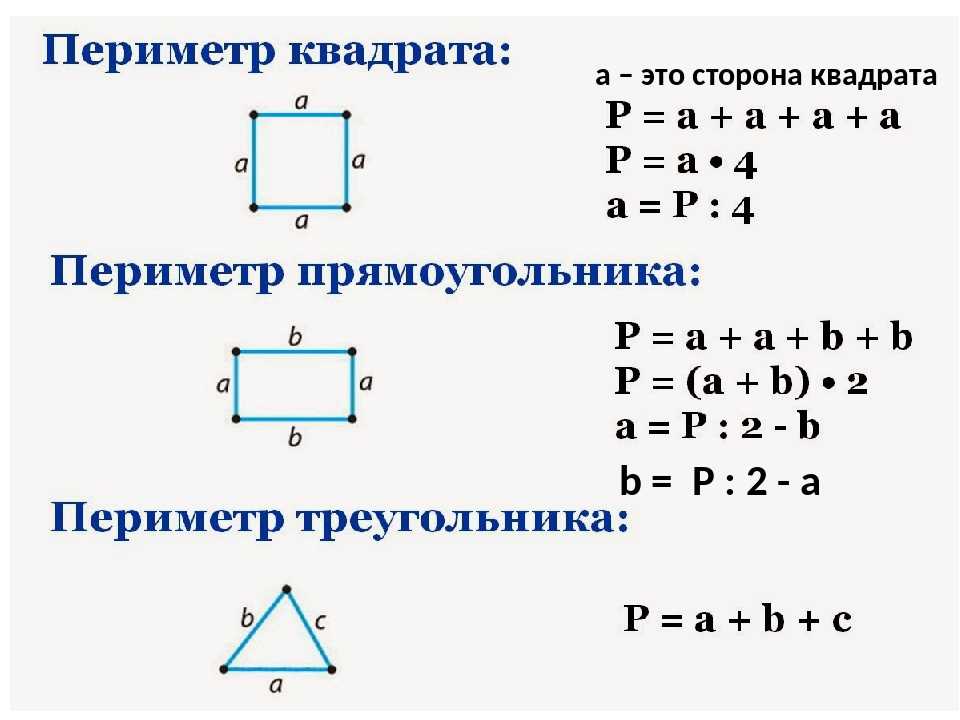

P — периметр параллелограмма

a — длина 1-ой стороны параллелограмма

b — длина 2-ой стороны параллелограмма

См. также: Программа для расчета периметра параллелограмма.


Формула периметра ромба:

1) Периметр ромба равен сумме 4-х длин его сторон или произведению длины любой его стороны на четыре (так как у ромба длины всех сторон равны).

P — периметр ромба

a — длина стороны ромба

См. также: Программа для расчета периметра ромба.

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Площадь и периметр прямоугольников и квадратов (Видео)

Здравствуйте! В этом видео показано, как найти площадь и периметр прямоугольника и квадрата .

Слово «периметр» происходит от греческого префикса per , что означает «вокруг», и греческого корня metron , что означает «мера». Таким образом, периметр фигуры — это мера или расстояние вокруг нее.

Слово «область» происходит от латинского языка и означает «открытое пространство». Таким образом, площадь фигуры — это размер открытого «пространства пола» внутри фигуры.

Итак, если вы покупаете каменную плитку для мощения патио, вам нужно знать площадь патио. Но если вы покупаете ограждение, чтобы обойти патио, вы хотите знать его периметр.

Чтобы найти периметра квадрата , сложите четыре стороны. Поскольку все четыре стороны квадрата равны, мы также можем просто умножить длину одной стороны на 4. Это дает нам формулу для периметра квадрата. Если у квадрата длина стороны s , тогда периметр квадрата равен \(P=s+s+s+s\) или \(P=4s\).

Например, предположим, что у вас есть небольшой квадратный садовый участок по 10 футов с каждой стороны. Тогда его периметр в 4 раза больше длины стороны 10 футов, а именно 40 футов. Итак, вам понадобится 40 футов забора, чтобы построить забор вокруг сада.

Обратите внимание, что периметр — это расстояние, поэтому мы измеряем его в простых единицах измерения, таких как футы, дюймы, метры или километры.

Вот вам пример.

Предположим, у вас есть небольшой квадрат со стороной 7 мм. Каков его периметр? Будьте внимательны, чтобы указать единицы вашего ответа. Приостановите видео сейчас, пока вы работаете над решением, а затем нажмите кнопку воспроизведения, чтобы сравнить свой ответ с моим.

Периметр маленького квадрата в 4 раза больше длины стороны 7 мм, что равно 28 мм.

Чтобы найти периметра прямоугольника , вы можете просто сложить четыре стороны, как вы это сделали с квадратом. Но так как противоположные стороны прямоугольника равны, вы также можете добавить удвоенную длину плюс удвоенную ширину. Это дает нам формулу периметра \(P=2l+2w\), где l — длина, а w — ширина прямоугольника.

Например, предположим, что у вас есть прямоугольный внутренний дворик размером 20 футов в длину и 15 футов в ширину. 2 раза по 20 футов — это 40 футов, а 2 раза по 15 футов — это 30 футов. Итак, мы добавляем 40 футов и 30 футов, чтобы получить периметр 70 футов.

Опять же, это означает, что нам нужно будет купить 70-футовое ограждение, чтобы обойти внутренний дворик.

Теперь твоя очередь! Предположим, у вас есть прямоугольный садовый участок длиной 45 футов и шириной 25 футов. Каков его периметр? Не забудьте указать единицы вашего ответа. Приостановите видео сейчас, пока вы работаете над решением. Затем нажмите кнопку воспроизведения, чтобы сравнить свой ответ с моим.

2 раза 45-футовая длина равна 90 футам, а 2 раза 25-футовая ширина равна 50 футам. Мы добавляем 90 футов и 50 футов, чтобы получить 140 футов по периметру садового участка.

Теперь давайте посмотрим, как найти площади этих фигур. На этот раз начнем с прямоугольника. Чтобы найти площадь прямоугольника , мы умножаем длину на ширину. Это дает нам формулу площади \(A=lw\), где снова l представляет длину, а w представляет ширину.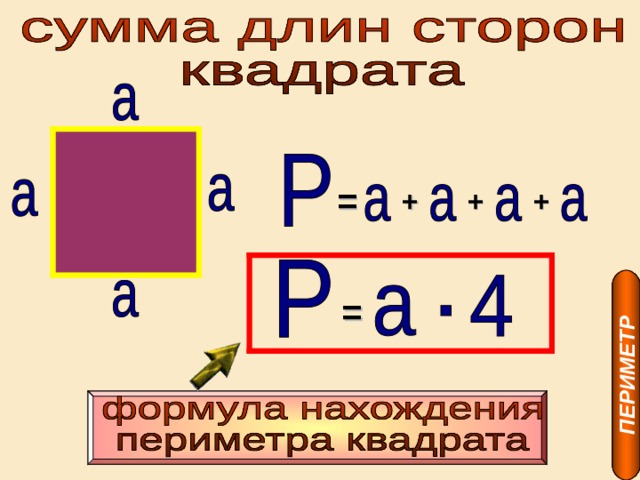 9{2}\). Поскольку мы умножили две единицы футов друг на друга, мы возвели эту единицу в наш ответ. Площадь всегда измеряется в квадратных единицах.

Мы можем разделить прямоугольник на каждый фут по длине и ширине, чтобы разделить прямоугольник на 12 квадратных футов, необходимых для покрытия пола плиткой.

Вот еще один пример, который вы можете попробовать самостоятельно.

Предположим, прямоугольная парковка имеет длину 15 метров и ширину 12 метров. Какова площадь стоянки? Будьте внимательны, чтобы указать единицы вашего ответа. Приостановите видео, пока не рассчитаете свое решение. Затем нажмите кнопку воспроизведения и сравните свой ответ с моим. 9{2}\).

Обратите внимание, что если мы разделим квадрат на каждый фут вдоль каждой стороны, мы разделим внутреннюю часть на 16 квадратов по 1 футу с каждой стороны. Мы называем каждый из этих маленьких квадратов квадратных футов , и требуется 16 из них, чтобы выложить плиткой пол этого шкафа. Именно это мы имеем в виду, когда говорим, что площадь квадрата составляет 16 квадратных футов. Помните, мы всегда измеряем площадь в квадратных единицах, таких как квадратные футы, квадратные дюймы, квадратные метры или квадратные мили.

Вот вам пример. 9{2}\). Вы не забыли сказать «квадратные сантиметры», а не просто «сантиметры» в своем ответе? Некоторые учителя и тесты засчитают ваш ответ неправильно, если вы используете неправильные единицы измерения, поэтому будьте очень осторожны, записывая свои единицы!

В этом уроке мы научились находить периметр и площадь квадратов и прямоугольников. Периметр фигуры — это расстояние вокруг нее, измеряемое в простых единицах измерения, таких как футы или метры. Периметр квадрата в четыре раза больше длины стороны, а периметр прямоугольника в два раза больше длины плюс в два раза больше ширины. 9{2}\)
 
Прямоугольник: \(A=lw\)

 

Все это можно свести к четырем формулам, которые часто встречаются в математике и которые стоит запомнить. Помните, что квадрат — это особый тип прямоугольника, поэтому, если вы можете вспомнить только формулы площади и периметра прямоугольника, вы можете использовать их для нахождения площади и периметра квадрата.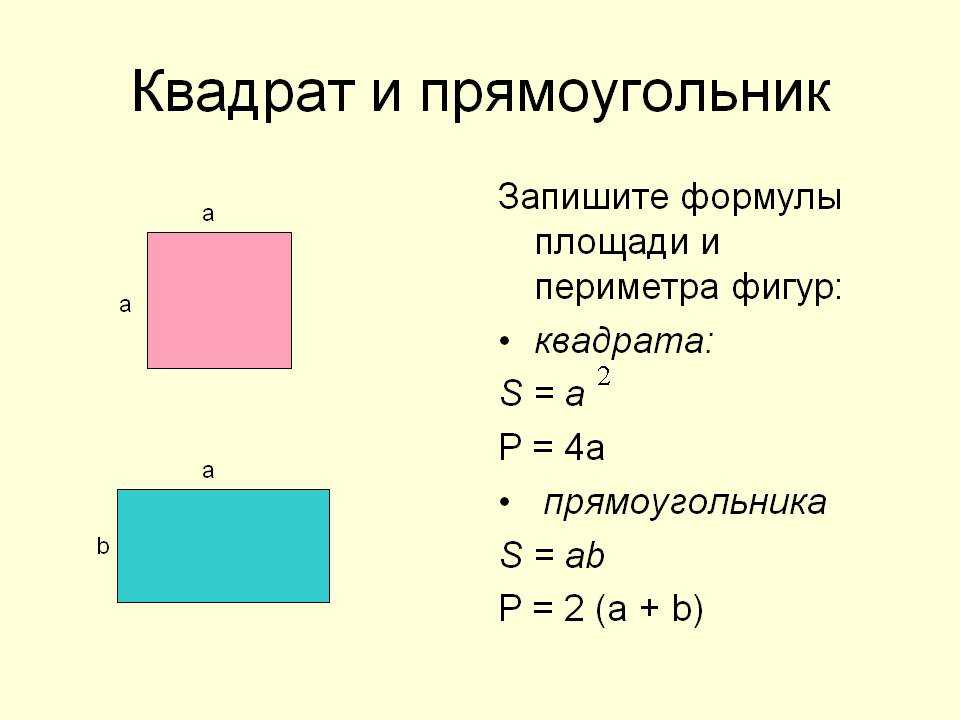

Надеюсь, это видео было полезным. Спасибо за просмотр и удачной учебы!

Периметр квадрата с калькулятором- Math Open Reference

Периметр квадрата с калькулятором — Math Open Reference

Открытый справочник по математике

Главная Контакт О Тематический указатель

Определение: Общее расстояние вокруг внешней стороны квадрат

Попробуйте это Перетащите любую оранжевую точку, чтобы изменить размер квадрата. Периметр вычисляется по мере перетаскивания.

Как найти периметр квадрата

Как и у любого многоугольника, периметр — это общее расстояние вокруг внешней стороны, которое можно найти, сложив длины каждой стороны. В случае квадрата все четыре стороны имеют одинаковую длину, значит, периметр в четыре раза больше длины стороны. Или как формула: где:
S длина любой стороны

На рисунке выше перетащите любую оранжевую точку, чтобы изменить размер квадрата. По показанной длине стороны рассчитайте периметр и убедитесь, что ваш результат соответствует формуле в верхней части диаграммы.

No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *