Как правильно решить пример без скобок?
Как правильно решить пример без скобок?
Запомните правило:
- Если в примере нет скобок, сначала выполняем действия умножения и деления по порядку, слева направо. …
- Если в примере есть скобки, то сначала мы выполняем действия в скобках, затем умножение и деление, и затем — сложение и вычитание начиная слева направо.
Какое первое действие в примере без скобок?
Если в выражение без скобок входят не только действия сложения и вычитания, но и умножения и деления, или оба этих действия, то сначала выполняют по порядку (слева направо) умножение и деление, а затем сложение и вычитание.
Какие первые действия в математике?
Сначала умножение и деление, затем сложение и вычитание В школе дается следующее правило, определяющее порядок выполнения действий в выражениях без скобок: действия выполняются по порядку слева направо, причем сначала выполняется умножение и деление, а затем – сложение и вычитание.
Что сначала делается сложение или умножение?
При умножении двух разных единиц измерения получается новая единица измерения, при сложении единицы измерения не меняются. При умножении мы получаем эту самую новую единицу измерения. Если она такая же, как и у первого слагаемого, тогда мы можем выполнить сложение. Это просто правило.
Что это вычитание?
Вычитание — операция обратная сложению. Вычитание возможно только, если оба аргумента принадлежат одному множеству элементов (имеют одинаковый тип).
Что такое сложение и вычитание?
Сложение – это объединение объектов в одно целое. Результатом сложения чисел является число, называемое суммой чисел (слагаемых). Вычитание – это такое действие, в котором отнимают меньшее число от большего. Большее число называется уменьшаемым, меньшее – вычитаемым, результат вычитания – разностью.
Как решать дроби Сложение и вычитание?
Чтобы сложить дроби с одинаковыми знаменателями, надо сложить их числители, а знаменатель оставить без изменений. Чтобы вычесть дроби с одинаковыми знаменателями, надо из числителя первой дроби вычесть числитель второй, а знаменатель опять же оставить без изменений.
Чтобы вычесть дроби с одинаковыми знаменателями, надо из числителя первой дроби вычесть числитель второй, а знаменатель опять же оставить без изменений.
Как называется сложение в математике?
Сложение чисел Результат сложения двух или более чисел называется суммой, а сами числа — слагаемыми. … Складываем числа, аналогично положительным, записываем результат со знаком «минус». Например, (-6)+(-5,3)=-(6+5,3)=-11,3. От перестановки мест слагаемых сумма не изменяется a+b=b+a.
Как называется в математике плюс?
Знаки «плюс» и «минус» (+ и −) — математические символы, используемые для обозначения операций сложения и вычитания, а также положительных и отрицательных величин.
Как называется математическое действие Если стоит знак плюс?
В стране математики живут не только цифры и числа, но и разные математические знаки. Сегодня вы с Лисёнком познакомитесь с ними. … В математике это действие называется сложением и ставится знак плюс.
Как называется действие с минусом?
Вычитание – действие обратное сложению. Уменьшаемое – число, из которого вычитают. Вычитаемое – число, которое вычитают. Разность – результат вычитания.
Как называется при умножении?
Так же, как и при сложении и вычитании, числа при умножении имеют свое название. Первое число при умножении называется множитель. Второе число при умножении тоже называется множитель. Результат умножения называют произведение.
Что такое результат умножения?
Умноже́ние — одна из основных математических операций над двумя аргументами (множителями или сомножителями). Иногда первый аргумент называют множимым, а второй множителем; результат умножения двух аргументов называется их произведением.
Как умножить два отрицательных числа?
Умножение отрицательных чисел Правило умножения отрицательных чисел: чтобы умножить два отрицательных числа, нужно перемножить их модули. Это значит, что для любых отрицательных чисел -a, -b верно равенство: (-а) * (-b) = a * b.
Это значит, что для любых отрицательных чисел -a, -b верно равенство: (-а) * (-b) = a * b.
Как умножить натуральное число на отрицательное?
Правило умножения отрицательных чисел заключается в том, что для того, чтобы умножить два отрицательных числа, необходимо перемножить их модули. Данное правило записывается так: для любых отрицательных чисел –a, −b данное равенство считается верным. (−а)⋅(−b)=a⋅b.
§ Порядок действий в решении примеров по математике
Похоже, вы используете блокировщик рекламы. Наш сайт существует и развивается только за счет дохода от рекламы.
Пожалуйста, добавьте нас в исключения блокировщика.
Скрыть меню
На главную страницу
Войти при помощи
Темы уроков
Начальная школа
- Геометрия: начальная школа
- Действия в столбик
- Деление с остатком
- Законы арифметики
- Периметр
- Порядок действий
- Разряды и классы.
 Разрядные слагаемые
Разрядные слагаемые - Счет в пределах 10 и 20
Математика 5 класс
- Взаимно обратные числа и дроби
- Десятичные дроби
- Натуральные числа
- Нахождение НОД и НОК
- Округление чисел
- Перевод обыкновенной дроби в десятичную
- Площадь
- Проценты
- Свойства сложения, вычитания, умножения и деления
- Среднее арифметическое
- Упрощение выражений
- Уравнения 5 класс
- Числовые и буквенные выражения
Математика 6 класс
- Масштаб
- Модуль числа
- Окружность. Площадь круга
- Отношение чисел
- Отрицательные и положительные числа
- Периодическая дробь
- Признаки делимости
- Пропорции
- Рациональные числа
- Система координат
- Целые числа
Алгебра 7 класс
- Алгебраические дроби
- Как применять формулы сокращённого умножения
- Многочлены
- Одночлены
- Системы уравнений
- Степени
- Уравнения
- Формулы сокращённого умножения
- Функция в математике
Геометрия 7 класс
- Точка, прямая и отрезок
- Что такое аксиома и теорема
Алгебра 8 класс
- Квадратичная функция.
 Парабола
Парабола - Квадратные неравенства
- Квадратные уравнения
- Квадратный корень
- Неравенства
- Системы неравенств
- Стандартный вид числа
- Теорема Виета
Алгебра 9 класс
- Возрастание и убывание функции
- Нули функции
- Область определения функции
- Отрицательная степень
- Среднее
геометрическое
Алгебра 10 класс
- Иррациональные числа
Алгебра 11 класс
- Факториал
Всё, что ты говоришь, говорит о тебе, и особенно то, что ты говоришь о других. Поль Валери
на главную
Введите тему
Русский язык Поддержать сайт
При расчётах примеров нужно соблюдать определённый порядок действий.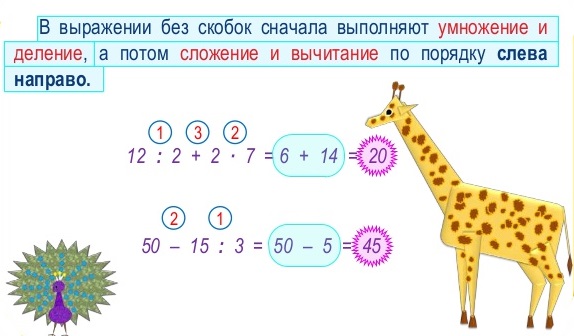 С помощью правил ниже, мы
разберёмся в каком порядке выполняются действия и для чего нужны скобки.
С помощью правил ниже, мы
разберёмся в каком порядке выполняются действия и для чего нужны скобки.
Если в выражении скобок нет, то:
- сначала выполняем слева направо все действия умножения и деления;
- а потом слева направо все действия сложения и вычитания.
Рассмотрим порядок действий в следующем примере.
Напоминаем вам, что порядок действий в математике расставляется слева направо (от начала к концу примера).
При вычислении значения выражения можно вести запись двумя способами.
Первый способ
- Каждое действие записывается отдельно со своим номером под примером.
- После выполнения последнего действия ответ обязательно записывается в исходный пример.
Запомните!
При расчёте результатов действий с двузначными и/или трёхзначными числами обязательно приводите свои расчёты в столбик.
Второй способ
- Второй способ называется запись «цепочкой».
 Все вычисления проводятся в точно таком же порядке
действий, но результаты записываются сразу после знака равно.
Все вычисления проводятся в точно таком же порядке
действий, но результаты записываются сразу после знака равно.
Запомните!
Если выражение содержит скобки, то сначала выполняют действия в скобках.
Внутри самих скобок действует правило порядка действий как в выражениях без скобок.
Если внутри скобок находятся ещё одни скобки, то сначала выполняются действия внутри вложенных (внутренних) скобок.
Порядок действий и возведение в степень
Если в примере содержится числовое или буквенное выражение в скобках, которое надо возвести в степень, то:
- Сначала выполняем все действия внутри скобок
- Затем возводим в степень все скобки и числа, стоящие в степени, слева направо (от начала к концу примера).
- Выполняем оставшиеся действия в обычном порядке
Порядок работы
Обновлено 11 февраля 2017 г. | Infoplease Staff
Если у вас есть математическая задача, включающая более одной операции, например сложение и вычитание или вычитание и умножение , что вы делаете в первую очередь?
Пример #1 : 6 – 3 x 2 = ?
- Вы сначала выполняете вычитание (6 — 3 = 3), а затем умножение (3 x 2 = 6 )?
- Или вы начинаете с умножения (3 x 2 = 6), а затем вычитаете (6 – 6 = 9).
 0011 0 )?
0011 0 )?
PEMDAS
В подобных случаях мы следуем порядку операций . Заказ, в котором следует выполнять операции, сокращается как Pemdas :
- P Arentheses
- E Xponents
- M Ultiplication и D IVIS A дополнение и S вычитание (слева направо)
(Один из способов запомнить это — подумать о фразе P аренда E извините M y D ухо A unt S в приведенном выше примере ally.) занимаемся умножением и вычитанием. M умножение происходит на шаг раньше S вычитания, поэтому сначала мы умножаем 3 x 2, а затем вычитаем сумму из 6, в результате чего получается 0.
?
- Нет P арентез.
- Нет компонентов E .
- Начнем с умножения M и ivision D , работая слева направо.
ПРИМЕЧАНИЕ: Несмотря на то, что умножение предшествует делению в PEMDAS, они выполняются на одном шаге слева направо. Сложение и вычитание также выполняются на одном шаге.
Сложение и вычитание также выполняются на одном шаге. - 30 ÷ 5 = 6 , остается 6 x 2 + 1 = ?
- 6 х 2 = 12 , остается 12 + 1 = ?
- Затем мы делаем A дополнение: 12 + 1 = 13
Обратите внимание, что если бы мы выполнили умножение перед делением, то получили бы неверный ответ:
17 5 x 2 = 10 , осталось 30 ÷ 10 + 1 = ?
- 30 ÷ 10 = 3 , остается 3 + 1 = ?
- 3 + 1 = 4 (отключить на 9!)
Последний пример для продвинутых учащихся, использующий все шесть операций:
Пример #3 : 5 + (4 – 2) 2 x 3 ÷ 6 – 1 = ?
- Начните с P арентез: 4 – 2 = 2 . (Несмотря на то, что вычитание обычно выполняется на последнем шаге, поскольку оно заключено в скобки, мы делаем это первым.) Получается 5 + 2 2 x 3 ÷ 6 – 1 = ?
- Затем E xponents: 2 2 = 4 .
 Теперь у нас есть 5 + 4 x 3 ÷ 6 – 1= ?
Теперь у нас есть 5 + 4 x 3 ÷ 6 – 1= ? - Затем M умножение и D ivision, начиная слева: 4 x 3 = 12 , оставляя нас с 5 + 12 ÷ 6 – 1 = ?
- Затем двигаемся вправо: 12 ÷ 6 = 2 , составляя задачу 5 + 2 – 1 = ?
- Затем A добавление и S вычитание, начиная слева: 5 + 2 = 7 , оставляя 7 – 1 = ?
- Наконец, переход вправо: 7 — 1 = 6
(для получения дополнительной практики, попробуйте нашу игру за заказ!)
| Тяничные эквиваленты общих фракций | . Десятичные эквиваленты обыкновенных дробей Числа и формулы .com/ipa/0/9/3/3/3/4/A0933340.html Источники + Наши общие источники
Правило PEMDAS — ChiliMathПоиск Правило PEMDAS (аббревиатура от «Пожалуйста, извините, моя дорогая тетя Салли») представляет собой набор правил, определяющих приоритет порядка вычислений, то есть, какую операцию выполнять первой. Ниже показан пример, в котором есть два возможных ответа. Первое решение дает неверный ответ, потому что оно вычисляет числовое выражение слева направо. В то время как второе решение является правильным, потому что оно следует правилам Порядка операций. Упростите числовое выражение. Неверное решение: Правильное решение: Порядок действийШаг 1 : В верхней части списка не забывайте группировать все символы 02ВСЕГДА. Примерами символов группировки являются круглые скобки ( ), скобки и фигурные скобки { }. Для вложенных символов группировки проработайте их изнутри и снаружи. Шаг 2 : Экспоненциальные выражения вычисляются или вычисляются перед выполнением любой из четырех основных арифметических операций, а именно: сложения, вычитания, умножения и деления. Шаг 3 : Далее умножьте и/или разделите слева направо, прежде чем выполнять сложение и вычитание. Это говорит нам о том, что умножение и деление имеют более высокий уровень важности, чем сложение и вычитание. Шаг 4 : Наконец, добавьте и/или вычтите то, что идет первым слева направо. PEMDASPEMDAS — это мнемоническое устройство, которое может помочь нам запомнить порядок операций, который, как мы уже знаем, означает «9».0236 P аренда E извините M y D ухо A unt S союзник». P – Parentheses E – Exponents M – Multiplication D – Division A – Addition S – Subtraction Just a quick caution, the операции умножения и деления имеют одинаковый уровень приоритета. Точно так же сложение и вычитание равны по степени важности. Выполните операцию, которая идет первой, когда вы работаете над ней слева направо. Примеры применения правила PEMDASПример 1 : Упростите следующее выражение, используя порядок операций. Решение : Обратите внимание, что задействованы три операции. Основываясь на порядке операций, умножение имеет приоритет над сложением и вычитанием, поэтому мы будем умножать первыми. Затем вычтите, а затем сложите, так как операция вычитания предшествует сложению слева направо. Пример 2 : Упростите следующее выражение, используя порядок операций. Решение : Символ группировки имеет наивысший приоритет, что означает, что мы должны сначала упростить все внутри. В скобках указаны операции деления и умножения. |

 Разрядные слагаемые
Разрядные слагаемые Парабола
Парабола Все вычисления проводятся в точно таком же порядке
действий, но результаты записываются сразу после знака равно.
Все вычисления проводятся в точно таком же порядке
действий, но результаты записываются сразу после знака равно.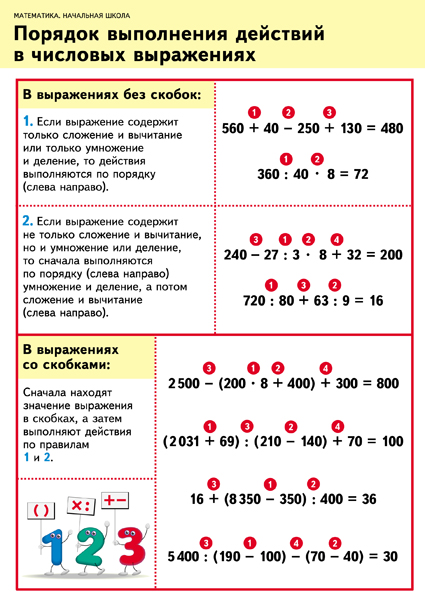 0011 0 )?
0011 0 )?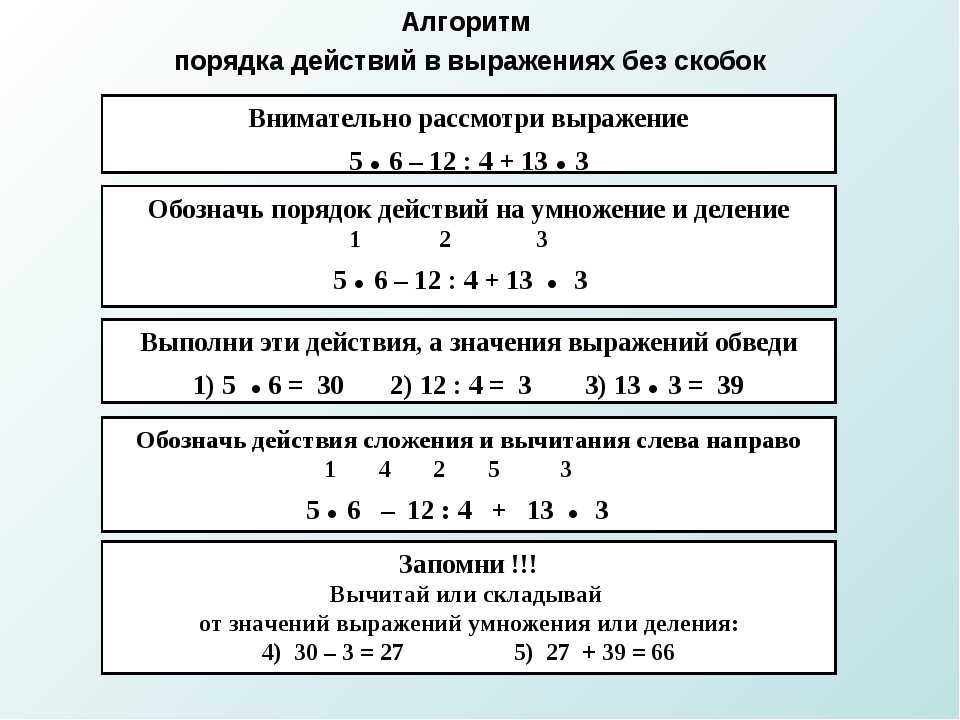 Сложение и вычитание также выполняются на одном шаге.
Сложение и вычитание также выполняются на одном шаге. Теперь у нас есть 5 + 4 x 3 ÷ 6 – 1= ?
Теперь у нас есть 5 + 4 x 3 ÷ 6 – 1= ? 

 Чтобы решить, когда умножать или делить, всегда выполняйте тот, который появляется первым слева направо.
Чтобы решить, когда умножать или делить, всегда выполняйте тот, который появляется первым слева направо.