Ответ
ОТВЕТ: 75.
Ответ
ОТВЕТ: 41.
Ответ
ОТВЕТ: 6.
Ответ
ОТВЕТ: 11,5.
Реклама
Поддержать нас
Решение Ященко ОГЭ 2023 Вариант №16 (36 вариантов) Математика
Решение заданий варианта №16 из сборника ОГЭ 2023 по математике И. В. Ященко 36 типовых вариантов ФИПИ школе. ГДЗ решебник для 9 класса. Ответы с решением. Полный разбор всех заданий.
В. Ященко 36 типовых вариантов ФИПИ школе. ГДЗ решебник для 9 класса. Ответы с решением. Полный разбор всех заданий.
ЧАСТЬ 1
Задание 1-5.
В жилых домах установлены бытовые электросчётчики, которые фиксируют расход электроэнергии в киловатт-часах (кВт·ч). Учёт расхода электроэнергии может быть однотарифным, двухтарифным или трёхтарифным.
При однотарифном учёте стоимость 1 кВт · ч электроэнергии не меняется в течение суток. При двухтарифном и трёхтарифном учёте она различна в зависимости от времени суток (сутки разбиты на периоды, называемые тарифными зонами).
В таблице дана стоимость 1 кВт · ч электроэнергии в рублях в 2021 году.
В квартире у Петра Сергеевича установлен трёхтарифный счётчик, и в 2021 году Николай Андреевич оплачивал электроэнергию по трёхтарифному учёту.
На рисунке точками показан расход электроэнергии в квартире Петра Сергеевича по тарифным зонам за каждый месяц 2021 года.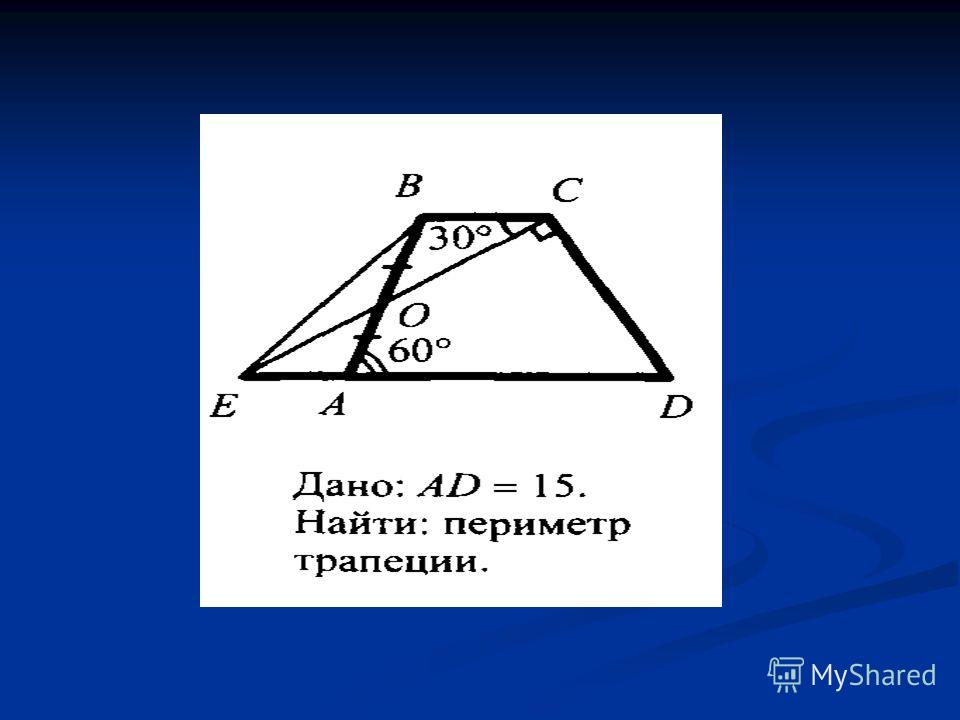 Для наглядности точки соединены линиями.
Для наглядности точки соединены линиями.
Задание 6.
Найдите значение выражения (\frac{2}{15}+\frac{5}{12})\cdot \frac{16}{11}.
Задание 7.
На координатной прямой точки А, В, С и D соответствуют числам -\frac{1}{50}; \frac{1}{50}; -\frac{11}{15}; -\frac{11}{50}.
Какой точке соответствует число -\frac{11}{50}?
1) A 2) B 3) C 4) D
Задание 8.
Найдите значение выражения 9√7·2√2·√14.
Задание 9.
Решите уравнение x2 – 4 = 2x – 1.
Если уравнение имеет более одного корня, в ответ запишите меньший из корней.
Задание 10.
Вероятность того, что новая шариковая ручка пишет плохо (или не пишет), равна 0,14. Покупатель в магазине выбирает одну шариковую ручку. Найдите вероятность того, что эта ручка пишет хорошо.
Задание 11.
Установите соответствие между графиками функций и формулами, которые их задают.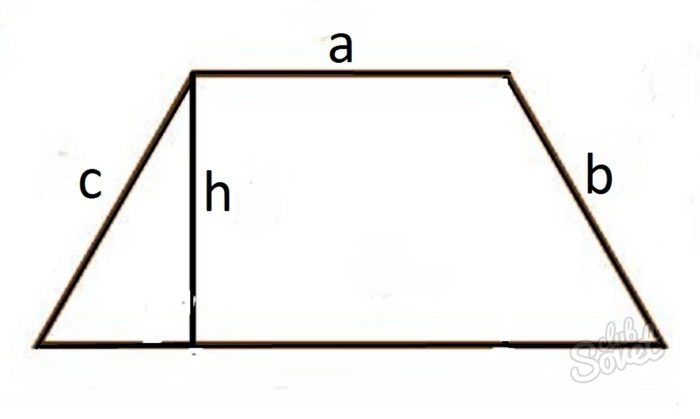
ФОРМУЛЫ
А) y=\frac{1}{6x}
Б) y=-\frac{6}{x}
В) y=\frac{6}{x}
ГРАФИКИ
В таблице под буквой укажите соответствующий номер.
Задание 12.
Потенциальная энергия тела (в джоулях) в поле тяготения Земли вблизи её поверхности вычисляется по формуле Е = mgh, где m – масса тела (в килограммах), g – ускорение свободного падения (в м/с2), a h – высота (в метрах), на которой находится это тело, относительно поверхности. Пользуясь этой формулой, найдите m (в килограммах), если g = 9,8 м/с2, h = 5 м, а E = 196 Дж.
Задание 13.
Укажите неравенство, решение которого изображено на рисунке.
1) x2 – 16 ≤ 0
2) x2 – 4x ≤ 0
3) x2 – 4x ≥ 0
4) x2 – 16 ≥ 0
Задание 14.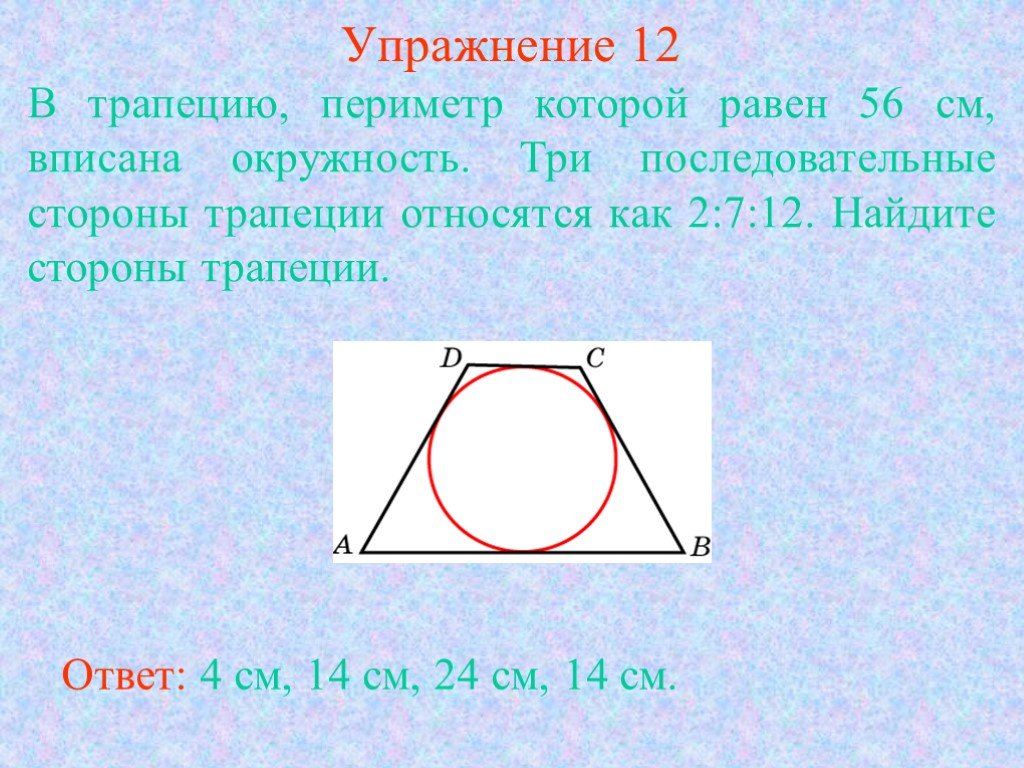
В ходе распада радиоактивного изотопа его масса уменьшается вдвое каждые 6 минут. В начальный момент масса изотопа составляла 640 мг. Найдите массу изотопа через 42 минуты. Ответ дайте в миллиграммах.
Задание 15.
В треугольнике ABC угол С равен 90°, М – середина стороны АВ, АВ = 64, ВС = 44. Найдите СМ.
Задание 16.
Касательные в точках A и В к окружности с центром в точке О пересекаются под углом 56°. Найдите угол АВО. Ответ дайте в градусах.
Задание 17.
Высота равнобедренной трапеции, проведённая из вершины С, делит основание AD на отрезки длиной 8 и 17. Найдите длину основания ВС.
Задание 18.
На клетчатой бумаге с размером клетки 1×1 изображён треугольник. Найдите его площадь.
Задание 19.
Какое из следующих утверждений верно?
1) Диагонали ромба равны. {2}-6x}.
{2}-6x}.
Определите, при каких значениях k прямая у = kx имеет с графиком ровно одну общую точку.
Задание 23.
Отрезки АВ и DC лежат на параллельных прямых, а отрезки АС и BD пересекаются в точке М. Найдите МС, если АВ = 14, DC = 30, АС = 39.
Задание 24.
В остроугольном треугольнике ABC проведены высоты AA1 и BB1. Докажите, что углы BB1A1 и BAA1 равны.
Задание 25.
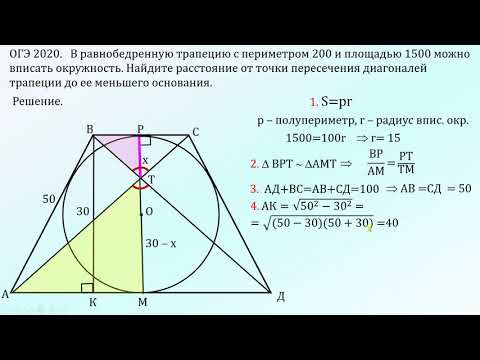
В равнобедренную трапецию, периметр которой равен 20, а площадь равна 20, можно вписать окружность. Найдите расстояние от точки пересечения диагоналей трапеции до её меньшего основания.
Источник варианта: Сборник ОГЭ 2023 по математике. Типовые экзаменационные варианты. 36 вариантов. Под редакцией И.В. Ященко.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 5 / 5. Количество оценок: 2
Количество оценок: 2
Оценок пока нет. Поставь оценку первым.
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.
- Запись опубликована:24.11.2022
- Рубрика записи+ Типовые экзаменационные варианты ОГЭ
- Автор записи:Andrei Maniakin
РЕШЕНИЕ: Вопрос: Дан равнобедренный треугольник с меньшим основанием 0f 2, периметром 70 и острыми углами при основании 60 градусов, найдите площадь трапеции. Проделанная работа: я знаю
РЕШЕНИЕ: Вопрос: Дан равнобедренный треугольник с меньшим основанием 0f 2, периметром 70 и острыми углами при основании 60 градусов, найдите площадь трапеции. Проделанная работа на данный момент: я знаю Алгебра ->
Настраиваемые средства решения задач Word
-> Геометрия
-> РЕШЕНИЕ: Вопрос: Дан равнобедренный треугольник с меньшим основанием 0f 2, периметром 70 и острыми углами при основании 60 градусов, найдите площадь трапеции.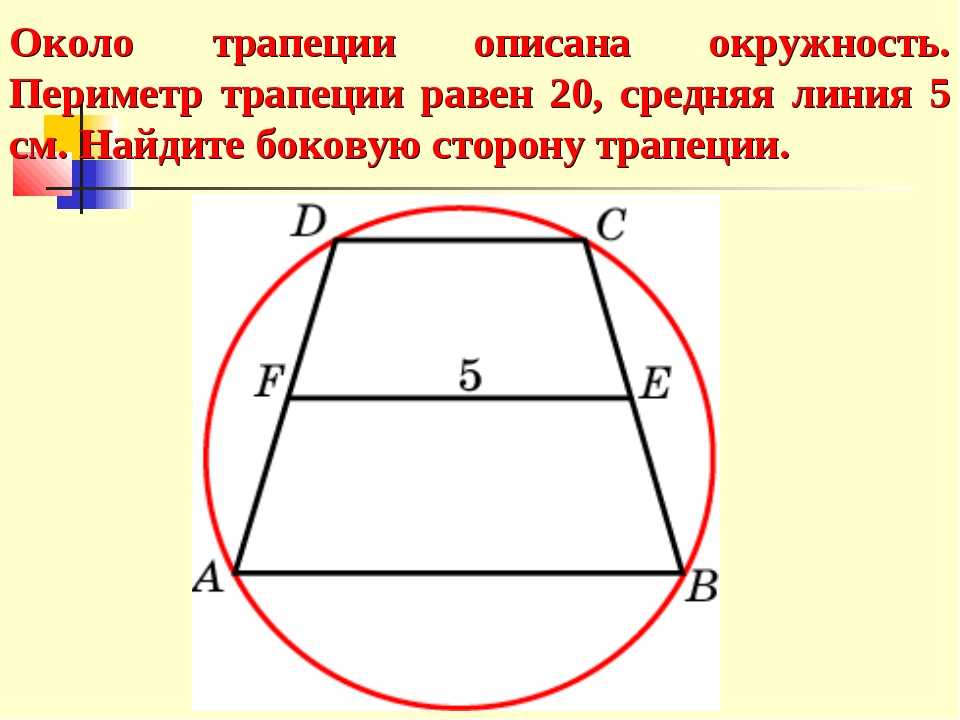 Проделанная работа на данный момент: я знаю Войти
Проделанная работа на данный момент: я знаю Войти
|
|
√ Трапеция (Виды, Формула площади и периметра, Примеры)
by Sigma
Геометрия — одна из областей математики. Он имеет множество форм, одна из которых — плоская геометрия. В плоской геометрии есть четырехугольник, который имеет множество разновидностей. Один из них трапециевидный.
Он имеет множество форм, одна из которых — плоская геометрия. В плоской геометрии есть четырехугольник, который имеет множество разновидностей. Один из них трапециевидный.
В повседневной жизни трапецию можно встретить в сумочке, бриджах и коробке из-под попкорна в кинотеатре.
Содержание
Определение трапецииТрапеция — одна из специальных фигур плоской геометрии. По определению, трапеция — это четырехугольник (четырехсторонняя форма), у которого пара параллельных сторон находится напротив. Кроме того, суммарные углы друг напротив друга составляют 180°.
В общем случае трапеция имеет основания сверху и снизу (a и b), высоту (h) и наклонную сторону (ножки).
Трапеция имеет разные названия в США и Великобритании. Различия:
| US | British | |
| Trapezoid | It has a pair of parallel sides | It has not parallel sides |
| Trapezium | Непараллельные стороны | Имеют пару параллельных сторон |
Есть несколько видов трапеций.
Прямая трапеция имеет пару параллельных прямых и два прямых угла.
2. Равнобедренная трапецияРавнобедренная трапеция имеет одинаковые углы при основании. Следовательно, наклонные стороны (ножки) имеют одинаковую длину.
3. Разносторонняя трапецияРазносторонняя трапеция – это разновидность трапеции, которая имеет неравные стороны и равные углы .
Площадь трапецииПлощадь трапеции с параллельными сторонами и высота (высота)
Площадь = A = [(a+b)/2] x h
Периметр трапеции 3 Длина периметра 90 означает все стороны. Другими словами, периметр трапеций равен сумме всех длин.Периметр = P = a + b + c + d
Медиана трапеции Медиана означает среднюю часть чего-либо.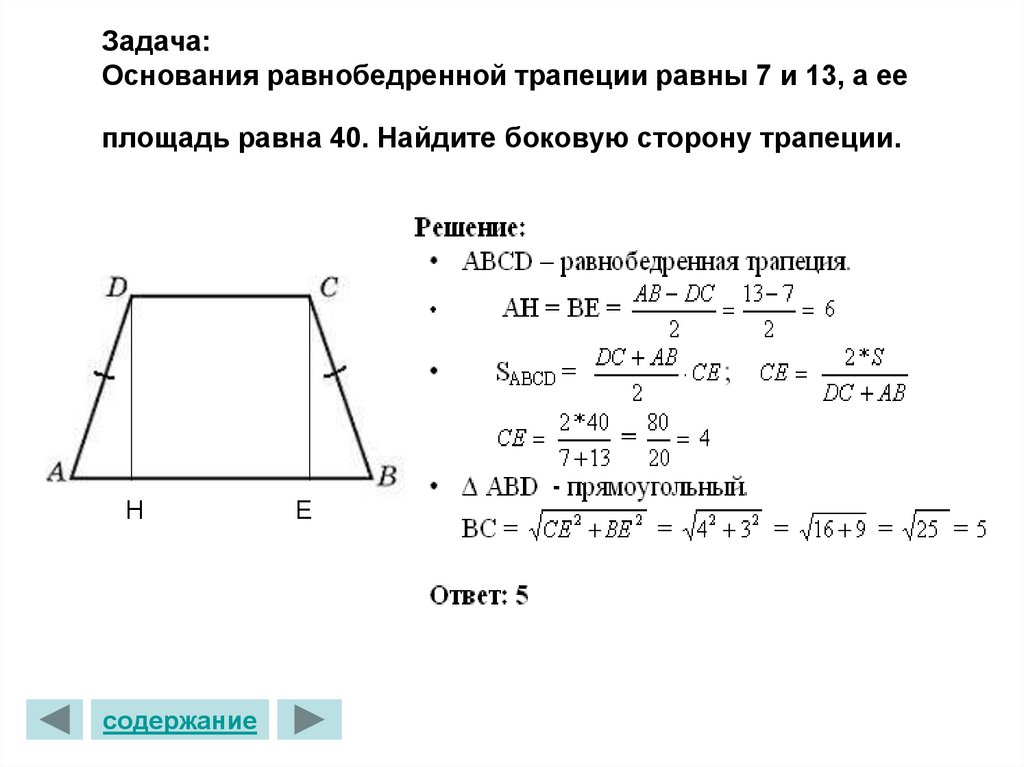 Под медианой трапеции понимается линия, разделяющая ее на две части, каждая из которых имеет половину высоты. Он параллелен основаниям (верхнему и нижнему).
Под медианой трапеции понимается линия, разделяющая ее на две части, каждая из которых имеет половину высоты. Он параллелен основаниям (верхнему и нижнему).
Длина медианы является средней длины параллельной линии.
Медиана = (a+b)/2
Примеры1. Определите, какие утверждения верны.
а. Трапеция это прямоугольник
б. У трапеции всегда прямой угол.
д. Равнобедренная трапеция имеет одинаковую длину наклонных сторон.
Пример
а. Трапеция — это прямоугольник ( false , потому что прямоугольник — это особая форма трапеции)
б. У трапеции всегда прямой угол. ( false , есть только прямая трапеция с прямыми углами)
c. Трапеция всегда имеет четыре стороны ( верно , потому что трапеция имеет форму четырехугольника).
д. Равнобедренная трапеция имеет одинаковую длину наклонных сторон ( верно , потому что у нее одинаковые углы в основании, следовательно, у нее одинаковая длина наклонных сторон)
2.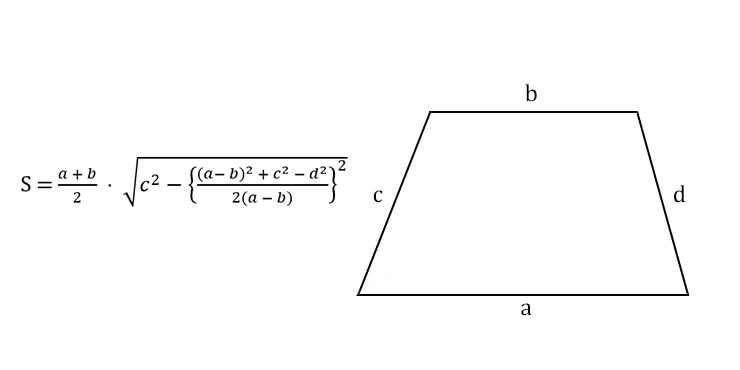

 Сложные задачи
Сложные задачи 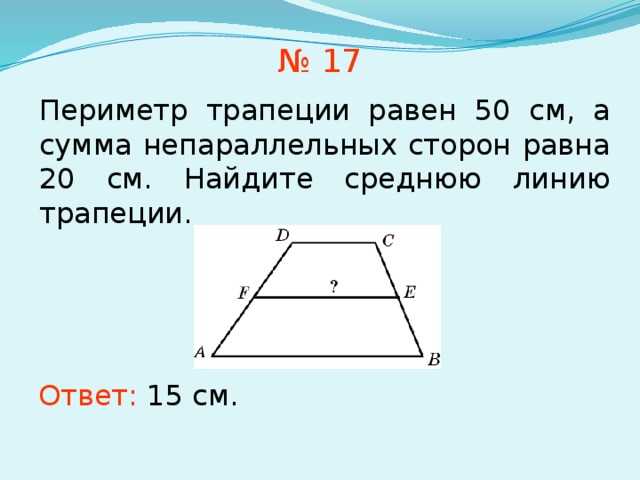 И мы знаем, что
правый сегмент внизу еще и потому, что
прямоугольный треугольник слева и один справа
конгруэнтны.
Теперь нам говорят, что периметр равен 70.
Таким образом, чтобы сформировать периметр, мы складываем все четыре стороны
трапеция.
Левая сторона трапеции равна
Нижняя сторона это сумма
Правая сторона
Верхняя сторона есть.
Таким образом, сумма всех этих должна равняться 70:
Мы решаем это для X и получаем 22
Итак, теперь мы знаем, что нижняя сторона
и это большее основание трапеции.
И его высота.
Теперь мы можем найти площадь, используя , и
, в формуле
.
Эдвин
И мы знаем, что
правый сегмент внизу еще и потому, что
прямоугольный треугольник слева и один справа
конгруэнтны.
Теперь нам говорят, что периметр равен 70.
Таким образом, чтобы сформировать периметр, мы складываем все четыре стороны
трапеция.
Левая сторона трапеции равна
Нижняя сторона это сумма
Правая сторона
Верхняя сторона есть.
Таким образом, сумма всех этих должна равняться 70:
Мы решаем это для X и получаем 22
Итак, теперь мы знаем, что нижняя сторона
и это большее основание трапеции.
И его высота.
Теперь мы можем найти площадь, используя , и
, в формуле
.
Эдвин