Периметр квадрата как посчитать: Найти периметр квадрата со стороной 3 см

Онлайн калькулятор периметра вписанного в круг квадрата. Как узнать периметр вписанного в круг квадрата.

При помощи нашего калькулятора вы легко сможете узнать периметр вписанного в круг квадрата.

Вычислить периметр вписанного квадрата через:	R — радиус кругаD — диаметр кругаS — площадь кругаP — периметр круга
Радиус круга R:

Для того что бы найти периметр вписанного в круг квадрата, нам необходимо узнать длину ребра этого квадрата. Для этого нам необходимо разделить квадрат по диагонали на два равнобедренных треугольника, при этом основание у этих треугольников будет равно диаметру круга.

Следующим действиям мы должны определиться с известной нам величиной круга в которую вписан квадрат, а именно нам должна быть известна:

1. либо площадь круга, обозначаемая буквой S,
2. либо периметр круга, обозначаемый буквой P,
3. либо радиус круга, обозначаемый буквой R,
4. либо диаметр круга, обозначаемый буквой D.

Начнем по порядку, мы имеем равнобедренный прямоугольный треугольник и для того, что бы узнать длину его ребер нам необходимо воспользоваться теоремой Пифагора исходя из которой

c² = 2a²,
Таким образом
a = √c²/2

Теперь для того что бы найти длину ребра треугольника (которое равно стороне нашего квадрата) нам необходимо узнать длину основания треугольника, которое равно диаметру круга

D = c

1. Если нам известна площадь круга в который вписан квадрат то для нахождения диаметра нам необходимо воспользоваться следующей формулой:

D=2√S/π

2. Если нам известна длина круга в который вписан квадрат то для нахождения диаметра нам необходимо воспользоваться следующей формулой:

D=P/π

3. Если нам известен радиус круга в который вписан квадрат то для нахождения диаметра нам необходимо воспользоваться следующей формулой:

D=2R

Соответственно если мы знаем диаметр круга который равен основанию треугольника полученного путем разделения квадрата на две части по диагонали,

c=D

мы можем узнать длину сторон квадрата используя теорему Пифагора

a = √c²/2

после того как мы получили значение длины стороны вписанного квадрата равную a, для получения его периметра нам необходимо полученное значение умножить на 4.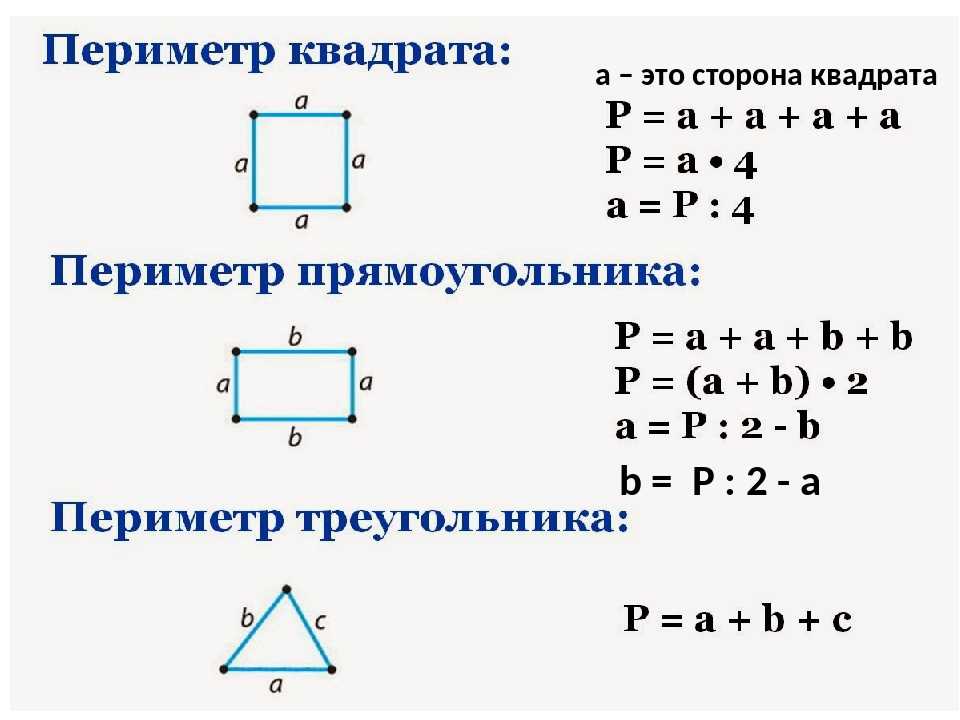

S = 4a

Вычислить периметр вписанного квадрата через R — радиус круга

Вычислить периметр вписанного квадрата через D — диаметр круга

Вычислить периметр вписанного квадрата через S — площадь круга

Вычислить периметр вписанного квадрата через P — периметр круга

Периметр квадрата и прямоугольника. Способы определения и примеры решения. :: SYL.ru

Часто на просторах интернета можно найти насмешки по поводу того, как знания по математике — интегралы, дифференциалы, тригонометрические функции и прочие разделы предмета — не помогают облегчить жизнь человека.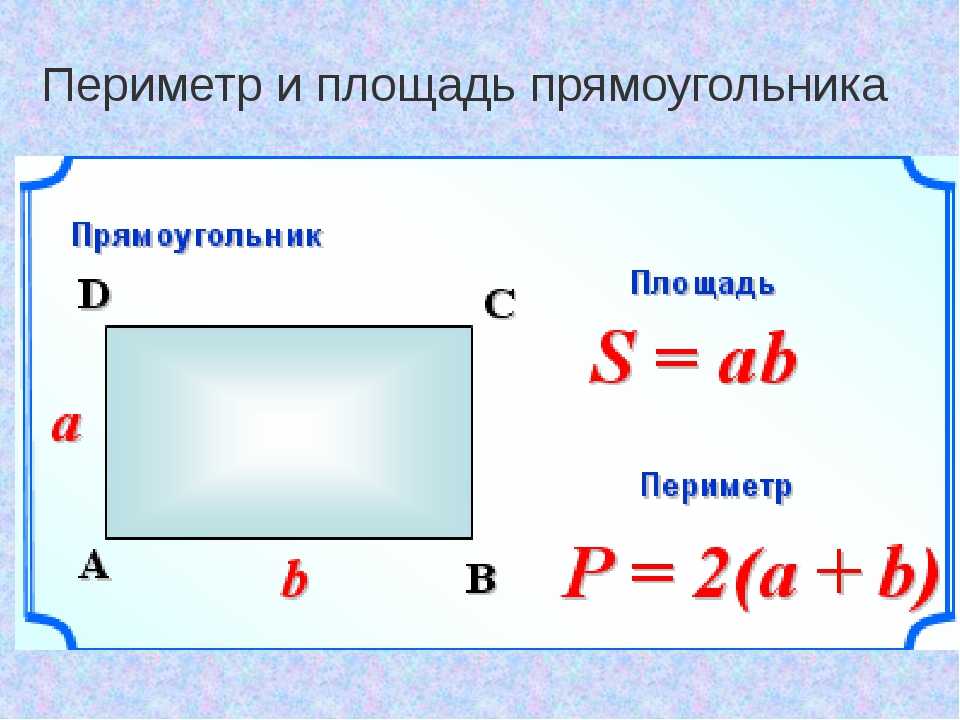 Такие шутки напрасны, ведь как выручает умение правильно рассчитывать периметр квадрата, прямоугольника и других геометрических фигур в строительных работах. Расход материала: плитки, обоев, напольного покрытия — не определить без понимания элементарных математических формул и геометрических фигур.

Свойства квадрата

Любые вычисления в математике базируются на свойствах объекта. Чтобы ответить на вопрос: «Чему равен периметр квадрата?» — рекомендуется вспомнить отличительные характеристики этой фигуры.

1. Равенство всех сторон.
2. Наличие четырех углов величиной 90 градусов.
3. Параллельность сторон.
4. Поворотная симметрия. При вращении фигуры ее вид остается неизменным.
5. Возможность описать и вписать окружность.
6. Диагонали при пересечении делят друг друга пополам.
7. Площадь фигуры характеризует заполненное квадратом место в двухмерном пространстве.
8. Периметр фигуры не что иное, как сумма длин его сторон.
9. Из предыдущего свойства вытекает, что единицами измерения величины периметра будут единицы длины: м, см, дм и другие.

Для подсчета плинтусов для завершения ремонта в квадратном помещении, необходимо знать длину комнаты. Для этого необходимо посчитать ее периметр.

Периметр

В переводе с греческого языка слово означает «измерять вокруг». Термин применим ко всем замкнутым фигурам: квадрату, окружности, прямоугольнику, треугольнику, трапеции и прочим. Знания по определению периметра элементарных фигур необходимы для решения сложных геометрических задач с объектами неправильной формы. Например, для расчета плинтусов в комнату планировкой типа «Г», или как еще называют, «сапожком», потребуется определить периметр квадрата и прямоугольника. Ведь форма помещения состоит из этих элементарных фигур.

Общепринятое обозначение такой величины – буква Р. Каждой фигуре с учетом ее свойств присуща своя формула для определения периметра.

Свойства прямоугольника

1. Равенство противоположных сторон.
2. Равенство диагоналей.
3. Возможность описать окружность.
4. Высоты прямоугольника равны его сторонам.
5. Сумма углов равна 360 градусов, и все углы прямые.
6. Параллельность противоположных сторон.
7. Перпендикулярность прилегающих сторон.
8. Сумма квадратов диагоналей прямоугольника равна сумме квадратов его сторон.
9. Пересекаясь, диагонали делят друг друга пополам.
10. Невозможность вписать в фигуру окружность.

Периметр квадрата

В зависимости от установленных (известных) параметров квадрата, существуют разные формулы для определения его периметра. Простой задачей является расчет периметра при установленной длине его стороны (с). В этом случае Р=с+с+с+с или 4*с. Например, длина стороны квадрата 7 см, тогда периметр фигуры буде 28 см (4*7).

В первом случае все понятно, но как найти периметр квадрата, зная его площадь? И тут все предельно ясно. Поскольку площадь фигуры определяется умножением одной стороны на другую, а у квадрата все стороны равны, необходимо извлечь корень из известной величины. Пример: есть квадрат с площадью 25 дм².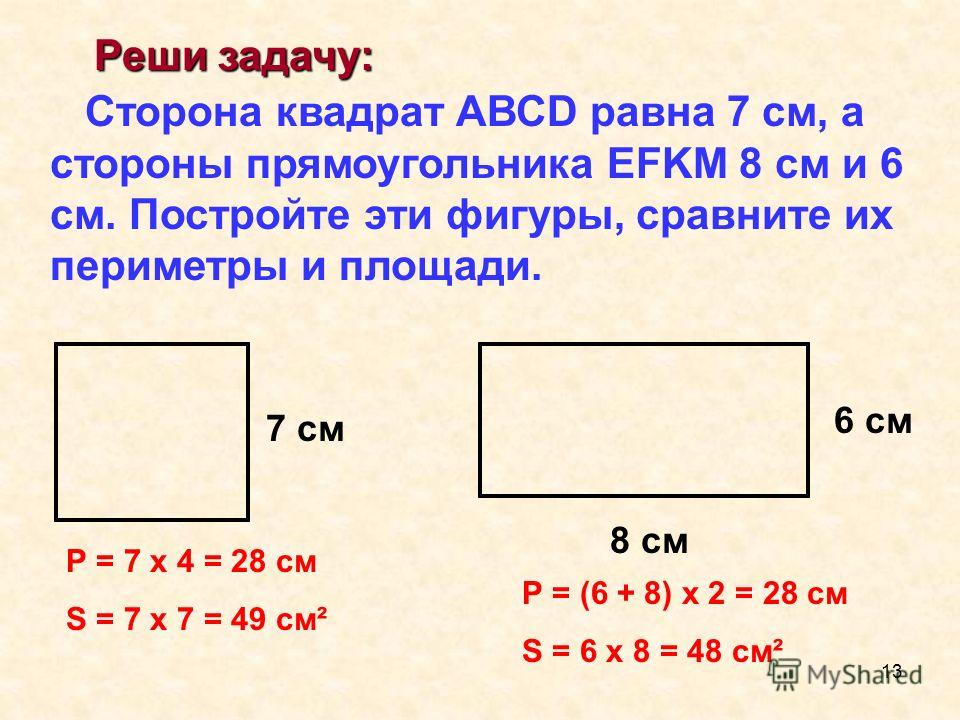 Корень из 25 равен 5 – эта величина характеризует длину стороны квадрата. Теперь, подставляя найденную величину — 5 дм² — в первоначальную формулу периметра, можно решить задачу. Ответом будет значение в 20 дм. То есть 4 умножили на 5, получили искомую величину.

Квадрат и окружность

Из свойств рассматриваемой фигуры выплывает, что в квадрат можно вписать окружность и также ее описать вокруг фигуры.

Первый вариант – нахождение периметра по радиусу описанной окружности. Вписанным считается квадрат, вершины которого находятся на окружности. Радиус окружности равен 1/2 длине диагонали. Выходит, что диаметр равен диагонали. Теперь необходимо рассмотреть прямоугольный треугольник, который получился в результате деления диагональю квадрата. Решение задачи сводится к нахождению сторон этого треугольника. ВС – это известная величина, диаметр описанной окружности. Допустим, он равен 3 см. Теорема Пифагора в случае с равными сторонами треугольника, будет выглядеть так: 2с²=3² . В формуле обозначение с – это длина стороны треугольника и квадрата; 3 – известная величина гипотенузы. Отсюда, с=√9/2. Зная сторону квадрата, его периметр посчитать не проблема.

Особенностью вписанной окружности является деление сторон квадрата пополам. Поэтому радиус равняется половине длины стороны квадрата. Тогда сторона с=2*радиус. Периметр квадрата в этом случае равен 4*2*радиус или 8 радиусам окружности.

Периметр прямоугольника

Самая элементарная формула определения периметра прямоугольника через известные величины его сторон выглядит так: Р=2(а+b), где а и b — длины сторон фигуры.

Диагональ прямоугольника аналогично квадрату делит фигуру пополам, образуя прямоугольный треугольник. Однако задача усложняется тем, что стороны этого треугольника неравные. В случае с известной величиной одной из сторон и диагонали, вторую можно найти, следуя теореме Пифагора: д²=а²+в², где а и в – стороны фигуры, а д – диагональ.

Если неизвестна ни одна из сторон, тогда в дело вступают знания тригонометрии: синусы, косинусы и другие функции.

Нахождение периметра по описанной окружности и известному диаметру сводится к тому, что диаметр равен длине диагонали фигуры. Дальше решение задачи определяется по наличию известных величин. Если даны углы, тогда через тригонометрические функции. Если дана сторона, ответ будет найден через теорему Пифагора.

Прямоугольник и тригонометрические функции

Для наглядности приведен пример решения задачи. Дано: прямоугольник АВСД; длина диагонали (d) 20 см; угол ф – 30°. Найти периметр фигуры.

Из тригонометрии необходимо вспомнить следующее: синус угла в прямоугольном треугольнике равен отношению противоположного катета к гипотенузе. Синус 30° (существуют таблицы, по которым можно определить значения тригонометрических функций для правильных углов) равен 1/2. Получается 1/2 = отношению в к d. Неизвестная величина в будет равна d/2=20/2=10 см.

Для расчета периметра следует найти вторую сторону фигуры. Можно через теорему Пифагора, так как известны длины гипотенузы и одного из катетов или опять через отношение сторон для косинуса угла.

Косинус угла ф выражается как отношение прилежащего катета к гипотенузе и равен √3/2.

√3/2=n/d, n=(d*√3)/2 или 10*√3. После извлечения корня из 3, получаем длину стороны треугольника: 10*1,73=17,3 см.

Периметр равен 2(17,3+10)=2*27,3=54,6 см.

Периметр и отношение сторон

В школьной программе встречаются задачи по геометрии, когда длины сторон прямоугольника выражены их отношением друг к другу. Рассмотрение решения подобной задачи представлено ниже.

Известно, что сумма длин всех сторон прямоугольника, то есть его периметр, равен 84 см. Отношение длины (д) к ширине (ш) – 3:2. Найти стороны фигуры.

Решение: пусть длина будет 3х, а ширина 2х, согласно соотношению из условия задачи. Формула периметра прямоугольника с полученными данными длин сторон будет следующей: 3х+3х+2х+2х = 84. Далее, 10х = 84, х=8,4 см. Подставив х в выражение длины и ширины прямоугольника, можно найти искомые величины. Длина будет: 3*8,4 = 25,2 см; ширина: 2*8,4 = 16,8 см.

Статья посвящена решению наиболее часто встречаемых задач в школьной программе. И это далеко не все способы нахождения периметра квадрата и прямоугольника.

Программа Python для нахождения периметра квадрата

Питон Джава С С++ HTML CSS JavaScript PHP SQL Контрольный опрос

В этой статье мы создали несколько программ на Python, чтобы найти и распечатать периметр квадрата на основе длины его стороны, введенной пользователем во время выполнения. Вот список программ:

• Найти периметр квадрата без функции
• Использование определяемой пользователем функции
• Использование класса

Прежде чем запускать эти программы, давайте сначала напомним вам об используемой здесь формуле.

Формула для нахождения периметра квадрата

Чтобы найти периметр любого квадрата, используйте следующую формулу:

 per = 4*side 

Здесь per указывает периметр, а сторона указывает длину стороны квадрата.

То есть, как вы все знаете, периметр квадрата можно вычислить, сложив все его четыре стороны, или просто умножение любой стороны на 4.

Следовательно, если длина стороны квадрата равна 2 метрам, то его периметр будет равен 2+2+2+2 или 4*2 , что равно 16 .

Найти периметр квадрата без функции

Чтобы вычислить периметр квадрата в Python, вы должны попросить пользователя ввести длину стороны квадрата, затем используйте приведенную выше формулу и рассчитайте периметр, как показано в программе, приведенной ниже:

 print("Введите длину стороны квадрата:")
с = интервал (ввод ())
р = 4*с
print("\nПериметр = ", p) 

Приведенный ниже снимок показывает начальный вывод, созданный этой программой Python:

Теперь введите ввод, скажем, 5 в качестве длины стороны квадрата, и нажмите клавишу ENTER , чтобы найти и напечатайте значение периметра, как показано на снимке ниже:

Модифицированная версия предыдущей программы

В этой программе end= используется для пропуска автоматического перехода на новую строку с помощью

print() . И {:.2f} есть используется с format() для печати значения p только до двух знаков после запятой.

 print("Введите длину стороны: ", end="")
с = с плавающей запятой (ввод ())
р = 4*с
print("\nPerimeter = {:.2f}".format(p)) 

Вот пример запуска с пользовательским вводом 3.4 в качестве длины стороны квадрата:

Найти периметр квадрата с помощью функции

Эта программа делает то же задание, что и предыдущее, но с использованием определяемой пользователем функции с именем findPerSqr() . Этот Функция получает в качестве аргумента длину любой стороны квадрата и возвращает значение площади.

 по определению findPerSqr(x):
    вернуть 4*х

print("Введите длину стороны: ", end="")
с = с плавающей запятой (ввод ())

p = найтиPerSqr(s)
print("\nPerimeter = {:.2f}".format(p)) 

Эта программа выводит тот же результат, что и предыдущая программа.

Найти периметр квадрата с помощью класса

Это последняя программа в этой статье, созданная с использованием класса , объектно-ориентированной функции Python. Доступ к функции-члену класса осуществляется через его объект. Поэтому мы создали объект с именем об и через этот объект мы получили доступ к функции-члену с именем findPerSqr() класса CodesCracker .

 класс CodesCracker:
    def найтиPerSqr (я, х):
        вернуть 4*х

print("Введите длину стороны: ", end="")
с = с плавающей запятой (ввод ())

ob = Взломщик кодов()
p = ob.findPerSqr(s)
print("\nPerimeter = {:.2f}".format(p)) 

Та же программа на других языках

• Java Вычислить периметр квадрата
• C Расчет периметра квадрата
• С++ Вычисление периметра квадрата

Онлайн-тест Python

---

« Предыдущая программаСледующая программа »

---

Поделись, пожалуйста:

---

Подпишитесь на нас/Нравится на Facebook

---

Подпишитесь на нас на YouTube

Калькулятор периметра квадрата

Периметр квадрата — Периметр квадрата определяется как длина границы квадрата. Для квадрата периметр вычисляется путем сложения четырех его сторон. Мы знаем, что все стороны квадрата равны, а значит, его периметр будет в 4 раза больше его стороны, то есть в 4 раза больше стороны.

Примеры расчетов периметра квадрата

Периметр квадрата 7 м

Периметр квадрата 3 см

Периметр квадрата 9 см

Периметр квадрата 6 в

Периметр квадрата 5 ярдов

Периметр квадрата 4 ярда

Периметр квадрата 8 м

Периметр квадрата 2 см

Периметр квадрата 5 футов

Периметр квадрата 6 ярдов

Периметр квадрата 4 м

Периметр квадрата 7 футов

Периметр квадрата 9 ярдов

Периметр квадрата 2 м

Периметр квадрата 8 футов

Периметр квадрата 3 см

Периметр квадрата 9 футов

Периметр квадрата 6 в

Периметр квадрата 5 ярдов

Периметр квадрата 4 м

Периметр квадрата 44 см

Периметр квадрата 60 футов

Периметр квадрата 59 футов

Периметр квадрата 44 в

Периметр квадрата 13 м

Периметр квадрата 70 м

Периметр квадрата 14 см

Периметр квадрата 98 в

Периметр квадрата 56 ярдов

Периметр квадрата 62 м

Периметр квадрата 42 см

Периметр квадрата 26 футов

Периметр квадрата 66 см

Периметр квадрата 62 фута

Периметр квадрата 33 м

Периметр квадрата 31 ярд

Периметр квадрата 93 ярда

Периметр квадрата 42 м

Периметр квадрата 95 футов

Периметр квадрата 73 см

Квадрат представляет собой плоскую форму с четырьмя сторонами равной длины, с прямым углом 90° на каждой стороне.

Каждая сторона противоположна и параллельна друг другу. Ширина и длина квадрата равны. Периметром квадрата называется вся его часть, выходящая за пределы его равных сторон. Это пустое пространство вокруг границы квадрата. Периметр рассчитывается для измерения границы, необходимой для ограждения квадратной комнаты. Периметр квадрата измеряется путем умножения размера стороны на 4,9.0003

Этот небольшой калькулятор предназначен для вычисления периметра квадрата. Это бесплатный онлайн-инструмент для автоматического определения области, которая задается в заданном вопросе.

Формула периметра квадрата

Универсальная формула для вычисления периметра квадрата:

4a= 4*a, где a равно стороне квадрата.

Чтобы измерить периметр квадрата, нам нужно знать длину его сторон и умножить длину сторон на 4. Все четыре стороны имеют одинаковую длину. Они обозначаются единицей измерения или сантиметром.

Необходимые шаги:

Шаг 1- Запишите длины сторон, указанные в вопросе

Шаг 2- Обозначьте длину как «а»

Шаг 3- Напишите формулу- 4a = 4*a

Шаг 4- вставьте значения, указанные в вопросе, так, как написано в формуле.

Шаг 5- умножить данные стороны на 4

Шаг 6- Полученный результат является мерой периметра в назначенных ему единицах измерения

Пример 1- Найдите периметр квадрата со стороной 100 см

Решение-

Шаг 1- данная сторона как «а» равна 100 см.

Шаг 2- 4a=4*a

Шаг 3- 4*100= 400

Шаг 4- Периметр квадрата равен 400 см

Пример 2- Нас могут попросить найти сторону квадрата квадрат. Например, найдите сторону квадрата, периметр которого равен 196 м.

Решение-

Шаг 1- площадь = 196 м

Шаг 2- 4a= 4*a

Шаг 3- 196= 4*a => 196/4= a => a=49

Шаг 4- сторона квадрата равна 49

Пример 3- Можно задать отношение периметров 2-х квадратов. Например, если отношение площадей двух квадратов 225:256, то отношение их периметров будет-

Решение-

Шаг 1- сторона квадрата будет «а».