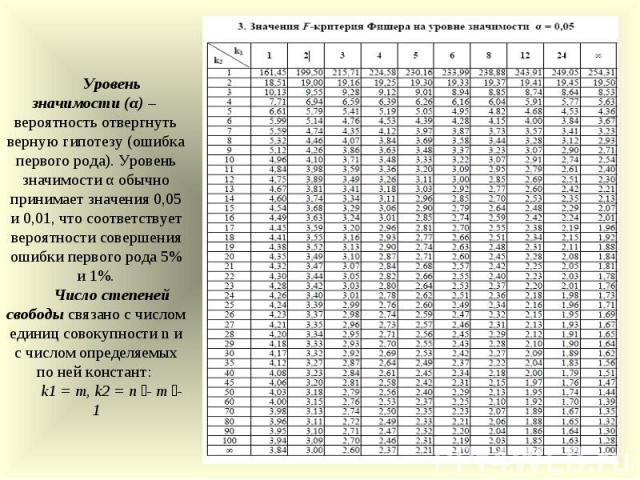
Коэффициенты Стьюдента | это… Что такое Коэффициенты Стьюдента?
Толкование
- Коэффициенты Стьюдента
Кванти́ли (проценти́ли) распределе́ния Стью́дента (коэффициенты Стьюдента) — числовые характеристики, широко используемые в задачах математической статистики таких как построение доверительных интервалов и проверка статистических гипотез.
Содержание
- 1 Определение
- 2 Замечания
- 3 Таблица квантилей
- 3.1 Пример
- 4 См. также
Определение
Пусть Fn — функция распределения Стьюдента t(n) с n степенями свободы, и . Тогда α-квантилью этого распределения называется число tα,n такое, что
- .
Замечания
- Прямо из определения следует, что случайная величина, имеющая распределение Стьюдента с

- Функция Fnстрого возрастает для любого . Следовательно, определена её обратная функция , и
- .
- Функция не имеет простого представления. Однако, возможно вычислить её значения численно.
- Распределение t(n) симметрично. Следовательно,
- t1 − α,n = − tα,n.
Таблица квантилей
Нижеприведённая таблица получена с помощью функции tinv пакета tα,n, необходимо найти строку, соответствующую нужному n, и колонку, соответствующую нужному α. Искомое число находится в таблице на их пересечении.
Пример
- t0.2,4 = 0.2707;
- t0.8,4 = − t0.2,4 = − 0.2707.
См. также
- Распределение Стьюдента;
- Доверительный интервал для математического ожидания нормальной выборки.
Квантили tα,n
two-tailed test 1-0.  9/2
9/21-0.8/2 1-0.7/2 1-0.6/2 1-0.5/2 1-0.4/2 1-0.3/2 1-0.2/2 1-0.1/2 1-0.05/2 1-0.02/2 one-tailed test 1-0.9 1-0.8 1-0.7 1-0.6 1-0.5 1-0.4 1-0.3 1-0.2 1-0.1 1-0.05 1-0.02 1 0.1584 0.3249 0.5095 0.7265 1.0000 1.3764 1.9626 3.0777 6.3138 12.7062 31.8205 2 0.1421 0.2887 0.4447 0.8165 1.0607 1.3862 1.8856 2.9200 4.3027 6.9646 3 0.1366 0.2767 0.4242 0.5844 0.7649 0.9785 1.2498 1.6377 2.3534 3.1824 4.5407 4 0.1338 0.  2707
27070.4142 0.5686 0.7407 0.9410 1.1896 1.5332 2.1318 2.7764 3.7469 5 0.1322 0.2672 0.4082 0.5594 0.7267 0.9195 1.1558 1.4759 2.0150 2.5706 3.3649 6 0.1311 0.2648 0.4043 0.5534 0.7176 0.9057 1.1342 1.4398 1.9432 2.4469 3.1427 7 0.1303 0.2632 0.4015 0.5491 0.7111 0.8960 1.1192 1.4149 1.8946 2.3646 2.9980 8 0.1297 0.2619 0.3995 0.5459 0.7064 0.8889 1.1081 1.3968 1.8595 2.3060 2.8965 9 0.1293 0.2610 0.3979 0.  5435
54350.7027 0.8834 1.0997 1.3830 1.8331 2.2622 2.8214 10 0.1289 0.2602 0.3966 0.5415 0.6998 0.8791 1.0931 1.3722 1.8125 2.2281 2.7638 11 0.1286 0.2596 0.3956 0.5399 0.6974 0.8755 1.0877 1.3634 1.7959 2.2010 2.7181 12 0.1283 0.2590 0.3947 0.5386 0.6955 0.8726 1.0832 1.3562 1.7823 2.1788 2.6810 13 0.1281 0.2586 0.3940 0.5375 0.6938 0.8702 1.0795 1.3502 1.7709 2.1604 2.6503 14 0.1280 0.2582 0.3933 0.5366 0.  6924
69240.8681 1.0763 1.3450 1.7613 2.1448 2.6245 15 0.1278 0.2579 0.3928 0.5357 0.6912 0.8662 1.0735 1.3406 1.7531 2.1314 2.6025 16 0.1277 0.2576 0.3923 0.5350 0.6901 0.8647 1.0711 1.3368 1.7459 2.1199 2.5835 17 0.1276 0.2573 0.3919 0.5344 0.6892 0.8633 1.0690 1.3334 1.7396 2.1098 2.5669 18 0.1274 0.2571 0.3915 0.5338 0.6884 0.8620 1.0672 1.3304 1.7341 2.1009 2.5524 19 0.1274 0.2569 0.3912 0.5333 0.6876 0.  8610
86101.0655 1.3277 1.7291 2.0930 2.5395 20 0.1273 0.2567 0.3909 0.5329 0.6870 0.8600 1.0640 1.3253 1.7247 2.0860 2.5280 21 0.1272 0.2566 0.3906 0.5325 0.6864 0.8591 1.0627 1.3232 1.7207 2.0796 2.5176 22 0.1271 0.2564 0.3904 0.5321 0.6858 0.8583 1.0614 1.3212 1.7171 2.0739 2.5083 23 0.1271 0.2563 0.3902 0.5317 0.6853 0.8575 1.0603 1.3195 1.7139 2.0687 2.4999 24 0.1270 0.2562 0.3900 0.5314 0.6848 0.8569 1.  0593
05931.3178 1.7109 2.0639 2.4922 25 0.1269 0.2561 0.3898 0.5312 0.6844 0.8562 1.0584 1.3163 1.7081 2.0595 2.4851 26 0.1269 0.2560 0.3896 0.5309 0.6840 0.8557 1.0575 1.3150 1.7056 2.0555 2.4786 27 0.1268 0.2559 0.3894 0.5306 0.6837 0.8551 1.0567 1.3137 1.7033 2.0518 2.4727 28 0.1268 0.2558 0.3893 0.5304 0.6834 0.8546 1.0560 1.3125 1.7011 2.0484 2.4671 29 0.1268 0.2557 0.3892 0.5302 0.6830 0.8542 1.0553 1. 
1.6991 2.0452 2.4620 30 0.1267 0.2556 0.3890 0.5300 0.6828 0.8538 1.0547 1.3104 1.6973 2.0423 2.4573 31 0.1267 0.2555 0.3889 0.5298 0.6825 0.8534 1.0541 1.3095 1.6955 2.0395 2.4528 32 0.1267 0.2555 0.3888 0.5297 0.6822 0.8530 1.0535 1.3086 1.6939 2.0369 2.4487 33 0.1266 0.2554 0.3887 0.5295 0.6820 0.8526 1.0530 1.3077 1.6924 2.0345 2.4448 34 0.1266 0.2553 0.3886 0.5294 0.6818 0.8523 1.0525 1.3070 1.  6909
69092.0322 2.4411 35 0.1266 0.2553 0.3885 0.5292 0.6816 0.8520 1.0520 1.3062 1.6896 2.0301 2.4377 36 0.1266 0.2552 0.3884 0.5291 0.6814 0.8517 1.0516 1.3055 1.6883 2.0281 2.4345 37 0.1265 0.2552 0.3883 0.5289 0.6812 0.8514 1.0512 1.3049 1.6871 2.0262 2.4314 38 0.1265 0.2551 0.3882 0.5288 0.6810 0.8512 1.0508 1.3042 1.6860 2.0244 2.4286 39 0.1265 0.2551 0.3882 0.5287 0.6808 0.8509 1.0504 1.3036 1.6849 2.  0227
02272.4258 40 0.1265 0.2550 0.3881 0.5286 0.6807 0.8507 1.0500 1.3031 1.6839 2.0211 2.4233 41 0.1264 0.2550 0.3880 0.5285 0.6805 0.8505 1.0497 1.3025 1.6829 2.0195 2.4208 42 0.1264 0.2550 0.3880 0.5284 0.6804 0.8503 1.0494 1.3020 1.6820 2.0181 2.4185 43 0.1264 0.2549 0.3879 0.5283 0.6802 0.8501 1.0491 1.3016 1.6811 2.0167 2.4163 44 0.1264 0.2549 0.3878 0.5282 0.6801 0.8499 1.0488 1.3011 1.6802 2.0154 2.  4141
414145 0.1264 0.2549 0.3878 0.5281 0.6800 0.8497 1.0485 1.3006 1.6794 2.0141 2.4121 46 0.1264 0.2548 0.3877 0.5281 0.6799 0.8495 1.0483 1.3002 1.6787 2.0129 2.4102 47 0.1263 0.2548 0.3877 0.5280 0.6797 0.8493 1.0480 1.2998 1.6779 2.0117 2.4083 48 0.1263 0.2548 0.3876 0.5279 0.6796 0.8492 1.0478 1.2994 1.6772 2.0106 2.4066 49 0.1263 0.2547 0.3876 0.5278 0.6795 0.8490 1.0475 1.2991 1.6766 2.0096 2.4049 50 0.  1263
12630.2547 0.3875 0.5278 0.6794 0.8489 1.0473 1.2987 1.6759 2.0086 2.4033 100 0.1260 0.2540 0.3864 0.5261 0.6770 0.8452 1.0418 1.2901 1.6602 1.9840 2.3642 1000 0.1257 0.2534 0.3854 0.5246 0.6747 0.8420 1.0370 1.2824 1.6464 1.9623 2.3301
Wikimedia Foundation. 2010.
Игры ⚽ Поможем сделать НИР
- Коэффициенты Ламэ
- Коялович, Войцех
Полезное
Классические методы статистики: t-критерий Стьюдента
Начать, пожалуй, стоит с математических допущений, на которых основан критерий Стьюдента. Основных таких допущений, как известно, два:
Кроме того, в своей исходной форме, t-критерий предполагает независимость сравниваемых выборок.
Проверка указанных требований к данным должна всегда предшествовать формальному статистическому анализу, в котором задействован критерий Стьюдента (к сожалению, многие исследователи забывают об этом). Способы проверки этих требований я рассмотрю в будущих сообщениях. Сейчас же пока отметим, что условие нормальности распределения данных становится не таким жестким при «больших» объемах выборок, а для выборок с разными дисперсиями существует особая модификация t-критерия (критерий Уэлча; см. также ниже).
Этот вариант критерия Стьюдента служит для проверки нулевой гипотезы о равенстве среднего значения (\(mu_1\)) генеральной совокупности, из которой была взята выборка, некоторому известному значению (\(mu_0\)):
Рассчитанное значение критерия мы можем далее интерпретировать следующим образом, исходя из свойств t-распределения: если это значение попадает в т.н. область отклонения нулевой гипотезы (см. рисунок ниже), то мы вправе отклонить проверяемую нулевую гипотезу.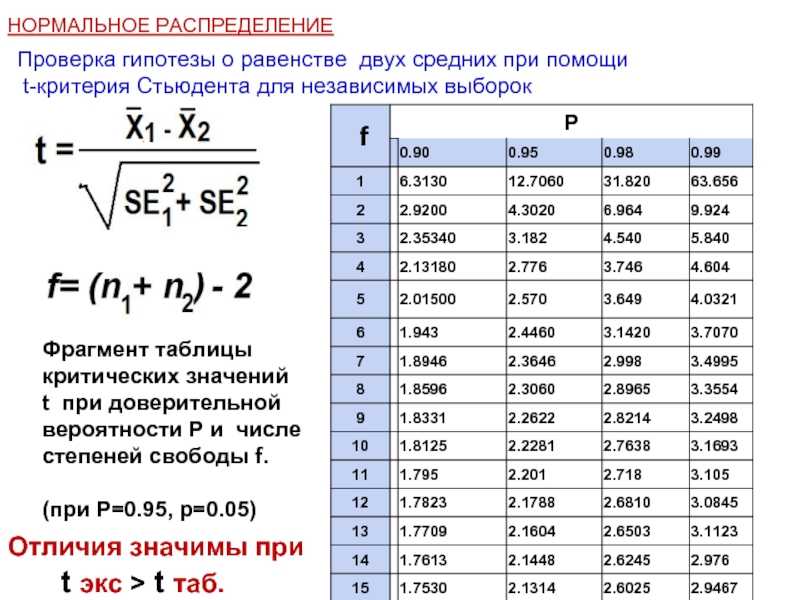 Область отклонения нулевой гипотезы для критерия Стьюдента определяется заранее принятым уровнем значимости (например, \(\alpha=0.05\)) и числом степеней свободы.
Область отклонения нулевой гипотезы для критерия Стьюдента определяется заранее принятым уровнем значимости (например, \(\alpha=0.05\)) и числом степеней свободы.
Эквивалентным подходом к интерпретации результатов теста будет следующий: допустив, что нулевая гипотеза верна, мы можем рассчитать, насколько велика вероятность получить t-критерий, равный или превышающий то реальное значение, которое мы рассчитали по имеющимся выборочным данным. Если эта вероятность оказывается меньше, чем заранее принятый уровень значимости (например, \(P < 0.05\)), мы вправе отклонить проверяемую нулевую гипотезу. Именно такой подход сегодня используется чаще всего: исследователи приводят в своих работах P-значение, которое легко рассчитывается при помощи статистических программ. Рассмотрим, как это можно сделать в системе R.
Предположим, у нас имеются данные по суточному потреблению энергии, поступающей с пищей (кДж/сутки), для 11 женщин (пример заимствован из книги Altman D. G. (1981) Practical Statistics for Medical Research, Chapman & Hall, London):
G. (1981) Practical Statistics for Medical Research, Chapman & Hall, London):
d.intake <- c(5260, 5470, 5640, 6180, 6390, 6515, 6805, 7515, 7515, 8230, 8770)
Среднее значение для этих 11 наблюдений составляет:
mean(d.intake) [1] 6753.6
Вопрос: отличается ли это выборочное среднее значение от установленной нормы в 7725 кДж/сутки? Разница между нашим выборочным значением и этим нормативом довольно прилична: 7725 — 6753.6 = 971.4. Но насколько велика эта разница статистически? Ответить на этот вопрос поможет одновыборочный t-тест. Как и другие варианты t-теста, одновыборочный тест Стьюдента выполняется в R при помощи функции t.test():
t.test(d.intake, mu = 7725)
One Sample t-test
data: d.intake
t = -2.8208, df = 10, p-value = 0.01814
alternative hypothesis: true mean is not equal to 7725
95 percent confidence interval:
5986.348 7520.925
sample estimates:
mean of x
6753. 636
636Видим, что для имеющихся выборочных данных t-критерий составляет -2.821 при 10 степенях свободы (df). Вероятность получить такое (либо большее) значение t при условии, что проверяемая нулевая гипотеза верна, оказалась весьма мала: p-value = 0.01814 (во всяком случае, это меньше 5%). Следовательно (см. выше), мы можем отклонить проверяемую нулевую гипотезу о равенстве выборочного среднего значения нормативу и принять альтернативную гипотезу (alternative hypothesis: true mean is not equal to 7725). Делая это, мы рискуем ошибиться с вероятностью менее 5%.
Помимо t-критерия, количества степеней свободы, Р-значения и выборочного среднего (sample estimates: mean of x), программа рассчитала также 95%-ный доверительный интервал (95 percent confidence interval) для истинной разницы между выборочным средним значением суточного потребления энергии и нормативом. Если бы мы повторили аналогичный тест много раз для разных групп из 11 женщин, то в 95% случаев эта разница оказалась бы в диапазоне от 5986. {2}\) — выборочные оценки дисперсии. При соблюдении условия о равенстве групповых дисперсий приведенная формула приобретает более простой вид (подробнее см. здесь). Интерпретация t-критерия, рассчитанного для двух выборок, выполняется точно так же, как и в случае с одной выборкой (см. выше).
{2}\) — выборочные оценки дисперсии. При соблюдении условия о равенстве групповых дисперсий приведенная формула приобретает более простой вид (подробнее см. здесь). Интерпретация t-критерия, рассчитанного для двух выборок, выполняется точно так же, как и в случае с одной выборкой (см. выше).
Рассмотрим пример о суточном расходе энергии (expend) у худощавых женщин (lean) и женщин с избыточным весом (obese), приведенный в книге Питера Дальгаарда (Dalgaard P (2008) Introductory statistics with R. Springer). Данные из этого примера (подробнее см. ?energy) входят в состав пакета ISwR, сопровождающего книгу (если он у Вас не установлен, выполните команду install.packages(«ISwR»)):
library(ISwR) data(energy) attach(energy) energy expend stature 1 9.21 obese 2 7.53 lean 3 7.48 lean 4 8.08 lean 5 8.09 lean 6 10.15 lean 7 8.40 lean 8 10.88 lean 9 6.13 lean 10 7.90 lean 11 11.51 obese 12 12.79 obese 13 7.05 lean 14 11.85 obese 15 9.97 obese 16 7.48 lean 17 8.79 obese 18 9.69 obese 19 9.68 obese
Соответствующие средние значения потребления энергии в рассматриваемых группах пациенток составляют (подробнее о примененной ниже функции tapply() см. здесь):
tapply(expend, stature, mean) lean obese 8.07 10.30
Различаются ли эти средние значения статистически? Проверим гипотезу об отсутствии разницы при помощи t-теста:
t.test(expend ~ stature)
Welch Two Sample t-test
data: expend by stature
t = -3.8555, df = 15.919, p-value = 0.001411
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-3.459167 -1.004081
sample estimates:
mean in group lean mean in group obese
8.066154 10.297778Обратите внимание на использование знака ~ в вызове функции t.test(). Это стандартный для R способ записи формул, описывающих связь между переменными. В нашем случае выражение expend ~ stature можно расшифровать как «зависимость суточного потребления энергии (expend) от статуса пациентки (stature)».
В нашем случае выражение expend ~ stature можно расшифровать как «зависимость суточного потребления энергии (expend) от статуса пациентки (stature)».
Согласно полученному значению P (p-value = 0.001411), средние значения потребления энергии у женщин из рассматриваемых весовых групп статистически значимо различаются. Отвергая нулевую гипотезу о равенстве этих средних значений, мы рискуем ошибиться с вероятностью лишь около 0.1%. При этом истинная разница между средними значениями с вероятностью 95% находится в диапазоне от -3.5 до -1.0 (см. 95 percent confidence interval).
Следует подчеркнуть, что при выполнении двухвыборочного t-теста R по умолчанию принимает, что дисперсии сравниваемых совокупностей не равны, и, как следствие, выполняет t-тест в модификации Уэлча (подробнее см. здесь). Мы можем изменить такое поведение программы, воспользовавшись аргументом var.equal = TRUE: (от variance — дисперсия, и equal — равный):
t.test(expend ~ stature, var.equal = TRUE) Two Sample t-test data: expend by stature t = -3.9456, df = 20, p-value = 0.000799 alternative hypothesis: true difference in means is not equal to 0 95 percent confidence interval: -3.411451 -1.051796 sample estimates: mean in group lean mean in group obese 8.066154 10.297778
Р-значение стало еще меньше, и мы так же, как и после теста в модификации Уэлча, можем сделать вывод о наличии существенной разницы между средними. Однако такое совпадение выводов будет иметь место не всегда и, следовательно, на разницу между групповыми дисперсиями (или ее отсутствие) следует обращать серьезное внимание при выборе и интерпретации того или иного варианта t-теста.
Сравнение двух зависимых (= парных) выборок
Зависимыми, или парными, являются две выборки, содержащие результаты измерений какого-либо количественного признака, выполненных на одних и тех же объектах. Во многих исследованиях какой-то определенный отклик измеряется у одних и тех же объектов до и после экспериментального воздействия. При такой схеме эксперимента исследователь более точно оценивает эффект воздействия именно потому, что прослеживает его у одних и тех же объектов.
При такой схеме эксперимента исследователь более точно оценивает эффект воздействия именно потому, что прослеживает его у одних и тех же объектов.
Но как в таких случаях оценить наличие эффекта от воздействия статистически? В общем виде критерий Стьюдента можно представить как
\[t = \frac{\text{оценка параметра} — \text{истинное значение параметра}}{\text{ст. ошибка оценки параметра}}\]
Нас интересует «истинное значение параметра» — среднее изменение какого-либо количественного признака как результат экспериментального воздействия — обозначим его \(\delta\). Оценкой этого истинного параметра является наблюдаемое (выборочное) среднее изменение признака. Тогда t-критерий примет вид
\[t = \frac{\bar{d} — \delta}{S_{\bar{d}}} \]
Если нулевая гипотеза заключается в равенстве истинного эффекта нулю, формула для парного критерия Стьюдента примет вид
\[t = \frac{\bar{d}}{S_{\bar{d}}} \]
В книге П. Дальгаарда (Dalgaard 2008) имеется пример о суточном потреблении энергии, измеренном у одних и тех же 11 женщин до и после периода менструаций:
Дальгаарда (Dalgaard 2008) имеется пример о суточном потреблении энергии, измеренном у одних и тех же 11 женщин до и после периода менструаций:
data(intake) # из пакета ISwR
attach(intake)
intake
pre post
1 5260 3910
2 5470 4220
3 5640 3885
4 6180 5160
5 6390 5645
6 6515 4680
7 6805 5265
8 7515 5975
9 7515 6790
10 8230 6900
11 8770 7335Индивидуальные разницы в потреблении энергии у этих женщин составляют:
post - pre [1] -1350 -1250 -1755 -1020 -745 -1835 -1540 -1540 [9] -725 -1330 -1435
Усреднив эти индивидуальные разницы, получим
mean(post - pre) [1] -1320.5
Задача заключается в том, чтобы оценить, насколько статистически значимо эта средняя разница отличается от нуля. Применим парный критерий Стьюдента (обратите внимание на использование аргумента paired = TRUE):
t.test(pre, post, paired = TRUE)
Paired t-test
data: pre and post
t = 11. 9414, df = 10, p-value = 3.059e-07
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
1074.072 1566.838
sample estimates:
mean of the differences
1320.455
9414, df = 10, p-value = 3.059e-07
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
1074.072 1566.838
sample estimates:
mean of the differences
1320.455Как видим, рассчитанное программой P-значение оказалось намного меньше 0.05, что позволяет нам сделать заключение о наличии существенной разницы в потреблении энергии у исследованных женщин до и после менструации. Истинная величина эффекта (в абсолютном выражении) с вероятностью 95% находится в интервале от 1074.1 до 1566.8 кДж/сутки.
Приведенные выше примеры охватывают наиболее типичные случаи применения критерия Стьюдента. За рамками этого сообщения остаются т.н. односторонние варианты t-теста, когда проверяемая нулевая гипотеза заключается в том, что одно из сравниваемых средних значений больше (или меньше) другого. Однако можно отметить, что односторонний вариант t-теста легко реализуется при помощи функции t. test() в сочетании с аргументом alternative, который может принимать одно из трех значений — «two.sided» («двухсторонний»; выбирается программой по умолчанию), «greater» («больше») или «less» («меньше»).
test() в сочетании с аргументом alternative, который может принимать одно из трех значений — «two.sided» («двухсторонний»; выбирается программой по умолчанию), «greater» («больше») или «less» («меньше»).
Распределение | Что это такое и как его использовать (с примерами)
Опубликован в 28 августа 2020 г. к Ребекка Беванс. Отредактировано 9 июля 2022 г.
Распределение t , также известное как t -распределение Стьюдента, представляет собой способ описания данных, которые следуют кривой нормального распределения при нанесении на график, с наибольшим количеством наблюдений, близких к среднему, и меньшим количеством наблюдений в хвосты.
Это тип нормального распределения, используемый для небольших выборок, когда дисперсия данных неизвестна.
В статистике t -распределение чаще всего используется для:
- Найдите критические значения для доверительного интервала, когда данные примерно нормально распределены.

- Найдите соответствующее p -значение из статистического теста, использующего t -распределение ( t -тесты, регрессионный анализ).
Содержание
- Что такое t-распределение?
- T-распределение и стандартное нормальное распределение
- T-распределение и t-показатели
- Часто задаваемые вопросы о t-распределении
Что такое
t -распределение?Распределение t — это тип нормального распределения, который используется для небольших выборок. Нормально распределенные данные образуют форму колокола при нанесении на график, с большим количеством наблюдений около среднего и меньшим количеством наблюдений в хвостах.
t -распределение используется, когда данные примерно нормально распределены, что означает, что данные имеют форму колокола, но дисперсия совокупности неизвестна. Дисперсия в t -распределении оценивается на основе степеней свободы набора данных (общее количество наблюдений минус 1).
Это более консервативная форма стандартного нормального распределения , также известного как распределение z . Это означает, что оно дает более низкую вероятность центру и более высокую вероятность хвостам, чем стандартное нормальное распределение.
Пример: t -распределение по сравнению с z -распределение Если вы измеряете средний балл теста по выборке только из 20 учащихся, вы должны использовать t -распределение для оценки доверительного интервала вокруг среднего значения. Если вы используете распределение z , ваш доверительный интервал будет искусственно точным. T — распределение и стандартное нормальное распределение При увеличении степеней свободы (общее количество наблюдений минус 1) 9Распределение 0005 t будет все ближе и ближе соответствовать стандартному нормальному распределению, также известному как распределение z , пока они не станут почти идентичными.
Свыше 30 степеней свободы распределение t примерно совпадает с распределением z . Таким образом, распределение z можно использовать вместо распределения t при больших размерах выборки.
Распределение z предпочтительнее t -распределение, когда дело доходит до статистических оценок, потому что оно имеет известную дисперсию. Он может дать более точные оценки, чем t -распределение, дисперсия которого аппроксимируется с использованием степеней свободы данных.
Получение отзывов о языке, структуре и форматировании
Профессиональные редакторы вычитывают и редактируют вашу статью, уделяя особое внимание:
- Академический стиль
- Расплывчатые предложения
- Грамматика
- Согласованность стиля
См. пример
Т -распределение и т -баллы t -оценка представляет собой число стандартных отклонений от среднего в t -распределении.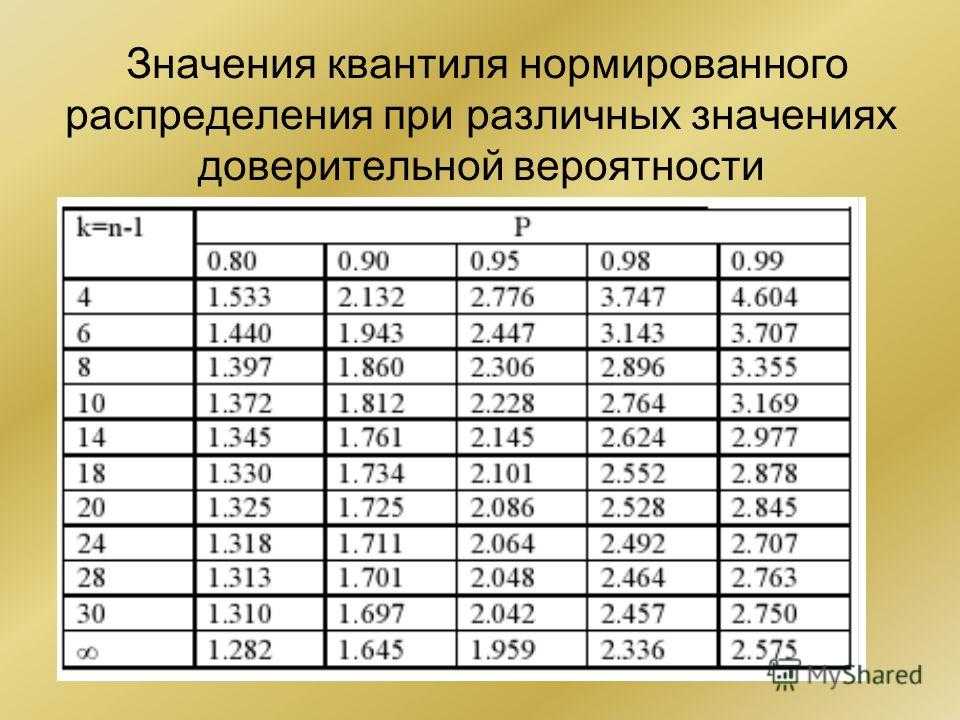 Обычно вы можете найти результат t в таблице t или воспользоваться онлайн-калькулятором t .
Обычно вы можете найти результат t в таблице t или воспользоваться онлайн-калькулятором t .
В статистике t -оценки в основном используются для нахождения двух вещей:
- Верхняя и нижняя границы доверительного интервала, когда данные примерно нормально распределены.
- p -значение тестовой статистики для t -тестов и регрессионных тестов.
Доверительные интервалы используют t -показателей для вычисления верхней и нижней границ интервала прогнозирования. Оценка t , используемая для получения верхней и нижней границ, также известна как критическое значение из t или t *.
Пример доверительного интервалаВы выбрали 20 учащихся из двух разных классов для оценки средних результатов стандартизированного теста и хотите узнать, есть ли разница между двумя группами.
Используя двусторонний t -критерий, вы получаете оценку разницы между двумя классами и доверительный интервал вокруг этой оценки. Из теста t вы обнаружите, что разница в среднем балле между классом 1 и классом 2 составляет 4,61, с 95% доверительный интервал от 3,87 до 5,35.
Поскольку доверительный интервал не пересекает ноль и на самом деле очень далек от нуля, маловероятно, что эта разница в результатах тестов могла возникнуть при нулевой гипотезе об отсутствии различий между группами.
T -баллы и p -значенияСтатистические тесты генерируют тестовую статистику, показывающую, насколько далеки ваши данные от нулевой гипотезы статистического теста. Затем они вычисляют p — значение, описывающее вероятность того, что ваши данные появятся, если нулевая гипотеза верна.
Статистика теста для t -тестов и регрессионных тестов представляет собой t -оценку. В то время как большинство статистических программ автоматически вычисляют соответствующее значение p для оценки t , вы также можете найти значения в таблице t , используя ваши степени свободы и t -оценку, чтобы найти значение p .
Значение t , которое дает значение p ниже вашего порога статистической значимости, известно как критическое значение t или t *.
Пример p-значения. Двусторонний t -критерий разницы результатов теста дает t -значение 12,79. Это означает, что разница в средних групповых значениях составляет 12,79 стандартных отклонений от среднего значения распределения нулевой гипотезы.Степени свободы 38 (n–1 для каждой группы). Глядя на это в t -table (или вычислив его в вашей любимой статистической программе) вы найдете p -значение < 0,001.
Этот вывод, как и вывод из доверительного интервала, предполагает, что вы вряд ли обнаружите такую большую разницу, если истинная разница в средних результатах теста равна нулю.
Часто задаваемые вопросы о t-распределении
- Что такое t-распределение? org/Answer»>
- Что такое t-оценка?
t -значение (также известное как t -значение) эквивалентно количеству стандартных отклонений от среднего значения t -распределения.
Показатель t — это тестовая статистика, используемая в t -тестах и регрессионных тестах.
 Его также можно использовать для описания того, насколько далеко от среднего находится наблюдение, когда данные следуют т -распределение.
Его также можно использовать для описания того, насколько далеко от среднего находится наблюдение, когда данные следуют т -распределение.- Что такое тестовая статистика?
Статистика теста — это число, рассчитанное с помощью статистического теста. Он описывает, насколько ваши наблюдаемые данные далеки от нулевой гипотезы об отсутствии связи между переменными или отсутствии различий между группами выборок.
Тестовая статистика показывает, насколько две или более группы отличаются от общего среднего значения генеральной совокупности или насколько линейный наклон отличается от наклона, предсказанного нулевой гипотезой. В разных статистических тестах используются разные статистические данные.
- Что такое критическое значение? org/Answer»>
Распределение t — это способ описания набора наблюдений, где большинство наблюдений падают близко к среднему, а остальные наблюдения составляют хвосты с обеих сторон. Это тип нормального распределения, используемый для небольших выборок, когда дисперсия данных неизвестна.
Распределение t образует колоколообразную кривую при нанесении на график. Его можно описать математически, используя среднее значение и стандартное отклонение.
Критическое значение — это значение статистики теста, которое определяет верхнюю и нижнюю границы доверительного интервала или определяет порог статистической значимости в статистическом тесте. Он описывает, как далеко от среднего значения распределения вы должны уйти, чтобы покрыть определенное количество общей вариации данных (т. е. 90%, 95%, 99%).
Если вы строите 95% доверительный интервал и используете порог статистической значимости p = 0,05, то ваше критическое значение будет одинаковым в обоих случаях.
Процитировать эту статью Scribbr
Если вы хотите процитировать этот источник, вы можете скопировать и вставить цитату или нажать кнопку «Цитировать эту статью Scribbr», чтобы автоматически добавить цитату в наш бесплатный генератор цитирования.
Беванс, Р. (2022, 09 июля). Т-распределение | Что это такое и как его использовать (с примерами).
Скриббр. Проверено 22 марта 2023 г., с https://www.scribbr.com/statistics/t-distribution/
Процитировать эту статью
Полезна ли эта статья?
Вы уже проголосовали. Спасибо 🙂 Ваш голос сохранен 🙂 Обработка вашего голоса…
Ребекка работает над докторской диссертацией по почвенной экологии, а в свободное время пишет. Она очень рада, что может поболтать о статистике со всеми вами.
т Распределение Основные понятия | Реальная статистика с использованием Excel
Основные понятия Проверка гипотезы с одной выборкой, описанная в разделе «Проверка гипотез с использованием центральной предельной теоремы с использованием нормального распределения», подходит, когда известно стандартное отклонение распределения совокупности, а совокупность либо нормально распределена или выборка достаточно велика, чтобы применить центральную предельную теорему.
Проблема в том, что стандартное отклонение генеральной совокупности обычно неизвестно. Один из подходов к решению этой проблемы заключается в использовании стандартного отклонения s выборки в качестве аппроксимации стандартного отклонения σ для генеральной совокупности. Лучшим подходом является использование t-распределения.
Pdf и основные свойстваОпределение 1 : ( Студенческий ) т распределение с к степеней свободы , сокращенно T ( k ) имеет функцию распределения вероятностей (pdf)
, где Γ(y) — гамма-функция, как описано в разделе Гамма-функция.
Ключевые статистические свойства распределения t:
- Среднее = 0 для k > 0
- Медиана = 0
- Режим = 0
- Диапазон = (-∞, ∞)
- Дисперсия = тыс. ⁄ ( тыс. – 2) для тыс.
 > 2
> 2 - Асимметрия = 0 для k > 3
- Эксцесс = 6 ⁄ ( к – 4) для к > 4
Общая форма функции плотности вероятности распределения t напоминает колоколообразную форму нормально распределенной случайной величины со средним значением 0 и дисперсией 1, за исключением того, что она немного ниже и шире. По мере роста числа степеней свободы распределение t приближается к стандартному нормальному распределению, и в действительности приближение довольно близкое для K ≥ 30.
Рисунок 1 — Диаграмма T -распределения по градусам свободы
Другие свойствасвойство 1 : если x имеет нормальное дистрибьютор 555555555 года. , ?
Щелкните здесь для доказательства свойства 1.
свойство 2 : для выборок достаточно большого размера n со средним x̄ и стандартным отклонением s случайная величина
3 имеет распределение 0 T
3
( н – 1).
Доказательство: Это следует из свойства 1 центральной предельной теоремы.
НаблюденияТестовая статистика в свойствах 1 и 2 такая же, как
из центральной предельной теоремы с заменой стандартного отклонения совокупности σ на стандартное отклонение выборки s . Что делает это настолько полезным, так это то, что обычно стандартное отклонение совокупности неизвестно, в то время как стандартное отклонение выборки известно.
Если выборка составляет значительную часть (конечной) совокупности (например, более 5%), то стандартную ошибку s/ в свойствах 1 и 2 следует заменить на
, где N – численность населения.
Функции рабочего листаExcel Functions : Excel обеспечивает следующие функции для распределения T:
T.DIST ( x , DF , CUM 9006). f ( x ) для распределения t, когда cum = FALSE и соответствующая кумулятивная функция распределения F ( x ), когда включая = ИСТИНА.
T.ОБР ( p,df ) = значение x такое, что T.DIST( x, df , TRUE) = p df , т.е. х, df , ИСТИНА).
Кроме того, Excel предоставляет следующие функции рабочего листа:
T.DIST.RT ( x , df ) = правая часть распределения t с размерами x и df степеней свободы.0003
T.DIST.2T ( x , df ) = сумма правого хвоста распределения t с df степеней свободы при x плюс левый хвост при -06,5 -x6,
где x ≥ 0 (функция выдает значение ошибки, когда x < 0).
T.ОБР.2T ( p , df ) = значение x такое, что T.DIST.2T( x , df ) = 9000 .РАСП.2T( x , df )
Обратите внимание, что правый хвост на x , T.DIST.RT( x , df ) = 1 – T. DIST( x 0d 0 , TRUE 0, , ). Поскольку распределение t симметрично относительно x = 0, левый хвост при — x также равен T.DIST.RT( x , df ) и сумме правого и левого хвостов, T.DIST .2T( x , df ) равно 2* T.DIST.RT( x , df ).
DIST( x 0d 0 , TRUE 0, , ). Поскольку распределение t симметрично относительно x = 0, левый хвост при — x также равен T.DIST.RT( x , df ) и сумме правого и левого хвостов, T.DIST .2T( x , df ) равно 2* T.DIST.RT( x , df ).
Так как распределение t симметрично относительно x = 0, мы имеем следующие эквивалентности:
T.DIST (- x , df , ИСТИНА) = 1 – T.DIST ( x , df , TRUE) = T.DIST .RT( x , df )
T.DIST.RT(- x , df ) = 1 – T.DIST.RT( x , df ) 900 x , df , ИСТИНА)
T.ОБР(1- p , df ) = T.ОБР.2T(2* p , df
) для Как правило, мы используем T.DIST.RT и T.DIST.2T для одностороннего и двустороннего t-тестов соответственно. Мы используем T.ОБР.(1- p, df ) и T.ОБР.2T( p, df ) для односторонних и двусторонних критических значений соответственно.
Функции Excel : Вышеуказанные функции недоступны для версий Excel до Excel 2010. В Excel 2007 и более ранних версиях вместо них используются следующие функции, где x ≥ 0, DF > 0 и Хвосты = 1 или 2:
TDIST ( x, DF , Хвосты ) = T.DIST.RT ( x, DF ), если хвосты = 1 и = T.DIST.2T( x, df ) if tails = 2
TINV ( p, df ) = T.INV.2T( p, df )
функции более подробно описаны в разделе Встроенные статистические функции.
На рис. 2 приведены примеры использования этих функций рабочего листа Excel.
Рисунок 2 – Примеры функций распределения t
Функции для нецелочисленных df округляется до ближайшего меньшего целого числа. Таким образом, df = 3,7 обрабатывается так же, как df = 3.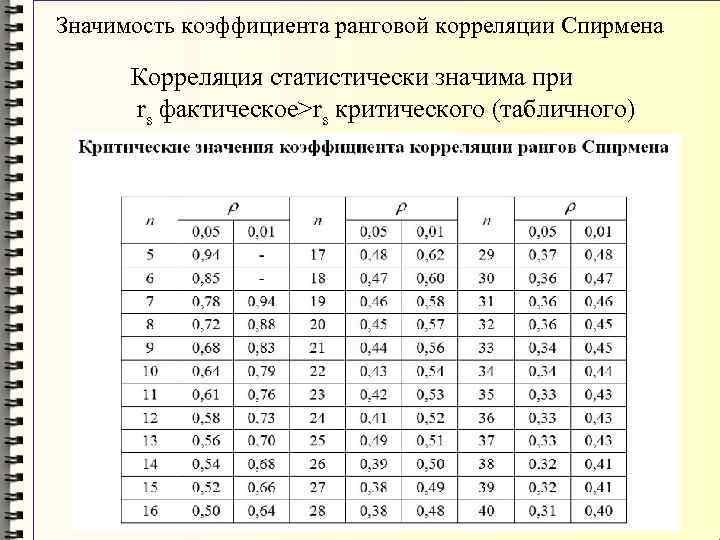


 9/2
9/2 2707
2707 5435
5435 6924
6924 8610
8610 0593
0593
 6909
6909 0227
0227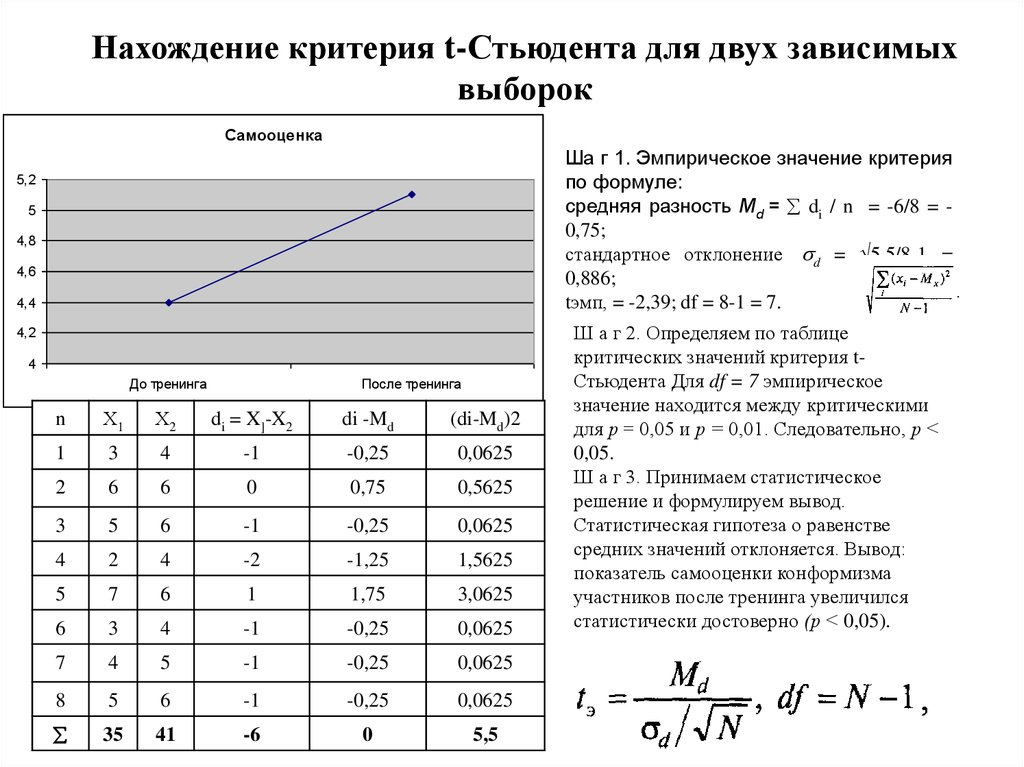 4141
4141 1263
1263 636
636 05 lean
14 11.85 obese
15 9.97 obese
16 7.48 lean
17 8.79 obese
18 9.69 obese
19 9.68 obese
05 lean
14 11.85 obese
15 9.97 obese
16 7.48 lean
17 8.79 obese
18 9.69 obese
19 9.68 obese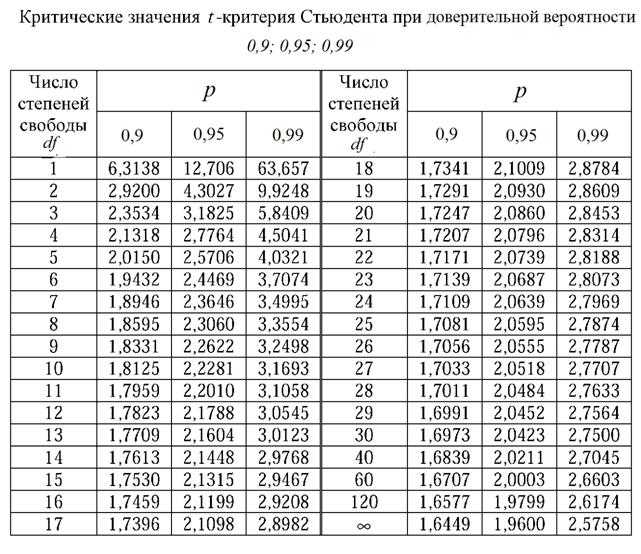 test(expend ~ stature, var.equal = TRUE)
Two Sample t-test
data: expend by stature
t = -3.9456, df = 20, p-value = 0.000799
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-3.411451 -1.051796
sample estimates:
mean in group lean mean in group obese
8.066154 10.297778
test(expend ~ stature, var.equal = TRUE)
Two Sample t-test
data: expend by stature
t = -3.9456, df = 20, p-value = 0.000799
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-3.411451 -1.051796
sample estimates:
mean in group lean mean in group obese
8.066154 10.297778 9414, df = 10, p-value = 3.059e-07
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
1074.072 1566.838
sample estimates:
mean of the differences
1320.455
9414, df = 10, p-value = 3.059e-07
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
1074.072 1566.838
sample estimates:
mean of the differences
1320.455
 Его также можно использовать для описания того, насколько далеко от среднего находится наблюдение, когда данные следуют т -распределение.
Его также можно использовать для описания того, насколько далеко от среднего находится наблюдение, когда данные следуют т -распределение. Скриббр.
Проверено 22 марта 2023 г.,
с https://www.scribbr.com/statistics/t-distribution/
Скриббр.
Проверено 22 марта 2023 г.,
с https://www.scribbr.com/statistics/t-distribution/ > 2
> 2