Формула площади параллелограмма через диагонали: Площадь параллелограмма — найти онлайн и формула

Параллелограмм – это разновидность четырехугольников, у которого противоположные стороны параллельны друг другу.

Классический параллелограмм выглядит вот так:

Впервые об этой фигуре подробно написал древнегреческий математик Евклид в своем известном произведении «Начала». Он же рассказал и о двух частных случаях параллелограмма, которые нам сегодня хорошо известны.

Это и прямоугольник, у которого противоположные стороны не только параллельны друг другу, но и пересекаются под прямым углом. И квадрат, у которого помимо параллельности противоположных сторон, все стороны еще и равны между собой.

И наконец, не лишним будет вспомнить, что подразумевается под термином «площадь».

Площадь геометрической фигуры – это размер плоскости, которая находится внутри сторон фигуры.

Ну а теперь объединим эти два понятия и расскажем, как надо считать площадь параллелограмма.

Формулы для расчета площади параллелограмма

Есть три основных формулы для вычисления площади параллелограмма:

1. если известна длина стороны и высота, проведенная к ней;
2. если известны длины сторон и углы между ними;
3. если известны длины диагоналей и угол между ними.

Теперь о каждом из этих способов подробнее.

Как найти площадь параллелограмма, если известны сторона и высота

Возьмем для примера такой параллелограмм:

В нем указаны две высоты – BE и BF. Напомню, что высота — это отрезок, который опускается из вершины на противоположную сторону под прямым углом.

В данном случае площадь считается весьма просто. Надо всего лишь перемножить длину высоты и длину стороны, к которой она проведена.

И то же самое касается, если знать длины стороны DC и высоты BF. Тогда для вычисления площади достаточно их перемножить.

Кстати, у этой формулы есть весьма интересное доказательство. Так как у параллелограмма противоположные стороны параллельны и равны, то можно взять треугольник ABE и переставить его к стороне CD. Вот так это будет выглядеть:

В результате мы получим прямоугольник, у которого нам известны длины обеих сторон (высота параллелограмма превратилась в одну из сторон). А как известно, площадь прямоугольника равна произведению его сторон.

Формула площади параллелограмма, если известны стороны и угол

Площадь параллелограмма можно посчитать, если известны длины обеих его сторон и величина острого угла между ними.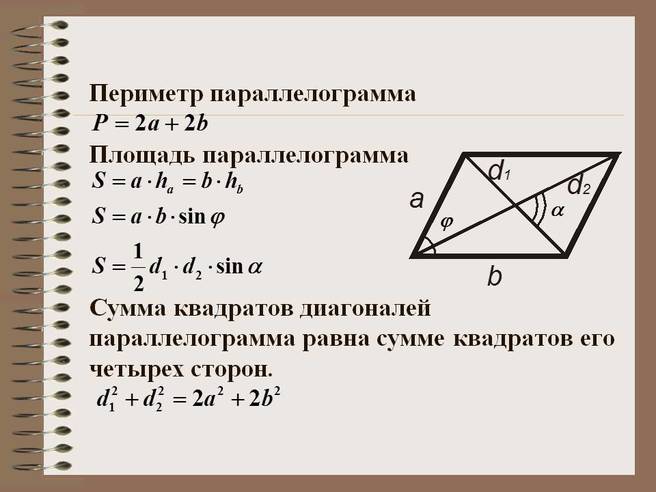

Собственно, этот способ вытекает из предыдущего, Просто по исходным данным нужно вычислить высоту параллелограмма, а уже потом по ней посчитать площадь.

Согласно тригонометрии, синус острого угла в прямоугольнике равен отношению противоположного катета к гипотенузе. В нашем примере таким катетом является высота, а гипотенузой сторона «а». И получается:

Соответственно, чтобы посчитать значение высоты надо:

И наша конечная формула для расчета площади будет выглядеть следующим образом:

Как найти площадь параллелограмма через диагонали

Этот способ используется крайне редко, но знать его все равно нужно. Во всяком случае, на экзаменах у школьников такие примеры вполне могут встретиться.

В данном случае для вывода формулы используются весьма непростые математические вычисления. И мы не будем ими вас загружать. А просто покажем конечный результат:

Соответственно, здесь d1 и d2 – длины диагоналей, а y – острый угол между ними.

Вот и все, что мы хотели рассказать о вычислении площади параллелограмма.

Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru

Эта статья относится к рубрикам:

• Математика

Как найти площадь параллелограмма abcd: формула через стороны, диагонали

Sign in

Password recovery

Восстановите свой пароль

Ваш адрес электронной почты

MicroExcel.ru Математика Геометрия Нахождение площади параллелограмма: формула и примеры

Параллелограмм – это геометрическая фигура; четырехугольник, у которого противоположные стороны равны и параллельны.

• Формула вычисления площади
  • По длине стороны и высоте
  • По двум сторонам и углу между ними
  • По двум диагоналям и углу между ними
• Примеры задач

Формула вычисления площади

По длине стороны и высоте

Площадь параллелограмма (S) равняется произведению длины его стороны и высоты, проведенной к ней:

S = a ⋅ h

По двум сторонам и углу между ними

Площадь параллелограмма находится путем умножения длин его обеих сторон и синуса угла между ними:

S = a ⋅ b ⋅ sin α

По двум диагоналям и углу между ними

Площадь параллелограмма равна одной второй произведения длин его диагоналей, умноженного на синус угла между ними:

S = ¹/₂ ⋅ d ₁ ⋅ d ₂ ⋅ sin α

Примеры задач

Задание 1
Найдите площадь параллелограмма, если длина его стороны равняется 7 см, а высоты – 4 см.

Решение:
Используем первую формулу, в которой задействованы известные нам по условиям задания значения: S = 4 см * 7 см = 28 см².

Задание 2
Найдите площадь параллелограмма, если его стороны равны 6 и 8 см, а угол между ними – 30°.

Решение:
Применим вторую формулу, рассмотренную выше: S = 6 см * 8 см * sin 30° = 24 см².

Задание 3
Найдите площадь параллелограмма с диагоналями, равными 4 и 6 см. Угол между ними составляет 90°.

Решение:
Воспользуемся формулой, в которой фигурируют диагонали: S = 1/2 * 4 см * 6  см * sin 90° = 12 см².

ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ

Таблица знаков зодиака

Нахождение площади трапеции: формула и примеры

Нахождение длины окружности: формула и задачи

Римские цифры: таблицы

Таблица синусов

Тригонометрическая функция: Тангенс угла (tg)

Нахождение площади ромба: формула и примеры

Нахождение объема цилиндра: формула и задачи

Тригонометрическая функция: Синус угла (sin)

Геометрическая фигура: треугольник

Нахождение объема шара: формула и задачи

Тригонометрическая функция: Косинус угла (cos)

Нахождение объема конуса: формула и задачи

Таблица сложения чисел

Нахождение площади квадрата: формула и примеры

Что такое тетраэдр: определение, виды, формулы площади и объема

Нахождение объема пирамиды: формула и задачи

Признаки подобия треугольников

Нахождение периметра прямоугольника: формула и задачи

Формула Герона для треугольника

Что такое средняя линия треугольника

Нахождение площади треугольника: формула и примеры

Нахождение площади поверхности конуса: формула и задачи

Что такое прямоугольник: определение, свойства, признаки, формулы

Разность кубов: формула и примеры

Степени натуральных чисел

Нахождение площади правильного шестиугольника: формула и примеры

Тригонометрические значения углов: sin, cos, tg, ctg

Нахождение периметра квадрата: формула и задачи

Теорема Фалеса: формулировка и пример решения задачи

Сумма кубов: формула и примеры

Нахождение объема куба: формула и задачи

Куб разности: формула и примеры

Нахождение площади шарового сегмента

Что такое окружность: определение, свойства, формулы

Найдите площадь параллелограмма с помощью диагоналей

Главная » Площадь геометрических фигур » Найдите площадь параллелограмма с помощью диагоналей

Последнее обновление: 27 марта 2021 г. автор: Ido Sarig · Этот веб-сайт получает доход от рекламы и использует файлы cookie · Условия использования · Политика конфиденциальности

В другой задаче мы нашли площадь параллелограмма, диагонали которого перпендикулярны, используя длины этих диагоналей и длин одной из его сторон.

На самом деле нам нужна была только длина стороны, чтобы показать, что диагонали перпендикулярны. Как только мы это установили, мы знали, что это особый параллелограмм, который также является ромбом.

Это позволило легко найти площадь, даже не используя сторону, поскольку площадь ромба — это просто произведение его диагоналей, деленное на два.

Но, как мы упоминали в этой задаче, если у нас есть длины диагоналей и одной стороны, мы можем вычислить площадь любого параллелограмма, даже если диагонали не перпендикулярны. В этой задаче мы покажем, как это сделать.

Задача

ABDC — параллелограмм со стороной 11 единиц, а длина диагонали 24 единицы и 20 единиц.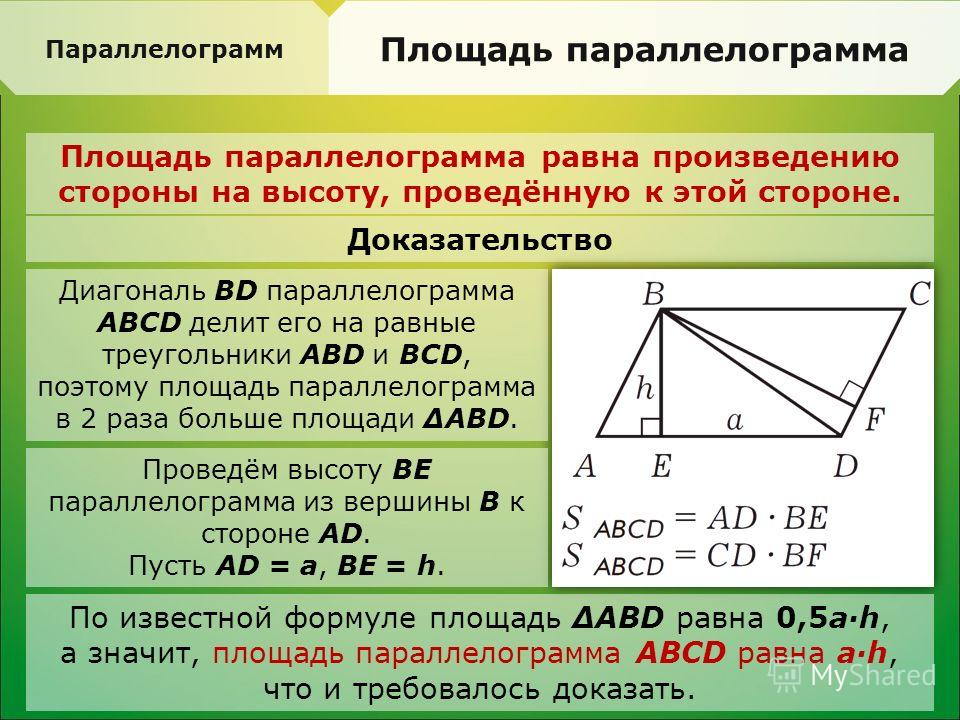 Найдите его площадь.

Стратегия

Диагонали делят параллелограмм на 4 треугольника. В другой задаче мы видели, что эти 4 треугольника имеют равные площади.

Даже если мы этого не помним, легко восстановить сделанное нами там доказательство. Мы знаем, что диагонали параллелограмма делят друг друга пополам, поэтому треугольники ΔABO и ΔADO, например, имеют одинаковый размер основания и одинаковую высоту, поэтому они имеют одинаковую площадь.

И то же самое для любой другой пары смежных треугольников в параллелограмме. Итак, если мы найдем площадь хотя бы одного из этих треугольников, мы получим площадь параллелограмма, умножив ее на четыре.

Так как диагонали делят друг друга пополам и мы знаем их длины, у нас есть весь периметр треугольника ΔADO. Как найти площадь треугольника, если известен его периметр? Мы можем использовать формулу Герона.

Для треугольника со сторонами a, b и c полупериметр s равен (a+b+c)/2. Формула Герона дает его площадь как √[s⋅(s-a)⋅(s-b)⋅(s-c)].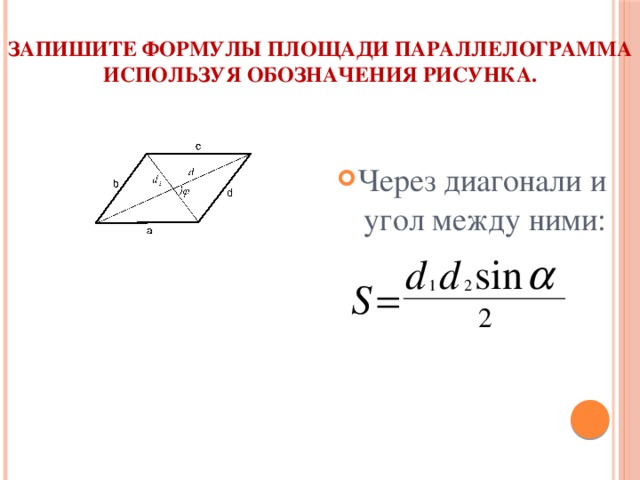

Теперь мы можем подставить значения нашей задачи для a, b и c, получить площадь треугольника ΔADO, а затем умножить на 4, чтобы получить площадь параллелограмма.

Решение

(1) a= 11 //данно
(2) b=10 //AC=20, задано, диагонали параллелограмма делят друг друга пополам, поэтому AO=10
(3) c=12 // BD=24, учитывая, что диагонали параллелограмма делят друг друга пополам, поэтому DO=12
(4) s=(a+b+c)/2=(11+10+12)/2=16,5 //(1) , (2), (3), замена
(5)A _ΔADO =√[s⋅(s-a)⋅(s-b)⋅(s-c)] // Формула Герона
(6) A _ΔADO =√[ 16,5*(16,5-10)*(16,5-11)*(16,5-12)]=√2654,4375≈51,52
(7)A _ABCD =4*A _ΔADO // Диагонали делят параллелограмм на 4 равновеликих треугольника
(8) A _ABCD = 206.08

Примечание

Стоит отметить, что площадь параллелограмма нельзя получить, используя только диагонали. Кроме того, необходимо иметь либо длину одной стороны, либо один из углов параллелограмма. Чтобы понять, почему, наглядным образом представьте диагонали как две жесткие палки, соединенные в точке пересечения ослабленным винтом или гвоздем. Вы можете повернуть две диагонали вокруг этого соединения и сформировать другой параллелограмм (соединив конечные точки диагоналей).

Эти параллелограммы имеют разные площади. Если сделать диагонали почти параллельными друг другу — получится параллелограмм с близкой к нулю высотой и, следовательно, близкой к нулю площадью. Но по мере того, как вы создаете больший угол между диагоналями, площадь параллелограмма будет увеличиваться.

Об авторе

Идо Сариг — руководитель отдела высоких технологий со степенью бакалавра вычислительной техники. Его цель — помочь вам разработать лучший подход к решению геометрических задач. Вы можете связаться с ним по адресу [email protected]

Площадь параллелограмма по диагоналям и стороне

Главная » Площадь геометрических фигур » Площадь параллелограмма по диагоналям и стороне

Последнее обновление: 30 сентября 2019 г. автор: Ido Sarig · Этот веб-сайт получает доход от рекламы и использует файлы cookie · Условия использования · Политика конфиденциальности высота параллелограмма в эту сторону.

Но что делать, если у нас нет этих измерений (бок, высота)? Что, если вместо этого нам представят длину одной стороны и длину обеих диагоналей?

Давайте посмотрим, как мы все еще можем вычислить площадь параллелограмма в этом случае, в следующей задаче.

Задача

Параллелограмм имеет длину стороны 13 единиц, а длину диагонали 24 единицы и 10 единиц. Найдите его площадь.

Стратегия

Есть два способа начать думать об этой проблеме, и оба приведут нас к одному и тому же решению.

Поскольку у нас есть обе диагонали, мы можем начать с размышлений о свойствах диагоналей в параллелограммах — они делят друг друга пополам. Итак, если у нас есть диагонали в 24 и 10 единиц, они делят друг друга пополам на отрезки в 12 и 5 единиц соответственно:

Итак, теперь у нас есть треугольник со сторонами 5, 12 и 13 — пифагорейская тройка, что означает, что треугольник является прямоугольным, и мы можем легко вычислить его площадь как катет x катет /2, или 5×12/2=30.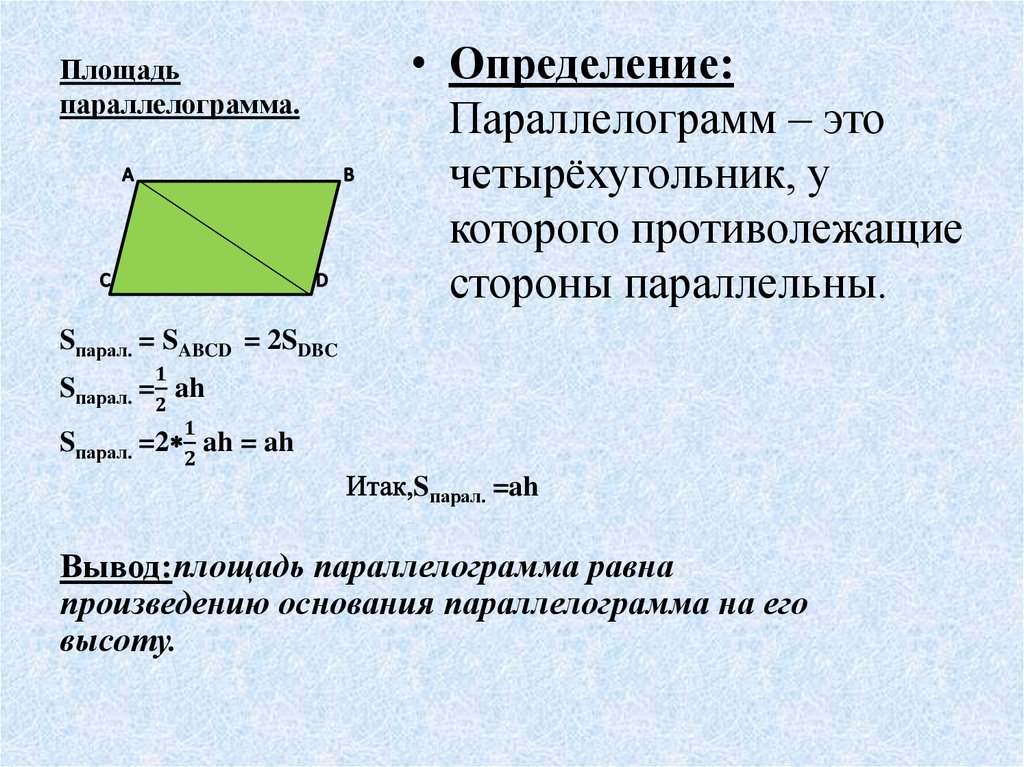

Но если m∠AOB=90°, то m∠AOD=90°, так как ∠AOB и ∠AOD — линейная пара, сумма которых составляет 180°. Тогда треугольники ΔAOB и ΔAOD конгруэнтны (соотношение сторона-угол-сторона), как и треугольники ΔAOB и ΔCOB (также сторона-угол-сторона). Итак, у нас есть 4 треугольника площадью 30, составляющих площадь параллелограмма, площадь которого, таким образом, 4×30=120.

Еще один способ решить эту задачу — вспомнить, что если параллелограмм — ромб, то его площадь равна произведению диагоналей, деленному на два. Это потому, что ромб — это тоже воздушный змей, а мы показали, что площадь воздушного змея — это половина произведения его диагоналей.

Итак, если мы докажем, что параллелограмм является ромбом, мы можем использовать это напрямую. Мы можем приступить к доказательству того, что этот параллелограмм действительно является ромбом, используя тот факт, что если диагонали параллелограмма перпендикулярны, то это ромб, а выше мы показали, что эти диагонали действительно перпендикулярны.