Формула площади прямоугольника 3: Площадь фигур. Площадь прямоугольника — урок. Математика, 3 класс.

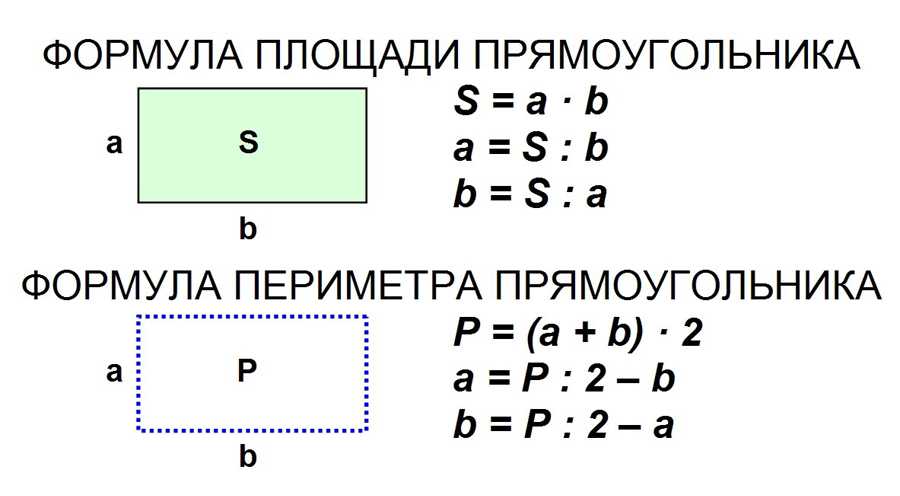
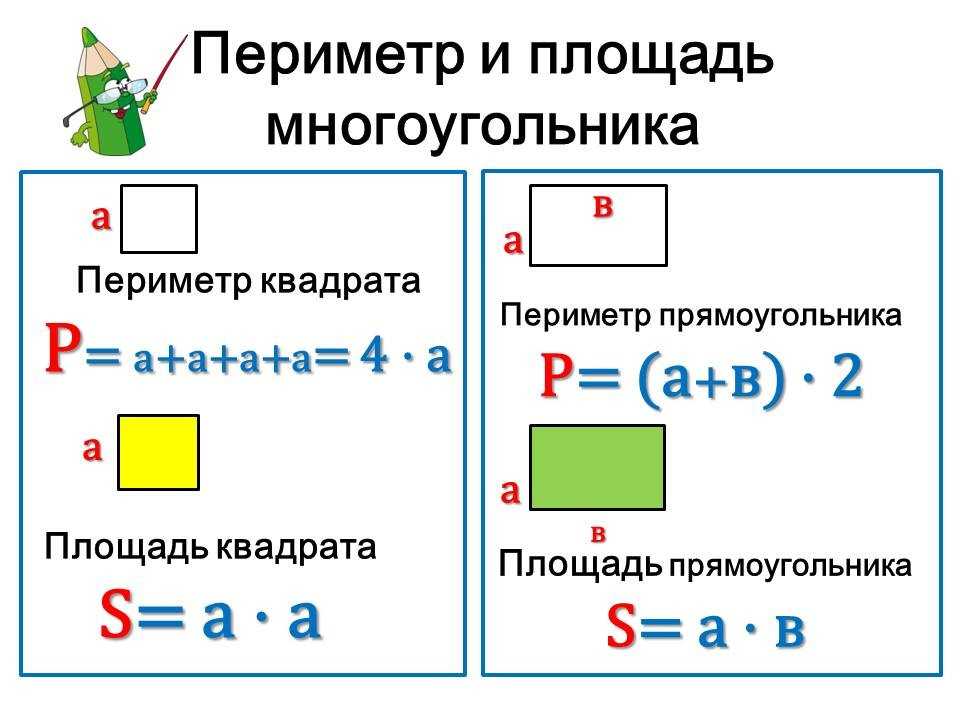
Как найти площадь прямоугольника 3 класс примеры

Статьи › Находится › Как находится площадь прямоугольника формула

Чтобы найти площадь прямоугольника, надо найти произведение длин его сторон. 2 см ⋅ 4 см = 8 см 2. Длина и ширина прямоугольника должны быть выражены (записаны) в одинаковых единицах длины.

1. Как найти площадь прямоугольника в 3 классе
2. Как найти площадь прямоугольника двумя способами 3 класс
3. Как найти площадь третий класс
4. Как вычислять площадь прямоугольника
5. Как найти площадь и периметр прямоугольника 3 класс
6. Как можно найти пример и площадь прямоугольника
7. Как найти периметр прямоугольника в 3 классе
8. Как найти стороны прямоугольника 3 класс
9. Как решить задачу найди площадь прямоугольника
10. Как найти площадь и периметр треугольника 3 класс
11. Как объяснить ребенку что такое площадь
12. Что такое периметр и площадь 3 класс
13. Как правильно посчитать площадь
14. Как найти длину прямоугольника 3 класс
15. Как найти площади
16. Как найти площадь если известны 3 стороны
17. Как найти площадь квадрата или прямоугольника
18. Как найти ширину прямоугольника 3 класс
19. Как вычислить площадь прямоугольника ABCD
20. Как вычислить площадь прямоугольника зная его периметр
21. Как найти площадь треугольника в третьем классе
22. Как найти периметр в 3 классе

Как найти площадь прямоугольника в 3 классе

Когда известно значение длины и ширины фигуры

Для вычисления необходимо умножить их друг на друга. S = a × b, где S — площадь; a, b — длина и ширина.

Как найти площадь прямоугольника двумя способами 3 класс

S = а * b, где a — длина прямоугольника, b — ширина прямоугольника.

Как найти площадь третий класс

S = a × a = a2, где S — площадь, a — сторона. Эту формулу проходят в 3 классе. Остальные формулы третьеклассникам знать пока не нужно, но они пригодятся ученикам 8 класса.

Как вычислять площадь прямоугольника

2) Для вычисления площади прямоугольника нужно умножить его длину на ширину. Формула для вычисления площади прямоугольника имеет следующий вид: S = a*b.

Как найти площадь и периметр прямоугольника 3 класс

Ответы1. Периметр прямоугольника — это сумма всех его сторон. Формула нахождения площади прямоугольника: S = a × b, где а — ширина, b — длина прямоугольника.

Как можно найти пример и площадь прямоугольника

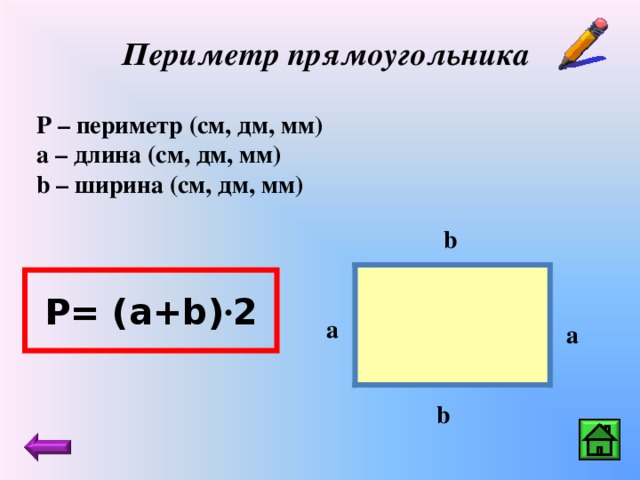
Площадь прямоугольника равна произведению его длины и ширины. S = · b, где S — площадь, — длина, b — ширина прямоугольника.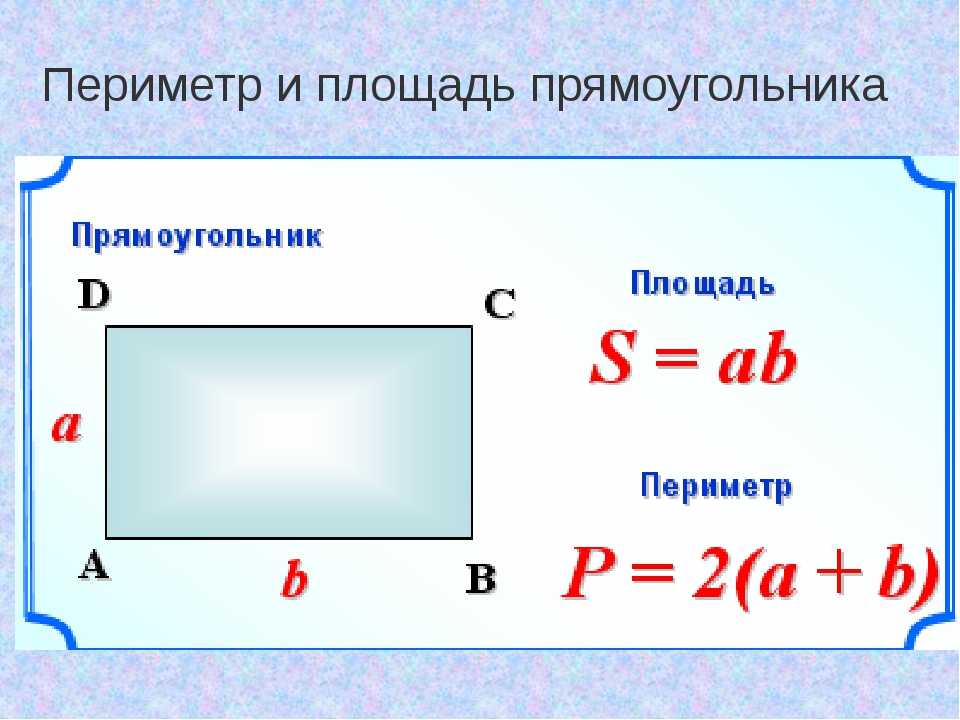 Периметр прямоугольника равен удвоенной сумме его длины и ширины. P = (+ b) · 2, где P — периметр, — длина, b — ширина прямоугольника.

Как найти периметр прямоугольника в 3 классе

Формула нахождения периметра прямоугольника

P = a + b + c + d, где a, b, c, d — стороны. P = 2 × (a + b), где a и b — соседние стороны.

Как найти стороны прямоугольника 3 класс

А = S: b, где S — площадь прямоугольника, b — сторона прямоугольника.

Как решить задачу найди площадь прямоугольника

Площадь прямоугольника равна произведению длин его сторон. Запишем формулу для вычисления площади прямоугольника: S = a × b, где S — площадь прямоугольника, а — длина, b — ширина.

Как найти площадь и периметр треугольника 3 класс

Формула площади треугольника:

• Самая простая формула для расчета площади это произведение основания и высоты треугольника, поделенное на 2: S = (a · h)/2,
• Вторая формула для расчета площади треугольника: по радиусу вписанной окружности и периметру: S = (r · P)/2 = r · p.

Как объяснить ребенку что такое площадь

Площадь находят мерками, квадратиками (поэтому и единицы площади квадратные — так детям понятнее). Если фигура — прямоугольник, её делят на равные квадратики и считают их. Так можно делать с небольшими фигурами, которые помещаются в тетрадках.

Что такое периметр и площадь 3 класс

Ответы2. Периметром (P) называют сумму всех сторон. Чтобы найти периметр, нужно сложить все стороны. Площадь (S) показывает размер фигуры.

Как правильно посчитать площадь

Для этого необходимо с помощью рулетки измерить длину и ширину пола, а затем умножить значения между собой. Так можно узнать площадь комнаты в квадратных метрах по полу. Если у комнаты есть выступающие части, то для подсчета площади необходимо вычесть их площадь из общего размера комнаты.

Как найти длину прямоугольника 3 класс

Для того, чтобы найти длину этого прямоугольника нужно из данной величины периметра вычесть две ширины прямоугольника и полученный результат разделить на два.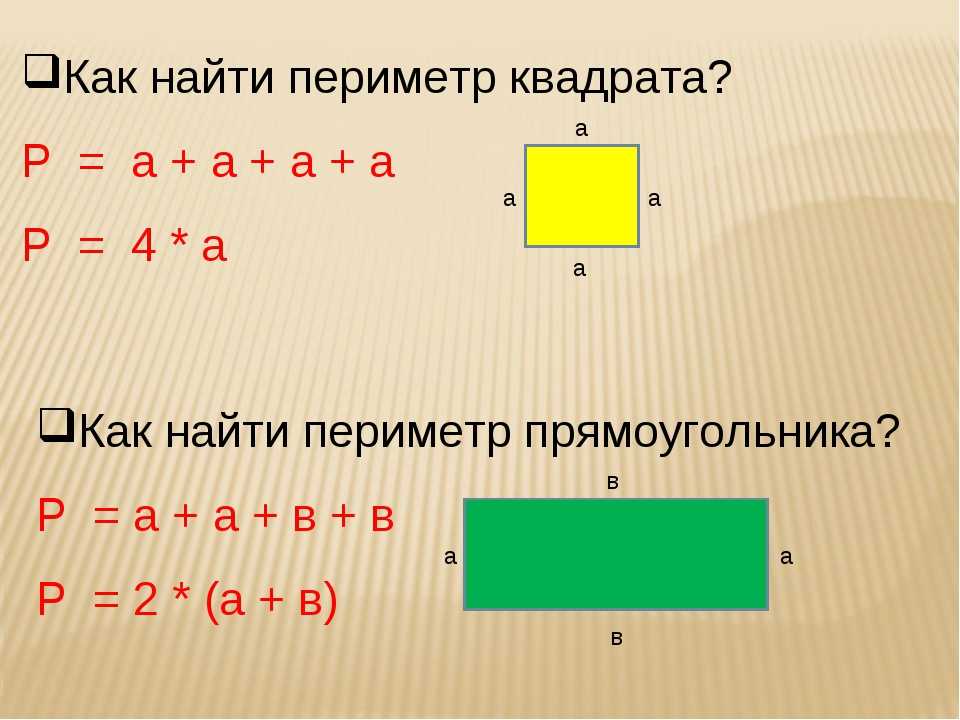

Как найти площади

S = a ⋅ b, где a и b — длина и ширина.

Как найти площадь если известны 3 стороны

Для того, чтобы найти площадь треугольника давайте вспомним и применим формулу Герона для нахождения площади треугольника. Формула Герона: S = √(p(p — a)(p — b)(p — c)), где p — полу периметр, который найдем так: p = (a + b + c)/2.

Как найти площадь квадрата или прямоугольника

1) Для того, чтобы найти площадь прямоугольника нужно умножить длину на ширину. S = a * b. 2) Для того, чтобы найти площадь квадрата нужно умножить сторону саму на себя.

Как найти ширину прямоугольника 3 класс

Ширину можно вычислить по длине, если известна еще площадь или периметр прямоугольника. Например, зная площадь и длину, можно найти ширину по формуле а = S/b. А зная периметр и длину, можно вычислить ширину по формуле a = (P — 2b) / 2.

Как вычислить площадь прямоугольника ABCD

Площадь прямоугольника — есть произведение его ширины и длины: S пр. 2).

Как вычислить площадь прямоугольника зная его периметр

Умножьте периметр на длину известной стороны. Найдите квадрат известной стороны и умножьте полученное число на 2.5. Если известны любая сторона и периметр:

• S — искомая площадь прямоугольника;
• a — известная сторона;
• P — периметр прямоугольника (равен сумме всех сторон).

Как найти площадь треугольника в третьем классе

Площадь треугольника равна половине произведения длины высоты треугольника и длины стороны, к которой проведена высота S ABC = a ⋅ h 2.

Как найти периметр в 3 классе

Как найти периметр фигуры:

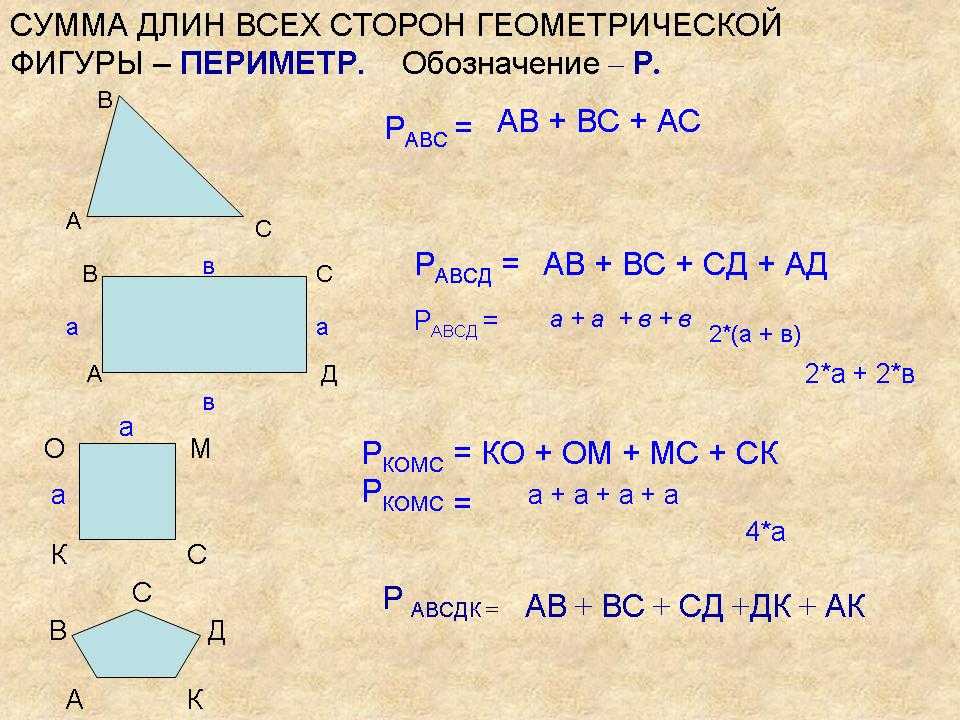
• Периметр — это сумма длин всех сторон многоугольника.
• P = 3 ⋅ a, где a — длина стороны.
• P = 2 ⋅ (a + b), где a — одна сторона, b — соседняя сторона.

Площадь. Формула площади прямоугольника — презентация онлайн

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

1. Цель урока:

ЦЕЛЬ УРОКА:
• Образовательные
1. Воспроизведение и коррекция необходимых
знаний и умений по данной теме.
2. Анализ заданий и способов их выполнения.
3. Рационализация способа выполнения заданий.
4. Самостоятельное выполнение заданий для
проверки знаний, умений, навыков.
Развивающие
1. Развитие приёмов умственной и исследовательской
деятельности.
Воспитательные
1. Воспитывать у учащихся навыки учебного труда.
2. Воспитывать культуру устной и письменной
математической речи.
3. Прививать интерес к истории математики.

2. Оборудование:

ОБОРУДОВАНИЕ:
1. Математика: учебник для 5 кл.
общеобразоват. учреждений/ Н.Я.
Виленкин, В.И. Жохов и др., М.:
«Сайтком», 2
2. Конверты у каждого из учащихся с
набором различных фигур для
практической работы
3. Тест у каждого из учащихся для
проверки знаний, умений и навыков.
4. Чертёжные инструменты.

3. Урок в 5 классе на тему: Площадь. Формула площади прямоугольника

УРОК В 5 КЛАССЕ
НА ТЕМУ:
ПЛОЩАДЬ. ФОРМУЛА ПЛОЩАДИ
ПРЯМОУГОЛЬНИКА
Учитель Хлебодаровской СОШ:
Бойкова Н.Г.

4. 1.Организационный момент.

1.ОРГАНИЗАЦИОННЫЙ
МОМЕНТ.
«Три пути ведут к знанию:
Путь размышления – это путь самый
благородный.
Путь подражания – это путь самый легкий.
И путь опыта – это путь самый горький»
Конфуций

5. Устный чет

УСТНЫЙ ЧЕТ
1.
2.
3.
4.
5.
6.
7.
8.
9.
48:4 =
12+23=
24•3=
36-18 =
8•0=
18+13=
76:2=
99:9=
70-35=
10. 2•19=
11. 18•1=
12. 47-9=
13. 16+58 =
14. 9•8=
15. 64-33=
16. 55:1=
17. 84+15=
18. 0:31=

6. Работа по готовым рисункам. Вычислить площадь фигуры:

РАБОТА ПО ГОТОВЫМ РИСУНКАМ.
ВЫЧИСЛИТЬ ПЛОЩАДЬ ФИГУРЫ:

7. 1) Работа с раздаточным материалом.

1) РАБОТА С РАЗДАТОЧНЫМ МАТЕРИАЛОМ.
На каждой парте набор
разноцветных
многоугольников, из них
сначала выбираются
четырехугольники, а из
четырехугольников –
прямоугольники и
квадраты, причем в
каждом наборе по два
неравных
прямоугольника и два
неравных квадрата.
2) Задание: сделав
необходимые измерения,
найти площади
прямоугольника и
квадрата. Результаты
измерений — значение
площади — записываются
на обратной стороне
шаблона. Шаблоны
подписываются и сдаются
учителю на проверку.
Физкультминутка (игра “истинно — ложно”)
Если высказывание верно, то учащиеся делают наклоны вправовлево и хлопают в ладоши (на счет 4). Если высказывание неверно,
то учащиеся приседают и тянутся руками вверх.
1. Делить на нуль нельзя.
2. 32 = 6
3. Квадрат — это прямоугольник.
4. У квадрата все стороны равны
5. У любого треугольника 3 вершины, 3 угла, 2 стороны.
6. сегодня 22 декабря
7. 2*2=5
8. 5 «б» класс — самый дружный в школе!
6. Решение задач из учебника: №717,720.
№ 717
a = 28 см.
b = ? см, в 7 р. <
S = ? см2
1) 28 : 7 = 4 (см) — ширина прямоугольника.
2) 4 • 28 = 112 (см2)
Ответ: площадь прямоугольника равна 112 см2.
№720
S = 36 см2
a = ? см.
S = a2
a = 6 (см)
6 • 6 = 36 (см2)
Ответ: сторона квадрата равна 6 см.
Самостоятельная работа в виде теста в двух вариантах
1. Площадь прямоугольника определяется по формуле:
а) S = a2; б) S = a • b; в) S = 2 • (a+b).
2.Площадь квадрата со стороной 7 см равна:
2
2
а) 59 см ; б) 28 см ; в) 49 см
2
4. Периметр квадрата равен 64 см. Площадь его равна:
а) 128 см2; б) 64 см2; в) 256 см2.

11. а) 46 см2;

А) 46 СМ2;
а) 46 см2;
б) 18 см2;
в) 72 см2.
Итоги урока. Рефлексия.
1. О каких геометрических фигурах шел разговор на уроке?
2. Что нужно знать, чтобы найти площади прямоугольника, квадрата?
3. Пригодятся ли вам в жизни полученные знания? Где?
4. Что на уроке было самым сложным, простым?
5. Выставление оценок.

13. Спасибо за урок

Домашняя работа
СПАСИБО ЗА УРОК

English     Русский Правила

Формула прямоугольника — GeeksforGeeks

Прямоугольник относится к семейству параллелограммов, а параллелограммы относятся к типу четырехугольников. Качество прямоугольника в том, что все его внутренние углы равны 90°. Противоположные стороны прямоугольника равны, однако соседние стороны не обязательно должны быть равными. Давайте посмотрим на формулы, связанные с прямоугольником, например, периметр прямоугольника, площадь прямоугольника и т. д.

Площадь прямоугольника

Площадь можно охарактеризовать как пространство, занимаемое ровной поверхностью определенной формы.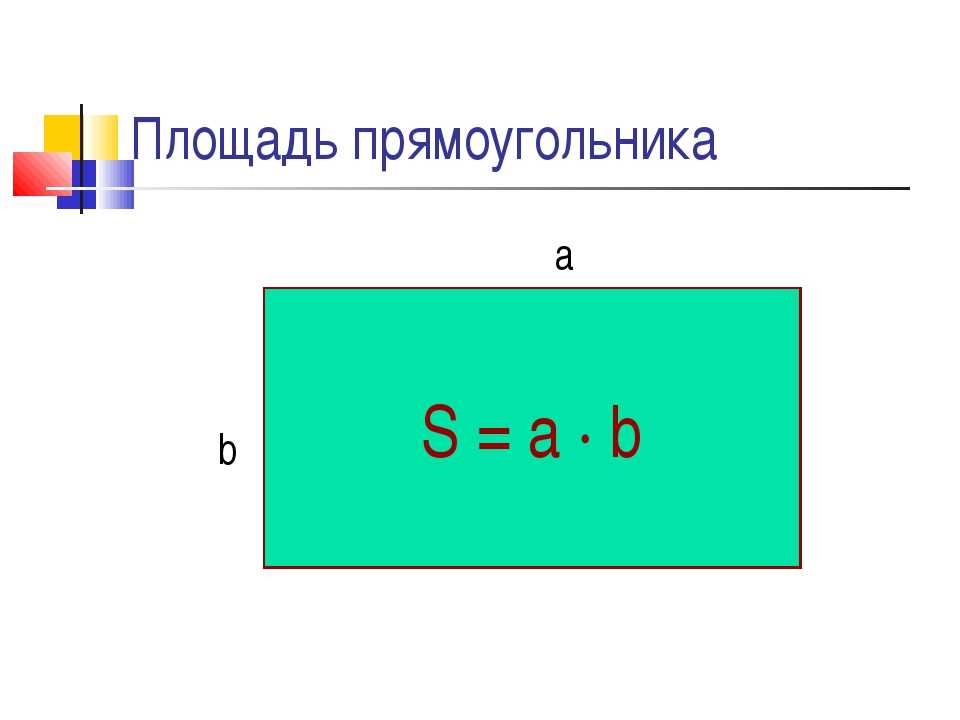 Она оценивается как «количество» квадратных единиц (квадратных сантиметров, квадратных дюймов, квадратных футов и т. д.). Площадь прямоугольника — это количество единичных квадратов, которые могут втиснуться в прямоугольник. Несколько примеров прямоугольных форм — это ровные поверхности экранов ПК, планшетов, классных досок и т. д.

Формула площади прямоугольника

Уравнение площади прямоугольника используется для определения площади прямоугольника внутри его границ. Рецепт площади «A» прямоугольника, длина и ширина которого равны «l» и «w» по отдельности, представляет собой элемент «l × w».

Площадь прямоугольника = (длина × ширина) квадратных единиц.

Доказательство:

 

Площадь прямоугольника ABCD = площадь треугольника ABC + площадь треугольника ADC

= 2 × площадь основания треугольника ABC

20002 (

= AB × BC

= Длина × Ширина

Вычисление площади прямоугольника

Площадь прямоугольника равна произведению его длины на ширину.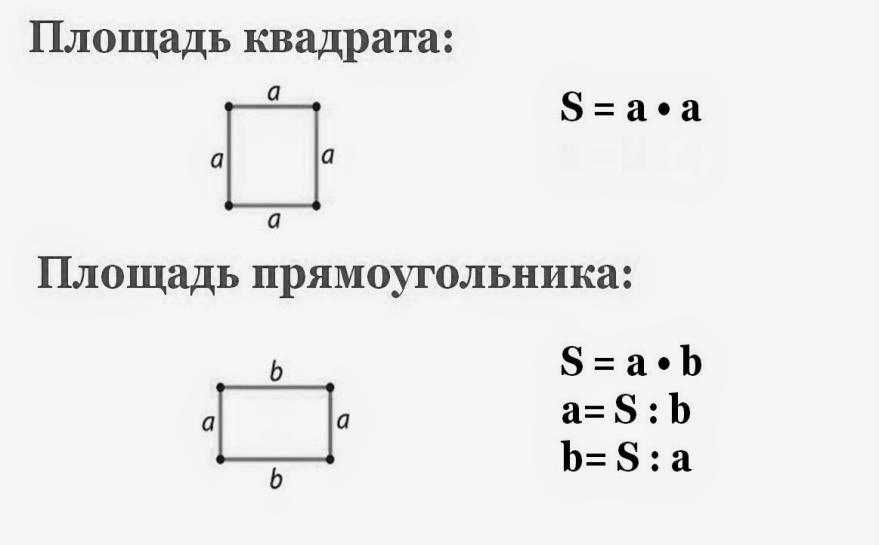 Следуйте средствам, указанным ниже, чтобы отследить площадь прямоугольника:

1. Шаг 1 : Обратите внимание на компоненты длины и ширины из предоставленной информации.
2. Шаг 2: Найдите результат значений длины и ширины.
3. Шаг 3: Дайте ответ в квадратных единицах.

Площадь прямоугольника по диагонали

Диагональ прямоугольника — это прямая линия внутри прямоугольника, пересекающая его противоположные вершины. В прямоугольнике две диагонали и обе имеют одинаковую длину. Мы можем отследить диагональ прямоугольника, используя теорему Пифагора.

(Diagonal) ² = (Length) ² + (Breadth) ²

(Length) ² = (Diagonal) ² – (Breadth) ²

Length = √ {(Диагональ) ² – (Ширина) ² }

Теперь формула для вычисления площади прямоугольника: Длина × Ширина. В качестве альтернативы мы можем записать эту формулу как √{(Диагональ) ² – (Ширина) ² } × Ширина.

Площадь прямоугольника = ширина (√{(Диагональ) ² – (Ширина) ² }).

Периметр прямоугольника

Периметр прямоугольника можно считать одной из значимых формул прямоугольника. Это абсолютное расстояние, пройденное прямоугольником вокруг его внешней стороны. В математике вы столкнетесь с многочисленными математическими формами и размерами, у которых есть площадь, периметр и даже объем (для трехмерных фигур). Вы также освоите уравнения для такого большого количества границ. Часть экземпляров различной формы представляет собой круг, квадрат, многоугольник, четырехугольник и т. д. В этой статье вы сосредоточитесь на жизненно важном элементе прямоугольника, например, периметре.

Периметр определяет длину фигуры. Предположим, что для квадрата, каждая из сторон которого эквивалентна, периметр квадрата будет в несколько раз больше его стороны. Из-за круга периметр называется периферией, которая определяется в свете его протяженности. Прежде чем мы выясним периметр данного прямоугольника, давайте сначала узнаем, что такое прямоугольник.

Периметр прямоугольника — это полное расстояние, пройденное его пределами или сторонами. Поскольку у прямоугольника четыре стороны, по этим линиям периметр прямоугольника будет равен сумме каждой из четырех сторон. Поскольку периметр является прямой мерой, соответственно, единицей измерения периметра прямоугольника будут метры, сантиметры, дюймы, футы и так далее.

Периметр прямоугольника Формула

Периметр не что иное, как граница. На приведенной выше диаграмме у нас есть 4 стороны. Сложив эти 4 стороны, мы получим периметр прямоугольника.

Сумма с каждой стороны = L+ L+ B+ B

SO 2L+ 2B

Периметр прямоугольника = 2 (L+ B)

Применение периметра прямоугольника

1. Мы можем решить по длине. прямоугольного поля или питомника для его ограждения с использованием реберного рецепта
2. Очень хорошо может быть использован для некоторых ремесленных и художественных начинаний, например, для украшения границы прямоугольного картона яркими полосками или веревками
3. Для обустройства прямоугольного бассейна длина заплывов характеризуется кромкой
4. Для плана развития дома мы хотим определить предел использования существенного, который мыслим уравнением границы

Примеры вопросов

Вопрос 1: Найдите площадь прямоугольника, длина которого 21 единица, ширина 11 единицы измерения.

Решение:

Дано, длина = 21 единица и ширина = 11 единиц.

Формула определения площади прямоугольника: A = длина × ширина (l × b).

Подставьте 21 вместо «l» и 11 вместо «w» в этом уравнении.

Итак, площадь прямоугольника = 21 × 11 = 231 кв.

Вопрос 2: Найдите площадь прямоугольника длиной 12 мм и шириной 8 мм.

Решение:

Длина прямоугольника = 12 мм.

Ширина прямоугольника = 8 мм.

Площадь прямоугольника = длина × ширина

= 12 × 8 кв. мм.

= 96 кв.мм.

Вопрос 3: Нахождение площади прямоугольника, длина которого 10,5 см, а ширина 5,5 см.

Решение:

Длина прямоугольника (l) = 10,5 см

Ширина прямоугольника (b) = 5,5 см

Площадь прямоугольника = длина × ширина (l × b)

Площадь прямоугольника = 10,5 × 5,5

= 57,75 см ² .

Вопрос 4: Площадь прямоугольника 32 см ² . Найдите его длину, если его ширина 4 см.

Решение:

Площадь прямоугольника = 32 см ²

Шегота прямоугольника = 4 см

Длина прямоугольника = площадь прямоугольника/Шета прямоугольника

= 32 см ² /4 см

= 8 см.

Итак, длина прямоугольника 8 см.

Вопрос 5: Найдите периметр прямоугольника, длина и ширина которого равны 11 см и 5,5 см соответственно.

Решение:

Длина = 11 см и Ширина = 5,5 см 2(11 + 5,5) см

P = 2 × 16,5 см

Следовательно, периметр прямоугольника = 33 см.

Вопрос 6: Прямоугольный двор имеет длину 12 см и периметр 60 см. Найдите его ширину.

Решение: 

Периметр = 60 см

Длина = 10 см

Пусть W — ширина.

Из формулы

Периметр, P = 2(длина + ширина)

Подставляя значения,

60 = 2(12 + ширина)

12 + W = 30

W = 31 – 12

Следовательно, ширина 20см.

Вопрос 7: Найдите периметр прямоугольника, длина и ширина которого равны 12 см и 4 см соответственно.

Решение:

Дано,

Длина = 12 см

Ширина = 4 см

Периметр прямоугольника = 2 (длина + ширина)

= 2 (12 + 4) См

= 2 × 16 см

Следовательно, периметр прямоугольника = 32 см.

Вопрос 8: Найдите периметр прямоугольника, длина которого 21 см, а ширина 13 см.

Решение:

Дано,

Длина = 21 см

Ширина = 13 см

Периметр прямоугольника = 2 (длина + ширина)

= 2 (21 + 13) См

= 2 × 34 см

Следовательно, периметр прямоугольника = 68см.

Мэтуэй | Популярные проблемы

9(1/2) 92-4*-1+2 92

1	Найдите том	сфера (5)	
2	Найти площадь	круг (5)	
3	Найдите площадь поверхности	сфера (5)	
4	Найти площадь	круг (7)	
5	Найти площадь	круг (2)	
6	Найти площадь	круг (4)	
7	Найти площадь	круг (6)	
8
11	Найти простую факторизацию	741
12	Найдите том	сфера (3)	
13	Оценить	3 квадратный корень из 8*3 квадратный корень из 10
14	Найти площадь	круг (10)	
15	Найти площадь	круг (8)	
16	Найдите площадь поверхности	сфера (6)	
17	Найти простую факторизацию	1162
18	Найти площадь	круг (1)	
19	Найдите длину окружности	круг (5)	
20	Найдите том	сфера (2)	
21	Найдите том	сфера (6)	
22	Найдите площадь поверхности	сфера (4)	
23	Найдите том	сфера (7)	
24	Оценить	квадратный корень из -121
25	Найти простую факторизацию	513
26	Оценить	квадратный корень из 3/16* квадратный корень из 3/9
27	Найдите том	коробка (2)(2)(2)	
28	Найдите длину окружности	круг (6)	
29	Найдите окружность	круг (3)	
30	Найдите площадь поверхности	сфера (2)	
31	Оценить	2 1/2÷22000000
32	Найдите Том	коробка (5)(5)(5)	
33	Найдите том	коробка (10)(10)(10)	
34	Найдите длину окружности	круг (4)	
35	Преобразование в проценты	1,7
36	Оценить	(5/6)÷(4/1)
37	Оценить	3/5+3/5
38	Оценить	ф(-2)	92
40	Найти площадь	круг (12)	
41	Найдите том	коробка (3)(3)(3)	
42	Найдите том	коробка (4)(4)(4)
45	Найти простую факторизацию	228
46	Оценить	0+0
47	Найти площадь	круг (9)	
48	Найдите длину окружности	круг (8)	
49	Найдите длину окружности	круг (7)	
50	Найдите том	сфера (10)	
51	Найдите площадь поверхности	сфера (10)	
52	Найдите площадь поверхности	сфера (7)	
53	Определить, является простым или составным	5
60	Преобразование в упрощенную дробь	2 1/4
61	Найдите площадь поверхности	сфера (12)	
62	Найдите том	сфера (1)	
63	Найдите длину окружности	круг (2)	
64	Найдите том	коробка (12)(12)(12)	
65	Добавить	2+2=
66	Найдите площадь поверхности	коробка (3)(3)(3)	
67	Оценить	корень пятой степени из 6* корень шестой из 7
68	Оценить	7/40+17/50
69	Найти простую факторизацию	1617
70	Оценить	27-(квадратный корень из 89)/32
71	Оценить	9÷4
72	Оценка 92
74	Оценить	1-(1-15/16)
75	Преобразование в упрощенную дробь	8
76	Оценка	656-521	9-2
79	Оценить	4-(6)/-5
80	Оценить	3-3*6+2
81	Найдите площадь поверхности	коробка (5)(5)(5)	
82	Найдите площадь поверхности	сфера (8)	
83	Найти площадь	круг (14)	
84	Преобразование в десятичное число	5 ноября
85 9-2
88	Оценить	1/2*3*9
89	Оценить	4/4-17/-4
90	Оценить	11. No related posts. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт