Как найти площадь равнобедренного треугольника? Ответ на webmath.ru
Содержание:
- Формула
- Примеры вычисления площади равнобедренного треугольника
Формула
Чтобы найти площадь равнобедренного треугольника (рис. 1), необходимо вычислить произведение половины основания этого треугольника на его высоту:
$$\mathrm{S}_{\Delta}=\frac{1}{2} a h_{a}$$
Напомним, что треугольник называется равнобедренным, если его две стороны равны. Равные стороны называются боковыми сторонами рассматриваемого треугольника, а третья сторона — основанием.
Примеры вычисления площади равнобедренного треугольника
Пример
Задание. Найти площадь равнобедренного треугольника $ABC$, если известно, что его основание равно 4 м, а высота, проведенная к этому основанию — 6 м.
Решение. Искомая площадь равна произведению высоты на основание, деленному на два:
$\mathrm{S}_{\Delta A B C}=\frac{4 \cdot 6}{2}=\frac{24}{2}=12$ (м2)
 {2}}=\sqrt{25-16}=\sqrt{9}=3$ (cм)
{2}}=\sqrt{25-16}=\sqrt{9}=3$ (cм)
А тогда искомая площадь
$\mathrm{S}_{\Delta A B C}=\frac{1}{2} A C \cdot B H=\frac{8 \cdot 3}{2}=4 \cdot 3=12$ (см2)
Ответ. $\mathrm{S}_{\Delta A B C}=12$ (см2)
Остались вопросы?
Здесь вы найдете ответы.
Площадь равнобедренного треугольника с прямым углом составляет 16 см кв. Каким образом можно вычислить длину гипотенузы данной треугольной фигуры?
Обозначим через х катет имеющегося равнобедренного треугольника, имеющего прямой угол. В этом случае его площадь будет представлять собой ½ длины его катета, возведенную в квадратную степень. Это значит, что квадрат катета равен двум площадям треугольника (2S). В нашем случае это:
2S = 2*16 = 32 см кв.
Для того чтобы найти длину катета, нужно извлечь корень квадратный из числа 32:
х = 4*√2 см.
Теперь можно высчитать длину гипотенузы, которая будет равна:
х / sin45 = 8 см.
Ответ: Длина гипотенузы равна 8 см.
Имеется равнобедренный треугольник площадью 192 см кв. Его основание составляет 32 см. Как можно вычислить периметр данной треугольной фигуры?
Дан треугольник АВС, в котором АВ=ВС и АС=32 см.
Проведем к основанию треугольника высоту ВН, также являющуюся медианой.
Площадь треугольника равна половине произведения длины его основания на высоту:
S=АС*ВН/2
Из этой формулы можно выразить ВН:
ВН=2S/АС=2*192/32=12 см.
Известно, что в равнобедренном треугольнике две стороны равны:
АВ=ВС=√(ВН²+(АС/2)²)=√(144+256)=20 см.
Теперь можно высчитать периметр (Р) треугольника АВС, который будет равен сумме длин его сторон:
Р=2АВ+АС=40+32=72 см.
Ответ: Периметр равнобедренного треугольника АВС равен 72 см.
Длина гипотенузы равнобедренного треугольника, имеющего прямой угол, составляет 12 см. Как найти площадь данного треугольника?
Обозначим буквой х катет имеющегося треугольника.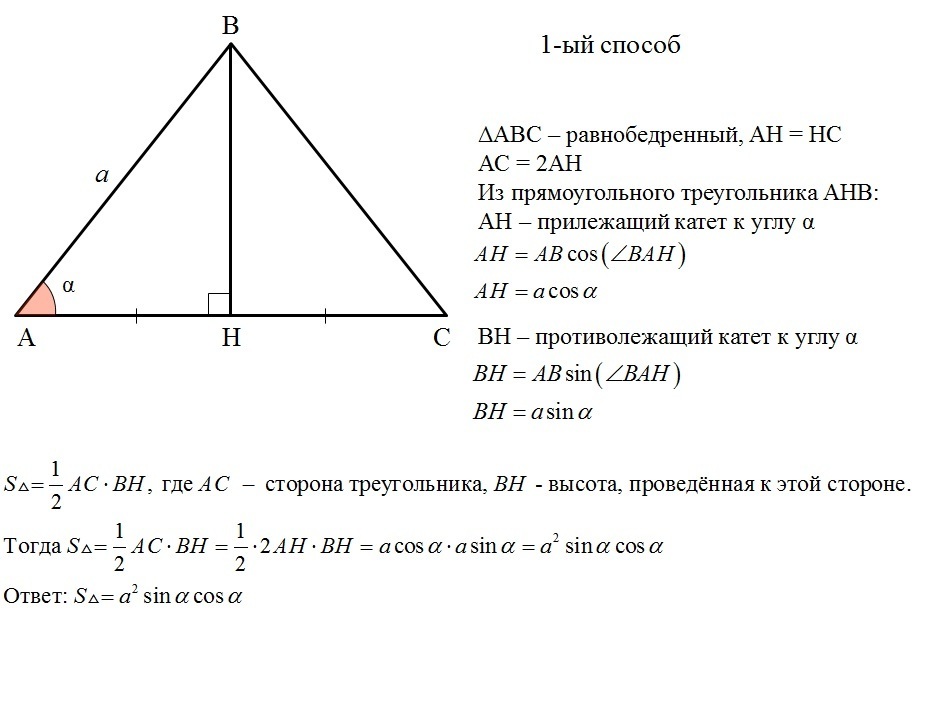 Тогда по теореме
Пифагора:
Тогда по теореме
Пифагора:
12²=x² + x², что равно 144=2х²
Отсюда находим значение х:
x²=72, x=√72
Зная длину катета равнобедренного треугольника, можно найти его площадь (S):
S = √72 * √72/2 = 36 см кв.
Ответ: Площадь треугольника равна 36 см кв.
Дан равнобедренный треугольник, угол в основании которого составляет 25 градусов. Площадь данной фигуры равна 16 см кв. Есть еще один равнобедренный треугольник с углом 130 градусов и площадью 4з см кв. Чему будет равно отношение оснований этих двух треугольных фигур?
Разберемся с первым из треугольников. Так как он является равнобедренным, то оба угла при его основании будут равны. Зная о том, что сумма всех углов треугольника равна 180 градусом, мы можем найти третий угол треугольника, находящийся при его вершине:
180-25-25=130 градусов.
Переходим ко второму треугольнику. Известно, что угол при его вершине
равен 230 градусом. Исходя из этого можно рассчитать величины его углов,
расположенных в основании фигуры:
Исходя из этого можно рассчитать величины его углов,
расположенных в основании фигуры:
(180-130)/2=25 градусов.
Очевидно, что треугольники являются подобными на основании равенства углов.
Следует определить коэффициент подобия двух треугольных фигур. Квадрат коэффициента подобия будет равен отношению площадей треугольников:
49/16=kˆ2
Отсюда выражаем k:
k=7/4
Коэффициент подобия представляет собой отношение основания первой подобной треугольной фигуры ко второй. Это значит, что:
С/c=k = 7/4
Ответ: Отношение оснований двух треугольников равно 7/4.
Чему равна площадь равнобедренного треугольника с прямым углом при условии, что длина его гипотенузы составляет с?
Площадь (S) треугольника с прямым углом составляет ½ часть произведения
его катетов. Принимая во внимание тот факт, что треугольник является
равнобедренным, можно утверждать, что длины его катетов равны. Их можно
обозначить через х. В этом случае формулу для расчета площади треугольника
можно записать в следующем виде:
Их можно
обозначить через х. В этом случае формулу для расчета площади треугольника
можно записать в следующем виде:
S=½x*x=½x²
Согласно теореме Пифагора, действительной для прямоугольного треугольника:
с²=х²+х²=2x²
x²=½c²
Подставим в формулу площади получившееся равенство:
S=½*½с²=¼с² см.кв.
Ответ: Площадь равнобедренного треугольника равна ¼с² см кв.
Как можно рассчитать площадь равнобедренного треугольника, если длина его высоты и основания – величины известные?
Площадь (S) любой треугольной фигуры рассчитывается путем деления пополам произведения длины его основания (с) и высоты (h):
S = ½ c*h
Как найти площадь равнобедренного треугольника?
Площадь каждого треугольника, в том числе и равнобедренного, рассчитывается как половина, взятая от произведения длины высоты треугольника и его основания. Формула имеет следующий вид:
S=1/2 *a*h
Пусть а = 150 см.
Проводим высоту к основанию треугольника. Она же будет являться и медианой по той причине, что треугольник равнобедренный. В результате образовался треугольник с прямым углом и гипотенузой, длина которой равна 85 см. Один из катетов треугольника равен h, а второй рассчитывается как а/2:
150/2=75 см.
Теперь можно рассчитать длину второго катета (на основании теоремы Пифагора):
h=√85²-75²=√7225-5625=√1600=40 см.
Когда все необходимые для расчета площади треугольника величины известны, можно найти ее значение:
S=1/2 *a*h=1/2 *150*40=3000 см.
Как можно найти площадь треугольника при условии, что он является равнобедренным, и его периметр равен 100 см, а основание – 48 см?
Вычислим длину боковой стороны равнобедренного треугольника, отняв от его периметра длину основания и разделив полученное число на 2:
(100-48):2=26 см.
Тогда площадь равнобедренного треугольника с заданными параметрами будет равна:
S=b/4*√(4a²-b²)=12*√(2704-2304)=12*20=240 cм кв.
Чему равна площадь равнобедренного треугольника, длины сторон которого составляют 10 см и 12 см (сумма длин его катетов)?
К основанию равнобедренного треугольника проведем высоту, делящую его на две равные треугольные фигуры, каждая из которых имеет угол 90 градусов и катет длиной 12/2 = 6 см. Гипотенуза подобных треугольников имеет длину 10 см.
В случае с прямоугольным треугольником может быть применима теорема Пифагора, которая поможет найти катет, являющийся высотой треугольника:
h² = 10² — 6² = 64 см
Избавимся от квадратов:
h = 8 см.
Тогда площадь треугольника будет равна:
S = 12 * 8 : 2 = 48 см кв.
Как рассчитать площадь равнобедренного треугольника, если известно о том, что длина его гипотенузы составляет 44 см?
Введем условные обозначения, согласно которым х – это длина одного из
катетов равнобедренного треугольника. В этом случае длина второго катета
тоже будет равна х.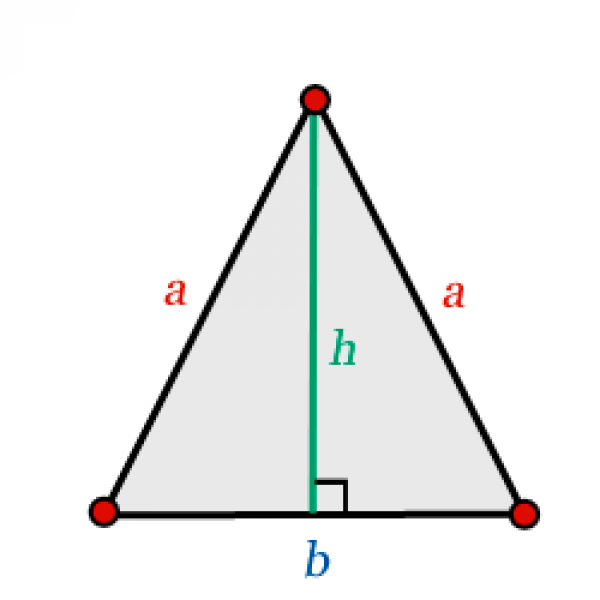
х²+ х² = 44²
2х² = 1936
Отсюда можем найти значение х:
x=√968
Найдя длину катета равнобедренного треугольника, можно вычислить его площадь (S), равную ½ произведения длин его катетов:
S = √968*√968/2 = 484 см кв.
Каким образом возможно высчитать площадь равнобедренного треугольника через стороны и длину его основания?
Располагая сведениями о длине основания (b) и стороны (a) треугольной фигуры с равными катетами, возможно рассчитать площадь (S) этой фигуры. С этой целью следует пользоваться приведенной ниже формулой:
S = b/4×√ 4× a²-b².
Возможно ли определить площадь равнобедренного треугольника через его боковые стороны и образованный ими угол?
Информация о длине боковых сторон (а) треугольной фигуры с катетами равной
длины и размере угла (α), который образован этими катетами, позволит
определить площадь этой фигуры.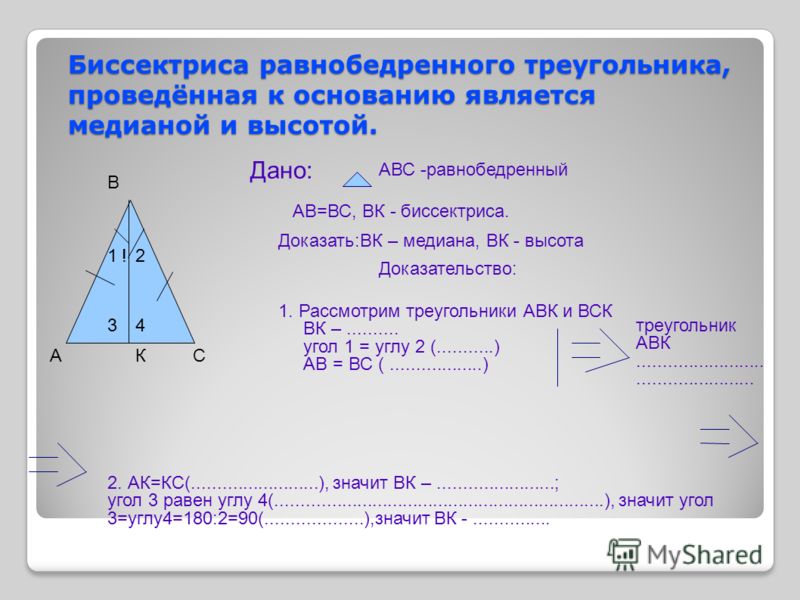 В этом поможет следующая формула:
В этом поможет следующая формула:
S = 1/2a2 * sin(α).
Как можно высчитать площадь равнобедренного треугольника при условии, что известна длина его основания и угол?
Для расчета площади треугольной фигуры с катетами равной длины, при условии, что известна их длина (а), основание (b) и угол, который образован основанием и одним из катетов(α), используется следующая формула:
S = ½ * a * b * sin(α)
Длина основания равнобедренного треугольника превышает длину его боковой стороны на 3 см. Периметр данной треугольной фигуры равен 30 см. Как можно высчитать длину основания данного равнобедренного треугольника?
Примем неизвестную длину основания равнобедренного треугольника за х. В данном случае длина каждой из боковых сторон, которые в равнобедренном треугольнике равны, будет составлять (х-3). Известно, что периметр (Р) треугольника равен 30 см. Тогда:
Р = 3х-6 = 30 см.
Отсюда можно вывести х:
х = (30+6)/3 = 12 см.
Ответ: Длина основания равна 12 см.
Высота, проведенная в равнобедренном треугольнике, равна 15 см. Длина основания данной фигуры превышает длину его боковой стороны на 15 см. Как найти основание равнобедренного треугольника в этом случае?
Примем х за длину основания равнобедренного треугольника. Тогда длина его боковой стороны будет составлять (х-15). Высота, проведенная в треугольнике с прямым углом, также представляет собой его медиану, которая делит его на две равных треугольных фигуры. Следует рассмотреть одну из образовавшихся треугольных фигур. Для начала вычислим ее основания, используя теорему Пифагора:
с2 = а2 + b2 = (15)²+(0,5x)²=(x-15)²
Из этого получается:
225-x²-30x+225-0,25x²
0=0,75x²-30x
x(0,75x-30)=0
x¹=0 см.
x=40 см.
Очевидно, что сторона треугольной фигуры не может иметь длину, равную 0см.
Поэтому можно сделать вывод о том, что ее длина составляет 40 см.
По какой формуле можно высчитать площадь равнобедренного треугольника?
Для ответа на поставленный вопрос следует провести высоту из вершины того угла равнобедренного треугольника, который является противоположным его основанию. После этого длину проведенной высоты (а) нужно умножить на длину основания фигуры (b), а затем разделить полученное значение на два. Формула расчета площади треугольной фигуры, которая является равнобедренной, выглядит следующим образом:
S=a*b/2, или S=1/2a* b.
В равнобедренном треугольнике к его основанию проведена высота, длина которой равна 1,2 см. Длина самого основания фигуры составляет 3,2 см. Как рассчитать длину боковой стороны этого равнобедренного треугольника?
Вычислим половину длины основания данного равнобедренного треугольника:
3,2/2 = 1,6 см.
Имеется треугольник с прямым углом и катетами, длины которых равны 1,2 см
и 1,6 см. Требуется определить длину его гипотенузы. Ее можно вычислить,
используя теорему Пифагора:
Ее можно вычислить,
используя теорему Пифагора:
с²=а²+в²
с² = 1,2² + 1,6² = 1,44 + 2,56 = 4
Осталось только извлечь корень квадратный из 4:
с=√4=2 см.
Ответ: Длина боковой стороны равнобедренного треугольника равна 2 см.
Один из углов равнобедренного треугольника является тупым. Одна сторона данной фигуры составляет 14 см, а другая – 8 см. Чему равно основание треугольника с двумя равными сторонами?
Известно, что углы, расположенные у основания равнобедренного треугольника, всегда являются острыми, иначе сумма всех трех углов превышала бы 180 градусов. Исходя из этого, можно сделать вывод о том, что тупой угол расположен у вершины данной треугольной фигуры.
Доказанным фактом является то, что та сторона фигуры, которая расположена
напротив тупого угла, имеет большую длину, чем сторона, лежащая против
острого угла треугольника. Это позволяет утверждать, что длина основания
данного треугольника больше длины его боковой стороны.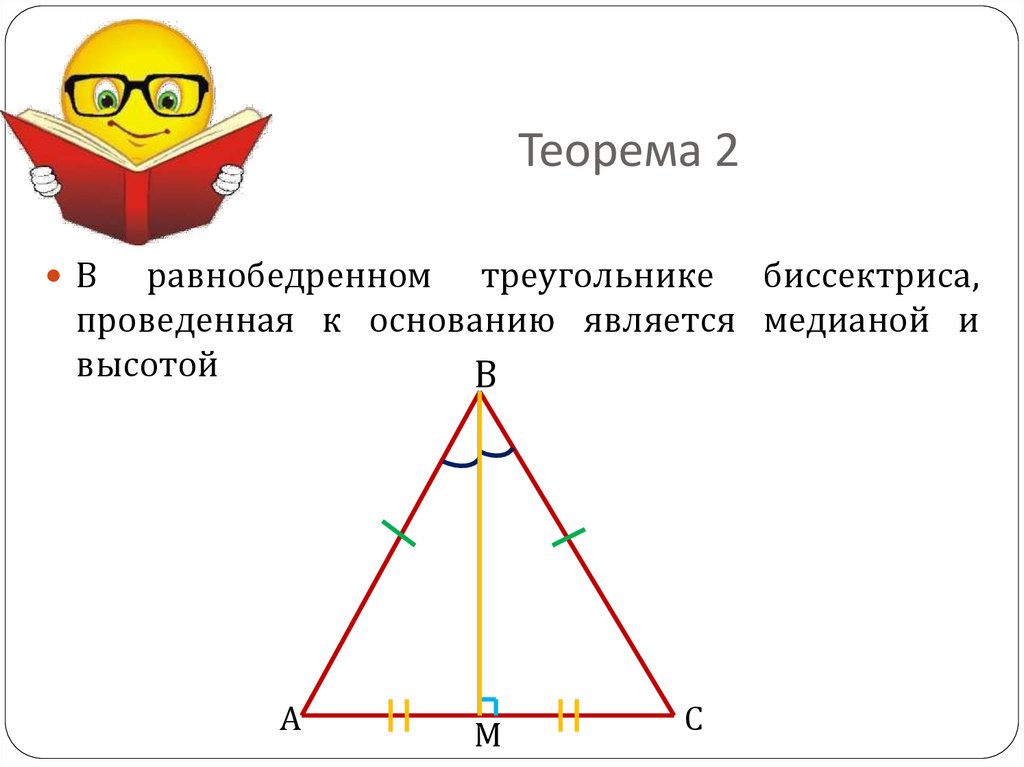 По причине того,
что треугольная фигура является равнобедренной, и известны длины двух ее
сторон (8 см и 14 см), можно говорить о том, что неизвестная сторона будет
составлять 8 см или 14 см. Если предположить, что длина неизвестной
стороны равна 14 см, тогда длина основания будет составлять 8 см, что
невозможно, так как противоречит утверждению о расположении больших сторон
напротив тупых углов. Это означает, что длина третьей стороны треугольника
равна 8 см, а основание в данном случае составляет 14 см.
По причине того,
что треугольная фигура является равнобедренной, и известны длины двух ее
сторон (8 см и 14 см), можно говорить о том, что неизвестная сторона будет
составлять 8 см или 14 см. Если предположить, что длина неизвестной
стороны равна 14 см, тогда длина основания будет составлять 8 см, что
невозможно, так как противоречит утверждению о расположении больших сторон
напротив тупых углов. Это означает, что длина третьей стороны треугольника
равна 8 см, а основание в данном случае составляет 14 см.
Равнобедренный треугольник имеет сторону длиной 29 см. Высота, проведенная в нем, составляет 21 см. Чему равно основание треугольника с указанными параметрами?
Для решения данной задачи следует воспользоваться теоремой Пифагора:
с²=а²+в²
Отсюда можно выразить квадрат длины неизвестной стороны, который будет равен разности квадратов известной стороны и высоты:
29²-21² = 400.
Для того чтобы узнать длину основания равнобедренного треугольника, нужно извлечь корень квадратный из числа 400, а затем умножить полученное число на 2:
√400*2 = 20*2 = 40 см.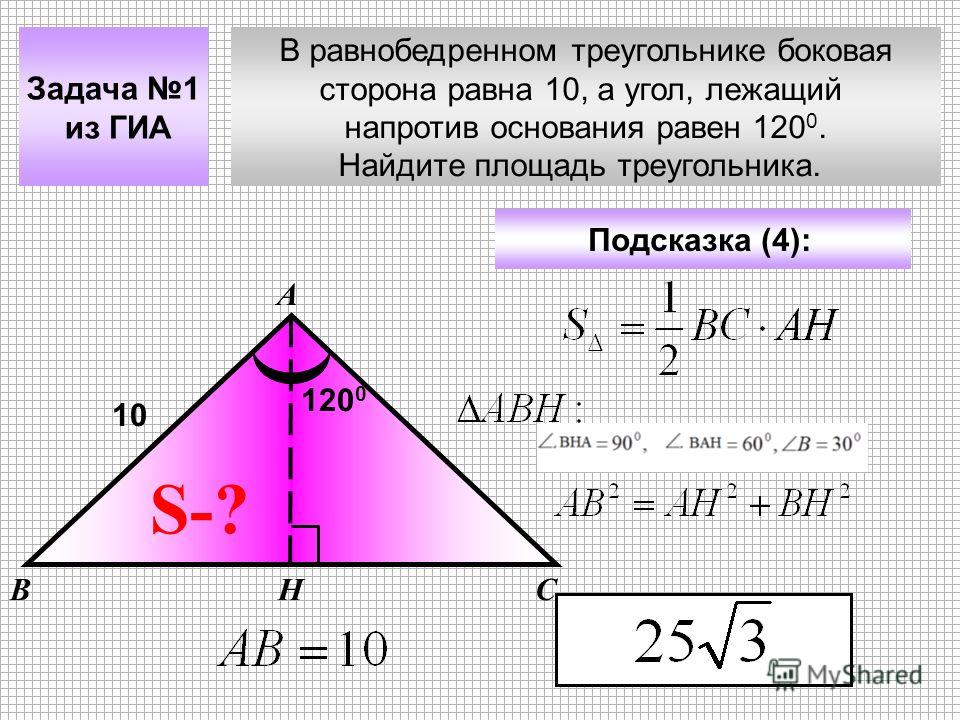
Ответ: Длина основания равнобедренного треугольника равна 40 см.
Читать дальше: как найти площадь равностороннего треугольника.
Обсудить на форуме |
Площадь равнобедренного треугольника – формула, определение, примеры
Площадь равнобедренного треугольника – это пространство, заключенное между сторонами треугольника. Помимо общей формулы площади равнобедренного треугольника, которая равна половине произведения основания и высоты треугольника, для вычисления площади треугольников используются разные формулы в зависимости от их классификации по сторонам. Эти различные типы в зависимости от сторон приведены ниже:
Помимо общей формулы площади равнобедренного треугольника, которая равна половине произведения основания и высоты треугольника, для вычисления площади треугольников используются разные формулы в зависимости от их классификации по сторонам. Эти различные типы в зависимости от сторон приведены ниже:
- Равносторонний треугольник — треугольник, у которого все стороны равны.
- Равнобедренный треугольник — треугольник, у которого любые две стороны/углы равны.
- Разносторонний треугольник — треугольник, все стороны которого не равны.
Давайте подробно разберем площадь равнобедренного треугольника в следующем разделе.
| 1. | Какова площадь равнобедренного треугольника? |
| 2. | Формулы площади равнобедренного треугольника |
| 3. | Площадь равнобедренного треугольника с использованием сторон |
4. | Площадь равнобедренного треугольника по формуле Герона |
| 5. | Площадь равнобедренного треугольника с использованием тригонометрии (SAS и ASA) |
| 6. | Площадь равнобедренного прямоугольного треугольника |
| 7. | Часто задаваемые вопросы о площади равнобедренного треугольника |
Какова площадь равнобедренного треугольника?
Площадь равнобедренного треугольника — это полное пространство или область, занимаемая между сторонами равнобедренного треугольника в двумерном пространстве. Равнобедренный треугольник определяется как треугольник, у которого две равные стороны, что также означает два равных угла. Вот некоторые свойства равнобедренного треугольника, которые отличают его от других типов треугольников:
- Две равные стороны равнобедренного треугольника называются катетами , а угол между ними называется углом при вершине или углом при вершине.

- Сторона, противоположная углу при вершине, называется основанием, а углы при основании равны.
- Перпендикуляр из угла при вершине делит пополам основание и угол при вершине.
Площадь равнобедренного треугольника выражается в квадратных единицах. Следовательно, некоторые единицы измерения, которые можно использовать для представления площади равнобедренного треугольника, это м 2 , см 2 , дюймов 2 , ярдов 2 и т. д.
Формулы площади равнобедренного треугольника
Площадь равнобедренного треугольника относится к общему пространству, занимаемому фигурой в 2D. Площадь равнобедренного треугольника можно рассчитать разными способами на основе известных элементов равнобедренного треугольника. Общая основная формула, которую можно использовать для расчета площади равнобедренного треугольника с использованием высоты, задается как (1/2) × основание × высота 9.0003
В следующей таблице приведены различные формулы, которые можно использовать для расчета площади равнобедренного треугольника для другого набора известных параметров.
| Известные параметры данного равнобедренного треугольника | Формула для расчета площади (в квадратных единицах) |
| А = ½ × ширина × высота |
| A = ½[√(a 2 − b 2 ⁄4) × b] |
| А = ½ × b × a × sin(α) |
| А = [а 2 × sin (β/2) × sin (α)] |
| A = ½ × a 2 |
где,
- b = основание равнобедренного треугольника
- а = мера равных сторон равнобедренного треугольника
- α = мера равных углов равнобедренного треугольника
- β = угол, противоположный основанию
Площадь равнобедренного треугольника с использованием сторон
Если известны длины равных сторон и основания равнобедренного треугольника, то можно вычислить высоту или высоту треугольника.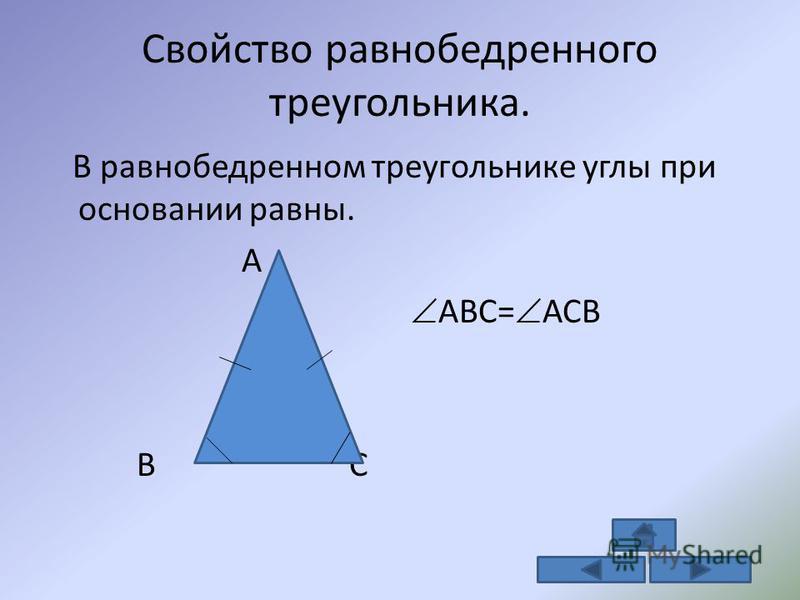 Формула для вычисления площади равнобедренного треугольника с использованием сторон задается следующим образом:
Формула для вычисления площади равнобедренного треугольника с использованием сторон задается следующим образом:
Площадь равнобедренного треугольника с использованием только сторон = ½[√(a 2 — b 2 /4) × b]
где,
- b = основание равнобедренного треугольника
- h = высота равнобедренного треугольника
- a = длина двух равных сторон
Вывод:
Из рисунка выше мы знаем:
BD = DC = ½ BC = ½ b (перпендикуляр от угла при вершине делит основание пополам)
AB = AC = a (равные стороны равнобедренного треугольника)
Применяя теорему Пифагора для ΔABD, получаем:
а 2 = (б/2) 2 + (АД) 2
AD = √(a 2 − b 2 /4)
Высота равнобедренного треугольника = √(a 2 − b 2 /4)
Кроме того, мы знаем, что общая площадь треугольника определяется как:
Площадь = ½ × b × h
Заменяющее значение высоты:
Площадь равнобедренного треугольника с использованием только сторон = ½[√(a 2 − b 2 /4) × b]
Площадь равнобедренного треугольника по формуле Герона
Формула площади равнобедренного треугольника может быть легко получена с помощью формулы Герона, как описано в следующих шагах.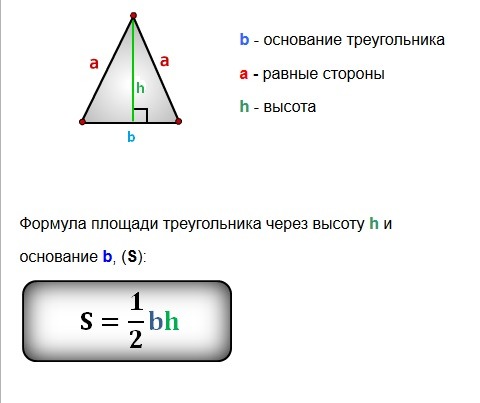 Формула Герона используется для нахождения площади треугольника, когда даны измерения его трех сторон.
Формула Герона используется для нахождения площади треугольника, когда даны измерения его трех сторон.
Вывод:
Формула Герона для нахождения площади A треугольника, стороны которого равны a, b и c:
A = √s(s-a)(s-b)(s-c)
где,
- a, b и c — стороны треугольника.
- с — полупериметр треугольника.
Мы знаем, что периметр треугольника со сторонами a, b и c равен a + b + c. Здесь s — половина периметра треугольника, поэтому его называют полупериметром.
Таким образом, полупериметр равен:
s = (a + b + c)/2
Теперь для равнобедренного треугольника
s = ½(a + a + b)
⇒ s = ½ (2a + b)
или, s = a + (b/2)
Кроме того,
Площадь = √[s(s-a)(s-b)(s-c)]
или, Площадь = √[s (s−a) 2 (s−b)]
⇒ Площадь = (s−a) × √[s (s−b)]
Подстановка значения «s»
⇒ Площадь = (a + b/2 − a) × √[(a + b/2) × ((a + b/2) − b)]
⇒ Площадь = b/2 × √[(a + б/2) × (а — б/2)]
Площадь равнобедренного треугольника = b/2 × √(a 2 − b 2 /4) квадратных единиц
где,
- b = основание равнобедренного треугольника
- а = длина двух равных сторон
Площадь равнобедренного треугольника с использованием тригонометрии (SAS и ASA)
Формула для нахождения площади равнобедренного треугольника по длине двух сторон и углу между ними или по двум углам и длине между ними может быть рассчитана с использованием основных понятий тригонометрии.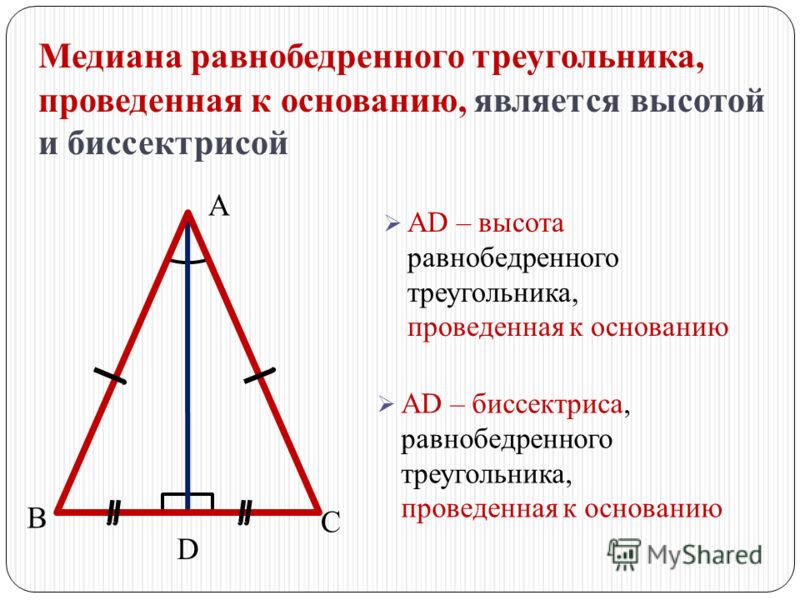
Используя 2 стороны и угол между ними:
Площадь = ½ × b × a × sin(α) квадратных единиц
где,
- b = основание равнобедренного треугольника
- а = длина двух равных сторон
- α = угол между неравными сторонами
Используя 2 угла и длину между ними:
Площадь = [a 2 × sin(β/2) × sin(α)] квадратных единиц
где,
- a = длина двух равных сторон
- α, β = углы равнобедренного треугольника
Площадь равнобедренного прямоугольного треугольника
Прямоугольный равнобедренный треугольник определяется как равнобедренный треугольник, один из углов которого равен 90°. Формула для расчета площади равнобедренного прямоугольного треугольника может быть выражена следующим образом:
Площадь = ½ × a 2
, где a — длина равных сторон.
Вывод:
Обозначим равные стороны прямоугольного равнобедренного треугольника как «а», как показано на рисунке ниже:
Длина гипотенузы BC может быть рассчитана с помощью теоремы Пифагора,
BC 2 = a 2 + a 2
BC = 90½03 основание высота
Площадь = ½ × a × a = a 2 /2 квадратных единиц
Примеры площади равнобедренного треугольника
Пример 1: Найдите площадь равнобедренного треугольника, если длина основания 10 см, а высота 17 см?
Решение:
Основание треугольника (b) = 10 см
Высота треугольника (h) = 17 см
Площадь равнобедренного треугольника = (1/2) × b × h
= ( 1/2) × 10 × 17
= 5 × 17
= 85 см 2
Ответ: Площадь данного равнобедренного треугольника равна 85 см 2 .

Пример 2: Найдите длину основания равнобедренного треугольника, площадь которого 243 см 2 , а высота треугольника 9 см.
Решение:
Площадь треугольника, A = 243 см 2
Высота треугольника (h) = 9 см
Основание треугольника = b =?
Площадь равнобедренного треугольника = (1/2) × b × h
243 = (1/2) × b × 9
243 = (b × 9)/2
b = (243 × 2)/ 9
b = 54 см
Ответ: Высота данного равнобедренного треугольника равна 54 см.
Пример 3: Найдите длины равных сторон равнобедренного треугольника с основанием 24 см и площадью 60 см 2 .
Решение:
Мы знаем, что
Основание равнобедренного треугольника = 24 см
Площадь равнобедренного треугольника = 60 см 2 − b 2 /4)
Следовательно,
60 = (24/2)√(a 2 — 24 2 /4)
60 = 12√ (A 2 — 144)
5 = √ (A 2 -144)
квадрат обе стороны, мы получили,
25 25 25)
.
 = a 2 −144
= a 2 −144a 2 = 169
⇒a = 13 см
Ответ: Длина равных сторон данного равнобедренного треугольника равна 13 см.
перейти к слайдуперейти к слайдуперейти к слайду
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Записаться на бесплатный пробный урок
Практические вопросы по площади равнобедренного треугольника
перейти на слайдперейти на слайд
Часто задаваемые вопросы о площади равнобедренного треугольника
Что означает площадь равнобедренного треугольника?
Площадь фигуры — это область, ограниченная фигурой. Таким образом, площадь равнобедренного треугольника означает все пространство, заключенное в равнобедренном треугольнике.
Что такое равнобедренный треугольник?
Равнобедренный треугольник определяется как треугольник, у которого две равные стороны, что также означает два равных угла.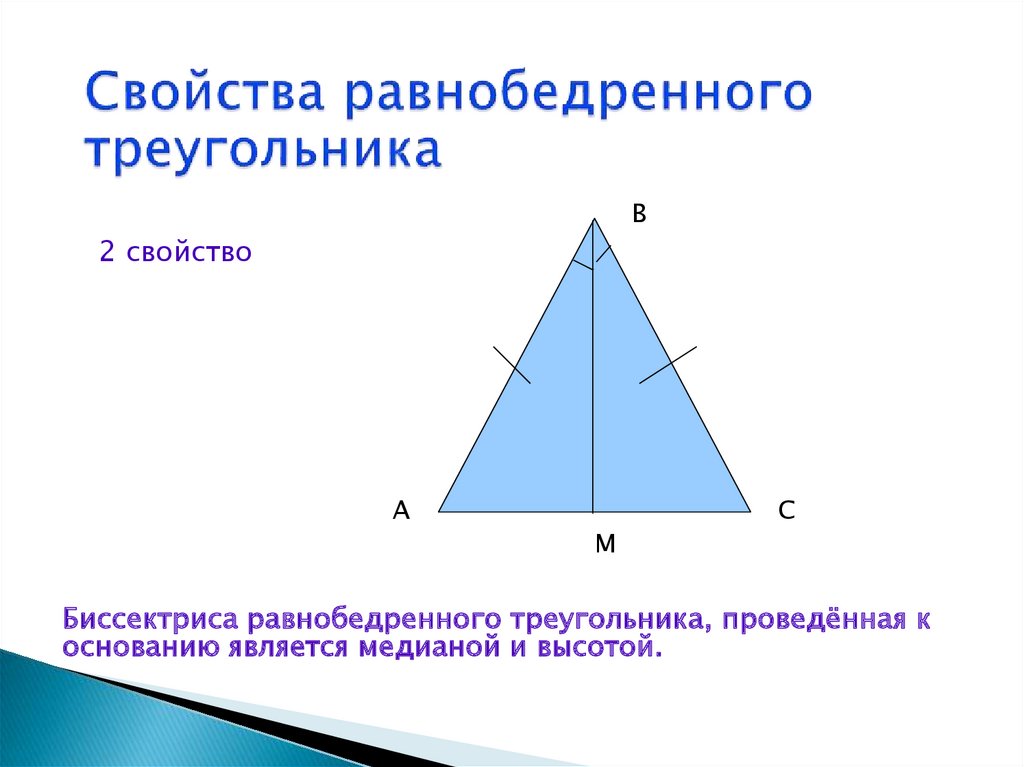 Вот некоторые свойства равнобедренного треугольника, которые отличают его от других типов треугольников:
Вот некоторые свойства равнобедренного треугольника, которые отличают его от других типов треугольников:
- Две равные стороны равнобедренного треугольника называются катетами , а угол между ними называется углом при вершине или углом при вершине.
- Сторона, противоположная углу при вершине, называется основанием, а углы при основании равны.
- Перпендикуляр из угла при вершине делит пополам основание и угол при вершине.
Какая формула площади равнобедренного треугольника?
Площадь равнобедренного треугольника относится к общему пространству, занимаемому фигурой в 2D. Площадь равнобедренного треугольника можно рассчитать разными способами на основе известных элементов равнобедренного треугольника.
- При использовании основания и высоты: площадь = ½ × ширина × высота
- Используя все три стороны: Площадь = ½[√(a 2 − б 2 ⁄4) × б]
- Используя длину двух сторон и угол между ними: Площадь = ½ × b × a × sin(α)
- Используя два угла и расстояние между ними: A = [a 2 ×sin(β/2)×sin(α)]
- Формула площади равнобедренного прямоугольного треугольника: Площадь = ½ × a 2
где
b = основание равнобедренного треугольника
a = мера равных сторон равнобедренного треугольника
α = мера равных углов равнобедренного треугольника
β = мера угла, противоположного основанию
Как найти высоту, используя площадь равнобедренного треугольника?
Высоту или высоту равнобедренного треугольника можно вычислить, применив теорему Пифагора для любых двух сторон.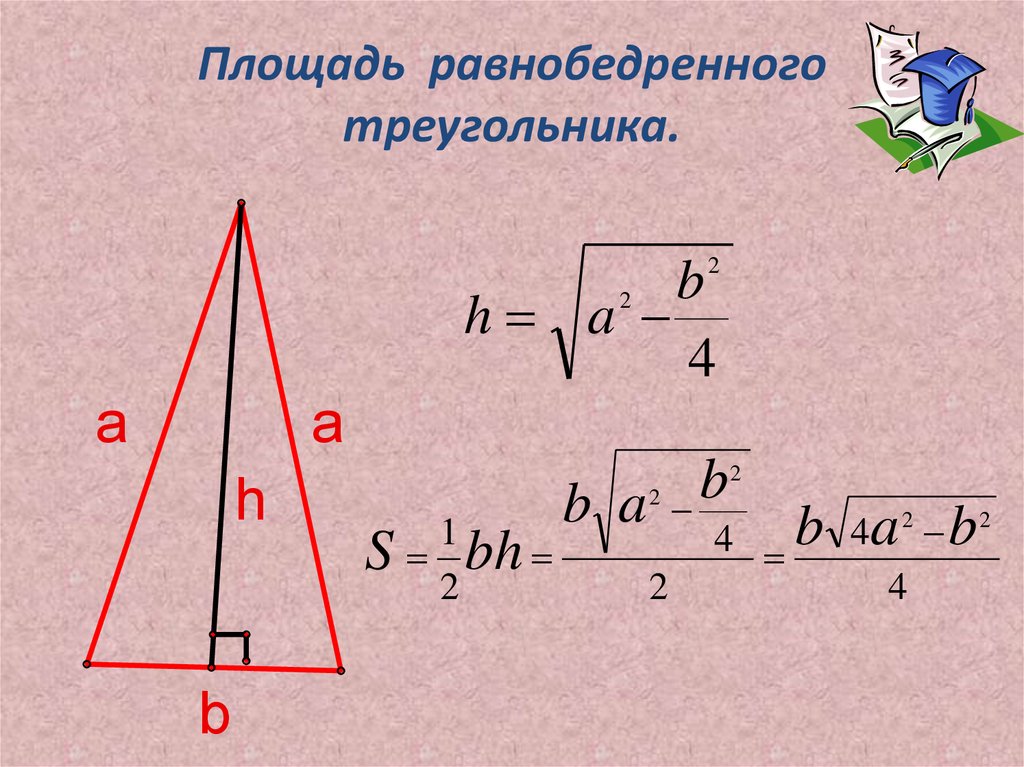 Формула для расчета высоты равнобедренного треугольника дается как,
Формула для расчета высоты равнобедренного треугольника дается как,
Высота равнобедренного треугольника = √(a 2 − b 2 /4) единиц
, где
b = основание равнобедренного треугольника
a = мера равных сторон равнобедренного треугольника
Что такое периметр и площадь равнобедренного треугольника?
Периметр равнобедренного треугольника определяется как длина границы равнобедренного треугольника. Формула для периметра равнобедренного треугольника дается как P = 2a + b единиц. В то время как площадь — это общая область, покрытая равнобедренным треугольником, определяемая как ½ [√ (a 2 — b 2 ⁄4) × b]
где
- b = основание равнобедренного треугольника
- а = мера равных сторон равнобедренного треугольника
Как найти площадь равнобедренного треугольника без высоты?
Выражение для вычисления площади равнобедренного треугольника без высоты можно вычислить по формуле Герона.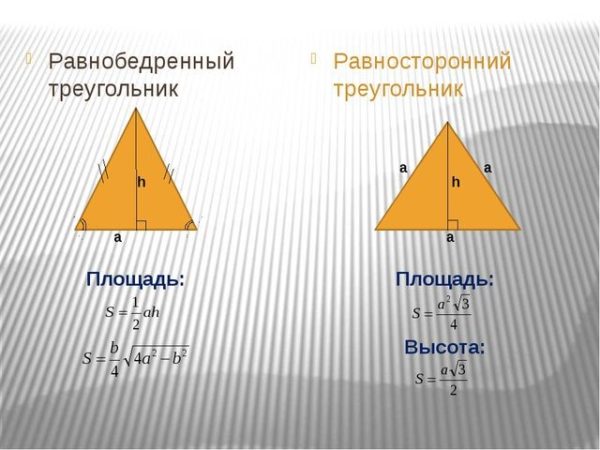 Формула для расчета площади равнобедренного треугольника без высоты дается как,
Формула для расчета площади равнобедренного треугольника без высоты дается как,
Площадь равнобедренного треугольника = b/2 × √(a 2 − b 2 /4)
где
- b = основание равнобедренного треугольника
- а = мера равных сторон равнобедренного треугольника
Как найти площадь равнобедренного треугольника по двум сторонам и углу?
Площадь треугольника равна половине произведения данных двух сторон и синуса прилежащего к ним угла.
Формула площади треугольника с двумя сторонами и прилежащим углом (SAS) используется для нахождения общей формулы для расчета площади равнобедренного треугольника для SAS как,
Площадь = ½ × b × a × sin(α)
где
- b = основание равнобедренного треугольника
- а = мера равных сторон равнобедренного треугольника
- α = мера равных углов равнобедренного треугольника
Как найти площадь равнобедренного треугольника с тремя сторонами?
Площадь равнобедренного треугольника с тремя сторонами можно рассчитать по формуле Герона, то есть Площадь = \(\sqrt {s(s — a)(s — b)(s — c)} \). В равнобедренном треугольнике сторона с = стороне а. Общая формула для расчета площади равнобедренного треугольника имеет следующий вид:
В равнобедренном треугольнике сторона с = стороне а. Общая формула для расчета площади равнобедренного треугольника имеет следующий вид:
Площадь равнобедренного треугольника = b/2 × √(a 2 − b 2 /4)
где
- b = основание равнобедренного треугольника
- а = мера равных сторон равнобедренного треугольника
Формулы для равнобедренных треугольников — Что такое формулы для равнобедренных треугольников? Примеры
Равнобедренный треугольник в геометрии — это треугольник, две стороны которого имеют одинаковую длину. Два угла, лежащие напротив равных сторон, равны и всегда острые. Различные формулы для равнобедренных треугольников объясняются ниже. Две важные формулы для равнобедренных треугольников – площадь треугольника и периметр треугольника.
Что такое формулы равнобедренных треугольников?
В равнобедренном треугольнике две стороны одинаковой длины и две равные стороны соединяются под одинаковым углом к основанию, т.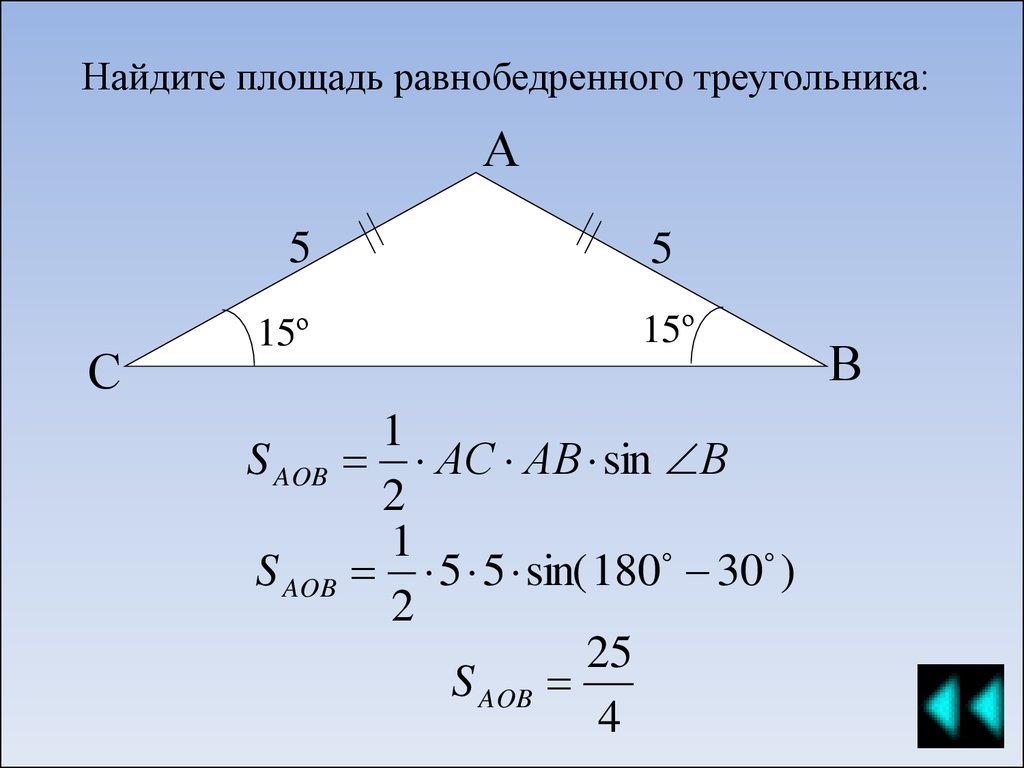 е. к третьей стороне. Таким образом, в равнобедренном треугольнике высота перпендикулярна от вершины, которая является общей для равных сторон. Такие особые свойства равнобедренного треугольника помогают нам рассчитать его площадь, а также высоту с помощью формул равнобедренного треугольника.
е. к третьей стороне. Таким образом, в равнобедренном треугольнике высота перпендикулярна от вершины, которая является общей для равных сторон. Такие особые свойства равнобедренного треугольника помогают нам рассчитать его площадь, а также высоту с помощью формул равнобедренного треугольника.
Формулы равнобедренного треугольника 9{2}}{4}}\)
(Здесь а — равная сторона, а b — основание треугольника.)
Площадь = 1/2 × abSinα
(Здесь a и b — длины двух сторон, а α — угол между этими сторонами.)
Периметр равнобедренного треугольника : В равнобедренном треугольнике три стороны: две равные стороны и одно основание. Для вычисления периметра равнобедренного треугольника используется выражение 2a + b , 9{2}}{4}}\)
Давайте проверим несколько примеров, чтобы лучше понять использование формул для равнобедренных треугольников.
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Записаться на бесплатный пробный урок
Примеры использования формул для равнобедренных треугольников
Пример 1: Определить площадь равнобедренного треугольника, у которого основание «b» равно 8 единицам, а боковая сторона «a» равна 5 единицам?
Решение: Применение теоремы Pythagoras ‘:
A 2 = (B/2) 2 + H 2
H 2 = A 2 -00999999999999999999999999999999 2 . = 5 2 — 4 2 что дает h = 3
Площадь A’ = (1/2) × b × h = (1/2) 8 × 3 = 12 единиц 2
5 0 Ответ: площадь равнобедренного треугольника – 12 единиц 2 .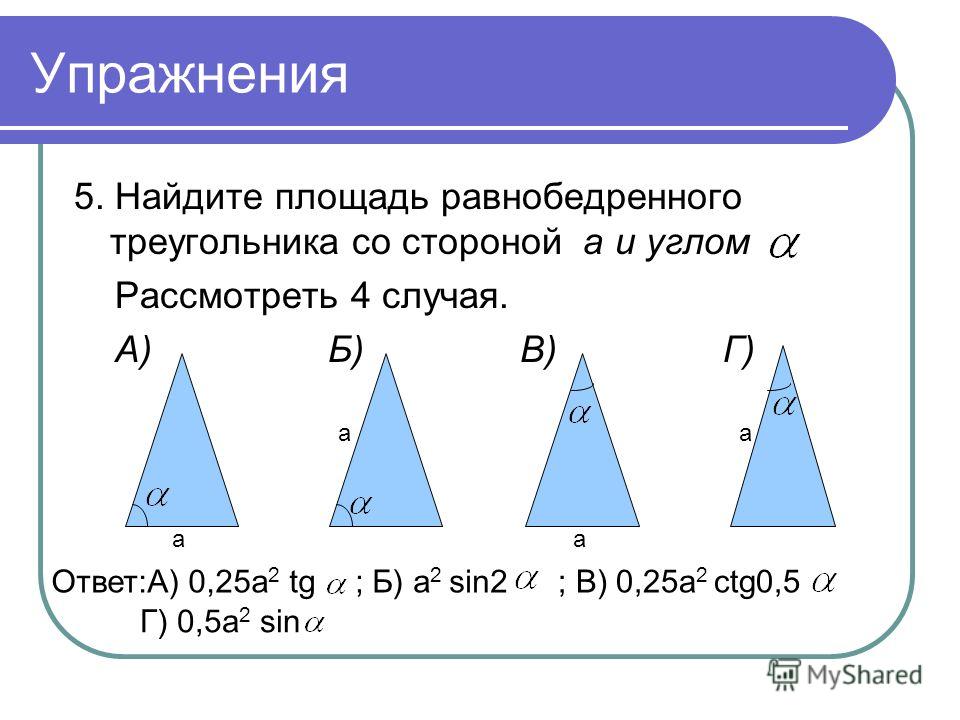
Пример 2: Найдите боковую сторону равнобедренного треугольника площадью 20 единиц 2 и база 10 единиц?
Решение: Используя формулу площади равнобедренного треугольника:
A = (1/2) b h = 20
Учитывая b = 10,
Найти: боковая сторона
h = 40 / 10 4
0 Применение теоремы Пифагоры:
A 2 = (B/2) 2 + H 2 = √ (5 2 + 4 2 ) = √41 + 4 2 ) = √41 + 4 2 ) =.0206
Ответ: боковая сторона равнобедренного треугольника равна √41.
Пример 3: Вычислите площадь, высоту и периметр равнобедренного треугольника, если две его равные стороны имеют длину 6 единиц, а третья сторона равна 8 единицам.
Решение:
Дано a = b = 6 единиц, c = 8 единиц
Чтобы найти: площадь, высоту и периметр равнобедренного треугольника
Периметр равнобедренного треугольника,
P = 2×a + b
P = 2×6 + 8
= 20 ед. 8 2 /4)
h = √(36−16)
h = √20 ед. 8×√20
= √20/4 квадратных единиц
Ответ:
Часто задаваемые вопросы о формулах для равнобедренных треугольников
Что такое формула равнобедренного треугольника в геометрии? 9{2}}{4}}\)
(Здесь a и b — длины двух сторон, а α — угол между этими сторонами.)
Как использовать формулу равнобедренного треугольника?
Мы можем использовать формулы равнобедренного треугольника следующим образом:
- Шаг 1: Проверьте параметр (площадь, периметр или высоту), который нужно получить или рассчитать.
- Шаг 2. Определите сторону равнобедренного треугольника и подставьте значение в нужную формулу — площадь, периметр или высоту.


 Метод геометрических мест
Метод геометрических мест Первый признак подобия
Первый признак подобия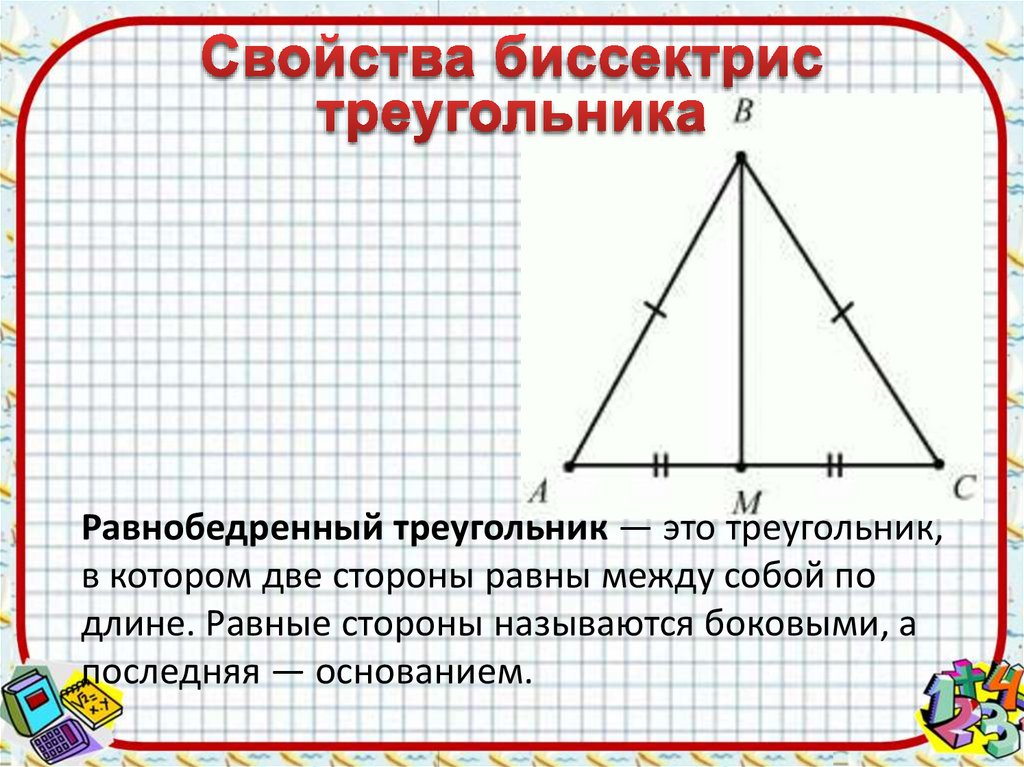 Правильний чотирикутник (квадрат)
Правильний чотирикутник (квадрат)
 Свойства и признаки параллельности.
Свойства и признаки параллельности. Решение задач
Решение задач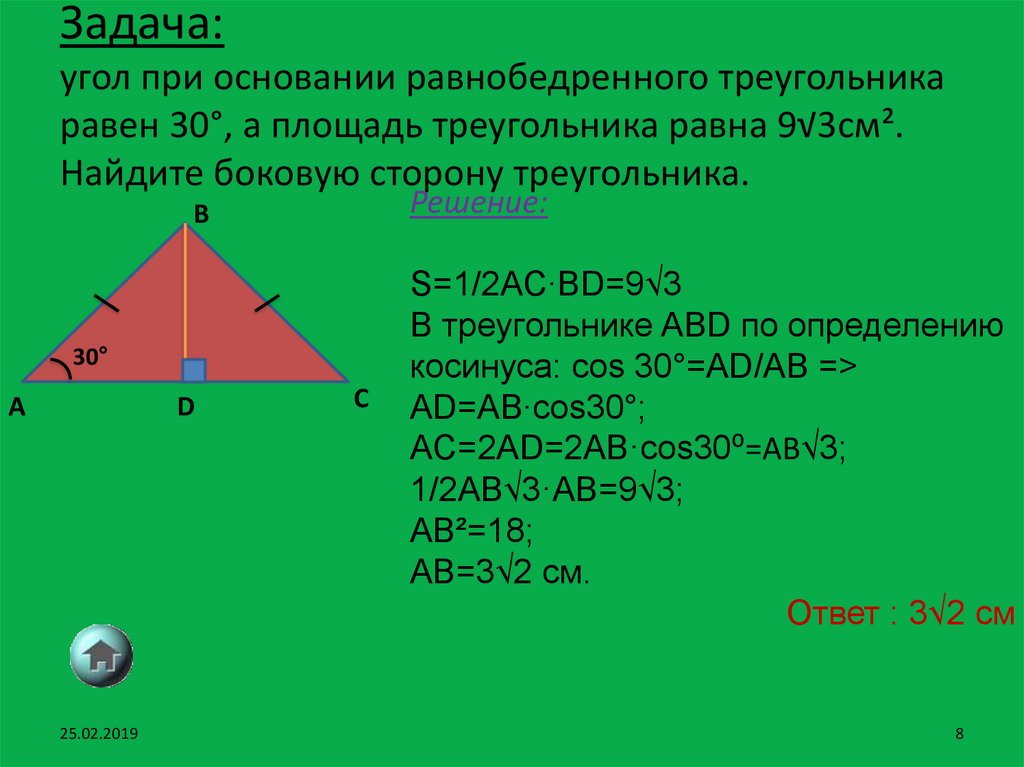 Шар. Куля
Шар. Куля Формулы снабжены пояснениями и комментариями. На отдельном рисунке приведено соответствие условных обозначений формул и элементов равнобедренного треугольника. Далее приведен раздел с примерами решения задач.
Формулы снабжены пояснениями и комментариями. На отдельном рисунке приведено соответствие условных обозначений формул и элементов равнобедренного треугольника. Далее приведен раздел с примерами решения задач.
 д. Просто найдите наиболее подходящую на рисунке слева. Для самых любопытных в тексте справа поясняется, почему формула явяляется правильной и как именно с ее помощью находится площадь.
д. Просто найдите наиболее подходящую на рисунке слева. Для самых любопытных в тексте справа поясняется, почему формула явяляется правильной и как именно с ее помощью находится площадь.  Высота делит этот прямоугольник на два малых прямоугольника, при этом стороны треугольника являются их диагоналями, которые делят их ровно пополам. Таким образом, площадь равнобедренного треугольника и будет равна половине произведения боковой стороны на высоту). См. также Формулу 5
Высота делит этот прямоугольник на два малых прямоугольника, при этом стороны треугольника являются их диагоналями, которые делят их ровно пополам. Таким образом, площадь равнобедренного треугольника и будет равна половине произведения боковой стороны на высоту). См. также Формулу 5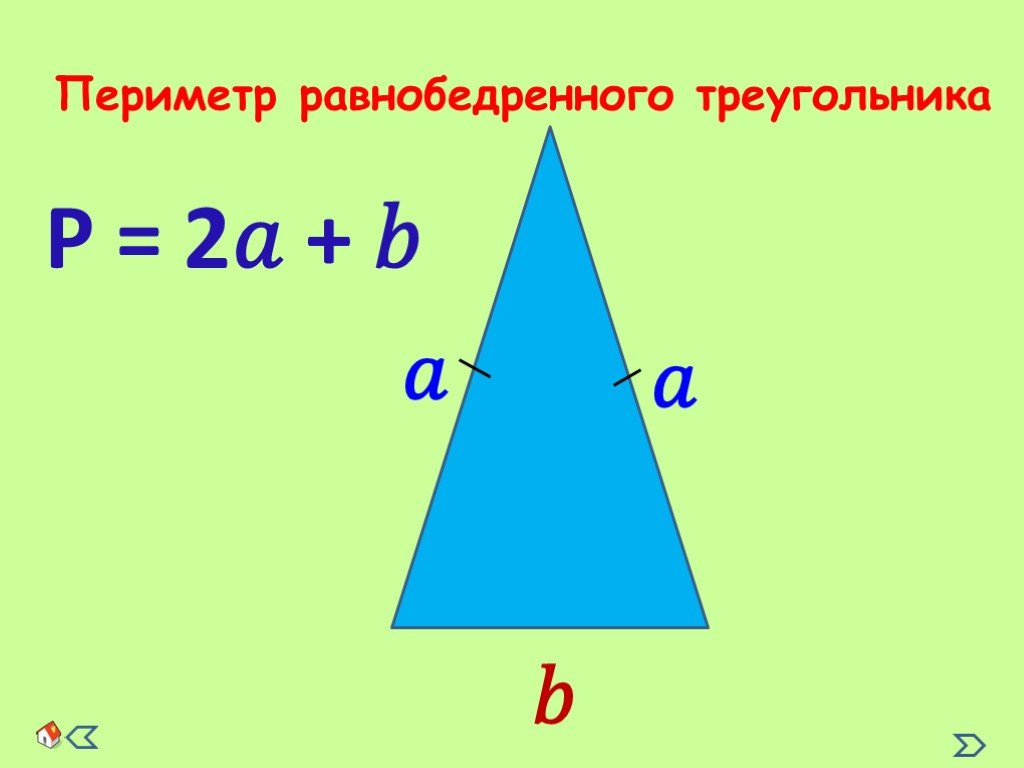 Если присмотреться внимательнее, то станет очевидно, что половина основания (b/2) умноженная на tg(β/2) даст нам высоту треугольника. Поскольку высота в равнобедренном треугольнике является, одновременно, биссектрисой и медианой, то tg(β/2) — это отношение половины основания (b/2) к высоте — tg(β/2) = (b/2)/h. Откуда h = b / (2 tg(β/2) ). В итоге формула снова будет сведена к более простой Формуле 5, которая вполне очевидна.
Если присмотреться внимательнее, то станет очевидно, что половина основания (b/2) умноженная на tg(β/2) даст нам высоту треугольника. Поскольку высота в равнобедренном треугольнике является, одновременно, биссектрисой и медианой, то tg(β/2) — это отношение половины основания (b/2) к высоте — tg(β/2) = (b/2)/h. Откуда h = b / (2 tg(β/2) ). В итоге формула снова будет сведена к более простой Формуле 5, которая вполне очевидна. Боковая сторона является гипотенузой, поэтому из квадрата боковой стороны (а) вычтем квадрат второго катета. Поскольку он равен половине основания (b/2) то его квадрат будет равен b2/4. Извлечение корня из данного выражения и даст нам высоту. Что и видно в Формуле 6. Если числитель и знаменатель умножить на два, а потом двойку числителя внести под знак корня, получим второй вариант той же самой формулы, который написан через знак «равно».
Боковая сторона является гипотенузой, поэтому из квадрата боковой стороны (а) вычтем квадрат второго катета. Поскольку он равен половине основания (b/2) то его квадрат будет равен b2/4. Извлечение корня из данного выражения и даст нам высоту. Что и видно в Формуле 6. Если числитель и знаменатель умножить на два, а потом двойку числителя внести под знак корня, получим второй вариант той же самой формулы, который написан через знак «равно».  Обратите внимание на обозначения переменных! Не перепутайте α и β, а также a и b!
Обратите внимание на обозначения переменных! Не перепутайте α и β, а также a и b!
 Поскольку треугольник равнобедренный, то она примет более простой вид (см. формулу 1 в списке формул выше):
Поскольку треугольник равнобедренный, то она примет более простой вид (см. формулу 1 в списке формул выше):  Оба прямоугольных треугольника равны между собой. Гипотенузы — это стороны равнобедренного треугольника, поэтому они равны, один из катетов — общий, а, поскольку, BK одновременно является и биссектрисой и высотой, то, соответствующие углы также равны. Поэтому нам будет достаточно найти площадь одного из них и умножить полученное число на два.
Оба прямоугольных треугольника равны между собой. Гипотенузы — это стороны равнобедренного треугольника, поэтому они равны, один из катетов — общий, а, поскольку, BK одновременно является и биссектрисой и высотой, то, соответствующие углы также равны. Поэтому нам будет достаточно найти площадь одного из них и умножить полученное число на два.


 = a 2 −144
= a 2 −144