Как привести дробные числа к общему знаменателю. Как привести дроби к общему знаменателю
Чтобы понять, как складывать дроби с разными знаменателями, сначала изучим правило, а затем рассмотрим конкретные примеры.
Чтобы сложить или вычесть дроби с разными знаменателями, надо:
1) Найти(НОЗ) данных дробей.
2) Найти дополнительный множитель к каждой дроби. Для этого новый знаменатель нужно разделить на старый.
3) Умножить числитель и знаменатель каждой дроби на дополнительный множитель и сложить или вычесть дроби с одинаковыми знаменателями.
4) Проверить, является ли полученная в результате дробь правильной и несократимой.
В следующих примерах надо сложить или вычесть дроби с разными знаменателями:
1) Чтобы вычесть дроби с разными знаменателями, сначала ищем наименьший общий знаменатель данных дробей. Выбираем большее из чисел и проверяем, делится ли оно на меньшее. 25 на 20 не делится. Умножаем 25 на 2. 50 на 20 не делится.
Умножаем 25 на 3. 75 на 20 не делится. Умножаем 25 на 4. 100 на 20 делится. Значит, наименьший общий знаменатель равен 100.
2) Чтобы найти дополнительный множитель к каждой дроби, надо новый знаменатель разделить на старый. 100:25=4, 100:20=5. Соответственно, к первой дроби дополнительный множитель 4, ко второй — 5.
3) Умножаем числитель и знаменатель каждой дроби на дополнительный множитель и вычитаем дроби по правилу вычитания дробей с одинаковыми знаменателями.
4) Полученная дробь — правильная и несократимая. Значит, это — ответ.
1) Чтобы сложить дроби с разными знаменателями, сначала ищем наименьший общий знаменатель. 16 на 12 не делится. 16∙2=32 на 12 не делится. 16∙3=48 на 12 делится. Значит, 48 — НОЗ.
2) 48:16=3, 48:12=4. Это — дополнительные множители к каждой дроби.
3) умножаем числитель и знаменатель каждой дроби на дополнительный множитель и складываем новые дроби.
4)Полученная в результате дробь — правильная и несократимая.
1) 30 на 20 не делится.
2) чтобы найти дополнительный множитель к каждой дроби, надо новый знаменатель поделить на старый: 60:20=3, 60:30=2.
3) умножаем числитель и знаменатель каждой дроби на дополнительный множитель и вычитаем новые дроби.
4) полученную дробьна 5.
1) 8 на 6 не делится. 8∙2=16 на 6 не делится. 8∙3=24 делится и на 4, и на 6. Значит, 24 — это и есть НОЗ.
2) чтобы найти дополнительный множитель к каждой дроби, нужно новый знаменатель разделить на старый. 24:8=3, 24:4=6, 24:6=4. Значит, 3, 6 и 4 — дополнительные множители к первой, второй и третьей дроби.
3) умножаем числитель и знаменатель каждой долби на дополнительный множитель. Складываем и вычитаем. Полученная дробь — неправильная, поэтому необходимо выделить целую часть.
На этом уроке мы рассмотрим приведение дробей к общему знаменателю и решим задачи по этой теме. Дадим определение понятию общего знаменателя и дополнительного множителя, вспомним о взаимно простых числах.
Тема: Сложение и вычитание дробей с разными знаменателями
Урок: Приведение дробей к общему знаменателю
Повторение. Основное свойство дроби.
Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.
Например, числитель и знаменатель дроби можно разделить на 2. Получим дробь . Эту операцию называют сокращением дроби. Можно выполнить и обратное преобразование, умножив числитель и знаменатель дроби на 2. В этом случае говорят, что мы привели дробь к новому знаменателю. Число 2 называют дополнительным множителем.
Вывод. Дробь можно привести к любому знаменателю кратному знаменателю данной дроби. Для того чтобы привести дробь к новому знаменателю, ее числитель и знаменатель умножают на дополнительный множитель.
1. Приведите дробь к знаменателю 35.
Число 35 кратно 7, то есть 35 делится на 7 без остатка. Значит, это преобразование возможно. Найдем дополнительный множитель. Для этого разделим 35 на 7. Получим 5. Умножим на 5 числитель и знаменатель исходной дроби.
2. Приведите дробь к знаменателю 18.
Найдем дополнительный множитель. Для этого разделим новый знаменатель на исходный. Получим 3. Умножим на 3 числитель и знаменатель данной дроби.
3. Приведите дробь к знаменателю 60.
Разделив 60 на 15, получим дополнительный множитель. Он равен 4. Умножим числитель и знаменатель на 4.
4. Приведите дробь к знаменателю 24
В несложных случаях приведение к новому знаменателю выполняют в уме. Принято только указывать дополнительный множитель за скобочкой чуть правее и выше исходной дроби.
Дробь можно привести к знаменателю 15 и дробь можно привести к знаменателю 15. У дробей и общий знаменатель 15.
Общим знаменателем дробей может быть любое общее кратное их знаменателей.
Для простоты дроби приводят к наименьшему общему знаменателю. Он равен наименьшему общему кратному знаменателей данных дробей.
Пример. Привести к наименьшему общему знаменателю дроби и .
Сначала найдем наименьшее общее кратное знаменателей данных дробей. Это число 12. Найдем дополнительный множитель для первой и для второй дроби. Для этого 12 разделим на 4 и на 6. Три — это дополнительный множитель для первой дроби, а два — для второй. Приведем дроби к знаменателю 12.
Мы привели дроби и к общему знаменателю, то есть мы нашли равные им дроби, у которых один и тот же знаменатель.
Правило. Чтобы привести дроби к наименьшему общему знаменателю, надо
Во-первых, найти наименьшее общее кратное знаменателей этих дробей, оно и будет их наименьшим общим знаменателем;
Во-вторых, разделить наименьший общий знаменатель на знаменатели данных дробей, т. е. найти для каждой дроби дополнительный множитель.
В-третьих, умножить числитель и знаменатель каждой дроби на ее дополнительный множитель.
а) Привести к общему знаменателю дроби и .
Наименьший общий знаменатель равен 12. Дополнительный множитель для первой дроби — 4, для второй — 3. Приводим дроби к знаменателю 24.
б) Привести к общему знаменателю дроби и .
Наименьший общий знаменатель равен 45. Разделив 45 на 9 на 15, получим, соответственно, 5 и 3. Приводим дроби к знаменателю 45.
в) Привести к общему знаменателю дроби и .
Общий знаменатель — 24. Дополнительные множители, соответственно, — 2 и 3.
Иногда бывает трудно подобрать устно наименьшее общее кратное для знаменателей данных дробей. Тогда общий знаменатель и дополнительные множители находят с помощью разложения на простые множители.
Привести к общему знаменателю дроби и .
Разложим числа 60 и 168 на простые множители. Выпишем разложение числа 60 и добавим недостающие множители 2 и 7 из второго разложения. Умножим 60 на 14 и получим общий знаменатель 840. Дополнительный множитель для первой дроби — это 14.
Дополнительный множитель для второй дроби — 5. Приведем дроби к общему знаменателю 840.
Список литературы
1. Виленкин Н.Я., Жохов В.И., Чесноков А.С. и др. Математика 6. — М.: Мнемозина, 2012.
2. Мерзляк А.Г., Полонский В.В., Якир М.С. Математика 6 класс. — Гимназия, 2006.
3. Депман И.Я., Виленкин Н.Я. За страницами учебника математики. — Просвещение, 1989.
4. Рурукин А.Н., Чайковский И.В. Задания по курсу математика 5-6 класс. — ЗШ МИФИ, 2011.
5. Рурукин А.Н., Сочилов С.В., Чайковский К.Г. Математика 5-6. Пособие для учащихся 6-х классов заочной школы МИФИ. — ЗШ МИФИ, 2011.
6. Шеврин Л.Н., Гейн А.Г., Коряков И.О. и др. Математика: Учебник-собеседник для 5-6 классов средней школы. Библиотека учителя математики. — Просвещение, 1989.
Можно скачать книги, указанные в п.1.2. данного урока.
Домашнее задание
Виленкин Н.Я., Жохов В.И., Чесноков А.С. и др. Математика 6. — М.: Мнемозина, 2012. (ссылка см. 1.2)
Домашнее задание: №297, №298, №300.
Другие задания: №270, №290
В данном материале мы разберем, как правильно приводить дроби к новому знаменателю, что такое дополнительный множитель и как его найти. После этого сформулируем основное правило приведения дробей к новым знаменателям и проиллюстрируем его примерами задач.
Понятие приведения дроби к другому знаменателю
Вспомним основное свойство дроби. Согласно ему, обыкновенная дробь a b (где a и b – любые числа) имеет бесконечное количество дробей, которые равны ей. Такие дроби можно получить, умножив числитель и знаменатель на одинаковое число m (натуральное). Иными словами, все обыкновенные дроби могут быть заменены другими вида a · m b · m . Это и есть приведение исходного значения к дроби с нужным знаменателем.
Привести дробь к другому знаменателю можно, умножив ее числитель и знаменатель на любое натуральное число. Главное условие – множитель должен быть одинаков для обоих частей дроби. В итоге получится дробь, равная исходной.
Проиллюстрируем это примером.
Пример 1
Привести дробь 11 25 к новому знаменателю.
Решение
Возьмем произвольное натуральное число 4 и умножим обе части исходной дроби на него. Считаем: 11 · 4 = 44 и 25 · 4 = 100 . В итоге получилась дробь 44 100 .
Все подсчеты можно записать в таком виде: 11 25 = 11 · 4 25 · 4 = 44 100
Выходит, любую дробь можно привести к огромному количеству разных знаменателей. Вместо четверки мы могли бы взять другое натуральное число и получить еще одну дробь, эквивалентную исходной.
Но не любое число может стать знаменателем новой дроби. Так, для a b в знаменателе могут стоять только числа b · m , кратные числу b . Вспомните основные понятия деления – кратные числа и делители. Если число не кратно b , но делителем новой дроби оно быть не может. Поясним нашу мысль примером решения задачи.
Пример 2
Вычислить, возможно ли приведение дроби 5 9 к знаменателям 54 и 21 .
Решение
54 кратно девятке, которая стоит в знаменателе новой дроби (т.
е. 54 можно разделить на 9). Значит, такое приведение возможно. А 21 мы разделить на 9 не можем, поэтому такое действие для данной дроби выполнить нельзя.
Понятие дополнительного множителя
Сформулируем, что такое дополнительный множитель.
Определение 1
Дополнительный множитель представляет собой такое натуральное число, на которое умножают обе части дроби для приведения ее к новому знаменателю.
Т.е. когда мы выполняем это действие с дробью, мы берем для нее дополнительный множитель. Например, для приведения дроби 7 10 к виду 21 30 нам потребуется дополнительный множитель 3 . А получить дробь 15 40 из 3 8 можно с помощью множителя 5 .
Соответственно, если мы знаем знаменатель, к которому необходимо привести дробь, то мы можем вычислить для нее и дополнительный множитель. Разберем, как это сделать.
У нас есть дробь a b , которую можно привести к некоторому знаменателю c ; вычислим дополнительный множитель m . Нам надо произвести умножение знаменателя исходной дроби на m .
У нас получится b · m , а по условию задачи b · m = c . Вспомним, как связаны между собой умножение и деление. Эта связь подскажет нам следующий вывод: дополнительный множитель есть не что иное, как частное от деления c на b , иначе говоря, m = c: b .
Таким образом, для нахождения дополнительного множителя нам нужно разделить требуемый знаменатель на исходный.
Пример 3
Найдите дополнительный множитель, с помощью которого дробь 17 4 была приведена к знаменателю 124 .
Решение
Используя правило выше, мы просто разделим 124 на знаменатель первоначальной дроби – четверку.
Считаем: 124: 4 = 31 .
Выполнять расчеты такого типа часто требуется при приведении дробей к общему знаменателю.
Правило приведения дробей к указанному знаменателю
Перейдем к определению основного правила, с помощью которого можно привести дроби к указанному знаменателю. Итак,
Определение 2
Для приведения дроби к указанному знаменателю нужно:
- определить дополнительный множитель;
- умножить на него и числитель, и знаменатель исходной дроби.
Как применить это правило на практике? Приведем пример решения задачи.
Пример 4
Выполните приведение дроби 7 16 к знаменателю 336 .
Решение
Начнем с вычисления дополнительного множителя. Разделим: 336: 16 = 21 .
Полученный ответ умножаем на обе части исходной дроби: 7 16 = 7 · 21 16 · 21 = 147 336 . Так мы привели исходную дробь к нужному знаменателю 336 .
Ответ: 7 16 = 147 336 .
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Как привести алгебраические (рациональные) дроби к общему знаменателю?
1) Если в знаменателях дробей стоят многочлены, нужно попытаться одним из известных способов.
2) Наименьший общий знаменатель (НОЗ) состоит из всех множителей, взятых в наибольшей степени.
Наименьший общий знаменатель для чисел устно ищем как наименьшее число, которое делится на остальные числа.
3) Чтобы найти дополнительный множитель к каждой дроби, надо новый знаменатель разделить на старый.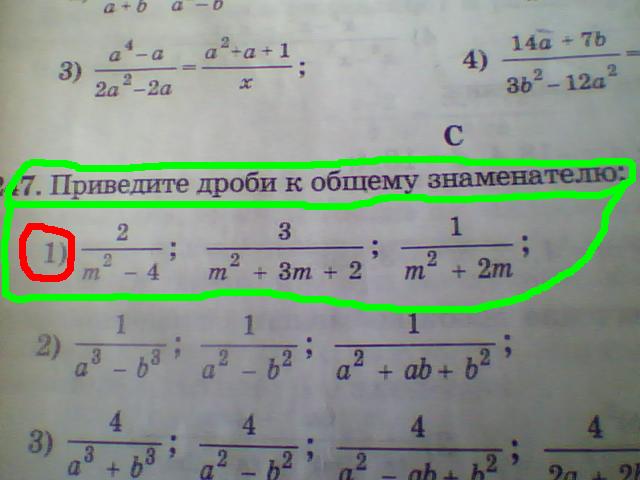
4) Числитель и знаменатель первоначальной дроби умножаем на дополнительный множитель.
Рассмотрим примеры приведения алгебраических дробей к общему знаменателю.
Чтобы найти общий знаменатель для чисел, выбираем большее число и проверяем, делится ли оно на меньшее. 15 на 9 не делится. Умножаем 15 на 2 и проверяем, делится ли полученное число на 9. 30 на 9 не делится. Умножаем 15 на 3 и проверяем, делится ли полученное число на 9. 45 на 9 делится, значит, общий знаменатель для чисел равен 45.
Наименьший общий знаменатель состоит из всех множителей, взятых в наибольшей степени. Таким образом, общий знаменатель данных дробей равен 45 bc (буквы принято записывать в алфавитном порядке).
Чтобы найти дополнительный множитель к каждой дроби, надо новый знаменатель разделить на старый. 45bc:(15b)=3c, 45bc:(9c)=5b. Умножаем числитель и знаменатель каждой дроби на дополнительный множитель:
Сначала ищем общий знаменатель для чисел: 8 на 6 не делится, 8∙2=16 на 6 не делится, 8∙3=24 на 6 делится.
Каждую из переменных нужно включить в общий знаменатель один раз. Из степеней берем степень с большим показателем.
Таким образом, общий знаменатель данных дробей равен 24a³bc.
Чтобы найти дополнительный множитель к каждой дроби, нужно новый знаменатель разделить на старый: 24a³bc:(6a³c)=4b, 24a³bc:(8a²bc)=3a.
Дополнительный множитель умножаем на числитель и знаменатель:
Многочлены, стоящие в знаменателях данных дробей, нужно . В знаменателе первой дроби — полный квадрат разности: x²-18x+81=(x-9)²; в знаменателе второй — разность квадратов: x²-81=(x-9)(x+9):
Общий знаменатель состоит из всех множителей, взятых в наибольшей степени, то есть равен (x-9)²(x+9). Находим дополнительные множители и умножаем их на числитель и знаменатель каждой дроби:
У дробей бывают различные или одинаковые знаменатели. Одинаковый знаменатель или по-другому называют общий знаменатель у дроби. Пример общего знаменателя:
\(\frac{17}{5}, \frac{1}{5}\)
Пример разных знаменателей у дробей:
\(\frac{8}{3}, \frac{2}{13}\)
Как привести к общему знаменателю дроби?
У первой дроби знаменатель равен 3, у второй равен 13.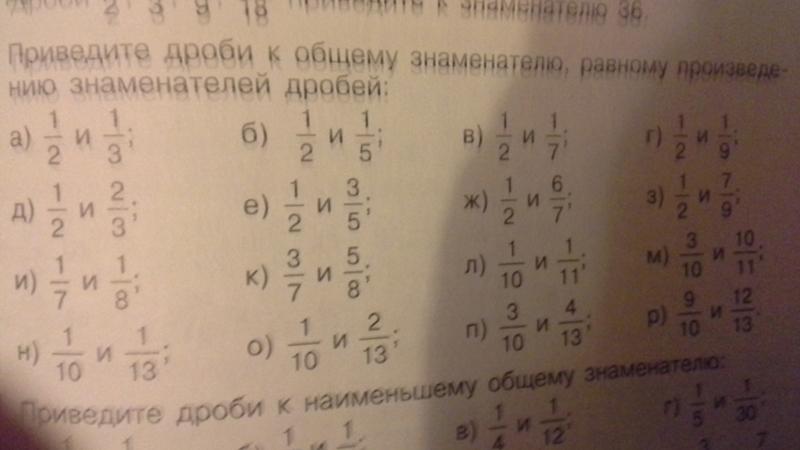
Нужно найти такое число, чтобы делилось и на 3 и на 13. Это число 39.
Первую дробь нужно умножить на дополнительный множитель 13. Чтобы дробь не изменилась умножаем обязательно и числитель на 13 и знаменатель.
\(\frac{8}{3} = \frac{8 \times \color{red} {13}}{3 \times \color{red} {13}} = \frac{104}{39}\)
Вторую дробь умножаем на дополнительный множитель 3.
\(\frac{2}{13} = \frac{2 \times \color{red} {3}}{13 \times \color{red} {3}} = \frac{6}{39}\)
Мы привели к общему знаменателю дроби:
\(\frac{8}{3} = \frac{104}{39}, \frac{2}{13} = \frac{6}{39}\)
Наименьший общий знаменатель.
Рассмотрим еще пример:
Приведем дроби \(\frac{5}{8}\) и \(\frac{7}{12}\) к общему знаменателю.
Общий знаменатель для чисел 8 и 12 могут быть числа 24, 48, 96, 120, …, принято выбирать наименьший общий знаменатель в нашем случае это число 24.
Наименьший общий знаменатель – это наименьшее число, на которое делиться знаменатель первой и второй дроби.
Как найти наименьший общий знаменатель?
Методом перебора чисел, на которое делиться знаменатель первой и второй дроби и выбрать из них самое наименьшее.
Нам нужно дробь со знаменателем 8 умножить на 3, а дробь со знаменателем 12 умножить на 2.
\(\begin{align}&\frac{5}{8} = \frac{5 \times \color{red} {3}}{8 \times \color{red} {3}} = \frac{15}{24}\\\\&\frac{7}{12} = \frac{7 \times \color{red} {2}}{12 \times \color{red} {2}} = \frac{14}{24}\\\\ \end{align}\)
Если у вас сразу не получиться привести дроби к наименьшему общему знаменателю в этом ничего страшного нет, в дальнейшем решая пример вам может быть придется полученный ответ
Общей знаменатель можно найти для любых двух дробей это может быть произведение знаменателей этих дробей.
Например:
Приведите дроби \(\frac{1}{4}\) и \(\frac{9}{16}\) к наименьшему общему знаменателю.
Самый простой способ найти общий знаменатель – это произведение знаменателей 4⋅16=64. Число 64 это не наименьший общий знаменатель. По заданию нужно найти именно наименьший общий знаменатель. Поэтому ищем дальше. Нам нужно число, которое делиться и на 4, и на 16, это число 16. Приведем к общему знаменателю дроби, умножим дробь со знаменателем 4 на 4, а дробь со знаменателем 16 на единицу. Получим:
\(\begin{align}&\frac{1}{4} = \frac{1 \times \color{red} {4}}{4 \times \color{red} {4}} = \frac{4}{16}\\\\&\frac{9}{16} = \frac{9 \times \color{red} {1}}{16 \times \color{red} {1}} = \frac{9}{16}\\\\ \end{align}\)
Какой общий знаменатель у чисел 6 и 8?
Таким образом, наше наименьшее общее кратное 8 и 6, которое также является наименьшим общим знаменателем этих двух дробей, будет 24 .
Запрос на удаление |
Посмотреть полный ответ на khanacademy.org
Какой наименьший общий знаменатель у 6 и 8?
Число 24 является LCM 6 и 8.
Запрос на удаление |
Посмотреть полный ответ на byjus. com
Каковы общие кратные чисел 6 и 8?
Таким образом, первые три общих кратных 6 и 8 = 24, 48, 72.
Запрос на удаление |
Посмотреть полный ответ на byjus.com
Какое наименьшее число 6 и 8?
Часто задаваемые вопросы по НОК чисел 6 и 8
НОК чисел 6 и 8 равно 24. Чтобы найти наименьшее общее кратное (НОК) чисел 6 и 8, нам нужно найти кратные 6 и 8 (кратные 6 = 6, 12 , 18, 24; кратные 8 = 8, 16, 24, 32) и выберите наименьшее кратное, которое точно делится на 6 и 8, то есть 24.
Запрос на удаление |
Посмотреть полный ответ на cuemath.com
Как мне найти общий знаменатель?
Мы можем получить общие знаменатели, умножив числитель (вверху) и знаменатель (внизу) на одну и ту же сумму.
Запрос на удаление |
Полный ответ см. на сайте splashlearn.com
LCM и GCF 6 и 8
Каков общий знаменатель 6 и 9?
LCM 6 и 918.
Запрос на удаление |
Посмотреть полный ответ на byjus.com
Почему вы находите общий знаменатель?
Для того, чтобы сложить или вычесть одну дробь из другой, они должны иметь общий знаменатель, или одинаковый знаменатель. Это потому, что невозможно сложить две дроби, имеющие разное количество частей.
Запрос на удаление |
Посмотреть полный ответ на сайте Study.com
Каков наибольший общий делитель чисел 6 и 8?
HCF 6 и 8 равен 2. Чтобы вычислить наибольший общий делитель 6 и 8, нам нужно разложить каждое число на множители (множители 6 = 1, 2, 3, 6 и множители 8 = 1, 2, 4, 8). ) и выберите наибольший множитель, который точно делит и 6, и 8. то есть 2.
|
Посмотреть полный ответ на byjus.com
Каковы LCM и GCF 6 и 8?
Пример 1: Найдите НОД чисел 6 и 8, если их НОК равен 24. Следовательно, наибольший общий делитель чисел 6 и 8 равен 2. Пример 2: Для двух чисел НОД = 2 и НОК = 24.
Запрос на удаление |
Посмотреть полный ответ на cuemath.com
Имеют ли числа 6 и 8 общие делители?
Следовательно, общие делители чисел 6 и 8 равны 1 и 2.
Запрос на удаление |
Посмотреть полный ответ на byjus.com
Как быстрее всего найти общий знаменатель?
Самый простой способ найти общий знаменатель пары дробей — умножить числитель и знаменатель одной дроби на знаменатель другой.
|
Посмотреть полный ответ на quickanddirtytips.com
Каков общий знаменатель для 2 и 4?
НОК 2 и 4 равно 4. НОК любых двух целых чисел в математике — это значение, которое без остатка делится на два значения. Наименьшее число среди всех общих кратных 2 и 4 — это НОК 2 и 4. (2, 4, 6, 8, 10,… ) и (4, 8, 12, 16,… ) — первые несколько кратных 2 и 4 соответственно.
Запрос на удаление |
Посмотреть полный ответ на byjus.com
Что является примером общего знаменателя?
Дроби, имеющие одинаковые знаменатели, такие знаменатели называются общими знаменателями. Рассмотрим следующие примеры: 1/2 + 1/2 = 1 и 3/4 + 1/4 = 1. В обоих случаях знаменатели у дробей общие, поэтому вычислить ответ несложно.
Запрос на удаление |
Посмотреть полный ответ на cuemath. com
Что такое знаменатель числа 6?
Знаменатель – это нижнее число дроби.
Значит, в дроби 3/8 знаменатель равен 8. В дроби 5/6 знаменатель равен 6.
Запрос на удаление |
Посмотреть полный ответ на theschoolrun.com
Каковы общие знаменатели чисел 6 и 7?
Ответ на этот вопрос 42. LCM 6 и 7 с использованием различных методов показаны в этой статье для справки. НОК двух ненулевых целых чисел, 6 и 7, — это наименьшее натуральное число 42, которое без остатка делится как на 6, так и на 7.
Запрос на удаление |
Посмотреть полный ответ на byjus.com
Каковы общие знаменатели чисел 4 и 7?
Что такое LCM 4 и 7? Ответ на этот вопрос 28.
Запрос на удаление |
Посмотреть полный ответ на byjus. com
Каковы общие знаменатели чисел 4 и 9?
LCM 4 и 9 равно 36.
Запрос на удаление |
Посмотреть полный ответ на byjus.com
Каков первый шаг в поиске общего знаменателя?
Шаг 1: Найдите наименьший общий знаменатель. Кратные 6: 6, 12, 18, 24 и т. д. Кратные 9: 9, 18, 27 и т. д. Наименьшее число, на которое и 6, и 9 делятся без остатка, равно 18.
Запрос на удаление |
Посмотреть полный ответ на content.byui.edu
Что такое общий знаменатель дроби?
Что такое общий знаменатель? Когда знаменатели двух или более дробей совпадают, они являются общими знаменателями.
Запрос на удаление |
Посмотреть полный ответ на mathsisfun.com
Какой общий знаменатель у 6 и 4?
LCM 4 и 6 равно 12.
|
Посмотреть полный ответ на byjus.com
Какой общий знаменатель у чисел 3 и 8?
Что такое LCM 3 и 8? Ответ на этот вопрос 24.
Запрос на удаление |
Посмотреть полный ответ на byjus.com
← Предыдущий вопрос
Бака какой национальности?
Следующий вопрос →
Почему в конце концов Дейзи остается с Томом?
Наименьшее общее кратное. Сравнение дробей — Полный курс арифметики
| Пример 6. Что больше, | 1 2 | или | 3 8 | ? |
Ответить . Приведите общий знаменатель. Выберите LCM из 2 и 8, что само по себе равно 8. Пример 2 выше.
| Будем менять | 1 2 | в эквивалентную дробь со знаменателем 8: |
| 1 2 | = | 4 8 | . |
| Знаменатели теперь одинаковы, и мы можем сравнить | 4 8 | с | 3 8 | . |
Видим:
| 4 8 | больше, чем | 3 8 | . |
То есть
| 1 2 | больше, чем | 3 8 | . |
| Пример 7. Что больше, | 3 4 | или | 25 32 | ? |
Ответить . Снова сделаем знаменатели одинаковыми, а затем сравним числители. В качестве общего знаменателя мы выберем НОК 4 и 32, что само по себе равно 32.
| Мы вышлем | 3 4 | со знаменателем 32. | При умножении обоих |
терминов по 8,
| 3 4 | = | 24 32 | . |
| Теперь мы сравниваем | 3 4 | или |
| 24 32 | с | 25 32 | . |
| 25 больше, чем 24; поэтому | 25 32 | больше, чем | 3 4 | . |
| Пример 8. Что больше, | 5 6 | или | 7 9 | ? |
Ответить . В качестве общего знаменателя выберите НОК из 6 и 9.
Ответить . Выберите 18.
| 5 6 | = | 15 18 | , | 7 9 | = | 14 18 | . |
| Чтобы изменить | 5 6 | , мы умножили оба члена на 3. Чтобы изменить | 7 9 | , мы |
умножил оба члена на 2.
Мы выбираем общее кратное знаменателей, потому что мы меняем знаменатели, умножая их
| Теперь 15 больше, чем 14. Следовательно, | 5 6 | больше, чем | 7 9 | . |
Сложение дробей (как мы увидим в Уроке 25) требует той же техники, что и их сравнение, потому что знаменатели — единицы измерения — должны быть одинаковыми. Например,
| 5 6 | + | 7 9 | = | 15 18 | + | 14 18 |
| = | 29 18 | . | ||||
В следующем разделе, вопрос 4, мы увидим, как сравнивать дроби путем перекрестного умножения.