Формулы площади треугольника 8 класс онлайн-подготовка на Ростелеком Лицей
Различные формулы площади треугольника
Площадь – одна из важных характеристик фигуры на плоскости. Можно сказать так: чем больше краски нужно для того, чтобы покрасить фигуру, тем больше ее площадь (см. рис. 1).
Рис. 1. Чем больше краски нужно для того, чтобы покрасить фигуру, тем больше ее площадь
Любое измерение – это сравнение с эталоном. Для площади в качестве эталона выбрали площадь квадрата со стороной (она равна кв. ед.) (см. рис. 2). Поэтому раньше вычисление площади называлось квадратурой.
Рис. 2. Площадь квадрата со стороной м равна
Понятно, что вычислять площадь, каждый раз разбивая фигуру на квадраты, неудобно (да и не всегда возможно). Поэтому для различных типов фигур были выведены формулы для вычисления площади (см. рис. 3).
Рис. 3. Для различных типов фигур выведены формулы для вычисления площади
Поскольку треугольник – базовая и одна из самых важных фигур, то для него было получено сразу несколько различных формул. Их основное отличие – элементы треугольника, которые в них используются.
Их основное отличие – элементы треугольника, которые в них используются.
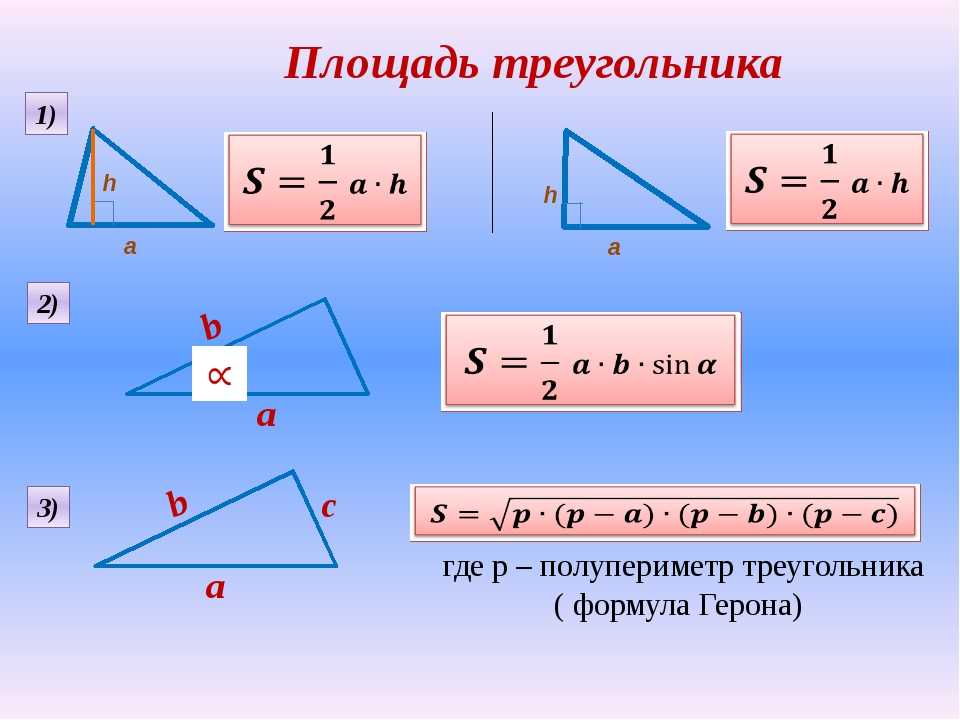
Так, помимо «классической» формулы – через высоту и основание (см. рис. 4):
Рис. 4. Произвольный треугольник со сторонами и высотой , проведенной к стороне
на этом уроке мы будем рассматривать:
1. вычисление площади треугольника по двум сторонам и углу между ними (см. рис. 5):
Рис. 5. Произвольный треугольник со сторонами и углом , лежащим между сторонами и
2. по трем сторонам – формула Герона (см. рис. 6):
где – полупериметр:
Рис. 6. Произвольный треугольник со сторонами
3. с использованием радиуса описанной окружности (см. рис. 7):
Рис. 7. Окружность радиуса описана около произвольного треугольника со сторонами
4. с использованием радиуса вписанной окружности (см. рис. 8):
рис. 8):
где – полупериметр:
Рис. 8. Произвольный треугольник со сторонами описан около окружности радиуса
Единицы измерения
Обратите внимание, что в большинстве задач, с которыми вы будете сталкиваться на уроках математики, длины отрезков, площади фигур и т. д. будут даваться без единиц измерения, например: длины сторон треугольника равны . Обычно подразумевают «условные единицы». Но что это значит? Можно дать эквивалентную формулировку: длины стороны треугольника равны , и , где – это сколько-то сантиметров (метров, километров, ярдов, …) (см. рис. 9).
Рис. 9. Прямоугольный треугольник со сторонами , и , где – единица измерения (см, м, км, ярды и т. д.)
Тогда любая длина в рамках данной задачи будет пропорциональна этой условной единице . Например, высота такого треугольника, проведенная к гипотенузе, будет равна усл. ед., или см (м, км, …) (см. рис. 10).
Рис. 10. Прямоугольный треугольник со сторонами , и и высотой см (м, км, …), проведенной к гипотенузе
Таким образом, решив задачу для условных единиц, мы можем использовать решение для любых единиц измерения, используя нужный нам . То же касается и площади – у данного треугольника она будет равна кв. ед., или (, , …).
То же касается и площади – у данного треугольника она будет равна кв. ед., или (, , …).
При этом надо помнить: если в условии все же указаны единицы измерения (например, все длины даны в сантиметрах), то, во-первых, надо следить, чтобы все величины при вычислениях были с одинаковыми единицами измерения (чтобы не умножить метры на сантиметры), а во-вторых, не забывать указывать получившиеся единицы для найденных величин.
Формула площади произвольного треугольника
Начнем изучение формул для вычисления площади треугольника с той, которую мы вывели самой первой:
Пожалуй, это наиболее часто используемая формула.
Вспомним, как мы вывели эту формулу. Вспомним, что площадь прямоугольника со сторонами и равна (см. рис. 11):
Рис. 11. Прямоугольник со сторонами и
Проведем диагональ, получим два прямоугольных треугольника. Они равны: катеты равны, как противоположные стороны прямоугольника (см. рис. 12). Значит, их площади одинаковы.
рис. 12). Значит, их площади одинаковы.
Рис. 12. Если провести диагональ в прямоугольнике, то получится два равных прямоугольных треугольника
Получаем, что площадь прямоугольного треугольника с катетами и равна:
Для произвольного треугольника можно рассмотреть два случая. Если высота проведена из вершины острого угла (см. рис. 13), то треугольник делится на два прямоугольных, для каждого из которых верна формула площади:
Рис. 13. Произвольный остроугольный треугольник, где проведенная к стороне высота делит на отрезки, равные и
Если же высота проведена из вершины тупого угла, то она проходит вне треугольника (см. рис. 14). Тогда площадь исходного треугольника не сумма, а разность площадей двух прямоугольных:
Рис. 14. Произвольный тупоугольный треугольник, где проведенная к стороне высота проходит вне треугольника
Итак, площадь произвольного треугольника можно вычислить по формуле (см. рис. 15):
15):
где – длина любой из сторон треугольника, а – длина высоты, проведенной к этой стороне.
Рис. 15. Произвольный треугольник с высотой , проведенной к стороне
Что нам дает эта формула?
1. С ее помощью можно вычислить площадь треугольника, зная длины стороны и высоты, которая к ней проведена. Например, сторона равна , высота . Площадь треугольника равна :
2. Два треугольника с одинаковыми основаниями и высотой имеют равные площади.
Возьмем два параллельных рельса, расстояние между которыми равно . На одном рельсе отметим отрезок длиной . На втором рельсе возьмем точку и соединим с концами отрезка. Получим треугольник (см. рис. 16). Высота его равна расстоянию между рельсами, т. е. , а основание равно . Площадь равна .
Рис. 16. На одном из параллельных рельсов, расстояние между которыми равно , отметили отрезок длиной , а на втором – взяли точку и соединили с концами отрезка
Начнем двигать точку по верхнему рельсу (см. рис. 17). Треугольник начинает растягиваться и менять форму. Но длины основания и высоты у него не меняются. Следовательно, не меняется и площадь.
рис. 17). Треугольник начинает растягиваться и менять форму. Но длины основания и высоты у него не меняются. Следовательно, не меняется и площадь.
Рис. 17. При движении точки по верхнему рельсу треугольник измененной формы имеет ту же площадь, т. к. длины основания и высоты остаются теми же
Этот факт мы использовали, когда доказывали, что медиана делит треугольник на два равновеликих треугольника. Действительно, у этих треугольников общая высота, а основания равны, так как основание медианы – середина стороны (см. рис. 18).
Рис. 18. Медиана делит треугольник на два равновеликих треугольника
3. Использовать эту формулу можно для вычисления длин сторон или высот, даже если вычислять площадь и не требуется.
Пример 1. В треугольнике сторона , сторона , высота . Найти высоту (см. рис. 19).
Рис. 19. Иллюстрация к примеру 1
Решение.
Приравняем площади треугольника, вычисленные для сторон и :
Выразим :
Ответ: .
Фактически мы здесь можем использовать не формулу для вычисления площади треугольника, а следствие из нее:
где – высоты, проведенные к соответствующим сторонам.
Пример 2. В треугольнике длины сторон равны: , , . Найти высоту, проведенную к большей стороне (см. рис. 20).
Рис. 20. Иллюстрация к примеру 2
Решение.
Заметим, что это египетский треугольник. Его стороны подчиняются соотношению:
Следовательно, по обратной теореме Пифагора, он прямоугольный (см. рис. 21). Большая сторона является гипотенузой.
Рис. 21. Иллюстрация к примеру 2
С одной стороны, площадь прямоугольного треугольника можно найти как полупроизведение катетов:
С другой – как полупроизведение гипотенузы на высоту, проведенную из прямого угла:
Приравнивая, получаем:
Ответ: .
Формула площади равностороннего треугольника
Используем формулу для выведения формулы площади правильного треугольника. Поскольку правильный треугольник задается одним элементом – длиной своей стороны, то логично, что и его площадь должна выражаться через сторону.
Поскольку правильный треугольник задается одним элементом – длиной своей стороны, то логично, что и его площадь должна выражаться через сторону.
Опустим высоту (она является биссектрисой и медианой) (см. рис. 22).
Рис. 22. Равносторонний треугольник со стороной и высотой , являющейся и биссектрисой, и медианой
Тогда:
Используем теорему Пифагора для треугольника (см. рис. 23).
Рис. 23. Рассматриваемый прямоугольный треугольник
Получаем:
Откуда:
Тогда площадь равностороннего треугольника равна:
Эта формула может встречаться довольно часто, но запоминать ее необязательно – при необходимости ее всегда можно вывести.
Площадь треугольника через две стороны и угол между ними
Высота треугольника нам будет известна далеко не всегда. Гораздо чаще у нас будут возникать задачи, в которых площадь надо найти, зная стороны и углы треугольника.
Рассмотрим треугольник со сторонами . Проведем высоту к стороне (см. рис. 24).
Рис. 24. Произвольный треугольник со сторонами , высотой и углом между сторонами и
Нам известна формула площади:
Рассмотрим левый прямоугольный треугольник (см. рис. 25):
Рис. 25. Рассматриваемый левый прямоугольный треугольник
По определению синуса (отношение противолежащего катета к гипотенузе):
Откуда:
Тогда:
Обратите внимание, что в полученной формуле длина высоты нам уже не нужна. Теперь, чтобы вычислить площадь треугольника, достаточно знать две любые стороны и угол (синус угла) между ними.
Например, вычислим площадь треугольника со сторонами и и углом между ними. Воспользуемся полученной формулой:
Получаем:
Рассмотрим еще один пример.
Пример 3. Площадь равнобедренного треугольника равна , а угол при вершине (см. рис. 26). Найти его боковые стороны.
26). Найти его боковые стороны.
Рис. 26. Иллюстрация к примеру 3
Решение.
Раз дана площадь и угол, то имеет смысл попробовать использовать только что полученную формулу (при этом, раз треугольник равнобедренный, то стороны, образующие угол , равны между собой):
Ответ: .
Формула площади треугольника через радиус описанной окружности
Вспомним еще раз формулу площади треугольника через синус угла:
Была у нас еще одна формула, где фигурировал синус и длина стороны – это теорема синусов (см. рис. 27):
Рис. 27. Окружность радиуса описана около произвольного треугольника со сторонами и углом между сторонами и
Можем выразить синус угла через длину стороны и радиус описанной окружности:
Подставим полученное выражение в формулу для площади:
Таким образом, мы получили еще одну формулу площади треугольника. На этот раз через радиус описанной окружности.
На самом деле, полученная формула площади избыточная. Чтобы по этой формуле найти площадь треугольника, нужно знать элемента: длины всех трех сторон, да еще и радиус описанной окружности. Хотя третий признак равенства треугольников говорит нам, что треугольник однозначно задается тремя своими сторонами, поэтому его площадь мы должны уметь находить по трем сторонам. И такая формула для вычисления площади действительно есть – она называется формулой Герона. К ней мы сейчас перейдем, а пока обсудим, зачем же нужна полученная формула.
Дело в том, что она чаще используется не в таком виде:
а в виде:
т. е. для вычисления радиуса описанной окружности.
Эту формулу удобно применять, если вам известны три стороны треугольника и нужно найти радиус описанной окружности. Можно, конечно, использовать теорему синусов:
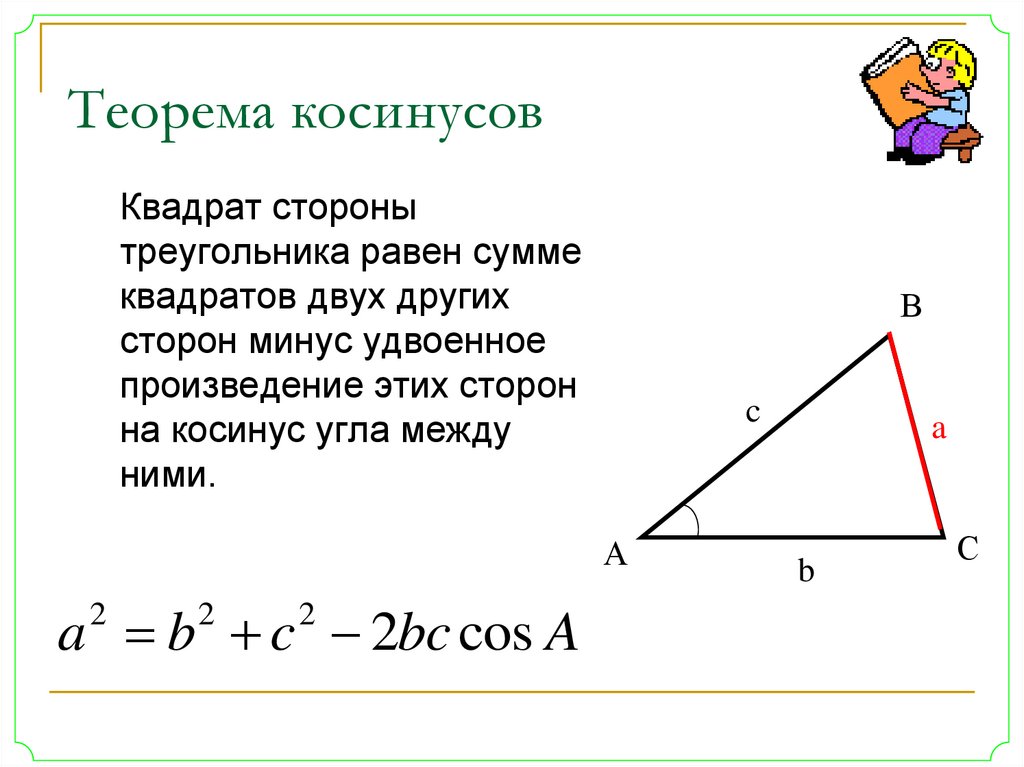
Но в этом случае нам потребуется найти синус одного из углов треугольника. Чтобы это сделать, придется выразить косинус из теоремы косинусов:
А затем, используя основное тригонометрическое тождество, найти синус:
Данная же формула позволяет не заниматься поиском углов – достаточно найти площадь треугольника через формулу Герона и подставить все значения в формулу .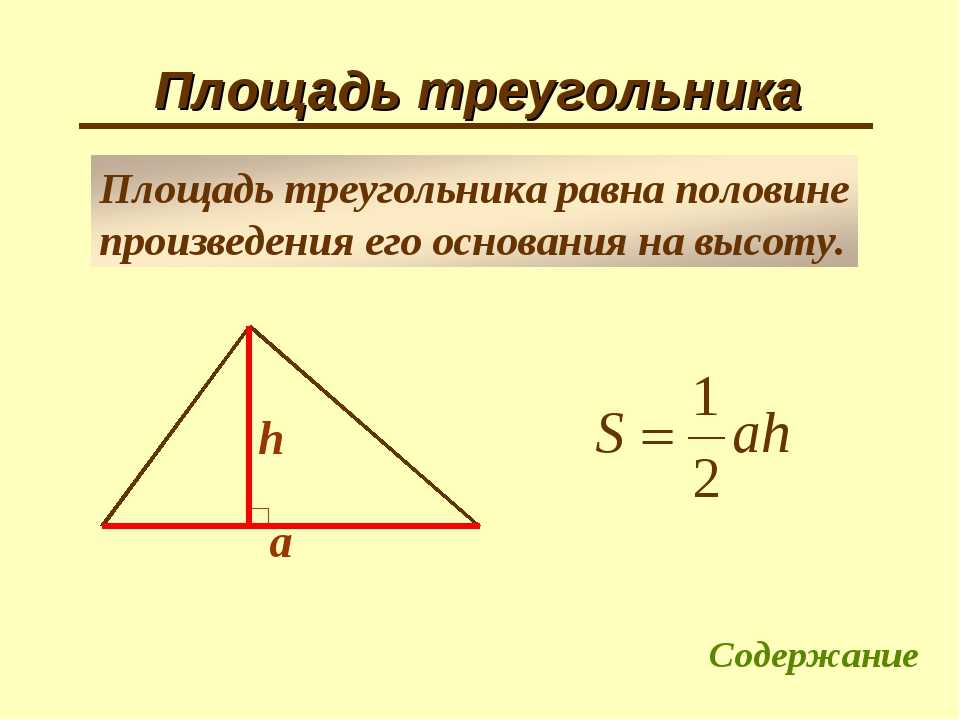
Два способа нахождения радиуса описанной окружности
Пример 1.
Пусть нам дан треугольник со сторонами . Найти радиус описанной окружности.
Решение.
Способ 1 (формула Герона).
Найдем его площадь, используя формулу Герона:
где – полупериметр треугольника:
Получаем:
Тогда:
Радиус описанной окружности равен:
Способ 2 (теоремы синусов и косинусов).
Попробуем теперь найти радиус описанной окружности данного треугольника без использования площади – используя теоремы синусов и косинусов. Найдем один из углов, используя теорему косинусов:
Откуда:
Используем основное тригонометрическое тождество, чтобы найти синус этого угла и воспользоваться теоремой синусов:
Обратите внимание: формально синус мог получиться и со знаком минус, но для углов треугольника синус может принимать только положительные значения.
Откуда:
Ответ: .
Конечно, это дело вкуса, но, кажется, что первый способ нахождения радиус описанной окружности гораздо менее трудоемкий.
Формула Герона
Итак, чтобы найти площадь треугольника, зная длины его сторон, удобно использовать формулу, которая называется формулой Герона (по фамилии ученого, который включил ее в свой труд «Метрика»):
где – это полупериметр:
Например, если стороны треугольника равны (см. рис. 28), то его площадь легко вычислить с использованием формулы Герона:
Рис. 28. Треугольник со сторонами
Использование этой теоремы, как вы видели, совсем не сложно. А вот доказательство достаточно длинное. С ним вы можете ознакомиться ниже.
Доказательство формулы Герона
Доказательство.
Рассмотрим треугольник со сторонами (см. рис. 29).
Рис. 29. Произвольный треугольник со сторонами и высотой , проведенной к стороне
У нас есть формула для площади треугольника:
Наша задача – выразить через .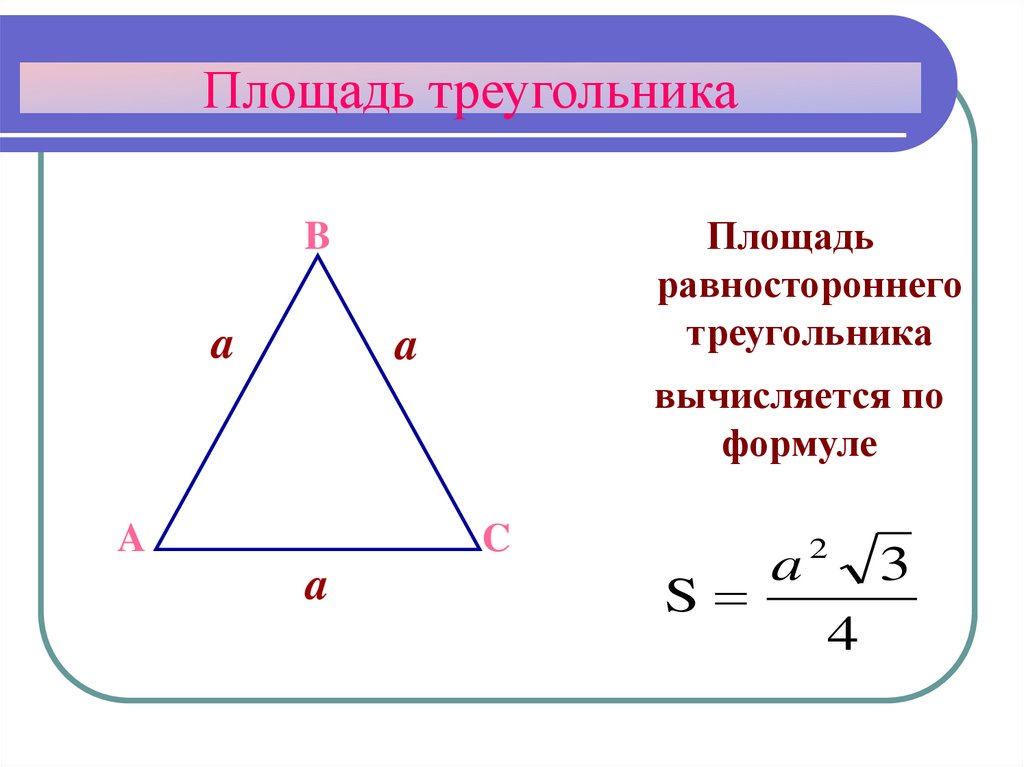 Обозначим для краткости (см. рис. 30):
Обозначим для краткости (см. рис. 30):
Рис. 30. Обозначения:
Высота является катетом и в левом, и в правом прямоугольных треугольниках. Используя теорему Пифагора для треугольников и , получаем:
Или:
Поскольку , то:
Откуда:
Теперь можем выразить из треугольника высоту через :
Заметим, что:
Получаем:
Откуда:
Осталось подставить в формулу для площади:
Доказано.
Пример 4. В треугольнике стороны равны . Найти радиус описанной окружности (см. рис. 31).
Рис. 31. Иллюстрация к примеру 4
Решение.
Зная три стороны и площадь треугольника, радиус описанной окружности можно найти из формулы:
А площадь, зная длины трех сторон, мы можем найти по формуле Герона:
Получаем:
Ответ: .
Формула площади треугольника через радиус вписанной окружности
Раз есть формула, связывающая площадь треугольника и радиус описанной окружности, должна быть и формула, связывающая площадь треугольника и радиус вписанной окружности.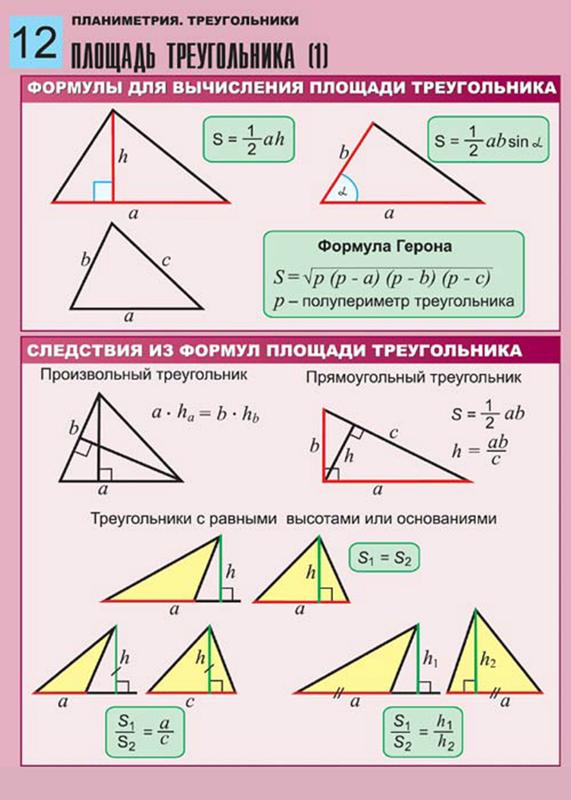
Мы доказали, что в любой треугольник можно вписать окружность. Если соединить центр этой окружности со всеми тремя вершинами, то исходный треугольник разобьется на три новых (мы уже доказывали, что эти три отрезка – части биссектрис соответствующих углов треугольника) (см. рис. 32).
Рис. 32. Отрезки, которые соединяют центр вписанной в треугольник окружности с тремя вершинами, – части биссектрис соответствующих углов треугольника
Во всех этих трех малых треугольниках высоты равны радиусу вписанной окружности.
Рис. 33. В трех полученных треугольниках высоты равны радиусу вписанной окружности
Применяя к каждому треугольнику формулу площади и складывая полученные выражения, имеем:
где – полупериметр:
Получили новую формулу площади – произведение полупериметра на радиус вписанной окружности:
Отметим несколько важных моментов: во-первых, эту формулу можно обобщить на случай любого описанного многоугольника. Попробуйте провести доказательство, например, для четырехугольника, используя точно такую же схему, как и для треугольника (см. рис. 34).
Попробуйте провести доказательство, например, для четырехугольника, используя точно такую же схему, как и для треугольника (см. рис. 34).
Рис. 34. В четырехугольник вписана окружность, ее центр соединен отрезками с четырьмя вершинами, а отрезки, в свою очередь, разбивают четырехугольник на четыре малых треугольника, высоты которых равны радиусу вписанной окружности
Во-вторых, в отличие от формулы с радиусом описанной окружности, эту формулу нельзя назвать избыточной. Конечно, чаще всего, чтобы найти полупериметр, нужно знать длины всех сторон треугольника, но формально для применения этой формулы знать длины всех трех сторон треугольника необязательно – достаточно знать именно полупериметр.
Наконец, эту формулу чаще используют именно для нахождения радиуса вписанной окружности (в других формулах он у нас не фигурировал, поэтому для нас это будет единственный способ):
Например, зная три стороны треугольника и используя формулу Герона для нахождения площади, несложно найти радиус вписанной окружности по этой формуле.
Пример 5. В равнобедренном треугольнике основание равно , а боковая сторона – . Найти радиус вписанной окружности.
Рис 35. Иллюстрация к примеру 5
Решение.
Итак,
Радиус вписанной окружности практически всегда мы будем искать по формуле:
Осталось найти площадь. В общем случае можно было бы воспользоваться формулой Герона (можете попробовать решить эту задачу таким способом и убедиться, что получится такой же ответ). Мы же «схитрим» и воспользуемся тем, что треугольник равнобедренный и высота, проведенная к основанию, является также биссектрисой и медианой (см. рис. 36).
Рис. 36. Иллюстрация к примеру 5
Поэтому несложно найти ее длину, используя теорему Пифагора:
Откуда:
Тогда площадь треугольника:
Получаем:
Ответ: .
Заключение
В завершение урока давайте посмотрим на все формулы сразу.
Первые три формулы используют элементы самого треугольника (стороны, углы, высоты). В частности, формула Герона позволяет нам находить площадь по трем сторонам треугольника. Формула с синусом – по двум сторонам и углу между ними. Если нам известна сторона и два угла, то можно применить теорему синусов, чтобы найти еще одну сторону, а дальше задача сводится к предыдущей – мы знаем уже две стороны и угол между ними. Оставшиеся две формулы мы чаще будем использовать не для нахождения площади треугольника, а для вычисления радиусов вписанной и описанной окружности.
В частности, формула Герона позволяет нам находить площадь по трем сторонам треугольника. Формула с синусом – по двум сторонам и углу между ними. Если нам известна сторона и два угла, то можно применить теорему синусов, чтобы найти еще одну сторону, а дальше задача сводится к предыдущей – мы знаем уже две стороны и угол между ними. Оставшиеся две формулы мы чаще будем использовать не для нахождения площади треугольника, а для вычисления радиусов вписанной и описанной окружности.
Нужно ли все их запоминать? Конечно, желательно, ведь каждая из них может быть полезна в той или иной задаче, в зависимости от исходных данных. Вместе с тем важно помнить: треугольник почти всегда однозначно задается любыми тремя своими элементами. Поэтому, используя различные свойства треугольника, а также теоремы синусов, косинусов, можно найти недостающие элементы треугольника и применить именно ту формулу, которую вы помните. Так, если вы не уверены в формуле Герона, то, используя теорему косинусов и основное тригонометрическое тождество, можете найти синус одного из углов и воспользоваться формулой с двумя сторонами и синусом угла между ними.
Список литературы
Александров А.Д., Вернер А.Л., Рыжик В.И. Геометрия, 8 класс. Учебник. – М.: «Просвещение», 2018.
Бутузов В.Ф., Кадомцев С.Б., Прасолов В.В./Под ред. Садовничего В.А. Геометрия, 8 класс. Учебник. – М.: «Просвещение», 2018.
Мерзляк А.Г., Полонский В.Б., Якир М.С., Геометрия, 8 класс. Учебник. – М.: издательский центр «ВЕНТАНА-ГРАФ», 2018.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
Интернет-портал yaklass.ru (Источник)
Интернет-портал 100formul.ru (Источник)
Интернет-портал ru.onlinemschool.com (Источник)
Домашнее задание
В треугольнике угол , , а высота делит сторону на отрезки , . Найти площадь треугольника и длину высоты, проведенной к стороне .
Найти площадь треугольника, две стороны которого равны и , а градусная мера угла между ними равна .
Найти радиус окружности, вписанной в равносторонний треугольник со стороной .
Вычислить площадь треугольника по формуле. Как рассчитать площадь треугольника
Инструкция
Стороны и углы считаются основными элементами а . Треугольник полностью определяется любой из следующих своих основных элементов: либо тремя сторонами, либо одной стороной и двумя углами, либо двумя сторонами и углом между ними. Для существования треугольника , задаваемого тремя сторонами a, b, c, необходимо и достаточно выполнение неравенств, называемых неравенствами треугольника :
a+b > c,
a+c > b,
b+c > a.
Для построения треугольника по трем сторонам a, b, c, необходимо из точки С отрезка СВ=a как из провести циркулем окружность радиусом b. Затем аналогичным образом провести из точки B окружность радиусом равным стороне c. Точка их пересечения A – третья вершина искомого треугольника ABC, где АВ=c, CB=a, CA=b — стороны треугольника . Задача имеет , если стороны a, b, c, удовлетворяют неравенствам треугольника указанным в шаге 1.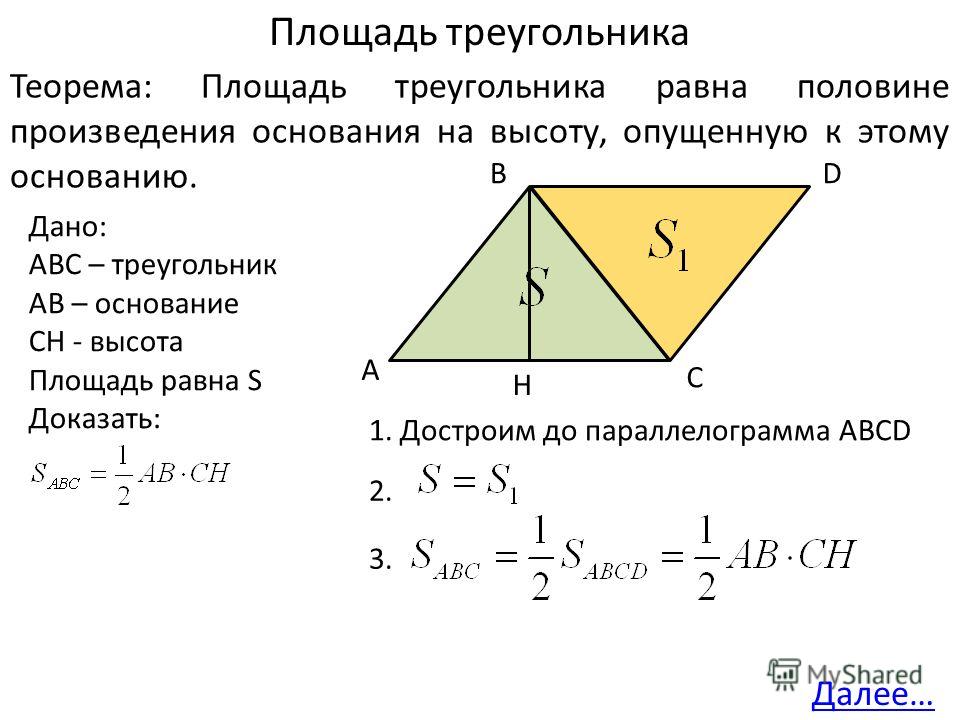
Если треугольник является прямоугольным, то есть один из его углов равен 90°, а стороны, его образующие, катетами, третья сторона гипотенузой. В данном случае площадь равняется произведению катетов, деленному на два.
S=ab/2
Чтобы найти площадь треугольника , можно воспользоваться одной из многочисленных формул. Формулу выбирайте в зависимости от того, какие данные уже известны.
Вам понадобится
- знание формул для нахождения площади треугольника
Инструкция
Если вы знаете величину одной из сторон и величину высоты, опущенной на эту сторону из противолежащего ей угла, то можно найти площадь по следующей : S = a*h/2, где S — площадь треугольника, a — одна из сторон треугольника, а h — высота, к стороне a.
Существует известная для определения площади треугольника, если известны три его стороны. Она формулой Герона. Для упрощения ее записи вводят промежуточную величину — полупериметр: p = (a+b+c)/2, где a, b, c — .
Предположим, что вам известна одна из сторон треугольника и три угла. Тогда легко найти площадь треугольника: S = a²sinα sinγ / (2sinβ), где β — угол, противолежащий стороне a, а α и γ — прилежащие к стороне углы.
Видео по теме
Обратите внимание
Самая общая формула, которая подходит для всех случаев — это формула Герона.
Источники:
Поиск площади треугольника — одна из самых распространенных задач школьной планиметрии. Знания трех сторон треугольника достаточно для определения площади любого треугольника. В частных случаях и равностороннего треугольников достаточно знать длины двух и одной стороны соответственно.
Вам понадобится
- длины сторон треугольников, формула Герона, теорема косинусов
Инструкция
Формула Герона для площади треугольника следующим образом: S = sqrt(p(p-a)(p-b)(p-c)). Если расписать полупериметр p, то получится: S = sqrt(((a+b+c)/2)((b+c-a)/2)((a+c-b)/2)((a+b-c)/2)) = (sqrt((a+b+c)(a+b-c)(a+c-b)(b+c-a)))/4.
Видео по теме
Для проведения ремонтных работ бывает необходимо измерить площадь стен. Так проще рассчитать необходимое количество краски или обоев. Для измерений лучше всего воспользоваться рулеткой или сантиметровой лентой. Замеры следует проводить уже после того, как стены были выровнены.
Вам понадобится
- -рулетка;
- -стремянка.
Инструкция
Чтобы посчитать площадь стен, вам необходимо знать точную высоту потолков, а также произвести замеры длины по полу. Делается это следующим образом: возьмите сантиметр, проложите его над плинтусом. Обычно сантиметра для всей длины не хватает, поэтому закрепите его в углу, затем размотайте на максимальную длину. В этой точке поставьте отметку карандашом, запишите полученный результат и дальнейшее измерение проводите тем же образом, начиная с последней точки замера.
Стандартная потолков в типовых — 2 метра 80 сантиметров, 3 метра и 3 метра 20 сантиметров, в зависимости от дома. Если дом был построен до 50-х годов, то, скорее всего, реальная высота несколько ниже указанной. Если вы вычисляете площадь для ремонтных работ, то небольшой запас не повредит — считайте, исходя из стандарта. Если все же необходимо знать реальную высоту — проведите замеры . Принцип аналогичен измерению длины, но потребуется стремянка.
Перемножьте полученные показатели — это и есть площадь вашей стены . Правда, при покрасочных работах или для необходимо вычесть
Учтите, что замеры длины и ширины комнаты проводить вдвоем, так легче зафиксировать сантиметр или рулетку и, соответственно, получить более точный результат. Проводите один и тот же замер несколько раз, чтобы убедиться в точности полученных цифр.
Видео по теме
Нахождение объема треугольника действительно нетривиальная задача. Дело в том, что треугольник — двухмерная фигура, т.е. он целиком лежит в одной плоскости, а это значит, что у него попросту нет объема. Разумеется нельзя найти то, чего не существует. Но не будем опускать руки! Можно принять следующее допущение — объем двухмерной фигуры, это ее площадь. Площадь треугольника мы и будем искать.
Вам понадобится
- лист бумаги, карандаш, линейка, калькулятор
Инструкция
Начертите на листе бумаги при помощи линейки и карандаша. Внимательно рассмотрев треугольник, вы сможете убедиться, что у него действительно нет , так как он нарисован на плоскости. Подпишите стороны треугольника: пусть одна сторона будет стороной «а», другая — стороной «b», и третья — стороной «c». Подпишите вершины треугольника буквами «А», «B» и «C».
Подпишите вершины треугольника буквами «А», «B» и «C».
Измерьте линейкой любую сторону треугольника и запишите получившийся результат. После этого восстановите перпендикуляр к измеренной стороне из противоположной ей вершины, такой перпендикуляр будет высотой треугольника. В случае, представленном на рисунке, перпендикуляр «h» восстановлен к стороне «c» из вершины «A». Измерьте получившуюся высоту линейкой и запишите результат измерения.
Может случиться, что вам будет сложно восстановить точный перпендикуляр. В этом случае вам следует воспользоваться другой формулой. Измерьте все стороны треугольника линейкой. После этого подсчитайте полупериметр треугольника «p», сложив получившиеся длины сторон и разделив их сумму пополам. Имея в своем распоряжении значение полупериметра, вы можете по формуле Герона. Для этого необходимо извлечь квадратный корень из следующего : p(p-a)(p-b)(p-c).
Вы получили искомую величину площади треугольника. Задача нахождения объема треугольника не решена, но как говорилось выше, объема не . Вы можете найти объем , которая по сути треугольником в трехмерном мире. Если представить, что наш первоначальный треугольник стал трехмерной пирамидой, то объем такой пирамиды будет произведению длины ее основания на полученную нами площадь треугольника.
Вы можете найти объем , которая по сути треугольником в трехмерном мире. Если представить, что наш первоначальный треугольник стал трехмерной пирамидой, то объем такой пирамиды будет произведению длины ее основания на полученную нами площадь треугольника.
Обратите внимание
Подсчеты будут тем точнее, чем тщательнее вы будете производить измерения
Источники:
- Калькулятор “Все во все” — портал по справочным величинам
- объем треугольника в 2019
Три точки, однозначно определяющие треугольник в Декартовой системе координат — это его вершины. Зная их положение относительно каждой из координатных осей можно вычислить любые параметры этой плоской фигуры, включая и ограничиваемую ее периметром площадь . Это можно сделать несколькими способами.
Инструкция
Используйте формулу Герона для расчета площади треугольника . В ней задействованы размеры трех сторон фигуры, поэтому вычисления начините с . Длина каждой стороны должна быть равна корню из суммы квадратов длин ее проекций на координатные оси.
Для упрощения расчетов введите вспомогательную переменную — полупериметр (Р). Из , что это половина суммы длин всех сторон: Р = ½*(AB+BC+AC) = ½*(√((X₁-X₂)² + (Y₁-Y₂)² + (Z₁-Z₂)²) + √((X₂-X₃)² + (Y₂-Y₃)² + (Z₂-Z₃)²) + √((X₁-X₃)² + (Y₁-Y₃)² + (Z₁-Z₃)²).
Ниже приведены формулы нахождения площади произвольного треугольника которые подойдут для нахождения площади любого треугольника, независимо от его свойств, углов или размеров. Формулы представлены в виде картинки, здесь же приведены пояснения по применению или обоснованию их правильности. Также на отдельном рисунке указаны соответствия буквенных обозначений в формулах и графических обозначений на чертеже.
Примечание . Если же треугольник обладает особыми свойствами (равнобедренный, прямоугольный, равносторонний), можно использовать формулы, приведенные ниже, а также дополнительно специальные, верные только для треугольников с данными свойствами, формулы:
- «Формулы площади равностороннего треугольника»
Формулы площади треугольника
Пояснения к формулам :
a, b, c — длины сторон треугольника, площадь которого мы хотим найти
r — радиус вписанной в треугольник окружности
R — радиус описанной вокруг треугольника окружности
h — высота треугольника, опущенная на сторону
p — полупериметр треугольника, 1/2 суммы его сторон (периметра)
α — угол, противолежащий стороне a
треугольника
β — угол, противолежащий стороне b
треугольника
γ — угол, противолежащий стороне c
треугольника
h a , h b , h c
Обратите внимание, что приведенные обозначения соответствуют рисунку, который находится выше, чтобы при решении реальной задачи по геометрии Вам визуально было легче подставить в нужные места формулы правильные значения.
- Площадь треугольника равна половине произведения высоты треугольника на длину стороны на которую эта высота опущена (Формула 1). Правильность этой формулы можно понять логически. Высота, опущенная на основание, разобьет произвольный треугольник на два прямоугольных. Если достроить каждый из них до прямоугольника с размерами b и h, то, очевидно, площадь данных треугольников будет равна ровно половине площади прямоугольника (Sпр = bh)
- Площадь треугольника равна половине произведения двух его сторон на синус угла между ними (Формула 2) (см. пример решения задачи с использованием этой формулы ниже). Несмотря на то, что она кажется непохожей на предыдущую, она легко может быть в нее преобразована. Если из угла B опустить высоту на сторону b, окажется, что произведение стороны a на синус угла γ по свойствам синуса в прямоугольном треугольнике равно проведенной нами высоте треугольника, что и даст нам предыдущую формулу
- Площадь произвольного треугольника может быть найдена через произведение половины радиуса вписанной в него окружности на сумму длин всех его сторон (Формула 3), проще говоря, нужно полупериметр треугольника умножить на радиус вписанной окружности (так легче запомнить)
- Площадь произвольного треугольника можно найти, разделив произведение всех его сторон на 4 радиуса описанной вокруг него окружности (Формула 4)
- Формула 5 представляет собой нахождение площади треугольника через длины его сторон и его полупериметр (половину суммы всех его сторон)
- Формула Герона (6) — это представление той же самой формулы без использования понятия полупериметра, только через длины сторон
- Площадь произвольного треугольника равна произведению квадрата стороны треугольника на синусы прилежащих к этой стороне углов деленного на двойной синус противолежащего этой стороне угла (Формула 7)
- Площадь произвольного треугольника можно найти как произведение двух квадратов описанной вокруг него окружности на синусы каждого из его углов.
 (Формула 8)
(Формула 8) - Если известна длина одной стороны и величины двух прилежащих к ней углов, то площадь треугольника может быть найдена как квадрат этой стороны, деленный на двойную сумму котангенсов этих углов (Формула 9)
- Если известна только длина каждой из высот треугольника (Формула 10), то площадь такого треугольника обратно пропорциональна длинам этих высот, как по Формуле Герона
- Формула 11 позволяет вычислить площадь треугольника по координатам его вершин , которые заданы в виде значений (x;y) для каждой из вершин. Обратите внимание, что получившееся значение необходимо взять по модулю, так как координаты отдельных (или даже всех) вершин могут находиться в области отрицательных значений
Примечание . Далее приведены примеры решения задач по геометрии на нахождение площади треугольника. Если Вам необходимо решить задачу по геометрии, похожей на которую здесь нет — пишите об этом в форуме. В решениях вместо символа «квадратный корень» может применяться функция sqrt(), в которой sqrt — символ квадратного корня, а в скобках указано подкоренное выражение .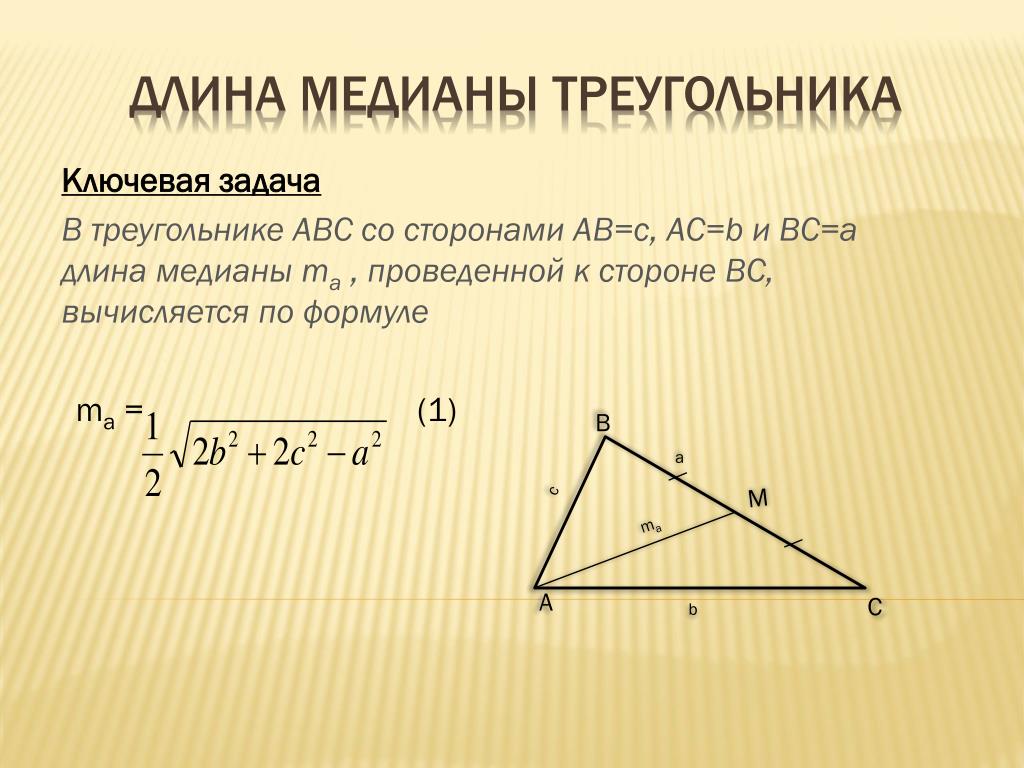 Иногда для простых подкоренных выражений может использоваться символ √
Иногда для простых подкоренных выражений может использоваться символ √
Стороны треугольника равны 5 и 6 см. Угол между ними составляет 60 градусов. Найдите площадь треугольника .
Решение .
Для решения этой задачи используем формулу номер два из теоретической части урока.
Площадь треугольника может быть найдена через длины двух сторон и синус угла межу ними и будет равна
S=1/2 ab sin γ
Поскольку все необходимые данные для решения (согласно формуле) у нас имеются, нам остается только подставить значения из условия задачи в формулу:
S = 1/2 * 5 * 6 * sin 60
В таблице значений тригонометрических функций найдем и подставим в выражение значение синуса 60 градусов . Он будет равен корню из трех на два.
S = 15 √3 / 2
Ответ : 7,5 √3 (в зависимости от требований преподавателя, вероятно, можно оставить и 15 √3/2)
Задача. Найти площадь равностороннего треугольникаНайти площадь равностороннего треугольника со стороной 3см.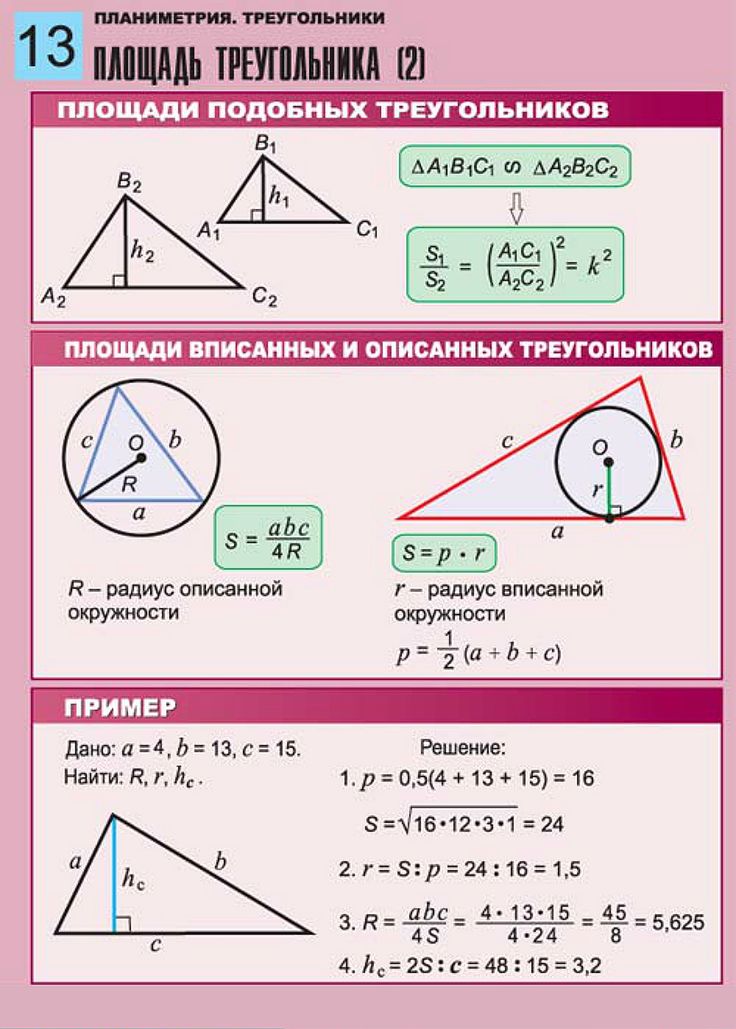
Решение .
Площадь треугольника можно найти по формуле Герона:
S = 1/4 sqrt((a + b + c)(b + c — a)(a + c — b)(a + b -c))
Поскольку a = b = c формула площади равностороннего треугольника примет вид:
S =
√3 / 4 * a 2
S =
√3 / 4 * 3 2
Ответ : 9 √3 / 4.
Задача. Изменение площади при изменении длины сторон
Во сколько раз увеличится площадь треугольника, если стороны увеличить в 4 раза?
Решение .
Поскольку размеры сторон треугольника нам неизвестны, то для решения задачи будем считать, что длины сторон соответственно равны произвольным числам a, b, c. Тогда для того, чтобы ответить на вопрос задачи, найдем площадь данного треугольника, а потом найдем площадь треугольника, стороны которого в четыре раза больше. Соотношение площадей этих треугольников и даст нам ответ на задачу.
Далее приведем текстовое пояснение решения задачи по шагам. Однако, в самом конце, это же самое решение приведено в более удобном для восприятия графическом виде. Желающие могут сразу опуститься вниз решения.
Желающие могут сразу опуститься вниз решения.
Для решения используем формулу Герона (см. выше в теоретической части урока). Выглядит она следующим образом:
S = 1/4 sqrt((a + b + c)(b + c — a)(a + c — b)(a + b -c))
(см. первую строку рисунка внизу)
Длины сторон произвольного треугольника заданы переменными a, b, c.
Если стороны увеличить в 4 раза, то площадь нового треугольника с составит:
S 2 = 1/4 sqrt((4a + 4b + 4c)(4b + 4c — 4a)(4a + 4c — 4b)(4a + 4b -4c))
(см. вторую строку на рисунке внизу)
Как видно, 4 — общий множитель, который можно вынести за скобки из всех четырех выражений по общим правилам математики.
Тогда
S 2 = 1/4 sqrt(4 * 4 * 4 * 4 (a + b + c)(b + c — a)(a + c — b)(a + b -c)) — на третьей строке рисунка
S 2 = 1/4 sqrt(256 (a + b + c)(b + c — a)(a + c — b)(a + b -c)) — четвертая строка
Из числа 256 прекрасно извлекается квадратный корень, поэтому вынесем его из-под корня
S 2 = 16 * 1/4 sqrt((a + b + c)(b + c — a)(a + c — b)(a + b -c))
S 2 = 4 sqrt((a + b + c)(b + c — a)(a + c — b)(a + b -c))
(см. пятую строку рисунка внизу)
пятую строку рисунка внизу)
Чтобы ответить на вопрос, заданный в задаче, нам достаточно разделить площадь получившегося треугольника, на площадь первоначального.
Определим соотношения площадей, разделив выражения друг на друга и сократив получившуюся дробь.
Формул для вычисления площади треугольника в интернете можно найти свыше 10. Немало из них применяется в задачах с известными сторонами и углами треугольника. Однако есть ряд сложных примеров где по условию задания известны только одна сторона и углы треугольника, или радиус описанной или вписанной окружности и еще одна характеристика. В таких случаях простую формулу применить не удастся.
Приведенные ниже формулы позволят решить 95 процентов задач в которых требуется найти площадь треугольника.
Перейдем к рассмотрению распространенных формул площади.
Рассмотрим треугольник изображен на рисунке ниже
На рисунке и далее в формулах введены классические обозначения всех его характеристик
a,b,c
– стороны треугольника,
R
– радиус описанной окружности,
r
– радиус вписанной окружности,
h[b],h[a],h[c]
– высоты, проведенные в соответствии со сторонами a,b,c.
alpha, beta,hamma –
углы возле вершин.
1. Площадь равна половине произведения стороны треугольника на высоту опущенной к этой стороне. На языке формул это определение можно записать так
Таким образом, если известна сторона и высота — то площадь найдет каждый школьник.
Кстати, из этой формулы можно вывести одну полезную зависимость между высотами
2. Если учесть, что высота треугольника через соседнюю сторону выражается зависимостью
То с первой формулы площади следуют однотипные вторые
Внимательно посмотрите на формулы — их легко запомнить, поскольку в произведении фигурирует две стороны и угол между ними. Если правильно обозначить стороны и углы треугольника (как на рисунке выше) то получим две стороны a,b и угол связан с третьей С (hamma).
3. Для углов треугольника справедливо соотношение
Зависимость позволяет применять в вычислениях следующие формулы площади треугольника
Примеры на эту зависимость встречаются крайне редко, но помнить что есть такая формула Вы должны.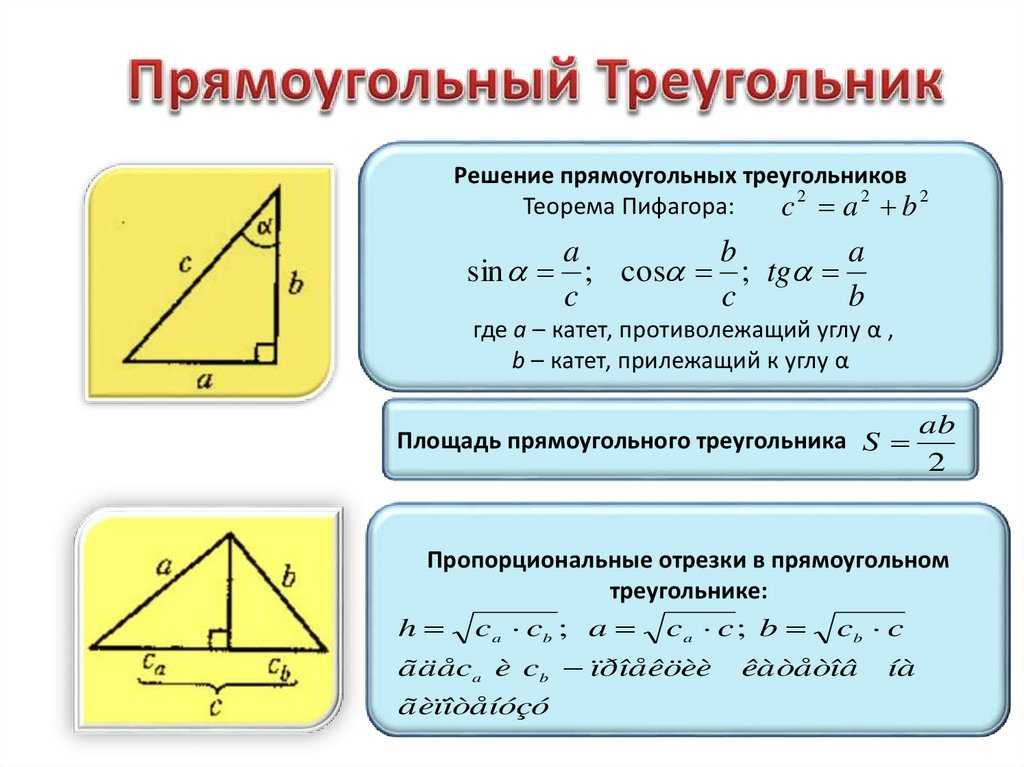
4. Если известна сторона и два прилегающих угла то площадь находится по формуле
5. Формула площади через сторону и котангенс прилегающих углов следующая
Перестановкой индексов можете получить зависимости для других сторон.
6. Приведенная ниже формула площади используется в задачах когда вершины треугольника заданы на плоскости координатами . В этом случае площадь равна половине определителя взятого по модулю.
7. Формула Герона
применяют в примерах с известными сторонами треугольника.
Сначала находят полупериметр треугольника
А затем определяют площадь по формуле
или
Ее довольно часто используют в коде программ калькуляторов.
8. Если известны все высоты треугольника то площадь определяют по формуле
Она сложна для вычисления на калькуляторе, однако в пакетах MathCad, Mathematica, Maple площадь находится на «раз два ».
9.
Следующие формулы используют известны радиусы вписанных и описанных окружностей.
В частности, если известно радиус и стороны треугольника, или его периметр то площадь вычисляется согласно формуле
10. В примерах где задано стороны и радиус или диаметр описанной окружности площадь находят по формуле
11. Следующая формула определяет площадь треугольника через сторону и углы треугольника.
Ну и напоследок — частные случаи:
Площадь прямоугольного треугольника
с катетами a
и b
равна половине их произведения
Формула площади равностороннего (правильного) треугольника
=
= одной четвертой произведения квадрату стороны на корень из тройки.
Треугольник — это одна из самых распространенных геометрических фигур, с которой мы знакомимся уже в начальной школе. С вопросом, как найти площадь треугольника, сталкивается каждый школьник на уроках геометрии. Так, какие же особенности нахождения площади данной фигуры можно выделить? В данной статье мы рассмотрим основные формулы, необходимые для выполнения такого задания, а также разберем виды треугольников.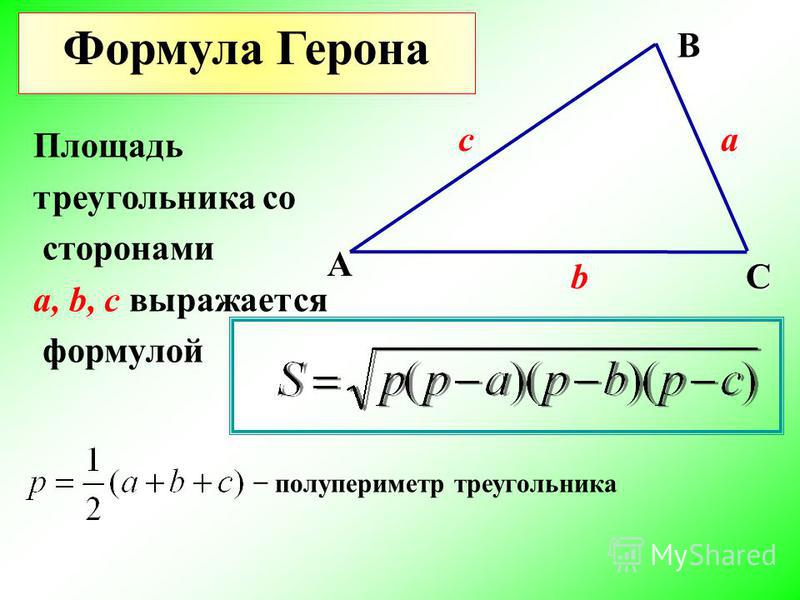
Виды треугольников
Найти площадь треугольника можно абсолютно разными способами, потому что в геометрии выделяется не один вид фигур, содержащих три угла. К таким видам относятся:
- Тупоугольный.
- Равносторонний (правильный).
- Прямоугольный треугольник.
- Равнобедренный.
Рассмотрим подробнее каждый из существующих типов треугольников.
Такая геометрическая фигура считается наиболее распространенной при решении геометрических задач. Когда возникает необходимость начертить произвольный треугольник, на помощь приходит именно этот вариант.
В остроугольном треугольнике, как понятно по названию, все углы острые и в сумме составляют 180°.
Такой треугольник также очень распространен, однако встречается несколько реже остроугольного. Например, при решении треугольников (т. е. известно несколько его сторон и углов и нужно найти оставшиеся элементы) иногда требуется определить, является угол тупым или нет. Косинус — это отрицательное число.
В величина одного из углов превышает 90°, поэтому оставшиеся два угла могут принимать маленькие значения (например, 15° или вовсе 3°).
Чтобы найти площадь треугольника данного типа, необходимо знать некоторые нюансы, о которых мы поговорим дальше.
Правильный и равнобедренный треугольники
Правильным многоугольником называется фигура, включающаяся в себя n углов, у которой все стороны и углы равны. Таким и является правильный треугольник. Так как сумма всех углов треугольника составляет 180°, то каждый из трех углов равен 60°.
Правильный треугольник, благодаря его свойству, также называют равносторонней фигурой.
Стоит также отметить, что в правильный треугольник можно вписать только одну окружность и около него можно описать только одну окружность, причем их центры расположены в одной точке.
Помимо равностороннего типа, можно также выделить равнобедренный треугольник, несильно от него отличающийся. В таком треугольнике две стороны и два угла равны между собой, а третья сторона (к которой прилегают равные углы) является основанием.
На рисунке показан равнобедренный треугольник DEF, углы D и F которого равны, а DF является основанием.
Прямоугольный треугольник
Прямоугольный треугольник назван так потому, что один из его углов прямой, то есть равен 90°. Другие же два угла в сумме составляют 90°.
Самая большая сторона такого треугольника, лежащая против угла в 90° является гипотенузой, остальные же две его стороны — это катеты. Для данного типа треугольников применима теорема Пифагора:
Сумма квадратов длин катетов равна квадрату длины гипотенузы.
На рисунке изображен прямоугольный треугольник BAC с гипотенузой AC и катетами AB и BC.
Чтобы найти площадь треугольника с прямым углом, нужно знать числовые значения его катетов.
Перейдем к формулам нахождения площади данной фигуры.
Основные формулы нахождения площади
В геометрии можно выделить две формулы, которые подходят для нахождения площади большинства видов треугольников, а именно для остроугольного, тупоугольного, правильного и равнобедренного треугольников.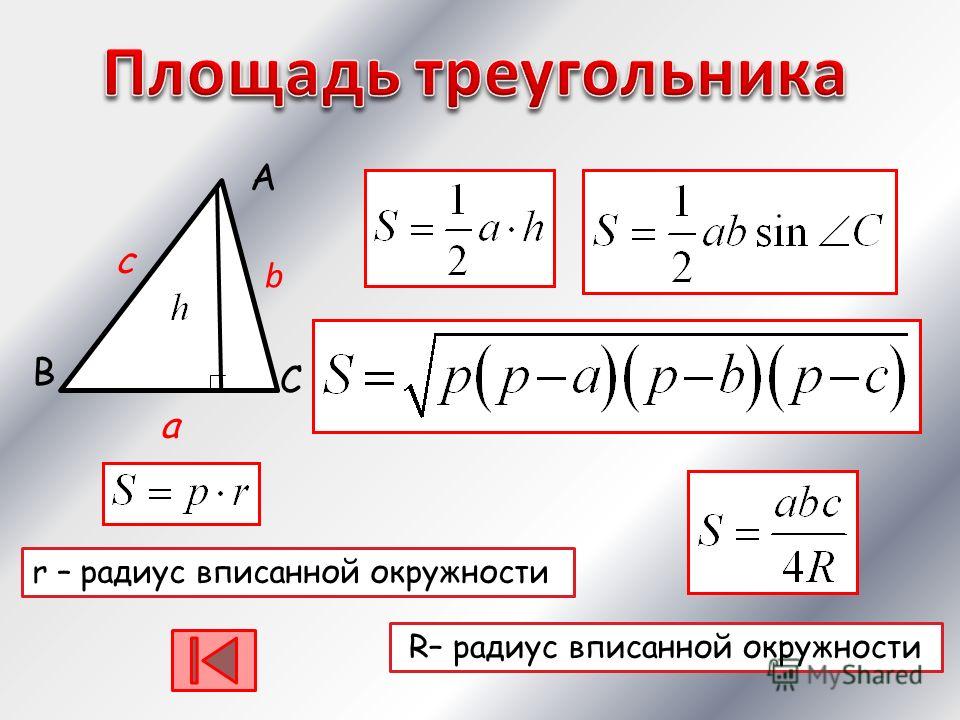 Разберем каждую из них.
Разберем каждую из них.
По стороне и высоте
Данная формула является универсальной для нахождения площади, рассматриваемой нами фигуры. Для этого достаточно знать длину стороны и длину проведенной к ней высоты. Сама формула (половина произведения основания на высоту) выглядит следующим образом:
где A — сторона данного треугольника, а H — высота треугольника.
Например, чтобы найти площадь остроугольного треугольника ACB, нужно умножить его сторону AB на высоту CD и разделить получившееся значение на два.
Однако не всегда бывает легко найти площадь треугольника таким способом. Например, чтобы воспользоваться этой формулой для тупоугольного треугольника, необходимо продолжить одну из его сторон и только после этого провести к ней высоту.
На практике данная формула применяется чаще остальных.
По двум сторонам и углу
Данная формула, как и предыдущая подходит для большинства треугольников и по своему смыслу является следствием формулы нахождения площади по стороне и высоте треугольника. То есть рассматриваемую формулу можно легко вывести из предыдущей. Ее формулировка выглядит так:
То есть рассматриваемую формулу можно легко вывести из предыдущей. Ее формулировка выглядит так:
S = ½*sinO*A*B,
где A и B — это стороны треугольника, а O — угол между сторонами A и B.
Напомним, что синус угла можно посмотреть в специальной таблице, названной в честь выдающегося советского математика В. М. Брадиса.
А теперь перейдем к другим формулам, подходящим только для исключительных видов треугольников.
Площадь прямоугольного треугольника
Помимо универсальной формулы, включающей в себя необходимость проводить высоту в треугольнике, площадь треугольника, содержащего прямой угол, можно найти по его катетам.
Так, площадь треугольника, содержащего прямой угол, — это половина произведения его катетов, или:
где a и b — катеты прямоугольного треугольника.
Правильный треугольник
Данный вид геометрических фигур отличается тем, что его площадь можно найти при указанной величине лишь одной его стороны (так как все стороны правильного треугольника равны). Итак, встретившись с задачей «найти площадь треугольника, когда стороны равны», нужно воспользоваться следующей формулой:
Итак, встретившись с задачей «найти площадь треугольника, когда стороны равны», нужно воспользоваться следующей формулой:
S = A 2 *√3 / 4,
где A — это сторона равностороннего треугольника.
Формула Герона
Последний вариант для нахождения площади треугольника — это формула Герона. Для того чтобы ею воспользоваться, необходимо знать длины трех сторон фигуры. Формула Герона выглядит так:
S = √p·(p — a)·(p — b)·(p — c),
где a, b и c — это стороны данного треугольника.
Иногда в задаче дано: «площадь правильного треугольника — найти длину его стороны». В данном случае нужно воспользоваться уже известной нам формулой нахождения площади правильного треугольника и вывести из нее значение стороны (или ее квадрата):
A 2 = 4S / √3.
Экзаменационные задачи
В задачах ГИА по математике встречаются множество формул. Помимо этого, достаточно часто необходимо найти площадь треугольника на клетчатой бумаге.
В данном случае удобнее всего провести высоту к одной из сторон фигуры, определить по клеткам ее длину и воспользоваться универсальной формулой для нахождения площади:
Итак, после изучения представленных в статье формул, у вас не возникнут проблемы при нахождении площади треугольника любого вида.
Как вы можете помнить из школьной программы по геометрии, треугольник – это фигура, образованная из трех отрезков, соединяющихся тремя точками, не лежащими на одной прямой. Треугольник образует три угла, отсюда и название фигуры. Определение может быть и иным. Треугольник можно так же назвать многоугольником с тремя углами, ответ будет так же верным. Треугольники делятся по числу равных сторон и по величине углов в фигурах. Так выделяют такие треугольники, как равнобедренный, равносторонний и разносторонний, а так же прямоугольный, остроугольный и тупоугольный, соответственно.
Формул вычисления площади треугольника очень много. Выбирать, как найти площадь треугольника, т.е. какой формулой воспользоваться, только вам. Но стоит отметить лишь некоторые обозначения, которые используются во многих формулах вычисления площади треугольника. Итак, запоминайте:
S – это площадь треугольника,
a, b, c – это стороны треугольника,
h – это высота треугольника,
R – это радиус описанной окружности,
p – это полупериметр.
Вот основные обозначения, которые могут вам пригодиться, если вы совершенно забыли курс геометрии. Ниже будут приведены наиболее понятные и не сложные варианты вычисления неизвестной и загадочной площади треугольника. Это не сложно и пригодится как вам в домашних нуждах, так и для помощи своим детям . Давайте вспомним, как вычислить площадь треугольника проще простого:
В нашем случае площадь треугольника равна: S = ½ * 2,2 см. * 2,5 см. = 2,75 кв.см. Помните, что площадь измеряется в квадратных сантиметрах (кв.см.).
Прямоугольный треугольник и его площадь.
Прямоугольный треугольник – это треугольник, у которого один угол равен 90 градусам (потому называется прямым). Прямой угол образуют две перпендикулярные линии (в случае с треугольником – два перпендикулярных отрезка). В прямоугольном треугольнике прямой угол может быть только один, т.к. сумма всех углов одного любого треугольника равна 180 градусам. Получается, что 2 других угла должны делить между собой оставшиеся 90 градусов, например 70 и 20, 45 и 45 и т.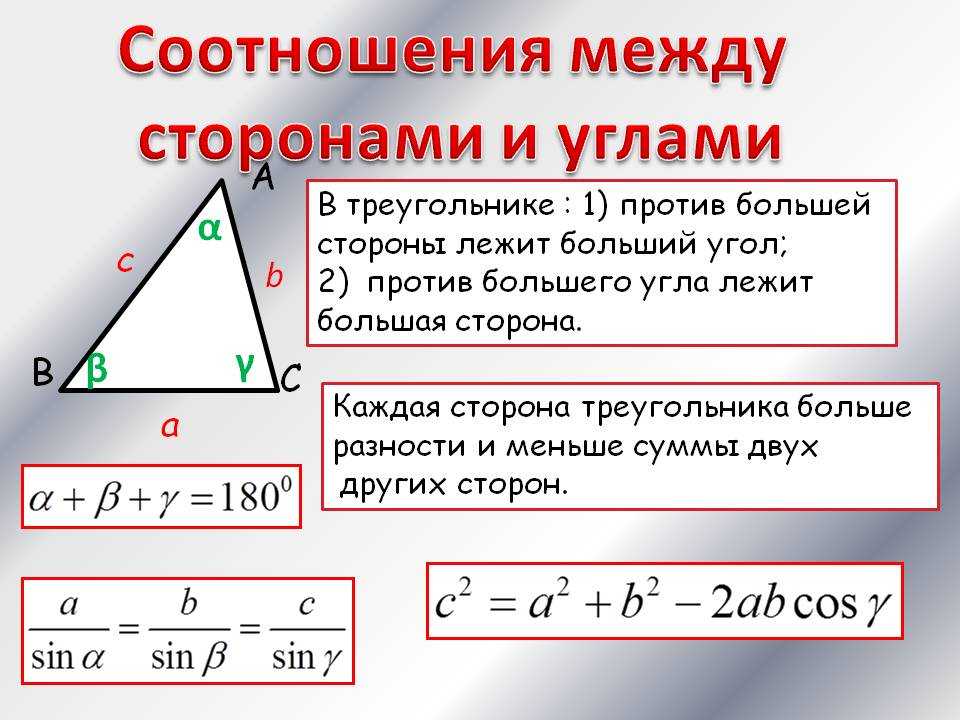 д. Итак, основное вы вспомнили, осталось узнать, как найти площадь прямоугольного треугольника. Представим, что перед нами вот такой прямоугольный треугольник, и нам необходимо найти его площадь S.
д. Итак, основное вы вспомнили, осталось узнать, как найти площадь прямоугольного треугольника. Представим, что перед нами вот такой прямоугольный треугольник, и нам необходимо найти его площадь S.
1. Самый простой способ определения площади прямоугольного треугольника высчитывается по следующей формуле:
В нашем случае, площадь прямоугольного треугольника равна: S = 2,5 см. * 3 см. / 2 = 3,75 кв.см.
В принципе, больше нет необходимости выверения площади треугольника иными способами, т.к. в быту пригодится и поможет только этот. Но существуют и варианты измерения площади треугольника через острые углы.
2. Для других способов вычисления необходимо иметь таблицу косинусов, синусов и тангенсов. Посудите сами, вот какие варианты вычисления площадей прямоугольного треугольника еще можно использовать:
Мы решили воспользоваться первой формулой и с небольшими помарками (чертили в блокноте и использовали старую линейку и транспортир), но у нас вышел верный расчет:
S = (2,5*2,5)/(2*0,9)=(3*3)/(2*1,2). У нас вышли такие результаты 3,6=3,7, но с учетом сдвига клеток, этот нюанс нам можно простить.
У нас вышли такие результаты 3,6=3,7, но с учетом сдвига клеток, этот нюанс нам можно простить.
Равнобедренный треугольник и его площадь.
Если перед вами стоит задача вычислить формулу равнобедренного треугольника, то проще всего воспользоваться главной и как считается классической формулой площади треугольника.
Но для начала, перед тем, как найти площадь равнобедренного треугольника, узнаем, что это за фигура такая. Равнобедренным треугольником называется треугольник, у которого две стороны имеют одинаковую длину. Эти две стороны называются боковыми, третья сторона называется основанием. Не путайте равнобедренный треугольник с равносторонним, т.е. правильным треугольником, у которого все три стороны равны. В таком треугольнике нет особых тенденций к углам, точнее к их величине. Однако углы у основания в равнобедренном треугольнике равны, но отличаются от угла между равными сторонами. Итак, первую и главную формулу вы уже знаете, осталось узнать, какие еще формулы определения площади равнобедренного треугольника известны:
Площадь прямого треугольника – формула через катеты
4. 3
3
Средняя оценка: 4.3
Всего получено оценок: 240.
4.3
Средняя оценка: 4.3
Всего получено оценок: 240.
Прямоугольный треугольник отличается от произвольных целым рядом параметров. Это и значение сторон, которое можно рассчитать по теореме Пифагора; возможность напрямую использовать тригонометрические функции и несколько специфичных формул, предназначенных для расчета площади именно прямоугольных треугольников. Именно об этих формулах и пойдет речь в данной статье.
Формула площади прямоугольного треугольника
В классическом случае, площадь треугольника находится как половина произведение стороны на высоту, проведенную к этой стороне.
Рис. 1. Площадь произвольного треугольника.В прямоугольном треугольнике для двух из трех сторон высоты и сами стороны совпадают. Рассмотрим на примере.
Дан прямоугольный треугольник АВС с прямым углом при вершине В. Для катета ВС высотой будет катет АВ, а для катета АВ высотой служит сторона ВС.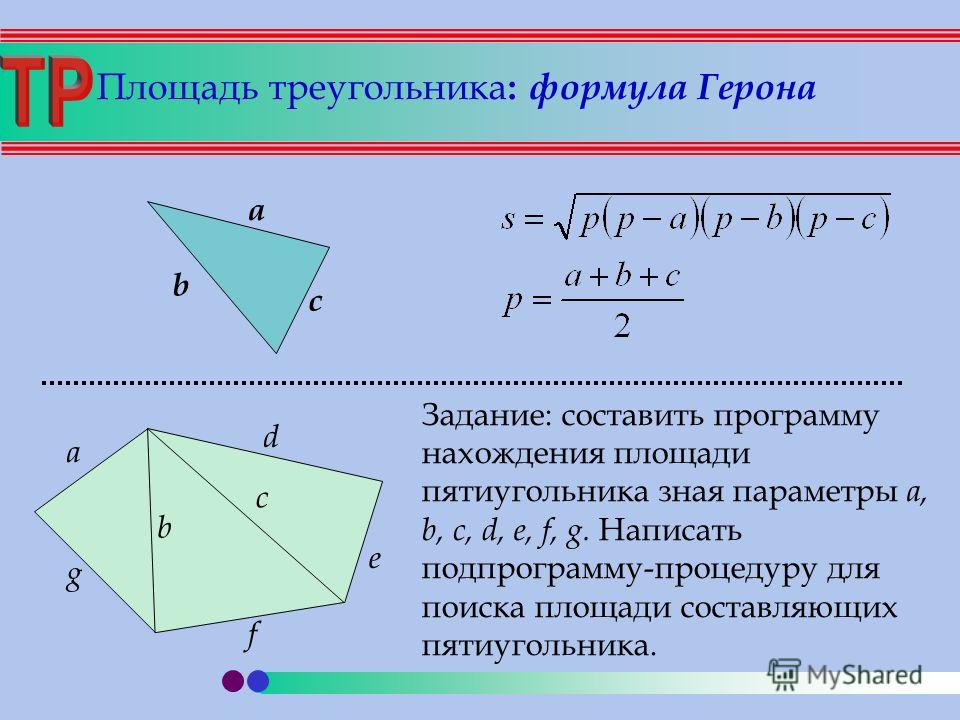 Только гипотенуза нуждается в дополнительных построениях для нахождения высоты.
Только гипотенуза нуждается в дополнительных построениях для нахождения высоты.
Именно из этих особенностей и вытекает формула площади прямого треугольника.
$S= {1\over2}a*b$ где a и b это катеты треугольника. То есть значение двух сторон просто подставили в классическую формулу. В итоге получается самая простая из возможных формул для нахождения площади прямоугольного треугольника. Рассмотрим несколько неклассических ситуаций, когда значение катетов неизвестно.
Если в задаче о прямоугольном треугольнике дается значение высоты, то имеется в виду перпендикуляр, проведенный к гипотенузе.
Задача
- В прямоугольном треугольнике высота равняется 8, а острый угол при гипотенузе 60 градусов. Найти площадь прямого треугольника.
Для каждой геометрической задачи существует, как минимум 3 решения.
Конкретно в нашем случае можно выделить два простых способа:
- Найти гипотенузу и определить значение площади по классической формуле.

- Найти каждый из катетов и найти площадь через катеты.
Рассмотрим каждый из вариантов, чтобы иметь представление о возможных путях решения подобных задач.
Обозначим треугольник АВС, проведем высоту ВН. Угол АСВ равен 60 градусов. Найдем гипотенузу. Она состоит из двух отрезков АН и НС. Найдем каждый из отрезков, сложим их и получим искомое значение.
АН найдем из прямоугольного треугольника АНВ с прямым углом у вершины Н. Сумма острых углов в прямоугольном треугольнике всегда равна 90 градусам. Значит Угол ВАС=90-60=30.
Воспользуемся тригонометрической функцией. Воспользуемся значением тангенса:
$$tg(BAC)= {BH\over AH}=\sqrt{3}$$ – значение тангенса можно взять из таблицы Брадиса или запомнить его для трех характерных углов 30, 45 и 60 градусов.
$$АН={ВН\over\sqrt{3}}= {8\over\sqrt{3}}=4,62$$
Получившийся результат мы округлим до сотых. Не стоит бояться получившихся длинных дробных значений. В вычислениях они встречаются постоянно, нужно просто правильно округлять полученные значения.
По схожей схеме вычислим НС из прямоугольного треугольника ВНС.
$$tg(НСВ)={ВН \over НС}={1 \over \sqrt{3}}$$
$$HC={BH\over tg(HCB)}={BH\over{1\over\sqrt{3}}}=BH*\sqrt{3}=8*\sqrt{3}=13,87$$
Значение снова округлим до сотых. Два получившихся значения сложим и посчитаем значение площади.
АС=АН+НС=4,62+13,87=18,49
$$S={1\over2}*BH*AC={1\over2}*8*18,49=73,96$$
Приведем решение через катеты и сравним результаты.
В прямоугольном треугольнике ВНС сторона ВС выступает гипотенузой. Воспользуемся значением синуса:
$$sin(ACB)={BH\over BC}={\sqrt{3}\over2}$$
Значение синуса для угла в 60 градусов является табличным значением.
$$BC=BH/sin(ACB)=8/(\sqrt{3}/2)=16/\sqrt{3}=9,23$$
Подобным методом определим значение второго катета из треугольника АНВ:
$$sin(BAH)=BH/AB=1/2$$
$$AB=BH/(1/2)=BH*2=16$$
Оба катета найдены, можно подсчитать значение площади:
$$S=1/2*AB*BC=1/2*16*9,23=73,84$$
Получившиеся значения схожи.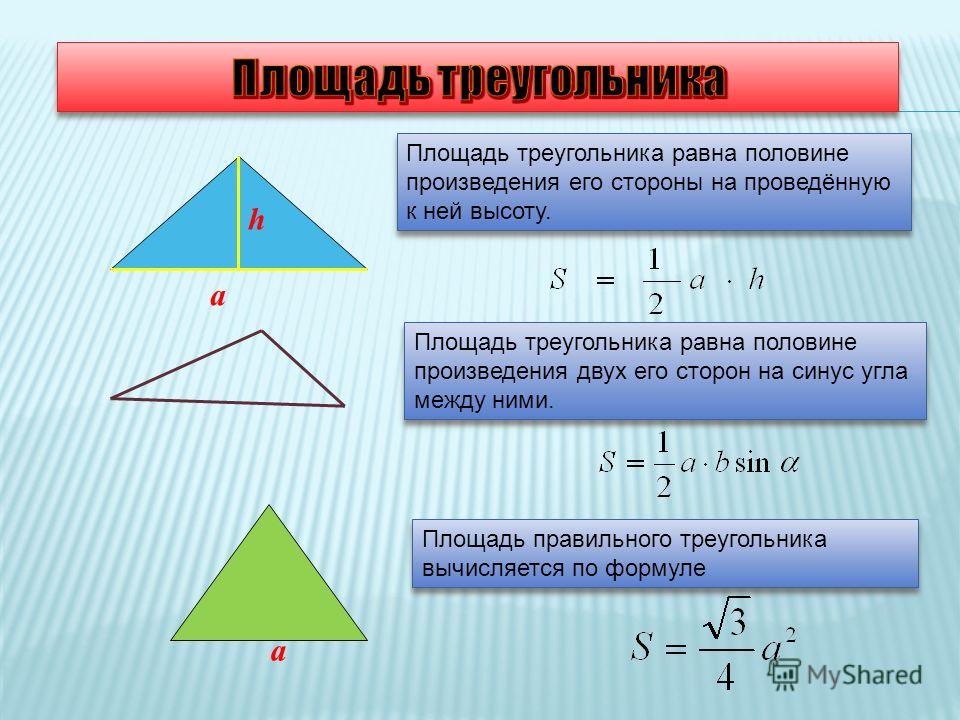 Различие в сотых легко объясняется округлениями, которые выполнялись для удобства расчета. В подобных вычислениях расхождение в единицу считается допустимым.
Различие в сотых легко объясняется округлениями, которые выполнялись для удобства расчета. В подобных вычислениях расхождение в единицу считается допустимым.
Что мы узнали?
Мы досконально разобрали формулу нахождения площади прямоугольного треугольника. Показали другие варианты нахождения площади, подробно разобрали различные пути решения задач на нахождение площади прямоугольного треугольника.
Тест по теме
Доска почёта
Чтобы попасть сюда — пройдите тест.
Иван Ульянов
7/10
Александр Барсов
8/10
Оценка статьи
4.3
Средняя оценка: 4.3
Всего получено оценок: 240.
А какая ваша оценка?
Формула Герона для площади треугольника
Формула Герона для площади треугольникаСодержание
Главная страница
ТЕОРЕМА
Для треугольника со стороной a , b и c и площадь K , мы имеем
ДОКАЗАТЕЛЬСТВО
Поскольку доказательство формулы Герона «круговое» и длинное, мы разделим его на три основные части.
Часть А
Пусть O будет центром вписанной окружности. Пусть r будет радиусом этой окружности (рис. 7). Как видим, ОД = ОЕ = ОФ = r .Теперь, применяя обычную формулу площади треугольников, получаем:
Площадь ( BOC ) = (основание) (высота) = ( BC ) ( OE ) = ar
Площадь ( COA ) = (основание) (высота) = ( AC ) ( OF ) = br
rs
Часть Б
Теперь, используя предложение 1, мы можем видеть, что ABC теперь состоит из трех пар конгруэнтных треугольников, а именно Так как соответствующие части конгруэнтных треугольников конгруэнтны, мы имеем
Так как соответствующие части конгруэнтных треугольников конгруэнтны, мы имеемТеперь продлите основание треугольника AB до точки G , так что AG = CE . В настоящее время,
BG = BD + AD + AG = BD + AD + CE по конструкции
Теперь, поскольку BG = с ,
с — с = БГ — АВ = АГ
с — б = БГ — АС
 н.э. + CE ) — ( CE + г. н.э. .
н.э. + CE ) — ( CE + г. н.э. .Эти равенства просто помогают нам визуализировать отрезки s — a , s — b и s — c .
Часть С
Теперь постройте OL таким образом, чтобы он был перпендикулярен OB и пересекал AB в точке K (рис. 8).Затем постройте AM таким образом, чтобы он был перпендикулярен AB и пересекал OL в точке H (рис. 9).
Далее подключите BH (рисунок 10).
По предложению 4 четырехугольник AHBO является вписанным четырехугольником.
Пожалуйста, не расстраивайтесь из-за следующей алгебры. Их можно визуализировать с помощью рисунка 10.
Теперь давайте сосредоточимся на углах около O .
 (***)
(***) Очевидно, < DOA + < DOB = < AOB . (****)
Теперь мы видим, что треугольник COF подобен треугольнику BHA .
Эквивалентно,
Точно так же треугольник KAH подобен KDO . Это потому, что < KAH и < KDO равны 90 градусам, а < AKH = < DKO .
В сочетании с (V*) , получаем:

Теперь посмотрите на треугольник BOK . По предложению 2 видим, что треугольник ODB и треугольник KDO подобны.
Теперь добавьте 1 к обеим сторонам (V**) :
Умножение этого уравнения слева на BG/BG и справа на BD/BD дает:
Из части А площадь треугольника ABC = K = rs .
Это дает формулу Герона:
Площадь треугольника с тремя сторонами
Чтобы найти площадь треугольника с тремя сторонами, воспользуемся формулой Герона. Площадь треугольника можно вычислить с помощью различных формул. Основная формула, используемая для нахождения площади треугольника, представляет собой ½ × основание × высота, где «основание» — это сторона треугольника, на которой образована высота, а «высота» — это длина высоты, проведенная к « Основание» из противоположной ему вершины. Однако, если высота треугольника неизвестна, а нам нужно найти площадь треугольника с тремя разными сторонами, используется формула Герона. Эта формула была выведена греческим математиком, известным как Герон Александрийский. Давайте рассмотрим различные формулы, которые используются для нахождения площади треугольника с тремя сторонами.
1. | Площадь треугольника с тремя сторонами Формула |
| 2. | Доказательство площади треугольника с 3 сторонами Формула |
| 3. | Часто задаваемые вопросы о площади треугольника с 3 сторонами |
Площадь треугольника с тремя сторонами Формула
Чтобы найти площадь треугольника с тремя сторонами, мы используем формулу Герона, которая гласит, что если a, b и c — три стороны треугольника, то его площадь равна
Площадь = √[s(s-a)(s-b)(s-c)]
Здесь «s» — полупериметр треугольника, т. е. s = (a + b + c)/2.
Давайте посмотрим, как найти площадь треугольника с 3 сторонами, заданными как: 3, 6 и 7. Мы знаем, что a = 3, b = 6 и c = 7, полупериметр, s = (a + b + c)/2 = (3 + 6 + 7)/2 = 8. Найдем площадь треугольника по формуле Герона.
A = √[s(s-a)(s-b)(s-c)]
= √[8(8-3)(8-6)(8-7)]
= √[8 × 5 × 2 × 1]
= √(80)
≈ 8,94
Доказательство площади треугольника с 3 сторонами Формула
Доказательство формулы площади треугольника с тремя сторонами можно вывести следующим образом.
Рассмотрим показанный выше треугольник со сторонами a, b, c и углами, противоположными сторонам, как угол A, угол B, угол C.
Используя закон косинусов, cos A = (b 2 + c 2 — а 2 ) / 2bc.
Использование одного из тригонометрических тождеств, 92]}\\[0,2 см] &= \dfrac{1}{4} \sqrt{(b+c+a)(b+c-a)(a+b-c)(a-b+c)}\\[ 0.2cm] \end{align} \)
Мы знаем, что полупериметр треугольника равен s = (a + b + c)/2. Отсюда
a + b + c = 2s
b + c — a = 2s — 2a
a + b — c = 2s — 2c
a — b + c = 2s — 2b
Подставляя все эти значения на последнем шаге,
\( \begin{align}& \text{Area } \\[0.2cm]&= \dfrac{1}{4} \sqrt{2s (2s-2a)(2s-2c )(2s-2b)}\\[0,2 см] &= \dfrac{4}{4} \sqrt{s(s-a)(s-c)(s-b)}\\[0,2 см] &= \sqrt{s( s-a)(s-b)(s-c)} \end{align}\)
Итак, мы доказали формулу Герона.
Площадь треугольника с 3 сторонами Примеры
Пример 1: Три стороны данного треугольника составляют 8 единиц, 11 единиц и 13 единиц.
 Найдите его полупериметр и его площадь.
Найдите его полупериметр и его площадь.Решение:
Мы знаем, что формула, которая используется для нахождения площади треугольника с 3 сторонами, такова: Площадь = √[s(s-a)(s-b)(s-c)], где ‘a’, ‘ b’, ‘c’ — три стороны, а s — полупериметр треугольника. В этом случае а = 8; b = 11, c = 13, а полупериметр равен s = 8 + 11 + 13 = 32/2 = 16
Рассчитаем площадь треугольника с тремя сторонами по формуле Герона.
A =√[s(s-a)(s-b)(s-c)]
= √[16(16-8)(16-11)(16-13)]
= √[16 × 8 × 5 × 3]
= √16 × √8 × √5 × √3
= 4 × 2√2 × √5 ×√3
= 8 √30 = 43,817 единица 2
5 ∴ 900 Площадь данного треугольника = 43,817 ед. 2
Пример 2: Если три стороны треугольника равны 4 единицам, 6 единицам и 8 единицам соответственно, найдите площадь треугольника.
Решение:
Чтобы найти площадь треугольника с 3 заданными сторонами, мы используем формулу: A =√[s(s-a)(s-b)(s-c)]
Стороны данного треугольника 4 единицы, 6 единиц и 8 единиц.

Полупериметр треугольника равен
s = (a + b + c)/2 = (4 + 6 + 8)/2 = 18/2 = 9.
Теперь найдем площадь треугольника по формуле Герона:
A =√[s(s-a)(s-b)(s-c)]
= √[9(9-4)(9-6)( 9-8)]
= √[9× 5 × 3 × 1]
= 3 √15 = 11,61 квадратных единиц
∴ Площадь треугольника = 11,61 квадратных единиц.
перейти к слайдуперейти к слайду
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Записаться на бесплатный пробный урок
Практические вопросы по площади треугольника с тремя сторонами
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о площади треугольника с 3 сторонами
Какова площадь треугольника с тремя сторонами?
Площадь треугольника с 3 сторонами можно рассчитать по формуле Герона, согласно которой площадь треугольника равна √[s(s-a)(s-b)(s-c)], где a, b и c — три разные стороны, а s — полупериметр треугольника, который можно рассчитать следующим образом: полупериметр = (a + b + c)/2
Какова площадь треугольника с тремя равными сторонами?
Если треугольник имеет 3 равные стороны, он называется равносторонним треугольником. Площадь равностороннего треугольника можно рассчитать по формуле Площадь = a 2 (√3/4), где а — сторона треугольника. Например, если сторона равностороннего треугольника равна 6 единицам, его площадь будет рассчитываться следующим образом. Площадь = a 2 (√3/4), Площадь = 6 2 (√3/4) = 15,59 квадратных единиц.
Площадь равностороннего треугольника можно рассчитать по формуле Площадь = a 2 (√3/4), где а — сторона треугольника. Например, если сторона равностороннего треугольника равна 6 единицам, его площадь будет рассчитываться следующим образом. Площадь = a 2 (√3/4), Площадь = 6 2 (√3/4) = 15,59 квадратных единиц.
Какова площадь треугольника с тремя сторонами и высотой?
Если мы знаем стороны треугольника вместе с его высотой, мы можем использовать основную формулу площади треугольника. Площадь треугольника = 1/2 × основание × высота. Например, если высота (высота) треугольника = 8 ед., а сторона треугольника, на которой образована высота, задана (основание) = 7 ед., мы можем найти его площадь по формуле, Площадь треугольника = 1/2 × основание × высота. Площадь = 1/2 × 7 × 8 = 28 квадратных единиц.
Какова площадь треугольника с тремя сторонами и углом?
Если стороны треугольника даны вместе с прилежащим к ним углом, площадь треугольника можно рассчитать по формуле Площадь = (ab × sin C)/2, где «a» и «b» — две данным сторонам, а С — угол между ними. Этот метод также известен как метод «боковой угол в сторону». Например, если две стороны треугольника равны 5 единицам и 7 единицам, а угол между ними равен 60°, то площадь = (7 × 5 × sin 60)/2 = 15,15 квадратных единиц.
Этот метод также известен как метод «боковой угол в сторону». Например, если две стороны треугольника равны 5 единицам и 7 единицам, а угол между ними равен 60°, то площадь = (7 × 5 × sin 60)/2 = 15,15 квадратных единиц.
Какова площадь треугольника со сторонами 3, 5, 7?
Если три стороны треугольника равны 3, 5 и 7, его площадь можно рассчитать по формуле площадь = √[s(s-a)(s-b)(s-c)]. В этом случае a = 3, b = 5, c = 7 и s (полупериметр) = 7,5. Подставляя значения в формулу, √[7,5(7,5-3)(7,5-5)(7,5-7)] = √(7,5 × 4,5 × 2,5 × 0,5) = 6,49 единицы 2
Что такое неправильный треугольник ?
Неправильный треугольник — это треугольник, у которого все три стороны имеют разную длину. Он также известен как разносторонний треугольник (если все три стороны различны).
Как найти площадь неправильного треугольника?
Мы используем формулу Герона, чтобы найти площадь неправильного треугольника. Неправильный треугольник означает треугольник, стороны которого различны по длине.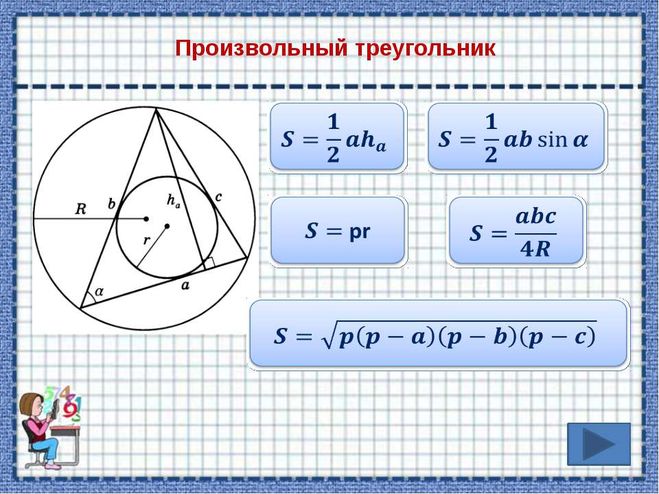 Согласно формуле Герона: Площадь = √[s(s-a)(s-b)(s-c)], где a, b и c — стороны треугольника, а s — полупериметр треугольника.
Согласно формуле Герона: Площадь = √[s(s-a)(s-b)(s-c)], где a, b и c — стороны треугольника, а s — полупериметр треугольника.
Как найти длину сторон треугольника только с 3 углами?
Напомним, что два подобных треугольника имеют одинаковые углы, но разные стороны (стороны пропорциональны). Таким образом, существует бесконечное число треугольников с одним и тем же набором любых трех заданных углов. Таким образом, невозможно найти стороны треугольника, если мы просто знаем все 3 угла, нам нужно знать хотя бы одну сторону, чтобы определить две другие стороны.
Для чего используется формула Герона?
Формула Герона используется для нахождения площади треугольника с тремя разными сторонами. Формула Герона записывается как Площадь = √[s(s-a)(s-b)(s-c)], где a, b и c — стороны треугольника, а s — полупериметр треугольника.
В честь кого названа формула Герона?
Формула Герона названа в честь Герона Александрийского, греческого математика, который нашел площадь треугольника, используя 3 стороны. Вот почему формула √[s(s-a)(s-b)(s-c)] известна как формула Герона.
Вот почему формула √[s(s-a)(s-b)(s-c)] известна как формула Герона.
Скачать БЕСПЛАТНО учебные материалы
Рабочий лист по площади
геометрия — Как вычислить площадь пересечения произвольного треугольника с квадратом?
Итак, сегодня весь день бился с откровенно уже бесящей проблемой.
Учитывая набор вершин треугольника на плоскости (всего 3 точки, 6 свободных параметров), мне нужно вычислить площадь пересечения этого треугольника с единичным квадратом, определяемым {0,0} и {1,1 }. (Я выбрал это, потому что любой квадрат в 2D может быть преобразован в это, и одно и то же преобразование может переместить 3 вершины).
Итак, теперь задача упрощена до 6 параметров, 3 пунктов… что, я думаю, достаточно мало, чтобы я захотел закодировать полное решение/найти полное решение.
(я хотел бы, чтобы это выполнялось на графическом процессоре буквально для более чем 2 миллионов треугольников каждые <0,5 секунды, если это возможно. что касается необходимости упрощения/отсутствия структур данных/библиотек)
С точки зрения моей попытки решения , у меня.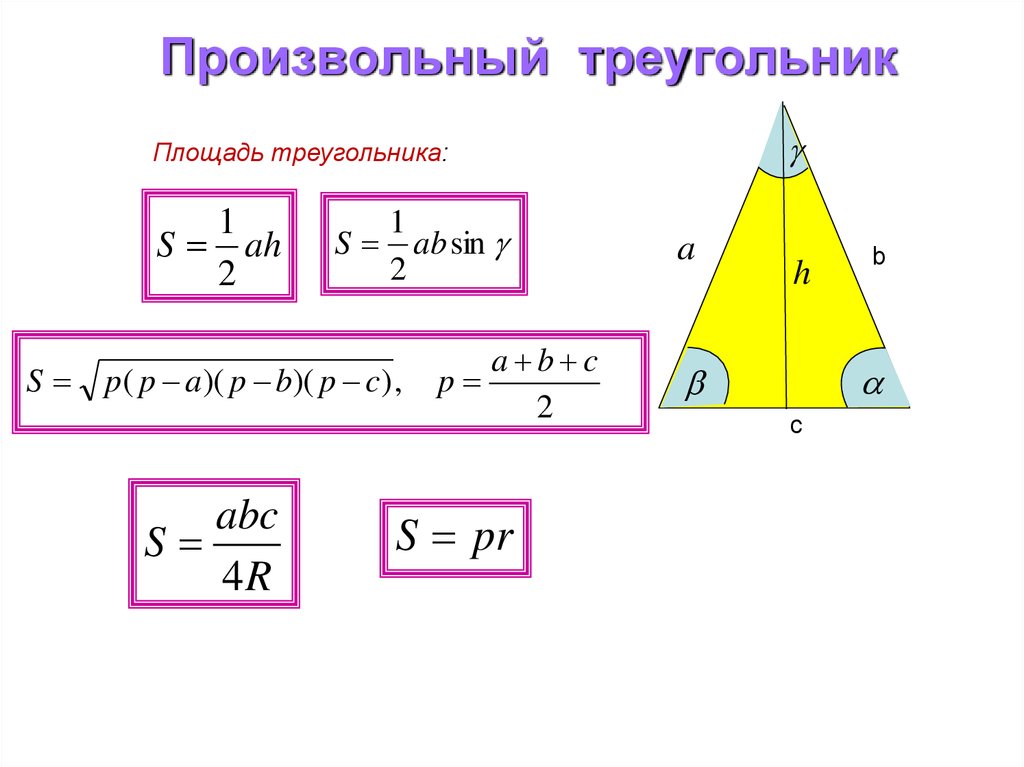 .. есть список способов, которые я придумал, ни один из которых не кажется быстрым или… специфичным для хорошего случая (слишком общего).
.. есть список способов, которые я придумал, ни один из которых не кажется быстрым или… специфичным для хорошего случая (слишком общего).
Вариант 1: Найдите вложенный многоугольник, это может быть что угодно от треугольника до 6-угольника. Сделайте это, используя некоторые алгоритмы пересечения выпуклого многоугольника за время O (n), которые я нашел. Затем я бы отсортировал эти точки пересечения (новые вершины, до 7 из них O(n log n)) в порядке по часовой стрелке или против часовой стрелки, чтобы я мог запустить простой алгоритм площади на точках (на основе функции Грина) ( О(n) снова). Это самое быстрое, что я могу сделать для произвольного выпуклого n-угольника, пересекающегося с другим m-угольником. Однако… моя проблема определенно не такая сложная, это частный случай, поэтому у нее должно быть лучшее решение…
Вариант 2:
Поскольку я знаю, что это треугольник и единичный квадрат, я могу просто найти список точек пересечения более грубым способом (вместо того, чтобы использовать какой-то алгоритм, который.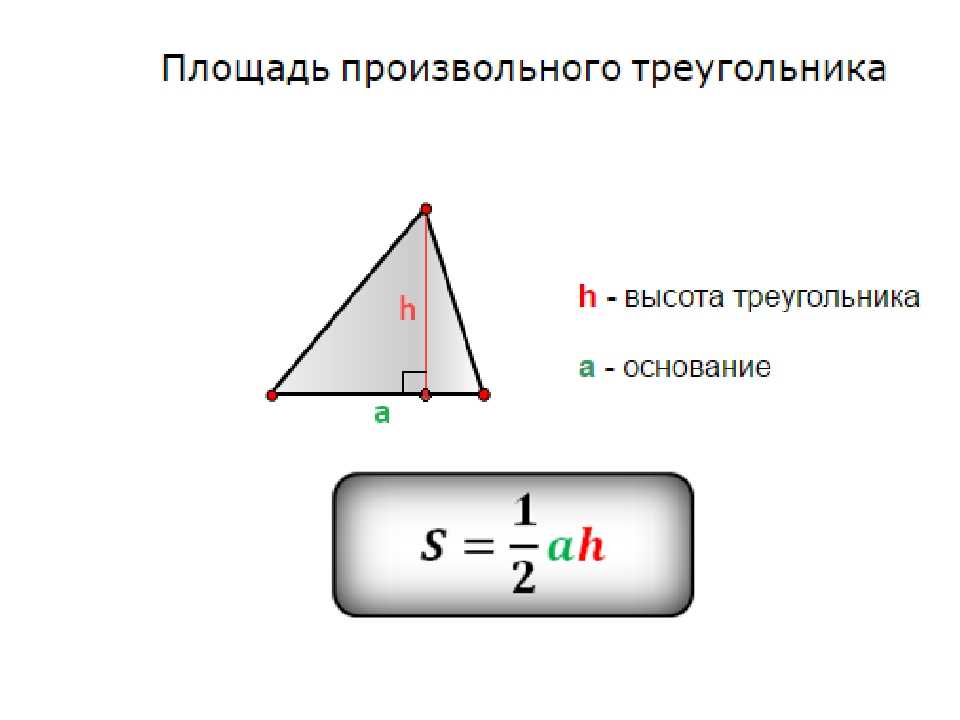 .. откровенно говоря, немного разочаровывает в реализации, как указано выше)
.. откровенно говоря, немного разочаровывает в реализации, как указано выше)
Там всего 19 точек для проверки. 4 точки — углы квадрата внутри треугольника. 3 точки — это треугольник внутри квадрата. И тогда для каждой линии треугольника каждая будет пересекать 4 линии из квадрата (например, линии y=0, y=1, x=0, x=1). это еще 12 баллов. Итак, 12+3+4 = 19точки для проверки. Как только у меня будет максимум 6, минимум 3 точки, которые делают это пересечение, я могу использовать один из двух методов, которые я могу придумать.
2a: Отсортируйте их по возрастанию значения x и просто разложите фигуру на подтреугольники / 4-угольники, каждая с простой формулой, основанной на ограничивающих верхней и нижней линиях. суммировать площади.
или 2b: Снова отсортируйте точки пересечения некоторым циклическим способом, а затем рассчитайте площадь на основе функции зелени.
К сожалению, насколько я могу судить, это все равно оказывается таким же сложным. Я могу начать разбивать все случаи еще немного, чтобы найти точки пересечения, так как я знаю, что это просто 0 и 1 для квадрата, что заставляет математику отбрасывать некоторые термины . .. но это не обязательно просто.
.. но это не обязательно просто.
Вариант 3: Начать разделение проблемы на основе различных условий. Например. 0, 1, 2 или 3 точки треугольника внутри квадрата. Затем для каждого случая пройдите все возможное количество пересечений, а затем для каждого из этих случаев многоугольников однозначно запишите решение площади.
Вариант 4: некоторая формула со ступенчатыми функциями Хэвисайда. Это тот, который мне нужен больше всего, я подозреваю, что он будет немного… большим, но, может быть, я оптимистично смотрю на то, что это возможно, и что это будет самое быстрое время выполнения вычислений, когда у меня будет формула.
— В целом, я знаю, что это можно решить с помощью какой-нибудь высокоуровневой библиотеки (например, clipper). Я также понимаю, что написание общих решений не так сложно при использовании различных структур данных (связный список с последующей его сортировкой). И все эти случаи были бы в порядке, если бы мне просто нужно было сделать это несколько раз.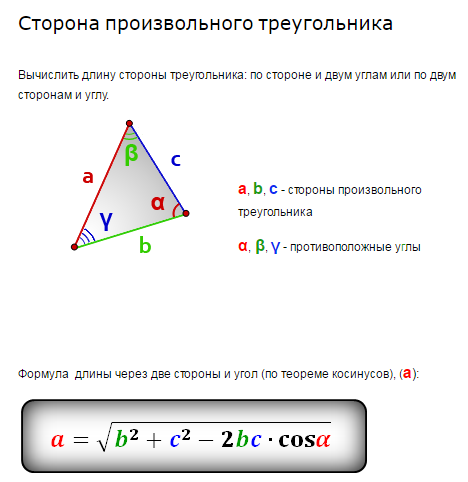 Но, поскольку мне нужно запустить его как шаг обработки изображения, порядка> 9* 1024*1024 раза на изображение, и я снимаю изображения со скоростью .. скажем, 1 кадр/с (технически я хочу увеличить эту скорость как можно быстрее, но нижняя граница составляет 1 секунду, чтобы вычислить 9 миллионов этих пересечений треугольников территориальные проблемы). Это может быть невозможно на процессоре, и это нормально, я, вероятно, все равно реализую это в Cuda, но я хочу увеличить скорость для этой проблемы.
Но, поскольку мне нужно запустить его как шаг обработки изображения, порядка> 9* 1024*1024 раза на изображение, и я снимаю изображения со скоростью .. скажем, 1 кадр/с (технически я хочу увеличить эту скорость как можно быстрее, но нижняя граница составляет 1 секунду, чтобы вычислить 9 миллионов этих пересечений треугольников территориальные проблемы). Это может быть невозможно на процессоре, и это нормально, я, вероятно, все равно реализую это в Cuda, но я хочу увеличить скорость для этой проблемы.
Редактировать: Итак, я остановился на варианте 2b. Поскольку возможных пересечений всего 19, из которых не более 6 определяют форму, я сначала нахожу эти 3–6 вершин. Затем я сортирую их в циклическом (против часовой стрелки) порядке. А затем я нахожу площадь, вычисляя площадь этого многоугольника.
Вот мой тестовый код, который я написал для этого (это для Игоря, но должен читаться как псевдокод) К сожалению, он немного затянут, но… Я думаю, кроме моего дрянного алгоритма сортировки (не должно быть больше 20 свопы, так что не так много накладных расходов на написание лучшей сортировки).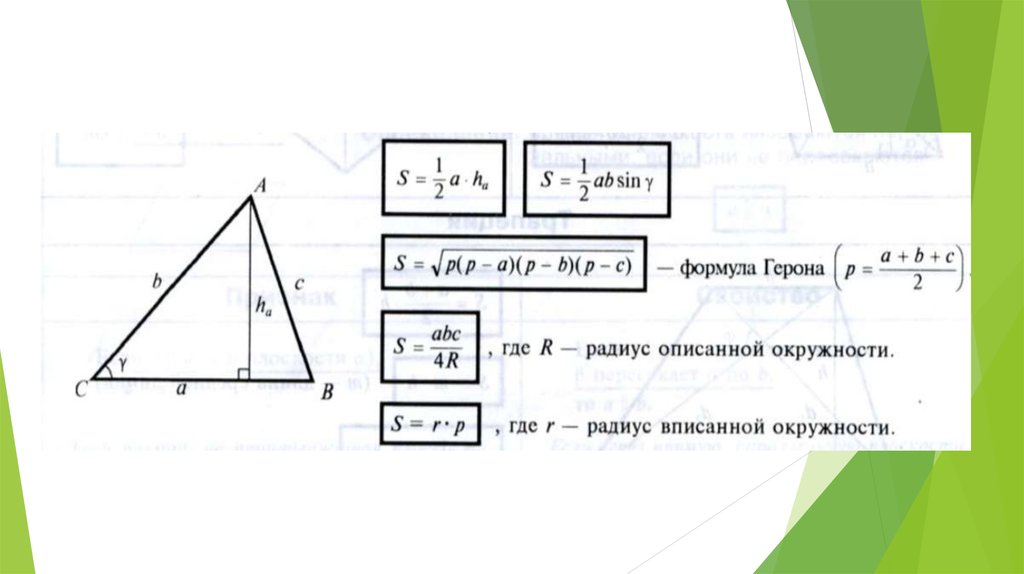 .. кроме этой сортировки, я не думаю, что смогу сделать это быстрее. Тем не менее, я открыт для любых предложений или упущений, которые я мог иметь при выборе этого варианта.
.. кроме этой сортировки, я не думаю, что смогу сделать это быстрее. Тем не менее, я открыт для любых предложений или упущений, которые я мог иметь при выборе этого варианта.
функция calculateAreaUnitSquare(xPos, yPos) волна xPos волна yPos // Во-первых, создайте массив назначения. Не более 7 возможных результатов для этой геометрии. Сделать/o/N=(7) outputVertexX = NaN Сделать/o/N=(7) outputVertexY = NaN переменная pointsfound = 0 // Проверяем 4 угла квадрата // Делаем это, проверяя каждый угол относительно параметризованной плоскости, описанной базисными векторами p2-p0 и p1-p0. // (например, спроецировать на точку - p0 на p2-p0 и на p1-p0. Используя соответствующее масштабирование параметризации (не единицу). // Когда у нас есть параметризация, можно проверить, находится ли он внутри треугольника, проверив, что u и v ограничены u>0, v>0 1-u-v > 0 переменная denom = yPos[0]*xPos[1]-xPos[0]*yPos[1]-yPos[0]*xPos[2]+yPos[1]*xPos[2]+xPos[0]*yPos[ 2]-xPos[1]*yPos[2] //переменная u00 = yPos[0]*xPos[1]-xPos[0]*yPos[1]-yPos[0]*Xx+yPos[1]*Xx+xPos[0]*Yx-xPos[1] *Yx //переменная v00 = -yPos[2]*Xx+yPos[0]*(Xx-xPos[2])+xPos[0]*(yPos[2]-Yx)+yPos[2]*Yx переменная u00 = (yPos[0]*xPos[1]-xPos[0]*yPos[1])/деном переменная v00 = (yPos[0]*(-xPos[2])+xPos[0]*(yPos[2]))/denom переменная u01 =(yPos[0]*xPos[1]-xPos[0]*yPos[1]+xPos[0]-xPos[1])/деном переменная v01 =(yPos[0]*(-xPos[2])+xPos[0]*(yPos[2]-1)+xPos[2])/деном переменная u11 = (yPos[0]*xPos[1]-xPos[0]*yPos[1]-yPos[0]+yPos[1]+xPos[0]-xPos[1])/деном переменная v11 = (-yPos[2]+yPos[0]*(1-xPos[2])+xPos[0]*(yPos[2]-1)+xPos[2])/denom переменная u10 = (yPos[0]*xPos[1]-xPos[0]*yPos[1]-yPos[0]+yPos[1])/деном переменная v10 = (-yPos[2]+yPos[0]*(1-xPos[2])+xPos[0]*(yPos[2]))/denom если(u00 >= 0 && v00 >=0 && (1-u00-v00) >=0) outputVertexX[найдены точки] = 0 outputVertexY[найденные точки] = 0 точек найдено+=1 конец если(u01 >= 0 && v01 >=0 && (1-u01-v01) >=0) outputVertexX[найдены точки] = 0 outputVertexY[найденные точки] = 1 точек найдено+=1 конец если(u10 >= 0 && v10 >=0 && (1-u10-v10) >=0) outputVertexX[найдены точки] = 1 outputVertexY[найденные точки] = 0 точек найдено+=1 конец если(u11 >= 0 && v11 >=0 && (1-u11-v11) >=0) outputVertexX[найдены точки] = 1 outputVertexY[найденные точки] = 1 точек найдено+=1 конец // Проверяем 3 точки на треугольник.Это легко, просто посмотрите, ограничено ли оно единичным квадратом. если есть то добавьте. переменная я = 0 для (я = 0; я <3; я + = 1) если (xPos[i] >= 0 && xPos[i] <= 1 ) if(yPos[i] >=0 && yPos[i] <=1) if(!((xPos[i] == 0 || xPos[i] == 1) && (yPos[i] == 0 || yPos[i] == 1)) )) outputVertexX[найденные точки] = xPos[i] outputVertexY[найденные точки] = yPos[i] точек найдено+=1 конец конец конец конец для // Проверяем пересечения. // Процедура: цикл по трем линиям треугольника. // Для каждой строки // Проверяем вертикальность // Если не по вертикали, найти точку пересечения y с линиями x=0 и x=1. // если y точка пересечения находится между 0 и 1, то добавляем точку // Проверяем горизонтальность // если не горизонтально, найти точку пересечения x с линиями y=0 и y=1 // если точка пересечения x находится между 0 и 1, то добавляем точку для (я = 0; я <3; я + = 1) переменная iN = mod(i+1,3) если(xPos[i] != xPos[iN]) переменная tx0 = xPos[i]/(xPos[i] - xPos[iN]) переменная tx1 = (xPos[i]-1)/(xPos[i] - xPos[iN]) если (tx0 > 0 && tx0 < 1) переменная yInt = (yPos[iN]-yPos[i])*tx0+yPos[i] если (yInt > 0 && yInt <1) outputVertexX[найдены точки] = 0 outputVertexY[найденные точки] = yInt точек найдено+=1 конец конец если (tx1 > 0 && tx1 < 1) yInt = (yPos[iN]-yPos[i])*tx1+yPos[i] если (yInt > 0 && yInt <1) outputVertexX[найдены точки] = 1 outputVertexY[найденные точки] = yInt точек найдено+=1 конец конец конец если(yPos[i] != yPos[iN]) переменная ty0 = yPos[i]/(yPos[i] - yPos[iN]) переменная ty1 = (yPos[i]-1)/(yPos[i] - yPos[iN]) если (ty0 > 0 && ty0 < 1) переменная xInt = (xPos[iN]-xPos[i])*ty0+xPos[i] если (xInt > 0 && xInt <1) outputVertexX[найденные точки] = xInt outputVertexY[найденные точки] = 0 точек найдено+=1 конец конец если (ty1 > 0 && ty1 < 1) xInt = (xPos[iN]-xPos[i])*ty1+xPos[i] если (xInt > 0 && xInt <1) outputVertexX[найденные точки] = xInt outputVertexY[найденные точки] = 1 точек найдено+=1 конец конец конец конец для // Теперь у нас есть все 6 вершин, которые нам нужны.
2) ) : 0 // Теперь отсортируем оставшиеся вершины по этому угловому смещению. Это сориентирует точки выпуклого многоугольника в его максимальном размере / ориентации против часовой стрелки. // (Эта сортировка дерьмовая, но теоретически будет не более 25 свопов. Что в общей схеме операций не так уж и плохо. переменная j for(i=1; i<найденых точек; i+=1) for(j=i+1; j<найденых точек; j+=1) если (углы [j] > углы [i]) переменная tempX = outputVertexX[j] переменная tempY = outputVertexY[j] выходная вершинаX[j] = выходнаявершинаX[i] outputVertexY[j] = outputVertexY[i] outputVertexX[i] = tempX outputVertexY[i] = tempY переменная tempA = углы [j] углы [j] = углы [i] углы [я] = темпА конец конец для конец для // Теперь список упорядочен! // теперь вычисляем площадь по списку ориентированных против часовой стрелки точек на выпуклом многоугольнике. // имеет простую и легкую математическую формулу: http://www.

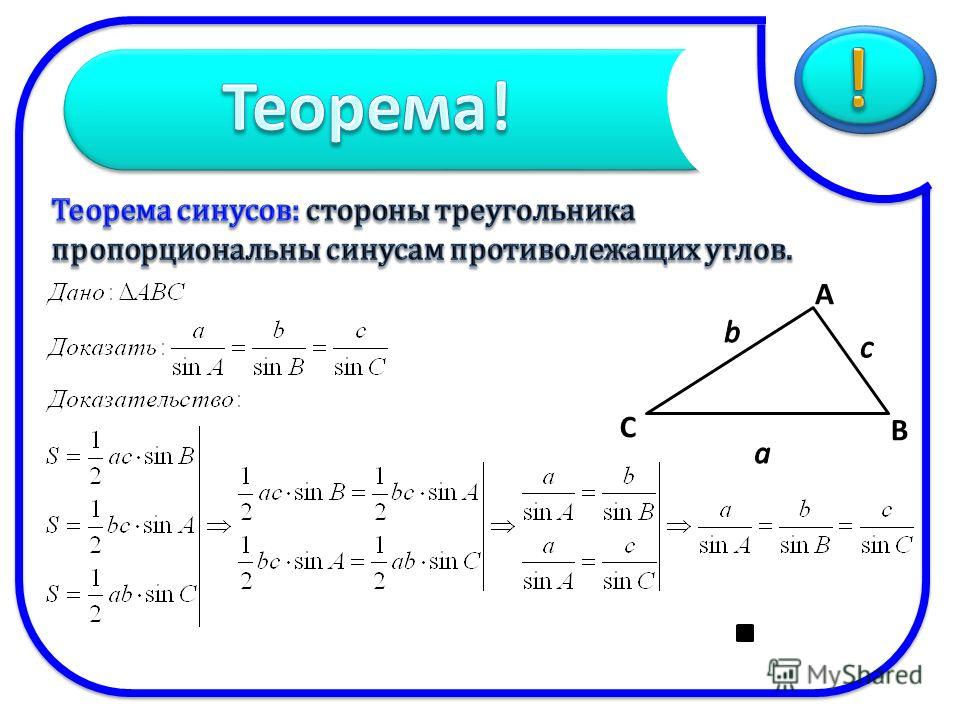 (Формула 8)
(Формула 8)
 Найдите его полупериметр и его площадь.
Найдите его полупериметр и его площадь.
 Это легко, просто посмотрите, ограничено ли оно единичным квадратом. если есть то добавьте.
переменная я = 0
для (я = 0; я <3; я + = 1)
если (xPos[i] >= 0 && xPos[i] <= 1 )
if(yPos[i] >=0 && yPos[i] <=1)
if(!((xPos[i] == 0 || xPos[i] == 1) && (yPos[i] == 0 || yPos[i] == 1)) ))
outputVertexX[найденные точки] = xPos[i]
outputVertexY[найденные точки] = yPos[i]
точек найдено+=1
конец
конец
конец
конец для
// Проверяем пересечения.
// Процедура: цикл по трем линиям треугольника.
// Для каждой строки
// Проверяем вертикальность
// Если не по вертикали, найти точку пересечения y с линиями x=0 и x=1.
// если y точка пересечения находится между 0 и 1, то добавляем точку
// Проверяем горизонтальность
// если не горизонтально, найти точку пересечения x с линиями y=0 и y=1
// если точка пересечения x находится между 0 и 1, то добавляем точку
для (я = 0; я <3; я + = 1)
переменная iN = mod(i+1,3)
если(xPos[i] != xPos[iN])
переменная tx0 = xPos[i]/(xPos[i] - xPos[iN])
переменная tx1 = (xPos[i]-1)/(xPos[i] - xPos[iN])
если (tx0 > 0 && tx0 < 1)
переменная yInt = (yPos[iN]-yPos[i])*tx0+yPos[i]
если (yInt > 0 && yInt <1)
outputVertexX[найдены точки] = 0
outputVertexY[найденные точки] = yInt
точек найдено+=1
конец
конец
если (tx1 > 0 && tx1 < 1)
yInt = (yPos[iN]-yPos[i])*tx1+yPos[i]
если (yInt > 0 && yInt <1)
outputVertexX[найдены точки] = 1
outputVertexY[найденные точки] = yInt
точек найдено+=1
конец
конец
конец
если(yPos[i] != yPos[iN])
переменная ty0 = yPos[i]/(yPos[i] - yPos[iN])
переменная ty1 = (yPos[i]-1)/(yPos[i] - yPos[iN])
если (ty0 > 0 && ty0 < 1)
переменная xInt = (xPos[iN]-xPos[i])*ty0+xPos[i]
если (xInt > 0 && xInt <1)
outputVertexX[найденные точки] = xInt
outputVertexY[найденные точки] = 0
точек найдено+=1
конец
конец
если (ty1 > 0 && ty1 < 1)
xInt = (xPos[iN]-xPos[i])*ty1+xPos[i]
если (xInt > 0 && xInt <1)
outputVertexX[найденные точки] = xInt
outputVertexY[найденные точки] = 1
точек найдено+=1
конец
конец
конец
конец для
// Теперь у нас есть все 6 вершин, которые нам нужны.
Это легко, просто посмотрите, ограничено ли оно единичным квадратом. если есть то добавьте.
переменная я = 0
для (я = 0; я <3; я + = 1)
если (xPos[i] >= 0 && xPos[i] <= 1 )
if(yPos[i] >=0 && yPos[i] <=1)
if(!((xPos[i] == 0 || xPos[i] == 1) && (yPos[i] == 0 || yPos[i] == 1)) ))
outputVertexX[найденные точки] = xPos[i]
outputVertexY[найденные точки] = yPos[i]
точек найдено+=1
конец
конец
конец
конец для
// Проверяем пересечения.
// Процедура: цикл по трем линиям треугольника.
// Для каждой строки
// Проверяем вертикальность
// Если не по вертикали, найти точку пересечения y с линиями x=0 и x=1.
// если y точка пересечения находится между 0 и 1, то добавляем точку
// Проверяем горизонтальность
// если не горизонтально, найти точку пересечения x с линиями y=0 и y=1
// если точка пересечения x находится между 0 и 1, то добавляем точку
для (я = 0; я <3; я + = 1)
переменная iN = mod(i+1,3)
если(xPos[i] != xPos[iN])
переменная tx0 = xPos[i]/(xPos[i] - xPos[iN])
переменная tx1 = (xPos[i]-1)/(xPos[i] - xPos[iN])
если (tx0 > 0 && tx0 < 1)
переменная yInt = (yPos[iN]-yPos[i])*tx0+yPos[i]
если (yInt > 0 && yInt <1)
outputVertexX[найдены точки] = 0
outputVertexY[найденные точки] = yInt
точек найдено+=1
конец
конец
если (tx1 > 0 && tx1 < 1)
yInt = (yPos[iN]-yPos[i])*tx1+yPos[i]
если (yInt > 0 && yInt <1)
outputVertexX[найдены точки] = 1
outputVertexY[найденные точки] = yInt
точек найдено+=1
конец
конец
конец
если(yPos[i] != yPos[iN])
переменная ty0 = yPos[i]/(yPos[i] - yPos[iN])
переменная ty1 = (yPos[i]-1)/(yPos[i] - yPos[iN])
если (ty0 > 0 && ty0 < 1)
переменная xInt = (xPos[iN]-xPos[i])*ty0+xPos[i]
если (xInt > 0 && xInt <1)
outputVertexX[найденные точки] = xInt
outputVertexY[найденные точки] = 0
точек найдено+=1
конец
конец
если (ty1 > 0 && ty1 < 1)
xInt = (xPos[iN]-xPos[i])*ty1+xPos[i]
если (xInt > 0 && xInt <1)
outputVertexX[найденные точки] = xInt
outputVertexY[найденные точки] = 1
точек найдено+=1
конец
конец
конец
конец для
// Теперь у нас есть все 6 вершин, которые нам нужны. 2) ) : 0
// Теперь отсортируем оставшиеся вершины по этому угловому смещению. Это сориентирует точки выпуклого многоугольника в его максимальном размере / ориентации против часовой стрелки.
// (Эта сортировка дерьмовая, но теоретически будет не более 25 свопов. Что в общей схеме операций не так уж и плохо.
переменная j
for(i=1; i<найденых точек; i+=1)
for(j=i+1; j<найденых точек; j+=1)
если (углы [j] > углы [i])
переменная tempX = outputVertexX[j]
переменная tempY = outputVertexY[j]
выходная вершинаX[j] = выходнаявершинаX[i]
outputVertexY[j] = outputVertexY[i]
outputVertexX[i] = tempX
outputVertexY[i] = tempY
переменная tempA = углы [j]
углы [j] = углы [i]
углы [я] = темпА
конец
конец для
конец для
// Теперь список упорядочен!
// теперь вычисляем площадь по списку ориентированных против часовой стрелки точек на выпуклом многоугольнике.
// имеет простую и легкую математическую формулу: http://www.
2) ) : 0
// Теперь отсортируем оставшиеся вершины по этому угловому смещению. Это сориентирует точки выпуклого многоугольника в его максимальном размере / ориентации против часовой стрелки.
// (Эта сортировка дерьмовая, но теоретически будет не более 25 свопов. Что в общей схеме операций не так уж и плохо.
переменная j
for(i=1; i<найденых точек; i+=1)
for(j=i+1; j<найденых точек; j+=1)
если (углы [j] > углы [i])
переменная tempX = outputVertexX[j]
переменная tempY = outputVertexY[j]
выходная вершинаX[j] = выходнаявершинаX[i]
outputVertexY[j] = outputVertexY[i]
outputVertexX[i] = tempX
outputVertexY[i] = tempY
переменная tempA = углы [j]
углы [j] = углы [i]
углы [я] = темпА
конец
конец для
конец для
// Теперь список упорядочен!
// теперь вычисляем площадь по списку ориентированных против часовой стрелки точек на выпуклом многоугольнике.
// имеет простую и легкую математическую формулу: http://www.