Формула сумма 4 степени: Формулы сокращённого умножения

Содержание

Таблицы с формулами сокращенного умножения по алгебре 7 класса

Ниже представлены таблицы с формулами сокращенного умножения для различных степеней (квадрат, куб, четвертая и n-я степень), которые изучаются в школьной программе по алгебре 7 и более старших классов.

Формулы для квадратов


Квадрат суммы	(a + b)² = a² + 2ab + b²
Квадрат разности	(a — b)² = a² — 2ab + b²
Разность квадратов	a² — b² = (a + b)(a — b)
Квадрат суммы 3 слагаемых	(a + b + c)² = a² + b² + c² + 2ab + 2ac + 2bc

microexcel. ru

Формулы для кубов


Куб суммы	(a + b)³ = a³ + 3a²b + 3ab² + b³
Куб разности	(a — b)³ = a³ — 3a²b + 3ab² — b³
Сумма кубов	a³ + b³ = (a + b)(a² — ab + b²)
Разность кубов	a³ — b³ = (a — b)(a² + ab + b²)
Куб суммы 3 слагаемых	(a + b + с)³ = a³ + b³ + с³ + 3a²b + 3a²с + 3ab² + 3aс² + 3b²с + 3bc² + 6abc

microexcel. ru

Формулы для четвертой степени


Четвертая степень суммы	(a + b)⁴ = a⁴ + 4a³b + 6a²b² + 4ab³ + b⁴
Четвертая степень разности	(a — b)⁴ = a⁴ — 4a³b + 6a²b² — 4ab³ + b⁴
Разность четвертых степеней	a⁴ — b⁴ = (a — b)(a + b)(a² + b²)

microexcel. ru

Формулы для степени n


n-я степень суммы	ru/wp-content/uploads/2020/04/n-stepen-summy-6.png" class="stbSkipLazy aligncenter size-full" width="750" height="1245" data-full="https://microexcel.ru/wp-content/uploads/2020/04/n-stepen-summy-6.png" />» data-order=»<img src="https://microexcel.ru/wp-content/uploads/2020/04/n-stepen-summy-6.png" class="stbSkipLazy aligncenter size-full" width="750" height="1245" data-full="https://microexcel.ru/wp-content/uploads/2020/04/n-stepen-summy-6.png" />»>
сумма n-ых степеней	..- ab<sup>n-2</sup> + b<sup>n-1</sup>)</em></span></nobr><br><nobr><span class="math"><em>n</em></span> — нечетное положительное число</nobr>» data-order=»<nobr><span class="math"><em>a<sup>n</sup> + b<sup>n</sup> = (a+b)(a<sup>n-1</sup> — a<sup>n-2</sup>b +…- ab<sup>n-2</sup> + b<sup>n-1</sup>)</em></span></nobr><br><nobr><span class="math"><em>n</em></span> — нечетное положительное число</nobr>»>aⁿ + bⁿ = (a+b)(a^n-1 — a^n-2b +…- ab^n-2 + b^n-1) n — нечетное положительное число
разность n-ых степеней	..+ ab<sup>n-2</sup> + b<sup>n-1</sup>)</em></span></nobr><br><nobr><span class="math"><em>n</em></span> — любое натуральное число</nobr>» data-order=»<nobr><span class="math"><em>a<sup>n</sup> — b<sup>n</sup> = (a-b)(a<sup>n-1</sup> + a<sup>n-2</sup>b +…+ ab<sup>n-2</sup> + b<sup>n-1</sup>)</em></span></nobr><br><nobr><span class="math"><em>n</em></span> — любое натуральное число</nobr>»>aⁿ — bⁿ = (a-b)(a^n-1 + a^n-2b +…+ ab^n-2 + b^n-1) n — любое натуральное число

microexcel.ru

Разложение суммы 4 степени. Калькулятор онлайн.Упрощение многочлена.Умножение многочленов

В предыдущем уроке мы разобрались с разложением на множители. Освоили два способа: вынесение общего множителя за скобки и группировку. В этом уроке — следующий мощный способ: формулы сокращённого умножения . В краткой записи — ФСУ.

Формулы сокращённого умножения (квадрат суммы и разности, куб суммы и разности, разность квадратов, сумма и разность кубов) крайне необходимы во всех разделах математики. Они применяются в упрощении выражений, решении уравнений, умножении многочленов, сокращении дробей, решении интегралов и т.д. и т.п. Короче, есть все основания разобраться с ними. Понять откуда они берутся, зачем они нужны, как их запомнить и как применять.

Разбираемся?)

Откуда берутся формулы сокращённого умножения?

Равенства 6 и 7 записаны не очень привычно. Как бы наоборот. Это специально.) Любое равенство работает как слева направо, так и справа налево. В такой записи понятнее, откуда берутся ФСУ.

Они берутся из умножения.) Например:

(a+b) 2 =(a+b)(a+b)=a 2 +ab+ba+b 2 =a 2 +2ab+b 2

Вот и всё, никаких научных хитростей. Просто перемножаем скобки и приводим подобные. Так получаются все формулы сокращённого умножения. Сокращённое умножение — это потому, что в самих формулах нет перемножения скобок и приведения подобных. Сокращены.) Сразу дан результат.

ФСУ нужно знать наизусть. Без первых трёх можно не мечтать о тройке, без остальных — о четвёрке с пятёркой.)

Зачем нужны формулы сокращённого умножения?

Есть две причины, выучить, даже зазубрить эти формулы. Первая — готовый ответ на автомате резко уменьшает количество ошибок. Но это не самая главная причина. А вот вторая…

Если Вам нравится этот сайт…

Кстати, у меня есть ещё парочка интересных сайтов для Вас.)

Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)

можно познакомиться с функциями и производными.

Для того что бы упростить алгебраические многочлены, существуют формулы сокращенного умножения . Их не так уж и много и они легко запоминаются, а запомнить их нужно. Обозначения которые используются в формулах, могут принимать любой вид (число или многочлен).

Первая формула сокращенного умножения называется разность квадратов . Она заключается в том что из квадрата одного числа отнимается квадрат второго числа равен величине разности данных чисел, а также их произведению.

а 2 — b 2 = (а — b)(a + b)

Разберем для наглядности:

22 2 — 4 2 = (22-4)(22+4)=18 * 26 = 468
9а 2 — 4b 2 c 2 = (3a — 2bc)(3a + 2bc)

Вторая формула о сумме квадратов . Звучит она как, сумма двух величин в квадрате равняется квадрату первой величины к ней прибавляется двойное произведение первой величины умноженное на вторую, к ним прибавляется квадрат второй величины.

(а + b) 2 = a 2 +2ab + b 2

Благодаря данной формуле, становится намного проще вычислять квадрат от большого числа, без использования вычислительной техники.

Так к примеру: квадрат от 112 будет равен
1) В начале разберем 112 на числа квадраты которых нам знакомы
112 = 100 + 12
2) Вписываем полученное в скобки возведенные в квадрат
112 2 = (100+12) 2
3) Применяя формулу, получаем:
112 2 = (100+12) 2 = 100 2 + 2 * 100 * 12 + 122 = 10000 + 2400+ 144 = 12544

Третья формула это квадрат разности . Которая гласит о том, что две вычитаемые друг друга величины в квадрате равняются, тому что, от первой величины в квадрате отнимаем двойное произведение первой величины умноженное на вторую, прибавляя к ним квадрат второй величины.

(а +b) 2 = а 2 — 2аb + b 2

где (а — b) 2 равняется (b — а) 2 . В доказательство чему, (а-b) 2 = а 2 -2аb+b 2 = b 2 -2аb + а 2 = (b-а) 2

Четвертая формула сокращенного умножения называется куб суммы . Которая звучит как: две слагаемые величины в кубе равны кубу 1 величины прибавляется тройное произведение 1 величины в квадрате умноженное на 2-ую величину, к ним прибавляется тройное произведение 1 величины умноженной на квадрат 2 величины, плюс вторая величина в кубе.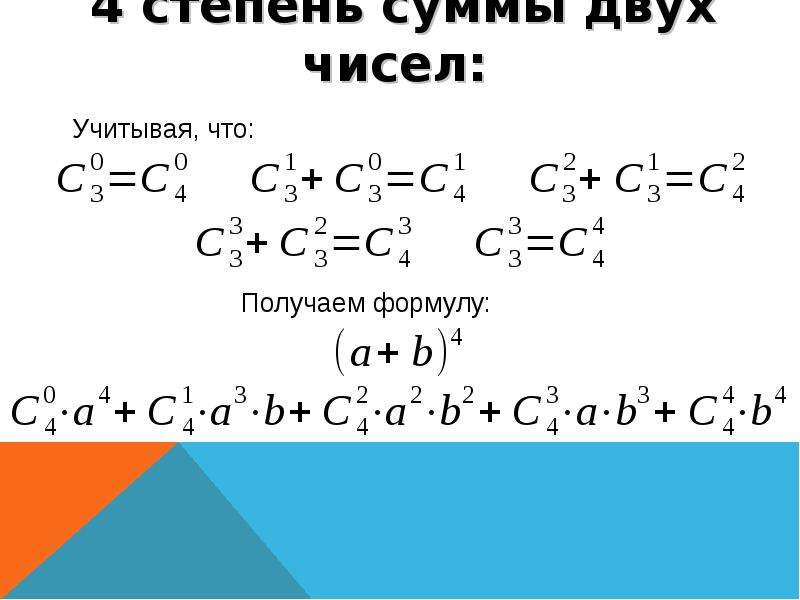

(а+b) 3 = а 3 + 3а 2 b + 3аb 2 + b 3

Пятая, как вы уже поняли называется куб разности . Которая находит разности между величинами, как от первого обозначения в кубе отнимаем тройное произведение первого обозначения в квадрате умноженное на второе, к ним прибавляется тройное произведение первого обозначения умноженной на квадрат второго обозначения, минус второе обозначение в кубе.

(а-b) 3 = а 3 — 3а 2 b + 3аb 2 — b 3

Шестая называется — сумма кубов . Сумма кубов равняется произведению двух слагаемых величин, умноженных на неполный квадрат разности, так как в середине нет удвоенного значения.

а 3 + b 3 = (а+b)(а 2 -аb+b 2)

По другому можно сказать сумму кубов можно назвать произведение в двух скобках.

Седьмая и заключительная, называется разность кубов (ее легко перепутать с формулой куба разности, но это разные вещи). Разность кубов равняется произведению от разности двух величин, умноженных на неполный квадрат суммы, так как в середине нет удвоенного значения.

а 3 — b 3 = (а-b)(а 2 +аb+b 2)

И так формул сокращенного умножения всего 7, они похожи друг на друга и легко запоминаются, единственно важно не путаться в знаках. Они так же рассчитаны на то, что их можно использовать в обратном порядке и в учебниках собрано довольно много таких заданий. Будьте внимательны и все у вас получится.

Если у вас появились вопросы по формулам, обязательно пишите их в комментариях. Будем рады ответить вам!

Если Вы находитесь в декретном отпуске, но хотите зарабатывать деньги. Просто перейдите по ссылке Интернет бизнес с Орифлейм . Там все очень подробно написано и показано. Будет интересно!

Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.

Сбор и использование персональной информации

Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.

От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.

Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.

Какую персональную информацию мы собираем:

Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.

Как мы используем вашу персональную информацию:

Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.

Раскрытие информации третьим лицам

Мы не раскрываем полученную от Вас информацию третьим лицам.

Исключения:

В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.

Защита персональной информации

Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.

Соблюдение вашей конфиденциальности на уровне компании

Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.

Формулы сокращенного выражения очень часто применяются на практике, так что их все желательно выучить наизусть. До этого момента нам будет служить верой и правдой , которую мы рекомендуем распечатать и все время держать перед глазами:

Первые четыре формулы из составленной таблицы формул сокращенного умножения позволяют возводить в квадрат и куб сумму или разность двух выражений. Пятая предназначена для краткого умножения разности и суммы двух выражений. А шестая и седьмая формулы используются для умножения суммы двух выражений a и b на их неполный квадрат разности (так называют выражение вида a 2 −a·b+b 2 ) и разности двух выражений a и b на неполный квадрат их суммы (a 2 +a·b+b 2 ) соответственно.

Стоит отдельно заметить, что каждое равенство в таблице представляет собой тождество . Этим объясняется, почему формулы сокращенного умножения еще называют тождествами сокращенного умножения.

При решении примеров, особенно в которых имеет место разложение многочлена на множители , ФСУ часто используют в виде с переставленными местами левыми и правыми частями:

Три последних тождества в таблице имеют свои названия. Формула a 2 −b 2 =(a−b)·(a+b) называется формулой разности квадратов , a 3 +b 3 =(a+b)·(a 2 −a·b+b 2 ) — формулой суммы кубов , а a 3 −b 3 =(a−b)·(a 2 +a·b+b 2 ) — формулой разности кубов . Обратите внимание, что соответствующим формулам с переставленными частями из предыдущей таблицы фсу мы никак не назвали.

Дополнительные формулы

В таблицу формул сокращенного умножения не помешает добавить еще несколько тождеств.

Сферы применения формул сокращенного умножения (фсу) и примеры

Основное предназначение формул сокращенного умножения (фсу) объясняется их названием, то есть, оно состоит в кратком умножении выражений. Однако сфера применения ФСУ намного шире, и не ограничивается кратким умножением. Перечислим основные направления.

Несомненно, центральное приложение формулы сокращенного умножения нашли в выполнении тождественных преобразований выражений . Наиболее часто эти формулы используются в процессе упрощения выражений .

Пример.

Упростите выражение 9·y−(1+3·y) 2 .

Решение.

В данном выражении возведение в квадрат можно выполнить сокращенно, имеем 9·y−(1+3·y) 2 =9·y−(1 2 +2·1·3·y+(3·y) 2) . Остается лишь раскрыть скобки и привести подобные члены: 9·y−(1 2 +2·1·3·y+(3·y) 2)= 9·y−1−6·y−9·y 2 =3·y−1−9·y 2 .

Применяют для упрощения вычислений, а также разложение многочленов на множители, быстрого умножения многочленов. Большинство формул сокращенного умножения можно получить из бинома Ньютона — в этом Вы скоро убедитесь.

Формулы для квадратов применяют в вычислениях чаще. Их начинают изучать в школьной программе начиная с 7 класса и до конца обучения формулы для квадратов и кубов школьники должны знать на зубок. 7.

Решение. Что такое бином Ньютона Вы вероятно уже знаете. Если нет то ниже приведены биномиальные коэффициенты

Они образуются следующим образом: по краю идут единицы, коэффициенты между ними в нижней строке образуют суммированием соседних верхних. Если ищем разницу в каком-то степени, то знаки в расписании чередуются от плюса к минусу. Таким образом для седьмого порядка получим такой расклад

Внимательно также посмотрите как меняются показатели — для первой переменной они уменьшаются на единицу в каждом следующем слагаемом, соответственно для второй — на единицу растут. В сумме показатели всегда должны быть равны степени разложения (=7 ).

Думаю на основе приведенного выше материала Вы сможете решить задачи на бином Ньютона. Изучайте формулы сокращенного умножения и применяйте везде, где это может упростить вычисления и сэкономит время выполнения задания.

Все формулы сокращенного умножения, объяснения, примеры

Будут и задачи для самостоятельного решения, к которым можно посмотреть ответы.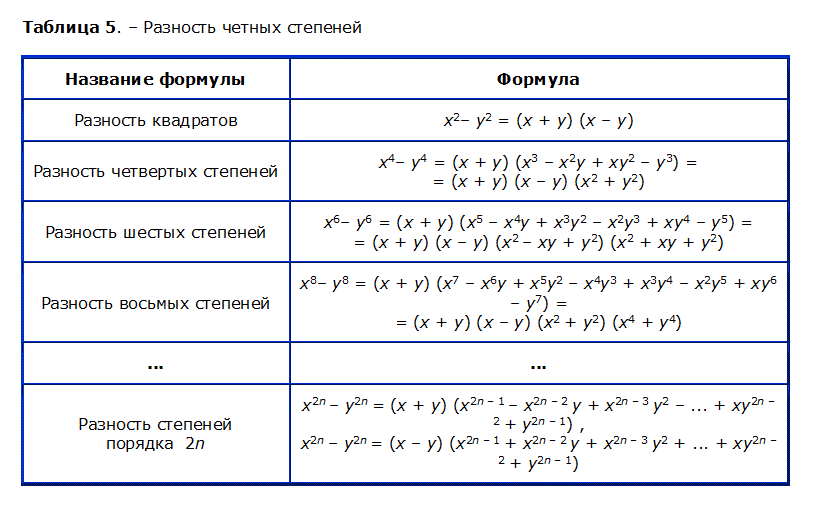

Формулы сокращённого умножения позволяют производить тождественные преобразования выражений — многочленов. С их помощью многочлены можно разложить на множители, а применяя формулы в обратном порядке — представлять произведения двучленов, квадраты и кубы в виде многочленов. Рассмотрим все общепринятые формулы сокращённого умножения, их вывод, распространённые задачи на тождественные преобразования выражений с помощью этих формул, а также домашние задания (ответы к ним открываются по ссылкам).

Формулой квадрата суммы называется равенство

(квадрат суммы двух чисел равен квадрату первого числа плюс удвоенное произведение первого числа на второе плюс квадрат второго числа).

Вместо a и b в эту формулу могут быть подставлены любые числа.

Формула квадрата суммы часто применяется для упрощения вычислений. Например,

С помощью формулы квадрата суммы многочлен можно разложить на множители, а именно, представить в виде произведения двух одинаковых множителей .

Формула следует из правила умножения многчлена на многочлен:

Пример 1. Записать в виде многочлена выражение

Решение. По формуле квадрата суммы получаем

Пример 2. Записать в виде многочлена выражение

Решение. По формуле квадрата суммы получаем

Применить формулу сокращённого умножения самостоятельно, а затем посмотреть решение

Формулой квадрата разности называется равенство

(квадрат разности двух чисел равен квадрату первого числа минус удвоенное произведение первого числа на второе плюс квадрат второго числа).

Формула квадрата разности часто применяется для упрощения вычислений. Например,

С помощью формулы квадрата разности многочлен можно разложить на множители, а именно, представить в виде произведения двух одинаковых множителей .

Формула следует из правила умножения многчлена на многочлен:

Пример 5. Записать в виде многочлена выражение

Решение. По формуле квадрата разности получаем

Применить формулу сокращённого умножения самостоятельно, а затем посмотреть решение

Часто в многочлене второй степени содержится квадрат суммы или разности, но содержится в скрытом виде. Чтобы получить полный квадрат в явном виде, нужно преобразовать многочлен. Для этого, как правило, одно из слагаемых многочлена представляется в виде удвоенного произведения, а затем к многочлену прибавляется и из него вычитается одно и то же число.

Пример 7. Рассмотрим многочлен второй степени

Решение. Этот многочлен можно преобразовать следующим образом:

Здесь мы представили 5x в виде удвоенного произведения 5/2 на x, прибавили к многочлену и вычли из него одно и то же число , далее применили формулу квадрата суммы для двучлена .

Итак, мы доказали равенство

показывающее, что многочлен второй степени

равен полному квадрату плюс число .

Пример 8. Рассмотрим многочлен второй степени

Решение. Проведём над ним следующие преобразования:

Здесь мы представили 8x в виде удвоенного произведения x на 4, прибавили к многочлену и вычли из него одно и то же число 4², применили формулу квадрата разности для двучлена x − 4.

Итак, мы доказали равенство

показывающее, что многочлен второй степени

равен полному квадрату плюс число −16.

Применить формулу сокращённого умножения самостоятельно, а затем посмотреть решение

Формулой куба суммы называется равенство

(куб суммы двух чисел равен кубу первого числа плюс утроенное произведение квадрата первого числа на второе, плюс утроенное произведение первого числа на квадрат второго и плюс куб второго числа).

С помощью формулы куба суммы многочлен можно разложить на множители, а именно, представить в виде произведения трёх одинаковых множителей .

Формула куба суммы выводится так:

Пример 10. Записать в виде многочлена выражение

Решение. По формуле куба суммы получаем

Применить формулу сокращённого умножения самостоятельно, а затем посмотреть решение

Формулой куба разности называется равенство

(куб разности двух чисел равен кубу первого числа минус утроенное произведение квадрата первого числа на второе, плюс утроенное произведение первого числа на квадрат второго минус куб второго числа).

Формула куба разности выводится так:

Пример 12. Записать в виде многочлена выражение

Решение. По формуле куба разности получаем

Применить формулу сокращённого умножения самостоятельно, а затем посмотреть решение

Формулой разности квадратов называется равенство

(разность квадратов двух чисел равна произведению суммы эти чисел на их разность).

С помощью формулы куба суммы любой многочлен вида можно разложить на множители.

Доказательство формулы получено с применением правила умножения многочленов:

Пример 14. Записать в виде многочлена произведение

Решение. По формуле разности квадратов получаем

Пример 15. Разложить на множители

Решение. Это выражение в явной форме ни под одно тождество не подходит. Но число 16 можно представить в виде степени с основанием 4: 16=4². Тогда исходное выражение примет иной вид:

а это уже формула разности квадратов, и, применив эту формулу, получим

Применить формулу сокращённого умножения самостоятельно, а затем посмотреть решение

Формулой суммы кубов называется равенство

(сумма кубов двух чисел равна произведению суммы эти чисел на неполный квадрат разности этих чисел).

Неполным квадратом разности a и b называется многочлен .

С помощью формулы куба суммы любой многочлен вида можно разложить на множители.

Доказательство формулы получено с применением правила умножения многочленов:

Пример 17. Записать в виде многочлена произведение

Решение. Возводим в третью степень слагаемые в первых скобках и получаем их сумму:

Тот же результат получаем, выполняя умножение выражений в скобках по правилам умножения многочленов:

Применить формулу сокращённого умножения самостоятельно, а затем посмотреть решение

Формулой разности кубов называется равенство

(разность кубов двух чисел равна произведению разности эти чисел на неполный квадрат суммы этих чисел).

Неполным квадратом разности a и b называется многочлен .

С помощью формулы куба суммы любой многочлен вида можно разложить на множители.

Пример 19. Записать в виде многочлена произведение

Решение. Возводим в третью степень слагаемые в первых скобках:

Получаем разность этих кубов:

Применить формулу сокращённого умножения самостоятельно, а затем посмотреть решение

Другие темы в блоке «Школьная математика»

Формулы сокращенного умножения 💣

Формулы сокращенного умножения

Вместо букв a, b могут быть любые числа, переменные или даже целые выражения. Для быстрого решения задач лучше выучить основные 7 формул сокращенного умножения (ФСУ) наизусть. Да, алгебра такая, нужно быть готовым много запоминать.

Ниже удобная табличка, которую можно распечатать и использовать, как закладку для быстрого запоминания формул.

Как читать формулы сокращенного умножения

Учимся проговаривать формулы сокращенного выражения:

Разность квадратов двух выражений равна произведению их разности и их суммы.

Квадрат суммы двух выражений равен квадрату первого плюс удвоенное произведение первого на второе плюс квадрат второго.

Квадрат разности двух выражений равен квадрату первого минус удвоенное произведение первого на второе плюс квадрат второго.

Сумма кубов двух выражений равна произведению суммы первого и второго на неполный квадрат их разности.

Разность кубов двух выражений равна произведению разности первого и второго на неполный квадрат их суммы.

Куб суммы двух выражений равен кубу первого плюс утроенное произведение квадрата первого на второе плюс утроенное произведение первого на квадрат второго плюс куб второго.

Куб разности двух выражений равен кубу первого минус утроенное произведение квадрата первого на второе плюс утроенное произведение первого на квадрат второго минус куб второго.

Доказательство формул сокращенного умножения

Напомним, что разность квадратов двух чисел a и b равна произведению их разности и их суммы: a² — b² = (a — b) * (a + b).

Иначе говоря, произведение суммы a и b на их разность равна разности их квадратов: (a — b) * (a + b) = a² — b².

Важно знать, что разность квадратов не равна квадрату разности: a² — b² ≠ (a — b)².

Докажем, что a² — b² = (a — b) * (a + b).

Поехали:

Используя искусственный метод, прибавим и отнимем одно и тоже a * b.
+ a * b — a * b = 0
a² — b² = a² — b² + ab — ab

Сгруппируем иначе: a² — b² + a * b — a * b = a² — a * b + a * b — b²

Продолжим группировать: a² — a * b — b² +a * b = (a² — a * b) + (a * b — b²)

Вынесем общие множители за скобки:
(a² — a * b) + (a * b — b²) = a *(a — b) + b *(a — b)

Вынесем за скобки (a — b). a * (a — b) + b * (a — b) = (a — b) * (a + b)

Результат доказательства: a² — b² = (a — b) * (a + b)

Для того, чтобы доказать в обратную сторону: (a — b) * (a + b) = a² — b², нужно раскрыть скобки: (a — b) * (a + b) = a * a + a * b — b * a — b * b = a² — b².

Остальные ФСУ можно доказать аналогичным методом.

Дополнительные формулы сокращенного умножения

К таблице основных ФСУ следует добавить еще несколько важных тождеств, которые пригодятся для решения задач.

Бином Ньютона

Формула для разложения на отдельные слагаемые целой неотрицательной степени суммы двух переменных. Записывается вот так:

Пример вычисления биномиальных коэффициентов, которые стоят в строке под номером n в треугольнике Паскаля:

ФСУ для квадрата и куба суммы и разности — являются частными случаями формулы бинома Ньютона при n = 2 и n = 3.

Формула возведения в квадрат суммы трех, четырех и более слагаемых

Пригодится, если слагаемых в сумме, которую нужно возвести в степень, больше, чем два.

(a₁+a₂+…+a_n)² = a₁² + a₂² + … + a_n-1² + a_n² + 2 * a₁ * a₂ + 2 * a₁ * a₃ + 2 * a₁ * a₄ + … +

+ 2 * a₁ * a_n-1 + 2 * a₁ * a_n + 2 * a₂ * a₃ + 2 * a₂ * a₄ + … + 2 * a₂ * a_n-1 + 2 * a₂ * a_n +…+

+ 2 * a_n-1 * a_n

Читается так: квадрат суммы n слагаемых равен сумме квадратов всех этих слагаемых и удвоенных произведений всех возможных пар этих слагаемых.

Формула разности n-ых степеней двух слагаемых

aⁿ − bⁿ = (a − b) * (a^n-1 + a^n-2 * b + a^n-3 * b² + … + a * b^n-2 + b^n-1).

Для четных показателей можно записать так:

a^2*m − b^2*m = (a² − b²) *(a^2*m−2 + a^2*m−4 * b² + a^2*m−6 * b⁴ + … + b^2*m−2).

Для нечетных показателей:

a^2*m+1 − b^2*·m+1 = (a − b) * (a^2*m + a^2*m−1 * b + a^2*m−2 * b² + … + b^2*m).

Частными случаями являются формулы разности квадратов и кубов при n = 2 и n = 3. Для разности кубов b можно также заменить на −b.

Решение задач

Давайте потренируемся и рассмотрим примеры с дробями.

Задание 1

Что сделать: вычислить квадрат произведения (55 + 10)².

Как решаем: воспользуемся формулой квадрата суммы: (55 + 10)² = 55² + 2 * 55 * 10 + 10² = 3025 + 1100 + 100 = 4225.

Задание 2

Что сделать: упростить выражение 64 * с³ – 8.

Как решаем: применим разность кубов: 64 * с³ – 8 = (4 * с)³ – 2³ = (4 * с – 2)((4 * с)² + 4 * с * 2 + 2²) = (4 * с – 2)(16 * с² + 8 * с + 4).

Задание 3

Что сделать: раскрыть скобки (7 * y — x) * (7 * y + x).

Как решаем:

Произведем умножение: (7 * y — x) * (7 * y + x) = 7 * y * 7 * y + 7 * y * x — x * 7 * y — x * x = 49 * y² + 7 * y * x — 7 * y * x — x² = 49 * y² — x².
Используем формулу сокращенного умножения: (7 * y — x) * (7 * y + x) = (7 * y)² — x² = 49 * y² — x².

Многочленов бояться не стоит, просто совершайте последовательно каждое действие. С формулами решать задачки быстрее и удобнее — сохраняйте шпаргалку, запоминайте и радуйте своих учителей 🙂

Формулы сокращенного умножения. Примеры

Формулы сокращенного умножения применяют для упрощения вычислений, а также разложение многочленов на множители, быстрого умножения многочленов. Большинство формул сокращенного умножения можно получить из бинома Ньютона — в этом Вы скоро убедитесь.

Формулы для кубов не сильно сложные и их нужно знать при сведении многочленов к стандартному виду, для упрощения подъема суммы или разности переменной и числа к кубу.

Формулы обозначены красным получают из предыдущих группировкой подобных слагаемых.

Формулы для четвертого и пятого степени в школьном курсе мало кому пригодятся, однако есть задачи при изучении высшей математики где нужно вычислять коэффициенты при степенях.

Формулы для степени n расписаны через биномиальные коэффициенты с использованием факториалов следующие

Примеры применения формул сокращенного умножения

Пример 1. Вычислить 51^2. 7.

Формулы сокращённого умножения. Неполный квадрат суммы и разности

При выполнении преобразований разных выражений часто встречаются некоторые частные случаи умножения. Равенства, выражающие эти случаи, называются формулами сокращённого умножения.

Формулы сокращённого умножения — это выражения, в которых пропущены промежуточные вычисления, поэтому их и называют сокращёнными.

a² + b² = (a + b)² — 2ab — сумма квадратов;

a² — b² = (a + b)(a — b) — разность квадратов;

(a + b)² = a² + 2ab + b² — квадрат суммы;

(a — b)² = a² — 2ab + b² — квадрат разности;

a³ + b³ = (a + b)(a² — ab + b²) — сумма кубов;

a³ — b³ = (a — b)(a² + ab + b²) — разность кубов;

(a + b)³ = a³ + 3a²b + 3ab² + b³ — куб суммы;

(a — b)³ = a³ — 3a²b + 3ab² — b³ — куб разности.

Обратите внимание, что a и b в формулах сокращённого умножения могут быть как числами, так и выражениями.

Разложение формул сокращенного умножения

Рассмотрим каждую формулу подробнее и приведём доказательство верности формул сокращённого умножения.

Сумма квадратов двух чисел равна разности квадрата суммы этих чисел и их удвоенного произведения:

a² + b² = (a + b)² — 2ab.

Доказательство: выполним преобразование правой части формулы, приведём подобные члены и получим левую часть формулы:

(a + b)² — 2ab = (a + b)(a + b) — 2ab = a² + ab + ab + b² — 2ab = a² + b².

Разность квадратов двух чисел равна произведению суммы этих чисел на их разность:

a² — b² = (a + b)(a — b).

Доказательство: выполним умножение многочленов из правой части формулы, приведём подобные члены и получим левую часть формулы:

(a + b)(a — b) = a² — ab + ab — b² = a² — b².

Квадрат суммы двух чисел равен сумме квадрата первого числа, удвоенного произведения первого числа на второе и квадрата второго числа:

(a + b)² = a² + 2ab + b².

Доказательство: представим степень в виде произведения, выполним умножение и приведение подобных членов:

(a + b)² = (a + b)(a + b) = a² + ab + ab + b² = a² + 2ab + b².

Квадрат разности двух чисел равен квадрату первого числа, минус удвоенное произведение первого числа на второе, плюс квадрат второго числа:

(a — b)² = a² — 2ab + b².

Доказательство: представим степень в виде произведения, выполним умножение и приведение подобных членов:

(a — b)² = (a — b)(a — b) = a² — ab — ab + b² = a² — 2ab + b².

Сумма кубов двух чисел равна произведению суммы первого и второго числа на неполных квадрат разности этих чисел:

a³ + b³ = (a + b)(a² — ab + b²).

(a + b)(a² — ab + b²) = a³ — a²b + ab² + a²b — ab² + b³ = a³ + b³.

Разность кубов двух чисел равна произведению разности первого и второго числа на неполный квадрат суммы этих чисел:

a³ — b³ = (a — b)(a² + ab + b²).

(a — b)(a² + ab + b²) = a³ + a²b + ab² — a²b — ab² — b³ = a³ — b³.

Куб суммы двух чисел равен сумме четырёх слагаемых: куб первого числа, утроенное произведение квадрата первого числа на второе число, утроенное произведение первого числа на квадрат второго и куб второго числа:

(a + b)³ = a³ + 3a²b + 3ab² + b³.

Доказательство: представим степень в виде произведения, выполним умножение и приведение подобных членов:

(a + b)³ = (a + b)(a + b)² = (a + b)(a² + 2ab + b²) = a³ + 2a²b + ab² + a²b + 2ab² + b³ = a³ + 3a²b + 3ab² + b³.

Куб разности двух чисел равен кубу первого числа, минус утроенное произведение квадрата первого числа на второе число, плюс утроенное произведение первого числа на квадрат второго, минус куб второго числа:

(a — b)³ = a³ — 3a²b + 3ab² — b³.

Доказательство: представим степень в виде произведения, выполним умножение и приведение подобных членов:

(a — b)³ = (a — b)(a — b)² = (a — b)(a² — 2ab + b²) = a³ — 2a²b + ab² — a²b + 2ab² — b³ = a³ — 3a²b + 3ab² — b³.

Неполный квадрат суммы

Выражение:

a² + 2ab + b²

это квадрат суммы, которое также называется полным квадратом суммы, относительно выражения:

a² + ab + b²,

которое называется неполным квадратом суммы. Неполный квадрат суммы — это сумма квадратов двух чисел и их произведения. Неполный квадрат суммы отличается от полного только произведением чисел, которое не удваивается.

Неполный квадрат разности

Выражение:

a² — 2ab + b²

это квадрат разности, который также называется полным квадратом разности относительно выражения:

a² — ab + b²,

которое называется неполным квадратом разности. {2}}\)

Потренируйся – преобразуй следующие выражения:

Справился? Закрепим тему. Выбери из приведенных ниже выражений те, которые можно представить в виде квадрата суммы или разности.

3 $, которые настроены таким образом, чтобы использовать все четыре измерения. $$ \ begin {array} {c | c | c} \ begin {array} {cc} {\ color {красный} \ bullet} & {\ color {красный} \ bullet} \\ {\ цвет {красный} \ пуля} и {\ цвет {красный} \ пуля} \ end {array} & \ begin {array} {cc} {\ color {красный} \ bullet} & {\ color {красный} \ bullet} \\ {\ цвет {красный} \ пуля} и {\ цвет {красный} \ пуля} \ end {array} & \ begin {array} {cc} {\ color {синий} \ bullet} & {\ color {синий} \ bullet} \\ {\ цвет {синий} \ пуля} и {\ цвет {синий} \ пуля} \ конец {массив} \\\ hline \ begin {array} {cc} {\ color {зеленый} \ bullet} & {\ color {зеленый} \ bullet} \\ {\ цвет {зеленый} \ пуля} и {\ цвет {зеленый} \ пуля} \ end {array} & \ begin {array} {cc} {\ color {красный} \ bullet} & {\ color {синий} \ bullet} \\ {\ color {зеленый} \ bullet} и {\ color {magenta} \ bullet} \ end {array} & \ begin {array} {cc} {\ color {синий} \ bullet} & {\ color {синий} \ bullet} \\ {\ цвет {синий} \ пуля} и {\ цвет {синий} \ пуля} \ конец {массив} \\\ hline \ begin {array} {cc} {\ color {зеленый} \ bullet} & {\ color {зеленый} \ bullet} \\ {\ цвет {зеленый} \ пуля} и {\ цвет {зеленый} \ пуля} \ end {array} & \ begin {array} {cc} {\ color {magenta} \ bullet} & {\ color {magenta} \ bullet} \\ {\ color {magenta} \ bullet} и {\ color {magenta} \ bullet} \ end {array} & \ begin {array} {cc} {\ color {magenta} \ bullet} & {\ color {magenta} \ bullet} \\ {\ color {magenta} \ bullet} и {\ color {magenta} \ bullet} \ конец {массив} \\ \ end {array} $$ Это прямоугольный гиперсолид $ 2 \ times2 \ times3 \ times3 $, состоящий из четырех копий $ 1 \ cdot1 ^ 3 + 1 \ cdot2 ^ 3 $.

5 $ в свою конфигурацию.

полигонов — Основы работы с полигонами — Подробно

Слово многоугольник представляет собой сочетание двух греческих слов: «поли» означает «много» и «гон». означает угол. У многоугольника помимо углов есть стороны и вершины. «Три» означает «три», поэтому самый простой многоугольник называется треугольник, потому что у него три угла. Он также имеет три стороны и три вершины. Треугольник всегда компланарен, чего нельзя сказать о многих из них. другие полигоны.

Правильный многоугольник — многоугольник, все углы и стороны которого совпадают или равны. Вот некоторые правильные многоугольники.

Мы можем использовать формула, чтобы найти сумму внутренних углов любого многоугольника. В этой формуле буква n обозначает количество сторон или углов многоугольника.

сум углов = (n — 2) 180 °

Давайте воспользуемся формула, чтобы найти сумму внутренних углов треугольника. Запасной 3 для п. Получаем, что сумма равна 180 градусам. Это важный факт, о котором следует помнить.

сум углов = (n — 2) 180 °
= (3 — 2) 180 ° = (1) 180 ° = 180 °

Чтобы найти сумма внутренних углов четырехугольника, мы можем снова использовать формулу. На этот раз замените n на 4. Мы находим, что сумма внутренних углов четырехугольника 360 градусов.

сум углов = (n — 2) 180 °
= (4-2) 180 ° = (2) 180 ° = 360 °

Полигоны могут быть разделенными на треугольники, нарисовав все диагонали, которые можно нарисовать из одной единственной вершины.Давайте попробуем это с четырехугольником, показанным здесь. Из вершине A мы можем провести только одну диагональ к вершине D. Четырехугольник может поэтому разделим на два треугольника.

Если вы посмотрите вернувшись к формуле, вы увидите, что n — 2 дает количество треугольников в многоугольнике, и это число умножается на 180, сумма мер всех внутренних углов в треугольнике. Вы видите, где «н — 2 «происходит от? Это дает нам количество треугольников в многоугольнике.Как Как вы думаете, много ли треугольников будет у 5-стороннего многоугольника?

Вот пятиугольник, 5-сторонний многоугольник. Из вершины A можно провести две диагонали, разделяющие пятиугольник на три треугольника. Умножаем 3 раза на 180 градусов, чтобы найти сумма всех внутренних углов пятиугольника, составляющая 540 градусов.

сум углов = (n — 2) 180 °
= (5-2) 180 ° = (3) 180 ° = 540 °

Ссылки по теме:
Определения многоугольников, формулы полигонов (площадь, периметр) и имена полигонов (таблицы и формулы)

Лемма о подтверждении связи / Формула суммы степеней

Вот, формула суммы степеней:

Формула суммы степеней утверждает, что для графа G = (V, E) сумма степеней вдвое превышает количество ребер. Давайте посмотрим на K ₃, полный граф (со всеми возможными ребрами) с 3 вершинами.

Во-первых, напомним, что градусов означает количество ребер, которые входят в вершину . Вершина — это , инцидентная ребру, если вершина является одной из двух вершин, которые соединяет ребро. В случае K ₃ каждая вершина имеет два инцидентных ей ребра. Фактически, для всех K графов (полных графов) каждая вершина имеет n-1 градус, n — количество вершин.Наркотик.

Итак, для каждой вершины в наборе V мы увеличиваем нашу сумму на количество ребер, инцидентных этой вершине. Или, по-другому, постройте последовательность степеней для графика и просуммируйте ее: sum ([2, 2, 2]) # 6 . Эта сумма в два раза больше количества ребер. Наш граф должен иметь 6/2 ребер.

Бит «удвоенное количество ребер» может показаться произвольным. Но каждое ребро имеет двух вершин, инцидентных ему. В формуле суммы степеней мы суммируем степень, количество ребер, инцидентных каждой вершине.Степень — это свойство, связанное с ребрами. Ребра — это соединения между двумя вершинами. Суммирование степеней каждой вершины неизбежно приведет к пересчету ребер.

Свойства, которые мы можем получить из этой формулы

Все, что умножено на 2, является четным. Так как сумма степеней в два раза больше количества ребер, результат должен быть четным, и количество ребер тоже должно быть четным.

Обладая вышеуказанными знаниями, мы можем узнать, возможно ли описание графа. Это полезно в головоломке, подобной той, которую я нашел в этой книге:

На недавнем математическом семинаре 9 математиков поздоровались друг с другом, пожав друг другу руки.Возможно ли, чтобы на семинаре каждый математик пожал руку ровно 7 людям?

Каждый математик пожал бы руку 7 другим, что равносильно рукопожатию каждому математику, за исключением вас и еще одного человека.

График, возможно, и не выскочил на вас, но с его помощью можно хорошо решить эту головоломку. Думайте о каждом математике как о вершине, а рукопожатие — как о ребре.

Можно ли получить граф с 9 вершинами и 7 ребрами? Применяя формулу суммы степеней, мы можем сказать «нет».

Суммируя степени всех 9 вершин, мы получаем 63, так как 9 * 7 = 63 . Поскольку сумма степеней вдвое больше количества ребер, мы знаем, что будет 63 ÷ 2 ребер или 31,5 ребра. Поскольку половинное рукопожатие — просто неудобный момент, мы знаем, что этот график невозможен.

Ненавижу говорить математикам, что они не могут пожать друг другу руки. Можем ли мы вместо этого попросить 9 математиков пожать руку 8 другим математикам?

Можно ли получить граф с 9 вершинами и 8 ребрами?

Суммирование 8 градусов 9 раз дает 72, что означает 36 ребер.

Сумма внутренних и внешних углов (многоугольники, пятиугольники …) // Tutors.

com

Определение суммы внутренних и внешних углов

Полигоны подобны домикам в мире двумерной геометрии. Они создают внутреннее, называемое внутренним, и внешнее, называемое экстерьером. Вы можете измерять внутренние и внешние углы. Вы также можете сложить суммы всех внутренних углов и суммы всех внешних углов правильных многоугольников. Наша формула работает с треугольниками, квадратами, пятиугольниками, шестиугольниками, четырехугольниками, восьмиугольниками и многим другим.

Видео
Что такое правильный многоугольник?
Сумма внутренних углов многоугольника
Сумма внутренних углов

Сумма внешних углов

Что такое правильный многоугольник?

Чтобы многоугольник был правильным многоугольником, он должен удовлетворять этим четырем требованиям:

Быть двумерным
Ограничьте пространство, создав интерьер и экстерьер
Используйте только отрезки для сторон
Все стороны равны друг другу по длине и все внутренние углы равны по размеру

Сумма внутренних углов многоугольника

Правильные многоугольники существуют без ограничений (теоретически), но по мере того, как у вас появляется все больше и больше сторон, многоугольник все больше и больше похож на круг. Правильный многоугольник с наименьшим количеством сторон — тремя — и есть равносторонний треугольник. Правильный многоугольник с большинством сторон, обычно используемый в классах геометрии, вероятно, двенадцатигранник, или 12-угольник, с 12 сторонами и 12 внутренними углами:

Довольно необычно, не правда ли? Но только потому, что у него есть все эти стороны и внутренние углы, не думайте, что вы не можете много разобраться в нашем двенадцатиугольнике. Предположим, например, что вы хотите знать, к чему складываются все эти внутренние углы в градусах?

Сумма внутренних углов

Треугольники — это просто.Их внутренние углы складываются в 180 °. Точно так же квадрат (правильный четырехугольник) добавляет 360 °, потому что квадрат можно разделить на два треугольника.

Слово «многоугольник» означает «много углов», хотя большинство людей, кажется, замечают стороны больше, чем углы, поэтому они создали такие слова, как «четырехугольник», что означает «четыре стороны».

Правильный многоугольник имеет столько же внутренних углов, сколько и сторон, поэтому треугольник имеет три стороны и три внутренних угла. Квадратный? По четыре каждого.Пентагон? Пять и так далее. У нашего двенадцатиугольника 12 сторон и 12 внутренних углов.

Формула суммы внутренних углов

Формула для суммы внутренних углов этого многоугольника очень проста. Пусть n равно количеству сторон любого правильного многоугольника, который вы изучаете. Вот формула:

Сумма внутренних углов = (n — 2) × 180 °

Сумма углов в треугольнике

Вы можете это сделать. Попробуйте сначала с нашим равносторонним треугольником:

(п — 2) × 180 °

(3 — 2) × 180 °

Сумма внутренних углов = 180 °

Сумма углов квадрата

И снова попробуйте для квадрата:

(п — 2) × 180 °

(4 — 2) × 180 °

2 × 180 °

Сумма внутренних углов = 360 °

Как найти один внутренний угол

Чтобы найти размер одного внутреннего угла, вы просто берете эту сумму для всех углов и делите ее на n, количество сторон или углов в правильном многоугольнике.

Новая формула очень похожа на старую:

Один внутренний угол = (n — 2) × 180 ° n

Опять же, проверьте это на равносторонний треугольник:

(3 — 2) × 180 ° 3

180 ° 3

Один внутренний угол = 60 °

А для квадрата:

(4 — 2) × 180 ° 4

2 × 180 ° 4

360 ° 4

Один внутренний угол = 90 °

Эй! Оно работает! И работает каждый раз . Давайте теперь займемся этим двенадцатигранником.

Примеры внутренних углов

Помните, как выглядит 12-сторонний двенадцатигранник? Найдем сумму внутренних углов, а также один внутренний угол:

Найдите сумму внутренних углов двенадцатиугольника

(п — 2) × 180 °

(12 — 2) × 180 °

10 × 180 °

Сумма внутренних углов = 1800 °

А теперь найдем один внутренний угол

(п — 2) × 180 ° с.

(12-2) × 180 ° 12

10 × 180 ° 12

1,800 ° 12

Один внутренний угол = 150 °

Отлично!

Сумма внешних углов

Каждый правильный многоугольник имеет внешних углов . Это , а не угол отражения (более 180 °), создаваемый вращением от внешней стороны одной стороны к другой. Это распространенное заблуждение. Например, в равностороннем треугольнике внешний угол равен , а не 360 ° — 60 ° = 300 °, как если бы мы вращались от одной стороны до конца вокруг вершины к другой стороне.

Внешние углы создаются путем расширения одной стороны правильного многоугольника за пределы формы и последующего измерения в градусах от этой удлиненной линии до следующей стороны многоугольника.

Поскольку вы расширяете сторону многоугольника, этот внешний угол обязательно должен составлять дополнительных к внутреннему углу многоугольника. Вместе внутренние и внешние углы в сумме составляют 180 °.

Для нашего равностороннего треугольника внешний угол любой вершины равен 120 °. Для квадрата внешний угол составляет 90 °.

Формула внешнего угла

Если вы предпочитаете формулу, вычтите внутренний угол из 180 °:

Внешний угол = 180 ° — внутренний угол

Примеры внешних углов

Что осталось в нашей коллекции правильных многоугольников? Этот двенадцатигранник! Мы знаем, что любой внутренний угол составляет 150 °, поэтому внешний угол составляет:

180 ° — 150 °

Внешний угол = 30 °

Проверка работы

Внимательно посмотрите на три внешних угла, которые мы использовали в наших примерах:

Треугольник = 120 °

Квадрат = 90 °

Додекагон = 30 °

Приготовьтесь удивляться.Умножьте каждое из этих измерений на количество сторон правильного многоугольника:

Треугольник = 120 ° × 3 = 360 °
Квадрат = 90 ° × 4 = 360 °
Двенадцатьугольник = 30 ° × 12 = 360 °

Каждый раз, когда вы складываете (или умножаете, что является быстрым сложением) суммы внешних углов любого правильного многоугольника, вы всегда получаете 360 °.

Это похоже на магию, но геометрическая причина этого на самом деле проста: чтобы перемещаться вокруг этих фигур, вы делаете один полный оборот на 360 °.

Тем не менее, эту идею легко запомнить: каким бы сложным и многогранным ни был правильный многоугольник, сумма его внешних углов всегда равна 360 ° . {\ circ} $$

Задача 3

Какова сумма внутренних углов многоугольника (пятиугольника)?

Покажи ответ

Задача 4

Какова сумма размеров внутренних углов многоугольника (шестиугольника)?

Покажи ответ

Видео Учебное пособие

по внутренним углам многоугольника

Определение правильного многоугольника:

Правильный многоугольник — это просто многоугольник, все стороны которого имеют одинаковую длину, а все углы имеют одинаковую величину.Вы, наверное, слышали о равностороннем треугольнике — двух наиболее известных и наиболее часто изучаемых типах правильных многоугольников.

Примеры правильных многоугольников

Обычный шестиугольник Обычный Пентагон Подробнее о правильных многоугольниках здесь .
Измерение одного внутреннего угла
Форма Формула Сумма внутренних углов
Обычный Пентагон $$ (\ красный 3-2) \ cdot180 $$ $$ 180 ^ {\ circ} $$
$$ \ red 4 $$ многоугольник
(четырехугольник) $$ (\ красный 4-2) \ cdot 180 $$ $$ 360 ^ {\ circ} $$
$$ \ red 6 $$ многоугольник
(шестигранник) $$ (\ красный 6-2) \ cdot 180 $$ $$ 720 ^ {\ circ} $$
А как насчет одного внутреннего угла?
Чтобы найти размер одного внутреннего угла правильного многоугольника (многоугольника со сторонами равной длины и углами одинаковой меры) с n сторонами, мы вычисляем сумму внутренних углов или $$ (\ red n-2) \ cdot 180 $$ и затем разделите эту сумму на количество сторон или $$ \ red n $$. {\ circ}
долл. США
Нахождение 1 внутреннего угла правильного многоугольника
Задача 5
Каков размер 1 внутреннего угла правильного восьмиугольника?
Покажи ответ
Задача 6
Вычислить размер 1 внутреннего угла правильного двенадцатиугольника (12-сторонний многоугольник)?
Покажи ответ
Задача 7
Вычислить размер 1 внутреннего угла правильного шестиугольника (16-стороннего многоугольника)?
Покажи ответ
Задача вызова
Каков размер 1 внутреннего угла пятиугольника?
Покажи ответ
На этот вопрос нельзя ответить , потому что форма не является правильным многоугольником .Вы можете использовать эту формулу, чтобы найти единственный внутренний угол, только если многоугольник правильный!
Рассмотрим, например, неправильный пятиугольник внизу.
Вы можете сказать, просто взглянув на картинку, что $$ \ angle A и \ angle B $$ не совпадают.
Мораль этой истории. Хотя вы можете использовать нашу формулу, чтобы найти сумму , внутренних углов любого многоугольника (правильного или неправильного), вы можете , а не использовать формулу этой страницы для измерения единственного угла — кроме случаев, когда многоугольник правильный .
Как насчет меры внешнего угла?
Внешние углы многоугольника
Формула суммы внешних углов:
Сумма размеров внешних углов многоугольника, по одному в каждой вершине, равна 360 °.
Измерение единственного внешнего угла
Формула , чтобы найти 1 угол правильного выпуклого многоугольника с n сторонами =
$$ \ angle1 + \ angle2 + \ angle3 = 360 ° $$
$$ \ угол1 + \ угол2 + \ угол3 + \ угол4 = 360 ° $$
$$ \ угол1 + \ угол2 + \ угол3 + \ угол4 + \ угол5 = 360 ° $$
Практика Задачи
Задача 8
Вычислить размер 1 внешнего угла правильного пятиугольника?
Покажи ответ
Задача 9
Каков размер 1 внешнего угла правильного десятиугольника (10-сторонний многоугольник)?
Покажи ответ
Задача 10
Каков размер 1 внешнего угла правильного двенадцатиугольника (12-стороннего многоугольника)?
Покажи ответ
Задача вызова
Каков размер 1 внешнего угла пятиугольника?
Покажи ответ
На этот вопрос нельзя ответить , потому что форма не является правильным многоугольником . Хотя вы знаете, что сумма внешних углов равна 360, вы можете использовать формулу, чтобы найти единственный внешний угол, только если многоугольник правильный!
Рассмотрим, например, пятиугольник, изображенный ниже. Хотя мы знаем, что все внешние углы в сумме составляют 360 °, мы можем увидеть, просто посмотрев, что каждый $$ \ angle A \ text {and} и \ angle B $$ не совпадают ..
Определить количество сторон от углов
Можно определить, сколько сторон имеет многоугольник, исходя из того, сколько градусов составляет его внешний или внутренний угол.
Задача 11
Если каждый внешний угол равен 10 °, сколько сторон у этого многоугольника?
Покажи ответ
Задача 12
Если каждый внешний угол равен 20 °, сколько сторон у этого многоугольника?
Покажи ответ
Задача 13
Если каждый внешний угол составляет 15 °, сколько сторон у этого многоугольника?
Покажи ответ
Задача вызова
Если каждый внешний угол равен 80 °, сколько сторон у этого многоугольника?
Покажи ответ На этот вопрос нет решения.
Когда вы используете формулу для нахождения единственного внешнего угла для определения количества сторон, вы получаете десятичную дробь (4.5), что невозможно. Подумайте об этом: как многоугольник может иметь 4,5 стороны? У четырехугольника 4 стороны. У пятиугольника 5 сторон.
Теорема о сумме треугольников
— объяснение и примеры
Мы знаем, что разные треугольники имеют разные углы и длины сторон, но одно остается неизменным — каждый треугольник состоит из трех внутренних углов и трех сторон, которые могут быть одинаковой длины или разной длины.
Например, прямоугольный треугольник имеет один угол, равный точно 90 градусам, и два острых угла.
Равнобедренные треугольники имеют два равных угла и две равные длины сторон. Равносторонние треугольники имеют одинаковые углы и одинаковую длину сторон. Треугольники из шкалы имеют разные углы и разную длину сторон.
Несмотря на то, что все эти треугольники различаются по углам или длинам сторон, все они подчиняются одним и тем же правилам и свойствам.
Из этой статьи вы узнаете о:
Теорема о сумме треугольников,
внутренние углы треугольника и
Как использовать теорему о сумме треугольников, чтобы найти внутренние углы треугольника?
Что такое внутренний угол треугольника?
В геометрии внутренние углы треугольника — это углы, которые образуются внутри треугольника.
Внутренние углы имеют следующие свойства:
Сумма внутренних углов составляет 180 градусов (теорема о сумме углов треугольника).
Все внутренние углы треугольника больше 0 °, но меньше 180 °.
Биссектрисы всех трех внутренних углов пересекаются внутри треугольника в точке, называемой центром, которая является центром внутренней окружности треугольника.
Сумма каждого внутреннего угла и внешнего угла равна 180 ° (прямая линия).
Что такое теорема о сумме углов треугольника?
Одно общее свойство треугольников состоит в том, что все три внутренних угла в сумме составляют 180 градусов. Это подводит нас к важной теореме в геометрии, известной как теорема о сумме углов треугольника.
Согласно теореме о сумме углов треугольника, сумма трех внутренних углов в треугольнике всегда равна 180 °.
Мы можем это как:
∠a + ∠b + ∠c = 180 °
Как найти внутренние углы треугольника?
Когда известны два внутренних угла треугольника, можно определить третий угол с помощью теоремы о сумме углов треугольника.Чтобы найти третий неизвестный угол треугольника, вычтите сумму двух известных углов из 180 градусов.
Давайте рассмотрим несколько примеров проблем:
Пример 1
Треугольник ABC таков, что ∠A = 38 ° и ∠B = 134 °. Рассчитайте ∠C.
Решение
По теореме о сумме углов треугольника имеем;
∠A + ∠B + ∠C = 180 °
⇒ 38 ° + 134 ° + ∠Z = 180 °
⇒ 172 ° + ∠C = 180 °
Вычтем обе стороны на 172 °
⇒ 172 ° — 172 ° + ∠C = 180 ° — 172 °
Следовательно, ∠C = 8 °
Пример 2
Найдите недостающие углы x в треугольнике, показанном ниже.
Решение
По теореме о сумме углов треугольника (сумма внутренних углов = 180 °)
⇒ x + x + 18 ° = 180 °
Упростите, объединив похожие термины.
⇒ 2x + 18 ° = 180 °
Вычтите обе стороны на 18 °
⇒ 2x + 18 ° — 18 ° = 180 ° — 18 °
⇒ 2x = 162 °
Разделим обе стороны на 2
⇒ 2x / 2 = 162 ° / 2
х = 81 °
Пример 3
Найдите недостающие углы внутри треугольника ниже.
Решение
Это равнобедренный прямоугольный треугольник; следовательно, один угол равен 90 °
⇒ x + x + 90 ° = 180 °
⇒ 2x + 90 ° = 180 °
Вычесть обе стороны на 90 °
⇒ 2x + 90 ° — 90 ° = 180 ° — 90 °
⇒ 2x = 90 °
⇒ 2x / 2 = 90 ° / 2
х = 45 °
Пример 4
Найдите углы треугольника, второй угол которого превышает первый угол на 15 °, а третий угол на 66 ° больше второго.
Решение
Let;
1 ^ST угол = x °
2 ^ND угол = (x + 15) °
3 ^RD угол = (x + 15 + 66) °
По теореме о сумме углов треугольника,
х ° + (х + 15) ° + (х + 15 + 66) ° = 180 °
Соберите похожие условия.
⇒ 3x + 81 ° = 180 °
⇒ 3x = 180 ° — 81 °
⇒ 3x = 99
х = 33 °
Теперь подставим x = 33 ° в три уравнения.
1 ^ST угол = x ° = 33 °
2 ^ND угол = (x + 15) ° = 33 ° + 15 ° = 48 °
3 ^RD угол = (x + 15 + 66) ° = 33 ° + 15 ° + 66 ° = 81 °
Следовательно, три угла треугольника равны 33 °, 48 ° и 81 °.
Пример 5
Найдите недостающие внутренние углы на следующей диаграмме.
Решение
Угол y ° и (2x + 10) ° — дополнительные углы (сумма 180 °)
Следовательно,
⇒ y ° + (2x + 10) ° = 180 °
⇒ y + 2x = 170 ° ……………… (i)
Также, по теореме о сумме углов треугольника,
⇒ x + y + 65 ° = 180 °
⇒ x + y = 115 ° ………………… (ii)
Решите два одновременных уравнения заменой
⇒ y = 170 ° — 2x
⇒ x + 170 ° — 2x = 115 °
⇒ -x = 115 ° -170 °
х = 55 °
Но, y = 170 ° — 2x
= 170 ° — 2 (55) °
⇒ 170 ° — 110 °
.
у = 60 °
Следовательно, недостающие углы равны 60 ° и 55 °
Пример 6
Вычислите значение x для треугольника с углами; x °, (x + 20) ° и (2x + 40) °.
Решение
Сумма внутренних углов = 180 °
x ° + (x + 20) ° + (2x + 40) ° = 180 °
Упростить.
х + х + 2х + 20 ° + 40 ° = 180 °
4x + 60 ° = 180 °
Вычтем 60 с обеих сторон.
4x + 60 ° — 60 ° = 180 ° — 60 °
4x = 120 °
Теперь разделите обе стороны на 4.
4x / 4 = 120 ° / 4
х = 30 °
Следовательно, углы треугольника равны 30 °, 50 ° и 100 °.
Пример 7
Найдите недостающие углы на схеме ниже.
Решение
Треугольник ADB и BDC — равнобедренные треугольники.
DBC = ∠DCB = 50 °
∠ BAD = ∠ DBA = x °
Следовательно,
50 ° + 50 ° + ∠BDC = 180 °
∠BDC = 180 ° — 100 °
∠BDC = 80 °
Но, z ° + 80 ° = 180 ° (Углы на прямой)
Следовательно, z = 100 °
В треугольнике ADB:
z ° + x + x = 180 °
100 ° + 2x = 180 °
2x = 180 ° — 100 °
2x = 80 °
х = 40 °
<noscript><img src='/800/600/https/fsd.multiurok.ru/html/2019/03/15/s_5c8b434543ebf/img4.jpg' /></noscript> youtube.com/embed/zWECG5Kig7U?rel=0;controls=0;showinfo=0;theme=light» frameborder=»0″ allowfullscreen=»allowfullscreen»/>
Предыдущий урок | Главная страница | Следующий урок
Углы треугольника — Бесплатная справка по математике
Углы могут быть добавлены
Как и обычные числа, углы можно складывать для получения суммы, возможно, с целью определения меры неизвестного угла.Иногда мы можем определить недостающий угол, потому что знаем, что сумма должна быть определенным значением. Помните — сумма градусов углов в любом треугольнике равна 180 градусам. Ниже изображен треугольник ABC, где угол A = 60 градусов, угол B = 50 градусов и угол C = 70 градусов.
Если сложить все три угла в любом треугольнике, мы получим 180 градусов. Итак, мера угла A + угол B + угол C = 180 градусов. Это верно для любого треугольника в мире геометрии. Мы можем использовать эту идею, чтобы найти величину угла (углов), для которой градус отсутствует или не указан.
Нахождение недостающего угла
В треугольнике ABC ниже угол A = 40 градусов и угол B = 60 градусов. Какова мера угла C?
Мы знаем, что сумма мер любого треугольника равна 180 градусам. Используя тот факт, что угол A + угол B + угол C = 180 градусов, мы можем найти меру угла C.
угол A = 40
угол B = 60
угол C = мы не знаем.
Чтобы найти угол C, мы просто подставляем формулу выше и решаем относительно C.
A + B + C = 180
C = 180 — A — B
C = 180-40-60
C = 80
Чтобы проверить правильность 80 градусов, давайте сложим все три угловые меры. Если мы получим 180 градусов, то наш ответ для угла C правильный.
Поехали:
40 + 60 + 80 = 180
180 = 180 … Проверяет!
Не всегда нужно подставлять эти значения в уравнение и решать. Как только вы освоитесь с такого рода проблемами, вы сможете сказать: «Хорошо, 40 + 60 = 100, поэтому другой угол должен быть 80!» и это намного быстрее.
Равносторонние треугольники
Если треугольник равносторонний, каков градус каждого из его углов?
Помните, что все стороны равностороннего треугольника имеют равной меры . У них также, как вы узнаете, равные углы! Пусть x = градус каждого угла. У треугольников три угла, поэтому мы прибавим x ТРИ раза.
У нас это:
x + x + x = 180
3x = 180
x = 60
Имеет смысл, правда? Если все углы равны и в сумме они равны 180, то это должно быть 60 градусов!
Соотношение углов
Углы треугольника в градусах находятся в соотношении 4: 5: 9.
Каков градус НАИБОЛЬШЕГО угла треугольника?
Обратите внимание, что наименьший угол представлен наименьшим числом в данном соотношении. Наименьшее из приведенных чисел — 4, верно? Поскольку это соотношение, мы должны умножить все эти значения (4,5,9) на некоторый общий коэффициент, чтобы получить фактические углы. (Например, 60 и 80 находятся в соотношении 3: 4 с коэффициентом 20)
Пусть 4x = мера наименьшего угла треугольника. Теперь мы можем сказать, что 5x и 9x = градусы остальных углов треугольника.Мы просто складываем 4x + 5x + 9x, приравниваем сумму к 180 градусам и решаем относительно x. Найдя x, мы подставляем значение x в 4x и упрощаем, чтобы найти меру наименьшего угла треугольника.
4x + 5x + 9x = 180
9x + 9x = 180
18x = 180
x = 180/18
x = 10
Мы нашли значение x, но это НЕ означает, что мы закончили.
Чтобы найти величину наименьшего угла треугольника, умножаем 4 на 10. Итак, 4 x 10 = 40.
Ответ — 40 градусов.
Помните, сумма углов треугольника равна 180 градусам. Просто возьмите то, что вам дано в задаче, и попытайтесь определить, в результате чего итоговый угол в сумме составит 180 градусов.
Урок, проводимый г-ном Фелизом
Воспользуйтесь «Калькулятором треугольников» ниже:
.
No related posts.