Формула тангенса: Как найти тангенс угла а? Формула нужна

Формула — Эквивалентность тангенса

Формула Эквивалентность тангенса

\[\mathrm{tg}{x} \underset{x \to 0}{\sim} x\]

 

Доказательство

\[\lim_{x \to 0} { \frac{\mathrm{tg}{x}}{x} } = \lim_{x \to 0} { \frac{\frac{\sin{x}}{\cos{x}}}{x} } = \lim_{x \to 0} { \frac{\frac{\sin{x}}{x}}{\cos{x}} } = \frac{\lim_{x \to 0} { \frac{\sin{x}}{x} }}{\lim_{x \to 0} { \cos{x} }} = \frac{1}{1} = 1\]

изменить / сообщить об ошибке

связанные материалы

Формула Эквивалентность синуса

\[\sin{x} \underset{x \to 0}{\sim} x\]

изменить / сообщить об ошибке

Формула Эквивалентность арксинуса

\[\arcsin{x} \underset{x \to 0}{\sim} x\]

изменить / сообщить об ошибке

Формула Эквивалентность арктангенса

\[\mathrm{arctg}{x} \underset{x \to 0}{\sim} x\]

изменить / сообщить об ошибке

Формула Эквивалентность косинуса

\(1 — \cos x \underset{x \to 0}{\sim} \frac{x^2}{2}\)

 

Доказательство

\[\lim_{x \to 0} \frac{1 — \cos x}{\frac{x^2}{2}} = \lim_{x \to 0} \frac{2\sin^2{\frac{x}{2}}}{\frac{x^2}{2}} = \lim_{x \to 0} \frac{2\sin^2{\frac{x}{2}}}{{2 (\frac{x}{2})^2 }} = \lim_{x \to 0} \frac{\sin{\frac{x}{2}}}{{\frac{x}{2} }} \frac{\sin{\frac{x}{2}}}{{\frac{x}{2} }} = \lim_{x \to 0} \frac{\sin{\frac{x}{2}}}{{\frac{x}{2} }} \lim_{x \to 0} \frac{\sin{\frac{x}{2}}}{{\frac{x}{2} }} = 1 \cdot 1 = 1\]

изменить / сообщить об ошибке

Формула Эквивалентность логарифма

Входящие величины

\(a\) — число >0 и ≠ 1

\[\log_a(1+x) \underset{x \to 0}{\sim} \frac{x}{\ln a}\]

\[a = e \Rightarrow \ln(1+x) \underset{x \to 0}{\sim} x\]

 

Доказательство

\[\frac{\log_a(1+x)}{\dfrac{x}{\ln a}} = \ln a \cdot \frac{1}{x} \cdot \log_a(1+x) = \ln a \cdot \log_a(1+x)^\frac{1}{x} = \ln a \cdot \frac{\ln(1+x)^{\frac{1}{x}}}{\ln a} = \ln(1+x)^{\frac{1}{x}}\]

Для вычисления предела правой части воспользуемся непрерывностью логарифма и вторым замечательным пределом:

\[\lim_{x \to 0} \frac{\log_a(1+x)}{\dfrac{x}{\ln a}} = \lim_{x \to 0}\ln(1+x)^{\frac{1}{x}} = \ln\lim_{x\to0}(1+x)^{\frac{1}{x}} = \ln e=1\]

 

 

изменить / сообщить об ошибке

Формула Эквивалентность показательной функции

Входящие величины

\(a\) — число > 0 и ≠ 1

\[a^x — 1 \underset{x \to 0}{\sim} x\ln a\]

\[a = e \Rightarrow e^x — 1 \underset{x \to 0}{\sim} x\]

 

Доказательство

сделаем замену \(z = \log_a(1+x)\) и выразим \(x\) через \(z\): \(x = a^z — 1\). z — 1 \sim z\ln a\) при \(z \to 0\). В этой формуле осталось лишь сменить обозначение переменного  на 

изменить / сообщить об ошибке

Определение Эквивалентные бесконечно малые функции

Бесконечно малые функции \(\alpha(x)\) и \(\beta(x)\) называются эквивалентными или равносильными бесконечно малыми одного порядка при \(x \to a\), если: 

\(\lim_{x \to a}{\frac{\alpha(x)}{\beta(x)}} = 1\)

Обозначают:

 \(\alpha(x) \sim \beta(x)\) при \(x \to a\) или просто \(\alpha(x) \underset{x \to a}{\sim} \beta(x)\)

изменить / сообщить об ошибке

Тангенс угла диэлектрических потерь, определение, формула расчета, мостовая схема

Все диэлектрики, используемые в качестве изоляторов, сохраняют свои свойства до определённых значений напряжений и токов. Кроме этого, в процессе долговременной эксплуатации происходит постепенная деградация диэлектрических характеристик. Периодический контроль параметров электроизоляции особенно важен для оборудования, работающего под высоким постоянным или переменным напряжением. Например, такие жизненно важные объекты, как трансформаторные подстанции, автотрансформаторы, генераторы, линии электропередач и высоковольтные изоляторы должны регулярно контролироваться с помощью специальных приборов. Одним из основных измеряемых параметров диэлектрических свойств является тангенс угла диэлектрических потерь tg δ.

• Определение тангенса угла диэлектрических потерь
• Что такое мостовая схема
• Формула расчёта
• Какие значения используют для расчёта
• Факторы, увеличивающие (ТУДП)
• Заключение

Определение тангенса угла диэлектрических потерь

Для исследования свойств диэлектриков в качестве образцов для измерений берутся конденсаторы, в которых пространство между обкладками заполняется испытуемым диэлектриком. Идеальный конденсатор характеризуется двумя признаками:

1. При постоянном напряжении на обкладках ток утечки равен нулю вплоть до напряжения пробоя, то есть ja = 0. 2.

2. При переменном напряжении на обкладках сдвиг по фазе φ между током и напряжением равен в точности 90°.

Обкладки конденсатора под воздействием переменного напряжения поочерёдно заряжаются и разряжаются. Энергия, полученная во время заряда, возвращается обратно в сеть во время разряда. Величина ёмкостного тока, умноженная на напряжение равна ёмкостной мощности. Если бы существовал идеальный диэлектрик, то из сети потреблялась бы только ёмкостная (реактивная мощность). Но в реальных диэлектриках часть энергии электрического поля всегда необратимо преобразуется в тепло. Таким образом возникают диэлектрические потери, численно равные электрической мощности, идущей на нагрев диэлектрика, находящегося в переменном электрическом поле.

На Рис.1 представлена векторная диаграмма токов, протекающих через диэлектрик, рассеивающий часть электрической энергии в тепловую.

Здесь:

— U — напряжение на обкладках конденсатора;

— I — полный ток;

— Ia ,Ic — активная и ёмкостная компоненты полного тока;

— φ — фазовый сдвиг между приложенным напряжением и полным током;

— δ — угол между полным током I и ёмкостным Ic.

Рис.1 Векторная диаграмма токов в диэлектрике с потерями.

Из треугольника токов на Рис.1 следует, что:

tg δ = Ia / Ic (1).

То есть отношение активной компоненты тока к ёмкостной называется тангенсом угла диэлектрических потерь (ТУДП). Величина обратная ТУДП называется добротностью Q изоляции:

Q = 1/ tg δ (2).

Для идеального диэлектрика угол δ = 0, тогда и tg δ = 0. Величина ТУДП характеризует общее состояние изоляции, являясь интегральным параметром потерь. На рост активной составляющей влияют различные внутренние дефекты, наличие влаги, загрязнений и поляризационные процессы. От чего зависит ТУДП? В качестве диэлектриков могут применяться как газообразные, твердые и жидкие материалы. В зависимости от электрофизических свойств материалов различают следующие диэлектрические потери, вызывающие нагрев диэлектрика и изменение значений tg δ:

— Ионизационные потери, характерные для газов.

— Релаксационные потери в жидких диэлектриках, связанные с релаксационной поляризацией.

— Потери в веществах, обладающих дипольной поляризацией.

— Высокочастотные резонансные потери.

— Потери, связанные с неоднородностью структуры твердых, аморфных материалов.

— Потери в отдельных веществах, обладающих одновременно сквозной электропроводностью и поляризационным рассеянием.

Что такое мостовая схема

Для измерения электрического сопротивления англичанином С.Х.Кристи в 1833 г. была придумана электрическая схема, которую в 1843 г. усовершенствовал Ч.Уитстон.

Устройство получило название — мост (мостик) Уитстона. Принцип работы моста Уитстона показан на Рис.2. Имеется два плеча R-R2 и R1-R2. Здесь R — измеряемое сопротивление, R2 — известное, подобранное заранее) сопротивление, R1 — переменный резистор (реостат), регулировкой которого достигается выполнение условия равенства потенциалов в «мостике» на регистраторе V (гальванометр), то есть отсутствие тока через него:

V_R/R  = VR₁/R₁ (3).

Формула (3) — условие балансировки моста.

Рис. Принципиальная схема моста Уитстона для измерения сопротивлений.

Для измерения ёмкостей немецкий изобретатель Г.Шеринг (1880-1959) предложил аналогичное устройство, названное в его честь мостом Шеринга. Эта версия мостового устройства используется в качестве для приборов, с помощью которых измеряются величина ёмкости и tg δ. Принципиальная схема одного из вариантов такого моста, работающего при протекании переменного тока, показана на Рис. .

Рис. Принципиальная схема моста Шеринга.

Обозначения на схеме:

— CX — экспериментальный образец (ёмкость с диэлектриком, ТУДП, которого получают после измерения ёмкости).

— CN — образцовый, калиброванный образец конденсатора.

— C4 — набор (магазин) ёмкостей, служащих для балансировки моста.

— G — гальванометр (стрелочный или электронный прибор).

— R3 — переменное, подстроечное сопротивление.

— R4 — постоянное, калиброванное сопротивление.

На Фото 1 показан пример прибора на базе моста Шеринга.

Фото 1.

Формула расчёта

Мощность тока, уходящая в тепло равна произведению напряжения U на активную составляющую переменного тока IА:

P = U * I = U * I cos φ = U * IА = U * IC * tg δ (4).

Реактивная составляющая переменного тока с частотой ω вычисляется по формуле:

IC = U * ω * С (5).

Тогда мощность P равна: P = U2 * ω * С * tg δ (6). Поскольку активная мощность по закону Джоуля-Ленца равна:

P = U2 / R (7),

то из (6) и (7) следует, что:

tg δ = 1/( ω * С * R) (8).

Выражение (8) — основная формула для вычисления ТУДП. Ёмкость и сопротивление получают путем измерений с помощью приборов на основе мостовых схем.

Какие значения используют для расчёта

Для корректных расчётов ТУДП изоляционных деталей электрооборудования используются следующие значения:

— Частота переменного тока 50 Гц, соответствующая частоте в линиях электропередач. При повышении частоты ТУДП снижается.

— Расчёты производятся для комнатной температуре 20°С, что обычно соответствуют температурам измерений 10-20°С.

— Напряжения, используемые м измерительных мостах, находятся в диапазоне от 0,2*Uном до Uном через интервал 0,2 * Uном, где Uном — номинальное напряжение для испытуемого изделия. Типичный диапазон: 3,0-10,0 кВ.

Факторы, увеличивающие (ТУДП)

Основные факторы, влияющие на величину ТУДП: температура окружающей среды, частота переменного тока, напряжение электрического поля и влажность.

Температура

Повышение температуры вызывает увеличение tg δ, т.к. происходит рост проводимости, вызванный активизацией колебаний и перемещений отдельный зарядов и диполей в полярных диэлектриках.

Частота

С ростом частоты tg δ снижается, если причиной потерь является проводимость диэлектрика. В этом случае активная компонента тока не зависит от частоты, а реактивная (ёмкостная) растёт прямо пропорционально частоте, поэтому отношение IА к IС , т.е. tg δ уменьшаться с ростом частоты. Если основной причиной потерь является поляризация, то tg δ при определённой частоте будет иметь максимум с последующим спадом. В сложных диэлектриках присутствуют потери обоих типов, поэтому результат получается путём суммирования обоих типов.

Влажность

Присутствие влаги в любом виде (жидком, газообразном) вызывает существенное увеличение tg δ. Основная причина связана с тем, что увлажнение уменьшает удельное сопротивление (повышает проводимость).

Напряжение электрического поля

Если основным механизмом потерь является ионизация атомов диэлектрика, то заметное увеличение tg δ начинается с Ui — напряжения, вызывающего ионизации газового фрагмента. В случае отсутствия газовых включений tg δ не зависит от напряжения.

Заключение

Измерительный контроль значений ТУДП позволяет отслеживать состояние изоляционных свойств электрооборудования. Например, измерение tg δ трансформаторного масла, являющегося основным изолятором в силовых трансформаторах высоковольтных подстанций, позволяет избежать выхода из строя объектов энергоснабжения. Полученные значения ТУДП дают информацию о текущем качестве изоляции. Измерение ТУДП необходимо производить в соответствии с требованиями действующих стандартов на конкретные изделия (электрическая аппаратура, трансформаторы, генераторы, кабельная продукция).

Понравилась статья? Расскажите друзьям:

Оцените статью, для нас это очень важно:

Проголосовавших: 1 чел.
Средний рейтинг: 5 из 5.

9.3: Формулы двойного угла, половинного угла и приведения

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

1525

• OpenStax
• OpenStax

Цели обучения

• Использование формул двойного угла для нахождения точных значений
• Использовать формулы двойного угла для проверки тождества
• Используйте формулы сокращения для упрощения выражения
• Используйте формулы половинного угла, чтобы найти точные значения

Велосипедные рампы, сделанные для соревнований (см. рисунок \(\PageIndex{1}\)) должны различаться по высоте в зависимости от уровня навыков участников. Для продвинутых участников угол, образованный рампой и землей, должен быть \(\theta\) таким, что \(\tan \theta=\dfrac{5}{3}\). Угол делится пополам для новичков. Какая крутизна пандуса для новичков? В этом разделе мы исследуем три дополнительные категории тождеств, которые мы можем использовать, чтобы ответить на такие вопросы, как этот.

Рисунок \(\PageIndex{1}\): Велосипедные рампы для опытных райдеров имеют более крутой наклон, чем для новичков.

Использование формул двойного угла для нахождения точных значений

В предыдущем разделе мы использовали формулы сложения и вычитания для тригонометрических функций. Теперь еще раз взглянем на те же формулы. Формулы двойного угла являются частным случаем формул сумм, где \(\alpha=\beta\). Вывод формулы двойного угла для синуса начинается с формулы суммы

\[\sin(\alpha+\beta)=\sin \alpha \cos \beta+\cos \alpha \sin \beta\]

Если мы позволим \(\alpha=\beta=\theta\), то у нас есть

\[\begin{align*} \sin(\theta+\theta)&= \sin \theta \cos \theta+\cos \theta \sin \theta\\[4pt] \sin(2\theta) &= 2\sin \theta \cos \theta \end{align*}\]

Получение двойного угла для косинуса дает нам три варианта. Во-первых, исходя из формулы суммы \(\cos(\alpha+\beta)=\cos \alpha \cos \beta−\sin \alpha \sin \beta\), и пусть \(\alpha=\beta=\ тета\), у нас есть 92\theta} \end{align}\]

Как: Зная тангенс угла и квадрант, в котором он расположен, используйте формулы двойного угла, чтобы найти точное значение

1. Нарисуйте треугольник для отражения данная информация.
2. Определите правильную формулу двойного угла.
3. Подставьте значения в формулу на основе треугольника.
4. Упростить.

Пример \(\PageIndex{1}\): Использование формулы двойного угла для нахождения точного значения, включающего тангенс

Учитывая, что \(\tan \theta=−\dfrac{3}{4}\) и \(\theta\) находится в квадранте II, найдите следующее:

1. \(\sin(2\theta) \)
2. \(\cos(2\тета)\)
3. \(\загар(2\тета)\)

Решение

Если мы нарисуем треугольник, чтобы отразить предоставленную информацию, мы сможем найти значения, необходимые для решения задач на изображении. Нам даны \(\tan \theta=−\dfrac{3}{4}\), такие что \(\theta\) находится в квадранте II. Тангенс угла равен противолежащей стороне относительно прилежащей стороны, а поскольку  \(\theta\)  находится во втором квадранте, прилежащая сторона находится на 92\\[4pt] c&= 5 \end{align*}\]

Теперь мы можем нарисовать треугольник, подобный показанному на рисунке \(\PageIndex{2}\).

Рисунок \(\PageIndex{2}\)

1. Начнем с написания формулы двойного угла для синуса.

   \(\sin(2\theta)=2 \sin \theta \cos \theta\)

   Мы видим, что нам нужно найти \(\sin \theta\) и \(\cos \theta\). На основании рисунка \(\PageIndex{2}\) мы видим, что гипотенуза равна \(5\), поэтому \(\sin θ=35\), \(\sin θ=35\) и \(\ cos θ=−45\). Подставьте эти значения в уравнение и упростите. 92}\\[4pt]
   &= \dfrac{-\dfrac{3}{2}}{1-\dfrac{9}{16}}\\[4pt]
   &= -\dfrac{3}{ 2}\left(\dfrac{16}{7}\right)\\[4pt]
   &= -\dfrac{24}{7}
   \end{align*}\]

Упражнение \(\PageIndex{1}\)

Учитывая \(\sin \alpha=\dfrac{5}{8}\), с \(\theta\) в квадранте I, найдите \(\cos( 2\альфа)\).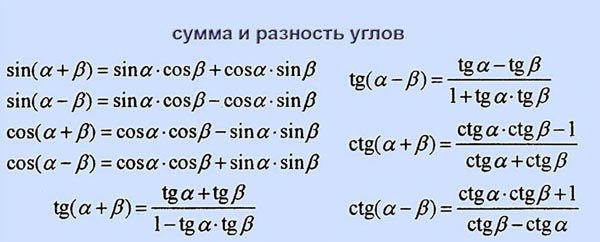

Ответить

\(\cos(2\alpha)=\dfrac{7}{32}\)

Пример \(\PageIndex{2}\): использование формулы двойного угла для косинуса без точных значений 92 3x \end{align*}\]

Анализ

Этот пример показывает, что мы можем использовать формулу двойного угла, не имея точных значений. Он подчеркивает, что шаблон — это то, что нам нужно помнить, и что тождества верны для всех значений в области определения тригонометрической функции.

Использование формул двойного угла для проверки тождественности

Установление тождества с использованием формул двойного угла выполняется с использованием тех же шагов, которые мы использовали для получения формул суммы и разности. Выберите более сложную часть уравнения и перепишите ее, пока она не совпадет с другой стороной. 92 \theta}{\tan \theta}}\\[4pt] &= \dfrac{2}{\cot \theta-\tan \theta} \qquad \text {Используйте взаимное тождество для } \dfrac{1}{ \tan \theta} \end{align*}\]

Анализ

Вот случай, когда более сложная часть исходного уравнения оказалась справа, но мы решили работать с левой частью. Однако, если бы мы выбрали для перезаписи левую часть, мы бы работали в обратном направлении, чтобы получить эквивалентность. Например, предположим, что мы хотели показать

92 \тета\)

Использование формул приведения для упрощения выражения

Формулы двойного угла можно использовать для получения формул приведения, которые являются формулами, которые мы можем использовать для уменьшения мощности данного выражения, включающего четные степени синуса или косинуса. Они позволяют нам переписать четные степени синуса или косинуса в терминах первой степени косинуса. Эти формулы особенно важны в курсах математики более высокого уровня, в частности исчисления. Также называемые формулами уменьшения степени, включены три тождества, которые легко выводятся из формул двойного угла. 92 x\\[4pt]
&= \dfrac{1}{4}+\dfrac{1}{2} \cos(2x)+\dfrac{1}{8}+\dfrac{1}{8} \cos(4x)\\[4pt]
&= \dfrac{3}{8}+\dfrac{1}{2} \cos(2x)+\dfrac{1}{8} \cos(4x)
\end{align*}\]

Анализ

Решение находится с помощью формулы приведения дважды, как уже отмечалось, и формулы полного квадрата из алгебры. 3(2x)=\left[ \dfrac {1}{2} \sin(2x) \right] [ 1−\cos(4x) \) 92 x\\[4pt] &= \dfrac{10}{4}+\dfrac{10}{2} \cos(2x)+\dfrac{10}{8}+\dfrac{10}{8}\ cos(4x)\\[4pt] &= \dfrac{30}{8}+5\cos(2x)+\dfrac{10}{8}\cos(4x)\\[4pt] &= \dfrac{ 15}{4}+5\cos(2x)+\dfrac{5}{4}\cos(4x) \end{align*}\]

Использование формул половинного угла для нахождения точных значений

Следующий набор тождеств — это набор из формул половинного угла , которые могут быть получены из формул приведения, и мы можем использовать их, когда имеем угол, равный половине размер специального угла. Если мы заменим \(\theta\) на \(\dfrac{\alpha}{2}\), формула половинного угла для синуса будет найдена путем упрощения уравнения и решения для \(\sin\left(\dfrac{ \alpha}{2}\right)\). Обратите внимание, что формулам половинного угла предшествует знак \(\pm\) . Это не означает, что допустимы как положительные, так и отрицательные выражения. Скорее, это зависит от квадранта, в котором заканчивается \(\dfrac{\alpha}{2}\) . 92\left(\dfrac{\alpha}{2}\right)&= \dfrac{1-\cos\left(2\cdot \dfrac{\alpha}{2}\right)}{1+\cos\ влево (2\cdot \dfrac{\alpha}{2}\right)}\\[4pt] \tan\left(\dfrac{\alpha}{2}\right)&= \pm \sqrt{\dfrac{ 1-\cos \alpha}{1+\cos \alpha}} \end{align*}\]

ФОРМУЛЫ ПОЛУУГЛОВ

Формулы для полууглов следующие:

\[\begin{ выравнивание} \sin\left(\dfrac{\alpha}{2}\right)&=\pm \sqrt{\dfrac{1-\cos\alpha}{2}} \label{halfsine} \\[4pt] \cos \left(\dfrac{\alpha}{2} \right) &=\pm \sqrt{\dfrac{1+\cos \alpha}{2}} \\[4pt] \tan\left(\dfrac {\alpha}{2}\right) &=\pm \sqrt{\dfrac{1-\cos\alpha}{1+\cos\alpha}} =\dfrac{\sin\alpha}{1+\cos \alpha} =\dfrac{1-\cos\alpha}{\sin\alpha}\end{align}\] 9{\circ}}{2}}\\[4pt]
&= \sqrt{\dfrac{1-\dfrac{\sqrt{3}}{2}}{2}}\\[4pt]
&= \sqrt{\dfrac{\dfrac{2-\sqrt{3}}{2}}{2}}\\[4pt]
&= \sqrt{\dfrac{2-\sqrt{3}}{4} }\\[4pt]
&= \dfrac{\sqrt{2-\sqrt{3}}}{2}
\end{align*}\]

Помните, что мы можем проверить ответ с помощью графического калькулятора.

Анализ

Обратите внимание, что мы использовали только положительный корень, потому что \(\sin(15°)\) положительно.

Практическое руководство: Зная тангенс угла и квадрант, в котором находится угол, найдите точные значения тригонометрических функций половины угла.

1. Нарисуйте треугольник для представления данной информации.
2. Определите правильную формулу половинного угла.
3. Подставьте значения в формулу на основе треугольника.
4. Упростить.

Пример \(\PageIndex{8}\): поиск точных значений с использованием тождеств половинного угла

квадрант III, найдите точное значение следующего:

1. \(\sin\left(\dfrac{\alpha}{2}\right)\)
2. \(\cos\влево(\dfrac{\alpha}{2}\вправо)\)
3. \(\загар\влево(\dfrac{\alpha}{2}\вправо)\)

Решение

Используя данную информацию, мы можем нарисовать треугольник, показанный на рисунке \(\PageIndex{3}\). Используя теорему Пифагора, мы находим, что гипотенуза равна 17. Следовательно, мы можем вычислить {17}\).

Рисунок \(\PageIndex{3}\)

1. Прежде чем мы начнем, мы должны помнить, что если \(α\) находится в квадранте III, то \(180°<\alpha<270°\), поэтому \(\ dfrac{180°}{2}<\dfrac{\alpha}{2}<\dfrac{270°}{2}\). Это означает, что конечная сторона  \(\dfrac{\alpha}{2}\) находится в квадранте II, так как \(90°<\dfrac{\alpha}{2}<135°\). Чтобы найти \(\sin \dfrac{\alpha}{2}\), начнем с записи формулы половинного угла для синуса. Затем мы подставляем значение косинуса, которое мы нашли из треугольника на рисунке \(\PageIndex{3}\), и упрощаем. \[\begin{align*} \sin \dfrac{\alpha}{2}&= \pm \sqrt{\dfrac{1-\cos \alpha}{2}}\\[4pt] &= \pm \ sqrt{\dfrac{1-(-\dfrac{15}{17})}{2}}\\[4pt] &= \pm \sqrt{\dfrac{\dfrac{32}{17}}{2} }\\[4pt] &= \pm \sqrt{\dfrac{32}{17}\cdot \dfrac{1}{2}}\\[4pt] &= \pm \sqrt{\dfrac{16}{ 17}}\\[4pt] &= \pm \dfrac{4}{\sqrt{17}}\\[4pt] &= \dfrac{4\sqrt{17}}{17} \end{align*} \] Мы выбираем положительное значение \(\sin \dfrac{\alpha}{2}\) , потому что угол заканчивается в квадранте II, а синус положителен в квадранте II.
2. Чтобы найти \(\cos \dfrac{\alpha}{2}\), мы напишем формулу половинного угла для косинуса, подставим значение косинуса, которое мы нашли из треугольника на рисунке \(\PageIndex{3} \) и упростить. \[\begin{align*} \cos \dfrac{\alpha}{2}&= \pm \sqrt{\dfrac{1+\cos \alpha}{2}}\\[4pt] &= \pm \ sqrt{\dfrac{1+\left(-\dfrac{15}{17}\right)}{2}}\\[4pt] &= \pm \sqrt{\dfrac{\dfrac{2}{17} {2}}\\[4pt] &= \pm \sqrt{\dfrac{2}{17}\cdot \dfrac{1}{2}}\\[4pt] &= \pm \sqrt{\dfrac {1}{17}}\\[4pt] &= -\dfrac{\sqrt{17}}{17} \end{align*}\] Мы выбираем отрицательное значение \(\cos \dfrac{\alpha {2}\) , потому что угол находится в квадранте II, потому что косинус отрицателен в квадранте II.
3. Чтобы найти \(\tan \dfrac{\alpha}{2}\), запишем формулу половинного угла для тангенса. Снова подставляем значение косинуса, которое мы нашли из треугольника на рисунке \(\PageIndex{3}\), и упрощаем. \[\begin{align*} \tan \dfrac{\alpha}{2}&= \pm \sqrt{\dfrac{1-\cos \alpha}{1+\cos \alpha}}\\[4pt] &= \pm \sqrt{\dfrac{1-\left(-\dfrac{15}{17}\right)}{1+\left(-\dfrac{15}{17}\right)}}\\ [4pt] &= \pm \sqrt{\dfrac{\dfrac{32}{17}}{\dfrac{2}{17}}}\\[4pt] &= \pm \sqrt{\dfrac{32} {2}}\\[4pt] &= -\sqrt{16}\\[4pt] &= -4 \end{align*}\] Мы выбираем отрицательное значение \(\tan \dfrac{\alpha} {2}\) потому что \(\dfrac{\alpha}{2}\)  лежит в квадранте II, а тангенс отрицателен в квадранте II.

Упражнение \(\PageIndex{5}\)

Учитывая, что \(\sin \alpha=−\dfrac{4}{5}\) и \(\alpha\)  лежит в квадранте IV, найдите точное значение из \(\cos \left(\dfrac{\alpha}{2}\right)\).​​​​​

Ответ

\(-\dfrac{2}{\sqrt{5}}\)

Пример \(\PageIndex{9}\): Нахождение измерения половинного угла

Теперь вернемся к задаче, поставленной в начале раздела. Велосипедная рампа сконструирована для соревнований высокого уровня с углом \(θ\) , образованным рампой и землей. Еще одна рампа должна быть построена вполовину меньшей крутизны для соревнований новичков. Если \(tan θ=53\) для соревнований более высокого уровня, каково измерение угла для соревнований новичков? 92&=34\\[4pt] c&=\sqrt{34} \end{align*}\]

Рисунок \(\PageIndex{4}\)

Мы видим, что \(\cos \theta=\dfrac{3} {\ sqrt {34}} = \ dfrac {3 \ sqrt {34}} {34} \). Мы можем использовать формулу половинного угла для тангенса: Поскольку \(\tan \theta\) находится в первом квадранте, то и \(\tan \dfrac{\theta}{2}\).

\[\begin{align*}
\tan \dfrac{\theta}{2}&= \sqrt{\dfrac{1-\dfrac{3\sqrt{34}}{34}}{1+\ dfrac{3\sqrt{34}}{34}}}\\[4pt]
&= \sqrt{\dfrac{\dfrac{34-3\sqrt{34}}}{34}}{\dfrac{34+ 3\sqrt{34}}{34}}}\\[4pt] 9{−1}(0,57)≈29,7°\). Таким образом, угол рампы для соревнований новичков равен \(≈29,7°\).

Медиа

Доступ к этим онлайн-ресурсам для получения дополнительных инструкций и практики с формулами двойного угла, половинного угла и сокращения.

• Двухугольные удостоверения
• Полуугольные тождества

Ключевые уравнения

Формулы двойного угла	\(\sin(2\theta)=2\sin \theta \cos \theta\) 92 \тета=\dfrac{1−\cos(2\theta)}{1+\cos(2\theta)}\)
Формулы полууглов	\(\sin \dfrac{\alpha}{2}=\pm \sqrt{\dfrac{1−\cos \alpha}{2}}\) \(\cos \dfrac{\alpha}{2}=\pm \sqrt{\dfrac{1+\cos \alpha}{2}}\) \(\tan \dfrac{\alpha}{2}=\pm \sqrt{\dfrac{1−\cos \alpha}{1+\cos \alpha}}\) \(=\dfrac{\sin \alpha}{1+\cos \alpha}\) \(=\dfrac{1−\cos \alpha}{\sin \alpha}\)

Ключевые понятия

• Тождества двойных углов выводятся из формул суммы основных тригонометрических функций: синуса, косинуса и тангенса. См. Пример \(\PageIndex{1}\), Пример \(\PageIndex{2}\), Пример \(\PageIndex{3}\) и Пример \(\PageIndex{4}\).
• Формулы редукции особенно полезны в математических вычислениях, поскольку они позволяют уменьшить мощность тригонометрического члена. См. Пример \(\PageIndex{5}\) и Пример \(\PageIndex{6}\).
• Формулы половинного угла позволяют нам найти значение тригонометрических функций, содержащих половинные углы, независимо от того, известен исходный угол или нет. См. Пример \(\PageIndex{7}\), Пример \(\PageIndex{8}\) и Пример \(\PageIndex{9}\).

---

Эта страница под названием 9.3: Формулы двойного угла, половинного угла и сокращения распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована OpenStax с помощью исходного контента, который был отредактирован в соответствии со стилем и стандартами платформа LibreTexts; подробная история редактирования доступна по запросу.

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или Страница

   Автор

   ОпенСтакс

   Лицензия

   СС BY

   Версия лицензии

   4,0

   Программа OER или Publisher

   ОпенСтакс

   Показать страницу TOC

   нет

2. Теги

   1. формулы двойного угла
   2. формула половинного угла
   3. формулы половинного угла
   4. Теорема Пифагора
   5. формулы приведения
   6. источник@https://openstax. org/details/books/precalculus

Формула тангенса с примерами решения

Формула тангенса

Формулы тангенса используются для вычисления функций тангенса в математике. Функция тангенса также обозначается как тангенс. Касательная функция получается путем деления перпендикуляра на основание.

О теме 

В тригонометрии существует шесть типов соотношений или функций. Тангенс функция является примером этих функций. Различные тригонометрические тождества и формулы вычисляют функцию тангенса. Существуют различные формулы касательной функции, вычисленные из этих тождеств и формул.

Предположим, треугольник прямоугольный. Прямоугольный треугольник содержит три стороны: основание, перпендикуляр и гипотенузу. Простая формула функции тангенса:

тангенс = Перпендикуляр/Основание 

С другой стороны, другая формула для функции тангенса вычисляется с учетом острого угла в прямоугольном треугольнике.

tan = противоположная сторона / смежная сторона

В этой формуле противолежащая сторона — это сторона прямоугольного треугольника, противоположная углу x. Прилежащая сторона – это сторона прямоугольного треугольника, примыкающая к углу x. Существует множество формул для смежных углов. Все эти формулы подробно описаны в следующем разделе.

Формула

Общая формула:

(на основе сторон тригонометрии)

tan = перпендикуляр/основание

(относительно угла x в прямоугольном треугольнике)

tan = противоположная сторона/4 смежная сторона

tan = противоположная сторона/4 смежная сторона

Sin и cos Формула тангенса:

tan x = (sin x) / (cos x)

Формулы тангенса с использованием тождества обратной величины:

tan x = 1 / (cot x)

Формулы тангенса с использованием тождества Пифагора:

тангенс х = ± √( сек ² x – 1)

Формула тангенса тождества кофункции:

tan x = cot (90° – x) (OR)

tan x = cot (π/2 – x)

Сумма и разность Формула тангенса:

tan (A – B) = (tan A – tan B) / (1 + tan A tan B)

tan (A + B) = (tan A + tan B) / (1 – tan A tan B)

Формула касательной двойного угла:

tan 2x = (2 tan x) / (1 – tan ² x)

Формула касательной тройного угла:

tan 3x = (3 tan x – tan ³ x) / (1 – 3tan ² x)

Тангенс половины угла Формула:

tan (x/2) = (1 – cos x) / (sin x)

tan (x/2) =± √[(1 – cos x) / (1 + cos x)]

Решенные примеры

1.