Периметр правильного треугольника – формула, примеры
4.6
Средняя оценка: 4.6
Всего получено оценок: 145.
4.6
Средняя оценка: 4.6
Всего получено оценок: 145.
Правильный треугольник особенно выделяется на фоне других фигур. Любой параметр такого треугольника может быть определен из длины стороны. Особенной простотой отличается нахождение периметра.
Определения
Для начала вспомним несколько определений, которые потребуются для того, чтобы решать задачи на нахождение периметра правильного треугольника:
- Правильным треугольником является треугольник, все стороны которого равны, а каждый из углов составляет 60 градусов.
- Правильный треугольник является частным случаем равнобедренного, поэтому любая высота правильного треугольника будет являться биссектрисой и медианой.
- Некоторые формулы для произвольного треугольника при применении к правильному треугольнику можно значительно упростить с помощью теоремы Пифагора.

Периметр треугольника
Что такое периметр? Это сумма длин всех сторон.
Формула периметра одинакова для любой фигуры. Это всегда сумма длин всех сторон.
Рис. 1. Различные фигуры.Конкретно для правильного треугольника, нужно вспомнить, что все стороны этой фигуры равны между собой. Сторон у треугольника 3, а значит, формула периметра выглядит следующим образом:
$$P=3a$$
Пример
Сложную задачу на нахождение периметра правильного треугольника придумать нелегко. Поэтому решим интересную, но простую задачу на заданную тематику. В процессе решения рассмотрим применение теоремы Пифагора для решения задач с правильным треугольником.
Площадь правильного треугольника АВС равняется $9\sqrt{3}$
Рис. 2. Рисунок к задаче.Любую характеристику правильного треугольника можно найти, если есть хотя бы одна из длин. Неважно, будет это сторона, площадь, периметр, медиана или биссектриса. Любой длины будет достаточно для решения задачи.
Вспомним формулу площади треугольника и упростим ее для правильного треугольника.
Из этой формулы выразим значение стороны:
$$a=\sqrt{4S\over{\sqrt{3}}}=\sqrt{{4*{9\over{\sqrt{3}}}}\over{\sqrt{3}}}=6$$
Теперь найти периметр не составит проблем.
$$P=3a=3*6=18$$
Что мы узнали?
Мы привели формулу периметра правильного треугольника. На примере показали, как можно найти площадь правильного треугольника через площадь. На том же примере показали примерный ход решения любой задачи на решение правильного треугольника.
Тест по теме
Доска почёта
Чтобы попасть сюда — пройдите тест.
Оценка статьи
4.6
Средняя оценка: 4.6
Всего получено оценок: 145.
А какая ваша оценка?
Периметр треугольника. Онлайн калькулятор.
Периметр треугольника по сторонам
Введите длины сторон треугольника
a =
b =
c =
Формула периметра треугольника по сторонам
P=a+b+c
Где a, b и c — стороны треугольника
Периметр треугольника по средним линиям
Введите длины средних линий
MN =
NK =
KM =
Формула периметра треугольника по средним линиям
P=MN×2+NK×2+KM×2
Где MN, NK и KM — средние линии треугольника
Периметр треугольника по двум сторонам и углу между ними
Введите стороны и угол между ними
a =
b =
α =
Формула периметра треугольника по двум сторонам и углу между ними
Где a, b — стороны треугольника, α — угол между сторонами
Периметр прямоугольного треугольника по катету и гипотенузе
Введите катет
Введите гипотенузу
Формула периметра прямоугольного треугольника по катету и гипотенузе
Где a — гипотенуза, b — катет
Периметр прямоугольного треугольника по катетам
Введите первый катет
Введите второй катет
Формула периметра прямоугольного треугольника по двум катетам
Где a и b — катеты
Периметр равнобедренного треугольника по основанию и высоте
Введите основание
Введите высоту
Формула периметра равнобедренного треугольника по основанию и высоте
Где h — высота, a — основание
Периметр равнобедренного треугольника по боковой стороне и основанию
Введите сторону
Введите основание
Формула периметра равнобедренного треугольника по боковой стороне и основанию
Где b — боковые стороны, a — основание
Периметр равностороннего треугольника по высоте
Введите высоту
Формула периметра равностороннего треугольника по высоте
Где h — высота
Периметр равностороннего треугольника по площади вписанной окружности
Введите площадь
Формула периметра равностороннего треугольника по площади вписанной окружности
Где S — площадь вписанной окружности
Периметр прямоугольного треугольника по гипотенузе и углу
Введите гипотенузу
Введите угол
Формула периметра прямоугольного треугольника по гипотенузе и углу
P=c×sin(α) + c×cos(α)+c
Где с — гипотенуза, α — угол
Периметр прямоугольного треугольника по катету и прилежащему углу
Введите катет
Введите угол
Формула периметра прямоугольного треугольника по катету и прилежащему углу
P=b×tg(α)+b+b/cos(α)
Где b — катет, α — прилежащий угол
Периметр прямоугольного треугольника по катету и противолежащему углу
Введите катет
Введите угол
Формула периметра прямоугольного треугольника по катету и противолежащему углу
P=a+a/tg(α)+a/sin(α)
Где a — катет, α — противолежащий угол
Связь площади и периметра треугольника
Связь площади и периметра треугольника — Открытый справочник по математикеГлавная Контакт О Тематический указатель
Треугольник с фиксированной
периметр
может иметь много разных
области.
Попробуйте это Перетащите оранжевую точку на треугольник ниже. Треугольник будет иметь фиксированную периметр, но площадь будет разной.
Распространенной ошибкой является предположение, что треугольник с фиксированной периметр также должен иметь фиксированный область. это точно , а не , как видно из рисунка выше. Когда вы перетаскиваете оранжевую точку A, треугольник будет поддерживать фиксированный периметр. Но, как видите, площадь сильно различается.
Когда A находится на полпути между B и C, площадь максимальна. Когда вы перетащите его в одну сторону, вы увидите площадь уменьшается, как в формуле вверху, так и замечая, что внутри нее может поместиться все меньше и меньше квадратов. В конце концов, когда A находится на одной линии с B и C, площадь равна нулю.
Площадь максимальна, когда треугольник равнобедренный. То есть, когда обе стороны имеют одинаковую длину. Тщательно отрегулируйте A выше чтобы создать равнобедренный треугольник и отметить, что площадь наибольшая, когда AC и AB имеют одинаковую длину (9,0)
Попробуйте со строкой
Сделайте петлю из нити и проденьте ее вокруг двух булавок (соответствующих двум точкам B и C выше). Натяните нить третьей булавкой, чтобы получился треугольник. Когда вы перемещаете любую булавку с натянутой струной,
вы будете делать треугольники с разными площадями, но периметр фиксирован (длина петли веревки).
Натяните нить третьей булавкой, чтобы получился треугольник. Когда вы перемещаете любую булавку с натянутой струной,
вы будете делать треугольники с разными площадями, но периметр фиксирован (длина петли веревки).Связь Эллипса
На рисунке выше установите флажок «Показать след», затем перетащите точку А вокруг базовой линии. Полученная форма представляет собой эллипс.Почему это? Определение эллипса
«Линия, образующая замкнутый контур, где сумма расстояний от двух точек (фокусов) до каждой точки на линии постоянна»
Точки B и C образуют два фокуса. Поскольку расстояние от В до С фиксировано, а периметр фиксирован, то сумма расстояний АВ и АС равна константа — условие, необходимое для формирования эллипса.Узнайте больше об эллипсах
Описанный выше эксперимент со струной на самом деле представляет собой практический способ рисования эллипса.
См. Рисование эллипса с помощью веревки и двух булавок. Дополнительные сведения об эллипсах см. также
Определение эллипса.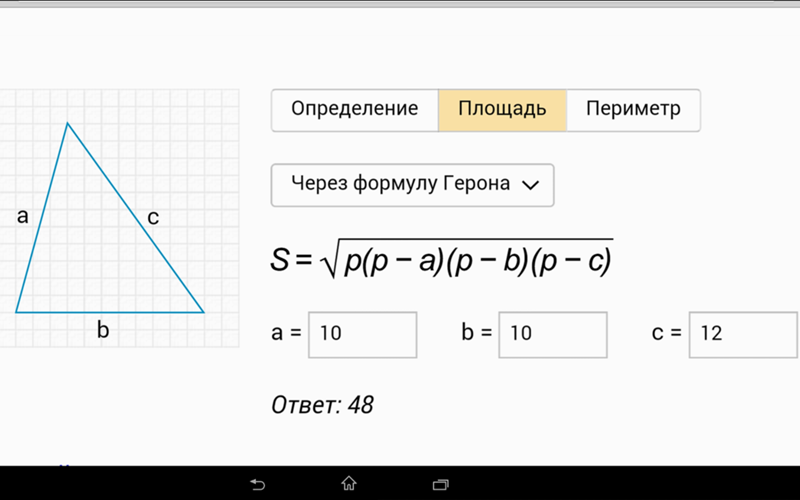
Другие темы треугольника
Общий
- Определение треугольника
- Гипотенуза
- Уголки внутренние треугольные
- Наружные треугольные углы
- Теорема о внешнем угле треугольника
- Теорема Пифагора
- Доказательство теоремы Пифагора
- Пифагоровы тройки
- Треугольник, описанный вокруг окружности
- Треугольник вписанный в окружность
- Медианы треугольника
- Высота треугольника
- Средняя линия треугольника
- Неравенство треугольника
- Соотношение сторона/угол
Периметр/площадь
- Периметр треугольника
- Площадь треугольника
- Формула Герона
- Площадь равностороннего треугольника
- Площадь методом «боковой угол сторона»
- Площадь треугольника с фиксированным периметром
Треугольные типы
- Прямоугольный треугольник
- Равнобедренный треугольник
- Разносторонний треугольник
- Равносторонний треугольник
- Равнобедренный треугольник
- Тупоугольный треугольник
- Остроугольный треугольник
- Треугольник 3-4-5
- 30-60-90 треугольник
- 45-45-90 треугольник
Треугольные центры
- Центр треугольника
- Центр окружности треугольника
- Центроид треугольника
- Ортоцентр треугольника
- Линия Эйлера
Конгруэнтность и подобие
- Конгруэнтные треугольники
Решение треугольников
- Решение треугольника
- Закон синусов
- Закон косинусов
Тесты и упражнения с треугольниками
- Викторина типа треугольник
- Проблема с мячиком
- Сколько треугольников?
- Спутниковые орбиты
(C) 2011 Copyright Math Open Reference.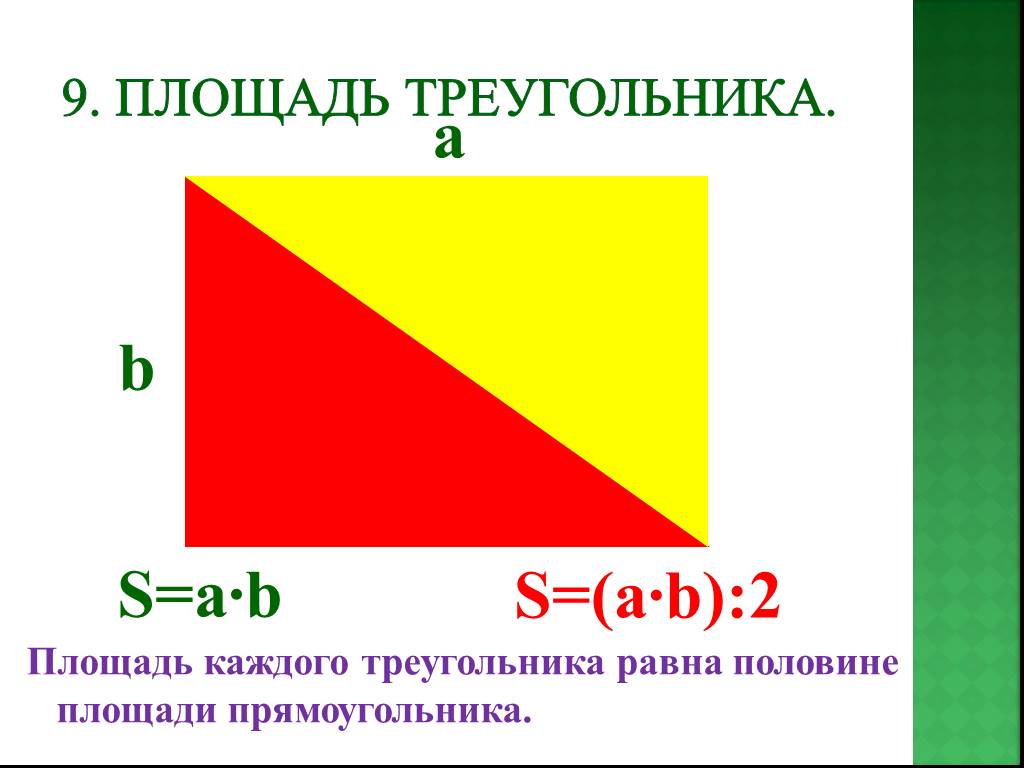
Все права защищены
4.6: Площадь и периметр треугольников
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 2176
Площадь равна половине произведения основания на высоту, а периметр равен сумме сторон.
Формула площади треугольника равна половине площади параллелограмма .
Рисунок \(\PageIndex{1}\)Площадь треугольника: \(A=\dfrac{1}{2} bh\) или \(A=\dfrac{bh}{2}\).
Рисунок \(\PageIndex{2}\)Что, если бы вам дали треугольник и размеры его основания и высоты? Как можно найти общее расстояние вокруг треугольника и количество места, которое он занимает?
2 \\ 92\) и основание \(24\: m\)?В вопросах 6-11 мы собираемся вывести формулу площади равностороннего треугольника.
Рисунок \(\PageIndex{7}\)- Что за треугольник \(\Delta ABD\)? Найдите \(AD\) и \(BD\).
- Найдите площадь \(\Delta ABC\).
- Если каждая сторона равна \(x\), что такое \(AD\) и \(BD\)?
- Если каждая сторона равна \(x\), найдите площадь \(\Delta ABC\).
- Используя формулу №9, найдите площадь равностороннего треугольника со стороной 12 дюймов.
- Используя формулу №9, найдите площадь равностороннего треугольника со стороной 5 дюймов.
Обзор (ответы)
Чтобы просмотреть ответы на обзор, откройте этот PDF-файл и найдите раздел 10.3.
Словарь
| Срок | Определение |
|---|---|
| Площадь | Площадь — это пространство внутри периметра двумерной фигуры.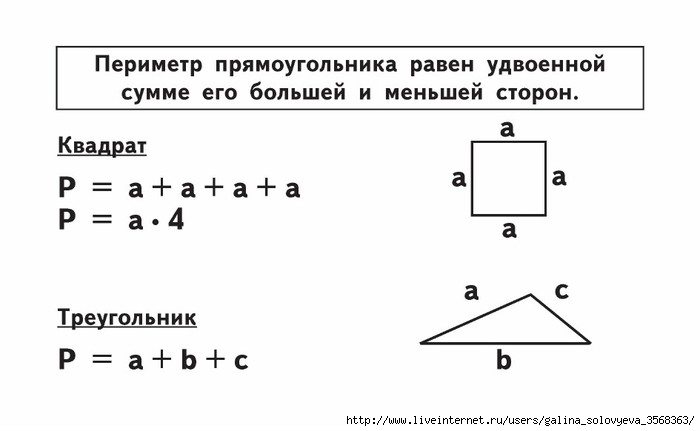 |
| Периметр | Периметр — это расстояние вокруг двумерной фигуры. |
| Перпендикулярный | Перпендикулярные прямые — это прямые, пересекающиеся под углом 90∘. Произведение наклонов двух перпендикулярных прямых равно -1. |
| Прямоугольный | Прямой угол – это угол, равный 90 градусам. |
| Прямоугольный треугольник | Прямоугольный треугольник — это треугольник, у которого один угол равен 90 градусов. |
| Площадь параллелограмма | Площадь параллелограмма равна произведению основания на высоту: \(A = bh\). |
| Площадь треугольника | Площадь треугольника равна половине площади параллелограмма. Отсюда формула: \(A=\dfrac{1}{2}bh\) или \(A=\dfrac{bh}{2}\). |
Дополнительные ресурсы
Интерактивный элемент
ВИДЕО: Область треугольника (целые числа)
Действия: Область и периметр для обсуждения Triangles
.
Практика: Площадь и периметр треугольников
Реальный мир: Периметр
Эта страница под названием 4.6: Площадь и периметр треугольников распространяется под лицензией CK-12 и была создана, изменена и/или курирована Фондом CK-12 с помощью исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts.

