Читать дальше: как найти косинус угла между векторами.
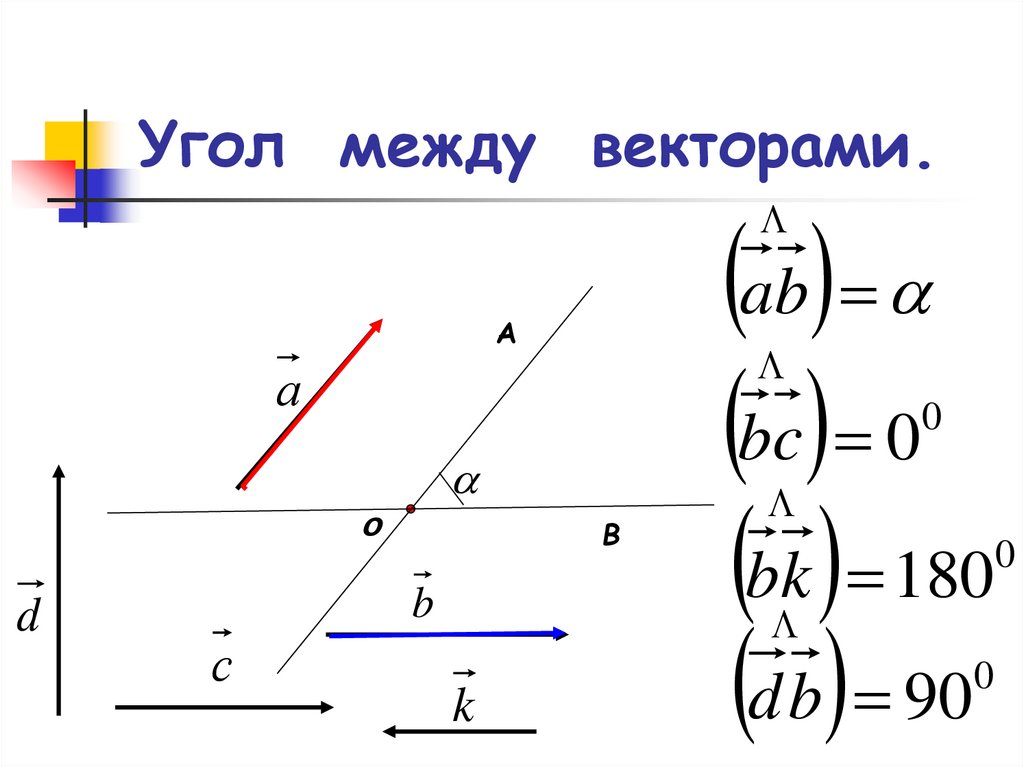
Угол между векторами.
Навигация по странице:
- Определение угла между векторами
- Формула вычисления угла между векторами
- Примеры задач на вычисление угла между векторами
- плоские задачи
- пространственные задачи
Онлайн калькулятор. Вычисление угла между векторами.
Определение. Углом между двумя векторами, отложенными от одной точки, называется кратчайший угол, на который нужно повернуть один из векторов вокруг своего начала до положения сонаправленности с другим вектором.
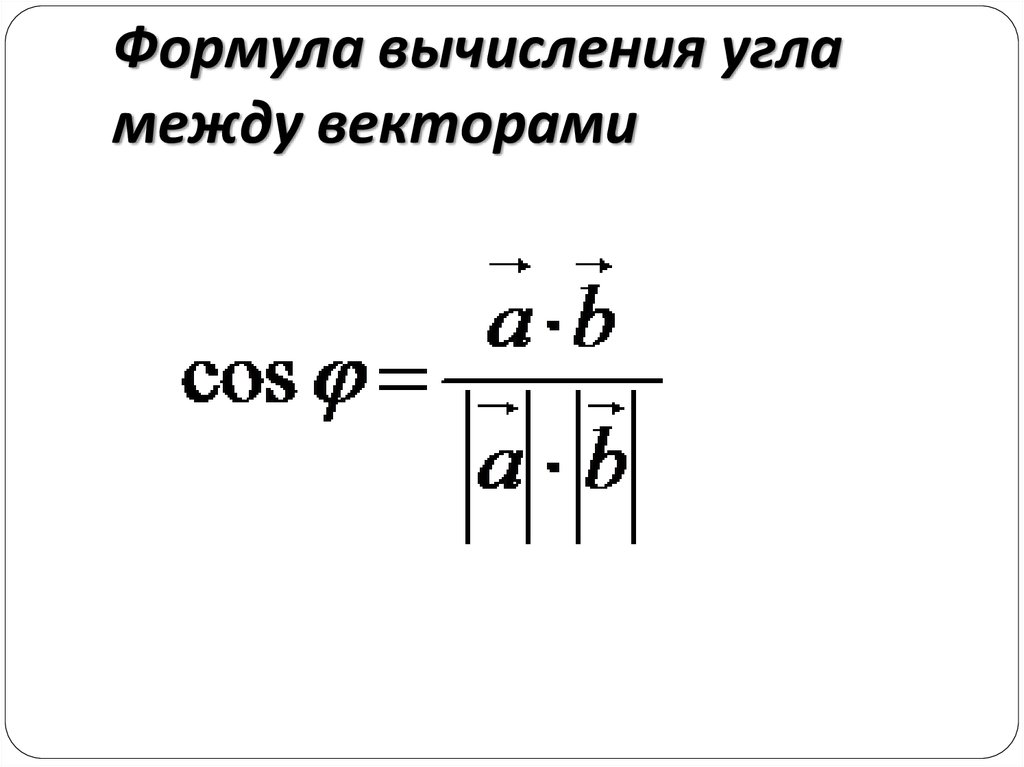
Основное соотношение. Косинус угла между векторами равен скалярному произведению векторов, поделенному на произведение модулей векторов.
Формула вычисления угла между векторами
| cos α = | a·b |
| |a|·|b| |
Примеры задач на вычисление угла между векторами
Примеры вычисления угла между векторами для плоских задачи
Пример 1. Найти угол между векторами a = {3; 4} и b = {4; 3}.
Найти угол между векторами a = {3; 4} и b = {4; 3}.
Решение: Найдем скалярное произведение векторов:
a·b = 3 · 4 + 4 · 3 = 12 + 12 = 24.
Найдем модули векторов:
|a| = √32 + 42 = √9 + 16 = √25 = 5
|b| = √42 + 32 = √16 + 9 = √25 = 5
Найдем угол между векторами:
| cos α = | a · b | = | 24 | = | 24 | = 0.96 |
| |a| · |b| | 5 · 5 | 25 |
Пример 2. Найти угол между векторами a = {7; 1} и b = {5; 5}.
Решение: Найдем скалярное произведение векторов:
a·b = 5 · 7 + 1 · 5 = 35 + 5 = 40.
Найдем модули векторов:
|a| = √72 + 12 = √49 + 1 = √50 = 5√2
|b| = √52 + 52 = √25 + 25 = √50 = 5√2
Найдем угол между векторами:
| cos α = | a · b | = | 40 | = | 40 | = | 4 | = 0. 8 8 |
| |a| · |b| | 5√2 · 5√2 | 50 | 5 |
Примеры вычисления угла между векторами для пространственных задач
Пример 3. Найти угол между векторами a = {3; 4; 0} и b = {4; 4; 2}.
Решение: Найдем скалярное произведение векторов:
a·b = 3 · 4 + 4 · 4 + 0 · 2 = 12 + 16 + 0 = 28.
Найдем модули векторов:
|a| = √32 + 42 + 02 = √9 + 16 = √25 = 5
|b| = √42 + 42 + 22 = √16 + 16 + 4 = √36 = 6
Найдем угол между векторами:
| cos α = | a · b | = | 28 | = | 14 |
| |a| · |b| | 5 · 6 | 15 |
Пример 4. Найти угол между векторами a = {1; 0; 3} и b = {5; 5; 0}.
Решение: Найдем скалярное произведение векторов:
a·b = 1 · 5 + 0 · 5 + 3 · 0 = 5.
Найдем модули векторов:
|a| = √12 + 02 + 32 = √1 + 9 = √10
|b| = √52 + 52 + 02 = √25 + 25 = √50 = 5√2
Найдем угол между векторами:
| cos α = | a · b | = | 5 | = | 1 | = | √5 | = 0.1√5 |
| |a| · |b| | √10 · 5√2 | 2√5 | 10 |
Вектора Вектор: определение и основные понятия Определение координат вектора заданного координатами его начальной и конечной точки Модуль вектора. Длина вектора Направляющие косинусы вектора Равенство векторов Ортогональность векторов Коллинеарность векторов Компланарность векторов Угол между векторами Проекция вектора Сложение и вычитание векторов Умножение вектора на число Скалярное произведение векторов Векторное произведение векторов Смешанное произведение векторов Линейно зависимые и линейно независимые вектора Разложение вектора по базису
Онлайн калькуляторы с векторами
Онлайн упражнения с векторами на плоскости
Онлайн упражнения с векторами в пространстве
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Калькулятор угла между двумя векторами.
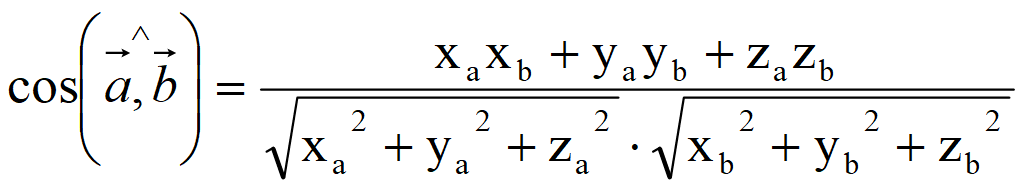 2D и 3D векторы
2D и 3D векторыС помощью этого калькулятора угла между двумя векторами вы быстро научитесь находить угол между двумя векторами. Неважно, находятся ли ваши векторы в 2D или 3D , а также являются ли их представления координатами или начальными и конечными точками — наш инструмент является беспроигрышным вариантом в любом случае. Поиграйте с калькулятором и проверьте определения и пояснения ниже; если вы ищете формулу угла между двумя векторами, вы обязательно найдете их там.
Раз уж вы здесь, ищете решения своих векторных задач, можем ли мы предположить, что вы также интересуетесь векторными операциями? Проверьте другие инструменты Omni в разделе координатной геометрии.
Формулы угла между двумя векторами
В этом параграфе вы найдете формулы для угла между двумя векторами — и только формулы. Если вы хотите понять, как мы их получаем, перейдите непосредственно к следующему параграфу,  {\ гидроразрыва {1} {2}} \ большой) \ большой)
\end{split}angle=arccos((xa⋅xb+ya⋅yb)/((xa2+ya2)21⋅(xb2+yb2)21))
{\ гидроразрыва {1} {2}} \ большой) \ большой)
\end{split}angle=arccos((xa⋅xb+ya⋅yb)/((xa2+ya2)21⋅(xb2+yb2)21))
- Векторы между начальной и конечной точкой:
Для вектора a\boldsymbol aa:
A=(x1,y1,z1)\scriptsize A =(x_1,y_1,z_1)A=(x1,y1,z1)
And:
B =(x2,y2,z2)\scriptsize B =(x_2,y_2,z_2)B=(x2,y2,z2)
Таким образом, вектор a\boldsymbol aa равен:
a=(x2−x1, y2,y1)\scriptsize\boldsymbol a = (x_2-x_1,y_2,y_1)a=(x2−x1,y2,y1)
Для вектора b\boldsymbol bb:
C=(x3, y3,z3)\scriptsize C =(x_3,y_3,z_3)C=(x3,y3,z3)
And:
D=(x4,y4,z4)\scriptsize D =(x_4,y_4,z_4)D=(x4,y4,z4)
Итак, вектор b\boldsymbol bb:
b=(x4−x3,y4−y3)\scriptsize\boldsymbol{b}=(x_4-x_3,y_4-y_3)b=(x4−x3,y4−y3)
And:
угол =arccos(((x2−x1)⋅(x4−x3)+(y2−y1)⋅(y4−y3))/((((x2−x1)2+(y2−y1)2)12⋅((x4 −x3)2+(y4−y3)2)12))\scriptsize\begin{split} \mathrm{угол} &= \mathrm{arccos}\bigg(\Big((x_2-x_1)\cdot(x_4-x_3)\\ &\!\!\!\!\!\!\!\!\!+(y_2-y_1)\cdot(y_4-y_3)\Big)\\ &\!\!\!\!\!\!\!\!\!/\Big(\big((x_2-x_1)^2+(y_2-y_1)^2\big)^{\frac{1 {2}}\\ &\!\!\!\!\!\!\!\!\!\cdot\!\big((x_4-x_3)^2+(y_4-y_3)^2\big)^{\frac{1 }{2}}\Большой)\Большой) \end{split}angle=arccos(((x2−x1)⋅(x4−x3)+(y2−y1)⋅(y4−y3))/(((x2− x1)2+(y2−y1)2)21⋅((x4−x3)2+(y4−y3)2)21))
Угол между двумя трехмерными векторами
- Векторы, представленные координатами:
a=(xa,ya,za)\scriptsize\boldsymbol a = (x_a,y_a,z_a)a=(xa,ya,za)
И:
b=(xb,yb,zb )\scriptsize\boldsymbol b = (x_b,y_b,z_b)b=(xb,yb,zb)
Тогда:
angle=arccos((xa⋅xb+ya⋅yb+za⋅zb)/ ((xa2+ya2+za2)12⋅(xb2+yb2+zb2)12))\scriptsize \начать{разделить} &\mathrm{угол} \!=\! \mathrm{arccos}\bigg((x_a\cdot x_b+y_a\cdot y_b+z_a\cdot z_b)\\ &\!\!/\Большой(\большой(x_a^2+y_a^2+z_a^2\big)^{\frac{1}{2}}\cdot\big(x_b^2+y_b^2+ z_b ^ 2 \ большой) ^ {\ гидроразрыва {1} {2}} \ большой) \ большой) \end{split}angle=arccos((xa⋅xb+ya⋅yb+za⋅zb)/((xa2+ya2+za2)21⋅(xb2+yb2 +zb2)21))
- Векторы между начальной и конечной точкой:
Для вектора a\boldsymbol{a}a:
A=(x1,y1,z1)\scriptsize A = (x_1,y_1,z_1)A=(x1,y1,z1)
И:
B=(x2,y2,z2)\scriptsize B =(x_2,y_2,z_2)B=(x2,y2,z2)
Итак:
a=(x2−x1,y2−y1 ,z2−z1)\scriptsize\boldsymbol{a} = (x_2-x_1,y_2-y_1,z_2-z_1)a=(x2-x1,y2-y1,z2-z1)
Для вектор b\boldsymbol{b}b:
C=(x3,y3,z3)\scriptsize C = (x_3,y_3,z_3)C=(x3,y3,z3)
And:
D=(x4,y4,z4)\scriptsize D =(x_4,y_4,z_4)D=(x4,y4,z4)
Итак:
b=(x4−x3 ,y4−y3,z4−z3)\scriptsize\boldsymbol{b}=(x_4-x_3,y_4-y_3,z_4-z_3)b=(x4−x3,y4−y3,z4−z3 )
Найдите окончательную формулу аналогично двумерной версии:
angle=arccos(((x2−x1)⋅(x4−x3)+(y2−y1)⋅(y4−y3)+(z2−z1)⋅ (z4−z3))/(((x2−x1)2+(y2−y1)2+(z2−z1)2)12⋅((x4−x3)2+(y4−y3)2+(z4− z3)2)12))\scriptsize\begin{split} \mathrm{угол} &= \mathrm{arccos}\bigg(\Big((x_2-x_1)\cdot(x_4-x_3)\\ &\!\!\!\!\!\!\!\!+(y_2-y_1)\cdot(y_4-y_3)+(z_2-z_1)\\ &\!\!\!\!\!\!\!\!\cdot(z_4-z_3)\Big)/\Big(\big((x_2-x_1)^2+(y_2-y_1)^2\ \ &\!\!\!\!\!\!\!\!+(z_2-z_1)^2\big)^{\frac{1}{2}}\!\cdot\!\big((x_4 -x_3)^2+(y_4-y_3)^2\\ &\!\!\!\!\!\!\!\!+(z_4-z_3)^2\big)^{\frac{1}{2}}\Big)\bigg) \end{split}angle=arccos(((x2-x1)⋅(x4-x3)+(y2-y1)⋅(y4-y3)+(z2-z1) ⋅(z4−z3))/(((x2−x1)2+(y2−y1)2+(z2−z1)2)21⋅((x4−x3) 2+(y4−y3)2+(z4−z3)2)21))
Также можно иметь один угол, определяемый координатами, а другой определяемый начальной и конечной точками, но мы не позволим, чтобы это еще больше затеняло этот раздел. Все, что имеет значение, это то, что наш калькулятор угла между двумя векторами имеет все возможные комбинации, доступные для вас.
Все, что имеет значение, это то, что наш калькулятор угла между двумя векторами имеет все возможные комбинации, доступные для вас.
Как найти угол между двумя векторами?
Хорошо, вышеприведенный абзац был чем-то вроде TL;DR . Чтобы лучше понять формулы для угла между двумя векторами, давайте проверим, откуда они берутся:
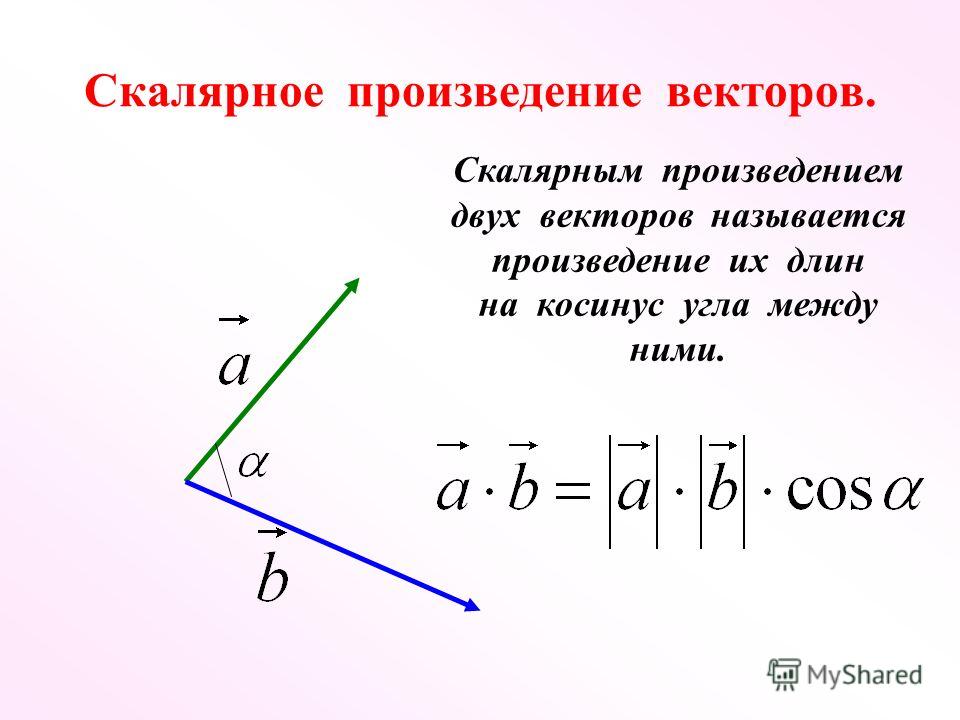
Начните с базовой геометрической формулы для расчета скалярного произведения:
Скалярное произведение определяется как произведение модулей векторов на косинус угла между ними (обозначается здесь как α\alphaα):
a⋅b=∣a∣×∣b∣×cos(α)\boldsymbol{a}\cdot\boldsymbol{b} = |\boldsymbol{a}|\times|\boldsymbol{b}|\times \cos(\alpha)a⋅b=∣a∣×∣b∣×cos(α)
🙋 Наш калькулятор векторной величины здесь, чтобы помочь, если вам нужно обновить эту другую важную векторную величину!
Затем, сделайте угол предметом уравнения :
Разделить на произведение величин векторов:
cos(α)=(a⋅b∣a∣×∣b∣)\scriptsize\cos(\alpha) = \left(\frac{\boldsymbol{a}\cdot\boldsymbol{b}}{| \boldsymbol{a}|\times|\boldsymbol{b}|}\right)cos(α)=(∣a∣×∣b∣a⋅b)
Найдите арккосинус обеих сторон:
α =arccos(a⋅b∣a∣×∣b∣)\scriptsize\alpha = \mathrm{arccos}\left(\frac{\boldsymbol{a}\cdot\boldsymbol{b}}{|\boldsymbol{a} |\times|\boldsymbol{b}|}\right)α=arccos(∣a∣×∣b∣a⋅b)
После этого нам нужно освежить определение величины векторов :
. {\ гидроразрыва {1} {2}} \ большой) \ большой)
\end{split}α=arccos((xa⋅xb+ya⋅yb+za⋅zb)/((xa2+ya2+za2)21⋅(xb2+yb2 +zb2)21))
{\ гидроразрыва {1} {2}} \ большой) \ большой)
\end{split}α=arccos((xa⋅xb+ya⋅yb+za⋅zb)/((xa2+ya2+za2)21⋅(xb2+yb2 +zb2)21))И все!
Кроме того, если ваши векторы имеют другую форму (вы знаете их начальную и конечную точки), вам необходимо заранее выполнить некоторые вычисления. Цель состоит в том, чтобы привести их к стандартной векторной записи.
Если вектор вашего примера описывается начальной точкой B=(x1,y1)B=(x_1, y_1)B=(x1,y1) и конечной точкой B=(x2,y2)B=(x_2 , y_2)B=(x2,y2), то vectora\boldsymbol{a}a может быть выражен как:
a=(x2−x1,y2−y1)\scriptsize\boldsymbol{a} = (x_2- x_1,y_2-y_1)a=(x2−x1,y2−y1)
Все еще не понятно? Без проблем! Мы подготовили несколько примерных расчетов, чтобы убедиться, что все предельно ясно.
Угол между двумя трехмерными векторами — пример
Предположим, что мы хотим найти угол между двумя векторами:
a=(3,6,1)\scriptsize\boldsymbol{a} = (3, 6, 1)a =(3,6,1)
и b\boldsymbol{b}b определяется как вектор между точками A=(1,1,2)A = (1, 1, 2)A=(1,1, 2) и B=(-4,-8,6)B=(-4,-8,6)B=(-4,-8,6) .

Что нам нужно сделать?
- Сначала вычислить вектор b\boldsymbol{b}b , учитывая начальную и конечную точки:
b=(−4−1,−8−1,6−2)=(−5,−9,4)\scriptsize\boldsymbol{b} = (-4-1,-8-1,6- 2) = (-5,-9,4)b=(−4−1,−8−1,6−2)=(−5,−9,4)
- Затем найти скалярное произведение векторов a\boldsymbol{a}a и b\boldsymbol{b}b:
a⋅b=(3×−5)+(6×−9)+(1×4)=−15−54+4=−65\scriptsize \начать{разделить} \boldsymbol{a}\cdot\boldsymbol{b}&= (3 \times -5) + (6 \times-92}\\ &=\sqrt{122}\приблизительно11.045 \end{split}∣b∣=(−5)2+(−9)2+42
=122
≈11,045
- Наконец, используйте преобразованное уравнение скалярного произведения :
α=arccos(a⋅b∣a∣×∣b∣)=arccos(−656,782×11,045)=arccos(−0,86767)=150,189°≈150,2°\scriptsize\begin{split} \alpha &= \mathrm{arccos}\left(\frac{\boldsymbol{a}\cdot\boldsymbol{b}}{|\boldsymbol{a}|\times|\boldsymbol{b}|}\right) \\[1em] &=\mathrm{arccos}\left(\frac{-65}{6,782\times11,045}\right) \\[1em] &=\mathrm{arccos}(-0,86767) \\[1em] &=150,189\градус\приблизительно150,2\градус \end{split}α=arccos(∣a∣×∣b∣a⋅b)=arccos(6,782×11,045−65)=arccos(−0,86767)=150,189°≈150,2°
И вот вы идти! Вы только что вычислили угол между двумя трехмерными векторами.
 Поздравляем!
Поздравляем!Если вы хотите узнать больше о понятиях координатной геометрии, мы рекомендуем воспользоваться калькулятором средней скорости изменения.
Как использовать калькулятор угла между двумя векторами?
Итак, как работает наш калькулятор угла между двумя векторами? Следуйте этим пошаговым инструкциям:
- Выберите векторное пространство . Рассмотрим тот же пример, что и в предыдущем пункте. Наши векторы и точки имеют три координаты, поэтому нам нужно выбрать опцию 3D .
- Выберите представление первого вектора . Первый вектор имеет стандартную запись, поэтому мы оставляем значение по умолчанию: представление координат .
- Введите первый вектор . Введите x=3x = 3x=3, y=6y = 6y=6, z=1z = 1z=1.
- Выберите представление второго вектора . На этот раз нам нужно изменить его на точечное представление .
- Введите значения второго вектора .
 Входные данные A=(1,1,2)\boldsymbol A = (1,1,2)A=(1,1,2) и B=(−4,−8,6)\boldsymbol B = (-4, -8,6)B=(−4,−8,6) в соответствующие поля.
Входные данные A=(1,1,2)\boldsymbol A = (1,1,2)A=(1,1,2) и B=(−4,−8,6)\boldsymbol B = (-4, -8,6)B=(−4,−8,6) в соответствующие поля. - Инструмент нашел угол между двумя 3D-векторами в тот момент, когда вы заполнили последнее поле. В нашем случае это 150,2°150,2\градус 150,2° — это, конечно, тот же результат, который мы получили при ручных вычислениях.
Часто задаваемые вопросы
Что такое вектор?
Вектор — это представление физической величины, которое имеет как величину, так и направление.
Как определить угол, образованный двумя векторами?
Угол между двумя векторами определяется с помощью арккосинуса скалярных произведений двух векторов и произведения их модулей.
Как рассчитать угол между двумя векторами в 2D?
Чтобы вычислить угол между двумя векторами в 2D-пространстве:
- Найдите скалярное произведение векторов.
- Разделите скалярное произведение на величину первого вектора.

- Разделить результат на величину второго вектора.
Математически угол
αмежду двумя векторами может быть записан как:
α = arccos[(xa * xb + ya * yb) / (√(xa² + ya²) * √(xb² + yb²))]Как рассчитать угол между двумя векторами в 3D?
Чтобы вычислить угол между двумя векторами в трехмерном пространстве:- Найдите скалярное произведение векторов.
- Разделите скалярное произведение на величину первого вектора.
- Разделить результат на величину второго вектора.
Математически угол
αмежду двумя векторами может быть записан как:
α = arccos[(xa * xb + ya * yb + za * zb) / (√(xa² + ya² + za²) * √(xb² + yb² + zb²))]Математика — угол между векторами
Как вычислить угол между двумя векторами?
Это относительно просто, поскольку для двумерных вращений существует только одна степень свободы. Если v1 и v2 нормализованы так, что |v1|=|v2|=1, тогда
angle = acos(v1v2)
, где:
- = «точечное» произведение (см.
 рамку справа на странице ).
рамку справа на странице ). - acos = arc cos = функция, обратная косинусу, см. страницу тригонометрии.
- |v1|= величина v1.
Единственная проблема в том, что это не даст всех возможных значений от 0° до 360° или от -180° до +180°. Другими словами, он не скажет нам, находится ли v1 впереди или позади v2, переход от v1 к v2 — это противоположное направление от v2 к v1.
В большинстве математических библиотек acos обычно возвращает значение от 0 до π (в радианах), что составляет от 0° до 180°.
Если мы хотим, чтобы значение + или — указывало, какой вектор впереди, то нам, вероятно, нужно использовать функцию atan2 (как описано на этой странице). используя:
угол 2 относительно 1= atan2(v2.y,v2.x) — atan2(v1.y,v1.x)
Для обсуждения вопросов, которые следует учитывать при использовании этой формулы, см. страница здесь.
Axis Angle Result
Это проще всего вычислить, используя представление оси-угла, потому что:
- угол определяется как acos скалярного произведения из двух (нормализованных) векторов: v1v2 = |v1||v2| cos(угол)
- ось задается перекрестным произведением
два вектора, длина этой оси равна |v1 x v2| = |v1||v2| грех (угол).

как описано здесь
это взято из этого обсуждения.
Итак, если v1 и v2 нормированы так, что |v1|=|v2|=1, то
угол = acos(v1v2)
ось = норма(v1 x v2)
Если векторы параллельны (угол = 0 или 180 градусов), то длина v1 x v2 будет равен нулю, потому что sin(0)=sin(180)=0. В нулевом случае ось делает не имеет значения и может быть чем угодно, потому что вокруг него нет вращения. в 180-градусный случай, когда ось может быть любой под углом 90 градусов к векторам, поэтому представляет собой целый ряд возможных осей.
угол (градусы) грех(угол) cos(угол) v1v2 v1 x v2 0 0 1 1 0,0,0 90 1 0 0 длина блока 180 0 -1 -1 0,0,0 270 -1 0 0 длина блока Результат кватерниона
Одним из подходов может быть определение кватерниона, который при умножении на вектор поворачивает его:
p 2 =q * p 1
Это работает почти так, как описано на этой странице.

Однако, чтобы повернуть вектор, мы должны использовать эту формулу:
p 2 =q * p 1 * conj(q)
где:
- p 2 = вектор, представляющий точку после поворота
- q = кватернион, представляющий вращение.
- p 1 = вектор, представляющий точку до поворота
Это немного запутанно, чтобы решить для q, поэтому я благодарен minorlogic за следующий подход, который преобразует результат угла оси в кватернион:
Угол оси может быть преобразован в кватернион следующим образом, пусть x,y,z,w равны элементы кватерниона, они могут быть выражены через угол оси, как объяснено здесь.
угол = arcos(v1v2/ |v1||v2|)
ось = норма (v1 x v2)
с = грех (угол/2)
х = ось.х * с
у = ось.у * с
z = ось.z *s
w = cos(угол/2)Мы можем использовать эту формулу триггера половинного угла на этом страница: sin(угол/2) = 0,5 sin(угол) / cos(угол/2)
, поэтому замена в формуле кватерниона дает:
s = 0,5 sin(угол) / cos(угол/2)
х = норма (v1 x v2). x *s
x *s
у = норма (v1 x v2).y *s
z = норма(v1 x v2).z *s
w = cos(угол/2)умножить x,y,z и w на 2* cos(угол/2) (это денормализует кватернион но мы всегда можем нормализовать позже)
x = норма(v1 x v2).x * sin(угол)
y = норма(v1 x v2).y * sin(угол)
z = норма(v1 x v2).z * sin(угол)
w = 2 * cos(угол/2) * cos(угол/2)теперь замените формулу триггера половинного угла на это страница: cos(угол/2) = sqrt(0.5*(1 + cos(угол))
x = норма(v1 x v2).x * sin(угол)
y = норма(v1 x v2).y * sin(угол)
z = норма(v1 x v2).z * sin(угол)
w = 1 + cos (угол), потому что |v1 x v2| = |v1||v2| sin(угол) мы можем нормализовать (v1 x v2), разделив это с sin(угол),
также применяется v1v2 = |v1||v2| cos(угол) так,
х = (v1 х v2).x / |v1||v2|
y = (v1 x v2).y/ |v1||v2|
z = (v1 x v2).z/ |v1||v2|
w = 1 + v1v2 / |v1||v2|Если v1 и v2 уже нормализованы, то |v1||v2|=1, поэтому
x = (v1 x v2).
 x
x
у = (v1 x v2).y
z = (v1 x v2).z
w = 1 + v1v2Если v1 и v2 еще не нормализованы, то умножьте на |v1||v2| дает:
х = (v1 х v2).x
у = (v1 x v2).y
z = (v1 x v2).z
ш = |v1||v2| + v1v2Результат матрицы
Использование кватерниона для преобразования матрицы здесь мы получаем:
1 — 2*qy 2 — 2*qz 2 2*qx*qy — 2*qz*qw 2*qx*qz + 2*qy*qw 2*qx*qy + 2*qz*qw 1 — 2*qx 2 — 2*qz 2 2*qy*qz — 2*qx*qw 2*qx*qz — 2*qy*qw 2*qy*qz + 2*qx*qw 1 — 2*qx 2 — 2*qy 2 , поэтому, подставив приведенный выше результат кватерниона в матрицу, мы получим:
(v1 x v2).x = v1.y * v2.z — v2.y * v1.z
(v1 x v2).y = v1.z * v2.x — v2.z * v1.

 {\ гидроразрыва {1} {2}} \ большой) \ большой)
\end{split}α=arccos((xa⋅xb+ya⋅yb+za⋅zb)/((xa2+ya2+za2)21⋅(xb2+yb2 +zb2)21))
{\ гидроразрыва {1} {2}} \ большой) \ большой)
\end{split}α=arccos((xa⋅xb+ya⋅yb+za⋅zb)/((xa2+ya2+za2)21⋅(xb2+yb2 +zb2)21))
 Поздравляем!
Поздравляем! Входные данные A=(1,1,2)\boldsymbol A = (1,1,2)A=(1,1,2) и B=(−4,−8,6)\boldsymbol B = (-4, -8,6)B=(−4,−8,6) в соответствующие поля.
Входные данные A=(1,1,2)\boldsymbol A = (1,1,2)A=(1,1,2) и B=(−4,−8,6)\boldsymbol B = (-4, -8,6)B=(−4,−8,6) в соответствующие поля.
 рамку справа на странице ).
рамку справа на странице ).
 x *s
x *s 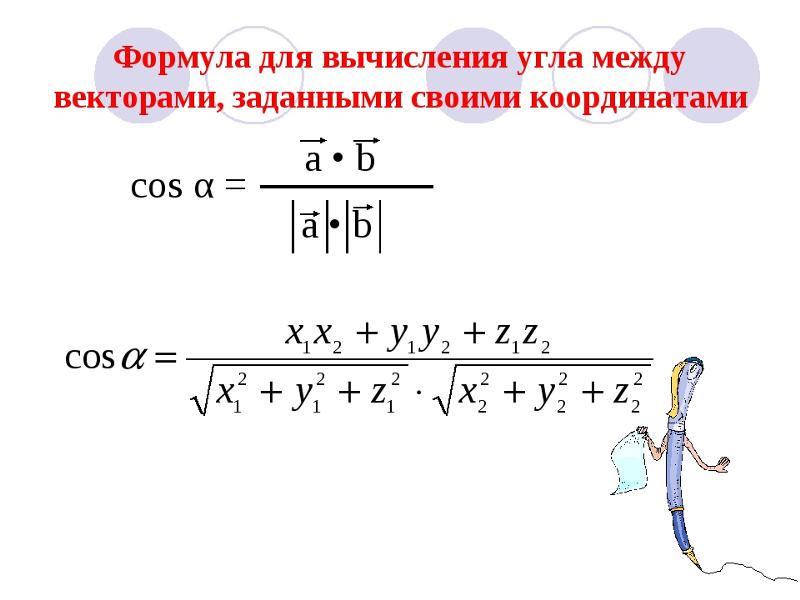 x
x