Произведение синусов и косинусов: формулы, примеры
В данной статье рассмотрены формулы произведения синусов, косинусов, а также формулы произведения синуса на косинус. Допустим, есть необходимость вычислить произведение синусов или косинусов углов α и β. Формулы произведения позволяют перейти от произведения к сумме или разности синусов и косинусов углов α+β и α-β.
Приведем формулы произведения синуса на синус, косинуса на косинус и синуса на косинус.
Формулы произведения. Список
Приведем формулировки, а затем и сами формулы.
- Произведение синусов углов α и β равно полуразности косинуса угла α-β и косинуса угла α+β.
- Произведение косинусов углов α и β равно полусумме косинуса угла α-β и косинуса угла α+β.
- Произведение синуса угла α на косинус угла β равно полусумме синуса угла α-β и синуса угла α+β.
Для любых α и β справедливы формулы
- sin α·sin β=12cosα-β-cosα+β;
- cos α·cos β=12cosα-β+cosα+β;
- sin α·cos β=12sinα-β+sinα+β.
Вывод формул
Вывод описанных выше формул проводится с помощью формул сложения и на основе свойства равенства. Согласно этому свойству, если левую и правую части верного равенства сложить соответственно с левой и правой частями другого верного равенста, то в результате получится еще одно верное равенство. Покажем вывод формул произведения.
Сначала запишем формулы косинуса суммы и косинуса разности:
cosα+β=cos α·cos β-sin α·sin βcosα-β=cos α·cos β+sin α·sin β
Сложим эти равенства и получим:
cosα+β+cosα-β=cos α·cos β-sin α·sin β+cos α·cos β+sin α·sin βcosα+β+cosα-β=2·cos α·cos β
Отсюда
cos α·cos β=12cosα+β+cosα-β
Формула произведения косинусов доказана.
Перепишем формулу косинуса суммы следующим образом:
-cos(α+β)=-cos α·cosβ+sin α·sinβ
Добавим к равенству формулу cosα-β=cos α·cos β+sin α·sinβ.
Получим:
-cos(α+β)+cosα-β=-cos α·cosβ+sin α·sinβ+cos α·cos β+sin α·sinβ-cos(α+β)+cosα-β=2·sin α·sinβsin α·sinβ=12(cosα-β-cos(α+β))
Таким образом, выведена формула произведения синусов.
Теперь возьмем формулу синуса суммы, формулу синуса разности, и сложим их левые и правые части
sinα+β=sin α·cos β+cos α·sin βsinα-β=sin α·cos β-cos α·sin βsinα+β+sinα-β=sin α·cos β+cos α·sin β+sin α·cos β-cos α·sin βsinα+β+sinα-β=2sin α·cos βsin α·cos β=12(sinα+β+sinα-β)
Формула произведения синуса на косинус выведена.
Примеры использования
Приведем примеры использования формул произведения синусов, косинусов и синусов на косинус при решении задач.
Пусть α=60°, β=30°. Возьмем формулу произведения синусов и подставим в нее конкретные значения.
sin α·sin β=12(cosα-β-cosα+β)sin 60°·sin 30° =12(cos60°-30°-cos60°+30°)sin 60°·sin 30°=12(cos30°-cos90°)sin 60°·sin 30°=12(32-0)=34
Теперь вычислим значение выражения, обратившись к таблице основных значений тригонометрических функций.
sin60°·sin30°=32·12=34.
Таким образом, мы проверили формулу на практике и убедились, что формула справедлива.
Пример.
Формулы произведенияНужно sin 75° умножить на cos 15° и вычислить точное значение произведения.
Мы не располагаем точными значениями синуса и косинуса данных углов, однако можем вычислить точное значение произведения sin 75°·cos 15° c помощью формулы произведения синуса на косинус.
sin 75°·cos 15°=12sin(75°-15°+sin(75°+15°))sin 75°·cos 15°=12sin60°+sin90°=1232+1=3+24
Также формулы произведения используются преобразования тригонометрических выражений.
Решение задач
от 1 дня / от 150 р.
Курсовая работа
от 5 дней / от 1800 р.
Автор: Ирина Мальцевская
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Формула умножения синуса на косинус. Сумма и разность синусов и косинусов: вывод формул, примеры
Одним из разделов математики, с которыми школьники справляются с наибольшими трудностями, является тригонометрия.
Неудивительно: для того чтобы свободно овладеть этой областью знаний, требуется наличие пространственного мышления, умение находить синусы, косинусы, тангенсы, котангенсы по формулам, упрощать выражения, уметь применять в вычислениях число пи. Помимо этого, нужно уметь применять тригонометрию при доказательстве теорем, а это требует либо развитой математической памяти, либо умения выводить непростые логические цепочки.
Истоки тригонометрии
Знакомство с данной наукой следует начать с определения синуса, косинуса и тангенса угла, однако прежде необходимо разобраться, чем вообще занимается тригонометрия.
Исторически главным объектом исследования данного раздела математической науки были прямоугольные треугольники. Наличие угла в 90 градусов дает возможность осуществлять различные операции, позволяющие по двум сторонам и одному углу либо по двум углам и одной стороне определять значения всех параметров рассматриваемой фигуры. В прошлом люди заметили эту закономерность и стали активно ею пользоваться при строительстве зданий, навигации, в астрономии и даже в искусстве.
Начальный этап
Первоначально люди рассуждали о взаимоотношении углов и сторон исключительно на примере прямоугольных треугольников. Затем были открыты особые формулы, позволившие расширить границы употребления в повседневной жизни данного раздела математики.
Изучение тригонометрии в школе сегодня начинается с прямоугольных треугольников, после чего полученные знания используются учениками в физике и решении абстрактных тригонометрических уравнений, работа с которыми начинается в старших классах.
Сферическая тригонометрия
Позже, когда наука вышла на следующий уровень развития, формулы с синусом, косинусом, тангенсом, котангенсом стали использоваться в сферической геометрии, где действуют иные правила, а сумма углов в треугольнике всегда больше 180 градусов. Данный раздел не изучается в школе, однако знать о его существовании необходимо как минимум потому, что земная поверхность, да и поверхность любой другой планеты, является выпуклой, а значит, любая разметка поверхности будет в трёхмерном пространстве «дугообразной».
Возьмите глобус и нитку. Приложите нитку к двум любым точкам на глобусе, чтобы она оказалась натянутой. Обратите внимание — она обрела форму дуги. С такими формами и имеет дело сферическая геометрия, применяющаяся в геодезии, астрономии и других теоретических и прикладных областях.
Прямоугольный треугольник
Немного узнав про способы применения тригонометрии, вернемся к базовой тригонометрии, чтобы в дальнейшем разобраться, что такое синус, косинус, тангенс, какие расчёты можно с их помощью выполнять и какие формулы при этом использовать.
Первым делом необходимо уяснить понятия, относящиеся к прямоугольному треугольнику. Во-первых, гипотенуза — это сторона, лежащая напротив угла в 90 градусов. Она является самой длинной. Мы помним, что по теореме Пифагора её численное значение равно корню из суммы квадратов двух других сторон.
Например, если две стороны равны 3 и 4 сантиметрам соответственно, длина гипотенузы составит 5 сантиметров. Кстати, об этом знали ещё древние египтяне около четырех с половиной тысяч лет назад.
Две оставшиеся стороны, которые образуют прямой угол, носят название катетов. Кроме того, надо помнить, что сумма углов в треугольнике в прямоугольной системе координат равняется 180 градусам.
Определение
Наконец, твердо понимая геометрическую базу, можно обратиться к определению синуса, косинуса и тангенса угла.
Синусом угла называется отношение противолежащего катета (т. е. стороны, располагающейся напротив нужного угла) к гипотенузе. Косинусом угла называется отношение прилежащего катета к гипотенузе.
Запомните, что ни синус, ни косинус не может быть больше единицы! Почему? Потому что гипотенуза — это по умолчанию самая длинная Каким бы длинным ни был катет, он будет короче гипотенузы, а значит, их отношение всегда будет меньше единицы. Таким образом, если у вас в ответе к задаче получился синус или косинус со значением, большим, чем 1, ищите ошибку в расчётах или рассуждениях. Этот ответ однозначно неверен.
Наконец, тангенсом угла называется отношение противолежащей стороны к прилежащей.
Тот же самый результат даст деление синуса на косинус. Посмотрите: в соответствии с формулой мы делим длину стороны на гипотенузу, после чего делим на длину второй стороны и умножаем на гипотенузу. Таким образом, мы получаем то же самое соотношение, что и в определении тангенса.
Котангенс, соответственно, представляет собой отношение прилежащей к углу стороны к противолежащей. Тот же результат мы получим, разделив единицу на тангенс.
Итак, мы рассмотрели определения, что такое синус, косинус, тангенс и котангенс, и можем заняться формулами.
Простейшие формулы
В тригонометрии не обойтись без формул — как найти синус, косинус, тангенс, котангенс без них? А ведь именно это требуется при решении задач.
Первая формула, которую необходимо знать, начиная изучать тригонометрию, говорит о том, что сумма квадратов синуса и косинуса угла равна единице. Данная формула является прямым следствием теоремы Пифагора, однако позволяет сэкономить время, если требуется узнать величину угла, а не стороны.
Многие учащиеся не могут запомнить вторую формулу, также очень популярную при решении школьных задач: сумма единицы и квадрата тангенса угла равна единице, деленной на квадрат косинуса угла. Присмотритесь: ведь это то же самое утверждение, что и в первой формуле, только обе стороны тождества были поделены на квадрат косинуса. Выходит, простая математическая операция делает тригонометрическую формулу совершенно неузнаваемой. Помните: зная, что такое синус, косинус, тангенс и котангенс, правила преобразования и несколько базовых формул вы в любой момент сможете сами вывести требуемые более сложные формулы на листе бумаги.
Формулы двойного угла и сложения аргументов
Ещё две формулы, которые требуется выучить, связаны со значениями синуса и косинуса при сумме и разности углов. Они представлены на рисунке ниже. Обратите внимание, что в первом случае оба раза перемножается синус и косинус, а во втором складывается попарное произведение синуса и косинуса.
Также существуют формулы, связанные с аргументами в виде двойного угла.
Они полностью выводятся из предыдущих — в качестве тренировки попробуйте получить их самостоятельно, приняв угол альфа равным углу бета.
Наконец, обратите внимание, что формулы двойного угла можно преобразовать так, чтобы понизить степень синуса, косинуса, тангенса альфа.
Теоремы
Двумя основными теоремами в базовой тригонометрии являются теорема синусов и теорема косинусов. С помощью этих теорем вы легко сможете понять, как найти синус, косинус и тангенс, а значит, и площадь фигуры, и величину каждой стороны и т. д.
Теорема синусов утверждает, что в результате деления длины каждой из сторон треугольника на величину противолежащего угла мы получим одинаковое число. Более того, это число будет равно двум радиусам описанной окружности, т. е. окружности, содержащей все точки данного треугольника.
Теорема косинусов обобщает теорему Пифагора, проецируя её на любые треугольники. Оказывается, из суммы квадратов двух сторон вычесть их произведение, умноженное на двойной косинус смежного им угла — полученное значение окажется равно квадрату третьей стороны.
Таким образом, теорема Пифагора оказывается частным случаем теоремы косинусов.
Ошибки по невнимательности
Даже зная, что такое синус, косинус и тангенс, легко совершить ошибку из-за рассеянности внимания или ошибки в простейших расчётах. Чтобы избежать таких ошибок, ознакомимся с наиболее популярными из них.
Во-первых, не следует преобразовывать обыкновенные дроби в десятичные до получения окончательного результата — можно и ответ оставить в виде обыкновенной дроби, если в условии не оговорено обратное. Такое преобразование нельзя назвать ошибкой, однако следует помнить, что на каждом этапе задачи могут появиться новые корни, которые по задумке автора должны сократиться. В этом случае вы напрасно потратите время на излишние математические операции. Особенно это актуально для таких значений, как корень из трёх или из двух, ведь они встречаются в задачах на каждом шагу. То же касается округлений «некрасивых» чисел.
Далее, обратите внимание, что к любому треугольнику применима теорема косинусов, но не теорема Пифагора! Если вы по ошибке забудете вычесть удвоенное произведение сторон, умноженное на косинус угла между ними, вы не только получите совершенно неверный результат, но и продемонстрируете полное непонимание предмета.
Это хуже, чем ошибка по невнимательности.
В-третьих, не путайте значения для углов в 30 и 60 градусов для синусов, косинусов, тангенсов, котангенсов. Запомните эти значения, ведь синус 30 градусов равен косинусу 60, и наоборот. Их легко перепутать, вследствие чего вы неизбежно получите ошибочный результат.
Применение
Многие ученики не спешат приступать к изучению тригонометрии, поскольку не понимают её прикладного смысла. Что такое синус, косинус, тангенс для инженера или астронома? Это понятия, благодаря которым можно вычислить расстояние до далёких звёзд, предсказать падение метеорита, отправить исследовательский зонд на другую планету. Без них нельзя построить здание, спроектировать автомобиль, рассчитать нагрузку на поверхность или траекторию движения предмета. И это только самые очевидные примеры! Ведь тригонометрия в том или ином виде используется повсюду, начиная от музыки и заканчивая медициной.
В заключение
Итак, вы синус, косинус, тангенс. Вы можете использовать их в расчётах и успешно решать школьные задачи.
Вся суть тригонометрии сводится к тому, что по известным параметрам треугольника нужно вычислить неизвестные. Всего этих параметров шесть: длины трёх сторон и величины трёх углов. Всё различие в задачах заключается в том, что даются неодинаковые входные данные.
Как найти синус, косинус, тангенс исходя из известных длин катетов или гипотенузы, вы теперь знаете. Поскольку эти термины обозначают не что иное, как отношение, а отношение — это дробь, главной целью тригонометрической задачи становится нахождение корней обычного уравнения либо же системы уравнений. И здесь вам поможет обычная школьная математика.
Я не буду убеждать вас не писать шпаргалки. Пишите! В том числе, и шпаргалки по тригонометрии. Позже я планирую объяснить, зачем нужны шпаргалки и чем шпаргалки полезны. А здесь — информация, как не учить, но запомнить некоторые тригонометрические формулы. Итак — тригонометрия без шпаргалки!Используем ассоциации для запоминания.
1. Формулы сложения:
косинусы всегда «ходят парами»: косинус-косинус, синус-синус.
И еще: косинусы — «неадекватны». Им «все не так», поэтому они знаки меняют: «-» на «+», и наоборот.
Синусы — «смешиваются» : синус-косинус, косинус-синус.
2. Формулы суммы и разности:
косинусы всегда «ходят парами». Сложив два косинуса — «колобка», получаем пару косинусов- «колобков». А вычитая, колобков точно не получим. Получаем пару синусов. Еще и с минусом впереди.
Синусы — «смешиваются» :
3. Формулы преобразования произведения в сумму и разность.
Когда мы получаем пару косинусов? Когда складываем косинусы. Поэтому
Когда мы получаем пару синусов? При вычитании косинусов. Отсюда:
«Смешение» получаем как при сложении, так и при вычитании синусов. Что приятнее: складывать или вычитать? Правильно, складывать. И для формулы берут сложение:
В первой и в третьей формуле в скобках — сумма. От перестановки мест слагаемых сумма не меняется.
а во вторых — сумму
Шпаргалки в кармане дают спокойствие: если забыл формулу, можно списать. А дают уверенность: если воспользоваться шпаргалкой не удастся, формулы можно легко вспомнить.
Соотношения между основными тригонометрическими функциями – синусом, косинусом, тангенсом и котангенсом — задаются тригонометрическими формулами . А так как связей между тригонометрическими функциями достаточно много, то этим объясняется и обилие тригонометрических формул. Одни формулы связывают тригонометрические функции одинакового угла, другие – функции кратного угла, третьи – позволяют понизить степень, четвертые – выразить все функции через тангенс половинного угла, и т.д.
В этой статье мы по порядку перечислим все основные тригонометрические формулы, которых достаточно для решения подавляющего большинства задач тригонометрии.
Навигация по странице.
Основные тригонометрические тождества
Основные тригонометрические тождества задают связь между синусом, косинусом, тангенсом и котангенсом одного угла. Они вытекают из определения синуса, косинуса, тангенса и котангенса, а также понятия единичной окружности . Они позволяют выразить одну тригонометрическую функцию через любую другую.
Подробное описание этих формул тригонометрии, их вывод и примеры применения смотрите в статье .
Формулы приведения
Формулы приведения следуют из свойств синуса, косинуса, тангенса и котангенса , то есть, они отражают свойство периодичности тригонометрических функций, свойство симметричности, а также свойство сдвига на данный угол. Эти тригонометрические формулы позволяют от работы с произвольными углами переходить к работе с углами в пределах от нуля до 90
градусов.
Обоснование этих формул, мнемоническое правило для их запоминания и примеры их применения можно изучить в статье .
Формулы сложения
Тригонометрические формулы сложения показывают, как тригонометрические функции суммы или разности двух углов выражаются через тригонометрические функции этих углов. Эти формулы служат базой для вывода следующих ниже тригонометрических формул.
Формулы двойного, тройного и т.д. угла
Формулы двойного, тройного и т.д. угла (их еще называют формулами кратного угла) показывают, как тригонометрические функции двойных, тройных и т.д. углов () выражаются через тригонометрические функции одинарного угла . Их вывод базируется на формулах сложения.
Более детальная информация собрана в статье формулы двойного, тройного и т.д. угла .
Формулы половинного угла
Формулы половинного угла показывают, как тригонометрические функции половинного угла выражаются через косинус целого угла .
Эти тригонометрические формулы следуют из формул двойного угла.
Их вывод и примеры применения можно посмотреть в статье .
Формулы понижения степени
Тригонометрические формулы понижения степени призваны содействовать переходу от натуральных степеней тригонометрических функций к синусам и косинусам в первой степени, но кратных углов. Иными словами, они позволяют понижать степени тригонометрических функций до первой.
Формулы суммы и разности тригонометрических функций
Основное предназначение формул суммы и разности тригонометрических функций заключается в переходе к произведению функций, что очень полезно при упрощении тригонометрических выражений. Указанные формулы также широко используются при решении тригонометрических уравнений, так как позволяют раскладывать на множители сумму и разность синусов и косинусов.
Формулы произведения синусов, косинусов и синуса на косинус
Переход от произведения тригонометрических функций к сумме или разности осуществляется посредством формул произведения синусов, косинусов и синуса на косинус .
Copyright by cleverstudents
Все права защищены.
Охраняется законом об авторском праве. Ни одну часть сайта www.сайт, включая внутренние материалы и внешнее оформление, нельзя воспроизводить в какой-либо форме или использовать без предварительного письменного разрешения правообладателя.
Тригонометрические тождества
tg \alpha = \frac{\sin \alpha}{\cos \alpha}, \enspace ctg \alpha = \frac{\cos \alpha}{\sin \alpha}
tg \alpha \cdot ctg \alpha = 1
Данное тождество говорит о том, что сумма квадрата синуса одного угла и квадрата косинуса одного угла равна единице, что на практике дает возможность вычислить синус одного угла, когда известен его косинус и наоборот.
При преобразовании тригонометрических выражений очень часто используют данное тождество, которое позволяет заменять единицей сумму квадратов косинуса и синуса одного угла и также производить операцию замены в обратном порядке.
Нахождение тангенса и котангенса через синус и косинус
tg \alpha = \frac{\sin \alpha}{\cos \alpha},\enspace
Данные тождества образуются из определений синуса, косинуса, тангенса и котангенса. Ведь если разобраться, то по определению ординатой y
является синус, а абсциссой x
— косинус. Тогда тангенс будет равен отношению \frac{y}{x}=\frac{\sin \alpha}{\cos \alpha}
, а отношение \frac{x}{y}=\frac{\cos \alpha}{\sin \alpha}
— будет являться котангенсом.
Добавим, что только для таких углов \alpha , при которых входящие в них тригонометрические функции имеют смысл, будут иметь место тождества , ctg \alpha=\frac{\cos \alpha}{\sin \alpha} .
Например: tg \alpha = \frac{\sin \alpha}{\cos \alpha} является справедливой для углов \alpha , которые отличны от \frac{\pi}{2}+\pi z , а ctg \alpha=\frac{\cos \alpha}{\sin \alpha} — для угла \alpha , отличного от \pi z , z — является целым числом.
Зависимость между тангенсом и котангенсом
tg \alpha \cdot ctg \alpha=1
Данное тождество справедливо только для таких углов \alpha , которые отличны от \frac{\pi}{2} z . Иначе или котангенс или тангенс не будут определены.
Опираясь на вышеизложенные пункты, получаем, что tg \alpha = \frac{y}{x} , а ctg \alpha=\frac{x}{y} . Отсюда следует, что tg \alpha \cdot ctg \alpha = \frac{y}{x} \cdot \frac{x}{y}=1 . Таким образом, тангенс и котангенс одного угла, при котором они имеют смысл, являются взаимно обратными числами.
Зависимости между тангенсом и косинусом, котангенсом и синусом
tg^{2} \alpha + 1=\frac{1}{\cos^{2} \alpha}
— сумма квадрата тангенса угла \alpha
и 1
, равна обратному квадрату косинуса этого угла.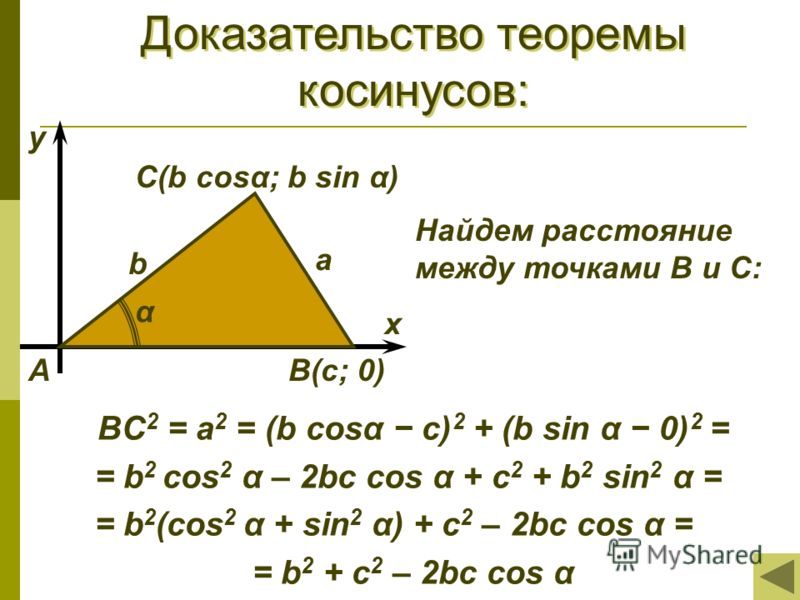
{2} \alpha = 1
. Это уравнение имеет два решения \cos \alpha = \pm \sqrt{1-\frac34}=\pm\sqrt\frac14
.
По условию \frac{\pi}{2}
Для того, чтобы найти ctg \alpha , воспользуемся формулой ctg \alpha = \frac{\cos \alpha}{\sin \alpha} . Соответствующие величины нам известны.
ctg \alpha = -\frac12: \frac{\sqrt3}{2} = -\frac{1}{\sqrt 3} .
Формулы для заучивания
Формулы сокращенного умножения
Формула разности квадратов: .
Формула квадрата суммы: .
Формула квадрата разности: .
Формула куба суммы: .
Формула куба разности: .
Формула суммы кубов: .
Формула разности кубов: .
Обобщения формул сокращенного умножения
1.
2.
3. Формула бинома Ньютона:
,
где , , ; ;
Свойства логарифмов
Основное логарифмическое тождество: .
Логарифм произведения: .
Логарифм частного: .
Логарифм степени: .
Формула перехода к новому основанию: .
Формула связи:
Свойства степеней
Умножение степеней с одинаковым основанием: .
Деление степеней с одинаковым основанием: .
Возведение степени в степень: .
Умножение степеней с разными основаниями, но одинаковыми показателями:.
,
Формулы тригонометрии
Нечетность синуса , четность косинуса .
Синус суммы: .
Синус разности: .
Косинус суммы: .
Косинус разности: .
Основное тригонометрическое тождество: .
Синус двойного угла: .
Косинус двойного угла: .
Формулы понижения: степени:.
Выражение синуса и косинуса через тангенс угла: , .
Выражение синуса и косинуса через тангенс половинного угла: .
Формулы преобразования суммы или разности в произведение
Сумма синусов: .
Разность синусов: .
Сумма косинусов: .
Разность косинусов: .
Формулы преобразования произведения в сумму или разность
Произведение синуса на косинус: .
Произведение синуса на синус: .
Произведение косинуса на косинус: .
Таблица значений тригонометрических функций
0 | ||||||||
0 | 1 | 0 | -1 | 0 | ||||
1 | 0 | -1 | 0 | 1 | ||||
0 | 1 | — | 0 | — | 0 | |||
— | 1 | 0 | — | 0 | — |
Прогрессии
Формула — го члена арифметической прогрессии
Здесь
—
первый член арифметической прогрессии,
—
разность прогрессии.
Формула суммы первых членов арифметической прогрессии
Формула — го члена геометрической прогрессии
Здесь — первый член геометрической прогрессии, — знаменатель прогрессии.
Формула суммы первых членов геометрической прогрессии
Формула суммы бесконечно убывающей геометрической прогрессии
Свойства гиперболических функций
1. , 2. ,
3. , 4. ,
5. ,
Формулы приведения
1. , 2.,
3. , 4. ,
5. , 6. ,
7.
,
8.
,
9. , 10. ,
11. , 12. ,
13. , 14.
15. 16.
Таблица производных
1. , 2. ,
3. , 4. ,
5. , 6. ,
7. , 8. ,
9. , 10. ,
11. , 12. ,
13. , 14. ,
15. , 16. ,
17. ,
18. , ,
19. , ,
20. , ,
21. , .
Таблица интегралов
1. 2.
3. , 4. ,
5. 6. ,
7. , 8. . ,
9. , 10. ,
11.
,
12..
,
13. , 14. ,
15. , 16. ,
17. , 18. ,
19. , 20. ,
21. ,
22. ,
23. ,
24. , 25. ,
26. , 27. .
28. , 29. ,
30. ,
31. ,
Замечания.
Если то
Рекуррентная формула для нахождения интеграла
, ,
Интегрирование тригонометрических функций: методы и примеры
- Подынтегральное выражение можно преобразовать из произведения тригонометрических функций в сумму
- Интеграл произведения степеней синуса и косинуса одного и того же аргумента
- Использование метода замены переменной
- Универсальная тригонометрическая подстановка
Будут и задачи для самостоятельного решения, к которым можно
посмотреть ответы.
Рассмотрим интегралы, в которых подынтегральная функция представляет собой произведение синусов и косинусов первой степени от икса, умноженного на разные множители, то есть интегралы вида
(1)
Воспользовавшись известными тригонометрическими формулами
(2)
(3)
(4)
можно преобразовать каждое из произведений в интегралах вида (31) в алгебраическую сумму и проинтегрировать по формулам
(5)
и
(6)
- Пригодится: тригонометрические тождества для преобразования выражений
Пример 1. Найти интеграл от тригонометрической функции
Решение. По формуле (2) при
имеем
Поэтому
Применяя далее формулу (5), получим
Пример 2.
Найти интеграл от тригонометрической функции
Решение. По формуле (3) при получаем следующее преобразование подынтегрального выражения:
Поэтому
Применяя далее формулу (6), получим
Для самопроверки при расчетах можно воспользоваться калькулятором неопределённых интегралов онлайн.
- Пригодится: тригонометрические тождества для преобразования выражений
Пример 3. Найти интеграл от тригонометрической функции
Решение. По формуле (4) при получаем следующее преобразование подынтегрального выражения:
Применяя формулу (6), получим
Рассмотрим теперь интегралы от функций, представляющих собой произведение степеней синуса и косинуса одного и того же аргумента, т.
е.
(7)
В частных случаях один из показателей (m или n) может равняться нулю.
При интегрировании таких функций используется то, что чётную степень косинуса можно выразить через синус, а дифференциал синуса равен cos x dx (или чётную степень синуса можно выразить через косинус, а дифференциал косинуса равен — sin x dx).
Следует различать два случая: 1) хотя бы один из показателей m и n нечётный; 2) оба показателя чётные.
Пусть имеет место первый случай, а именно показатель n = 2k + 1 — нечётный. Тогда, учитывая, что
получим
Подынтегральное выражение представлено в таком виде, что одна его часть – функция только синуса, а другая – дифференциал синуса. Теперь с помощью замены переменной t = sin x решение сводится к интегрированию многочлена относительно t.
Если же только степень m нечётна, то поступают аналогично, выделяя множитель sinx, выражая остальную часть подынтегральной функции через cos x и
полагая t = cos x. Этот приём можно использовать и
при интегрировании частного степеней синуса и косинуса, когда хотя бы один из показателей — нечётный.
Всё дело в том, что частное степеней синуса и косинуса — это частный случай их произведения: когда тригонометрическая
функция находится в знаменателе подынтегрального выражения, её степень — отрицательная. Но бывают и случаи частного
тригонометрических функций, когда их степени — только чётные. О них — следующем абзаце.
Если же оба показателя m и n – чётные, то, используя тригонометрические формулы
понижают показатели степени синуса и косинуса, после чего получится интеграл того же типа, что и выше.
Поэтому интегрирование следует продолжать по той же схеме. Если же один из чётных показателей — отрицательный,
то есть рассматривается частное чётных степеней синуса и косинуса, то данная схема не годится. Тогда используется
замена переменной в зависимости от того, как можно преобразовать подынтегральное выражение. Такой случай будет
рассмотрен в следующем параграфе.
- Пригодится: тригонометрические тождества для преобразования выражений
Пример 4. Найти интеграл от тригонометрической функции
Решение. Показатель степени косинуса – нечётный. Поэтому представим
в виде
и произведём замену переменной t = sin x (тогда dt = cos x dx). Тогда получим
Возвращаясь к старой переменной, окончательно найдём
Для самопроверки при расчетах можно воспользоваться калькулятором неопределённых интегралов онлайн.
Пример 5. Найти интеграл от тригонометрической функции
.
Решение. Показатель степени косинуса, как и в предыдущем примере – нечётный, но больше. Представим
в виде
и произведём замену переменной t = sin x (тогда dt = cos x dx). Тогда получим
Раскроем скобки
и получим
Возвращаясь к старой переменной, получаем решение
Пример 6. Найти интеграл от тригонометрической функции
Решение. Показатели степени синуса и косинуса – чётные. Поэтому преобразуем подынтегральную функцию так:
Тогда получим
Во втором интеграле произведём замену переменной, полагая t = sin2x.
Тогда (1/2)dt = cos2x dx. Следовательно,
а
Окончательно получаем
- Пригодится: тригонометрические тождества для преобразования выражений
Найти интеграл от тригонометрической функции самостоятельно, а затем посмотреть решение
Пример 7. Найти интеграл от тригонометрической функции
.
Посмотреть правильное решение и ответ.
Нет времени вникать в решение? Можно заказать работу!
Метод замены переменной при интегировании тригонометрических функций можно применять
в случаях, когда в подынтегральном выражении присутствует только синус или только косинус, произведение
синуса и косинуса, в котором или синус или косинус — в первой степени, тангенс или котангенс, а также
частное чётных степеней синуса и косинуса одного и того же аргумента.
При этом можно производить перестановки не только sinx = t и sinx = t,
но и tgx = t и ctgx = t.
Пример 8. Найти интеграл от тригонометрической функции
.
Решение. Произведём замену переменной: , тогда . Получившееся подынтегральное выражение легко интегрируется по таблице интегралов:
.
Возвращаясь к первоначальной переменной, окончательно получаем:
Для самопроверки при расчетах можно воспользоваться калькулятором неопределённых интегралов онлайн.
- Пригодится: тригонометрические тождества для преобразования выражений
Пример 9. Найти интеграл от тригонометрической функции
.
Решение. Преобразуем тангенс в отношение синуса и косинуса:
.
Произведём замену переменной: , тогда . Получившееся подынтегральное выражение представляет собой табличный интеграл со знаком минус:
.
Возвращаясь к первоначальной переменной, окончательно получаем:
.
Пример 10. Найти интеграл от тригонометрической функции
.
Решение. Произведём замену переменной: , тогда .
Преобразуем подынтегральное выражение, чтобы применить тригонометрическое тождество :
Производим замену переменной, не забывая перед интегралом поставить знак минус (смотрите выше, чему равно dt). Далее раскладываем подынтегральное выражение на множители и интегрируем по таблице:
.
Возвращаясь к первоначальной переменной, окончательно получаем:
.
Для самопроверки при расчетах можно воспользоваться калькулятором неопределённых интегралов онлайн.
Найти интеграл от тригонометрической функции самостоятельно, а затем посмотреть решение
Пример 11. Найти интеграл от тригонометрической функции
.
Посмотреть правильное решение и ответ.
- Пригодится: тригонометрические тождества для преобразования выражений
Универсальную тригонометрическую подстановку можно применять в случаях, когда подынтегральное выражение не подпадает под случаи, разобранные в предыдущих параграфах. В основном, когда синус или косинус (или и то, и другое) находятся в знаменателе дроби. Доказано, что синус и косинус можно заменить другим выражением, содержащим тангенс половины исходного угла следующим образом:
где .
Тогда .
Но заметим, что универсальная тригонометрическая подстановка часто влечёт за собой довольно сложные алгебраические преобразования, поэтому её лучше применять, когда никакой другой метод не работает. Разберём примеры, когда вместе с универсальной тригонометрической подстановкой используются подведение под знак дифференциала и метод неопределённых коэффициентов.
Пример 12. Найти интеграл от тригонометрической функции
.
Решение. Решение. Воспользуемся универсальной тригонометрической подстановкой. Тогда
.
Дроби в числителе и знаменателе умножаем на , а двойку выносим и ставим перед знаком интеграла. Тогда
Чтобы в результате преобразований прийти к табличному интегралу, попытаемся получить в
знаменателе полный квадрат. Для этого умножим числитель и знаменатель подынтегрального выражения на 2.
Применяем интегрирование подведением под знак дифференциала. Получим
К полученному результату преобразований можем теперь применить табличный интеграл 21. В результате получаем окончательное решение:
.
Пример 13. Найти интеграл от тригонометрической функции
.
Решение. Решение. Воспользуемся универсальной тригонометрической подстановкой. Тогда
.
Дроби в числителе и знаменателе умножаем на , а двойку выносим и ставим перед знаком интеграла. Тогда
.
Чтобы в результате преобразований прийти к табличному интегралу, попытаемся получить в знаменателе полный квадрат. Для этого умножим числитель и знаменатель подынтегрального выражения на 3. Применяем интегрирование подведением под знак дифференциала. Получим
К полученному результату преобразований можем теперь применить табличный интеграл 21.
В результате
получаем окончательное решение:
.
Пример 14. Найти интеграл от тригонометрической функции
.
Решение. Решение. Воспользуемся универсальной тригонометрической подстановкой. Тогда
Используем метод неопределённых коэффициентов. Получим следующее подынтегральное выражение:
Чтобы найти коэффициенты, решим систему уравнений:
Теперь получаем:
Используем подведение под знак дифференциала:
К последнему слагаемому применяем замену переменной , тогда . Получаем:
Преобразуем и вернём на место первоначальную переменную и окончательно получим решение:
- Пригодится: тригонометрические тождества для преобразования выражений
| Назад | Листать | Вперёд>>> |
К началу страницы
Пройти тест по теме Интеграл
Начало темы «Интеграл»
Неопределённый интеграл: основные понятия, свойства, таблица неопределённых интегралов
Найти неопределённый интеграл: начала начал, примеры решений
Метод замены переменной в неопределённом интеграле
Интегрирование подведением под знак дифференциала
Метод интегрирования по частям
Интегрирование дробей
Интегрирование рациональных функций и метод неопределённых коэффициентов
Интегрирование некоторых иррациональных функций
Продолжение темы «Интеграл»
Определённый интеграл
Несобственные интегралы
Площадь плоской фигуры с помощью интеграла
Объём тела вращения с помощью интеграла
Вычисление двойных интегралов
Длина дуги кривой с помощью интеграла
Площадь поверхности вращения с помощью интеграла
Определение работы силы с помощью интеграла
10.
Тригонометрия — MAPHY.COMНекоторые рекомендации к выполнению тригонометрических преобразований
При выполнении тригонометрических преобразований следуйте следующим советам:
- Не пытайтесь сразу придумать схему решения примера от начала до конца.
- Не пытайтесь преобразовывать сразу весь пример. Продвигайтесь вперёд маленькими шагами.
- Помните, что кроме тригонометрических формул в тригонометрии можно по-прежнему применять все справедливые алгебраические преобразования (вынесение за скобку, сокращение дробей, формулы сокращённого умножения и так далее).
- Верьте, что всё будет хорошо.
Основные тригонометрические формулы
Большинство формул в тригонометрии часто применяется как справа налево, так и слева направо, поэтому учить эти формулы нужно так хорошо, чтобы Вы легко смогли применить некоторую формулу в обоих направлениях. Запишем для начала определения тригонометрических функций. Пусть имеется прямоугольный треугольник:
Тогда, определение синуса:
Определение косинуса:
Определение тангенса:
Определение котангенса:
Основное тригонометрическое тождество:
Простейшие следствия из основного тригонометрического тождества:
Формулы двойного угла.
Синус двойного угла:
Косинус двойного угла:
Тангенс двойного угла:
Котангенс двойного угла:
Дополнительные тригонометрические формулы
Тригонометрические формулы сложения.
Синус суммы:
Синус разности:
Косинус суммы:
Косинус разности:
Тангенс суммы:
Тангенс разности:
Котангенс суммы:
Котангенс разности:
Тригонометрические формулы преобразования суммы в произведение. Сумма синусов:
Разность синусов:
Сумма косинусов:
Разность косинусов:
Сумма тангенсов:
Разность тангенсов:
Сумма котангенсов:
Разность котангенсов:
Тригонометрические формулы преобразования произведения в сумму. Произведение синусов:
Произведение синуса и косинуса:
Произведение косинусов:
Формулы понижения степени.
Формула понижения степени для синуса:
Формула понижения степени для косинуса:
Формула понижения степени для тангенса:
Формула понижения степени для котангенса:
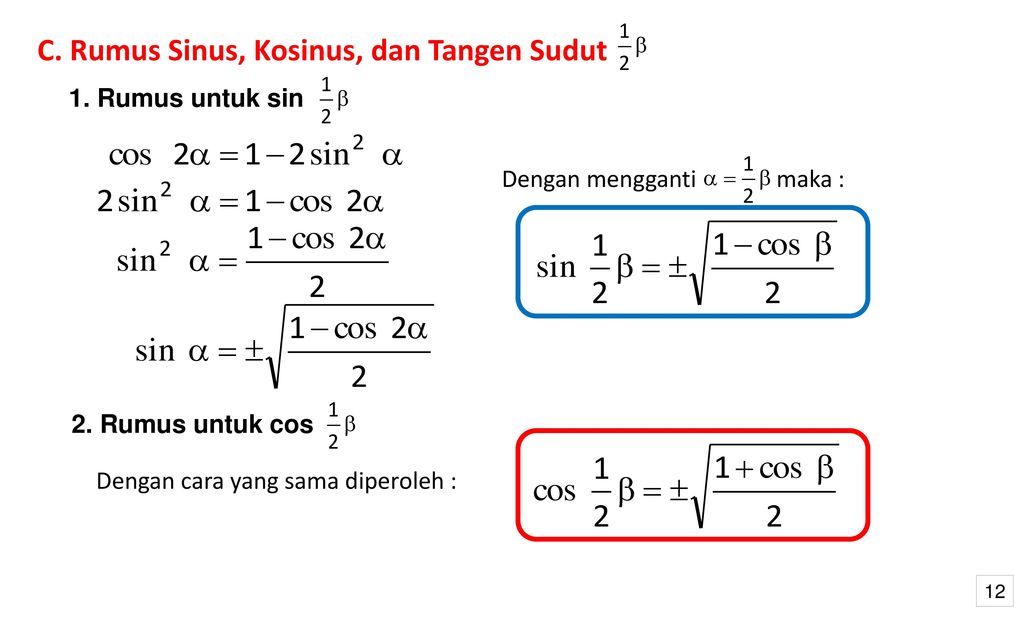
Формулы половинного угла. Формула половинного угла для тангенса:
Формула половинного угла для котангенса:
Тригонометрические формулы приведения
Функцию косинус называют кофункцией функции синус и наоборот. Аналогично функции тангенс и котангенс являются кофункциями. Формулы приведения можно сформулировать в виде следующего правила:
- Если в формуле приведения угол вычитается (прибавляется) из 90 градусов или 270 градусов, то приводимая функция меняется на кофункцию;
- Если же в формуле приведения угол вычитается (прибавляется) из 180 градусов или 360 градусов, то название приводимой функции сохраняется;
- При этом перед приведенной функцией ставится тот знак, который имеет приводимая (т. е. исходная) функция в соответствующей четверти, если считать вычитаемый (прибавляемый) угол острым.
е. исходная) функция в соответствующей четверти, если считать вычитаемый (прибавляемый) угол острым.Формулы приведения задаются в виде таблицы:
Тригонометрическая окружность
По тригонометрической окружности легко определять табличные значения тригонометрических функций:
Тригонометрические уравнения
Для решения некоторого тригонометрического уравнения его нужно свести к одному из простейших тригонометрических уравнений, которые будут рассмотрены ниже. Для этого:
- Можно применять тригонометрические формулы приведенные выше. При этом не нужно пытаться преобразовать сразу весь пример, а нужно двигаться вперед маленькими шагами.
- Нужно не забывать о возможности преобразовать некоторое выражение и с помощью алгебраических методов, т.е. например, вынести что-нибудь за скобку или, наоборот, раскрыть скобки, сократить дробь, применить формулу сокращенного умножения, привести дроби к общему знаменателю и так далее.
- При решении тригонометрических уравнений можно применять метод группировки. При этом нужно помнить, что для того чтобы произведение нескольких множителей было равно нолю, достаточно чтобы любой из них был равен нолю, а остальные существовали.
- Применяя метод замены переменной, как обычно, уравнение после введения замены должно стать проще и не содержать первоначальной переменной. Также нужно не забыть выполнить обратную замену.
- Помните, что однородные уравнения часто встречаются и в тригонометрии.
- Раскрывая модули или решая иррациональные уравнения с тригонометрическими функциями нужно помнить и учитывать все тонкости решения соответствующих уравнений с обычными функциями.
- Помните про ОДЗ (в тригонометрических уравнениях ограничения на ОДЗ в основном сводятся к тому, что делить на ноль нельзя, но не забываем и о других ограничениях, особенно о положительности выражений в рациональных степенях и под корнями четных степеней). Также помните, что значения синуса и косинуса могут лежать только в пределах от минус единицы до плюс единицы включительно.
Также помните, что значения синуса и косинуса могут лежать только в пределах от минус единицы до плюс единицы включительно.Главное, если не знаете, что делать, делайте хоть что-нибудь, при этом главное правильно использовать тригонометрические формулы. Если то, что Вы при этом получаете становиться все лучше и лучше, значит продолжайте решение, а если становиться хуже, значит вернитесь к началу и попробуйте применить другие формулы, так поступайте пока не наткнетесь на правильный ход решения.
Формулы решений простейших тригонометрических уравнений. Для синуса существует две равнозначные формы записи решения:
Для остальных тригонометрических функций запись однозначна. Для косинуса:
Для тангенса:
Для котангенса:
Решение тригонометрических уравнений в некоторых частных случаях:
принцесса, доктор, астроном и математика
youtube.com/embed/PCHUKWOx2AQ» frameborder=»0″ allowfullscreen=»allowfullscreen»> Анна Малкова (автор книги для подготовки к ЕГЭ, ведущая годового Онлайн-курса подготовки к ЕГЭ на 100 баллов, руководитель компании «ЕГЭ-студия» (Курсы ЕГЭ)).
Знаете ли вы, что с одной из тригонометрических формул связана настоящая приключенческая история? Эта история так повлияла на развитие науки, что неизвестно, какой была бы наша цивилизация, если бы все это не случилось. А герои нашей истории – король, доктор, принцесса и астроном.
Давайте отправимся в Шотландию конца XVI века.
Началось все с того, что король Шотландский задумал жениться. Но так получилось, что ни одной подходящей девушки он не нашел у себя на родине в Шотландии и решил, что невесту надо искать за морем, в Дании. «Но не самому же искать невесту, – подумал король. – Смотреть на их портреты, приглашать на свидания… Как это все утомительно!» И король отправил в Данию за невестой придворного доктора, которого звали Джон Крэйг.
Но приключения только начинались. Корабль, на котором плыл Джон Крэйг попал в шторм, не доплыв до Копенгагена. Хорошо, что по близости оказался остров Вен. На острове стояла лучшая обсерватория того времени. Она была построена знаменитым астрономом Тихо Браге и называлась Ураниборг, замок Урании, богини астрономии. Тихо Браге – один из величайших астрономов в истории Европы. В ноябре 1572 года Тихо Браге заметил в созвездии Кассиопея необычайно яркую звезду. Это была вспышка сверхновой. Тихо Браге занимался изучением комет и понял, что кометы имеют внеземное происхождение. Он измерил длину года с точностью до секунды. Материалы его наблюдений помогли его приемнику Кеплеру открыть законы движения планет.
Все знали, что Тихо Браге обладает необыкновенно острым зрением и владеет новейшими по тем временам методами вычислений.
Путешественников приютили в обсерватории, и доктор Крэйг смог вести ученые беседы с Тихо Браге. Астроном рассказал доктору Крэйгу об одном из таких методов.
Представьте себе, как сложно было производить математические вычисления в XVI веке, не имея ни калькуляторов, ни компьютеров, имея только счеты и вычисляя в столбик. Например, нужно перемножить 2 числа m и n. Если речь идет об астрономии, это могли быть восьмизначные числа. Представьте, 2 восьмизначных числа перемножить в столбик и не ошибиться. Оказалось, что Тихо Браге пользовался другим методом. Он использовал формулу преобразования произведения косинусов в сумму.
Подбирались по таблице значений косинуса такие числа а и b, чтобы m и n оказывались косинусами этих чисел.
Но что делать, если, например, m=375? Ведь нет такого угла, у которого косинус будет равен 375.
Но 375 можно записать как 0,375 умноженное на 1000.
Например, n=16431=0,16431 умножить на 10 в 5 степени.
Тогда в нашей формуле могут быть числа m и n, если по модулю они не превосходят 1, а могут быть числа m1 и n1 такие, что отличаются от исходных степенями десятки.
Нам осталось по таблицам косинусов подобрать такие числа а и b, что косинус а =m1, косинус b=n1. После этого мы складываем а+b и находим по таблице косинус (а+b). Вычитаем а – b и находим косинус (а-b). Затем мы складываем 2 косинуса и делим пополам.
Так нам удалось избежать умножения больших чисел и заменить его более простым сложением.
Впечатленный этим удивительным методом, доктор Крэйг, вернувшись в Шотландию, рассказал о нем своему другу, математику Джону Неперу. «Отлично! – сказал Непер. – Но зачем нам косинусы, ведь у нас есть логарифмы!»
Если вы знакомы с логарифмами, то, конечно, вы знаете формулу
Это при условии
В этой формуле мы тоже видим, как из логарифма произведения получается сумма логарифмов.
Оставалось только разработать таблицу логарифмов. Этим и занялся математик Непер. В результате вычисление значительно упростились.
Например, нам нужно найти произведение чисел b и с. Эти числа тоже могут быть семи или восьмизначными.
Мы находим по таблице логарифмов логарифм числа b по какому-нибудь удобному основанию а. Находим логарифм с по тому же основанию. Складываем эти 2 числа и получаем результат. Этот результат является логарифмом произведения b на с по тому же основанию. Находим в таблице этот логарифм b на с и находим, от какого числа по основанию а его взяли, то есть произведение b на c.
«Но к чему такие сложности?» – скажите вы. – «Применение всех этих формул для преобразования произведения косинусов, сумму косинусов. Или, как здесь, из логарифма произведения сделать сумму логарифмов… Не проще ли было взять калькулятор и посчитать?»
Нет, не проще, потому что калькуляторов не было. Более того, применение логарифмов и упрощение вычислений ускорило развитие цивилизации. Начали развиваться астрономия, а вместе с ней – мореплавание, торговля и промышленность. Технический прогресс ускорился. И, в том числе, приблизилось то время, когда мы можем пользоваться компьютерами, калькуляторами и мобильными телефонами.
А что могло бы произойти, если бы вся эта история не случилась?
Пишите в комментариях!
7.4 Формулы «сумма-произведение» и «произведение-сумма» — предварительное исчисление 2e
Цели обучения
В этом разделе вы:
- Экспресс-продукты в сумме.
- Выразите суммы как продукты.
Рисунок 1 Оркестр Калифорнийского университета в Лос-Анджелесе (кредит: Эрик Чан, Flickr).
Группа марширует по полю, создавая потрясающий звук, который поддерживает толпу. Этот звук распространяется как волна, которую можно интерпретировать с помощью тригонометрических функций. Например, на рисунке 2 представлена звуковая волна для музыкальной ноты A. В этом разделе мы исследуем тригонометрические тождества, лежащие в основе таких повседневных явлений, как звуковые волны.
Рисунок 2
Выражение произведений в виде сумм
Мы уже изучили ряд формул, полезных для расширения или упрощения тригонометрических выражений, но иногда нам может понадобиться выразить произведение косинуса и синуса в виде суммы.
Мы можем использовать формулы произведения на сумму, которые выражают произведения тригонометрических функций в виде сумм. Давайте сначала исследуем тождество косинуса, а затем тождество синуса.
Выражение произведений в виде суммы косинуса
Мы можем вывести формулу произведения на сумму из тождеств суммы и разности для косинуса. Если мы сложим два уравнения, то получим:
cosαcosβ+sinαsinβ=cos(α−β)+cosαcosβ−sinαsinβ=cos(α+β)________________________________2cosαcosβ=cos(α−β)+cos(α+β)cosαcosβ+sinαsinβ=cos(α−β)+cosαcosβ− sinαsinβ=cos(α+β)________________________________2cosαcosβ=cos(α−β)+cos(α+β)
Затем делим на 22, чтобы выделить произведение косинусов:
cosαcosβ=12[cos(α−β)+cos(α+β)]cosαcosβ=12[cos(α−β)+cos(α+β)]
Как
Произведение косинусов выразите в виде суммы.
- Напишите формулу произведения косинусов.
- Подставить данные углы в формулу.
- Упростить.
Пример 1
Запись произведения в виде суммы с использованием формулы произведения косинуса на сумму
Запишите следующее произведение косинусов в виде суммы: 2cos(7×2)cos3x2.2cos(7×2)cos3x2.
Решение
Начнем с написания формулы произведения косинусов:
cosαcosβ=12[cos(α−β)+cos(α+β)]cosαcosβ=12[cos(α−β)+cos(α+β) ]
Затем мы можем подставить данные углы в формулу и упростить.
2cos (7×2) cos (3×2) = (2) (12) [cos (7×2–3×2)+cos (7×2+3×2)] = [cos (4×2)+cos (10×2)] = cos2x+cos5x2cos (7×2 )cos(3×2)=(2)(12)[cos(7×2−3×2)+cos(7×2+3×2)] = [cos(4×2)+cos(10×2)] = cos2x+cos5x
Попытайся #1
Используйте формулу произведения на сумму, чтобы записать произведение в виде суммы или разности: cos(2θ)cos(4θ).
cos(2θ)cos(4θ).
Выражение произведения синуса и косинуса в виде суммы
Далее мы получим формулу произведения на сумму для синуса и косинуса из формул суммы и разности для синуса. Если мы сложим сумму и разность тождеств, то получим:
sin(α+β)=sinαcosβ+cosαsinβ+ sin(α−β)=sinαcosβ−cosαsinβ________________________________________________sin(α+β)+sin(α−β)=2sinαcosβsin(α+β)=sinαcosβ+cosαsinβ+ β)=sinαcosβ−cosαsinβ_________________________________________sin(α+β)+sin(α−β)=2sinαcosβ
Затем делим на 2, чтобы выделить произведение косинуса и синуса:
sinαcosβ=12[sin(α+β)+sin(α−β)]sinαcosβ=12[sin(α+β)+sin(α−β)]
Пример 2
Запись произведения в виде суммы, содержащей только синус или косинус
Выразите следующее произведение в виде суммы, содержащей только синус или косинус и не содержащей произведений: sin(4θ)cos(2θ).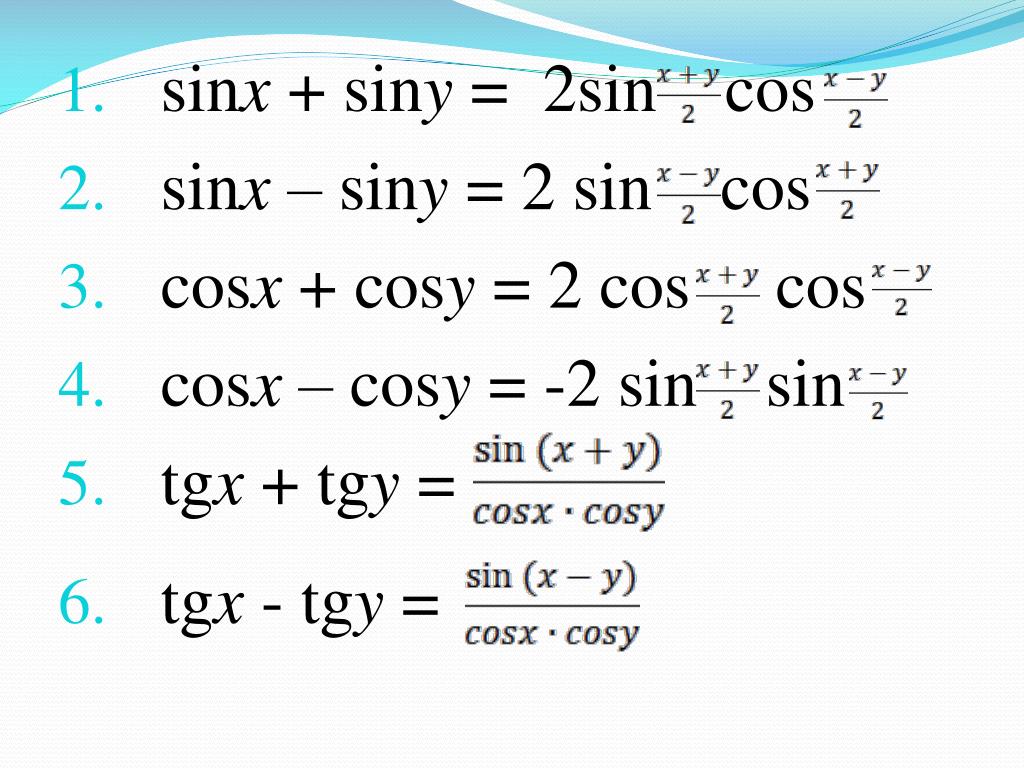
sin(4θ)cos(2θ).
Решение
Напишите формулу произведения синуса и косинуса. Затем подставьте данные значения в формулу и упростите.
sinαcosβ=12[sin(α+β)+sin(α−β)]sin(4θ)cos(2θ)=12[sin(4θ+2θ)+sin(4θ−2θ)]=12[sin( 6θ)+sin(2θ)]sinαcosβ=12[sin(α+β)+sin(α−β)]sin(4θ)cos(2θ)=12[sin(4θ+2θ)+sin(4θ−2θ) ]=12[sin(6θ)+sin(2θ)]
Попытайся #2
Используйте формулу произведения на сумму, чтобы записать произведение в виде суммы: sin(x+y)cos(x−y).sin(x+y)cos(x−y).
Выражение произведений синусов через косинус
Выражение произведения синусов через косинус также получается из тождеств суммы и разности для косинуса. В этом случае мы сначала вычтем две формулы косинуса:
cos(α−β)=cosαcosβ+sinαsinβ− cos(α+β)=−(cosαcosβ−sinαsinβ)____________________________________________________cos(α−β)−cos(α+β)=2sinαsinβ cos(α−β)=cosαcosβ+sinαsinβ − cos(α+β)=−(cosαcosβ−sinαsinβ)_________________________________________________________________cos(α−β)−cos(α+β)=2sinαsinβ
Затем делим на 2, чтобы выделить произведение синусов:
sinαsinβ=12[cos(α−β)−cos(α+β)]sinαsinβ=12[cos(α−β)−cos(α+β)]
Аналогичным образом мы могли бы выразить произведение косинусов через синус или вывести другие формулы произведения на сумму.
Формулы произведения к сумме
Формулы произведения на сумму следующие:
cosαcosβ=12[cos(α−β)+cos(α+β)]cosαcosβ=12[cos(α−β)+cos(α+β) ]
sinαcosβ=12[sin(α+β)+sin(α−β)]sinαcosβ=12[sin(α+β)+sin(α−β)]
sinαsinβ=12[cos(α−β) )−cos(α+β)]sinαsinβ=12[cos(α−β)−cos(α+β)]
cosαsinβ=12[sin(α+β)−sin(α−β)]cosαsinβ=12 [sin(α+β)−sin(α−β)]
Пример 3
Выразите произведение в виде суммы или разности
Запишите cos(3θ)cos(5θ)cos(3θ)cos(5θ) в виде суммы или разности.
Решение
У нас есть произведение косинусов, поэтому начнем с написания соответствующей формулы. Затем подставляем данные углы и упрощаем.
cosαcosβ=12[cos(α−β)+cos(α+β)]cos(3θ)cos(5θ)=12[cos(3θ−5θ)+cos(3θ+5θ)] =12[cos( 2θ)+cos(8θ)] Использовать четно-нечетное тождество. cosαcosβ=12[cos(α−β)+cos(α+β)]cos(3θ)cos(5θ)=12[cos(3θ−5θ)+cos(3θ+5θ)] =12[cos(2θ) +cos(8θ)]Использовать четно-нечетное тождество.
Попытайся #3
Используйте формулу произведения на сумму для вычисления cos11π12cosπ12.cos11π12cosπ12.
Выражение сумм в виде произведений
Некоторые проблемы требуют обратного процесса, который мы только что использовали. Формулы суммы к произведению позволяют нам выразить суммы синуса или косинуса в виде произведений. Эти формулы могут быть получены из тождеств произведения на сумму. Например, с помощью нескольких замен мы можем получить тождество суммы и произведения для синуса. Пусть u+v2=αu+v2=α и u−v2=β.u−v2=β.
Затем
90 004 −u−v2 =2v2 =vТаким образом, заменив αα и ββ в формуле произведения на сумму подстановочными выражениями, мы получим
sinαcosβ=12[sin(α+β)+sin(α−β)] sin(u+v2)cos(u−v2)=12[sinu+sinv]Подставить вместо (α+β) и (α−β )2sin(u+v2)cos(u−v2)=sinu+sinv sinαcosβ=12[sin(α+β)+sin(α−β)] sin(u+v2)cos(u−v2)=12[ sinu+sinv] Замените для (α+β) и (α−β)2sin(u+v2)cos(u−v2)=sinu+sinv
Другие тождества суммы к произведению получаются аналогично.
Формулы суммы к произведению
Формулы суммы к произведению следующие:
sinα+sinβ=2sin(α+β2)cos(α−β2)sinα+sinβ=2sin(α+β2)cos(α−β2)
sinα −sinβ=2sin(α−β2)cos(α+β2)sinα−sinβ=2sin(α−β2)cos(α+β2)
cosα−cosβ=−2sin(α+β2)sin(α−β2) cosα−cosβ=−2sin(α+β2)sin(α−β2)
cosα+cosβ=2cos(α+β2)cos(α−β2)cosα+cosβ=2cos(α+β2)cos(α−β2 )
Пример 4
Запись разности синусов в виде произведения
Запишите следующую разность синусов в виде произведения: sin(4θ)−sin(2θ).sin(4θ)−sin(2θ).
Решение
Начнем с написания формулы разности синусов.
sinα-sinβ=2sin(α-β2)cos(α+β2)sinα-sinβ=2sin(α-β2)cos(α+β2)
Подставьте значения в формулу и упростите.
sin (4θ) −sin (2θ) = 2sin (4θ — 2θ2) cos (4θ+2θ2) = 2sin (2θ2) cos (6θ2) = 2sinθcos (3θ) sin (4θ) −sin (2θ) = 2sin ( 4θ−2θ2)cos(4θ+2θ2) =2sin(2θ2)cos(6θ2) =2sinθcos(3θ)
Попытайся #4
Используйте формулу преобразования суммы в произведение, чтобы записать сумму в виде произведения: sin(3θ)+sin(θ).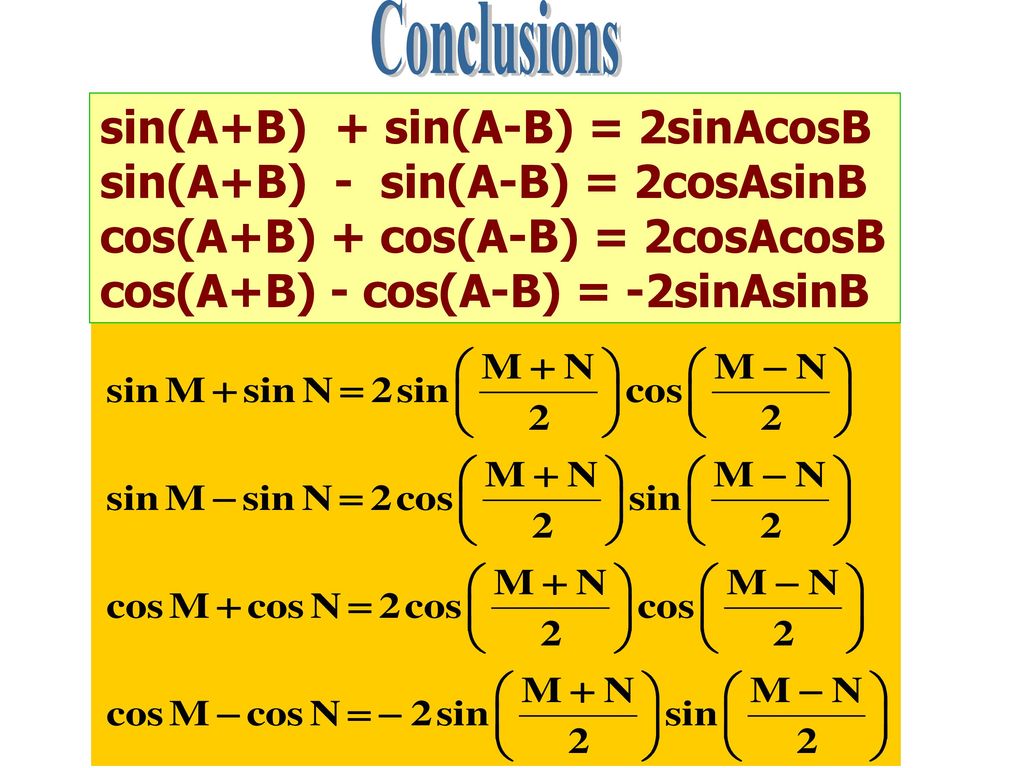
sin(3θ)+sin(θ).
Пример 5
Вычисление с использованием формулы произведения суммы
Вычисление cos(15∘)−cos(75∘).cos(15∘)−cos(75∘).
Решение
Начнем с написания формулы разности косинусов.
cosα-cosβ=-2sin(α+β2)sin(α-β2)cosα-cosβ=-2sin(α+β2)sin(α-β2)
Затем подставляем данные углы и упрощаем.
cos (15∘) −cos (75∘) = — 2sin (15∘+75∘2) sin (15∘ — 75∘2) = −2sin (45∘) sin (-30∘) = −2 ( 22) ( — 12) = 22cos (15∘) −cos (75∘) = — 2sin (15∘+75∘2) sin (15∘ — 75∘2) = −2sin (45∘) sin (−30∘ ) =−2(22)(−12) =22
Пример 6
Удостоверение личности
Докажите тождество:
cos(4t)−cos(2t)sin(4t)+sin(2t)=−tantcos(4t)−cos(2t)sin(4t)+sin(2t)=−tant
Решение
Мы начнем с левой части, более сложной части уравнения, и перепишем выражение, пока оно не совпадет с правой частью.
cos(4t)−cos(2t)sin(4t)+sin(2t)=−2sin(4t+2t2)sin(4t−2t2)2sin(4t+2t2)cos(4t−2t2) = −2sin( 3t) sint2sin (3t) стоимость = −2sin (3t) sint2sin (3t) стоимость = −sintcost = −tantcos (4t) -cos (2t) sin (4t)+sin (2t) = — 2sin (4t+2t2) sin (4t — 2t2) 2sin (4t+2t2) cos (4t — 2t2) = −2sin (3t) sint2sin (3t) стоимость = −2sin (3t) sint2sin (3t) стоимость = −sintcost = −tant
Анализ
Напомним, что проверка тригонометрических тождеств имеет свой собственный набор правил. Процедуры решения уравнения не совпадают с процедурами проверки личности. Когда мы подтверждаем тождество, мы выбираем одну сторону для работы и делаем замены до тех пор, пока эта сторона не превратится в другую сторону.
Пример 7
Проверка идентичности с использованием формул двойного угла и обратных идентичностей
Проверка идентичности csc2θ−2=cos(2θ)sin2θ.csc2θ−2=cos(2θ)sin2θ.
Решение
Для проверки этого уравнения мы объединим несколько тождеств.
Мы будем использовать формулу двойного угла и обратные тождества. Мы будем работать с правой частью уравнения и перепишем ее, пока она не совпадет с левой частью.
cos (2θ) sin2θ = 1-2sin2θsin2θ = 1sin2θ — 2sin2θsin2θ = csc2θ —2cos (2θ) sin2θ = 1-2sin2θsin2θ = 1sin2θ —2sin2θ = csc2θ — 2
Попытайся #5
Проверить тождество tanθcotθ−cos2θ=sin2θ.tanθcotθ−cos2θ=sin2θ.
7.4 Секционные упражнения
Устный
1.
Начиная с произведения на формулу суммирования sinαcosβ=12[sin(α+β)+sin(α−β)],sinαcosβ=12[sin(α+β)+sin(α−β)], объясните, как определите формулу для cosαsinβ.cosαsinβ.
2.
Объясните два различных метода вычисления cos(195°)cos(105°),cos(195°)cos(105°), один из которых использует произведение для суммирования. Какой способ проще?
3.
Объясните ситуацию, когда мы должны преобразовать уравнение из суммы в произведение, и приведите пример.
4.
Объясните ситуацию, когда мы должны преобразовать уравнение из произведения в сумму, и приведите пример.
Алгебраический
Для следующих упражнений перепишите произведение как сумму или разность.
5.
16sin(16x)sin(11x)16sin(16x)sin(11x)
6.
20cos(36t)cos(6t)20cos(36t)cos(6t)
7.
2sin(5x)cos(3x)2sin(5x)cos(3x)
8.
10cos(5x)sin(10x)10cos(5x)sin(10x)
9.
грех(-x)sin(5x)sin(-x)sin(5x)
10.
sin(3x)cos(5x)sin(3x)cos(5x)
Для следующих упражнений перепишите сумму или разность в виде произведения.
11.
cos(6t)+cos(4t)cos(6t)+cos(4t)
12.
грех(3х)+грех(7х)грех(3х)+грех(7х)
13.
cos(7x)+cos(-7x)cos(7x)+cos(-7x)
14.
sin(3x)−sin(−3x)sin(3x)−sin(−3x)
15.
cos(3x)+cos(9x)cos(3x)+cos(9x)
16.
sinh-sin(3h)sinh-sin(3h)
Для следующих упражнений оцените произведение для следующего, используя сумму или разность двух функций.
17.
cos(45°)cos(15°)cos(45°)cos(15°)
18.
cos(45°)sin(15°)cos(45°)sin(15°)
19.
sin(-345°)sin(-15°)sin(-345°)sin(-15°)
20.
sin(195°)cos(15°)sin(195°)cos(15°)
21.
sin(-45°)sin(-15°)sin(-45°)sin(-15°)
В следующих упражнениях оцените произведение, используя сумму или разность двух функций. Оставьте в терминах синуса и косинуса.
22.
cos(23°)sin(17°)cos(23°)sin(17°)
23.
2sin(100°)sin(20°)2sin(100°)sin(20°)
24.
2sin(-100°)sin(-20°)2sin(-100°)sin(-20°)
25.
sin(213°)cos(8°)sin(213°)cos(8°)
26.
2cos(56°)cos(47°)2cos(56°)cos(47°)
Для следующих упражнений перепишите сумму как произведение двух функций. Оставьте в терминах синуса и косинуса.
27.
sin(76°)+sin(14°)sin(76°)+sin(14°)
28.
cos(58°)-cos(12°)cos(58°)-cos(12°)
29.
sin(101°)−sin(32°)sin(101°)−sin(32°)
30.
cos(100°)+cos(200°)cos(100°)+cos(200°)
31.
sin(-1°)+sin(-2°)sin(-1°)+sin(-2°)
Для следующих упражнений подтвердите тождество.
32.
cos(a+b)cos(a-b)=1-tanatanb1+tanatanbcos(a+b)cos(a-b)=1-tanatanb1+tanatanb
33.
4sin(3x)cos(4x)=2sin(7x)−2sinx4sin(3x)cos(4x)=2sin(7x)−2sinx
34.
6cos(8x)sin(2x)sin(-6x)=-3sin(10x)csc(6x)+36cos(8x)sin(2x)sin(-6x)=-3sin(10x)csc(6x)+ 3
35.
sinx+sin(3x)=4sinxcos2xsinx+sin(3x)=4sinxcos2x
36.
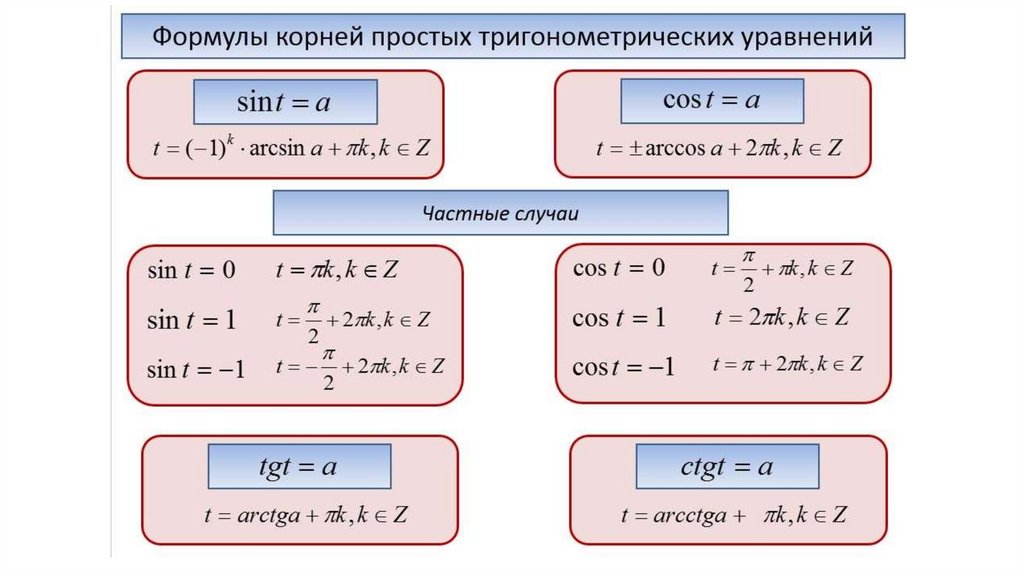
2(cos3x-cosxsin2x)=cos(3x)+cosx2(cos3x-cosxsin2x)=cos(3x)+cosx
37.
2tanxcos(3x)=secx(sin(4x)−sin(2x))2tanxcos(3x)=secx(sin(4x)−sin(2x))
38.
cos(a+b)+cos(a−b)=2cosacosbcos(a+b)+cos(a−b)=2cosacosb
Цифровой
Для следующих упражнений перепишите сумму как произведение двух функций или произведение как сумму двух функций. Дайте ответ в виде синусов и косинусов. Затем оцените окончательный ответ численно, округлив до четырех знаков после запятой.
39.
cos(58∘)+cos(12∘)cos(58∘)+cos(12∘)
40.
sin(2∘)−sin(3∘)sin(2∘)−sin(3∘)
41.
cos(44∘)−cos(22∘)cos(44∘)−cos(22∘)
42.
cos(176∘)sin(9∘)cos(176∘)sin(9∘)
43.
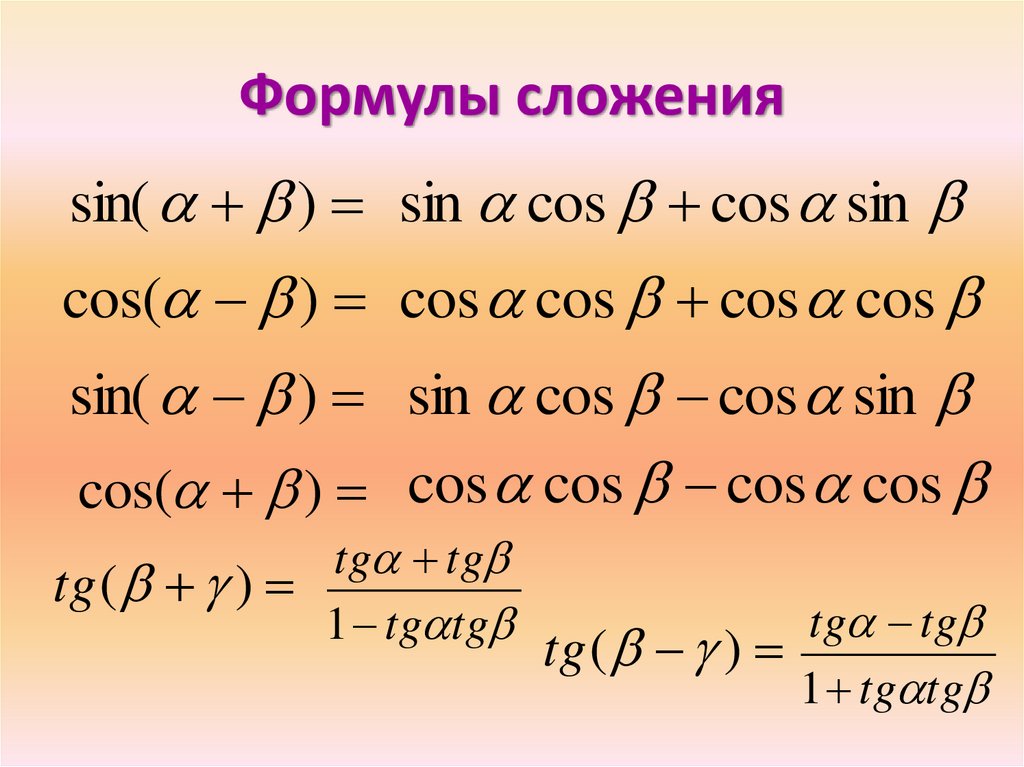
sin(−14∘)sin(85∘)sin(−14∘)sin(85∘)
Технология
Для следующих упражнений алгебраически определите, является ли каждое из заданных выражений истинным тождеством. Если это не тождество, замените правую часть выражением, эквивалентным левой части. Проверьте результаты, построив графики обоих выражений на калькуляторе.
44.
2sin(2x)sin(3x)=cosx-cos(5x)2sin(2x)sin(3x)=cosx-cos(5x)
45.
cos(10θ)+cos(6θ)cos(6θ)−cos(10θ)=cot(2θ)cot(8θ)cos(10θ)+cos(6θ)cos(6θ)−cos(10θ)=cot( 2θ)кроватка(8θ)
46.
sin(3x)−sin(5x)cos(3x)+cos(5x)=tanxsin(3x)−sin(5x)cos(3x)+cos(5x)=tanx
47.
2cos(2x)cosx+sin(2x)sinx=2sinx2cos(2x)cosx+sin(2x)sinx=2sinx
48.
sin(2x)+sin(4x)sin(2x)−sin(4x)=−tan(3x)cotxsin(2x)+sin(4x)sin(2x)−sin(4x)=−tan(3x)cotx
В следующих упражнениях упростите выражение до одного члена, затем нарисуйте исходную функцию и вашу упрощенную версию, чтобы убедиться, что они идентичны.
49.
sin(9t)−sin(3t)cos(9t)+cos(3t)sin(9t)−sin(3t)cos(9t)+cos(3t)
50.
2sin(8x)cos(6x)−sin(2x)2sin(8x)cos(6x)−sin(2x)
51.
грех(3x)-sinxsinxsin(3x)-sinxsinx
52.
cos(5x)+cos(3x)sin(5x)+sin(3x)cos(5x)+cos(3x)sin(5x)+sin(3x)
53.
sinxcos(15x)−cosxsin(15x)sinxcos(15x)−cosxsin(15x)
Расширения
Для следующих упражнений докажите следующие формулы произведения суммы.
54.
sinx-siny=2sin(x-y2)cos(x+y2)sinx-siny=2sin(x-y2)cos(x+y2)
55.
cosx+cosy=2cos(x+y2)cos(x−y2)cosx+cosy=2cos(x+y2)cos(x−y2)
Для следующих упражнений подтвердите тождество.
56.
sin(6x)+sin(4x)sin(6x)−sin(4x)=tan(5x)cotxsin(6x)+sin(4x)sin(6x)−sin(4x)=tan(5x)cotx
57.
cos(3x)+cosxcos(3x)−cosx=−cot(2x)cotxcos(3x)+cosxcos(3x)−cosx=−cot(2x)cotx
58.
cos(6y)+cos(8y)sin(6y)−sin(4y)=cotycos(7y)sec(5y)cos(6y)+cos(8y)sin(6y)−sin(4y)=cotycos( 7г)сек(5г)
59.
cos(2y)−cos(4y)sin(2y)+sin(4y)=tanycos(2y)−cos(4y)sin(2y)+sin(4y)=tany
60.
sin(10x)−sin(2x)cos(10x)+cos(2x)=tan(4x)sin(10x)−sin(2x)cos(10x)+cos(2x)=tan(4x)
61.
cosx-cos(3x)=4sin2xcosxcosx-cos(3x)=4sin2xcosx
62.
(cos(2x)−cos(4x))2+(sin(4x)+sin(2x))2=4sin2(3x)(cos(2x)−cos(4x))2+(sin(4x) +грех(2x))2=4sin2(3x)
63.
tan(π4−t)=1−tant1+tanttan(π4−t)=1−tant1+tant
14.2 — Тригонометрические тождества
14.2 — Тригонометрические тождества14.2 — Тригонометрические тождества
Мы начнем этот раздел с формулировки около 20 основных тригонометрических тождеств. Вы можете обратиться к книги, такие как « Справочник по математическим функциям », Абрамовица и Стегуна и многих других. Чтобы понять их, мы организуем разделите их на 9 групп и обсудите каждую группу.Затем мы заканчиваем этот раздел 7 примерами.
Сравнение тождеств и уравнений: Тождество — это утверждение, которое всегда верно, тогда как уравнение истинно только при определенных условиях. Например
3 х + 2 х = 5 хэто тождество, которое всегда верно, независимо от значения x , тогда как
3 х = 15уравнение (точнее, условное уравнение), верное только если x = 5.
A Тригонометрическое тождество — это тождество, содержащее тригонометрическое функции sin, cos, tan, cot, sec или csc. Тригонометрические тождества можно использовать для:
- Упрощение тригонометрических выражений.
- Решение тригонометрических уравнений.
- Докажите, что одно тригонометрическое выражение эквивалентно другому, так что мы можем заменить первое выражение вторым выражением. Второе выражение может дать нам новое понимание некоторых приложений. что первый не показывает.
Взаимные тождества
1а. 1б. 1с.
Эта группа тождеств утверждает, что csc и sin взаимно обратны, что sec и cos обратны, и что cot и tan обратны.
Они следуют непосредственно из определений тригонометрических функций.
(Нажмите здесь, чтобы увидеть их снова.)
Многие математики считают их просто основными
упрощения, которые нужно использовать, чтобы избавиться от csc, sec и кроватки в пользу
грех, кос и загар. Тождества с отрицательным углом
2а. потому что (- θ ) = потому что ( θ ) 2б. грех (- θ ) = — грех ( θ ) 2с. загар (- θ ) = — загар ( θ )
Эти тождества описывают лево-правую симметрию кривых cos, sin и tan. Многие математики считают эти тождества просто базовыми.
упрощения, используемые для избавления от отрицательных углов внутри
потому что, грех или загар.Графически тождество (2а) говорит о том, что высота кривой cos для отрицательного угла совпадает с высотой кривой cos для соответствующего положительного угла. Говорят, что любая кривая, обладающая этим свойством, имеет даже симметрия .
Тождество (2b) говорит о том, что высота кривой sin для отрицательного угла это минус высоты для соответствующего положительного угла. Говорят, что любая кривая, обладающая этим свойством, имеет нечетную симметрию .
Тождество (2с) говорит о том, что кривая тангенса также имеет нечетную симметрию.
Тождества «сдвиг влево на 90°»
3а.3б. 3с.
График слева объясняет тождество (3а). Он показывает, что сдвиг кривой sin к осталось 90 ° (или на π / 2 радиана или ¼ цикла) дает кривую cos. График справа объясняет тождество (3b). Это показывает, что сдвиг кривой cos к влево на 90 ° (или на π / 2 радиана или ¼ цикла) дает перевернутая кривая греха.
Тождество (3c) можно доказать, используя тождества (3a) и (3b) и немного алгебры.
Эти тождества также считаются базовыми упрощениями и используются для получения избавиться от 9сдвиг 0°. Используя их повторно, их можно использовать для получения избавиться от сдвигов на 180°, 270°, 360° и т. д.Теорема Пифагора
4. грех 2 ( θ ) + cos 2 ( θ ) = 1
Это тригонометрическая форма теоремы Пифагора.
Обратите внимание, что обозначение sin 2 ( θ ) означает (sin( θ )) 2 , и то же самое касается cos. Другими словами, вы должны сначала взять грех, а затем возвести его в квадрат. Причина не размещения показатель степени в конце должен дать понять, что это не угол θ , который в квадрате, скорее это sin от θ , которое возведено в квадрат.
Тождество (4) считается базовым упрощением. Мы также можем изменить его в качестве
1 − sin 2 ( θ ) = cos 2 ( θ )или как
1 − cos 2 ( θ ) = sin 2 ( θ )и они также считаются основными упрощениями, когда они используются для заменить два члена слева на один член справа.
Чтобы доказать тождество (4), просто постройте прямоугольный треугольник с гипотенузой 1
и угол θ . Тогда основание и высота равны
cos( θ ) и sin( θ ), и
оригинальная форма
теорема Пифагора, а именно а 2 + б 2 = в 2 ,
превращается в тождество (4).
График справа иллюстрирует теорему Пифагора. показывая, как высота sin 2 ( θ ) кривая (красная) и высота потому что 2 ( θ ) кривая (синяя) добавить к всегда равному 1 (черная пунктирная линия).
Мы также можем записать теорему Пифагора в двух других формах. Если мы разделим обе части тождества (4) на cos 2 ( θ ) и упростить, тогда это читается
1 + тангенс 2 ( θ ) = сек 2 ( θ )В противном случае, если мы разделим обе стороны тождества (4) по греху 2 ( θ ) и упростите, тогда получится
1 + детская кроватка 2 ( θ ) = csc 2 ( θ )
| Тождества, которые мы обсуждали до сих пор (тождества с 1 по 4), на самом деле просто упрощения, которые всегда применяются слева направо (т.  е. путем замены
левостороннее выражение везде, где оно встречается справа
выражение.) Остальные тождества (тождества с 5 по 9, обсуждаются далее)
указаны так, что левая часть представляет собой комбинированную форму .
некоторого выражения, а правая часть — это , разбитая на части форма .
Их можно применять в любом направлении в зависимости от того, чего мы хотим добиться:
|
Этот метод используется для создания более компактных выражений .Коричневая идентичность
5.
Это тождество следует из определения sin, cos и tan. Чтобы получить его, просто разделите отношение sin на отношение cos и упростите. Результатом является соотношение для загара:
Сумма углов тождеств
6а. sin( α ± β ) = sin( α )·cos( β ) ± cos( α )·sin( β ) 6б. 6с.
Эти тождества описывают, как разбить тригонометрическую функцию суммы или разность углов α и β в тригонометрические функции отдельных углов α и β .
На самом деле это 6 тождеств, 3 происходят от использования верхних знаков и 3 происходят от использования нижних знаков. Например, тождество (6c) с нижние знаки гласят:
Распространенной ошибкой является игнорирование этих тождеств и убеждение, что, например,
грех( α + β ) = sin( α )+ sin( β ) НЕПРАВИЛЬНО!Это неправильно! Это может быть правильно, только если грех кривая представляла собой прямую линию, проходящую через начало координат, а не волнистую кривую.
Вот пример, который использует тождество (6a) для описания того, что происходит, когда синусоидальная волна
смещен влево на 30°.
Можно (но сложнее) использовать тождество (6а) в обратном направлении и покажите, как сумма sin и cos может быть выражена как sin со сдвигом фазы. Нажмите здесь, чтобы увидеть пример этого.
Сейчас мы докажем, что грех( α + β ) = sin( α )·cos( β ) + cos( α )·sin( β ).
Доказательство: На рисунке показан большой желтый косой треугольник с двумя маленькими внутри него прямоугольные треугольники. Примените закон синусов к большому треугольнику.
Используйте тот факт, что sin( γ ) = ч / c и далее умножьте ( a + b ) на другую сторону.
Разверните правую сторону, а затем используйте два маленьких треугольника в
картинку, чтобы заменить каждую дробь соответствующей тригонометрической функцией. Мы сделали.Тождество (6а) с верхним знаком, а именно:
грех( α + β ) = sin( α )·cos( β ) + cos( α )·sin( β )которую мы только что доказали, вероятно, является наиболее важная идентичность группы. Любая другая идентичность в группе (и в фактически почти любое тригонометрическое тождество) может быть получено из него. Например:
- Тождество греха ( α − β )
можно получить, написав его как sin( α + (− β )),
применяя тождество (6a), а затем используя тождества отрицательного угла (2a) и (2b),
помыть.
- Идентичность для cos( α + β ) может быть получена с помощью
используя тождество (3а), чтобы записать его как грех со сдвигом фазы:
sin(( α + 90°) + β ),
затем применяя тождество (6а), а затем снова используя (3а) для очистки. - Идентификация tan ( α + β ) может быть получена путем деления тождества (6а) на (6б).
Тождества двойного угла
7а. sin(2 α ) = 2·sin( α )·cos( α ) 7б. cos(2 α знак равно cos 2 ( α ) − sin 2 ( α ) = 1 − 2 sin 2 ( α )
= 2 cos 2 ( α ) − 1
7с.
Эти тождества являются частными случаями тождеств (6а), (6б) и (6в). с верхними знаками, которые гласили: Пусть β равно α и тождества (7а), (7б), (7в) сразу выскочит. Тождество (7b) записывается в 3 разных формах. Вторая и третья формы результат использования теоремы Пифагора о первой форме. Они являются предпочтительными формами, потому что они включают только грех или только cos, и не оба.
Эти тождества используются для преобразования тригонометрической функции дважды угол в тригонометрическую функцию самого угла.
Тождества половинного угла
Если мы решим вторую форму тождества (7b) для sin 2 ( α ) и третья форма для cos 2 ( α ), тогда мы получаем эти два тождества: Если мы теперь изменим название угла α на A /2, то они становятся так называемыми тождествами половинного угла:
8а. 8б.
Эти тождества используются для преобразования тригонометрической функции половину угла в тригонометрическую функцию самого угла.
Идентификаторы продуктов
Если мы сложим или вычтем тождества (6а) и (6б) в различных комбинациях тогда мы получаем так называемые идентификаторы продуктов:
9а. грех( α )·sin( β ) = ½ [cos( α — β ) — cos( α + β )] 9б. sin( α )·cos( β ) = ½[sin( α + β ) + грех( α − β )] 9с. cos( α )·cos( β ) = ½[cos( α + β ) + cos( α − β )]
Они полезны для изменения произведений тригонометрических функций. в суммы тригонометрических функций или наоборот.
Примеры
Мы закончим этот раздел семью примерами. Первые три примера показывают, как можно использовать тождества от 1 до 9 для доказательства новых тригонометрические тождества.Последние четыре примера показывают, как преобразовать тригонометрическое выражение в другое форма приводит к новым открытиям, которые ранее не были очевидны. Примеры приходят из электротехники, где переменный ток (переменный ток) имеет вид волна греха.
Тригонометрические тождества также используются для решения тригонометрических уравнений.
Эта тема рассматривается в следующем разделе.
| Как доказать тригонометрическое тождество:
|
Пример 1. Докажите тригонометрическое тождество
Решение: Выполните следующие шаги: Детали шагов:
- Используйте идентичность загара чтобы заменить функцию tan на sin/cos в левой части (слева).
- Сделайте то же самое с правой стороны. Также с загара и детской кроватки функции обратны, замените функцию кроватки с кос/син.
- Правая часть теперь представляет собой сложную дробь (дробь, которая содержит больше дробей). Соедините дроби в числитель и дроби в знаменателе.
- Использовать
правило инвертирования и умножения
делить дроби и упрощать.
Две стороны теперь идентичны, поэтому идентичность доказана.
Пример 2. В этом примере есть две новые функции:
- Есть несколько разных углов.
- Нам нужно сравнить две стороны, чтобы понять, что делать.
Докажите тригонометрическое тождество Решение: Выполните следующие шаги:
Детали шагов:
- Используйте взаимные тождества для замены sec и csc функции с cos и sin.
- Сравнивая две стороны, мы замечаем, что углы на правой стороне равны 4 х и х . У нас могут быть такие же углы на левой стороне, если мы заменим угол 5 х на сумму углов 4 х + х .
- Применить идентичность суммы углов к sin(4 x + x ) в числителе.
- Разбейте одну дробь на две. Две стороны теперь идентичны, поэтому идентичность доказана.
Пример 3.
Новая функция здесь заключается в том, что правая часть представляет собой дробь.
а левой нет. Нам придется сделать это дробью.
Докажите тригонометрическое тождество
Решение: Выполните следующие шаги: Детали шагов:
- Поскольку угол справа вдвое больше угла слева, замените угол 2 α на RHS с помощью тождество с двойным углом для греха.
- RHS имеет знаменатель sin( α ) + cos( α ). Чтобы получить тот же знаменатель на LHS, мы применяем НЛОО к нему; то есть мы умножаем и разделить LHS на ту же величину, а именно sin( α ) + cos( α ).
- Расширьте числитель.
- Используйте теорему Пифагора. Две стороны теперь идентичны, поэтому идентичность доказана.
Пример 4. Добавление синусоидальной и косинусной волн одной частоты производит другую волну той же частоты
(a) Докажите идентичность
где справа C и φ задаются формулой (b) Используйте тождество, чтобы выразить сумму двух синусоидальные волны,y 1 = 3 sin( θ ) и y 2 = 4 cos( θ ),как одиночная синусоидальная волна со сдвигом фазы.
Затем изобразите все три сигнала на графике.Часть решения (a): Потому что легче разбить углы, чем объединив их, мы будем работать над правой частью этого тождества и преобразовать его в левосторонний.
Прежде всего обратите внимание, что пара уравнений для C и φ описывает преобразование вектора из прямоугольные в полярные координаты. Ссылаясь на рисунок справа, вектор равен ( A , B ) в прямоугольных координатах и C ∠ φ в полярных координатах. Для использования на шаге 3 доказательства обратите внимание, что на диаграмме также показано, что
A = C cos( φ ) и B = C sin( φ ).Вот шаги доказательства:
Детали шагов:
- Использовать сумму углов тождества
чтобы грех разорвал углы θ и φ .
- Расшир.
- Используйте тот факт (упомянутый выше), что A = C cos( φ ) и B = C sin( φ ). Две стороны теперь идентичны так что тождество доказано.
Часть решения (b): Теперь мы будем использовать тождество, подтвержденное в части (a). чтобы выразить сумму y = 3 sin( θ ) + 4 cos( θ ) как одиночная синусоидальная волна со сдвигом фазы. Пусть А = 3 и В = 4 в тождестве. Это дает поэтому сумма сигналов y 1 = 3 sin( θ ) и y 2 = 4 cos( θ ) равно
y = 5 sin( θ + 53,13°)На графике справа показаны отдельные сигналы зеленым и синим цветом, а результирующая форма волны красного цвета. (Кликните сюда чтобы увидеть, как можно изобразить красную волну.
) Примечания:
- Значение этого примера в том, что он показывает, что сложение двух синусоидальных сигналов той же частоты приводит к другой синусоидальной форме сигнала на той же частоте, но с фазовым сдвигом. Сравните этот результат с результатом, найденным в следующем примере.
- Мы можем добавить любое количество противофазных синусоидальных или косинусных волн той же частоты
для создания одиночного греха со сдвигом фазы, выполнив следующие шаги:
- Разбейте каждый сигнал на sin и cos, применив идентификатор справа влево (в тренере по алгебре нажмите кнопку Разбить триггер ),
- Добавить все синусы и добавить все косинусы,
- Объединить оставшиеся sin и cos, применяя тождество слева направо (в тренере по алгебре нажмите кнопку Объединить триггер ).
- Одна из наиболее важных ситуаций, связанных с
противофазные волны в сети переменного тока (AC). Примером является
электроэнергетическая сеть континента. Каждый генератор, подключенный к
сеть должна выдавать напряжение, совпадающее по фазе с
все остальные генераторы в сети. В противном случае напряжения будут иметь тенденцию к отмене.
Пример 5. Волны с немного отличающимися частотами производят удары
(a) Докажите тождество
(b) Левую часть тождества можно рассматривать как сумму два синусоидальных сигнала с немного другими частотами. Графики сигналов y 1 и г 2 на одном графике и сравните их. (c) Теперь постройте их сумму на другом графике. Эта задача будет
очень трудно, если бы не тождество, доказанное в части (а).
Идентификацию можно использовать для преобразования суммы сигналов в один термин.
Покажите, что этот единственный член можно интерпретировать как синусоидальную волну с
медленно изменяющаяся амплитуда. Используйте сторону с одним термином идентичности, чтобы построить сюжет.
Часть решения (а): По сути, мы доказываем идентичность продукта (9b). Ключевая идея доказательства состоит в том, чтобы заметить, что углы 21 t и 19 t можно подумать о 20 т ± 1 т а потом ломать углы кроме суммы углов тождества.
Вот шаги доказательства:
Детали шагов:
- Правая сторона имеет углы t и 20 т . Чтобы получить те же углы на левой стороне, напишите 21 t как 20 т + 1 т и 19 т как 20 т − 1 т .
- Примените идентичность суммы углов для греха к обоим терминам.
Эта личность говорит
sin( α ± β ) = sin( α )·cos( β ) ± cos( α )·sin( β )
В этом случае пусть α = 20 t и β = 1 t . - Упрощение.
Часть решения (b): Вот график двух синусоидальные формы волны:
Обратите внимание, что форма волны с угловая скорость ω = 21 (синий) колеблется немного быстрее, чем форма волны с ω = 19 (зеленый). Синий имеет 10,5 циклов за указанное время, а зеленый — 9,5 циклов; на один цикл меньше. В результате в определенные моменты времени, например, в момент времени t = 0 и t = 3,14 волны 90 518 в фазе 90 519 (то есть пики вместе), а в другое время, например, в момент времени t = 1,57 волны 180° вне фазы , (то есть один находится на гребне, когда другой находится во впадине).
Часть решения (с): Было бы очень сложно добавить осциллограммы графически.
Все, что мы можем сказать наверняка, это то, что когда они находятся в фазе, они добавляют к
дают амплитуду 1, и когда они сдвинуты по фазе на 180°, они
отменить, чтобы получить амплитуду 0.
Что более информативно, так это построить график другой стороны тождества, а именно
y = cos( t ) · sin(20 t ).Этот график показан ниже красным цветом. Мы видим, что множитель cos( t ) в этом произведении играет роль медленно изменяющаяся амплитуда для быстро меняющееся колебание sin(20 t ). То есть у нас есть синусоидальная волна sin(20 t ), но в определенные моменты времени она имеет малая амплитуда, а в другое время она имеет большую амплитуду.
Чтобы построить этот график, мы сначала нарисуем один цикл кривой г = потому( т ) (и его негатив), оба показаны серым цветом. Это называется конверт и используется в качестве ориентира. Затем рисуем кривую y = sin(20 t ) внутри конверта. Рисуем 20 колебаний и растягиваем и сжимаем их до помещается внутрь конверта.
Примечания:
- В акустике периодическая конструктивная и деструктивная интерференция известна как ударов . Биты могут сильно раздражать, если они вызваны, скажем, сдвоенные двигатели самолета, работающие с немного разными скоростями. Но они может быть полезно, например, для проверки того, настроены ли две гитарные струны.
- При производстве электроэнергии каждый генератор, подключенный к электрическая сеть должна вырабатывать напряжение той же частоты, что и все остальные генераторы в сети. В противном случае напряжения будут иметь тенденцию периодически отменяться.
Пример 6. Электрическая мощность, рассеиваемая резистором
Обычно используются два типа электрического тока: постоянного тока (DC) и переменного тока (AC).
- Постоянный ток – это постоянный во времени ток. Обычно это
производится батареей. Для этого примера рассмотрим постоянный ток
0,7071 ампер:
i = 0,7071 ампер
- Переменный ток — это ток, который течет туда и обратно
в электрической цепи и описывается
синусоидальная функция времени.
Обычно он вырабатывается электрическим генератором. Для этого примера
будем использовать переменный ток амплитудой 1,0 ампер:
i = 1,0 sin( t ) ампер
Когда электрический ток проходит через резистор (такой как тостер или лампочка) он рассеивает тепло или световую энергию. Сила (т. е. скорость, с которой рассеивается энергия) определяется формулой
р = i 2 Р ,где p — мощность в ваттах, i — мощность ток в амперах, а R – это сопротивление резистора в омах.
Если ток изменяется со временем, то
мощность должна быть рассчитана в каждый момент времени по этой формуле.
Мы говорим, что формула дает мгновенная мощность .Задача: Показать, что постоянный ток 0,7071 ампер и переменный ток с амплитудой 1,0 ампер рассеивает одинаковую мощность в резисторе 1000 Ом, а именно 500 Вт, при усреднении по времени .
Решение: Основная идея показана на графиках ниже, где мы нанесли количество i 2 , соответствующее графики я показано выше:
Слева мы видим, что квадрат постоянного тока i = 0,7071 дает константу i 2 = 0,5. Когда это i 2 умножается на R = 1000 Ом это дает постоянную мощность p = 500 Вт.
Справа мы видим, что возведение в квадрат синусоидального тока i = 1,0 sin( t ) дает другую форму волны , i 2 = 1,0 sin 2 ( t ), со следующими характеристиками:
- Оба, когда и = + 1
а когда i = −1, то i 2 = 1, и всякий раз, когда i = 0, тогда i 2 = 0 также.
- Форма волны выглядит как косинусоидальная кривая, перевернутая вверх дном и приподнятая к средняя высота 0,5.
Вот доказательство того, что средняя высота i 2 кривая ½.
- Начните с: i = 1,0 sin( t ) и возведите в квадрат: i 2 = 1,0 sin 2 ( t ).
- Использовать тождество половинного угла (8a), измененное следующим образом: .
- Интерпретировать правую часть идентификатора. Это
синусоидальный сигнал плюс постоянная составляющая.
- Последний член представляет собой составляющую постоянного тока. Это вызывает i 2 , чтобы иметь среднее значение ½.
Примечания:
- Этот пример показал, что переменный ток амплитудой 1 ампер равен эффективен в качестве постоянного тока 0,7071 ампер при питании резистора такого как лампочка или тостер. Этот результат можно обобщить. Эффективное значение (также называемое среднеквадратичным значением) любого переменного тока находится путем умножения его амплитуды на 0,7071.
- В случаях, когда частота переменного тока высока, среднее значение
мощности важнее, чем мгновенная мощность. Пример — когда
через кухонный тостер проходит переменный ток частотой 60 Гц. Элемент тостера не имеет
время нагрева и остывания при изменении тока и просто остается на одном постоянном уровне
температура. Другим примером является тот же самый ток частотой 60 Гц, протекающий через люминесцентную лампу. легкий. В этом случае свет фактически включается и выключается при изменении тока.
но человеческий глаз не может реагировать достаточно быстро, чтобы увидеть это. В обеих ситуациях мы
больше интересует средняя мощность, чем мгновенная мощность.
Пример 7. Электроэнергия, вырабатываемая генератором
В электрической цепи, показанной справа, генератор производит энергию и нагрузку потребляет эту энергию. Мощность, потребляемая нагрузкой, равна мощности, вырабатываемой генератором. Это закон сохранения энергии.
Если нагрузкой является резистор, то в предыдущем примере показано, как рассчитать мощность, потребляемую резистором. В этом примере мы делаем два изменения:
- Изучаем мощность, которую производит генератор.
- Пусть нагрузка содержит катушку индуктивности или конденсатор.
Катушка индуктивности — это любое устройство, которое создает магнитное поле, когда ток
течет через него. Пример — электродвигатель.
Конденсатор — это любое устройство, которое создает электрическое поле, когда электрический заряд
хранится в нем. На самом деле каждая цепь имеет некоторую емкость и некоторую индуктивность.
либо случайно, либо намеренно.
Основным следствием нагрузки, имеющей индуктивность или емкость, является то, что переменный ток и напряжение, вырабатываемые генератором, могут быть не совпадает по фазе с до 90°.
Например, на рисунке показано напряжение не в фазе с током, с напряжение опережает ток на 60°.
р = i v ,где i — сила тока в амперах в этот момент, а v — сила тока в амперах. напряжение генератора в вольтах. Предположим, что генератор вырабатывает переменный ток
i = I 0 sin ( ωt )и что нагрузка такова, что напряжение не совпадает по фазе с током на угол φ .
(Фазовый сдвиг φ может быть положительным или отрицательным.)v = V 0 sin ( ωt+φ )Поскольку i и v меняются со временем, то же самое p . Но, как и в предыдущем примере, вместо мгновенной мощности нас интересует средняя мощность.
Задача: Найдите среднюю мощность, выдаваемую генератором.
Решение: Выполняем те же действия, что и в предыдущем примере. Подставляя данное i и v в формуле степени дает
Произведение тригонометрических функций можно превратить в сумму тригонометрических функции с использованием тождества (9a), которое говорит, что грех( α )·sin( β ) = ½ [cos( α — β ) — cos( α + β )]. Если мы сделаем замены α→ωt+φ а также β→ωt тогда тождество (9а) имеет видsin( ωt+φ )·sin( ωt ) = ½[cos( φ ) − cos(2 ωt+φ )]Подставляя это в формулу для p , получаем или расширение, Поскольку φ — константа (помните, что это фазовый сдвиг между v и i ) мгновенная мощность p снова равна синусоидальный сигнал с постоянной составляющей.
Постоянная составляющая дает среднюю мощность, Некоторые специальные грузы. - Идеальные резисторы: i и v находятся в фазе ( φ = 0), поэтому приведенная выше формула дает . С В 0 = I 0 R это также может быть написано как Это согласуется с результатом, который мы получили в предыдущем примере, что это было р среднее = ( I действующий ) 2 R где I действующий = 0,7071 I 0
- Идеальные катушки индуктивности: φ = +90 или и идеальных конденсатора: φ = −90 o .
В обоих случаях приведенная выше формула дает
р среднее = 0,
Как это может быть? Объясняется это тем, что катушки индуктивности и конденсаторы поглощают энергию в течение половины каждого цикла, поскольку они создают свои магнитные и электрические поля а затем отдать энергию обратно в генератор в другой половине цикла, когда поля разрушаются.
Обратите внимание, что в точках a и b мгновенная мощность фактически отрицательна. Причина в том, что в эти моменты i и v имеют противоположные знаки. и объяснение, как упоминалось выше, заключается в том, что мощность возвращается к генератору. Также обратите внимание, что если φ = 0, то красная кривая сводится к i 2 кривая в предыдущем примере.
| Упражнения для тренера по алгебре |
Если вы нашли эту страницу в веб-поиске, вы не увидите
Оглавление в рамке слева.
Щелкните здесь, чтобы отобразить его.
простых триггерных тождеств с формулой Эйлера — BetterExplained
Общеизвестно, что триггерные личности трудно запомнить: вот как выучить их, не теряя рассудка.
Исходя из теоремы Пифагора и подобных треугольников, мы можем найти связи между sin, cos, tan и friends (читайте статью о тригонах).
Можем ли мы пойти глубже? Может быть, мы можем связать синус с самим (син-цепцией). С точки зрения математики, мы ищем такие формулы (полная шпаргалка):
Вместо того, чтобы запоминать эти плохие мамочки, давайте научимся 92, а, б$. Это полезно при разложении на множители, упрощении уравнений и так далее.
Connections In Trig
Давайте переведем триггер на простой английский язык. Что это значит?
Помня, что синус — это «высота (в процентах от макс.)», это уравнение спрашивает: Если мы сложим два угла, какова будет их общая высота?
Быстрая догадка может состоять в том, чтобы объединить отдельные высоты:
Выглядит аккуратно, но не совсем правильно. Если мы продолжаем складывать углы, их высота увеличивается до максимума (100%), а затем начинает уменьшаться.
Связь между углом и высотой не может быть простым сложением.
Теперь вот странная вещь: я могу нарисовать, какой должна быть новая высота ( Вот она! ), но я не могу превратить свой рисунок в уравнение.
Или можно?
Рисование с помощью формулы Эйлера
Формула Эйлера позволяет нам создать круговой путь, используя комплексные числа:
Важно отметить, что умножение комплексных чисел приводит к вращению. Ага! Мы можем использовать формулу Эйлера, чтобы нарисовать нужное нам вращение: 92$, давайте умножим части:
Теперь мы говорим! Эта версия легко разделяет горизонтальное положение (реальная составляющая) и вертикальное положение (мнимая составляющая):
- Суммарная высота: $ \sin(a + b) = \sin(a)\cos(b) + \sin(b) \cos(a) $
- Суммарная ширина: $ \cos(a + b) = \cos(a)\cos(b) – \sin(a)\sin(b) $
Бум: два надоедливых триггерных тождества за одно вычисление. Неплохая сделка.
Понимание уравнения
Теперь, когда мы нашли уравнение, давайте вникнем в его значение. Когда мы складываем высоты, вот что происходит:
- Полная высота синего треугольника ($\sin(a)$) не может быть использована, так как красный треугольник не простирается так далеко. (Почему? Когда мы добавляем угол $b$, мы движемся под более крутым углом с той же гипотенузой. Мы увеличиваем расстояние по вертикали и теряем расстояние по горизонтали.) уменьшая его в $\cos(b)$ раз.
- Полную высоту красного треугольника ($\sin(b)$) также нельзя использовать, так как он находится под углом. Мы «переворачиваем» $\sin(b)$, уменьшая его в $\cos(a)$ раз.
Помните, что синус и косинус представляют собой проценты. В этом случае
или
Конечно, мы бы использовали как , чтобы получить полную высоту каждого треугольника. Но на диаграмме мы видим, что $a$ скользит назад, а $b$ скручивается, поэтому высота, которую мы получаем на самом деле , уменьшается. Думайте о каждом косинусе как о налоге на ваш рост, уменьшая сумму, которую вы забираете домой. ( Иметь рост 0,90? Это хорошо, Papa Cosine позволит вам сохранить 75%. Оплати остальное, сука! ).
Теперь, что происходит с малыми углами, такими как $\sin(.01 + .02)?$
Мы могли бы подключить и пыхтить это. Но я предполагаю, что результат примерно такой:
Почему? Моя мысленная диаграмма для малых углов такова:
Нет заметной разницы между идеальными высотами ($\sin(a)$ и $\sin(b)$) и «облагаемыми» версиями ($\sin(a )\cos(b)$ и $\sin(b)\cos(a)$).
- Для крошечных углов $\sin(a + b)$ является вертикальной линией. Он почти не теряет высоты из-за скольжения или скручивания частей.
- Для малых углов косинус (удерживаемый процент) близок к 100%. Мы сохраняем большую часть высоты, которая у нас есть.
- $\sin(x) \sim x$ — распространенное приближение для малых углов (часто используется в исчислении). По сути, он говорит, что $\sin(x)$ — это строка для короткого периода времени. Для малых углов $\sin(a + b) \sim \sin(a) + \sin(b) \sim a + b$.
Для косинуса у нас аналогичная диаграмма:
- На этот раз коэффициент преобразования совпадает (косинус с косинусом, синус с синусом).
- Полная ширина первого треугольника ($\cos(a)$) уменьшается, чтобы соответствовать ширине второго.
- Синусоида отрицательна, так как она отталкивает нас назад, уменьшая наш рост. Мы можем использовать подобные треугольники, чтобы извлечь этот кусок.
Обычно я не думаю о деталях на диаграмме, хотя приятно несколько раз посмотреть, как они работают. Если вам просто нужно триггерное тождество, прокрутите его алгебраически с помощью формулы Эйлера.
Зачем нам триггерные личности?
Хороший вопрос. Несколько причин:
1. Потому что надо (худшая причина). Многие триггерные классы заставляют вас запоминать эти идентификаторы, чтобы позже вы могли пройти тест (аргх). Вам не нужно запоминать их, вы можете выработать формулу примерно за минуту. Сохраните свое драгоценное место в мозгу для чего-то другого.
2. Теперь мы можем «разложить» триггерные функции на более простые части. Теперь мы можем разделить синус на более мелкие части, что полезно в исчислении.
Например, чтобы найти производную синуса, нам нужно:
и пусть $dx$ станет равным нулю. С этим сложно работать напрямую, но, используя формулу $\sin(a + b)$, мы имеем
Когда $dx$ стремится к нулю, $\cos(dx) = 1$ (нулевой угол равен полной ширине ), поэтому мы имеем:
И когда $dx$ стремится к нулю, $\sin(dx)$ и $dx$ становятся равными:
Подставляя это, мы получаем $\cos(a)$ как производная от $\sin(a)$. Фу! Работа с триггерными функциями не всегда проста, но, по крайней мере, выполнима.
3. Эффективен в вычислительном отношении. Если вы занимаетесь компьютерной графикой и часто вычисляете синус/косинус (скажем, для скалярных произведений), тригонометрические тождества являются полезными сокращениями. В прошлом эти тождества использовались аналогично таблицам журналов, чтобы упростить ручные вычисления.
4. Математика заключается в том, чтобы видеть связи. Поскольку тригонометрические функции являются производными от окружностей и экспоненциальных функций, кажется, что они появляются повсюду. Иногда вы упрощаете сценарий, переходя от триггера к экспонентам или наоборот.
5. Углубите свои знания о формуле Эйлера. Освойте формулу Эйлера, и вы освоите круги. И оттуда, мир! ( Примечание редактора: кажется, что мизинец Калида прикреплен ко рту. Мы работаем над этим. )
Видите ли, формула Эйлера позволяет нам нарисовать окружность и считать положение. Это восхитительно! Мы можем избежать большого количества болезненной геометрии с помощью нескольких умножений. Если вы занимаетесь продвинутой математикой, пусть Леонард Эйлер глубоко проникнет в вашу душу, это того стоит. Он хорошая компания.
На сегодня все. Счастливая математика.
Приложение: Ресурсы и расширенные формулы
Вы можете изменить параметры $a$ и $b$ для создания новых идентификаторов.
Формула вычитания: замените B на -B
Формула с двойным углом: замените B на
. формулу двойного угла и найти $\sin(a)$, который равен половине угла, используемого в $\sin(2a)$. Триг без слез (отличный ресурс и название) имеет больше деталей:
http://brownmath.com/twt/double.htm
Несколько других полезных ссылок:
- http://www.tc.umn.edu/~nydic001/docs/unpubs/Eulers_Formula_and_Trig_Identities.pdf
- https://www.wyzant.com/resources/lessons/math/trigonometry/eulers-formula-trig-identities
- http://www.ctralie.com/Teaching/Euler/
- http://kunklet.people.cofc.edu/MATh320/euler.pdf
Другие публикации из этой серии
- Как интуитивно выучить тригонометрию
- Легкие триггерные тождества с формулой Эйлера
- Интуиция по закону косинусов
- Интуиция для закона синусов
- Как выучить триггерные производные
Множественные тождества угловых косинусов и синусов
Мы знаем тождества для sin(2 x ) и cos(2 x ), но как насчет sin( nx ) и cos( nx )? Я нашел способ найти тождества для cos( nx ) и других свойств, связанных с sin(9я(х)\). Сначала мы находим тождества от cos(3 x ) к cos(10 x ) исключительно в терминах cos x , используя формулу суммы косинуса. Они перечислены здесь:
Таблица 1: Косинусные тождества для n = от 1 до 10
| cos(1 x ) | 1cos 1 x | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| cos(2 x ) | 2cos 2 x – 1 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| cos(3 x ) | 4 cos 3 90 518 x 90 519 – 3 cos 90 719 1 90 720 90 518 x 90 519 90 569 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| cos(4 x ) | 8cos 4 x – 8cos 2 x + 1 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| cos(5 x ) | 16cos 5 x – 20cos 3 x + 5cos 1 x | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| cos(6 x ) | 32cos 6 х – 48cos 4 x + 18cos 2 x – 1 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| cos(7 x ) | 64cos 7 x – 112cos 5 x + 56cos 3 x – 7cos 1 0 0 3 x | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| cos(8 x ) | 128cos 8 x – 256cos 6 x + 160cos 4 x – 32cos 2 0518 х + 1 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| cos(9 x ) | 256cos 9 x – 576cos 7 x + 432cos 5 x – 120cos 3 x + 9cos 1 x | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| cos(10 x ) | 512cos 10 x – 1280cos 8 x + 1120cos 6 x – 400cos 4 x + 50cos 9я(х)\). {n} 2i-1\): 2 8 18 32 50 72 …..
9{i_1} 2i_2-1\): 8 48 160 400 840 1568 2688 Продолжайте этот процесс, чтобы найти необходимое количество строк.
Столбец 1 содержит коэффициент членов высшей степени.
Столбец 2 должен начинаться с одного 0 и 1. Столбец 3 должен начинаться с трех нулей и 1. Столбец 4 должен начинаться с пяти нулей и 1 и так далее. Каждый раз, когда добавляется нечетное количество нулей и добавляется 1, потому что для cos(2 n x ), где 2 n — четное число, наш тригонометрический полином заканчивается положительной или отрицательной единицей. многочлена легко определить, потому что они чередуются. Наконец, приведенная выше таблица строк и столбцов представляет коэффициенты тригонометрического полинома для cos( нх ). (Строка n представляет коэффициенты тригонометрического полинома cos( n x ).) Все эти тождества можно подтвердить с помощью графической утилиты. Мы рассмотрели тождества только для cos( nx ). Тождества sin( nx ) необычны. Поскольку sin(2 x ) равно 2sin x · cos x , sin(2 n x ), где 2 n равно четному, не может быть выражен исключительно через sin x 9{2}х — 1 \) |
Обратите внимание, что если вы измените порядок и замените косинус на синус для нечетных степеней, мы сможем получить многоугольную идентичность функции синуса.
Должна быть закономерность для четных тождеств синуса, но я еще не исследовал ее. Мы можем вычесть косинус из четных тождеств синуса.
Последовательность Фибоначчи
Последовательность Фибоначчи имеет тенденцию появляться в самых странных местах, как это происходит в треугольнике Паскаля. Наш тригонометрический полином не является исключением для появления последовательности Фибоначчи. Давайте посмотрим на коэффициенты cos( nx ) поближе.
Сложите члены по диагонали слева направо, чтобы получить последовательность: 1, 1, 2, 3, 5, 8, 13, 21….
Узор из квадратов
При получении производные от тождеств и сложение их коэффициентов.
| Производная | Сумма коэффициентов | |
| cos(1 x ) | –1sin 1 x | –1 |
| cos(2 x ) | –4cos 1 x sin 1 x | –4 9056 |
| cos(3 x ) | –12cos 2 x sin 1 x + 3sin 1 x | –12 + 3 = –9 |
| cos(4 x ) | –32cos 3 x sin 1 x + 16cos 0 1 0518 x sin 1 x | –32 + 16 = –16 |
| cos(5 x ) | –80cos 4 x sin 1 x + 60cos 2 x sin 1 x – 5sin 1 x | –80 + 60 – 5 = –25 |
| cos(6 x ) | –192cos 5 x sin 1 x + 192cos 3 x sin 1 x – 36cos 1 x sin 1 x | 2 –192 + 193|
| cos(7 x ) | –448cos 6 x sin 1 x + 560cos 4 x sin 1 x – 168cos 2 x sin 1 x + 7sin 1 x | –448 + 560 – 168 + 7 = –49 |
| cos(8 x ) | –1024cos 7 x sin 1 x + 1536cos 5 x sin 1 x – 640cos 3 x sin 1 x + 64cos 1 x sin 1 x | –1024 + 1536 – 640 + 64 = –64 94 |
| cos(9 x ) | –2304cos 8 x sin 1 x + 4032cos 6 x sin 1 x – 2160cos 4 x sin 1 x + 360cos 2 x sin 1 x – 9sin 1 x | –2304 + 4032 – 2160 + 360 – 9 = –81 |
| cos(10 x ) | –5120cos 9 x sin 1 x + 10240cos 7 0 180519 sin 1 x – 6720cos 5 x sin 1 x + 1600cos 3 x sin 1 x – 100cos 1 x sin 1 х | –5120 + 10240 – 6720 + 1600 = 100 = –100 |
У нас есть шаблон квадратов при сложении коэффициентов производных.
Доказательство тождества общего тригонометрического полинома
Метод нахождения тождества cos( 9{2}x + 1 \)
Проверяет ли это? Давайте попробуем непонятное число… скажем, 0,7. Итак, мы имеем \(\cos(12\cdot 0,7) = \cos(8,4) \приблизительно -0,51\).
И результат по вольфраму: Результат подтверждает.
Объяснение урока: Формула Эйлера для тригонометрических тождеств
В этом объяснении мы научимся использовать формулу Эйлера формула для доказательства тригонометрических тождеств, таких как двойной угол и половинный угол.
Когда мы впервые узнаем о тригонометрических функциях и
экспоненциальные функции, они, кажется, имеют мало общего. Тригонометрический
функции периодические, а в случае синуса и косинуса ограничены сверху и снизу
1 и −1,
тогда как экспоненциальная функция непериодична и не имеет верхней границы. Однако,
Формула Эйлера показывает, что
благодаря введению комплексных чисел эти, казалось бы, не связанные друг с другом идеи,
на самом деле тесно связаны
и, во многих отношениях, как две стороны одной медали.
Определение: Формула Эйлера
Формула Эйлера утверждает, что для любого действительного числа 𝜃, 𝑒=𝜃+𝑖𝜃.косинус
Эту формулу также называют соотношением Эйлера.
Формула Эйлера применяется во многих областях математики, такие как функциональный анализ, дифференциальные уравнения и анализ Фурье. Кроме того, его приложения распространяться на физику и инженерии в таких разнообразных областях, как обработка сигналов, электротехника, и квантовая механика. В этом объяснении мы сосредоточимся на его приложениях в тригонометрии — в особенно производные тригонометрических тождеств.
В первом примере мы покажем, как мы можем вывести тригонометрические личности с помощью одного свойств экспоненциальной функции, а затем применяя Формула Эйлера.
Пример 1. Использование формулы Эйлера для получения тригонометрических тождеств
- Использование формулы Эйлера для выражения 𝑒 в
через синус и косинус.
- Учитывая, что 𝑒𝑒=1, что тригонометрический тождество может быть получено путем разложения экспонент в терминах тригонометрических функций?
Ответ
Часть 1
Переписывание 𝑒=𝑒,() мы можем применить формулу Эйлера, чтобы получить 𝑒=(−𝜃)+𝑖(−𝜃).cossin
Используя нечетные/четные тождества для синуса и косинуса, sinsincoscos(−𝜃)=−𝜃,(−𝜃)=𝜃, у нас есть 𝑒=𝜃−𝑖𝜃.cossin
Часть 2
Используя тождество Эйлера и наш ответ из части 1, мы можем переписать 𝑒𝑒=(𝜃+𝑖𝜃)(𝜃−𝑖𝜃).коссинкоссин
Раскрывая скобки, имеем 𝑒𝑒=𝜃−𝑖𝜃𝜃+𝑖𝜃𝜃−𝑖𝜃.coscossincossinsin
Наконец, мы можем упростить это, чтобы получить 𝑒𝑒=𝜃+𝜃.cossin
Следовательно, учитывая, что 𝑒𝑒=1,
мы доказали тригонометрическое тождество
синкос𝜃+𝜃≡1.
Как мы видели в последнем примере, используя свойства экспоненциальной функцию и применяя формулу Эйлера, мы можем вывести тригонометрические тождества. Следующий пример будет показать универсальность этого метода.
Пример 2. Тригонометрические тождества из формулы Эйлера
Какие тригонометрические тождества можно получить, применяя формулу Эйлера? идентичность 𝑒()?
Ответ
Первое, что нам нужно сделать, это применить одно из свойств экспоненты функция. Очевидным выбором здесь является мультипликативное свойство: 𝑒=𝑒𝑒.()
Теперь, когда у нас есть два разных, но равных выражения, мы можем применить формулу Эйлера к каждому, чтобы получить cossincossincossin(𝜃+𝜑)+𝑖(𝜃+𝜑)=(𝜃+𝑖𝜃)(𝜑+𝑖𝜑).
Раскрывая скобки справа, имеем cossincoscossinsincossinsin(𝜃+𝜑)+𝑖(𝜃+𝜑)=𝜃𝜑+𝑖𝜃𝜑+𝑖𝜃𝜑+𝑖𝜃𝜑.
Собирая одинаковые члены в правой части, находим, что
cossincoscossinsincossinsincos(𝜃+𝜑)+𝑖(𝜃+𝜑)=(𝜃𝜑−𝜃𝜑)+𝑖(𝜃𝜑+𝜃𝜑).
Наконец, мы можем приравнять действительную и мнимую части, чтобы получить следующие два тригонометрических тождества: coscoscossinsincossinsincos(𝜃+𝜑)=𝜃𝜑−𝜃𝜑,(𝜃+𝜑)=𝜃𝜑+𝜃𝜑.
Пример 3. Формулы двойного угла из формулы Эйлера
Используйте формулу Эйлера, чтобы вывести формулу для cos2𝜃 и sin2𝜃 с точки зрения греха𝜃 и потому𝜃.
Ответ
Прежде всего нам нужно рассмотреть, какое свойство экспоненциальной функции мы можем применить, чтобы получить два разных, но равных выражения. Так как мы ищем для тождеств в 2𝜃 имеет смысл рассматривать выражение 𝑒. На данный момент имеется два очевидный выбор свойств экспоненциальной функции для использования, либо мощность правило или мультипликативное правило. В обоих этих случаях мы получим один и тот же результат: 𝑒=𝑒.
Применяя формулу Эйлера к обоим этим выражениям, мы имеем
cossincossin2𝜃+𝑖2𝜃=(𝜃+𝑖𝜃).
Раскрывая скобки, имеем cossincoscossinsincossincossin2𝜃+𝑖2𝜃=𝜃+2𝑖𝜃𝜃+𝑖𝜃=𝜃−𝜃+2𝑖𝜃𝜃.
действительную и мнимую части можно приравнять получить два следующих тригонометрических тождества: coscossinsincossin2𝜃=𝜃−𝜃,2𝜃=2𝜃𝜃.
Используя аналогичный метод, мы можем вывести формулы множественных углов для грех𝑛𝜃 и cos𝑛𝜃 для больших значений 𝑛. Однако, чтобы упростить вывод, мы можем использовать биномиальную теорему.
Биномиальная теорема
Для любого целого числа 𝑛, (𝑎+𝑏) = 𝑎+𝐶𝑎𝑏+𝐶𝑎𝑏+⋯+𝐶𝑎𝑏+⋯+𝐶𝑎𝑏+𝑏, где 𝐶=𝑛𝑟𝑛−𝑟. Иногда, 𝐶 обозначается 𝑛𝑟 или 𝐶.
В следующем примере мы покажем, как мы можем использовать биномиальную теорему для упрощения вывод формул кратных углов для синуса и косинуса.
Пример 4. Формулы кратных углов из формулы Эйлера
- Используйте формулу Эйлера, чтобы вывести формулу для
cos6𝜃 и sin6𝜃
с точки зрения греха𝜃 и
потому что𝜃.
- Следовательно, выразите tan6𝜃 через загар𝜃.
Ответ
Часть 1
Используя свойства показательной функции, мы можем написать 𝑒=𝑒.
Используя формулу Эйлера, мы можем переписать это как cossincossin6𝜃+𝑖6𝜃=(𝜃+𝑖𝜃).
Используя биномиальную теорему, мы можем раскрыть скобки следующим образом: CossincossossossIncossOssOssInsInIn6𝜃+𝑖6𝜃 = 𝜃+𝐶𝜃 (𝑖𝜃)+𝐶𝜃𝑖𝜃+𝐶𝜃𝑖𝜃+𝐶𝜃𝑖𝜃+𝐶𝜃𝑖𝜃+𝑖𝜃.
Замена в долах 𝐶 и упрощая, имеем CossincoscossossIncossOssOssOssInsin6𝜃+𝑖6𝜃 = 𝜃+6𝑖𝜃𝜃+15𝑖𝜃𝜃+20𝑖𝜃𝜃+15𝑖𝜃𝜃+6𝑖𝜃𝜃+𝑖𝜃.
Оценка полномочий 𝑖, мы получаем CossincossossossIncossOssOssInsInIn6𝜃+𝑖6𝜃 = 𝜃+6𝑖𝜃𝜃 — 15𝜃𝜃 — 20𝑖𝜃𝜃+15𝜃𝜃+6𝑖𝜃𝜃 — 𝜃.
. Приравнивая реальные и мнимые части, мы приходим к следующему
два тождества:
coscoscossincossinsinsincossincossincossin6𝜃=𝜃−15𝜃𝜃+15𝜃𝜃−𝜃,6𝜃=6𝜃𝜃−20𝜃𝜃+6𝜃𝜃. 0005
Часть 2
Используя тождества из части 1, мы можем написать tansincoscossossossossossossInsInsin6𝜃 = 6𝜃6𝜃 = 6𝜃𝜃 — 20𝜃𝜃+6𝜃𝜃𝜃 — 15𝜃𝜃+15𝜃𝜃 — 𝜃.
, чтобы выразить это с точки зрения Tan𝜃, нам нужно разделить оба числитель и знаменатель через cos𝜃, что приводит к тантантантантантантан6𝜃=6𝜃−20𝜃+6𝜃1−15𝜃+15𝜃−𝜃.
Одно из интересных применений формулы Эйлера состоит в том, что мы можем вывести выражение для sin𝜃 и cos𝜃 с точки зрения 𝑒 и 𝑒. В первом примере мы видели, что мы можем выразить 𝑒 через синус и косинус как
| 𝑒=𝜃−𝑖𝜃.коссин | (1) |
Добавление этого к формуле Эйлера дает 𝑒+𝑒=𝜃+𝑖𝜃+𝜃−𝑖𝜃=2𝜃.cossincossincos
Отсюда, разделив на 2, получим следующую формулу косинуса: cos𝜃=12𝑒+𝑒.
Точно так же мы можем вывести формулу для синуса, рассматривая разницу
между уравнением (1)
и формула Эйлера выглядит следующим образом:
𝑒−𝑒=𝜃+𝑖𝜃−(𝜃−𝑖𝜃)=2𝑖𝜃. cossincossinsin
Разделив на 2𝑖, получим sin𝜃=12𝑖𝑒−𝑒.
Эти две формулы интересны сами по себе. Однако с целью этого объяснителя, мы продемонстрируем, как их можно использовать для получения далее тригонометрические тождества.
Пример 5. Формулы произведения на сумму из формулы Эйлера
- Выведите два тригонометрических воображаемые части 𝑒+𝑒()().
- Аналогично, какие два тригонометрических тождества можно получить, рассматривая действительная и мнимая части 𝑒−𝑒()()?
Ответ
Часть 1
Начнем с применения мультипликативного свойства экспонент к переписыванию 𝑒+𝑒=𝑒𝑒+𝑒𝑒.()()
𝑒+𝑒=𝑒𝑒+𝑒.()()
Используя определение косинуса в терминах экспоненциальной функции,
cos𝜑=12𝑒+𝑒,
мы можем переписать это как
𝑒+𝑒=2𝜑𝑒. ()()cos
Теперь мы можем использовать формулу Эйлера, чтобы переписать это как коссинкоссинкоскоссин(𝜃+𝜑)+𝑖(𝜃+𝜑)+(𝜃−𝜑)+𝑖(𝜃−𝜑)=2𝜑(𝜃+𝑖𝜃).
Сгруппировав действительную и мнимую части в обеих частях уравнения, мы получим ((𝜃+𝜑)+(𝜃−𝜑))+𝑖((𝜃+𝜑)+(𝜃−𝜑))=2𝜃𝜑+2𝑖𝜃𝜑.coscossinsincossossincos
Приравнивая действительную и мнимую части, получаем следующие два тригонометрические тождества: coscoscoscossincossinsin𝜃𝜑=12((𝜃+𝜑)+(𝜃−𝜑)),𝜃𝜑=12((𝜃+𝜑)+(𝜃−𝜑)).
Часть 2
Аналогичным методом можно рассмотреть выражение 𝑒−𝑒()(). Применение свойств экспоненциальная функция, мы можем переписать это как 𝑒−𝑒=𝑒𝑒−𝑒𝑒.()()
Выделив 𝑒, мы можем выразить это как 𝑒−𝑒=𝑒𝑒−𝑒.()()
Используя определение синуса в терминах показательной функции,
грех𝜑=12𝑖𝑒−𝑒,
мы можем переписать это как
𝑒−𝑒=2𝑖𝜑𝑒. ()()грех
Теперь мы можем применить формулу Эйлера к обеим частям уравнения, чтобы получить cossincossinsincossin(𝜃+𝜑)+𝑖(𝜃+𝜑)−((𝜃−𝜑)+𝑖(𝜃−𝜑))=2𝑖𝜑(𝜃+𝑖𝜃).
Сгруппировав действительную и мнимую части в обеих частях уравнения, мы получим ((𝜃+𝜑)−(𝜃−𝜑))+𝑖((𝜃+𝜑)−(𝜃−𝜑))=−2𝜃𝜑+2𝑖𝜃𝜑.coscossinsinsinsincossin
Приравнивая действительную и мнимую части, получаем следующие два тригонометрические тождества: sinsincoscossinsinsinsin𝜃𝜑=12((𝜃−𝜑)−(𝜃+𝜑)),𝜃𝜑=12((𝜃+𝜑)−(𝜃−𝜑)).
В этом последнем примере мы используем определения синуса и косинуса в терминах комплексная экспонента Функция для выражения степеней синуса и косинуса в терминах формул множественных углов.
Пример 6. Степени кратных углов из формулы Эйлера
- Используйте формулу Эйлера для выражения sincos𝜃𝜃
в виде 𝑎𝜃+𝑏3𝜃+𝑐5𝜃sinsinsin, где 𝑎, 𝑏,
и 𝑐 — константы, которые необходимо найти.
- Следовательно, найдите решения sinsin5𝜃−3𝜃=0 в интервале 0≤𝜃𝜋. Дай свой ответ в точной форме.
Ответ
Часть 1
Используя определения синуса и косинуса в терминах комплексной экспоненты, sincos𝜃=12𝑖𝑒−𝑒,𝜃=12𝑒+𝑒, мы можем переписать выражение как sincos𝜃𝜃=12𝑖𝑒−𝑒12𝑒+𝑒.
Следовательно, sincos𝜃𝜃=−132𝑖𝑒−𝑒𝑒+𝑒.
Используя биномиальную теорему, мы можем расширить каждый из наборов скобок следующим образом: sincos𝜃𝜃=−132𝑖𝑒−3𝑒+3𝑒−𝑒𝑒𝑒+2+.
Теперь мы можем раскрыть две круглые скобки, чтобы получить sincos𝜃𝜃 = −132𝑖𝑒 — 3𝑒+3𝑒- 𝑒+2𝑒−6𝑒+6𝑒−2𝑒+𝑒−3𝑒+3𝑒−𝑒.
Сбор терминов 𝑒 с 𝑒 условия приводят к синкос𝜃𝜃=−132𝑖𝑒−𝑒−𝑒−𝑒−2𝑒.
Следовательно,
Sincos𝜃𝜃 = 116212𝑖𝑒 — 𝑒+12𝑖𝑒 — 𝑒 — 12𝑖𝑒-𝑒 .
Теперь мы можем использовать определение синуса в терминах комплекса экспоненциально, чтобы переписать это как sincossinsinsin𝜃𝜃=116(2𝜃+3𝜃−5𝜃).
Часть 2
Используя наш ответ из части 1, мы видим, что sinsinsincos5𝜃−3𝜃=2𝜃−16𝜃𝜃.
Следовательно, нахождение решений sinsin5𝜃−3𝜃=0 эквивалентно нахождению решений 0=2𝜃−16𝜃𝜃.sinsincos
Мы можем факторизовать это уравнение следующим образом: 0=2𝜃1−8𝜃𝜃.sinsincos
Это имеет решения, если либо sin𝜃=0, либо 1−8𝜃𝜃=0sincos. Принимая во внимание первый случай, учитывая, что 0≤𝜃𝜋, грех𝜃=0 когда 𝜃=0.
Теперь мы можем рассмотреть случай, когда 1−8𝜃𝜃=0sincos. Используя формулу двойного угла для синуса, sinsincos2𝜃=2𝜃𝜃, мы можем переписать это как 1−22𝜃=0.sin
Следовательно,
грех2𝜃=12.
Извлекая квадратный корень из обеих частей уравнения, получаем sin2𝜃=±1√2.
Начиная с положительного квадратного корня для 𝜃 в диапазоне 0≤𝜃𝜋, sin2𝜃=1√2 когда 𝜃=𝜋8 или 3𝜋8. Точно так же для отрицательного квадратного корня sin2𝜃=−1√2, когда 𝜃=5𝜋8 или 7𝜋8.
Следовательно, решения sinsin5𝜃−3𝜃=0 для 𝜃 в диапазоне 0≤𝜃𝜋 являются 𝜃=0,𝜋8,3𝜋8,5𝜋8,7𝜋8.
Ключевые моменты
- Использование формулы Эйлера в сочетании со свойствами экспоненциальная функция, мы можем вывести много тригонометрических тождеств, таких как пифагорейское тождество, сумма и разность формулы и формулы множественных углов.
- Мы можем использовать теорему Эйлера, чтобы выразить синус и косинус
в терминах комплексной экспоненциальной функции как
sincos𝜃=12𝑖𝑒−𝑒,𝜃=12𝑒+𝑒.
Используя эти формулы, мы можем вывести дальнейшие тригонометрические тождества,
например, сумма к продукту
формулы и формулы для выражения степеней синуса и косинуса и произведения
два с точки зрения нескольких углов.
- Мы можем использовать тождества, полученные из формулы Эйлера, чтобы помогите нам упростить интегралы и решить тригонометрические уравнения.
7.4 Доказательство тригонометрических тождеств | mhf4utrigonometry
7.4 Доказательство тригонометрических тождеств
Полезные видео
Шаг 4) Сравните левую сторону с правой. Заметили, как они одинаковы? Поздравляем! Вы только что доказали тригонометрическое тождество!
Хотите верьте, хотите нет, но большую часть этой главы вы имели дело с тригонометрическими тождествами.
Тригонометрическое тождество записывается в виде уравнения и просто утверждает, что обе части уравнения эквивалентны.
Однако к тригонометрическому тождеству нельзя относиться так, как мы обычно относимся к уравнениям. Почему? Потому что на самом деле мы не пытаемся решить что-то вроде того, как мы обычно решаем уравнения, поэтому мы на самом деле не пытаемся изолировать переменную (никаких изолированных переменных и т. д.).
Кроме того, метод, при котором мы выполняем одни и те же операции с обеих сторон уравнения (например, умножение, деление, сложение и т. д.), не обязательно используется. Это потому, что нам это не обязательно действительно нужно (ничего не решая). В конечном счете, мы всего лишь пытаемся доказать, что обе части уравнения эквивалентны.
При доказательстве мы имеем дело с обеими частями уравнения отдельно, как если бы каждая из них была отдельным выражением; упрощая левую сторону, упрощая правую сторону и затем сравнивая их.
Итак, что мы делаем? Ну, большая часть тригонометрических тождеств упрощается. На самом деле это все так. Мы упрощаем обе стороны, пока они не будут выглядеть одинаково.
При доказательстве мы имеем дело с обеими частями уравнения по отдельности, как если бы каждая была отдельным выражением; упрощая левую сторону, упрощая правую сторону и затем сравнивая их.
В вашем распоряжении несколько инструментов для упрощения. Во-первых, все формулы двойного угла, формулы составного угла и обратные тригонометрические отношения могут быть заменены (или исключены) при упрощении. Другие тождества включают частные тождества и пифагорейские тождества. Все это указано ниже.
Кроме того, вы всегда можете расшириться, что может привести к тому, что вы узнаете другую личность или выработаете другие стратегии.
ВАЖНОЕ ПРИМЕЧАНИЕ: слово идентичность используется для описания эквивалентности двух вещей. Тригонометрические тождества констатируют эквивалентность нескольких других тождеств (например, двойного угла, пифагорейского тождества и т. д.), но на самом деле констатируют их эквивалентность.
ПОЛЕЗНЫЕ СОВЕТЫ
Иногда предлагается сначала начать с более запутанной и сложной стороны. Вы можете разработать другую технику, сохраняя ее более аккуратной.
Если это покажется вам полезным, вы можете полностью переписать обе части уравнения в личности, которые вы заметите.
По возможности используйте факторинг и общий знаменатель.
Превратите единицы в то, что вы хотите! Заманчиво сразу использовать тождество Пифагора, но вы можете преобразовать 1 во что угодно, представив его в виде эквивалентной дроби (т.
е. cos x cos x).Если знаменатель двучленный, попробуйте умножить на сопряженные числа! Поскольку сопряжение может быть установлено равным единице, все, что вы на самом деле делаете, это умножение на единицу. Но так как сопряжение является обратным знаком, оно позволяет исключить некоторые термины. Нажмите на ссылку ниже, чтобы узнать, как использовать технику умножения на сопряжение.
При решении тригонометрических тождеств может возникнуть путаница. Чтобы облегчить себе задачу, упростите на клочке бумаги или сбоку и подпишите обратно. Это поможет сделать вещи более аккуратными, и вы сможете легче организовать свои мысли.
Попробуйте преобразовать все в виде синуса или косинуса. Вы обнаружите, что относительно легче определить другие личности и упростить.
Щелкните здесь
Зачем нам утруждать себя всеми этими трудностями только для того, чтобы доказать, что две вещи эквивалентны? Ну, это потому, что иногда тригонометрические тождества не всегда верны.
По сути, с помощью тригонометрических тождеств мы пытаемся доказать их истинность. Другие тождества, такие как частные тождества и составной угол, подтвердились, но как насчет их случайной комбинации?
Это вам предстоит доказать. Ниже приведен пример, который продемонстрирует, как применять методы и приемы, которые мы обсуждали ранее.
Примеры вопросов
Уровень 1/2
Уровень 3
3. Объясните, почему мы не решаем тригонометрические тождества, как мы обычно решаем уравнения, описывая определение тождества.
Контрольные ответы
Уровень 4
4. Составьте схему, которая суммирует все, что вы узнали о тригонометрических тождествах. Включите примеры, приемы, приемы и пошаговые описания того, как доказывать тригонометрические тождества.
Наверх
Другие полезные ссылки
Purple Math
Дополнительная практика
Ключевые понятия/советы
ЩЕЛКНИТЕ ДЛЯ СОВЕТОВ
Вы также можете проверить тождественность, нарисовав каждую сторону отдельно и показав, что они эквивалентны.