Формула уравнение касательной: Уравнение касательной к графику функции — урок. Алгебра, 10 класс.

как составить и решить задачу с его помощью

Задания, связанные с нахождением уравнения касательной, часто вызывают трудности у учеников старших классов. Подобные задачи встречаются и на ЕГЭ по математике. Они могут иметь различную формулировку. К примеру, школьникам предлагают определить тангенс угла наклона касательной или написать, чему будет равна производная в какой-либо конкретной точке. Для решения всех подобных заданий нужно придерживаться простой последовательности действий, которая будет подробно рассмотрена ниже.

Содержание:

• Как составлять уравнение касательной в заданной точке
  • Алгоритм написания уравнения
• Задачи на написание уравнения касательной
• Видео

Как составлять уравнение касательной в заданной точке

При написании уравнения будем использовать следующие обозначения:

• x0 — заданная в условии точка, принадлежащая функции, через которую проводится касательная;
• f(x) — исходная функция;
• f'(x) — производная от функции;
• k — угловой коэффициент.

Перед написанием уравнения следует проверить существование функции в заданной точке касания, является ли она непрерывной и дифференцируемой в ней. Например, гипербола f(x) = 14 / (x + 11) прерывается в x = –11, а g(x) = |8x + 9|, хоть и является непрерывной на всей числовой прямой, в x = 0 не является дифференцируемой.

Алгоритм написания уравнения

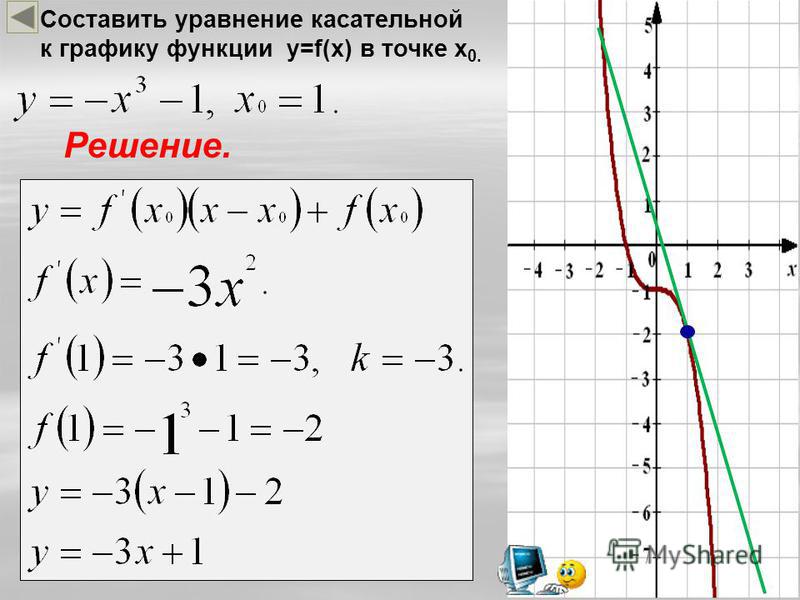
После проверки можно приступать к нахождению уравнения. Разберем несложную задачу, в которой нужно найти касательную к f(x) = 3x³ – 6x² + 2x – 1 в x0 = 1. Для этого будем следовать данному алгоритму:

1. Вычислим f(x0). Для этого просто подставим значение 1 в функцию: f(1) = 3·1³ – 6·1² + 2·1 – 1 = –2.
2. Теперь необходимо записать производную: f'(x) = 9x² – 12x + 2.
3. Подсчитаем значение производной в x0: f'(1) = 9·1² – 12·1 + 2 = –1.
4. Необходимо подставить все найденные выше значения в общую формулу: y = f(x0) + f'(x0)(x – x0). После этого получаем: y = –2 + (–1)·(x – 1) = –x – 1.

В результате приобретает вид: y = –x – 1. Изобразим графики исходной функции и касательной в x0 = 1.

Рассмотрим уравнение более подробно. Как уже было сказано ранее, в общем виде оно имеет вид y = kx + b. В задачах, встречающихся на ЕГЭ, часто нужно рассчитать угловой коэффициент, тангенс угла наклона или же определить, чему будет равна производная в точке касания. Их роль выполняет k — коэффициент, находящийся перед x. Для полученного в примере уравнения k = –1.

Рассмотрим некоторые виды заданий, для решения которых необходимо уметь выписывать касательную к функции в конкретной точке.

Задачи на написание уравнения касательной

Различают несколько типов задач на уравнение касательной в определенной точке. Самый первый и простой тип уже был разобран при написании алгоритма решения подобных заданий. В них необходимо выписать уравнение или коэффициент k. Условием определяется исходная функция и точка касания.

Ко второму типу относятся задачи, в которых известно k, но неизвестно, где происходит касание. Как правило, в их формулировках указывается, что касательная будет проходить параллельна по отношению к оси абсцисс (тогда подразумеваем k = 0), или к какой-либо линейной функции (тогда угловой коэффициент касательной совпадает с коэффициентом k линейной функции). Рассмотрим, как нужно рассуждать, решая такие задания.

Записать уравнение касательной для параболы f(x) = 2x² – 3, если известно, что она будет параллельна y = –8x + 2.

• Поскольку касательная параллельна заданной прямой, можно сделать вывод, что угол их наклона совпадает. Запишем, что k = f'(x0) = –8.
• Возьмем от функции производную: f'(x) = 4x.
• Определим точку касания. Для этого приравняем производную к числу k: 4x = –8. Решим уравнение и найдем x0 = –2.
• Вычислим, чему будет равна функция в этой точке: f(–2) = 2·(–2)² – 3 = –11.
• Теперь мы располагаем всеми необходимыми данными для записи уравнения. Подставим их в формулу для нахождения уравнения: y = –11 + (–8)(x – (–2)) = –8x – 27.

В третьем типе заданий в условии задается функция и точка, которая не принадлежит ее графику, но лежит на ее касательной.

Написать уравнение касательной к кубической функции g(x) = 2x³, если известно, что она проходит через точку Q(0;–0,5).

• Поскольку точка принадлежит касательной, подставим ее координаты в общий вид уравнения: –0,5 = g(x0) + g'(x0)(– x0).
• Запишем производную: g'(x) = 6x².
• Очевидно, что g(x0) = 2·(x0)³, a g'(x0) = 6·(x0)². Подставим в общий вид: –0,5 = 2·.(x0)³ + 6·(x0)²(– x0). Решим уравнение, и из него определим абсциссу точки касания: x0 = 0,5.
• Подсчитываем значение функции в точке: g(0,5) = 2·0,5³ = 0,25.
• Вычисляем производную в точке касания: g'(0,5) = 6·0,5² =1,5.
• В заключение записываем готовое уравнение, подставив в него рассчитанные данные: y = 0,25 + 1,5(x – 0,5) = 1,5x – 0,5.

Часто встречаются различные графические задачи, не требующие подробного решения. Пример такого задания приведен ниже.

Показан график функции, которая определена на участке [–7;7]. Необходимо выяснить, сколько точек существует на промежутке [–4;6], в которых касательная к изображенной функции будет параллельна y = –66.

Будем рассуждать так. Прямая y = –66 проходит параллельно оси абсцисс. Это значит, что ее угловой коэффициент, а также значение производной в точке, где произошло касание, и угол наклона касательной будут нулевыми. Это возможно лишь в точках экстремума. Подсчитать их количество не составит труда: 4 максимума и 3 минимума, т. е. 7 точек. Однако –5 не входит в промежуток, заданный условием. Поэтому окончательным ответом будет число 6.

Видео

Закрепить это тему вам поможет видео.

Уравнение касательной по двум точкам. Касательная к графику функции в точке

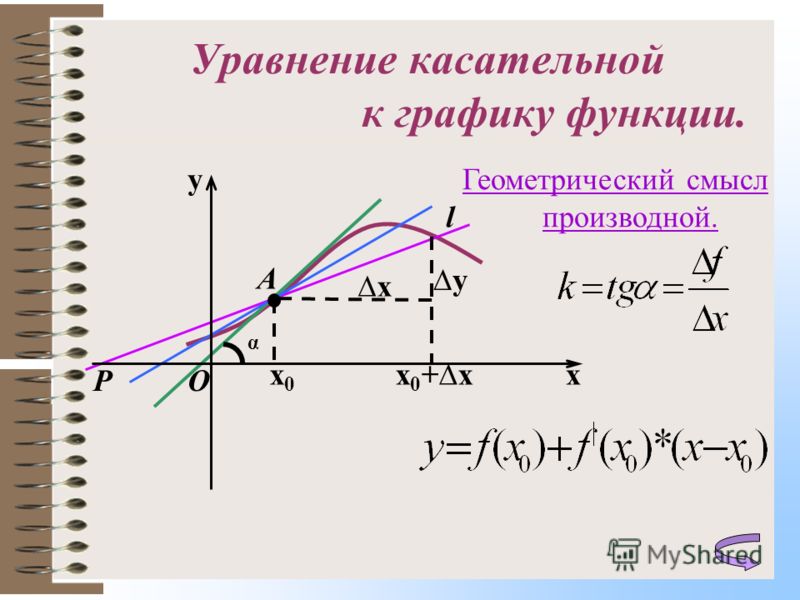
Касательная – это прямая, проходящая через точку кривой и совпадающая с ней в этой точке с точностью до первого порядка (рис. 1).

Другое определение : это предельное положение секущей при Δx →0.

Пояснение : Возьмем прямую, пересекающую кривую в двух точках:

А и b (см.рисунок). Это секущая. Будем поворачивать ее по часовой стрелке до тех пор, пока она не обретет только одну общую точку с кривой. Так мы получим касательную.

Строгое определение касательной:

Касательная к графику функции f , дифференцируемой в точке x о , — это прямая, проходящая через точку (x о ; f (x о )) и имеющая угловой коэффициент f ′(x о ).

Угловой коэффициент имеет прямая вида y = kx + b . Коэффициент k и является угловым коэффициентом этой прямой.

Угловой коэффициент равен тангенсу острого угла, образуемого этой прямой с осью абсцисс:

k = tg α

Здесь угол α – это угол между прямой y = kx + b и положительным (то есть против часовой стрелки) направлением оси абсцисс.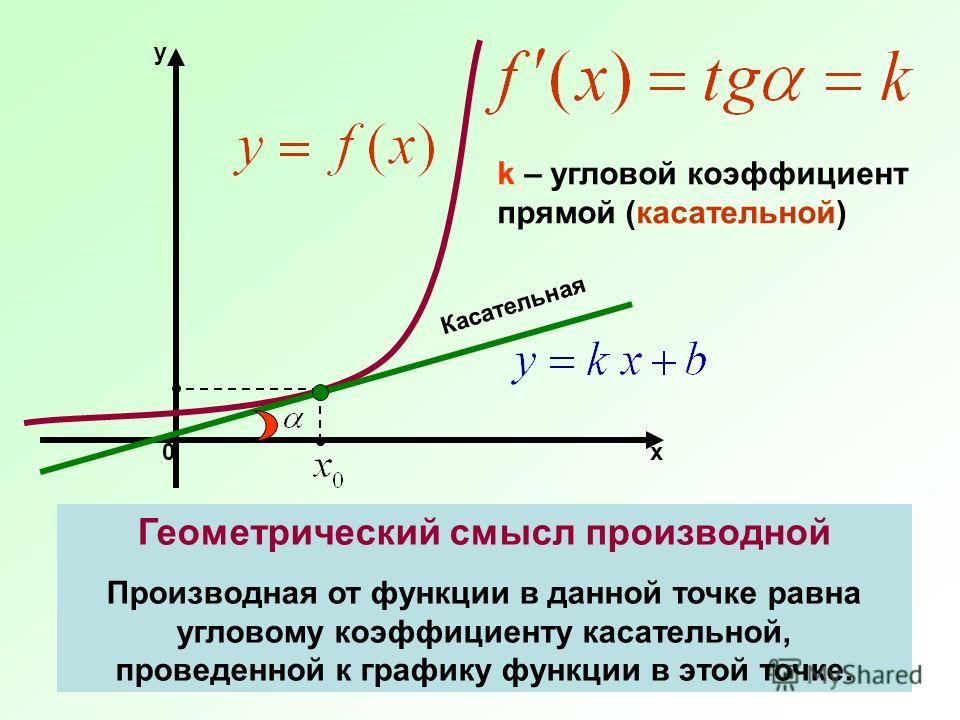

Он называется углом наклона прямой (рис.1 и 2).

Если угол наклона прямой y = kx + b острый, то угловой коэффициент является положительным числом. График возрастает (рис.1).

Если угол наклона прямой y = kx + b тупой, то угловой коэффициент является отрицательным числом. График убывает (рис.2).

Если прямая параллельна оси абсцисс, то угол наклона прямой равен нулю. В этом случае угловой коэффициент прямой тоже равен нулю (так как тангенс нуля есть ноль). Уравнение прямой будет иметь вид y = b (рис.3).

Если угол наклона прямой равен 90º (π/2), то есть она перпендикулярна оси абсцисс, то прямая задается равенством x = c , где c – некоторое действительное число (рис.4).

Уравнение касательной к графику функции y = f (

x ) в точке x о :

Пример : Найдем уравнение касательной к графику функции f (x ) = x 3 – 2x 2 + 1 в точке с абсциссой 2.

Решение .

Следуем алгоритму.

1) Точка касания x о равна 2. Вычислим f (x о ):

f (x о ) = f (2) = 2 3 – 2 ∙ 2 2 + 1 = 8 – 8 + 1 = 1

2) Находим f ′(x ). Для этого применяем формулы дифференцирования, изложенные в предыдущем разделе. Согласно этим формулам, х 2 = 2х , а х 3 = 3х 2 . Значит:

f ′(x ) = 3х 2 – 2 ∙ 2х = 3х 2 – 4х .

Теперь, используя полученное значение f ′(x ), вычислим f ′(x о ):

f ′(x о ) = f ′(2) = 3 ∙ 2 2 – 4 ∙ 2 = 12 – 8 = 4.

3) Итак, у нас есть все необходимые данные: x о = 2, f (x о ) = 1, f ′(x о ) = 4. Подставляем эти числа в уравнение касательной и находим окончательное решение:

у = f (x о ) + f ′(x о ) (x – x о ) = 1 + 4 ∙ (х – 2) = 1 + 4х – 8 = –7 + 4х = 4х – 7.

Ответ : у = 4х – 7.

Инструкция

Определяем угловой коэффициент касательной к кривой в точке М.
Кривая, представляющая собой график функции y = f(x), непрерывна в некоторой окрестности точки М (включая саму точку М).

Если значения f‘(x0) не существует, то либо касательной нет, либо она проходит вертикально. Ввиду этого, наличие производной функции в точке х0 обусловлено существованием невертикальной касательной, соприкасающейся с графиком функции в точке (х0, f(х0)). В этом случае угловой коэффициент касательной равен будет f»(х0). Таким образом, становится ясен геометрический смысл производной – расчет углового коэффициента касательной.

Найдите значение абсциссы точки касания, которую обозначаются буквой «а». Если она совпадает с заданной точкой касательной, то «а» будет ее х-координате. Определите значение функции f(a), подставив в уравнение функции величину абсциссы.

Определите первую производную уравнения функции f’(x) и подставьте в него значение точки «а».

Возьмите общее уравнение касательной, которое определяется как y = f(a) = f (a)(x – a), и подставьте в него найденные значения a, f(a), f «(a). В результате будет найдено решение графика и касательной.

Решите задачу иным способом, если заданная точка касательной не совпала с точкой касания. В этом случае необходимо в уравнение касательной вместо цифр подставить «а». После этого вместо букв «х» и «у» подставьте значение координат заданной точки. Решите получившееся уравнение, в котором «а» является неизвестной. Поставьте полученное значение в уравнение касательной.

Составьте уравнение касательной с буквой «а», если в условии задачи задано уравнение функции и уравнение параллельной линии относительно искомой касательной. После этого необходимо производную функции , чтобы координату у точки «а». Подставьте соответствующее значение в уравнение касательной и решите функцию.

Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.

Сбор и использование персональной информации

Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.

От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.

Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.

Какую персональную информацию мы собираем:

• Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.

Как мы используем вашу персональную информацию:

• Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
• Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
• Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
• Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.

Раскрытие информации третьим лицам

Мы не раскрываем полученную от Вас информацию третьим лицам.

Исключения:

• В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
• В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.

Защита персональной информации

Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.

Соблюдение вашей конфиденциальности на уровне компании

Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.

Касательная — это прямая , которая касается графика функции в одной точке и все точки которой находятся на наименьшем расстоянии от графика функции. Поэтому касательная проходит касательно графика функции под определённым углом и не могут проходить через точку касания несколько касательных под разными углами.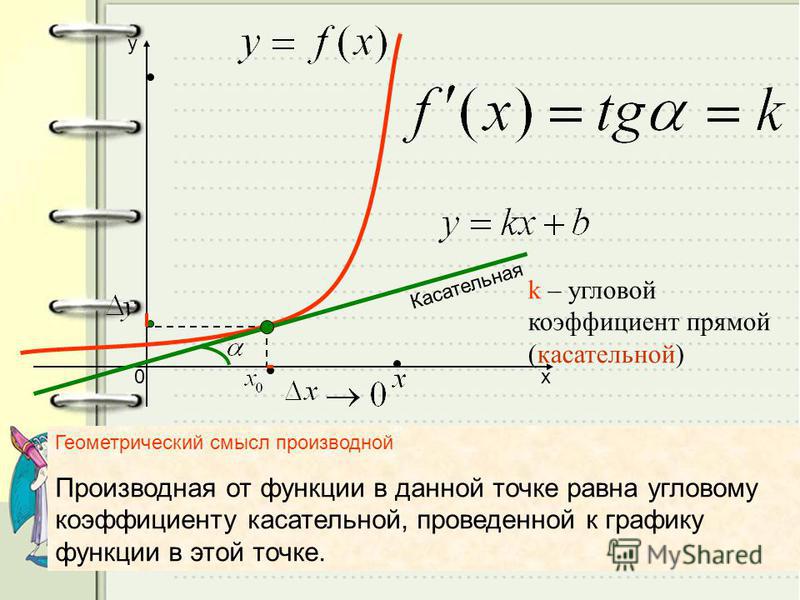 Уравнения касательной и уравнения нормали к графику функции составляются с помощью производной.

Уравнение касательной выводится из уравнения прямой .

Выведем уравнение касательной, а затем — уравнение нормали к графику функции.

y = kx + b .

В нём k — угловой коэффициент.

Отсюда получаем следующую запись:

y — y 0 = k (x — x 0 ) .

Значение производной f «(x 0 ) функции y = f (x ) в точке x 0 равно угловому коэффициенту k = tgφ касательной к графику функции, проведённой через точку M 0 (x 0 , y 0 ) , где y 0 = f (x 0 ) . В этом состоит геометрический смысл производной .

Таким образом, можем заменить k на f «(x 0 ) и получить следующее уравнение касательной к графику функции :

y — y 0 = f «(x 0 )(x — x 0 ) .

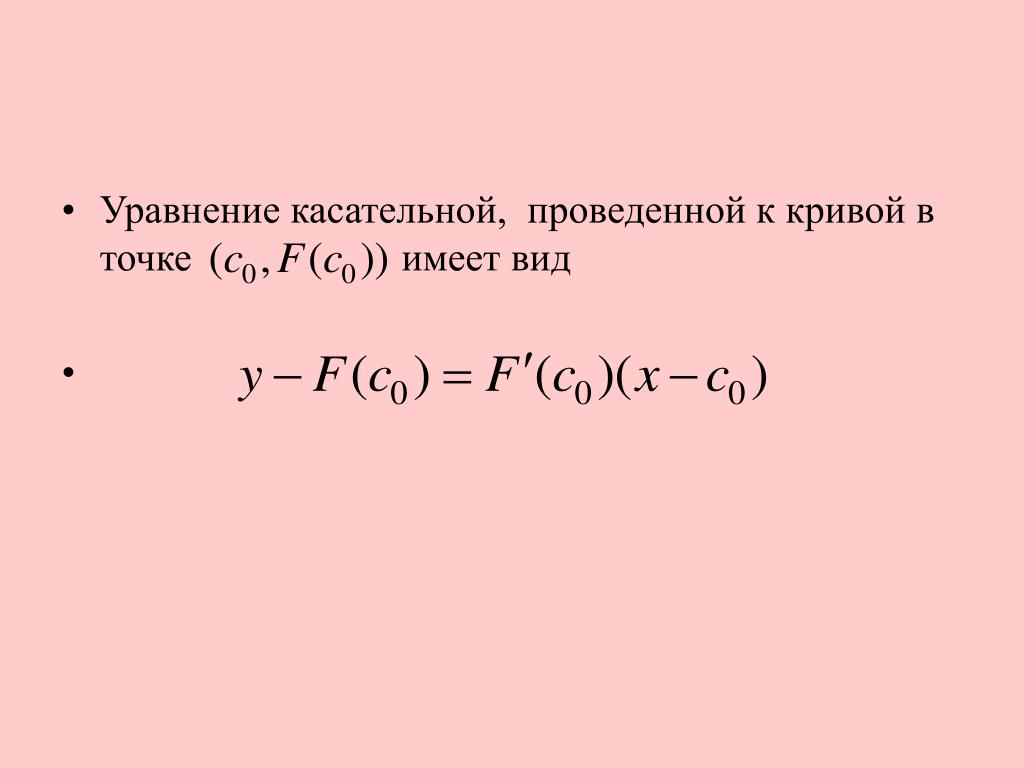
В задачах на составление уравнения касательной к графику функции (а мы уже скоро к ним перейдём) требуется привести получившееся по вышеприведённой формуле уравнение к уравнению прямой в общем виде . Для этого нужно все буквы и числа перенести в левую часть уравнения, а в правой части оставить ноль.

Теперь об уравнении нормали. Нормаль — это прямая, проходящая через точку касания к графику функции перпендикулярно касательной. Уравнение нормали :

(x — x 0 ) + f «(x 0 )(y — y 0 ) = 0

Для разминки первый же пример прелагается решить самостоятельно, а затем посмотреть решение. Есть все основания надеяться, что для наших читателей эта задача не будет «холодным душем».

Пример 0. Составить уравнение касательной и уравнение нормали к графику функции в точке M (1, 1) .

Пример 1. Составить уравнение касательной и уравнение нормали к графику функции , если абсцисса точки касания .

Найдём производную функции:

Теперь у нас есть всё, что требуется подставить в приведённую в теоретической справке запись, чтобы получить уравнение касательной. Получаем

В этом примере нам повезло: угловой коэффициент оказался равным нулю, поэтому отдельно приводить уравнение к общему виду не понадобилось. Теперь можем составить и уравнение нормали:

На рисунке ниже: график функции бордового цвета, касательная зелёного цвета, нормаль оранжевого цвета.

Следующий пример — тоже не сложный: функция, как и в предыдущем, также представляет собой многочлен, но угловой коэффициен не будет равен нулю, поэтому добавится ещё один шаг — приведение уравнения к общему виду.

Пример 2.

Решение. Найдём ординату точки касания:

Найдём производную функции:

.

Найдём значение производной в точке касания, то есть угловой коэффициент касательной:

Подставляем все полученные данные в «формулу-болванку» и получаем уравнение касательной:

Приводим уравнение к общему виду (все буквы и числа, отличные от нуля, собираем в левой части, а в правой оставляем ноль):

Составляем уравнение нормали:

Пример 3. Составить уравнение касательной и уравнение нормали к графику функции , если абсцисса точки касания .

Решение. Найдём ординату точки касания:

Найдём производную функции:

.

Найдём значение производной в точке касания, то есть угловой коэффициент касательной:

.

Находим уравнение касательной:

Перед тем, как привести уравнение к общему виду, нужно его немного «причесать»: умножить почленно на 4. Делаем это и приводим уравнение к общему виду:

Составляем уравнение нормали:

Пример 4. Составить уравнение касательной и уравнение нормали к графику функции , если абсцисса точки касания .

Решение. Найдём ординату точки касания:

.

Найдём производную функции:

Найдём значение производной в точке касания, то есть угловой коэффициент касательной:

.

Получаем уравнение касательной:

Приводим уравнение к общему виду:

Составляем уравнение нормали:

Распространённая ошибка при составлении уравнений касательной и нормали — не заметить, что функция, данная в примере, — сложная и вычислять её производную как производную простой функции. Следующие примеры — уже со сложными функциями (соответствующий урок откроется в новом окне).

Пример 5. Составить уравнение касательной и уравнение нормали к графику функции , если абсцисса точки касания .

Решение. Найдём ординату точки касания:

Внимание! Данная функция — сложная, так как аргумент тангенса (2x ) сам является функцией. Поэтому найдём производную функции как производную сложной функции.

Статья дает подробное разъяснение определений, геометрического смысла производной с графическими обозначениями. Будет рассмотрено уравнение касательной прямой с приведением примеров, найдено уравнения касательной к кривым 2 порядка.

Yandex.RTB R-A-339285-1 Определение 1

Угол наклона прямой y = k x + b называется угол α , который отсчитывается от положительного направления оси о х к прямой y = k x + b в положительном направлении.

На рисунке направление о х обозначается при помощи зеленой стрелки и в виде зеленой дуги, а угол наклона при помощи красной дуги.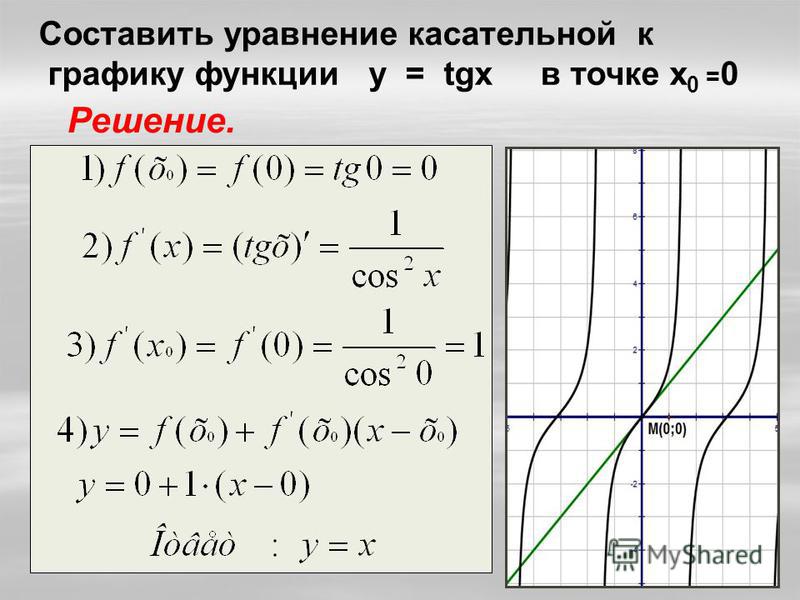 Синяя линия относится к прямой.

Определение 2

Угловой коэффициент прямой y = k x + b называют числовым коэффициентом k .

Угловой коэффициент равняется тангенсу наклона прямой, иначе говоря k = t g α .

• Угол наклона прямой равняется 0 только при параллельности о х и угловом коэффициенте, равному нулю, потому как тангенс нуля равен 0 . Значит, вид уравнения будет y = b .
• Если угол наклона прямой y = k x + b острый, тогда выполняются условия 0 0 , причем имеется возрастание графика.
• Если α = π 2 , тогда расположение прямой перпендикулярно о х. Равенство задается при помощи равенства x = c со значением с, являющимся действительным числом.
• Если угол наклона прямой y = k x + b тупой, то соответствует условиям π 2

Определение 3

Секущей называют прямую, которая проходит через 2 точки функции f (x) . Иначе говоря, секущая – это прямая, которая проводится через любые две точки графика заданной функции.

По рисунку видно, что А В является секущей, а f (x) – черная кривая, α — красная дуга, означающая угол наклона секущей.

Когда угловой коэффициент прямой равняется тангенсу угла наклона, то видно, что тангенс из прямоугольного треугольника А В С можно найти по отношению противолежащего катета к прилежащему.

Определение 4

Получаем формулу для нахождения секущей вида:

k = t g α = B C A C = f (x B) — f x A x B — x A , где абсциссами точек А и В являются значения x A , x B , а f (x A) , f (x B) — это значения функции в этих точках.

Очевидно, что угловой коэффициент секущей определен при помощи равенства k = f (x B) — f (x A) x B — x A или k = f (x A) — f (x B) x A — x B , причем уравнение необходимо записать как y = f (x B) — f (x A) x B — x A · x — x A + f (x A) или
y = f (x A) — f (x B) x A — x B · x — x B + f (x B) .

Секущая делит график визуально на 3 части: слева от точки А, от А до В, справа от В. На располагаемом ниже рисунке видно, что имеются три секущие, которые считаются совпадающими, то есть задаются при помощи аналогичного уравнения.

По определению видно, что прямая и ее секущая в данном случае совпадают.

Секущая может множественно раз пересекать график заданной функции. Если имеется уравнение вида у = 0 для секущей, тогда количество точек пересечения с синусоидой бесконечно.

Определение 5

Касательная к графику функции f (x) в точке x 0 ; f (x 0) называется прямая, проходящая через заданную точку x 0 ; f (x 0) , с наличием отрезка, который имеет множество значений х, близких к x 0 .

Пример 1

Рассмотрим подробно на ниже приведенном примере. Тогда видно, что прямая, заданная функцией y = x + 1 , считается касательной к y = 2 x в точке с координатами (1 ; 2) . Для наглядности, необходимо рассмотреть графики с приближенными к (1 ; 2) значениями. Функция y = 2 x обозначена черным цветом, синяя линия – касательная, красная точка – точка пересечения.

Очевидно, что y = 2 x сливается с прямой у = х + 1 .

Для определения касательной следует рассмотреть поведение касательной А В при бесконечном приближении точки В к точке А. Для наглядности приведем рисунок.

Секущая А В, обозначенная при помощи синей линии, стремится к положению самой касательной, а угол наклона секущей α начнет стремиться к углу наклона самой касательной α x .

Определение 6

Касательной к графику функции y = f (x) в точке А считается предельное положение секущей А В при В стремящейся к А, то есть B → A .

Теперь перейдем к рассмотрению геометрического смысла производной функции в точке.

Перейдем к рассмотрению секущей А В для функции f (x) , где А и В с координатами x 0 , f (x 0) и x 0 + ∆ x , f (x 0 + ∆ x) , а ∆ x обозначаем как приращение аргумента. Теперь функция примет вид ∆ y = ∆ f (x) = f (x 0 + ∆ x) — f (∆ x) . Для наглядности приведем в пример рисунок.

Рассмотрим полученный прямоугольный треугольник А В С. Используем определение тангенса для решения, то есть получим отношение ∆ y ∆ x = t g α . Из определения касательной следует, что lim ∆ x → 0 ∆ y ∆ x = t g α x . По правилу производной в точке имеем, что производную f (x) в точке x 0 называют пределом отношений приращения функции к приращению аргумента, где ∆ x → 0 , тогда обозначим как f (x 0) = lim ∆ x → 0 ∆ y ∆ x .

Отсюда следует, что f » (x 0) = lim ∆ x → 0 ∆ y ∆ x = t g α x = k x , где k x обозначают в качестве углового коэффициента касательной.

То есть получаем, что f ’ (x) может существовать в точке x 0 причем как и касательная к заданному графику функции в точке касания равной x 0 , f 0 (x 0) , где значение углового коэффициента касательной в точке равняется производной в точке x 0 . Тогда получаем, что k x = f » (x 0) .

Геометрический смысл производной функции в точке в том, что дается понятие существования касательной к графику в этой же точке.

Чтобы записать уравнение любой прямой на плоскости, необходимо иметь угловой коэффициент с точкой, через которую она проходит. Его обозначение принимается как x 0 при пересечении.

Уравнение касательной к графику функции y = f (x) в точке x 0 , f 0 (x 0) принимает вид y = f » (x 0) · x — x 0 + f (x 0) .

Имеется в виду, что конечным значением производной f » (x 0) можно определить положение касательной, то есть вертикально при условии lim x → x 0 + 0 f » (x) = ∞ и lim x → x 0 — 0 f » (x) = ∞ или отсутствие вовсе при условии lim x → x 0 + 0 f » (x) ≠ lim x → x 0 — 0 f » (x) .

Расположение касательной зависит от значения ее углового коэффициента k x = f » (x 0) . При параллельности к оси о х получаем, что k k = 0 , при параллельности к о у — k x = ∞ , причем вид уравнения касательной x = x 0 возрастает при k x > 0 , убывает при k x

Пример 2

Произвести составление уравнения касательной к графику функции y = e x + 1 + x 3 3 — 6 — 3 3 x — 17 — 3 3 в точке с координатами (1 ; 3) с определением угла наклона.

Решение

По условию имеем, что функция определяется для всех действительных чисел. Получаем, что точка с координатами, заданными по условию, (1 ; 3) является точкой касания, тогда x 0 = — 1 , f (x 0) = — 3 .

Необходимо найти производную в точке со значением — 1 . Получаем, что

y » = e x + 1 + x 3 3 — 6 — 3 3 x — 17 — 3 3 » = = e x + 1 » + x 3 3 » — 6 — 3 3 x » — 17 — 3 3 » = e x + 1 + x 2 — 6 — 3 3 y » (x 0) = y » (- 1) = e — 1 + 1 + — 1 2 — 6 — 3 3 = 3 3

Значение f ’ (x) в точке касания является угловым коэффициентом касательной, который равняется тангенсу наклона.

Тогда k x = t g α x = y » (x 0) = 3 3

Отсюда следует, что α x = a r c t g 3 3 = π 6

Ответ: уравнение касательной приобретает вид

y = f » (x 0) · x — x 0 + f (x 0) y = 3 3 (x + 1) — 3 y = 3 3 x — 9 — 3 3

Для наглядности приведем пример в графической иллюстрации.

Черный цвет используется для графика исходной функции, синий цвет – изображение касательной, красная точка – точка касания. Рисунок, располагаемый справа, показывает в увеличенном виде.

Пример 3

Выяснить наличие существования касательной к графику заданной функции
y = 3 · x — 1 5 + 1 в точке с координатами (1 ; 1) . Составить уравнение и определить угол наклона.

Решение

По условию имеем, что областью определения заданной функции считается множество всех действительных чисел.

Перейдем к нахождению производной

y » = 3 · x — 1 5 + 1 » = 3 · 1 5 · (x — 1) 1 5 — 1 = 3 5 · 1 (x — 1) 4 5

Если x 0 = 1 , тогда f ’ (x) не определена, но пределы записываются как lim x → 1 + 0 3 5 · 1 (x — 1) 4 5 = 3 5 · 1 (+ 0) 4 5 = 3 5 · 1 + 0 = + ∞ и lim x → 1 — 0 3 5 · 1 (x — 1) 4 5 = 3 5 · 1 (- 0) 4 5 = 3 5 · 1 + 0 = + ∞ , что означает существование вертикальной касательной в точке (1 ; 1) .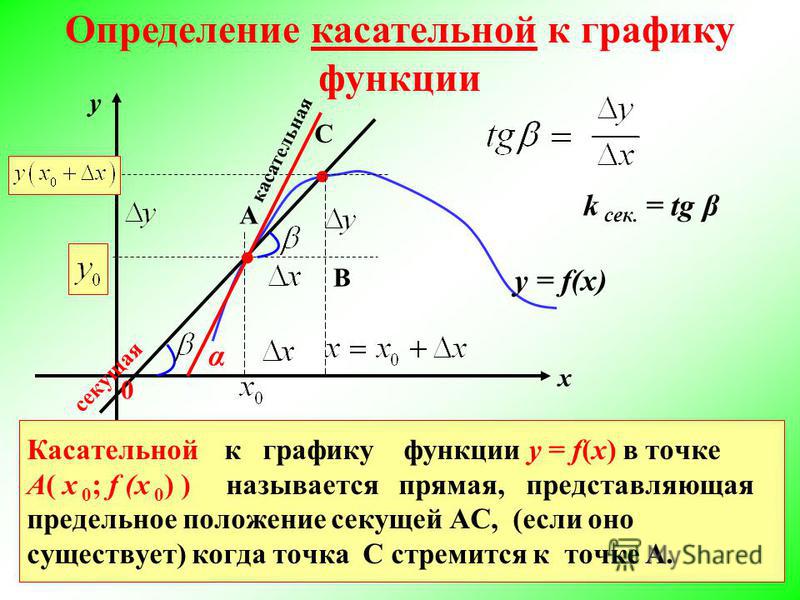

Ответ: уравнение примет вид х = 1 , где угол наклона будет равен π 2 .

Для наглядности изобразим графически.

Пример 4

Найти точки графика функции y = 1 15 x + 2 3 — 4 5 x 2 — 16 5 x — 26 5 + 3 x + 2 , где

1. Касательная не существует;
2. Касательная располагается параллельно о х;
3. Касательная параллельна прямой y = 8 5 x + 4 .

Решение

Необходимо обратить внимание на область определения. По условию имеем, что функция определена на множестве всех действительных чисел. Раскрываем модуль и решаем систему с промежутками x ∈ — ∞ ; 2 и [ — 2 ; + ∞) . Получаем, что

y = — 1 15 x 3 + 18 x 2 + 105 x + 176 , x ∈ — ∞ ; — 2 1 15 x 3 — 6 x 2 + 9 x + 12 , x ∈ [ — 2 ; + ∞)

Необходимо продифференцировать функцию. Имеем, что

y » = — 1 15 x 3 + 18 x 2 + 105 x + 176 » , x ∈ — ∞ ; — 2 1 15 x 3 — 6 x 2 + 9 x + 12 » , x ∈ [ — 2 ; + ∞) ⇔ y » = — 1 5 (x 2 + 12 x + 35) , x ∈ — ∞ ; — 2 1 5 x 2 — 4 x + 3 , x ∈ [ — 2 ; + ∞)

Когда х = — 2 , тогда производная не существует, потому что односторонние пределы не равны в этой точке:

lim x → — 2 — 0 y » (x) = lim x → — 2 — 0 — 1 5 (x 2 + 12 x + 35 = — 1 5 (- 2) 2 + 12 (- 2) + 35 = — 3 lim x → — 2 + 0 y » (x) = lim x → — 2 + 0 1 5 (x 2 — 4 x + 3) = 1 5 — 2 2 — 4 — 2 + 3 = 3

Вычисляем значение функции в точке х = — 2 , где получаем, что

1. y (- 2) = 1 15 — 2 + 2 3 — 4 5 (- 2) 2 — 16 5 (- 2) — 26 5 + 3 — 2 + 2 = — 2 , то есть касательная в точке (- 2 ; — 2) не будет существовать.
2. Касательная параллельна о х, когда угловой коэффициент равняется нулю. Тогда k x = t g α x = f » (x 0) . То есть необходимо найти значения таких х, когда производная функции обращает ее в ноль. То есть значения f ’ (x) и будут являться точками касания, где касательная является параллельной о х.

Когда x ∈ — ∞ ; — 2 , тогда — 1 5 (x 2 + 12 x + 35) = 0 , а при x ∈ (- 2 ; + ∞) получаем 1 5 (x 2 — 4 x + 3) = 0 .

1 5 (x 2 + 12 x + 35) = 0 D = 12 2 — 4 · 35 = 144 — 140 = 4 x 1 = — 12 + 4 2 = — 5 ∈ — ∞ ; — 2 x 2 = — 12 — 4 2 = — 7 ∈ — ∞ ; — 2 1 5 (x 2 — 4 x + 3) = 0 D = 4 2 — 4 · 3 = 4 x 3 = 4 — 4 2 = 1 ∈ — 2 ; + ∞ x 4 = 4 + 4 2 = 3 ∈ — 2 ; + ∞

Вычисляем соответствующие значения функции

y 1 = y — 5 = 1 15 — 5 + 2 3 — 4 5 — 5 2 — 16 5 — 5 — 26 5 + 3 — 5 + 2 = 8 5 y 2 = y (- 7) = 1 15 — 7 + 2 3 — 4 5 (- 7) 2 — 16 5 — 7 — 26 5 + 3 — 7 + 2 = 4 3 y 3 = y (1) = 1 15 1 + 2 3 — 4 5 · 1 2 — 16 5 · 1 — 26 5 + 3 1 + 2 = 8 5 y 4 = y (3) = 1 15 3 + 2 3 — 4 5 · 3 2 — 16 5 · 3 — 26 5 + 3 3 + 2 = 4 3

Отсюда — 5 ; 8 5 , — 4 ; 4 3 , 1 ; 8 5 , 3 ; 4 3 считаются искомыми точками графика функции.

Рассмотрим графическое изображение решения.

Черная линия – график функции, красные точки – точки касания.

1. Когда прямые располагаются параллельно, то угловые коэффициенты равны. Тогда необходимо заняться поиском точек графика функции, где угловой коэффициент будет равняться значению 8 5 . Для этого нужно решить уравнение вида y » (x) = 8 5 . Тогда, если x ∈ — ∞ ; — 2 , получаем, что — 1 5 (x 2 + 12 x + 35) = 8 5 , а если x ∈ (- 2 ; + ∞) , тогда 1 5 (x 2 — 4 x + 3) = 8 5 .

Первое уравнение не имеет корней, так как дискриминант меньше нуля. Запишем, что

1 5 x 2 + 12 x + 35 = 8 5 x 2 + 12 x + 43 = 0 D = 12 2 — 4 · 43 = — 28

Другое уравнение имеет два действительных корня, тогда

1 5 (x 2 — 4 x + 3) = 8 5 x 2 — 4 x — 5 = 0 D = 4 2 — 4 · (- 5) = 36 x 1 = 4 — 36 2 = — 1 ∈ — 2 ; + ∞ x 2 = 4 + 36 2 = 5 ∈ — 2 ; + ∞

Перейдем к нахождению значений функции. Получаем, что

y 1 = y (- 1) = 1 15 — 1 + 2 3 — 4 5 (- 1) 2 — 16 5 (- 1) — 26 5 + 3 — 1 + 2 = 4 15 y 2 = y (5) = 1 15 5 + 2 3 — 4 5 · 5 2 — 16 5 · 5 — 26 5 + 3 5 + 2 = 8 3

Точки со значениями — 1 ; 4 15 , 5 ; 8 3 являются точками, в которых касательные параллельны прямой y = 8 5 x + 4 .

Ответ: черная линия – график функции, красная линия – график y = 8 5 x + 4 , синяя линия – касательные в точках — 1 ; 4 15 , 5 ; 8 3 .

Возможно существование бесконечного количества касательных для заданных функций.

Пример 5

Написать уравнения всех имеющихся касательных функции y = 3 cos 3 2 x — π 4 — 1 3 , которые располагаются перпендикулярно прямой y = — 2 x + 1 2 .

Решение

Для составления уравнения касательной необходимо найти коэффициент и координаты точки касания, исходя из условия перпендикулярности прямых. Определение звучит так: произведение угловых коэффициентов, которые перпендикулярны прямым, равняется — 1 , то есть записывается как k x · k ⊥ = — 1 . Из условия имеем, что угловой коэффициент располагается перпендикулярно прямой и равняется k ⊥ = — 2 , тогда k x = — 1 k ⊥ = — 1 — 2 = 1 2 .

Теперь необходимо найти координаты точек касания. Нужно найти х, после чего его значение для заданной функции. Отметим, что из геометрического смысла производной в точке
x 0 получаем, что k x = y » (x 0) . Из данного равенства найдем значения х для точек касания.

Получаем, что

y » (x 0) = 3 cos 3 2 x 0 — π 4 — 1 3 » = 3 · — sin 3 2 x 0 — π 4 · 3 2 x 0 — π 4 » = = — 3 · sin 3 2 x 0 — π 4 · 3 2 = — 9 2 · sin 3 2 x 0 — π 4 ⇒ k x = y » (x 0) ⇔ — 9 2 · sin 3 2 x 0 — π 4 = 1 2 ⇒ sin 3 2 x 0 — π 4 = — 1 9

Это тригонометрическое уравнение будет использовано для вычисления ординат точек касания.

3 2 x 0 — π 4 = a r c sin — 1 9 + 2 πk или 3 2 x 0 — π 4 = π — a r c sin — 1 9 + 2 πk

3 2 x 0 — π 4 = — a r c sin 1 9 + 2 πk или 3 2 x 0 — π 4 = π + a r c sin 1 9 + 2 πk

x 0 = 2 3 π 4 — a r c sin 1 9 + 2 πk или x 0 = 2 3 5 π 4 + a r c sin 1 9 + 2 πk , k ∈ Z

Z — множество целых чисел.

Найдены х точек касания. Теперь необходимо перейти к поиску значений у:

y 0 = 3 cos 3 2 x 0 — π 4 — 1 3

y 0 = 3 · 1 — sin 2 3 2 x 0 — π 4 — 1 3 или y 0 = 3 · — 1 — sin 2 3 2 x 0 — π 4 — 1 3

y 0 = 3 · 1 — — 1 9 2 — 1 3 или y 0 = 3 · — 1 — — 1 9 2 — 1 3

y 0 = 4 5 — 1 3 или y 0 = — 4 5 + 1 3

Отсюда получаем, что 2 3 π 4 — a r c sin 1 9 + 2 πk ; 4 5 — 1 3 , 2 3 5 π 4 + a r c sin 1 9 + 2 πk ; — 4 5 + 1 3 являются точками касания.

Ответ: необходимы уравнения запишутся как

y = 1 2 x — 2 3 π 4 — a r c sin 1 9 + 2 πk + 4 5 — 1 3 , y = 1 2 x — 2 3 5 π 4 + a r c sin 1 9 + 2 πk — 4 5 + 1 3 , k ∈ Z

Для наглядного изображения рассмотрим функцию и касательную на координатной прямой.

Рисунок показывает, что расположение функции идет на промежутке [ — 10 ; 10 ] , где черная прямя – график функции, синие линии – касательные, которые располагаются перпендикулярно заданной прямой вида y = — 2 x + 1 2 . Красные точки – это точки касания.

Канонические уравнения кривых 2 порядка не являются однозначными функциями. Уравнения касательных для них составляются по известным схемам.

Касательная к окружности

Для задания окружности с центром в точке x c e n t e r ; y c e n t e r и радиусом R применяется формула x — x c e n t e r 2 + y — y c e n t e r 2 = R 2 .

Данное равенство может быть записано как объединение двух функций:

y = R 2 — x — x c e n t e r 2 + y c e n t e r y = — R 2 — x — x c e n t e r 2 + y c e n t e r

Первая функция располагается вверху, а вторая внизу, как показано на рисунке.

Для составления уравнения окружности в точке x 0 ; y 0 , которая располагается в верхней или нижней полуокружности, следует найти уравнение графика функции вида y = R 2 — x — x c e n t e r 2 + y c e n t e r или y = — R 2 — x — x c e n t e r 2 + y c e n t e r в указанной точке.

Когда в точках x c e n t e r ; y c e n t e r + R и x c e n t e r ; y c e n t e r — R касательные могут быть заданы уравнениями y = y c e n t e r + R и y = y c e n t e r — R , а в точках x c e n t e r + R ; y c e n t e r и
x c e n t e r — R ; y c e n t e r будут являться параллельными о у, тогда получим уравнения вида x = x c e n t e r + R и x = x c e n t e r — R .

Касательная к эллипсу

Когда эллипс имеет центр в точке x c e n t e r ; y c e n t e r с полуосями a и b , тогда он может быть задан при помощи уравнения x — x c e n t e r 2 a 2 + y — y c e n t e r 2 b 2 = 1 .

Эллипс и окружность могут быть обозначаться при помощи объединения двух функций, а именно: верхнего и нижнего полуэллипса.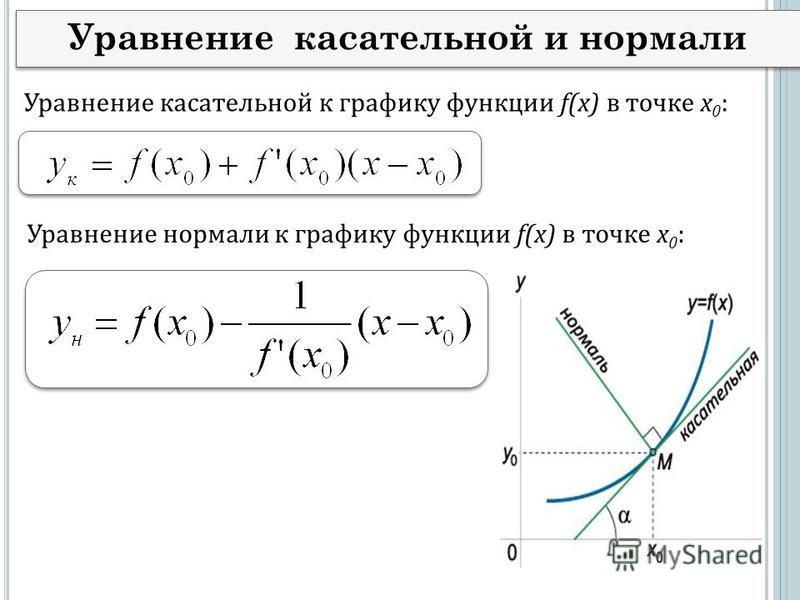 Тогда получаем, что

y = b a · a 2 — (x — x c e n t e r) 2 + y c e n t e r y = — b a · a 2 — (x — x c e n t e r) 2 + y c e n t e r

Если касательные располагаются на вершинах эллипса, тогда они параллельны о х или о у. Ниже для наглядности рассмотрим рисунок.

Пример 6

Написать уравнение касательной к эллипсу x — 3 2 4 + y — 5 2 25 = 1 в точках со значениями x равного х = 2 .

Решение

Необходимо найти точки касания, которые соответствуют значению х = 2 . Производим подстановку в имеющееся уравнение эллипса и получаем, что

x — 3 2 4 x = 2 + y — 5 2 25 = 1 1 4 + y — 5 2 25 = 1 ⇒ y — 5 2 = 3 4 · 25 ⇒ y = ± 5 3 2 + 5

Тогда 2 ; 5 3 2 + 5 и 2 ; — 5 3 2 + 5 являются точками касания, которые принадлежат верхнему и нижнему полуэллипсу.

Перейдем к нахождению и разрешению уравнения эллипса относительно y . Получим, что

x — 3 2 4 + y — 5 2 25 = 1 y — 5 2 25 = 1 — x — 3 2 4 (y — 5) 2 = 25 · 1 — x — 3 2 4 y — 5 = ± 5 · 1 — x — 3 2 4 y = 5 ± 5 2 4 — x — 3 2

Очевидно, что верхний полуэллипс задается с помощью функции вида y = 5 + 5 2 4 — x — 3 2 , а нижний y = 5 — 5 2 4 — x — 3 2 .

Применим стандартный алгоритм для того, чтобы составить уравнение касательной к графику функции в точке. Запишем, что уравнение для первой касательной в точке 2 ; 5 3 2 + 5 будет иметь вид

y » = 5 + 5 2 4 — x — 3 2 » = 5 2 · 1 2 4 — (x — 3) 2 · 4 — (x — 3) 2 » = = — 5 2 · x — 3 4 — (x — 3) 2 ⇒ y » (x 0) = y » (2) = — 5 2 · 2 — 3 4 — (2 — 3) 2 = 5 2 3 ⇒ y = y » (x 0) · x — x 0 + y 0 ⇔ y = 5 2 3 (x — 2) + 5 3 2 + 5

Получаем, что уравнение второй касательной со значением в точке
2 ; — 5 3 2 + 5 принимает вид

y » = 5 — 5 2 4 — (x — 3) 2 » = — 5 2 · 1 2 4 — (x — 3) 2 · 4 — (x — 3) 2 » = = 5 2 · x — 3 4 — (x — 3) 2 ⇒ y » (x 0) = y » (2) = 5 2 · 2 — 3 4 — (2 — 3) 2 = — 5 2 3 ⇒ y = y » (x 0) · x — x 0 + y 0 ⇔ y = — 5 2 3 (x — 2) — 5 3 2 + 5

Графически касательные обозначаются так:

Касательная к гиперболе

Когда гипербола имеет центр в точке x c e n t e r ; y c e n t e r и вершины x c e n t e r + α ; y c e n t e r и x c e n t e r — α ; y c e n t e r , имеет место задание неравенства x — x c e n t e r 2 α 2 — y — y c e n t e r 2 b 2 = 1 , если с вершинами x c e n t e r ; y c e n t e r + b и x c e n t e r ; y c e n t e r — b , тогда задается при помощи неравенства x — x c e n t e r 2 α 2 — y — y c e n t e r 2 b 2 = — 1 .

Гипербола может быть представлена в виде двух объединенных функций вида

y = b a · (x — x c e n t e r) 2 — a 2 + y c e n t e r y = — b a · (x — x c e n t e r) 2 — a 2 + y c e n t e r или y = b a · (x — x c e n t e r) 2 + a 2 + y c e n t e r y = — b a · (x — x c e n t e r) 2 + a 2 + y c e n t e r

В первом случае имеем, что касательные параллельны о у, а во втором параллельны о х.

Отсюда следует, что для того, чтобы найти уравнение касательной к гиперболе, необходимо выяснить, какой функции принадлежит точка касания. Чтобы определить это, необходимо произвести подстановку в уравнения и проверить их на тождественность.

Пример 7

Составить уравнение касательной к гиперболе x — 3 2 4 — y + 3 2 9 = 1 в точке 7 ; — 3 3 — 3 .

Решение

Необходимо преобразовать запись решения нахождения гиперболы при помощи 2 функций. Получим, что

x — 3 2 4 — y + 3 2 9 = 1 ⇒ y + 3 2 9 = x — 3 2 4 — 1 ⇒ y + 3 2 = 9 · x — 3 2 4 — 1 ⇒ y + 3 = 3 2 · x — 3 2 — 4 и л и y + 3 = — 3 2 · x — 3 2 — 4 ⇒ y = 3 2 · x — 3 2 — 4 — 3 y = — 3 2 · x — 3 2 — 4 — 3

Необходимо выявить, к какой функции принадлежит заданная точка с координатами 7 ; — 3 3 — 3 .

Очевидно, что для проверки первой функции необходимо y (7) = 3 2 · (7 — 3) 2 — 4 — 3 = 3 3 — 3 ≠ — 3 3 — 3 , тогда точка графику не принадлежит, так как равенство не выполняется.

Для второй функции имеем, что y (7) = — 3 2 · (7 — 3) 2 — 4 — 3 = — 3 3 — 3 ≠ — 3 3 — 3 , значит, точка принадлежит заданному графику. Отсюда следует найти угловой коэффициент.

Получаем, что

y » = — 3 2 · (x — 3) 2 — 4 — 3 » = — 3 2 · x — 3 (x — 3) 2 — 4 ⇒ k x = y » (x 0) = — 3 2 · x 0 — 3 x 0 — 3 2 — 4 x 0 = 7 = — 3 2 · 7 — 3 7 — 3 2 — 4 = — 3

Ответ: уравнение касательной можно представить как

y = — 3 · x — 7 — 3 3 — 3 = — 3 · x + 4 3 — 3

Наглядно изображается так:

Касательная к параболе

Чтобы составить уравнение касательной к параболе y = a x 2 + b x + c в точке x 0 , y (x 0) , необходимо использовать стандартный алгоритм, тогда уравнение примет вид y = y » (x 0) · x — x 0 + y (x 0) . Такая касательная в вершине параллельна о х.

Следует задать параболу x = a y 2 + b y + c как объединение двух функций.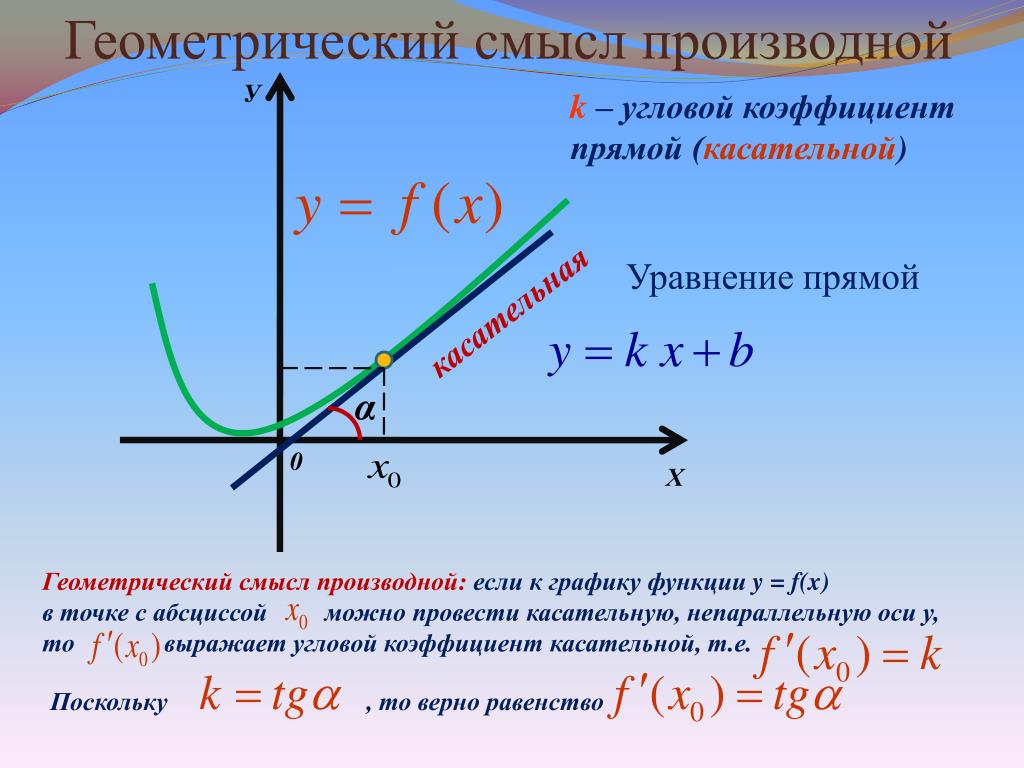 Поэтому нужно разрешить уравнение относительно у. Получаем, что

x = a y 2 + b y + c ⇔ a y 2 + b y + c — x = 0 D = b 2 — 4 a (c — x) y = — b + b 2 — 4 a (c — x) 2 a y = — b — b 2 — 4 a (c — x) 2 a

Графически изобразим как:

Для выяснения принадлежности точки x 0 , y (x 0) функции, нежно действовать по стандартному алгоритму. Такая касательная будет параллельна о у относительно параболы.

Пример 8

Написать уравнение касательной к графику x — 2 y 2 — 5 y + 3 , когда имеем угол наклона касательной 150 ° .

Решение

Начинаем решение с представления параболы в качестве двух функций. Получим, что

2 y 2 — 5 y + 3 — x = 0 D = (- 5) 2 — 4 · (- 2) · (3 — x) = 49 — 8 x y = 5 + 49 — 8 x — 4 y = 5 — 49 — 8 x — 4

Значение углового коэффициента равняется значению производной в точке x 0 этой функции и равняется тангенсу угла наклона.

Получаем:

k x = y » (x 0) = t g α x = t g 150 ° = — 1 3

Отсюда определим значение х для точек касания.

Первая функция запишется как

y » = 5 + 49 — 8 x — 4 » = 1 49 — 8 x ⇒ y » (x 0) = 1 49 — 8 x 0 = — 1 3 ⇔ 49 — 8 x 0 = — 3

Очевидно, что действительных корней нет, так как получили отрицательное значение. Делаем вывод, что касательной с углом 150 ° для такой функции не существует.

Вторая функция запишется как

y » = 5 — 49 — 8 x — 4 » = — 1 49 — 8 x ⇒ y » (x 0) = — 1 49 — 8 x 0 = — 1 3 ⇔ 49 — 8 x 0 = — 3 x 0 = 23 4 ⇒ y (x 0) = 5 — 49 — 8 · 23 4 — 4 = — 5 + 3 4

Имеем, что точки касания — 23 4 ; — 5 + 3 4 .

Ответ: уравнение касательной принимает вид

y = — 1 3 · x — 23 4 + — 5 + 3 4

Графически изобразим это таким образом:

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

Касательная плоскость и нормаль к явно заданной поверхности.

Касательной плоскостью к поверхности в ее точке $M_0$ (точка касания) называется плоскость, содержащая в себе все касательные к кривым, проведенным на поверхности через эту точку.

Нормалью к поверхности называется прямая, перпендикулярная к касательной плоскости и проходящая через точку касания.

Если уравнение поверхности имеет вид $$F(x,y,z)=0,$$ то уравнение касательной плоскости в точке $M_0(x_0, y_0, z_0)$ есть $$F_x'(x_0, y_0, z_0)(x-x_0)+F_y'(x_0, y_0, z_0)(y-y_0)+F_z'(x_0, y_0, z_0)(z-z_0)=0.$$

Уравнение нормали $$\frac{x-x_0}{F_x'(x_0, y_0, z_0)}=\frac{y-y_0}{F_y'(x_0, y_0, z_0)}=\frac{z-z_0}{F_z'(x_0, y_0, z_0)}.$$

В случае задания поверхности в явной форме $$z=f(x, y)$$ уравнение касательной плоскости в точке $M_0(x_0, y_0, z_0)$ имеет вид $$z-z_0=f_x'(x_0, y_0)(x-x_0)+f_y'(x_0, y_0)(y-y_0),$$ а уравнение нормали $$\frac{x-x_0}{f_x'(x_0, y_0)}=\frac{y-y_0}{f_y'(x_0, y_0)}=\frac{z-z_0}{-1}.$$

Примеры:

7.229. а) Найти уравнения касательной плоскости и нормали к поверхности $z=\sin x\cos y$ в точке $(\pi/4, \pi/4, \pi/4).$

Решение.

Для поверхности $$z=f(x, y)$$ уравнение касательной плоскости в точке $M_0(x_0, y_0, z_0)$ имеет вид $$z-z_0=f_x'(x_0, y_0)(x-x_0)+f_y'(x_0, y_0)(y-y_0),$$ а уравнение нормали $$\frac{x-x_0}{f_x'(x_0, y_0)}=\frac{y-y_0}{f_y'(x_0, y_0)}=\frac{z-z_0}{-1}.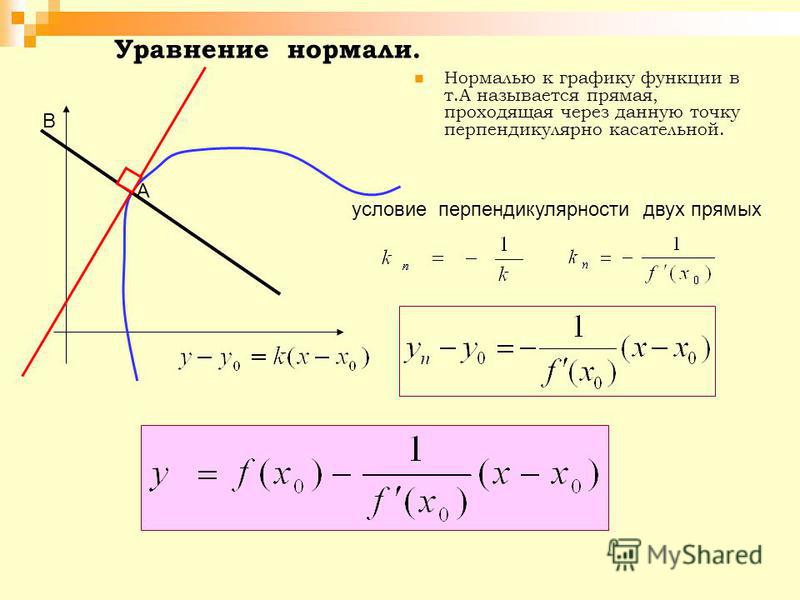 2-2x+6y=4$ найти уравнение нормали, параллельной прямой $\frac{x+2}{1}=\frac{y}{3}=\frac{z+1}{4}.$

 

 

Уравнение тангенсов и нормалей

Производные используются для нахождения скорости изменения функции по отношению к переменным. Чтобы найти скорость изменения функции по переменной, необходимо дифференцировать ее по этой переменной. Скорость изменения функции y = f(x) по отношению к x определяется как dy/dx или f'(x). Например, y = x ² + x, тогда dy/dx = f'(x) = d(x ² + x)/dx = 2x + 1.

Когда две переменные (пусть x = f(t ) и y = g(t)) варьируется по другой переменной t, то скорость изменения рассчитывается по цепному правилу. Скорость изменения y по отношению к x равна: dy/dx = (dy/dt) × (dt/dx). Например, x = t и y = 2t, тогда dy/dx вычисляется как: dx/dt = 1 или dt/dx = 1 и dy/dt = 2. Следовательно, dy/dx = (dy/dt) × ( dt/dx) = 2 × 1 = 2. Следовательно, скорость изменения y по отношению к x рассчитывается как скорость изменения y по отношению к t и скорость изменения t по отношению к x.

Применение производных

Производные в основном используются в математике для определения изменения значения любой переменной по отношению к другой переменной. В реальной жизни также рассматриваются и обсуждаются производные. Например, слово скорость упоминается очень часто, но мало кто знает, что скорость — это тоже производная, скорость — это изменение расстояния по отношению ко времени. Давайте рассмотрим некоторые важные приложения производных,

• Чтобы найти скорость изменения функции по отношению к переменным.
• Для поиска касательных и нормальных кривых.
• Чтобы найти максимальное и минимальное значение функции.
• Определение возрастания или убывания функции и интервала возрастания или убывания функции.
• Чтобы найти вогнутость (независимо от того, является ли функция вогнутой вверх или вогнутой вниз) функции.
• Для расчета скорости по смещению и ускорения по скорости (скорость — это изменение смещения во времени, а ускорение — это изменение скорости во времени).
• Чтобы найти приблизительное значение некоторых величин (например, квадратный корень, кубический корень из числа).

Касательная и нормаль 

Касательная к кривой в данной точке — это прямая линия, которая касается кривой в данной точке (не пересекает кривую, а только касается кривой в данной точке). Принимая во внимание, что Нормальная — это прямая линия, перпендикулярная касательной.

Следовательно, произведение наклона касательной и нормали равно -1 . Пусть обозначенный наклон касательной и нормали равен м _{T и м N соответственно. Тогда}

м _T × m _N = -1 .

Если касательная составляет угол Θ с осью x, то наклон касательной = м _T = tan Θ .

Так, м _Т × м _N = -1 Итак, tan Θ × м _N =

3 -1 9.

Следовательно, наклон нормали равен -1/tan Θ или -cot Θ .

Уравнение касательной и нормали

Наклон касательной к кривой, уравнение которой y = f(x) в точке ) в точке a ). Следовательно, уравнение касательной в форме точка-наклон имеет вид

(y – f(a))/(x – a) = f'(a),  

и с использованием уравнения m _T × m _Н = -1 , 

Уравнение нормали: 

(y – f(a))/(x – a) = -1/f'(a) .

Примеры задач 

Вопрос 1: y = x ² — уравнение кривой, найдите уравнение касательной и нормали в точке (1, 1).

Решение:

Первое дифференцирование y = x ² , y’ = 2x .

Наклон касательной в точке (1, 1) равен 2 × 1 = 2, а наклон нормали равен -1/2 .

Следовательно, уравнение касательной в точке (1, 1) имеет вид: (y – 1)/(x – 1) = 2 => y = 2x – 1

И уравнение нормали в точке (1, 1): (y – 1)/(x – 1) = -1/2 = 2y = -x + 3 .

Вопрос 2: у = х ⁴ + х ² уравнение кривой, найти уравнение касательной и нормали в точке (1, 2) дифференцируем y = x ⁴ + x ² , получаем y’ = 4x ³ + 2x .

Наклон касательной в точке (1, 2) равен 4 × (1) ³ + 2 × 1 = 6 и наклон нормали -1/6 .

Следовательно, уравнение касательной в точке (1, 2) имеет вид: (y – 2)/(x – 1) = 6 => y = 6x – 4

И уравнение нормали в точке (1, 2 ) равно: (y – 2)/(x – 1) = -1/6 => 6y = -x + 13 .

Вопрос 3: y = x уравнение кривой, найти уравнение касательной и нормали в точке (1, 1).

Решение:

Сначала продифференцируем y = x, получим y’ = 1.

Наклон касательной в точке (1, 1) равен 1, а наклон нормали равен -1.

Следовательно, уравнение касательной в точке (1, 1) имеет вид: (y – 1)/(x – 1) = 1 => y = x

А уравнение нормали в точке (1, 1) имеет вид: ( y – 1)/(x – 1) = -1 => 2y = -x + 2.

Вопрос 4: x = t и y = t – уравнение кривой, найдите уравнение касательной и нормали в точке t = 2.

Решение:

Сначала продифференцируем x = t, получим dx/dt = 1 или dt/dx = 1,

И дифференцировать y = t, dy/dt = 1.

Следовательно, dy/dx = (dy/dt) × (dt/dx) = 1 × 1 = 1.

Наклон касательной в точке t = 2 равно 1, а наклон нормали равен -1.

Следовательно, уравнение касательной в точке в точке t = 2 имеет вид: (y – 2)/(x – 2) = 1 => y = x

А уравнение нормали в точке в точке t = 2 имеет вид (y – 2)/(x – 2) = -1 => y = -x + 4.

Вопрос 5: x = t и y = t ² есть уравнение кривой и, найдите уравнение касательной и нормально в точке t = 1,

Решение:

Сначала продифференцируем x = t, dx/dt = 1 или dt/dx = 1.

И продифференцируем y = t ² , dy/dt = 2t = 2 × 1 2.

Следовательно, dy/dx = (dy/dt) × (dt/dx) = 2 × 1 = 2.

Наклон касательной в точке t = 1 равен 2, а наклон нормали равен -1 /2.

Следовательно, уравнение касательной в точке в точке t = 1 равно (y – 1)/(x – 1) = 2 => y = 2x – 1.

И уравнение нормали в точке в точке t = 1 имеет вид (у – 1)/(х – 1) = -1/2 => 2у = -х + 3,

Что такое уравнение касательной?

В вычислениях вы неизбежно столкнетесь с уравнением касательной. Что именно представляет собой это уравнение? Эта статья объяснит все, что вам нужно знать об этом.

1 Определения ключевых терминов и формул

2 Основной метод нахождения уравнения касательной линии

3 Методы решения задач, связанных с уравнением касательной линии

3. 1 Определите максимальное и минимальное количество баллов

3.2 Раскройте уравнение нормального

3.3 Вертикальные и горизонтальные касательные линии

4 Подведение итогов

Изучая исчисление, вы узнаете, что наклон кривой постоянно меняется, когда вы перемещаетесь по графику. Этим она отличается от прямой. Вы можете описать каждую точку на графике наклоном.

Касательная — это просто прямая линия с наклоном, которая проходит прямо из той же самой точной точки на графике. Когда мы хотим найти уравнение для тангенса, нам нужно сделать вывод, как взять производную исходного уравнения, с которым мы работаем.

При поиске уравнения касательной вам понадобятся и точка, и наклон. Вы сможете определить наклон касательной, вычислив значение производной в месте касания. Здесь сходятся линия и точка.

Что касается связанного с этим уравнения нормали, «нормальная» линия определяется как линия, перпендикулярная касательной. Эта линия будет проходить через точку касания. Теперь, когда мы кратко рассмотрели, что такое уравнение касательной, мы рассмотрим основные термины и формулы, с которыми вам нужно будет ознакомиться, чтобы найти уравнение касательной.

Определения ключевых терминов и формул

Изображение через: Flickr

Прежде чем мы перейдем к тому, как найти уравнение касательной линии, мы рассмотрим основные термины, которые вам необходимо знать. Имея четкое представление об этих терминах, вы сможете прийти к правильному ответу при поиске уравнения.

• Касательная – это прямая линия, которая соприкасается с функцией в точке и только в этой конкретной точке. Эта линия едва соприкасается с функцией, но соприкасается и соответствует наклону кривой. Эта линия также параллельна в точке встречи. Вы также можете просто назвать это касательной.

• Секущая линия – это линия, пересекающая функцию. Эта линия будет во второй точке и пересекается в двух точках на кривой. Вы также можете просто назвать это секущей.

• Формула пересечения наклона . Это формула y = mx + b, где m – наклон линии, а b – точка пересечения с осью y. Вы будете использовать эту формулу для линии.

• Формула точки-наклона – Это формула y – y1 = m (x-x1), в которой используется точка наклона линии, к которой относится x1, y1. Наклон линии представлен m, что даст вам формулу пересечения наклона.

Теперь, когда ключевые термины и формулы понятны, вы готовы найти уравнение касательной. Вы должны повторить свои шаги и убедиться, что вы правильно применили формулы. В противном случае вы получите результат, который отклоняется от правильно атрибутированного уравнения.

Основной метод нахождения уравнения касательной

Изображение с: Flickr

Когда мы готовы найти уравнение касательной, нам нужно пройти несколько шагов. . Если вы выполните все эти шаги последовательно, вы найдете результат, который вы ищете.

Существует несколько способов найти уравнение касательной, а это значит, что один метод может оказаться для вас проще, чем другой. Мы рассмотрим несколько способов найти уравнение. Ниже приведен первый способ.

Запишите функцию и начертите касательную

Хотя вы можете набраться смелости и отказаться от использования графика для иллюстрации касательной, это облегчит вам жизнь, нарисовав ее так, чтобы вы могли ее увидеть. Это потому, что это облегчает отслеживание и определение того, все ли сделано правильно на пути к нахождению уравнения. Вы захотите нарисовать функцию на миллиметровой бумаге с касательной, проходящей через заданную точку.

Используйте производную для наклона

Далее вам нужно взять первую производную (f’x), которая представляет наклон касательной где-то, где угодно, на f(x), пока он находится на точке.

Введите координату x в f(x)

Возьмите точку, которую вы используете, чтобы найти уравнение, и найдите ее координату x. Когда вы вводите эту координату в f'(x), вы получаете наклон касательной.

Преобразование уравнения касательной линии в форму точка-наклон

Теперь вам нужно преобразовать уравнение касательной линии в форму точка-наклон. Преобразование будет выглядеть так: y – y1 = m(x – x1). В этом уравнении m представляет наклон, а x1, y1 — точки на вашей линии. Поздравляем! Вы нашли уравнение касательной.

Подтверждение уравнения касательной

Несмотря на то, что вы можете быть уверены, что нашли уравнение для касательной, вы все равно должны убедиться, что получили правильный результат. Полезно иметь для этого графический калькулятор, чтобы упростить вам задачу, хотя вы также можете использовать бумагу. Вы начертите начальную функцию, а также касательную. Если вы подтверждаете вручную, посмотрите на график, который вы сделали ранее, и посмотрите, нет ли ошибок.

Методы решения задач, связанных с уравнением касательной линии

Есть несколько других методов, которые стоит рассмотреть, поскольку они относятся к уравнению касательной линии. Знание этого поможет вам найти крайние точки на графике, уравнение нормали, а также вертикальные и горизонтальные линии.

Определите максимальную и минимальную точки

При использовании этого метода первым шагом будет определение крайних точек на графике. Это максимальные и минимальные баллы, учитывая, что один выше любых других баллов, а другой ниже любых баллов. Помните, что касательная всегда будет иметь нулевой наклон в максимальной и минимальной точках.

Следует отметить, что наличие наклона 0 не гарантирует, что крайние точки будут правильными. Чтобы быть уверенным, что вы нашли экстремальные точки, вы должны сделать следующие шаги:

1. Возьмем первую производную функции, которая даст f'(x). Полученное уравнение будет для наклона касательной.
2. Найдите f'(x) = 0. Это позволит выявить вероятные максимальные и минимальные точки.
3. Возьмите вторую производную функции, которая даст f”(x). Это скажет вам о скорости, с которой сдвигается наклон касательной.
4. Для вероятных максимальных и минимальных точек, которые вы обнаружили ранее, введите координату x a в f”(x). Теперь вам нужно будет проверить, является ли это положительным или отрицательным. Если он положительный, вы нашли минимум а. Если он отрицательный, вы нашли максимум. Третий результат, который вы получите, — это точка перегиба, когда f”(a) равняется нулю.
5. Когда вы обнаружите крайнюю точку a , вам нужно будет найти f(a), чтобы узнать координату y.

Раскройте уравнение нормали

«Нормаль» к кривой в определенной точке проходит через эту точку. Однако его наклон перпендикулярен касательной. Если вы хотите найти уравнение нормали, вам нужно будет сделать следующее:

1. Найдите наклон касательной, который представлен как f'(x).
2. Если у вас есть точка x = a, вам нужно будет найти наклон касательной в этой же точке.
3. Теперь вам нужно найти наклон нормали, вычислив -1 / f'(a).
4. Запишите уравнение нормали в формате точка-наклон.

Вертикальные и горизонтальные касательные

Чтобы узнать, где у функции есть касательная по горизонтали или по вертикали, нам придется пройти несколько шагов.

1. При поиске горизонтальной касательной с наклоном, равным нулю, возьмите производную функции и установите ее равной нулю.
2. Получите и идентифицируйте значение x  .
3. Возьмите исходную функцию, чтобы вывести значение y . В результате у вас теперь есть местоположение точки.
4. При поиске вертикальной касательной с неопределенным наклоном возьмите производную функции и приравняйте знаменатель к нулю.
5. Получите и определите значение x.
6. Возьмите исходную функцию, чтобы вывести значение y . В результате у вас теперь есть местоположение точки.

При поиске вертикальных и горизонтальных касательных следует помнить о двух вещах. В случае горизонтальных касательных необходимо убедиться, что знаменатель не равен нулю ни в точках x , ни в точках y . В случае вертикальных касательных нужно убедиться, что числитель не равен нулю ни в точках x , ни в точках y .

Подведение итогов

Изображение взято с Flickr

Поздравляем с нахождением уравнения касательной! Теперь вы можете быть уверены, что у вас есть методология для нахождения уравнения касательной. Это может показаться сложным процессом, но достаточно просто, если вы попрактикуетесь несколько раз. Главное — понять ключевые термины и формулы. Наличие графика в качестве визуального представления наклона и касательной также упрощает процесс.

Уравнение касательной и нормали

Производные находят множество применений в науке, технике и даже социальных науках. Некоторые из приложений в области науки оценивают скорость изменения величин или находят уравнения касательной к кривой. Мы будем обсуждать понятие касательной и нормали к кривой.

Касательные и нормали подобны любым другим прямым линиям в данной точке кривой. Касательная параллельна кривой в точке, а нормаль проходит перпендикулярно кривой. Уравнение касательной и нормали можно вычислить так же, как и любую другую прямую. Но чтобы найти градиент касательных и нормалей к кривой, учащимся понадобится производная.

Если наклон касательной к кривой y = f(x) в точке a равен f'(a) (производная f(x) в точке (a).

Тогда уравнение касательной в форме точка-наклон имеет вид (y – f(a))/(x – a) = f'(a), и с использованием уравнения mT × mN = −1,

 

Уравнение нормали равно

(y – f(a))/(x – a) = −1/f'(a).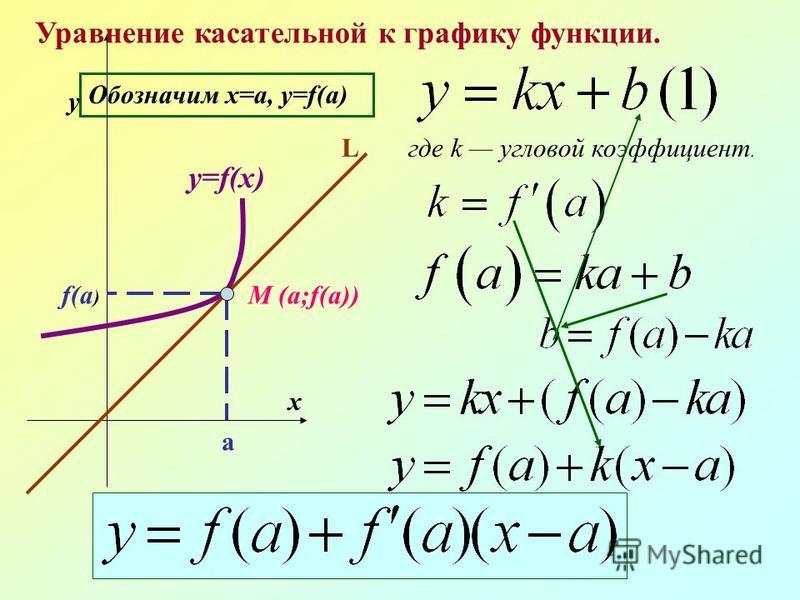

Изучение производных приводит к одному из выводов, поскольку dy/dx геометрически представляет в любой точке (x,y) наклон кривой y =f(x).

Важным термином, который следует запомнить, является градиент. Градиент кривой в точке определяется как наклон этой касательной к кривой в этой конкретной точке.

Двигаясь дальше, угол касательной играет важную роль при нахождении уравнения прямой.

Поэтому ниже приведены некоторые ключевые моменты, которые следует помнить об угле касательной к кривой в точке:

1. ,y) образует положительное направление оси x, то в этом случае точка A = tan Ψ = (dy/dx)A. Наклон касательной к кривой остается y =f(x).

2. В этом случае, когда касательная к кривой параллельна оси x, тогда Ψ = 0. Это означает, что tan Ψ будет равен нулю и, следовательно, (dy/dx)A также будет равен нулю.

3. Когда касательная к кривой параллельна оси y, тогда Ψ = ⊼/2 = cot Ψ = 0 и, следовательно, (dy/dx)A становится равным 0. 

4. Последний случай когда касательная параллельна оси x, что означает, что Ψ ≠ 0. Далее это приводит к уравнению tan Ψ ≠ (dy/dx)A ≠ 0. Следовательно, наклон нормали к кривой в точке A становится равным A = −1/(dy/dx)A.

Выполнение этих пунктов выше может помочь вам продвинуться дальше в поиске уравнения касательной и нормали.

Уравнение касательной

Дана кривая y =f(x) с точкой A (x1, y1). Следовательно, наклон касательной становится равным (dy/dx)x = x1; у = у1.

Теперь, когда мы узнали, как рассчитать наклон, мы можем просто продолжить, следуя концепции координатной геометрии, согласно которой уравнение прямой имеет вид

(y − y1) = m(x − x1) , где м – уклон.

Теперь мы можем заменить «m» в приведенном выше уравнении на (dy/dx)x = x1 ; у = у1 . Теперь новое уравнение касательной к кривой в точке A (x1, y1) равно

(y − y1) = (dy/dx)x = x1; у = у1 (х — х1).

Вышеупомянутое уравнение является уравнением формулы тангенса. Таким образом, выполните эти три простых шага, чтобы найти уравнение касательной к кривой в точке A (x1, y1).

Шаг 1: Первым и главным шагом должно быть нахождение (dy/dx) из данного уравнения кривой y = f(x).

Шаг 2: Следующий шаг включает в себя нахождение значения (dy/dx) в точке A (x1, y1). Этот метод позволяет вычислить «m» или наклон этой точки. Следовательно, m = (dy/dx)x = x1; у = у11.

Шаг 3: Последний шаг — запомнить уравнение прямой из координатной геометрии, которое имеет вид (y − y1) = m(x − x1).

Значение m заменяется наклоном уравнения касательной, рассчитанным выше:

(y − y1) = (dy/dx)x = x1 ; у = у1 (х — х1).

Уравнение нормали

Если задано уравнение кривой y = f(x), то нахождение уравнения нормали в точке кривой A (x1, y1) начинается с нахождения наклона. Наклон нормали к кривой в точке A (x1, y1) равен A = A = −1/ (dy/dx)x = x1; у = у1.

Поскольку теперь нам известен наклон, мы можем перейти к нахождению уравнения нормальной линии в точке кривой A (x1, y1), используя формулу, полученную из координатной геометрии:

(y − y1) = m(x − x1), где m — наклон.

Здесь следует отметить, что, хотя уравнение для нормальной линии такое же, как и для касательной, значение наклона здесь отличается. Наклон для нормали равен −1/(dy/dx)x = x1; у = у1 .

(y − y1) = [ −1/ (dy/dx)x = x1 ; y = y1](x − x1)

Ниже приведены три шага, которые можно выполнить один за другим при нахождении уравнения нормали к кривой в точке A (x1, y1):

Шаг 1: Определить уравнение кривой y = f(x). Как только это установлено, найдите (dy/dx) из данного уравнения кривой; у = f (х).

Шаг 2: Следующий шаг очень важен, так как он включает в себя вычисление наклона уравнения нормали к кривой в точке A (x1, y1). Для этого найдите значение (dy/dx) в точке A (x1, y1). Формула наклона нормали: m = −1/(dy/dx)x = x ₁ ; у = у ₁ .

Шаг 3: Последним шагом является замена значения наклона в уравнении (y − y1) = m(x − x1). Решив это, вы успешно нашли уравнение для нормали.

Вышеупомянутые шаги очень просты. При решении уравнения нормали обращайтесь к этим шагам в указанном порядке. Выполнение этих шагов может ускорить процесс нахождения уравнения нормали к кривой.

Проведите быструю проверку выводов, чтобы не допускать ошибок при ответах на вопросы по этой теме. Кроме того, выполните простые шаги, упомянутые выше, чтобы лучше понять уравнение касательной и нормали.

Важные формулы касательной и нормали 

Ниже приведены важные формулы касательной и нормали к любой кривой в заданной точке.

No related posts.