Как решить функцию: Ошибка: 404 Материал не найден

Решение задач на функции по математике с примерами

Оглавление:

Сначала идёт подробная теория по функциям, а потом примеры решения задач по функциям.

Функция

К оглавлению…

Функция считается заданной, если каждому соответствует единственное по определенному правилу вычисленное , где и — числовые множества. Говорят, что зависит от , и функция — это зависимость переменной от переменной . Множество называется областью определения функции, множество — областью значений функции. Переменную называют независимой переменной, а переменную — зависимой. Переменная является функцией от , что записывается Для записи функций используются и другие буквы: и т. п.

Переменная называется аргументом функции, — ее значением.

Функция может быть задана формулой, таблицей и другими способами. Если функция задана формулой, и область определения функции не указана, то считается, что область определения состоит из всех значений независимой переменной, при которых эта формула имеет смысл.

Например, если то область определения функции все , кроме , т. е.

Если — многочлен, то называется целой рациональной функцией; если — это дробно-рациональная функция. Например, — целая рациональная функция 3-й степени; —— дробно-рациональная функция.

Введем понятие координатной плоскости. Проведем на плоскости через точку две взаимно перпендикулярных прямые и — оси координат. Ось называется осью абсцисс, ось — осью ординат, точка — началом координат. Этой точкой каждая из осей разбивается на две полуоси, одна из которых — положительная, другая — отрицательная.

Каждой точке плоскости ставится в соответствие пара чисел ; — координаты точки. Это записывается , — абсцисса точки, — ордината. Значение определяется как расстояние от начала координат до основания перпендикуляра, опущенного из точки на ось ; значение — расстояние от начала координат до основания перпендикуляра, опущенного из точки на .Для определения значений и на осях выбираются единичные отрезки.

Оси координат разбивают плоскость на 4 четверти: I, II, III и IV. В I четверти обе координаты положительны, во II — координата отрицательна, положительна, в III — обе координаты отрицательны, в IV — положительна, отрицательна. Приведенное описание — это прямоугольная декартова система координат. Графиком функции называется множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты — соответствующим значениям функции. График представляет собой линию на плоскости, непрерывную или разрывную.

Линейная функция

К оглавлению…

Функция вида где и — числа, называется линейной функцией, ее область определения т.е. . Область значений линейной функции , т. е., если ; если , то .

График линейной функции — прямая линия, угол наклона которой к оси определяется числом (угловой коэффициент). Если — угол наклона, то если , то прямая параллельна .

Например, график функции — прямая .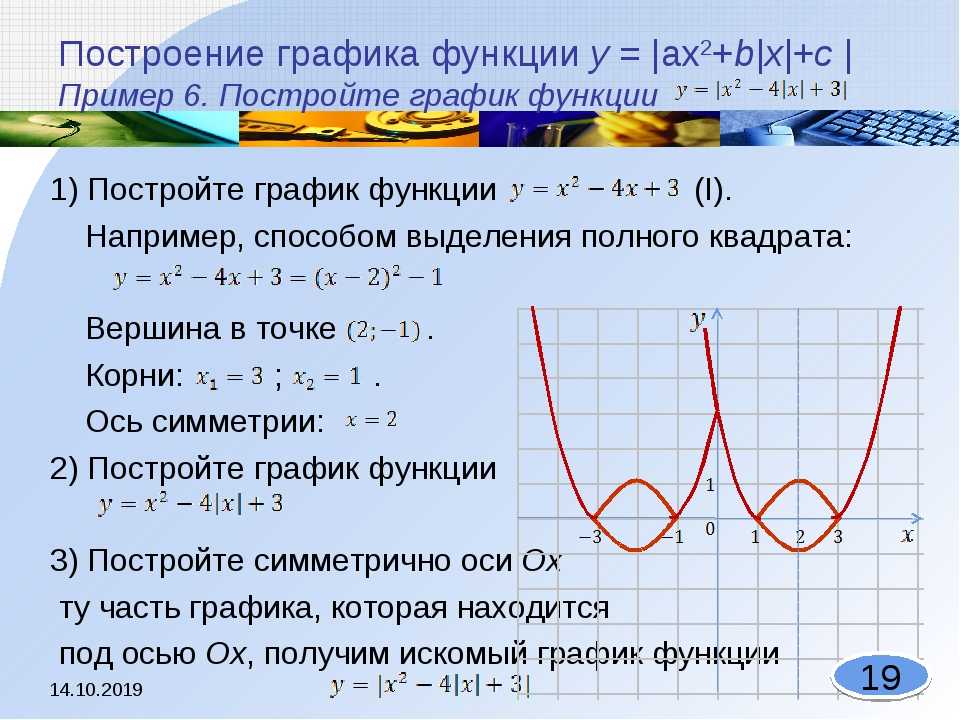

График линейной функции строится по двум точкам, т. к. две точки определяют прямую единственным образом.

Квадратичная функция

К оглавлению…

Функция , где называется квадратичной. Область определения квадратичной функции, или График квадратичной функции называется параболой, ее ветви направлены вверх, если , и вниз, если . И в том, и в другом случае парабола имеет вершину, координаты которой вычисляются по следующим формулам:;. Обычно при необходимости по формуле вычисляют , a получают подстановкой в формулу , т. е. . Парабола имеет вертикальную ось симметрии, проходящую через вершину. Построение параболы часто сводится к нахождению точек пересечения графика с т.е. корней уравнения , если они существуют, и координат вершины. Если корней нет, то находят еще несколько точек.

Например, график функции имеет вершину в т. , т.к. и проходит через точки и . Построим графики функций и

1)

2)Корни уравнения те же

Из графиков видно, что множество значений квадратичной функции , если , и если

Эта функция называется обратной пропорциональностью. Область ее определения т. к. .

Множество значений График этой функции называется гиперболой;

он не имеет точек пересечения с осями и и имеет эти оси в качестве асимптот, т. е. прямых, к которым кривая бесконечно приближается.

График расположен в I и III четвертях, если и во II и IV четвертях, если .

Например, построим график . Он проходит через точки График симметричен относительно начала координат.

Степенная функция с целым показателем

К оглавлению…

Степенной функцией с целым показателем называется функция вида , где — целое число. Отметим, что частными случаями такой степенной функции являются линейная функция , квадратичная функция обратная пропорциональность Графики этих функций представлены ниже.

1) Показатель степени — нечетное положительное число, например,

График называется кубической параболой.
2) — четное положительное число ., например,

3) — нечетное отрицательное число например,

4) — четное отрицательное число например ,

Показательная функция

К оглавлению…

Функция где называется показательной. При этом Функция имеет различные графики при и

1) ; если возрастает, то также возрастает, например,

2) ; если возрастает, то убывает, например,

Логарифмическая функция

К оглавлению…

Функция , где и , называется логарифмической. Так же, как и в случае показательной функции, существуют 2 графика логарифмической функции: при и при . Например,

Тригонометрические функции

К оглавлению…

Тригонометрическими функциями называются функции

1) График — синусоида, период

2) График — синусоида, период

3) период

4) период .

Функции: относятся к элементарным. К ним присоединяют еще

График функции

Преобразование графиков функции

К оглавлению…

Одним из способов построения графиков является способ получения из графика функции графиков функций следующего вида:

Построение нового графика происходит на основе графика элементарной функции путем его преобразования.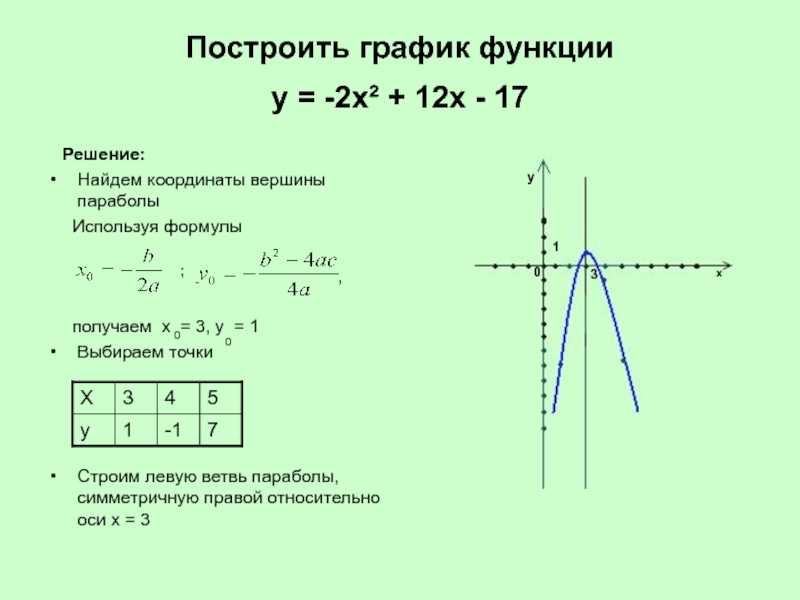

В 1-м случае график получается из графика путем сдвига этого графика как единого целого вдоль оси ординат на единиц. Например, построим график функции Сначала построим график и затем сдвинем его на 3 единицы вниз.

Во 2-м случае график получается из графика путем сдвига вдоль оси абсцисс на единиц влево, если , и вправо, если . Например, построим график

В 3-м случае для построения графика надо растянуть график в раз вдоль оси ординат при неиз —

менной оси абсцисс. Если , то растяжение часто называют сжатием. Например, построим графики:

В 4-м случае для построения графика надо растянуть или сжать вдоль оси абсцисс при неизменной оси ординат график Если , происходит растяжение, если — сжатие. Например, построим графики и

В 5-м случае для получения графика из графика нужно отразить его симметрично относительно оси абсцисс. Например, построим график функции .

В 6-м случае для получения графика из графика нужно отразить его симметрично относительно оси ординат. Например, построим график функции .

В 7-м случае для получения графика из графика нужно отразить симметрично относительно оси абсцисс часть графика, лежащую ниже этой оси. Например, построим график

В 8-м случае для получения графика из графика нужно заменить часть графика, лежащую слева от оси ординат, графиком, симметричным части графика, лежащей справа от оси ординат. Например, построим график

9-й случай — это получение обратной функции. Такими взаимно обратными функциями являются и

Для построения обратной функции нужно функцию симметрично отразить относительно биссектрисы прямого угла I четверти координатной плоскости. Например, графики и

Свойства функций

К оглавлению…

1) Четность. Функция называется четной, если на всей области определения называется нечетной, если на всей области определения Например,

— четные функции.

— нечетные функции.

График четной функции симметричен относительно оси ординат; график нечетной функции симметричен относительно начала координат.

2) Периодичность. Функция называется периодической, если на всей области определения где — период.

Например, функции — периодические с периодом ; функции — периодичес-кие с периодом . Период функции равен , аналогично для

3) Возрастание. Функция возрастает на некотором интервале из области определения, если для любых и из этого интервала таких, что , выполняется

4) Убывание. Функция убывает на некотором интервале из области определения, если для любых и из этого интервала таких, что выполняется .

5) Экстремумы. Точка называется точкой минимума функции , если для всех из некоторой окрестности выполняется . Само значение — минимум функции (min). Точка называется точкой максимума функции , если для всех из некоторой окрестности выполняется Само значение в этом случае называется максимумом функции (max). Выше приведена таблица свойств элементарных функций.

Производная функции

К оглавлению…

Допустим, областью определения функции является интервал Возьмем точку и точку в окрестности точки ; тогда разность называется приращением аргумента в точке .

— приращение функции в точке .

Число называется пределом функции в точке , если для любого при всех , достаточно близких к , выполняется неравенство . Обозначается

производная функции равна пределу отношения приращения функции к приращению аргумента, если такой предел существует и конечен. Производная функции также обозначается

Производные элементарных функций

К оглавлению…

Правила вычисления производных

К оглавлению…

Если для функций и существуют производные и , то:

Если функция имеет производную на некотором интервале, то она называется дифференцируемой на этом интервале.

Если в каждой точке интервала , то возрастает на этом интервале.

Если в каждой точке интервала, то на этом интервале убывает.

Если на интервале имеет производную и и если при и при то точка является точкой максимума функции ; при этом

И наоборот, если при тех же условиях при и при , то точка — точка минимума функции , при этом .

Уравнение касательной к графику функции

К оглавлению…

Касательная к графику в точке , если дифференци-руема в точке , — это прямая, проходящая через точку и имеющая угловой коэффициент Уравнение касательной:

Например, напишем уравнение касательной к функции в точке

Уравнение касательной:

Исследование функций и построение графиков

К оглавлению…

Исследование функции, т.е. наиболее полное описание ее свойств, производится, как правило, для построения ее графика и состоит из нескольких пунктов:

1. область определения функции;
2. область значений функции;
3. четность, нечетность функции;
4. периодичность функции;
5. определение нулей функции, т.е. значений , в которых функция обращается нуль, и значения, которое принимает функция при ;
6. интервалы возрастания и убывания функции;
7. экстремумы функции;
8. нахождение, если это необходимо, дополнительных точек для построения графика.

Иногда к перечисленным пунктам добавляют еще нахождение интервалов знакопостоянства функции.

Однако для построения графика не всегда бывает необходимо проводить исследование по полной схеме, достаточно тех пунктов, которые дают возможность построить график. Так, бывает трудно найти область значений функции и нули функции.

Пример. Исследовать функцию и построить ее график..

1.Область определения .

3.функция четная.

Метод интервалов:

Функция возрастает на интервалах: и при на этих интервалах функция убывает.

7. и — эти значения называют критическими точками.

Только там, где , возможны экстремумы функции. Экстремумы легко определить по схеме.

Стрелка, направленная вверх, означает возрастание функции, вниз — убывание.

Если в критической точке возрастание функции сменяется убыванием, то в этой точке — максимум, если наоборот — минимум.

8.Составим небольшую таблицу:

Строим график. Область значений функции, которую сразу определять было сложно,

Наибольшее и наименьшее значения функции

К оглавлению…

Решение многих практических задач часто сводится к нахождению наибольшего и наименьшего значений непрерывной на отрезке функции. Правило нахождения этих значений таково: чтобы найти наибольшее и наименьшее значения функции, имеющей на отрезке конечное число критических точек, нужно вычислить значения функции во всех критических точках и на концах отрезка, а затем из полученных чисел выбрать наибольшее и наименьшее.

Например, найдем наименьшее и наибольшее значения функции на отрезке

критические точки.

Составим таблицу:

Итак, наименьшее значение а наибольшее 5, часто это записывают так:

Первообразная и интеграл

К оглавлению…

Функция называется первообразной для функции на некотором промежутке, если для всех из этого промежутка

Например, функция -первообразная для функции при так как

Любая первообразная для при может быть записана как где — одна из первообразных для при а — произвольное число.

Нахождение первообразной для функции — действие, обратное нахождению производной. Исходя из этого, можно составить таблицу первообразных некоторых функций.

Три правила нахождения первообразных

К оглавлению…

1. Если — первообразная для , a — первообразная для , то — первообразная для
2. Если — первообразная для и — число, то — первообразная для .
3. Если — первообразная для, и — числа и , то — первообразная для

Например, найдем первообразные.

Пусть функция непрерывна на отрезке и не меняет знака на этом отрезке. Тогда фигуру, ограниченную графиком этой функции, отрезком и прямыми называют криволинейной трапецией.

Например,

Заштрихованная фигура — криволинейная трапеция.

Для вычисления площади криволинейной трапеции применяется формула:

В нашем примере

Площадь криволинейной трапеции может быть получена так же, как где — сумма площадей прямоугольников, на которые разбивается криволинейная трапеция. Основания прямоугольников и (площадь трапеции). Суммирование площадей называется интегрированием, а площадь трапеции выражается как интеграл, т.е.

— формула Ньютона-Лейбница.

Для удобства используют запись:

Например,

Вычислим площадь фигуры, ограниченной линиями:

Сделаем чертеж.

где — площадь криволинейной трапеции,

ограниченной синусоидой, осью и прямыми и — площадь 6 6 прямоугольника, ограниченного прямыми

Решение задач на функции

К оглавлению…

Найти область определения функций

К оглавлению…

Найти область значений функции

К оглавлению…

Построить график функций методом преобразования

К оглавлению…

Какие из следующих функций являются чётными? нечётными? не являются ни чётными, ни нечётными?

К оглавлению…

Определить период функций

К оглавлению…

Найти производные функций

К оглавлению…

Касательная к графику функции

К оглавлению…

Задача №160

Написать уравнение касательной к графику функции в точке

Решение, — уравнение касательной, где

Задача №161

Найти тангенс ума наклона касательной, проходящей через точку графика функции

Решение:

Задача №162

Написать уравнение касательной к графику функции в точке

Задача №163

Найти точки графика функции в которых касательная параллельна оси абсцисс.

Решение:

Если прямая , то угол между ними равен , т. е.

Задача №164

Под каким углом пересекается с осью график функции

Решение:

Угол пересечения определяется углом между касательной к графику в точке пересечения и осью .

— уравнение касательной, где — угол наклона касательной к в точке .

Задача №165

Под каким углом пересекается с осью график функции

Решение. График пересекается с в точке

— угол наклона касательной в точке к

— угол наклона касательной в этой же точке к ;

Задача №166

Найти все значения , при которых касательные к графикам функций в точках с абсциссой параллельны.

Решение:

Параллельность касательных означает равенство их угловых коэффициентов. Поэтому

Задача №167

К параболе в точке с абсциссой проведена касательная. Найти точку пересечения этой касательной с .

Решение:

— уравнение касательной.

При пересечении с

Ответ: точка

Задача №168

Найти координаты точки пересечения двух касательных, проведенных к графику функции в точке с абсциссой и в точке с абсциссой

Решение:

Задача №169

Найти уравнения общих касательных к параболам и

Решение:

1) Касательная к проходит через точку с абсциссой этой параболы. Уравнение касательной:

2) Касательная к проходит через точку с абсциссой этой параболы. Уравнение касательной:

Эти касательные — одна и та же прямая, следовательно их угловые коэффициенты и свободные члены совпадают.

Уравнения касательной к функциив точке с абсциссой

Задача №170

Вычислите площадь треугольника, ограниченного осями координат и касательной к графику функции в точке с абсциссой

Решение:

Сделаем схематический чертеж. Функция гипербола, т. к.

Эта гипербола имеет асимптоты и Т. к. , начертим только одну ветвь гиперболы.

— Уравнение касательной.

Эта прямая пересекается с при в точке и пересекается с при в точке

Задача №171

Найти угол между касательными, проведенными из точки к параболе

Решение:

Сделаем чертеж. касательной к графику в точке с абсциссой .

Эта прямая проходит через точку , поэтому Возьмем касательную к правой ветви параболы; и

Угол между касательными

Ответ:

Задача №172

В точке к графику функции проведена касательная. Найти длину ее отрезка, заключенного между осями координат.

Решение:

Уравнение касательной к графику функции при.

Прямая пересекает ось в точке и ось в точке Расстояние между этими точками:

Ответ:

Задача №173

Найти уравнения тех касательных к графику функции которые вместе с осями координат ограничивают треугольник площади .

Решение:

Прямая отсекает на осях и следующие отрезки:

при

при имеет катеты и

Уравнение касательной

Исследование функций и построение графиков

К оглавлению…

Наибольшее и наименьшее значение функции

К оглавлению…

Первообразная и интеграл

К оглавлению…

Эта лекция взята со страницы решения задач по математике:

Решение задач по математике

Возможно вам будут полезны эти страницы:

Степенная функция, ее свойства и график 9 класс онлайн-подготовка на Ростелеком Лицей

 

 

Тема: Числовые функции

 

Урок: Степенная функция её свойства и график

 

 

1. Введение

 

 

На этом уроке мы начнем рассматривать степенную функцию с отрицательным показателем.

 

 

2. График и свойства функции

 

 

Сначала мы познакомимся с функцией т. е. с функциями вида:

 

Рассмотрим график функции

Можно воспользоваться таблицей, а можно проанализировать уже известные нам графики (рис. 1,2).

Изучая графики функций можно себе представить, как будет выглядеть график функции  (рис. 3).

Функция четная, поэтому мы можем изучить и изобразить график на луче и симметрично отобразить относительно оси y.

Если  xвозрастает, то и возрастает, а убывает.

При  функция не существует.

 

Прочтем график.

Если  то у возрастает,

Если то у убывает,

1.

2. Функция четная, График симметричен относительно оси y.

3. Функция убывает на луче  и возрастает на луче

4. Функция ограничена снизу и не ограничена сверху.

5. Функция не имеет ни наибольшего, ни наименьшего значения.

6. Функция непрерывна на луче  и на луче

7.

8. Функция выпукла вниз на луче  и на луче

Функция имеет асимптоты, рассмотрим их.

Асимптота – это такая прямая, к которой данная кривая неограниченно приближается.

При

Ось xявляется горизонтальной асимптотой, её уравнение .

При

При

Ось yявляется вертикальной асимптотой, ее уравнение .

Рассмотрим интервалы знакопостоянства функции (рис. 4).

На луче  функция положительна, на луче  функция положительна, и только при функция не существует.

Рассмотрим типовые неравенства.

 

3. Примеры

 

 

Свойства функции – ключ к решению многих задач.

 

1. Найти все значения параметра m, при каждом из которых уравнение

имеет хотя бы одно решение.

Решение:

Изобразим график функции , она определена при всех x кроме (рис. 5).

Это значит, что любое значение  достигается хотя бы при одном значении аргумента.

Заметим, что если мы задаем  то получаем два решения, .

2. Решить уравнение с параметром:

Решение:

Необходимо построить график функции  пересечь его семейством прямых , найти точки пересечения и выписать ответ (рис. 5а).

Нет решений при

Два различных решения при

Мы подробно рассмотрели график и свойства функции  Рассмотрим график и свойства подобных функций в общем виде.

 

4. График и свойства функции

 

 

Функция

 

Все эти функции проходят через  фиксированные характерные точки (-1; 1) и (1; 1) (рис. 6).

Асимптоты: горизонтальная  и вертикальная

Свойства функции:

2. Функция четная.

3. Убывает на луче  и возрастает на луче

4. Ограничена снизу и не ограничена сверху.

5. Не имеет ни наибольшего, ни наименьшего значения.

6. Непрерывна на луче  и на луче

8. Выпукла вниз на луче  и на луче

Рассмотрим взаимное расположение кривых (рис. 7).

Обе кривые проходят через две фиксированные точки:

 

5. Примеры

 

 

1. Найдите область значений функции:

 

Решение:

Если  , то y убывает,

Ответ:

Кривая сдвинута по оси xна три единицы вправо. Функциямонотонно возрастает при

Ответ:

 

6. Заключение

 

 

Мы рассмотрели функцию  На следующем уроке мы познакомимся с функциями вида  т.е. с функциями и т.д.

 

 

Список рекомендованной литературы

1. Мордкович А.Г. и др. Алгебра 9 кл.: Учеб. Для общеобразоват. Учреждений.- 4-е изд. – М.: Мнемозина, 2002.-192 с.: ил.

2. Мордкович А.Г. и др. Алгебра 9 кл.: Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Т. Н. Мишустина и др. — 4-е изд. — М.: Мнемозина, 2002.-143 с.: ил.

3. Макарычев Ю. Н. Алгебра. 9 класс : учеб.для учащихся общеобразоват. учреждений / Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, И. Е. Феоктистов. — 7-е изд., испр. и доп. — М.: Мнемозина, 2008.

4. Алимов Ш.А., Колягин Ю.М., Сидоров Ю.В. Алгебра. 9 класс. 16-е изд. — М., 2011. — 287 с.

5. Мордкович А. Г. Алгебра. 9 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений / А. Г. Мордкович, П. В. Семенов. — 12-е изд., стер. — М.: 2010. — 224 с.: ил.

6. Алгебра. 9 класс. В 2 ч. Ч. 2. Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Л. А. Александрова, Т. Н. Мишустина и др.; Под ред. А. Г. Мордковича. — 12-е изд., испр. — М.: 2010.-223 с.:ил.

 

Рекомендованные ссылки на ресурсы интернет

1. Открытая математика (Источник)

2. Задачи (Источник)

3. Решу ЕГЭ (Источник)

 

Рекомендованное домашнее задание

Мордкович А.Г. и др. Алгебра 9 кл.: Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Т. Н. Мишустина и др. — 4-е изд. — М. : Мнемозина, 2002.-143 с.: ил.

№№ 332(а, в), 333(a, г), 335.

 

 

Функции с числом е

  Функции с числом е. Друзья! На сайте «Математический тандем» проходит конкурс «Лучший комментатор декабря 2012 года», так что добро пожаловать, будут призы. В данной статье мы с вами рассмотрим задачи, входящие в сотав типовых заданий экзамена по математике, связанные с исследованием функций (где присутствует число е).

Рекомендую вам ещё раз внимательно прочитать статью «Исследование функций. Это нужно знать!» и освежить в памяти изложенную информацию. Не устану повторять, что для того чтобы решать задачи на нахождение наибольшего или наименьшего значения, задачи на нахождение экстремумов, важно понимать свойства производной для исследования функций, знать таблицу производных и правила дифференцирования.

После решения каждой задачи есть разъяснения другого подхода к решению (я обещал вам «хитрости» — они здесь). Рекомендую посмотреть, выглядит график показательной функции

.

Рассмотрим задачи:

Найдите наименьшее значение функции у = (х–17)е^х–16 

на отрезке [15;17].

Мы знаем, что для того, чтобы найти наибольшее или наименьшее значение функции на отрезке, необходимо вычислить её значение на границах заданного интервала и в точках, где производная равна нулю. Действуем по алгоритму:

1. Найдём производную заданной функции:

2. Найдем нули производной на заданном отрезке, то есть приравниваем производную к нулю и вычислим корни уравнения:

*Выражение е^х-16 не равно нулю ни при каких х, так как известно, что показательная функция имеет положительные значения на всей области определения.

3. Определяем принадлежит ли найденная точка интервалу.

Точка х = 16  принадлежит интервалу  [15;17]. Значит значение функции будем вычислять в точках  15, 16 и 17:

*Учтите, что число е ≈ 2,71.  Это нецелое число и неконечная десятичная дробь, поэтому любое выражение с этим числом в подобных задачах на ЕГЭ не является верным ответом, но вы всё равно его проанализируйте. В данной задаче, если мы  –2 разделим на число 2,71  то результат будет лежать в пределах от –1 до 0 (можно посчитать столбиком для проверки).

4. Делаем вывод.

Таким образом, наименьшее значение функции равно  –1.

Ответ: –1

В этой статье  я обещал вам какие-то там «хитрости», которые можно использовать при решении. Если вы поняли теорию производной и знаете, как находить максимальные и минимальные значения, то тогда читайте дальше — представленный приём будет хорошим дополнительным «инструментом» и позволит решать подобные задания мгновенно.

Итак! Мы знаем, что ответом в задачах на ЕГЭ в части В должно быть целое число, либо конечная десятичная дробь.

Посмотрите на данную функцию. Сразу можно сказать, что  значение функции будет являться целым числом только при х = 16 или при х = 17,  и  ни при каких других значениях х. Поэтому достаточно вычислить:

и далее записать ответ.

Ещё один путь решения (без нахождения производной). Сразу подставляем в функцию все целые значения из интервала (их всего три 15, 16 и 17), вычисляем и выбираем наименьшее значение:

Решите самостоятельно:

Посмотреть решение 

 

Найдите точку минимума функции у = (х + 18)е^х-18   

1. Найдём производную заданной функции:

2. Найдем нули производной:

Получаем, что х = –19.  

*Выражение е^х-18 не равно нулю ни при каких х, так как известно, что показательная функция имеет положительные значения на всей области определения.

3. Определим знаки производной функции на интервалах (подставляем любые произвольные значения в производную) и изобразим на рисунке поведение функции:

В точке х = –19 функция меняет знак с отрицательного на положительный, значит это искомая точка минимума.

Ответ: –19 

Как решать быстрее данный тип задач?

Когда мы получили производную и приравняли её к нулю:

(х + 19)е^х–18 = 0

Далее получили, что х=–19. Данное решение и будет являться ответом задачи. 

*То есть, в при решении данного типа задач, можно обойтись без определения знаков производной на интервалах. Но будьте осторожны! В других заданиях на нахождение максимума (минимума), где получите несколько нулей производной, её знаки на интервалах нужно определять обязательно.

Решите самостоятельно:

Посмотреть решение 

 

Найдите точку максимума функции у = (3х² – 15х + 15)е^7–х

Найдём производную заданной функции:

Найдем нули производной:

Число е^7-х не может быть равно нулю, так как степень положительного числа всегда даст в результате число положительное. 

Решаем  – 3 (х–5)(х–2) = 0.  Получим х₁ = 5  и  х₂ = 2 .

Определим знаки производной функции (подставляя любые значения из интервалов в найденную производную) и изобразим на рисунке поведение функции:

В точке х = 5 функция меняет знак с положительного на отрицательный, значит это искомая точка максимума.

Ответ: 5

Решите самостоятельно:

Посмотреть решение 

 

Найдите наибольшее значение функции у = (22 – х)е

х–21  

на отрезке [16;25].

Найдём производную заданной функции:

Найдем нули производной:

Число е^х-21 не может быть равно нулю, так как степень положительного числа всегда даст в результате число положительное, значит х = 21.

Полученное значение принадлежит интервалу [16;25].

Вычислим значения данной в условии функции в точках 16, 21  и 25:

*То есть на границах интервала и в точке, где производная обращается в нуль.

Первый результат меньше единицы (это понятно и без вычислений).

Третий результат так же меньше единицы (отрицательное число).

Значит наибольшее значение функции на заданном  интервале равно 1.

*Помните, что ответы с числом е (по требованиеям ЕГЭ) не являются верными.

Ответ: 1

Если у вас всё-таки неразрешимые проблемы с нахождением производной, то подставляйте в исходную функцию все целые значения из интервала и выбирайте наибольшее полученное значение.

*Кроме того, по данной функции сразу видно, что её значение будет целым числом только при х = 21 или при х = 22.

Можете подставить только их в функцию, далее произвести вычисления и выбрать наибольшее значение.

Решите самостоятельно:

Посмотреть решение 

 

Найдите наибольшее значение функции у = (2х² – 10х + 10)е ^х

на отрезке [–4; 3].

Необходимо определить значения на границах интервала, и в точках, где производная обращается в нуль.

Найдём производную заданной функции:

Найдем нули производной:

Произведение множителей равно нулю, когда какой либо из этих множителей  равен нулю.

Число е^х не может быть равно нулю, так как степень положительного числа всегда даст в результате число положительное.

Значит  решением  являются корни: х₁=0  и  х₂=3

Обе точки принадлежат интервалу [–4;3], х=3 совпадает с границей интервала.

Вычисляем значения функции в точках: – 4, 0 и 3:  

Значит наибольшее значение функции равно 10.

Ответ: 10

*Как вы уже поняли, можно в заданную функцию можно подставить все целые значения х из интервала, и таким образом найти наибольшее значение функции. Но в данном случае придётся перебрать 8 чисел (–4;–3;–2;–1;0;1;2;3).

Решите самостоятельно:

Посмотреть решение 

 

Найдите наименьшее значение функции  у = (х + 44)²е^–44–х    

на отрезке  [– 46; –43] 

Найдём производную заданной функции:

Обратите внимание, что результат мы представили сразу в виде множителей, это будет удобно при вычислении нулей производной.

Найдем нули производной:

Решением являются корни:  х₁= – 44   и   х₂= – 42. 

Заданному интервалу [– 46;–43]  принадлежит только точка  х = – 44.

Вычисляем значения функции в точках – 46, – 44 и – 43, то есть на границах интервала и в точке, где производная равна нулю:

Наименьшее значение функции равно 0.

Ответ: 0

*Как это задание решить быстро?

Учитывая, что ответом должно быть целое число, видно что значение данной функции будет целым только при х= – 44 и х= 44.

указанному в условии интервалу принадлежит х= – 44, вычисляем:

Решите самостоятельно:

Посмотреть решение 

В данной рубрике продолжим рассматривать задачи, не пропустите!

На этом закончим. Всем удачи!

С уважением, Александр Крутицких. 

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

{2}+3x – 4[/latex], оцените каждое из следующих условий.

1. [латекс]f\влево(2\вправо)[/латекс]
2. [латекс]ф(а)[/латекс]
3. [латекс]f(a+h)[/латекс]
4. [латекс]\dfrac{f\left(a+h\right)-f\left(a\right)}{h}[/latex]

Показать решение

Попробуйте

Учитывая функцию [латекс]g\left(m\right)=\sqrt{m — 4}[/latex], вычислите [латекс]g\left(5\right)[/latex].

Показать решение

В дополнение к функциям оценки 9{2}+2p[/латекс], найдите [латекс]ч\влево(п\вправо)=3[/латекс].

Показать решение

Как: решить функцию.

1. Замените результат в формуле указанным значением.
2. Найдите входную переменную, которая делает утверждение верным.

В следующем видео показан еще один пример решения функции.

Попробуйте

Учитывая функцию [латекс]g\left(m\right)=\sqrt{m — 4}[/latex], решить [латекс]g\left(m\right)=2[ /латекс].

Показать решение

Вычисление функций, выраженных в формулах

Некоторые функции определяются математическими правилами или процедурами, выраженными в форме уравнения .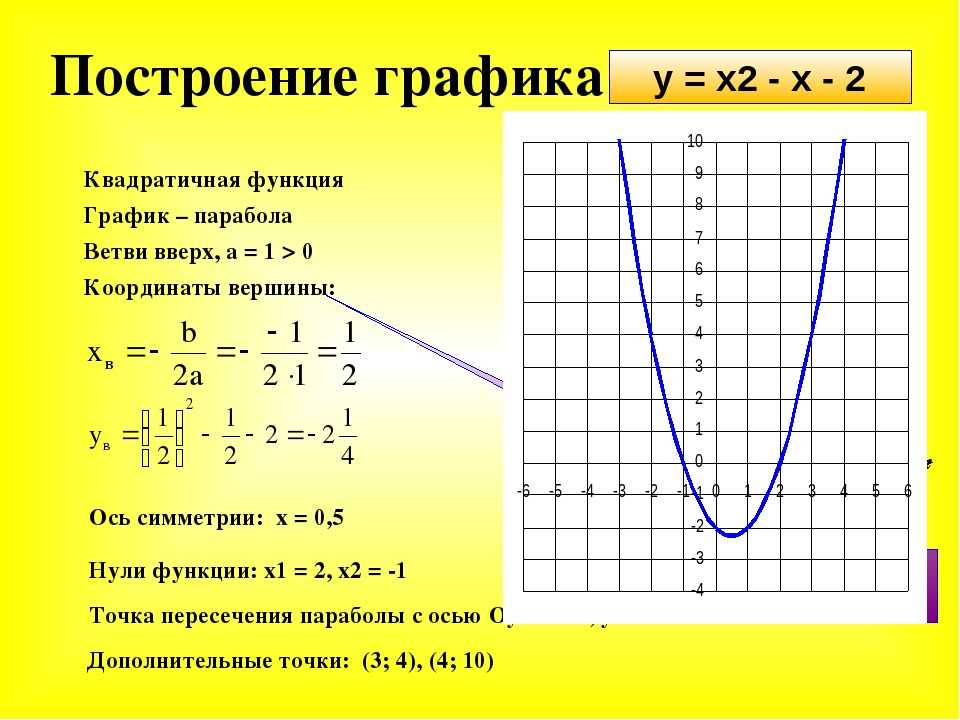 Если возможно выразить выход функции с помощью формулы , включающей входную величину, то мы можем определить функцию в алгебраической форме. Например, уравнение [латекс]2n+6p=12[/латекс] выражает функциональную связь между [латекс]n[/латекс] и [латекс]p[/латекс]. Мы можем переписать его, чтобы решить, является ли [latex]p[/latex] функцией [latex]n[/latex].

функции, уравнения и формулы

Мы видели, что уравнение типа [latex]ax+by=c[/latex] можно записать в другой форме, решив уравнение для одной из переменных. Если мы решим это линейное уравнение для y , его можно будет записать в виде линии, состоящей из пересечения наклона, [латекс]у = mx+b[/латекс].

Некоторые формулы могут быть записаны в виде функций путем решения одной из переменных. Например, вы видите, как решить формулу для прямоугольника с периметром 21 фут, [латекс]21 = 2l + 2w[/латекс] для длины?

Как: Дана функция в виде уравнения, напишите ее алгебраическую формулу.

1. Решите уравнение, чтобы изолировать выходную переменную с одной стороны от знака равенства, с другой стороны как выражение, которое включает только входную переменную.
2. Используйте все обычные алгебраические методы для решения уравнений, такие как прибавление или вычитание одной и той же величины из обеих частей или умножение или деление обеих частей уравнения на одну и ту же величину.

Пример: нахождение уравнения функции

Выразите отношение [latex]2n+6p=12[/latex] в виде функции [latex]p=f\left(n\right)[/latex], если возможно .

Показать решение

Посмотрите это видео, чтобы увидеть еще один пример того, как выразить уравнение в виде функции.

Иногда отношения между переменными нельзя выразить в виде функции. См. приведенный ниже пример для получения дополнительной информации.

Пример: выражение уравнения окружности в виде функции 9{y}[/latex], если мы хотим выразить [latex]y[/latex] как функцию [latex]x[/latex], не существует простой алгебраической формулы, включающей только [latex]x[/latex] что равно [латекс]у[/латекс]. Однако каждый [латекс]x[/латекс] определяет уникальное значение для [латекс]у[/латекс], и существуют математические процедуры, с помощью которых [латекс]у[/латекс] можно найти с любой желаемой точностью. В этом случае мы говорим, что уравнение дает неявное (подразумеваемое) правило для [latex]y[/latex] как функции [latex]x[/latex], даже если формулу нельзя записать явно.

Вычисление функции, заданной в табличной форме

Как мы видели выше, мы можем представлять функции в виде таблиц. И наоборот, мы можем использовать информацию в таблицах для написания функций, и мы можем оценивать функции, используя таблицы. Например, насколько хорошо наши питомцы помнят приятные воспоминания, которыми мы делимся с ними? Существует городская легенда, что у золотой рыбки память 3 секунды, но это всего лишь миф.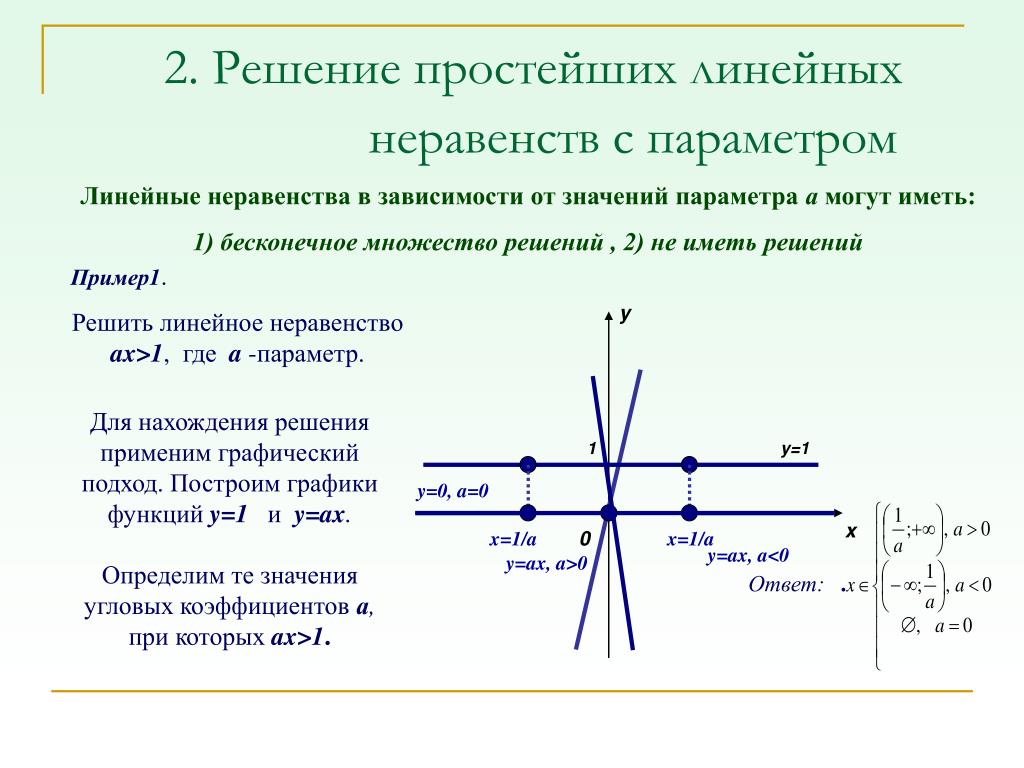 Золотая рыбка может помнить до 3 месяцев, а бета-рыбка имеет память до 5 месяцев. И если память щенка не превышает 30 секунд, то взрослая собака может помнить 5 минут. Это мизер по сравнению с кошкой, память которой длится 16 часов.

Функцию, связывающую тип питомца с длительностью его памяти, легче визуализировать с помощью таблицы. См. таблицу ниже.

Домашнее животное	Объем памяти в часах
Щенок	0,008
Взрослая собака	0,083
Кат	16
Золотая рыбка	2160
Бета-рыба	3600

Иногда вычисление функции в виде таблицы может оказаться более полезным, чем использование уравнений. Здесь давайте вызовем функцию [latex]P[/latex].

Домен функции — это тип питомца, а диапазон — действительное число, представляющее количество часов, в течение которых сохраняется память питомца. Мы можем оценить функцию [latex]P[/latex] по входному значению «золотая рыбка». Мы бы написали [латекс]P\влево(\текст{золотая рыбка}\вправо)=2160[/латекс]. Обратите внимание, что для вычисления функции в форме таблицы мы идентифицируем входное значение и соответствующее выходное значение из соответствующей строки таблицы. Табличная форма для функции [latex]P[/latex] кажется идеально подходящей для этой функции, в большей степени, чем ее запись в форме абзаца или функции.

Как сделать: Имея функцию, представленную в виде таблицы, определите конкретные выходные и входные значения.

1. Найдите заданный вход в строке (или столбце) входных значений.
2. Идентифицируйте соответствующее выходное значение в паре с этим входным значением.
3. Найдите указанные выходные значения в строке (или столбце) выходных значений, отмечая каждый раз, когда появляется это выходное значение.
4. Определите входное значение(я), соответствующее данному выходному значению.

Пример: вычисление и решение табличной функции

Используя приведенную ниже таблицу,

1. Вычислите [латекс]г\влево(3\вправо)[/латекс].
2. Решить [латекс]г\влево(п\вправо)=6[/латекс].

[латекс]n[/латекс]	1	2	3	4	5
[латекс]g(n)[/латекс]	8	6	7	6	8

Показать решение

Попробуйте

Используя таблицу из предыдущего примера, вычислите [latex]g\left(1\right)[/latex] .

Показать решение

Поиск значений функции на графике

упорядоченные пары входов и выходов

Мы можем рассматривать функцию как набор входов и соответствующих им выходов. То есть мы можем рассматривать функцию как набор упорядоченных пар [латекс]\влево(х, у\вправо).[/латекс]

Помните, что в записи функции [латекс]у = f(х) [/latex], поэтому упорядоченные пары, содержащие входы и выходы, можно записать в виде ( ввод ,  вывод ) или [латекс]\влево(х, f(х)\вправо)[/латекс].

Вычисление функции с помощью графика также требует нахождения соответствующего выходного значения для заданного входного значения, только в этом случае мы находим выходное значение, глядя на график. Решение функционального уравнения с использованием графика требует нахождения всех экземпляров заданного выходного значения на графике и наблюдения за соответствующим входным значением (значениями).

Пример: Чтение значений функции из графика

92+x+4[/latex] с использованием обозначения функций.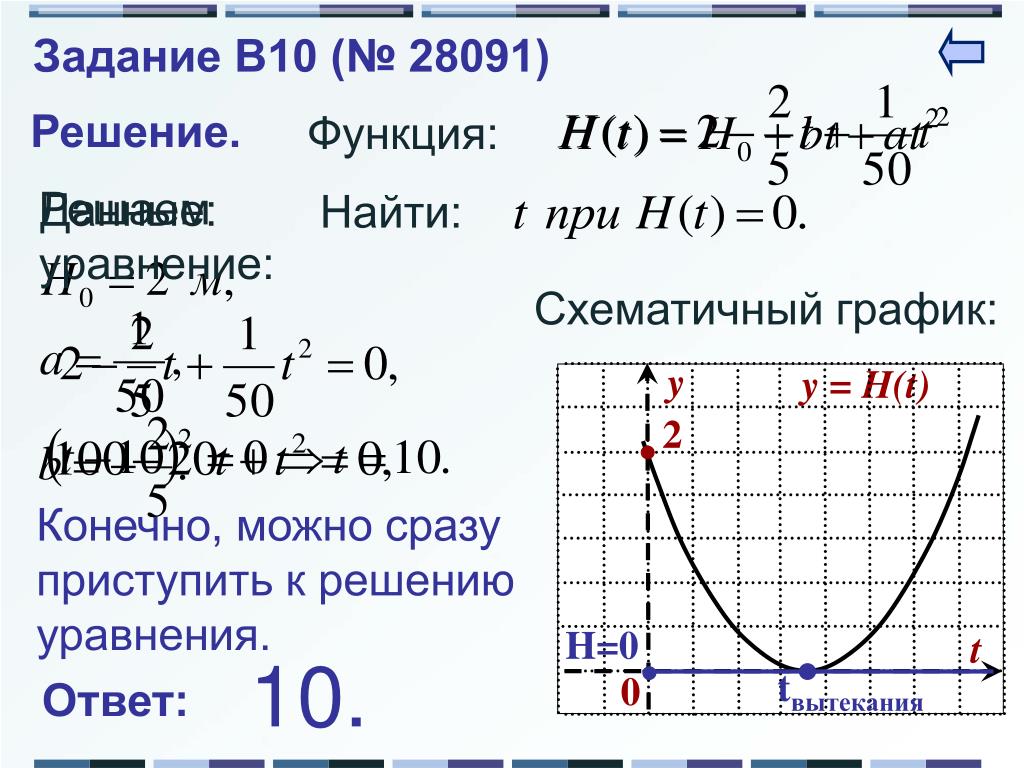

Вычислить функцию в [latex]x=1[/latex]

Создайте таблицу значений, которая ссылается на функцию. Включите как минимум интервал [latex][-5,5][/latex] для [latex]x[/latex]-значений.

Решить функцию для [латекс]f(0)[/латекс]

Исчисление I — Функции

Показать мобильное уведомление Показать все примечания Скрыть все примечания

Уведомление для мобильных устройств

Похоже, вы используете устройство с «узкой» шириной экрана ( т. е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.

Раздел 1-1: Функции

В этом разделе мы постараемся убедиться, что вы знакомы с функциями и обозначениями функций. Оба будут появляться почти в каждом разделе в классе исчисления, поэтому вам нужно будет иметь дело с ними.

Во-первых, что такое функция? Простейшее определение состоит в том, что уравнение будет функцией, если для любого \(x\) в области определения уравнения (область — это все \(x\), которые могут быть подставлены в уравнение), уравнение будет дают ровно одно значение \(y\), когда мы оцениваем уравнение при определенном \(x\).

Обычно это легче понять на примере.

Пример 1. Определите, является ли каждый из следующих функций функциями.

92} = 3 + 1 = 4\]

Теперь есть два возможных значения \(y\), которые мы могли бы использовать здесь. Мы могли бы использовать \(y = 2\) или \(y = — 2\). Поскольку есть два возможных значения \(y\), которые мы получаем из одного \(x\), это уравнение не является функцией.

Обратите внимание, что это должно иметь место только для одного значения \(x\), чтобы уравнение не было функцией.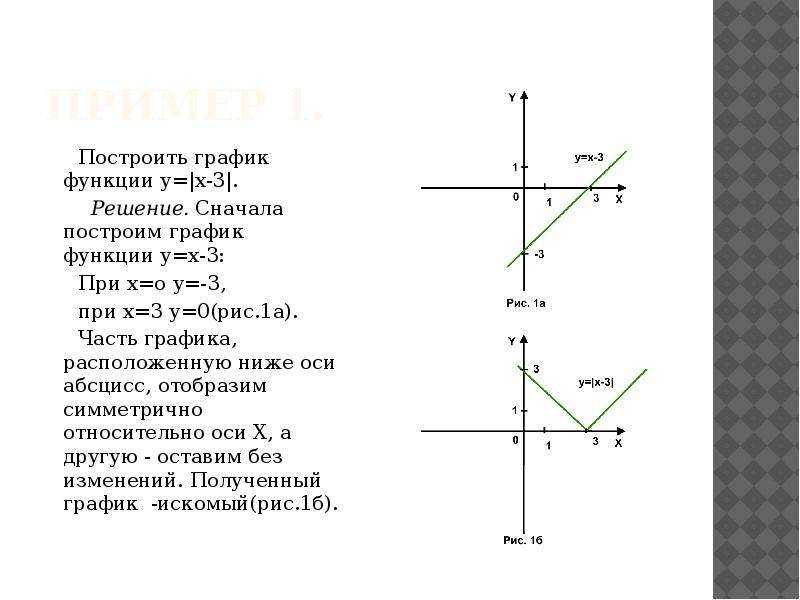 Например, мы могли бы использовать \(x = — 1\), и в этом случае мы бы получили одиночное \(y\) (\(y = 0\)). Однако из-за того, что происходит при \(x = 3\), это уравнение не будет функцией. 92} — 5x + 3\\ \end{выровнено} \\ & \vdots & \end{массив}\]

Напомним, что это НЕ буква, умноженная на \(x\), это просто причудливый способ написания \(y\).

Итак, почему это полезно? Что ж, давайте возьмем приведенную выше функцию и получим значение функции в точке \(x = -3\). Используя обозначение функции, мы представляем значение функции в точке \(x = -3\) как \(f\left(-3 \right)\). Обозначение функций дает нам хороший компактный способ представления значений функций. 92} + 6x — 11\) найти каждое из следующих.

1. \(ж\влево( 2 \вправо)\)
2. \(f\влево( { — 10} \вправо)\)
3. \(ж\влево(т\вправо)\)
4. \(f\влево({t — 3} \вправо)\)
5. \(f\влево( {x — 3} \вправо)\)
6. \(f\влево( {4x — 1} \вправо)\)

Показать все решения Скрыть все решения

a \(f\left( 2 \right)\) Показать решение 92} + 32х — 18\]

Эта мало чем отличается от предыдущей части.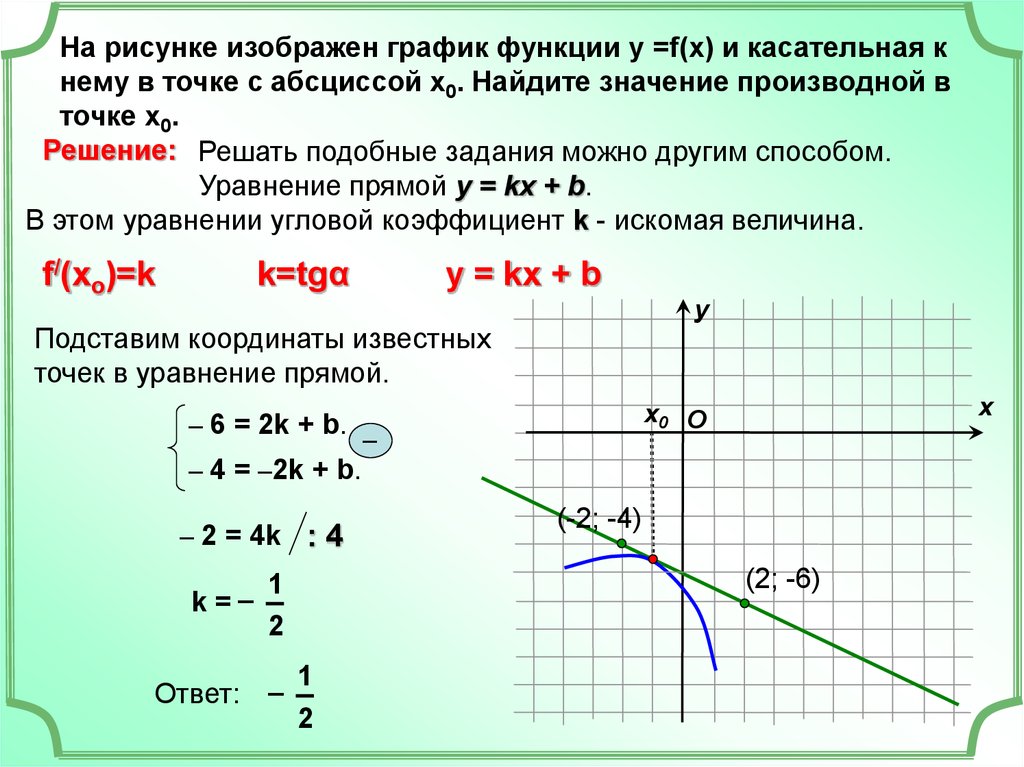 Все, что мы сделали, это изменили уравнение, которое мы подставляли в функцию.

На протяжении всего курса исчисления мы будем находить корни функций. Корень функции есть не что иное, как число, для которого функция равна нулю. Другими словами, нахождение корней функции \(g\left( x \right)\) эквивалентно решению

\[г\влево( х \вправо) = 0\] 92} — 4\влево( 3 \вправо)\влево( 2 \вправо)} }}{{2\влево( 3 \вправо)}}\\ & = \frac{{6 \pm \sqrt {12} } {6}\\ & = \ frac{{6 \pm \sqrt {\left( 4 \right)\left( 3 \right)}}}}{6}\\ & = \frac{{6 \pm 2 \sqrt 3 }}{6}\\ & = \frac{{3 \pm \sqrt 3 }}{3}\\ & = 1 \pm \frac{1}{3}\sqrt 3 \\ & = 1 \pm \frac{1}{{\sqrt 3}}\end{align*}\]

Чтобы напомнить вам, как упрощать радикалы, мы привели несколько форм ответа.

Для завершения задачи вот полный список всех корней этой функции.

\[t = 0,\,\,t = \frac{{3 + \sqrt 3 }}{3},\,\,\,t = \frac{{3 — \sqrt 3 }}{3}\ ]

Обратите внимание, что мы не использовали окончательную форму для корней из квадратного.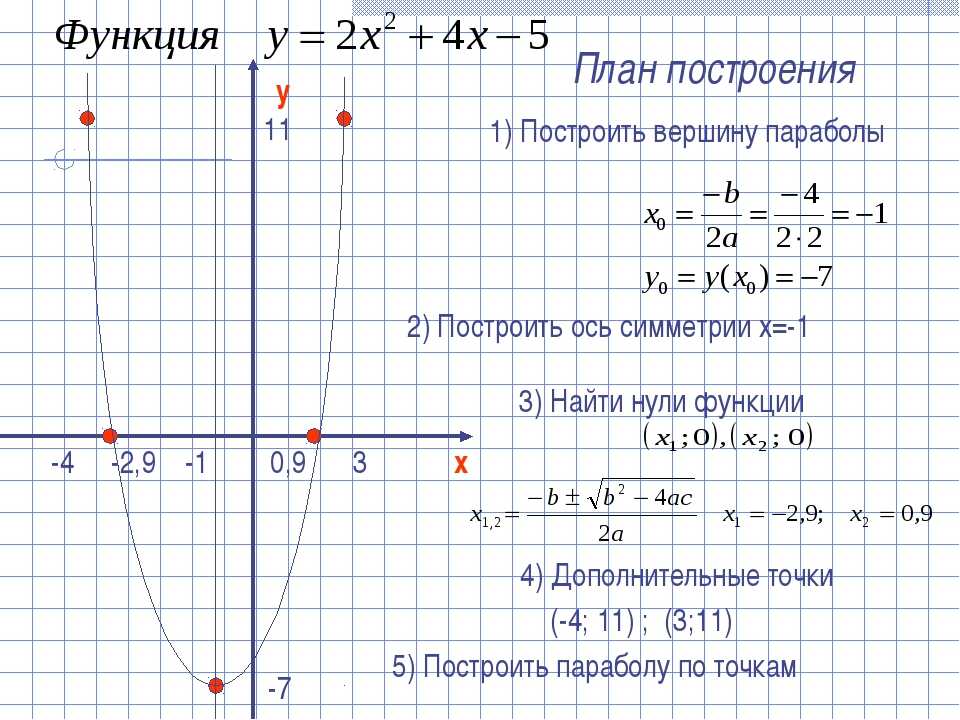 Обычно мы останавливаемся на упрощении для таких корней. Также обратите внимание, что ради практики мы разбили компактную форму для двух корней квадратного уравнения. Вы должны быть в состоянии сделать это, поэтому убедитесь, что вы можете.

В этом примере было несколько моментов, кроме поиска корней функций.

Первое, что нужно было напомнить вам о квадратной формуле. Это не последний раз, когда он вам понадобится в этом классе.

Во-вторых, чтобы вы привыкли видеть «беспорядочные» ответы. На самом деле ответы в приведенном выше примере не так уж и беспорядочны. Тем не менее, большинство студентов после занятий по алгебре очень привыкли видеть в качестве ответов только целые числа и случайные «хорошие» дроби.

Итак, честное предупреждение. На этом уроке я часто намеренно делаю ответы «грязными», чтобы вы отвыкли всегда ожидать «хороших» ответов. В «реальной жизни» (что бы это ни было) ответ редко представляет собой простое целое число, например два. В большинстве задач ответом будет десятичная дробь, полученная из неупорядоченной дроби, и/или ответ, содержащий радикалы.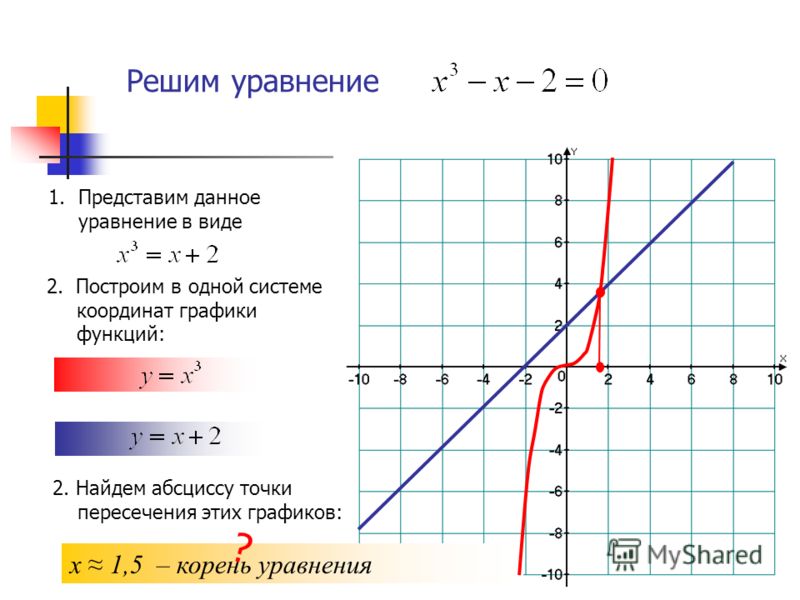

Одна из наиболее важных идей о функциях состоит в том, что домен и диапазон функции. Проще говоря, область определения функции — это набор всех значений, которые можно вставить в функцию, и при этом функция существует и имеет действительное число для значения. Итак, для домена нам нужно избегать деления на ноль, квадратных корней из отрицательных чисел, логарифмов из нуля и логарифмов из отрицательных чисел (если вы не знакомы с логарифмами, мы рассмотрим их чуть позже), 92} + 12х + 5\)

1. \(f\влево( z \вправо) = \влево| {z — 6} \вправо | — 3\)
2. \(г\влево( х \вправо) = 8\)

Показать все решения Скрыть все решения

a \(f\left( x \right) = 5x — 3\) Показать решение

Мы знаем, что это линия, а не горизонтальная линия (потому что наклон равен 5, а не нулю…). Это означает, что эта функция может принимать любое значение, поэтому диапазоном являются все действительные числа.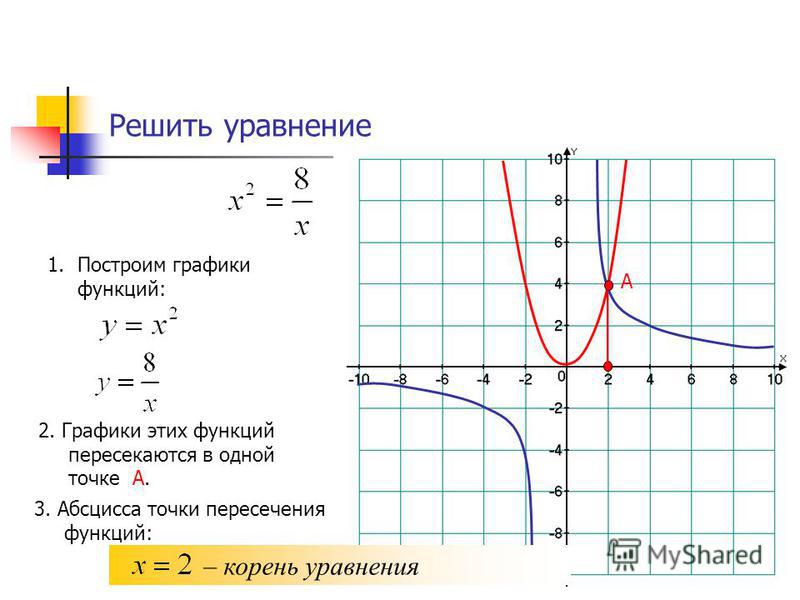 Используя «математическую» запись, это

\[{\rm{Диапазон}}:\,\,\,\влево( { — \infty ,\infty } \вправо)\]

В более общем смысле это полином, и мы знаем, что можем подставить любое значение в полином, поэтому областью определения в этом случае также являются все действительные числа или

. \[{\rm{Домен}}:\,\,\, — \infty < x < \infty \hspace{0,25 дюйма}{\rm{or}} \hspace{0,25 дюйма} \left( { - \infty ,\infty } \справа)\]

b \(g\left( t \right) = \sqrt {4 — 7t} \) Показать решение

Это квадратный корень, а мы знаем, что квадратный корень всегда положительный или нулевой. Тогда мы знаем, что диапазон будет

. \[{\rm{Диапазон}}:\,\,\,\влево [{0,\infty} \вправо)\]

Для домена нам нужно немного поработать, но немного. Нам нужно убедиться, что мы не извлекаем квадратные корни из каких-либо отрицательных чисел, поэтому нам нужно это потребовать,

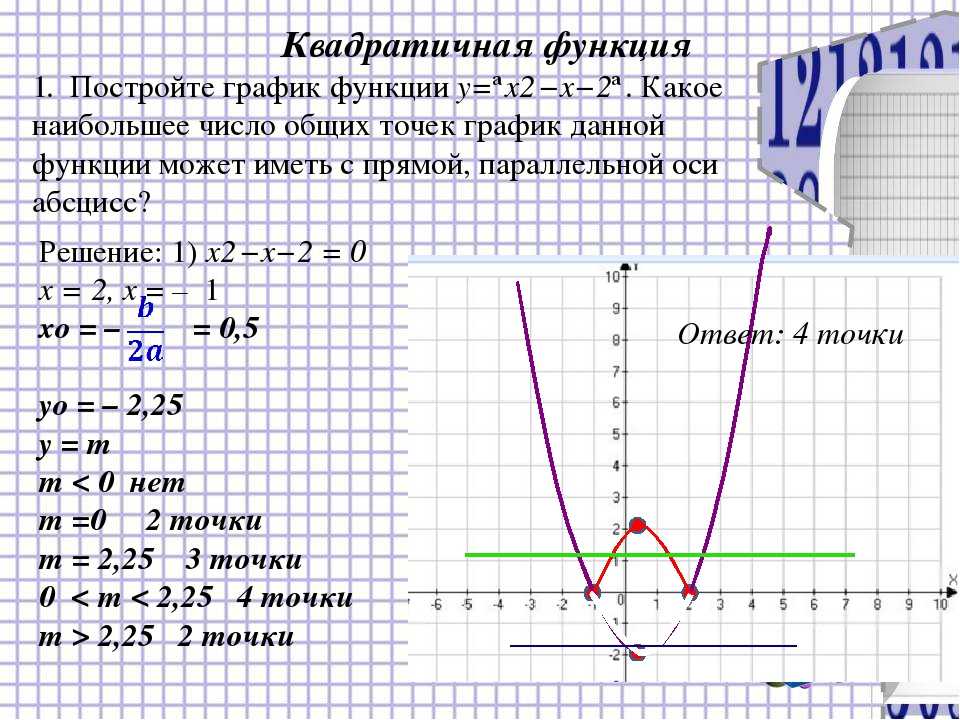. 2}\) отрицателен), и поэтому вершина будет самой высокой точкой на графике. Если мы знаем вершину, мы можем получить диапазон. Тогда вершина равна 92} + 12\влево( 3 \вправо) + 5 = 23\hspace{0,25 дюйма}\hspace{0,25 дюйма} \Стрелка вправо \hspace{0,25 дюйма}\влево({3,23} \right)\]

Итак, как обсуждалось, мы знаем, что это будет самая высокая точка на графике или наибольшее значение функции, а парабола будет принимать все значения меньше этого, поэтому диапазон тогда будет

\[{\rm{Диапазон}}:\,\,\,\влево( { — \infty ,23} \вправо]\]

d \(f\left( z \right) = \left| {z — 6} \right| — 3\) Показать решение

Эта функция содержит абсолютное значение, и мы знаем, что абсолютное значение будет либо положительным, либо нулевым. В этом случае абсолютное значение будет равно нулю, если \(z = 6\), и поэтому часть абсолютного значения этой функции всегда будет больше или равна нулю. Мы вычитаем 3 из части абсолютного значения, поэтому мы знаем, что диапазон будет

. \[{\rm{Диапазон}}:\,\,\,\влево[ { — 3,\infty } \вправо)\]

Мы можем подставить любое значение в абсолютное значение, и поэтому домен снова состоит из действительных чисел или,

\[{\rm{Домен}}:\,\,\, — \infty < z < \infty \hspace{0,25 дюйма}{\rm{или}} \hspace{0,25 дюйма} \left( { - \infty ,\infty } \справа)\]

e \(g\left( x \right) = 8\) Показать решение

Поначалу эта функция может показаться сложной, но на самом деле она самая простая в этом наборе примеров. Это постоянная функция, поэтому любое значение \(x\), которое мы подставляем в функцию, даст значение 8. Это означает, что диапазон представляет собой одно значение или 9.0011

\[{\rm{Диапазон}}:\,\,\,8\]

Домен состоит из действительных чисел,

\[{\rm{Домен}}:\,\,\, — \infty < x < \infty \hspace{0,25 дюйма}{\rm{или}} \hspace{0,25 дюйма} \left( { - \infty ,\infty } \справа)\]

В общем, определение диапазона функции может быть несколько затруднено. 2} — t — 6 = \left( {t — 3} \right)\left( {t + 2} \right) = 0\]

Итак, функция будет равна нулю при \(t = — 2\) и \(t = 3\). Напомним, что эти точки будут единственным местом, где функция может изменить знак . В этих точках не требуется менять знак, но это будут единственные точки, в которых функция может менять знак. Это означает, что все, что нам нужно сделать, — это разбить числовую прямую на три области, которые избегают этих двух точек, и проверить знак функции в одной точке в каждой из областей. Если функция положительна в одной точке области, она будет положительной и во всех точках этой области, поскольку она не содержит ни одной из точек, в которых функция может менять знак. У нас будет аналогичная ситуация, если функция отрицательна для контрольной точки.

Итак, вот числовая строка, показывающая эти вычисления.

Отсюда мы видим, что единственная область, в которой квадратичная функция (в ее модифицированной форме) будет отрицательной, находится в средней области.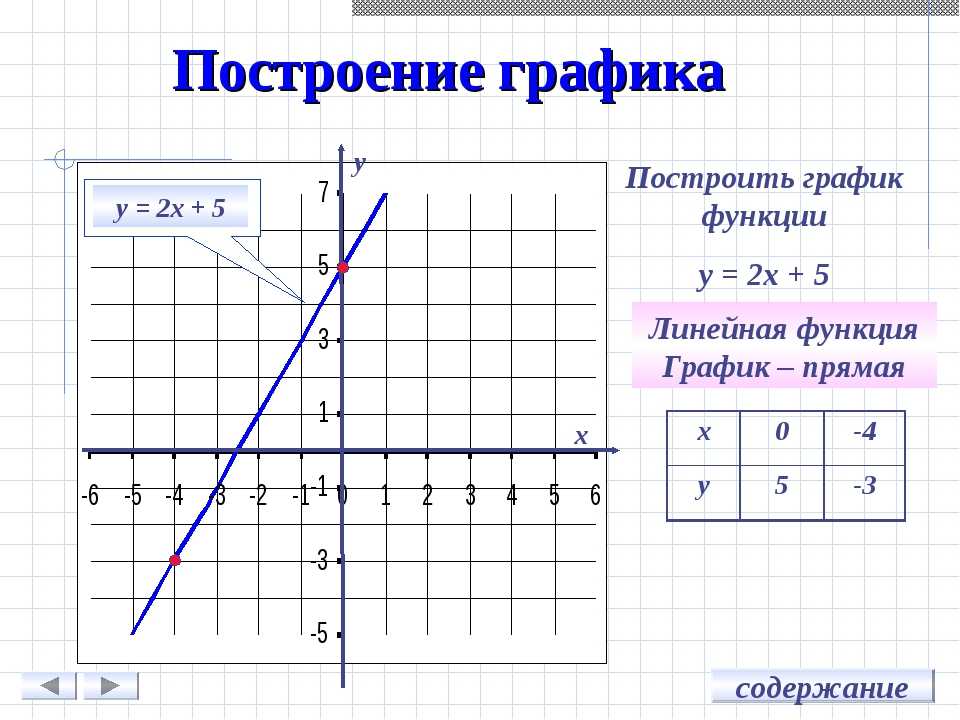 Вспоминая, что мы получили модифицированную область, умножив квадратное число на -1, это означает, что квадратное число под корнем будет положительным только в средней области, и поэтому домен для этой функции тогда будет

. \[{\rm{Домен}}:\,\,\, — 2 \le t \le 3 \hspace{0,25 дюйма} {\rm{или}} \hspace{0,25 дюйма} \left[ { — 2, 3} \справа]\] 92} — 9 > 0\]

Обратите внимание, что нам нужно, чтобы неравенство здесь было строго больше нуля, чтобы избежать деления на ноль. Мы можем либо решить это методом из предыдущего примера, либо, в данном случае, достаточно легко решить путем проверки. Домен в данном случае

\[{\rm{Домен}}:\,\,\,x < - 3\,\,\& \,\,x > 3\hspace{0,25 дюйма}{\rm{или}} \hspace{0,25 in} \left( { — \infty , — 3} \right)\,\,\& \,\,\left( {3,\infty } \right)\]

Следующая тема, которую нам нужно здесь обсудить, это композиция функций . Композиция \(f(x)\) и \(g(x)\) равна

\[\left( {f \circ g} \right)\left( x \right) = f\left( {g\left( x \right)} \right)\]

Другими словами, композиции оцениваются путем подстановки второй указанной функции в первую указанную функцию. Обратите внимание, что здесь важен порядок. Изменение порядка чаще всего приводит к другому ответу. 92} — x + 10\) и \(g\left( x \right) = 1 — 20x\) найти каждое из следующих.

1. \(\влево( {f \circ g} \вправо)\влево( 5 \вправо)\)
2. \(\влево( {f \circ g} \вправо)\влево( x \вправо)\)
3. \(\влево( {g \circ f} \вправо)\влево( x \вправо)\)
4. \(\влево( {g \circ g} \вправо)\влево( x \вправо)\)

Показать все решения Скрыть все решения

a \(\left( {f \circ g} \right)\left( 5 \right)\) Показать решение

В этом случае у нас есть число вместо \(x\), но это работает точно так же. 2} — 100x + 12\end{align*}\] 92} + 20x — 199\конец{выравнивание*}\]

И еще раз подчеркну. Этот ответ отличается от предыдущей части. В композиции важен порядок.

d \(\left( {g \circ g} \right)\left( x \right)\) Показать решение

В данном случае не горячитесь по поводу того, что это одна и та же функция. Состав по-прежнему работает так же.

\[\begin{align*}\left( {g \circ g} \right)\left( x \right) & = g\left( {g\left( x \right)} \right)\\ & = г\влево( {1 — 20x} \вправо)\\ & = 1 — 20\влево( {1 — 20x} \вправо)\\ & = 400x — 19\конец{выравнивание*}\]

Давайте рассмотрим еще один пример, который приведет нас к следующему разделу.

Пример 7. Даны \(f\left( x \right) = 3x — 2\) и \(g\left( x \right) = \frac{1}{3}x + \frac{2}{3}\ ) найти каждое из следующих.

1. \(\влево( {f \circ g} \вправо)\влево( x \вправо)\)
2. \(\влево( {g \circ f} \вправо)\влево( x \вправо)\)

Показать все решения Скрыть все решения

a \(\left( {f \circ g} \right)\left( x \right)\) Показать решение

\[\begin{align*}\left( {f \circ g} \right)\left( x \right) & = f\left( {g\left( x \right)} \right)\\ & = е \ влево ( {\ гидроразрыва {1} {3} х + \ гидроразрыва {2} {3}} \ справа) \\ & = 3 \ влево ( {\ гидроразрыва {1} {3} х + \ гидроразрыва {2 }{3}} \right) — 2\\ & = x + 2 — 2\\ & = x\end{align*}\]

b \(\left( {g \circ f} \right)\left( x \right)\) Показать решение

\[\begin{align*}\left( {g \circ f} \right)\left( x \right) & = g\left( {f\left( x \right)} \right)\\ & = g\left( {3x — 2} \right)\\ & = \frac{1}{3}\left( {3x — 2} \right) + \frac{2}{3}\\ & = x — \frac{2}{3} + \frac{2}{3}\\ & = x\end{align*}\]

В данном случае два состава были одинаковыми, и на самом деле ответ был очень простым.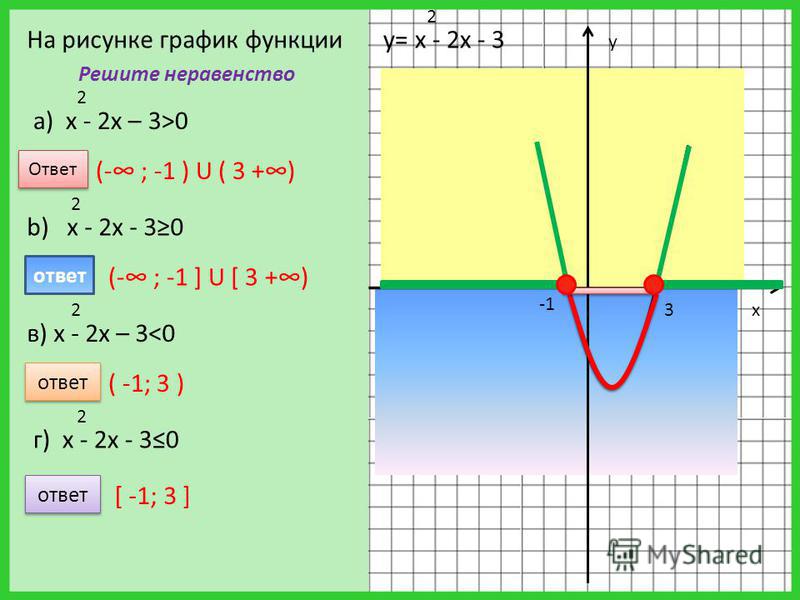

\[\left( {f \circ g} \right)\left( x \right) = \left( {g \circ f} \right)\left( x \right) = x\]

Обычно этого не происходит. Однако, когда две композиции равны \(x\), между этими двумя функциями существует очень хорошая взаимосвязь. Мы рассмотрим эту связь в следующем разделе.

Как решить уравнение в R – КОЛИЧЕСТВЕННАЯ ОПРЕДЕЛЕНИЕ ЗДОРОВЬЯ

В этой статье будет использоваться функция uniroot.all() из пакета rootSolve для поиска всех решений уравнения в заданном интервале (или области).

Ввод: uniroot.all() принимает 2 аргумента: функция f и интервал.

Как это работает: Ищет в интервале все возможные корни f .

Вывод: uniroot.all() возвращает вектор всех корней f за интервал.

Вот несколько примеров:

1.

Найдите решение простой функции: \(|x| + 4 = 0\)

Сначала введем функцию в R:

 библиотека (rootSolve)
# написание функции
f1 = функция (х) {
  абс (х) - 4
} 

Затем мы наносим функцию на график, чтобы попытаться визуально определить, сколько у нее решений (т. е. где и сколько раз она пересекает линию y = 0). Это поможет нам определить интервал (область), в котором мы будем искать решение.

 # попробуем построить функцию
# в диапазоне [-50, 50]
х = -50:50
график (х, f1 (х), тип = 'л')
# добавляем горизонтальную линию на y = 0
abline(h = 0, col = 'синий') 

Вывод:

Итак, мы видим, что функция пересекает синюю линию в 2 точках и что область значений [-50, 50] покрывает все решения функции f.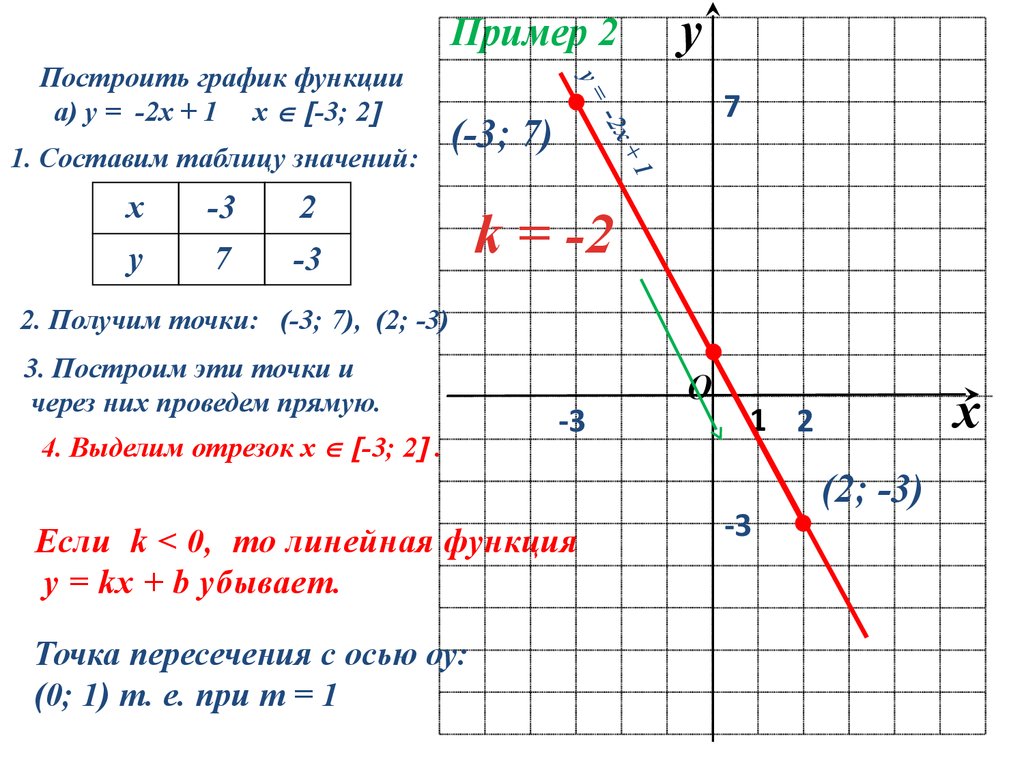

Далее мы будем использовать uniroot.all(), чтобы найти все решения f свыше [-50, 50]

 roots = uniroot.all(f1, c(-50, 50))
# print(roots) outputs: -4 4
# построение графика корней f1
точки (x = корни, y = rep (0, длина (корни)), col = "красный", pch = 16, cex = 1,5) 

Вывод:

2. Найдите решение более сложной функции: \(\frac{\sqrt{x}}{(x + 2)} – \frac{1}{4} = 0\)

 library(rootSolve)
# написание функции
f2 = функция (х) {
  кврт(х) / (х + 2) - 1/4
} 

Далее мы построим график функции на интервале [0, 100] (поскольку он содержит \(\sqrt{x}\), нет смысла пробовать отрицательные значения).

 # попробуем построить функцию
# в диапазоне [0, 100]
х = 0:100
график (х, f2 (х), тип = 'л')
# добавляем горизонтальную линию на y = 0
abline(h = 0, col = 'синий') 

Вывод:

Мы видим, что функция f имеет 2 решения в области [0,100].

Давайте точно найдем, что это такое:

 uniroot.all(f2, c(0, 100))
# выходы: 0,3431545 11,6568502
# построим решения
points(x = корни, y = rep(0, length(root)), col = "red", pch = 16, cex = 1.5) 

Вывод:

3. Найдите решение функции: \ (\frac{1}{x} = 0\)

Этот пример показывает, что uniroot. all() имеет некоторые недостатки. Иногда он не может найти все корни за указанный интервал, а иногда даже выдает неверный ответ.

 библиотека (rootSolve)
# написание функции
f3 = функция (х) {
  1/х
} 

Построение графика функции в области значений [-50, 50].

 х = -50:50
график (х, f3 (х), тип = 'л')
abline(h = 0, col = 'blue') 

Вывод:

Мы видим, что \(\frac{1}{x} = 0\) не имеет решений.

Ладно, бежим uniroot.all() на f3:

 # поиск корней f3
корни = uniroot.
No related posts.