Формула вероятность безотказной работы: 5.1. Вероятность безотказной работы

Содержание

Оценки времени безотказной работы

Планы с восстановлением отказавших элементов

Планы без замены отказавших элементов
Несмещенные оценки для вероятности безотказной работы

Оценке параметра экспоненциального закона , мы уделяем много внимания по двум причинам.

Во-первых, экспоненциальный закон находит серьезные применения в задачах теории надежности, к настоящему времени имеется большое число работ, посвященных этому вопросу. Во-вторых, для случая показательного закона многие задачи удается разрешить в явной форме, выписав ответ в виде простых формул.

Таким образом, на примере показательного закона можно изложить основные идеи методов получения оценок, не затемняя их сложными расчетами. Уместно также будет заметить, что обычно в литературе по надежности, предполагают при оценке параметров закона Вейбулла , что значение параметра р нам известно.

Однако при таком предположении закон Вейбулла заменой времени может быть сведен к показательному закону. Так называемый логарифмически показательный закон, для которого , также заменой переменных может быть сведен к показательному.

Таким образом, приводимые ниже оценки с учетом замены времени могут быть использованы и в этих случаях.

В качестве основного параметра, для которого в настоящем параграфе строятся оценки, выбрано значение . Однако можно было бы строить оценки для параметра , равного среднему значению времени безотказной работы.

В ряде случаев может возникнуть необходимость получения оценок для вероятности безотказной работы в течение заданного времени . В конце статьи даны формулы для несмещенных оценок , соответствующие планам [N, Б, r], [N, B, r].

Планы с восстановлением отказавших элементов

Вначале рассмотрим планы испытаний с восстановлением отказавших элементов [N, B, r], [N, B, T], [N, B, (r, T)].

Для этих планов моменты наблюдаемых отказов образуют пуассоновский поток с интенсивностью .

Действительно, так как времена безотказной работы каждого элемента взаимно независимо, то последовательность моментов , замен элементов в k-й ячейке стенда образует процесс восстановления, у которого интервалы являются взаимно независимыми показательно распределенными случайными величинами, .

Но такой процесс восстановления является пуассоновским потоком с интенсивностью, равной . Моменты замен элементов (отказов) взаимно независимы, поэтому взаимно независимы пуассоновские потоки моментов замен, соответствующие N различным ячейкам стенда.

Так как поток всех отказов, которые происходят при испытаниях, является суперпозицией

N взаимно независимых пуассоновских потоков с интенсивностями , то он также будет пуассоновским потоком с интенсивностью .

План [N, B, T]. В случае плана [N, B, T] мы наблюдаем пуассоновский поток отказов с интенсивностью в течение времени Т.

Пусть — число наблюдаемых отказов, которые произошли в моменты . Плотность вероятности этого события можно получить следующим образом. Вероятность того, что первый отказ произойдет в интервале , равна , условная вероятность того, что второй отказ произойдет в интервале при условии, что первый отказ произошел в интервале , равна и т.д.

Наконец, условная вероятность того, что — й отказ произошел в интервале , а в интервале других отказов не было при условии, что отказы произошли в интервалах , равна .

Вероятность события, что отказы произошли в интервалах , равна произведению этих условных вероятностей,

Таким образом, плотность вероятностей наступления отказов в моменты равна

(1)

Вероятность, того что за время испытаний Т не произойдет ни одного отказа, равна

(2)

Рассматривая, (1) и (2) как функции правдоподобия, получаем уравнение максимального правдоподобия

(3)

решение которого имеет вид (4)

Так как , то оценкой параметра является (5)

Так как , то

(6)

т. е. оценка (5) является несмещенной.

(7)

(7′)

Можно показать, что эта оценка является эффективной. Заметим также, что из вида плотности (1) следует, что в случае плана [N, B, T] достаточной статистикой является только число отказов, происшедших за время испытаний, а сами моменты отказов никакой дополнительной информации о параметре не содержат.

Рассмотрим несколько примеров.

Пример 1. Испытания проводились по плану [N=100, B, T=200]. Отказы произошли в моменты . Общее число отказов . По формуле (5) находим, что

План [N, B, r]. Для плана [N, B, r], рассуждая аналогичным образом, получаем, что вероятность того, что отказы произойдут в интервалах , равна

Отсюда следует, что плотность вероятностей наступления отказов в моменты равна

(8)

Из (8) следует, что достаточной статистикой для оценки параметра является момент , наступления r-го отказа.

Уравнение максимального правдоподобия имеет вид

(9)

откуда получаем оценку (10)

Заметим теперь, что , т.е. является суммой r интервалов между последовательными отказами. Эти интервалы являются взаимно независимыми случайными величинами с плотностями вероятностей, равными . Поэтому плотность вероятностей , равная свертке r плотностей , имеет вид

(11)

Из (11) и (10) получаем

(12)

Следовательно, оценка , полученная методом максимального правдоподобия, является смещенной, а при r=1 ее математическое ожидание равно бесконечности. Смещение легко устранить, если рассмотреть оценку

(13)

Из (13) и (12) следует, что . Вспомнив, что , получаем несмещенную оценку для

(14)

Для дисперсий оценок (13), (14) имеют место формулы

(15)

(16)

Дисперсии оценок существуют только для значений r>2.

Пример 2. Испытания проводились в соответствии с планом . Момент регистрации десятого отказа . Из формулы (14) находим оценку

План [N, b, (r, T)]. При исследовании более общего плана [N, b, (r, T)] испытания прекращаются в момент Т, и при этом наблюдается отказов, или в момент появления r-го отказа, если . В первом случае плотность вероятности наступления отказов в моменты записывается по формуле (1), а во втором случае плотность вероятности наступления отказов в моменты — по формуле (8). Используя метод максимального правдоподобия, получаем оценку для

По аналогии с только что разобранным случаем плана [N, b, r] мы можем улучшить эту оценку, устранив смещение. Вводим оценку

(17)

которая является несмещенной. Действительно, воспользовавшись формулу для условных математических ожиданий, получаем

Аналогичным способом можно найти дисперсию этой оценки

(18)

Для несмещенной оценки параметров имеем

(19)

(20)

В заключение отметим изящный результат, полученный Л.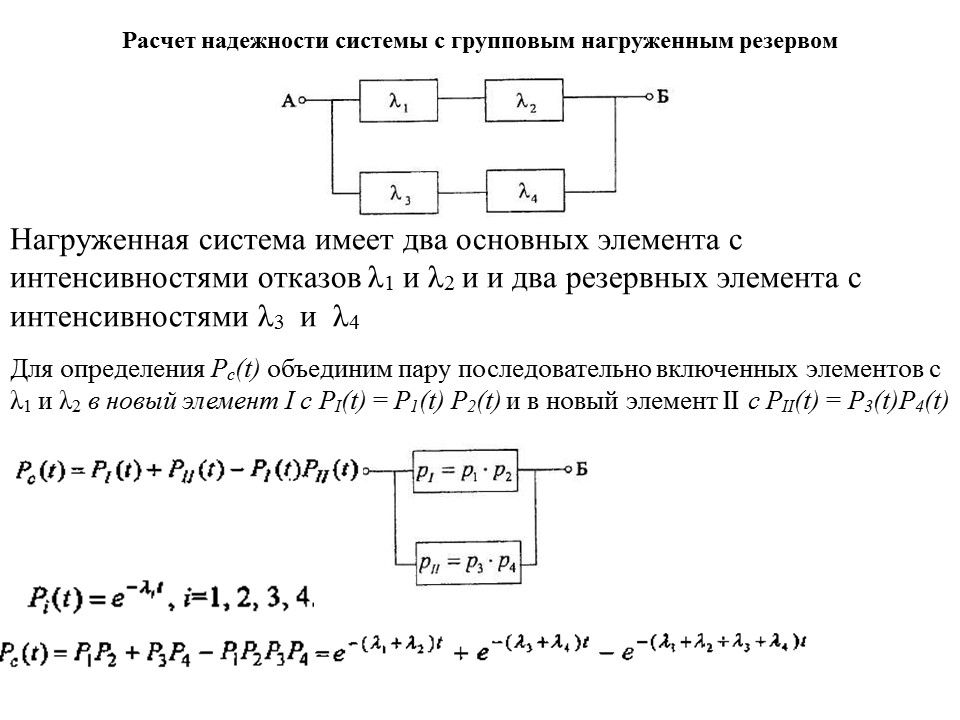 Н. Большевым. Существует общий класс планов проведения испытаний, в которых момент остановки испытаний t* определялся как момент первого достижения траекторией (t, d(t)) границы множества G. Здесь d(t) — число элементов, отказавших к моменту t.

Предположим, что граница Г множества G является невозрастающей функцией от t (рис. 1).

Рис. 1. График множества G и его границы

Точки границы Г разбиваются на два класса. Назовем точку точкой класса А, если правее ее на уровне d все точки не принадлежат множеству G. Точки класса А обведены на рис.1 кружками. Точки границы Г, не являющиеся точками класса А, назовем точками класса Б.

Эти точки на рис. 1 показаны тонкими сплошными линиями. Л.Н. Большев показал, что несмещенная оценка для параметра строится следующим образом. Если в момент первого достижения траекторией (t, d(t)) границы Г точка (t*, d(t*)) есть точка класса А, то оценка определяется по формуле

Если же точка (t*, d(t*)) есть точка класса Б, то оценка для находится по формуле

Заметим, что с вероятностью единица момент достижения точек класса Б совпадает с моментом наступления отказа.

Планы без замены отказавших элементов

Рассмотрим теперь планы, в которых отказавшие элементы не заменяются новыми.

План [N, Б T]. Выражение для плотности вероятностей того, что при испытаниях по плану [N, Б, T] отказы произойдут в моменты , можно получить следующим образом.

Плотность вероятностей того, что в эти моменты откажут элементы с номерами , равна, в силу взаимной независимости моментов отказов, произведению плотностей вероятности для моментов отказов каждого из этих элементов, умноженных на вероятность того, что в интервале (0, Т) отказов у остальных N — d(t) элементов не произойдет, т.е. равна

(21)

Событие, состоящее в том, что моменты отказов равны , может осуществиться способами, так как из N чисел можно сделать N…N — d(t)+1 различных выборок номеров . Умножая (21) на , получаем выражение для искомой плотности вероятностей

(22)

Таким образом, в случае плана [N, Б T] достаточными статистиками будут: число d(t) элементов, отказавших за время Т, и сумма времен, в течение которых проработал каждый элемент, т. е. суммарная наработка элементов за время проведения испытаний. Из (22) получаем, что

(23)

Отсюда имеем (24)

Таким образом, оценка максимального правдоподобия равна (25)

Эта оценка является смещенной. Точный подсчет смещения приводит к очень громоздким формулам, которые мы опускаем. По этой же причине мы опускаем формулу для дисперсии .

Заметим, что для сравнительно надежных элементов при плотность условного распределения момента отказа, происшедшего в интервале (0, T) равна , а среднее значение каждого приближенно можно считать равным T/2. Отсюда для d(t) > 10 и , исходя из закона больших чисел, можно считать, что .

Подставив это выражение в знаменатель формулы (25), получаем

(26)

Формулой (26) часто пользуются на практике. Следует, однако, иметь в виду, что она применима при . Если считать, что формула (25) слишком сложна, то для оценки также можно исходить из формулы оценки вероятности по частоте.

Оценкой для вероятности безотказной работы элемента является отношение числа элементов N — d(t), безотказно проработавших в течение времени Т, к общему числу N элементов. Приравняв оценку к теоретическому значению вероятности, получаем для нахождения оценки уравнение

откуда (27)

Этой формулой можно воспользоваться для значений . Заметим, что смещение оценки (27) является бесконечным, так как с положительной вероятностью может получиться, что d(t) = N.

Пример 3. Испытания проводились в соответствии с планом [N=100, Б, T=500]. Отказы произошли в моменты

Общее число отказавших элементов d(500) = 11, суммарная наработка

= 31 + 49 + 90 + 135 + 161 + 249 + 323 + 353 + 383 + 436 + 477 + 89*500 = 47 147

По формуле (25) находим оценку для параметра

Если исходить из упрощенной формулы (26), то .

План [N, Б, r]. Для плана [N, Б, r] плотность вероятностей появления отказов в моменты получаем из рассуждений, аналогичных тем, которые были использованы для плана [N, Б, T].

Плотность вероятностей, того, что в моменты откажут элементы с номерами , а остальные N — r элементов в интервале не дадут отказов, равна .

Учитывая, что число возможных наборов по r различных цифр из N равно N(N — 1)…(N -r +1), получаем, что плотность вероятностей наступления r отказов в моменты

Из этой формулы следует, что достаточной статистикой является суммарная наработка всех испытываемых элементов.

(29)

Заметим, что, введя новые переменные , плотность (28) можно, учитывая (29), переписать в виде

(30)

При этом мы учитываем, что якобиан перехода от координат к координатам равен 1.

Из (30) следует, что случайные величины являются взаимно независимыми, при этом плотность равна , соответственно плотность случайной величины равна .

Таким образом, из (30) следует, что s является суммой r взаимно независимых показательно распределенных случайных величин.

Отсюда получаем, что плотность распределения суммарной наработки равна (31)

Прологарифмировав плотность (28), находим

откуда получаем уравнение максимального правдоподобия

Оценка максимального правдоподобия имеет вид (32)

Использовав выражение (31) для плотности вероятностей суммарной наработки, находим, что

Таким образом, оценка является смещенной. Это смещение можно устранить, если использовать оценку … (33)

Дисперсия этой оценки равна

(34)

Пример 4. Испытания проводились в соответствии с планом [N=50, Б, r=8]. Моменты отказов равны . Значение суммарной наработки = 91+145+221+285+317+328+411+496(50-7)=21 965.

По формуле (33) находим оценку для параметра :
План [N, Б, (r,T)]. Если используется план [N, Б, (r,T)], то испытания прекращаются либо в момент T, если , либо в момент , если . Соответственно в первом случае плотность вероятностей наступления d(t) отказов в моменты записывается по формуле (22), а во втором, для моментов отказов — по формуле (28). Как и в случае плана [N, B, (r,T)], находим, что оценка максимального правдоподобия имеет вид

По аналогии с предыдущим случаем мы можем использовать улучшенную оценку для случая . Окончательно получаем

(35)

Эта оценка является смещенной; ввиду громоздкости формул, выражающих смещение и дисперсию, мы вынуждены пропустить их.

План [N, Б, (r, HS0)]. В заключение рассмотрим еще один план проведения стендовых испытаний, который также находит практическое применение. Проводятся испытания N элементов без восстановления отказавших. Испытания прекращаются в тот момент, когда либо суммарная наработка испытываемых элементов станет равной заданному до начала испытаний числу S0, либо в момент отказа r-го отказа элемента, если при этом суммарная наработка оказывается меньше S0. Такой план сокращено будем обозначать через [N, Б, (r, HS0)].

Если обозначить через число N(t) элементов, оставшихся исправными к моменту t, то суммарная наработка S(t) испытываемых элементов к моменту t равна . Допустим, что отказы элементов произошли в моменты , тогда суммарная наработка к моменту времени t задается формулой

t0 = 0, если d(t) = 0. Испытания прекращаются в тот момент s, когда либо суммарная наработка

(36)

(при этом d(s)<r), либо в момент tr отказа r-го элемента

(37)

Выше было показано, что при испытаниях N элементов без восстановления отказавших случайные величины являются взаимно независимыми, одинаково распределенными с плотностью .

Таким образом, условия (36) и (37) фактически означают, что мы наблюдаем пуассоновский поток отказов с интенсивностью и прекращаем наблюдения либо в «момент» S0, либо в «момент» S(tr) наступления r-го отказа. Но задачу оценки параметра пуассоновского потока мы уже решили, разбирая случай плана [N, B, (r,T)]. Чтобы воспользоваться оценкой (17), в ней надо считать и в формуле для дисперсии оценки (18) считать = .

Окончательно,

(38)

находится по формуле (35). Эта оценка несмещенная, ее дисперсия в соответствии с формулой (18) равна

(20)

Как это следует из рассмотрения плана [N, B, (r,T)], достаточными статистиками будут d(t0), если S(tr) > S0, и S(tr), если S(tr) < S0.

Пример 5. Испытания проводятся в соответствии с планом [N=100, Б, (r=5, HS=10000)]. Первый отказ наступил в момент t(1)=34, значение суммарной наработки SБ(t(1))=3400<10000. Второй отказ был зарегистрирован в момент t(2)=75, значение суммарной наработки стало равным SБ(t(2))=7459<10000. В интервале от t(2)=75 до t(0)=100,71 отказы не наблюдались. В момент t(0)=100,71 значение суммарной наработки достигло заданного уровня 10 000. В соответствии с верхней частью формулы (38) находим

Несмещенные оценки для вероятности безотказной работы

Одним из наиболее важных показателей надежности является вероятность безотказной работы в течение заданного времени T3. В случае показательного закона эта вероятность. Используя полученные выше формулы для оценок параметра , можно в качестве оценки для рассматривать

(39)

Можно показать, что эта оценка при увеличении числа N испытываемых элементов является состоятельной и асимптотически эффективной, если только — асимптотически эффективная оценка для .

Однако при конечных значениях N оценка, задаваемая формулой (39), является смещенной. Это смещение может быть весьма существенным в практически важном случае, когда R(T3) близка к единице.

Величина смещения зависит также от типа плана, в соответствии с которым проводятся испытания. Так же как и для оценок параметра , можно поставить задачу отыскания несмещенных оценок для .

Основная идея построения несмещенных оценок с минимальными дисперсиями заключается в следующем. Сначала отыскивают несмещенную оценку для заданной функции от неизвестного параметра.

Если эта несмещенная оценка — функция от достаточной статистики (и притом единственная), то она имеет наименьшую дисперсию. Если же эта несмещенная оценка не является функцией от достаточной статистики, то в качестве новой несмещенной оценки рассматривается условное математическое ожидание от исходной оценки при условии, что фиксировано значение достаточной статистики.

В начало

Содержание портала

Вероятность безотказной работы — Энциклопедия по экономике

Надежность биологических систем — это свойство клеток, органов, систем организма выполнять специфические функции, сохраняя характерные для них величины в течение определенного времени, составляющего, как правило, продолжительность жизни.

Основной характеристикой надежности систем служит вероятность безотказной работы. Организм повышает свою надежность различными способами [c.97]
Аналогичное требование относится и к установлению оптимальных значений показателей надежности — одному из важнейших свойств электроизделий. Усложнение в ряде случаев конструкций, увеличение числа элементов в них, интенсификация режимов работы электрооборудования приводят к возрастанию количества отказов, поскольку, как следует из теории надежности, вероятность безотказной работы изделия находится в обратной зависимости от числа элементов в конструкции. В результате затраты на ремонт электрических машин и аппаратов в несколько раз превышают первоначальные вложения на их приобретение. [c.240]

Рис. 4. Зависимость обобщающего показателя эффективности от вероятности безотказной работы реактора УЗК

Показатель эффективности функционирования оборудования (1), рассчитанный на стадии проектирования с учетом функции вероятности безотказной работы (рис.

2 и 3) может служить в качестве основного критерия при рассмотрении вопросов технического перевооружения (замены аппаратов). [c.54]
Безотказность показывает свойство изделия непрерывно сохранять работоспособность в течение некоторого времени или некоторой наработки, выражающееся в вероятности безотказной работы, средней наработке до отказа, интенсивности отказов. [c.195]

Такая универсальность позволяет использовать одни и те же математические формулы при исследовании самых различных потоков отказов изделий. Кроме того, этот закон удобен при аппроксимации статистических данных, так как распределение вероятностей безотказной работы изделий может быть сведено к линейной функции, что позволит довольно просто определять параметры распределения. [c.63]

Оператор 8. Расчет (вероятностей безотказной работы изделий по каждому месяцу года. [c.64]

Пример. Пусть вероятность безотказной работы изделия-аналога составляет 92 %, а расчетный показатель вероятности безотказной работы проектируемого изделия — 96%. Тогда, на основании выражения (3.4), получим [c.37]

Надежность продукта можно представить как надежность, складывающуюся на трех этапах при проектировании, производстве и эксплуатации. В этом случае надежность продукта можно оценить по темпам роста количества отказов в период эксплуатации п или по вероятности безотказной работы продукта Р (т) во времени т (рис. 4.6). [c.180]

Надежность изделий количественно выражается через / показатель продолжительности безотказной работы. Это — среднее время работы между двумя неисправностями , Для многих изделий (часть низковольтной аппаратуры, светотехники и пр. ) первый же отказ является и последним в истории данного изделия, т. е. продолжительность безотказной работы, под которой следует понимать, что данное изделие будет сохранять свои потребительские свойства в соответствующих условиях эксплуатации в течение определенного времени. Показатель вероятности безотказной работы выражается гарантийным сроком службы изделия. [c. 67]

P(f) — вероятность безотказной работы [c.174]

Вероятность безотказной работы характеризует вероятность отсутствия отказов при заданных условиях эксплуатации в течение определенного заданного интервала времени [c.174]

Вероятность безотказной работы — убывающая функция времени, обладающая следующими свойствами в начальный момент времени (при t = 0) ДО) = 1, а при /— > оо Р (t) стремится к нулю. [c.174]

Рис. 3. Зависимость вероятности безотказной работы от количества ГСЭ.

Потребительская ценность какого-либо эффекта может оказаться существенно отличной от стоимостной оценки. Поэтому при выборе генерального направления технической политики более осязаемыми являются натуральные измерители наиболее дефицитных ресурсов (труда, материалов, времени, площади и т. п.) и внеэкономических (научных, социальных, технических) эффектов. Так, например, для трубопроводных систем чрезвычайно важным эффектом является повышение надежности в условиях эксплуатации, причем выраженное приращением вероятности безотказной работы трубопровода за достаточно длительный период (35 — 50 лет) и снижением ожидаемого числа аварий на 1000 км в год.

[c.112]

Этой задаче посвящена обширная социологическая литература (см., например, книгу [70]) и поэтому нет необходимости останавливаться на ней подробно. Однако следует отметить важность четкой постановки вопроса, обеспечивающей однозначность его понимания экспертами. Например, на вопрос назовите важнейшее свойство данной продукции — несколько экспертов могут ответить — надежность. Но неопределенность этих ответов очень велика. Один эксперт под надежностью понимает вероятность безотказной работы, другой — наработку на отказ, третий — срок службы до первого ремонта, четвертый — срок службы до полного физического износа и т. д. Поэтому вопрос должен быть сформулирован таким образом, чтобы получить на него четкий и однозначный ответ. Кроме того, следует принимать во внимание, что эксперту так же, как и любому человеку, трудно без значительной ошибки выносить решение, когда приходится учитывать более семи альтернатив, например, назначать весомость более чем семи свойствам. Поэтому нельзя представлять экспертам список, в котором, например, несколько десятков свойств, и требовать от них назначить весомости этл. м свойствам. Как же поступать в тех случаях, когда учитывается более семи свойств продукции Свойства должны быть представлены в виде иерархической структурной схемы, о которой говорилось раньше, таким образом, чтобы количество свойств, объединяемых в любую группу, было не больше семи (табл. 3). [c.56]

Интенсивность отказов вероятность безотказной работы в течение заданного времени средняя наработка на отказ [c.107]

Поэтому для определения вероятностей чаще всего применяются косвенные методы, позволяющие по известным вероятностям одних событий определять вероятности других, с ними связанных. С этой целью обычно сложные схемы разлагают на ряд более простых схем, для которых вероятности наступления искомых событий известны или могут быть сравнительно легко определены экспериментальным путем. Например, для определения вероятности безотказной работы сложной электронной системы экспериментальным путем устанавливают со- [c.10]

Вероятность безотказной работы P(t) — вероятность того, что в заданном интервале времени или в пределах заданной наработки не возникнет отказ изделия. Вероятность безотказной работы оценивается по формуле [c.50]

N — число изделий, подвергнутых испытанию N(t) — число изделий, отказавших к моменту времени t. Если задана плотность наработки до отказа f(t), то вероятность безотказной работы аналитически определяется по формуле [c.50]

Пример 1. Найти вероятность безотказной работы двигателя автомобиля ГАЗ-51А до 45 тыс. км пробега (по данным табл. 9) [c.50]

Определим вероятность безотказной работы в течение t —100 ч рассматриваемого типа подшипников. [c.51]

P(t) —вероятность безотказной работы за время t. [c.52]

В стандарт на аттестованные электродвигатели впервые в практике электромашиностроения заложены количественные показатели надежности срок службы электродвигателей — 18 лет вероятность безотказной работы при двух годах эксплуатации— 0,99, при 10 годах — 0,95, при 18 годах — 0,90. [c.63]

Надежность складывается из безотказности, ремонтопригодности и ряда других показателей и зависит от долговечности составных частей изделий. Безотказность — это свойство изделия непрерывно сохранять работоспособность в течение некоторой наработки или некоторого времени. Характеризуется величинами наработки на отказ, вероятностью безотказной работы и др. Ремонтопригодность— свойство изделия, заключающееся в его приспособленности к предупреждению, обнаружению причин отказов и устранению их при техническом обслуживании и ремонте. Среди показателей ремонтопригодности выделяют среднее время вос-стгновления изделий в часах. [c.216]

Важнейшие требования к автоматическому оборудованию — надежность его работы. Надежность (безотказность процесса или оборудования) характеризуется способностью функционировать в соответствии с техническими условиями в течение заданного периода времени при установленных требованиях эксплуатации. В комплексе аппаратуры Импульс-2 и Депеша-2 вероятность безотказной работы за 10000 ч составляет не менее 0,9, а средний срок службы не менее 8 лет. Для обеспечения надежной работы автоматизированного комплекса необходимо правильно сформировать весь технологический процесс в виде определенной системы, включающей оборудование, агрегаты, вспомогательные устройства, оперативную диспетчерскую связь и т. д. Отказы в производственной системе распре-дейяются на следующие группы отказы оборудования отказы КИП и А отказы, вызываемые обслуживающим персоналом. [c.182]

Анализ вероятности безотказной работы реакторов в зависимости от числа циклов коксования (рис. 2) проводился с учетом усталостной природы разрушений в оболочках реакторов. Для сравнения рассматривалась надежность аппаратов двухреакторного блока УЗК ПО «Омскнефте-оргсинтез». [c.52]

На рисунках 2 и 3 представлена вероятность безотказной работы реакторов УЗК АО НУНПЗ и реакторов УЗК ПО «Омскнефтеоргсинтез». [c.53]

Если вероятность безотказной работы по закону Вейбула определяется уравнением [1] [c.46]

Коэффициенты с и D в этом случае определяются по методу наименьших квадратов, следовательно, могут быть определены и параметры закона распределения Вейбула, причем для вычисления значений вероятностей безотказной работы изделий предлагается использовать приближенную формулу [21 [c.46]

Действительно, если вероятность безотказной работы по закону Вейбулла определяется уравнением [c. 63]

По этим формулам можно находить параметры закона распределения Вейбулла, причем для вычисления значений вероятностей безотказной работы изделий предлагается использовать приближенную формулу [14] [c.63]

Проводится детальная классификация технико-экономических показателей качества изделий с целью выявления таких из них, которые в большей или меньшей мере оказывают влияние на величину потребности. Проведенный анализ показателей качества показал, что нет необходимости учитывать в расчетах все изменяющиеся показатели качества, так как многие из них практически или совсем не влияют на изменение величины потребности, или это влияние незначительное, или возможность изменения потребности находится в функции еще целого ряда факторов. Реальное влияние на изменение потребности оказывают такие из них, как производительность (объем работы) изделия безотказность и срок службы. В дальнейших исследованиях ограничимся рассмотрением только этих трех основных показателей. Следует заметить, что для различных изделий существуют различные показатели, характеризующие выбранные основные характеристики. Например, производительность и объем работы. Для турбогенераторов, сверхпроводниковых синхронных компенсаторов, коллекторных, синхронных и асинхронных электрических машин, гидрогенераторов — это номинальная мощность для безколлекторных регулируемых машин и регулируемых электроприводов — момент вращения для светотехнического оборудования — световой поток и мощность ламп для оборудования по производству оптического волокна — скорость вытяжки оптического волокна для коммутационной аппаратуры — число коммутируемых цепей для магистральных и промышленных электровозов — мощность для щеток электрических машин, вращающихся, — плотность тока для электросварочного оборудования — скорость сварки (резки) и др. Показатель безотказности изделий характеризует такие свойства изделий, как наработка на отказ, интенсивность отказов, вероятность безотказной работы, коэффициент готовности и др. И наконец, срок службы характеризуется количеством лет эксплуатации, ресурсом работы, ресурсом до капитального ремонта, межремонтным периодом. [c.38]

Пример 2. Определить вероятность безотказной работы подшипников А305 (см. табл. 8), исходя из закона распределения наработок до отказа. [c.50]

Известно [46], что наработка до отказа подшипников распределена по закону Вейбулла, для которого вероятность безотказной работы [c.50]

Как рассчитать и решить для успеха и неудачи | Вероятность

Изображение выше представляет успех и неудачу.

Для расчета успеха и неудачи необходимы два основных параметра: x и N.

Где;

x = количество успехов
N = общее количество испытаний или элементов

Давайте решим пример;
Найти результат, если x равно 12, а N равно 14?

Это означает, что;

x = количество успехов = 12
n = общее количество испытаний или предметов = 14

P (успех) = ^x ⁄ _N
P (успех) = ¹² ~ ₁₄
P (успех) = ¹² ~ ₁₄
P (успех) = ^{Разделив числитель и знаменатель на 2
P(успех) = ⁶ ⁄ ₇
P(успех) = 0,857}

Следовательно, успех равно 0,857.

Формула расчета отказа:

P(отказ) = ^{(N – x)} ⁄ _N

Где;

x = количество успехов
N = общее количество попыток или элементов

Давайте решим пример;
Найти ошибку, когда x равно 12, а N равно 14.

Это означает, что;

x = количество успехов = 12
N = общее количество попыток или элементов = 14

P(неудача) = ^{(n — x)} ⁄ _n
P (сбой) = ^{(14 — 12)} ⁄ ₁₄
P (сбой) = ² ⁄ ₁₄
Диализация Нумератора и денообразования на денатор на ⁄ ₁₄
2
P(отказ) = ¹ ⁄ ₇
P(отказ) = 0,142

Следовательно, отказ равен 0,142.

Калькулятор Никзома – Энциклопедия калькулятора способна вычислять успех и неудачу.

Чтобы получить ответ и расчет успеха и неудачи, используйте калькулятор Nickzom – The Calculator Encyclopedia. Во-первых, вам нужно получить приложение.

Вы можете получить это приложение любым из следующих способов:

Web – https://www.nickzom.org/calculator-plus

Чтобы получить доступ к профессиональной версии через Интернет, вам необходимо регистрация и подписка на 1500 NGN за год , чтобы иметь полный доступ ко всем функциям.
Вы также можете попробовать демо-версию через https://www.nickzom.org/calculator

Android (платная) – https://play.google.com/store/apps/details?id=org .nickzom.nickzomcalculator
Android (бесплатно) – https://play.google.com/store/apps/details?id=com.nickzom.nickzomcalculator
Apple (платно) – https://itunes.apple .com/us/app/nickzom-calculator/id1331162702?mt=8
После того, как вы получили приложение энциклопедии калькулятора, перейдите к0007 Карта калькулятора, , затем нажмите Вероятность под Математика .

Теперь нажмите Успех и неудача под Вероятность

На приведенном ниже снимке экрана показана страница или действие для ввода ваших значений, чтобы получить ответ об успехе и неудаче в соответствии с соответствующими параметрами, которые x и N.

Теперь введите значения правильно и соответственно для параметров, как того требует x IS 12 и N IS 14.

Наконец, нажмите на расчет

, как вы можете видеть на скриншоте выше, Calczom Calculator — Calculator Encycloped Solves для успеха. и отказ, также представляет формулу, работы и шаги.

Опубликовано Январь 4, 2020 Автор Loveth IdokoКатегории МатематикаТеги энциклопедия калькулятора, математика, N, калькулятор nickzom, вероятность, успех и неудача, x

AMPLE — Расчет вероятности отказа

Изложенное ниже является основой для определения характеристик вероятности отказа (PoF), которые используются для расчета стоимости риска.

Мы предположили, что актив имеет доминирующий вид отказа (например, отказ обмотки трансформатора).

Были распознаны два типа поведения PoF:

Случайные сбои имеют постоянную вероятность с течением времени. Примерами являются электронные компоненты и сложные электрические активы.
Для ветхих активов PoF увеличивается с возрастом или использованием по мере износа.

Возникают отклонения в этих формах поведения, например, «детская смертность», изменения в нагрузке и «укладывание в постель».

Статистику отказов можно получить из:

Известных внутренних и внешних исторических данных
Оценка на основе опыта и экспертных знаний
Актуарные данные
Ускоренные испытания.

Существует математическая зависимость между мгновенной вероятностью отказа r(t), частотой отказов f(t) и средним временем между отказами. Если мы можем определить одну из этих характеристик, мы можем рассчитать остальные, чтобы определить текущие и будущие затраты на риск.

(a) Мгновенная вероятность отказа в зависимости от возраста r(t)

Мы можем определить мгновенную PoF типа актива, задав опытному и опытному персоналу вопрос: «Для среднего актива возраста x, какова PoF в год Икс».

Затем можно построить кривую наилучшего соответствия, представляющую «стандартную кривую» для мгновенной PoF актива этого типа.

Этот стандарт является общим руководством, и каждый актив должен быть оценен на предмет того, имеет ли он более высокую или меньшую вероятность отказа, чем стандарт. То есть, падает ли фактическая кривая для конкретного актива выше или ниже стандарта.

(b) Частота отказов f(t)

Мы можем определить частоту отказов f(t), задав вопрос: «Если бы у нас была сотня таких активов в таком состоянии, сколько, по вашему мнению, вышло бы из строя в этом году». Затем этот вопрос следует повторить для последующих лет.

Затем можно построить кривую наилучшего соответствия, представляющую «стандартную кривую» для частоты отказов этого типа активов.

Опять же, нам нужно рассмотреть, как частота отказов конкретного актива может отличаться от стандартной.

Среднее время наработки на отказ (MTBF)

Мы можем определить среднее время наработки на отказ, задав вопрос: если бы у вас была сотня таких активов, какое среднее время наработки на отказ вы ожидаете.

Поскольку многие активы не могут выйти из строя, эта характеристика будет более точной, если будет рассчитана на основе других характеристик или собранных данных.

Мгновенная вероятность отказа в зависимости от возраста — общая кривая

Общие кривые, использованные в исследованиях SCAR и SMEAR, обеспечивают общую аппроксимацию, достаточную для начальной оценки риска.

Текущий PoF r(t) определяется путем задания вопроса «через сколько лет вы на 100% уверены, что этот актив выйдет из строя». т. е. r(t) = 1, S f(t) = 1.

Из общей кривой мы можем определить текущую PoF.

Характеристики отказов

Наиболее часто понимаемой характеристикой является текущая мгновенная PoF и ее изменение со временем по мере износа актива.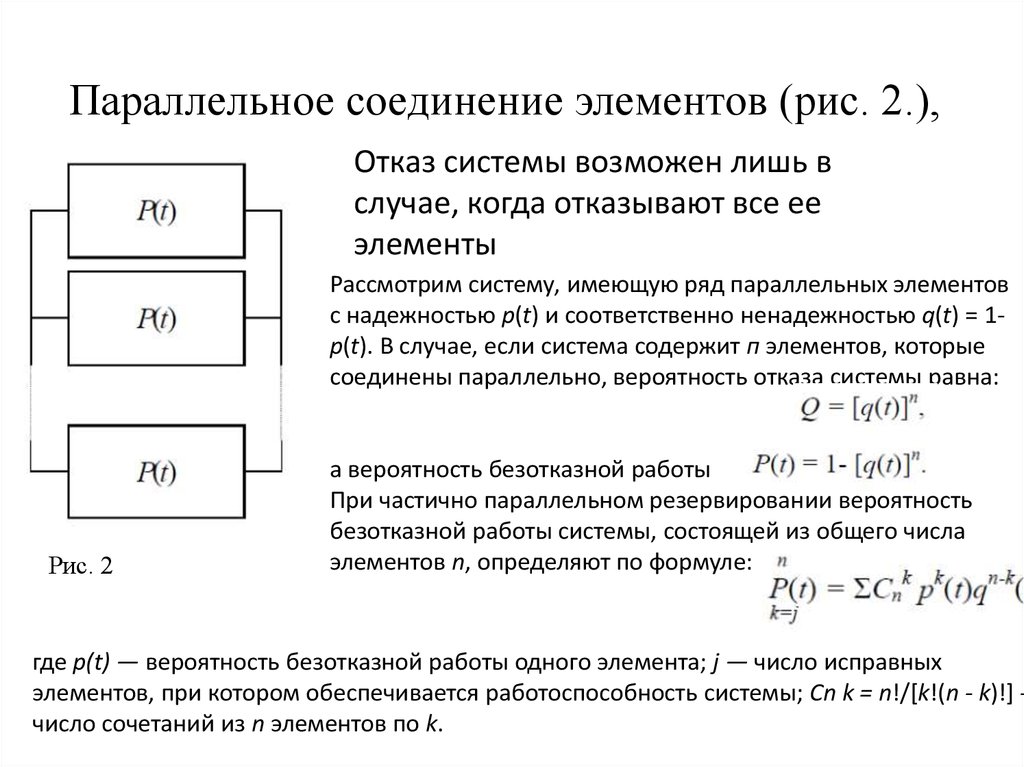

Для оценки частоты требуются опытные инженеры, разбирающиеся в теории вероятностей. Это более сложная для понимания концепция, но она дает подходящие результаты.

С помощью этих двух методов можно определить частотную кривую для расчета стоимости риска для использования в процессе ORDM.

Данные

Следующие данные могут быть использованы для прогнозирования вероятности отказа:

Исторические данные
Записи других органов, производителей и других источников .

Подробная электронная система инвентаризации очень помогает управляющим активами моделировать срок службы активов на основе:

собственного опыта
своего опыта работы с аналогичными активами на других должностях
опыта других органов власти
опыта и знаний производителя актива.

Владельцы активов не могут предсказать отказы активов со 100% точностью. Однако система инвентаризации с наилучшей доступной оценкой полезного срока службы может помочь выявить активы, срок полезного использования которых приближается к концу.

Таким образом, процесс выглядит следующим образом:

Запишите дату строительства актива
Дайте каждому активу наилучшую оценку фактического срока службы
Проверьте фактическое состояние активов, начиная с наиболее критического.

Этот подход оправдывает действия по мониторингу состояния.

Оценка

Вероятность отказа, как правило, связана с состоянием или характеристиками актива, при этом основными видами отказа являются:

Отказ емкости
Структурная целостность (катастрофический отказ) или нарушение условий.

Чтобы точно оценить текущую вероятность отказа, необходимо рассмотреть каждый из этих видов отказа.

Наибольшая стоимость риска для большинства сервисных органов связана с структурной целостностью или физическим отказом актива, и вероятность будет напрямую связана с физическим состоянием актива.

Ниже приведен пример эффективного срока службы актива и определения вероятности отказа:

В качестве альтернативы можно провести предварительную оценку состояния активов.

Активы, подверженные риску, выявляются посредством общей оценки их структурной целостности. The probability of failure can be assigned a ranking according to the structural integrity:

Asset Condition	Probability of Failure (in next 5 years)
Excellent	0.0
Very good	0.0
Good	0.0
Average	0.1
Below average	0.2
Бедные	0,3
Очень бедные	0,6 0,60353
Неудовлетворительный	0,7
	0,9

4999

0,9

4999

0,9

49999

0,9

Вероятность отказа (в ближайшие 5 лет)

Пример 1

Пример 2

Satisfactory

0.01

0.001

Moderate

0.1

0.01

Poor

0.5

0.1

Очень бедные

0,9

0,4

Установка коэффициентов вероятности является произвольной, однако важна относительная последовательность. Точность и надежность результатов анализа зависят только от введенных данных. Однако при последовательном подходе к оценке состояния можно получить полезную информацию, которая поможет определить активы, подверженные риску.

Типичная кривая затухания зависимости вероятности отказа показана ниже.

Практические вопросы

При прогнозировании вероятности отказа нам очень часто приходится полагаться на истории отказов и определять характер отказов в зависимости от фактического возраста активов на момент возникновения отказа.

Если доступно достаточное количество надежных записей об отказах, мы можем предсказать вероятное количество отказов по мере старения активов и, следовательно, вероятность отказа. По мере того, как будет собрано больше записей об отказах и мы поймем причины и способы отказа, мы сможем разработать профиль отказа и с уверенностью предсказать вероятность отказа. Тем временем нам, возможно, придется полагаться на некоторые неофициальные свидетельства неудач, прошлый опыт и местные знания полевого персонала.

Зная время, когда в конечном итоге произойдет сбой, мы можем построить график вероятной вероятности сбоя в промежуточный период.