1.2.6. Расчет вероятности безотказной работы прибора
Рассмотрим примеры, в которых требуется вычислить вероятностьь безотказной работы и вероятность отказа работы прибора, в состав которого входят несколько элементов и используются различные способы их соединения между собой.
Пример 1.14. Прибор состоит из двух независимо работающих элементов. Вероятность отказа первого элемента равна P1= 0,1, а второго – P2 = 0,2.
Рассмотрим событие A = {прибор откажет работать}.
1) Вычислим вероятность события A, если элементы соединены Последовательно,
Решение: Обозначим через A1 Событие, которое заключается в том, что откажет элемент А1 = {откажет первый элемент}, и через A2 —
A2 = {откажет второй элемент}.
Тогда данный прибор не будет работать (событие А), если выйдет из строя Хотя бы Один из элементов (или первый, или второй, или оба не будут работать).
P (A) = p (A1+A2) = p (A1) + p (A2) – p (A1 A2) = p (A1) + p (A2) – p (A1) p (A2) =
= p1+p2 — p1 p2 = 0,1 +0,2 – 0,1*0,2 = 0,28.
Итак, вероятность того, что данный прибор Откажет Р (А) = 0,28.
Состояние прибора, когда он работает правильно, есть событие А — противоположное событию А, когда прибор откажет.
Тогда, используя свойства вероятности, можно найти Вероятность правильной работы А Данного прибора по формуле:
р ( ) = 1 – р ( А) = 1 – 0,28 = 0,72.
2) Вычислим вероятность отказа прибора (событие А ), если элементы соединены параллельно:
Решение.
Данный прибор откажет в том случае, если Откажут оба элемента Одновременно. Следовательно, отказ прибора в этом случае может быть представлен как Произведение Событий А1 и А2 , т. е. A=A1A2 . Так как элементы перестают работать Независимо друг от друга, то из независимости событий A1 и A2 получаем P(A) = P(A1) P(A2) = P1 P2 = 0,1 * 0,2 = 0,02.
Определение. События A1 A2 ¼ AN называют Взаимно независимыми, если для любой их части выполняется равенство
P() = p() p()¼P(), (1.5)
1<=i1<i2 ¼<im<=n , m=2, ¼,n.
Пример 1.15. Прибор состоит из трех последовательно соединенных и независимо работающих друг от друга элементов.
Каждый из элементов может быть признан бракованным или стандартным:
Обозначим вероятность того, что первый элемент оказался бракованным,
Равной P1, второй элемент бракованный — P2, третий элемент бракованный — P3.
Прибор будем считать Бракованным, если хотя бы один из его элементов бракованный. Найти вероятность того, что прибор Стандартный.
Решение: Обозначим события
A1 = {первый элемент — стандартный},
A2 = {второй элемент — стандартный },
A3 = {третий элемент — стандартный }
A = {прибор стандартный }.
В данном случае прибор нормально работает в том случае, если все три элемента одновременно работают, т. е. все три элемента, входящие в прибор, стандартные. Тогда работу прибора можно описать как событие А, состоящее из Произведения трех Независимых Событий A=A1*A2*A3 , вероятность которого можно вычислить по формуле вероятности произведения независимых событий
P(A) = P(A1)P(A2)P(A3) =(1 – P1) (1- P2) (1 – P3).
Вероятность отказа прибора (событие А ) в данном случае есть величина, равная вероятности события, противоположного событию
Р ( А) = 1 – Р (А).
Примечание. Рассмотренные примеры 1.13, 1.14 и 1.15 являются аналогом решения контрольной задачи №3 (первого пункта задания) из методических указаний для выполнения контрольных работ.
Рассмотрим некоторые свойства независимых событий.
Свойство7. Если A и B независимы, то и B Независимы.
Свойство 8. Если событие A не зависит от событий B1 и B2, а события B1 и B2 несовместны, тогда события A и B1+ B2 независимы.
Свойство 9. Если события A, A1 и A2 взаимно независимы, тогда события A и A1+ A2 независимы.
Вопросы для самопроверки
1. В чем заключается геометрический подход к вычислению вероятности?
2. Чему равна вероятность суммы двух противоположных событий?
3. Перечислите основные свойства вероятности события.
4. Что такое независимые события?
| < Предыдущая | Следующая > |
|---|
1.2. Вероятность безотказной работы. Вероятность отказа
Безопасность жизнедеятельности в техносфере / Надежность технических систем и техногенный риск / 1.2. Вероятность безотказной работы. Вероятность отказа
Вероятностью безотказной работы аппаратуры называется вероятность того, что она будет сохранять свои характеристики (параметры) в заданных пределах в течение определенного промежутка времени при определенных условиях эксплуатации, или, короче, – вероятностью безотказной работы аппаратуры называется вероятность того, что в определенных условиях эксплуатации в пределах заданной продолжительности работы отказ не возникает.
В дальнейшем эта характеристика обозначается P(t).
Пусть t – время, в течение которого необходимо определить вероятность безотказной работы, а Т1 – время работы аппаратуры от ее включения до первого отказа. Тогда, согласно определению вероятности безотказной работы, справедливо выражение:
, (1.1)
т.е. вероятность безотказной работы – это вероятность того, что время Т1 от момента включения аппаратуры до ее отказа будет больше или равно времени t, в течение которого определяется вероятность безотказной работы.
Из определения вероятности безотказной работы видно, что эта характеристика является функцией времени. Она имеет следующие очевидные свойства:
1) P(t) является убывающей функцией времени;
2) ;
3) Р(0) = 1, .
На практике для определения P(t) из статистических данных об отказах аппаратуры обычно используются методы непосредственного подсчета вероятностей.
Вероятность безотказной работы определяется следующей статистической оценкой:
, (1.2)
где N0 –число образцов аппаратуры в начале испытания, n(t) – число отказавших образцов за время t.
При увеличении числа образцов N0 статистическая оценка вероятности обнаруживает устойчивость, т.е. слабо отличается от вероятности безотказной работы:
. (1.3)
На практике иногда более удобной характеристикой является вероятность неисправной работы, или вероятность отказов. Эта характеристика может быть полезна, например, при сравнение надежности резервированной и не резервированной систем. Исправная работа и отказ являются событиями несовместными и противоположными. Поэтому вероятность безотказной работы и вероятность отказа Q(t) связаны зависимостью:
Q (t) = 1 – P (t), (1.4)
или с учетом выражения (1.
1)
Q (t) = P (T1 t) (1.5)
Из выражения (1.5) видно, что вероятность отказа является интегральной функцией распределения времени работы (Т1) до отказа, т.е.
Q (t) = F (t) (1.6)
Производная от интегральной функции распределения есть дифференциальный закон (плотность) распределения:
. 1.7)
Тогда на основании выражений (1.6) и (1.7) получим:
, (1.8)
т.е.
производная от вероятности отказа подчиняется дифференциальному закону распределения времени работы (Т1) аппаратуры до ее отказа.
Для статистического определения вероятности отказа воспользуемся выражениями (1.4)и (1.3). Подставляя в выражение (1.4) вместо P(t) его выражение из формулы (1.3), получим:
.
(1.9)
Вероятность безотказной работы P(t), как количественная характеристика надежности, обладает следующими достоинствами:
1) характеризует изменение надежности во времени;
2) входит во многие другие характеристики аппаратуры, а поэтому может быть полезна широкому кругу лиц, занимающихся вопросами проектирования, эксплуатации, ремонта и т.п. Например, вероятность безотказной работы наряду с точностью и живучестью определяет боевую эффективность оружия, а поэтому является необходимой для исследователя военных операций и полководца. Она определяет также стоимость изготовления и эксплуатации аппаратуры, а поэтому может быть полезной инженеру-экономисту;
3) охватывает большинство факторов, существенно влияющих на надежность аппаратуры, и поэтому достаточно полно характеризует надежность;
4) может быть сравнительно просто получена расчетным путем до изготовления системы. Это позволяет выбрать оптимальную в смысле надежности структуру системы и ее принципиальную схему;
5) является удобной характеристикой надежности, как простейших элементов, так и сложных систем и даже комплексов.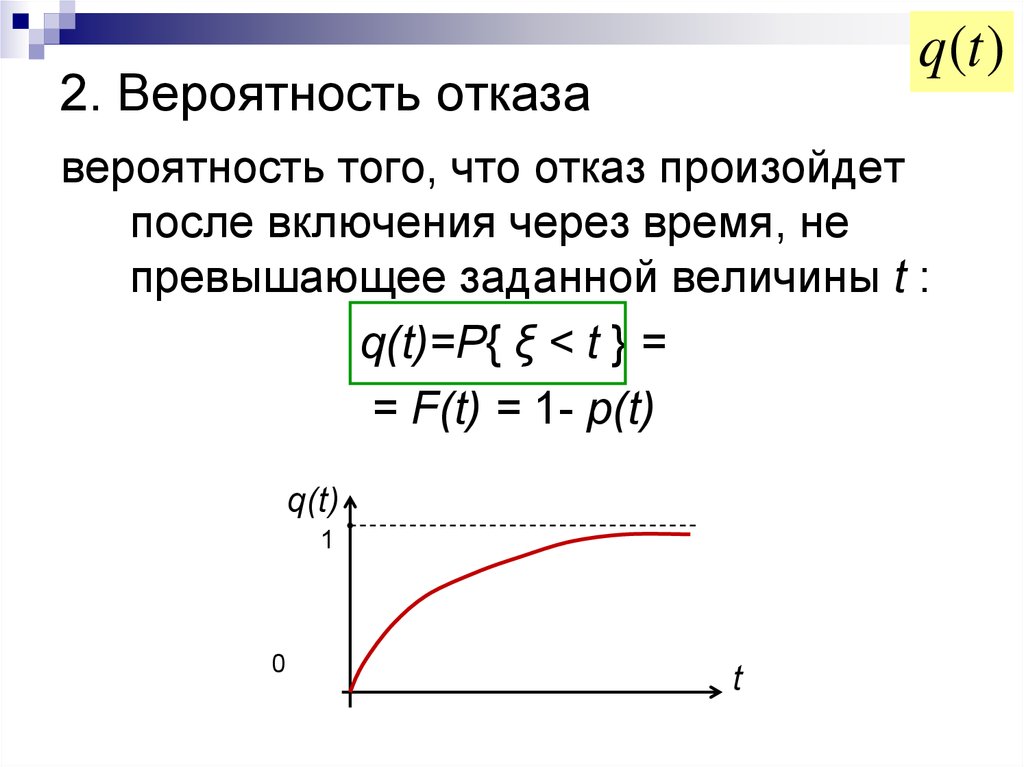
Указанные достоинства вероятности безотказной работы явились причиной наибольшего распространения этой характеристики.
Однако вероятность безотказной работы имеет также существенные недостатки:
1) характеризует надежность восстанавливаемых систем только до первого отказа, а поэтому является достаточно полной характеристикой надежности только систем разового использования;
2) не позволяет охарактеризовать зависимость между временными составляющими цикла эксплуатации; это не дает возможности установить, даже в вероятностном смысле, будет ли система готова к действию в данный момент времени или нет;
3) не всегда удобна для оценки надежности простых элементов, в особенности таких, у которых отсутствует старение;
4) по известной вероятности безотказной работы бывает трудно вычислить другие количественные характеристики надежности.
Эти недостатки позволяют сделать вывод, что вероятность безотказной работы, как, впрочем, и любая другая характеристика, не полностью характеризует такое свойство как надежность, и поэтому не может быть с ним отождествлена.
выживания — Как определить вероятность отказа, если отказов не было?
На этот вопрос было дано несколько хороших ответов, но недавно у меня была возможность просмотреть несколько ресурсов по этой теме, и я решил поделиться результатами.
Существует несколько возможных оценок для данных без сбоев. Обозначим $k=0$ как количество отказов и $n$ как объем выборки. Оценка максимального правдоподобия для вероятности отказа с учетом этих данных:
$$ P(K = k) = \frac{k}{n} = 0 \tag{1} $$
Такая оценка весьма неудовлетворительна, так как тот факт, что мы не наблюдали отказов в нашей выборке, едва ли доказывает, что они вообще невозможны. Знание об отсутствии данных предполагает, что существует или вероятность отказа, даже если этого не наблюдалось (пока). Наличие априорных знаний приводит нас к использованию байесовских методов, рассмотренных Бейли (1997), Раззаги (2002), Басу и др. (1996) и Ладбруком и Лью (2009).
Среди простых оценщиков оценщик с «верхней границей», который предполагает (Бейли, 1997)
, что было бы нелогично использовать оценку P в случай нулевого отказа, чтобы получить вероятность, превышающую предсказанную оценкой максимального правдоподобия в случае одного отказа разумная верхняя граница
определяется как
$$ \frac{1}{n} \tag{2} $$
.
Согласно обзору Ладбрука и Лью (2009 г.), другими возможными вариантами являются «правило трех» (см. здесь, Википедия или Эйпаш и др., 1995 г.)
$$ \frac{3}{n} \tag{3} $ $
или другие варианты:
$$ \frac{3}{n+1} \tag{4} $$
«правило 3.7» Ньюкомба и Альтмана (или 3.6):
$$ \frac {3.7}{n} \tag{5} $$
«новое правило четырех»:
$$ \frac{4}{n+4} \tag{6} $$
но согласно заключению Ладбрука и Лью (2009) «правило трех» «практически бесполезно», а «правило 3.6» (и 3.7) «имеют серьезные ограничения — они крайне неточны, если первоначальный размер выборки меньше 50», и они не действуют. рекомендую 9\frac{1}{n+1} \tag{8} $$
или для оценки среднего по таким предыдущим
$$ \frac{1}{n+2} \tag{9} $$
еще другой подход, предполагающий экспоненциальную картину отказов с постоянной интенсивностью отказов (распределения Пуассона), дает
$$ \frac{1/3}{n} \tag{10} $$
, если мы используем бета-приор с параметрами $a$ и $ b$ можно использовать формулу (см.
Razzaghi, 2002):
$$ \frac{a}{a+b+n} \tag{11} $$
, что при $a = b = 1$ приводит к равномерному до (9). Предполагая, что априор Джеффриса с $a = b = 0,5$, это приводит к
$$ \frac{1}{2(n+1)} \tag{12} $$
Обычно рекомендуются формулы Байеса (7)-(12). Basu et al (1996) рекомендует (11) с информативным априорным анализом, когда доступны некоторые априорные знания. Поскольку не существует единого наилучшего метода, я бы посоветовал изучить литературу перед тем, как приступить к анализу, особенно когда $n$ невелико.
Бейли, Р.Т. (1997). Оценка по данным нулевого отказа. Анализ рисков, 17 , 375-380.
Раззаги, М. (2002). Об оценке биномиальной вероятности успеха при нулевом появлении в выборке. Журнал современных прикладных статистических методов, 1 (2), 41.
Ладбрук, Дж., и Лью, М.Дж. (2009). Оценка риска редких осложнений: достаточно ли «правила трех»? ANZ журнал хирургии, 79 (7-8), 565-570.
Eypasch, E.
, Lefering, R., Kum, C.K., and Troidl, H. (1995). Вероятность нежелательных явлений, которые еще не произошли: статистическое напоминание. BMJ 311 (7005): 619–620.
Басу, А.П., Гейлор, Д.В., и Чен, Дж.Дж. (1996). Оценка вероятности возникновения опухоли для редкого рака с нулевым появлением в образце. Регуляторная токсикология и фармакология, 23 (2), 139-144.
байесовский расчет вероятности (отказа)
спросил
Изменено 5 лет назад
Просмотрено 187 раз
$\begingroup$
Я работаю над смертностью в 12 больницах, где проводят кардиохирургические операции у младенцев. Набор данных доступен здесь: набор данных Surg. Набор данных структурирован таким образом:
н р больница 47 0 А 148 18 Б 119 8 С ... ... ...
.. ... ...
где $n$ — количество операций, а $r$ — количество смертей. Моя цель — рассчитать вероятность отказа для каждой больницы $p_i$. Учебник, которому я следую (WinBUGS), сообщает, что
$r_i \sim Биномиальный(p_i, n_i)$
но мой вопрос: почему $p_i$ нельзя просто вычислить как $p_i = r_i/n_i$?
- вероятность
- байесовское
- биномиальное распределение
- winbugs
$\endgroup$
4
$\begingroup$
Вы можете использовать цитируемую вами формулу, но, похоже, вы предпочитаете использовать байесовский метод оценки, который включает в статистическую модель априорную информацию. Это два разных способа ведения статистики. Проверьте этот вопрос, чтобы узнать больше о том, что такое байесовская модель.
На самом деле, если вы вычислите вероятности различных значений $p_i$, вы обнаружите, что они имеют наибольшие пики в точках $r_i/n_i$.
На графике ниже вы видите профили правдоподобия для отдельных больниц, а вертикальные линии — точечные оценки $r_i/n_i$.
Обратите внимание, что при использовании неинформативного априорного $\pi(\theta) = 1$ (или $Beta(1,1)$) байесовские оценки $\pi(\theta|x) \propto f(x | \theta) \pi(\theta)$ такие же, как и при использовании подхода, основанного на правдоподобии, поэтому все три подхода приведут к одним и тем же точечным оценкам.
Таким образом, использование «чего-то большего», чем $r_i/n_i$, полезно для обработки неопределенности параметров, как заметил @jaradniemi в комментарии. С другой стороны, можно использовать более сложный подход, если (а) вы хотите построить иерархическую модель, в которой существует некоторая общая вероятность сбоя и специфические для сайта эффекты, или (б) вы можете использовать байесовский подход, чтобы включить некоторые нестандартные ситуации. -информация данных в вашей модели в качестве информативного априора.
$\endgroup$
1
$\begingroup$
Как отметил @jaradniemi, $r_i/n_i$ — это всего лишь оценка $p_i$.