Формулы арифметической и геометрической прогрессии 9 класс таблица: Арифметическая и геометрическая прогрессии — урок. Основной государственный экзамен 9 класс, Математика.

Арифметическая и геометрическая прогрессии, 9 класс

Петропавловская Ольга Анатольевна,

учитель математики МОУ «Гимназия № 20 имени Героя Советского Союза В. Б. Миронова», г. Саранск

Тема. Арифметическая и геометрическая прогрессии (9 класс)

Тип урока: обобщение знаний, формирование практических способов действий

Цели урока:

образовательные:

— исследовать связь между арифметической и геометрической прогрессиями;

— познакомить с понятием функции дискретной переменной;

— усвоить и отработать приемы построения графика функций дискретной переменной;

развивающие:

— развить умение наблюдать, подмечать закономерности, обобщать, проводить рассуждение по аналогии;

— сформировать умение строить и интерпретировать математическую модель в некоторой реальной ситуации;

воспитательные:

— показать связь математики с реальной действительностью, развить культуру и стиль мышления, математическую речь учащихся;

— формировать информационную культуру, интерес к информатике;

Технические средства: компьютеры, мультимедийный проектор, презентация «Арифметическая и геометрическая прогрессия», мультимедийный диск «Интерактивная математика. 5-9 классы».

Ход урока.

1. Организационный момент. Сообщение темы, целей урока.

2. Актуализация опорных знаний.

Учитель:

— вспомним:

1) определение арифметической и геометрической прогрессий,

2) формулы n-ных членов арифметической и геометрической прогрессий,

3) формулы суммы n первых членов арифметической и геометрической прогрессий,

4) характеристические свойства прогрессий.

(Соответствующие формулы ученики записывают на доске и в тетрадях).

3. Учитель:

-рассмотрим и решим 2 задачи.

ЗАДАЧА 1. Вертикальные стержни фермы имеют следующую длину: наименьший 3 дм, а каждый следующий длиннее на 2 дм.

ЗАДАЧА 2. В благоприятных условиях бактерии размножаются так, что на протяжении одной минуты одна из них делится на две.

Задания к задачам.

1. Запишите последовательность в соответствии с условием задачи.

2.Постройте график заданной прогрессии по данным задачи, если 1 ≤n ≤ 7 используя мультимедийный диск «Интерактивная математика. 5-9 классы».

3. Сформулируйте вывод о графике.

Учитель:

Какие сведения нам необходимы для построения графика?

Как вы считаете, существует ли здесь функциональная зависимость, обоснуйте свой ответ.

Охарактеризуйте область определения каждой из этих функций.

Следовательно, арифметическая и геометрическая прогрессии есть функции, заданные на множестве натуральных чисел. Внимательно рассмотрите графики этих последовательностей и сделайте выводы о членах этих прогрессий.

(вывод: при n=1,2,3 члены геометрической прогрессии увеличиваются незначительно, даже медленнее, чем члены арифметической прогрессии, но с увеличением номера члена члены геометрической прогрессии делают резкий скачок в сторону увеличения).

Сообщение ученика.

Об этой особенности членов геометрической прогрессии хорошо знал изобретатель шахмат много веков назад. До нас дошла легенда. Индийскому царю понравилась игра в шахматы. Он решил вознаградить изобретателя. Тот попросил за одну клетку шахматной доски — 1 пшеничное зерно, за 2 клетку- 2 зерна, за 3 клетку- 4 зерна, за 4 клетку- 8 зерен, за 5 клетку- 16 зерен и т.д. царь был очень огорчен тем, что изобретатель попросил столь ничтожную плату. И был удивлен, когда придворные математики сообщили ему требуемое количество зерен: 18 446 744 073 709 551 615 зерен, что составило 230 584 300 921 369 пудов.

Чтобы поместить такое количество зерна нужно построить амбар высотой 4 м, шириной- 10 м и длиной- 300000000 км. Это расстояние в 2 раза больше расстояния от земли до солнца. Чтобы получить такой урожай надо засеять пшеницей поверхность всей земли: океаны, моря, горы, пустыни, Арктику, Антарктику и получать средний урожай в течение 5 лет.

Учитель:

С формулой

связан случай с великим математиком К.Ф. Гауссом. Однажды на уроке, чтобы занять первоклассников, пока он будет заниматься с учениками 3-его класса, учитель велел сложить все числа от 1 до 100, надеясь, что это займет много времени. Едва учитель закончил чтение условия, Гаусс предъявил ответ, записанный на грифельной доске. Изумленный учитель понял, что это самый способный ученик в его практике. В дальнейшем Гаусс сделал много замечательных открытий. Его даже называли «царем математики».

Сформулируйте свойство членов конечной арифметической прогрессии, на основании которого маленький Гаусс решил эту задачу. (В конечной арифметической прогрессии суммы членов равноотстоящих от концов прогрессии равны между собой).

Как вы считаете, обладают ли похожим свойством члены конечной геометрической прогрессии? (В конечной геометрической прогрессии произведения членов равноотстоящих от концов прогрессии равны между собой). Докажем это свойство для конечной геометрической прогрессии b1, b2, b3, b4, b5, b6.

( Доказательство у доски:

b1*b6=b1*b1q5=b12q5

b2*b5=b1q*b1q4=b12q5

b3*b4=b1q2 *b1q3=b12q5.

Итак, b1*b6= b2*b5 =b3*b4.)

Решим задачу № 403 («Алгебра 9»,авторы Ш.А. Алимов и др.), в которой применяется одно из характеристических свойств прогрессий.

(№ 403. В арифметической прогрессии а3+а9=8. Найти S11).

Обратитесь еще раз к формулам n-ного члена прогрессий и их характеристическим свойствам.

Внимательно посмотрите, подумайте и скажите, что надо сделать, изменить в этих формулах, чтобы все увидели связь, которая существует между ними? (Да, похожи если заменить в формулах n-ного члена сложение умножением и умножение – возведение в степень. Родство прогрессий становится еще более заметным, если в формулах, выражающих характеристические свойства заменить сложение умножением, а деление на 2 – извлечением квадратного корня.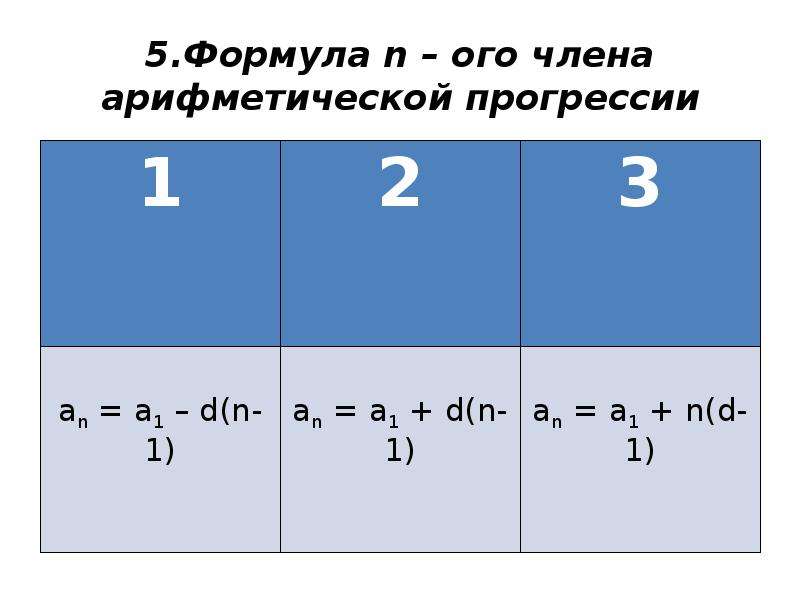 И тогда из характеристического свойства арифметической прогрессии получится характеристическое свойство геометрической прогрессии).

На связь между арифметической и геометрической прогрессиями первым в глубокой древности обратил внимание Архимед. В 1544 году вышла книга немецкого математика Штифеля «Общая арифметика», в которой он составил следующую таблицу:

Как вы считаете, есть ли какая-то закономерность, связывающая числа в строке? (В верхней строке арифметическая прогрессия с разностью единица. В нижней – геометрическая прогрессия со знаменателем 2).

Охарактеризуйте связь, существующую между строками таблицы? (Числа верхней строки есть показатели степени с основанием 2, а соответствующие числа нижней строки есть значение этой степени).

Таким образом, числа в нижней строке можно записать в виде последовательности:

2-4 ; 2-3 ; 2-2 ; 20 ; 21 ; 22 ; 23 ; 24 ; 25 ; 26; 27. Докажите взаимосвязь данной последовательности с темой урока? (Показатели степеней являются членами арифметической прогрессии, а сами степени составляют геометрическую прогрессию).

4. Итог урока.

1) Арифметическая и геометрическая прогрессии есть функции, заданные на множестве натуральных чисел.

2) В конечной арифметической прогрессии суммы членов равноотстоящих от концов равны.

3) В конечной геометрической прогрессии произведения членов равноотстоящих от концов равны.

4) Если показатели степеней являются членами арифметической прогрессии, то сами степени являются членами геометрической прогрессии.

5. Домашнее задание.

Докажите или опровергните тезис «3 числа могут составить одновременно арифметическую и геометрическую прогрессии».

ГДЗ Алгебра Дорофеев 9 класс Контрольные КР-5. Арифметическая и геометрическая прогрессии Вариант 3

Содержание

Авторы:Дорофеев, Кузнецова, Минаева

Тип:контрольные работы

1. Последовательность задана формулой n-го члена: b_n=n*(n+2).

а) Запишите первые 3 члена этой последовательности; найдите b_50.

б) Является ли членом этой последовательности число 442?

2. Одна из двух данных последовательностей является арифметической прогрессией, другая — геометрической прогрессией:

(a_n): 1; 10; 100; … ;

(у_n): 100; 200; 300; … .

а) Продолжите каждую из этих прогрессий, записав следующие три её члена.

б) Найдите 10-й член геометрической прогрессии.

3. Андрей готовился к экзамену по геометрии. За 5 дней ему надо было выучить 30 билетов. Успел ли Андрей выучить все билеты, если в первый день он выучил 1 билет, а в каждый следующий день учил в 2 раза больше билетов, чем в предыдущий?

4. Сколько отрицательных членов в арифметической прогрессии:

-37,8; -35,1; …?

5. Найдите сумму всех натуральных чисел первой сотни, которые при делении на 5 дают в остатке 1. {5} — 1 \right)}{2 — 1} =\]

\[= 32 — 1 = 31\ (билет) — он\ \]

\[сможет\ выучить\ за\ 5\ дней.\]

\[Ответ:да,\ успел.\]

\[\boxed{\mathbf{4.}}\]

\[Арифметическая\ прогрессия:\]

\[- 37,8;\ — 35,1;\ldots\]

\[a_{1} = — 37,8;\]

\[d = — 35,1 — ( — 37,8) = 2,7;\]

\[a_{n} = a_{1} + (n — 1) \cdot d\]

\[a_{1} + (n — 1) \cdot d < 0\]

\[- 37,8 + (n — 1) \cdot 2,7 < 0\]

\[(n — 1) \cdot 2,7 < 37,8\]

\[n — 1 < 14\]

\[n < 15\]

\[n = 14 — отрицательных\]

\[членов.\]

\[Ответ:14\ членов.\]

\[\boxed{\mathbf{5.}}\]

\[Числа\ первой\ сотни — это\ \]

\[числа\ от\ 11\ до\ 100.\]

\[a_{1} = 11;\ a_{2} = 16;\ \ a_{n} = 96:\]

\[d = a_{2} — a_{1} = 16 — 11 = 5.\]

\[a_{n} = a_{1} + d(n — 1)\]

\[96 = 11 + 5 \cdot (n — 1)\]

\[85 = 5n — 5\]

\[5n = 90\]

\[n = 18\ (чисел) -\]

\[удовлетворяющих\ условию.\]

\[S_{16} = \frac{a_{1} + a_{16}}{2} \cdot 18 =\]

\[= (11 + 96) \cdot 9 = 107 \cdot 9 = 863. {5}.\]

Ошибка или идея? Сообщить 📤

Мне не нравится на сайте, измените:Сделайте так, чтобы можно было:Решение неправильно/опечатка

Все номера

Вариант 2Вариант 3Вариант 4Вариант 1Вариант 2Вариант 3Вариант 4Вариант 1

Арифметическая прогрессия и геометрическая прогрессия

Слово «последовательность» в английском языке означает набор некоторых чисел или объектов таким образом, что он имеет первый член, второй член и так далее. Например, последовательности могут быть любыми. — Январь Февраль, …. это последовательность месяцев в году. Последовательности используются в реальных реальных жизнях людей каждый день. Дни недели также можно рассматривать как последовательность. Таким образом, становится необходимым изучать последовательности и находить в них закономерности, чтобы мы могли предсказывать следующие члены последовательности и извлекать из них информацию.

Последовательности

Рассмотрим последовательность: 2,4,6,8 и так далее. Различные числа, встречающиеся в нем, называются его членами. Они обозначаются ₁ , ₂ , ₃ … _n. Нижние индексы обозначают n-й термин. N-й член последовательности также называется общим членом последовательности, потому что мы можем вывести из него любой другой член, подставляя различные значения n. В этом случае

a ₁ = 2, a ₂ = 4, a ₃ = 6 и так далее…

Последовательность с конечным числом членов называется конечной последовательностью, и аналогично последовательность с бесконечным числом членов называется бесконечной последовательностью.

Последовательность можно рассматривать как функцию, областью определения которой является множество натуральных чисел или некоторое его подмножество. Иногда мы используем функциональное обозначение a(n) для a _n .

Серия

Для данной последовательности a ₁ , a ₂ , a ₃ … а _n . Приведенное ниже выражение называется рядом. Ряд может быть бесконечным или конечным в зависимости от количества членов в его последовательности. ∑ — общепринятое обозначение, используемое для обозначения серии. Это указывает на вовлеченное суммирование.

= a ₁ + a ₂ + a ₃ +… a _n 

Эти понятия порождают последовательности, известные как арифметическая прогрессия и геометрическая прогрессия.

Арифметическая прогрессия (А.П)

Рассмотрим последовательность 1, 3, 5, 7, ….. Обратите внимание, что в этой последовательности разница между последовательными элементами постоянна. Это означает, что на каждом шаге к каждому члену этой последовательности добавляется постоянное значение. Последовательность a ₁ , a ₂ , a ₃ … a _n можно назвать арифметической прогрессией, если _n+1 = a _n + d, где n — любое натуральное число. . В таком ряду a ₁ называется первым членом, а постоянный член d называется общей разностью AP. Таким образом, AP выглядит как

а, а + г, а + 2д, а + 3д ….. и так далее.

Число n для AP можно определить как

a _n = a ₁ + (n-1)d

Сумма n членов AP определяется как

S _п = 

или

S _N =

Геометрическая прогрессия (G.P)

Рассмотрите следующую последовательность, 2, 4, 8, 16… .. Здесь ясно, что каждый термин умножается на 2 в этом. последовательность. Такие последовательности, в которых последовательные члены умножаются на постоянное число, называются геометрическими прогрессиями. В более общем смысле последовательность a ₁ , a ₂ , a ₃ … a _n можно назвать геометрической прогрессией, если _n+1 = a _n . r, где n — любое натуральное число. В таком ряду a ₁ называется первым членом, а постоянный член r называется обыкновенным отношением Г.П. Итак, GP выглядит так:

a, ar, ar ² , ar ⁿ …. . и так далее.

Число n для GP может быть определено как

a _n = a ₁ r ^n-1

В общем, ВП может быть конечным и бесконечным, но в случае бесконечного ВП общее отношение должно быть между 0 и 1, иначе значения ВП доходят до бесконечности. Сумма ГП состоит из двух случаев:

Обозначим S _n are a + ar + ar ² + ….. ar ⁿ

Случай 1: Если r = 1, то ряд рушится до

а, а, а, а… и так далее.

S _n = na

Случай 2: Если r≠1, ряд остается прежним,

a + ar + ar ² + ….. ar ⁿ

S _n = 

Давайте рассмотрим некоторые текстовые задачи, связанные с этими понятиями 

Примеры задач

Вопрос 1: Биткойн-акции начинался с 5 долларов. После этого каждый день он повышается на 2 доллара. Найдите цену акции в конце 16-го дня.

Ответ: 

В приведенном выше вопросе каждый раз, когда к предыдущему термину добавляется постоянное число, получается новый термин. Это АП.

5, 7, 9, … и так далее.

Используя формулу для n-го члена AP.

a _n = a ₁ + (n-1)d

Здесь a ₁ обозначает первый член, а d обозначает общую разность. В этом случае

a ₁ = 5, d = 2 и n = 16

a ₁₀ = a ₁ + (16-1)d

⇒ a 9000 7 10 = 5 + (15 )2

⇒ а ₁₀ = 5 + 30

⇒ а ₁₀ = 35 

Таким образом, цена акций составляет 35 долларов.

Вопрос 2: Человек посадил 3 дерева при рождении сына. После этого в последующие дни рождения он каждый год сажал еще по 5 деревьев. Найдите количество деревьев в его дворе, когда его сыну исполнится 10 лет.

Ответ: 

В приведенном выше вопросе каждый раз, когда к предыдущему термину добавляется постоянное число, получается новый термин. Это АП.

3, 8, 13, … и так далее.

Используя формулу для n-го члена AP.

a _n = a ₁ + (n-1)d

Здесь a ₁ обозначает первый член, а d обозначает общую разность. В этом случае

a ₁ = 3, d = 5 и n = 10

a ₁₀ = a ₁ + (10-1)d

⇒ a ₁₀ = а ₁ + (9)d

⇒ a ₁₀ = 3 + 9(5)

⇒ a ₁₀ = 3 + 45 

⇒ a ₁₀ = 48

Итак, на его заднем дворе 48 деревьев. сейчас.

Вопрос 3. Английская рок-группа the1975 летом выпустила новый альбом, и за один день было продано 100 000 копий. Сейчас альбом возглавляет чарты, и каждый день продается на 20 000 копий больше, чем в предыдущий день. Найдите общий объем продаж альбомов за неделю.

Ответ: 

В приведенном выше вопросе каждый раз, когда к предыдущему термину добавляется постоянное число, получается новый термин. Это АП.

100 000; 120 000; 140 000; … и так далее.

Цель состоит в том, чтобы вычислить сумму последовательности в конце 10-го дня.

Используя формулу для суммы до n-го члена AP.

S _n = 

Здесь _{обозначает первый член, а d обозначает общую разность. В этом случае}

a = 100 000, d = 20 000 и n = 7

S _n =

⇒S ₇ =

⇒S ₇ =

⇒ S ₇ =

⇒ С ₇ =

⇒ С ₇ =

⇒S ₇ = 770000

Таким образом, общий объем продаж альбомов составляет 770 000 экземпляров.

Вопрос 4: Популяция оленей в Национальном парке Корбетт увеличивается. В 2015 году он был 1000, с тех пор он увеличивается, и каждый год становится в 2 раза. Найдите население в 2021 году. 

Решение.

Здесь каждый год население становится в 2 раза больше. Постоянное число умножается на предыдущий член, чтобы получить новый термин. Это геометрическая прогрессия.

1000, 2000… и так далее.

Здесь a = 1000 и r = 2

Используя формулу для n-го члена ГП

a _n = a ₁ r ^n-1

900 02 В 2021 г. n = 7. Подключение значения в формуле

a _n = a ₁ r ^n-1

⇒a _n = (1000)(2) ^{(7-1) 901 18}

⇒ _n = (1000)(2) ⁶

⇒a _n = (1000)(64)

⇒ a _n = 64000 

Сейчас в Национальном парке Корбетт должно быть 64 000 оленей.

Вопрос 5: У человека 2 родителя, 4 дедушки и бабушки, 8 прабабушек и дедушек и так далее. Найдите количество предков в последних 10 поколениях этой семьи.

Раствор.

 Здесь каждый год количество увеличивается в 2 раза. Постоянное число умножается на предыдущий член, чтобы получить новый термин. Это геометрическая прогрессия.

2,4 … и так далее.

Здесь a = 2 и r = 2

Используя формулу для n-го члена ГП 2021 г., n = 10. Подключение значения в формуле

a _n = a ₁ r ^n-1

⇒a _n = (2)(2) ^(10-1)

⇒ _n = (2)(2) ⁹

⇒a _n = (2) ¹⁰

⇒a _n = 64000 

Сейчас в Национальном парке Корбетт должно быть 64 000 оленей.

Вопрос 6: Вставьте два числа от 4 до 256 так, чтобы полученная последовательность стала GP.

Ответ:

Допустим, эти два числа равны x и y. Результирующая последовательность примет следующий вид:

4, x, y, 256

Эта последовательность состоит из четырех членов и является GP. Здесь

a = 4 и r = ?

Формула для n-го члена ГП равна  

a _n = a ₁ r ^n-1

4-й член 256,

256 = 4r ^{(4 – 1)}

64 = r ³

Это означает, что r = 4

Таким образом,

x = ar

⇒ x = (4)(4)

⇒ x= 16

y = ar ²

9 0002 ⇒ у = 4(4) ²

⇒ y = 64

Итак, нужно вставить два числа: 16 и 64

Вопрос 7: Количество бактерий в чашке равно 100, и каждый час они увеличиваются вдвое по сравнению с предыдущим значением. Найдите количество бактерий в чашке через 6 часов.

Ответ:

Здесь каждый год количество увеличивается в 2 раза. Постоянное число умножается на предыдущий член, чтобы получить новый термин. Это геометрическая прогрессия.

100,200, 400… и так далее.

Здесь a = 100 и r = 2

Используя формулу для суммы до n-го члена ГП

S _n =

n = 6. Подставляем значения в формулу

S _н =

⇒ С _n = 

⇒ S ₆ = 

⇒ S ₆ = 

⇒ S ₆ = 

9 0002 ⇒ S ₆ = 6300

Теперь в чашке должно быть 63 000 бактерий. .

n-й член геометрической последовательности

Горячая математика

Учитывая геометрическая последовательность с первым сроком а 1 и обыкновенное отношение р , н й (или общий) термин дан кем-то
а н «=» а 1 ⋅ р н − 1 .

Пример 1:

Найди 6 й член геометрической прогрессии 3 , 12 , 48 , … .

а 1 «=» 3 , р «=» 12 3 «=» 4 а 6 «=» 3 ⋅ 4 6 − 1 «=» 3 ⋅ 4 5 «=» 3072

Пример 2:

Найди 7 й термин для геометрической последовательности, в которой а 2 «=» 24 и а 5 «=» 3 .

Заменять 24 для а 2 и 3 для а 5 в формуле

а н «=» а 1 ⋅ р н − 1 .

а 2 «=» а 1 ⋅ р 2 − 1 → 24 «=» а 1 р а 5 «=» а 1 ⋅ р 5 − 1 → 3 «=» а 1 р 4

Решите первое уравнение для а 1 : а 1 «=» 24 р

Подставьте это выражение вместо а 1 во втором уравнении и решить для р .

3 «=» 24 р ⋅ р 4 3 «=» 24 р 3 1 8 «=» р 3 так р «=» 1 2

Заменитель р в первом уравнении и решить а 1 .

24 «=» а 1 ( 1 2 ) 48 «=» а 1

Теперь используйте формулу, чтобы найти а 7 .