Распределение Пуассона | это… Что такое Распределение Пуассона?
| Функция вероятности | |
| Функция распределения | |
| Обозначение | |
| Параметры | |
| Носитель | |
| Функция вероятности | |
| Функция распределения | |
| Математическое ожидание | |
| Медиана | |
| Мода | |
| Дисперсия | |
| Коэффициент асимметрии | |
| Коэффициент эксцесса | |
| Информационная энтропия | |
| Производящая функция моментов | |
| Характеристическая функция | |
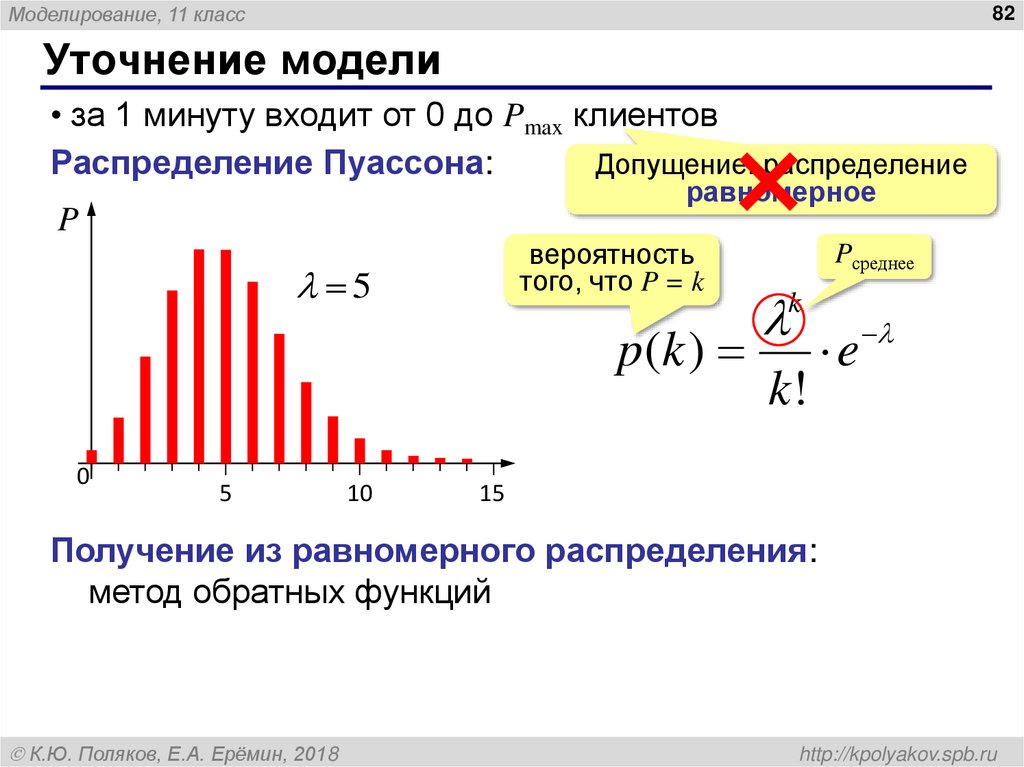
Распределение Пуассона — вероятностное распределение дискретного типа, моделирует случайную величину, представляющую собой число событий, произошедших за фиксированное время, при условии, что данные события происходят с некоторой фиксированной средней интенсивностью и независимо друг от друга.
Распределение Пуассона играет ключевую роль в теории массового обслуживания.
Содержание
|
Определение
Выберем фиксированное число и определим дискретное распределение, задаваемое следующей функцией вероятности:
- ,
где
- обозначает факториал числа ,
- — основание натурального логарифма.
Тот факт, что случайная величина имеет распределение Пуассона с параметром , записывается: .
Моменты
Производящая функция моментов распределения Пуассона имеет вид:
- ,
откуда
- ,
- .
Для факториальных моментов распределения справедлива общая формула:
- ,
где
А так как моменты и факториальные моменты линейным образом связаны, то часто для пуассоновского распределения исследуются именно факториальные моменты, из которых при необходимости можно вывести и обычные моменты.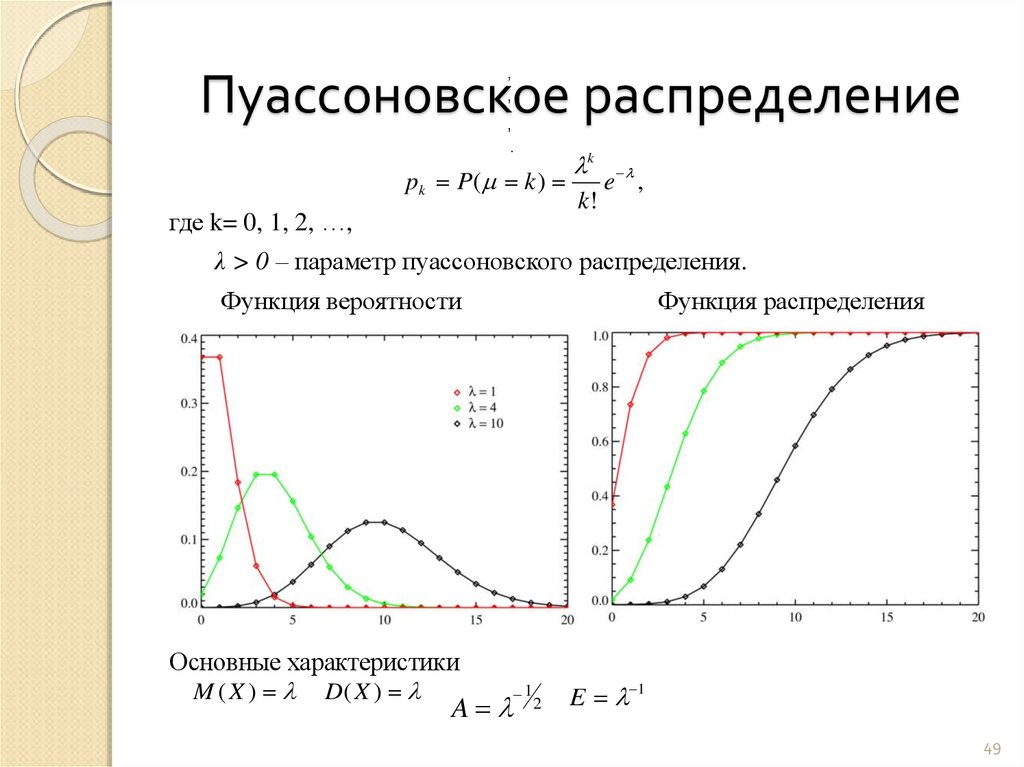
Свойства распределения Пуассона
- .
- Пусть , и . Тогда условное распределение при условии, что , биномиально. Более точно:
- .
История
Изначально распределение Пуассона было предложено для моделирования потока входящих телефонных звонков на коммутатор. Примеры других ситуаций, которые можно смоделировать, применив это распределение: поломки оборудования, длительность исполнения ремонтных работ стабильно работающим сотрудником, ошибка печати, рост колонии бактерий в чашке Петри, дефекты в длинной ленте или цепи и др.[1].
См. также
- Биномиальное распределение;
- Пуассон, Симеон Дени.
Примечания
- ↑ Ральф Винс , 2012
Литература
- Вентцель Е. С., Овчаров Л. А., Теория вероятностей и её инженерные приложения, М.
 : 2000, С. 135. — ISBN 978-5-406-00565-1.
: 2000, С. 135. — ISBN 978-5-406-00565-1. - Ральф Винс Математика управления капиталом: Методы анализа риска для трейдеров и портфельных менеджеров = The mathematics of money management risk analysis techniques for traders. — М.: «Альпина Паблишер», 2012. — 400 с. — ISBN 978-5-9614-1894-1
| п·Вероятностные распределения | ||
|---|---|---|
| Одномерные | Многомерные | |
| Дискретные: | Бернулли | биномиальное | геометрическое | гипергеометрическое | логарифмическое | отрицательное биномиальное | Пуассона | дискретное равномерное | мультиномиальное |
| Абсолютно непрерывные: | Бета | Вейбулла | Гамма | гиперэкспоненциальное | Колмогорова | Коши | Лапласа | логнормальное | нормальное (Гаусса) | логистическое | Накагами |Парето | полукруговое | непрерывное равномерное | Райса | Рэлея | Стьюдента | Фишера | хи-квадрат | экспоненциальное | variance-gamma | многомерное нормальное | копула |
Распределение Пуассона | это.
 .. Что такое Распределение Пуассона?
.. Что такое Распределение Пуассона?| Функция вероятности | |
| Функция распределения | |
| Обозначение | |
| Параметры | |
| Носитель | |
| Функция вероятности | |
| Функция распределения | |
| Математическое ожидание | |
| Медиана | |
| Мода | |
| Дисперсия | |
| Коэффициент асимметрии | |
| Коэффициент эксцесса | |
| Информационная энтропия | |
| Производящая функция моментов | |
| Характеристическая функция | |
Распределение Пуассона — вероятностное распределение дискретного типа, моделирует случайную величину, представляющую собой число событий, произошедших за фиксированное время, при условии, что данные события происходят с некоторой фиксированной средней интенсивностью и независимо друг от друга.
Распределение Пуассона играет ключевую роль в теории массового обслуживания.
Содержание
|
Определение
Выберем фиксированное число и определим дискретное распределение, задаваемое следующей функцией вероятности:
- ,
где
- обозначает факториал числа ,
- — основание натурального логарифма.
Тот факт, что случайная величина имеет распределение Пуассона с параметром , записывается: .
Моменты
Производящая функция моментов распределения Пуассона имеет вид:
- ,
откуда
- ,
- .
Для факториальных моментов распределения справедлива общая формула:
- ,
где
А так как моменты и факториальные моменты линейным образом связаны, то часто для пуассоновского распределения исследуются именно факториальные моменты, из которых при необходимости можно вывести и обычные моменты.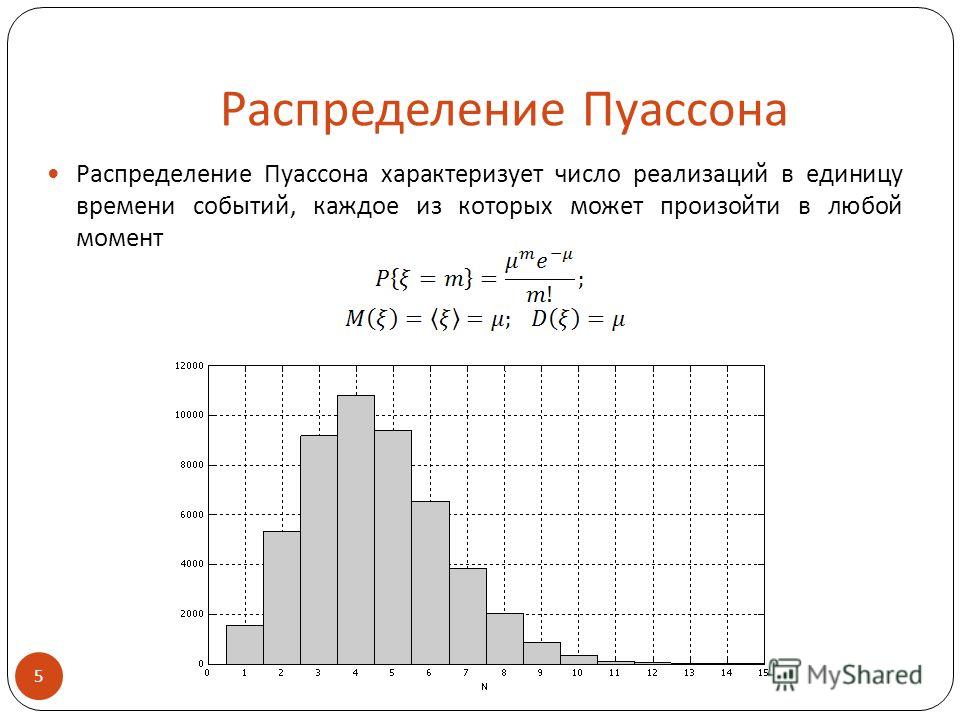
Свойства распределения Пуассона
- Сумма независимых пуассоновских случайных величин также имеет распределение Пуассона. Пусть . Тогда
- .
- Пусть , и . Тогда условное распределение при условии, что , биномиально. Более точно:
- .
История
Изначально распределение Пуассона было предложено для моделирования потока входящих телефонных звонков на коммутатор. Примеры других ситуаций, которые можно смоделировать, применив это распределение: поломки оборудования, длительность исполнения ремонтных работ стабильно работающим сотрудником, ошибка печати, рост колонии бактерий в чашке Петри, дефекты в длинной ленте или цепи и др.[1].
См. также
- Биномиальное распределение;
- Пуассон, Симеон Дени.
Примечания
- ↑ Ральф Винс , 2012
Литература
- Вентцель Е. С., Овчаров Л. А., Теория вероятностей и её инженерные приложения, М.
 : 2000, С. 135. — ISBN 978-5-406-00565-1.
: 2000, С. 135. — ISBN 978-5-406-00565-1. - Ральф Винс Математика управления капиталом: Методы анализа риска для трейдеров и портфельных менеджеров = The mathematics of money management risk analysis techniques for traders. — М.: «Альпина Паблишер», 2012. — 400 с. — ISBN 978-5-9614-1894-1
| п·Вероятностные распределения | ||
|---|---|---|
| Одномерные | Многомерные | |
| Дискретные: | Бернулли | биномиальное | геометрическое | гипергеометрическое | логарифмическое | отрицательное биномиальное | Пуассона | мультиномиальное |
| Абсолютно непрерывные: | Бета | Вейбулла | Гамма | гиперэкспоненциальное | Колмогорова | Коши | Лапласа | логнормальное | нормальное (Гаусса) | логистическое | Накагами |Парето | полукруговое | непрерывное равномерное | Райса | Рэлея | Стьюдента | Фишера | хи-квадрат | экспоненциальное | variance-gamma | многомерное нормальное | копула |
Формула распределения Пуассона и ее значение в финансах
Оглавление
Содержание
Что такое распределение Пуассона?
Как это работает
Формула
Распределение Пуассона в финансах
Часто задаваемые вопросы о распределении Пуассона
К
Адам Хейс
Полная биография
Адам Хейс, доктор философии, CFA, финансовый писатель с более чем 15-летним опытом работы на Уолл-стрит в качестве трейдера деривативов.
Узнайте о нашем редакционная политика
Обновлено 19 мая 2022 г.
Рассмотрено
Сомер Андерсон
Рассмотрено Сомер Андерсон
Полная биография
Сомер Дж. Андерсон — дипломированный бухгалтер, доктор бухгалтерского учета и профессор бухгалтерского учета и финансов, проработавший в сфере бухгалтерского учета и финансов более 20 лет. Ее опыт охватывает широкий спектр областей бухгалтерского учета, корпоративных финансов, налогов, кредитования и личных финансов.
Узнайте о нашем Совет финансового контроля
Факт проверен
Сюзанна Квилхауг
Факт проверен Сюзанна Квилхауг
Полная биография
Сюзанна — контент-маркетолог, писатель и специалист по проверке фактов. Она имеет степень бакалавра финансов в Государственном университете Бриджуотер и помогает разрабатывать контент-стратегии для финансовых брендов.
Узнайте о нашем редакционная политика
Инвестопедия / Джоуль Гарсия
Что такое распределение Пуассона?
В статистике распределение Пуассона — это распределение вероятностей, которое используется, чтобы показать, сколько раз событие может произойти в течение определенного периода. Другими словами, это счетное распределение. Распределения Пуассона часто используются для понимания независимых событий, которые происходят с постоянной скоростью в течение заданного интервала времени.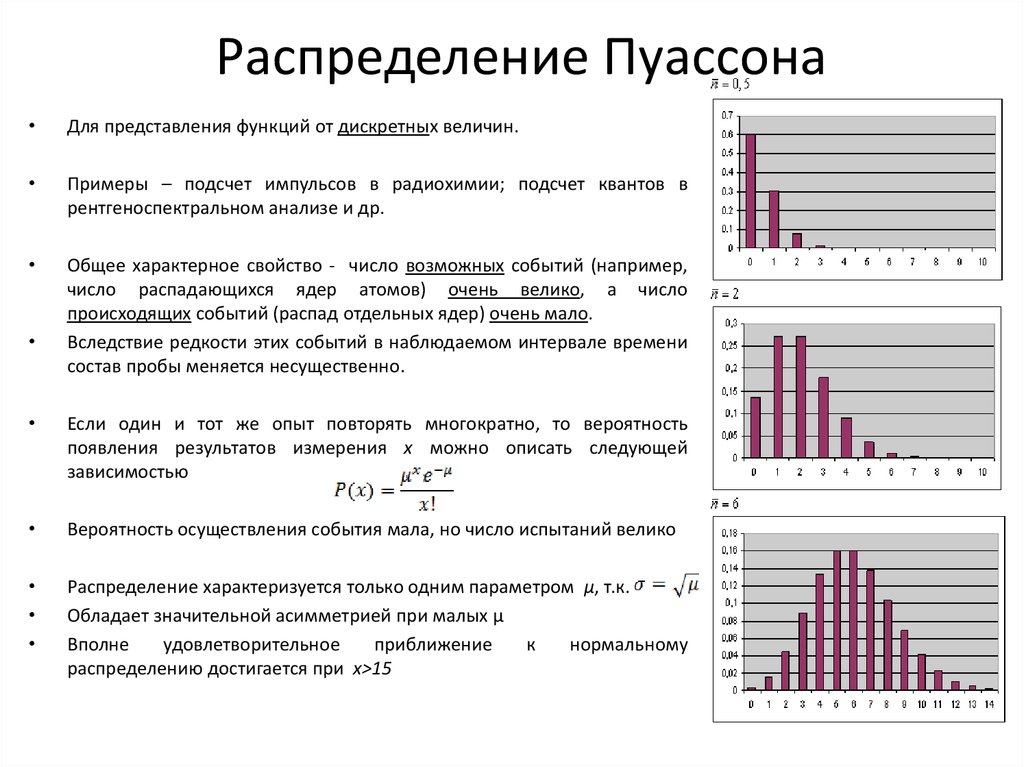 Он был назван в честь французского математика Симеона Дени Пуассона.
Он был назван в честь французского математика Симеона Дени Пуассона.
Распределение Пуассона является дискретной функцией, что означает, что переменная может принимать только определенные значения в (потенциально бесконечном) списке. Иными словами, переменная не может принимать все значения в любом непрерывном диапазоне. Для распределения Пуассона переменная может принимать только целые числа (0, 1, 2, 3 и т. д.), без дробей или десятичных знаков.
Ключевые выводы
- Распределение Пуассона, названное в честь французского математика Симеона Дени Пуассона, можно использовать для оценки того, сколько раз событие может произойти в течение «X» периодов времени.
- Распределения Пуассона используются, когда интересующая переменная является дискретной счетной переменной.
- Многие экономические и финансовые данные появляются в виде счетных переменных, например, сколько раз человек становится безработным в данном году, что позволяет анализировать их с помощью распределения Пуассона.

Понимание распределения Пуассона
Распределение Пуассона можно использовать для оценки вероятности того, что что-то произойдет «X» раз. Например, если среднее количество людей, которые покупают чизбургеры в сети быстрого питания в пятницу вечером в одном ресторане, составляет 200 человек, распределение Пуассона может ответить на такие вопросы, как «Какова вероятность того, что более 300 человек купить бургеры?» Таким образом, применение распределения Пуассона позволяет менеджерам вводить оптимальные системы планирования, которые не будут работать, скажем, при нормальном распределении.
Одним из самых известных исторических и практических применений распределения Пуассона была оценка ежегодного числа прусских кавалерийских солдат, убитых в результате ударов ногами. Современные примеры включают оценку количества автомобильных аварий в городе заданного размера; в физиологии это распределение часто используется для расчета вероятностных частот различных типов секреции нейротрансмиттеров.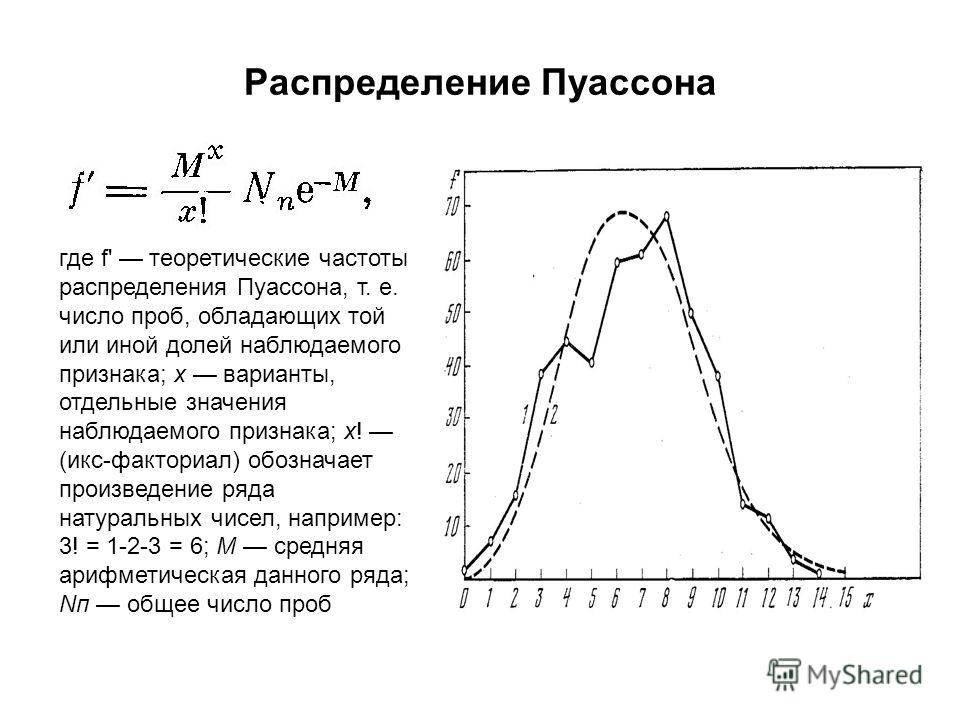 Или, если бы в видеомагазине каждую пятницу вечером в среднем было 400 покупателей, какова была бы вероятность того, что 600 покупателей пришли бы в любой конкретный вечер пятницы?
Или, если бы в видеомагазине каждую пятницу вечером в среднем было 400 покупателей, какова была бы вероятность того, что 600 покупателей пришли бы в любой конкретный вечер пятницы?
Формула распределения Пуассона
Формула распределения Пуассона. СК ТейлорГде:
- e число Эйлера ( e = 2,71828…)
- x количество вхождений
- х ! является факториалом x
- λ равно ожидаемому значению (EV) x , когда оно также равно его дисперсии
Учитывая данные, которые следуют распределению Пуассона, это выглядит графически как:
Пример распределения Пуассона. Инвестопедия В примере, изображенном на графике выше, предположим, что некоторый рабочий процесс имеет частоту ошибок 3%. Если мы дополнительно предположим 100 случайных испытаний, распределение Пуассона описывает вероятность получения определенного количества ошибок за некоторый период времени, например, за один день.
Если среднее значение очень велико, то распределение Пуассона является приблизительно нормальным распределением.
Распределение Пуассона в финансах
Распределение Пуассона также обычно используется для моделирования данных финансового подсчета, где сумма невелика и часто равна нулю. В качестве примера в финансах его можно использовать для моделирования количества сделок, которые типичный инвестор совершит в определенный день, что может быть равно 0 (часто), 1, 2 и т. д.
В качестве другого примера, эту модель можно использовать для прогнозирования количества «шоков» на рынке, которые произойдут в заданный период времени, скажем, за десятилетие.
Когда следует использовать распределение Пуассона?
Распределение Пуассона лучше всего применять для статистического анализа, когда рассматриваемая переменная является счетной переменной. Например, сколько раз X встречается на основе одной или нескольких независимых переменных. Например, чтобы оценить, сколько бракованных изделий сойдет с конвейера при различных исходных данных.
Какие предположения делает распределение Пуассона?
Чтобы распределение Пуассона было точным, все события независимы друг от друга, скорость событий во времени постоянна, и события не могут происходить одновременно. При этом среднее значение и дисперсия будут равны друг другу.
Является ли распределение Пуассона дискретным или непрерывным?
Поскольку оно измеряет дискретные значения, распределение Пуассона также является дискретным распределением. Это можно противопоставить нормальному распределению, которое является непрерывным.
Распределение Пуассона | Brilliant Math & Science Wiki
Содержание
- Условия использования
- Вероятности с распределением Пуассона
- Свойства распределения Пуассона
- Практическое применение
- Смотрите также
- Рекомендации
Распределение Пуассона применимо только при выполнении нескольких условий.
Условия распределения Пуассона:
- Событие может произойти любое количество раз в течение периода времени.
- События происходят независимо. Другими словами, если событие происходит, оно не влияет на вероятность другого события, происходящего в тот же период времени.
- Скорость возникновения постоянна; то есть скорость не меняется в зависимости от времени.
- Вероятность возникновения события пропорциональна продолжительности периода времени. Например, вероятность того, что событие произойдет за 2 часа, должна быть в два раза выше, чем вероятность того, что событие произойдет за 1 час.
Например, распределение Пуассона подходит для моделирования количества телефонных звонков, которые офис получит в полдень, если известно, что в этот период времени в среднем поступает 4 звонка в час.
- Хотя в среднем это 4 звонка, теоретически они могут получить любое количество звонков за этот период времени.

- События фактически независимы, поскольку нет оснований ожидать, что вызывающий абонент повлияет на шансы другого вызывающего абонента.
- Частота возникновения может считаться постоянной.
- Разумно предположить, что (например) вероятность получить звонок в первые полчаса такая же, как и вероятность получить звонок в последние полчаса.
Конечно, эта ситуация не является абсолютной идеальной теоретической подгонкой для распределения Пуассона. Например, офис, безусловно, не может принять триллион звонков за указанный период времени, поскольку в живых осталось менее триллиона человек, которые могут звонить. С практической точки зрения ситуация достаточно близка, чтобы распределение Пуассона хорошо моделировало поведение ситуации. 9{n-k}\) для \(k=0,1,2,3,\ldots,n\).
Теперь давайте возьмем ограничение выше, используя \(n \to \infty\). Вместо бесконечно малого \(p\) предположим, что задано, что \(np\), среднее значение функции распределения вероятностей, является некоторым конечным значением \(m\).
Найдите \(P(X=k)\) через \(m\) и \(k\) для этого нового распределения, где \(k=0,1,2,3,\ldots\), без поиска чего-либо или декламирования каких-либо формул по памяти.
Учитывая, что ситуация следует распределению Пуассона, существует формула, позволяющая вычислить вероятность наблюдения \(k\) событий за период времени для любого неотрицательного целого значения \(k\). 9{-2,5}}{4!} \приблизительно 0,133\\\\ &\ \\vточки \конец{выравнивание}\]
Распределение Пуассона с \(\lambda=2.5\)
Для этой формулы нет верхнего предела значения \(k\), хотя вероятность быстро приближается к 0 по мере увеличения \(k\). \(_\квадрат\)
Каждую минуту в ресторане быстрого питания к кассе подходит в среднем 2,8 клиента.
Предполагая, что количество клиентов, приближающихся к кассе в минуту, подчиняется распределению Пуассона, какова вероятность того, что 4 клиента подойдут к кассе в следующую минуту?
Округлите ответ до 3 знаков после запятой.
Распределение Пуассона можно использовать для вычисления вероятностей «меньше чем» и «больше чем», используя правило суммы и дополнительных вероятностей.
Статистик фиксирует количество автомобилей, подъезжающих к перекрестку. Он обнаружил, что каждую минуту к перекрестку подъезжает в среднем 1,6 автомобиля.
Если предположить, что количество автомобилей, подъезжающих к этому перекрестку, подчиняется распределению Пуассона, какова вероятность того, что 3 или более автомобилей подъедут к перекрестку в течение минуты? 9{-1,6}}{2!} \приблизительно 0,258 \\\\ \Стрелка вправо P(X \le 2) &= P(X=0) + P(X=1) + P(X=2) \\ &\примерно 0,783\\\\ \Стрелка вправо P(X \ge 3) &= 1-P(X \le 2) \\ &\примерно 0,217. \конец{выравнивание}\]
Следовательно, вероятность того, что в течение минуты к перекрестку подъедут 3 или более автомобилей, приблизительно равна \(0,217.\) \(_\квадрат\)
96,89% 97,89% 98,89% 99,89%
Когда производитель компьютерных дисков тестирует диск, он записывает данные на диск, а затем тестирует его с помощью сертификатора. Сертификатор подсчитывает количество пропущенных импульсов или ошибок. Количество ошибок в тестовой области на диске имеет распределение Пуассона с \(\lambda = 0,2\).
Сертификатор подсчитывает количество пропущенных импульсов или ошибок. Количество ошибок в тестовой области на диске имеет распределение Пуассона с \(\lambda = 0,2\).
Какой процент тестовых областей имеет две или меньше ошибок?
Есть и другие приложения распределения Пуассона, которые исходят из более открытых задач. Например, его можно использовать для определения количества персонала, необходимого в колл-центре.
Колл-центр получает в среднем 4,5 звонка каждые 5 минут. Каждый агент может обработать один из этих вызовов в течение 5 минут. Если вызов получен, но агент не может его принять, то этот вызывающий абонент будет переведен на удержание. Предполагая, что вызовы следуют распределению Пуассона, какое минимальное количество операторов необходимо дежурить, чтобы вызовы удерживались не более 10 % времени?
Чтобы все звонки были приняты, количество дежурных операторов должно быть больше или равно количеству полученных звонков. Если \(X\) — количество полученных вызовов, а \(k\) — количество агентов, то \(k\) должно быть установлено так, чтобы \(P(X > k)\le 0,1,\) или эквивалентно, \(P(X \le k) > 0,9{-4,5}}{7!} \приблизительно 0,082 &\подразумевает P(X\le 7)\приблизительно 0,913.
\конец{массив}\]
Если цель состоит в том, чтобы убедиться, что менее 10% вызовов помещаются на удержание, то операторы \(\boxed{7}\) должны быть на дежурстве. \(_\квадрат\)
Ожидаемое значение распределения Пуассона не должно вызывать удивления, поскольку каждое распределение Пуассона определяется своим математическим ожиданием.
Ожидаемое значение случайной величины Пуассона:
Учитывая дискретную случайную величину \(X\), которая следует распределению Пуассона с параметром \(\lambda,\), ожидаемое значение этой переменной равно 9{-\lambda}.\)
Найдите его стандартное отклонение.
Изображение предоставлено Wikidepia Skbkekas, функция массы вероятности распределения Пуассона
Режим лишь немного сложнее:
Режим случайной величины Пуассона:
Если \(\lambda\) не является целым числом, модой распределения Пуассона с параметром \(\lambda\) является \(\lfloor \lambda \rfloor\).
В противном случае и \(\lambda\), и \(\lambda-1\) являются режимами.
Медиана распределения Пуассона не имеет замкнутой формы, но известны ее границы:
Медиана случайной величины Пуассона:
Медиана \(\rho\) распределения Пуассона с параметром \(\lambda\) удовлетворяет
\[\lambda-\ln 2 \leq \rho \leq \lambda+\frac{1}{3}.\]
Сумма двух независимых пуассоновских случайных величин является пуассоновской случайной величиной.
Сумма независимых пуассоновских случайных величин: 9{-(\lambda_1+\lambda_2)}}{к!}.\]
Дэймон работает в вечернюю смену в кассе своей розничной торговли. В настоящее время открыты две кассы, но его коллега собирается пойти домой на день и закрыть свою кассу.
Количество клиентов, приближающихся к каждой кассе, является независимой случайной величиной Пуассона. Если на каждую кассу приходило в среднем 2 покупателя в минуту, какова вероятность того, что за минуту после того, как его коллега пойдет домой, к кассе Деймона подойдет более 4 покупателей?
Округлите ответ до 3 знаков после запятой.
Кроме того, распределение Пуассона можно рассматривать как предельный случай биномиального распределения. Если имеется \(n\) независимых испытаний, \(p\) — вероятность успешного испытания, а \(np\) остается постоянной, то это биномиальное распределение будет вести себя как распределение Пуассона по мере того, как \(n\) приближается к бесконечность.
Предельная теорема Пуассона:
Поскольку \(n\) стремится к бесконечности, а \(p\) приближается к \(0\), так что \(\lambda\) является константой с \(\lambda=np,\), биномиальное распределение с параметрами \(n \) и \(p\) аппроксимируется распределением Пуассона с параметром \(\lambda\): 9{-\lambda}}{к!}.\]
Это можно доказать, рассмотрев тот факт, что сходимость по производящим функциям момента влечет сходимость по распределению.
Классическим примером распределения Пуассона является количество прусских солдат, случайно убитых ногой лошади, поскольку это первый пример применения распределения Пуассона к большому набору данных реального мира.
За 20 лет наблюдались десять армейских корпусов, всего 200 наблюдений, и за это время 122 солдата были убиты ударом лошади. Вопрос в том, сколько смертей можно ожидать в течение года, что, как оказалось, прекрасно моделируется распределением Пуассона \((\)с \(\lambda=0,61):\)
# of deaths Predicted % Expected # of occurrences Actual # of occurrences 0 54.34 108.67 109 1 33.15 66.29 65 2 10.11 20.22 22 3 2.05 4.11 3 4 0.32 0.63 1 5 0.04 0.08 0 6 0.01 0.01 0 The interpretation of this data важно: поскольку распределение Пуассона измеряет частоту событий в предположении статистической случайности, совпадение ожидаемого распределения с фактическими данными предполагает, что фактические данные действительно были обусловлены случайностью.
Если фактические данные привели к гораздо большему количеству смертей, чем ожидалось, следует искать альтернативное объяснение (например, неадекватная подготовка, хитрый и изощренный заговор противника и т. д.). 9{-12}}{k!} \примерно 2,12\%,\]
, что означает, что в целом они могут чувствовать себя комфортно, имея под рукой только такое количество сотрудников, чтобы обработать 20 вызовов. Конечно, выбор порога зависит от контекста; например, в отделении неотложной помощи может потребоваться дополнительный персонал.
Короче говоря, список приложений очень длинный. Частичный список [1] недавно изученных явлений, которые подчиняются распределению Пуассона, приведен ниже:
- количество мутаций на данной цепи ДНК в единицу времени
- количество заявлений о банкротстве за месяц
- количество заездов на автомойку в час
- количество сбоев сети в день
- количество заражений файлового сервера вирусом в центре обработки данных в течение 24 часов
- количество остановов двигателей самолетов Airbus 330 на 100 000 летных часов
- количество пациентов с астмой, поступивших в данный час в поликлинику без предварительной записи
- количество голодающих, заходящих в ресторан McDonald’s в день
- количество несчастных случаев на производстве за заданное время производства
- число рождений, смертей, браков, разводов, самоубийств и убийств за определенный период времени
- количество клиентов, которые звонят, чтобы пожаловаться на проблему обслуживания в месяц
- количество посетителей веб-сайта в минуту
- количество звонков на горячую линию для потребителей за 5 минут
- количество телефонных звонков в минуту в малом бизнесе
- количество прибывающих к пункту взимания платы за дорожную магистраль в минуту между 3 часами ночи и и 4 утра в январе на Канзасе Магистраль.

 : 2000, С. 135. — ISBN 978-5-406-00565-1.
: 2000, С. 135. — ISBN 978-5-406-00565-1.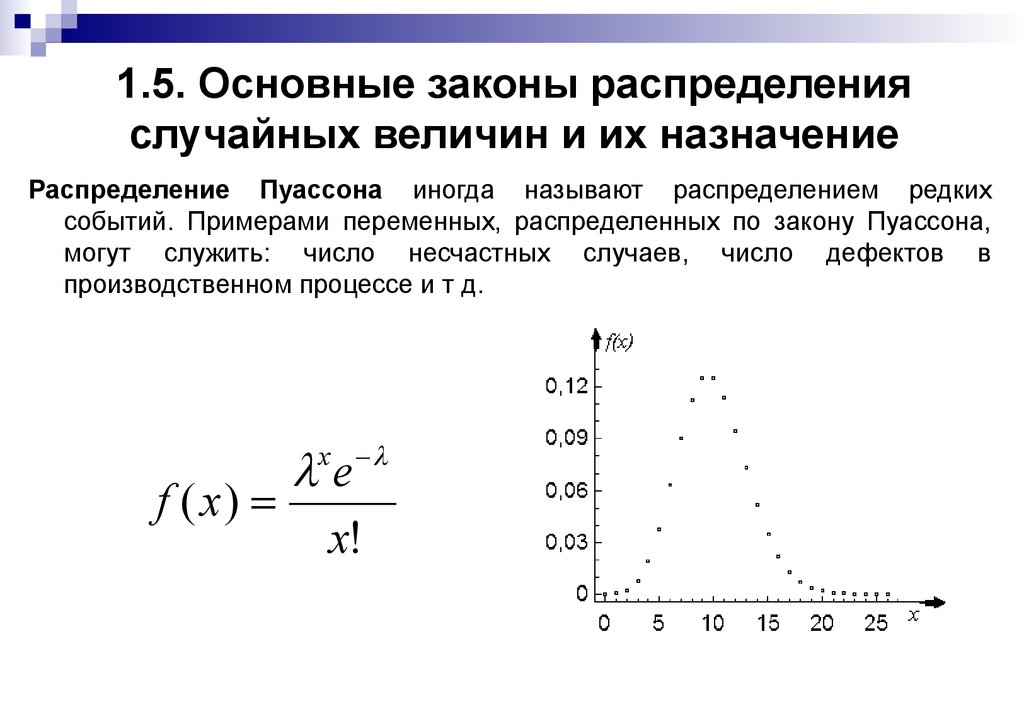 : 2000, С. 135. — ISBN 978-5-406-00565-1.
: 2000, С. 135. — ISBN 978-5-406-00565-1.

 \конец{массив}\]
\конец{массив}\] В противном случае и \(\lambda\), и \(\lambda-1\) являются режимами.
В противном случае и \(\lambda\), и \(\lambda-1\) являются режимами.
 За 20 лет наблюдались десять армейских корпусов, всего 200 наблюдений, и за это время 122 солдата были убиты ударом лошади. Вопрос в том, сколько смертей можно ожидать в течение года, что, как оказалось, прекрасно моделируется распределением Пуассона \((\)с \(\lambda=0,61):\)
За 20 лет наблюдались десять армейских корпусов, всего 200 наблюдений, и за это время 122 солдата были убиты ударом лошади. Вопрос в том, сколько смертей можно ожидать в течение года, что, как оказалось, прекрасно моделируется распределением Пуассона \((\)с \(\lambda=0,61):\) Если фактические данные привели к гораздо большему количеству смертей, чем ожидалось, следует искать альтернативное объяснение (например, неадекватная подготовка, хитрый и изощренный заговор противника и т. д.). 9{-12}}{k!} \примерно 2,12\%,\]
Если фактические данные привели к гораздо большему количеству смертей, чем ожидалось, следует искать альтернативное объяснение (например, неадекватная подготовка, хитрый и изощренный заговор противника и т. д.). 9{-12}}{k!} \примерно 2,12\%,\]