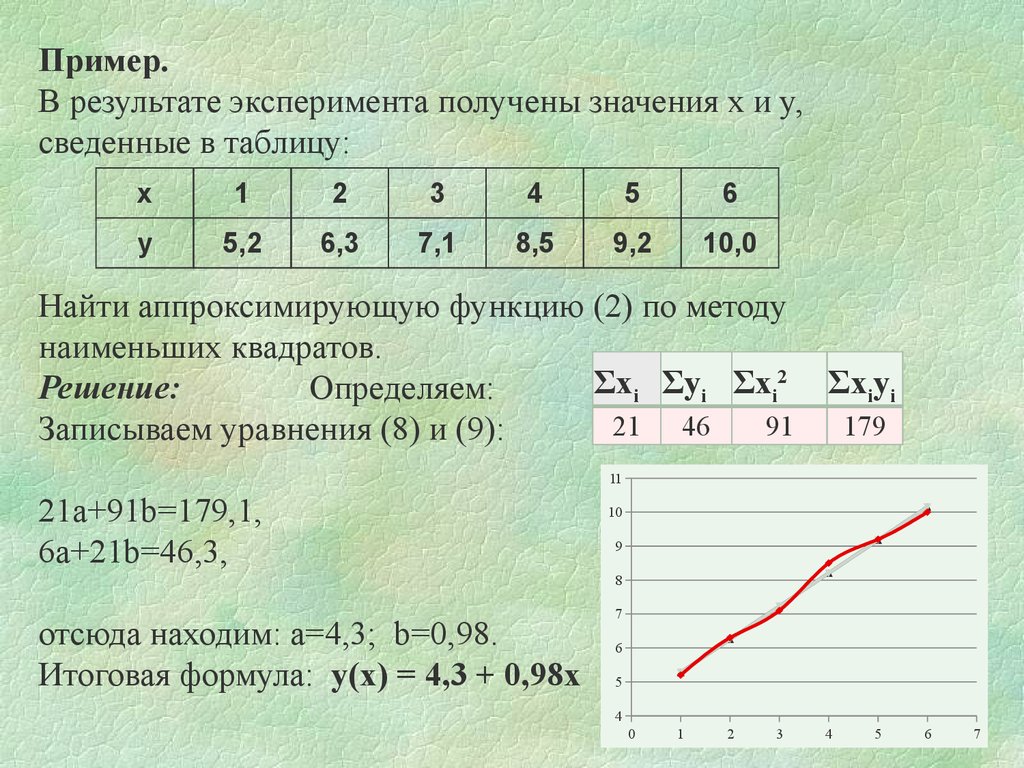
Моделирование в электроэнергетике — Аппроксимация опытных данных. Метод наименьших квадратов (МНК)
Аппроксимация опытных данных – это метод, основанный на замене экспериментально полученных данных аналитической функцией наиболее близко проходящей или совпадающей в узловых точках с исходными значениями (данными полученными в ходе опыта или эксперимента). В настоящее время существует два способа определения аналитической функции:
— с помощью построения интерполяционного многочлена n-степени, который проходит непосредственно через все точки заданного массива данных. В данном случае аппроксимирующая функция представляется в виде: интерполяционного многочлена в форме Лагранжа или интерполяционного многочлена в форме Ньютона.
— с помощью построения аппроксимирующего многочлена n-степени, который проходит в ближайшей близости от точек из заданного массива данных. Таким образом, аппроксимирующая функция сглаживает все случайные помехи (или погрешности), которые могут возникать при выполнении эксперимента: измеряемые значения в ходе опыта зависят от случайных факторов, которые колеблются по своим собственным случайным законам (погрешности измерений или приборов, неточность или ошибки опыта). В данном случае аппроксимирующая функция определяется по методу наименьших квадратов.
В данном случае аппроксимирующая функция определяется по методу наименьших квадратов.
Метод наименьших квадратов (в англоязычной литературе Ordinary Least Squares, OLS) — математический метод, основанный на определении аппроксимирующей функции, которая строится в ближайшей близости от точек из заданного массива экспериментальных данных. Близость исходной и аппроксимирующей функции F(x) определяется числовой мерой, а именно: сумма квадратов отклонений экспериментальных данных от аппроксимирующей кривой F(x) должна быть наименьшей.
Рис.1. Аппроксимирующая кривая, построенная по методу наименьших квадратов
Метод наименьших квадратов используется:
— для решения переопределенных систем уравнений, когда количество уравнений превышает количество неизвестных;
— для поиска решения в случае обычных (не переопределенных) нелинейных систем уравнений;
— для аппроксимации точечных значений некоторой аппроксимирующей функцией.
Аппроксимирующая функция по методу наименьших квадратов определяется из условия минимума суммы квадратов отклонений расчетной аппроксимирующей функции от заданного массива экспериментальных данных.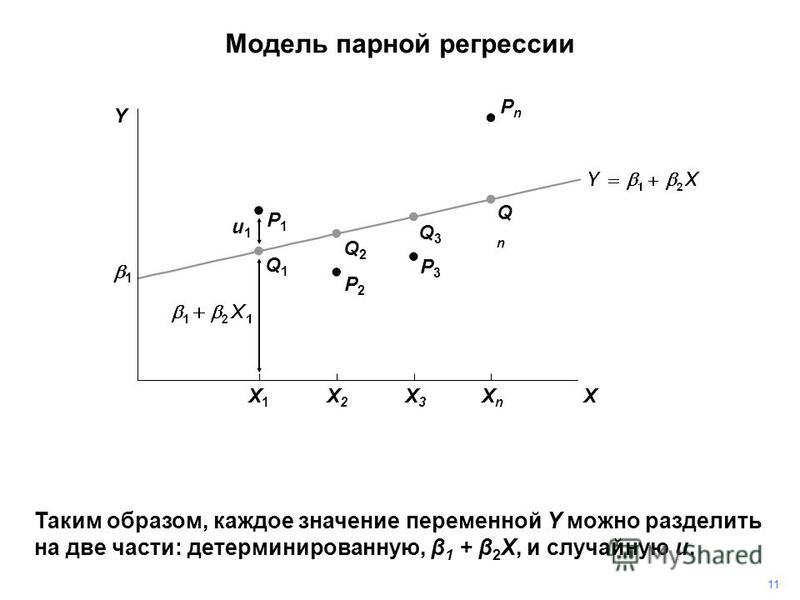 Данный критерий метода наименьших квадратов записывается в виде следующего выражения:
Данный критерий метода наименьших квадратов записывается в виде следующего выражения:
— значения расчетной аппроксимирующей функции в узловых точках ,
— заданный массив экспериментальных данных в узловых точках .
Квадратичный критерий обладает рядом «хороших» свойств, таких, как дифференцируемость, обеспечение единственного решения задачи аппроксимации при полиномиальных аппроксимирующих функциях.
В зависимости от условий задачи аппроксимирующая функция представляет собой многочлен степени m
Степень аппроксимирующей функции не зависит от числа узловых точек, но ее размерность должна быть всегда меньше размерности (количества точек) заданного массива экспериментальных данных.
∙ В случае если степень аппроксимирующей функции m=1, то мы аппроксимируем табличную функцию прямой линией (линейная регрессия).
∙ В случае если степень аппроксимирующей функции m=2, то мы аппроксимируем табличную функцию квадратичной параболой (квадратичная аппроксимация).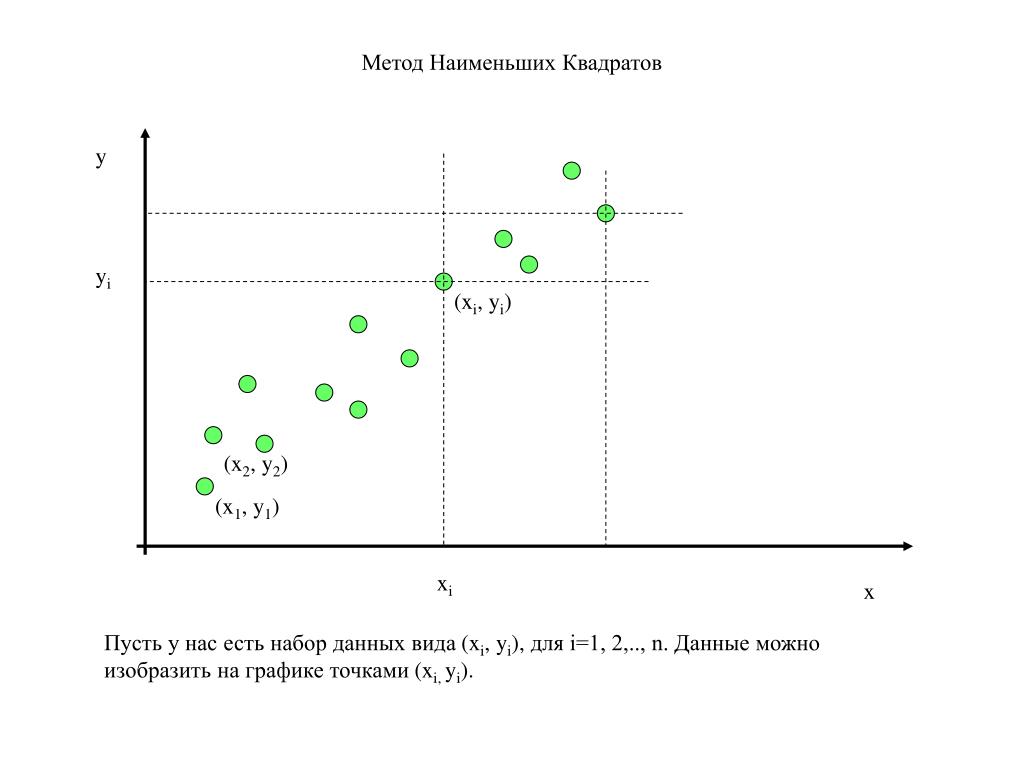
∙ В случае если степень аппроксимирующей функции m=3, то мы аппроксимируем табличную функцию кубической параболой (кубическая аппроксимация).
В общем случае, когда требуется построить аппроксимирующий многочлен степени m для заданных табличных значений, условие минимума суммы квадратов отклонений по всем узловым точкам переписывается в следующем виде:
— координаты узловых точек таблицы;
— неизвестные коэффициенты аппроксимирующего многочлена степени m;
— количество заданных табличных значений.
Необходимым условием существования минимума функции является равенству нулю ее частных производных по неизвестным переменным . В результате получим следующую систему уравнений:
Преобразуем полученную линейную систему уравнений: раскроем скобки и перенесем свободные слагаемые в правую часть выражения. В результате полученная система линейных алгебраических выражений будет записываться в следующем виде:
Данная система линейных алгебраических выражений может быть переписана в матричном виде:
В результате была получена система линейных уравнений размерностью m+1, которая состоит из m+1 неизвестных. Данная система может быть решена с помощью любого метода решения линейных алгебраических уравнений (например, методом Гаусса). В результате решения будут найдены неизвестные параметры аппроксимирующей функции, обеспечивающие минимальную сумму квадратов отклонений аппроксимирующей функции от исходных данных, т.е. наилучшее возможное квадратичное приближение. Следует помнить, что при изменении даже одного значения исходных данных все коэффициенты изменят свои значения, так как они полностью определяются исходными данными.
Данная система может быть решена с помощью любого метода решения линейных алгебраических уравнений (например, методом Гаусса). В результате решения будут найдены неизвестные параметры аппроксимирующей функции, обеспечивающие минимальную сумму квадратов отклонений аппроксимирующей функции от исходных данных, т.е. наилучшее возможное квадратичное приближение. Следует помнить, что при изменении даже одного значения исходных данных все коэффициенты изменят свои значения, так как они полностью определяются исходными данными.
Аппроксимация исходных данных линейной зависимостью (линейная регрессия)
В качестве примера, рассмотрим методику определения аппроксимирующей функции, которая задана в виде линейной зависимости. В соответствии с методом наименьших квадратов условие минимума суммы квадратов отклонений записывается в следующем виде:
— координаты узловых точек таблицы;
— неизвестные коэффициенты аппроксимирующей функции, которая задана в виде линейной зависимости.
Необходимым условием существования минимума функции является равенству нулю ее частных производных по неизвестным переменным. В результате получаем следующую систему уравнений:
Преобразуем полученную линейную систему уравнений.
Решаем полученную систему линейных уравнений. Коэффициенты аппроксимирующей функции в аналитическом виде определяются следующим образом (метод Крамера):
Данные коэффициенты обеспечивают построение линейной аппроксимирующей функции в соответствии с критерием минимизации суммы квадратов аппроксимирующей функции от заданных табличных значений (экспериментальные данные).
Алгоритм реализации метода наименьших квадратов
1. Начальные данные:
— задан массив экспериментальных данных с количеством измерений N
— задана степень аппроксимирующего многочлена (m)
2. Алгоритм вычисления:
2.1. Определяются коэффициенты для построения системы уравнений размерностью
— коэффициенты системы уравнений (левая часть уравнения)
— индекс номера строки квадратной матрицы системы уравнений
— индекс номера столбца квадратной матрицы системы уравнений
— свободные члены системы линейных уравнений (правая часть уравнения)
— индекс номера строки квадратной матрицы системы уравнений
2. 2. Формирование системы линейных уравнений размерностью .
2. Формирование системы линейных уравнений размерностью .
2.3. Решение системы линейных уравнений с целью определения неизвестных коэффициентов аппроксимирующего многочлена степени m.
2.4.Определение суммы квадратов отклонений аппроксимирующего многочлена от исходных значений по всем узловым точкам
Найденное значение суммы квадратов отклонений является минимально-возможным.
Аппроксимация с помощью других функций
Следует отметить, что при аппроксимации исходных данных в соответствии с методом наименьших квадратов в качестве аппроксимирующей функции иногда используют логарифмическую функцию, экспоненциальную функцию и степенную функцию.
Логарифмическая аппроксимация
Рассмотрим случай, когда аппроксимирующая функция задана логарифмической функцией вида:
Поиск неизвестных коэффициентов осуществляется по методу наименьших квадратов в соответствии со следующей системой уравнений.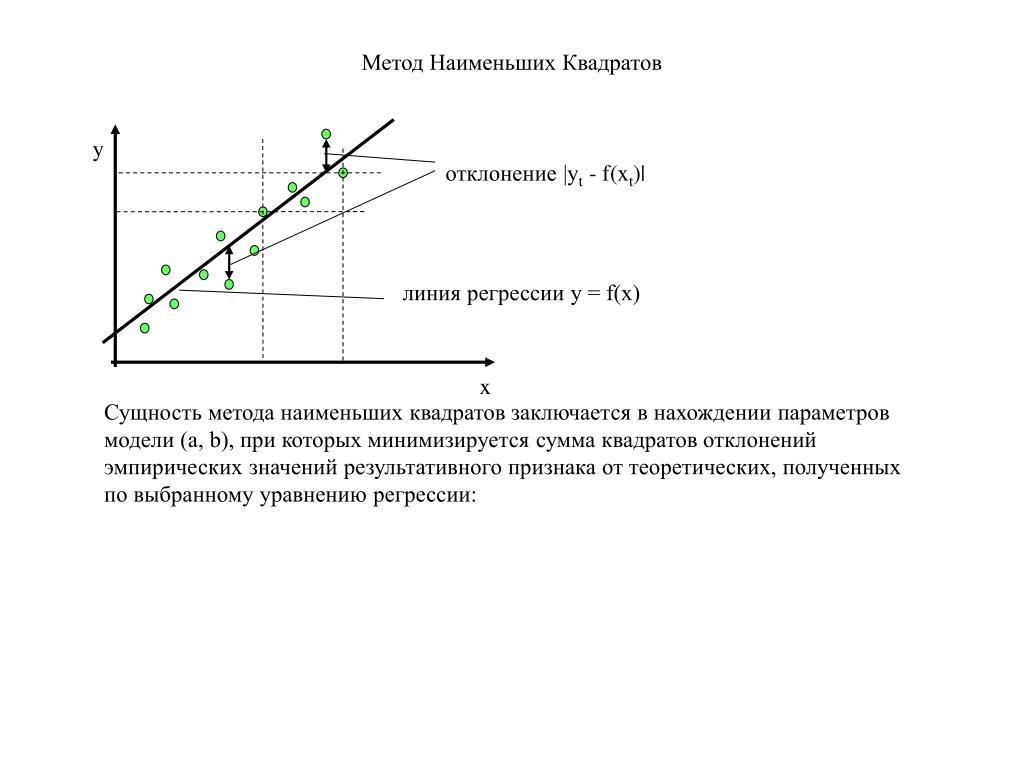
Решаем полученную систему линейных уравнений. Коэффициенты аппроксимирующей функции в аналитическом виде определяются следующим образом:
Экспоненциальная аппроксимация
Рассмотрим случай, когда аппроксимирующая функция задана экспоненциальной функцией вида:
Для применения метода наименьших квадратов экспоненциальная функция линеаризуется:
Поиск неизвестных коэффициентов осуществляется по методу наименьших квадратов в соответствии со следующей системой уравнений.
Решаем полученную систему линейных уравнений. Коэффициенты аппроксимирующей функции в аналитическом виде определяются следующим образом:
Степенная аппроксимация
Рассмотрим случай, когда аппроксимирующая функция задана степенной функцией вида:
Для применения метода наименьших квадратов степенная функция линеаризуется:
Поиск неизвестных коэффициентов осуществляется по методу наименьших квадратов в соответствии со следующей системой уравнений.
Решаем полученную систему линейных уравнений. Коэффициенты аппроксимирующей функции в аналитическом виде определяются следующим образом:
Выбор наилучшей аппроксимирующей функции определяется значением среднеквадратического отклонения. В связи с этим следует по методу наименьших квадратов определить несколько аппроксимирующих функций, а затем по критерию наименьшего среднеквадратического отклонения следует выбрать наиболее подходящую функцию.
Численное моделирование. Метод наименьших квадратов. (Лекция 7)
Сегодня: _________________ 2009 г.
Курс: Общий физический практикум
Склярова Елена Александровна
2. Лекция № 7
Сегодня: _________________ 2009 г.Лекция № 7
Тема: Численное моделирование
Содержание лекции:
1. Метод наименьших квадратов
3. Аппроксимация экспериментальных данных
Метод наименьших квадратов (МНК), идея которого принадлежитА.Лежандру, а теоретическое обоснование К.Гауссу. В соответствии с этим
методом, оценки параметров ai определяют из условия минимума суммы
квадратов отклонений измеренных значений yi от соответствующей ординаты
рассмотренной кривой
4.
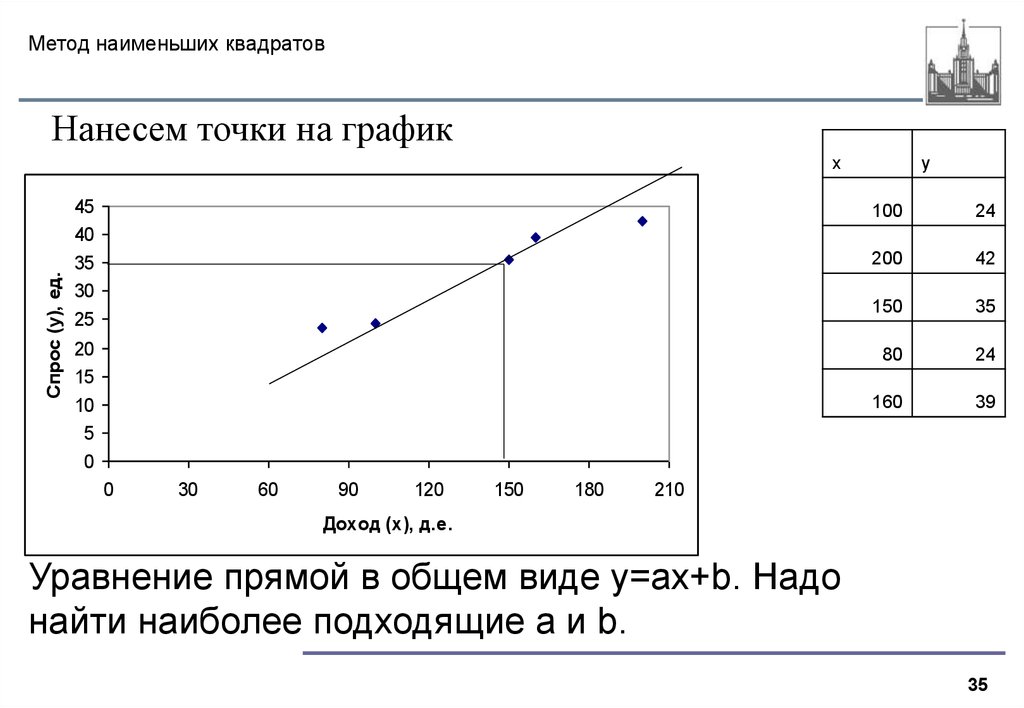 Метод наименьших квадратовПри обработке результатов измерений часто возникает необходимость
Метод наименьших квадратовПри обработке результатов измерений часто возникает необходимостьпостроить эмпирическую формулу, дающую аналитическое выражение
функциональной зависимости, заданной таблицей.
Общепринятым и весьма эффективным при решении подобных задач
является так называемый
метод наименьших квадратов, при котором
требование наилучшего согласования искомой кривой U = f(x) и
экспериментальных точек сводятся к тому, чтобы «сумма квадратов
отклонений» экспериментальных точек от искомой функции
U=
f(x, а, b, …) обращалась в минимум.
Метод наименьших квадратов — статистический прием, с помощью
которого неизвестные параметры модели оцениваются путем
минимизации
суммы
квадратов
отклонений
действительных
(эмпирических) значений от теоретических (из Глоссария по
естественным наукам).
5. Метод наименьших квадратов
«Метод наименьших квадратов» имеет перед другими методамиприближения существенные преимущества:
1.
он приводит к сравнительно простому математическому способу
определения параметров а, b, с, … искомого функционала;
2.
он дает довольно веское теоретическое обоснование с
вероятностной точки зрения.
6. Метод наименьших квадратов
Постановка задачиПусть результаты измерений
представлены
таблицей.
х
х1
х2
х3
…
U
U1
U2
U3
…
хn
Un
Если каждое из Ui (i = 1, 2, …, n) измеряется несколько раз, то в таблице Ui
заменяется средним арифметическим значением данной величины
1 m
(1)
U
U .
i
m k 1
ki
7. Метод наименьших квадратов
Далее выбираем общий вид функции U = f(x), зависящей отнескольких числовых параметров а, b, c, именно эти параметры и
требуется выбрать согласно методу наименьших квадратов так, чтобы
сумма квадратов отклонений Ui от f(xi) была минимальна. Запишем U как
функцию не только аргумента х, но и параметров а, b, c:
U = f(x, а, b, с, …)
(2)
Требуется выбрать а, b, c так, чтобы выполнялось условие
n
2
f
(
x
,
a
,
b
,
c
,.
 ..)
..)U
min .
i
i 1
(3)
8. Метод наименьших квадратов
Замечание:Следует заметить, что на практике не редко встречаются случаи, когда
экспериментальные данные при различных значениях аргумента
вследствие каких-либо причин обладают различной точностью. Это
имеет место тогда, когда дисперсии
SU21 , SU2 2 ,…, SU2 n неоднородны.
В этом случае необходимо минимизировать взвешенную сумму
квадратов отклонений экспериментальных и вычисленных значений
функции
(3’)
n
pi f ( x, a, b, c,…) U i min .
2
i 1
Здесь pi – веса наблюдений,
определяемые в соответствии с (1.37).
9. Метод наименьших квадратов
Найдем значения а, b, c, обращающие левую часть выражения вминимум.
Для этого продифференцируем ее по а, b, c и приравняем производные к
нулю:
xi 0
a
i 1
n
f
f ( xi , a, b, c,…) U i b xi 0
i 1
,
n
f
f i ( x, a, b, c,…) U i c xi 0
i 1
f
f
(
x
,
a
,
b
,
c
,.
 ..)
..)U
i
i
n
где
f
– значение частной производной функции f
xi f a ( xi , a, b, c)
a
по параметру а в точке xi,
f
xi ,
b
f
xi
c
– частные производные по параметрам b и с
искомого функционала
(4)
10. Метод наименьших квадратов
Решить систему (4) в общем виде нельзя, для этого необходимозадаться конкретным видом функции f.
Рассмотрим наиболее часто встречающийся на практике случай, когда f
является степенным полиномом, т.е.
f(x) = axm + bxm–1 + cxm–2 + … .
(5)
Рассмотрим два часто встречающихся на практике случая:
1)
когда функция f(x) линейна;
2)
когда функция f(x) выражается полиномом второй степени
(параболой).
11. Метод наименьших квадратов
Подбор параметров линейнойфункции методом наименьших
квадратов
В опыте зарегистрирована совокупность значений (хi, Ui), i = 1, 2, …, n
(табл.).
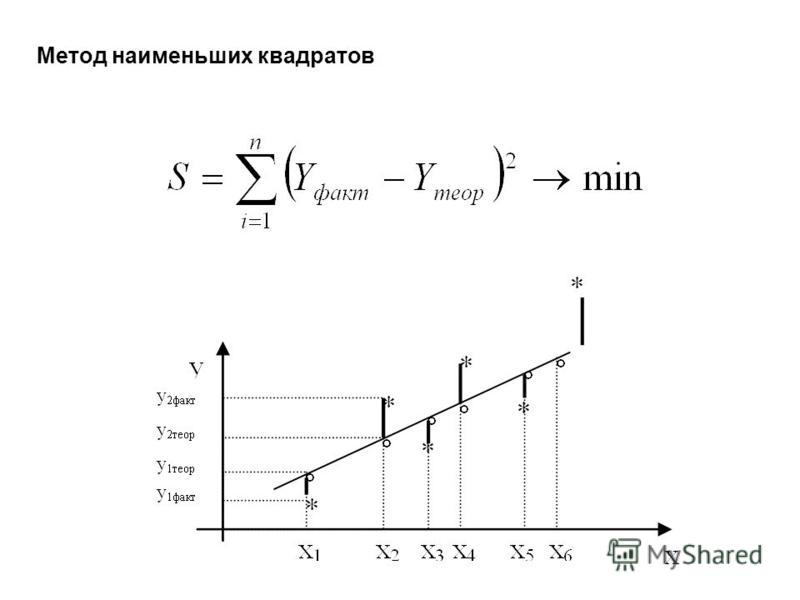
Требуется подобрать по методу наименьших квадратов параметры а, b
линейной функции
U = ax + b,
описывающей полученную экспериментальную зависимость U = f(x).
(6)
12. Метод наименьших квадратов
Для отклонений имеем выражения:U 1 (ax1 b) U1 ,
U 2 (ax2 b) U 2 ,
………………………….
U n (axn b) U n ,
n
( U i )
i 1
2
n
(axi b) U i F (a, b).
2
(7)
(8)
i 1
Таким образом, для случая линейного приближения сформулированная в
предыдущем параграфе задача сводится к исследованию на экстремум
функции двух переменных F(a, b).
13. Метод наименьших квадратов
Согласно системе (4), необходимые условия экстремума даютn
F (a, b)
2 (axi b) U i xi 0,
a
i 1
n
F (a, b)
2 (axi b) U i 0.
b
i 1
Поскольку
f
xi ,
a xi
f
1.
b xi
(9)
(10)
Сокращая на 2, получим систему (9) в виде (4). Далее преобразуем
уравнения (9) к виду
n
n
n
a b xi x i U i ,
i 1
i 1
i 1
n
n
a xi bn U i .
i 1
i 1
xi2
(11)
14. Метод наименьших квадратов
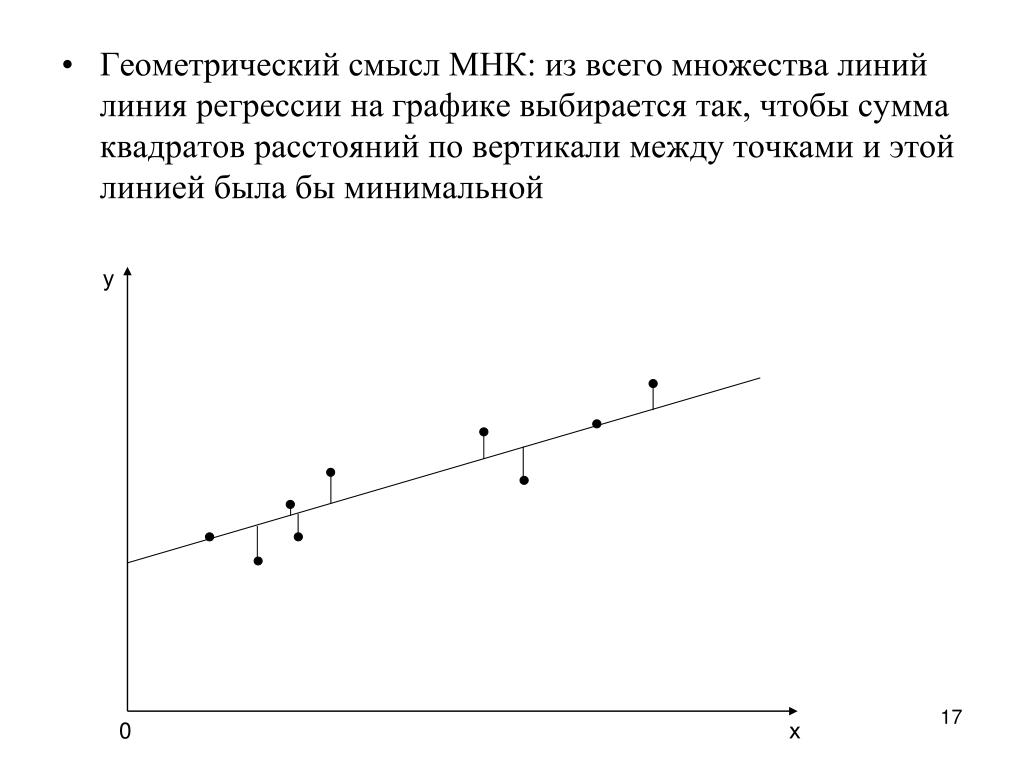
Решая систему (11), получимn
a
n
n xi U i xi
i 1
i 1
n
n
i 1
xi2
n
U i
i 1
n
xi
i 1
2
n
1 n
b U i a xi
n i 1
i 1
.
,
(12)
(13)
Определив из выражений (12) и (13) искомые а и b, мы найдем тем самым
искомую эмпирическую формулу в виде (6).
U = ax + b,
(6)
15. Метод наименьших квадратов
Теория дает возможность определить также дисперсию уклоненияточек от прямой и дисперсию коэффициентов а и b. Если
дисперсия
2точек,
2
– дисперсия
коэффи-циентов
а и b, тогда
2a
b
и
0
2
U
i
02 i 1
i 1
n 2
n n 2
n
(16)
2a 02
U i2
n
n
i 1
xi2
xi
i 1
n
2
,
2
(14)
n xiU i xi U i
i 1
i 1
i 1
,
n 2 n 2
n n 2 n xi xi
i 1
i 1
n
n
n
n
(15)
n
n
–
b2 02
n xi2
i 1
n
n
i 1
xi2
n
xi
i 1
2
.
16. Метод наименьших квадратов
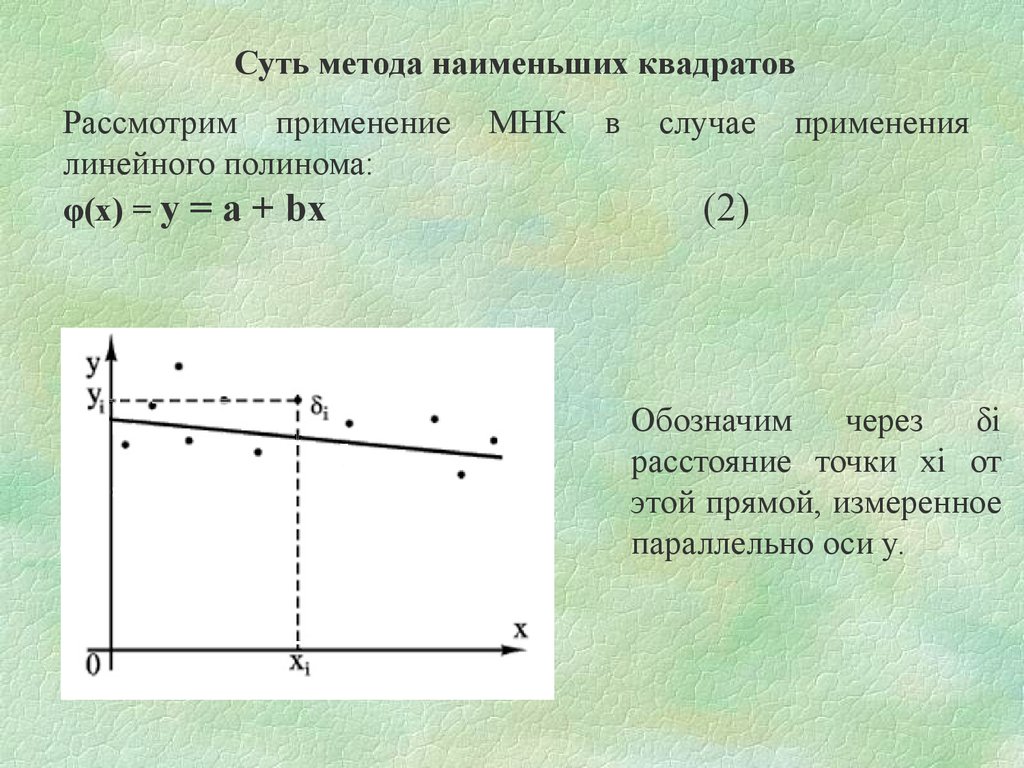
Примечание:Далеко не всякая зависимость описывается уравнением прямой линии. Однако
в ряде случаев можно путем несложных преобразований привести к линейной
более сложную зависимость.
k
Так, например, если
U l , то введя новую переменную
x
получим линейную связь между U и q.
1
q ,
x
17. Метод наименьших квадратов
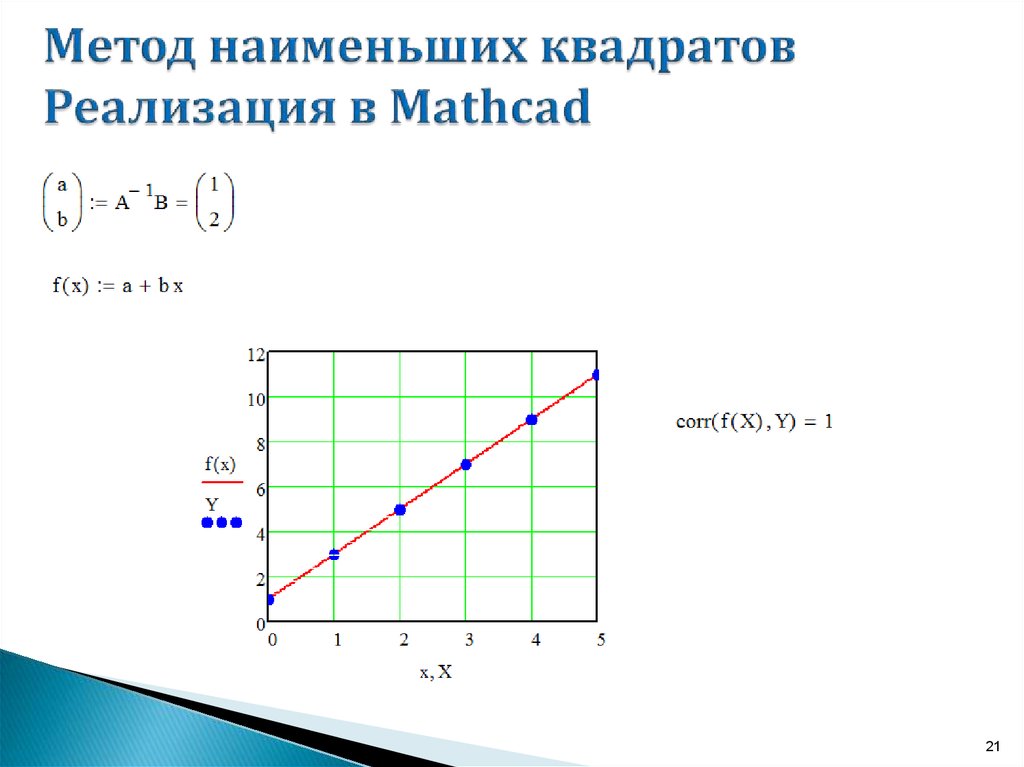
Пример.Пусть заданы результаты четырех измерений (рис.): y = 0 при x = 0; y = 1 при
x = 1; y = 2 при x = 3; y = 5 при x = 4.
Задача заключается в том, чтобы провести
~
y b0 b1t
через эти точки прямую
таким образом,
чтобы сумма квадратов отклонений
была минимальна.
Запишем уравнение, описывающее
проведение прямой
~
y b0 b1t
по результатам измерений.
Рис. 1. Аппроксимация прямой
линией.
18. Метод наименьших квадратов
Мыполучаем
систему:
1
1
1
1
переопределенную
0
0
1 b0 1
,
3 b1 2
4
5
или Xb=y. Нам
4 8
13 4
понадобится
1 матрица
T
T
1
X X
, ( X X )
.
обратная к ней:
8 26
20 4 2
XTX
и
Тогда решение b=(XTX)-1XTy по методу наименьших квадратов будет иметь вид
19.
 Метод наименьших квадратовТогда решение b=(XTX)-1XTy по методу наименьших квадратов будет иметь вид
Метод наименьших квадратовТогда решение b=(XTX)-1XTy по методу наименьших квадратов будет иметь вид0
b
13
4
1
1
1
1
1 0 .2
~ 0 1
b
.
b
4
2
0
1
3
4
2
1
.
1
1 20
5
Таким образом, оптимальная прямая задается уравнением
~
y 0.2 1.1t
20. Подбор параметров параболы второго порядка методом наименьших квадратов
В опыте зарегистрированы значения (хi, Ui), i = 1, 2, 3, …, n, сведенные втаблицу. Требуется методом наименьших квадратов подобрать параметры
квадратичной функции-параболы второго порядка
U = ax2 + bx + c,
(17)
сoответствующей наблюдаемой экспериментальной зависимости.
Итак, эмпирическую формулу ищем в виде
U = f(x, a, b, c).
(18)
Для отклонений имеем выражения
Ui = (a+ bxi + c) – Ui , i = 1, 2, …, n,
отсюда
U i
n
i 1
2
n
i 1
(axi2
x
bxi c) U i
2
F (a, b, c).
Здесь F(a, b, c) 0 и, следовательно, функция F(a, b, c) имеет минимум.

(19)
(20)
21. Подбор параметров параболы второго порядка методом наименьших квадратов
Необходимые условия экстремума даютn
F (a, b, c)
2 xi2 (axi2 bxi c) U i 0,
a
i 1
n
F (a, b, c)
2
2 xi (axi bxi c) U i 0,
b
i 1
n
F (a, b, c)
2
2 (axi bxi c) U i 0.
c
i 1
(21)
Систему (21) можно непосредственно записать, исходя из общей системы
(4), с учетом того, что
f
f
2
x
,
xi ,
i
a xi
b xi
f
1.
c xi
(22)
22. Подбор параметров параболы второго порядка методом наименьших квадратов
Аналогично тому, как это сделано в предыдущем параграфе, получимсистему нормальных уравнений:
n
a
xi4
n
b
xi3
n
c
xi2
n
2
xi U i ,
n
n
n
n
3
2
a xi b xi c xi xi U i ,
i 1
i 1
i 1
i 1
n
n
n
2
a xi b xi cn U i .
i 1
i 1
i 1
i 1
i 1
i 1
i 1
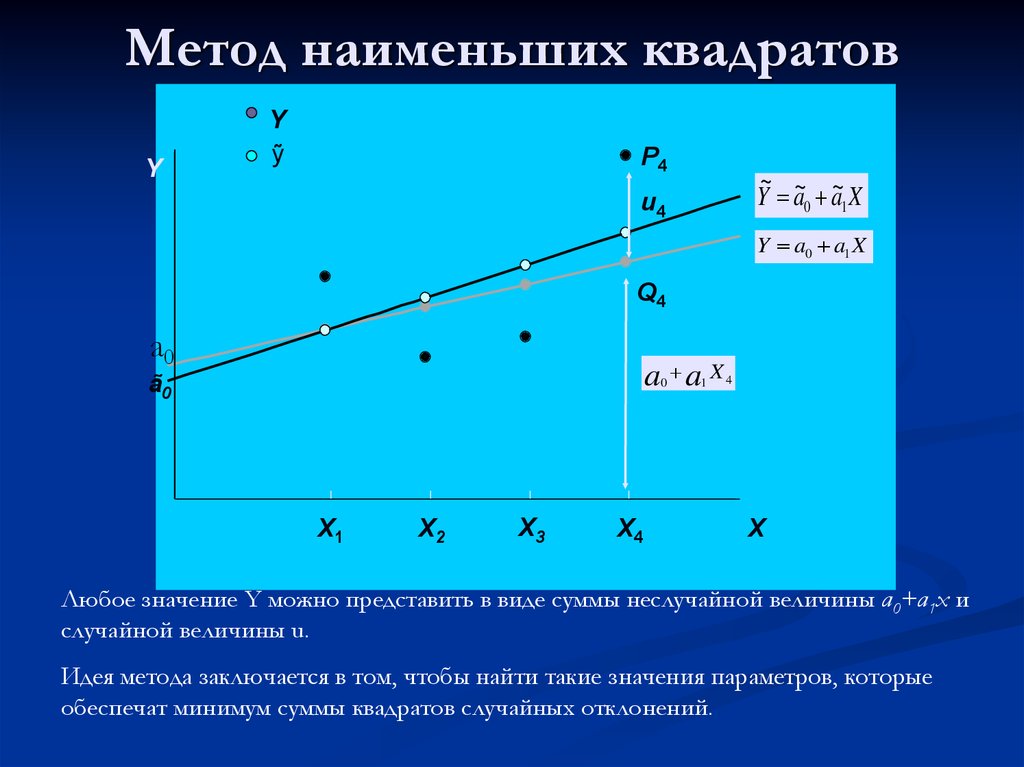
Решая систему (23), находим искомые коэффициенты a, b, c,
самым определяем искомую эмпирическую функцию.
(23)
и тем
23. Замечания о выборе эмпирической формулы
Способ наименьших квадратов не может дать ответа на вопрос о том, какоговида функция лучше всего аппроксимирует данные экспериментальные точки.
Вид функции должен быть задан на основании каких-то физических
соображений. Метод наименьших квадратов позволяет нам лишь выбрать,
какая из прямых, экспонент или парабол является лучшей прямой, лучшей
экспонентой или лучшей параболой.
Можно предложить лишь методику определения степени приближающего
полинома вида
U = axm + bxm–1 + cxm–2 + …
(24)
24. Замечания о выборе эмпирической формулы
хU
х1
U1
х2
U2
U k U k 1 U k ,
х3
U3
2
U k U k 1 U k ,
…………………………..
sU k s 1U k 1 s 1U k
…
…
хk
Uk
хk+1
Uk+1
…
…
xn
Un
U k
U k 1 U k
U k
,
xk 1 xk
xk 1 xk
U k 1 U k
2
Uk
,
xk 2 xk
.
 ………………………………….
………………………………….s 1
s 1
U k 1 U k
sU k
, s 1
xk s xk
…
…
25. Замечания о выборе эмпирической формулы
Можно усмотреть, что если результатыизмерения в точности удовлетворяют
линейному
закону,
разделенные
либо
то
первые
конечные
для
таблицы
постоянным
шагом
U3 U2
U k 1 U
U n Uразности
U 2 Uс
k
n 1
1
…
.
должны
быть
постоянны:
x2 x1
x3 x2
xk 1 xk
xn xn 1
(27)
Если
же
линейная
приближенно
имеющую
формула
отражает
место
лишь
фактически
зависимость,
то
выписанная цепочка точных равенств
заменится
цепочкой
приближенных
26. Пример
Предположим, что функцию f можно с высокой точностьюаппроксимировать многочленом Pm(x) некоторой степени m. Если
эта степень заранее неизвестна, то возникает проблема выбора
оптимальной степени аппроксимирующего многочлена в условиях,
когда исходные данные yi содержат случайные ошибки.

Для решения этой задачи можно принять следующий алгоритм: для
каждого m=0,1,2,.. вычисляется величина
За оптимальное значение степени многочлена следует принять то
значение m, начиная с которого величина стабилизируется или
начинает возрастать.
27. Метод наименьших квадратов
Пример1.
Приближение
функции
по
методу
наименьших
квадратов.
Пусть функция
задана
таблицей
своих
значений:
x
-3
-1
0
1
y
-4
-0.8
1.6
2.3
3
1.5
Приблизим функцию многочленом 2-ой степени. Для этого
вычислим коэффициенты нормальной системы уравнений:
,
,
,
,
,
28. Метод наименьших квадратов
Составим нормальную систему наименьших квадратов, котораяимеет вид:
Решение системы легко находится:
,
,
.
Таким образом, многочлен 2-ой степени найден:
29. Примеры
ПРИМЕР 2. Нахождение оптимальной степени многочлена.Определение параметров эмпирической зависимости.
 Часто из
Часто изфизических соображений следует, что зависимость y = f(x) между
величинами хорошо описывается моделью вида y = g(x, a0, a1, … am), где
вид зависимости g известен. Тогда применение критерия наименьших
квадратов приводит к задаче определения искомых параметров a0, a1, … am
из условия минимума функции:
30. Метод наименьших квадратов
Функция задана таблицей значенийНайти приближение функции многочленом оптимальной степени методом
наименьших квадратов.
Введем векторы исходных данных
Определим
базисные
функции.
Так
как
мы
приближаем
многочленом, базисные функции будут степенными функциями.
функцию
31. Метод наименьших квадратов
Определим аппроксимационный полином степениНапример, многочлен степени 2
Функция среднеквадратического отклонения многочлена степени n
32. Метод наименьших квадратов
Вычислим среднеквадратическое отклонение для многочленов степени 0,1,2 и 3Нарисуем графики многочленов и исходных данных
33.
 ПримерыПРИМЕР 3. Вывод нормальной системы уравнений для
ПримерыПРИМЕР 3. Вывод нормальной системы уравнений длянахождения параметров эмпирической зависимости.
Если зависимость от параметров a0, a1, … am нелинейна, то
экстремум функции
ищут методами минимизации функций нескольких
переменных.
34. Метод наименьших квадратов
Выведем систему уравнений для определениякоэффициентов a и b функции
,
осуществляющей среднеквадратичную аппроксимацию
заданной функции y = f(x) по
n+1 точкам. Составим функцию
и запишем для нее необходимое условие экстремума:
35. Метод наименьших квадратов
Тогда нормальная система примет вид:Получили линейную систему уравнений относительно неизвестных
параметров и, которая легко решается.
36. Примеры
Пусть дано решить систему уравненийa1x + b1y + c1z + … + n1 = 0
a2x + b2y + c2z + … + n2 = 0
(1)
a3x + b3y + c3z + … + n3 = 0
…
число которых более числа неизвестных x, у, z…
Чтобы решить их по способу Н.
 квадратов, составляют
квадратов, составляютновую систему уравнений, число которых равно числу
неизвестных и которые затем решаются по
обыкновенным правилам алгебры.
37. Примеры
Эти новые, или так называемые нормальные, уравнениясоставляются по следующему правилу: умножают сперва все
данные уравнения на коэффициенты у первой неизвестной х и,
сложив почленно, получают первое нормальное уравнение,
умножают все данные уравнения на коэффициенты у второй
неизвестной у и, сложив почленно, получают второе
нормальное уравнение и т. д.
[aa] = a1a1 + a2a2 +…
[ab] = a1b1 + a2b2 +…
[ac] = a1c1 + a2c2 +…
…
[ba] = b1a1 + b2a2 +…
[bb] = b1b1 + b2b2 +…
[bc] = b1c1 + b2c2 +…
38. Примеры
то нормальные уравнения представятся в следующемпростом виде:
[aa]x + [ab]y + [ac]z + … + [an] = 0
[ba]x + [bb]y + [bc]z + … + [bn] = 0
(2)
[ca]x + [cb]y + [cc]z + … + [cn] = 0
…
Легко заметить, что коэффициенты нормальных уравнений
весьма легко составляются из коэффициентов данных, и
притом коэффициент у первой неизвестной во втором
уравнении равен коэффициенту у второй неизвестной в
первом, коэффициент у первой неизвестной в третьем
уравнении равен коэффициенту у третьей неизвестной в
первом и т.
 д.
д.39. Примеры
Для пояснения сказанного ниже приведено решениепяти уравнений с двумя неизвестными:
5x — 8y — 16 = 0
8x — y — 32 = 0
16x + 8y — 55 = 0
9x + 7y — 32 = 0
9x + 20y — 29 = 0
Составив значения [aa], [ab].., получаем следующие
нормальные уравнения:
507x + 323у — 1765 = 0
323x + 578у — 1084 = 0,
откуда х = +3,55; у = — 0,109.
40. Примеры
Уравнения (1) представляют систему линейныхуравнений, то есть уравнений, в которых все
неизвестные входят в первой степени. В большинстве
случаев уравнения, связывающие наблюдаемые и
искомые величины, бывают высших степеней и даже
трансцендентные, но это не изменяет сущности дела:
предварительными изысканиями всегда можно найти
величины искомых с таким приближением, что затем,
разложив соответствующие функции в ряды и
пренебрегая высшими степенями искомых поправок,
можно привести любое уравнение к линейному.
Метод наименьших квадратов.

Пример.
Пусть на вход некоторого устройства подается
сигнал х, а на выходе измеряется сигнал y. Известно, что
величины x и y связаны функциональной зависимостью,
но какой именно – неизвестно. Требуется приближенно
определить эту функциональную зависимость y= (x) по
опытным данными. Пусть в результате измерений
получен ряд экспериментальных точек (xi,yi).
Известно, что через n точек можно всегда провести
кривую, аналитически выражаемую многочленом (n-1)-й
степени. Этот многочлен называют интерполяционным.
И вообще, замену функции (x) на функцию (x) так, что
их значения совпадают в заданных точках
(xi) = (xi) , i = 1,2, … n.
называют интерполяцией.
(25)
Метод наименьших квадратов
Однако такое решение проблемы не является
удовлетворительным, поскольку yi (xi) из-за
случайных ошибок измерения и влияния на
измерения значений yi помех и шумов в устройстве.
Так что
(26)
i
i
i
y ( x )
Где i– некоторая случайная ошибка.
 Поэтому
Поэтомутребуется провести кривую так, чтобы она в
наименьшей степени зависела от случайных ошибок.
Эта задача называется сглаживанием
(аппроксимацией) экспериментальной зависимости и
часто решается методом наименьших квадратов.
Сглаживающую кривую называют
аппроксимирующей.
Метод наименьших квадратов
Задача аппроксимации решается следующим
образом.
В декартовой прямоугольной системе координат
наносят точки (xi, yi). По расположению этих точек
высказывается предположение о принадлежности
искомой функции к определенному классу функций.
Например, линейная функция
(x)=a0+aix, квадратичная (x)=a0+a1x+ a2x2 и т.д. В
общем случае
(x)= (x, a0, a1, …an). Неизвестные параметры
функции a1, a2,… an определяются из требования
минимума суммы квадратов случайных ошибок, т.е.
минимума величины
n
n
2
(27)
i ( yi ( xi , a0 , a1 ,…, an )) 2
i 1
i 1
Величина называется также суммарной невязкой.
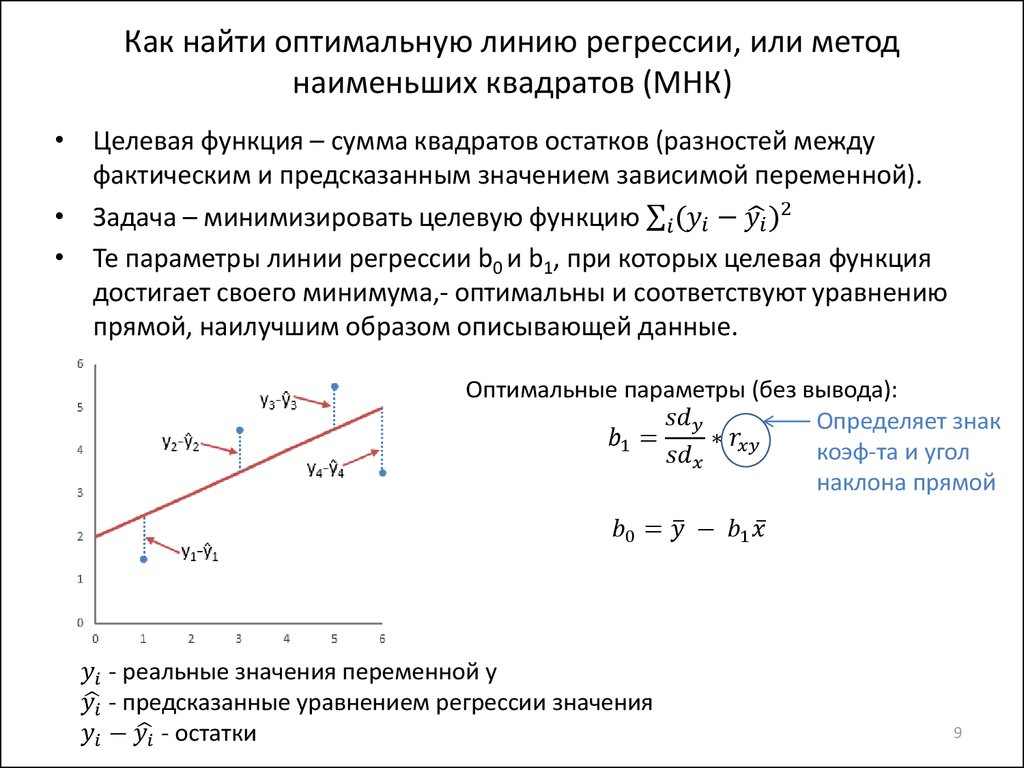
Метод наименьших квадратов
Необходимым условием минимума функции
нескольких переменных является обращение в нуль
частных производных невязки:
( yi ( xi , a0 , a1 ,…, an ))
0
a j
i 1
n
, j=0, 1, …r.
(28)
Решая систему уравнений, находим неизвестные
параметры aj и тем самым полностью определяем
функцию, которая наилучшим образом (в смысле
наименьших квадратов отклонений от исходных
точек или наименьшей суммарной невязки)
аппроксимирует (приближает) искомую функцию (x).
Метод наименьших квадратов
Остановимся подробнее на линейной зависимости
(x)=a0+aix.
Дифференцируя, получим следующую систему
уравнений
(1.5)
n
( yi a0 a1 xi ) 0
i 1
n
( y a a x )x 0
i
0
1 i
i
i 1
Из первого уравнения находим a0 = My — a1Mx ,
где
1 n
Mx xi ,
n i 1
1 n
My yi
n i 1
(29)
Метод наименьших квадратов
Подставляя выражение для a0 во второе
уравнение, найдем
Kxy
a1 2
S
(30)
где
1 n
Kxy ( xi Mx)( yi My ),
n i 1
1 n
2
S ( xi Mx) 2
n i 1
(31)
Kxy
Kxy
Таким образом, ( x) My S 2 Mx S 2 x(32)
есть искомая линейная функция.

Метод наименьших квадратов
Ввиду простоты расчетов аппроксимация
линейной зависимости используется довольно часто.
Кроме того, многие функции, зависящие от двух
параметров, можно линеаризовать путем замены
переменных.
Для этого необходимо подобрать такое
преобразование исходной зависимости y(x)= (x, a0,
a1, …an), в результате которого она приобретает
линейный вид v = b0 + b1 u. Далее решается задача
линейной аппроксимации для новой зависимости и
вычисленные коэффициенты b0 и b1
пересчитываются в коэффициенты a0 и a1.
Для ряда часто встречающихся
двухпараметрических зависимостей возможные
замены переменных (а также, обратные замены для
пересчета b0 и b1 в a0 и a1) приведены в табл. 1.1.
Примеры
Примеры
Примеры
Примеры
Примеры
Примеры
Лекция окончена
Нажмите клавишу <ESC> для выхода
STATS4STEM
Линейная регрессия: w это линия регрессии методом наименьших квадратов , и какое отношение она имеет к остаткам ?
Введение
Представьте, что у вас есть диаграмма рассеяния, полная точек, и вы хотите нарисовать линию, которая лучше всего соответствует вашим данным.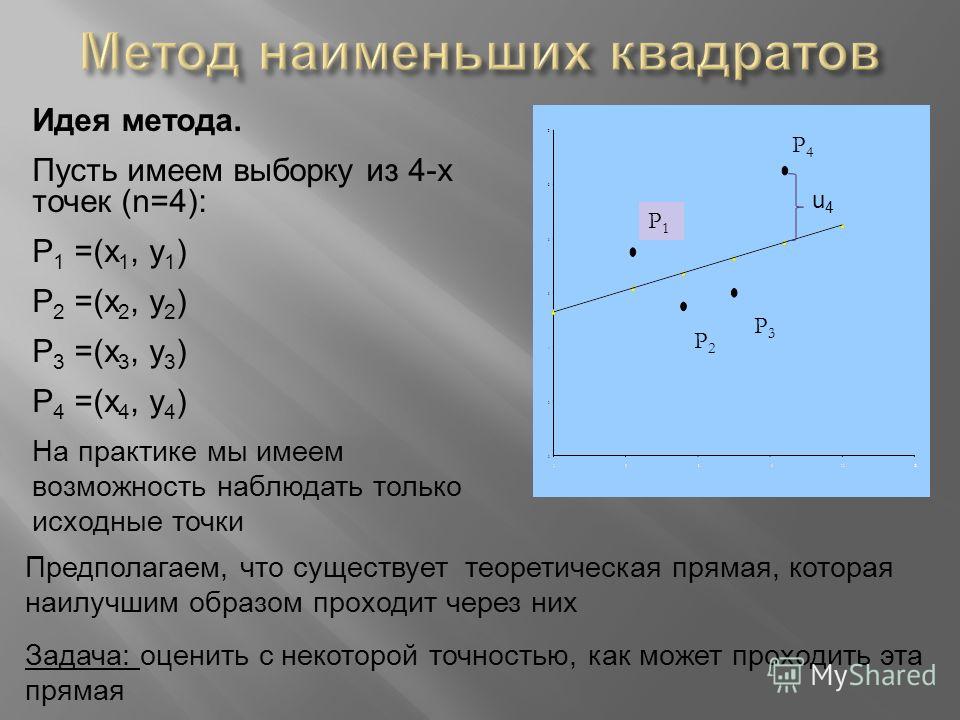 Эта лучшая линия — линия регрессии наименьших квадратов (сокращенно LSRL).
Эта лучшая линия — линия регрессии наименьших квадратов (сокращенно LSRL).
Общая формула LSRL
Формула : \(\widehat{y} = a + bx\)
Это верно, где \(\widehat{y} \) – прогнозируемое значение y при данном x, \(a\) — точка пересечения по оси y, \(b\) и — наклон.
Линия регрессии наименьших квадратов предсказывает \(\widehat{y} \)
Для каждого значения x линия регрессии наименьших квадратов дает предсказанное значение y, близкое к наблюдаемому значение y, но обычно немного отличается. Это предсказанное значение y называется «y-шляпой» и обозначается как \(\widehat{y} \). Наблюдаемое значение y просто называется «y».
Остатки
Обратим внимание на небольшой разрыв между наблюдаемым значением y (точка рассеяния, обозначенная y) и предсказанным значением y (точка на линии, обозначенная \(\widehat {у} \)).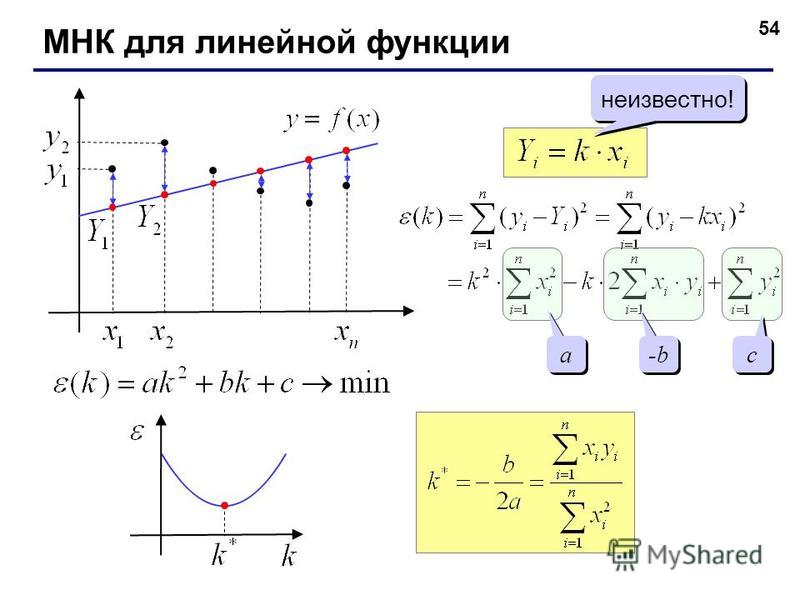 Этот разрыв называется остатком . Полное определение и формула приведены ниже:
Этот разрыв называется остатком . Полное определение и формула приведены ниже:
Определение: Остаток – это расстояние по вертикали между наблюдаемой точкой и вашим предсказанным значением Y.
Формула: 9Остаток 0004 = \(y — \widehat{y}\)
** ПОМНИТЕ: остаток наблюдается минус предсказанный!!
Для получения дополнительной информации об остатках нажмите здесь.
LSRL и остатки
К настоящему времени вы знаете, что линия регрессии методом наименьших квадратов проходит через диаграмму рассеяния точек и предсказывает значение y (\(\widehat{y} \)) для любого заданного x . Вы также знаете, что цель здесь состоит в том, чтобы создать максимально подходящую линию. Здесь вступают в игру остатки. LSRL подходит «лучше всего», поскольку уменьшает остатки.
Линия регрессии методом наименьших квадратов — это линия, минимизирующая сумму квадратов остатков.
Другими словами, для любой другой строки, кроме LSRL, сумма квадратов остатков будет больше. Это то, что делает LSRL единственной наиболее подходящей линией.
Это то, что делает LSRL единственной наиболее подходящей линией.
Расчет линии регрессии методом наименьших квадратов
Получив все точки данных, вы можете использовать свой калькулятор, чтобы найти LSRL.
Шаг 1 : Перейдите в STAT и нажмите EDIT. Затем введите все точки данных в списки 1 и 2.
Шаг 2 : Перейдите в STAT и щелкните правой кнопкой мыши на CALC. Затем нажмите LinReg. Нажав Enter и запустив эту функцию, вы получите наклон и точку пересечения по оси Y вашего LSRL, а также значения r и r 2 .
Если у вас нет точек данных, можно рассчитать LSRL вручную. Вам необходимо знать два ключевых факта:
(1) LSRL должен проходить через \(( \bar{x}, \bar{y} )\).
(2) Наклон LSRL (который при использовании формулы \(\widehat{y} = a + bx\) будет \(b\)) рассчитывается следующим образом: \(b = (r ) ({s_y \над s_x} )\)
Используя эту информацию, вы можете найти LSRL, как показано в примере ниже:
Используя таблицу справа, найдите уравнение для линии регрессии метода наименьших квадратов. |
|
Шаг 1 : Найдите наклон
\(b = 1,16\)
Шаг 2 : Найдите точку пересечения по оси Y
\(\widehat{y} = a + bx\)
\(33 = a + (1.16)(28) \)
\(a = 0,52\)
Шаг 3 : Собери все вместе! Заключение минимизирует сумму квадратов остатков.
Введение в подбор методом наименьших квадратов — MATLAB & Simulink
Введение в подбор по методу наименьших квадратов
Модель регрессии связывает данные отклика с данными предиктора с одним или несколькими
коэффициенты. Метод подбора — это алгоритм, который
вычисляет коэффициенты модели по набору входных данных. Curve Fitting Toolbox™ использует методы подбора наименьших квадратов, чтобы оценить коэффициенты
регрессионная модель.
Метод подбора — это алгоритм, который
вычисляет коэффициенты модели по набору входных данных. Curve Fitting Toolbox™ использует методы подбора наименьших квадратов, чтобы оценить коэффициенты
регрессионная модель.
Curve Fitting Toolbox поддерживает следующие методы подбора методом наименьших квадратов:
Линейный метод наименьших квадратов
Взвешенный метод наименьших квадратов
Робастный метод наименьших квадратов
Нелинейный метод наименьших квадратов
11 11 11 11 Тип регрессионной модели и свойства входных данных определить, какой метод наименьших квадратов наиболее подходит для оценки модели коэффициенты. 9является вектором размером n на 1 оценок ответов f – общая форма регрессии модель.
 i 9i)2
i 9i)2Предположения об ошибках
Разница между наблюдаемыми и истинными значениями для точки данных составляет вызвал ошибку . Потому что это невозможно наблюдать непосредственно, ошибка для точки данных аппроксимируется с точкой данных остаточный.
Методы подбора методом наименьших квадратов наиболее точны для наборов данных, которые не содержат большое количество случайных ошибок с экстремальными значениями. Статистический результаты, такие как достоверность и границы предсказания, предполагают, что ошибки нормально распределены. Методы подбора данных обычно делают два важных предположения об ошибке в данных, содержащих случайные вариации:
В методах подбора данных предполагается, что ошибки распределяются нормально, поскольку нормальное распределение часто обеспечивает адекватную аппроксимацию распределения многих измеряемых величин.
 Хотя метод наименьших квадратов
метод не предполагает нормально распределенных ошибок при расчете
оценки параметров, метод лучше всего работает для данных, которые не содержат
большое количество случайных ошибок с экстремальными значениями. Нормальное распределение
является одним из вероятностных распределений, в котором экстремальные случайные ошибки
необычный. Однако статистические результаты, такие как достоверность и прогноз
границы требуют нормально распределенных ошибок для их достоверности.
Хотя метод наименьших квадратов
метод не предполагает нормально распределенных ошибок при расчете
оценки параметров, метод лучше всего работает для данных, которые не содержат
большое количество случайных ошибок с экстремальными значениями. Нормальное распределение
является одним из вероятностных распределений, в котором экстремальные случайные ошибки
необычный. Однако статистические результаты, такие как достоверность и прогноз
границы требуют нормально распределенных ошибок для их достоверности.Если среднее значение остатков не равно нулю, проверьте, зависит от выбора модели или переменных-предикторов. Для примерки методы, отличные от метода взвешенных наименьших квадратов, Curve Fitting Toolbox дополнительно предполагает, что ошибки имеют постоянную дисперсию по значениям предикторов.
 Остатки, не имеющие
постоянная дисперсия указывает на то, что на подгонку может повлиять низкое качество
данные.
Остатки, не имеющие
постоянная дисперсия указывает на то, что на подгонку может повлиять низкое качество
данные.Linear Least Squares
Curve Fitting Toolbox использует линейный метод наименьших квадратов, чтобы подобрать линейную модель к данные. Линейная модель
Линейная модель степени м – 1 имеет матричную форму
y=Xβ+ε
где
y это n -на-1 вектор данных ответа.
β — вектор размером м х 1 неизвестных коэффициентов.

X является n — м конструкция матрица, содержащая м – 1 предиктор столбцы. Каждая предикторная переменная соответствует столбцу в х . Последний столбец в X — это столбец из единиц представляющий постоянный член модели.
ε является вектором размером n на 1 неизвестных ошибок.
Например, полином первой степени вида
y=p1x+p2
равно
[y1y2y3…yn]=[x1 1×2 1×3 1…xn 1]×[p1p2]
Вы не можете вычислить β напрямую, потому что ε неизвестно. Линейный метод наименьших квадратов аппроксимирует β путем вычисления вектора коэффициентов b , который минимизирует SSE.

(XTX)b=XTy
, где X T транспонирование матрицы X . Формула для б тогда
b=(XTX)−1XTy
Для решения системы одновременных линейных уравнений для неизвестные коэффициенты, используйте оператор обратной косой черты MATLAB ® (
mldivide). Потому что инвертирующий X T X может привести к недопустимые ошибки округления, оператор обратной косой черты использует декомпозицию QR с поворотом, который является устойчивым алгоритмом численно. Подробнее об арифметических операциях см. информация об операторе обратной косой черты и разложении QR. Вычислять
вектор подогнанных значений отклика х , замена b в формулу модели.
Вычислять
вектор подогнанных значений отклика х , замена b в формулу модели.Для примера подбора полиномиальной модели с использованием линейного метода наименьших квадратов метод подгонки, см. Подгонку полиномиальной модели к данным.
Взвешенный метод наименьших квадратов
Если ошибка данных ответа не имеет постоянной дисперсии между значениями данных предиктора, на подгонку могут влиять данные низкого качества. взвешенный метод наименьших квадратов использует коэффициенты масштабирования, называемые веса , чтобы повлиять на эффект ответа значения при расчете коэффициентов модели. Используйте взвешенный метод наименьших квадратов, если веса известны или если веса следовать определенной форме. 9i)2
где w i веса.
 Веса, которые вы указываете, должны преобразовывать дисперсии ответов.
к постоянному значению. Если вам известны дисперсии σi2 ошибок измерения в ваших данных, то веса
задаются формулой wi=1σi2. Кроме того, вы можете использовать остатки для оценки
ошибка в расчете σi2.
Веса, которые вы указываете, должны преобразовывать дисперсии ответов.
к постоянному значению. Если вам известны дисперсии σi2 ошибок измерения в ваших данных, то веса
задаются формулой wi=1σi2. Кроме того, вы можете использовать остатки для оценки
ошибка в расчете σi2.Взвешенная формула для SSE дает формулу для b
b=(XTWX)−1XTWy
, где W — диагональная матрица, такая что Wii=wi.
Для примера подбора полиномиальной модели с использованием взвешенного метод подгонки по методу наименьших квадратов, см. Улучшение подгонки модели с помощью весов.
Устойчивый метод наименьших квадратов
Экстремальные значения в ответных данных называются выбросы . Линейная аппроксимация по методу наименьших квадратов чувствительна к выбросы, потому что возведение остатков в квадрат увеличивает влияние этих данных баллов в расчете SSE.
 Используйте надежный метод подбора методом наименьших квадратов
если ваши данные содержат выбросы.
Используйте надежный метод подбора методом наименьших квадратов
если ваши данные содержат выбросы.Curve Fitting Toolbox предоставляет следующие надежные методы подбора методом наименьших квадратов:
Наименьшие абсолютные невязки (LAR) — этот метод находит кривую который минимизирует абсолютные остатки, а не квадратичные разности. Следовательно, крайние значения имеют меньше влияние на посадку.
Биквадрат веса — этот метод минимизирует взвешенную сумму квадраты, где вес, присвоенный каждой точке данных, зависит от того, насколько далеко точка находится от подобранной кривой. Точки рядом подобранная кривая получает полный вес. Точки дальше от кривой получить уменьшенный вес.
 Точки, находящиеся дальше от
кривая, чем ожидалось, случайным образом получить ноль
масса.
Точки, находящиеся дальше от
кривая, чем ожидалось, случайным образом получить ноль
масса.Метод двухквадратичных гирь часто предпочтительнее LAR потому что он одновременно пытается найти кривую, которая соответствует большая часть данных с использованием метода наименьших квадратов при минимизации влияния выбросов.
Подгонка робастных двухквадратичных грузов использует итерационно перевзвешенные алгоритм наименьших квадратов, который следует следующим шагам:
Подгонка модели методом взвешенных наименьших квадратов. Для на первой итерации алгоритм использует веса, равные единице если вы не укажете веса.
Рассчитайте скорректированные остатки и стандартизируйте их.
 скорректированные остатки приведены по
скорректированные остатки приведены поradj=ri1−hi
где ч я являются параметры, которые уменьшают вес точек данных, которые находятся далеко от подобранной кривой. Стандартизированные скорректированные остатки равны предоставлено
u=radjKs
где K =4,685 — настройка постоянная, а s является надежным стандартом отклонение, полученное путем деления среднего абсолютного отклонения (MAD) остатков на 0,6745.
Расчет робастных весов как функции и . Биквадратные веса даны by
wi={(1−(ui)2)2|ui|<10|ui|≥1
Если подгонка сходится, выйти из итерации процесс.
 В противном случае выполните следующую итерацию биквадрата
метод установки грузов, вернувшись к шагу 1.
В противном случае выполните следующую итерацию биквадрата
метод установки грузов, вернувшись к шагу 1.
Вместо минимизации влияния выбросов с помощью надежного метода наименьших квадратов подгонки, вы можете пометить точки данных, которые будут исключены из подгонки. Дополнительные сведения см. в разделе Удаление выбросов. информация.
Для примера подбора полиномиальной модели с использованием надежного метода наименьших квадратов. метод подгонки, см. Сравните надежные методы подгонки.
Нелинейный метод наименьших квадратов
Curve Fitting Toolbox использует нелинейный метод наименьших квадратов для подбора модель к данным. А нелинейная модель определяется как уравнение, нелинейное по коэффициентам или имеющее комбинацию линейные и нелинейные коэффициенты.
 Экспоненциальные модели, модели Фурье и Гаусса
нелинейны, например.
Экспоненциальные модели, модели Фурье и Гаусса
нелинейны, например.Нелинейная модель имеет матричную форму
y=f(X,β)+ε
, где
y представляет собой n -by-1 вектор данные ответа.
β представляет собой вектор размером м на 1 коэффициенты.
X n — м конструкция матрица.
f является нелинейной функцией β и X .
ε представляет собой n -by-1 вектор неизвестные ошибки.
В нелинейной модели, в отличие от линейной модели, приближенные коэффициенты b нельзя рассчитать с помощью матричных методов. Curve Fitting Toolbox использует следующий итеративный подход для расчета коэффициенты:
Инициализировать значения коэффициентов.
 Для некоторых
нелинейных моделей, набор инструментов обеспечивает эвристический подход для
расчет начальных значений. Для других моделей коэффициенты
инициализируются случайными значениями в интервале [0,1]. 9=f(X,b) и вычисляется с использованием якобиана функции f(X,β). Якобиан функции f(X,β) определяется как матрица частных производных
взятые по коэффициентам при β.
Для некоторых
нелинейных моделей, набор инструментов обеспечивает эвристический подход для
расчет начальных значений. Для других моделей коэффициенты
инициализируются случайными значениями в интервале [0,1]. 9=f(X,b) и вычисляется с использованием якобиана функции f(X,β). Якобиан функции f(X,β) определяется как матрица частных производных
взятые по коэффициентам при β.Отрегулируйте коэффициенты, используя один из этих нелинейные алгоритмы наименьших квадратов:
Trust-region — этот алгоритм используется по умолчанию. Ты должен использовать алгоритм доверенной области, если вы укажете коэффициентные ограничения. Алгоритм доверенной области может решать сложные нелинейные задачи больше эффективнее других алгоритмов и является улучшение по сравнению с популярным Levenberg-Marquardt алгоритм.

Левенберг-Марквардт — Если алгоритм доверенной области не дает разумной подгонки, и вы не имеют ограничения на коэффициенты, используйте Алгоритм Левенберга-Марквардта.
Если посадка удовлетворяет указанным критерии сходимости, выйти из итерации. В противном случае вернуться к шаг 2.
Curve Fitting Toolbox поддерживает использование весов и надежной подгонки для расчета SSE для нелинейных моделей.
Точность предсказаний нелинейной модели зависит от типа модель, критерии сходимости, набор данных и начальные значения присвоены коэффициенты. Если параметры по умолчанию не дают разумная подгонка, поэкспериментируйте с различными начальными значениями для модели коэффициенты, нелинейные алгоритмы наименьших квадратов и критерии сходимости.
 В общем, начните с изменения начальных значений коэффициента, потому что
нелинейные подгонки модели особенно чувствительны к начальным значениям для
коэффициенты модели. Дополнительные сведения см. в разделе Указание параметров подгонки и оптимизированных начальных точек.
информация об изменении параметров по умолчанию.
В общем, начните с изменения начальных значений коэффициента, потому что
нелинейные подгонки модели особенно чувствительны к начальным значениям для
коэффициенты модели. Дополнительные сведения см. в разделе Указание параметров подгонки и оптимизированных начальных точек.
информация об изменении параметров по умолчанию.Для примера подбора экспоненциальной модели с использованием нелинейного метод подгонки по методу наименьших квадратов, см. Подгонку экспоненциальной модели к данным.
Ссылки
[1] DuMouchel, W.H., и Ф. Л. О’Брайен. «Интеграция надежного варианта в множественную регрессию Вычислительная среда». Информатика и статистика: Материалы 21-го симпозиума по интерфейсу . Александрия, Вирджиния: Американская статистическая ассоциация, 19 лет.



 i 9i)2
i 9i)2 Хотя метод наименьших квадратов
метод не предполагает нормально распределенных ошибок при расчете
оценки параметров, метод лучше всего работает для данных, которые не содержат
большое количество случайных ошибок с экстремальными значениями. Нормальное распределение
является одним из вероятностных распределений, в котором экстремальные случайные ошибки
необычный. Однако статистические результаты, такие как достоверность и прогноз
границы требуют нормально распределенных ошибок для их достоверности.
Хотя метод наименьших квадратов
метод не предполагает нормально распределенных ошибок при расчете
оценки параметров, метод лучше всего работает для данных, которые не содержат
большое количество случайных ошибок с экстремальными значениями. Нормальное распределение
является одним из вероятностных распределений, в котором экстремальные случайные ошибки
необычный. Однако статистические результаты, такие как достоверность и прогноз
границы требуют нормально распределенных ошибок для их достоверности.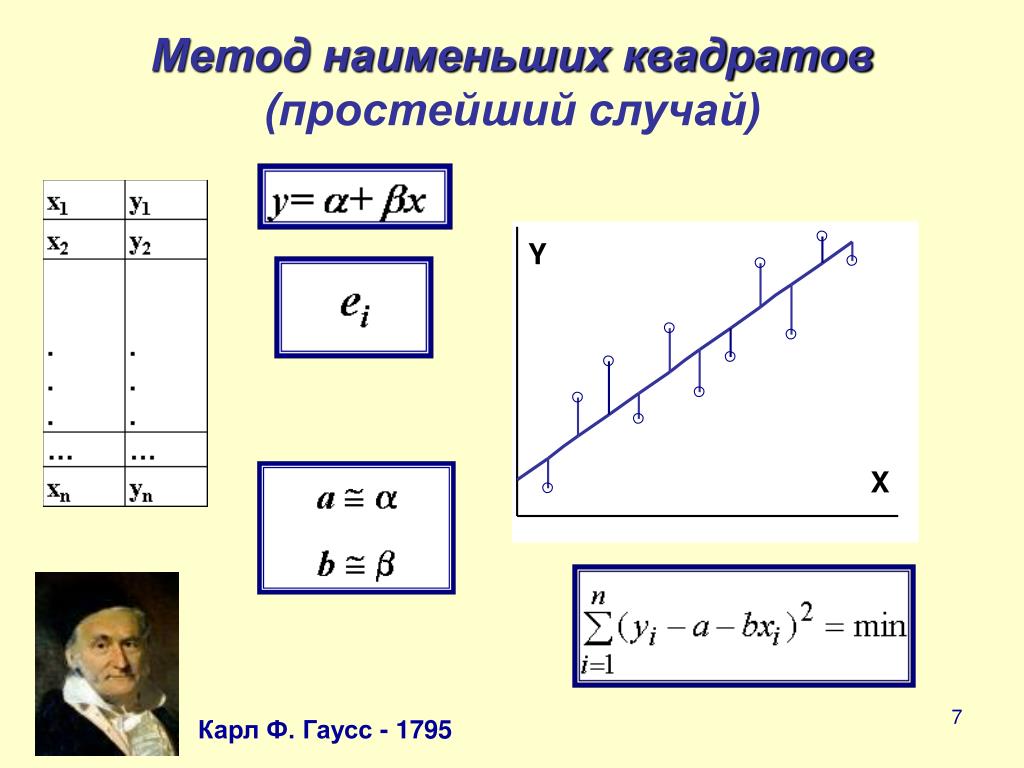 Остатки, не имеющие
постоянная дисперсия указывает на то, что на подгонку может повлиять низкое качество
данные.
Остатки, не имеющие
постоянная дисперсия указывает на то, что на подгонку может повлиять низкое качество
данные.