Векторы в пространстве и метод координат
Существует два способа решения задач по стереометрии
Первый — классический — требует отличного знания аксиом и теорем стереометрии, логики, умения построить чертеж и свести объемную задачу к планиметрической. Способ хорош тем, что развивает мозги и пространственное воображение.
Другой метод — применение векторов и координат. Это простые формулы, алгоритмы и правила. Он очень удобен, особенно когда времени до экзамена мало, а решить задачу хочется.
Если вы освоили векторы на плоскости и действия с ними — то и с векторами в пространстве разберетесь. Многие понятия окажутся знакомыми.
Система координат в пространствеВыберем начало координат. Проведем три взаимно перпендикулярные оси X, Y и Z. Зададим удобный масштаб.
Получилась система координат в трехмерном пространстве. Теперь каждая его точка характеризуется тремя числами — координатами по X, Y и Z. Например, запись M(−1; 3; 2) означает, что координата точки M по X (абсцисса) равна −1, координата по Y (ордината) равна 3, а координата по Z (аппликата) равна 2.
Векторы в пространстве определяются так же, как и на плоскости. Это направленные отрезки, имеющие начало и конец. Только в пространстве вектор задается тремя координатами x, y и z:
Как найти координаты вектора? Как и на плоскости — из координаты конца вычитаем координату начала.
Длина вектора в пространстве – это расстояние между точками A и B. Находится как корень квадратный из суммы квадратов координат вектора.
Пусть точка M – середина отрезка AB. Ее координаты находятся по формуле:
Для сложения векторов применяем уже знакомые правило треугольника и правило параллелограмма
Сумма векторов, их разность, произведение вектора на число и скалярное произведение векторов определяются так же, как и на плоскости. Только координат не две, а три. Возьмем векторы и .
Сумма векторов:
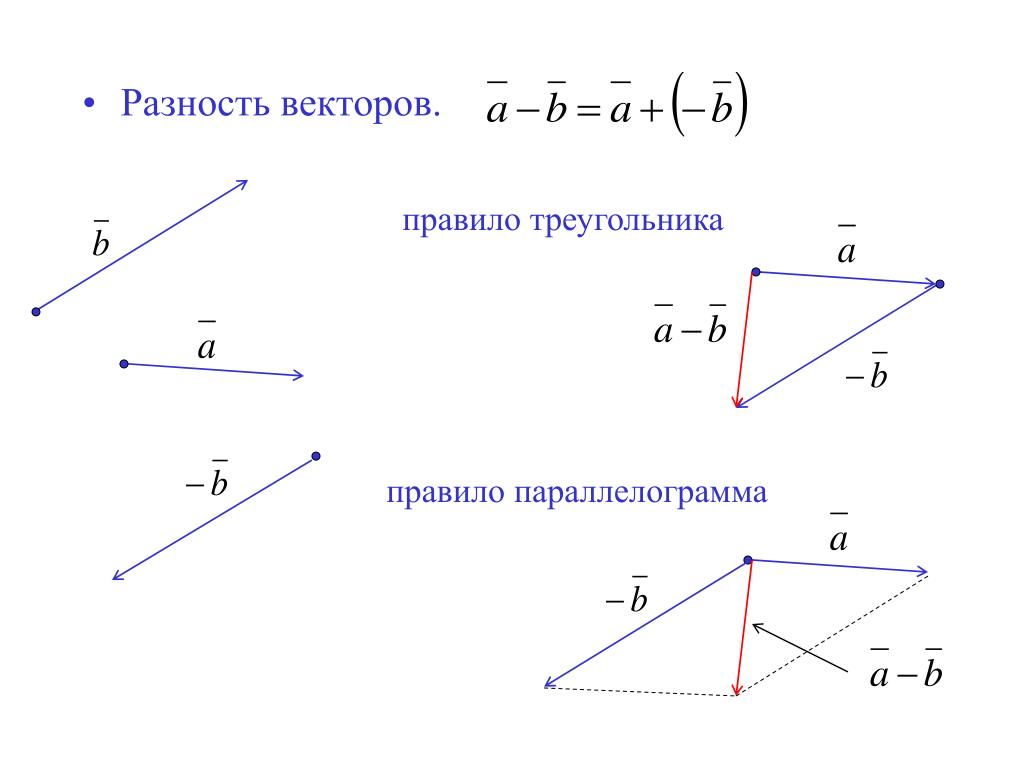
Разность векторов:
Произведение вектора на число:
Скалярное произведение векторов:
Косинус угла между векторами:
Последняя формула удобна для нахождения угла между прямыми в пространстве. Особенно если эти прямые – скрещиваются. Напомним, что так называются прямые, которые не параллельны и не пересекаются. Они лежат в параллельных плоскостях.
Особенно если эти прямые – скрещиваются. Напомним, что так называются прямые, которые не параллельны и не пересекаются. Они лежат в параллельных плоскостях.
1. В кубе ABCDA1B1C1D1 точки E и K — середины ребер соответственно A1B1 и B1C1. Найдите косинус угла между прямыми AE и BK.
Если вам достался куб — значит, повезло. Он отлично вписывается в прямоугольную систему координат. Строим чертеж:
Длина ребра куба не дана. Какой бы она ни была, угол между AE и BK от нее не зависит. Поэтому возьмем единичный куб, все ребра которого равны 1.
Прямые AE и BK — скрещиваются. Найдем угол между векторами и . Для этого нужны их координаты.
Запишем координаты векторов:
и найдем косинус угла между векторами и :
2. В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, точки E, K — середины ребер SB и SC соответственно. Найдите косинус угла между прямыми AE и BK.
Найдите косинус угла между прямыми AE и BK.
Лучше всего выбрать начало координат в центре основания пирамиды, а оси X и Y сделать параллельными сторонам основания.
Координаты точек A, B и C найти легко:
Из прямоугольного треугольника AOS найдем
Координаты вершины пирамиды:
Точка E — середина SB, а K — середина SC. Воспользуемся формулой для координат середины отрезка и найдем координаты точек E и K.
Найдем координаты векторов и
и угол между ними:
Покажем теперь, как вписать систему координат в треугольную призму:
3. В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, точка D — середина ребра A1B1. Найдите косинус угла между прямыми AD и BC1
Пусть точка A — начало координат. Возьмем ось X параллельно стороне BC, а ось Y перпендикулярно ей. Другими словами, на оси Y будет лежать отрезок AH, являющийся высотой треугольника ABC.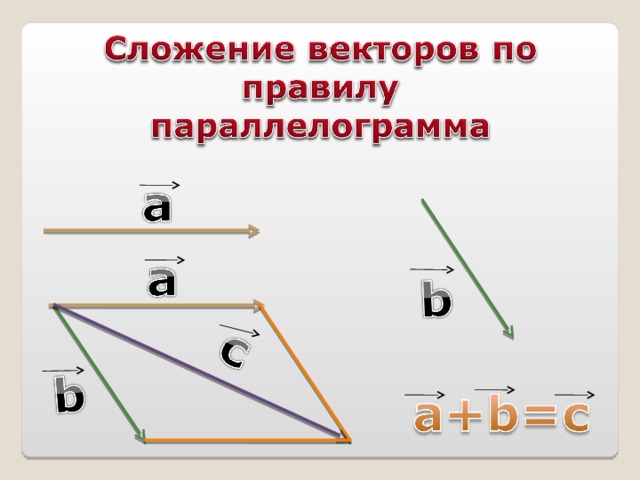 Нарисуем отдельно нижнее основание призмы.
Нарисуем отдельно нижнее основание призмы.
Запишем координаты точек:
Точка D — середина A1B1. Значит, пользуемся формулами для координат середины
отрезка.
Найдем координаты векторов и , а затем угол между ними:
Смотрите, как легко с помощью векторов и координат найти угол между прямыми. А если требуется найти угол между плоскостями или между прямой и плоскостью? Для решения подобных задач нам понадобится уравнение плоскости в пространстве.
Плоскость в пространстве задается уравнением:
Здесь числа A, B и C — координаты вектора, перпендикулярного этой плоскости. Его называют нормалью к плоскости.
Вместо x, y и z можно подставить в уравнение координаты любой точки, принадлежащей данной плоскости. Получится верное равенство.
Плоскость в пространстве можно провести через любые три точки, не лежащие на одной прямой. Поэтому для того, чтобы написать уравнение плоскости, берем координаты трех принадлежащих ей точек. Подставляем их по очереди в уравнение плоскости. Решаем полученную систему.
Подставляем их по очереди в уравнение плоскости. Решаем полученную систему.
Покажем, как это делается.
Напишем уравнение плоскости, проходящей через точки M (1; 0; 1), N (2; −2; 0) и K (4; 1; 2).
Уравнение плоскости выглядит так:
Подставим в него по очереди координаты точек M, N и K.
Для точки M:
То есть A + C + D = 0.
Для точки N:
Аналогично для точки K:
Получили систему из трех уравнений:
В ней четыре неизвестных: A, B, C и D. Поэтому одну из них мы выберем сами, а другие выразим через нее. Правило простое — вместо одной из переменных можно взять любое число, не равное нулю.
Пусть, например, D = −2. Тогда:
Выразим C и B через A и подставим в третье уравнение:
Решив систему, получим:
Уравнение плоскости MNK имеет вид:
Умножим обе части уравнения на −3. Тогда коэффициенты станут целыми:
Вектор — это нормаль к плоскости MNK.
Уравнение плоскости, проходящей через заданную точку имеет вид:
Угол между плоскостями равен углу между нормалями к этим плоскостям:
Не правда ли, знакомая формула? Скалярное произведение нормалей поделили на произведение их длин.
Заметим, что при пересечении двух плоскостей вообще-то образуется четыре угла.
Мы берем меньший из них. Поэтому в формуле стоит модуль скалярного произведения — чтобы косинус угла был неотрицателен.
4. В кубе ABCDA1B1C1D1 точки E и F — середины ребер соответственно A1B1 и A1D1. Найдите тангенс угла между плоскостями AEF и BDD1.
Строим чертеж. Видно, что плоскости AEF и BDD1 пересекаются где-то вне куба. В классическом решении пришлось бы строить линию их пересечения. Но векторно-координатный метод значительно всё упрощает. Не будем ломать голову над тем, по какой прямой пересекаются плоскости. Просто отметим координаты нужных нам точек и найдем угол между нормалями к плоскостям AEF и BDD1.
Просто отметим координаты нужных нам точек и найдем угол между нормалями к плоскостям AEF и BDD1.
Сначала — нормаль к плоскости BDD1. Конечно, мы можем подставить координаты точек B, D и D1 в уравнение плоскости и найти коэффициенты, которые и будут координатами вектора нормали. А можем сделать хитрее — увидеть нужную нормаль прямо на чертеже. Ведь плоскость BDD1 — это диагональное сечение куба. Вектор перпендикулярен этой плоскости.
Итак, первый вектор нормали у нас уже есть:
Напишем уравнение плоскости AEF.
Берем уравнение плоскости и по очереди подставляем в него, вместо x, y и z, соответствующие координаты точек A, E и F.
Упростим систему:
Пусть С = -1. Тогда A = B = 2.
Уравнение плоскости AEF:
Нормаль к плоскости AEF:
Найдем угол между плоскостями:
5. Основание прямой четырехугольной призмы BCDA1B1C1D1 — прямоугольник ABCD, в котором AB = 5, AD = √33. Найдите тангенс угла между плоскостью грани AA1D1D и плоскостью, проходящей через середину ребра CD перпендикулярно прямой B1D, если расстояние между прямыми A1C1 и BD равно √3.
Найдите тангенс угла между плоскостью грани AA1D1D и плоскостью, проходящей через середину ребра CD перпендикулярно прямой B1D, если расстояние между прямыми A1C1 и BD равно √3.
Эта задача наглядно показывает, насколько векторный метод проще классического. Попробуйте, для разнообразия, построить необходимые сечения и провести все доказательства — как это делается в «классике» 🙂
Строим чертеж. Прямую четырехугольную призму можно по-другому назвать «параллелепипед».
Замечаем, что длина и ширина параллелепипеда у нас есть, а вот высота — вроде не дана. Как же ее найти?
«Расстояние между прямыми A1C1 и BD равно √3». Прямые A1C1 и BD скрещиваются. Одна из них — диагональ верхнего основания, другая — диагональ нижнего. Вспомним, что расстояние между скрещивающимися прямыми равно длине их общего перпендикуляра. Общий перпендикуляр к A1C1 и BD — это, очевидно, OO1, где O — точка пересечения диагоналей нижнего основания, O1 — точка пересечения диагоналей верхнего. А отрезок OO1 и равен высоте параллелепипеда.
А отрезок OO1 и равен высоте параллелепипеда.
Итак, AA1 = √3
Плоскость AA1 D1 D — это задняя грань призмы на нашем чертеже. Нормаль к ней — это любой вектор, перпендикулярный задней грани, например, вектор или, еще проще, вектор .
Осталась еще «плоскость, проходящая через середину ребра CD перпендикулярно прямой B1D». Но позвольте, если плоскость перпендикулярна прямой B1D — значит, B1D и есть нормаль к этой плоскости! Координаты точек B1 и D известны:
Координаты вектора — тоже:
Находим угол между плоскостями, равный углу между нормалями к ним:
Зная косинус угла, находим его тангенс по формуле
Получим:
Ответ:
Угол между прямой m и плоскостью α тоже вычисляется с помощью скалярного произведения векторов.
Пусть — вектор, лежащий на прямой m (или параллельный ей), — нормаль к плоскости α.
Находим синус угла между прямой m и плоскостью α по формуле:
6. В кубе ABCDA1B1C1D1 точка E — середина ребра A1B1. Найдите синус угла между прямой AE и плоскостью BDD1.
Как всегда, рисуем чертеж и выбираем систему координат
Находим координаты вектора .
Нужно ли нам уравнение плоскости BDD1? В общем-то, без него можно обойтись. Ведь эта плоскость является диагональным сечением куба, а значит, нормалью к ней будет любой вектор, ей перпендикулярный. Например, вектор .
Найдем угол между прямой и плоскостью:
Ответ:
Расстояние от точки M с координатами x0, y0 и z0 до плоскости α, заданной уравнением Ax + By + Cz + D = 0, можно найти по формуле:
7. В основании прямоугольного параллелепипеда BCDA1B1C1D1 лежит прямоугольник ABCD со сторонами AB = , AD = . Высота параллелепипеда AA1 = . Найдите расстояние от точки A до плоскости A1DB.
Высота параллелепипеда AA1 = . Найдите расстояние от точки A до плоскости A1DB.
Построим чертеж и выпишем координаты точек:
Запишем уравнение плоскости A1DB. Вы помните, как это делается — по очереди подставляем координаты точек A1, D и B в уравнение Ax + Be + Cz + D
Решим эту систему. Выберем
Тогда
Уравнение плоскости A1DB имеет вид:
Дальше все просто. Находим расстояние от точки A до плоскости A1DB:
В некоторых задачах по стереометрии требуется найти расстояние от прямой до параллельной ей плоскости. В этом случае можно выбрать любую точку, принадлежащую данной прямой.
Как найти координаты вектора: формулы, примеры
Sign in
Password recovery
Восстановите свой пароль
Ваш адрес электронной почты
MicroExcel.ru Математика Геометрия Нахождение координат вектора
В данной публикации мы рассмотрим формулы, с помощью которых можно найти координаты вектора, заданного координатами его начальной и конечной точек, а также разберем примеры решения задач по этой теме.
- Нахождение координат вектора
- Примеры задач
Нахождение координат вектора
Для того, чтобы найти координаты вектора AB, нужно из координат его конечной точки (B) вычесть соответствующие координаты начальной точки (A).
Формулы для определения координат вектора
| Для плоских задач | AB = {Bx — Ax; By — Ay} |
| Для трехмерных задач | AB = {Bx — Ax; By — Ay; Bz — Az} |
| Для n-мерных векторов | .. B<sub>n</sub> — A<sub>n</sub>}</em></span>» data-order=»<span class="math"><em><span style="text-decoration: overline;">AB</span> = {B<sub>1</sub> — A<sub>1</sub>; B<sub>2</sub> — A<sub>2</sub>; … B<sub>n</sub> — A<sub>n</sub>}</em></span>»>AB = {B1 — A1; B2 — A2; … Bn — An} |
Примеры задач
Задание 1
Найдем координаты вектора AB, если у его точек следующие координаты: A = (2; 8), B = (5; 12).
Решение:
AB = {5 – 2; 12 – 8} = {3; 4}.
Задание 2
Определим координаты точки B вектора AB = {6; 14}, если координаты точки A = (2; 5).
Решение:
Координаты точки B можно вывести из формулы для расчета координат вектора:
Bx = ABx + Ax = 6 + 2 = 8.
By = ABy + Ay = 14 + 5 = 19.
Таким образом, B = (8; 19).
ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ
Таблица знаков зодиака
Нахождение площади трапеции: формула и примеры
Нахождение длины окружности: формула и задачи
Римские цифры: таблицы
Таблица синусов
Тригонометрическая функция: Тангенс угла (tg)
Нахождение площади ромба: формула и примеры
Нахождение объема цилиндра: формула и задачи
Тригонометрическая функция: Синус угла (sin)
Геометрическая фигура: треугольник
Нахождение объема шара: формула и задачи
Тригонометрическая функция: Косинус угла (cos)
Нахождение объема конуса: формула и задачи
Таблица сложения чисел
Нахождение площади квадрата: формула и примеры
Что такое тетраэдр: определение, виды, формулы площади и объема
Нахождение объема пирамиды: формула и задачи
Признаки подобия треугольников
Нахождение периметра прямоугольника: формула и задачи
Формула Герона для треугольника
Что такое средняя линия треугольника
Нахождение площади треугольника: формула и примеры
Нахождение площади поверхности конуса: формула и задачи
Что такое прямоугольник: определение, свойства, признаки, формулы
Разность кубов: формула и примеры
Степени натуральных чисел
Нахождение площади правильного шестиугольника: формула и примеры
Тригонометрические значения углов: sin, cos, tg, ctg
Нахождение периметра квадрата: формула и задачи
Теорема Фалеса: формулировка и пример решения задачи
Сумма кубов: формула и примеры
Нахождение объема куба: формула и задачи
Куб разности: формула и примеры
Нахождение площади шарового сегмента
Что такое окружность: определение, свойства, формулы
основные понятия.
 Координаты вектора. Длина вектора
Координаты вектора. Длина вектора- Понятие вектора
- Координаты вектора в прямоугольной декартовой системой координат в пространстве
- Условие коллинеарности векторов в координатах
- Длина вектора и направляющие косинусы
Будут и задачи для самостоятельного решения, к которым можно посмотреть ответы.
Тот факт, что вектор — это направленный отрезок, будет проще понять, остановившись на различиях между скалярными и векторными величинами.
В приведенной ниже таблице «Не векторы» — это скалярные величины или просто скаляры, а «Векторы» — векторные величины.
| Не векторы | Векторы |
| Масса | Сила тяжести |
| Длина | Путь |
| Время | Ускорение |
| Плотность | Давление |
| Температура | Скорость |
| Объем | |
| Площадь | |
| Модуль вектора |
Не векторы (скаляры) не имеют направления, а векторы имеют направление.
Вектор обязательно идёт от некоторой точки A по прямой к некоторой точке B. Числовое значение вектора — длина, а физическое и геометрическое — направление. Из этого и выводится первое, самое простое определение вектора. Итак, вектор — это направленный отрезок, идущий от точки A к точке B. Обозначается он так: .
А чтобы приступить к различным операциям с векторами, нам нужно познакомиться с ещё одним определением вектора.
Вектор — это вид представления точки, до которой требуется добраться из некоторой начальной точки. Например, трёхмерный вектор, как правило, записывается в виде (х, y, z). Говоря совсем просто, эти числа означают, как далеко требуется пройти в трёх различных направлениях, чтобы добраться до точки.
Пусть дан вектор. При этом x = 3 (правая рука указывает направо), y = 1 (левая рука указывает
вперёд), z = 5 (под точкой стоит лестница, ведущая вверх). По этим данным вы найдёте точку,
проходя 3 метра в направлении, указываемом правой рукой, затем 1 метр в направлении,
указываемом левой рукой, а далее Вас ждёт лестница и, поднимаясь на 5 метров, Вы, наконец,
окажетесь в конечной точке.
По этим данным вы найдёте точку,
проходя 3 метра в направлении, указываемом правой рукой, затем 1 метр в направлении,
указываемом левой рукой, а далее Вас ждёт лестница и, поднимаясь на 5 метров, Вы, наконец,
окажетесь в конечной точке.
Все остальные термины — это уточнения представленного выше объяснения, необходимые для различных операций над векторами, то есть, решения практических задач. Пройдёмся по этим более строгим определениям, останавливаясь на типичных задачах на векторы.
Физическими примерами векторных величин могут служить смещение материальной точки, двигающейся в пространстве, скорость и ускорение этой точки, а также действующая на неё сила.
Геометрический вектор представлен в двумерном и трёхмерном пространстве в виде направленного отрезка. Это отрезок, у которого различают начало и конец.
Если A — начало вектора, а B — его конец, то вектор обозначается
символом или одной строчной буквой . На рисунке
конец вектора указывается стрелкой (рис. 1)
На рисунке
конец вектора указывается стрелкой (рис. 1)
Длиной (или модулем) геометрического вектора называется длина порождающего его отрезка
Два вектора называются равными, если они могут быть совмещены (при совпадении направлений) путём параллельного переноса, т.е. если они параллельны, направлены в одну и ту же сторону и имеют равные длины.
В физике часто рассматриваются закреплённые векторы, заданные точкой приложения, длиной и направлением.
Если точка приложения вектора не имеет значения, то его можно переносить, сохраняя длину и направление в любую точку
пространства. В этом случае вектор называется свободным. В курсе высшей математики
векторы изучаются в разделе аналитической геометрии, где рассматриваются свободные векторы. Итак, если свободный вектор —
это вектор, начало которого может быть в любой точке пространства, то все векторы одинакового направления
и длины считаются равными.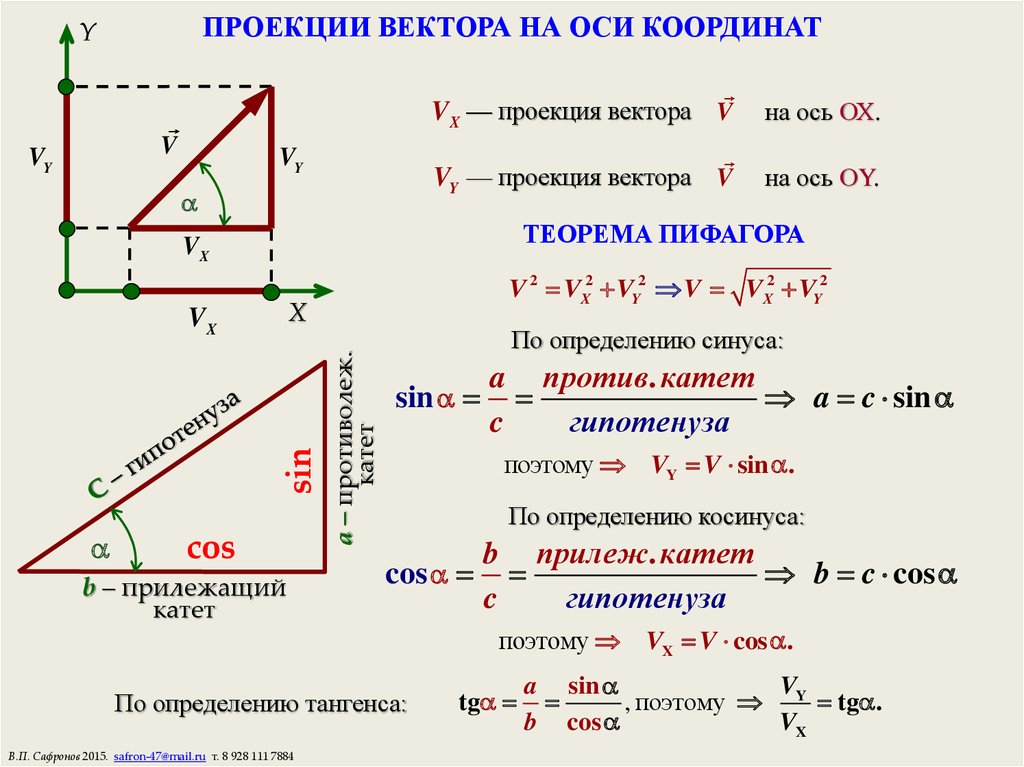
Перейти к операциям над векторами
Знакомство с прямоугольной декартовой системой координат в пространстве состоялось в соответствующем уроке
В упорядоченной системе координатных осей 0xyz ось Ox называется осью абсцисс, ось 0y – осью ординат, и ось 0z – осью аппликат.
С произвольной точкой М пространства свяжем вектор
,
называемый радиус-вектором точки М и спроецируем его на каждую из координатных осей. Обозначим величины соответствующих проекций:
Числа x, y, z называются координатами точки М , соответственно абсциссой, ординатой и аппликатой, и записываются в виде упорядоченной точки чисел: M (x; y; z) (рис.6).
Вектор единичной длины, направление которого совпадает с направлением оси, называют единичным вектором(или ортом) оси.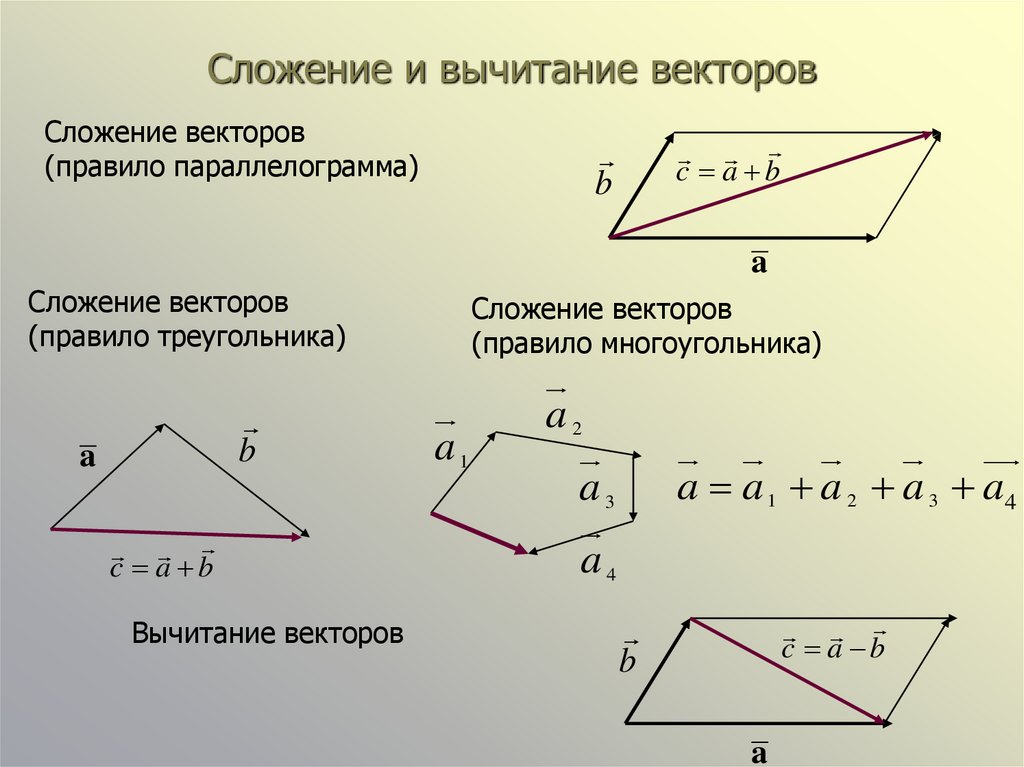
Соответственно орты координатных осей Ox, Oy, Oz
Теорема. Всякий вектор может быть разложен по ортам координатных осей:
(2)
Равенство (2) называется разложением вектора по координатным осям. Коэффициентами этого разложения являются проекции вектора на координатные оси. Таким образом, коэффициентами разложения (2) вектора по координатным осям являются координаты вектора.
После выбора в пространстве определённой системы координат вектор и тройка его координат однозначно определяют друг друга, поэтому вектор может быть записан в форме
(3)
Представления вектора в виде (2) и (3) тождественны.
Векторы называются коллинеарными, если они связаны отношением
.
Пусть даны векторы . Эти векторы коллинеарны, если координаты векторов связаны отношением
,
то есть, координаты векторов пропорциональны.
Пример 1. Даны векторы . Коллинеарны ли эти векторы?
Решение. Выясним соотношение координат данных векторов:
.
Координаты векторов пропорциональны, следовательно, векторы коллинеарны, или, что то же самое, параллельны.
Перейти к операциям над векторами
Нет времени вникать в решение? Можно заказать работу!
К началу страницы
Пройти тест по теме Векторы
Вследствие взаимной перпендикулярности координатных осей длина вектора
равна длине диагонали прямоугольного параллелепипеда, построенного на векторах
и выражается равенством
(4)
Вектор полностью определяется заданием двух точек (начала и конца), поэтому координаты вектора можно выразить через координаты этих точек.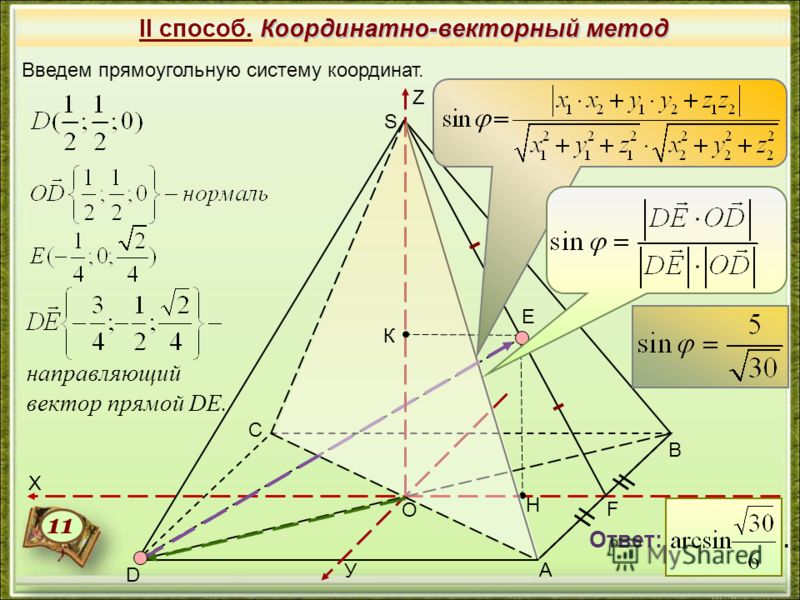
Пусть в заданной системе координат начало вектора находится в точке
а конец – в точке
(рис.8).
Тогда
Из равенства
следует, что
Отсюда
или в координатной форме
Следовательно, координаты вектора равны разностям одноимённых координат конца и начала вектора. Формула (4) в этом случае примет вид
(6)
Направление вектора определяют направляющие косинусы. Это косинусы углов, которые вектор образует с осями Ox, Oy и Oz. Обозначим эти углы соответственно α, β и γ. Тогда косинусы этих углов можно найти по формулам
,
,
.
Направляющие косинусы вектора являются также координатами орта этого вектора и, таким образом, орт вектора
или
.
Учитывая, что длина орта вектора равна одной единице, то есть
,
получаем следующее равенство для направляющих косинусов:
.
- Пригодится: тригонометрическая таблица (синусы, косинусы, тангенсы и котангенсы распространенных углов)
Пример 2. Найти длину вектора x = (3; 0; 4).
Решение. Длина вектора равна
Пример 3. Даны точки:
Выяснить, равнобедренный ли треугольник, построенный на этих точках.
Решение. По формуле длины вектора (6) найдём длины сторон и установим, есть ли среди них две равные:
Две равные стороны нашлись, следовательно необходимость искать длину третьей стороны отпадает, а заданный треугольник
является равнобедренным.
Перейти к операциям над векторами
Пример 4. Найти длину вектора и его направляющие косинусы, если .
Решение. Координаты вектора даны:
.
Длина вектора равна квадратному корню из суммы квадратов координат вектора:
.
Находим направляющие косинусы:
Решить задачу на векторы самостоятельно, а затем посмотреть решение
Пример 5. Найти длину, направляющие косинусы и орт вектора , если , .
Правильное решение и ответ.
- Пригодится: тригонометрическая таблица (синусы, косинусы, тангенсы и котангенсы распространенных углов)
Перейти к операциям над векторами
Нет времени вникать в решение? Можно заказать работу!
К началу страницы
Пройти тест по теме Векторы
| Назад | Листать | Вперёд>>> |
Поделиться с друзьями
Весь блок «Аналитическая геометрия»
- Векторы
- Понятие вектора, операции над векторами
- Сложение векторов: длина суммы векторов и теорема косинусов
- Скалярное произведение векторов, угол между двумя векторами
- Линейная зависимость векторов
- Базис системы векторов.
 Аффинные координаты
Аффинные координаты - Векторное произведение векторов, смешанное произведение векторов
- Плоскость
- Уравнения плоскости, взаимное расположение плоскостей
- Прямая на плоскости
- Уравнение прямой с угловым коэффициентом
- Общее уравнение прямой на плоскости
- Уравнение прямой в отрезках
- Каноническое уравнение прямой на плоскости
- Параметрические уравнения прямой на плоскости
- Нормальное уравнение прямой на плоскости, расстояние от точки до прямой
Вычислительная геометрия, или как я стал заниматься олимпиадным программированием.Часть 1 / Хабр
Здравствуйте, уважаемые хабравчане! Это моя вторая статья, и мне хотелось бы поговорить о вычислительной геометрии.
Немного истории
Я являюсь студентом уже 4 курса математического факультета, и до того как я начал заниматься программированием, я считал себя математиком на 100 процентов.
В конце первого курса мой преподаватель по информатике, который занимается олимпиадным программированием, обратил на меня внимание. Им как раз не хватало одного математика в команду. Так потихоньку меня начали приучать к олимпиадному программированию. Скажу честно, для меня это было очень сложно: для человека, который узнал слово Delphi на первом курсе. Однако мой преподаватель оказался очень грамотным специалистом и нашел хороший подход ко мне. Он начал давать мне математические задачи, который я сначала решал чисто математически, а уже потом писал код (с грехом пополам).
Мне очень нравится подход моего преподавателя: «разберись с этой темой, а потом расскажи нам, да так чтоб мы все поняли».
Итак, первой на самом деле важной задачей, с которой мне поручили разобраться, было именно вычислительная геометрия, необходимо было разобраться в типичных задач этого раздела информатики. И я решил подойти к этой задаче со всей ответственностью.
Я помню, как долго мучился с этими задачами, чтобы они прошли все тесты на сайте informatics. mccme. Зато теперь я очень рад, что прошел через все испытания и знаю, что же такое задачи вычислительной геометрии.
mccme. Зато теперь я очень рад, что прошел через все испытания и знаю, что же такое задачи вычислительной геометрии.
Вступление
«Вычислительная геометрия – это раздел информатики, изучающий алгоритмы решения геометрических задач. Такие задачи возникают в компьютерной графике, проектировании интегральных схем, технических устройств и др. Исходными данными в такого рода задачах могут быть множество точек, набор отрезков, многоугольники и т.п. Результатом может быть либо ответ на какой-то вопрос, либо какой-то геометрический объект».
Поскольку статья является достаточно большой я решил разбить ее на две части: первая часть посвящена многоугольникам, вторая – взаимному расположению различных геометрических объектов.
Немного теории о векторах
Отрезок, для которого указано, какой из его концов считается началом, а какой — концом, называется вектором. Любая точка пространства также может рассматриваться как вектор. Такой вектор называется нулевым. Начало и конец нулевого вектора совпадают, и он не имеет какого-либо определенного направления.
Такой вектор называется нулевым. Начало и конец нулевого вектора совпадают, и он не имеет какого-либо определенного направления.
Длиной ненулевого вектора AB называется длина отрезка AB. Длина нулевого вектора считается равной нулю.
Два ненулевых вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Если два ненулевых вектора AB и CD коллинеарны и если при этом лучи AB и CD сонаправлены, то векторы AB и CD называются сонаправленными, а если эти лучи не являются сонаправленными, то векторы AB и CD называются противоположно направленными. Нулевой вектор принято считать сонаправленным с любым вектором.
Скалярное произведение векторов
Скалярное произведение векторов — это число, равное произведению длин этих векторов на косинус угла между ними.
(a, b) = |a||b|cos∠(a, b)
Если векторы заданы своими координатами a(x1, y1), b(x2, y2) то скалярное произведение (a, b) = x1x2 + y1y2.
Косое произведение векторов
Псевдоскалярным или косым произведением векторов на плоскости называется число
[a, b] = |a||b|sinθ
где — угол вращения (против часовой стрелки) от a к b. Если хотя бы один из векторов a и b нулевой, то полагают [a, b] = 0.
Если векторы заданы своими координатами a(x1, y1), b(x2, y2) то косое произведение [a, b] = x1y2 — x2y1.
Геометрически косое произведение векторов представляет собой ориентированную площадь параллелограмма, натянутого на эти вектора.
Косое произведение векторов в задачах вычислительной геометрии занимает такое же почетное место, как рекурсии в комбинаторике. Это своего рода жемчужина вычислительной геометрии. Практически каждая задача вычислительной геометрии имеет более простое решение с помощью косового произведение вместо лобового решения.
А теперь займемся практикой
Начнем с треугольников
Задача №1
Задача очень простая, а именно: по введенным трем числам a, b, c определить существует ли треугольник с такими сторонами.
Решение
Понятно, что здесь нужно только проверить неравенство треугольника: a + b > c, a + c > b, b + c > a. Интересно, при изучении неравенства треугольника только ли у меня возник вопрос: не могут ли отрицательные числа тоже удовлетворять этим трем неравенствам? Оказывается, нет! Если мы сложим каждое неравенство, то получим a > 0, b > 0, c > 0. Поэтому неравенство треугольника является необходимым и достаточным условием существования треугольника.
Задача №2
Задача является очень похожей на предыдущую с той разницей, что треугольник задан не сторонами, а координатами вершин.
Решение
С первого взгляда решение кажется очевидным: вычислить стороны треугольника и свести задачу к предыдущей. Однако поскольку расстояние между двумя точками A(x1, y1), B(x2, y2) вычисляется по формуле √(x1-x2)2+(y1-y2)2 то при извлечении корня возможна потеря точности, что плохо скажется на проверке неравенства треугольника. Оказывается, что если треугольник задан координатами своих вершин, то вычислять длины его сторон и проверять неравенство треугольника не требуется. В этом случае треугольника не существует тогда и только тогда, когда данные три точки лежат на одной прямой. А это легко проверяется через косое произведение векторов. Если оно равно нулю, то векторы коллинеарные, то есть все три точки лежат на одной прямой.
Оказывается, что если треугольник задан координатами своих вершин, то вычислять длины его сторон и проверять неравенство треугольника не требуется. В этом случае треугольника не существует тогда и только тогда, когда данные три точки лежат на одной прямой. А это легко проверяется через косое произведение векторов. Если оно равно нулю, то векторы коллинеарные, то есть все три точки лежат на одной прямой.
Во всех следующих задачах будем считать, что треугольник существует, поскольку процедуру проверки существования треугольника мы только что рассмотрели.
Задача №3
Треугольник задан своими сторонами. Определить тип треугольника: тупоугольный, прямоугольный или остроугольный.
Решение
Вспомним, что представляют собой каждый вид треугольника.
Из курса геометрии известно, что напротив большей стороны лежит больший угол (он нам и нужен). Поэтому если мы выясним чему равен больший угол, то поймем тип треугольника:
- Угол больше 90° – треугольник тупоугольный
- Угол меньше 90°– треугольник остроугольный
- Угол равен 90°– треугольник прямоугольный
Воспользуемся теоремой косинусов:
Очевидно, что если косинус угла больше нуля то угол меньше 90°, если он равен нулю, то угол равен 90°, если он меньше нуля, то угол больше 90°.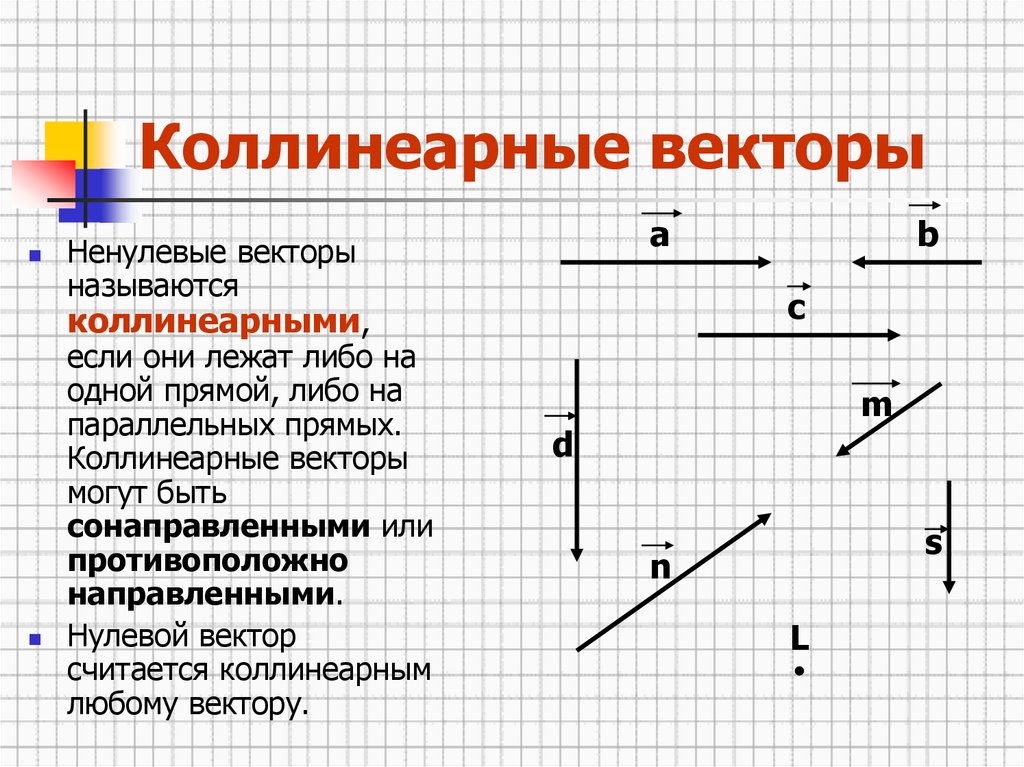 Однако немного поразмыслив можно понять, что вычислять косинус угла не обязательно, необходимо учесть лишь его знак:
Однако немного поразмыслив можно понять, что вычислять косинус угла не обязательно, необходимо учесть лишь его знак:
- Если cosα > 0, то a2 < b2 + c2 – треугольник остроугольный
- Если cosα = 0, то a2 = b2 + c2 – треугольник прямоугольный
- Если cosα < 0, то a2 > b2 + c2 – треугольник тупоугольный
где a – большая сторона.
Задача №4
Задача аналогична предыдущей задаче, только треугольник задан не своими сторонами, а координатами вершин.
Решение
Аналогично задаче 2 можно сказать, что эта задача полностью сводится к предыдущей задаче (так оно и есть). Однако, как и во второй задаче, решение можно упростить. Вообще, если треугольник задан координатами своих вершин, то всегда легче работать с ним через вектора, нежели вычислять стороны. Аналогично предыдущей задаче, необходимо определить каким является наибольший из углов треугольника. Вид угла легко определяется по знаку скалярного произведения образующих его векторов: оно положительно для острого угла, равно нулю для прямого угла и отрицательно для тупого угла. Поэтому необходимо посчитать все три скалярных произведения и перемножить их и по знаку данного числа можно судить о типе треугольника.
Аналогично предыдущей задаче, необходимо определить каким является наибольший из углов треугольника. Вид угла легко определяется по знаку скалярного произведения образующих его векторов: оно положительно для острого угла, равно нулю для прямого угла и отрицательно для тупого угла. Поэтому необходимо посчитать все три скалярных произведения и перемножить их и по знаку данного числа можно судить о типе треугольника.
Задача №5
По данным сторонам треугольника найти его площадь.
Решение
Очевидно решение, заключается в применение формулы Герона.
Кстати, никого не интересовало доказательство этой формулы?
Доказательство
Вот и все!
Задача №6
Вычислить площадь треугольника заданного координатами своих вершин.
Решение
Не будем говорить о решении, которое сводится к предыдущей задачи, а попробуем воспользоваться геометрическим смыслом косового произведения. Геометрически косое произведение двух векторов определяет ориентированную площадь параллелограмма натянутого на эти вектора. Поскольку диагональ параллелограмма разбивает его на два равновеликих треугольника, то можем найти площадь нашего треугольника, как половину площади параллелограмма.
Геометрически косое произведение двух векторов определяет ориентированную площадь параллелограмма натянутого на эти вектора. Поскольку диагональ параллелограмма разбивает его на два равновеликих треугольника, то можем найти площадь нашего треугольника, как половину площади параллелограмма.
Для векторов a(x1, y1), b(x2, y2)
S = (x1y2 — x2y1) / 2 — ориентированная площадь треугольника
Задача №7
Дана точка и треугольник заданный координатами своих вершин. Определить лежит ли точка внутри, на границе или вне этого треугольника.
Решение
У этой задачи есть два принципиально разных решения. Начнем с наименее привлекательного.
Метод площадей
Если сумма площадей треугольников AKB, AKC, BKC (не ориентированных, а «обычных») больше площади треугольника ABC точка лежит вне треугольника. Если же сумма первых трех площадей равна четвертой, то нужно проверить, не равна ли нулю одна из трех площадей. Если равна, то точка лежит на границе треугольника, иначе – внутри.
Если же сумма первых трех площадей равна четвертой, то нужно проверить, не равна ли нулю одна из трех площадей. Если равна, то точка лежит на границе треугольника, иначе – внутри.
Вычислять площади треугольников, естественно, надо через косое произведение векторов. Этот метод не очень хороший. Поскольку здесь используются сравнение чисел с плавающей точкой, а это в свою очередь может привести к принятию неверного решения при сравнении. Второй метод опять таки опирается на вектора, он намного эффективнее во всех отношениях.
Проверка полуплоскостей
Если хотя бы одна из сторон треугольника «разводит» противолежащую ей вершину и точку по разным полуплоскостям, то точка лежит вне треугольника. Иначе, если точка принадлежит хотя бы одной из прямых, содержащих стороны треугольника, то она находится на границе треугольника. Иначе точка лежит внутри треугольника.
В первом примере сторона AB разводит вершину C и точку K по разным полуплоскостям, поэтому точка лежит снаружи.
Задача №8
Вычисление площади многоугольника заданного координатами своих вершин.
Решение
Под многоугольником будем подразумевать простой многоугольник, то есть без самопересечений. При этом он может быть как выпуклым, так и не выпуклым.
Данную задачу можно решить двумя способами: вычисляя ориентированные площади трапеций и треугольников.
Метод трапеций
Для того чтобы посчитать площадь многоугольника нужно разбить его на трапеции, так как это показано на рисунке, а затем сложить ориентированные площади полученных трапеций это будет ориентированной площадью исходного многоугольника.
S = SA1A2 B2 B1 + SA2 A3 B3B2 + SA3A4B5B3 + SA4A5B6B5 + SA5A6B4 B6 + SA6A1 B1 B4
Площади трапеций считаем по известной формуле: полусумма оснований на высоту
SA1A2 B2 B1 = 0. 5 * (A1B1 + A2B2) *(B2 — B1)
5 * (A1B1 + A2B2) *(B2 — B1)
Поскольку полученная площадь является ориентированной, необходимо вычислить ее модуль.
Метод треугольников
Аналогично предыдущему методу можно разбивать многоугольник не на трапеции, а на треугольники, как показано на рисунке. В результате, сложив ориентированные площади этих треугольников, мы получим опять-таки ориентированную площадь многоугольника.
S = SOA1A2 + SOA2A3 + SOA3A4 + SOA4A5 + SOA5A6 + SOA6A1
Как вы видите задача вычисления площади многоугольника достаточна проста. Не знаю, почему, но мне больше нравится решать эту задачу методом разбиения на трапеции (наверно потому, что на всех олимпиадах я ее так решал). Тем более, что при втором решении площади треугольников надо вычислять через косое произведение. О формуле Герона надо забыть!!!
Тем более, что при втором решении площади треугольников надо вычислять через косое произведение. О формуле Герона надо забыть!!!
Задача №9
Многоугольник задан координатами своих вершин в порядке его обхода. Необходимо проверить является ли многоугольник выпуклым.
Решение
Напомню, что многоугольник называется выпуклым, если он лежит в одной полуплоскости относительно любой прямой, содержащей его сторону.
Задача опять сводится к вычислению косового произведения векторов, а именно у выпуклого многоугольника знаки косых произведений [Ai Ai+1, Ai+1 Ai+2] либо положительны, либо отрицательны. Поэтому если мы знаем направление обхода, то знак косых произведений для выпуклого многоугольника одинаков: он неотрицателен при обходе против часовой стрелки и неположителен при обходе по часовой стрелки.
Задача №10
Многоугольник (не обязательно выпуклый) на плоскости задан координатами своих вершин. Требуется подсчитать количество точек с целочисленными координатами, лежащих внутри него (но не на его границе).
Требуется подсчитать количество точек с целочисленными координатами, лежащих внутри него (но не на его границе).
Решение
Для решения этой задачи рассмотрим вспомогательную задачу: отрезок задан координатами своих концов, являющихся целыми числами. Необходимо посчитать количество целочисленных точек лежащих на отрезке. Понятно, что если отрезок вертикальный или горизонтальный, то необходимо вычесть координаты концов и добавить единицу. Интерес представляет случай, когда отрезок не является вертикальным или горизонтальным. Оказывается в этом случае необходимо достроить отрезок до прямоугольного треугольника и ответом будет число равное наибольшему общему делителю длин катетов этого треугольника плюс единица.
Для любого многоугольника с целочисленными координатами вершин справедлива формула Пика: S = n + m/2 — 1, где S – площадь многоугольника, n – количество целых точек лежащих строго внутри многоугольника, m – количество целых точек лежащих на границе многоугольника. Поскольку площадь многоугольника мы знаем как вычислять, то S известно. Так же мы можем вычислить количество целых точек лежащих на границе многоугольника, поэтому в формуле Пика остается лишь одна искомая неизвестная которую мы можем найти.
Поскольку площадь многоугольника мы знаем как вычислять, то S известно. Так же мы можем вычислить количество целых точек лежащих на границе многоугольника, поэтому в формуле Пика остается лишь одна искомая неизвестная которую мы можем найти.
Рассмотрим пример:
S = 16 + 4 + 4,5 + 6 + 1 + 2 = 33,5
m = 15
n = 33,5 – 7,5 +1 = 27 — точек лежит строго внутри многоугольника
Вот так вот решается эта задачка!
Вот и все! Надеюсь, Вам понравилась статья, и я напишу ее вторую часть.
Тест по теме «Векторы их определения, формулы»
Векторы
Вариант: 1
1. Геометрия – это наука о свойствах геометрических фигур.
2. Основные геометрические фигуры в пространстве: точка, прямая, плоскость.
3. Длина нулевого вектора равна нулю.
4. Сонаправленные векторы — если они коллинеарны и сонаправлены
5. Равные
вектора — если они сонаправленны и их длины равны.
6. Сумма нескольких векторов не зависит от того, в каком порядке они складываются.
7. Любые два ветора компланарные.
8. Если через точку пространства проведены три попарно перпендикулярные прямые, на каждой из них выбрано направление и выбрана единица измерения отрезков, то говорят, что задана прямоугольная система координат.
9. В прямоугольной системе координат каждой точке сопоставляется три числа, которые называются её координатами.
10. Каждая координата суммы двух или более векторов равна сумме соответствующих координат этих векторов
11. Напишите формулу длины вектора
12. Скалярным произведением двух векторов называется произведение их длины на косинус угла между ними.
13. Запишите формулу нахождения угла между векторами, зная координаты этих векторов /
14. Параллельный
перенос на вектор называется отображение
пространства на себя, при котором любая точка М переходит в точку М1,
что ММ1=.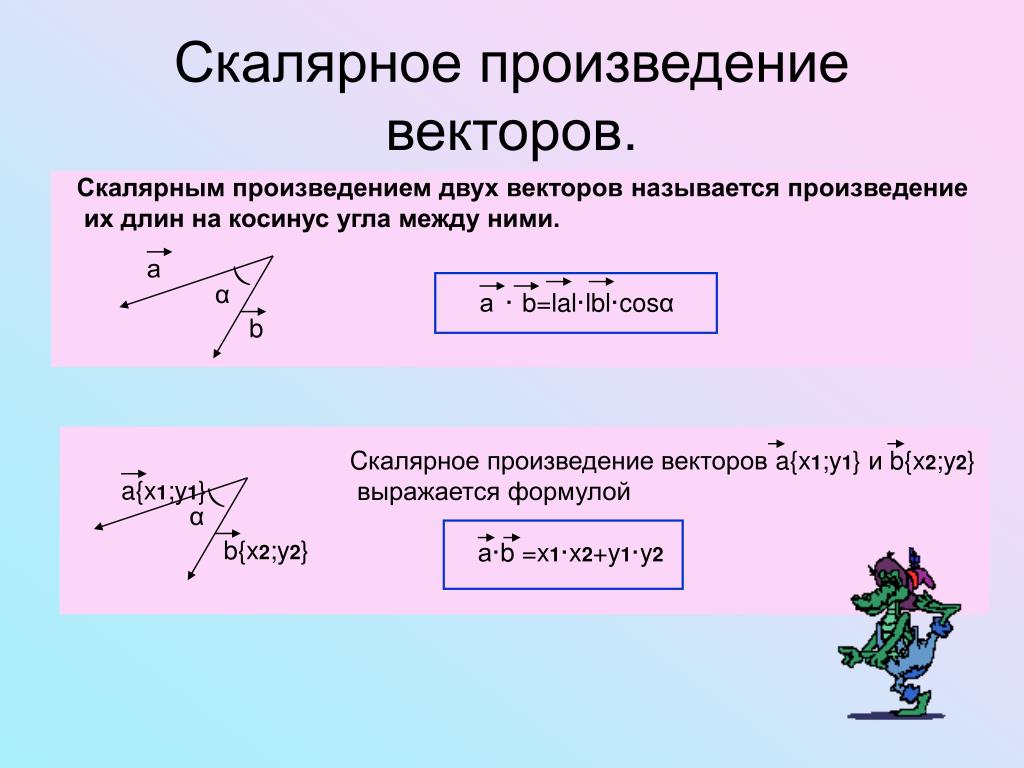
Векторы
Вариант: 2
1. Планиметрия – это раздел геометрии, в котором изучаются свойства фигур на плоскости.
2. Основные геометрические тела в пространстве: куб, тетраэдр, параллелепипед.
3. Дина ненулевого вектора называется длиной отрезка АВ.
4. Противоположно направленные векторы – если они коллинеарны и противоположно направленны
5. От любой точки можно отложить вектор, равный данному и при том только один.
6. Произведением ненулевого вектора на число к, называют такой вектор , длина которого =, причем вектор и сонаправленны при к>0 и противоположно направленны при к<0.
7. Три вектора, среди два которых два коллинеарны, также коллинеарны.
8. Прямые
с выбранными на них направлениями называется осями координат, а их общая
точка – началом координат.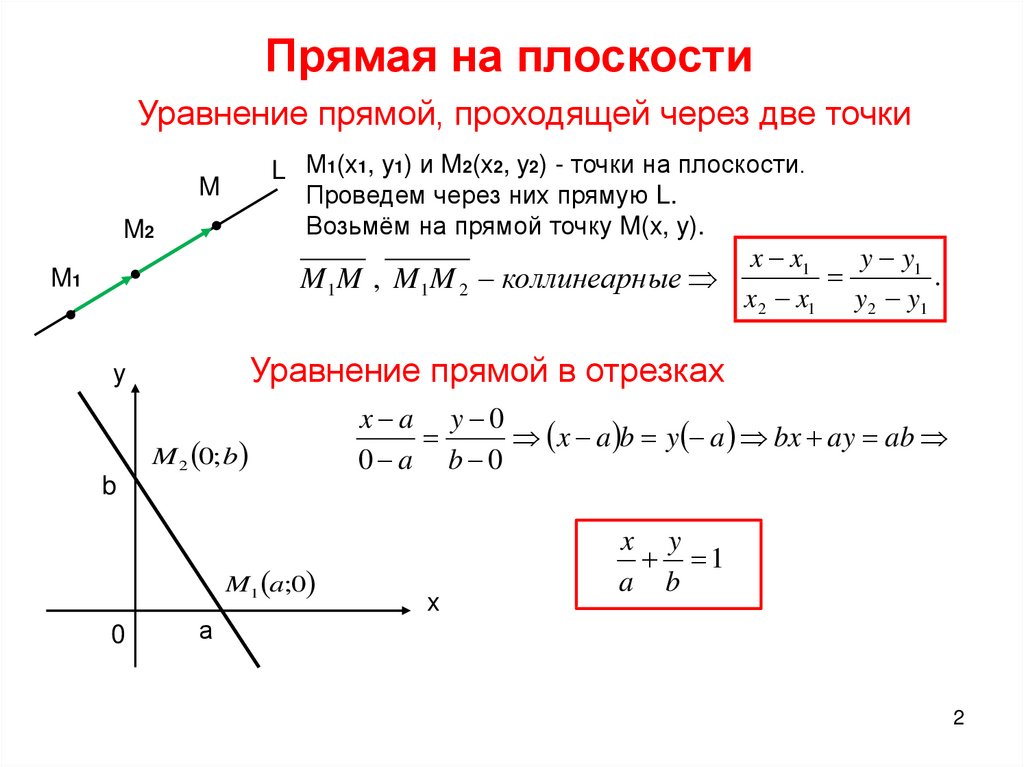
9. Перечислите единичные вектора – – единичный вектор по оси ОХ;
— единичный вектор по оси ОУ;
— единичный вектор по оси ОZ.
10. Каждая координата разности двух равна разности соответствующих координат этих векторов
11. Напишите формулу расстояния между двумя точками
12. Запишите формулу скалярного произведения двух векторов
13. Центральная симметрия-это отображение пространства на себя, при котором любая точка М переходит в симметричную ей точку М, относительно данного центра.
14. Параллельный перенос на вектор называется отображение пространства на себя, при котором любая точка М переходит в точку М1, что ММ1=.
Векторы
Вариант: 3
1. Основными геометрическими фигурами планиметрии являются точка и прямая.
2. Аксиома-утверждение
принимаемое без доказательств.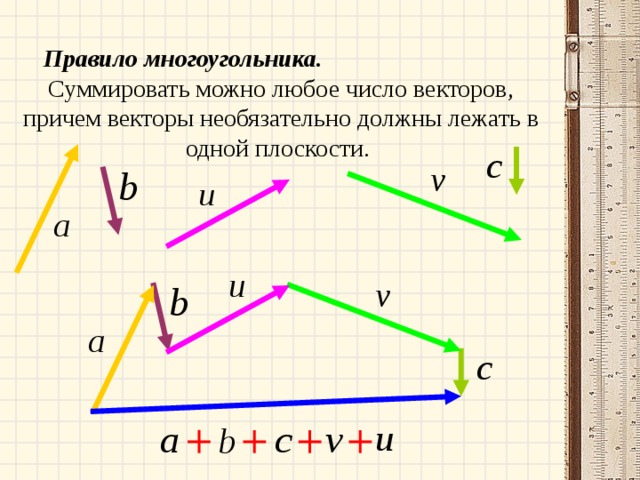
3. Длина ненулевого вектора обозначается .
4. Обозначаются сонаправленные векторы
5. Два ненулевых вектора называются противоположными, если их длины равны и они противоположно направлены.
6. Произведение нулевого вектора на любое число считается нулевым вектором.
7. Если векторы можно разложить по векторам и , т.е. представить в виде с=х+у,где х и у-некоторые числа, а и b векторы – комплананрны.
8. Перечислите оси координат в прямоугольной системе координат: х-абсцисса; у-ордината; z-аппликата.
9. Координаты нулевого вектора равны нулю.
10. Каждая координата произведения вектора на число равна произведению соответствующей координаты на это число
11. Если и сонаправленные =>угол между ними равен 0
12. Скалярное
произведение ненулевых векторов равна нулю тогда и только тогда, когда
эти векторы перпендикулярны.
13. Осевая симметрия – с осью а называется такое отображение пространства на себя, при котором любая точка М переходит в симметричную ей точку М, относительно оси а.
14. Параллельный перенос на вектор называется отображение пространства на себя, при котором любая точка М переходит в точку М1, что ММ1=.
Векторы
Вариант:4
1. Стереометрия – это раздел геометрии, в котором изучаются свойства геометрических фигур в пространстве.
2. Отрезок, для которого указано, какой из его концов считается началом, а какой – концом, называется вектором.
3. Коллинеарные векторы лежат на одной прямой или параллельных прямых.
4. Обозначаются противоположно направленные векторы
5. Разностью векторов и называется такой вектор, сумма которого с векторам .
6. Векторы
называются компланарными, если при откладывании их от одной и той же точки
они будут лежать в одной плоскости.
7. Любой вектор можно разложить по трем данным некомпланарным векторам, причем коэффицентф разложения определены единым образом.
8. Плоскости проходящие через оси координат ОХ и ОУ; ОУ и OZ, OX и OZ называются координатными плоскостями.
9. Координаты равных векторов соответственно равны.
10. Каждая координата середины отрезка равна полусумме соответствующих координат его концов.
11. Если и перпендикулярные =>угол между ними равен 900
12. Скалярный квадрат равен квадрату его длины.
13. Зеркальная симметрия (симметрий относительно плоскости альфа) называется такое отображение пространства на себя, при котором любая точка М переходит в симметричную ей относительно плоскости альфа точки М1.
14. Параллельный
перенос на вектор называется отображение
пространства на себя, при котором любая точка М переходит в точку М1,
что ММ1=.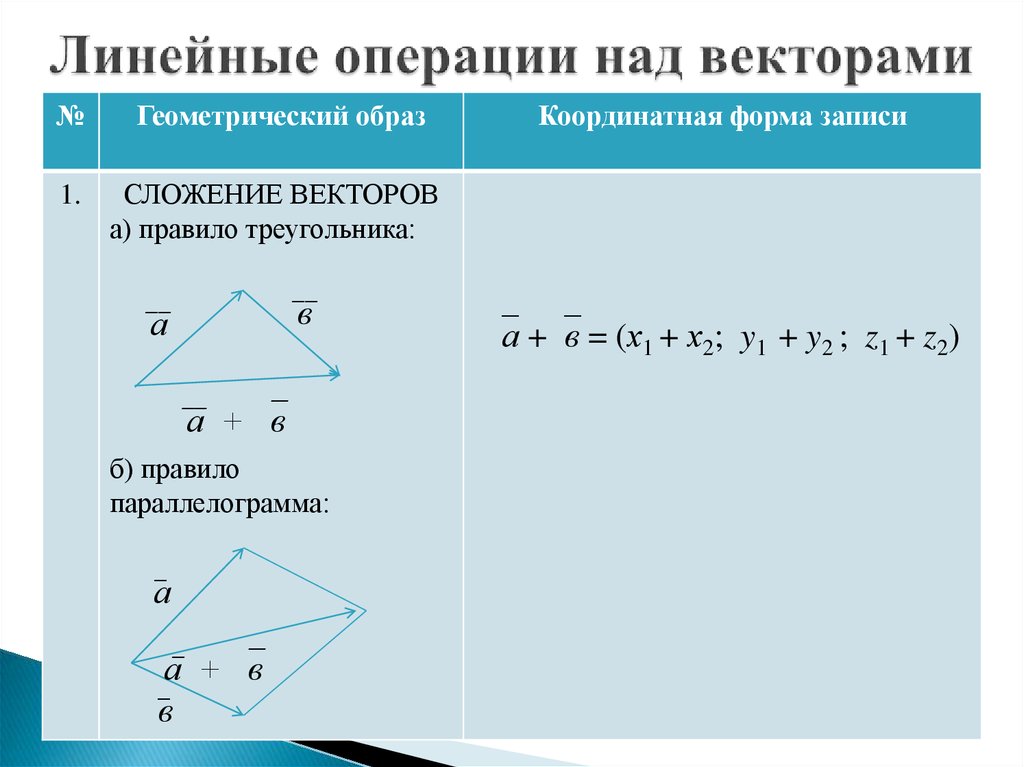
Векторы
Вариант: 1
1. Геометрия – это наука о ______________________________________________
2. Основные геометрические фигуры в пространстве: ________________________
3. Длина нулевого вектора ______________________________________________
4. Сонаправленные векторы — если они ____________________________________
5. Равные вектора — если они _____________________________________________
6. Сумма нескольких векторов ___________ от того, __________________________
7. Любые _____________________ компланарные.
8. Если через точку пространства проведены ____________________________________ на каждой из них выбрано направление и выбрана единица измерения отрезков, то говорят, что ______________________________________________________
9. В
прямоугольной системе координат каждой точке сопоставляется ________________,
которые называются ______________________.
10. Каждая координата суммы двух или более векторов равна сумме _________________________________________________________________
11. Напишите формулу длины вектора __________________
12. Скалярным произведением двух векторов называется ____________________________
13. Запишите формулу нахождения угла между векторами, зная координаты этих векторов ______________________________________________________
14. ______________________________ называется отображение пространства на себя, при котором любая точка М переходит в точку М1, что ММ1=.
Векторы
Вариант: 2
1. Планиметрия – это __________________, в котором изучаются _____________________________
2. Основные геометрические тела в пространстве: __________________________.
3. Дина
ненулевого вектора называется _________________________________.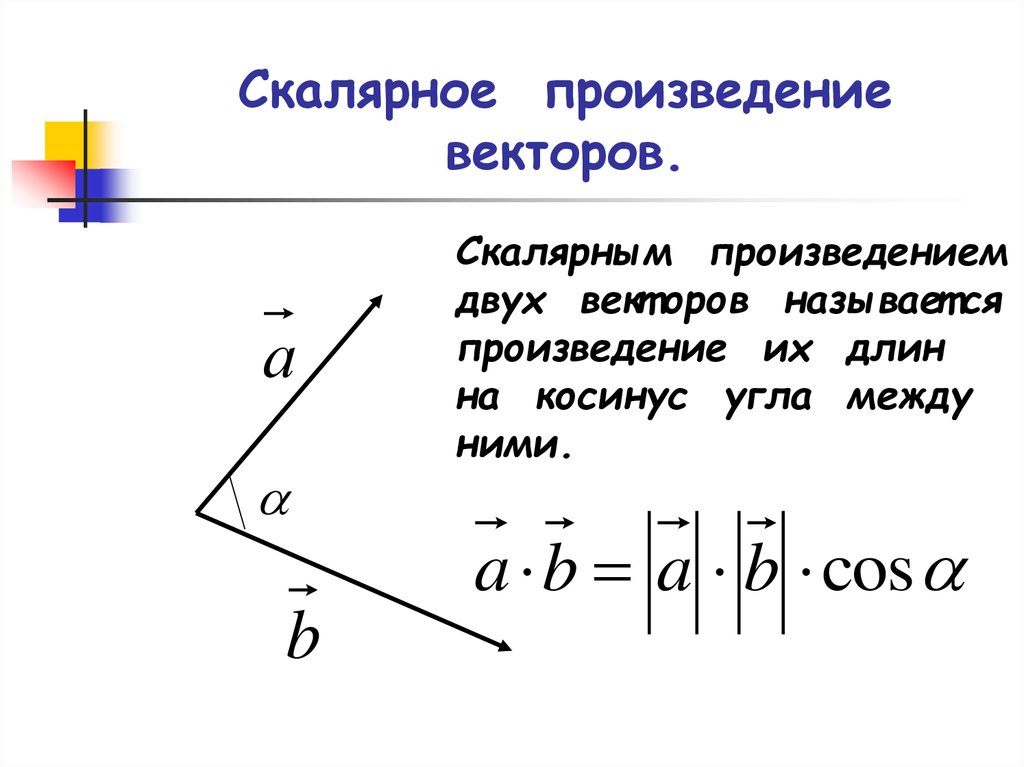
4. Противоположно направленные векторы – если они ___________________________________________________________________
5. От любой точки можно отложить вектор, ________________________________
6. Произведением ненулевого вектора на число к, называют такой вектор , ________________, причем _________________ при к>0 и _________________ при к<0.
7. Три вектора, _______________________________, также коллинеарны.
8. Прямые с выбранными на них направлениями называется _________________, а их общая точка – ___________________.
9. Перечислите единичные вектора – ______________________________________
10. Каждая координата разности двух равна _________________________________
11. Напишите формулу расстояния между двумя точками ______________________
12. Запишите формулу скалярного произведения двух векторов _________________
13. _________________-это
отображение пространства на себя, при котором любая точка М переходит в
симметричную ей точку М, относительно данного центра.
_________________-это
отображение пространства на себя, при котором любая точка М переходит в
симметричную ей точку М, относительно данного центра.
14. ______________________________ называется отображение пространства на себя, при котором любая точка М переходит в точку М1, что ММ1=.
Векторы
Вариант: 3
1. Основными геометрическими фигурами планиметрии являются ______________
2. Аксиома-________________________.
3. Длина ненулевого вектора обозначается _____________
4. Обозначаются сонаправленные векторы _____________
5. Два ненулевых вектора называются противоположными, если ___________________________________________________
6. Произведение нулевого вектора на любое число __________________________
7. Если
векторы можно разложить по
векторам и , т.е. представить в виде с=х+у, ____________________,
а и b
векторы – __________________.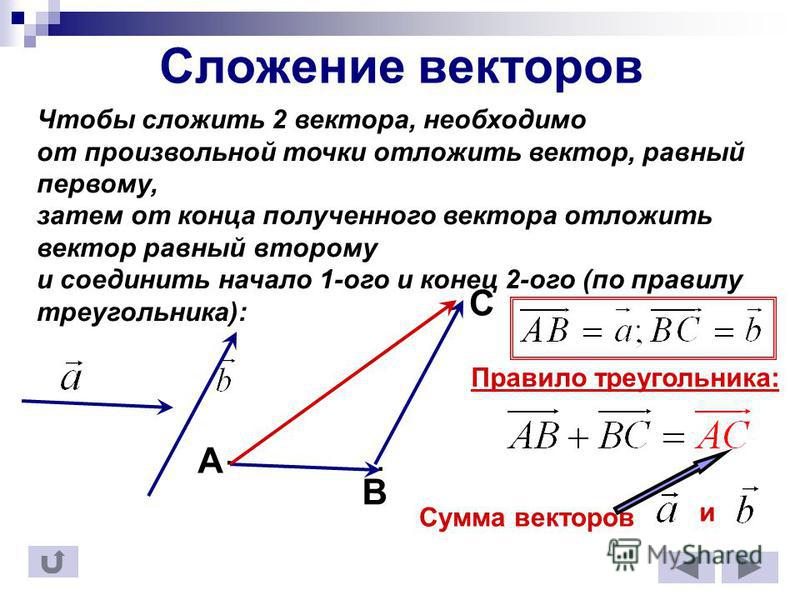
8. Перечислите оси координат в прямоугольной системе координат: __________________________
9. Координаты нулевого вектора ___________.
10. Каждая координата произведения вектора на число равна ___________________________________________________
11. Если и сонаправленные =>угол между __________
12. Скалярное произведение ненулевых векторов __________ тогда и только тогда, когда эти векторы ______________.
13. _______________ – с осью а называется такое отображение пространства на себя, при котором любая точка М переходит в симметричную ей точку М, относительно оси а.
14. ____________________________ называется отображение пространства на себя, при котором любая точка М переходит в точку М1, что ММ1=.
Векторы
Вариант:4
1. Стереометрия – это ____________, в котором изучаются _______________________
2. Отрезок,
для которого указано, какой из его концов считается началом, а какой – концом,
называется ______________
Отрезок,
для которого указано, какой из его концов считается началом, а какой – концом,
называется ______________
3. Коллинеарные векторы ________________________________________________
4. Обозначаются противоположно направленные векторы ___________
5. Разностью векторов и называется такой вектор, _________________________
6. Векторы называются компланарными, если _______________________________
___________________________________________________________________.
7. Любой вектор можно разложить _________________________, причем коэффицентф разложения определены единым образом.
8. Плоскости проходящие через оси координат ОХ и ОУ; ОУ и OZ, OX и OZ называются _____________________.
9. Координаты равных векторов ___________________.
10. Каждая координата середины отрезка равна _______________________________
11. Если и перпендикулярные =>угол между __________________
12. Скалярный
квадрат равен __________________________________
Скалярный
квадрат равен __________________________________
13. ____________________ (симметрий относительно плоскости альфа) называется такое отображение пространства на себя, при котором любая точка М переходит в симметричную ей относительно плоскости альфа точки М1.
14. __________________________ называется отображение пространства на себя, при котором любая точка М переходит в точку М1, что ММ1=.
Векторы основные формулы: Формулы векторов — ЭкоДом: Дом своими руками
Содержание
Формулы векторов
1. Координаты вектора
Если вектор задан координатами своих начала и конца: , то его координаты равны разности соответствующих координат конца и начала:
2. Длина или модуль вектора
Если вектор , то его длина равна корню квадратному из суммы квадратов координат:
3. Сумма векторов
Если векторы и заданы своими координатами, то суммой этих векторов есть вектор, координаты которого равны сумме соответствующих координат векторов-слагаемых:
4.
 Умножение вектора на число
Умножение вектора на числоЧтобы найти произведение вектора на некоторое число , нужно каждую координату заданного вектора умножить на это число:
5. Скалярное произведение векторов
Если векторы и заданы своими координатами, то их скалярное произведение равно сумме произведений соответствующих координат:
6. Векторное произведение векторов
Если векторы и заданы своими координатами в некотором ортонормированном базисе , то их векторное произведение находится по формуле:
7.
Смешанное произведение векторов
Если заданы три вектора и , то их смешанное произведение равно определителю, по строкам которого записаны координаты этих векторов:
Замечание. Обычно такой определитель вычисляется методом треугольников.
8. Угол между векторами
Косинус угла между двумя векторами и , заданными своими координатами, равен частному скалярного произведения этих векторов и произведению их модулей:
9.
 Проекция вектора на вектор
Проекция вектора на векторПроекция вектора на направление вектора равна отношение скалярного произведения этих векторов к модулю вектора :
|
Понравился сайт? Расскажи друзьям! |
| ||
11 класс.
Геометрия. Метод координат в пространстве. Скалярное произведение векторов. — Скалярное произведение векторов.
Комментарии преподавателя
Отложим от какой-нибудь точки O векторы и (см. рис. 1). Если векторы и не являются сонаправленными, то лучи ОА и ОВ образуют угол АОВ — угол между векторами, обозначим его . Если же векторы и — сонаправлены, то будем считать, что угол между ними равен 0°. Если угол между векторами равен 90°, то векторы называются перпендикулярными. На письме угол между векторами обозначают так: .
Скалярное произведение векторов находится по формуле: .
Рис. 1. Угол между векторами
Основные свойства скалярного произведения векторов:
1)
2)
3)
4)
Рассмотрим задачу на нахождение скалярного произведения векторов.
Задача 1. Дано: ABCDA1B1C1D1 – куб, O1 – центр A1B1C1D1 , AB=a (см. рис. 2).
Рис. 2.
Найти скалярные произведения векторов:
а) . Находим эти вектора на рисунке, они сонаправлены, значит угол между ними 0°, а эти вектора равны a. Получаем:
б) . Эти вектора параллельны и противоположно направлены, значит, угол между ними 180°. Модуль вектора — это диагональ квадрата, , . Получаем: .
в) . Так как эти вектора перпендикулярны (по рисунку), то косинус угла между ними равен 0. Значит, .
г) . Модули этих векторов равны — это диагонали квадратов. Чтобы найти угол между нужными векторами, рассмотрим треугольник A1C1B. Этот треугольник равносторонний, значит, угол равен 60°.
Этот треугольник равносторонний, значит, угол равен 60°.
·= — 2a2
д) . Эти вектора перпендикулярны, значит, .
е) . Длины этих векторов равны , так как они являются половинами диагоналей. Эти векторы противоположно направлены, угол между ними 180°.
Получаем:.
Задача 2. Дано: A(0;1;2), B(√2;1;2), C(√2;2;1), D(0;2;1). Доказать: ABCD – квадрат.
Решение:
1) Найдем координаты векторов, длины которых совпадают с длинами сторон четырехугольника. Координаты вектора – это разность координат конца и начала отрезка.
, , , . По координатам видно, что , . Доказано, что ABCD – параллелограмм.
2) Найдем модули эти векторов по формуле: .
Получаем: . Доказано, что ABCD – ромб.
3) Найдем один угол между векторами. .
Стороны попарно параллельны, стороны равны, и один угол равен 90°, значит остальные углы тоже равны 90°. Следовательно, ABCD – квадрат, что и требовалось доказать.
Следовательно, ABCD – квадрат, что и требовалось доказать.
ИСТОЧНИК
http://interneturok.ru/ru/school/geometry/11-klass/bmetod-koordinat-v-prostranstveb/skalyarnoe-proizvedenie-vektorov-2
http://www. youtube.com/watch?v=CJOt3vy20vs
http://www.youtube.com/watch?v=FhYroW_Ff6U
http://player.myshared.ru/1247089/data/images/img2.jpg
http://profege.ru/wp-content/uploads/2013/01/76c6ad7d219efe5add515e0e58a05100.jpg
http://portfoliosmolgu.ucoz.ru/_ph/8/2/757341327.jpg?1436847671
http://fs1261.gavitex.com/get/2398829017/skalyarnoe-proizvedenie-vektorov.rar
http://ok-t.ru/studopediaru/baza8/824194016948.files/image252.png
http://dok. opredelim.com/docs/index-42169.html
opredelim.com/docs/index-42169.html
http://www.metod-kopilka.ru/prezentaciya_k_zanyatiyu_po_teme_quotmetod_koordinat_v_prostranstvequot-42727.htm
http://school35.tuapse.ru/school_life/school_laboratorii/shtl%20mathematics/%D0%93%D1%83%D1%80%D0%B5%D0%B2%D0%B8%D1%87%20%D0%AD.%D0%93.%20%D0%BF%D1%80%D0%B5%D0%B7%D0%B5%D0%BD%D1%82%D0%B0%D1%86%D0%B8%D1%8F%20%D1%83%D0%B3%D0%BE%D0%BB%20%D0%BC%D0%B5%D0%B6%D0%B4%D1%83%20%D0%B2%D0%B5%D0%BA%D1%82%D0%BE%D1%80%D0%B0%D0%BC%D0%B8%20%D0%B2%20%D0%BF%D1%80%D0%BE%D1%81%D1%82%D1%80%D0%B0%D0%BD%D1%81%D1%82%D0%B2%D0%B5%20%D1%81%D0%BA%D0%B0%D0%BB%D1%8F%D1%80%D0%BD%D0%BE%D0%B5%20%D0%BF%D1%80%D0%BE%D0%B8%D0%B7%D0%B2%D0%B5%D0%B4%D0%B5%D0%BD%D0%B8%D0%B5. ppt
Формулы и уравнения векторной алгебры
Формулы и уравнения векторной алгебры
- Основные определения.
- Вектор (геометрический вектор) — это направленный отрезок (отрезок, у которого одна граничная точка считается начальной, другая – конечной).
На чертеже вектор обозначается стрелкойнад буквенным обозначением вектора также ставится стрелка .

Вектор, фигурирующий в определении, носит название связанного, или закрепленного вектора. - Закрепленный вектор — это направленный отрезок АВ, началом которого является точка А, а концом — точка В.
Свободный вектор — это множество всех закрепленных векторов, получающихся из фиксированного закрепленного вектора с помощью параллельного переноса. Обозначается .
Если же точка приложения вектора (точка A для вектора ) может быть выбрана произвольно, вектор называется свободным.
Если точка приложения может двигаться по линии действия вектора, говорят о скользящем векторе. Иначе говоря, свободный вектор является представителем бесконечного множества связанных или скользящих векторов. - Нулевой вектор — это вектор, у которого начало и конец совпадают:
- Коллинеарные векторы — это векторы, которые лежат на одной прямой, либо на параллельных прямых.
Нулевой вектор коллинеарен любому вектору.
- Три вектора называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях.
Если тройка векторов содержит нулевой вектор или пару коллинеарных векторов, то эти векторы компланарны. - Длина вектора (модуль) — это расстояние между началом и концом вектора. Обозначение: или
- Два вектора равны, если они коллинеарны, имеют одинаковую длину и направление. Например,
- Алгебраические операции над векторами.
- Операция сложения.
Суммой двух свободных векторов и называется свободный вектор , начало которого совпадает с началом первого, а конец — с концом второго, если совмещены конец вектора и начало вектора .
Сумма двух векторов и () — это вектор, идущий из начала вектора в конец вектора при условии, что начало вектора приложено к концу вектора (правило треугольника).Свойства операции сложения векторов:
1) Переместительное свойство: (коммутативность).
2) Сочетательное свойство: (ассоциативность).
3) Существует нулевой вектор , такой, что для любого вектора (особая роль нулевого вектора).
Нулевой вектор порождается нулевым закрепленным вектором, то есть точкой.
4) Для каждого вектора существует противоположный ему вектор , такой, что . Вектор называется вектором, противоположным вектору .
Правило параллелограмма (правило сложения векторов): если векторы и приложены к общему началу и на них построен параллелограмм, то сумма этих векторов представляет собой диагональ параллелограмма, идущую из общего начала векторов иВычитание векторов определяется через сложение: .
Другими словами, если векторы и приложены к общему началу, то разностью векторов и будет вектор , идущий из конца вектора к концу вектора . - Операция умножения вектора на число.
Произведением вектора на число называется вектор такой, что:
1) если λ > 0, ≠ , то получается из растяжением в λ раз: ;
2) если λ < 0, ≠ , то получается из растяжением в |λ| раз и последующим отражением: ;
3) если λ = 0 или , то .
Свойства операции умножения:
1) Распределительное свойство относительно суммы чисел: для любых действительных и всех (дистрибутивность).
2) Распределительное свойство относительно суммы векторов: (дистрибутивность).
3) Сочетательное свойство числовых сомножителей: (ассоциативность).
4) Существование единицы: .
- Ортонормированный базис. Декартова прямоугольная система координат.
- Ортонормированный базис (ОНБ) — это три взаимно перпендикулярных вектора с длинами, равными единице.
Обозначения:
- Базисные орты — это векторы .
- Зафиксированная точка О – это начало координат.
Отложим от точки O векторы .
Полученная система координат — это прямоугольная декартова система координат. - Декартовы координаты вектора — это координаты любого вектора в этом базисе:
Пример 11.
- Координатные оси — это прямые линии, проведенные через начало координат (точку O) по направлениям базисных векторов:
– порождает Ox;
– порождает Oy;
– порождает Oz.
- Абсцисса — это координата точки M (вектора в декартовой системе координат по оси Ox.
Ордината — это координата точки M (вектора в декартовой системе координат по оси Oy.
Аппликата — это координата точки M (вектора ) в декартовой системе координат по оси Oz. - Декартовы прямоугольные координаты x, y, z вектора равны проекциям этого вектора на оси Ox, Oy, Oz, соответственно. Иначе:
где α, β, γ – углы, которые составляет вектор с координатными осями Ox, Oy, Oz, соответственно, при этом cosα, cosβ, cosγ называются направляющими косинусами вектора . Пример 12.
Для направляющих косинусов справедливо соотношение: - Орт направления — это вектор единичной длины данного направления.
Формулы, уравнения, теоремы, примеры решения задач
Скалярное произведение векторов. Формулы и определение
Основные определения
Система координат — способ определить положение и перемещение точки или тела с помощью чисел или других символов.
Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Как найти координаты точки мы рассказали в этой статье.
Скаляр — это величина, которая полностью определяется в любой координатной системе одним числом или функцией.
Вектор — направленный отрезок прямой, для которого указано, какая точка является началом, а какая — концом.
Вектор с началом в точке A и концом в точке B принято обозначать как →AB. Векторы также можно обозначать малыми латинскими буквами со стрелкой или черточкой над ними, вот так: →a.
Скалярное произведение — это операция над двумя векторами, результатом которой является скаляр, то есть число, которое не зависит от выбора системы координат.
Результат операции является число. То есть при умножении вектор на вектор получается число. Если длины векторов |→a|, |→b| — это числа, косинус угла — число, то их произведение |→a|*|→b|*cos∠(→a, →b) тоже будет числом.
Чтобы разобраться в теме этой статьи, нам еще нужно узнать особенности угла между векторами.
Приходите тренироваться в детскую школу Skysmart. Ученики решают захватывающие задачки вместе с красочными героями на интерактивной платформе, чертят вместе с учителем на онлайн-доске и не боятся школьных контрольных.
Запишите ребенка на бесплатный вводный урок математики и начните заниматься в удовольствие уже завтра!
Угол между векторами
Угол между векторами ∠(→a, →b) может принимать значения от 0° до 180° градусов включительно. Аналитически это можно записать в виде двойного неравенства: 0°=<∠(→a; →b)=<180° либо 0°=<∠(→a; →b)=<π.
Значок угла ∠ можно опустить и писать просто: (→a;→b).
Пусть даны два вектора →a, →b.
Отложим их от некоторой точки О пространства: →OA = →a; →OB = →b. Тогда угол между векторами — это угол ∠AOB = (→a, →b).
Угол между векторами может быть прямым, тупым или острым. Рассмотрим каждый случай:
1. Если векторы сонаправлены, то угол между ними равен 0°.
Если векторы сонаправлены, то угол между ними равен 0°.
Так как косинус угла в 0° равен единице, то скалярное произведение сонаправленных векторов является произведением их длин. Если два вектора равны, то такое скалярное произведение называют скалярным квадратом.
2. Если угол между векторами равен 90°, то такие векторы перпендикулярны друг другу.
Так как косинус прямого угла равен 0, то скалярное произведение перпендикулярных векторов равно 0.
3. Если векторы направлены в разные стороны, тогда угол между ними 180°.
Так как косинус угла в 180° равен -1, то скалярное произведение противоположно направленных векторов равно отрицательному произведению их длин.
Также векторы могут образовывать тупой угол. Это выглядит так:
Важно!
Так как косинус тупого угла отрицательный, то скалярное произведение векторов, которые образуют тупой угол, является тоже отрицательным.
Скалярное произведение векторов
Определение скалярного произведения можно сформулировать двумя способами:
Скалярное произведение двух векторов a и b дает в результате скалярную величину, которая равна сумме попарного произведения координат векторов a и b.
- Геометрическая интерпретация.
Скалярным произведением двух векторов a и b будет скалярная величина, равная произведению модулей этих векторов, умноженная на косинус угла между ними:
→a * →b = →|a| * →|b| * cosα
- Алгебраическая интерпретация.
Что важно запомнить про геометрическую интерпретацию скалярного произведения:
- Если угол между векторами острый и векторы ненулевые, то скалярное произведение положительно, то есть cosα > 0.
- Если угол между векторами тупой и векторы ненулевые, то скалярное произведение отрицательно, так как cosα < 0.
- Если угол между векторами прямой, то скалярное произведение равно 0 так как , то есть cosα = 0.
Скалярное произведение в координатах
Вычисление скалярного произведения можно произвести через координаты векторов в заданной плоскости или в пространстве.
Скалярным произведением двух векторов на плоскости или в трехмерном пространстве в прямоугольной системе координат называется сумма произведений соответствующих координат векторов →a и →b.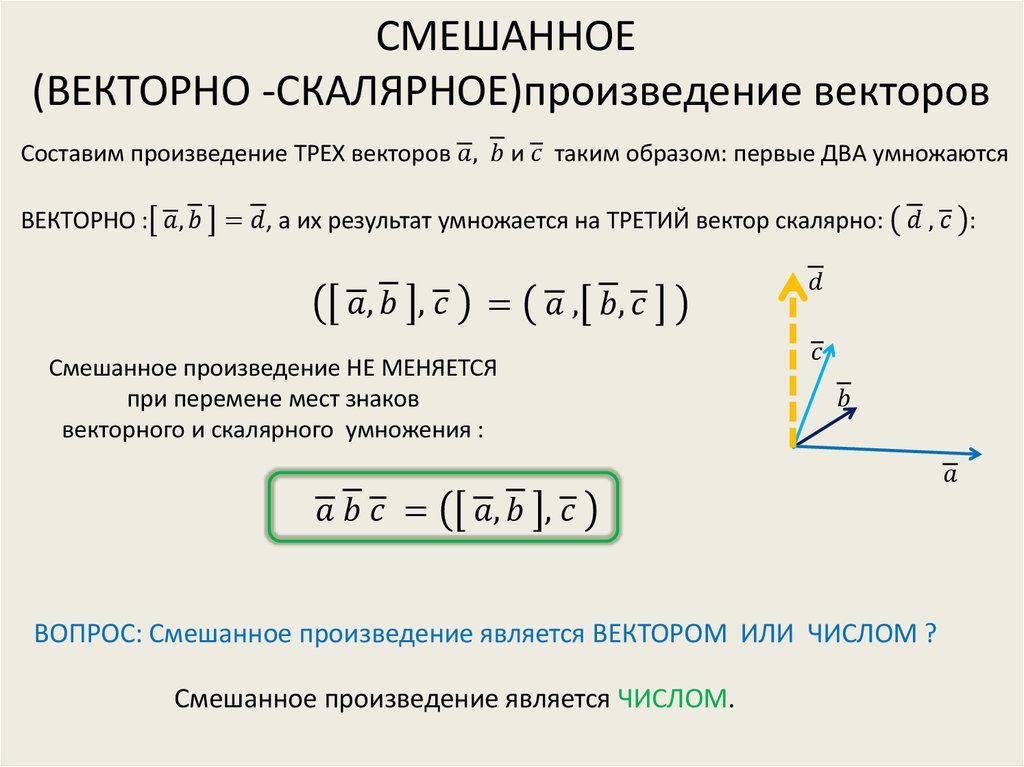
То есть для векторов →a = (ax, ay), →b = (bx, by) на плоскости в прямоугольной декартовой системе координат формула для вычисления скалярного произведения имеет вид: (→a, →b) = ax*bx + ay*by
А для векторов →a = (ax, ay, az), →b = (bx, by, bz) в трехмерном пространстве скалярное произведение в координатах находится так: (→a, →b) = ax*bx + ay*by + az*bz
Докажем это определение:
- Сначала докажем равенства
для векторов →a = (ax, ay), →b = (bx, by) на плоскости, заданных в прямоугольной декартовой системе координат.
Отложим от начала координат (точка О) векторы →OB = →b = (bx, by) и →OA = →a = (ax, ay)
Тогда, →AB = →OB — →OA = →b — →a = (bx — ax, by — ay)
- Будем считать точки О, А и В вершинами треугольника ОАВ. По теореме косинусов можно записать:
Так как:
то последнее равенство можно переписать так:
а по первому определению скалярного произведения имеем
откуда
- Вспомнив формулу вычисления длины вектора по координатам, получаем
- Абсолютно аналогично доказывается справедливость равенств (→a, →b) = |→a|*|→b|*cos(→a, →b) = ax*bx + ay*by + ax*bz для векторов →a = (ax, ay, az), →b = (bx, by, bz), заданных в прямоугольной системе координат трехмерного пространства.

- Формула скалярного произведения векторов в координатах позволяет заключить, что скалярный квадрат вектора равен сумме квадратов всех его координат: на плоскости (→a, →a) = ax2 + ay2 в пространстве (→a, →a) = ax2 + ay2 + az2.
Формулы скалярного произведения векторов заданных координатами
Формула скалярного произведения векторов для плоских задач
В плоской задаче скалярное произведение векторов a = {ax ; ay} и b = {bx ; by} можно найти по формуле:
a * b = ax * bx + ay * by
Формула скалярного произведения векторов для пространственных задач
В пространственной задаче скалярное произведение векторов a = {ax ; ay ; az} и b = {bx ; by ; bz} можно найти по формуле:
a * b = ax * bx + ay * by + az * bz
Формула скалярного произведения n-мерных векторов
В n-мерном пространстве скалярное произведение векторов a = {a1; a2; … ; an} и b = {b1; b2; … ; bn} можно найти по формуле:
a * b = a1 * b1 + a2 * b2 + … + an * bn
Свойства скалярного произведения
Свойства скалярного произведения векторов:
- Скалярное произведение вектора самого на себя всегда больше или равно нулю.
 В результате получается нуль, если вектор равен нулевому вектору.
В результате получается нуль, если вектор равен нулевому вектору.→а * →а > 0
→0 * →0 = 0
- Скалярное произведение вектора самого на себя равно квадрату его модуля:
→a * →a = →∣∣a∣∣2
- Операция скалярного произведения коммуникативна, то есть соответствует переместительному закону:
→a * →b = →b * →a
- Операция скалярного умножения дистрибутивна, то есть соответствует распределительному закону:
(→a + →b) * →c = →a * →c + →b * →c
- Сочетательный закон для скалярного произведения:
(k * →a) * →b = k * (→a * →b)
- Если скалярное произведение двух ненулевых векторов равно нулю, то эти векторы ортогональны, то есть перпендикулярны друг другу:
a ≠ 0, b ≠ 0, a * b = 0 <=> a ┴ b
Эти свойства очень легко обосновать, если отталкиваться от определения скалярного произведения в координатной форме и от свойств операций сложения и умножения действительных чисел.
Для примера докажем свойство коммутативности скалярного произведения (→a, →b) = (→b, →a)
По определению (→a, →b) = ax*bx + ay*by и (→b, →a) = bx*ax + by*ay. В силу свойства коммутативности операции умножения действительных чисел, справедливо ax*bx = bx*ax b ay*by = by*ay, тогда ax*bx + ay*by = bx*ax + by*ay.
В силу свойства коммутативности операции умножения действительных чисел, справедливо ax*bx = bx*ax b ay*by = by*ay, тогда ax*bx + ay*by = bx*ax + by*ay.
Следовательно, (→a, →b) = (→b, →a), что и требовалось доказать.
Аналогично доказываются остальные свойства скалярного произведения.
Следует отметить, что свойство дистрибутивности скалярного произведения справедливо для любого числа слагаемых, то есть,
и,
откуда следует:
Примеры вычислений скалярного произведения
Пример 1.
Вычислите скалярное произведение двух векторов →a и →b, если их длины равны 3 и 7 единиц соответственно, а угол между ними равен 60 градусам.
Как решаем:
У нас есть все данные, чтобы вычислить скалярное произведение по определению:
(→a,→b) = →|a| * →|b| * cos(→a,→b) = 3 * 7 cos60° = 3 * 7 * 1/2 = 21/2 = 10,5.
Ответ: (→a,→b) = 21/2 = 10,5.
Пример 2.
Найти скалярное произведение векторов →a и →b, если →|a| = 2, →|b| = 5, ∠(→a,→b) = π/6.
Как решаем:
Используем формулу →a * →b = →|a| * →|b| * cosα.
В данном случае:
→a * →b = →|a| * →|b| * cosα = 2 * 5 * cosπ/6 = 10 * √3/2 = 5√3
Ответ: →a * →b = 5√3.
Пример 3.
Как найти скалярное произведение векторов →a = 7*→m + 3*→n и →b = 5*→m + 8*→n, если векторы →m и →n перпендикулярны и их длины равны 3 и 2 единицы соответственно.
Как решаем:
По свойству дистрибутивности скалярного произведения имеем
Сочетательное свойство позволяет нам вынести коэффициенты за знак скалярного произведения:
В силу свойства коммутативности последнее выражение примет вид
Итак, после применения свойств скалярного произведения имеем
Осталось применить формулу для вычисления скалярного произведения через длины векторов и косинус угла между ними:
Ответ: (→a,→b) = 411.
Пример 4.
В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, найти косинус угла между прямыми AB1 и BC1.
Как решаем:
- Введем систему координат.
Если сделать выносной рисунок основания призмы, получим понятный плоскостной рисунок с помощью которого можно легко найти координаты всех интересующих точек.
- Точка А имеет координаты (0;0;0). Точка С — (1;0;0). Точка В — (1/2;√3/2;0). Тогда точка В1 имеет координаты (1/2;√3/2;1), а точка С1 – (1;0;1).
- Найдем координаты векторов →AB1 и →BC1:
- Найдем длины векторов →AB1 и →BC1:
- Найдем скалярное произведение векторов →AB1 и →BC1:
- Найдем косинус угла между прямыми AB1 и BC1:
Ответ: 1/4.
Пример 5.
а) Проверить ортогональность векторов: →a(1; 2; -4) и →b(6; -1; 1) .
б) Выяснить, будут ли перпендикулярными отрезки KL и MN, если K(3;5), L(-2;0), M(8;-1), N(1;4).
Как решаем:
а) Выясним, будут ли ортогональны пространственные векторы. Вычислим их скалярное произведение: →ab = 1*6 + 2*(-1) + (-4)*1 = 0, следовательно
б) Здесь речь идёт об обычных отрезках плоскости, а задача всё равно решается через векторы. Найдем их: →KL(-2-3; 0-5) = →KL(-5; -5), →MN(1-8; 4-(-1)) = →MN(-7;5)
Найдем их: →KL(-2-3; 0-5) = →KL(-5; -5), →MN(1-8; 4-(-1)) = →MN(-7;5)
Вычислим их скалярное произведение: →KL*→MN = -5*(-7) + (-5)*5 = 10 ≠ 0, значит, отрезки KL и MN не перпендикулярны.
Обратите внимание на два существенных момента:
- В данном случае нас не интересует конкретное значение скалярного произведения, важно, что оно не равно нулю.
- В окончательном выводе подразумевается, что если векторы не ортогональны, значит, соответствующие отрезки тоже не будут перпендикулярными. Геометрически это очевидно, поэтому можно сразу записывать вывод об отрезках, что они не перпендикулярны.
Ответ: а) →a перпендикулярно →b, б) отрезки KL, MN не перпендикулярны.
Пример 6.
Даны три вершины треугольника A(-1; 0), B(3; 2), C(5; -4). Найти угол при вершине B — ∠ABC.
Как решаем:
По условию чертеж выполнять не требуется, но для удобства можно сделать:
Требуемый угол ∠ABC помечен зеленой дугой. Сразу вспоминаем школьное обозначение угла: ∠ABC — особое внимание на среднюю букву B — это и есть нужная нам вершина угла.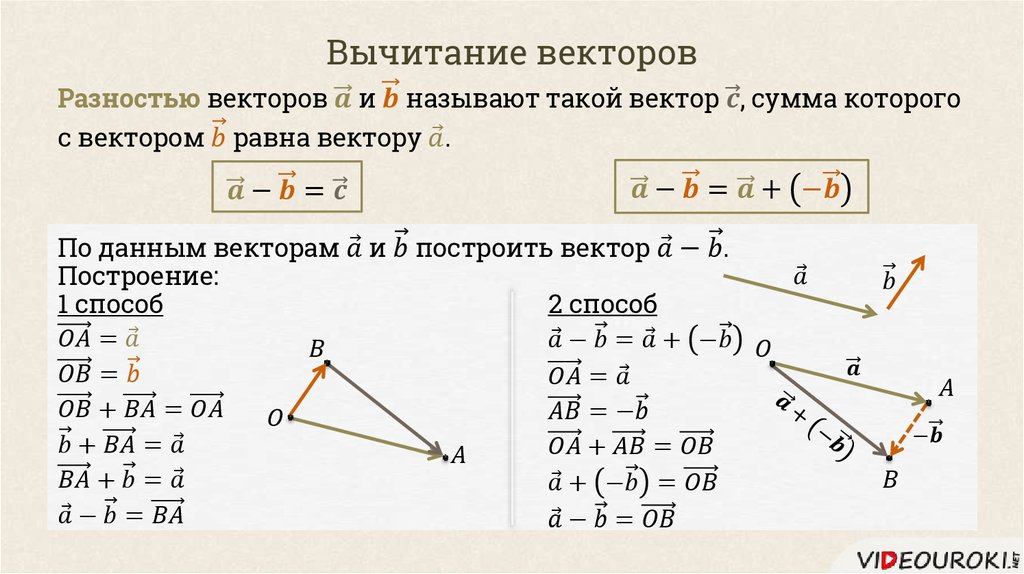 Для краткости можно также записать просто ∠B.
Для краткости можно также записать просто ∠B.
Из чертежа видно, что угол ∠ABC треугольника совпадает с углом между векторами →BA и →BC, иными словами: ∠ABC = ∠(→BA; →BC).
Найдем векторы:
Вычислим скалярное произведение:
Вычислим длины векторов:
Найдем косинус угла:
Когда такие примеры не будут вызывать трудностей, можно начать записывать вычисления в одну строчку:
Полученное значение не является окончательным, поэтому нет особого смысла избавляться от иррациональности в знаменателе.
Найдём сам угол:
Если посмотреть на чертеж, то результат действительно похож на правду. Для проверки угол также можно измерить и транспортиром.
Ответ: ∠ABC = arccos(1/5√2) ≈1,43 рад. ≈ 82°
Важно не перепутать, что в задаче спрашивалось про угол треугольника, а не про угол между векторами. Поэтому указываем точный ответ: arccos(1/5√2) и приближенное значение угла: ≈1,43 рад. ≈ 82°, которое легко найти с помощью калькулятора.
А те, кому мало и хочется еще порешать, могут вычислить углы ∠A, ∠C, и убедиться в справедливости канонического равенства ∠A + ∠B + ∠C = 180°.
Чтобы знания превратились в практический навык — запишите ребенка на бесплатный вводный урок математики в Skysmart. На занятии покажем, как все устроено, решим пару задачек и дадим рекомендации по программе обучения для вашего ребенка.
Скалярное произведение векторов
Геометрическая интерпретация. Скалярным произведением двух векторов a и b будет скалярная величина, равная произведению модулей этих векторов умноженного на косинус угла между ними:
a · b = |a| · |b| cos α
Алгебраическая интерпретация. Скалярным произведением двух векторов a и b будет скалярная величина, равная сумме попарного произведения координат векторов a и b.
Формулы скалярного произведения векторов заданных координатами
Формула скалярного произведения векторов для плоских задач
В случае плоской задачи скалярное произведение векторов a = {ax ; ay} и b = {bx ; by} можно найти воспользовавшись следующей формулой:
a · b = ax · bx + ay · by
Формула скалярного произведения векторов для пространственных задач
В случае пространственной задачи скалярное произведение векторов a = {ax ; ay ; az} и b = {bx ; by ; bz} можно найти воспользовавшись следующей формулой:
a · b = ax · bx + ay · by + az · bz
Формула скалярного произведения n -мерных векторов
В случае n-мерного пространства скалярное произведение векторов a = {a1 ; a2 ; . .. ; an} и b = {b1 ; b2 ; … ; bn} можно найти воспользовавшись следующей формулой:
.. ; an} и b = {b1 ; b2 ; … ; bn} можно найти воспользовавшись следующей формулой:
a · b = a1 · b1 + a2 · b2 + … + an · bn
Примеры задач на вычисление скалярного произведения векторов
Примеры вычисления скалярного произведения векторов для плоских задач
Пример 1. Найти скалярное произведение векторов a = {1; 2} и b = {4; 8}.
Решение: a · b = 1 · 4 + 2 · 8 = 4 + 16 = 20.
Пример 2. Найти скалярное произведение векторов a и b, если их длины |a| = 3, |b| = 6, а угол между векторами равен 60˚.
Решение: a · b = |a| · |b| cos α = 3 · 6 · cos 60˚ = 9.
Пример 3. Найти скалярное произведение векторов p = a + 3b и q = 5a — 3 b, если их длины |a| = 3, |b| = 2, а угол между векторами a и b равен 60˚.
Решение:
p · q = (a + 3b) · (5a — 3b) = 5 a · a — 3 a · b + 15 b · a — 9 b · b =
= 5 |a|2 + 12 a · b — 9 |b|2 = 5 · 32 + 12 · 3 · 2 · cos 60˚ — 9 · 22 = 45 +36 -36 = 45.
Пример 4. Найти скалярное произведение векторов (a + 2i)·(b — 2j),если a = {1; 2} и b = {4; -8}.
Решение: Запишем вектора a и b через ортонормированные базисные вектора i и j:
a = i + 2j
b = 4i — 8j
Тогда используя свойства ортов (i2 = 1, j2 = 1, i·j = 0)
(a + 2i)·(b — 2j) = (i + 2j + 2i)·(4i — 8j — 2j) = (3i + 2j)·(4i — 10j) = 12i2 — 30i·j + 12j·i — 20j2 = 12 — 0 + 0 — 20 = -8
Пример вычисления скалярного произведения векторов для пространственных задач
Пример 5. Найти скалярное произведение векторов a = {1; 2; -5} и b = {4; 8; 1}.
Решение: a · b = 1 · 4 + 2 · 8 + (-5) · 1 = 4 + 16 — 5 = 15.
Пример вычисления скалярного произведения для n -мерных векторов
Пример 6. Найти скалярное произведение векторов a = {1; 2; -5; 2} и b = {4; 8; 1; -2}.
Найти скалярное произведение векторов a = {1; 2; -5; 2} и b = {4; 8; 1; -2}.
Решение: a · b = 1 · 4 + 2 · 8 + (-5) · 1 + 2 · (-2) = 4 + 16 — 5 -4 = 11.
Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация / / Математический справочник / / Математика для самых маленьких. Шпаргалки. Детский сад, Школа. / / Понятие вектора. Действия с векторами, их свойства — сложение и вычитание векторов, умножение на число, коллинеарность. Скалярное умножение (произведение) векторов. Проекции, разложение векторов, координаты, действия в координатах, взаимное расположение Поделиться:
Поиск в инженерном справочнике DPVA. Введите свой запрос: | ||||||
Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста. Вложите в письмо ссылку на страницу с ошибкой, пожалуйста. | ||||||
Коды баннеров проекта DPVA. Консультации и техническая | Проект является некоммерческим. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса. Free xml sitemap generator | |||||
Онлайн калькуляторы, расчеты и формулы на GELEOT.RU
Векторы представляют собой особый раздел аналитической геометрии, который в том числе оказал значительное влияние на развитие физики. Сам по себе вектор выглядит как отрезок, который имеет начало и имеет конец, определен заданной конечными точками длиной этого отрезка. Но внутри вектора кроется множество других скрытых функций, за счет того что вектор задает направление. Поэтому если для отрезка не имеет значения какая точка названа началом, а какая концом, и чаще просто применяется принцип чтения «слева направо», то для векторов AB и BA – это диаметрально противоположные понятия.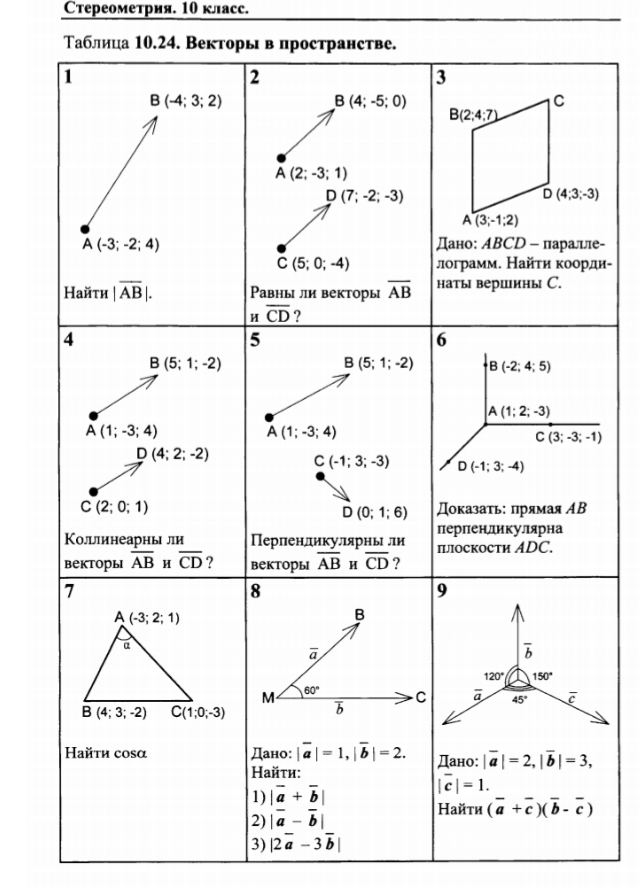
Итак, в векторе присутствует две важных составляющих – это его длина и направление. Тем не менее, координатами вектора задается не его фактическая длина, а местоположение на плоскости или в пространстве. Поэтому длина вектора, иначе называемая модуль вектора, вычисляется, используя прямоугольный треугольник с осями координат. Дальнейшие действия с вектором также чаще используют именно его координаты, нежели фактическую длину. Работе с векторами можно провести аналогию с целыми числами, — как только появляются отрицательные числа на числовой оси, приходится не только считать значение примера, но и все время обращать внимание на знаки. Так и с векторами, во всех действиях – будь то сложение, вычитание, умножение скалярное или векторное и другие действия, приходится не только учитывать реальные масштабы вектора – координаты, длина или угол, но и принимать в расчет его направление. К слову, направления векторов также находят отражение в знаках – обратный изначальному вектор всегда будет со знаком «минус».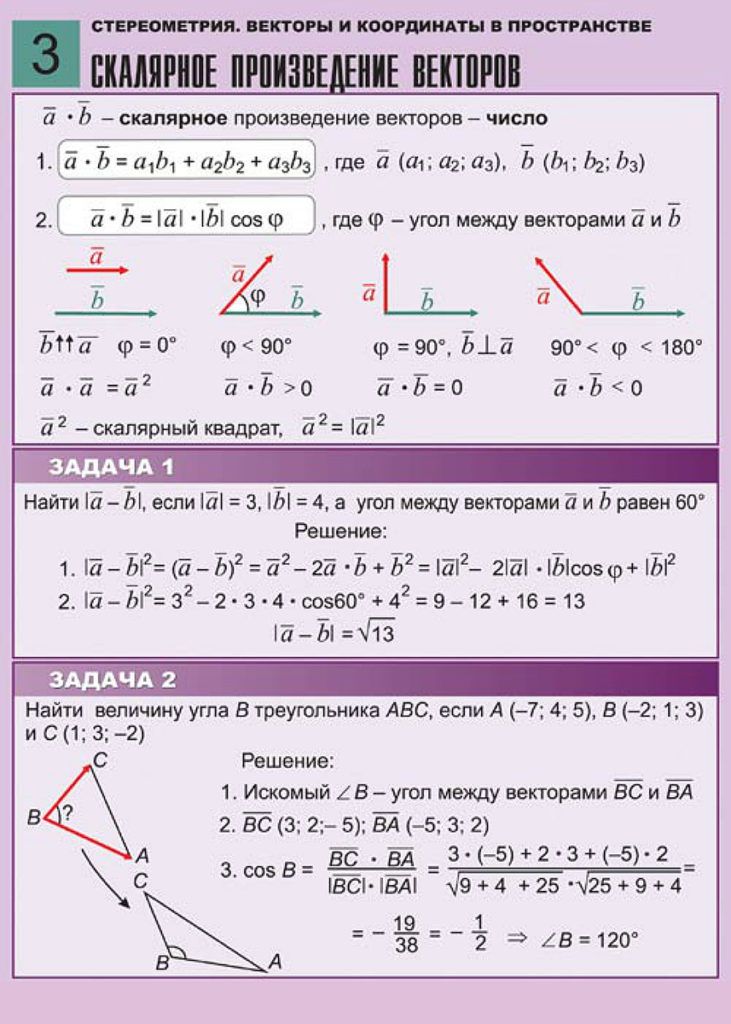
В данном разделе разложены все основные действия с векторами, такие как нахождение длины вектора, координат вектора, сложение векторов, вычитание векторов, скалярное произведение векторов, векторное произведение векторов, смешанное произведение трех векторов, вычисление угла между векторами и другие. Все расчет можно произвести для векторов на плоскости или для векторов в пространстве. Также доступен векторный калькулятор, который вычисляет все возможные параметры одного и более векторов, с заданными координатами точек вектора.
Векторов — Математика A-Level Revision
Векторная величина имеет как величину, так и направление. Ускорение, скорость, сила и перемещение — все это примеры векторных величин. Скалярная величина имеет только величину (поэтому направление не имеет значения). Примеры включают скорость, время и расстояние.
Единичные векторы
Единичный вектор — это вектор, который имеет величину 1. Обычно используются три важных единичных вектора, и это векторы в направлении осей x, y и z.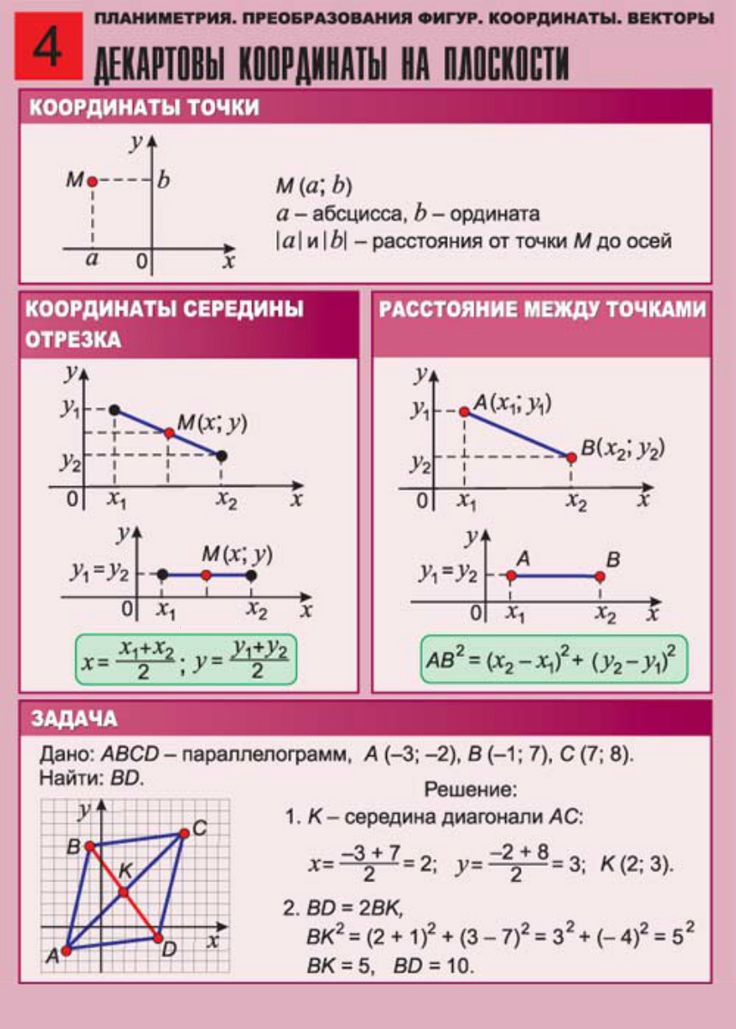 Единичный вектор в направлении оси x равен i , единичный вектор в направлении оси y равен j , а единичный вектор в направлении оси z равен k .
Единичный вектор в направлении оси x равен i , единичный вектор в направлении оси y равен j , а единичный вектор в направлении оси z равен k .
Запись векторов в этой форме может облегчить работу с векторами.
Величина вектора
Величину вектора можно найти с помощью теоремы Пифагора .
Обозначим величину вектора a через | a |
Векторы положения
Векторы положения — это векторы, определяющие положение точки относительно фиксированной точки (начала координат).
Например, точки A, B и C являются вершинами треугольника с векторами положения a , b и c соответственно:
Вы можете рисовать в исходной точке, где хотите.
Обратите внимание, что = — a + b = b — a , потому что вы можете добраться от A до B, перейдя от A к O, а затем перейдя от O к B.
Векторное уравнение прямой
Векторное уравнение прямой, проходящей через точку a и в направлении d :
Это означает, что для любого значения t точка r является точкой на прямой.
Если нам даны векторные уравнения двух разных линий, мы сможем определить, где пересекаются линии, из их уравнений.
Пример
Найдите, где пересекаются прямые с уравнениями r = i + j + t (3 i — j ) и r = — i + s ( j ).
Когда они пересекаются, мы можем приравнять уравнения друг другу:
i + j + t (3 i — j ) = — i + s ( j )
Коэффициенты приравнивания:
1 + 3t = -1 и 1 — t = s
Итак, t = -2/3 и s = 5/3
Таким образом, вектор положения точки пересечения задается путем подстановки t = -2/3 или s = 5/3 в одно из приведенных выше уравнений.Это дает — i +5 j /3.
Скалярное произведение
Предположим, у нас есть два вектора:
a i + b j + c k и d i + e j + f k , то их скалярное (или точечное) произведение: ad + be + fc. Итак, умножьте коэффициенты i вместе, коэффициенты j вместе и коэффициенты k вместе и сложите их все.
Итак, умножьте коэффициенты i вместе, коэффициенты j вместе и коэффициенты k вместе и сложите их все.
Обратите внимание, что это скалярное число (не вектор).
Запишем скалярное произведение двух векторов a и b как a · b .
Пример
Если a = i + 4 j — 2 k и b = 2 i + 4 j + 6 k , то a · b = 2 + 16 — 12 = 6
Угол между двумя векторами
Мы можем использовать скалярное произведение, чтобы найти угол между двумя векторами, благодаря следующей формуле:
Важным фактом является то, что два вектора перпендикулярны (ортогональны) тогда и только тогда, когда их скалярное произведение равно нулю.Это потому, что если q = 90 градусов выше, то a · b = 0.
В этом видео рассматриваются векторы и скаляры.
youtube.com/embed/Ea4SLWR0Z3E»>Величина и направление векторов
Величина вектора
Величина вектора
п
Q
→
это расстояние между начальной точкой
п
и конечная точка
Q
. В символах величина
п
Q
→
записывается как
|
п
Q
→
|
.
Если заданы координаты начальной и конечной точек вектора,
Формула расстояния
можно использовать для определения его величины.
|
п
Q
→
|
знак равно
(
Икс
2
—
Икс
1
)
2
+
(
y
2
—
y
1
)
2
Пример 1:
Найдите величину вектора
п
Q
→
чья начальная точка
п
Я сидел
(
1
,
1
)
и конечная точка находится в
Q
Я сидел
(
5
,
3
)
.
Решение:
Используйте формулу расстояния.
Подставьте значения
Икс
1
,
y
1
,
Икс
2
, а также
y
2
.
|
п
Q
→
|
знак равно
(
5
—
1
)
2
+
(
3
—
1
)
2
знак равно
4
2
+
2
2
знак равно
16
+
4
знак равно
20
≈
4.5
Величина
п
Q
→
около
4.5
.
Направление вектора
Направление вектора — это мера угла, который он образует с
горизонтальная линия
.
Для определения направления вектора можно использовать одну из следующих формул:
загар
θ
знак равно
y
Икс
, где
Икс
горизонтальное изменение и
y
это вертикальное изменение
или же
загар
θ
знак равно
y
2
—
y
1
Икс
2
—
Икс
1
, где
(
Икс
1
,
y
1
)
начальная точка и
(
Икс
2
,
y
2
)
конечная точка.
Пример 2:
Найдите направление вектора
п
Q
→
чья начальная точка
п
Я сидел
(
2
,
3
)
и конечная точка находится в
Q
Я сидел
(
5
,
8
)
.
Даны координаты начальной и конечной точек.Подставьте их в формулу
загар
θ
знак равно
y
2
—
y
1
Икс
2
—
Икс
1
.
загар
θ
знак равно
8
—
3
5
—
2
знак равно
5
3
Найдите обратный загар и воспользуйтесь калькулятором.
θ
знак равно
загар
—
1
(
5
3
)
≈
59
°
Вектор
п
Q
→
имеет направление около
59
°
.
Векторные уравнения
Угол между двумя плоскостями
Найден угол между двумя плоскостями
используя скалярное произведение.
Он равен острому углу, определяемому по
векторы нормали к плоскостям.
Пример
Рассчитать угол между плоскостями
π 1 : х + 2y -2z = 5
и π 2 : 6x -3y + 2z = 8
Расстояние между параллельными плоскостями
Пусть P будет точкой на плоскости π 1 : ax + by + cz = n
а.х = п
а Q — точка на плоскости π 2 : ax + by + cz = m
п. X =
м
Поскольку плоскости параллельны, они имеют общую нормаль: a
a = (a i + b j + c k )
Расстояние между самолетами
Пример
Рассчитать расстояние между плоскостями
π 1 : x + 2y — 2z = 5
и π 2 : 6x + 12y — 12z = 8
Копланарные векторы
Если существует связь между векторами a , b и c
так что c = λ a + μ b , где λ и μ — константы ,
, тогда векторы a, b и c копланарны.
Если три вектора копланарны,
c = λ a + μ b
Векторное уравнение плоскости
Из копланарного сечения выше
c = λ a + μ b
Когда используются векторы положения,
r = (1-λ-u) a + λ b + μ c — векторное уравнение плоскости .
Так как λ и b переменные, будет много возможных уравнений для плоскости.
Эффекты изменения λ и μ
Пример
Найдите векторное уравнение плоскости через точки
A (-1, -2, -3), B (-2,0,1) и C (-4, -1, -1)
Если λ = 2 и μ = 3
Когда A — известная точка на плоскости,
R — любая старая точка на плоскости, а b и c — векторы
.
параллельно плоскости,
векторное уравнение плоскости :
r = a + λ b + μ c
Уравнения линии
Линия может быть описана, когда на ней есть точка и
его вектор направления — вектор, параллельный прямой — известны.
На схеме ниже линия L проходит
через точки
A (x 1 , y 1 , z 1 ) и P (x, y, z).
u — вектор направления a i + b j + c k
Находясь на линии, он имеет то же направление, что и
любая параллельная линия.
O — происхождение.
a и p представляют собой векторы положения A и P.
Пример
Найдите векторное уравнение прямой, проходящей через
(3,2,1), которая параллельна вектору 2 i +3 j +4 k
Пример
Найти векторную форму уравнения
прямая, которая имеет параметрические уравнения
Пример
Найдите декартову форму прямой, у которой
вектор положения 3 i +2 j + k и параллелен
вектор i — j + k
Пример
Найдите векторное уравнение прямой, проходящей через
через A (1,2,3) и B (4,5,6)
Пример
Пример
Угол между прямой и плоскостью
Угол θ между прямой и плоскостью равен
дополнение угла между линией и
нормаль к плоскости.
Если линия имеет вектор направления u и
перпендикулярно плоскости a, затем
Пример
1)
2)
Пересечение двух прямых
Пример
Пересечение двух плоскостей
Найти уравнения линии пересечения
двух плоскостей, вектора направления и точки
на линии не требуется.
Поскольку линия пересечения лежит в обеих плоскостях,
вектор направления параллелен векторным произведениям
нормали каждой плоскости.
Пример
Найдите уравнение для линии пересечения
самолетов
-3x + 2y + z = -5
7x + 3y — 2z = -2
Расстояние от точки до плоскости
Чтобы найти расстояние от точки P до плоскости
- Найдите уравнение проекции PP ’, используя
нормаль к плоскости и точка P. - Найдите координаты P ’, перекресток
с самолетом. - Примените формулу расстояния к PP ’
Альтернативно
Пример
Найти расстояние между точкой (3,1, -2)
а плоскость x + 2y + 2z = — 4
Альтернативно
Расстояние от точки до линии
Чтобы найти расстояние от точки P до линии L
- Пусть линия имеет вектор направления u и параметр λ
- Найдите координаты PP ’, используя скалярное произведение с u
и точка P.
- Примените формулу расстояния к PP ’
Пересечение трех плоскостей
Чтобы решить пересечение,
использовать уравнения плоскости ax + by + cz + d = 0
для формирования расширенной матрицы, которая решается
для x, y и z.
Пересечение трех плоскостей может быть:
Одна точка
Найдено уникальное решение
Пример
Линия пересечения
Существует бесконечное количество решений
Пример
Параметрические уравнения
Две линии пересечения
Бесконечное количество решений
Пример
Использование второй строки
Заменить в первую строку
Подставить в третье уравнение
Три линии пересечения
Аналогично описанному выше.
Осмотрите каждую пару самолетов по очереди.
Пример
Плоскость пересечения
Два повторяющихся уравнения
Пример
Нет согласованности
Перекресток запрещен
Пример
Нет согласованности
Все плоскости параллельны
© Александр Форрест
Что такое вектор в математике? Список основных векторных формул и частей вектора
Что такое вектор?
Векторы могут быть определены несколькими способами в зависимости от контекста, в котором они используются. Вектор имеет как величину, так и направление, которое показано над направленным отрезком линии, где длина обозначает величину вектора, а стрелка указывает направление от хвоста к голове.
Вектор имеет как величину, так и направление, которое показано над направленным отрезком линии, где длина обозначает величину вектора, а стрелка указывает направление от хвоста к голове.
Два вектора похожи, если они имеют одинаковую величину и направление. Величина или направление вектора относительно положения не меняется. Но если вы растянете или переместите вектор от головы или хвоста, то изменится и величина, и направление.
Другими словами, вектор — это величина, имеющая как величину, так и направление.Есть скалярные величины, которые имеют только величину и измеряются вектором. Вектор важен не только в математике, но и в физике, такой как воздухоплавание, космос, путеводитель и т. Д. Пилоты используют векторные величины, сидя в самолете и безопасно перемещая его в другом направлении.
Если вы уверены в определении вектора и его использовании, следующим важным шагом будет изучение представления векторов. Они представлены в виде луча и пишутся строчными или прописными буквами. Как правило, один вектор представлен в обеих формах — алфавитах в верхнем и нижнем регистре. Если вектор записан в виде AB, то A — это хвост, а B — голова.
Как правило, один вектор представлен в обеих формах — алфавитах в верхнем и нижнем регистре. Если вектор записан в виде AB, то A — это хвост, а B — голова.
Список основных векторных формул
Векторы делятся на две основные категории: одна — это скалярное произведение, а другая — кросс-произведение. Список основных формул доступен для обеих категорий для решения геометрического преобразования в 2-х и 3-х измерениях. Эти формулы часто используются в физике и математике.{-1} \ frac {y} {x} \]
Части векторов
Части в векторах принимаются за углы, направленные к осям координат. Например, если какой-то вектор направлен на северо-запад, то его части будут вектором на запад и вектором на север. Итак, векторы делятся на две части, в основном, где имена могут быть разными, но концепция одинакова.
Зачем студентам нужны векторные формулы?
Изучив старые книги по геометрии, вы узнаете об эволюции векторов в алгебре и о том, как это полезно для студентов. Векторы изначально были названы алгеброй отрезков и ориентированы на перемещения. Давайте посмотрим на некоторые преимущества, по которым студенты должны изучать векторы в школе, а также во время учебы в высших учебных заведениях.
Векторы изначально были названы алгеброй отрезков и ориентированы на перемещения. Давайте посмотрим на некоторые преимущества, по которым студенты должны изучать векторы в школе, а также во время учебы в высших учебных заведениях.
Векторы важны как для физики, так и для математики, и было обнаружено, что они упрощают преобразование геометрии. Это означает, что можно быстро получить представление о геометрии и освоить важную часть линейной алгебры. Популярное применение векторов включает в себя механику частиц, механику жидкости, планарное описание, расчет траекторий, трехмерное движение и т. Д.
Другая область, где используются векторы, — это электромагнетизм, аналитическая геометрия, координатная геометрия и т. Д. С четким пониманием векторов студенты не только продвигаются в своей карьере, но и сдают различные конкурсные экзамены.
Введение, формула, свойства, решаемые примеры и часто задаваемые вопросы
Математическое представление физических величин, для которых можно определить как величину, так и направление, называется вектором. Вектор любой физической величины представлен в виде прямой линии со стрелкой. В векторном определении длина прямой линии обозначает величину вектора, а острие стрелки указывает его направление. Любые два вектора можно рассматривать как идентичные векторы, если они имеют одинаковую величину и направление. Лучшим примером вектора является сила, приложенная к объекту, потому что и сила, и направление приложенной силы влияют на ее действие на объект. Вращение или перемещение вектора вокруг себя никогда не изменит его величину.Изображение будет скоро загружено.
Вектор любой физической величины представлен в виде прямой линии со стрелкой. В векторном определении длина прямой линии обозначает величину вектора, а острие стрелки указывает его направление. Любые два вектора можно рассматривать как идентичные векторы, если они имеют одинаковую величину и направление. Лучшим примером вектора является сила, приложенная к объекту, потому что и сила, и направление приложенной силы влияют на ее действие на объект. Вращение или перемещение вектора вокруг себя никогда не изменит его величину.Изображение будет скоро загружено.
Vector Math
Vector Math находит широкий спектр приложений в различных областях алгебры, геометрии и физики. Как обсуждалось выше, вектор представлен в виде прямой линии со стрелкой. Конечные точки вектора обычно обозначаются заглавными буквами английского алфавита. Векторы символически представлены в виде конечных точек со стрелкой или строчной буквы со стрелкой. Изображение будет скоро загружено.
В приведенном выше векторе область, заключенная в скобку-цветок, указывает величину вектора, а острие стрелки указывает направление вектора. Этот вектор символически представлен как \ [\ overline {AB} \] или \ [\ overrightarrow {a} \]. Величина этого вектора задается как | AB | или | a |. Он представляет собой длину вектора и обычно вычисляется с помощью теоремы Пифагора. Основные математические операции, такие как сложение, вычитание и умножение, могут выполняться над векторами.Однако разделение двух векторов невозможно.
Словарь векторов:
Наиболее важные термины, связанные с векторами:
Нулевой вектор: вектор с нулевой величиной.
Единичный вектор: вектор с величиной, равной одной единице.
Вектор положения: вектор, обозначающий положение точки относительно ее начала координат.

Co Начальный вектор: два или более вектора с одной и той же начальной точкой.
Подобные и отличные векторы: Векторы с одинаковым направлением называются одинаковыми векторами, а векторы с разными направлениями называются разными векторами.
Копланарные векторы: векторы в одной плоскости.
Коллинеарный вектор: векторы, лежащие на одной прямой.
Равные векторы: два или более вектора с одинаковой величиной и направлением.
Вектор смещения: Вектор, указывающий смещение объекта из одной точки в другую.
Отрицательный вектор: Отрицательным для любого вектора является другой вектор с той же величиной, но в противоположном направлении.

Математические операции с вектором
1. Сложение вектора
Сложение вектора выполняется с любыми двумя векторами с использованием треугольного закона сложения векторов. Согласно этому закону, два добавляемых вектора представлены двумя сторонами треугольника с одинаковой величиной и направлением. Третья сторона дает величину и направление результирующего вектора сложения.Изображение будет скоро загружено.
2. Вычитание вектора
Рассмотрим два вектора a и b. Если вектор «a» должен быть вычтен из вектора «b», необходимо найти отрицательное значение вектора «a», и его следует добавить к вектору «b», используя закон треугольника.
3. Умножение векторов
Умножение любых двух векторов выполняется путем нахождения их «перекрестного произведения» или «скалярного произведения».
a b = | a || b | sin θ n̂ где, | a | величина вектора ‘a’ | b | — величина вектора ‘b’ θ — угол разделения двух векторов ‘a’ и ‘b’ n̂ — единичный вектор, представляющий направление умножения векторов |
a. где, | a | величина вектора ‘a’ | b | — величина вектора «b» θ — угол разделения двух векторов «a» и «b» |
Произведение двух векторов является векторной величиной. Он имеет как величину, так и направление, тогда как скалярное произведение двух векторов имеет только величину и не имеет направления. Итак, это скалярная величина.
Примеры векторной математики:
1.Найдите результирующий вектор сложения вектора a = (8,13) и вектора b = (12, 15).
Решение: вектор сложения ‘a’ и ‘b’, полученный как
c = a + b
c = (8, 13) + (12, 15)
c = (8 + 12) + ( 13 + 15)
c = (20, 27)
2. В одном из векторных вопросов k = (3, 4) и m = (7, 9). Вычтите вектор «k» из вектора «m».
Решение: Чтобы вычесть вектор «k» из вектора «m», необходимо найти отрицательный вектор «k».
Отрицательный вектор k = — k
= — (3, 4)
= (-3, -4)
Вычитание вектора k из вектора m дается как:
m — k = m + (-k)
= (7, 9) + (-3, -4)
= (7-3), (9-4)
= (4, 5)
3.{o} \]
\ [a \ cdot b = 63 \ times 0 \]
\ [a \ cdot b = 0 \ text {units} \]
Интересные факты:
Любой геометрический объект, который имеет как величину, так и направление, называется евклидовым вектором.
Матрицы также можно использовать с помощью определения вектора. Любая матрица с одной строкой или одним столбцом называется вектором-строкой или вектором-столбцом соответственно.
Векторный анализ | математика | Британника
Векторный анализ , раздел математики, который имеет дело с величинами, которые имеют как величину, так и направление. Некоторые физические и геометрические величины, называемые скалярами, можно полностью определить, указав их величину в подходящих единицах измерения. Таким образом, масса может быть выражена в граммах, температура — в градусах по некоторой шкале, а время — в секундах. Скаляры могут быть представлены графически точками на некоторой числовой шкале, такой как часы или термометр. Также существуют величины, называемые векторами, которые требуют указания направления, а также величины. Скорость, сила и смещение являются примерами векторов.Векторная величина может быть представлена графически направленным линейным сегментом, обозначенным стрелкой, указывающей в направлении векторной величины, при этом длина сегмента представляет величину вектора.
Некоторые физические и геометрические величины, называемые скалярами, можно полностью определить, указав их величину в подходящих единицах измерения. Таким образом, масса может быть выражена в граммах, температура — в градусах по некоторой шкале, а время — в секундах. Скаляры могут быть представлены графически точками на некоторой числовой шкале, такой как часы или термометр. Также существуют величины, называемые векторами, которые требуют указания направления, а также величины. Скорость, сила и смещение являются примерами векторов.Векторная величина может быть представлена графически направленным линейным сегментом, обозначенным стрелкой, указывающей в направлении векторной величины, при этом длина сегмента представляет величину вектора.
Подробнее по этой теме
аналитическая геометрия: векторный анализ
В евклидовом пространстве любой размерности векторы — направленные отрезки прямых — можно задавать координатами.Набор из n элементов (a1, …
Векторная алгебра.

Прототипом вектора является направленный отрезок линии A B (, см. Рисунок 1), который, как можно представить, представляет смещение частицы из ее начального положения A, в новое положение B . Чтобы отличать векторы от скаляров, принято обозначать векторы жирными буквами. Таким образом, вектор A B на рисунке 1 может быть обозначен как a , а его длина (или величина) — как | а |.Во многих задачах положение начальной точки вектора несущественно, поэтому два вектора считаются равными, если они имеют одинаковую длину и одинаковое направление.
Рисунок 1. Закон параллелограмма для сложения векторов
Encyclopædia Britannica, Inc.
Равенство двух векторов a и b обозначается обычным символическим обозначением a = b , а полезные определения элементарных алгебраических операций над векторами подсказывает геометрия.Таким образом, если A B = , а на рисунке 1 представляет смещение частицы от A до B , а затем частица перемещается в положение C , так что B C = b , ясно, что смещение от A до C может быть выполнено за одно смещение A C = c . Таким образом, логично записать a + b = c .Это построение суммы c , a и b дает тот же результат, что и закон параллелограмма, в котором результирующее c задается диагональю A C параллелограмма, построенного на векторах. A B и A D как стороны. Поскольку положение начальной точки B вектора B C = b несущественно, отсюда следует, что B C = A D .На рисунке 1 показано, что A D + D C = A C , так что коммутативный закон
Таким образом, логично записать a + b = c .Это построение суммы c , a и b дает тот же результат, что и закон параллелограмма, в котором результирующее c задается диагональю A C параллелограмма, построенного на векторах. A B и A D как стороны. Поскольку положение начальной точки B вектора B C = b несущественно, отсюда следует, что B C = A D .На рисунке 1 показано, что A D + D C = A C , так что коммутативный закон
Получите подписку Britannica Premium и получите доступ к эксклюзивному контенту.
Подпишитесь сейчас
используется для сложения векторов. Кроме того, легко показать, что ассоциативный закон
действительно, поэтому скобки в (2) можно опустить без каких-либо двусмысленностей.
Если s является скаляром, s a или a s определяется как вектор, длина которого | с || a | и направление которого совпадает с направлением a , когда s, положительно, и противоположно направлению a , если s, отрицательно.Таким образом, a и — a являются векторами, равными по величине, но противоположными по направлению. Приведенные выше определения и хорошо известные свойства скалярных чисел (представленных s и t ) показывают, что
Поскольку законы (1), (2) и (3) идентичны законам, встречающимся в обычной алгебре, вполне уместно использовать знакомые алгебраические правила для решения систем линейных уравнений, содержащих векторы. Этот факт позволяет вывести чисто алгебраическими средствами многие теоремы синтетической евклидовой геометрии, требующие сложных геометрических построений.
Произведения векторов.
Умножение векторов приводит к двум типам произведений: скалярному произведению и перекрестному произведению.
Точечное или скалярное произведение двух векторов a и b , записанное a · b , является действительным числом | a || b | cos ( a , b ), где ( a , b ) обозначает угол между направлениями a и b . Геометрически,
Если a и b расположены под прямым углом, тогда a · b = 0, и если ни a , ни b не является нулевым вектором, то исчезновение скалярного произведения показывает, что векторы перпендикуляр.Если a = b , то cos ( a , b ) = 1 и a · a = | a | 2 дает квадрат длины a .
Ассоциативные, коммутативные и дистрибутивные законы элементарной алгебры действительны для умножения векторов на точки.
Перекрестное или векторное произведение двух векторов a и b , записанное a × b , является вектором
, где n — вектор единичной длины, перпендикулярный плоскости a и b и направленный таким образом, что правый винт, повернутый от a к b , будет продвигаться в направлении n ( см. Рисунок 2).Если a и b параллельны, a × b = 0. Величина a × b может быть представлена площадью параллелограмма, имеющей соседние a и b . стороны. Кроме того, поскольку вращение от b к a противоположно вращению от a к b ,
Рисунок 2).Если a и b параллельны, a × b = 0. Величина a × b может быть представлена площадью параллелограмма, имеющей соседние a и b . стороны. Кроме того, поскольку вращение от b к a противоположно вращению от a к b ,
Рисунок 2: Перекрестное произведение, образованное умножением двух векторов
Encyclopædia Britannica, Inc.
Это показывает, что перекрестное произведение не коммутативно, а ассоциативный закон ( s a ) × b = s ( a × b ) и закон распределения
действительны для перекрестных произведений.
Системы координат.
Поскольку эмпирические законы физики не зависят от специального или случайного выбора систем отсчета, выбранных для представления физических отношений и геометрических конфигураций, векторный анализ является идеальным инструментом для изучения физической вселенной. Введение специальной системы отсчета или системы координат устанавливает соответствие между векторами и наборами чисел, представляющими компоненты векторов в этой системе координат, и вводит определенные правила работы с этими наборами чисел, которые следуют из правил операций на линии сегменты.
Введение специальной системы отсчета или системы координат устанавливает соответствие между векторами и наборами чисел, представляющими компоненты векторов в этой системе координат, и вводит определенные правила работы с этими наборами чисел, которые следуют из правил операций на линии сегменты.
Если выбран какой-то конкретный набор из трех неколлинеарных векторов (называемых базовыми векторами), то любой вектор A может быть однозначно выражен как диагональ параллелепипеда, ребра которого являются компонентами A в направлениях базовых векторов.Обычно используется набор из трех взаимно ортогональных единичных векторов (, т. Е. векторов длины 1) i , j , k , направленных вдоль осей знакомой декартовой системы отсчета ( см. Рисунок 3). . В этой системе выражение принимает вид
Рисунок 3: Разрешение вектора на три взаимно перпендикулярных компонента
Encyclopædia Britannica, Inc.
, где x , y и z — это проекции A на оси координат. Когда два вектора A 1 и A 2 представлены как
Когда два вектора A 1 и A 2 представлены как
, то использование законов (3) дает для их суммы
Таким образом, в декартовой системе отсчета сумма A 1 и A 2 является вектором, определяемым ( x 1 + y 1 , x 2 + y 2 , x 3 + y 3 ).Также скалярное произведение можно записать
с
Использование закона (6) дает
, так что векторное произведение представляет собой вектор, определяемый тройкой чисел, появляющихся как коэффициенты i , j и k в (9).
Если векторы представлены матрицами 1 × 3 (или 3 × 1), состоящими из компонентов ( x 1 , x 2 , x 3 ) векторов, можно перефразировать формулы (7) — (9) на языке матриц.Такая перефразировка предполагает обобщение концепции вектора на пространства размерности выше трех. Например, состояние газа обычно зависит от давления p , объема v , температуры T и времени t . Четверка чисел ( p , v , T , t ) не может быть представлена точкой в трехмерной системе отсчета. Но поскольку геометрическая визуализация не играет роли в алгебраических вычислениях, образный язык геометрии все еще можно использовать, введя четырехмерную систему отсчета, определяемую набором базовых векторов a 1 , a 2 , a 3 , a 4 с компонентами, определяемыми строками матрицы
Например, состояние газа обычно зависит от давления p , объема v , температуры T и времени t . Четверка чисел ( p , v , T , t ) не может быть представлена точкой в трехмерной системе отсчета. Но поскольку геометрическая визуализация не играет роли в алгебраических вычислениях, образный язык геометрии все еще можно использовать, введя четырехмерную систему отсчета, определяемую набором базовых векторов a 1 , a 2 , a 3 , a 4 с компонентами, определяемыми строками матрицы
Затем вектор x представляется в виде
.
, так что в четырехмерном пространстве каждый вектор определяется четверкой компонентов ( x 1 , x 2 , x 3 , x 4 ).
Исчисление векторов.
Частица, движущаяся в трехмерном пространстве, может быть расположена в каждый момент времени t с помощью вектора положения r , проведенного из некоторой фиксированной опорной точки O . Поскольку положение конечной точки r зависит от времени, r является векторной функцией t . Его компоненты в направлениях декартовых осей, представленные в O , являются коэффициентами i , j и k в представлении
Поскольку положение конечной точки r зависит от времени, r является векторной функцией t . Его компоненты в направлениях декартовых осей, представленные в O , являются коэффициентами i , j и k в представлении
.
Если эти компоненты являются дифференцируемыми функциями, производная r относительно t определяется по формуле
, который представляет скорость частицы v .Декартовы компоненты v появляются как коэффициенты i , j и k в (10). Если эти компоненты также дифференцируются, ускорение a = d v / d t получается путем дифференцирования (10):
Правила дифференцирования произведений скалярных функций остаются в силе для производных точечных и перекрестных произведений векторных функций, а подходящие определения интегралов векторных функций позволяют построить исчисление векторов, которое стало основным аналитическим инструментом в физических науках. и технологии.
и технологии.
Узнайте больше в этих связанных статьях Britannica:
аналитическая геометрия: векторный анализ
В евклидовом пространстве любой размерности векторы — направленные отрезки прямых — можно задавать координатами. Кортеж из n элементов ( 1 ,…, n ) представляет вектор в n-мерном пространстве, который проецируется на действительные числа a 1 ,…, n на осях координат.…
математика: линейная алгебра
Уиллард Гиббс занялся векторным анализом и смог распространить векторные методы на вычисления. Таким образом, они ввели меры бесконечно малых изменений векторного поля, которые под названиями div, grad и curl стали стандартными инструментами в изучении электромагнетизма и потенциала …
механика: Векторы
… и Британия соответственно) каждый из них применял векторный анализ, чтобы помочь выразить новые законы электромагнетизма, предложенные Джеймсом Клерком Максвеллом.
 …
…
Умножение векторов
Векторы — что это такое? дает введение в
предмет.
Есть два полезных определения умножения векторов в
в одном произведение — скаляр, а в другом — произведение
вектор. Нет операции деления векторов. В некоторых
школьные программы вы встретите скалярные произведения, но не векторные
продуктов, но мы обсуждаем оба типа умножения векторов в
в этой статье, чтобы дать более полное представление об основах
субъект
Скалярное умножение
Скалярное произведение
векторы $ {\ bf u} = (u_1, u_2, u_3) $ и $ {\ bf v} = (v_1, v_2, v_3) $
— скаляр, определенный как $$ {\ bf u.2 \ quad (2), $$ и если $ {\ bf i, j, k} $ — единичные векторы вдоль
оси тогда $$ {\ bf i.i} = {\ bf j.j} = {\ bf k.k} = 1, \ quad {\ rm
и} \ quad {\ bf i.j} = {\ bf j.k} = {\ bf k.i} = 0 \ quad (3). $$ Это
оставлено читателю, чтобы проверить из определения, что $$ {\ bf u.v} =
{\ bf v.u}, \ {\ rm и} \ ({\ bf u + v}). {\ bf w} = {\ bf u.w} + {\ bf
{\ bf w} = {\ bf u.w} + {\ bf
v.w}. $$ Это показывает, что мы можем расширять или умножать $$ {\ bf u.v} =
(u_1 {\ bf i} + u_2 {\ bf j} + u_3 {\ bf k}). (v_1 {\ bf i} + v_2 {\ bf j} + u_3 {\ bf
k}) $$ дает девять терминов. Используя уравнение (3), шесть из этих членов равны
ноль, а остальные три дают выражение $ u_1v_1 + u_2v_2 + u_3v_3 $
в соответствии с определением в уравнении (1).{-1} \ left ({{\ bf u.v} \ over | {\ bf
u} ||| {\ bf v} |} \ right) \ quad (7). $$ В трех измерениях мы можем использовать
более интуитивное определение угла с точки зрения поворота, но в
более высокие размеры необходимо иметь определение угла
такие как формула (7). Если мы воспользуемся этой формулой для определения угла, тогда
Правило косинуса следует прямо, поскольку они эквивалентны.
Обратите внимание, что произведение вектора-строки и вектора-столбца равно
определяется в терминах скалярного произведения, и это согласуется с
матричное умножение.$$ (u_1 \ u_2 \ u_3) \ left (\ begin {array} {cc}
v_1 \\ v_2 \\ v_3 \ end {array} \ right) = u_1v_1 + u_2v_2 +
u_3v_3. $$
$$
Векторное умножение
Векторное произведение двух
векторы $ {\ bf b} $ и $ {\ bf c} $, записываемые как $ {\ bf b} \ times {\ bf c} $
(и иногда называют крестом
product), это вектор $$ {\ bf b} \ times {\ bf c} = \ left (
\ begin {array} {cc} b_2c_3-b_3c_2 \\ b_3c_1 -b_1c_3 \\ b_1c_2 -b_2c_1
\ end {array} \ right) \ quad (8). $$ Существует альтернативное определение
векторного произведения, а именно, что $ {\ bf b} \ times {\ bf c} $ является
вектор величины $ | {\ bf b} || {\ bf c} | \ sin \ theta $ перпендикулярно
$ {\ bf b} $ и $ {\ bf c} $ и подчиняясь «правилу правой руки», и
докажем, что этот результат следует из данного определения
и что эти два определения эквивалентны.Приведено доказательство
позже для полноты, но сначала мы рассмотрим $ {\ bf b} \ times {\ bf
c} $ выражается через компоненты в направлениях $ {\ bf i,
j, k} $.
Из этого определения видно, что $ {\ bf b} \ times {\ bf c} = — {\ bf
c} \ times {\ bf b} $, поэтому эта операция не коммутативна. Если $ {\ bf i,
Если $ {\ bf i,
j, k} $ — единичные векторы вдоль осей, тогда из этого определения:
$$ {\ bf i} \ times {\ bf i} = {\ bf j} \ times {\ bf j} = {\ bf k} \ times {\ bf
k}, $$ и $$ \ eqalign {{\ bf i} \ times {\ bf j} & = {\ bf k}, \ quad
{\ bf j} \ times {\ bf i} = — {\ bf k} \ cr {\ bf j} \ times {\ bf k} & =
{\ bf i}, \ quad {\ bf k} \ times {\ bf j} = — {\ bf i} \ cr {\ bf k} \ times
{\ bf i} & = {\ bf j}, \ quad {\ bf i} \ times {\ bf k} = — {\ bf j}.} $$
Из определения следует, что $$ k ({\ bf b} \ times {\ bf c}) =
(k {\ bf b}) \ times {\ bf c} = {\ bf b} \ times (k {\ bf c}), \ quad \ quad
({\ bf a + b}) \ times {\ bf c} = ({\ bf a} \ times {\ bf c}) + ({\ bf
b} \ times {\ bf c}). $$ Расширение выражения $$ {\ bf b} \ times {\ bf
c} = (b_1 {\ bf i} + b_2 {\ bf j} + b_3 {\ bf k}) \ times (c_1 {\ bf i} +
c_2 {\ bf j} + c_3 {\ bf k}) $$ дает $$ (b_2c_3-b_3c_2) {\ bf i} +
(b_3c_1-b_1c_3) {\ bf j} + (b_1c_2-b_2c_1) {\ bf k} \ quad (9) $$ который
— формула для векторного произведения, заданная в уравнении (8).
Теперь мы докажем, что два определения умножения векторов
эквивалент. На схеме показаны направления векторов $ {\ bf
b} $, $ {\ bf c} $ и $ {\ bf b} \ times {\ bf c} $, которые образуют правую
вручил набор ».
Вы можете закончить чтение здесь, и это действительно больше
важно понимать, что есть два определения вектора
продукт, который может быть доказан как эквивалентный, чем он
механически проработать детали доказательства.
Теорема Вектор
произведение двух векторов $ {\ bf b} $ и $ {\ bf c} $ является вектором $ {\ bf
b} \ times {\ bf c} $ со следующими свойствами:
(i) $ {\ bf b} \ times {\ bf c} $ имеет
величина $ | {\ bf b} || {\ bf c} | \ sin \ theta $, где $ \ theta $ —
угол между направлениями $ {\ bf b} $ и $ {\ bf c} $;
(ii) $ {\ bf b} \ times {\ bf c} $ — это
перпендикулярно $ {\ bf b} $ и $ {\ bf c} $ с направлением, таким, что
векторы $ {\ bf b} $, $ {\ bf c} $ и $ {\ bf b} \ times {\ bf c} $ образуют
правый набор, как на схеме, так что $ {\ bf b} \ times {\ bf c} $
и $ {\ bf c} \ times {\ bf b} $ направлены в противоположные стороны.
Векторная геометрия — линейная алгебра с приложениями
Перейти к содержимому
В этой главе мы изучаем геометрию трехмерного пространства. Мы рассматриваем точку в трехмерном пространстве как стрелку из начала координат в эту точку. Это дает «картину» сути дела, которая действительно стоит тысячи слов.
векторов в
Ввести систему координат в трехмерном пространстве обычным способом. Сначала выберите точку, называемую , затем выберите три взаимно перпендикулярные линии, проходящие через , называемые , и , и установите числовую шкалу на каждой оси с нулем в начале координат. Данной точке в -пространстве мы связываем три числа , и с , как показано на рисунке 4.1.1.
Эти числа называются числом , и мы обозначаем точку как , или, чтобы подчеркнуть метку . Результат называется системой координат для трехмерного пространства, а результирующее описание трехмерного пространства называется .
Как и на плоскости, мы вводим векторы, отождествляя каждую точку с вектором
в , представленным от начала до, как на рисунке 4. 1.1. Неформально мы говорим, что точка имеет вектор , а этот вектор имеет точку . Таким образом, 3-пространство отождествляется с , и это отождествление будет проводиться на протяжении всей главы, часто без комментариев. В частности, термины «вектор» и «точка» взаимозаменяемы. Полученное описание трехмерного пространства называется . Обратите внимание, что происхождение .
1.1. Неформально мы говорим, что точка имеет вектор , а этот вектор имеет точку . Таким образом, 3-пространство отождествляется с , и это отождествление будет проводиться на протяжении всей главы, часто без комментариев. В частности, термины «вектор» и «точка» взаимозаменяемы. Полученное описание трехмерного пространства называется . Обратите внимание, что происхождение .
Длина и направление
Мы собираемся обсудить два фундаментальных геометрических свойства векторов в : длину и направление. Во-первых, если это вектор с точкой , вектор определяется как расстояние от начала координат до , то есть длина стрелки, представляющей . Следующие свойства длины будут часто использоваться.
Позвольте быть вектором.
- .
- тогда и только тогда, когда
- для всех скаляров.
Доказательство:
Пусть есть точка .
- На рис. 4.1.2 — гипотенуза прямоугольного треугольника , а значит, по теореме Пифагора.
 Но есть гипотенуза прямоугольного треугольника, значит. Теперь (1) следует путем исключения и извлечения положительных квадратных корней.
Но есть гипотенуза прямоугольного треугольника, значит. Теперь (1) следует путем исключения и извлечения положительных квадратных корней. - Если = 0, то по (1). Поскольку квадраты действительных чисел неотрицательны, отсюда следует, что и, следовательно, что . Обратное потому что.
- У нас так (1) дает
Следовательно, и мы закончили, потому что для любого действительного числа.
Если
, то . Точно так же, если
в 2-х пробелах, то .
Когда мы рассматриваем два ненулевых вектора как стрелки, исходящие из начала координат, геометрически ясно, что мы имеем в виду, говоря, что они имеют одинаковые или противоположные . Это приводит к принципиально новому описанию векторов.
Позвольте и быть векторами в . Тогда как матрицы тогда и только тогда, когда и имеют одинаковое направление и одинаковую длину.
Доказательство:
Если , они явно имеют одинаковое направление и длину. Обратно, пусть и — векторы с точками и соответственно. Если и имеют одинаковую длину и направление, то геометрически и должны быть одной и той же точкой.
Обратно, пусть и — векторы с точками и соответственно. Если и имеют одинаковую длину и направление, то геометрически и должны быть одной и той же точкой.
Отсюда , и , то есть .
Обратите внимание, что длина и направление вектора зависят от выбора системы координат в . Такие описания важны в приложениях, потому что физические законы часто формулируются в терминах векторов, и эти законы не могут зависеть от конкретной системы координат, используемой для описания ситуации.
Геометрические векторы
Если и являются различными точками в пространстве, стрелка от до имеет длину и направление.
Следовательно,
Предположим, что и любые две точки в . На рис. 4.1.4 отрезок от до обозначен и называется от до . Точка называется из , называется и обозначается .
Обратите внимание, что если любой вектор находится в точке с точкой, то он сам является геометрическим вектором, где находится начало координат. Обращение к «вектору» представляется оправданным в силу теоремы 4. 1.2, поскольку он имеет направление (от к ) и длину . Однако возникает проблема, поскольку два геометрических вектора могут иметь одинаковую длину и направление, даже если кончики и хвосты различны.
1.2, поскольку он имеет направление (от к ) и длину . Однако возникает проблема, поскольку два геометрических вектора могут иметь одинаковую длину и направление, даже если кончики и хвосты различны.
Например, и на рис. 4.1.5 имеют одинаковую длину и одинаковое направление (1 единица влево и 2 единицы вверх), поэтому по теореме 4.1.2 это один и тот же вектор! Наилучший способ понять этот кажущийся парадокс — это увидеть различия в одном и том же основном векторе. Когда это явление прояснено, это становится большим преимуществом, потому что, благодаря теореме 4.1.2, это означает, что один и тот же геометрический вектор может быть расположен в любом месте в пространстве; важна длина и направление, а не расположение кончика и хвоста. Эта возможность перемещать геометрические векторы очень полезна.
Закон параллелограмма
Теперь дадим внутреннее описание суммы двух векторов и в , то есть описание, зависящее только от длин и направлений, а не от выбора системы координат. Используя теорему 4.1.2, мы можем думать, что эти векторы имеют общий хвост. Если их кончики и соответственно, то они оба лежат в плоскости, содержащей , и , как показано на рисунке 4.1.6. Векторы и создают параллелограмм в , заштрихованный на рис. 4.1.6, называемый параллелограммом через и .
Используя теорему 4.1.2, мы можем думать, что эти векторы имеют общий хвост. Если их кончики и соответственно, то они оба лежат в плоскости, содержащей , и , как показано на рисунке 4.1.6. Векторы и создают параллелограмм в , заштрихованный на рис. 4.1.6, называемый параллелограммом через и .
Если мы теперь выберем систему координат на плоскости с началом, то закон параллелограмма на плоскости показывает, что их сумма является диагональю параллелограмма, который они определяют с хвостом . Это внутреннее описание суммы, поскольку оно не ссылается на координаты. Это обсуждение доказывает:
В параллелограмме, определяемом двумя векторами и , вектор является диагональю с тем же хвостом, что и .
Поскольку вектор можно расположить хвостом в любой точке, закон параллелограмма приводит к другому способу рассмотрения сложения векторов. На рис. 4.1.7 (а) сумма двух векторов и показана как заданная законом параллелограмма. Если его переместить так, чтобы его хвост совпал с кончиком (показан на (b)), то сумма видится как «сначала, а затем . Точно так же перемещение хвоста к кончику показывает в (с), что это «сначала, а затем». Это будет называться , и это дает наглядную иллюстрацию того, почему .
Точно так же перемещение хвоста к кончику показывает в (с), что это «сначала, а затем». Это будет называться , и это дает наглядную иллюстрацию того, почему .
Так как обозначает вектор из точки в точку , правило от кончика к хвосту принимает легко запоминающуюся форму
для любых точек , и .
Одна из причин важности правила «кончик к хвосту» заключается в том, что оно означает, что два или более вектора могут быть добавлены путем последовательного размещения их кончиком к хвосту. Это дает полезную «картину» суммы нескольких векторов и проиллюстрировано для трех векторов на рис. 4.1.8, где сначала рассматривается как , затем , затем .
Существует простой геометрический способ визуализации (матрицы) двух векторов. Если и расположены так, что у них есть общий хвост , и если и являются их соответствующими концами, то правило от кончика к хвосту дает . Следовательно, это вектор от кончика к кончику . Таким образом, оба и появляются как диагонали в параллелограмме, определяемом и (см. рис. 4.1.9.
Таким образом, оба и появляются как диагонали в параллелограмме, определяемом и (см. рис. 4.1.9.
Если и имеют общий хвост, то это вектор от вершины к вершине .
Одним из наиболее полезных применений вычитания векторов является то, что оно дает простую формулу для вектора из одной точки в другую и для расстояния между точками.
Пусть и две точки. Затем:
- .
- Расстояние между и равно
Можете ли вы доказать эти результаты?
Расстояние между и равно , а вектор от до равен
.
Следующая теорема говорит нам, что происходит с длиной и направлением скаляра, кратного данному вектору.
Если a — действительное число и вектор, то:
- Длина .
- Если , то направление такое же, как если бы ; напротив if
Доказательство:
Первое утверждение верно в силу теоремы 4.1.1.
Чтобы доказать второе утверждение, позвольте обозначить начало координат в Позвольте иметь точку и выбрать любую плоскость, содержащую и . Если мы установим систему координат на этой плоскости с началом, то такой результат следует из скалярного кратного закона на плоскости.
Если мы установим систему координат на этой плоскости с началом, то такой результат следует из скалярного кратного закона на плоскости.
Вектор называется if . Тогда
, и
являются единичными векторами, называемыми векторами.
Если показать, что это уникальный единичный вектор в том же направлении, что и
Решение:
Векторы в том же направлении, что и скалярные кратные, где . Но когда , то единичный вектор тогда и только тогда, когда .
Два ненулевых вектора вызываются, если они имеют одинаковое или противоположное направление.
Два ненулевых вектора и параллельны тогда и только тогда, когда один из них кратен другому.
Учитывая точки , , , и , определить, являются ли и параллельными.
Решение:
По теореме 4.1.3 и . Если
то , значит и , что невозможно. Следовательно, кратно , поэтому эти векторы не параллельны по теореме 4.1.5.
Линии в космосе
С помощью этих векторных методов можно очень просто описать прямые линии в пространстве. Для того, чтобы сделать это, нам сначала нужен путь к
Для того, чтобы сделать это, нам сначала нужен путь к
укажите ориентацию такой линии.
Мы называем ненулевой вектор вектором направления для прямой, если он параллелен для некоторой пары различных точек и на прямой.
Обратите внимание, что любой ненулевой скаляр, кратный , также будет служить вектором направления линии.
Мы используем тот факт, что существует ровно одна прямая, проходящая через конкретную точку и имеющая заданный вектор направления
. Мы хотим описать эту линию, задав условие на , и то, что точка лежит на этой линии. Пусть
и обозначают векторы и соответственно.
Затем
Следовательно, лежит на прямой тогда и только тогда, когда она параллельна — т. е. тогда и только тогда, когда для некоторого скаляра по теореме 4.1.5. Таким образом, вектор точки на линии тогда и только тогда, когда для некоторого скаляра .
Прямая, параллельная точке с вектором, задается как
Другими словами, точка с вектором находится на этой прямой тогда и только тогда, когда существует действительное число t такое, что .
В компонентной форме векторное уравнение становится
Приравнивание компонентов дает другое описание линии.
Прямая с вектором направления
задается как
Другими словами, точка находится на этой прямой тогда и только тогда, когда существует действительное число такое, что , , и .
Найдите уравнения прямой через точки и .
Решение:
Пусть
обозначает вектор от до . Тогда параллелен линии (и на линии), поэтому служит вектором направления для линии. Использование в качестве точки на линии приводит к параметрическим уравнениям
Обратите внимание, что если используется (а не ), уравнения равны
Они отличаются от предыдущих уравнений, но это просто результат изменения параметра. Фактически, .
Определить, пересекаются ли следующие прямые, и если да, то найти точку пересечения.
Решение:
Предположим, что вектор лежит на обеих линиях. Затем
Затем
где первое (второе) уравнение потому что лежит на первой (второй) строке. Следовательно, прямые пересекаются тогда и только тогда, когда три уравнения
есть решение. В этом случае и удовлетворяются все три уравнения, поэтому прямые пересекаются с , а точка пересечения равна
.
с использованием . Конечно, эту точку можно найти и от
с использованием .
Предположим, что даны точка и плоскость и требуется найти точку, лежащую на плоскости и ближайшую к , как показано на рис. 4.2.1.
Рисунок 4.2.1
Понятно, что требуется найти прямую, проходящую через нее, перпендикулярную плоскости, а затем получить как точку пересечения этой прямой с плоскостью. Для нахождения линии 90 247, перпендикулярной 90 248 плоскости, требуется способ определить, когда два вектора перпендикулярны. Это можно сделать, используя идею скалярного произведения двух векторов.
Скалярное произведение и углы
Для векторов
и
их скалярное произведение является числом, определенным
Поскольку это число, его иногда называют скалярным произведением и
. Если
и , то .
Пусть , и обозначают векторы в (или ).
- — действительное число.
- .
- .
- .
- для всех скаляров.
Читателям предлагается доказать эти свойства, используя определение скалярных произведений.
Убедитесь, что при , и .
Решение:
Применим теорему 4.2.1 несколько раз:
Существует внутреннее описание скалярного произведения двух ненулевых векторов в . Чтобы понять это, нам потребуется следующий результат из тригонометрии.
Если треугольник имеет стороны , , и , и если внутренний угол напротив, то
Рисунок 4.2.2
Доказательство:
Мы доказываем это, когда остро, то есть ; тупой случай аналогичен. На рис. 4.2.2 у нас есть и .
На рис. 4.2.2 у нас есть и .
Следовательно, теорема Пифагора дает
Закон косинусов следует, потому что для любого угла .
Обратите внимание, что закон косинусов сводится к теореме Пифагора, если угол прямой (потому что ).
Теперь пусть и ненулевые векторы, расположенные с общим хвостом. Затем они определяют уникальный угол в диапазоне
Этот угол будет называться углом между и . Ясно и параллельны, если есть или или . Обратите внимание, что мы не определяем угол между и, если один из этих векторов равен .
Следующий результат дает простой способ вычислить угол между двумя ненулевыми векторами с помощью скалярного произведения.
Пусть и ненулевые векторы. Если угол между и , то
Рисунок 4.2.4
Доказательство:
Мы рассчитываем двумя способами. Сначала примените закон косинусов к треугольнику на рис. 4.2.4, чтобы получить:
С другой стороны, мы используем теорему 4. 2.1:
2.1:
Сравнивая их, мы видим, что и результат следует.
Если и ненулевые векторы, теорема 4.2.2 дает внутреннее описание, поскольку , и угол между и не зависят от выбора системы координат. Более того, поскольку и ненулевые ( и ненулевые векторы), это дает формулу для косинуса угла:
Так как это можно использовать для поиска .
Вычислите угол между
и
.
Решение:
Вычислить . Теперь вспомним, что и определены так, что (, ) — точка на единичной окружности, определяемая углом (нарисованным против часовой стрелки, начиная с положительной оси). В данном случае мы знаем то и это. Потому что из этого следует.
Если и отличны от нуля, в предыдущем примере показано, что имеет тот же знак, что и , поэтому
В этом последнем случае (ненулевые) векторы перпендикулярны. В линейной алгебре используется следующая терминология:
Два вектора и называются \textbf{ортогональными}\index{ортогональными векторами}\index{векторами!ортогональными векторами}, если или или угол между ними равен .
Так как если либо или , то мы имеем следующую теорему:
Два вектора и ортогональны тогда и только тогда, когда .
Докажите, что точки , , и являются вершинами прямоугольного треугольника.
Решение:
Векторы вдоль сторон треугольника равны
Очевидно, что и являются ортогональными векторами. Это означает, что стороны и перпендикулярны, то есть угол в является прямым углом.
Проекции
В приложениях к векторам часто полезно записывать вектор как сумму двух ортогональных векторов.
Рисунок 4.2.5Если указан ненулевой вектор, основная идея состоит в том, чтобы иметь возможность записать произвольный вектор в виде суммы двух векторов,
где параллелен и ортогонален . Предположим, что и исходят из общего хвоста (см. рис. 4.2.5). Позвольте быть наконечником, и позвольте обозначать основание перпендикуляра от к линии через параллель к.
Тогда имеет необходимые свойства:
1. параллельно .
2. ортогонален .
3. .
Вектор на рис. 4.2.6 называется проекцией на .
Обозначается
На рис. 4.2.5 (а) вектор имеет то же направление, что и ; однако и иметь противоположные направления, если угол между и больше (см. рис. 4.2.5 (b)). Обратите внимание, что проекция равна нулю тогда и только тогда, когда и ортогональны.
Вычислить проекцию on очень легко.
Позвольте и быть векторами.
- Проекция на задается .
- Вектор ортогонален .
Доказательство:
Вектор параллелен и поэтому имеет форму для некоторого скаляра . Требование ортогональности и определяет . Фактически это означает, что по теореме 4.2.3. Если здесь подставляется, то условие равно
Отсюда следует, что , где допущение, гарантирующее, что .
Найти проекцию
на
и выразить, где параллельно и ортогонально .
Решение:
Проекция на
Следовательно, и это ортогонально по теореме 4.2.4 (в качестве альтернативы заметим, что ). Так как мы закончили.
Обратите внимание, что идею проекций можно использовать для нахождения кратчайшего расстояния от точки до прямой линии, в которой длина вектора ортогональна вектору направления линии.
Самолеты
Ненулевой вектор называется нормалью к плоскости, если он ортогонален каждому вектору на плоскости.
Например, единичный вектор является вектором нормали к плоскости.
Рис. 4.2.6Для данной точки и ненулевого вектора существует единственная плоскость, проходящая через нормаль , заштрихованная на рис. 4.2.6. Точка лежит на этой плоскости тогда и только тогда, когда вектор ортогонален ей, т. е. тогда и только тогда, когда . Потому что это дает следующий результат:
Плоскость, проходящая через нормаль
в качестве вектора нормали, определяется как
Другими словами, точка находится на этой плоскости тогда и только тогда, когда , , и удовлетворяют этому уравнению.
Найдите уравнение плоскости через
как обычно.
Решение:
Здесь общее скалярное уравнение принимает вид
Это упрощается до .
Если мы напишем , скалярное уравнение показывает, что каждая плоскость с нормальным
имеет линейное уравнение вида
(4.2)
для некоторой константы . И наоборот, график этого уравнения представляет собой плоскость с нормальным вектором (при условии, что , и не все равны нулю).
Найдите уравнение плоскости, через которую проходит параллельная плоскости с уравнением .
Решение:
Плоскость с уравнением имеет нормаль. Поскольку две плоскости параллельны, она служит нормалью к плоскости, которую мы ищем, поэтому уравнение для некоторых соответствует (4.2). Настаивая на том, что лежит на плоскости определяет ; то есть, . Следовательно, уравнение .
Рассмотрим точки и с векторами
и
.
Для вектора, отличного от нуля, скалярное уравнение плоскости с нормалью принимает векторную форму:
Плоскость с нормалью, проходящей через точку с вектором, определяется как
Другими словами, точка с вектором находится на плоскости тогда и только тогда, когда удовлетворяет этому условию.
Кроме того, уравнение (4.2) переводится следующим образом:
Каждая плоскость с нормалью имеет векторное уравнение для некоторого числа.
Найдите кратчайшее расстояние от точки до плоскости с помощью уравнения . Также найдите точку на этой плоскости, ближайшую к .
Решение:
У рассматриваемого самолета нормальный . Выберите любую точку на плоскости, скажем, и пусть это будет ближайшая к ней точка на плоскости (см. схему). Вектор от к равен . Теперь прямо с хвостом в . Тогда и проекция на :
Следовательно, расстояние равно . Для вычисления точки пусть
и
— векторы и . Затем
Это дает координаты .
Перекрестное произведение
Если , , и являются тремя различными точками, которые не все находятся на некоторой прямой, геометрически ясно, что существует единственная плоскость, содержащая все три. Векторы и оба лежат в этой плоскости, поэтому поиск нормали сводится к нахождению ненулевого вектора, ортогонального обоим и . Перекрестное произведение обеспечивает систематический способ сделать это.
Перекрестное произведение обеспечивает систематический способ сделать это.
Для заданных векторов и определите перекрестное произведение на
Поскольку это вектор, его часто называют векторным произведением . Существует простой способ запомнить это определение, используя вектора координат:
Это векторы длины, направленные вдоль положительных осей , и . Причина названия в том, что любой вектор можно записать как
.
Таким образом, векторное произведение можно описать следующим образом:
Если и два вектора, то
где определитель раскладывается по первому столбцу.
Если и , то
Обратите внимание, что это ортогонально обоим и в примере 4.2.11. В общем случае это верно, как можно проверить непосредственно вычислением и , и записано как первая часть следующей теоремы. Оно будет следовать из более общего результата, который вместе со второй частью будет доказан позже.
Позвольте и быть векторами в :
- является вектором, ортогональным обоим и .
- Если и отличны от нуля, то тогда и только тогда, когда и параллельны.
Напомним, что
Найдите уравнение плоскости через , , и .
Решение:
Векторы
и
лежат в плоскости, поэтому
— нормаль к плоскости (ортогональная к обоим и ). Следовательно, плоскость имеет уравнение
Так как лежит в плоскости у нас есть . Отсюда и уравнение. Можете ли вы проверить, что то же самое уравнение может быть получено, если и , или и , используются в качестве векторов на плоскости?
Перекрестное произведение двух -векторов и
было определено в разделе 4.2, где мы заметили, что его лучше всего запоминать с помощью определителя:
(4.3)
Здесь , и
— векторы координат, а определитель разложен по первому столбцу. Мы заметили (но не доказали) в теореме 4.2.5, что она ортогональна обоим и . Это легко следует из следующего результата.
Мы заметили (но не доказали) в теореме 4.2.5, что она ортогональна обоим и . Это легко следует из следующего результата.
Если , и , то .
Доказательство:
Напомним, что вычисляется путем умножения соответствующих компонентов и последующего сложения. Используя уравнение (4.3), получаем результат:
, где последний определитель расширен по столбцу 1.
Результат теоремы 4.3.1 можно кратко сформулировать следующим образом: если , , и три вектора из , то
где обозначает матрицу с , и в качестве ее столбцов. Теперь ясно, что ортогонален обоим и потому, что определитель матрицы равен нулю, если два столбца идентичны.
В силу (4.3) и теоремы 4.3.1 некоторые из следующих свойств перекрестного произведения следуют из
свойств определителей (их можно проверить и непосредственно).
Пусть , и обозначают произвольные векторы в .
- — это вектор.
- ортогонален обоим и .

- .
- .
- .
- для любого скаляра.
- .
- .
Мы видели некоторые из этих результатов в прошлом; Вы можете доказать 6,7 и 8?
Теперь мы подошли к фундаментальному соотношению между точечным и перекрестным произведениями.
Если и любые два вектора в , то
Доказательство:
Даны и , ввести систему координат и записать
и
в компонентной форме. Тогда все члены тождества могут быть вычислены с точки зрения компонентов.
Выражение для модуля вектора легко получить из тождества Лагранжа. Если угол между и , подстановка в тождество Лагранжа дает
, используя тот факт, что . Но неотрицательна в диапазоне , поэтому извлечение положительного квадратного корня из обеих сторон дает
Рисунок 4.3.1
Это выражение для не имеет отношения к системе координат и, более того, имеет хорошую геометрическую интерпретацию. Параллелограмм определяется векторами и имеет длину основания и высоту. Следовательно, площадь параллелограмма, образованного и равна
Параллелограмм определяется векторами и имеет длину основания и высоту. Следовательно, площадь параллелограмма, образованного и равна
Если и два ненулевых вектора и угол между и , то:
- площадь параллелограмма определяется и .
- и параллельны тогда и только тогда, когда .
Доказательство 2:
По (1) тогда и только тогда, когда площадь параллелограмма равна нулю. Площадь исчезает тогда и только тогда, когда и имеют одинаковое или противоположное направление, то есть тогда и только тогда, когда они параллельны.
Найдите площадь треугольника с вершинами , и .
Решение:
У нас есть
и . Площадь треугольника равна половине площади параллелограмма, образованного этими векторами, и поэтому равна . У нас есть
значит площадь треугольника
Рисунок 4.3.2 Если даны три вектора , , и , они определяют «сжатое» прямоугольное тело, называемое параллелепипедом (рис. 4.3.2), и часто полезно иметь возможность найти объем такого тела . Основанием твердого тела является параллелограмм, определяемый и , поэтому он имеет площадь . Высота тела — это длина проекции на . Отсюда
4.3.2), и часто полезно иметь возможность найти объем такого тела . Основанием твердого тела является параллелограмм, определяемый и , поэтому он имеет площадь . Высота тела — это длина проекции на . Отсюда
Таким образом, объем параллелепипеда равен . Это доказывает
Объем параллелепипеда определяется тремя векторами , и определяется как .
Найдите объем параллелепипеда, заданного векторами
Решение:
По теореме 4.3.1, .
Следовательно, объем равен по теореме 4.3.5.
Теперь мы можем дать внутреннее описание перекрестного произведения.
Если вектор взять в правую руку и пальцы сгибаются от угла к углу , большой палец указывает в направлении
Чтобы показать, почему это так, введите координаты в следующим образом: Пусть и имеют общий хвост , выберите начало координат в точке , выберите ось так, чтобы она указывала в положительном направлении, а затем выберите ось так, чтобы она находилась в плоскости – и положительная ось находится на той же стороне оси, что и . Тогда в этой системе и имеем составную форму
Тогда в этой системе и имеем составную форму
и
где и . Можете ли вы нарисовать график на основе описания здесь?
Правило правой руки утверждает, что оно должно указывать в положительном направлении. Но наше определение дает
и имеет положительное направление, потому что .
License
Linear Algebra with Applications by Xinli Wang находится под лицензией Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, если не указано иное.
Поделиться этой книгой
Поделиться в Твиттере
Векторная геометрия – объяснение и примеры
Моделирование важно во всех разделах математики, включая векторную геометрию . Это:
«Изучение геометрических представлений векторов, а именно представления в виде отрезков
направленных линий или стрелок».
В этой теме мы обсудим следующие аспекты векторной геометрии:
- Что такое вектор в геометрии?
- Определение вектора в геометрии
Что такое вектор в геометрии?
Величины, имеющие как величину, так и направление, известны как векторы. Мы можем использовать график для визуального представления векторов. Например, вектор, соединяющий две точки A и B, называется:
Мы можем использовать график для визуального представления векторов. Например, вектор, соединяющий две точки A и B, называется:
AB
Вектор в стандартном положении будет иметь начало координат в качестве начальной точки.
В компонентной или столбцовой форме векторы записываются упорядоченной парой (x, y). Вектор, записанный в таком виде, начинается в начале координат и заканчивается в точке упорядоченной пары.
отрицательное заданного вектора находится путем изменения направления вектора на противоположное. В этом случае его величина (или длина) такая же, как у исходного вектора.
Например, вектор:
BA = – AB
является отрицательным вектором AB, и:
|| ВА || = ||- AB || = || АВ ||
Определение вектора в геометрии
Если заданы две точки P и Q, стрелка от P до Q будет иметь длину и направление.
Предположим, что P и Q — две произвольные точки в пространстве R 3 . Отрезок линии от P до Q обозначается как PQ. В геометрии это называется вектором от P до Q.
Этот вектор будет иметь величину и направление. Точка P называется хвостом (или начальной точкой) вектора PQ, , а точка Q называется кончиком (или головой или конечной точкой) вектора PQ . Его длина обозначается как || PQ ||.
Предположим, точка P имеет координаты (x 1 , y 1 ), а точка Q имеет координаты (x 2 , y 2 ) в плоскости R 2 8 . Затем длина вектора PQ определяется шагами, указанными ниже.
Шаг 1: Сначала вычтите первую составляющую точки P из первой составляющей точки Q. Затем найдите квадрат полученной разности.
Шаг 2: Аналогичным образом вычтите второй компонент точки P из второго компонента точки Q и возведите это число в квадрат.
Шаг 3: Затем сложите два квадрата вместе.
Шаг 4: Наконец, извлеките квадратный корень из числа, полученного на третьем шаге. Это скалярное число будет длиной вектора.
- Обратите внимание, что длина или величина вектора является скалярной величиной.
Теперь давайте попробуем несколько примеров, чтобы попрактиковаться в работе с векторной геометрией.
Пример 1
Имея две точки, O в начале координат (0,0) и A с координатами (3,2), определите длину ||OA||.
Решение:
Сравнивая компоненты, получаем
(x 1 , y 1 ) = (0,0) и (x 2 , y ) 2 = 3, y ) 2 .
Используя вышеупомянутую формулу для нахождения длины двух векторов a, мы имеем: 92 )
Дополнительное упрощение дает нам:
‖ OA ‖ = √(9+4)
‖ OA ‖ = √13. 2 ) 92 )
2 ) 92 )
‖ AB ‖ = √1+ 0
‖ AB ‖ = 1
Таким образом, || АВ || = 1 — длина вектора, соединяющего две точки.
Пример 3
На рисунке ниже даны два вектора AB = 2 a и BC = 3 b, . Точка D — это середина BE, а E — середина BC.
Используя приведенную выше информацию, определите следующие векторы через a and b:
- (a) BC
- (b) BD
- (c) AD
Solution:
- ( а) Используя треугольный закон сложения векторов, мы имеем
ВС = ВА + АС
. Отметим связь между ВА и вектором известной длины, АВ 3 : 3 :0004 = ( — AB ) + AC Замена известных значений AB и AC дают нам : = -2 A + 3

Таким образом, BC = -2 a + 3 b длина вектора.
- (b) Так как Е дано как середина ВС, а D — середина ВЕ, то D — одна четвертая часть расстояния до н.э.0194
Подстановка значения BC , найденного в части (a), дает нам:
= ¼ (-2 a + 3 b )
= -1/2 a
0 б
.Таким образом, BD = -1/2 a + 3/4 b длина вектора.
- (c) Используя треугольный закон сложения векторов, мы имеем:
AD = AB + BD
Подставляя известные значения AB и AC дает нам:
= 2 a + (-1/2 a + 3/4 b )
Это можно упростить: -1/2 a ) + 3/4 b
= 3/2 a + 3/4 b .

Таким образом, AD = 3/2 a + 3/4 b — это длина вектора.
Пример 4
Пусть A = (2, 0, -4) и B = (2, 1, -2) две точки в пространстве Р 3 . Если 2 a – || б || b = 3/2 ( a – 2 x ), where a = OA , b = OB and x = OX and X = (x 1 , x 2 , x 3 ), найдите значения x 1 , x 2 и x 3 .
Решение :
Получаем соотношение:
2 a – || б || b = 3/2 ( a – 2 x ),
Где a = (2, 0, -4), b = (2, 1, -2) и x = (х 1 , х 2 , х 3 ).

Сначала оценим норму (величину) || б || используя предыдущие определения и процедуру нахождения величины вектора, начальная точка которого находится в начале координат. Это дает нам:
|| б || = √(2 2 + 1 2 + (-2) 2 )
= √(4 + 1 + 4)
= √9
=3
Следовательно, || б || = 3. Теперь имеем:
|| б || b = 3 (2, 1, -2)
= (3∙2, 3∙1, 3∙(-2))
= (6, 3, -6)
Аналогично имеем:
2 a = 2 (2, 0, -4) = (4, 0, -8).
Следовательно, левая часть станет
2 a – || б || б = (4, 0, -8) – (6, 3, -6)
= (4-6, 0-3 , -8-(-6))
= (-2, -3) , -8+6)
= (-2, -3, -2).
Правая часть примет вид:
3/2 ( a – 2 x ) = 3/2 ((4, 0, -8)– 2(x 1 , x 2 , x 3 ))
= 3/2 ((4, 0, -8) – (2x 1 , 2x 2 , 2x 3 ))
= 3/2 (4-2x 1 , 2x 2 , -8-2x 3 ).

Теперь, подставляя эти значения в левую и правую части уравнения, получаем:
2 а – || б || b = 3/2 ( a – 2 x )
(-2, -3, -2) = 3/2 (4-2x 1 , 2x 2 , -8-2x 3 )
2 (-2, -3, -2) = 3 (4-2x 1 , 2x 2 , -8-2x 3 )
(-4, -6, — 4) = (3(4-2x 1 ), 3(2x 2 ), 3(-8-2x 3 )).
Сравнение компонентов x, y и z дает нам:
-4 = 3(4-2x 1 )
-4 = 12 -6x 1
6x 1 = 12 -4
6x 1 = 8
x 1 = 8/6
. 3.
-6 = 3 (2x 2 )
-6 = 6x 2
x 2 = -6/6/6
Следовательно, x 2 = -1
-4 = 3 (x 2 = -1
-4 = 3 (x 2 = -1
. -8-2x 3 )
-4= -24 -6x 3
6x 3 = -24 + 4
6x 3 = -20
х 3 = -20/6
Следовательно, х 3 = -10/3.

Таким образом:
х 1 = 4/3, х 2 = -1 и х 3 = -10/3.
Практические вопросы- По двум точкам, V = (2, 5, 1) и C = (3, -2, 1), определите длину вектора VC .
- По двум точкам, G = (5, 5) и H = (4, -10), определить || ОГ || и || ОХ || 2 , где O = (0, 0) — начало координат.
- В треугольнике ABC CB = 4CX, XA = 5XY, а Z — середина треугольника AB. Пусть СХ = м и БЗ = n .
- (a) Determine the length of XB and XA in terms of m and n
- (b) Show that CZ = (4 м + n )
- (C) Оценка ‖ CY ‖/‖ CZ ‖ и (ACY ACY)/(область ACZ)
- Let Abcdef BE BA BAR BAR HEXAGON, и Let
- LET ABCDEF BE BA BA BAR HEXAGON и LET .
 .
. - LET ABCDEF BE BA BA BAR HEXAGON и LET .
- (а) Объясните, почему вектор ED = n .
- (б) Если ВС = м и СД = р, найти АС и н.э. 9 найти 4 (
4 9 найти)0193 ФД .
- Дана прямая ABC, пусть BC = 3 AB . Если OA = a и AB = b, то выразить OC через a и b .
Ответы
- || ВК || = 5√2
- || ОГ || = 5√2, || OH ||² = 116
- В данном треугольнике
- (a) XB = 3 M и XA = 3 M +2 N
- (B) CZ = CB+BZ = 4m+N (B) CZ = CB+BZ = 4m+N
- (B) CZ = CB+BZ = 4M+N
- (B) CZ = CB+BZ = 4m+N
- (B) CZ = CB+BZ = 4m+N
- (B) CZ = CB+BZ = 4m+N
- (B).
 Значения: ‖ CY ‖/‖ CZ ‖ = 2/5 и (ACY ACY)/(ACZ ACZ) = 2/5
Значения: ‖ CY ‖/‖ CZ ‖ = 2/5 и (ACY ACY)/(ACZ ACZ) = 2/5 - (B).
- (a) Напротив AB .
- (б) Если БК = м и КД = р . Then AC = n + m and AD = n + m + p
- (c) FD = -( m + n ) ( т. е. отрицательный вектор AC ).
- OC = a +4 b
Векторные формулы — важные определения, примеры и часто задаваемые вопросы
Каждый объект, имеющий как величину, так и направление, называется вектором.
Вектор можно изобразить геометрически как участок направляющей линии со стрелкой, обозначающей направление, и длиной, равной величине вектора. От хвоста к голове показана ориентация вектора. Мы рассмотрим определение вектора и некоторые векторные формулы с примерами по этой теме. Давайте посмотрим на идею!
Векторная формула
Понятие векторной формулы
В математике вектор — это представление объекта, которое включает в себя как величину, так и направление.
Если два вектора имеют одинаковое направление и величину, они одинаковы. Это означает, что если мы возьмем вектор и перенесем его в другое место, то получим новый вектор. Вектор, который мы получаем в конце этой фазы, выглядит так, и это тот же вектор, который был у нас в начале.
В физике векторы, представляющие силу и скорость, являются двумя распространенными примерами векторов. Мощность и скорость действуют одинаково. Величина вектора будет означать интенсивность силы или относительную скорость скорости. Поскольку смещение напрямую связано с расстоянием, расстояние и смещение не совпадают.
Величина вектора будет означать интенсивность силы или относительную скорость скорости. Поскольку смещение напрямую связано с расстоянием, расстояние и смещение не совпадают.
Стрелка обычно используется для обозначения вектора.
Также, чья длина пропорциональна величине и чье направление совпадает с количеством. Масштабированные векторные диаграммы со значениями часто используются для описания векторных величин. Вектор смещения будет описан на векторной диаграмме.
[Изображение будет загружено в ближайшее время]
Некоторые важные определения и вектор Все формулы
Векторные формулы Математика
Величина
9{2}}\]Направление
Направление вектора часто выражается как угол поворота против часовой стрелки вокруг его «хвоста» строго на восток.
Вектор с направлением 30 градусов — это вектор, повернутый на 30 градусов против часовой стрелки относительно строго на восток с использованием этого соглашения.
Векторная формула Физика
Сила
Векторная сумма двух или более сил представлена равнодействующей силой, которая является единственной силой.
Подобно тому, как две силы с величинами F1 и F2 действуют на частицу, эффект следующий:
[Изображение скоро будет загружено]
Скорость
Скорость изменения направления объекта представлена вектором скорости.
Величина вектора скорости указывает скорость объекта, а направление вектора указывает направление объекта.
[Изображение будет загружено в ближайшее время]
Треугольный закон сложения
Треугольный закон сложения векторов гласит, что когда два вектора представлены как две стороны треугольника одного порядка величины и направления, величина и направление результирующий вектор представлен третьей стороной треугольника.
Поскольку две силы, Вектор А и Вектор В, действуют в одном направлении, результирующее значение R является суммой двух векторов.
[Изображение скоро будет загружено]
Формула треугольного закона сложения: \[\bar{R}\] = \[\bar{A}\] + \[\bar{B}\]
Параллелограммный закон сложения
Когда две степени, формула вектора A вектора B, выражены противоположными сторонами параллелограмма, результирующая представлена диагональю параллелограмма, взятой из того же положения.
[Изображение скоро будет загружено]
Формула треугольного закона сложения: \[\bar{R}\] = \[\bar{A}\] + \[\bar{B}\]
Вычитание векторов
Если две степени, вектор А и вектор В, действуют в противоположных направлениях, то разница между двумя векторами используется для описания результирующего R.
В результате формула вычитания векторов имеет вид \[\ bar{R}\] = \[\bar{A}\] — \[\bar{B}\]
-мерная геометрия.
Таблица векторных формул трехмерной геометрии также доступна на каждом веб-сайте.
Примеры векторной формулы
Q.1) Найдите сложение и вычитание заданных векторов.
(2,3,4) и (5,7,8)
(6,3,2) и (7,5,3)
Ответ:
Используя треугольник по закону сложения заданы векторы
а) (2,3,4) и (5,7,8)
⇒ {2+5,3+7,4+8}
⇒ {7,10 ,12}
б) (6,3,2) и (7,5,3)
⇒ {6+7,3+5,2+3}
⇒ {13,8,5}
Используя закон вычитания векторов, данный вектор равен
а) (2,3,4) и (5,7,8)
⇒ {2-5,3-7,4-8}
⇒ {-3,-4,-4}
б) (6,3,2) и ( 7,5,3)
⇒ {6-7,3-5,2-3}
⇒ {-1,-2,-1}
Величина и направление векторов
Горячая математикаВеличина вектора
Величина вектора
п
Вопрос
→
это расстояние между начальной точкой
п
и конечная точка
Вопрос
. В символах величина
п
Вопрос
→
записывается как
|
п
Вопрос
→
|
.
В символах величина
п
Вопрос
→
записывается как
|
п
Вопрос
→
|
.
Если заданы координаты начальной и конечной точек вектора, то Формула расстояния можно использовать для нахождения его величины.
| п Вопрос → | знак равно ( Икс 2 − Икс 1 ) 2 + ( у 2 − у 1 ) 2
Пример 1:
Найдите величину вектора
п
Вопрос
→
чья начальная точка
п
я сидела
(
1
,
1
)
и конечная точка находится в
Вопрос
я сидела
(
5
,
3
)
.
Решение:
Используйте формулу расстояния.
Подставьте значения Икс 1 , у 1 , Икс 2 , а также у 2 .
| п Вопрос → | знак равно ( 5 − 1 ) 2 + ( 3 − 1 ) 2 знак равно 4 2 + 2 2 знак равно 16 + 4 знак равно 20 ≈ 4,5
Величина
п
Вопрос
→
около
4,5
.
Направление вектора
Направление вектора — это мера угла, который он образует с горизонтальная линия .
Для нахождения направления вектора можно использовать одну из следующих формул:
загар θ знак равно у Икс , куда Икс горизонтальное изменение и у вертикальное изменение
или же
загар θ знак равно у 2 − у 1 Икс 2 − Икс 1 , куда ( Икс 1 , у 1 ) является начальной точкой и ( Икс 2 , у 2 ) является конечной точкой.
Пример 2:
Найдите направление вектора
п
Вопрос
→
чья начальная точка
п
я сидела
(
2
,
3
)
и конечная точка находится в
Вопрос
я сидела
(
5
,
8
)
.
Заданы координаты начальной и конечной точки. Подставляем их в формулу загар θ знак равно у 2 − у 1 Икс 2 − Икс 1 .
загар θ знак равно 8 − 3 5 − 2 знак равно 5 3
Найдите обратный загар, затем воспользуйтесь калькулятором.
θ знак равно загар − 1 ( 5 3 ) ≈ 59 °
Вектор п Вопрос → имеет направление около 59° .
Векторные уравнения и интервалы
Цели
- Понять эквивалентность между системой линейных уравнений и векторным уравнением.
- Изучите определение Span{x1,x2,…,xk} и как рисовать изображения пролетов.
- Рецепт: решить векторное уравнение с использованием расширенных матриц / определить, находится ли вектор в интервале.
- Картинки: противоречивая система уравнений, непротиворечивая система уравнений, охватывает R2 и R3.
- Словарное слово: векторное уравнение .

- Основное словарное слово: диапазон .
Уравнение, включающее векторы с n координатами, аналогично n уравнениям, включающим только числа. Например, уравнение
хC126D+yC-1-2-1D=C8163D
упрощается до
Cx2x6xD+C-y-2y-yD=C8163DorCx-y2x-2y6x-yD=C8163D.
Чтобы два вектора были равны, все их координаты должны быть равны, так что это просто система линейных уравнений
Ex-y=82x-2y=166x-y=3.
Определение
Векторное уравнение — это уравнение, включающее линейную комбинацию векторов с возможными неизвестными коэффициентами.
Спрашивать, имеет ли векторное уравнение решение, это то же самое, что спрашивать, является ли данный вектор линейной комбинацией некоторых других заданных векторов.
Например, приведенное выше векторное уравнение спрашивает, является ли вектор (8,16,3) линейной комбинацией векторов (1,2,6) и (−1,2,−1).
На самом деле нас волнует решение систем линейных уравнений, а не решение векторных уравнений. Весь смысл векторных уравнений в том, что они дают нам другой, более геометрический способ рассмотрения систем линейных уравнений.
Весь смысл векторных уравнений в том, что они дают нам другой, более геометрический способ рассмотрения систем линейных уравнений.
Чтобы действительно решить векторное уравнение
хC126D+yC-1-2-1D=C8163D,
нужно решить систему линейных уравнений
Ex-y=82x-2y=166x-y=3.
Это означает формирование расширенной матрицы
C1-182-2166-13Dи уменьшение ряда. Обратите внимание, что столбцы расширенной матрицы являются векторами из исходного векторного уравнения , поэтому на самом деле нет необходимости записывать систему уравнений: можно напрямую перейти от векторного уравнения к расширенной матрице, «сложив векторы вместе». ». В следующем примере мы выполняем сокращение строки и находим решение.
Пример
Рецепт: Решение векторного уравнения
В общем, векторное уравнение
x1v1+x2v2+···+xkvk=b
, где v1,v2,. ..,vk,b — векторы в Rn, а x1,x2,…,xk — неизвестные скаляры, имеет тот же набор решений, что и линейная система с расширенной матрицей
..,vk,b — векторы в Rn, а x1,x2,…,xk — неизвестные скаляры, имеет тот же набор решений, что и линейная система с расширенной матрицей
, столбцами которого являются vi и b.
Теперь у нас есть три эквивалентных способа представить себе линейную систему:
- В виде системы уравнений:
ч3х1+3х2-2х3=7х1-х2-3х3=5
- В качестве расширенной матрицы: Ф23-271-1-35Г
- В виде векторного уравнения (x1v1+x2v2+···+xnvn=b):
x1F21G+x2F3-1G+x3F-2-3G=F75G
Третий по своей природе геометрический: он поддается рисованию картинок.
Будет важно знать, что такое всех линейных комбинаций набора векторов v1,v2,…,vk в Rn. Другими словами, мы хотели бы понимать множество всех векторов b в Rn таких, что векторное уравнение (относительно неизвестных x1,x2,…,xk)
x1v1+x2v2+···+xkvk=b
имеет решение (т.е. непротиворечиво).
Определение
Пусть v1,v2,. ..,vk — векторы в Rn. Диапазон элементов v1,v2,…,vk представляет собой набор всех линейных комбинаций элементов v1,v2,…,vk и обозначается Span{v1,v2,…,vk}. В символах:
..,vk — векторы в Rn. Диапазон элементов v1,v2,…,vk представляет собой набор всех линейных комбинаций элементов v1,v2,…,vk и обозначается Span{v1,v2,…,vk}. В символах:
Span{v1,v2,…,vk}=Ax1v1+x2v2+···+xkvk|x1,x2,…,xkinRB
Мы также говорим, что Span{v1,v2,…,vk} — это подмножество , натянутое на или , порожденное векторами v1,v2,…,vk.
Приведенное выше определение является первым из нескольких основных определений , которые мы встретим в этом учебнике. Они важны в том смысле, что составляют сущность предмета линейной алгебры: изучение линейной алгебры означает (частично) изучение этих определений. Все определения важны, но очень важно, чтобы вы выучили и поняли определения, помеченные как таковые.
Эквивалент означает, что для любого заданного списка векторов v1,v2,…,vk,b либо все три утверждения верны, либо все три утверждения ложны.
Рисунок 10. Это изображение несовместимой линейной системы : вектор w в правой части уравнения x1v1+x2v2=w не лежит в промежутке v1,v2. Убедитесь в этом сами, попробовав решить уравнение x1v1+x2v2=w, перемещая ползунки и уменьшая ряды. Сравните эту цифру.
Убедитесь в этом сами, попробовав решить уравнение x1v1+x2v2=w, перемещая ползунки и уменьшая ряды. Сравните эту цифру.Фотографии пролетов
Рисование изображения Span{v1,v2,…,vk} аналогично рисованию всех линейных комбинаций v1,v2,…,vk.
Span{v}vSpan{v,w}vwSpan{v,w}vwFigure11Изображения пролетов в R2.Span{v}vSpan{v,w}vwvwuSpan{u,v,w}Span{u,v,w}vwuFigure12Изображения пролеты в R3. Размах двух неколлинеарных векторов — это плоскость, содержащая начало координат и головы векторов. Обратите внимание, что три компланарных (но не коллинеарных) вектора охватывают плоскость, а не трехмерное пространство, точно так же, как два коллинеарных вектора охватывают прямую, а не плоскость.Интерактив: диапазон двух векторов в R2
Interactive: диапазон двух векторов в R3
Interactive: диапазон трех векторов в R3
Комментарии, исправления или предложения? (требуется бесплатная учетная запись GitHub)
геометрия — формула, связывающая три копланарных вектора
Задавать вопрос
спросил 93$ такие, что:
- Все векторы $\mathbf{\vec{u}}$, $\mathbf{\vec{v}}$ и $\mathbf{\vec{w}}$ не являются ноль (т.
 е. $\mathbf{\vec{0}}\notin\{\mathbf{\vec{u}},\mathbf{\vec{v}},\mathbf{\vec{w}}\}$ ).
е. $\mathbf{\vec{0}}\notin\{\mathbf{\vec{u}},\mathbf{\vec{v}},\mathbf{\vec{w}}\}$ ). - Векторы $\mathbf{\vec{u}}$ и $\mathbf{\vec{v}}$ неколлинеарны (т. е. $\mathbf{\vec{u}}\wedge\mathbf{\vec {v}}\neq\mathbf{\vec{0}}$).
- Векторы $\mathbf{\vec{u}}$, $\mathbf{\vec{v}}$ и $\mathbf{\vec{w}}$ компланарны (т. е. [$\mathbf{\vec {u}}$,$\mathbf{\vec{v}}$,$\mathbf{\vec{w}}]=0$). 93$, что я заявляю следующим образом:
$$[\mathbf{\vec{u}},\mathbf{\vec{v}},\mathbf{\vec{w}}]\neq 0 \ подразумевает \mathbf{\vec{x}}=\displaystyle \ frac {[\ mathbf {\ vec {x}}, \ mathbf {\ vec {v}}, \ mathbf {\ vec {w}}]} {[\ mathbf {\ vec {u}}, \ mathbf { \vec{v}},\mathbf{\vec{w}}]}\mathbf{\vec{u}}+\frac{[\mathbf{\vec{u}},\mathbf{\vec{x} },\mathbf{\vec{w}}]}{[\mathbf{\vec{u}},\mathbf{\vec{v}},\mathbf{\vec{w}}]}\mathbf{\ vec{v}}+\frac{[\mathbf{\vec{u}},\mathbf{\vec{v}},\mathbf{\vec{x}}]}{[\mathbf{\vec{u} }},\mathbf{\vec{v}},\mathbf{\vec{w}}]}\mathbf{\vec{w}}$$
Я задаю свой вопрос выше в поисках аналогичной формулы, связывающей три компланарных евклидовых вектора, если она вообще существует.


 Аффинные координаты
Аффинные координаты





 В результате получается нуль, если вектор равен нулевому вектору.
В результате получается нуль, если вектор равен нулевому вектору. Коллинеарные векторы. Действия с векторами и их свойства — сложение и
Коллинеарные векторы. Действия с векторами и их свойства — сложение и ru
ru


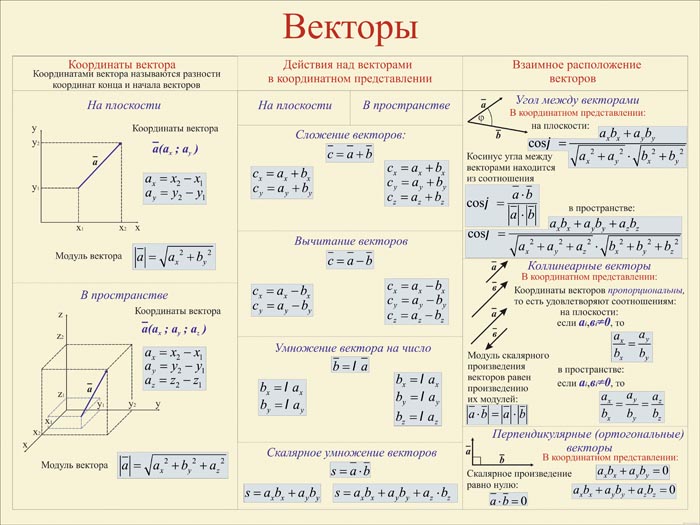 b = | a || b | cos θ
b = | a || b | cos θ