| 1 | Оценить с использованием заданного значения | квадратный корень из 50 | |
| 2 | Оценить с использованием заданного значения | квадратный корень из 45 | |
| 3 | Вычислить | 5+5 | |
| 4 | Вычислить | 7*7 | |
| 5 | Разложить на простые множители | 24 | |
| 6 | Преобразовать в смешанную дробь | 52/6 | |
| 7 | Преобразовать в смешанную дробь | 93/8 | |
| 8 | Преобразовать в смешанную дробь | 34/5 | |
| 9 | График | y=x+1 | |
| 10 | Оценить с использованием заданного значения | квадратный корень из 128 | |
| 11 | Найти площадь поверхности | сфера (3) | |
| 12 | Вычислить | 54-6÷2+6 | |
| 13 | График | y=-2x | |
| 14 | Вычислить | 8*8 | |
| 15 | Преобразовать в десятичную форму | 5/9 | |
| 16 | Оценить с использованием заданного значения | квадратный корень из 180 | |
| 17 | График | y=2 | |
| 18 | Преобразовать в смешанную дробь | 7/8 | |
| 19 | Вычислить | 9*9 | |
| 20 | Risolvere per C | C=5/9*(F-32) | |
| 21 | Упростить | 1/3+1 1/12 | |
| 22 | График | y=x+4 | |
| 23 | График | y=-3 | |
| 24 | График | x+y=3 | |
| 25 | График | x=5 | |
| 26 | Вычислить | 6*6 | |
| 27 | Вычислить | 2*2 | |
| 28 | Вычислить | 4*4 | |
| 29 | Вычислить | 1/2+(2/3)÷(3/4)-(4/5*5/6) | |
| 30 | Вычислить | 1/3+13/12 | |
| 31 | Вычислить | 5*5 | |
| 32 | Risolvere per d | 2d=5v(o)-vr | |
| 33 | Преобразовать в смешанную дробь | 3/7 | |
| 34 | График | y=-2 | |
| 35 | Определить наклон | y=6 | |
| 36 | Перевести в процентное соотношение | 9 | |
| 37 | График | y=2x+2 | |
| 38 | График | y=2x-4 | |
| 39 | График | x=-3 | |
| 40 | Решить, используя свойство квадратного корня | x^2+5x+6=0 | |
| 41 | Преобразовать в смешанную дробь | 1/6 | |
| 42 | Преобразовать в десятичную форму | 9% | |
| 43 | Risolvere per n | 12n-24=14n+28 | |
| 44 | Вычислить | 16*4 | |
| 45 | Упростить | кубический корень из 125 | |
| 46 | Преобразовать в упрощенную дробь | 43% | |
| 47 | График | x=1 | |
| 48 | График | y=6 | |
| 49 | График | y=-7 | |
| 50 | График | y=4x+2 | |
| 51 | Определить наклон | y=7 | |
| 52 | График | y=3x+4 | |
| 53 | График | y=x+5 | |
| 54 | График | 3x+2y=6 | |
| 55 | Решить, используя свойство квадратного корня | x^2-5x+6=0 | |
| 56 | Решить, используя свойство квадратного корня | x^2-6x+5=0 | |
| 57 | Решить, используя свойство квадратного корня | x^2-9=0 | |
| 58 | Оценить с использованием заданного значения | квадратный корень из 192 | |
| 59 | Оценить с использованием заданного значения | квадратный корень из 25/36 | |
| 60 | Разложить на простые множители | 14 | |
| 61 | Преобразовать в смешанную дробь | 7/10 | |
| 62 | Risolvere per a | (-5a)/2=75 | |
| 63 | Упростить | x | |
| 64 | Вычислить | 6*4 | |
| 65 | Вычислить | 6+6 | |
| 66 | Вычислить | -3-5 | |
| 67 | Вычислить | -2-2 | |
| 68 | Упростить | квадратный корень из 1 | |
| 69 | Упростить | квадратный корень из 4 | |
| 70 | Найти обратную величину | 1/3 | |
| 71 | Преобразовать в смешанную дробь | 11/20 | |
| 72 | Преобразовать в смешанную дробь | 7/9 | |
| 73 | Найти НОК | 11 , 13 , 5 , 15 , 14 | , , , , |
| 74 | Решить, используя свойство квадратного корня | x^2-3x-10=0 | |
| 75 | Решить, используя свойство квадратного корня | x^2+2x-8=0 | |
| 76 | График | 3x+4y=12 | |
| 77 | График | 3x-2y=6 | |
| 78 | График | y=-x-2 | |
| 79 | График | y=3x+7 | |
| 80 | Определить, является ли полиномом | 2x+2 | |
| 81 | График | y=2x-6 | |
| 82 | График | y=2x-7 | |
| 83 | График | y=2x-2 | |
| 84 | График | y=-2x+1 | |
| 85 | График | y=-3x+4 | |
| 86 | График | y=-3x+2 | |
| 87 | График | y=x-4 | |
| 88 | Вычислить | (4/3)÷(7/2) | |
| 89 | График | 2x-3y=6 | |
| 90 | График | x+2y=4 | |
| 91 | График | x=7 | |
| 92 | График | x-y=5 | |
| 93 | Решить, используя свойство квадратного корня | x^2+3x-10=0 | |
| 94 | Решить, используя свойство квадратного корня | x^2-2x-3=0 | |
| 95 | Найти площадь поверхности | конус (12)(9) | |
| 96 | Преобразовать в смешанную дробь | 3/10 | |
| 97 | Преобразовать в смешанную дробь | 7/20 | |
| 98 | Преобразовать в смешанную дробь | 2/8 | |
| 99 | Risolvere per w | V=lwh | |
| 100 | Упростить | 6/(5m)+3/(7m^2) |
Как рассчитать медиану выборки?
Как рассчитать медиану выборки?
mediāna «середина») набора чисел — число, которое находится в середине этого набора, если его упорядочить по возрастанию. Таким образом, медиана — это такое число, что половина из элементов набора больше него, а другая половина меньше (строго говоря, это верно только если все элементы набора различны).
Таким образом, медиана — это такое число, что половина из элементов набора больше него, а другая половина меньше (строго говоря, это верно только если все элементы набора различны).
Что такое медиана и мода?
Мода (Mo) представляет собой значение изучаемого признака, повторяющееся с наибольшей частотой, т. … мода – значение признака, встречающееся чаще всего. Медианой (Me) называется значение признака, приходящееся на середину ранжированной (упорядоченной) совокупности, т.
Как найти медианное значение?
Онлайн калькулятор для нахождения медианы ряда чисел. Медианой (серединой) набора чисел называется число стоящее посередине упорядоченного по возрастанию ряда чисел. Если количество чисел в ряду чётное, то медианой ряда является полусумма двух стоящих посередине чисел.
Что такое медиана и ее свойства?
Медианой треугольника называют отрезок, соединяющий вершину треугольника с серединой противоположной стороны (рис 1).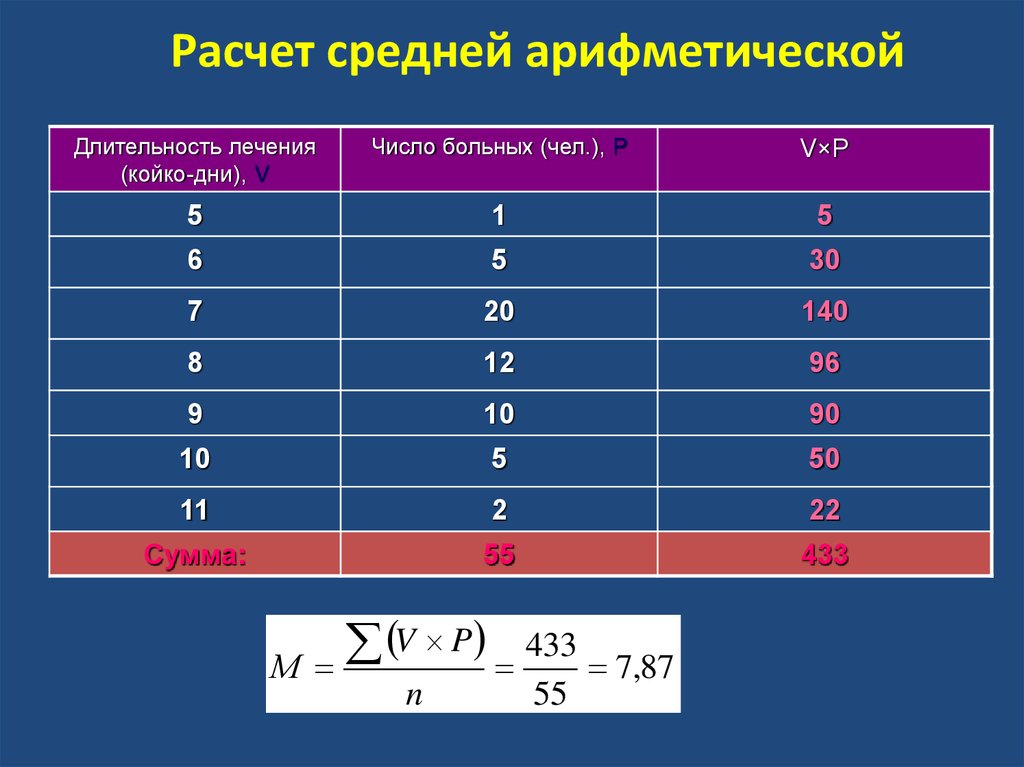 Поскольку в каждом треугольнике имеется три вершины, то в каждом треугольнике можно провести три медианы. … Медиана треугольника делит его на два треугольника равной площади (равновеликих треугольника).
Поскольку в каждом треугольнике имеется три вершины, то в каждом треугольнике можно провести три медианы. … Медиана треугольника делит его на два треугольника равной площади (равновеликих треугольника).
Что такое медиана в массиве?
Медиана массива. … такое значение, которое после сортировки массива A[1…n] будет равно: элементу A[n / 2 + 1], при нечетном n и (A[n / 2] + A[n / 2 + 1]) / 2.
Как найти длину медианы?
Длина медианы треугольника е. медиана треугольника равняется половине корня квадратного из удвоенной суммы квадратов двух сторон минус квадрат третьей стороны.
Как медиана делит угол?
Так давайте разбираться. На самом деле, медиана — это такой отрезок, который проведён из вершины к противоположной стороне, деля её при этом на два одинаковых отрезка. Как Вы можете увидеть, то медиана делит не угол пополам, а сторону, к которой проведена. А угол пополам будет делить биссектриса.
В каком отношении медианы делятся точкой пересечения?
Основное свойство Все три медианы треугольника пересекаются в одной точке, которая называется центроидом или центром тяжести треугольника, и делятся этой точкой на две части в отношении 2:1, считая от вершины.
В каком отношении делятся медианы равностороннего треугольника?
Вспоминаем, что медианы точкой пересечения делятся в отношении 2:1, считая от вершины.
Как вывести формулу медианы треугольника?
Длина медианы, проведенной к стороне треугольника равна половине корня квадратного из удвоенного произведения суммы квадратов двух других сторон минус квадрат этой стороны.
Что такое медиана в прямоугольном треугольнике?
Медиана прямоугольного треугольника, проведённая из вершины прямого угла, равна половине гипотенузы. Признак прямоугольного треугольника: Если в треугольнике медиана равна половине стороны, к которой она проведена, то такой треугольник является прямоугольным.
Чему равен катет лежащий против угла в 30 градусов?
Катет, лежащий против угла 30 градусов, равен половине гипотенузы.
Как найти медиану равностороннего треугольника?
Найти медиану биссектрису высоту равностороннего треугольника
- Формула для вычисления высоты = биссектрисы = медианы.
- В равностороннем треугольнике: все высоты, биссектрисы и медианы, равны. …
- L — высота=биссектриса=медиана
- a — сторона треугольника
Как доказать что треугольник прямоугольный по сторонам?
Так вот, прямоугольный треугольник обладает такими свойствами:
- Сумма квадратов катетов прямоугольного треугольника равна квадрату его гипотенузы
- Медиана прямоугольного треугольника равна половины гипотенузы
- сумма двух острых углов прямоугольного треугольника равна 90 градусов
Как узнать Остроугольный ли треугольник по сторонам?
Если квадрат наибольшей стороны меньше суммы квадратов двух других сторон: с² треугольник остроугольный. Если квадрат наибольшей стороны больше суммы квадратов двух других сторон: с² > a²+b² – треугольник тупоугольный.
Если квадрат наибольшей стороны больше суммы квадратов двух других сторон: с² > a²+b² – треугольник тупоугольный.
Как определить вид треугольника по его сторонам?
Поскольку всего три стороны, то можно составить три варианта сложения двух сторон: a + b , b + c , a + c . Первую сумму сравниваем с оставшейся стороной , вторую — с a и третью — с b . Если хотя бы в одном случае сумма окажется не больше третьей стороны, то делается вывод, что треугольник не существует.
Как определить прямоугольный треугольник или нет?
Прямоуго́льный треуго́льник — это треугольник, в котором один угол прямой (то есть 90 градусов). Соотношения между сторонами и углами прямоугольного треугольника лежат в основе тригонометрии.
Как отличить остроугольный треугольник от Тупоугольного?
Остроугольный треугольник — это треугольник, у которого все углы острые. Прямоугольный треугольник — это треугольник, у которого есть прямой угол. Тупоугольный треугольник — треугольник, все стороны которого есть тупой угол.
Тупоугольный треугольник — треугольник, все стороны которого есть тупой угол.
Как найти высоту в прямоугольном треугольнике?
Примеры решения задач
| Задание | В прямоугольном треугольнике катеты равны см и см. Найти высоту , опущенную на гипотенузу . |
|---|---|
| Решение | Пусть катет см, а см (рис. 2). Тогда по теореме Пифагора гипотенуза см Площадь прямоугольного треугольника равна половине произведения катетов, т.е. Высоту найдем по формуле |
| Ответ | см |
Как найти катет зная катет и угол?
Катет прямоугольного треугольника равен его гипотенузе, умноженной на синус противолежащего или на косинус прилежащего к этому катету угла. Катет равен другому катету, умноженному на тангенс противолежащего или котангенс прилежащего к первому катету угла.
Как найти длины катетов?
Она лежит напротив прямого угла. Длина гипотенузы может быть найдена различными способами. Если известна длина обоих катетов, то ее размер вычисляется по теореме Пифагора: сумма квадратов двух катетов равняется квадрату гипотенузы. К примеру: катет a = 3 см, катет b = 4 см.
Длина гипотенузы может быть найдена различными способами. Если известна длина обоих катетов, то ее размер вычисляется по теореме Пифагора: сумма квадратов двух катетов равняется квадрату гипотенузы. К примеру: катет a = 3 см, катет b = 4 см.
Как найти гипотенузу зная катет и угол между ними?
Найти можно через тригонометрическую функцию Sin или Cos угла. Так как Sin = противолежащий катет/гипотенуза, а Cos = прилежащий катет/гипотенуза, то если известный угол прилежащий к катету гипотенуза = 3/Cos40 = 3.
Как найти длину гипотенузы зная угол и катет?
Формула: sin=a/c, где а – катет, лежащий против данного угла, а с – гипотенуза. Далее преобразуем формулу и получаем: a=sin*c. Пример. Гипотенуза равна 10 см, угол А равен 30 градусов.
Как найти гипотенузу в прямоугольном треугольнике?
Гипотенуза (греч. ὑποτείνουσα, натянутая) — самая длинная сторона прямоугольного треугольника, противоположная прямому углу. Длина гипотенузы прямоугольного треугольника может быть найдена с помощью теоремы Пифагора: Квадрат длины гипотенузы равен сумме квадратов длин катетов.
Длина гипотенузы прямоугольного треугольника может быть найдена с помощью теоремы Пифагора: Квадрат длины гипотенузы равен сумме квадратов длин катетов.
Как найти гипотенузу в равнобедренном треугольнике?
Найти ее можно как квадратный корень из удвоенного произведения квадрата катета – это следствие из теоремы Пифагора и равенства катетов, как боковых сторон равнобедренного треугольника.
Как найти синус угла?
Чтобы найти синус и косинус угла в прямоугольном треугольнике, нужно вспомнить определения. Синус угла равен отношению противоположного катета к гипотенузе. Косинус угла равен отношению прилежащего катета к гипотенузе.
Среднее арифметическое чисел. Мода. Медиана. Размах ряда чисел – онлайн-тренажер для подготовки к ЕНТ, итоговой аттестации и ВОУД
Запомнить
Восстановить пароль
Регистрация
Конспект
Среднее арифметическое нескольких величин – это отношение суммы величин к их количеству.
Правило. Чтобы вычислить среднее арифметическое нескольких чисел, нужно взять сумму этих чисел и разделить все на количество слагаемых. Частное и будет средним арифметическим этих чисел.
Например: найдем среднее арифметическое чисел 2; 6; 9; 15.
У нас четыре числа, значит надо их сумму разделить на четыре. Это и будет среднее арифметическое данных чисел: (2 + 6 + 9 + 15) : 4 = 8.
Размах ряда чисел – это разность между наибольшим и наименьшим из этих чисел.
Например: найдем размах чисел 2; 5; 8; 12; 33.
Наибольшее число здесь – 33, наименьшее – 2. Значит, размах составляет 31, т. е.: 33 – 2 = 31.
Мода ряда чисел – это число, которое встречается в данном ряду чаще других.
Например: найдем моду ряда чисел 1; 7; 3; 8; 7; 12; 22; 7; 11; 22; 8.
Чаще всего в этом ряде чисел встречается число 7 (3 раза). Оно и является модой данного ряда чисел.
Медианой упорядоченного ряда чисел с нечетным числом членов называется число, записанное посередине, а медианой упорядоченного ряда чисел с четным числом членов называется среднее арифметическое двух чисел, записанных посередине.
Медианой произвольного ряда чисел называется медиана соответствующего упорядоченного ряда.
Например: в ряде чисел 2; 5; 9; 15; 21 медианой является число 9, находящееся посередине.
Найдем медиану в ряде чисел 4; 5; 7; 11; 13; 19.
Здесь четное количество чисел (6). Поэтому ищем не одно, а два числа, записанных посередине. Это числа 7 и 11. Находим среднее арифметическое этих чисел: (7 + 11) : 2 = 9. Число 9 является медианой данного ряда чисел.
Вопросы
В институте сдавали зачет по высшей математике. В группе было 10 человек, и они получили соответствующие оценки: 3; 5; 5; 4; 4; 4; 3; 2; 4; 5.
Какую оценку получали чаще всего? Каков средний балл сдавшей зачет группы?
Дан ряд чисел: 175; 172; 179; 171; 174; 170; 172; 169.
Найдите медиану и размах ряда.

Дан ряд чисел: 175; 172; 179; 171; 174; 170; 172; 169.
Найдите моду ряда и среднее арифметическое ряда.
Имеются следующие данные о месячной заработной плате пяти рабочих (тг): 126000; 138000; 132000; 141000; 150000.
Найдите среднюю заработную плату.
Магазин продает 8 видов булочек по следующим ценам: 31; 22; 24; 27; 30; 36; 19; 27.
Найдите разность среднего арифметического и медианы этого набора.
Найдите объем и медиану числового ряда.
9; 7; 1; 1; 11; 5; 1.
Товарные запасы хлопчатобумажных тканей в магазине за первое полугодие составили (тыс.
 тг) на начало каждого месяца:
тг) на начало каждого месяца:I II III IV V VI VII 37 34 35 32 36 33 38 Определите средний товарный запас хлопчатобумажных тканей за первое полугодие.
Провели несколько измерений случайной величины: 2,5; 2,2; 2; 2,4; 2,9; 1,8.
Найдите среднее арифметическое этого набора чисел.
Провели несколько измерений случайной величины: 6; 18; 17; 14; 4; 22.
Найдите медиану этого набора чисел.

Провели несколько измерений случайной величины:
800; 3200; 2000; 2600; 2900; 2000. Найдите моду этого набора чисел.
-
Магазин продает 8 видов хлеба по следующим ценам: 60, 75, 80, 85, 90, 100, 110, 120 тенге.
Найдите разность среднего арифметического и медианы этого набора.
-
Дан числовой ряд: 1; 7; 3; 8; 7; 12; 22; 7; 11; 22; 7,8.
Найдите среднее арифметическое, размах и моду.
Сообщить об ошибке
Инструмент для работы с графами онлайн
Визуализация графа, поиск кратчайшего пути и многое другое. В разделе Справка вы найдете обучающие видео.
В разделе Справка вы найдете обучающие видео.
Graph
Создание алгоритмы
Вставьте ваш алгоритм ниже и нажмите «Выполнить»Задайте матрицу смежности. Используйте запятую «,» в качестве разделителя
Для мультиграфа матрица содержит значения минимальных дуг между вершинами.
Мартрица имеет неправильный формат. Используйте запятую «,» в качестве разделителя. Матрица должна иметь одинаковое количество столбцов и строк.
Задайте матрицу инцидентности. Используйте запятую «,» в качестве разделителя
Мартрица имеет неправильный формат. Используйте запятую «,» в качестве разделителя.
Ваш алгоритм отправлен на модерацию и в случае успеха он будет добавлен на сайт.
Ошибка создания графа. Матрица смежности имеет неправильный формат. Нажимте кнопку «исправить матрицу» чтобы исправить матрицу или кнопку «справка» чтобы открыть справку о формате матрицы
Нажимте кнопку «исправить матрицу» чтобы исправить матрицу или кнопку «справка» чтобы открыть справку о формате матрицы
Ошибка создания графа. Матрица инцидентности имеет неправильный формат. Нажимте кнопку «исправить матрицу» чтобы исправить матрицу или кнопку «справка» чтобы открыть справку о формате матрицы
Какие функции нам добавить в первую очередь?
Пожалуйста, напишите, какого алгоритма вам не хватает. Поддержвать проект.
Сервис уже поддерживает следущий функционал: Поиск пути алгоритмом Дейкстры, матрицу смежности, матрицу инцидентности.
Прозрачность
Выделите и перемещайте объекты или перемещайте рабочую область.
Перемещайте курсор для перемещения объекта
Выделите и перемещайте объекты или перемещайте рабочую область.
Перемещайте курсор для перемещения объекта
Кликните на рабочую область, чтобы добавить вершину. Нумерация вершин
Выделите первую вершину для создания дуги
Выделите вторую вершину, которую хотите соединить
Выделите вершину, из которой хотите найти кратчайших путь
Выделите конечную вершину кратчайшего пути
Расстояние между вершинами %d
Пути не существует
Кликните по объекту, который хотите удалить
Добавить ребро
Ориентированную
Неориентированную
Матрица смежности
Сохранить
Отмена
Мин. расстояние =
Матрица инцидентности
Сохранение графа
закрыть
Число компонентов связности графа равно
Число слабо связных компонентов равно
Что вы думаете о сайте?
Имя (email для ответа)
Написать
Отправить
Напишите нам
исправить матрицу
справка
Матрица имеет неправильный формат
Сохранение изображения графа
Полный отчёт
Краткий отчёт
Граф не содержит Эйлеров цикл
Граф содержит Эйлеров цикл
Обработка. ..
..
Добавить вершину
Переименовать вершину
Переименовать
ru
Изменить вес
ненагруженный
Групповое переименование
Опрос
Рекомендовать алгоритмы
Граф не содержит Эйлерову цепь
Граф содержит Эйлерову цепь
Граф минимальных расстояний.
Нажмите для сохранения
Показать матрицу расстояний
Матрица расстояний
Выделите исток максимального потока
Выделите сток максимального потока
Максимальный поток из %2 в %3 равен %1
Поток из %1 в %2 не существует
Сток
Граф не содержит Гамильтонов цикл
Граф содержит Гамильтонов цикл
Граф не содержит Гамильтонову цепь
Граф содержит Гамильтонову цепь
Выбирете начальную вершину обхода
Порядок обхода:
Изгиб дуги
Отменить
Сохранить граф
По умолчанию
Стиль отрисовки вершины
Стиль отрисовки дуги
Цвет фона
Мультиграф не поддерживает все алгоритмы
ненагруженный
Выделите несколько объектов используя Cmd⌘.
Выделите несколько объектов используя Ctrl.
Перемещайте группу.
Копировать
Удалить
Поиск в ширину
Раскраска графа
Найти компоненты связности
Поиск в глубину
Найти Эйлеров цикл
Найти Эйлерову цепь
Алгоритм Флойда — Уоршелла
Упорядочить граф
Найти Гамильтонов цикл
Найти Гамильтонову цепь
Поиск максимального потока
Поиск минимального остовного дерева
Визуализация на основе весов
Поиск радиуса и диаметра графа
Поиск кратчайший путь алгоритмом Дейкстры
Рассчитать степень вершин
Вес минимального остовного дерева равен
Мы игнорировали ориентацию дуг при рассчете.
Граф не является связным
Выделите первый граф для проверки на изоморфизм. Кликните по любой вершине графа
Выделите второй граф для проверки на изоморфизм. Кликните по любой вершине графа
Кликните по любой вершине графа
Выделите граф, которому должны быть изоморфны подграфов. Кликните по любой вершине графа
Выделите граф в котором необходимо найти изоморфные подграфы. Кликните по любой вершине графа
Графы изоморфны
Графы не изоморфны
Количество изоморфных подграфов равно
Граф не содержит изоморфных подграфов
Поиск изоморфных подграфов
Изоморфных подграф №
Для использования алгоритма необходимо создать хотя бы 2 не связных графа
Проверка изоморфности графов
Граф не является связным
Граф содержит только одну вершину
Радиус графа
Диаметр графа
Центральная
Периферийная
Максимальная степень вершин графа равна
Найденное количество цветов
Готово
Действия
Стиль обычной дуги
Стиль выделенной дуги
Стиль обычной вершины
Стиль выделенной вершины
Поиск всех путей
Количество путей из
в
равно
Путь №
Выделите конечную вершину
Выделите начальную вершину
Найти все кратчайшие пути от вершины
Расстояние от
Путь до
Поиск самого длинного пути
Длина самого длинного пути ровна
Особые действия
Поменять направление всех дуг
Сделать все дуги неориентированными
Сделать все дуги ориентированными
Структурные средние — мода, медиана, квартиль, дециль.
 Решение задач и контрольных работ по статистике онлайн
Решение задач и контрольных работ по статистике онлайн
Краткая теория
Наиболее широкое применение в статистике имеют структурные средние, к числу которых относятся мода и медиана (непараметрические средние).
Мода — величина признака (варианта), которая встречается в ряду распределения с наибольшей частотой (весом). К моде (Мо) прибегают для выявления величины признака, имеющей наибольшее распространение (цена на рынке, по которой было совершено наибольшее число продаж данного товара, номер обуви, который пользуется наибольшим спросом у покупателей и т. д.). Мода используется только в совокупностях большой численности. В дискретном ряду мода находится как варианта, имеющая наибольшую частоту. В интервальном ряду сначала находится модальный интервал, то есть интервал, обладающий наибольшей частотой, а затем – приближенное значение модальной величины признака по формуле:
– нижняя граница модального интервала
— величина модального интервала
– частота интервала, предшествующего модальному
– частота модального интервала
– частота интервала, следующего за модальным
Квантили -
величины, разделяющие совокупность на определенной количество равных по
численности элементов частей. Самый известный квантиль – медиана, делящая совокупность на две равные части. Кроме медианы часто используются квартили, делящие ранжированный ряд на 4 равные части, децили -10 частей и перцентили — на 100
частей.
Самый известный квантиль – медиана, делящая совокупность на две равные части. Кроме медианы часто используются квартили, делящие ранжированный ряд на 4 равные части, децили -10 частей и перцентили — на 100
частей.
Медиана - величина признака у единицы, находящейся в середине ранжированного (упорядоченного) ряда. Если ряд распределения представлен конкретными значениями признака, то медиана (Me) находится как серединное значение признака.
Если ряд распределения дискретный, то медиана находится как серединное значение признака (например, если число значений нечетное – 45, то соответствует 23 значению признака в ряду значений, расположенных в порядке возрастания, если число значений четное – 44, то медиана соответствует полусумме 22 и 23 значений признака).
Если ряд распределения интервальный, то первоначально
находят медианный интервал, который содержит единицу, находящуюся в середине
ранжированного ряда.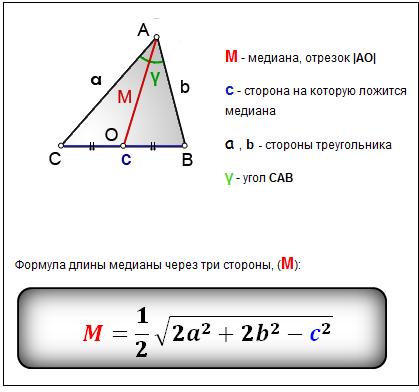 Для определения этого интервала сумму частот
делят пополам и на основании последовательного накопления (суммирования)
частот интервалов, начиная с первого, находят интервал, где расположена
медиана. Значение медианы в интервальном ряду вычисляют по формуле:
Для определения этого интервала сумму частот
делят пополам и на основании последовательного накопления (суммирования)
частот интервалов, начиная с первого, находят интервал, где расположена
медиана. Значение медианы в интервальном ряду вычисляют по формуле:
— нижняя граница медианного интервала
— величина медианного интервала
— сумма частот ряда
– сумма накопленных частот в интервалах, предшествующих медианному
– частота медианного интервала
Квартили — это значения
признака в ранжированном ряду, выбранные таким образом, что 25% единиц
совокупности будут меньше величины
, 25% единиц будут заключены между
и
; 25% -
между
и
,
остальные 25% превосходят
. Квартили определяются по формулам,
аналогичным формуле для расчета медианы. Для интервального ряда:
Для интервального ряда:
Децилем называется структурная переменная, делящая распределение на 10 равных частей по числу единиц в совокупности. Децилей 9, а децильных групп 10. Децили определяются по формулам, аналогичным формуле для расчета медианы и квартилей.
В целом общая формула для расчета квантилей в интервальном ряду такова:
– порядковый номер квантиля
– размерность квантиля (на сколько частей эти квартили делят совокупность)
– нижняя граница квантильного интервала
– ширина квантильного интервала
— накопленная частота предквантильного интервала
Для дискретного ряда номер квантиля можно найти по формуле:
Примеры решения задач
Задача 1
(дискретный ранжированный ряд)
В результате исследований установлен среднемесячный доход жильцов одного подъезда:
|
1. |
1.8 |
2 |
2.5 |
2.8 |
2.8 |
2.8 |
3.0 |
3.6 |
3.8 |
|
3.9 |
4 |
5.8 |
5.9 |
6 |
6 |
6 |
6.8 |
7 |
7 |
Определите:
Модальный
и медианный доход, квартили и децили дохода.
Решение
Имеем уже ранжированный ряд — значения дохода жильцов распределены по возрастанию.
Мода — наиболее часто встречающееся значение. В данном случае имеем ряд с двумя модами.
и
Медиана — такое значение признака, которое делит упорядоченное множество данных пополам.
Квартили — значения признака в ранжированном ряду, выбранные таким образом, что 25% единиц совокупности будут меньше величины ; 25% единиц будут заключены между и ; 25% — между и ; остальные 25% превосходят .
Дицили делят ряд на 10 равных частей:
Если не находите примера, аналогичного вашему, если сами не успеваете выполнить работу, если впереди экзамен по предмету и нужна помощь — свяжитесь со мной:
ВКонтакте
WhatsApp
Telegram
Я буду работать с вами, над вашей проблемой, пока она не решится.
Задача 2
(интервальный ряд)
Для определения среднего размера вклада в кредитном учреждении были получены следующие данные:
| Размер вклада, тыс.р. | до 10.0 | 10.0-16.0 | 16.0-22.0 | 22.0-28.0 | 28.0-34.0 | Свыше 34.0 |
| Удельный вес вкладов, % | 5.0 | 8.0 | 15.0 | 22.0 | 30.0 | 20.0 |
Рассчитайте
структурные средние (моду, медиану,
квартили).
Решение
Вычислим моду размера вклада:
Мода — варианта, которой соответствует наибольшая частота.
Мода вычисляется по формуле:
- начало модального интервала
- величина интервала
- частота модального интервала
- частота интервала, предшествующего модальному
- частота интервала, следующего за модальным
Таким образом, наибольшее количество вкладов имеют размер 30,7 тыс.р.
Медиана — варианта, находящаяся в середине ряда распределения.
Расчет медианы производится по формуле:
-начало (нижняя граница) медианного интервала
-величина интервала
-сумма всех частот ряда
-частота медианного интервала
-сумма накопленных частот вариантов до медианного
Таким образом, половина вкладов имеет размер до 28 тыс. р.,
другая половина — более 28 тыс.р.
р.,
другая половина — более 28 тыс.р.
Вычислим квартили:
Таким образом 25% вкладов меньше 20,8 тыс.р., 25% вкладов лежат в интервале от 20,8 тыс.р. до 28 тыс.р., 25% лежат в интервале от 28 тыс.р. до 33 тыс.р., 25% больше величины в 33 тыс.р.
Задача 3
Постройте графики для вариационного ряда. На графике покажите моду, медиану, среднюю, квартили.
| Возраст детей (лет) | Число детей (доли) |
| 0-3 | 0.15 |
| 3-6 | 0.2 |
| 6-9 | 0.4 |
| 9-12 |
0. 2 2
|
| 12-15 | 0.05 |
Решение
Вычислим среднюю : Для этого просуммируем произведения середин интервалов и соответствующих частот, и полученную сумму разделим на сумму частот.
Вычисление моды интервального ряда на графике
Построим гистограмму.
Мода определяется по гистограмме распределения. Для этого выбирается самый высокий прямоугольник, который в данном случае является модальным. Затем правую вершину модального прямоугольника соединяют с правым верхним углом предыдущего прямоугольника. А левую вершину модального прямоугольника – с левым верхним углом последующего прямоугольника. Далее из точки их пересечения опускают перпендикуляр на ось абсцисс.
Абсцисса точки пересечения этих прямых и будет модой распределения
Гистограмма
По гистограмме получаем, что
Вычисление медианы и квартилей интервального ряда на графике
Построим кумулятивную кривую частот (график накопленных частот)
| 0-3 | 3-6 | 6-9 | 9-12 | 12-15 | |
0. 15 15
|
0.35 | 0.75 | 0.95 | 1 |
Кумулятивная кривая частот
На получившимся графике накопленных частот из последней получившейся точки (в нашем примере) проведем линию перпендикулярную к оси она так же является максимальной высотой. Поделим ее на 4 части. Через полученные точки строим параллельную оси линии которая должна пересекать высоту к оси и кумуляту. От места пересечения кумуляты опускаем перпендикуляры. Получившиеся точки есть квартили и медиана (квартиль при ).
Вывод к задаче
Таким образом
средний возраст детей 6,9 лет. Наибольшее количество детей имеют возраст 7,5
лет. Четверть детей младше 4,5 лет, а самая старшая четверть детей старше 9,1
лет. Половина детей имеет возраст менее 7,3 лет, другая половина – более 7,3
лет.
Половина детей имеет возраст менее 7,3 лет, другая половина – более 7,3
лет.
Новые приключения медианы йодурии | Герасимов
С начала 1990-х почти до конца нулевых годов отечественная тиреоидология развивалась под знаком “медианы йодурии”. Появление доступных методик, таких как определение концентрации йода в моче (КЙМ) и оценка объема щитовидной железы (ЩЖ) с помощью ультразвукового сканирования (УЗИ), помноженное на бескрайние просторы России, открыло невозделанное поле для эпидемиологических исследований. Аналогичные процессы происходили и в других частях света, и, применяя марксистскую терминологию, происходящее в то время можно было бы назвать “первоначальным накоплением капитала”, если под капиталом понимать новые знания о природе и распространенности йодного дефицита.
Опять же в силу бескрайности просторов Россия остается одной из немногих стран в мире, в которых в течение последних 25 лет не было проведено общенационального исследования распространенности йодного дефицита. Вместо этого во многих регионах страны были выполнены (иногда неоднократно) автономные проекты, включающие исследование КЙМ у школьников (реже – у других групп населения) с расчетом медианной КЙМ (мКЙМ) или, просто говоря, “медианы йодурии”. Несмотря на недостатки такого подхода (отсутствие единых критериев выбора кластеров и целевых групп населения), уже к началу нулевых годов исследования были проведены во всех федеральных округах и большинстве крупных регионов и показали, что практически на всей территории Российской Федерации потребление йода было недостаточным [1]. Снижение мКЙМ выявили даже там, где его меньше всего ожидали, – на берегу Черного моря и у жителей острова Сахалин, за исключением небольшой популяции корейцев, традиционно использующих в питании много морепродуктов и морских водорослей.
Вместо этого во многих регионах страны были выполнены (иногда неоднократно) автономные проекты, включающие исследование КЙМ у школьников (реже – у других групп населения) с расчетом медианной КЙМ (мКЙМ) или, просто говоря, “медианы йодурии”. Несмотря на недостатки такого подхода (отсутствие единых критериев выбора кластеров и целевых групп населения), уже к началу нулевых годов исследования были проведены во всех федеральных округах и большинстве крупных регионов и показали, что практически на всей территории Российской Федерации потребление йода было недостаточным [1]. Снижение мКЙМ выявили даже там, где его меньше всего ожидали, – на берегу Черного моря и у жителей острова Сахалин, за исключением небольшой популяции корейцев, традиционно использующих в питании много морепродуктов и морских водорослей.
Наиболее тяжелый йодный дефицит был выявлен в Туве, где среди воспитанников интернатов и домов ребенка были обнаружены недавние случаи йододефицитного кретинизма, а мКЙМ была ниже 20 мкг/л. В отличие от ряда других стран (например, Китая) только в одном населенном пункте России (г. Туринске Свердловской области) был выявлен природный избыток йода в питьевой воде, а мКЙМ у школьников составила 719 мкг/л, что было примерно в 6 раз выше, чем в соседнем городе [2].
В отличие от ряда других стран (например, Китая) только в одном населенном пункте России (г. Туринске Свердловской области) был выявлен природный избыток йода в питьевой воде, а мКЙМ у школьников составила 719 мкг/л, что было примерно в 6 раз выше, чем в соседнем городе [2].
Не обошлось и без “перегибов на местах”, что понудило тогдашнего научного редактора журнала “Проблемы эндокринологии” профессора В. Фадеева еще в 2003 г. открыть дискуссию на сайте “Тиронет”1 под названием “Медиана йодурии от измученного редактора” и начать ее словами: “Люди, опомнитесь!!!” Возможно, что нервный срыв был вызван чтением подобного рода текста: “Продолжающееся воздействие антропоэкологического напряжения может закончиться переходом нейроэндокринных гомеостатических систем организма на новый биоэнергетический уровень, который выражается в изменении состояния здоровья, характеризующегося как преморбидное состояние или хронизация негативных процессов” [3].
Также возникли сложности с интерпретацией выявленных в процессе эпидемиологических исследований расхождений степени выраженности йодного дефицита по показателям мКЙМ по отношению к частоте зоба по данным УЗИ. Часто получалось, что мКЙМ у школьников на фоне проводимых профилактических мероприятий возрастала до оптимальных показателей, в то время как частота зоба если и снижалась, то ненамного и оставалась выше эндемического порога в 5%.
Часто получалось, что мКЙМ у школьников на фоне проводимых профилактических мероприятий возрастала до оптимальных показателей, в то время как частота зоба если и снижалась, то ненамного и оставалась выше эндемического порога в 5%.
В статьях весьма авторитетных специалистов стали появляться утверждения, что “проведение йодной профилактики снижает напряженность зобной эндемии, но не ликвидирует ее полностью”. Что существуют некие таинственные “экопатогены”, которые “крайне неблагоприятно влияют на функцию щитовидной железы и тем самым способствуют формированию зоба”, “а в генезе зоба в большинстве регионов России в настоящее время помимо дефицита йода существенную роль играют и другие зобогенные факторы, в основном экопатогены”. При этом “в тех случаях, когда в генезе зоба ведущую роль играют экопатогены, а не дефицит йода, лечение йодсодержащими препаратами неэффективно”. В ответ я посвятил пару статей разбору этих явных и надуманных проблем [4, 5].
Нельзя не признать, что ранние руководства помониторингу йодного дефицита, выпущенные под эгидой ВОЗ, ЮНИСЕФ и Глобальной сети по йоду2 (ГСЙ), перечисляли индикаторы оценки йодного дефицита, как говорится, “через запятую”, не оценивая приоритетность и информативность тех или иных методов. У некоторых исследователей даже возникало впечатление, что для исследования йодного статуса населения необходимо применять всю батарею индикаторов (частоту зоба, экскрецию йода с мочой, уровень тиреоглобулина в крови и частоту повышения более 3% уровней неонатального тиреотропного гормона (ТТГ) свыше 5 мИЕ/л). Только в самой последней редакции руководства ВОЗ, ЮНИСЕФ и ГСЙ [6], выпущенной в 2007 г., приоритетным и наиболее информативным методом оценки текущего статуса йодной обеспеченности населения было названо определение йода в моче.
У некоторых исследователей даже возникало впечатление, что для исследования йодного статуса населения необходимо применять всю батарею индикаторов (частоту зоба, экскрецию йода с мочой, уровень тиреоглобулина в крови и частоту повышения более 3% уровней неонатального тиреотропного гормона (ТТГ) свыше 5 мИЕ/л). Только в самой последней редакции руководства ВОЗ, ЮНИСЕФ и ГСЙ [6], выпущенной в 2007 г., приоритетным и наиболее информативным методом оценки текущего статуса йодной обеспеченности населения было названо определение йода в моче.
Однако с момента выпуска руководства [6] прошло более 10 лет, и возникла необходимость дать обновленные рекомендации, основанные на опыте и ошибках последних 10–15 лет. У читателя не должно возникнуть впечатления, что проблемы с “медианой йодурии” возникали только в российских исследованиях; они, увы, носили массовый характер. Поэтому в ЮНИСЕФ было проведено техническое консультативное совещание по мониторингу программ йодирования соли, по результатам которого были подготовлены рекомендации [7], опубликованные в 2018 г. С любезного согласия д-ра Р. Купки, советника по микронутриентам штаб-квартиры ЮНИСЕФ в Нью-Йорке, наш журнал опубликовал в этом номере перевод данных рекомендаций с небольшой редакторской адаптацией [8].
С любезного согласия д-ра Р. Купки, советника по микронутриентам штаб-квартиры ЮНИСЕФ в Нью-Йорке, наш журнал опубликовал в этом номере перевод данных рекомендаций с небольшой редакторской адаптацией [8].
Естественно, в этой колонке я не буду пересказывать содержание рекомендаций, но попытаюсь остановиться на некоторых моментах, наиболее, на мой взгляд, интересных для читателей тиреоидологического журнала.
Начну с того, чему в рекомендациях уделено всего несколько строчек, но что может быть важным для эндокринологов, которые в России являются наиболее преданными сторонниками программ йодной профилактики. А сказано там буквально следующее: оценка распространенности зоба (с использованием УЗИ, а тем более пальпации) в эпидемиологических исследованиях не является надежным индикатором статуса йодного потребления. При этом показатели объема ЩЖ и распространенности зоба оказались нечувствительными к быстрым изменениям уровня потребления йода3. Также имела место существенная субъективность при оценке зобов небольшого размера даже при использовании УЗИ.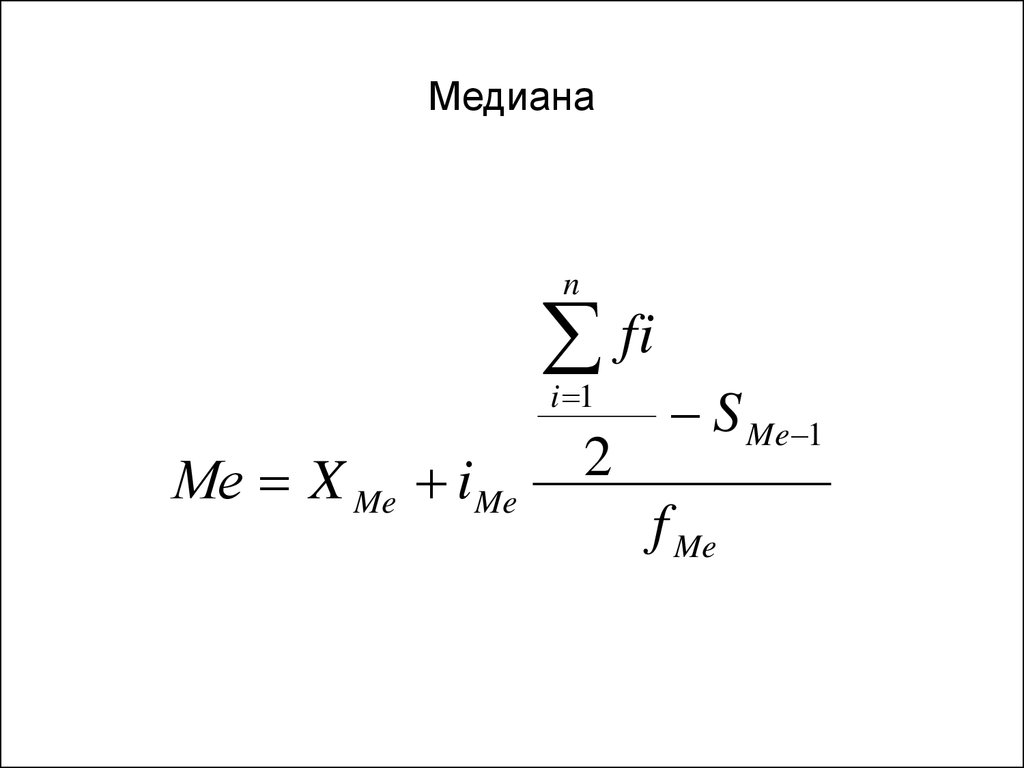 Все это не новости. Новость в том, что впервые четко сформулирована рекомендация прекратить исследование распространенности зоба при рутинных обследованиях статуса йодной обеспеченности населения, отдавая предпочтение анализу показателей мКЙМ, являющейся наилучшим индикатором потребления йода с питанием.
Все это не новости. Новость в том, что впервые четко сформулирована рекомендация прекратить исследование распространенности зоба при рутинных обследованиях статуса йодной обеспеченности населения, отдавая предпочтение анализу показателей мКЙМ, являющейся наилучшим индикатором потребления йода с питанием.
Ни в коем случае нельзя понимать эту рекомендацию как запрет ученым изучать состояние ЩЖ при различном йодном статусе населения. Речь идет именно о рутинных исследованиях, проводимых в странах и регионах с определенными интервалами для мониторинга программ йодной профилактики.
В новых рекомендациях [7] впервые четко указано, что обследования на базе школ для оценки статуса йодной обеспеченности населения имеют определенные ограничения по дизайну. Выбор школьников как целевой группы был обусловлен в первую очередь относительной простотой сбора материала (образцов соли и мочи для определения йода) в учебных заведениях по сравнению с домохозяйствами. Показатели мКЙМ у школьников достаточно точно отражают степень обеспеченности йодом общей популяции (general population), но не беременных и кормящих женщин, потребность в йоде у которых повышена.
Например, в принятой к публикации в следующем номере журнала статье из Беларуси показано, что мКЙМ у школьников (общенациональная когорта из 873 детей) составляла 191 мкг/л, ровно посередине диапазона от 100 до 300 мкг/л, что свидетельствует об оптимальном уровне йодной обеспеченности общей популяции. Вместе с тем мКЙМ у беременных женщин (121 мкг/л; общенациональная когорта из 700 женщин) указывает на неадекватный статус йодной обеспеченности: оптимальный диапазон составляет 150–250 мкг/л [9]. Это нередкая ситуация: две трети европейских стран, в которых были проведены обследования, сообщили о неадекватном йодном обеспечении беременных. При этом мКЙМ могла быть оптимальной в общей популяции [10].
Школьные обследования также могут неточно отражать йодный статус всего населения в странах или регионах, где действуют широкомасштабные программы школьного питания (с использованием йодированной соли или иных йодных добавок). Это имеет прямое отношение к России: при скудости профилактических мер для преодоления йодной недостаточности именно школьники чаще всего получают обогащенные йодом хлеб и другие продукты в рамках программ питания организованных коллективов. И если в уездном городе N мКЙМ у школьников оптимальная, это может не отражать статус йодной обеспеченности у остальных обывателей, не охваченных заботой государства российского.
И если в уездном городе N мКЙМ у школьников оптимальная, это может не отражать статус йодной обеспеченности у остальных обывателей, не охваченных заботой государства российского.
Новые рекомендации [7] также расширяют диапазон мКЙМ, указывающий на адекватное потребление йода у школьников, с 100–199 до 100–299 мкг/л. При этом осталась неизменной интерпретация мКЙМ более 300 мкг/л как “избыточное” потребление йода у школьников. Согласно прежнему руководству [6], существовал отдельный диапазон мКЙМ от 200 до 299 мкг/л, именованный как “более чем адекватное” потребление йода. Это вызывало вопросы и недоумение: чем “более чем адекватное” потребление йода отличается от “избыточного”? Ответ дало большое многонациональное исследование функции щитовидной железы у детей в зависимости от величины потребления йода, поведенное в 2013 г. Оно показало отсутствие дисфункции щитовидной железы у школьников при мКЙМ в диапазоне 100–299 мкг/л [11].
Нужно иметь в виду, что, по мнению составителей новых рекомендаций [7], расширение адекватного диапазона мКЙМ у школьников не должно распространяться на женщин репродуктивного возраста и вообще взрослых лиц. По мнению ведущих специалистов4 , диапазоны мКЙМ у детей в целом должны с определенной осторожностью распространяться на взрослых лиц, нормативы для которых пока еще не разработаны.
По мнению ведущих специалистов4 , диапазоны мКЙМ у детей в целом должны с определенной осторожностью распространяться на взрослых лиц, нормативы для которых пока еще не разработаны.
Таким образом, мКЙМ является наилучшим индикатором статуса йодной обеспеченности населения, а мКЙМ у школьников в диапазоне от 100 до 299 мкг/л указывает на отсутствие дефицита йода в общей популяции. Типичной ошибкой, указанной в рекомендациях [7], является представление о том, что лица с КЙМ <100 мкг/л имеют дефицит йода. Потребление йода с питанием и, следовательно, КЙМ являются очень вариабельными изо дня в день (особенно при анализе уровня йода в разовой порции мочи). Даже у лиц, среднее потребление йода у которых достаточно для поддержания нормальной функции ЩЖ, могут случаться отдельные дни и часы, когда КЙМ снижается до <100 мкг/л. В результате в популяциях с адекватным потреблением йода всегда будут встречаться показатели КЙМ <100 мкг/л. Вместе с тем эти показатели не являются индикативными для оценки распространенности дефицита йода среди населения. Об этом писали уже не раз, но ошибки в интерпретации данных носили массовый характер.
Об этом писали уже не раз, но ошибки в интерпретации данных носили массовый характер.
Отчасти такая трактовка данных объясняется тем, что бюрократам в органах здравоохранения (не исключая ВОЗ!) не очень понятна суть “медианы йодурии”. Им нужны конкретные цифры “больных” и “здоровых”. Когда в качестве основного индикатора для оценки выраженности йодного дефицита использовалась заболеваемость или распространенность зоба, то все было в порядке. А как интерпретировать “медиану йодурии”? Вот и стали “больными” считать тех, у кого КЙМ при эпидемиологических исследованиях была <100 мкг/л.
Например, мКЙМ в 122 мкг/л, полученная при обследовании общенациональной репрезентативной когорты школьников в Швейцарии, указывает на отсутствие йодного дефицита в общей популяции этой замечательной страны. Неправильно интерпретировать долю образцов мочи с уровнем йода <100 мкг/л (в приведенном выше примере таковых было 40%) как процент населения с йодным дефицитом. В равной мере 10% школьников с мКЙМ ≥300 мкг/л нельзя интерпретировать как долю населения, якобы имеющего избыточное потребление йода.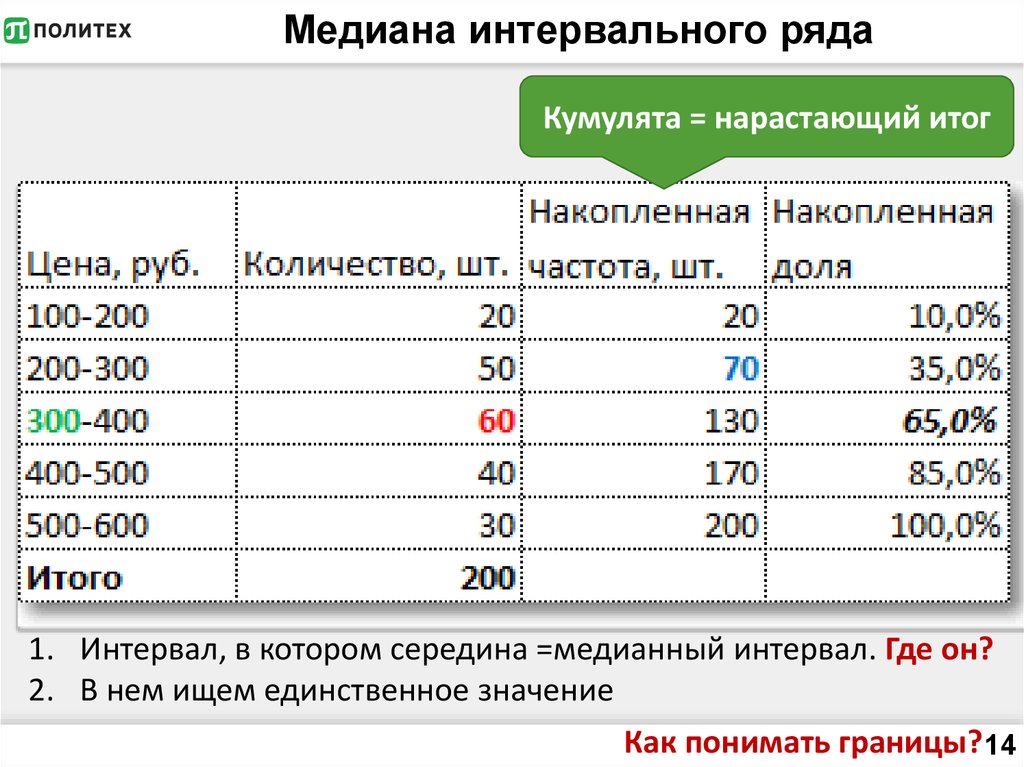
Следует сказать, что в настоящее время ведется активный поиск новых методических подходов к тому, как использовать показатели КЙМ для определения доли лиц в популяции с дефицитом и избытком йода. В двух больших обследованиях, проведенных в Армении и Грузии в 2016–2017 гг., были впервые использованы оригинальные подходы для расчета не только мКЙМ, но и суточных показателей поступления йода с питанием, что позволяло вычислить долю лиц с низким и высоким потреблением йода [12]. Но эта тема выходит за рамки настоящей публикации и требует отдельного разговора.
В начале этой колонки я предположил, что эра “медианы йодурии” в отечественной тиреоидологии закончилась в конце нулевых годов. А после наступил естественный спад интереса к проблеме. Какой смысл повторных обследований йодной обеспеченности населения, если профилактические мероприятия в основном носят формальный характер? Определенным разочарованием была неспособность правительственных органов и Государственной Думы в течение уже более 15 лет принять закон, регулирующий (даже в ограниченном масштабе) обязательное йодирование соли.
В недавно опубликованной статье [13] сотрудники НМИЦ эндокринологии Минздрава России проанализировали показатели заболеваемости и распространенности отдельных форм йододефицитных заболеваний у детей (0–14 лет), подростков (15–17 лет) и взрослых лиц (старше 18 лет) за период с 2009 по 2015 г.
Результаты были вполне ожидаемыми: заболеваемость эндемическим и другими формами нетоксического зоба детей за изученный период возросла с 41,4 до 44,2 случаев, а взрослых – с 910,5 до 978,4 случаев на 100 тыс. населения. При этом заболеваемость зобом у подростков несколько снизилась (может быть, сказался эффект использования йодированной соли в школьном питании?). Также был отмечен существенный рост заболеваемости и распространенности субклинического гипотиреоза во всех возрастных группах. Даже признавая несовершенство приведенной выше статистики, рассчитанной по данным обращаемости населения в медицинские учреждения, можно сделать вывод о фактическом провале системы профилактики йодного дефицита в стране.
Скажу прямо: сегодня я не вижу необходимости возобновления широкомасштабных полевых эпидемиологических исследований статуса йодной обеспеченности населения России (как на национальном, так и региональном уровне). Вернуться к “медиане йодурии” можно только после того, как будут приняты законодательные акты, регламентирующие эффективные мероприятия по использованию йодированной соли в хлебопекарной промышленности, общественном питании и повышению ее доступности в розничной торговле.
Но и сидеть сложа руки тоже неправильно: нужно внедрять методы оценки, практически не требующие дополнительных затрат. Например, одним из перспективных индикаторов оценки статуса йодной обеспеченности является частота повышения уровня неонатального ТТГ свыше 5 мМЕ/л. Согласно руководству [6], при оптимальном статусе йодной обеспеченности частота случаев увеличения ТТГ свыше 5 мМЕ/л не должна превышать 3%.
За последние годы в России была создана эффективная система скрининга новорожденных на врожденный гипотиреоз (ВГ). В 2015 г. такой скрининг проводился в 85 субъектах Федерации, а доля охвата новорожденных скринингом составила 99,1% [14]. Учитывая то, что все лаборатории уже имеют базы данных по уровню ТТГ у новорожденных, на мой взгляд, не должно возникнуть существенных проблем с расчетом процентной доли уровней ТТГ в крови свыше 5 мМЕ/л. По крайней мере, такие наблюдения в течение уже более 20 лет проводят в Тюменской области. И за этот период времени частота неонатального ТТГ снизилась с 44% в 1993 г. до 5,0–5,4% в 2013–2015 гг. [15].
В 2015 г. такой скрининг проводился в 85 субъектах Федерации, а доля охвата новорожденных скринингом составила 99,1% [14]. Учитывая то, что все лаборатории уже имеют базы данных по уровню ТТГ у новорожденных, на мой взгляд, не должно возникнуть существенных проблем с расчетом процентной доли уровней ТТГ в крови свыше 5 мМЕ/л. По крайней мере, такие наблюдения в течение уже более 20 лет проводят в Тюменской области. И за этот период времени частота неонатального ТТГ снизилась с 44% в 1993 г. до 5,0–5,4% в 2013–2015 гг. [15].
Однако использование данных скрининга ВГ для целей мониторинга йодной обеспеченности имеет свои ограничения. Хотя неонатальный ТТГ полезен для выявления умеренной и тяжелой степени дефицита йода, его следует с осторожностью рекомендовать для оценки в регионах с оптимальным йодным обеспечением и при легком йодном дефиците. В статье из Грузии, опубликованной в этом же номере [16] , было показано, что частота повышения уровня ТТГ >5 мМЕ/л у новорожденных уменьшилась с 4,46% в 2009 г. до 3,5% в 2015 г. Однако только в г. Тбилиси частота ТТГ >5 мМЕ/л была ниже 3% – уровня отсечения для адекватного обеспечения питания йодом. В других регионах страны (Западная и Восточная Грузия) частота ТТГ >5 мМЕ/л составляла 3,8 и 4,4% соответственно, что можно было бы ошибочно интерпретировать как легкий дефицит йода. На самом деле, по данным общенационального репрезентативного обследования, проведенного в 2017 г., мКЙМ у беременных женщин составляла 211 мкг/л, а у школьников – 298 мкг/л [12].
до 3,5% в 2015 г. Однако только в г. Тбилиси частота ТТГ >5 мМЕ/л была ниже 3% – уровня отсечения для адекватного обеспечения питания йодом. В других регионах страны (Западная и Восточная Грузия) частота ТТГ >5 мМЕ/л составляла 3,8 и 4,4% соответственно, что можно было бы ошибочно интерпретировать как легкий дефицит йода. На самом деле, по данным общенационального репрезентативного обследования, проведенного в 2017 г., мКЙМ у беременных женщин составляла 211 мкг/л, а у школьников – 298 мкг/л [12].
Возможной причиной повышения частоты ТТГ >5 мМЕ/л было то, что в национальную когорту новорожденных в Грузии входили недоношенные дети. Кроме того, у какой-то части детей кровь для анализа ТТГ собрали вне рекомендованного периода (2–5 дней после родов) из-за быстрой выписки родильниц из медицинского учреждения. Исключение из общей когорты упомянутых групп новорожденных, у которых чаще встречается транзиторная гипертиротропинемия, по данным пока не опубликованного исследования, проведенного в Армении, снижало частоту ТТГ >5 мМЕ/л до менее 3%5. Следует добавить, что в Армении уже пару десятилетий тому назад достигнуто устойчивое оптимальное потребление йода всем населением с мКЙМ 242 мкг/л у школьников, 226 мкг/л у беременных [17].
Следует добавить, что в Армении уже пару десятилетий тому назад достигнуто устойчивое оптимальное потребление йода всем населением с мКЙМ 242 мкг/л у школьников, 226 мкг/л у беременных [17].
Завершая свою уже непомерно растянувшуюся колонку, скажу, что “медиана йодурии” стала теперь главным действующим лицом мониторинга программ йодной профилактики и приключения ее только начинаются.
Примечания:
- https://forums.rusmedserv.com/showthread.php?t=4654
- До переименования в 2012 г. – Международный совет по контролю за йододефицитными заболеваниями (ICCIDD).
- Именно этот реальный феномен, по всей видимости, стал причиной мифа об “экопатогенах”.
- М. Zimmermann – персональное сообщение (2017).
- Hutchings – персональное сообщение (2018).
1. Герасимов Г.А., Фадеев В.В., Свириденко Н.Ю., и др. Йододефицитные заболевания в России. Простое решение сложной проблемы. – М.: Адамантъ, 2002. [Gerasimov GA, Fadeev VV, Sviridenko NY, et al. Yododefitsitnye zabolevaniya v Rossii. Prostoe reshenie slozhnoy problemy. Moscow: Adamant; 2002. (In Russ.)]
Yododefitsitnye zabolevaniya v Rossii. Prostoe reshenie slozhnoy problemy. Moscow: Adamant; 2002. (In Russ.)]
2. Кияев А.В., Платонова Н.М., Абдулхабирова Ф.Х., и др. Влияние избыточного потребления йода на функциональное состояние щитовидной железы и спектр ее патологии у жителей г. Туринска, Свердловской области. // Клиническая и экспериментальная тиреоидология. – 2015. – Т. 11. – №1. – С. 43-49. [Kiyaev AV, Platonova NM, Abdulhabirova FM, et al. Influence of excessive iodine intake on the thyroid function and spectrum of thyroid abnormalities in population of Turinsk, Sverdlovsk Region, of Russia. Clinical and experimental thyroidology. 2015;11(1):43-49. (In Russ.)] doi: 10.14341/ket2015143-49.
3. Андрюков Б.Г., Кику П.Ф., Семенова В.В. Гигиеническая оценка влияния факторов среды обитания Приморского края на заболеваемость щитовидной железы. // Гигиена и санитария. – 2005. – №4. – C. 6-9. [Andryukov BG, Kiku PF, Semenova VV. Hygienic assessment of the impact of environmental factors of the Primorye Territory on the incidence of thyroid diseases. Gig Sanit. 2005;(4):6-9. (In Russ.)]
Gig Sanit. 2005;(4):6-9. (In Russ.)]
4. Герасимов Г.А. Отзыв на дискуссионную статью Э.П. Касаткиной “Диффузный нетоксический зоб. Вопросы классификации и терминологии”. // Проблемы эндокринологии. – 2001. – Т. 47. – №6. – С. 12-15. [Gerasimov GA. Otzyv na diskussionnuyu stat’yu E.P. Kasatkinoy “Diffuznyy netoksicheskiy zob. Voprosy klassifikatsii i terminologii”. Problems of endocrinology. 2001;47(6):12-15. (In Russ.)]
5. Герасимов Г.А. Куда катится колесо, или вновь о простом решении сложной проблемы. // Клиническая и экспериментальная тиреоидология. – 2006. – Т. 2. – №4. – С. 4-7. [Gerasimov GA. Where does the wheel roll or again about simple solution of the difficult problem. Clinical and experimental thyroidology. 2006;2(4):4-7. (In Russ.)]
6. World Health Organization. Assessment of iodine deficiency disorders and monitoring their elimination: a guide for programme managers. Geneva: WHO; 2007.
7. UNICEF. Guidance of the monitoring of salt iodization programmes and determination of population iodine status [Internet]. UNICEF, 2018 [cited 2018 Jul 22]. Avaliable from: https://www.unicef.org/nutrition/files/Monitoring-of-Salt-Iodization.pdf
UNICEF, 2018 [cited 2018 Jul 22]. Avaliable from: https://www.unicef.org/nutrition/files/Monitoring-of-Salt-Iodization.pdf
8. ЮНИСЕФ; Глобальная сеть по йоду. Рекомендации по мониторингу программ йодирования соли и оценке статуса йодной обеспеченности населения (русскоязычная версия) // Клиническая и экспериментальная тиреоидология. – 2018. – Т. 14. – №2. – C. 100-112 [UNICEF; IGN. Guidance on the monitoring of salt iodization programmes and determination of population iodine status: Russian language version. Clinical and experimental thyroidology. 2018;14(2):100-112 (In Russ.)] doi: 10.14341/ket9734.
9. Мохорт Т.В., Петренко С.В., Леушев Б.Ю., и др. Оценка йодного обеспечения детей школьного возраста и беременных женщин в Республике Беларусь в 2017–2018 годах. // Клиническая и экспериментальная тиреоидология. – 2018. – Т. 14. – №3. (в печати). [Mokhort TV, Petrenko SV, Leushev BY, et al. Assessment of iodine provision of school-age children and pregnant women in the Republic of Belarus in 2017–2018. Clinical and experimental thyroidology. 2018;14(3) (in press). (In Russ.)] doi: 10.14341/ket9732.
Clinical and experimental thyroidology. 2018;14(3) (in press). (In Russ.)] doi: 10.14341/ket9732.
10. Zimmermann MB, Gizak M, Abbott K, et al. Iodine deficiency in pregnant women in Europe. Lancet Diabetes Endocrinol. 2015;3(9):672-674. doi: 10.1016/s2213-8587(15)00263-6.
11. Zimmermann MB, Aeberli I, Andersson M, et al. Thyroglobulin is a sensitive measure of both deficient and excess iodine intakes in children and indicates no adverse effects on thyroid function in the UIC range of 100-299 mug/L: a UNICEF/ICCIDD study group report. J Clin Endocrinol Metab. 2013;98(3):1271-1280. doi: 10.1210/jc.2012-3952.
12. Gerasimov G, Sturua L, Ugulava T, van der Haar F. Georgia celebrates optimal iodine nutrition. IDD Newsletter. 2018;46(1):2-4.
13. Трошина Е.А., Платонова Н.М., Панфилова Е.А., Панфилов К.О. Аналитический обзор по результатам мониторинга основных эпидемиологических характеристик йододефицитных заболеваний у населения Российской Федерации за период 2009–2015 гг. // Проблемы эндокринологии. – 2018. – Т. 64. – №1. – С. 21-37. [Troshina EA, Platonova NM, Panfilova EA, Panfilov KO. The analytical review of monitoring of the basic epidemiological characteristics of iodine deficiency disorders among the population of the Russian Federation for the period 2009–2015. Problems of endocrinology. 2018;64(1): 21-37. (In Russ.)] doi: 10.14341/probl9308.
// Проблемы эндокринологии. – 2018. – Т. 64. – №1. – С. 21-37. [Troshina EA, Platonova NM, Panfilova EA, Panfilov KO. The analytical review of monitoring of the basic epidemiological characteristics of iodine deficiency disorders among the population of the Russian Federation for the period 2009–2015. Problems of endocrinology. 2018;64(1): 21-37. (In Russ.)] doi: 10.14341/probl9308.
14. Дедов И.И., Безлепкина О.Б., Вадина Т.А., и др. Скрининг на врожденный гипотиреоз в Российской Федерации. // Проблемы эндокринологии. – 2018. – Т. 64. – №1. – С. 14-20. [Dedov II, Bezlepkina OB, Vadina TA., et al. Screening for congenital hypothyroidism in the Russian Federation. Problems of endocrinology. 2018;64(1):14-20. (In Russ.)] doi: 10.14341/probl8752.
15. Суплотова Л.А., Макарова О.Б., Ковальжина Л.С., Шарухо Г.В. Профилактика йодного дефицита в Тюменской области: успех или неудача? // Клиническая и экспериментальная тиреоидология. – 2015. – Т. 11. – №3. – C. 39-46. [Suplotova LA, Makarova OB, Kovalzhina LS, Sharuho GV. Prevention of iodine deficiency in the Tyumen region: success or failure? Clinical and experimental thyroidology. 2015;11(3):39-46. (In Russ.)] doi: 10.14341/ket2015339-46.
Prevention of iodine deficiency in the Tyumen region: success or failure? Clinical and experimental thyroidology. 2015;11(3):39-46. (In Russ.)] doi: 10.14341/ket2015339-46.
16. Barnabishvilli N, Gerasimov G, Azikuri T. The results of neonatal TSH screening do not agree with indicators of the optimal iodine status of pregnant women in the Republic of Georgia. Clinical and experimental thyroidology. 2018;14(2):81-85. doi: 10.14341/ket9777.
17. Hutchings N, Gerasimov G. Salt iodization in Armenia: a model for sustained success. IDD Newsletter. 2017;45(4):2-4.
Калькулятор среднего, медианы, моды, диапазона
Для расчета укажите числа, разделенные запятой.
| 10, 2, 38, 23, 38, 23, 21 |
Калькулятор статистики | Калькулятор стандартного отклонения | Калькулятор размера выборки
Среднее
Слово среднее, которое является омонимом для нескольких других слов в английском языке, также неоднозначно даже в области математики. В зависимости от контекста, будь то математический или статистический, значение «среднего» меняется. В простейшем математическом определении наборов данных в качестве среднего используется среднее арифметическое, также называемое математическим ожиданием или средним значением. В этой форме среднее относится к промежуточному значению между дискретным набором чисел, а именно к сумме всех значений в наборе данных, деленной на общее количество значений. Уравнение для расчета среднего арифметического практически идентично уравнению для расчета статистических концепций генеральной совокупности и выборочного среднего, с небольшими различиями в используемых переменных:
В зависимости от контекста, будь то математический или статистический, значение «среднего» меняется. В простейшем математическом определении наборов данных в качестве среднего используется среднее арифметическое, также называемое математическим ожиданием или средним значением. В этой форме среднее относится к промежуточному значению между дискретным набором чисел, а именно к сумме всех значений в наборе данных, деленной на общее количество значений. Уравнение для расчета среднего арифметического практически идентично уравнению для расчета статистических концепций генеральной совокупности и выборочного среднего, с небольшими различиями в используемых переменных:
Среднее значение часто обозначается как x̄ , произносится как «x bar», и даже в других случаях, когда переменная не равна x , штриховое обозначение является обычным индикатором некоторой формы среднего значения. В конкретном случае среднего значения совокупности вместо использования переменной x̄ используется греческий символ мю или μ . Точно так же или, скорее, сбивает с толку, выборочное среднее в статистике часто обозначается с большой буквы X̄ . Учитывая набор данных 10, 2, 38, 23, 38, 23, 21, суммирование выше дает:
Точно так же или, скорее, сбивает с толку, выборочное среднее в статистике часто обозначается с большой буквы X̄ . Учитывая набор данных 10, 2, 38, 23, 38, 23, 21, суммирование выше дает:
8 | = | = 22,143 |
Как упоминалось ранее, это одно из самых простых определений среднего, а некоторые другие включают взвешенное среднее арифметическое (которое отличается только тем, что одни значения в наборе данных вносят больший вклад, чем другие) и среднее геометрическое. Правильное понимание данных ситуаций и контекстов часто может предоставить человеку инструменты, необходимые для определения того, какой статистически значимый метод использовать. В общем, среднее значение, медиана, мода и диапазон в идеале должны быть рассчитаны и проанализированы для данной выборки или набора данных, поскольку они объясняют различные аспекты данных и, если их рассматривать отдельно, могут привести к искажению данных, как это будет продемонстрировано в следующих разделах.
Медиана
Статистическая концепция медианы — это значение, которое делит выборку данных, совокупность или распределение вероятностей на две половины. Поиск медианы по существу включает в себя поиск значения в выборке данных, которая имеет физическое расположение между остальными числами. Обратите внимание, что при вычислении медианы конечного списка чисел важен порядок выборок данных. Обычно значения перечислены в порядке возрастания, но нет реальной причины, по которой перечисление значений в порядке убывания приведет к другим результатам. В случае, когда общее количество значений в выборке данных нечетное, медиана — это просто число в середине списка всех значений. Если выборка данных содержит четное количество значений, медиана представляет собой среднее значение двух средних значений. Хотя это может сбивать с толку, просто помните, что хотя медиана иногда требует вычисления среднего значения, когда возникает этот случай, оно будет включать только два средних значения, тогда как среднее значение включает все значения в выборке данных. В нечетных случаях, когда есть только две выборки данных или есть четное количество выборок, где все значения одинаковы, среднее значение и медиана будут одинаковыми. При том же наборе данных, что и раньше, медиана будет получена следующим образом:
В нечетных случаях, когда есть только две выборки данных или есть четное количество выборок, где все значения одинаковы, среднее значение и медиана будут одинаковыми. При том же наборе данных, что и раньше, медиана будет получена следующим образом:
2,10,21, 23 ,23,38,38
После перечисления данных в порядке возрастания и определения нечетного числа значений становится ясно, что 23 является медианой для данного случая. Если бы к набору данных было добавлено другое значение:
2,10,21, 23 , 23 ,38,38,1027892
Поскольку число значений четное, медиана будет средней два средних числа, в данном случае 23 и 23, среднее значение которых равно 23. Обратите внимание, что в этом конкретном наборе данных добавлен выброс (значение, выходящее далеко за пределы ожидаемого диапазона значений), значение 1,027,892, не оказывает реального влияния на набор данных. Однако если для этого набора данных вычислить среднее значение, результатом будет 128 505,875. Это значение явно не является хорошим представлением семи других значений в наборе данных, которые намного меньше и ближе по значению, чем среднее значение и выброс. Это главное преимущество использования медианы при описании статистических данных по сравнению со средним значением. Хотя оба, а также другие статистические значения должны рассчитываться при описании данных, если можно использовать только одно из них, медиана может обеспечить лучшую оценку типичного значения в заданном наборе данных, когда между значениями существуют чрезвычайно большие различия.
Это значение явно не является хорошим представлением семи других значений в наборе данных, которые намного меньше и ближе по значению, чем среднее значение и выброс. Это главное преимущество использования медианы при описании статистических данных по сравнению со средним значением. Хотя оба, а также другие статистические значения должны рассчитываться при описании данных, если можно использовать только одно из них, медиана может обеспечить лучшую оценку типичного значения в заданном наборе данных, когда между значениями существуют чрезвычайно большие различия.
Режим
В статистике режим — это значение в наборе данных, имеющее наибольшее количество повторений. Набор данных может быть мультимодальным, то есть иметь более одного режима. Например:
2,10,21,23,23,38,38
И 23, и 38 появляются дважды каждое, что делает их оба модами для набора данных выше.
Подобно среднему и медиане, мода используется как способ выражения информации о случайных величинах и популяциях. Однако, в отличие от среднего и медианы, мода — это понятие, которое можно применять к нечисловым значениям, таким как марка тортильи, которую чаще всего покупают в продуктовом магазине. Например, при сравнении брендов Tostitos, Mission и XOCHiTL, если обнаружится, что при продаже чипсов из тортильи XOCHITL является модой и продается в соотношении 3: 2: 1 по сравнению с чипсами из тортильи марок Tostitos и Mission соответственно, соотношение может быть использовано для определения того, сколько мешков каждой марки необходимо хранить. В случае, если за определенный период продается 24 пакета чипсов из тортильи, в магазине будет 12 пакетов чипсов XOCHITL, 8 пакетов Tostitos и 4 пакета Mission при использовании режима. Если, однако, магазин просто использовал среднее значение и продал по 8 пакетов каждого, он потенциально мог бы потерять 4 продажи, если бы покупатель хотел только чипсы XOCHiTL, а не какой-либо другой бренд. Как видно из этого примера, важно учитывать всевозможные статистические значения при попытке сделать выводы о любой выборке данных.
Однако, в отличие от среднего и медианы, мода — это понятие, которое можно применять к нечисловым значениям, таким как марка тортильи, которую чаще всего покупают в продуктовом магазине. Например, при сравнении брендов Tostitos, Mission и XOCHiTL, если обнаружится, что при продаже чипсов из тортильи XOCHITL является модой и продается в соотношении 3: 2: 1 по сравнению с чипсами из тортильи марок Tostitos и Mission соответственно, соотношение может быть использовано для определения того, сколько мешков каждой марки необходимо хранить. В случае, если за определенный период продается 24 пакета чипсов из тортильи, в магазине будет 12 пакетов чипсов XOCHITL, 8 пакетов Tostitos и 4 пакета Mission при использовании режима. Если, однако, магазин просто использовал среднее значение и продал по 8 пакетов каждого, он потенциально мог бы потерять 4 продажи, если бы покупатель хотел только чипсы XOCHiTL, а не какой-либо другой бренд. Как видно из этого примера, важно учитывать всевозможные статистические значения при попытке сделать выводы о любой выборке данных.
Диапазон
Диапазон набора данных в статистике — это разница между наибольшим и наименьшим значениями. Хотя диапазон имеет разные значения в разных областях статистики и математики, это его самое основное определение, которое используется в предоставленном калькуляторе. Используя тот же пример:
2,10,21,23,23,38,38
38 — 2 = 36
Диапазон в этом примере равен 36. Как и в среднем, на диапазон могут существенно влиять очень большие или маленькие значения. Используя тот же пример, что и ранее:
2,10,21, 23 , 23 ,38,38,1027892
Диапазон в этом случае будет 1 027 890 по сравнению с 36 в предыдущем случае. Таким образом, важно тщательно анализировать наборы данных, чтобы гарантировать учет выбросов.
Калькулятор средней медианной моды с простым пошаговым решением
Калькулятор средней медианной моды
Значения данных (разделенные запятыми, максимум 50 значений): *
298,107,237,115,114,192,130,102,150,250,298
Решение:
Среднее значение:
Среднее значение набора данных обычно называют средним. Вы найдете среднее значение, взяв сумму всех значений данных и разделив эту сумму на общее количество значений данных. Формула среднего значения населения
$$ \mu = \frac{{\sum}x}{N} $$
Формула среднего значения выборки:
$$ \bar{x} = \frac{{\sum}x}{n} $$
Обе эти формулы используют один и тот же математический процесс: найдите сумму значений данных и разделите на общее количество. Для значений данных, введенных выше, решение:
$$ \frac{2730}{14} = 195$$
Вы найдете среднее значение, взяв сумму всех значений данных и разделив эту сумму на общее количество значений данных. Формула среднего значения населения
$$ \mu = \frac{{\sum}x}{N} $$
Формула среднего значения выборки:
$$ \bar{x} = \frac{{\sum}x}{n} $$
Обе эти формулы используют один и тот же математический процесс: найдите сумму значений данных и разделите на общее количество. Для значений данных, введенных выше, решение:
$$ \frac{2730}{14} = 195$$
Медиана:
Медиана набора данных находится путем упорядочивания набора данных по возрастанию и определения среднего числа. Если в наборе данных имеется нечетное количество значений данных, медиана представляет собой одно число. Если в наборе данных имеется четное количество значений данных, медиана представляет собой среднее значение двух средних чисел. Сортируя набор данных для введенных выше значений, мы имеем:
$$ 102, 107, 114, 115, 130, 150, 192, 207, 219, 237, 263, 298, 298, 298 $$
Так как в этом наборе данных четное число значений данных, есть два средних числа. При 14 значениях данных средние числа — это значения данных в позициях 7 и 8. Это 192 и 207. Медиана — это среднее этих чисел. У нас есть $$ {\frac{192 + 207}{2}} $$
Следовательно, медиана
$$ 199,5 $$
При 14 значениях данных средние числа — это значения данных в позициях 7 и 8. Это 192 и 207. Медиана — это среднее этих чисел. У нас есть $$ {\frac{192 + 207}{2}} $$
Следовательно, медиана
$$ 199,5 $$
Режим:
Режим — это число, которое появляется чаще всего. Набор данных может иметь несколько режимов. Если он имеет две моды, набор данных называется бимодальным. Если все значения данных имеют одинаковую частоту, все значения данных являются модами. Здесь режим(ы) равен/являются
Калькулятор среднего значения средней моды находит меры центральной тенденции. Сначала калькулятор даст вам ответ, а затем предложит пошаговое решение , чтобы вы могли легко научиться решать задачу самостоятельно. Среднее значение — это среднее значение набора чисел. Медиана — это среднее число/числа, расположенные в числовом порядке. Наконец, мода — это число, которое появляется чаще всего.
После того, как вы закончите расчет показателей центральной тенденции, взгляните на Калькулятор диапазона, дисперсии и стандартного отклонения. Статистика никогда не была проще … Вы ПОЛУЧИЛИ это!
Статистика никогда не была проще … Вы ПОЛУЧИЛИ это!
Среднее значение, медиана и мода являются показателями центральной тенденции в статистике. Другими словами, это числа, которые мы используем для измерения и описания центра распределения. Когда студенты начинают изучать распределения на курсах статистики, преподаватели и учебники преподают среднее значение, медиану и моду в качестве одних из первых тем курса. Даже учителя начальной школы знакомят своих учеников с мерами центральной тенденции, поэтому учащиеся начальной школы также могут использовать калькулятор среднего медианного режима. Здесь мы рассмотрим, как найти среднюю медиану и моду вручную. Затем вы можете использовать калькулятор среднего медианного режима, чтобы проверить свою работу.
Как найти среднее
Среднее значение обычно известно как среднее набора чисел. Большинство учащихся хорошо знакомы со средними показателями и часто используют их для определения своей успеваемости в классе. Как найти среднее значение в математике? Мы находим среднее значение, складывая все числа набора данных, а затем разделяя их на общее количество значений.
Как найти среднее значение в математике? Мы находим среднее значение, складывая все числа набора данных, а затем разделяя их на общее количество значений.
$$ \text{mean} = \frac{\sum{\text{значения данных}}}{\text{total}} $$
В математике мы используем символ суммирования $\sum$, чтобы обратите внимание, что мы должны сложить все числа вместе.
Если вы изучаете статистику AP, статистику на уровне колледжа или что-то еще, выходящее за рамки математики средней школы, вы будете использовать специальные символы для обозначения среднего значения. Символически, вы обозначите совокупность как «mu» $\mu$ и обозначите размер совокупности как N. Вы обозначите среднюю выборку как «x-bar» $\bar{x}$, и вы обозначите размер выборки на n. Формула среднего значения генеральной совокупности:
$$ \mu = \frac{\sum{x}}{N} $$
Формула выборочного среднего:
$$ \bar{x} = \frac{\sum {x}}{n} $$
В каждой из этих формул x представляет каждое из чисел в наборе данных. Итак, $\sum{x}$ — это сумма всех значений данных.
Итак, $\sum{x}$ — это сумма всех значений данных.
Вот как найти среднее значение в наборе данных 3, 5, 9, 15, 17. Среднее значение генеральной совокупности равно
$$ \mu = \frac{3 + 5 + 9 + 15+ 17}{5} $$
$$ \mu = \frac{49}{5} = 9,8 $$
Вы можете использовать приведенный выше калькулятор среднего среднего режима и ввести значения 3, 5, 9,15, 17, чтобы убедиться, что среднее 9.8.
Как найти медиану?
Что означает медиана в математике? Когда вы упорядочиваете все числа в наборе данных в порядке возрастания, медиана — это число, которое попадает точно посередине. Если есть два числа, которые находятся посередине, медиана является средним значением этих двух чисел.
3, 5, 9, 15, 17
Медиана приведенного выше набора данных равна 9. 9 – это число в середине.
Теперь рассмотрим следующий набор данных:
3, 5, 9, 15, 17, 20
Как найти медиану в этом случае? Здесь нам нужно найти медиану четных чисел. Для этого мы берем среднее из двух средних чисел. Медиана этого набора данных представляет собой среднее значение 9и 15. То есть
Медиана этого набора данных представляет собой среднее значение 9и 15. То есть
$$ \frac{9 + 15}{2} = 12 $$
Теперь используйте Калькулятор средней средней моды выше, чтобы проверить, что медиана теперь равна 12.
Что такое мода?
Что означает режим в математике? При описании набора данных частота значения данных — это количество раз, когда это значение встречается. Значение данных с наибольшей частотой или то, которое встречается чаще всего, является режимом. Набор данных может иметь две моды, если два числа имеют одинаковую максимальную частоту. Мы говорим, что распределение бимодальное, если оно имеет две моды. Иногда, если есть более двух чисел с наибольшей частотой, мы будем говорить, что набор данных не имеет моды. Однако с помощью приведенного выше калькулятора среднего среднего режима найденный режим будет включать все числа с наибольшей частотой.
В наборе данных 3, 5, 9, 15, 17, 9 какой режим? Значение данных 9 имеет частоту 2, в то время как все остальные числа имеют частоту 1. 9 имеет наибольшую частоту и, следовательно, 9 является модой. Вы можете использовать Калькулятор средней средней моды выше, чтобы убедиться, что мода равна 9.
9 имеет наибольшую частоту и, следовательно, 9 является модой. Вы можете использовать Калькулятор средней средней моды выше, чтобы убедиться, что мода равна 9.
Вот несколько примеров средней медианы и моды в статистике.
Пример 1. Найдите среднее значение
Найдите среднее значение генеральной совокупности для набора данных: 85, 78, 92, 65
Решение:
Так как задача требует найти среднее значение генеральной совокупности, правильным символом для среднего является $ \mu $. Формула средней генеральной совокупности:
$$ \mu = \frac{85 + 78 + 92 + 65}{4} $$
$$ \mu = \frac{ 320}{4} = 80$$
Следовательно , среднее значение генеральной совокупности, $ \mu $, равно 80.
Вы можете вырезать и вставить этот набор данных в приведенный выше калькулятор режима среднего среднего и убедиться, что среднее значение равно 80.
Пример 2: найти медиану
Найти медиана для следующего набора данных:
72, 75, 77, 80, 81, 81, 84, 86, 87, 88, 89, 91, 93, 94, 94, 94, 97, 99, 100
Медиана — это среднее число. Поскольку в этом наборе данных 19 значений данных, среднее число — это число на 10-й позиции. То есть 88. Медиана равна 88.
Поскольку в этом наборе данных 19 значений данных, среднее число — это число на 10-й позиции. То есть 88. Медиана равна 88.
Давайте добавим еще одно значение данных в начало набора данных, чтобы получить в общей сложности 20 значений данных. Мы включим 71.
71, 72, 75, 77, 80, 81, 81, 84, 86, 87, 88, 89, 91, 93, 94, 94, 94, 97, 99, 100
Поскольку существует четный набор значений данных, медиана является средним значением двух средних чисел. При 20 значениях данных два средних значения находятся на позициях 10 и 11. Эти два числа равны 87 и 88. Среднее значение 87 и 88 равно:
$$ \text{median} = \frac{87 + 88}{ 2} $$
$$ \text{медиана} = 87,5 $$
Следовательно, медиана этого набора данных равна 87,5.
Вы можете вырезать и вставить этот набор данных в Калькулятор среднего среднего режима выше и убедиться, что медиана равна 87,5.
Пример 3. Определение режима
71, 72, 75, 77, 80, 81, 81, 84, 86, 87, 88, 89, 91, 93, 94, 94, 94, 97, 99, 100
Режим — это значение данных, которое появляется чаще всего. Это значение данных с наибольшей частотой. В этом наборе данных значение данных 94 имеет частоту 3, что больше, чем частота любого другого значения данных. Таким образом, режим равен 94.
Это значение данных с наибольшей частотой. В этом наборе данных значение данных 94 имеет частоту 3, что больше, чем частота любого другого значения данных. Таким образом, режим равен 94.
Вы можете вырезать и вставить этот набор данных в калькулятор среднего среднего режима выше и убедиться, что режим равен 9.4.
Найдите среднее значение с дополнительной оценкой выброса
Когда мы вычисляем среднее значение, мы обнаруживаем, что выброс сильно влияет на ответ. Выброс в наборе данных — это значение, которое намного меньше или намного больше, чем все остальные значения. Рассмотрим пример тестовых оценок. Предположим, что значения данных в Примере 1 выше представляют 4 оценки за тест.
85, 78, 92, 65
Мы обнаружили, что среднее значение этого набора данных равно 80. Теперь рассмотрим 5-ю оценку теста, равную 20. Мы считаем 20 выбросом, потому что он намного меньше, чем остальная часть теста. оценки.
85, 78, 92, 65, 20
Итак, что теперь значит?
$$ \mu = \frac{85 + 78 + 92 + 65 + 20}{5} $$
$$ \mu = \frac{ 340}{5} = 68 $$
Следовательно, новый среднее значение равно 68. Среднее значение, которое изменяется с 80 до 68, представляет собой большую разницу. Значение выброса 20 сильно влияет на среднее значение. Считаете ли вы, что оценка 68 представляет собой типичное значение в этом наборе данных?
Среднее значение, которое изменяется с 80 до 68, представляет собой большую разницу. Значение выброса 20 сильно влияет на среднее значение. Считаете ли вы, что оценка 68 представляет собой типичное значение в этом наборе данных?
Найдите медиану с дополнительной оценкой выброса
Если бы мы упорядочили исходные 4 оценки за тест и нашли медиану, мы бы вычислили ее как среднее между 78 и 85.
65, 78, 85, 92
$$ \text{медиана} = \frac{78 + 85}{2} $$
$$ \text{медиана} = \frac{163}{2} = 81,5 $$
Таким образом, медиана исходных 4 тестовых оценок равна 81,5.
Теперь давайте включим в набор данных пятую тестовую оценку 20 и найдем новую медиану. Итак, теперь наш набор данных равен
20, 65, 78, 85, 92
При нечетном числе значений данных медиана является средним числом. Здесь это значение равно 78. Итак, новая медиана с включенным выбросом – 78.
Что это значит? Среднее значение и медиана исходного набора данных были соответственно 80 и 81,5. Но когда мы включили выброс в набор данных, среднее значение и медиана стали равными 68 и 78. Хотя среднее значение уменьшилось на 12 пунктов с включенным выбросом, медиана уменьшилась на 3,5 пункта. Мы видим, что выброс сильно влияет на среднее значение, но лишь незначительно влияет на медиану. Поэтому мы говорим, что медиана более точно описывает типичную тестовую оценку, потому что она более устойчива (не так подвержена влиянию) к любым выбросам в наборе данных.
Но когда мы включили выброс в набор данных, среднее значение и медиана стали равными 68 и 78. Хотя среднее значение уменьшилось на 12 пунктов с включенным выбросом, медиана уменьшилась на 3,5 пункта. Мы видим, что выброс сильно влияет на среднее значение, но лишь незначительно влияет на медиану. Поэтому мы говорим, что медиана более точно описывает типичную тестовую оценку, потому что она более устойчива (не так подвержена влиянию) к любым выбросам в наборе данных.
Для нормального колоколообразного распределения
Среднее значение, медиана и мода находятся примерно в центре нормального колоколообразного распределения. Следовательно, мы можем оценить, что все они имеют одинаковое значение.
Средняя медиана и мода имеют одно и то же значение при нормальном распределении в форме колокола.
Вот пример набора данных с одинаковыми средним значением, медианой и модой. Вы можете убедиться, что меры центральной тенденции одинаковы, вставив этот набор данных в Калькулятор среднего среднего режима.
1, 2, 2, 3, 3, 3, 4, 4, 4, 4, 5, 5, 5, 5, 5, 6, 6, 6, 6, 7, 7, 7, 8, 8, 9
Для распределений с асимметрией влево или с отрицательной асимметрией
В распределениях с асимметрией влево или с отрицательной асимметрией в левой части распределения имеются низкие оценки, потенциально являющиеся выбросами, и они вытягивают левый хвост влево. Как мы видели в приведенном выше примере, выбросы сильно влияют на среднее значение, в то время как выбросы незначительно влияют на медиану. В режиме остается значение данных с наибольшей частотой. Следовательно, выбросы не влияют на моду.
Если мы посмотрим на изображение асимметричного левого распределения, мы поместим среднее значение в крайнее левое положение. Затем мы помещаем медиану в положение где-то посередине среднего значения и моды. Наконец, мы помещаем режим в позицию, где мы видим самый высокий пик графика, потому что это значение наибольшей частоты. Это наглядный пример того, как на среднее значение больше всего влияют выбросы, на медиану выбросы влияют незначительно, а на моду выбросы не влияют. Следовательно, порядок трех значений по горизонтальной оси следующий: среднее, затем медиана, затем мода.
Следовательно, порядок трех значений по горизонтальной оси следующий: среднее, затем медиана, затем мода.
Для распределений с перекосом вправо или с положительным перекосом
Когда распределение скошено вправо или скошено положительно, в правой части распределения есть высокие баллы, потенциально выбросы, перетаскивающие правый конец вправо. Как и в случае с асимметричным левым распределением, выбросы сильно влияют на среднее значение, а на медиану — незначительно. На режим не влияют выбросы.
Если мы посмотрим на изображение асимметричного распределения вправо, то среднее значение будет расположено дальше всего вправо. Это значение тянется в направлении перекошенного хвоста. Поскольку выбросы в правом хвосте лишь незначительно влияют на медиану, она будет располагаться где-то посередине среднего значения и моды. И снова мода будет располагаться на самом высоком пике графика, в положении наибольшей частоты. Следовательно, порядок трех значений по горизонтальной оси — мода, медиана и среднее значение.
Следовательно, порядок трех значений по горизонтальной оси — мода, медиана и среднее значение.
Приведенный выше калькулятор средней медианной моды поможет вам рассчитать три показателя центральной тенденции. Следующим шагом является развитие понимания мер изменчивости. Существуют три меры изменчивости: диапазон, дисперсия и стандартное отклонение. Из них стандартное отклонение будет широко представлено в курсе статистики на уровне колледжа.
Калькулятор размаха, дисперсии и стандартного отклонения — лучший онлайн-ресурс для обучения вычислению трех показателей изменчивости вручную. Он дает четкие шаги о том, как решить проблему самостоятельно. Чтобы лучше понять меры изменчивости, см. «Определение дисперсии и стандартного отклонения» и «Как найти стандартное отклонение и дисперсию».
Поиск диапазона и расчет среднего числа в наборе
Расчет среднего и диапазона
Математическое определение
- Среднее значение
- Среднее значение всех данных в наборе.

- Медиана
- Значение в наборе, наиболее близкое к середине диапазона.
- Режим
- Значение, которое чаще всего встречается в наборе данных.
- Диапазон
- Разница между наибольшими и наименьшими данными в наборе данных.
Пример расчета
Расчет среднего значения, медианы, моды и диапазона для 3, 19, 9, 7, 27, 4, 8, 15, 3, 11.
Как найти среднее значение (или среднее значение)
Чтобы вычислить среднее значение, сложите числа: 3+3+4+7+8 +9+11+15+19+27=106, затем разделите его на количество точек данных 106/10=10,6.
Как найти медиану
В порядке возрастания числа 3, 3, 4, 7, 8, 9, 11, 15, 19, 27. Всего имеется 10 чисел, поэтому 5-е и 6-е числа используются для вычислить медиану. (8+9)/2 = 8,5
Если бы в ряду было 9 чисел, а не 10, вы бы взяли 5-е число и не нужно было бы усреднять 2 средних числа. Два средних числа нужно усреднять только в том случае, если набор данных содержит четное количество точек данных.
Как найти режим
Единственное число, которое появляется несколько раз, это 3, так что это режим.
Как найти диапазон
Чтобы вычислить диапазон, вычтите наименьшее число из наибольшего числа 27-3=24.
Среднее значение, медиана и мода: тренды данных, обнаружение аномалий и использование в спорте знать, если мы иметь хорошую оценку. Когда дело доходит до покупки дорогих товаров, мы часто спрашиваем средняя цена для поиска лучших предложений.
Это всего лишь несколько примеров того, как средние значения используются в реальная жизнь.
В этом разделе вы узнаете о различных типах средних показателей, о том, как они рассчитываются и применяются в различных областях, особенно в спорте.
Что означает термин «средний»?
Когда люди описывают «среднее» группы чисел, они часто ссылаются на среднее арифметическое. Это один из 3 различных типов среднего, включая медиану и моду.
Говоря языком разговора, большинство людей просто говорят «средний», когда
они действительно имеют в виду среднее значение. Арифметика означает и среднее
слова-синонимы, которые используются взаимозаменяемо, согласно Dictionary.com.
Арифметика означает и среднее
слова-синонимы, которые используются взаимозаменяемо, согласно Dictionary.com.
Рассчитывается путем сложения чисел в наборе и деления на общее число в наборе — так поступает большинство людей, когда находят среднее значение. См. пример ниже.
Среднее
Набор: 8, 12, 9, 7, 13, 10
Среднее = (8 + 12 + 9+ 7 + 13 + 10) / 6
= 59 / 6
= 9,83
Среднее или среднее арифметическое в этом примере равно 9,83 .
Медиана
Медиана , с другой стороны, является другим типом среднее, представляющее среднее число в упорядоченной последовательности чисел. Этот работает, упорядочивая последовательность чисел (в порядке возрастания), а затем определяя число, которое находится в середине набора. См. пример ниже.
Средняя медиана
Набор: 22, 26, 29, 33, 39 , 40, 42, 47, 53
В этом примере 39 является медианой или средним значением в наборе.
Режим
Режим в основном является наиболее частым значением, которое повторяется в наборе значений. Например, если в вашем наборе есть 21, 9, 14, 3, 11, 33, 5, 9, 16, 21, 5, 9, какой режим?
Ответ 9, потому что это значение повторяется 3 раза.
В статистике среднее, медиана и мода — все термины, используемые для измерить центральную тенденцию в выборке данных. Это иллюстрируется обычным график распределения ниже.
График нормального распределения используется для визуализации стандартного отклонения при анализе данных. Распределение статистических данных показывает, как часто встречаются значения в наборе данных.
На приведенном выше графике проценты представляют количество значений, попадающих в каждый раздел. Выделенные проценты в основном показывают, какая часть данных находится близко к середине графика.
Какая связь между средним, медианой и модой?
На первый взгляд может показаться, что связи нет
между средним, медианой и модой. Но есть эмпирический
отношения, которые существуют при измерении центра набора данных.
Но есть эмпирический
отношения, которые существуют при измерении центра набора данных.
Математики заметили, что обычно разница между медианой и модой, а это разница в 3 раза между средним и медианой.
Эмпирическая взаимосвязь выражается следующей формулой:
Среднее – Мода = 3 (Среднее – Медиана)
Давайте рассмотрим пример данных о населении, основанных на 50 штатах. Например, среднее значение населения составляет 7 миллионов, а медиана 4,8. млн и режим 1,5 млн.
- Среднее = 7 миллионов
- Медиана = 4,8 миллиона
- Мода = 1,5 миллиона
Среднее – Мода = 3 (Среднее – Медиана)
7 миллионов – 1,5 миллиона = 3(7 миллионов – 4,8 миллионов)
5,5 миллионов = 3(2,2)
5,5 миллион = 6,6 миллиона
Обратите внимание: Профессор математики Кортни Тейлор, доктор философии. заявил, что это не точное соотношение. Когда вы делаете расчеты, цифры не всегда точны. Но соответствующие цифры будут относительно близки.
Асимметричные или искаженные данные
Согласно Microeconomicsnotes.com, когда значения среднего, медианы и моды не равны, то распределение асимметрично или асимметрично. Степень асимметрии представляет степень, в которой набор данных отличается от нормального распределения.
Когда среднее значение больше, чем медиана, а медиана больше моды (Среднее > Медиана > Мода), является положительно асимметричным распределением . Он описывается как «перекошенный к вправо», потому что длинный конец кривой направлен вправо.
На примере графика ниже медиана и мода расположены слева от среднего.
С другой стороны, в отрицательном асимметричное распределение, среднее меньше медианы, а медиана меньше чем мода (среднее < медиана < мода). Длиннохвостовой конец направлен к левая сторона графика.
На приведенном ниже графике показаны медиана и мода, расположенные справа от среднего значения.
Отличие среднего от медианы: устойчивые числовые сводки
В наборе данных, когда среднее значение велико, читатель может предположить
медиана также будет высокой. Однако это не всегда следует.
Однако это не всегда следует.
Разница между средним значением и медианой становится очевидной, когда набор данных имеет выдающееся несоизмеримое значение. Эта ситуация привлекает внимание концепция стойкости числовые сводки. Устойчивая статистика представляет собой числовую сводку, в которой крайние значения не оказывают существенного влияния на его стоимость.
Давайте продемонстрируем это, показав, как присутствие Билла Гейтса влияет на среднее и медианное богатство, когда он входит в комнату.
Например, 10 человек обедают в ресторане. Назовем его набором А. В таблице ниже показаны их доходы от самого низкого до самого высокого.
Общий доход людей в ресторане составляет 506 000 долларов США, со средним доходом 50 600 долларов.
Поскольку в наборе 10 человек, для получения медианы мы
необходимо добавить значения 5 th и 6 th (Kat and Luigi’s
годовой доход) и разделите на 2.
Медиана = (46 000 + 49 000) / 2 = 95000/2
= 47 500
Средний доход группы составляет 47 500 долларов.
Диапазон представляет собой разницу между наименьшим доходом (Раффи) и самый высокий доход (Джон), который составляет 46 000 долларов.
Установить годовой доход
Теперь, если Джон выйдет из ресторана и войдет Билл Гейтс, как это повлияет на статистику годового дохода группы? Давайте назовем эту следующую группу набор B.
По данным Forbes, Билл Гейтс составил $90 млрд с 2017 по 2018 год.
Set B Годовой доход
С Биллом Гейтсом общий доход теперь составляет 90 миллиардов долларов плюс низкий доход людей в ресторане. Средний доход и диапазон группы сейчас слишком высока.
Однако медиана остается прежним и составляет около 47 500 долларов.
Медиана показывает, что она лучше отражает фактическое состояние людей.
финансовый статус. Точно так же мы можем сказать, что Билл Гейтс является исключением с годовым
доход, исчисляемый миллиардами.
Этот пример показывает, что среднее значение и диапазон не являются устойчивыми до крайних значений. В то время как медиана, как численное обобщение, обычно показывает сопротивление.
Что это нам говорит? Наличие экстремальных значений или выбросов указывает на то, что распределение асимметрично. Экстремальные значения обычно смещают среднее значение в сторону хвоста.
Значение выявления асимметрии
Наблюдение асимметрии на графике дает аналитикам более четкое представление тенденции набора данных. Например, если вы собрали данные о 500 студентах, которые сдавали Scholastic Assessment Test, вы хотели бы знать тенденцию оценки.
Если вы нанесете данные на график, вы поймете, что это положительно
перекошено, если имеется несколько высоких результатов и большинство значений сгруппированы
к нижней стороне шкалы. Если баллы стремятся в большую сторону
шкалы, с несколькими низкими баллами , распределение отрицательное
перекошенный.
В финансах инвесторы обращают внимание на асимметрию при анализе обратная раздача. Это важно, потому что позволяет им увидеть крайние диапазоны данных вместо того, чтобы просто сосредоточиться на средних значениях.
Распределение показывает асимметрию (степень асимметрии) или эксцесс когда доходность падает на 90 140 за пределы 90 143 нормального распределения. Меры эксцесса выбросы в любом хвосте асимметричного графа. Он вычисляет степень график имеет пик по сравнению с нормальным распределением.
Как это помогает инвесторам? Наблюдение за асимметрией или эксцессом помогает аналитикам прогнозировать риски, возникающие при сравнении модели с нормальным распределением с набором данных с тенденцией к более высокому стандартному отклонению. Риск определяется путем расчета того, насколько числа далеки от нормального распределения.
Как определить аномалии данных
В статистике выбросы
или аномалии — это необычные наблюдения, не принадлежащие определенной популяции.
При размещении на графике это точки, которые падают далеко из значений набора данных. Исследователи обычно находят выбросы на основе больших, хорошо структурированных данных. данные.
Насколько отличным должно быть значение, чтобы оно считалось выбросом? Чтобы определить это, можно использовать межквартильный диапазон (IQR).
IQR описывается как сводка из 5 чисел, которая содержит:
- Минимальное значение набора данных
- Первый квартиль (Q 1 ) – Что такое четверть пути через последовательность набора данных
- Медиана
- Третий квартиль (Q 3 ) Который три четверти последовательности всех данных
- Максимальное значение набора данных
Межквартильный размах (IQR) также похож на размах, но
считается менее чувствительным к экстремальным значениям (устойчивая статистика). Найти
это, вы должны взять первый
квартиль и вычесть третий квартиль. Это показывает, как данные распространяются
вокруг медианы.
IQR = Q 3 – Q 1
Обнаружение выбросов с использованием IQR
Практически все наборы данных могут быть описаны с помощью 5 сводка по номеру. Вот как вы можете использовать IQR для поиска выбросов:
- Вычислите межквартильный размах для набора данных
- Умножьте IQR на 1,5
- Добавьте IQR x 1,5 к третьему квартилю. правило: Любое значение больше этого является выбросом.
- Вычтите IQR x 1,5 из первого квартиля. правило: Любое значение меньше этого является выбросом.
Вот пример. Предположим, вы нашли выброс для следующего набора данных:
1, 5, 6, 6, 9, 10, 10, 11, 12, 13, 18
5 сводка чисел:
- Минимальное значение = 1
- Q 1 = 6
- Медиана = 10
- Q 3 = 12
- Максимальное значение = 18
IQR = Q 3 — Q 10002 — Q 3 — Q 10002 — Q 3 — Q 19058. х 1,5 = ?
х 1,5 = ?
6 x 1,5 = 9
9 + Q 3 = ?
9 + 12 = 21 (любое значение больше 21 является выбросом)
6 – Q 1 = ?
6 – 9 = -3 ( любое значение меньше -3 является выбросом)
Пока в наборе нет значений меньше -3 или больше 21. Хотя максимальное значение 18 на 5 пунктов больше, чем 13, оно не считается выбросом для этого набора данных.
Использование средних статистических данных в спортивной аналитике
В спорте аналитика, исследователи собирают статистику для измерения потенциала и способностей профессиональных спортсменов.
Согласно конкурентному преимуществу Athletic Performance Center, показатели спортивных результатов имеют отношение к общее спортивное развитие. Чтобы добиться успеха в любой спортивной сфере, люди должны достичь определенного уровня атлетизма, чтобы соревноваться на продвинутом уровне.
Фактически, многие профессиональные спортивные команды консультируются
статистики, чтобы помочь спортсменам отслеживать свои конкурентные преимущества. Это руководство
их в улучшении их силовых и кондиционных процедур.
Это руководство
их в улучшении их силовых и кондиционных процедур.
Отслеживание показателей эффективности помогает спортсменам выполнять 4 важных вещи:
- Помогает им узнать свой текущий уровень или базовый уровень.
- Как только они улучшаются, это позволяет им конкурировать на более высокий спортивный уровень.
- Позволяет спортсменам определять индивидуальные тренировки потребности.
- Помогает снизить риск получения травм.
Рейтинг популярных видов спорта
Средний показатель (BA) — это показатель производительности, используемый в бейсболе, крикете и софтболе. Это измеряет количество средних пробежек, которые игрок может набрать, прежде чем выйти из игры.
Это старейший измерительный прибор, которым измеряют тесто. успех. Более высокий BA означает, что у отбивающего больше шансов набрать очки без выход.
БА рассчитывается путем деления количества попаданий игрока на его
общее количество летучих мышей для значения от 0,000 до 1,000.
Согласно веб-сайту Высшей лиги бейсбола, BA всей лиги в последние годы оставался около 0,260. Для лучших отбивающих в игре, они могут превышать 0,300.
Тем не менее, некоторые выдающиеся спортсмены бьют выше 0,400, что составляет 4 попадания на каждые 10 ударов летучими мышами. MLB заявляет, что нет игрок делал это на протяжении всего сезона со времен Теда Уильямса. (0,406) из Бостон Ред Сокс в 1941.
В сезоне 1994 года, сокращенном забастовкой, Тони Гвинн был близок к тому, чтобы забить 400 мячей, забив 394 мяча при 164 попаданиях из 419 мячей в 110 играх.
Вот таблица игроков Главной лиги бейсбольной лиги, в которой показаны средние показатели лидеров регулярного сезона с 1985 по 2019 год:
В баскетболе процент бросков с игры (FG) используется для измерения того, насколько эффективно команда забивает мяч во время игры.
FG учитывает все удары, сделанные игроком. Однако он не включает штрафные броски, которые измеряются независимо как процент штрафных бросков.
Формула FG – это количество успешных выстрелов, разделенное на по общему количеству попыток выстрела.
FG 0,500 или 50% и выше обычно считается хорошим процент. Согласно Баскетболу Справка, активным игроком с самым высоким процентом в настоящее время является ДеАндре. Иордания с 66,96%.
Известные баскетболисты, такие как Майкл Джордан, имеют FG 49,69% с рейтингом 151, в то время как Леброн Джеймс занимает 111 место с 50,42%. Зал славы, такой как Карим Абдул-Джаббар, занимает 14-е место с 55,9.5%, а Мэджик Джонсон занимает 64-е место с 51,97%.
Basketball Reference определил 4 фактора, которые помогают командам выигрывать игры:
- Удары (40%)
- Перехваты (25%)
- Подборы (20%)
- Штрафные броски (15%)
4, стрельба является наиболее важным фактором, за которым следуют потери, подборы и штрафные броски. Однако другие утверждают, что помимо эффективного процента попаданий с игры, игра выигрывается при наличии надежной стратегии защиты.
Ниже представлена таблица игроков НБА с самым высоким процентом попаданий с игры.
Активные игроки выделены полужирным шрифтом .
* Указывает на члена Зала Славы
Многие лидеры по проценту бросков с игры — большие мужчины, которые склонны к данкам и броскам с высокой процентной вероятностью ближних бросков. В последние годы более широкое распространение получил трехочковый бросок. Оценка отличной универсальной стрельбы — 50-40-90, где игрок имеет 50% FG, 40% с трехочковой дистанции и 90% с линии штрафного броска.
Практический результат
Существует три типа средних значений, и это среднее, медиана и мода. Из трех наиболее часто используемым является арифметический иметь в виду. Он определяется путем сложения всех значений в наборе и деления его на общее количество факторов.
Вычисление среднего, медианы и моды позволяет исследователям
нормальное распределение или асимметрия на графике. В финансах инвесторы используют это, чтобы
измерить риск распределения прибыли. Чтобы обнаружить статистические выбросы, аналитики
используйте межквартильный диапазон.
Чтобы обнаружить статистические выбросы, аналитики
используйте межквартильный диапазон.
Вычисление средних значений особенно важно в спорте аналитика. Он используется для установления ориентиров и улучшения спортивных результатов. Метрики помочь спортсменам упорядочить силовые и кондиционные программы, а также избежать травмы.
Об авторе
Корин — страстный исследователь и автор финансовых тем, изучающих экономические тенденции, их влияние на население, а также способы помочь потребителям принимать более разумные финансовые решения. Другие ее тематические статьи можно прочитать на Inquirer.net и Manileno.com. Она имеет степень магистра творческого письма Филиппинского университета, одного из ведущих учебных заведений мира, и степень бакалавра коммуникативных искусств Колледжа Мириам.
Когда сомневаетесь, автосумма 😉
Калькулятор диапазона среднего среднего режима
Калькулятор диапазона среднего среднего режима представляет собой интеллектуальный инструмент, который позволяет вам вычислять средний режим среднего значения и диапазон для заданного набора данных. Читайте дальше, чтобы выполнить определенные расчеты набора данных с помощью нашего калькулятора среднего среднего режима!
Читайте дальше, чтобы выполнить определенные расчеты набора данных с помощью нашего калькулятора среднего среднего режима!
В статистике центральная тенденция (или мера центральной тенденции) называется центральным или типичным значением для распределения вероятностей. Говорят, что наиболее распространенными мерами центральной тенденции являются среднее арифметическое, медиана и мода.
Вы можете воспользоваться приведенным выше калькулятором среднего значения средней моды, чтобы найти меры центральной тенденции (среднее значение, медиана, мода). Этот калькулятор центральной тенденции не только помогает найти медиану средней моды, но также помогает рассчитать диапазон набора данных.
Что ж, перейдем к делу, просто прочитайте эту статью, чтобы узнать, как вычислить диапазон средней средней моды, что такое средняя медиана и мода (центральная тенденция) и диапазон, как найти среднее значение набора данных, медиана, режим и диапазон заданного набора данных и многое другое, что вам нужно знать!
Итак, начнем с термина «Среднее»
Что такое среднее значение в математике? Проще говоря, «среднее» — это среднее значение всех данных в наборе.
Математически «среднее» — это своего рода среднее значение, которое находят путем деления суммы набора чисел на количество чисел в наборе данных. Помните, что «среднее» — это не единственный вид среднего, это то, о чем думает большинство людей, рассматривая среднее значение. Вы можете использовать средства для нескольких видов полезных целей в своей повседневной жизни, в том числе от расчета времени, необходимого вам, чтобы добраться домой с работы, до расчета суммы, которую вы тратите в среднем за неделю.
Формула для среднего (арифметическая):
μ = ∑X / N
или
Среднее = сумма членов/число членов
Где;
- μ представляет собой среднее значение генеральной совокупности (ну, вместо этого вы можете использовать букву M для обозначения среднего значения выборки, но помните, что расчет такой же)
- ∑X означает сумму всех чисел
- N упоминается как общее количество номеров
Да, найти среднее значение для данного набора данных довольно просто, все, что вам нужно, чтобы выполнить указанные шаги, чтобы рассчитать среднее значение: давайте посмотрим на примере:
- Прежде всего необходимо определить набор значений, которые необходимо усреднить.
 Такие числа могут быть большими или маленькими, и даже их может быть сколько угодно. Помните, что вы должны использовать реальные числа, а не переменные
Такие числа могут быть большими или маленькими, и даже их может быть сколько угодно. Помните, что вы должны использовать реальные числа, а не переменные
Например: 2, 3, 4, 5, 6.
- Вы должны сложить свои значения вместе, чтобы найти сумму. Кроме того, для этого можно просто использовать калькулятор вручную или приложение для работы с электронными таблицами .
Например: 2 + 3 + 4+ 5+ 6 = 20
- Теперь вам нужно подсчитать количество значений в вашей группе. Вы должны посчитать все сложенные числа. Помните, что идентичные значения все равно должны учитываться, то есть, если в вашем наборе данных есть значения, которые повторяются, каждое из них по-прежнему учитывается при расчете вашей суммы. При подсчете количества значений не учитывайте сумму (ответ) всех сложенных чисел!
Пример: 2, 3, 4, 5, а также 6 дают в общей сложности пять значений.
- Наконец, вам нужно разделить сумму набора на количество значений.
 Результат называется медовухой (тип среднего) вашего набора. Да, это означает, что если каждое число в вашем наборе имеет среднее значение, то в сумме они будут равны .
Результат называется медовухой (тип среднего) вашего набора. Да, это означает, что если каждое число в вашем наборе имеет среднее значение, то в сумме они будут равны .
Пример: 20/5 = 4. Таким образом, 4 называется средним числом. Кроме того, вы можете проверить свои расчеты, просто умножив среднее значение на количество значений в наборе. В этом случае вы должны умножить 4 (среднее) на 5 (количество значений в наборе), и ваш результат будет 20 (4 × 5 = 20).
Кроме того, вы можете использовать приведенный выше калькулятор среднего для расчета среднего значения для заданного набора данных. Читайте дальше, чтобы узнать об этом умном калькуляторе среднего (среднего)!
О калькуляторе среднего: Этот калькулятор среднего поможет вам вычислить среднее (среднее) для заданного набора данных. Неважно, получены ли данные из популяции или из выборки, так как это действительно не влияет на расчет среднего значения. Вы можете попробовать приведенный выше калькулятор среднего среднего диапазона мод, чтобы вычислить среднее (среднее), медиану, моду и диапазон вместе с различными параметрами для заданного набора данных n.
Калькулятор центральной тенденции очень прост в использовании. Все, что вам нужно сделать, это выполнить указанные шаги, чтобы вычислить среднее значение для заданного набора данных.
Ввод:- Все, что вам нужно, чтобы ввести набор данных в специальное поле этого среднего калькулятора
После того, как вы ввели набор данных, для которого вы хотите найти среднее значение (среднее), просто нажмите кнопку расчета калькулятора режима среднего значения, инструмент покажет вам:
- Среднее (среднее)
- Медиана (средняя)
- Режим (наиболее распространенный)
- Диапазон (самый большой – самый маленький)
- Среднее геометрическое
- По возрастанию
- По убыванию
- Четные числа
- Нечетные числа
- Сумма чисел
- Максимальное количество
- Количество (общее количество)
- Столбчатая диаграмма заданного набора данных
Теперь давайте начнем с определения медианы в математике!
Что такое медиана в математике? Медиана называется средним значением в заданном наборе данных или представляет собой простую меру центральной тенденции. Когда вы ищете медиану в заданном наборе данных, который имеет нечетное количество общих чисел, процесс вычисления медианы слишком прост. Без сомнения, вычисление медианы в наборе данных с четным общим числом немного сложнее. Вы можете попробовать наш калькулятор медианы и использовать приведенную ниже формулу медианы для расчета медианы.
Когда вы ищете медиану в заданном наборе данных, который имеет нечетное количество общих чисел, процесс вычисления медианы слишком прост. Без сомнения, вычисление медианы в наборе данных с четным общим числом немного сложнее. Вы можете попробовать наш калькулятор медианы и использовать приведенную ниже формулу медианы для расчета медианы.
Формула для медианы:
Для расчета медианы будет учитываться эта формула:
Формула
Или
Медиана = среднее значение заданного набора данных
Чтобы найти медиану легко и успешно, проведите пальцем по экрану вниз!
Как вычислить медиану в нечетном наборе чисел:- Прежде всего, вы должны отсортировать числа в наборе данных от меньшего к большему. Если они зашифрованы, то вы должны выстроить их в ряд, начиная с наименьшего числа и заканчивая наибольшим числом. Если набор данных включает 5, 3, 1, 7, 2, то это будет как 1, 2, 3, 5, 7
- Теперь вам нужно найти число, которое находится ровно посередине заданного набора данных.
 Таким образом, ясно, что перед медианным числом стоит столько же чисел, сколько и за ним. Что ж, начните считать их, чтобы убедиться, что
Таким образом, ясно, что перед медианным числом стоит столько же чисел, сколько и за ним. Что ж, начните считать их, чтобы убедиться, что
Давайте посмотрим на этот набор данных 1, 2, 3, 5, 7 — вы можете видеть, что перед 3 стоят два числа, а также два числа позади него. Он показывает, что 3 — это число, которое находится ровно посередине
- Итак, медиана 1, 2, 3, 5, 7 равна 3. Помните, что медиана набора данных с нечетными номерами — это всегда число в сам набор данных. Имейте в виду, что медиана никогда не является числом, которого нет в последовательности.
Например; четный набор чисел: 2, 3, 1, 4
- Прежде всего, вы должны отсортировать свой набор чисел от меньшего к большему. Итак, снова используйте тот же первый шаг, что и упомянутый выше. Помните, что четный набор чисел будет иметь два числа точно посередине. Если набор данных включает 2, 3, 1, 4, то это будет 1, 2, 3, 4
- Теперь вам нужно найти среднее значение двух чисел в середине.
 Вы можете видеть, что 2 и 3 находятся посередине, поэтому здесь вам следует добавить 2 и 3, а затем просто разделить сумму на 2. Используйте приведенную выше формулу для нахождения среднего значения двух чисел (сумма двух средних числа) / 2
Вы можете видеть, что 2 и 3 находятся посередине, поэтому здесь вам следует добавить 2 и 3, а затем просто разделить сумму на 2. Используйте приведенную выше формулу для нахождения среднего значения двух чисел (сумма двух средних числа) / 2 - Итак, медиана этого набора данных с четным количеством чисел равна 2 ½. Итак, ясно, что медиана в четном наборе чисел не обязательно должна быть числом в самом наборе данных .
Наш калькулятор медианы — это интеллектуальный инструмент, который эффективно работает как средство поиска медианы. Проще говоря, калькулятор медианы поможет вам найти медиану из заданного набора данных. Читайте дальше, чтобы узнать, что вам нужно сделать, чтобы найти медиану!
Как найти медиану с помощью Калькулятора медианы:Вышеупомянутый искатель медианы имеет простой и удобный интерфейс, все, что вам нужно выполнить, чтобы найти значения медианы из заданного набора данных:
Ввод:- Все, что вам нужно, чтобы ввести набор данных в специальное поле вышеуказанного калькулятора медианы
- После того, как вы ввели набор данных, просто нажмите кнопку расчета — средство поиска медианы покажет вам медианное значение для заданного набора данных вместе со средним значением, режимом, диапазоном и другими статистическими данными
Теперь давайте узнаем определение режима в математике, как рассчитать режим набора данных вручную, пример расчета режима, калькулятор режима и многое другое.
Проведите вниз!
Что такое режим в математике?В режиме простого слова это значение, которое чаще всего встречается в наборе данных. Более конкретно, мода чисел — это число, которое чаще всего встречается в наборе данных. Помните, что набор данных не обязательно должен иметь только одну моду. Но когда два или более значения «связаны» как наиболее распространенные, можно сказать, что набор данных является бимодальным или мультимодальным соответственно. Другими словами, все наиболее распространенные числа являются модами множества. Просто попробуйте приведенный выше калькулятор среднего значения и моды, чтобы найти моду вместе с различными параметрами статистики.
Что ж, если вы хотите рассчитать режим чисел или режим (ы) набора данных, выполните указанные шаги.
Формула для режима:
Режим = наиболее повторяющийся элемент в наборе . Далее, вы должны подсчитать, сколько каждого числа. Число, которое появляется чаще всего, называется модусом чисел.
Давайте посмотрим на пример:
3, 7, 5, 13, 20, 23, 39, 23, 40, 23, 14, 12, 56, 23, 29
По порядку:
3, 5, 7, 12, 13 , 14, 20, 23, 23, 23, 23, 29, 39, 40, 56
По порядку становится легко увидеть, какие числа появляются чаще всего.
В этом примере режим чисел 23.
Другой пример режима:
{19, 8, 29, 35, 19, 28, 15}
Сначала расположите их по порядку:
{8 , 15, 19, 19, 28, 29, 35}
Здесь, 19это режим, поскольку он появляется дважды, а все остальные появляются только один раз.
Итак, как насчет более чем одного режима:У нас может быть более одного режима.
Да, иногда у нас может быть более одного режима.
Например:
{1, 3, 3, 3, 4, 4, 6, 6, 6, 9}
Пример: {1, 3, 3, 3, 4, 4, 6, 6, 6 , 9}
Здесь вы можете видеть, что 3 встречается три раза, как и 6.
Итак, это означает, что есть два режима, т.е. 3 и 6
Помните, что:
- Если ваш набор данных имеет два режима, то говорят, что он «бимодальный»
- Если ваш набор данных имеет более двух режимов, то он называется «мультимодальным»
Итак, подробнее о калькуляторе режимов!
О калькуляторе режимов: Калькулятор режимов — это интеллектуальный инструмент, который поможет вам вычислить значение режима набора чисел. Это означает, что этот калькулятор работает как средство поиска мод, которое помогает вам найти число, которое чаще всего встречается в наборе данных. Если набор данных имеет несколько режимов, лучше всего их найти с помощью калькулятора режимов.
Это означает, что этот калькулятор работает как средство поиска мод, которое помогает вам найти число, которое чаще всего встречается в наборе данных. Если набор данных имеет несколько режимов, лучше всего их найти с помощью калькулятора режимов.
Наш искатель мод довольно прост в использовании, все, что вам нужно, чтобы придерживаться заданных шагов, чтобы найти моду заданного набора данных в математике.
Ввод:
- Вы должны ввести набор данных, для которого вы хотите найти режим
- После того, как набор данных введен в указанное поле, нажмите кнопку расчета, этот калькулятор режимов покажет вам режим (наиболее распространенный), медиану, среднее значение, диапазон и определенные параметры для данного набора данных. .
Итак, читайте дальше, чтобы узнать определение диапазона в математике, пример расчета диапазона, как найти диапазон с помощью простого калькулятора диапазона и многое другое!
Что такое диапазон в математике? Математически диапазоном набора данных называется разница между наибольшим и наименьшим значением в наборе. Если вы хотите найти диапазон набора данных, вам следует упорядочить набор чисел от наименьшего к наибольшему, а затем вы должны вычесть наименьшее значение из наибольшего значения. Итак, давайте взглянем на приведенные шаги, и если вы хотите мгновенно найти диапазон чисел, просто попробуйте наш калькулятор диапазона среднего среднего режима.
Если вы хотите найти диапазон набора данных, вам следует упорядочить набор чисел от наименьшего к наибольшему, а затем вы должны вычесть наименьшее значение из наибольшего значения. Итак, давайте взглянем на приведенные шаги, и если вы хотите мгновенно найти диапазон чисел, просто попробуйте наш калькулятор диапазона среднего среднего режима.
Формула диапазона в математике:
Диапазон = наибольшее значение – наименьшее значение
Как вычислить диапазон чисел или набор данных:Например:
Допустим, набор данных содержит следующие числа:
{7, 8, 65, 8, 4, 7}.
- Прежде всего, вы должны расположить набор чисел в порядке от меньшего к большему. Ну вот как выглядит ваш набор данных: {4, 7, 7, 8, 8, 65}
- Теперь вы должны определить наименьшее и наибольшее число в наборе данных, в этом наборе данных наименьшее число равно 4, а наибольшее число равно 65
- Затем нужно вычесть наименьшее число из наибольшего.
 Наименьшее число 4, а наибольшее число 65, значит 65 — 4 = 61
Наименьшее число 4, а наибольшее число 65, значит 65 — 4 = 61 - Итак, диапазон этого конкретного набора данных составляет 61
Калькулятор диапазона работает эффективно как дальномер, который помогает вам вычислить диапазон чисел из заданного набора данных. В частности, калькулятор диапазона, который поможет вам найти разницу между наибольшим и наименьшим значением в наборе данных.
Как найти диапазон с помощью калькулятора диапазона:Да, расчет диапазона с помощью калькулятора становится довольно простым, вы просто выполняете указанные шаги, чтобы мгновенно найти диапазон заданного набора данных:
Ввод:- Все, что вам нужно, чтобы ввести свой набор данных в специальное поле дальномера
- После этого просто нажмите кнопку расчета, калькулятор диапазона мгновенно покажет вам значение диапазона набора данных, среднее значение, моду, медиану вместе с различными параметрами, которые вам нужно знать!
Чтобы найти это:
- Вы должны сложить все значения вашего набора данных и разделить на количество сложений, полученное значение называется средним значением набора данных
- Медиана называется средним числом набора данных в порядке от наименьшего к наибольшему
- Модой называется число, которое чаще всего встречается в вашем наборе данных
- Диапазон называется разницей между самым высоким и самым низким значениями в вашем наборе данных
Если вы не хотите зацикливаться на этих ручных вычислениях, просто введите свой набор данных в калькулятор диапазона среднего среднего режима и рассчитайте все за один раз!
Что делать, если в наборе данных нет моды? Режим набора данных указывает на число, которое встречается чаще всего. Если в вашем наборе данных нет числа, которое встречается чаще, чем любое другое, то это называется отсутствием режима для набора данных. Также возможно, что набор данных имеет более одного режима.
Если в вашем наборе данных нет числа, которое встречается чаще, чем любое другое, то это называется отсутствием режима для набора данных. Также возможно, что набор данных имеет более одного режима.
Предположим, что ваш набор данных:
8, 0, -3, 4, 12, 0, 5, -1, 0
Теперь, упорядочив набор данных от меньшего к большему, вы получите:
8, -3, -1, 0, 0, 0, 4, 5, 12
В этом наборе данных значение моды равно 0. во внимание, чтобы найти среднее (среднее) и диапазон вместе с медианой и модой для данного набора данных.
Ссылки:Из Википедии, свободной энциклопедии – Среднее (среднее) – Типы среднего – Среднее вероятностного распределения – Взвешенное арифметическое среднее – Среднее значение функции – также найдите моду, медиану, диапазон от источника из Википедии
Из источника wikihow – как найти медиану набора чисел – Найти медиану в нечетном и четном наборе чисел – Соавтор: Штатный редактор wikiHow
Из источника исследования – Как рассчитать среднее значение, медиану, моду и диапазон — меры центральной тенденции — и узнать больше обо всем!
Из авторизованного источника пурпурной математики — примеры среднего, медианы, моды и диапазона — узнайте больше о показателях центральной тенденции, диапазоне и различных параметрах
Калькулятор среднего, медианы, моды и диапазона
Среднее значение, медиана, мода и диапазон являются одними из важных понятий статистики. Все мы знаем, что статистика — это предмет, который целиком занимается данными или числами, их упорядочиванием и изучением. Когда у нас есть много данных, которые нужно изучить или проанализировать, важно иметь определенные параметры, которые сделают наше исследование лучше.
Все мы знаем, что статистика — это предмет, который целиком занимается данными или числами, их упорядочиванием и изучением. Когда у нас есть много данных, которые нужно изучить или проанализировать, важно иметь определенные параметры, которые сделают наше исследование лучше. Что подразумевает Центральная Тенденция?
Прежде чем перейти к знаниям о среднем значении, медиане и моде, нам нужно получить представление о термине, который очень важен для этих трех терминов — Центральная тенденция.
- Центральная тенденция — это статистический термин, представляющий центральную точку данного набора данных.
- Указывает, куда попадает большинство значений данного распределения данных.
- Центральную тенденцию можно представить как точку, вокруг которой группируются все значения заданного набора данных.

Теперь среднее значение, медиана, мода и диапазон являются такими центральными тенденциями, которые дают общее представление о данных данного набора данных. Каждый из них имеет свою методику расчета, и каждый из них передает различную картину данного набора данных. Давайте поймем это лучше, когда мы будем двигаться дальше.
Среднее
Это всем нам более знакомо. Нас использовали для расчета среднего значения заданного набора значений, и это среднее значение в статистике называется средним.
Среднее значение = Сумма всех значений или чисел в наборе данных, деленная на общее количество элементов в наборе данных.
Медиана
Данный набор данных может содержать значения из разных диапазонов. Их можно расположить таким образом, чтобы они располагались либо в порядке возрастания, либо в порядке убывания.
Когда вы упорядочиваете заданный набор данных либо в порядке возрастания, либо в порядке убывания, самое среднее значение является медианой данного набора данных.
Медиана = самый средний член данного набора данных, когда его значения расположены либо в возрастающем, либо в убывающем порядке.
Примечание. Если общее количество терминов четное, то среднее двух средних чисел является медианой данного набора данных.
Режим
В заданном наборе данных может быть много значений, которые повторяются или встречаются много раз в наборе данных. Такое число или значение, которое повторяется наибольшее количество раз в заданном наборе данных, называется его модой.
Режим = Значение или элемент, который повторяется наибольшее количество раз в заданном наборе данных.
Диапазон
Это разница между наибольшим и наименьшим значением заданного набора данных.
Диапазон = наибольшее значение – наименьшее значение
Пример
Рассмотрим пример данных, как показано ниже: 2, 5, 3, 6, 2, 6, 7, 9, 1.
Для этого набора данных значения средней медианы и моды следующие:
Среднее = (2 + 5 + 3 + 6 + 2 + 6 + 7 + 9 + 1) / 9 = 45 / 10 = 4,5
Медиана = Среднее значение (1,2,2,3,5,6,6,7,9) = 5
Mode = Наиболее повторяющиеся значения (1, 2, 2, 3, 5, 6, 6, 7, 9) = ( 2, 6 )
Диапазон = (наибольшее значение) 9 – (наименьшее значение) 1 = 8
Примечание. Те же расчеты остаются в силе, даже если значения в данном наборе данных представлены дробями или десятичными значениями. Нужна помощь по дробям или десятичным значениям? Проверьте наш онлайн-калькулятор дробей бесплатно.
Те же расчеты остаются в силе, даже если значения в данном наборе данных представлены дробями или десятичными значениями. Нужна помощь по дробям или десятичным значениям? Проверьте наш онлайн-калькулятор дробей бесплатно.
Математика — это не числа, уравнения, вычисления или алгоритмы; это о понимании. – Уильям Пол Терстон
Практическое применение среднего, медианы, моды и диапазона
Эти основные тенденции находят применение во многих статистических вычислениях. Например, в режиме реального времени рассмотрим центр обработки данных. Он содержит много оборудования, такого как серверы, охлаждающее оборудование, вентиляторы и т. д., которые потребляют электроэнергию. Датчики и интеллектуальные блоки питания используют эти основные тенденции для оценки различных статистических данных о мощности, потребляемой в данной стойке серверов и другого электрооборудования в центре обработки данных.
Кстати, знаете ли вы различные аспекты, которые учитываются при расчете стоимости электроэнергии? Проверьте их на нашем бесплатном онлайн-калькуляторе стоимости электроэнергии.
Как пользоваться калькулятором среднего, медианы, режима и диапазона CalculatorHut?
Этот бесплатный онлайн-калькулятор среднего, медианы, моды и диапазона от CalculatorHut позволяет вычислять эти значения для заданного набора данных. Вы можете ввести значения имеющегося у вас набора данных и очень легко рассчитать эти центральные тенденции.
Вы можете разместить это в виде виджета в своем блоге или на веб-сайте и сообщать читателям, сколько их устройство будет отображаться в ежемесячном счете за электроэнергию. Напишите нам по адресу [email protected], чтобы получить бесплатный настраиваемый виджет. CalculatorHut также имеет свое приложение с более чем 100 калькуляторами на различные темы — калькуляторы здоровья, финансовые калькуляторы, калькуляторы транспортных средств, математические калькуляторы, калькуляторы физики, калькуляторы химии и многие другие. Загрузите наше бесплатное приложение и носите мир вычислений в своем кармане.
Дайте нам знать, если вы хотите, чтобы мы добавили любой другой калькулятор в наш ассортимент. Мы будем рады служить вам. Удачных расчетов!!
Мы будем рады служить вам. Удачных расчетов!!
В реальной жизни не будь подлым! Будь медианой или модой!!
Калькулятор статистического среднего значения для среднего, медианы, моды и диапазона
Пример набора данных
Чтобы показать, как вычислять среднее значение, медиану, моду и диапазон, я буду использовать следующий набор данных:
36, 3, 8, 12, 15, 18, 22, 34, 8, 25, 17, 13, 23
Как вычислить среднее значение?
Среднее — это среднее всех чисел в наборе данных. Чтобы вычислить среднее значение набора чисел, вы складываете все числа вместе, а затем делите эту сумму на количество элементов в наборе.
| Набор данных: 36, 3, 8, 12, 15, 18, 22, 34, 8, 25, 17, 13, 23 36 + 3 + 8 + 12 + 15 + 18 + 22 + 34 + 8 + 25 + 17 + 13 + 23) ÷ 13 |
| Среднее значение = 234 ÷ 13 |
| Среднее значение = 18 |
Как вычислить медиану?
Медиана — это среднее число в наборе данных после сортировки набора данных от меньшего к большему. Чтобы вычислить медиану набора данных, вы подсчитываете количество элементов, а затем сортируете элементы от меньшего к большему. Далее, для нечетного числа элементов вы добавляете 1 к количеству элементов, а затем делите на 2, чтобы получить положение среднего числа. Из нашего примера набора данных медиана — это 7-е число в отсортированном списке, то есть число 17.
Чтобы вычислить медиану набора данных, вы подсчитываете количество элементов, а затем сортируете элементы от меньшего к большему. Далее, для нечетного числа элементов вы добавляете 1 к количеству элементов, а затем делите на 2, чтобы получить положение среднего числа. Из нашего примера набора данных медиана — это 7-е число в отсортированном списке, то есть число 17.
| Набор данных с нечетными номерами: 36, 3, 8, 12, 15, 18, 22, 34, 8, 25, 17, 13, 23 | |||||||||||||||||||||||||||
Количество элементов в наборе 171 81 | |||||||||||||||||||||||||||
| Средняя позиция = ((13 + 1) ÷ 2) | |||||||||||||||||||||||||||
| Средняя позиция = (14 ÷ 2) | |||||||||||||||||||||||||||
| Средняя позиция = 7 0 7 7 | |||||||||||||||||||||||||||
| Количество | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | ||||||||||||||
| Data Set | 3 | 8 | 8 | 12 | 13 | 15 | 17 | 18 | 22 | 23 | 25 | 34 | 36 | ||||||||||||||
| Median = 17 (7th number in sorted data set) | |||||||||||||||||||||||||||
Note that for an даже числа элементов, вы найдете среднее из двух средних чисел. Первая средняя позиция будет равна количеству элементов, разделенному на 2 минус 1. Вторая средняя позиция будет первой средней позицией плюс 1. Затем вы сложите два средних числа вместе и разделите на 2, чтобы найти среднее значение. Из нашего исправленного примера набора данных это дает вам среднее значение 16, что является средним значением 6-го и 7-го элементов (15 и 17).
Первая средняя позиция будет равна количеству элементов, разделенному на 2 минус 1. Вторая средняя позиция будет первой средней позицией плюс 1. Затем вы сложите два средних числа вместе и разделите на 2, чтобы найти среднее значение. Из нашего исправленного примера набора данных это дает вам среднее значение 16, что является средним значением 6-го и 7-го элементов (15 и 17).
| Четный набор данных: 36, 3, 8, 12, 15, 18, 22, 34, 8, 25, 17, 13 | ||||||||||||
| Количество элементов в наборе 12 | ||||||||||||
| 1-я средняя позиция = (число ÷ 2) — 1 | ||||||||||||
| 1-я средняя позиция = (12 ÷ 2) — 1 = 1-я средняя позиция | ||||||||||||
| 2 -я средняя позиция = 1 -я средняя позиция + 1 | ||||||||||||
| 2 -я средняя позиция = 6 + 1 = 7 | ||||||||||||
| 2 -е среднее число = 17 | ||||||||||||
| Среднее число средних чисел = (15 + 17 = 17 | ||||||||||||
. ) ÷ 2 = 16 ) ÷ 2 = 16 | ||||||||||||
| Count | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Data Set | 3 | 8 | 8 | 12 | 13 | 15 | 17 | 18 | 22 | 25 | 34 | 36 |
| Медиана = 16 (среднее значение 15 и 17) | ||||||||||||
Как рассчитать моду?
Режим — это число в наборе данных, которое наиболее часто повторяется в наборе. Чтобы найти режим, вы просто подсчитываете, сколько раз каждое уникальное число появляется в наборе данных. Число, которое появляется чаще всего, является режимом. В нашем примере набора данных чаще всего встречается число 8. Следовательно, мода набора данных — 8.
| Набор данных: 36, 3, 8, 12, 15, 18, 22, 34, 8, 25, 17, 13, 23, | ||||||||||||||||
| Сортированный набор данных | 3 | 8 | 3 | 8 | 8 | 12 | 13 | 15 | 17 | 18 | 22 | 23 | 25 | 34 | 36 | |
| Mode = 8 (8 appears the most often) | ||||||||||||||||
Обратите внимание, что набор данных может иметь более 1 режима. Например, если бы приведенный выше набор данных включал еще 3, то набор имел бы две моды: 3 и 8. Набор данных, имеющий две моды, называется 9.0140 бимодальный набор , тогда как набор данных, имеющий более двух режимов, называется мультимодальным набором .
Как рассчитать диапазон?
Диапазон — это разница между наибольшим числом в наборе и наименьшим числом в наборе. Чтобы найти диапазон, вы сортируете диапазон от меньшего к большему, чтобы определить минимальное и максимальное значения. Затем вы вычитаете минимальное значение из максимального значения, чтобы найти диапазон. В нашем примере минимальное значение равно 3, а максимальное — 36, что дает диапазон 33 (36 — 3).
Чтобы найти диапазон, вы сортируете диапазон от меньшего к большему, чтобы определить минимальное и максимальное значения. Затем вы вычитаете минимальное значение из максимального значения, чтобы найти диапазон. В нашем примере минимальное значение равно 3, а максимальное — 36, что дает диапазон 33 (36 — 3).
| Набор данных: 36, 3, 8, 12, 15, 18, 22, 34, 8, 25, 17, 13, 23 | ||||||||||||||||
| Сортируемые данные | 3 9003 | 8 80007 | 3 | 8. | 8 | 12 | 13 | 15 | 17 | 18 | 22 | 23 | 25 | 34 | 36 | 36 | 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 900036 9000 |


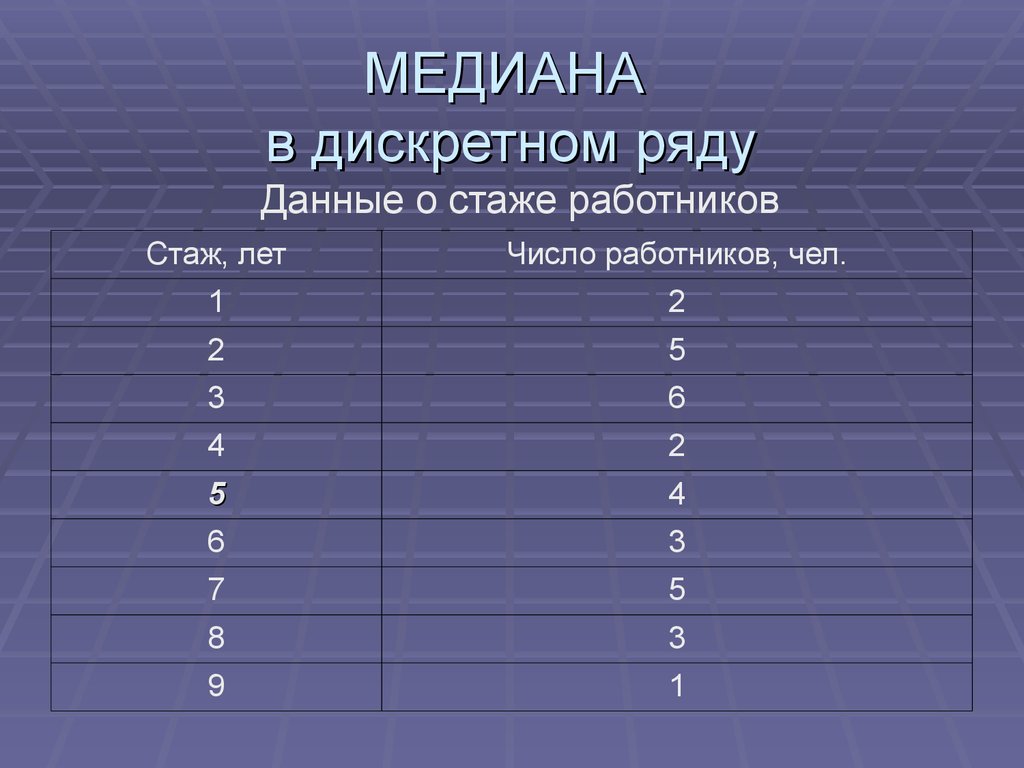
 тг) на начало каждого месяца:
тг) на начало каждого месяца:
 5
5