Формулы квадратичной функции: Построение графика квадратичной функции — урок. Алгебра, 8 класс.

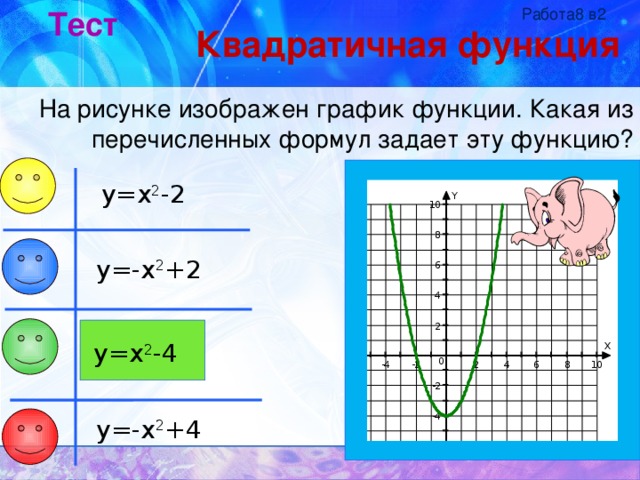
Свойства функции и её график. Взаимное расположение графика квадратичной функции и оси абсцисс.

О. Функция, задаваемая формулой называется квадратичной функцией.

Свойства:

1. Область определения функции: .

, т.к. значение квадратного трехчлена однозначно определено для любого действительного числа (почему?).

2. Множество значений функции:

Преобразуем квадратный трехчлен, задающий квадратичную функцию, выделив полный квадрат:

Введем обозначения: тогда .

Выражение может принимать любые неотрицательные значения в зависимости от x. Поэтому, при , а при

3. Периодичность:

Квадратичная функция не может быть периодической, т. к., например, свое значение она

принимает только в одной точке .

4. Чётность/нечётность

Если , то функция является функцией общего вида (не является ни четной, ни нечетной), т.к. , то есть и

Если , то функция имеет вид и , значит функция четная.

5. Точки пересечения графика с осями координат.

Точки пересечения с осью :

Точки пересечения с осью : , корни этого уравнения существуют, если , в противном случае точек пересечения с осью абсцисс нет.

Если , то точка пересечения одна и имеет координаты

Если , то квадратное уравнение имеет два корня, которые вычисляются по формулам: ,

Поэтому точек пересечения с осью две, и они имеют координаты и

6. Промежутки знакопостоянства функции:

Если : , то выражение вида для всех .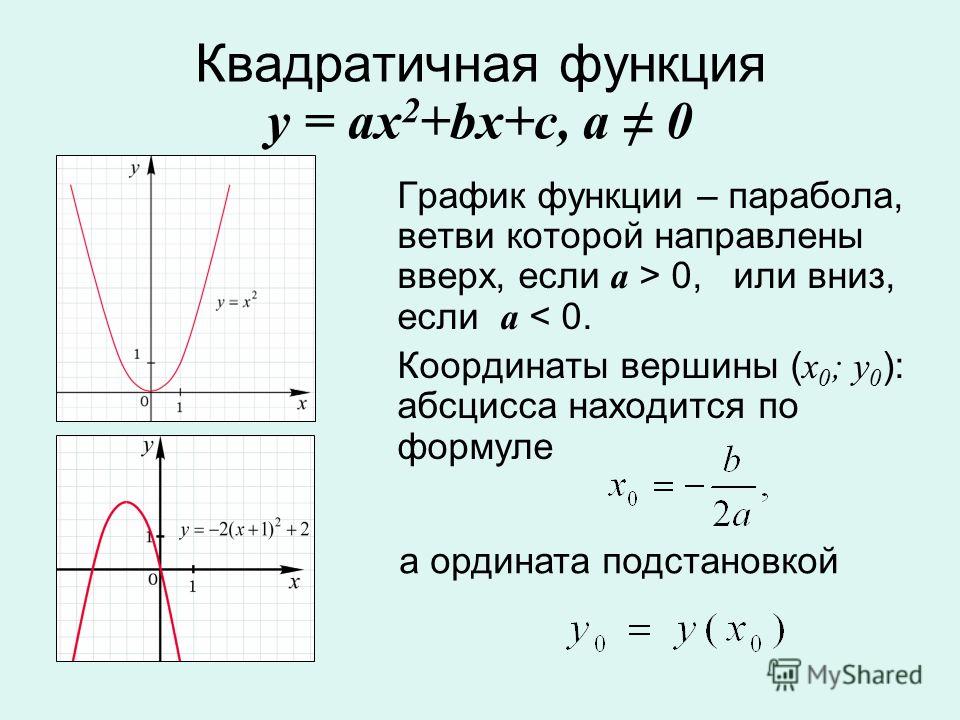 Значит, , .

: , тогда ,

: , где — корни уравнения .

Тогда при значения выражений, стоящих в скобках, будут иметь одинаковые знаки, значит, их произведение будет положительным, и при на данных промежутках квадратичная функция будет принимать положительные значения, а при — отрицательные.

Если , то наоборот, знаки выражений в скобках будут разными и, следовательно, из произведение будет отрицательным.

Тогда при на данном промежутке функция принимает отрицательные значения, а при — положительные.

7. Интервалы возрастания/убывания

Теорема.

Если , то функция является возрастающей при и убывающей при

Если , то функция является возрастающей при и убывающей при

Доказательство:

Пусть .

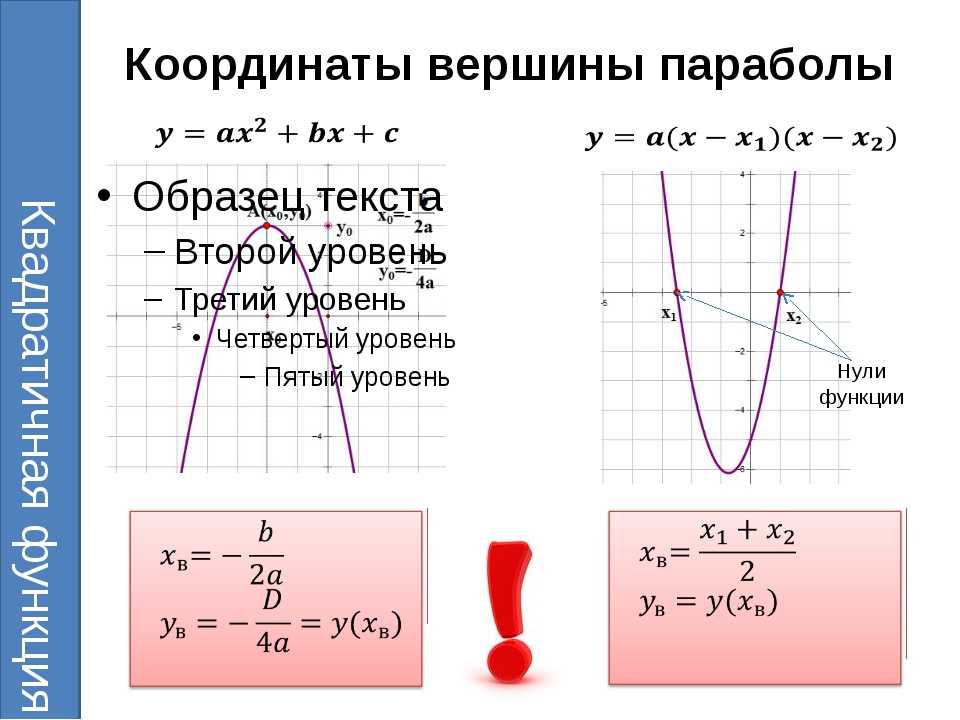
Рассмотрим разность значений квадратичной функции в точках , таких, что

при чем, . Тогда все три сомножителя в полученном выражении положительны. Это означает, что , т.е. , значит, если , то функция является возрастающей при .

Если , тогда последний сомножитель отрицателен (как сумма двух отрицательных чисел), а первые два положительны, тогда их произведение – отрицательно.

Т аким образом, , и функция убывает при .

Случай рассматривается аналогично (рассмотрите его самостоятельно).

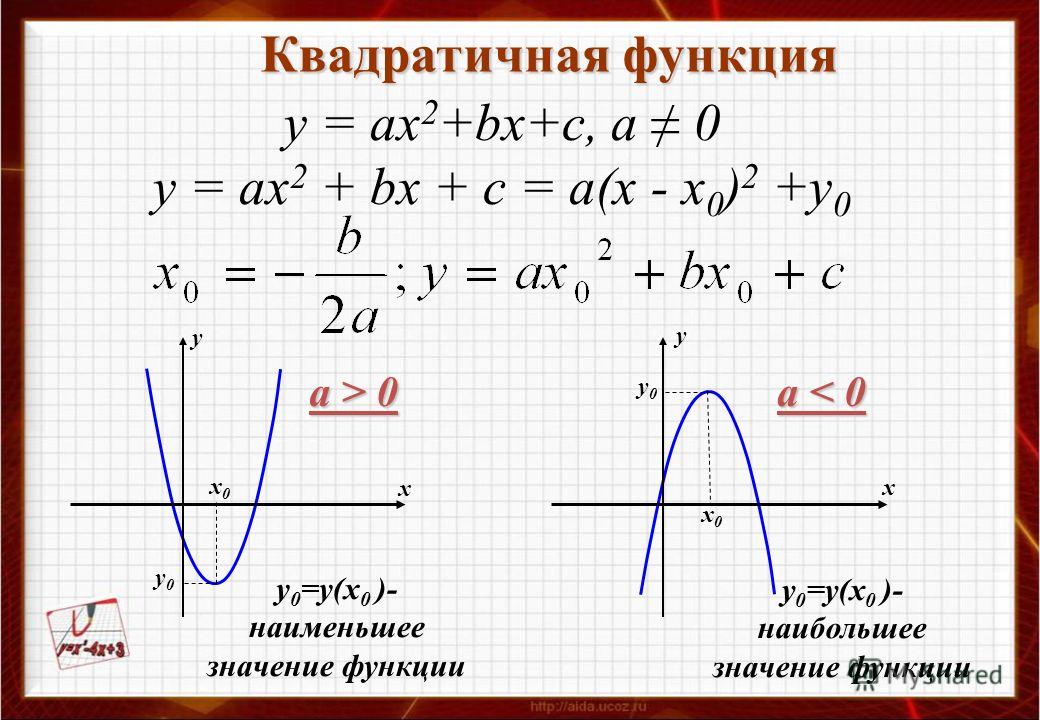
8. Наибольшее/наименьшее значение функции

Так как при функция возрастает на и убывает на , то при функция принимает наименьшее значение, и оно равно .

При функция возрастает на и убывает на , поэтому при функция принимает наибольшее значение и оно равно .

Формула квадратичной функции — GeeksforGeeks

Функцией называется алгебраическая функция, которую можно определить как корень полиномиальной функции. Это алгебраические выражения, содержащие конечное число членов, которые содержат как константы, так и переменные. Существует много типов алгебраических функций, некоторые из них — линейная функция, квадратичная функция, кубическая функция и т. д. Примеры:

• 2x ⇢ линейная функция
• x ² + 2x + 3 ⇢ квадратичная функция
• x ³ + x ² + 6x + 9 ⇢ кубическая функция

Формула квадратичной функции является полиномиальной функцией с одной или несколькими переменными. Стандартная форма квадратного уравнения:

f(x) = ax ² + bx + c , это говорит о том, что хотя бы один член в данном уравнении возведен в квадрат. В приведенном выше уравнении a, b, c — постоянные члены, а x — переменные.

f(x) = ax ² + bx + c,

Где a не равно 0, а a, b, c — действительные числа.

Степень полинома = 2.

Примеры квадратичных функций:

1. 4x ² + 3x + 5
2. 6x ² + x + 7
3. 7x ² + 5x
4. 9x ^2.

Любое уравнение имеет n корней, где n — степень многочлена. Корни квадратного уравнения равны

x = (-b ± √ (b²-4AC))/2a

Деривация для корней квадратичного уравнения

AX ² + BX + C = 0

1. СТАРЬ С AX ^{2 2} + B + C = 0
   1. . + bx + c=0
   2. Разделите уравнение на a x ² + (b/a) + c/a = 0
   3. Поместите c/a на другую сторону x ² + (b/a) x = -c/a
   4. Добавить (b/2a) ² в обе стороны x ² + (b/a)x + (b/2a) ² = -c/a + (b/2a) ²
   5. Левая сторона теперь имеет формат x ² + 2dx + d ² , где «d» — это «b/2a»

   Итак, перепишите это так: Квадрат” (x+b/2a) ² = -c/a + (b/2a) ²

Существуют различные типы корней квадратного уравнения, 

Чтобы найти природу корней, мы используем термин, называемый дискриминантом . Термин называется дискриминантом , потому что он определяет корни квадратного уравнения на основе его знака.

Существует 3 типа в природе корней, 

• Действительные и различные корни

Для действительных и различных корней дискриминант должен быть положительным, т.е. кривая уравнения пересекает ось x в двух разных точках.

• Действительные и равные корни

Для действительных и равных корней дискриминант равен нулю, т.е. b ² – 4ac = 0, Кривая уравнения пересекает ось x только в одной точке.

• Комплексные корни

Для комплексных корней дискриминант отрицателен, т.е.

Примеры задач

Вопрос 1: Запишите квадратичную функцию f(x) = (x – 9)(x + 3) в общем виде ax ² + bx + c.

Решение: 

Учитывая, функция как (x – 9)(x + 3)

= x ² + 3x – 9x – 27

= x ² – 6x – 27 является общей формой .

Вопрос 2: Найдите константы a, b, c в общей форме уравнения 4x ² + 5x + 9 = 0.

Ответ:

2 ^{x 90 равно 90 2} + 5x + 9 = 0, общее уравнение квадратного уравнения равно ax ² + bx + c = 0.

Следовательно, из ссылки на общее уравнение, a = 4, b = 5, c = 9.

Вопрос 3: Напишите квадратичную функцию f(x) = (x + 8)(x – 3) в общем виде ax ² + bx + c.

Решение :

Дана функция вида (х + 8)(х – 3)

= х ² – 3х + 8х – 24

= х 2900 общий вид

Вопрос 4: Найдите корни уравнения 2x ² – 4x + 2 = 0.

Решение: 

Здесь a = 2, b = -4, c = 2, чтобы найти корни уравнения, сначала нам нужно найти значение дискриминанта который помогает нам узнать природу корней.

дискриминант = b ² – 4ac = (-4) ² – 4(2)(2) = 16 – 16 = 0, что равно нулю. Значит, оно имеет действительные и равные корни.

корни = (−b ± √(b ² − 4ac)) / 2a

= (-(-4) ± √(0)) / 2(4) )

= 1 — корень уравнения.

Вопрос 5: Найдите корни уравнения 4x ² – 3x + 3.

Решение: 

Здесь a = 4, b = -3, c = 3, чтобы найти корни уравнения, сначала нам нужно найти значение дискриминанта, которое поможет нам узнать природу корней.

дискриминант = b ² – 4ac = (-3) ² – 4(4)(3) = 9 – 48 = -39, что отрицательно. Значит, у него сложные корни.

корни = (−b ± √(b ² − 4ac)) / 2a

= (-(-3) ± √-39 / 2(4) )

= (3 ± 39i)/8 корни квадратного уравнения.

Вопрос 6: Найдите корни квадратного уравнения 6x ² – 8x + 2 = 0.

Решение:

Здесь a = 6, b = 2, to -8, c найти корни уравнения, сначала нам нужно найти значение дискриминанта, которое поможет нам узнать природу корней.

дискриминант = b ² – 4ac = (-8)(-8) – 4(6)(2) = 64 – 48 = 16, что положительно. Итак, оно имеет реальные и отчетливые корни.

 x = (-b ± √ (b² – 4ac))/2a

= (-(-8) ± √((-8)(-8) – 4(6)(2))) / 2( 6)

= ( 8 ± √16) / 12

=  ( 8 ± 4)12

= 1/3 и 1 являются корнями уравнения.

Счет, математика и статистика — набор академических навыков

Квадратные уравнения и функции (экономика)

ContentsToggle Главное меню 1 Квадратные уравнения 2 Факторизация 2.1 Метод: when $a eq1$2.2 Видео Пример 3 Квадратная формула 4 Одновременное квадратичное уравнение 5 Квадратичные функции 6 Кубические функции 7 Рабочая тетрадь 8 Проверь себя 92+bx+c=0\], где $a\neq 0$, где $x$ — переменная, а $a,b$ и $c$ — константы.

Другими словами, это уравнение, в котором максимальная степень переменной (обычно $x$) равна $2$.

Решение квадратного уравнения означает нахождение значений $x$, удовлетворяющих уравнению (приравняем выражение слева от знака $=$ к нулю). Эти значения $x$ называются решением квадратного уравнения. Квадратные уравнения могут иметь два, одно или не иметь действительных решений. Решения квадратного уравнения соответствуют корням квадратной функции.

Существует два широко используемых метода решения квадратных уравнений: факторизация и квадратичная формула.

Факторизация

В некоторых случаях можно записать квадратное выражение в левой части квадратного уравнения как произведение двух линейных выражений, каждое из которых заключено в пару квадратных скобок. Запись квадратичного числа таким способом известна как факторизация квадратного числа или просто факторизация , потому что она включает в себя нахождение 92+(r+s)x+rs=0$ дает $(x+r)(x+s)$. Таким образом, корнями этого уравнения являются $(-r)$ и $(-s)$, так как мы можем видеть, что при подстановке любого из этих значений вместо $x$ выражение в одной из пар скобок становится равным нулю ( проверьте!), поэтому уравнение выполняется.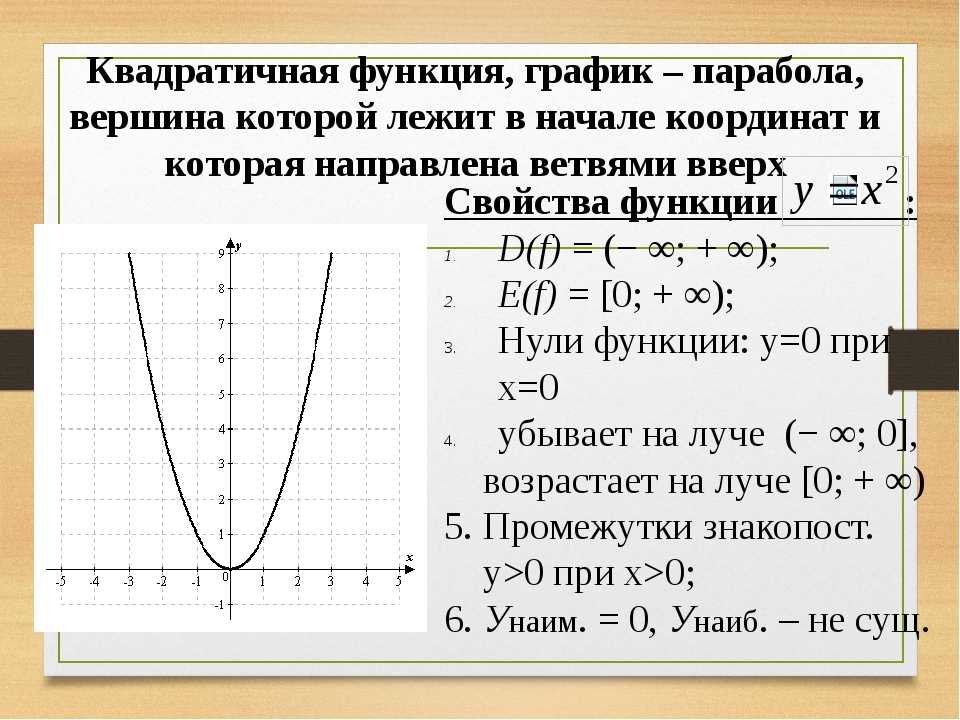

Мы знаем, что факторизация обратна раскрытию скобок. Поэтому раскрытие скобок — полезный способ проверить, правильно ли вы разложили квадратное выражение на множители. Убедитесь сами, что приведенная выше факторизация верна, раскрыв скобки. 9Тогда 2+5x+6$ равно $(x+A)(x+B)$, а корнями уравнения являются $(-A)$ и $(-B)$. Хороший способ отслеживать возможности для $A$ и $B$ — составить таблицу, в которой перечислены все значения для $A$ и $B$, произведение которых равно $6$:

1	6	6	7
(-1)	(-6)	6	(-7)
2	3	6	5
(-2)	(-3)	6	(-5)

Примечание : Для каждой пары чисел не имеет значения, что мы помещаем в «столбец A», а какое — в «столбец B».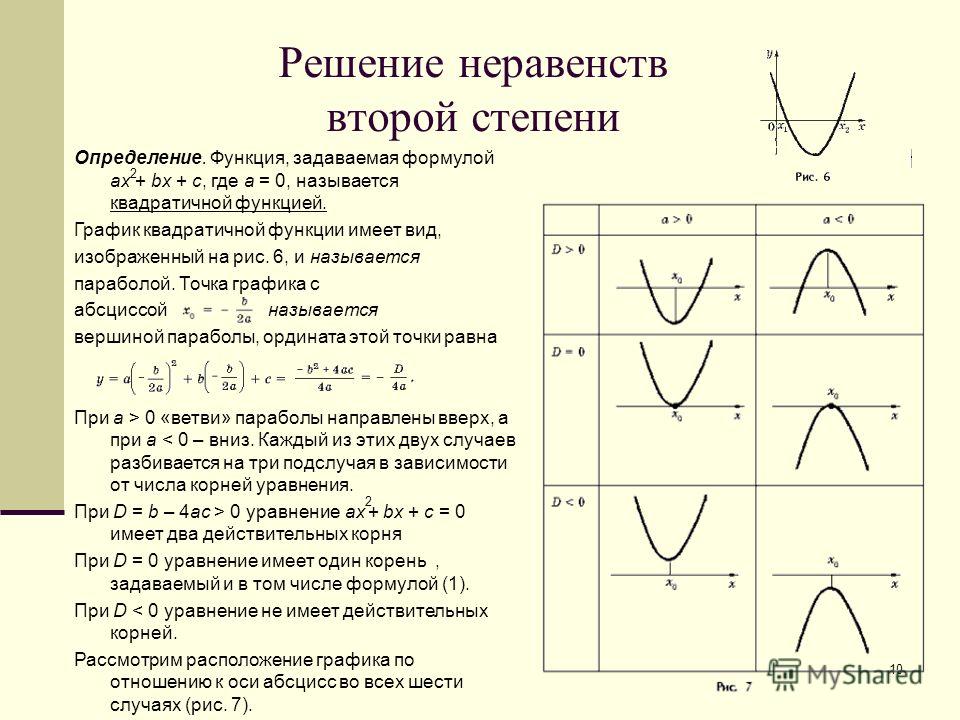 92-4ac\lt0$ действительных корней нет (каждый корень будет содержать мнимое число).

Дополнительную информацию и примеры использования квадратичной формулы для решения квадратных уравнений см. в разделе Квадратичная формула.

Одновременные квадратные уравнения

Мы можем решать пары одновременных квадратных уравнений. См. Решение одновременных линейных уравнений (экономика) для напоминания о том, как решать одновременные уравнения. Одновременные квадратные уравнения могут иметь до $2$ пар решений. 92+6x-20=0 \end{align} Теперь у нас есть одно квадратное уравнение, которое мы можем решить, используя описанные выше методы. Поскольку это уравнение сложно разложить на множители, мы будем использовать квадратичную формулу. Это дает $x=-5$ или $x=2$ (проверьте сами). Подстановка $x=-5$ в уравнение $\textbf{(2)}$ дает: \begin{align} y&-(-5)=3\\ \Rightarrow &y=-2 \end{align} So $x= -5$ и $y=-2$ — одно из решений. Сейчас мы найдем другое решение.

Подстановка $x=2$ в уравнение $\textbf{(2)}$ дает: \begin{align} y&-2=3\\ \Rightarrow &y=5 \end{align} Таким образом, другое решение $x=2 $ и $y=5$. 92+bx+c=0$ с помощью факторизации или квадратичной формулы.

График квадратичной функции имеет U-образную форму и называется параболой . Точка, в которой парабола меняет направление, называется точкой поворота функции.

Если $a\gt0$, то у нас есть парабола, открывающаяся вверх, которая выглядит как эта $\cup$, а точка поворота называется глобальным минимумом, потому что это точка, в которой график функции находится на

самом низком уровне. .

Если $a\lt0$, то у нас есть парабола, открывающаяся вниз, которая выглядит как эта $\cap$, а точка поворота называется глобальным максимумом, потому что это точка, в которой график функции достигает своего максимума .

Абсолютное значение $a$ определяет крутизну кривых параболы. Чем больше абсолютное значение $a$, тем круче кривая.