Формулы окружность геометрия: Формулы, как найти площадь круга

Содержание

какая основная, тригонометрические, математическая и геометрическая

Содержание:

Что такое окружность — определение и свойства
Через какие параметры ее можно найти
Формула длины окружности
Формула диаметра окружности
Формула радиуса окружности
Примеры задач с решением

Содержание

Что такое окружность — определение и свойства

Через какие параметры ее можно найти
Формула длины окружности
Формула диаметра окружности
Формула радиуса окружности
Примеры задач с решением

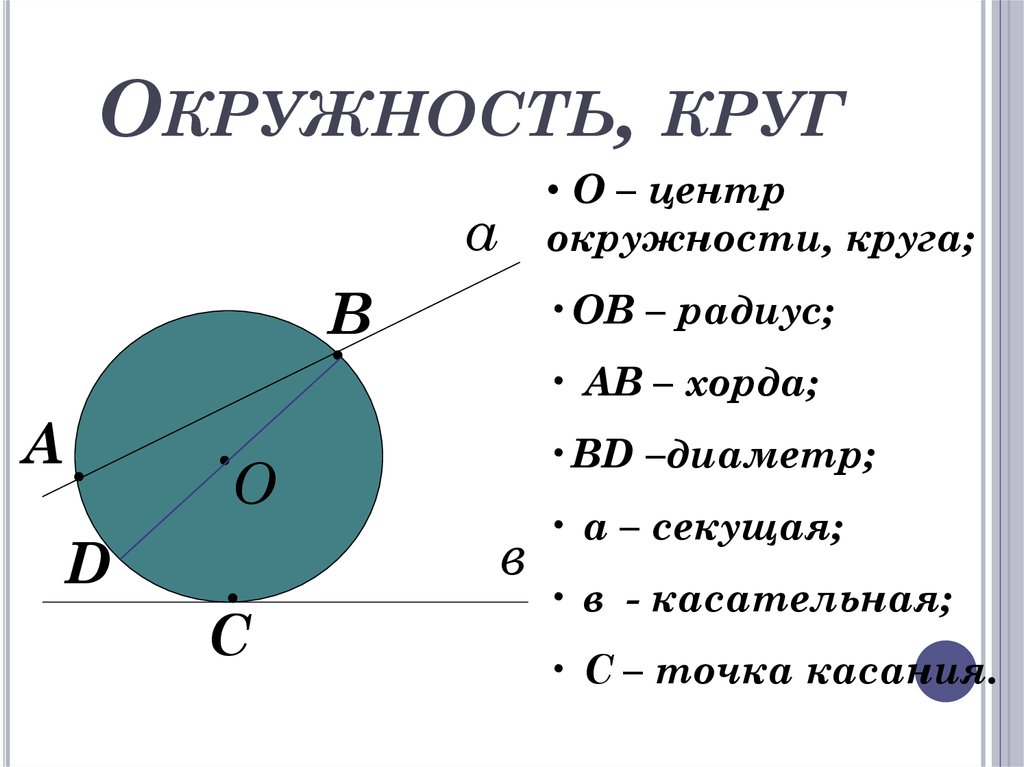
Что такое окружность — определение и свойства

Определение

Окружность является совокупностью множества точек, расположенных на плоскости, и равноудаленных от определенной точки О, которая представляет собой центр окружности.

Определение

Единичной окружностью называют такую окружность, радиус которой равен единице.

Определение

Круг представляет собой часть плоскости, которая ограничена окружностью.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Окружность обладает рядом характерных свойств:

Диаметр окружности в два раза больше, чем радиус окружности: D = 2r.
Минимальное расстояние от центра окружности к секущей (хорде) в любом случае меньше, чем радиус окружности.
Если существуют три точки, расположенные не на одной прямой, то через них можно провести единственно возможную окружность.
Из всех замкнутых кривых, обладающих аналогичной длиной, окружность обладает максимально возможной площадью.

При соприкосновении пары окружностей в определенной точке, эта точка расположена на прямой, которая проходит через центры заданных окружностей. {2} \)
Параметрическое уравнение окружности, которая имеет радиус r и центр в точке с координатами (a, b) в декартовой системе координат, записывают следующим образом:
$\begin{cases}x = a + r cos t\\y = b + r sin t\end{cases} $
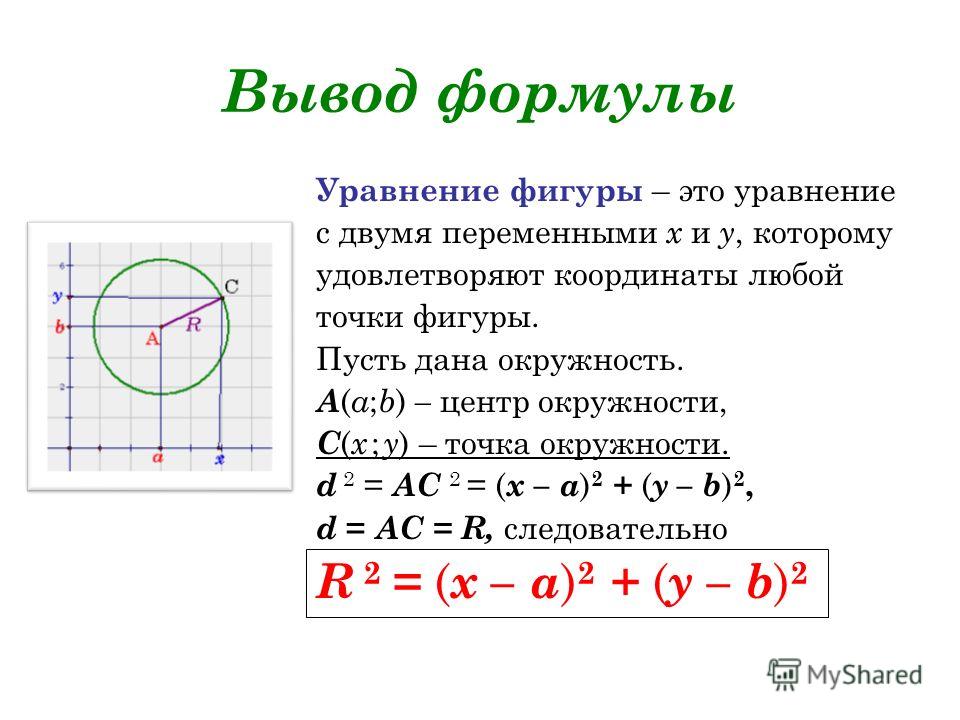
Формула длины окружности
Определение
Длиной окружности является длина замкнутой плоской кривой, которая ограничивает круг.
Длину окружности можно определить, зная ее диаметр:
$L = \pi D$
При известном радиусе длину окружности можно вычислить по формуле:
$L = 2\pi r$
Формула диаметра окружности
Определение
Диаметр окружности D является отрезком, соединяющим пару точек окружности и проходящим через ее центр.
Существует две формулы для определения диаметра окружности через радиус и длину:
$d = 2 * R$
$d = \frac{C}{\pi}$
Формула радиуса окружности
Определение
Радиус окружности R является геометрическим расстоянием, на которое удалена любая точка окружности от ее центра О. {2} = 6084\)
Ответ: площадь квадрата составляет 6084.
Задача 2
Диаметр окружности равен 5 см. Необходимо определить, какова длина заданной окружности.
Решение
Длину окружности можно рассчитать по формуле:
$L = \pi D$
Исходя из условий задачи, подставим значение диаметра в уравнение и выполним вычисления:
L = 3,14 * 5 = 15,7 (см)
Ответ: длина окружности равна 15,7 см.

Задача 3
Существует окружность с радиусом 3,5 м. Требуется определить длину данной окружности.
Решение
В первую очередь следует определить величину диаметра рассматриваемой окружности:
D = 2r = 3,5 * 2 = 7 (м)
Далее можно рассчитать длину окружности:
$L = \pi D = 3,14 * 7 = 21,98 (м)$
Ответ: длина окружности составляет 21,98 м.
Задача 4
Длина окружности составляет 7,85 м. Требуется определить радиус этой окружности.
Решение
Рассчитать радиус окружности, зная ее длину, можно путем деления длины на $2\pi:$
$R = \frac{C}{2\pi}$
Таким образом:
$R = \frac{7,85}{2 * 3,14} = \frac{7,85}{6,28} = 1,25 (м)$
Ответ: радиус окружности равен 1,25 м.

Насколько полезной была для вас статья?
У этой статьи пока нет оценок.

Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»

Поиск по содержимому

Урок геометрии в 9-м классе «Длина окружности»

О, сколько нам открытий чудных
Готовит просвещенья дух,
И опыт, сын ошибок трудных,
И гений, парадоксов друг,
И случай, бог изобретатель….

А.С. Пушкин
Цели:
1. Образовательные: ввести формулу длины окружности путем поисковой, исследовательской деятельности, показать перспективы ее использования при решении задач практического содержания, использовать материалы из истории открытия формулы и жизни выдающегося древнегреческого ученого Архимеда.
2. Воспитательные: воспитание патриотизма, целеустремленности, стремления к получению знаний.
Ход урока
I. Вводная беседа.
Тема нашего сегодняшнего занятия “Длина окружности”.
Что такое окружность? Как измерить её длину? Наглядное представление о длине окружности можно получить следующим образом. Представим себе нить в форме окружности. Разрежем её и растянем за концы. Длина полученного отрезка и есть длина окружности. Но не всегда длину окружности можно измерить с помощью нити. Поэтому вопрос о нахождении формулы для вычисления длины окружности волновал учёных с давних времён. И найти такую формулу посчастливилось древнегреческому учёному физику, математику, механику, изобретателю - Архимеду, жившему в III веке до н.э. Имя это вам уже знакомо. Вспомните, какие открытия Архимеда вы уже знаете?
1. Закон Архимеда о вытеснении объёма жидкости, равному объёму тела, погружённого в жидкость. Именно при открытии этого закона Архимед впервые произнёс “Эврика”, что означает “Нашёл”.
2. Архимед доказал, что медианы треугольника пересекаются в одной точке.
3. Архимед вывел формулу суммы бесконечной геометрической прогрессии.
Как математик Архимед много работал по изучению различных кривых. Одна из таких кривых - окружность. Архимед проделал тысячи измерений, чтобы найти формулу для вычисления длины окружности. Чтобы понять суть этого вывода я предлагаю вам выполнить практическую работу.
II. Практическая работа.
Оборудование: предмет, содержащий окружность; нить, линейка, циркуль, микрокалькулятор.
Ход работы
1. Измерить длину окружности l.
2. Измерить диаметр окружности D.
3. Найти отношение
Сравним отношения, которые у вас получились. Все они равны приближённо одному и тому же числу. Это число Архимед обозначил .
= 3,14159…(при вычислении используется 3,14).
Правило запоминания числа “Это я знаю и помню прекрасно”. (Количество букв в каждом слове этой фразы равно соответствующей цифре в записи числа ). Таким образом, мы установили, что отношение длины окружности к диаметру не зависит от окружности, т.е. одно и то же для всех окружностей. Отсюда l = D учитывая, что D=2R,

l = 2R
Вот такой изящный вывод длины окружности предложил Архимед.
III. Материалы из истории математики.
Об открытии этого великого учёного, о его проницательности и предвидении можно говорить много. На основании его исследований другими учёными Ньютоном и Лейбницем было открыто, через несколько тысячелетий, интегральное исчисление. Именно об Архимеде Ньютон говорил: “Мне было легче, я стоял на плечах гигантов…”.
Архимед был патриотом и помогал своему народу в борьбе с захватчиками. Когда римские легионеры направляли свои корабли к его родному острову Сицилия (местечко Сиракузы), он придумал способ поджигания вражеских кораблей с помощью больших зеркал, сфокусировав лучи солнца в одну точку. Корабли горели прямо на воде, и завоеватели вынуждены были отступить. Винт Архимеда применяется в различных машинах, служит для подъёма сыпучих грузов, перемещает детали на заводах. Архимед постоянно находился в поиске, им владел дух просвещения. И, может быть, о нём наш великий русский поэт А.С.Пушкин написал слова, которые являются эпиграфом к нашему сегодняшнему занятию.
IV. Закрепление изученного материала.
Решение задач практического содержания с применением формулы длины окружности. (Можно использовать любые задачи по данной теме. Например, из учебника Геометрия 7-9 Л.С. Атанасяна).
Задача 1.
Диаметр основания царь-колокола, находящегося в Московском Кремле, равен 6,6 м. Найдите длину окружности основания колокола.
Задача 2.
Тепловоз прошел 1413 м. Найдите диаметр колеса тепловоза, если известно, что оно сделало 300 оборотов.
Задача 3.
Вычислите длину круговой орбиты искусственного спутника Земли, если спутник вращается на расстоянии 320 км от Земли, а радиус Земли равен 6370 км.
V. Итоги урока.
Мы сегодня познакомились с замечательным открытием Архимеда, вывели формулу длины окружности. Работа по изучению гладких кривых продолжилась и после Архимеда. В настоящее время открыты замечательные кривые, свойства которых используются в народном хозяйстве. Вот некоторые примеры:

Цепная линия используется в расчетах, связанных с провисанием нитей — проводов, тросов.

Циклоида имеет непосредственное отношение к изобретению маятниковых часов.

Трактриса сыграла выдающуюся роль в связи с открытием Лобачевским неевклидовой геометрии.

Циссоида облегчила поиски решения задачи об удвоении куба.
P.S.
Для проведения урока оформляется стенд, где помещены материалы:
1. О жизни Архимеда и его открытиях.
2. Изображения окружности, ее диаметра и радиуса.
3. Последовательность выполнения практической работы.
4. Сведения о замечательных кривых с их изображением.
Кругов Формулы и теоремы | GMAT GRE Geometry Tutorial
Вот краткий обзор всестороннего члена семейства геометрических фигур — круга. В этом руководстве мы рассмотрим основные понятия, свойства, формулы и теоремы, необходимые для решения вступительных экзаменов MBA и MS.
Определение: Окружность — это простая замкнутая фигура, в которой все точки, лежащие на ней, равноудалены от точки, называемой центром.
Вот круг с центром O.
Вот некоторые основные сведения о круге и его свойствах:
Радиус : Отрезок, соединяющий центр круга с любой точкой на круге, называется радиусом. OB, OA, OX, OY — разные радиусы окружности на рисунке выше. Для любой окружности можно нарисовать бесконечное количество радиусов.
Диаметр : Отрезок, который проходит через центр и соединяет две точки на окружности, называется диаметром.

АВ — диаметр окружности. Как и в случае с радиусом, в окружности можно изобразить бесконечное количество диаметров.
Диаметр = 2 * радиус Или
Радиус = Диаметр / 2
Хорда : Отрезок, соединяющий любые две точки на окружности, является хордой. По кругу можно провести бесконечное количество хорд. XY — хорда окружности.
По-видимому, диаметр — это самая длинная хорда окружности.
Окружность:
Мерой расстояния вокруг края круга является длина окружности круга.
Длина окружности определяется по формуле
C = 2pr
Где C — длина окружности, а r — радиус.
Поскольку 2*радиус = диаметр, длина окружности также определяется как
C = pd
Значение p приблизительно равно 22/7 или 3,14159.

Площадь:
Площадь круга определяется по формуле
A = pr ²
Где r — радиус круга.
Поскольку r=d/2, площадь также определяется как
A = pd ² /4
Дуги и сектора :
Дуга является частью окружности окружности. XY — это дуга на рисунке выше.
Сектор – это площадь, покрываемая двумя радиусами и соединяющей их дугой. XLY и XOY — это два сектора на рисунке выше.
Длина дуги определяется по формуле (x/360) * 2pr
Площадь сектора определяется по формуле (x/360) * pr ²
Где x — угол, образуемый дуга и r радиус.
Центральный угол: Угол, одна вершина которого лежит в центре окружности, является центральным углом. ∠XOY — центральный угол на рисунке выше.
Вписанный угол: Угол, одна вершина которого лежит в одной части окружности, а два других конца лежат в другой части окружности, называется вписанным углом. ∠XLY, ∠OXY, ∠OYX — некоторые из вписанных углов на рисунке выше.

Вписанные углы, опирающиеся на одну дугу, равны.
Центральный угол в два раза больше соответствующего вписанного угла.
На рисунке выше
∠XOY = 2 ∠XLY
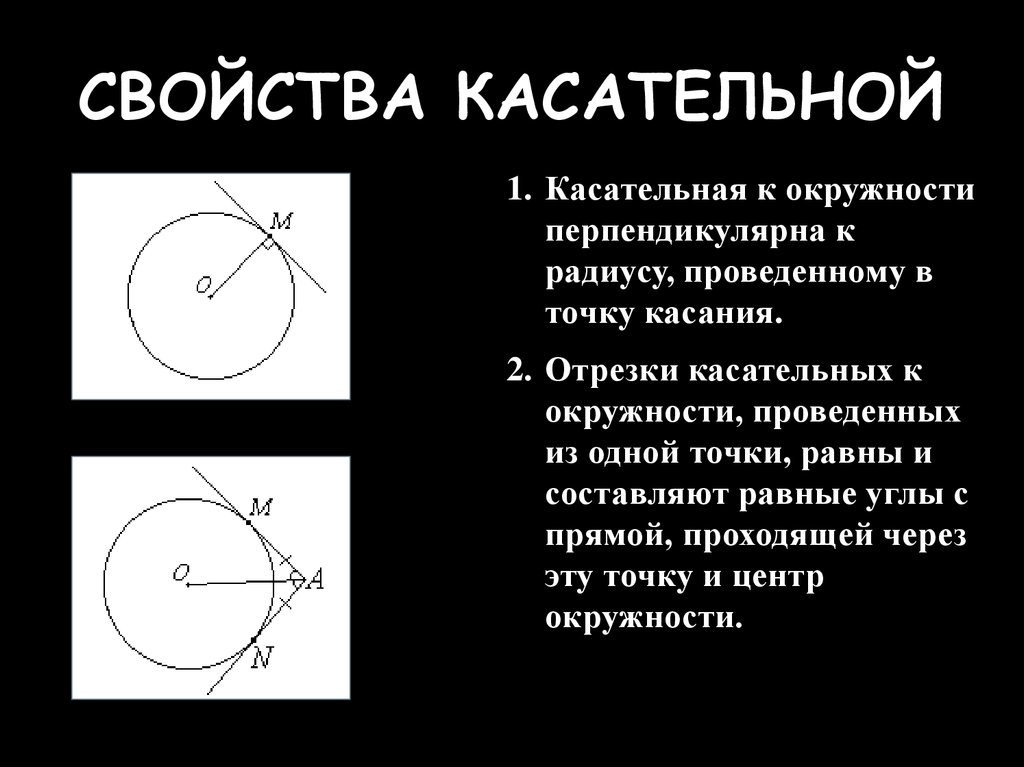
Касательная: Касательная окружности — это линия, которая касается окружности только в одной точке, не пересекая ее. MN — тангенс на рисунке выше.
Описанная окружность : Если многоугольник присутствует внутри окружности таким образом, что все его вершины лежат на окружности или только касаются окружности, то окружность называется описанной окружностью.
Примечание: Если треугольник вписан в окружность и если одна из сторон треугольника равна диаметру окружности, то диаметр действует как гипотенуза, а треугольник прямоугольный. Это называется теоремой Фалеса.

Вписанная окружность : Если окружность находится внутри многоугольника таким образом, что стороны многоугольника едва касаются окружности окружности, то окружность называется вписанной окружностью.
Полукруг: Полукруг — это половина круга.
Площадь полукруга = pr ² / 2
Длина окружности полукруга = половина периметра окружности + длина диаметра
→ (2pr/2) + 2r
→ pr+2r
→ r(2+p)

Задача 1: Площадь круга выше 81p. ∠DAB = 55°. Найдите центральный угол, образуемый дугой DB, площадь и длину окружности сектора DOB.
Решение:
Площадь круга = pr
2 = 81p
→ r ² = 81 и r = 9.
∠DB — вписанный угол. Вписанный угол равен половине центрального угла.
∠DAB = 55° → ∠DOB = 110°.
Площадь сектора DOB = (110/360)*81p = 24,75 p
Длина окружности сектора равна длине двух радиусов + длина дуги DB
Длина дуги DB = (110/360) *2*п*9 = 5,5 п
Окружность сектора DOB = 9 + 9 + 5,5p = 18 + 5,5p

Задача 2: Если QS — диаметр, QR = 6 и радиус = 5, найдите площадь заштрихованной области.
Решение:
Площадь заштрихованной области = Площадь круга – (Площадь треугольника QRS + Площадь полукруга)
Площадь круга = 25p
Площадь полукруга = 12,5p
Нахождение площади треугольника:
Согласно теореме Фалеса, если диаметр — это сторона треугольника, то она становится гипотенузой и треугольник прямоугольный.
Следовательно, ∠QRS = 90°.
Радиус = 5 → Диаметр, QS = 10
QR = 6 (дано)
Согласно теореме Pythagoras, QS ² = QR ² + RS ²
100 = 36 + RS ²60 2
100 = 36 + RS ²6060 2
100 = 36 + RS ²60 2
100 = 36 + RS ²60 2
100 = 36. → RS = 8. Мы также видим, что эта тройка кратна знаменитой пифагорейской тройке 3, 4, 5.
Площадь треугольника = основание * высота / 2 = 48 / 2 = 24
Площадь заштрихованной области = 25p – (24 + 12,5p) = (12,5p – 24) кв.ед.
Узнайте о многих других математических понятиях.

Есть ли у вас качества и навыки, чтобы стать успешным предпринимателем ? Посмотрите это видео, чтобы узнать
Песня MBA | Начните здесь | Истории успеха | проверка реальности | База знаний | Стипендии | Услуги
Круговая и координатная геометрия — mathscard online
Линейные графики и уравнения
$y=mx+c$
$m$ = градиент, $c$ = точка пересечения по вертикали.
$ m=\displaystyle \frac{y_2-y_1}{x_2-x_1}$
Параллельные линии имеют одинаковый градиент.
Рассмотрим строку, например:
градиент $m = \displaystyle {y-y_1\over x-x_1}$
$\quad \quad \Rightarrow y-y_{1}= m(x-x_{1})$
Это еще одна форма уравнения прямой линии.
Еще одна форма $ax + by + c = 0$
Середина прямой
Середина прямой, соединяющей точки $(x_{1},y_{1}) $ и $ (x_{2},y_{2})$.
Средняя точка $P$ =$\biggl [\displaystyle \frac{x_{1}+x_{2}}{2},\displaystyle \frac{y_{1}+y_{2}}{2}\biggr ]$
Расстояние между двумя точками
Возьмите две точки $(x_1, y_1)$ и $(x_2, y_2)$
92}$
Уравнение окружности
Для окружности с центром $(0,0)$ и радиусом $r$:
92$
Касательная и нормаль к окружности
Касательная к окружности — это прямая линия, которая ее касается.
9\circ $ касательной в точке, где касательная касается окружности.
Нормаль всегда проходит через центр окружности.
Градиенты
Если градиент касательной равен $m$, то градиент нормали равен $\displaystyle \frac{-1}{m}$.
Градиент нормали $(m_{n}) = \displaystyle \frac{-1}{\hbox{градиент касательной}(m_{t})}$
$\quad \quad \quad \quad \quad \quad \quad \rightarrow m_{t} \times m_{n} = -1$
Параметрические уравнения
Координаты точки на кривой можно определить с помощью параметрических уравнений.
No related posts.