Формулы площадь квадрата: Запишите формулу площади квадрата со стороной а и б. Вычислите площадь прямоугольника при а=2, 5…

Площадь квадрата онлайн

С помощю этого онлайн калькулятора можно найти площадь квадрата. Для нахождения площади квадрата, введите известные данные в ячейку и нажмите на кнопку «Вычислить». Теоретическую часть и численные примеры смотрите ниже.

Площадь квадрата. Определение

Определение 1. Площадь квадрата − это величина той части плоскости, которую занимает квадрат.

Единицы измерения площади квадрата

За единицу измерения площадей применяют квадрат, сторона которого равна единице измерения отрезков. В качестве единицы измерения площадей принимают квадраты со сторонами 1мм, 1см, 1дм, 1м и т.д (Рис.1). Такие квадраты назыают квадратным миллиметром, квадратным сантиметром, квадратным дециметром, квадратным метром и т.д., соответственно. Обозначаются они мм², см², дм², м² и т.д., соответственно.

Если выбрана единица измерения, то площадь измеряемого объекта (квадрата, треугольника, прямоугольника, многоугольника и т. д.)определяется положительным числом, которая определяет сколько раз единица измерения и ее части укладываются в данном объекте.

Для измерения отдельных плоских фигур используются специальные формулы. В данной статье мы выведем формулу для вычисления площади квадрата.

Площадь квадрата. Доказательство

Теорема 1. Площадь S квадрата со стороной a равна .

Доказательство. Пусть n целое неотрицательное число и пусть . Рассмотрим квадрат со стороной 1 (Рис.2). Разделим этот квадрат по ветрикали и по горизонлали на n равных частей. Получим маленьких квадратов состоронами . Поскольку площадь большого квадрата равна 1 (так как является единицей измерения), то очевидно, что площадь маленького квадрата равна:

а поскольку , то имеем:

Пусть теперь a является конечной десятичной дробью, содержащую n знаков после запятой. (Если n=0, то a будет целым числом). Тогда a можно представить в виде обыкновенной дроби, умножив и делив на :

откуда

где m − целое число.

Возьмем квадрат со стороной a и разделим его по горизонлали и вертикали на m ровных частей. Получим m² маленьких квадратов (Рис.3).

Тогда, учитывая (2), сторона каждого квадрата равна:

По формуле (1) площадь маленького квадрата равна:

Следовательно, площадь квадрата со стороной a равна:

Пусть, далее, число a представляет собой бесконечную десятичную дробь. Рассмотрим число a_n которая получается из a отбрасыванием всех десятичных знаков после запятой, начиная с (n+1)-го. Поскольку a отличается от a_n не более, чем на , то имеем:

откуда

Из неравенства (4) следует, что площадь S квадрата со стороной a заключена между площадью квадрата со стороной a_n и площадью квадрата со стороной (Рис.4), т.е.

При неограниченном увеличении числа n, число будет становиться сколь угодно малым и, следовательно, число будет сколь угодно мало отличаться от . Тогда из неравенства (5) следует, что число S будет мало отличаться от числа . Следовательно они равны, т.е. .

Площадь квадрата по стороне

Из вышеизложенного доказательства получили, что площадь квадрата равна:

где \( \small a \) сторона квадрата.

Пример 1. Сторона квадрата равна . Найти площадь квадрата.

Решение. Для нахождения плошади квадрата воспользуемся формулой (6). Подставляя в (6), получим:

Ответ:

Площадь квадрата по диагонали

Пусть известна диагональ \( \small d \) квадрата (Рис.5). Найдем площадь квадрата.

Для нахождения плошади квадрата, найдем сначала сторону \( \small a \) квадрата. Для этого воспользуемся теоремой Пифагора:

Подставляя (7) в (6), получим:

то есть площадь квадрата по диагонали вычисляется из следующей формулы:

Пример 2. Диагональ квадрата равна . Найти площадь квадрата.

Решение. Для нахождения плошади квадрата воспользуемся формулой (8). Подставляя в (8), получим:

Ответ:

Площадь квадрата по радиусу вписанной окружности

Пусть известен \( \small r \) радиус окружности вписанной в квадрат (Рис. 6). Найдем площадь квадрата.

Для нахождения плошади квадрата, найдем сначала сторону \( \small a \) квадрата. Нетрудно заметить, что радиус \( \small r \) равна половине стороны \( \small a \) квадрата, т.е.

Подставляя (9) в (6), получим:

или

Пример 3. Радиус вписанной в квадрат окружности равен . Найти площадь квадрата.

Решение. Для нахождения плошади квадрата воспользуемся формулой (10). Подставляя в (10), получим:

Ответ:

Площадь квадрата по радиусу описанной окружности

Пусть известен \( \small R \) радиус окружности описанной около квадрата (Рис.7). Найдем площадь квадрата.

Для нахождения плошади квадрата, найдем сначала сторону \( \small a \) квадрата. Восрользуемся теоремой Пифагора:

Подставляя (11) в (6), получим:

Пример 4. Радиус описанной окружности равен . Найти площадь квадрата.

Решение. Для нахождения площади квадрата воспользуемся формулой (12). Подставляя в (12), получим:

Ответ:

Площадь квадрата по периметру

Пусть известен периметр \( \small P \) квадрата.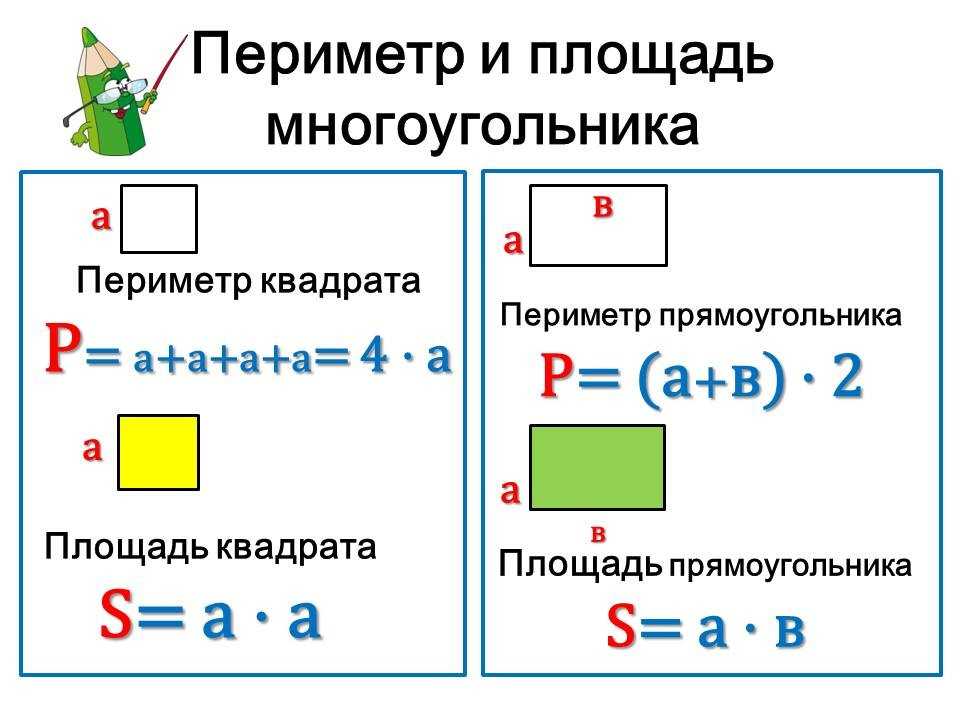 Найдем площадь квадрата. По периметру можно найти сторону квадрата:

Подставляя (13) в (6), получим:

то есть площадь квадрата через периметр равна:

Пример 5. Периметр квадрата равен . Найти площадь квадрата.

Решение. Для нахождения площади квадрата воспользуемся формулой (14). Подставляя в (14), получим:

Ответ:

Смотрите также:

• Квадрат. Онлайн калькулятор

Квадрат, свойства и формулы, площадь и периметр

Квадрат, свойства и формулы, площадь и периметр.

 

Поделиться в:

 

Квадрат – это правильный четырёхугольник, то есть четырёхугольник, у которого все углы равны и все стороны равны.

 

Квадрат (понятие, определение), диагональ квадрата

Свойства квадрата

Формулы квадрата. Площадь квадрата. Периметр квадрата

 

Квадрат (понятие, определение), диагональ квадрата:

Квадрат – это правильный четырёхугольник, то есть четырёхугольник, у которого все углы равны и все стороны равны.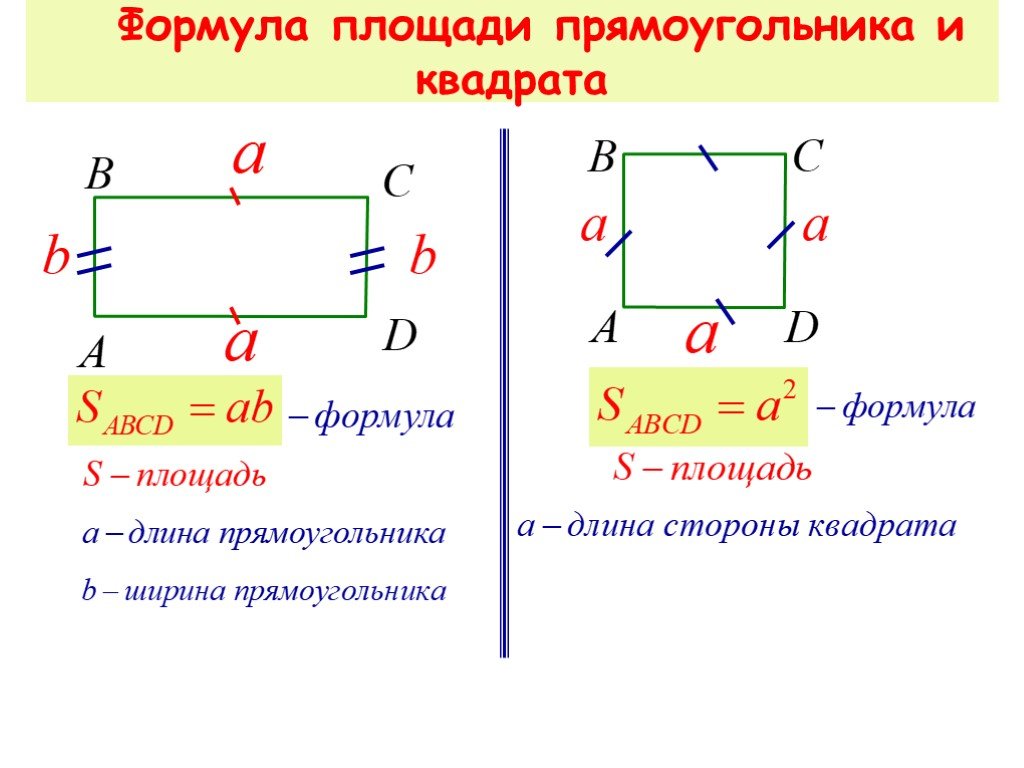

Квадрат – это четырехугольник, имеющий равные стороны и углы.

Рис. 1. Квадрат

Все углы квадрата прямые. Каждый из них прямой и равен 90°.

Таким образом, все квадраты отличаются друг от друга только длиной стороны.

Рис. 2. Квадрат и диагонали квадрата

Диагональ квадрата – это отрезок, соединяющий две вершины противоположных углов квадрата. AC и BD – это диагонали квадрата.

Квадрат является одновременно частным случаем других фигур: параллелограмма, ромба и прямоугольника. Поэтому квадрату присущи все свойства параллелограмма, ромба и прямоугольника.

Квадрат – это равносторонний прямоугольник.

Квадрат – это ромб с прямыми углами.

 

Свойства квадрата:

1. Длины всех сторон равны.

Рис. 3. Квадрат

AB = BC = CD = AD

2. Противоположные стороны квадрата параллельны.

Рис. 4. Квадрат

AB||CD,   BC||AD

3. Все углы квадрата прямые. Каждый из них равен 90°.

Рис. 5. Квадрат

∠ABC = ∠BCD = ∠CDA = ∠DAB = 90°

4. Сумма углов квадрата равна 360 градусам.

∠ABC + ∠BCD + ∠CDA + ∠DAB = 360°.

5. Диагонали квадрата равны между собой.

Рис. 6. Квадрат

AC = BD

6. Диагонали квадрата взаимно перпендикулярны. 

Рис. 7. Квадрат

AC ┴ BD 

7. Диагонали квадрата точкой пересечения делятся пополам.

 

Рис. 8. Квадрат

BO = OD = AO = OC 

8. Угол между диагональю и стороной квадрата равен 45 градусам.

 

Рис.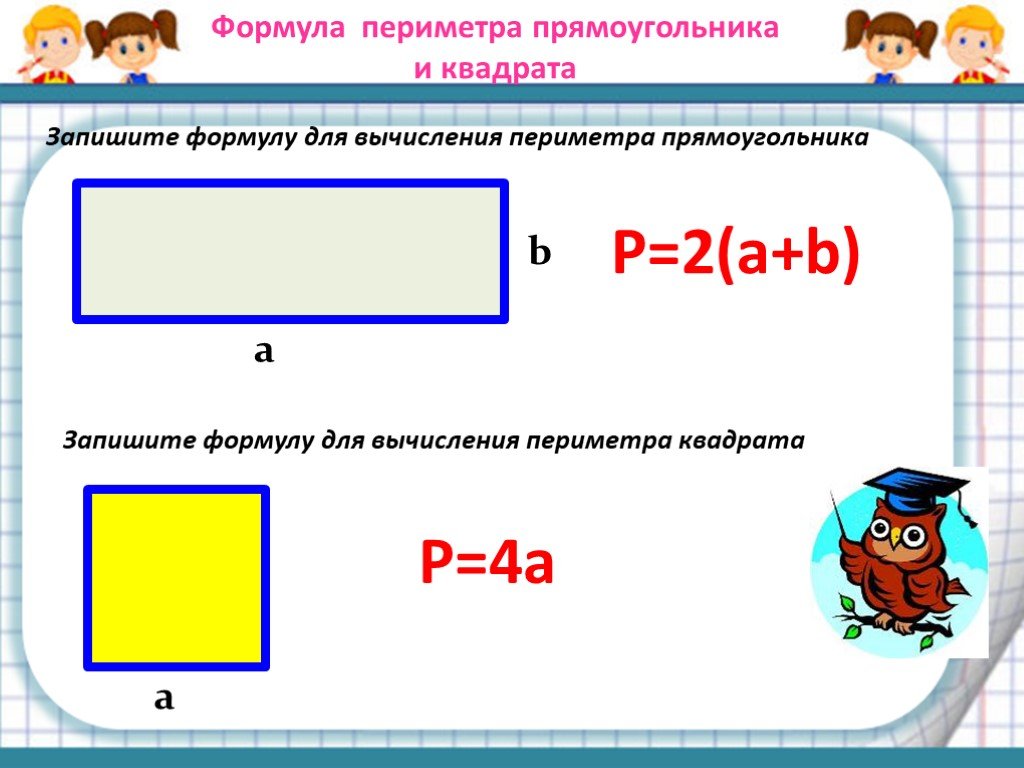 9. Квадрат

∠BCA = ∠ACD = ∠DAC = ∠CAB = 45° 

9. Диагонали квадрата являются биссектрисами углов и делят углы пополам.

Рис. 10. Квадрат

∠ABD = ∠DBC = ∠BCA = ∠ACD = ∠CDB = ∠BDA = ∠DAC = ∠CAB = 45°

10. Каждая из диагоналей делит квадрат на два равных равнобедренных прямоугольных треугольника.

Обе диагонали делят квадрат на 4 равных равнобедренных прямоугольных треугольника.

 

Рис. 11. Квадрат

△ABD = △CBD = △ABC = △ACD,

△AOB = △BOC = △COD = △AOD 

11. Точка пересечения диагоналей называется центром квадрата и также является центром вписанной и описанной окружности.

Рис. 12. Квадрат

 

Формулы квадрата. Площадь квадрата. Периметр квадрата:

Пусть a – длина стороны квадрата, d – диагональ квадрата, R – радиус описанной окружности квадрата, r – радиус вписанной окружности квадрата, P – периметр квадрата, S – площадь квадрата.

Формула диагонали квадрата:

 , , , , . 

Формула радиуса вписанной окружности квадрата:

Радиус вписанной окружности квадрата равен половине его стороны.

. 

Формула радиуса описанной окружности квадрата:

.

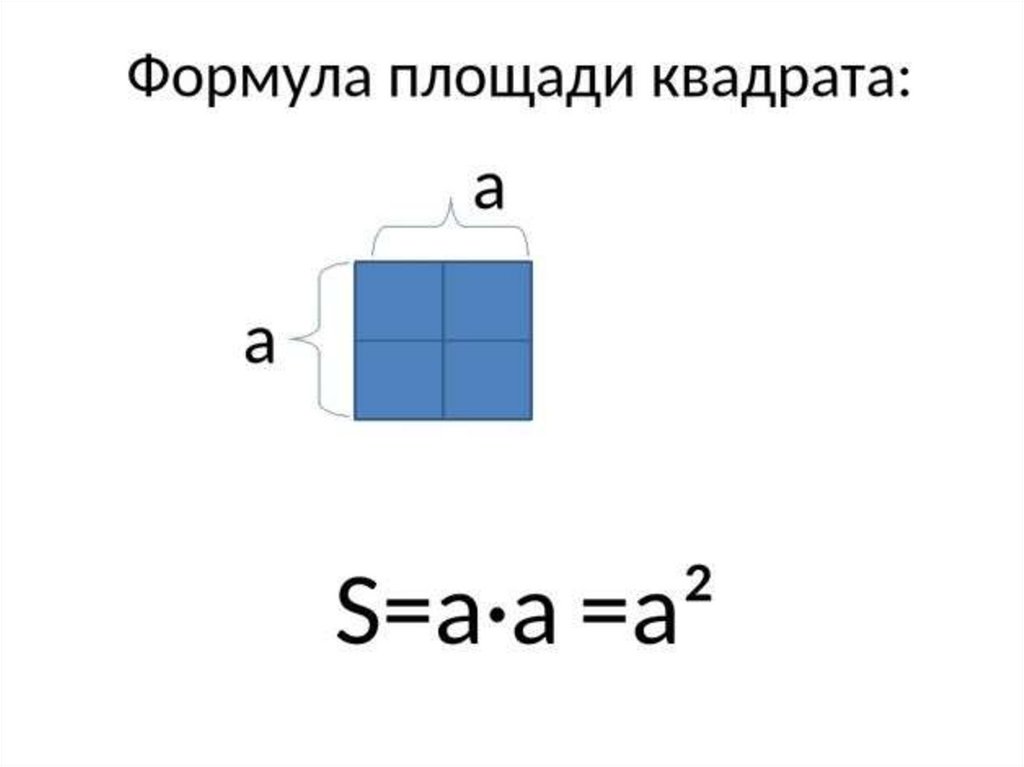
Формула периметра квадрата:

, , .

Формула площади квадрата:

, , , , .

 

Квадрат

Прямоугольник

Прямоугольный треугольник

Равнобедренный треугольник

Равносторонний треугольник

Шестиугольник

 

Примечание: © Фото https://www.pexels.com, https://pixabay.com

 

 

Коэффициент востребованности 2 822

Определение формулы с использованием различных методов

Квадрат — это тип многоугольника, у которого все четыре стороны одинаковы, а противоположные стороны параллельны. В математике, как и в геометрии, площадь изображается как пролет, занимаемый данным геометрическим объектом. В этой статье мы постараемся узнать о формуле площади квадрата и о том, как найти ее, используя диагональ, периметр и стороны. Площадь квадрата или любого объекта квадратной формы описывается как количество квадратных единиц, необходимых для заполнения квадрата.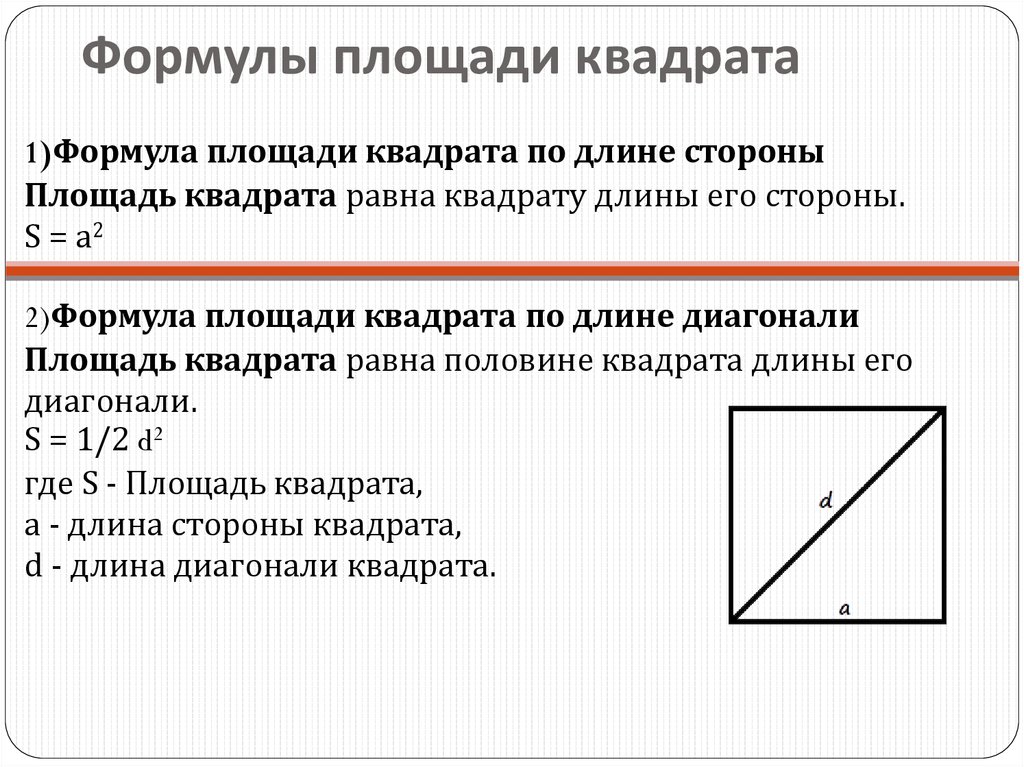 Мы узнаем больше об этой области и связанных терминах в заголовке ниже.

Площадь квадрата

Квадрат – это двумерный многоугольник, в котором диагонали делят друг друга пополам, а углы имеют одинаковую величину, т.е. 90 градусов. Площадь квадратной фигуры – это количество единичных квадратов, окружающих поверхность квадрата.

Поскольку все стороны квадрата равны, его площадь равна произведению двух его сторон. Площадь любого данного объекта рассчитывается в квадратных единицах, то есть в квадратных метрах, квадратных сантиметрах, квадратных дюймах, квадратных футах и ​​т. д. 92\).

Прочтите эту статью о площади треугольника.

Шаги для нахождения площади квадрата

Теперь, когда вы знаете формулу для вычисления площади с использованием периметра, диагонали и сторон, ниже приведены шаги, которые нужно выполнить, чтобы найти площадь поверхности квадрата.

Шаг 1: Для заданной квадратной фигуры получить данные. То есть получить значение стороны, диагонали или периметра.

Шаг 2: После того, как заданное значение будет ясно, вы можете выбрать формулу для использования.

Шаг 3: Подставив значения в данную формулу, вы получите площадь в единичных квадратах.

Методы нахождения площади квадрата

До сих пор мы обсуждали формулу площади поверхности квадрата, а теперь давайте разберемся с методами или процессом ее получения с использованием периметра, диагонали и сторон.

Площадь квадрата с использованием периметра

Формула периметра квадрата в математике = 4 × сторона.

Если периметр разделить на 4, получится уравнение для стороны квадрата.

Это сторона квадрата=периметр/4

Как только сторона будет получена, подставьте значение в формулу площади, и площадь может быть определена.

Пример: Периметр квадратной коробки равен 480 см. Определить площадь коробки. 2\)= 4 м × 4 м = 16 кв. м 92\).

Следовательно, длина стороны = \(\sqrt{Площадь}\) = \(\sqrt{2560}\) = 50,596 см.

Мы надеемся, что приведенная выше статья поможет вам понять и подготовиться к экзамену. Оставайтесь с нами в приложении Testbook, чтобы получать больше обновлений по связанным с математикой темам и другим подобным предметам. Кроме того, обратитесь к серии тестов, доступных для проверки ваших знаний по нескольким экзаменам.

Площадь квадрата Часто задаваемые вопросы

В.1 Какова площадь квадрата? 92}{2}\).

Q.4 Как найти сторону квадрата, если известна площадь?

Ответ 4 Чтобы найти сторону квадрата, если площадь задана, используйте данную формулу: сторона = \(\sqrt{Площадь}\).

В.5 Как найти площадь квадрата, если известен его периметр?

Ответ 5 Чтобы получить площадь квадрата, когда нам дан периметр, используйте следующие шаги: Разделите периметр на 4 и получите длину стороны.

Далее подставляем эту длину стороны в формулу площади и получаем ответ.

Скачать публикацию в формате PDF

Читать Подробнее посты

Вывод потенциальной формулы энергии, типы потенциальной энергии, и использует
Фактор волнового оборота: формула, прямолификаторы, значимость и использование
Celestial Bodies: Значение, типы. и интересные факты
Вертикальная линия на координатных плоскостях Уравнение, наклон, симметрия с примерами
Десятичные числа в повседневной жизни с приложениями, свойствами и примерами

Площадь квадрата — MathCracker.com

Инструкции: Используйте этот калькулятор, чтобы найти площадь квадрата с заданной стороной s. Пожалуйста, укажите сторону в поле формы ниже.

Подробнее об этой площади квадратного калькулятора

Этот калькулятор вычисляет площадь квадрата для указанной стороны. Сторона квадрата может быть любым допустимым числовым выражением. Например, это может быть любое число, такое как «3» или «6,56», или вы можете использовать такие выражения, как «1/3», «sqrt(3)» и т. д. сделать, это нажать «Рассчитать», и все шаги будут показаны.

Этот процесс очень прост и включает в себя возведение в квадрат значения предоставленной стороны. 92\]

Каковы шаги для вычисления площади квадрата

• Шаг 1: Определите сторону, которая дается, и назовите эту сторону «а»
• Шаг 2: Зная сторону «а», вычисляется площадь a * a = a²
• Шаг 3: При необходимости определите единицы «а» (если есть) и отдайте единицы области

Зачем вычислять площадь квадрата?

Существует бесчисленное множество приложений для вычисления площадей квадратов.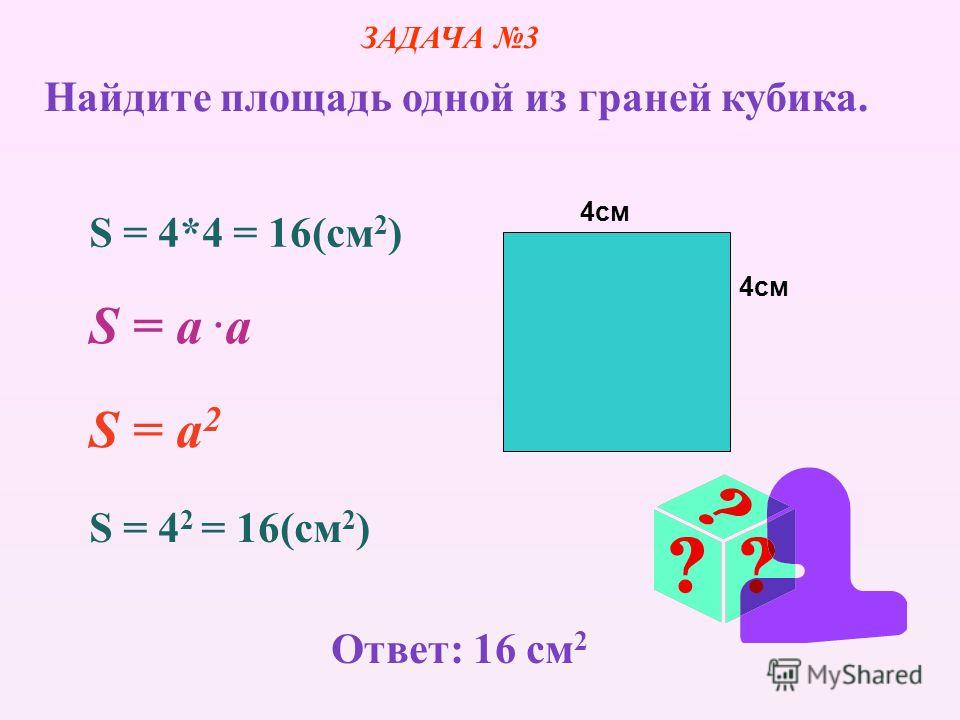 Например, вас может заинтересовать расчет площади помещения. площади земельного участка, для чего следует использовать формулу площади квадрата. 92 = 20,25 \]

Пример: Другой расчет площади

Вычислить площадь квадрата с диагональю d = 5.

Решение : Чтобы использовать известную нам формулу, мы сначала определяем сторону квадрата, которую нам нужно использовать. Но вместо стороны нам предоставили с диагональю.

По теореме Пифагора мы знаем, что \(d = a \sqrt{2}\), где d — диагональ, а a — сторона. Итак, мы можем найти сторону:

92 \]

Другие калькуляторы полезной площади

Также могут потребоваться другие геометрические формы. Вы можете вычислить площадь прямоугольника, например, используя очень простую формулу. Чуть более сложным является случай с площадью ромба, но все же следует тому же обоснованию, которое также похоже на то, что используется для вычисления площади треугольника.

В другой категории, из-за участия константы \(\pi\), вы можете использовать наши калькуляторы для площади круга и области эллипса, которые удивительно похожи.