Тангенс и котангенс суммы и разности аргументов, примеры
- Тангенс и котангенс суммы
- Тангенс и котангенс разности
- Примеры
п.1. Тангенс и котангенс суммы
Для вывода формул тангенса и котангенса суммы используем формулы синуса и косинуса суммы, полученные в §13 данного справочника.
\begin{gather*} tg(\alpha+\beta)=\frac{sin(\alpha+\beta)}{cos(\alpha+\beta)}=\frac{sin\alpha cos\beta+cos\alpha sin\beta}{cos\alpha cos\beta-sin\alpha sin\beta}=\frac{\frac{sin\alpha cos\beta+cos\alpha sin\beta}{cos\alpha cos\beta}}{\frac{cos\alpha cos\beta-sin\alpha sin\beta}{cos\alpha cos\beta}}=\\ =\frac{tg\alpha+tg\beta}{1-tg\alpha\cdot tg\beta}\\ \\ ctg(\alpha+\beta)=\frac{cos(\alpha+\beta)}{sin(\alpha+\beta)}=\frac{cos\alpha cos\beta-sin\alpha sin\beta}{sin\alpha cos\beta+cos\alpha sin\beta}= \frac{\frac{cos\alpha cos\beta-sin\alpha sin\beta}{sin\alpha sin\beta}}{\frac{sin\alpha cos\beta+cos\alpha sin\beta}{sin\alpha sin\beta}}=\\ =\frac{ctg\alpha\cdot ctg\beta-1}{ctg\alpha+ ctg\beta} \end{gather*}
п.
2. Тангенс и котангенс разностиДля вывода формулы тангенса и котангенса разности используем формулы синуса и косинуса разности, полученные в §13 данного справочника. \begin{gather*} tg(\alpha-\beta)=\frac{sin(\alpha-\beta)}{cos(\alpha-\beta)}=\frac{sin\alpha cos\beta-cos\alpha sin\beta}{cos\alpha cos\beta+sin\alpha sin\beta}=\frac{\frac{sin\alpha cos\beta-cos\alpha sin\beta}{cos\alpha cos\beta}}{\frac{cos\alpha cos\beta+sin\alpha sin\beta}{cos\alpha cos\beta}}=\\ =\frac{tg\alpha-tg\beta}{1+tg\alpha\cdot tg\beta}\\ \\ ctg(\alpha-\beta)=\frac{cos(\alpha-\beta)}{sin(\alpha-\beta)}=\frac{cos\alpha cos\beta+sin\alpha sin\beta}{sin\alpha cos\beta-cos\alpha sin\beta}= \frac{\frac{cos\alpha cos\beta+sin\alpha sin\beta}{sin\alpha sin\beta}}{\frac{sin\alpha cos\beta-cos\alpha sin\beta}{sin\alpha sin\beta}}=\\ =\frac{ctg\alpha\cdot ctg\beta+1}{ctg\beta-ctg\alpha}=-\frac{ctg\alpha\cdot ctg\beta+1}{ctg\alpha-ctg\beta} \end{gather*}
\begin{gather*} tg(\alpha+\beta) =\frac{tg\alpha+tg\beta}{1-tg\alpha\cdot tg\beta},\ \ \ ctg(\alpha+\beta) =\frac{ctg\alpha\cdot ctg\beta-1}{ctg\alpha+ ctg\beta}\\ \\ tg(\alpha-\beta) =\frac{tg\alpha-tg\beta}{1+tg\alpha\cdot tg\beta},\ \ \ ctg(\alpha-\beta)=-\frac{ctg\alpha\cdot ctg\beta+1}{ctg\alpha-ctg\beta} \end{gather*}
п.
2\alpha\)г*) \(tg\alpha tg\beta+tg\beta tg\gamma+tg\gamma tg\alpha\), если \(\alpha+\beta+\gamma=\frac\pi2\)
По условию \(\gamma=\frac\pi2-(\alpha+\beta)\). Подставляем: \begin{gather*} tg\alpha tg\beta+tg\beta tg\left(\frac\pi2-(\alpha+\beta)\right)+tg\left(\frac\pi2-(\alpha+\beta)\right)tg\alpha=\\ =tg\alpha tg\beta+ctg(\alpha+\beta)\cdot (tg\alpha+tg\beta)=tg\alpha tg\beta+\frac{tg\alpha+tg\beta}{tg(\alpha+\beta)}=\\ =tg\alpha tg\beta+\frac{(tg\alpha+tg\beta)(1-tg\alpha tg\beta)}{tg\alpha+tg\beta}=tg\alpha tg\beta+1-tg\alpha tg\beta=1 \end{gather*} Ответ: 1
Пример 3.Докажите, что \(\alpha+\beta=\frac\pi4\), если \(tg\alpha=\frac25,\ tg\beta=\frac37,\ \ 0\lt\alpha\lt\frac\pi2,\ \ 0\lt\beta\lt\frac\pi2\)
Найдем тангенс суммы: \begin{gather*} tg(\alpha+\beta)=\frac{tg\alpha+tg\beta}{1-tg\alpha\cdot tg\beta}=\frac{\frac25+\frac37}{1-\frac25\cdot\frac37}=\frac{\frac{14+15}{35}}{\frac{35-6}{35}}=\frac{29}{29}=1\\ \alpha+\beta=\frac\pi4+\pi k \end{gather*} По условию: \begin{gather*} \begin{cases} 0\lt\alpha\lt\frac\pi2\\ 0\lt\beta\lt\frac\pi2 \end{cases} \Rightarrow 0\lt\alpha+\beta\lt\pi\\ 0\lt\frac\pi4+\pi k\lt \pi\Rightarrow k = 0 \end{gather*} Значит: \(\alpha+\beta=\frac\pi4\)
Рейтинг пользователей
за неделю
- за неделю
- один месяц
- три месяца
Помогай другим
Отвечай на вопросы и получай ценные призы каждую неделю
См. подробности
Формулы суммы и разности двух углов – онлайн-тренажер для подготовки к ЕНТ, итоговой аттестации и ВОУД
Запомнить
Регистрация
Конспект
Формулы сложения выражают синус, косинус, тангенс и котангенс суммы и разности двух углов поворота \(\alpha \ и\ \beta\) через тригонометрические функции этих углов.
- Синус суммы: \(sin \left( {\alpha + \beta } \right) = sin \alpha \cdot cos \beta + cos \alpha \cdot sin \beta\).
\circ=\frac{\sqrt6-\sqrt2}4\).Вопросы
Найдите значение \(ctg15°\).
Упростите выражение.
\(\sqrt3cos\alpha-2cos(\alpha-\frac{\pi}6)\)
- Вычислите.
\(cos15° + sin15° · ctg30°\)
Найдите значение \(sin15°\).
Упростите.
\(\frac{sin(\alpha-\beta)+2cos\alpha\cdot sin\beta}{2cos\alpha\cdot cos\beta-cos(\alpha-\beta)}\)
Найдите \(ctg\alpha, \ если \ tg(\alpha+\frac{\pi}4)=0,2\).
{\circ}\)
Сообщить об ошибке
Тригонометрия
ТригонометрияТригонометрия коричневый — детская кроватка
Наиболее подходящим методом расчета составляющих сил является использование тригонометрических отношения, такие как sin, cos, тангенс угла. Отношение для sin и cos колеблется между 0 и 1.грех 0 = 0 и соз 0 = 1 грех 90 = 1 и соз 90 = 0 (а) (б) фигура 1 Посмотрите на единичный круг, показанный на рис.
1 (а). Грех (cos) угла
представляет собой отношение вертикальной и горизонтальной составляющих заданного
угол. Используя прямоугольный треугольник, показанный на рисунке 1 (б), мы можем вычислить
сторон любого прямоугольного треугольника. Следующие формулы используются для
расчет сторон:Векторы силы в большинстве случаев показаны под заданным углом, они равны гипотенуза прямоугольного треугольника. Нам нужно найти горизонталь и вертикальная составляющая вектора силы.
Вертикальный компонент: Напротив = Гипотенуза × грех ,и Горизонтальный компонент: Смежный = Гипотенуза × cos Эти утверждения всегда верны, если вы выбираете угол силы до горизонтальной опорной линии.
Если задан угол к вертикали
используйте дополнительный уголок (90 — Q)Тангенс и котангенс Если гипотенуза не нужна или не задана, мы можем вычислить длину вертикального или горизонтального или угла, используя загар или кроватку.
Опять же, тангенс угла равен
.Ниже показан простой способ справиться с sin, cos, tan и cot. Каждая формула состоят из трех цифр:
Sin = O pposit над ипотенузой H . Если у вас возникли проблемы с преобразованием формул, посмотрите на буквы в треугольник. они дают вам указание, как транспонировать формулу.
Значения sin и cos для наиболее распространенных углов. Правило греха
грех : грех : грех = а : б : с
а : грех = b : грех = c : грехКос правило
a ² = b ² + c ² — 2 bc x cos
b ² = c ² + a ² — 2 ac x cos
c ² = ² + б ² — 2 аб х косЧто такое тангенс тригонометрии. Свойства синуса, косинуса, тангенса и котангенса
ЕГЭ на 4? Разве ты не трепещешь от счастья?Вопрос, как говорится, интересный… Можно, можно на 4 пройти! И при этом не лопнуть.
.. Главное условие — регулярно заниматься. Вот основная подготовка к ЕГЭ по математике. Со всеми тайнами и загадками ЕГЭ, о которых в учебниках не прочтешь… Изучайте этот раздел, решайте побольше задач из разных источников — и все получится! Предполагается, что базовый раздел «Хватит тебе и троих!» не доставляет вам никаких проблем. А если вдруг… Переходите по ссылкам, не ленитесь!И начнем мы с великой и страшной темы.
Внимание!
В Спецразделе 555 есть дополнительный материал
.
Для тех, кто сильно «не очень…»
И для тех, кто «очень…»)Эта тема доставляет много проблем студентам. Считается одним из самых тяжелых. Что такое синус и косинус? Что такое тангенс и котангенс? Что такое числовой круг? Стоит задать эти безобидные вопросы, как человек бледнеет и пытается увести разговор в сторону… Но тщетно. Это простые понятия. И эта тема не сложнее других. Просто нужно с самого начала четко понимать ответы на эти самые вопросы.
Это очень важно. Если вы разобрались, вам понравится тригонометрия. Итак,Что такое синус и косинус? Что такое тангенс и котангенс?
Начнем с древних времен. Не волнуйтесь, мы пройдем все 20 столетий тригонометрии за 15 минут. И, незаметно для себя, повторим кусочек геометрии из 8 класса.
Нарисуйте прямоугольный треугольник со сторонами а, b, с и углом Х . Вот один.
Напомню, что стороны, образующие прямой угол, называются катетами. а и с — коньки. Их двое. Другая сторона называется гипотенузой. С — гипотенуза.
Треугольник и треугольник, подумай об этом! Что с ним делать? Но древние люди знали, что делать! Повторим их действия. Измерим сторону в . На рисунке клетки специально нарисованы, как это бывает в заданиях ЕГЭ. Сторона в равна четырем ячейкам. ХОРОШО. Измерим сторону а. Три клетки.
Теперь давайте разделим длину стороны a на длину стороны на . Или, как говорится, возьмем отношение к к в .
а/с = 3/4.В качестве альтернативы вы можете совместно использовать в на a. Получаем 4/3. Можно ли на разделить на С. гипотенуза С не считаем по ячейкам, но оно равно 5. Получаем а/с = 4/5. Короче говоря, вы можете разделить длины сторон друг на друга и получить какие-то числа.
И что? В чем смысл этого интересного занятия? Пока нет. Дурацкая работа, если честно.)
А теперь давайте сделаем это. Увеличим треугольник. Продлим стороны
Но это не их отношения!
Attitude a/c Было: а/с = 3/4, стало м/н = 6/8 = 3/4. Отношения других соответствующих сторон также не изменятся .
Можно произвольно изменять длины сторон в прямоугольном треугольнике, увеличивать, уменьшать, без изменения угла х – отношение соответствующих сторон не изменится . Можно проверить, а можно поверить на слово древним людям.Вот это очень важно! Отношения сторон в прямоугольном треугольнике никак не зависят от длин сторон (для одного и того же угла). Это настолько важно, что отношения сторон заслужили свои особые названия. Их имена, так сказать.) Знакомьтесь.
Чему равен синус угла x ? Это отношение противолежащего катета к гипотенузе:
sinx = a/c
чему равен косинус угла x ? Это отношение прилежащего катета к гипотенузе:
С osx = a/c
Чему равен тангенс угла x ? Это отношение противоположной ноги к соседней:
tgx= a/c
чему равен котангенс угла x ? Это отношение соседней ноги к противоположной:
ctgx = в/а
Все очень просто.
Синус, косинус, тангенс и котангенс — некоторые числа. Безразмерный. Просто цифры. Для каждого угла — свое.Почему я так скучно повторяюсь? Тогда что это нужно помнить . Как ни странно помню. Запоминание можно облегчить. Знакома фраза «Начнем издалека…»? Так что начните издалека.
Угол синуса равен отношению дальнего угла катета к гипотенузе. Косинус — это отношение ближайшего к гипотенузе.
Тангенс угла представляет собой отношение дальнего угла катетера к ближайшему. Котангенс — наоборот.
Уже проще, да?
Ну а если вспомнить, что в тангенсе и котангенсе сидят только катеты, а в синусе и косинусе фигурирует гипотенуза, то все станет совсем просто.
Все это славное семейство — синус, косинус, тангенс и котангенс еще называют тригонометрическими функциями .
А теперь вопрос к размышлению.
Почему мы говорим синус, косинус, тангенс и котангенс угла? Речь идет о взаимоотношениях сторон, вроде.
.. При чем тут угол? Посмотрим на вторую картинку. Точно такой же, как и первый.
Наведите указатель мыши на картинку. Я изменил угол х . увеличил его с х до х. Все отношения изменились! Отношение т/с стало 3/4, а соответствующее отношение т/у стало 6/4.
И все остальные отношения стали другими!
Следовательно, отношения сторон никак не зависят от их длин (под одним углом x), а резко зависят от этого самого угла! И только от него. Следовательно, термины синус, косинус, тангенс и котангенс относятся к углу . Угол здесь главный.
Следует иронически понимать, что угол неразрывно связан со своими тригонометрическими функциями. Каждый угол имеет свои синус и косинус. И почти у каждого свой тангенс и котангенс. Это важно. Считается, что если нам дан угол, то его синус, косинус, тангенс и котангенс мы знаем ! Наоборот. Зная синус или любую другую тригонометрическую функцию, мы знаем угол.
Существуют специальные таблицы, где для каждого угла записаны его тригонометрические функции. Таблицы Брейдиса называются. Их делают очень давно. Когда не было ни калькуляторов, ни компьютеров…
Конечно, тригонометрические функции всех углов невозможно запомнить. Вам нужно знать их только для нескольких углов, но об этом позже. А вот заклинание «Я знаю угол, значит, знаю его тригонометрические функции» — работает всегда!
Вот мы повторили геометрию из 8 класса. Она нам на ЕГЭ нужна? Нужна. Вот типичная задача с ЕГЭ.Для решения которого достаточно 8 класса.Приведена картинка:
Все. Данных больше нет. Нам нужно найти длину катета BC.
Клетки мало помогают, треугольник как-то неправильно расположен…. Нарочно, наверное… Из информации есть длина гипотенузы. 8 ячеек. Почему-то дан угол.
Тут надо сразу вспомнить о тригонометрии. Угол есть, значит, мы знаем все его тригонометрические функции. Какую функцию из четырех следует привести в действие? Давайте посмотрим, что мы знаем, не так ли? Мы знаем гипотенузу, угол, но нам нужно найти рядом с этим угловым катетом! Очевидно, косинус нужно привести в действие! Вот и запускаем.
Мы просто пишем по определению косинуса (отношение прилежащего катета к гипотенузе):cosC = BC/8
Угол C равен 60 градусам, а его косинус равен 1/2. Это нужно знать, без всяких таблиц! То есть:
1/2 = солнце/8
Элементарное линейное уравнение. Неизвестно — Вс . Кто разучился решать уравнения, прогуляйтесь по ссылке, остальные решите:
солнце = 4
Когда древние люди поняли, что каждый угол имеет свой набор тригонометрических функций, у них возник резонный вопрос. Разве синус, косинус, тангенс и котангенс не связаны друг с другом? Чтобы, зная одну функцию угла, можно было найти остальные? Без расчета самого угла?
Вот такие они были неугомонные…)
Связь между тригонометрическими функциями одного угла.
Конечно, синус, косинус, тангенс и котангенс одного и того же угла связаны между собой. Любая связь между выражениями задается в математике формулами. В тригонометрии существует огромное количество формул.
Но здесь мы рассмотрим самые основные из них. Эти формулы называются: основные тригонометрические тождества. Вот они:Эти формулы нужно знать железу. Без них в тригонометрии вообще делать нечего. Из этих основных тождеств следуют еще три вспомогательных тождества:
Сразу предупреждаю, что последние три формулы быстро выпадают из памяти. Почему-то.) Можно, конечно, вывести эти формулы из первых трех. Но, в трудную минуту… Сами понимаете.)
В стандартных задачах, таких как приведенные ниже, есть способ обойти эти забываемые формулы. А резко уменьшают ошибки по забывчивости, да и в расчетах тоже. Эта практика есть в разделе 555, урок «Связь между тригонометрическими функциями одного угла».
В каких задачах и как используются основные тригонометрические тождества? Самая популярная задача — найти какую-то функцию угла, если задана другая. В ЕГЭ такое задание присутствует из года в год.
) Например:Найдите значение sinx, если x — острый угол и cosx=0,8.
Задача почти элементарная. Ищем формулу, где есть синус и косинус. Вот эта формула:
sin 2 x + cos 2 x = 1
Подставляем сюда известную величину, а именно 0,8 вместо косинуса:
sin 2 x + 0,8 2 = 1
Ну и считаем, как обычно:
sin 2 x + 0,64 = 1
sin 2 x = 1 — 0,64
Здесь почти все. Мы вычислили квадрат синуса, осталось извлечь квадратный корень и ответ готов! Корень из 0,36 равен 0,6.
Задача почти элементарная. Но слово «почти» тут не напрасно… Дело в том, что подходит и ответ sinx=-0,6…(-0,6)2 тоже будет 0,36.
Получены два разных ответа. И вам нужен один. Второй неправильный. Как быть!? Да как обычно.) Внимательно читайте задание. Почему-то написано… если х острый угол… А в задачах каждое слово имеет смысл, да… Эта фраза — дополнительная информация к решению.
Острый угол – это угол меньше 90°. А при таких углах все тригонометрические функции — и синус и косинус, и тангенс с котангенсом — положительные.
Тех. здесь мы просто отбрасываем отрицательный ответ. Мы имеем право.Собственно, восьмиклассникам такие тонкости и не нужны. Они работают только с прямоугольными треугольниками, где углы могут быть только острыми. И не знают, счастливые, что есть отрицательные углы, и углы в 1000°… И все эти кошмарные углы имеют свои тригонометрические функции и с плюсом, и с минусом…
А вот для старшеклассников без учета знака — никак. Много знаний умножает печали, да…) И для правильного решения задача должна содержать дополнительную информацию (при необходимости). Например, это может быть:
Или как-то иначе. Вы увидите в приведенных ниже примерах.) Для решения таких примеров необходимо знать , в какую четверть попадает заданный угол x и какой знак имеет в этой четверти искомая тригонометрическая функция.
Эти основы тригонометрии обсуждаются на уроках, что такое тригонометрическая окружность, счет углов на этой окружности, радианная мера угла.
Иногда также необходимо знать таблицу синусов косинусов тангенсов и котангенсов.Итак, отметим самое главное:
Практические советы:
1. Запомните определения синуса, косинуса, тангенса и котангенса. Очень полезно.
2. Четко усваиваем: синус, косинус, тангенс и котангенс жестко связаны с углами. Мы знаем одно, значит, знаем другое.
3. Четко усваиваем: синус, косинус, тангенс и котангенс одного угла связаны между собой основными тригонометрическими тождествами. Нам известна одна функция, а значит, мы можем (при наличии необходимой дополнительной информации) вычислить все остальные.
А теперь, как обычно, решим. Сначала задания в объеме 8 класса. Но старшеклассники тоже могут…)
1. Рассчитайте значение tgA, если ctgA = 0,4.
2. β — угол в прямоугольном треугольнике. Найдите значение tgβ, если sinβ = 12/13.
3. Определить синус острого угла х, если tgx = 4/3.
4. Найти значение выражения:
6sin 2 5° — 3 + 6cos 2 5°
5.
(1+cosx), если sinx = 0,3 Найти значение выражения: Ответы (через точку с запятой, в беспорядке):
0,09; 3; 0,8; 2,4; 2,5
Случилось? Превосходно! Восьмиклассники уже могут ставить пятерки.)
Не все получилось? Задания 2 и 3 как-то не очень…? Без проблем! Для таких задач есть одна красивая техника. Все решается, практически, вообще без формул! А, значит, без ошибок. Этот прием описан в уроке: «Связь между тригонометрическими функциями одного угла» в разделе 555. Там же разобраны все остальные задачи.
Это были задачи типа ЕГЭ, но в урезанном варианте. ИСПОЛЬЗОВАНИЕ — легкое). А теперь почти те же задачи, но уже в полноценном виде. Для отягощенных знаниями старшеклассников.)
6. Найти значение tgβ, если sinβ = 12/13 и
7. Определить sinx, если tgx = 4/3, а x принадлежит интервалу (- 540°; — 450°).
8. Найдите значение выражения sinβ cosβ, если ctgβ = 1.
Ответы (в беспорядке):
0,8; 0,5; -2,4.
Здесь в задаче 6 угол задан как-то не очень однозначно… А в задаче 8 он вообще не задан! Это специально). Дополнительная информация берется не только из задачи, но и из головы.) Но если решитесь, то одно верное задание гарантировано!
Что делать, если вы еще не решили? Гм… Что ж, раздел 555 поможет здесь. Там подробно описаны решения всех этих задач, сложно не понять.
В этом уроке дается очень ограниченное представление о тригонометрических функциях. В пределах 8 класса. У пенсионеров есть вопросы…
Например, если угол Х (см. вторую картинку на этой странице) — сделать его немым!? Треугольник развалится! И как быть? Не будет ни катета, ни гипотенузы… Пропал синус…
Если бы древние люди не нашли выход из этой ситуации, у нас сейчас не было бы ни мобильных телефонов, ни телевизора, ни электричества. Да Да! Теоретическая основа всех этих вещей без тригонометрических функций — ноль без жезла. Но древние люди не подвели. Как они выкрутились — в следующем уроке.
Если вам нравится этот сайт…Кстати, у меня есть для вас еще парочка интересных сайтов.)
Вы можете потренироваться решать примеры и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
вы можете ознакомиться с функциями и производными.
1. Тригонометрические функции — это элементарные функции, аргументом которых является угол . Тригонометрические функции описывают отношения между сторонами и острыми углами в прямоугольном треугольнике. Области применения тригонометрических функций чрезвычайно разнообразны. Так, например, любые периодические процессы можно представить в виде суммы тригонометрических функций (рядов Фурье). Эти функции часто появляются при решении дифференциальных и функциональных уравнений.
2. К тригонометрическим функциям относятся следующие 6 функций: синус , косинус , тангенс , котангенс , секанс и косеканс .
Для каждой из этих функций существует обратная тригонометрическая функция.3. Удобно ввести геометрическое определение тригонометрических функций с помощью единичной окружности . На рисунке ниже показана окружность с радиусом r=1. На окружности отмечена точка M(x,y). Угол между радиус-вектором OM и положительным направлением оси Ox равен α.
4. синус угол α есть отношение ординаты y точки M(x,y) к радиусу r:
sinα=y/r.
Поскольку r=1, то синус равен ординате точки M(x,y).5. косинус угол α есть отношение абсциссы x точки M(x,y) к радиусу r:
cosα=x/r6. тангенс угол α есть отношение ординаты y точки M(x,y) к ее абсциссе x:
tanα=y/x,x≠07. Котангенс угол α есть отношение абсциссы x точки M(x,y) к ее ординате y:
cotα=x/y,y≠08. Секанс Угол α есть отношение радиуса r к абсциссе x точки M(x,y):
secα=r/x=1/x,x≠09. Косеканс угол α есть отношение радиуса r к ординате y точки M(x,y):
cscα=r/y=1/y,y≠010.
В единичной окружности проекции x, y точки M(x, y) и радиус r образуют прямоугольный треугольник, в котором x, y — катеты, r — гипотенуза. Поэтому приведенные выше определения тригонометрических функций применительно к прямоугольному треугольнику формулируются следующим образом:
синус угол α есть отношение противолежащего катета к гипотенузе.
косинус угол α есть отношение прилежащего катета к гипотенузе.
тангенсом углом α называется катет, противоположный прилежащему.
Котангенсом углом α называется прилежащий катет к противолежащему.
Секанс Угол α – это отношение гипотенузы к прилежащему катету.
Косеканс Угол α является отношением гипотенузы к противолежащему катету.11. График синусоидальной функции
y=sinx, домен: x∈R, домен: −1≤sinx≤112. График функции косинуса
y=cosx, домен: x∈R, диапазон: −1≤cosx≤113. График функции тангенса
y=tanx, домен: x∈R,x≠(2k+1)π/2, домен: −∞14.
График функции котангенса
y=cotx, область определения: x∈R,x≠kπ, область определения: −∞15. График секущей функции
y=secx, область определения: x∈R,x≠(2k+1)π/2, область определения: secx∈(−∞,−1]∪∪ОДЗ[-1; one] sin x = 0, при x = πk, где k ϵ Z cos x = 0, при x = π/2 + πk, где k ϵ Z sin x = 1, при x = π/2 + 2πk, где k ϵ Z cos x = 1, при x = 2πk, где k ϵ Z sin x = — 1, при x = 3π/2 + 2πk, где k ϵ Z cos x = — 1, при x = π + 2πk, где k ϵ Z sin (-x) = — sin x, т. е. нечетная функция cos (-x) = cos x, т. е. функция четная функция периодическая, наименьший период 2π sin x › 0, где x принадлежит четвертям I и II или от 0° до 180° (2πk, π + 2πk) cos x › 0, где x принадлежит четвертям I и IV или от 270° до 90° (- π/2 + 2πk, π/2 + 2πk) sin x ‹ 0, где x принадлежит четвертям III и IV или от 180° до 360° (π + 2πk, 2π + 2πk) cos x ‹ 0, где x принадлежит четвертям II и III или из 90 ° до 270° (π/2 + 2πk, 3π/2 + 2πk) возрастания на интервале [- π/2 + 2πk, π/2 + 2πk] возрастания на интервале [-π + 2πk, 2πk] убывает на промежутках [ π/2 + 2πk, 3π/2 + 2πk] убывает на промежутках производная (sin x)’ = cos x производная (cos x)’ = — sin x Определить, является функция четной или нет, очень просто.
Достаточно представить тригонометрический круг со знаками тригонометрических величин и мысленно «сложить» график относительно оси ОХ. Если знаки одинаковые, функция четная; в противном случае это странно.Введение радиан и перечисление основных свойств синусоиды и косинуса позволяют вывести следующую закономерность:
Проверить правильность формулы очень легко. Например, для x = π/2 синус равен 1, как и косинус x = 0. Проверку можно выполнить, просмотрев таблицы или проследив кривые функций для заданных значений.
Свойства тангенсоиды и котангенсоиды
Графики функций тангенса и котангенса существенно отличаются от синусоиды и косинуса. Значения tg и ctg обратны друг другу.
- Y = tgx.
- Тангенс стремится к значениям y при x = π/2 + πk, но никогда их не достигает.
- Наименьший положительный период тангеноида равен π.
- Tg(-x)=-tgx, т. е. функция нечетная.
- Tg x = 0, для x = πk.
- Функция увеличивается.
- Tg x › 0, для x ϵ (πk, π/2 + πk).
- Tg x ‹ 0, для x ϵ (— π/2 + πk, πk).
- Производная (tg x)’ = 1/cos 2 x .
Рассмотрим графическое представление котангенсоида ниже по тексту.
Основные свойства котангенсоида:
- Y = ctgx.
- В отличие от функций синуса и косинуса, в тангеноиде Y может принимать значения множества всех действительных чисел.
- Котангенсоид стремится к значениям y при x = πk, но никогда их не достигает.
- Наименьший положительный период котангенсоида равен π.
- Ctg(- x) = — ctg x, т. е. функция нечетная.
- Ctg x = 0, для x = π/2 + πk.
- Функция уменьшается.
- Ctg x › 0, для x ϵ (πk, π/2 + πk).
- Ctg x ‹ 0, для x ϵ (π/2 + πk, πk).
- Производная (ctg x)’ = — 1/sin 2 x Fix
Лекция: Синус, косинус, тангенс, котангенс произвольного угла
Синус, косинус произвольного угла
Чтобы понять, что такое тригонометрические функции, обратимся к окружности единичного радиуса.
Центр этой окружности находится в начале координат на плоскости координат. Для определения заданных функций воспользуемся радиус-вектором ИЛИ , которая начинается в центре круга, а точка R является точкой на круге. Этот радиус-вектор образует угол альфа с осью OH . Так как радиус окружности равен единице, то ИЛИ = R = 1 .Если из точки R опустить перпендикуляр на ось OH , то получится прямоугольный треугольник с гипотенузой, равной единице.
Если радиус-вектор движется по часовой стрелке, то это направление называется минус , но если против часовой стрелки — плюс .
Синус угла ИЛИ , является ординатой точки R векторов на окружности.
То есть для получения значения синуса заданного угла альфа необходимо определить координату В на поверхности.
Как было получено это значение? Зная, что синус произвольного угла прямоугольного треугольника есть отношение противолежащего катета к гипотенузе, получаем, что
А так как R=1 , то sin(α) = y 0 .
В единичной окружности значение ординаты не может быть меньше -1 и больше 1, что означает, что
Синус положительный в первой и второй четвертях единичной окружности, и отрицательный в третьей и четвертой .
Косинус угла данной окружности, образованной радиус-вектором ИЛИ , является абсциссой точки R векторов на окружности.
То есть для получения значения косинуса заданного угла альфа необходимо определить координату X на поверхности.
Косинусом произвольного угла в прямоугольном треугольнике является отношение прилежащего катета к гипотенузе, получаем, что
А так как R=1 , то cos(α) = x 0 .
В единичной окружности значение абсциссы не может быть меньше -1 и больше 1, значит
Косинус положителен в первом и четвертом квадрантах единичной окружности и отрицателен во втором и третьем.
тангенс произвольный угол вычисляется отношение синуса к косинусу.
\circ=\frac{\sqrt6-\sqrt2}4\).
{\circ}\)
1 (а). Грех (cos) угла
представляет собой отношение вертикальной и горизонтальной составляющих заданного
угол. Используя прямоугольный треугольник, показанный на рисунке 1 (б), мы можем вычислить
сторон любого прямоугольного треугольника. Следующие формулы используются для
расчет сторон:
Если задан угол к вертикали
используйте дополнительный уголок (90 — Q)
.. Главное условие — регулярно заниматься. Вот основная подготовка к ЕГЭ по математике. Со всеми тайнами и загадками ЕГЭ, о которых в учебниках не прочтешь… Изучайте этот раздел, решайте побольше задач из разных источников — и все получится! Предполагается, что базовый раздел «Хватит тебе и троих!» не доставляет вам никаких проблем. А если вдруг… Переходите по ссылкам, не ленитесь!
Это очень важно. Если вы разобрались, вам понравится тригонометрия. Итак,
а/с = 3/4.
Можно произвольно изменять длины сторон в прямоугольном треугольнике, увеличивать, уменьшать, без изменения угла х – отношение соответствующих сторон не изменится . Можно проверить, а можно поверить на слово древним людям.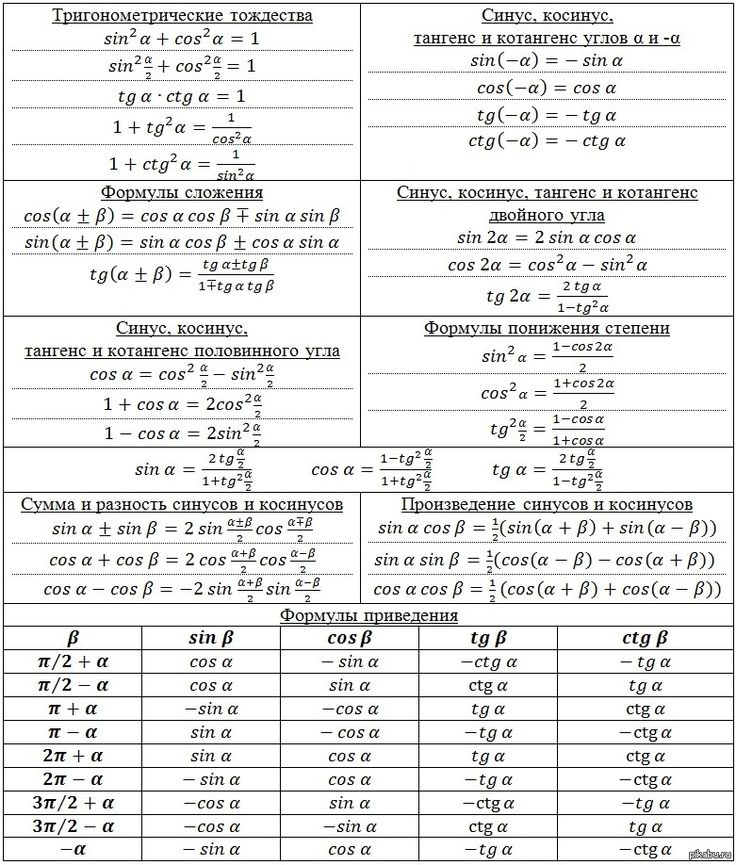
Синус, косинус, тангенс и котангенс — некоторые числа. Безразмерный. Просто цифры. Для каждого угла — свое.
.. При чем тут угол? 
Мы просто пишем по определению косинуса (отношение прилежащего катета к гипотенузе):
Но здесь мы рассмотрим самые основные из них. Эти формулы называются: основные тригонометрические тождества. Вот они: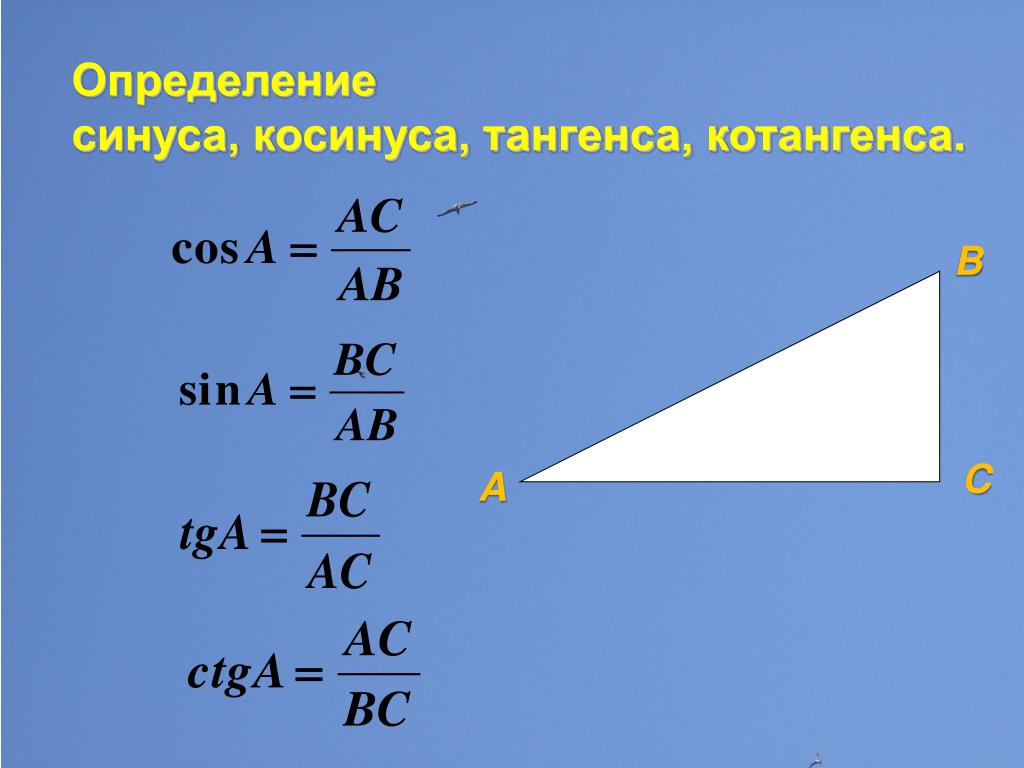
) Например:
Тех. здесь мы просто отбрасываем отрицательный ответ. Мы имеем право.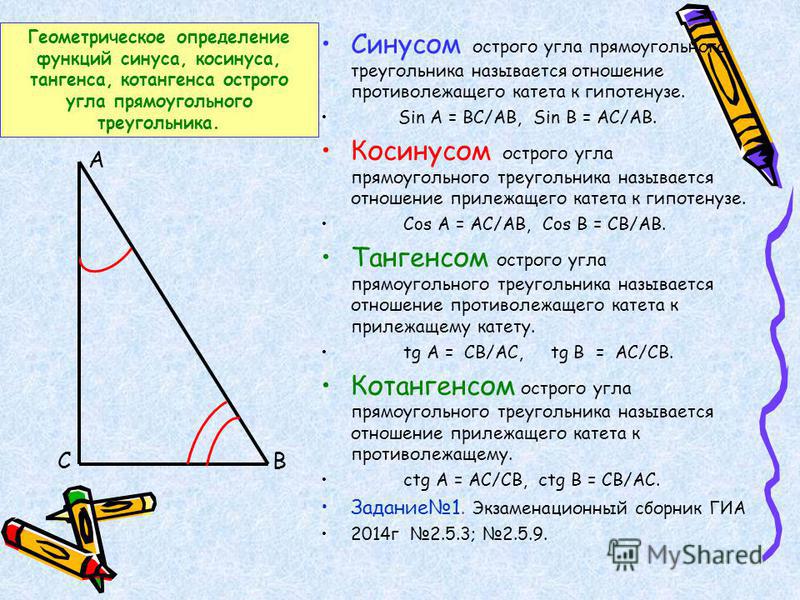
Иногда также необходимо знать таблицу синусов косинусов тангенсов и котангенсов.
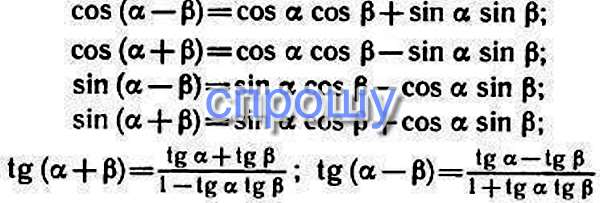Найти значение выражения: 