алгебра размещение
Вы искали алгебра размещение? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и алгебра сочетание, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «алгебра размещение».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как алгебра размещение,алгебра сочетание,алгебра сочетания,задачи на перестановку размещение и сочетание,количество перестановок из n по m,количество перестановок из n по n,количество размещений,комбинаторика перестановки размещения сочетания,комбинаторика размещение,комбинаторика размещение формула,комбинаторика размещения,комбинаторика размещения перестановки сочетания,комбинаторика размещения сочетания перестановки,комбинаторика сочетания перестановки размещения,комбинаторика сочетания размещения перестановки,комбинаторика формула размещение,математика перестановки,математика размещение,основные формулы комбинаторики перестановки сочетания размещения,основные формулы комбинаторики размещения сочетания перестановки,перестановка комбинаторика,перестановка размещение сочетание,перестановка размещение сочетание формулы,перестановка сочетание размещение,перестановка сочетание размещение формулы,перестановки и размещения,перестановки комбинаторика,перестановки размещения сочетания,перестановки размещения сочетания формулы,перестановки сочетания размещения,размещение алгебра,размещение комбинаторика,размещение комбинаторика формула,размещение математика,размещение перестановка сочетание,размещение перестановка сочетание формулы,размещение сочетание перестановка,размещение сочетание перестановка формулы,размещение теория вероятности,размещение формула,размещение формула комбинаторика,размещений,размещения и перестановки,размещения и сочетания,размещения комбинаторика,размещения перестановки и сочетания,размещения перестановки сочетания,размещения сочетания и перестановки,размещения формулы,сочетание алгебра,сочетание перестановка размещение,сочетание перестановка размещение формулы,сочетание размещение перестановка,сочетание размещение перестановка формулы,сочетания алгебра,сочетания и размещения формулы,сочетания перестановки размещения,сочетания примеры,сочетания размещения перестановки,сочетания размещения перестановки формулы,теория вероятности размещение,формула размещение,формула размещений,формула размещения,формула размещения в комбинаторике,формулы перестановка размещение сочетание,формулы перестановки размещения сочетания,формулы перестановки сочетания размещения,формулы размещения,формулы размещения перестановки сочетания,формулы размещения сочетания перестановки,формулы сочетания размещения перестановки,число размещений из n по k формула,элементы комбинаторики перестановки размещения сочетания,элементы комбинаторики перестановки сочетания размещения,элементы комбинаторики размещения перестановки сочетания,элементы комбинаторики сочетания размещения перестановки.
Решить задачу алгебра размещение вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
|
Навигация: Главная Случайная страница Обратная связь ТОП Интересно знать Избранные Топ: Определение места расположения распределительного центра: Фирма реализует продукцию на рынках сбыта и имеет постоянных поставщиков в разных регионах. Методика измерений сопротивления растеканию тока анодного заземления: Анодный заземлитель (анод) – проводник, погруженный в электролитическую среду (грунт, раствор электролита) и подключенный к положительному… Характеристика АТП и сварочно-жестяницкого участка: Транспорт в настоящее время является одной из важнейших отраслей народного хозяйства… Интересное: Уполаживание и террасирование склонов: Если глубина оврага более 5 м необходимо устройство берм. Варианты использования оврагов для градостроительных целей… Подходы к решению темы фильма: Существует три основных типа исторического фильма, имеющих между собой много общего… Искусственное повышение поверхности территории: Варианты искусственного повышения поверхности территории необходимо выбирать на основе анализа следующих характеристик защищаемой территории… Дисциплины: Автоматизация Антропология Археология Архитектура Аудит Биология Бухгалтерия Военная наука Генетика География Геология Демография Журналистика Зоология Иностранные языки Информатика Искусство История Кинематография Компьютеризация Кораблестроение Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Машиностроение Медицина Менеджмент Металлургия Метрология Механика Музыкология Науковедение Образование Охрана Труда Педагогика Политология Правоотношение Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Теология Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Энергетика Юриспруденция |
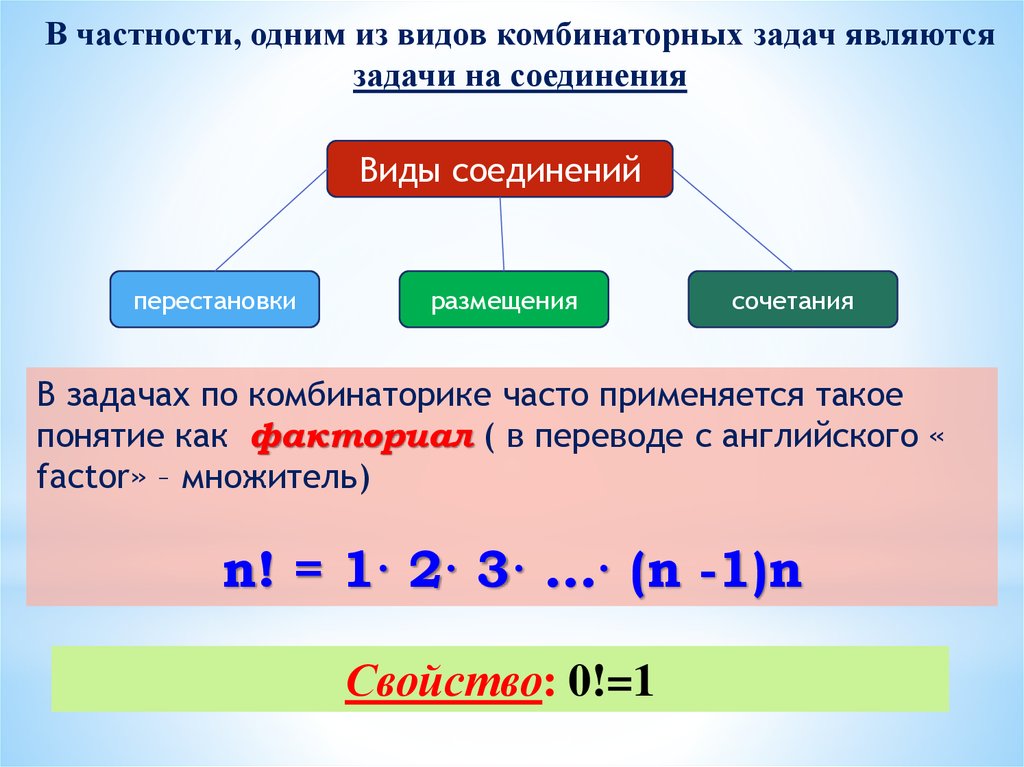
⇐ ПредыдущаяСтр 3 из 6Следующая ⇒ Формулы комбинаторики Рассмотрим задачу подсчета числа выборок из данного множества в общем виде. Сформулируем следующие определения: Размещения без повторения Размещением без повторения из n элементов по m называется всякое упорядоченное подмножество множества N, содержащее m различных элементов. Из определения следует, что два размещения отличаются друг от друга, как элементами, так и их порядком, даже если элементы одинаковы. Теорема 3. Число размещений без повторения равно произведению m сомножителей, наибольшим из которых является число n. Записывают: Перестановки без повторений Перестановками из n элементов называются различные упорядочения множества N. Из этого определения следует, что две перестановки отличаются только порядком элементов и их можно рассматривать как частный случай размещений. Теорема 4. Число различных перестановок без повторений вычисляется по формуле Сочетания без повторений Сочетанием без повторения из n элементов по m называется любое неупорядоченное подмножество множества N, содержащее m различных элементов. Из определения следует, что два сочетания различаются только элементами, порядок не важен. Теорема 5. Число сочетаний без повторений вычисляют по одной из следующих формул: Пример 1 а) 7 человек; б) 5 человек; в) 3 человека? Решение: а) Прежде всего надо выбрать 5 человек из 7 для посадки на стулья. Это можно сделать способом. С каждым выбором конкретной пятерки можно произвести перестановок местами. Замечание: Задачу можно решать, используя только теорему произведения, рассуждая следующим образом: для посадки на 1-й стул имеется 7 вариантов, на 2-й стул-6 вариантов, на 3-й -5, на 4-й -4 и на 5-й -3. Тогда число способов посадки 7 человек на 5 стульев равно . Решения обоими способами согласуются, так как б) Решение очевидно — в) — число выборов занимаемых стульев. — число размещений трех человек на трех выбранных стульях. Общее число выборов равно . Не трудно проверить формулы ; ; — число всех подмножеств множества, состоящего из n элементов. Вероятность суммы событий. Пусть А и В – два несовместных события. Тогда в соответствии с третьей аксиомой для вероятности имеем P(A+B) = P(A) + P(B). (3.6) Это равенство известно как теорема сложения вероятностей несовместных событий. Для классической схемы это свойство не нужно постулировать, т. Пример 3.5. Из колоды в 36 карт наугад вынимают 3 карты. Найти вероятность того, что среди них окажется хотя бы один туз. Решение. Введем следующие события: B={появление хотя одного туза}, A1={появление одного туза}, A2={появление двух тузов}, A3={появление трех тузов}. Очевидно, что B=A P(B) = P(A1)+P(A2)+P(A3) = Эту задачу можно решить иначе. Событие , противоположное событию В, состоит в том, что среди вынутых из колоды трех карт нет ни одного туза. ПосколькуP(B)+P( )=1, то P(B) = 1 – P( ) = Пусть А и В – два произвольных события, т.е. они, в общем случае, совместны. Запишем события А+В и В в виде A+B = A+B и B = B +BA. (объясните эти равенства, используя диаграммы Вьенна). P(A+B) = P(A) + P(B ), P(B) = P(B )+P(BA). Исключая P(B ),получим P(A+B) = P(A)+P(B)–P(AB). (3.7) Это равенство известно как теорема сложения вероятностей совместных событий. Полученная формула сложения вероятностей хорошо иллюстрируется при помощи диаграмм Вьенна. Здесь следует помнить, что вероятность события пропорциональна площади фигуры, которая соответствует данному событию. Событию А+В на рисунке соответствует вся заштрихованная фигура, площадь которой можно представить в виде суммы трех слагаемых SA+B=S1+S2+SAB, где S1 соответствует событию А–АВ, а S2 – событию В–АВ. Тогда, событию А будет соответствовать фигура с площадью SА= S1+SАВ, а событию В – SВ= S2+SАВ. В результате получим, что SА+В= SА+SВ–SАВ. Теорему сложения вероятностей можно обобщить на случай произвольного числа слагаемых. Вчастности, P(A+B+C) = P(A)+P(B)+P(C)–(AB)–P(AC)–P(BC)+P(ABC). (3.8) Докажите данную формулу самостоятельно. Пример 3.6. Два стрелка делают по одному выстрелу по мишени. Вероятность попадания для первого стрелка равна 0,8, для второго – 0,7. Какова вероятность поражения цели? Решение. Пусть A1={первый стрелок попал по цели}, A2={второй стрелок попал по цели}. Мишень будет поражена (событие В), если произойдет событие А1+А2. Поскольку события А1 и А2 совместны, но независимы, то P(А1+А2) = P(А1)+P(А2)–P(А1)P(А2) = 0,7+0,8–0,7×0,8 = 0,94. Отметим, что событие В можно записать также в виде A1 + A2+A1A2. P(B) = P(A1)P( )+P( )P(A2)+P(A1)P(A2) = = 0,8×0,3+0,2×0,7+0,7×0,8 = 0,94. Однако такой путь слишком длинный. ⇐ Предыдущая123456Следующая ⇒ Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций… Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции… Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства… Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)… |
Формулы комбинаций перестановок, трюки с примерами
В математике понятие перестановки используется в нескольких немного различающихся значениях, связанных с действием перестановки (перестановки) объектов или значений. Неформально перестановка набора объектов представляет собой расположение этих объектов в определенном порядке. Например, существует шесть перестановок множества {1,2,3}, а именно (1,2,3) , (1,3,2) , (2,1,3) , (2,3,1) , (3,1,2) и (3,2,1) . Можно определить анаграмму слова как перестановку его букв. Изучение перестановок в этом смысле вообще относится к области комбинаторики.
Например, существует шесть перестановок множества {1,2,3}, а именно (1,2,3) , (1,3,2) , (2,1,3) , (2,3,1) , (3,1,2) и (3,2,1) . Можно определить анаграмму слова как перестановку его букв. Изучение перестановок в этом смысле вообще относится к области комбинаторики.
Количество перестановок n различных объектов равно:
n×(n – 1) ×(n – 2) ×… ×2×1, это число называется «n факториал» и пишется «n!» .
В элементарной комбинаторике название «перестановки и комбинации» относится к двум связанным проблемам, обе из которых подсчитывают возможности выбора k различных элементов из множества n элементов, где для k-перестановок учитывается порядок выбора, но для k-сочетания игнорируется. Однако k-перестановки не соответствуют перестановкам, обсуждаемым в этой статье (если только k = n).
Факториал
Факториал — это когда после числа стоит восклицательный знак, поэтому оно представляет все положительные целые числа, предшествующие этому числу, после чего вы умножаете, чтобы решить факториал.
Обозначается n!. Следовательно, н! = 1 × 2 × 3 × … × (n – 1) × n
Например:
- 6! = 6 × 5 × 4 × 3 × 2 × 1 = 720
- 5! = 5 × 4 × 3 × 2 × 1 = 120
Формулы
Перестановка = n P r = n!/(n-r)!
Комбинация = n C r = n P r /r!
где n , r неотрицательные целые числа и r ≤ n .
- r — размер каждой перестановки.
- n — размер множества, из которого переставляются элементы.
- ! — оператор факториала.
Пример 1: Найдите количество перестановок и комбинаций:
н =6; r = 4.
Решение:
Шаг 1: Найдите факториал числа 6.
6! = 6 × 5 × 4 × 3 × 2 × 1 = 720
Шаг 2: Найдите факториал 6-4.
(6-4) ! = 2! = 2
Шаг 3: Разделите 720 на 2.
Перестановка = 720/2 = 360
Шаг 4: Найдите факториал числа 4.
4! = 4 × 3 × 2 × 1 = 24
Шаг 5: Разделите 360 на 24.
Комбинация = 360/24 = 15
Основные принципы счета
Если есть m способов сделать одно и n способов сделать другое, то существует m × n способов сделать и то, и другое. Фундаментальный принцип подсчета — это руководящее правило для определения количества способов выполнения двух задач.
Например:
- Допустим, вы хотите подбросить монетку и бросить кубик. Есть 2 способа подбросить монету и 6 способов бросить кубик. Тогда есть 2 × 6 = 12 способов, которыми вы можете подбросить монету и бросить кубик.
- Если вы хотите взять одну ноту на пианино и сыграть на одной струне на банджо, то есть 88 × 5 = 440 способов сделать и то, и другое.
- Если вы хотите вытянуть 2 карты из стандартной колоды из 52 карт, не заменяя их, то существует 52 способа вытянуть первую и 51 способ вытянуть вторую, так что всего 52 × 51 = 2652 способа вытяните две карты.

Принцип сложения
Если одно событие может произойти «m» способами, а другое событие может произойти «n» способами независимо от первого события, то любое из двух событий может произойти (m + n) способами .
Пример 2: В классе 10 мальчиков и 8 девочек. Классный руководитель хочет выбрать ученика для наблюдения за классом. Сколькими способами классный руководитель может сделать этот выбор?
Решение: Учитель может выбрать ученика для наблюдения двумя исключительными способами
- Выбрать мальчика среди 10 мальчиков, что можно сделать 10 способами ИЛИ
- Выбрать девочку среди 8 девочек, что можно сделать 8 способами.
Следовательно, согласно основному принципу сложения, мальчика или девочку можно выбрать 10 + 8 = 18 способами.
Принцип умножения
Если операцию можно выполнить «m» способами и после того, как она была выполнена любым из этих способов, вторую операцию можно выполнить «n» способами, то две операции последовательно можно выполнить (m × n) способами.
Пример 3: В классе 10 мальчиков и 8 девочек. Учитель хочет выбрать мальчика и девочку, которые будут представлять класс в функции. Сколькими способами учитель может сделать этот выбор?
Решение: Учитель должен выполнить два задания:
- Выбрать мальчика среди 10 мальчиков, что можно сделать 10 способами.
- Выбрать девушку среди 8 девушек, что можно сделать 8 способами.
Следовательно, необходимое количество способов = 10 × 8 = 80.
Методы выборки
- Процесс выборки можно разделить на следующие формы: ПОСЛЕДОВАТЕЛЬНОСТЬ.
- Порядок ВАЖЕН, и повторение НЕ РАЗРЕШЕНО, тогда каждый образец является ПЕРЕСТАВКОЙ.
- Порядок НЕ ВАЖЕН, и повторение РАЗРЕШЕНО, каждый образец является МНОЖЕСТВЕННЫМ.
- Порядок НЕ ВАЖЕН и повторение НЕ РАЗРЕШЕНО, каждый образец является КОМБИНАЦИЕЙ.
Перестановка
Перестановка — это расположение объектов без повторения, причем важен порядок. Другое определение перестановки — это количество возможных таких расположений.
Другое определение перестановки — это количество возможных таких расположений.
Количество перестановок «n» вещей, взятых «r» одновременно, обозначается как n P r Оно определяется как n P r
вы можете расположить объекты, это всегда будет целое число. Знаменатель в формуле всегда будет делиться на числитель без остатка.
Это также дает нам другое определение перестановок. n P n = n!
Пример 4: Список всех перестановок букв ABCD
Solution:
| ABCD | ABDC | ACBD | ACDB | ADBC | ADCB |
| BACD | BADC | BCAD | BCDA | BDAC | BDCA |
| CABD | CADB | CBAD | CBDA | CDAB | CDBA |
| DABC | DACB | DBAC | DBCA | DCAB | DCBA |
Теперь, если вам на самом деле не нужен список всех перестановок, вы можете использовать формулу для количества перестановок. Есть 4 объекта, и вы берете 4 за раз.
Есть 4 объекта, и вы берете 4 за раз.
4 P 4 = 4!/(4 – 4) ! = 4!/0! = 24/1 = 24.
Пример 5. Перечислите все три перестановки букв в слове РУКА
Решение:
| HAN | HNA | HAD | HDA | HND | HDN |
| AHN | ANH | AHD | ADH | AND | ADN |
| NHD | NDH | NAH | NHA | NAD | NDA |
| DHA | DAH | DAN | DNA | DHN | DNH |
Now, if you didn’t actually need a listing of all the permutations, you можно использовать формулу числа перестановок. Есть 4 объекта, и вы берете 3 за раз.
⁴ P ³ = 4!/(4-3) ! = 4!/1! = 24/1 = 24.
Циклические перестановки
Это перестановка вокруг круглого объекта, следует отметить, что у круглого объекта нет ни начала, ни конца, мы фиксируем один объект (или человека) и переставляем осталось.
Расположение вокруг круглого стола
Предположим, что пять человек A, B, C, D и E сидят по окружности круглого стола по порядку (у которого нет головы) . Теперь, сдвинув A, B, C, D и E на одну позицию против часовой стрелки, мы получим следующие расположения:
мы видим, что расположение на всех рисунках одинаковое.
∴ Количество круговых перестановок n разных вещей, взятых одновременно, равно (n – 1) !, если порядок по часовой стрелке и против часовой стрелки считать разными.
Пример 6. Сколькими способами можно рассадить 6 школьников вокруг круглого стола?
Решение: Задача представляет собой циклическую перестановку
Количество способов рассадить 6 студентов
= 1 × (6 – 1) ! = 5! = 5 × 4 × 3 × 2 × 1 = 120
Бусины или цветы (все разные) вокруг круглого ожерелья или гирлянды
Рассмотрим пять бусин A, B, C, D и E в ожерелье или пять цветы A, B, C и D, E в гирлянде и т. д. Если ожерелье или гирлянду слева перевернуть, мы получим расположение справа, т. е. против и по часовой стрелке порядок расположения не отличается.
д. Если ожерелье или гирлянду слева перевернуть, мы получим расположение справа, т. е. против и по часовой стрелке порядок расположения не отличается.
Таким образом, количество циклических перестановок «n» разных вещей взято.
все сразу равно:
1/2 (n–1)!, если порядок по часовой и против часовой стрелки считается некоторым.
Пример 7: Количество способов, которыми 10 человек могут сесть вокруг круглого стола так, чтобы ни у одного из них не было одинаковых соседей в любых двух расстановках.
Решение: 10 человек могут сидеть за круглым столом за 9! способы. Но вот приказы по часовой и против часовой стрелки будут давать одни и те же соседи. Следовательно, искомое количество способов = 1/2 × 9!
Условные перестановки
Когда условия применяются к тому, как устроены вещи, тогда случается, что перестановки называются условными.
Количество перестановок n вещей, использующих r за раз, в которых всегда встречается конкретная вещь = .
Пример 8. Сколько 4-значных чисел (повторение не допускается) можно составить, используя цифры 1-7, если в числе всегда будет 4?
Решение: Всего цифр (n) = 7
Всего способов составить число, если всегда присутствует 4
= r × n-1 P r-1 = 4 × ⁶P³ = 480. имеет n₁ объектов одного вида, n₂ второго рода, n₃ третьего рода и т. д., где n = n₁ + n₂ + n₃ + . . . + n k , Тогда число различимых перестановок n объектов равно
Пример 9. Сколькими различимыми способами можно написать буквы в BANANA?
Решение: В этом слове шесть букв, из которых три буквы А, две буквы Н и одна буква В. Таким образом, количество различных способов записи букв равно:
Количество перестановок n вещи, занимающие r за раз, в которых конкретная вещь никогда не происходит = .
Пример 10. Сколько различных слов из 3 букв можно составить из 5 гласных, если гласная «А» никогда не будет включена?
Решение: Всего букв (n) = 5
Итак, общее количество способов = n-1 P r = 5-1 P 3 = 4 P 3 = 24.
время, в течение которого m указанных вещей всегда собираются вместе = m!(n-m+1).
Пример 11. Сколькими способами можно расположить пять гласных a, e, i, o и u, если:
- две гласные e и i всегда вместе.
- две гласные e и i никогда не стоят вместе.
Решение: 1. По формуле m!(n – m + 1)!
Здесь n = 5, m = 2(e и i)
⇒ Требуемый номер. способов = 2!(5 – 2 + 1) ! = 2 × 4! = 48
2. Количество способов, когда e и i никогда не встречаются вместе
= общее количество. способов расположения 5 гласных
– нет. способов, когда e & i вместе = 5! – 48 = 72
Или используйте n! – м!(п – м + 1) ! = 5! – 48 = 72
Количество перестановок n различных вещей, взятых одновременно, при которых m указанных вещей никогда не сойдутся вместе = n!-m!(n-m+1)!
Число перестановок «n» вещей, взятых одновременно, когда «p» одинаковы одного вида, «q» одинаковы второго, «r» одинаково третьего и т. д.
д.
Пример 12: Сколько разных слов можно составить из букв мира МИССИСИППИ.
Решение: В слове MISSISSIPPI 4 I, 4S и 2P.
Таким образом, требуемое количество слов =
Количество перестановок «n» разных вещей, берущих «r» за раз, когда каждая вещь может быть повторена «r» раз = nr
Пример 13. Сколькими способами можно раздать 5 призов 4 мальчикам, если каждый мальчик имеет право на получение всех призов?
Решение: Любой из призов можно получить 4 способами; то любой из оставшихся 4 призов можно снова дать 4 способами, так как его может получить даже тот мальчик, который уже получил приз.
Следовательно, 5 призов можно раздать 4 × 4 × 4 × 4 × 4 = 4⁵ способами.
Комбинация
Комбинация — это расположение объектов без повторения и порядка, не имеющего значения. Другим определением комбинации является количество возможных таких схем.
Количество комбинаций «n» разнородных вещей, взятых «r» одновременно, обозначается как n C r или C(n, r) . Он определяется как n C r
Ключевым моментом для комбинации является то, что не допускается повторение объектов, и порядок не важен.
Пример 14. Перечислите все комбинации букв ABCD группами по 3.
Решение: Всего четыре комбинации (ABC, ABD, ACD и BCD). Ниже каждой из этих комбинаций перечислены шесть перестановок, которые эквивалентны как комбинации.
| ABC | ABD | ACD | BCD |
| ABC | ABD | ACD | BCD |
| ACB | ADB | ADC | BDC |
| BAC | BAD | CAD | CBD |
| BCA | BDA | CDA | CDB |
| CAB | DAB | DAC | DBC |
| CBA | DBA | DCA | DCB |

Решение: Общее количество способов
=
= = 4368.
Условные комбинации
Количество комбинаций n различных объектов, взятых одновременно, когда k конкретных объектов никогда не встречаются =
Количество выборов r объектов из n объектов, когда p отдельных объектов не находятся вместе ни в одном выборе = n C r – n-p C r-p
Количество выбранных r последовательных вещей из n вещей подряд = n – r + 1
Количество выбранных r последовательных вещей из n вещей по кругу =
количество комбинаций «n» разных вещей, использующих некоторые или все сразу =
Количество способов разделить m + n вещей на две группы, содержащие соответственно m и n вещей = m+n C n . n C n
Количество способов разделить ‘m + n + p’ вещей на три группы, содержащие соответственно ‘m’, ‘n’ и ‘p’ вещей = m+n+p C м . n+p C p =
n+p C p =
(i) Если m = n = p, т.е. Вещи «3m» разбиты на три равные группы, тогда количество комбинаций равно 9.0003
(ii) Buf, если «3m» вещей должны быть разделены между тремя людьми, то количество делений равно
Если mn отдельных предметов нужно разделить на m групп. Тогда число комбинаций равно , когда порядок групп не важен
и , когда важен порядок групп
Количество прямоугольников и квадратов
Количество прямоугольников любого размера в квадрате размера n × n и количество квадратов любого размера.
Количество прямоугольников любого размера в прямоугольнике размером n × p (n ,
Пример 16. Сколько клеток можно составить на шахматной доске?
Решение: Шахматная доска состоит из 9 равноотстоящих горизонтальных и вертикальных линий. Чтобы составить квадрат 1 × 1, мы должны выбрать из них две последовательные горизонтальную и вертикальную линии. Это можно сделать 8 × 8 = 8² способов.
Это можно сделать 8 × 8 = 8² способов.
Квадрат 2 × 2 требует трех последовательных горизонтальных и вертикальных линий, и мы можем сделать это 7 × 7 = 7² способов. Продолжая в том же духе, общее количество квадратов равно 9.0003
= 204.
Что нужно запомнить
0! = 1
Факториалы дробей и отрицательных целых чисел не определены.
;
N C x = N C y ⇒ x+ y = n
N C R = N C R+ = N C R+ = n C R+ = N C R+ = N C R+ = N C R+ = N C R+ = N C R+ = N C C R = . 1 C r
n C r = . н-1 С р-1
n C r = (n – r + 1) n C r-1
n C 1 = n C n-1 = n
Solved Examples
1. Prove that
Prove that
Solution:
= =
2. Prove that
Solution: We have
=
3. There 6 вопросов с несколькими вариантами ответов на экзамене. Сколько возможных последовательностей ответов, если в первых трех вопросах по 4 варианта, а в следующих трех по 5 вариантов?
Решение: На каждый из первых трех вопросов можно ответить 4 способами, а на каждый из следующих трех вопросов можно ответить 5 различными способами.
Отсюда искомое количество различных последовательностей ответов
= 4 × 4 × 4 × 5 × 5 × 5 = 8000.
4. Пять человек вошли в кабину лифта на первом этаже восьмиэтажного дома. дом. Предположим, что каждый из них может самостоятельно выйти из салона на любом этаже, начиная с первого. Каким общим числом способов каждый из пяти человек может покинуть каюту на любом из 7 этажей?
Решение: Любой из 5 человек может покинуть каюту 7 способами независимо от других.
Следовательно, необходимое количество способов = 7 × 7 × 7 × 7 × 7 = 7⁵.
5. Сколькими способами пять мальчиков и пять девочек могут образовать круг так, чтобы мальчики и девочки чередовались?
Решение: Поставив на стол одного мальчика, оставшихся можно разложить на 4! способы.
Будет 5 мест, по одному между двумя мальчиками
который могут заполнить 5 девушек из 5! способы.
Отсюда по принципу умножения искомое количество способов = 4! × 5! = 2880.
6. Сколькими способами можно рассадить 5 мальчиков и 5 девочек за круглым столом, при этом никакие две девочки не могут быть вместе?
Решение: Оставив одно место свободным между двумя мальчиками, можно сесть на 4! способы. Тогда на оставшихся 5 местах, 5 девушек сидят на 5! способы. Следовательно, искомое число = 4! × 5!
7. Сколько трехзначных чисел можно составить из цифр 1, 2, 3, 4, 5, если цифры могут повторяться?
Решение: Единичный разряд можно заполнить 5 способами, а так как повторы цифр разрешены, то и десятый разряд можно заполнить 5 способами.
Кроме того, сотое место можно заполнить также 5 способами.
Следовательно, искомое количество трехзначных чисел равно 5 × 5 × 5 = 125.
8. Сколькими способами можно расставить 8 человек по кругу?
Решение: Восемь человек можно расположить в круг
(8 – 1) ! = 7! = 5040.
ДАЛЕЕ: Комбинация перестановок
Перестановка и комбинация Важные формулы
Главная » Способности » Перестановка и комбинация » Важные формулы
Упражнение :: Перестановка и комбинация — Важные формулы
- 5 Важные2 формулы и комбинация Перестановка и комбинация – общие вопросы
Факторная запись:
Пусть n — целое положительное число. Затем факториал n , обозначаемый как n ! определяется как:
н! = п(п — 1)(п — 2) … 3.2.1.
Примеры:
Определяем 0! = 1 .

4! = (4 х 3 х 2 х 1) = 24.
5! = (5 х 4 х 3 х 2 х 1) = 120.
Варианты:
Различное расположение данного количества вещей путем взятия некоторых или всех одновременно называется перестановками.
Примеры:
Все перестановки (или расположения), сделанные с буквами a , b , c , взяв по две за раз, равны ( ab , ba , ac , ca , bc , cb ).
Все перестановки с буквами a , b , c , взятые все одновременно, составляют:
( abc , acb , bac , bca , каб , cba )
Количество перестановок:
Количество всех перестановок n вещей, взятых r за раз, равно:
n P r = n ( n — 1)( n — 2) .  .. ( n 92 — = 92 92 — )
.. ( n 92 — = 92 92 — )п ! ( н — р )! Примеры:
6 P 2 = (6 x 5) = 30.
7 P 3 = (7 х 6 х 5) = 210.
Кор. количество всех перестановок n вещей, взятых одновременно = n !.
Важный результат:
Если имеется n предметов, из которых p 1 одинаковы одного вида; p 2 похожи другого рода; P 3 — это третий вид, так и P R , как и R TH ,
Такие, что ( P 1 + 9249249249249249249249249249249249249249249249249249249249249249249249246 +
+
. … p r ) = n .
Тогда количество перестановок этих n объектов = п ! ( р 1 !).( р 2 )!…..( р р !) Комбинации:
Каждая из различных групп или выборок, которые могут быть образованы путем взятия некоторых или всех объектов, называется комбинацией .
Примеры:
Предположим, мы хотим выбрать двух из трех мальчиков A, B, C. Возможные варианты выбора: AB, BC и CA.
Примечание: AB и BA представляют один и тот же выбор.
Все комбинации, образованные a , b , c при взятии ab , bc , ca .
Единственная комбинация, которая может быть составлена из трех букв a , b , c , взятых одновременно, это abc .
Различные группы из 2-х из 4-х человек A, B, C, D:
AB, AC, AD, BC, BD, CD .
Обратите внимание, что ab ba — это две разные перестановки, но они представляют одну и ту же комбинацию.
Количество комбинаций:
Количество всех комбинаций из n вещей, взятых r за раз, составляет:
н С р = п ! = n ( n — 1)( n — 2) . 

 Увеличение объема продаж…
Увеличение объема продаж…
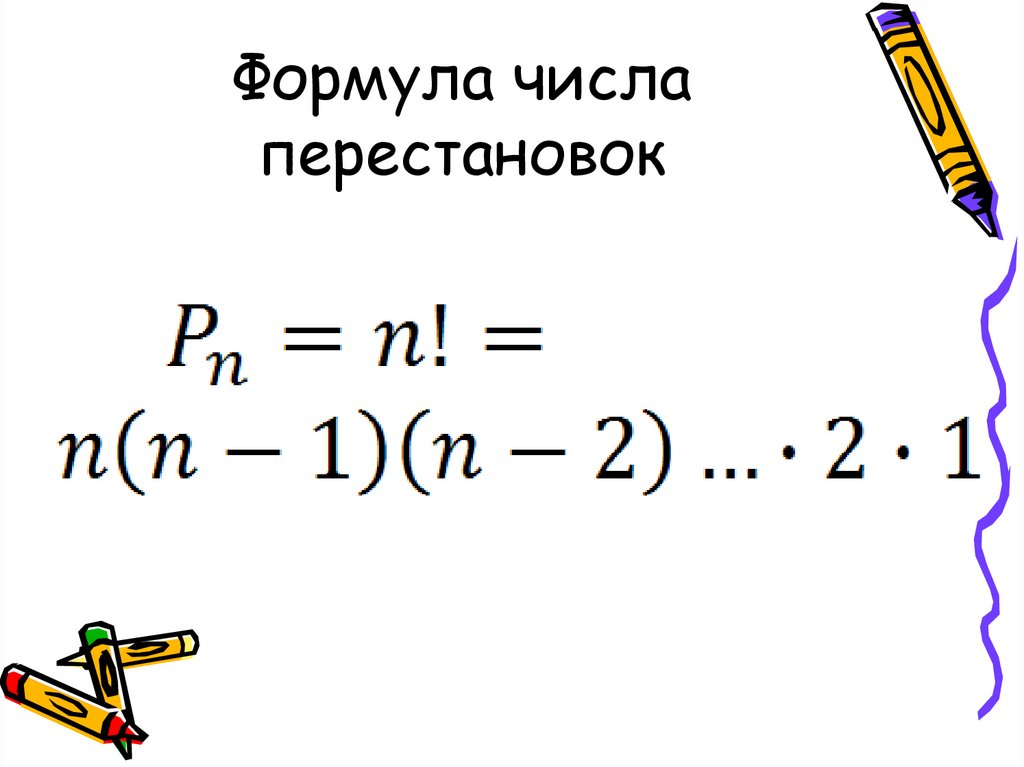
 Согласно теореме умножения искомое число способов посадки равно .
Согласно теореме умножения искомое число способов посадки равно . к. легко выводится из классического определения вероятности (доказать самостоятельно).
к. легко выводится из классического определения вероятности (доказать самостоятельно). Поскольку событие, стоящие в правых частях этих равенств, несовместны, то
Поскольку событие, стоящие в правых частях этих равенств, несовместны, то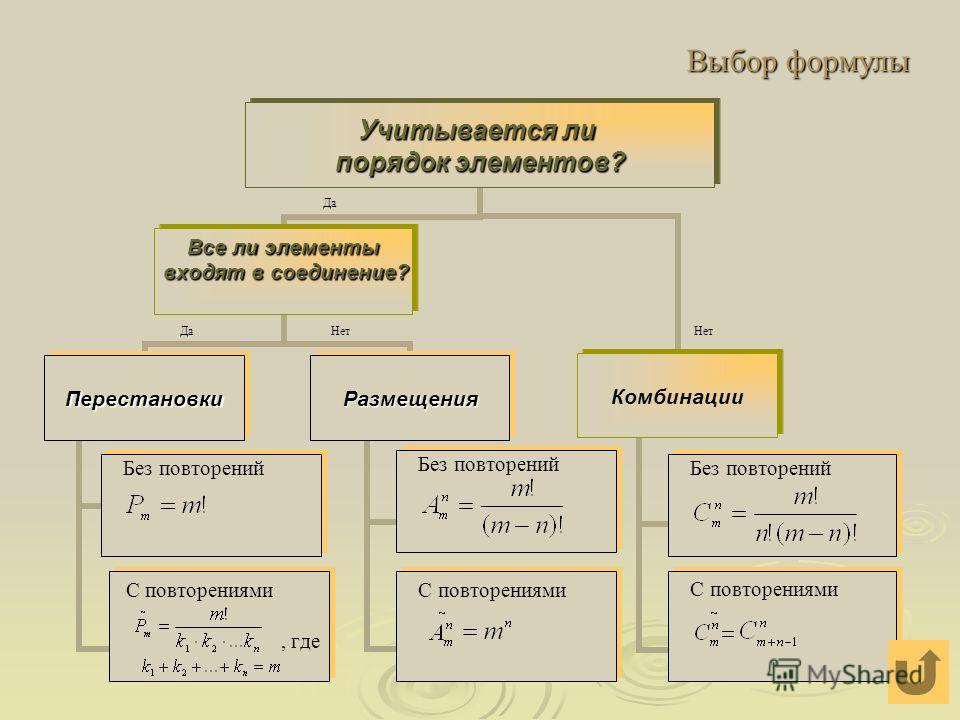 Полученное равенство соответствует теореме сложения вероятностей.
Полученное равенство соответствует теореме сложения вероятностей. Тогдаполучим
Тогдаполучим