Формулы сокращенного умножения кубов: Формулы сокращённого умножения

Формулы сокращенного умножения

Главная / i / t

• Квадрат суммы
• Квадрат разности
• Разность квадратов
• Сумма кубов
• Разность кубов
• Куб суммы
• Куб разности

Раскрывать скобки в таких выражениях довольно просто:

(x∙y)2 = (x∙y)∙(x∙y) = x∙x∙y∙y = x2∙y2

Это быстро можно сделать в случае, когда выражение в скобках содержит только операции умножения или деления. Но гораздо больше требуется промежуточных действий, чтобы раскрыть скобки с выражением, содержащим сумму или разницу двух чисел:

(x + y)2

(x − y)2

И чтобы избавиться от многократного повторения одних и тех же процедур существуют вот такие формулы сокращенного умножения:

Формулы сокращенного умножения

(x + y)2 = x2 + 2∙x∙y + y2

(x − y)2 = x2 − 2∙x∙y + y2

x2 − y2 = (x + y)∙(x − y)

x3 + y3 = (x + y)∙(x2 − x∙y + y2 )

x3 − y3 = (x − y)∙(x2 + x∙y + y2 )

(x + y)3 = x3 + 3∙x2∙y + 3∙x∙y2 + y3

(x − y)3 = x3 − 3∙x2∙y + 3∙x∙y2 − y3

Разберемся по порядку с каждой из этих формул.

Квадрат суммы

Возведем в квадрат следующее выражение:

(x + y)2

Квадратом числа называется умноженное дважды на само себя это число. В нашем случае в квадрат возведено число x+y, значит:

(x + y)2 = (x + y)∙(x + y)

Раскроем скобки:

(x + y)∙(x + y) = x∙x + x∙y + y∙x + y∙y

Дважды умноженный сам на себя x заменим на x2, аналогично заменим и y∙y на y2:

x∙x + x∙y + y∙x + y∙y = x2 + x∙y + y∙x + y2

Числа x∙y и y∙x всегда будут равны друг другу при совершенно любых x и y, поэтому вместо них можно оставить только число x∙y, умноженное на два:

x2 + x∙y + y∙x + y2 = x2 + 2∙x∙y + y2

Ни одно из всех этих преобразований не должно изменить значения первоначального выражения, значит, оно равно конечному:

(x + y)2 = x2 + 2∙x∙y + y2

Это формула сокращенного умножения называется «квадрат суммы».

Квадрат суммы двух чисел равен квадрату первого числа, плюс удвоенное произведение первого числа на второе, плюс квадрат второго числа:

(x + y)2 = x2 + 2∙x∙y + y2

Благодаря этой формуле нам теперь не придется многократно выполнять все вышеописанные процедуры.

Данное равенство будет выполняться при абсолютно любых x и y, такие выражения называются тождествами.

Тождеством называется равенство, верное при всех допустимых значениях входящих в него переменных.

Проверим сохранится ли равенство, если подставить в первую часть формулы вместо x число 3, а вместо y число 5:

(x + y)2 = (3 + 5)2 = 82 = 8∙8 = 64

Подставим эти же числа во вторую часть – будет тоже 64:

x2 + 2∙x∙y + y2 = 32 + 2∙3∙5 + 52 = 9 + 30 + 25 = 64

Равенство сохранилось – обе части равны друг другу.

Причину этой закономерности можно еще объяснить следующей геометрической иллюстрацией.

На рисунке изображен большой квадрат 8 на 8, состоящий из 8–ми рядов маленьких квадратиков, и каждый ряд состоит из 8–ми квадратиков. Чтобы посчитать количество маленьких квадратиков достаточно умножить 8 на 8:

8∙8 = 82

В этом выражении можно 8 поменять на 3+5, и посчитать количество квадратиков так:

(3 + 5)2 = 64

Но количество маленьких квадратиков можно посчитать и по-другому: сложить количество красных, зеленых и желтых квадратиков.

Чтобы посчитать количество красных квадратиков, нужно 3 умножить на 3:

3∙3 = 32 = 9

Количество зеленых вычислим так:

5∙5 = 52 = 25

Каждый из двух желтых прямоугольников состоит из 3 – х рядов, в каждом из которых 5 квадратиков, значит, количество желтых квадратиков можно определить так:

2∙3∙5 = 30

Сложим количество красных, зеленых и желтых квадратиков – получим тоже 64:

32 + 2∙3∙5 + 52 = 9 + 30 + 25 = 64

Очевидно, что оба способа подсчета квадратиков приведут к одному результату 64, значит:

(3 + 5)2 = 32 + 2∙3∙5 + 52

Первая часть этого выражения равна количеству квадратиков, которое подсчитано первым способом, вторая часть равна количеству квадратиков, которое подсчитано вторым способом.

С любыми другими числами равенство также будет всегда выполняться: например, пусть x=9, y=1, тогда:

(x + y)2 = (9 + 1)2 = 102 = 10∙10 = 100

x2 + 2∙x∙y + y2 = 92 + 2∙9∙1 + 12 = 81 + 18 + 1 = 100

Если одно из чисел равно нулю, равенство тоже сохранится: x=7, y=0

(x + y)2 = (7 + 0)2 = 72 = 7∙7 = 49

x2 + 2∙x∙y + y2 = 72 + 2∙7∙0 + 02 = 49 + 0 + 0 = 49

Как видите, это равенство верно при всех допустимых значениях.

Квадрат разности

Квадрат разности двух чисел равен квадрату первого числа, минус удвоенное произведение первого числа на второе, плюс квадрат второго числа.

(x − y)2 = x2 − 2∙x∙y + y2

Это тождество очень похоже на предыдущее. Чтоб убедиться, что это действительно тождество достаточно просто раскрыть скобки:

(x − y)2 = (x − y)∙(x − y)

(x − y)∙(x − y) = x2 − x∙y − y∙x + y2

С полной уверенностью можно заменить −x∙y−y∙x на −2∙x∙y, ибо это одно и то же:

x2 − x∙y − y∙x + y2 = x2 − 2∙x∙y + y2

И из первой части тождества получилась вторая, следовательно, это равенство верно для любых x и y:

Обе части этого тождества будут равны, даже когда x и y – дроби.

Пусть , :

Приведем дроби к общему знаменателю, чтобы отнять одну дробь от другой и возвести в квадрат:

А сейчас сделаем то же самое только уже через формулу:

Домножим все дроби, чтоб знаменатель был одинаковый и сложим их:

Пример

Упростить выражение:

(3∙a − b)2 + 6∙a∙b − b2

Воспользуемся формулой сокращенного умножения, чтобы раскрыть скобку:

(3∙a − b)2 + 6∙a∙b − b2 =

(3∙a)2 − 2∙3∙a∙b + b2 + 6∙a∙b − b2

Возведем в квадрат 3∙a и заменим 2∙3 на 6:

9∙a2 − 6∙a∙b + b2 + 6∙a∙b − b2

Чтобы было легче заметить, что делать дальше переставим похожие слагаемые поближе друг к другу:

9∙a2 − 6∙a∙b + 6∙a∙b + b2 − b2

Число −6∙a∙b+6∙a∙b при всех a и b будет равна нулю, как и число b2−b2, значит, их можно сократить:

9∙a2 + 6∙a∙b − 6∙a∙b + b2 − b2 = 9∙a2

Выражение стало намного проще – и теперь громоздкая изначальная конструкция равносильна 9∙a2:

(3∙a − b)2 + 6∙a∙b − b2 = 9∙a2

Пусть a=5, b=7, тогда значение первоначального выражения равно 225:

(3∙a − b)2 + 6∙a∙b − b2 =

(3∙5 − 7)2 + 6∙5∙7 − 72 =

=(15 − 7)2 + 210 − 49 =

82 + 210 − 49 = 64 + 210 − 49 = 225

Но у нас есть упрощенная версия того же выражения, и мы можем получить то же число 225 гораздо легче:

9∙a2 = 9∙52 = 9∙5∙5 = 225

Отсутствие числа b в выражении 9∙a2 означает, что от b ничего не зависит – попробуйте в первоначальном выражении число a оставить равным пяти, а вместо b подставьте любое другое число – получится тоже 225.

Разность квадратов

Еще одна очень популярная формула сокращенного умножения – «разность квадратов»:

Разность квадратов двух чисел равна произведению суммы этих чисел на их разность:

x2 − y2 = (x + y)∙(x − y)

Доказать это тождество очень легко:

(x + y)∙(x − y) = x∙x − x∙y + y∙x − y∙y =

x2 − x∙y + y∙x − y2 =

Сумма −x∙y+y∙x всегда будет равна нулю, какие числа вместо x и y мы бы ни подставляли, поэтому их можно просто убрать – от этого ничего не изменится:

x2 − x∙y + y∙x − y2 = x2 − y2

Проверим справедливость этого тождества:

Пусть x=124, y=123

(x + y)∙(x − y) = (124 + 123)∙(124 − 123) = 247∙1 = 247

x2 − y2 = 1242 − 1232 = 15376 − 15129 = 247

Вычисления в первом случае гораздо легче, чем во втором, поэтому, вместо вычисления значения выражения 1242 − 1232, иногда вычисляют значение выражения (124+123)∙(124 − 123).

Пример

Упростить выражение:

Чтобы в числителе появилась разность квадратов двух чисел, нужно заменить 9 на 32:

Теперь можно применить формулу:

Разделим числитель и знаменатель на число x+3, основное свойство дроби говорит, что от этого дробь не изменит значения:

Но обязательно следует учитывать, что до сокращения на x + 3, вместо x нельзя было подставить − 3 (будет деление на ноль), а после – уже можно. Поэтому сокращение на выражение, содержащее переменную, не всегда приводит к абсолютно тождественному выражению. В нашем случае первоначальное выражение тождественно конечному для всех x кроме случая, когда x = −3:

Подставим 100 вместо x в первое неупрощенное выражение – получим 97:

И подставим в упрощенное:

x − 3 = 100 − 3 = 97

Очевидно, что с упрощенным выражением легче работать чем с первоначальным.

Сумма кубов

Все следующие формулы используются гораздо реже чем предыдущие, но иногда они незаменимы.

Сумма кубов двух чисел равна произведению суммы этих чисел на неполный квадрат их разности:

x3 + y3 = (x + y)∙(x2 − x∙y + y2)

Раскроем скобки второй части этого тождества:

(x + y)∙(x2 − x∙y + y2) = x3 − x2∙y + x∙y2 + x2∙y − x∙y2 + y3

Сумма –x2∙y+x∙y2+x2∙y–x∙y2 равна нулю, уберем эту сумму, тогда из второй части тождества получится первая:

x3 + y3

Теперь проверим равенство на числах:

Пусть x=5, y=2

x3 + y3 = 53 + 23 = 125 + 8 = 133

Вторая часть тождетсва тоже будет равна 133:

(x + y)∙(x2 − x∙y + y2) =

(5 + 2)∙(52 − 5∙2 + 22 ) =

(7)∙(25 − 10 + 4) = 7∙19 = 133

Пример

Упростить выражение:

Число 125 равно числу 53, а 25=52, тогда их можно заменить:

В числителе появилась разница кубов, значит можно применить формулу:

Воспользуемся основным свойством дроби, чтобы сократить дробь:

Так как знаменатель x2 − 5∙x + 52 ни при одном действительном x никогда не будет равен нулю, то можно совершенно спокойно его сокращать, не беспокоясь за потерю равносильности.

Теперь при x=7, значение этого выражения можно вычислить так:

Но поскольку мы уже упростили это выражение, то тот же результат можно получить так:

x + 5 = 7 + 5 = 12

Разность кубов

Разность кубов двух чисел равна произведению разности этих чисел на неполный квадрат их суммы:

x3 − y3 = (x − y)∙(x2 + x∙y + y2)

Докажем это тождество:

(x − y)∙(x2 + x∙y + y2) =

x3 + x2∙y + x∙y2 − x2∙y − x∙y2 − y3 =

Сократим слагаемые, сумма которых равна нулю:

x3 + x2∙y + x∙y2 − x2∙y − x∙y2 − y3 =

x3 + y3

Аналогично убедимся в равенстве на тех же числах: x=5, y=3

x3 − y3 = 53 − 33 = 125 − 27 = 98

(x + y)∙(x2 − x∙y + y2) =

(5 − 3)∙(52 + 5∙3 + 32) =

(2)∙(25 + 15 + 9) = 2∙49 = 98

Куб суммы

Куб суммы двух чисел равен кубу первого числа, плюс утроенное произведение квадрата первого числа на второе, плюс утроенное произведение первого числа на квадрат второго, плюс куб второго числа

(x + y)3 = x3 + 3∙x2∙y + 3∙x∙y2 + y3

Чтобы доказать эту формулу нам потребуется сначала применить первое свойство степени:

(x + y)3 = (x + y)∙(x + y)2 =

По уже знакомой формуле квадрата суммы заменим вторую скобку:

(x + y)∙(x2 + 2∙x∙y + y2) =

И раскроем скобки по стандартной схеме:

(x + y)∙(x2 + 2∙x∙y + y2) = x3 + 2∙x2∙y + x∙y2 + x2∙y + 2∙x∙y2 + y3 =

Немного переставим слагаемые:

x3 + 2∙x2∙y + x2∙y + x∙y2 + 2∙x∙y2 + y3 =

К удвоенному x2∙y прибавляется одно x2∙y, следовательно, их сумму можно заменить утроенным x2∙y:

x3 + 3∙x2∙y + x∙y2 + 2∙x∙y2 + y3 =

Таким же образом поменяем x∙y2 + 2∙x∙y2 на 3∙x∙y2, которое имеет тот же смысл:

x3 + 3∙x2∙y + 3∙x∙y2 + y3 =

Так что теперь куб суммы можно посчитать не только так: x=6, y=4

(6 + 4)3 = 103 = 1000

Но еще и так:

63 + 3∙62∙4 + 3∙6∙42 + 43 = 216 + 432 + 288 + 64 = 1000

Пример

Упростить выражение:

Раскроем скобку в кубе по формуле:

Заменим на равное ему , заменим на , а 23 на 8:

Убираем слагаемые, сумма которых равна нулю, и потому никак не влияет на значение выражения:

Заменим 8 − 7 на 1:

По определению корня равен x, значит:

x + 1

Оказывается, что первоначальное сложное выражение равносильно такому простому конечному:

Проверить равносильность выражений можно на совершенно любом числе, например, пусть x будет равен 125, тогда изначальное выражение будет иметь значение 126:

(5 + 2)3 − 6∙(5)2 − 12∙5 − 7 =

(7)3 − 6∙25 − 60 − 7 =

343 − 150 − 60 − 7 = 126

Но вместо всех этих громоздких вычислений значения выражения при x=125 достаточно было воспользоваться его упрощенной версией, в которой просто нужно к 125 прибавить единицу и получить то же значение 126:

x + 1 = 125 + 1 = 126

Куб разности

Куб разности двух чисел равен кубу первого числа, минус утроенное произведение квадрата первого числа на второе, плюс утроенное произведение первого числа на квадрат второго, минус куб второго числа:

(x − y)3 = x3 − 3∙x2∙y + 3∙x∙y2 − y3

Доказательство этой формулы произведем по той же схеме, которая использовалась в предыдущий раз:

(x − y)3 =

(x − y)∙(x2 − 2∙x∙y + y2) =

x3 − 2∙x2∙y + x∙y2 − x2∙y + 2∙x∙y2 − y3 =

x3 − 2∙x2∙y − x2∙y + x∙y2 + 2∙x∙y2 − y3 =

x3 − 3∙x2∙y + x∙y2 + 2∙x∙y2 − y3 =

x3 − 3∙x2∙y + 3∙x∙y2 − y3

Пусть x=6, y=4, тогда куб разности этих чисел будет равен:

(6 − 4)3 = 23 = 8

Если посчитать, предварительно раскрыв скобки по формуле, то получится тоже восемь:

63 − 3∙62∙4 + 3∙6∙42 − 43 = 216 − 432 + 288 − 64 = 8

как раскладывается, формула сокращенного умножения, примеры с решением

Содержание:

• Что такое разность кубов и куб разности
• Вывод формулы разности кубов, как раскладывается
• Правила применения формул сокращенного умножения
  • Примеры задач с решением

Содержание

• Что такое разность кубов и куб разности
• Вывод формулы разности кубов, как раскладывается
• Правила применения формул сокращенного умножения
  • Примеры задач с решением

Что такое разность кубов и куб разности

Для возведения чисел и выражений в степень, а также для упрощения умножения используют формулы сокращенного умножения. 2+20y+25).\)

Насколько полезной была для вас статья?

Рейтинг: 4.00 (Голосов: 1)

Выделите текст и нажмите одновременно клавиши

«Ctrl» и «Enter»

Поиск по содержимому

Математический обзор факторинговых сумм или разностей кубов

Математический обзор факторинговых сумм или разностей кубов https://schooltutoring.com/help/wp-content/themes/movedo/images/empty/thumbnail.jpg 150 150 Дебора Дебора https://secure.gravatar.com/avatar/63fb4ad5c163b8f83de2f54371b9e040?s=96&d=mm&r=g 2 июля 2014 г. 2 декабря 2014 г.

Обзор

Суммы или разности кубов можно разложить аналогично другим квадратным уравнениям. Они следуют шаблону, который немного сложнее, чем факторизация квадратных уравнений.

Сумма кубов

Сумма кубов — это выражение, такое как x ³ + a ³ , где оба члена выражения являются совершенными кубами. Предположим, что выражение равно 8y ³ + 27. Одночлен 8y ³ является совершенным кубом числа 2y, потому что (2y) ³ равно 8y ³ . Точно так же константа 27 представляет собой совершенный куб числа 3, потому что 3 ³ равно 27.

Разность кубов

Разность кубов представляет собой выражение типа x ³ – a ³ , где оба члена выражения являются совершенными кубами. Предположим, что выражение 64x ³ – 125. Одночлен 64x ³ — это совершенный куб 4x, потому что (4x) ³ равно 64x ³ . Точно так же константа 125 — это совершенный куб числа 5, потому что 5 ³ равно 125. Совершенный куб может быть отрицательным действительным числом, потому что отрицательное действительное число, умноженное на отрицательное действительное число, является положительным, а положительное число, умноженное на отрицательное. число отрицательное число.

Рисунок 2: Разность кубов следует схеме x ³ – a ³ .

Разложение суммы кубов на множители

Сумма кубов x ³ + a ³ следует специальной схеме. Один множитель (x + a), а другой множитель — квадратичный многочлен, который уже в простейшем виде (x ² — ax + a ² ). Умножение (х + а) (х ² – топор + а ² ) равносильно сложению х(х ² – топор + а ² ) + а(х ² – топор + а). ² ). Первый член равен x ³ – ax ² + a ² x, а второй член равен ax ² – а ² х +а ³ . Соединяя термины вместе, мы получаем полное выражение: x ³ – ax ² + a ² x –a ² x + a ³ . Упрощенно выражение представляет собой сумму кубов x ³ + a ³ . Предположим, выражение 8y ³ +27. Следуя шаблону, его можно разложить как (2y + 3) (4y ² – 6y + 9).

Фактор разности кубов

Разность кубов x ³ – ³ также следует специальной схеме. Один множитель есть (х – а), а другой множитель – аналогичный квадратичный многочлен к сумме кубов, тоже уже в простейшем виде (х ² +ах +а ² ). Умножение (x – a)(x ² + ax + a ² ) равносильно сложению x(x ² + ax + a ² ) – a(x ² + ax + a ² ). Упрощенно выражение представляет собой разность кубов x ³ – a ³ . Предположим, что выражение равно x ³ – 216. Следуя шаблону, его можно разложить как (x – 6)(x ² + 6x + 36). Это то же самое, что х(х ² + 6х + 36) – 6(х ² +6х + 36). Если сложить вместе, то получится выражение x ³ + 6x ² + 36x – 6x ² – 36x – 216.

Рис. 3. Схема факторизации суммы двух кубов или разности двух кубов .

SOAP

Аббревиатура SOAP позволяет легко запомнить последовательность суммы или разности кубов. Если разлагаемое выражение представляет собой сумму кубов x ³ +a ³ , первый множитель (x + a) имеет тот же знак, что и x ³ + a ³ . Первая операция (х ² – топор) во втором сомножителе (х ² – топор + b ² ) имеет противоположный знак как х + а. Вторая операция во втором множителе (ax + b ² ) всегда положительна. Если факторизуемое выражение представляет собой разность кубов x ³ – a ³ , последовательность также соответствует SOAP. Первый множитель (х – а), тот же знак. Первая операция (х ² + ax) во втором сомножителе (x ² +ax + b ² ) имеет знак, противоположный знаку (x – a), а вторая операция (ax + b ² ) всегда положительна. Доказательство факторизации либо суммы кубов, либо разности кубов будет изучено на более продвинутых курсах математики в колледже.

Рисунок 4: Мнемоника для запоминания порядка знаков. (Он даже плавает!)

Заинтересованы в услугах репетитора по алгебре? Узнайте больше о том, как мы помогаем тысячам студентов каждый учебный год.

SchoolTutoring Academy — это первоклассная компания, предоставляющая образовательные услуги для учащихся K-12 и колледжей. Мы предлагаем программы репетиторства для учащихся K-12, классов AP и колледжей. Чтобы узнать больше о том, как мы помогаем родителям и учащимся в Alabaster, AL: посетите Tutoring in Alabaster, AL

Как найти площадь поверхности прямоугольной призмы (формула + видео)

Содержание

Нахождение площади поверхности всех прямоугольные призмы позволяет также найти площадь поверхности любого куба, поскольку куб является разновидностью прямоугольной призмы.

1. Что такое прямоугольная призма?
2. Какова площадь поверхности прямоугольной призмы?
3. Площадь поверхности прямоугольной призмы Формула
4. Как найти площадь поверхности прямоугольной призмы
5. Площадь поверхности прямоугольной коробки
6. Примеры расчета площади поверхности

Площадь поверхности прямоугольной призмы

Что такое прямоугольная призма?

Прямоугольная призма представляет собой шестигранное трехмерное тело, все грани которого являются прямоугольниками. Все шесть граней сходятся под прямым углом друг к другу. Противоположные грани равны.

Прямоугольная призма особого типа представляет собой куб , у которого все шесть граней конгруэнтны.

Какова площадь поверхности прямоугольной призмы?

Площадь поверхности прямоугольной призмы равна сумме площадей всех шести граней. Когда у вас есть куб, нахождение площади одной грани позволяет очень быстро найти общую площадь поверхности твердого тела, поскольку она будет в шесть раз больше площади одной грани.

Площадь поверхности прямоугольной призмы Формула

Нахождение площади поверхности всех прямоугольных призм (включая кубы) включает в себя как сложение, так и умножение. Вы должны знать ширину, длину и высоту призмы, прежде чем сможете применить эту формулу:

A = 2(ширина × длина) + 2(длина × высота) + 2(высота × ширина)

Мы можем использовать общие сокращения для ширины (w), длины (l) и высоты (h) и переформулировать формулу:

A = 2wl + 2lh + 2hw

Мы можем упростить это, выделив 2:

A = 2 wl + lh + hw

Поскольку каждая грань прямоугольной призмы имеет конгруэнтную противоположную грань, вы отслеживаете все шесть граней попарно.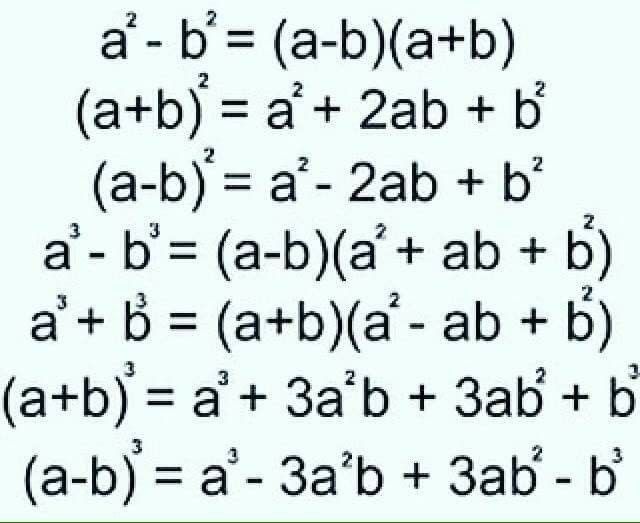 Использование формулы помогает предотвратить путаницу или отслеживать, какие грани вы измеряли. Вам нужны только три измерения.

Площадь поверхности прямоугольной коробки Формула

Для куба или прямоугольной коробки формула становится еще проще. Возьмите длину любого ребра, a :

A = 6a2

Это работает, потому что все измерения куба — ширина, высота и длина — одинаковы. Любые два измерения дадут площадь одной грани, а у куба шесть граней, поэтому площадь равна 6a2. Если вам трудно запомнить эту специальную формулу, вы всегда можете использовать общую формулу для прямоугольных призм.

Как найти площадь поверхности прямоугольной призмы

Вас попросили упаковать подарочную коробку, которую ваш математический клуб передаст вашему консультанту математического клуба. В коробке 100 сборников математических анекдотов, так что это прямоугольная призма хорошего размера. (Вы знаете, сколько книг в коробке? 😊)

[вставьте изображение коробки с размерами, как показано]

Размеры:

• Ширина — 30 см
• Длина — 15 см
• Высота — 20 см

Используйте формулу площади, чтобы узнать минимальное количество подарочной упаковки, которое вам понадобится. Сначала работайте; тогда загляните.

Составим уравнение для площади поверхности прямоугольной призмы, исходя из нашей формулы: + 300 + 600

A = 2 1350

A = 2700 см2

Хотя это звучит как много подарочной упаковки, это всего 0,27 м2. У вас есть лист подарочной упаковки размером 0,75 м × 0,5 м. Как вы думаете, вам будет достаточно?

Конечно, даже если вы оставите немного больше на перекрытие, ведь у вас есть 0,375 м2, а нужно всего 0,27 м2! (Вы знали, что в коробке всего 10 книг? 😲)

Площадь поверхности прямоугольной коробки

Теперь давайте посмотрим, как найти площадь поверхности прямоугольной призмы, коробки или куба.

Вы также должны упаковать хваленый куб корневого куба математического клуба для летнего хранения. У куба 12 конгруэнтных ребер по 45 см каждое. Сначала работайте; тогда загляните.

[вставьте изображение причудливой коробки с надписью Cube Root Cube]

Давайте составим уравнение для площади поверхности прямоугольной коробки, исходя из нашей формулы куба:

A = 6a2

A = 6452

A = 62 025

A = 62 025

A = 12,150 см вы будете использовать Постоянные записи старейшин клуба, чтобы обернуть ценный корневой куб куба. У вас есть 2 м2 их записей, датируемых 1960 годом. Хотя 12 150 см2 звучит много, это всего лишь 1 215 м2, поэтому у вас достаточно упаковки для хранения, чтобы защитить куб и его бесценное содержимое кубических корней.

Как рассчитать площадь поверхности Примеры

Потренируйтесь решать задачи на площадь поверхности для прямоугольных призм и кубов. Прежде чем смотреть ответы, попробуйте свои силы в обоих! Посмотрите, получите ли вы правильные ответы.

Вам нужно накрыть дорожную клетку для вашего домашнего удава, чтобы вы могли нести его в школьном автобусе. Какова площадь поверхности клетки?

[вставьте чертеж прямоугольной призмы, помеченной 1,5 ярда в длину, 0,25 ярда в ширину, 0,25 ярда в высоту; можно нарисовать улыбающуюся мультяшную змею внутри призмы]

A = 2 wl + lh + hw

A = 2 0.25 × 1.5 + 1.5 × 0.25 + 0.25 × 0.25

A = 2 0.375 + 0.375 + 0.0625

A = 2 8.125

A = 1.625 yds2

Давайте попробуем решить другую задачу на определение площади поверхности прямоугольного ящика.