Функции пределов: Ошибка 403 — доступ запрещён

Содержание

Определение предела функции по Гейне

11.1Определения предела по Коши и по Гейне

Определение предела функции, которое мы дали в предыдущей главе, называется также определением «по Коши». Напомним его:

Определение 1. (Предел функции по Коши) Пусть функция f(x) определена в некоторой проколотой окрестности точки x0. Говорят, что предел функции f(x) в точке x=x0 равен числу b, если для всякого ε>0 найдётся такое δ>0, что для всех x из проколотой δ-окрестности точки x0 значения функции лежат в ε-окрестности точки b.

Формально: утверждение

limx→x0f(x)=b

по определению означает, что

∀ε>0 ∃δ>0 ∀x∈˚Uδ(x0):f(x)∈Uε(b),

или (см. замечание 3 из предедыщей лекции 10):

∀ε>0 ∃δ>0 ∀x∈R:0<|x−x0|<δ⇒|f(x)−b|<ε.

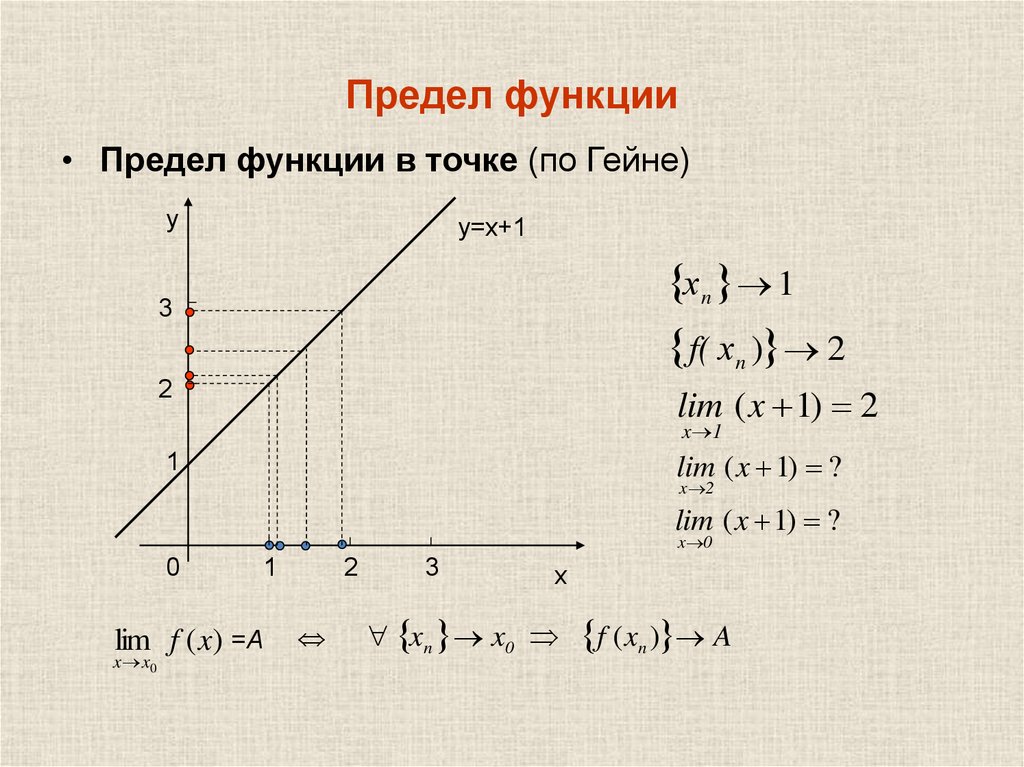
Для некоторых целей нам будет удобно использовать другое определение, известное как определение предела функции «по Гейне». Оно основано на понятии предела последовательности.

Определение 2. (Определение предела функции по Гейне.) Пусть снова функция f(x) определена в некоторой проколотой окрестности точки x0. Говорят, что предел функции f(x) в точке x=x0 равен числу b, если для любой последовательности {xn}, стремящейся к x0, все члены которой не равны x0, выполняется утверждение: последовательность значений функции f(x) в точках xn стремится к b: f(xn)→b при n→∞.

Формально:

∀{xn}:((∀n:xn≠x0)∧(limn→∞xn=x0))⇒limn→∞f(xn)=b.

∀{xn}:((∀n:xn≠x0)∧(limn→∞xn=x0))⇒⇒limn→∞f(xn)=b.

Это определение эквивалентно предыдущему (это мы чуть позже докажем) и хорошо согласуется с интуицией: например, на картинках в разделе примеры и мотивировка предыдущей лекции мы рисовали как раз последовательности значений x, и показывали (чисто визуально), что последовательность соответствующих значений функции стремится к нужному нам числу.

Нужно сказать про несколько тонкостей определения по Гейне:

Вообще говоря, не все значения f(xn) обязаны быть определены: возможно, какие-то из начальных членов последовательности {xn} лежат вне области определения функции f(x). Однако, мы знаем, что функция определена в некоторой проколотой окрестности точки x0, а последовательность xn стремится к x0, и значит, начиная с некоторого члена, обязательно окажется внутри той окрестности, где функция определена. Вместе с дополнительным условием о том, что члены последовательности не равны x0, это гарантирует, что по крайней мере начиная с некоторого n=N, все члены последовательности {f(xn)} определены. А поскольку начальные члены последовательности не влияют на предел, их можно просто отбросить.
Условие о том, что все члены последовательности {xn}, не равны x0, очень важно. Рассмотрим функцию
f(x)={1,x≠2;3,x=2.
из примера 12 с предыдущей лекции. Последовательность
xn={2,n=2k2+1n,n=2k+1
стремится к x0, при этом последовательность значений функции {f(xn)} имеет вид:
f(xn)={3,n=2k,1,n=2k+1,
и не имеет предела. Таким образом, если бы мы не требовали от последовательности {xn} никогда не посещать x0, нам пришлось бы сказать, что данная функция не имеет предела в точке 2, хотя согласно определению по Коши оно его имеет.
Требование xn≠x0 соответствует выбору проколотой окрестности для x0 в определении по Коши вместо обычной окрестности.
Заметим, что его также можно ослабить, и требовать, чтобы xn≠x0 не для всех n, а для всех, начиная с некоторого.
Тот факт, что в определении используется квантор всеобщности (для любой последовательности {xn}…), а не существования, также очень важен. Рассмотрим функцию
f(x)={x+1,x≤1;x−2,x>1.
из примера 13 с предыдущей лекции. У неё нет предела (по Коши) в точке x=1, поскольку при приближении по x к точке 1 справа или слева, значение функции f(x) приближается к разным числам (−1 и 2 соответственно).
Однако, если мы рассмотрим последовательность xn=1+1/n, она удовлетворяет всем условиям определения по Гейне, и при этом f(xn)→−1. Если бы достаточно было проверить лишь одну последовательность, мы могли бы сказать, что предел равен −1. Что не так: выбирая другую последовательность (например, xn=1−1/n), мы бы получили другой предел f(xn).

11.2Эквивалентность определений

Теорема 1. Определения предела по Коши и по Гейне эквивалентны.

Доказательство.

Из Коши следует Гейне. Пусть предел функции f при x→x0 равен b по Коши. Докажем, что тогда он равен b также и по Гейне.

Идея доказательства такая. Из определения по Коши следует, что если x близок к x0 (но при этом не равен x0), f(x) близко к b. Пусть последовательность xn стремится к x0 и никогда не посещает x0. Тогда если подождать достаточно долго, xn начнут быть близкими к x0 (и не равными x0). В этом случае, согласно определению по Коши, f(xn) окажутся близкими к b. Значит, f(xn) стремится к b.

Осталось чётко сформулировать, что значит в каждом случае означают слова «близко» и «достаточно долго».

Утверждение «предел функции f(x) при x→x0 равен b по Коши» формализуется так:

∀ε1>0 ∃δ1=δ1(ε1)>0 ∀x∈R:0<|x−x0|<δ1⇒|f(x)−b|<ε1.(11.1)

Докажем, что в этом случае определение по Гейне тоже выполняется. Пусть xn — произвольная последовательность, стремящаяся к x0 и никогда не посещающая x0. Тогда для всякого ε2>0 найдётся такое N2=N2(ε2), что для всех n>N2, выполняется неравенство |xn−x0|<ε2. Дополнительно известно, что для всех натуральных n, xn≠x0. Таким образом, для всех n>N2, выполняется неравенство

0<|xn−x0|<ε2.

Иными словами, все члены последовательности, начиная с номера N2+1, лежат в проколотой ε2-окрестности точки x0. Формально:

∀ε2>0 ∃N2=N2(ε) ∀n>N2:0<|xn−x0|<ε2.(11.2)

Мы хотим доказать, что в этом случае f(xn)→b. Иными словами, нам нужно доказать, что для всякого ε>0 найдётся такое N=N(ε), что для всех n>N выполняется неравенство |f(xn)−b|<ε.

Сравним утверждения (11.1) и (11.2). Утверждение (11.1) говорит, что если мы хотим сделать f(x) близким к b, то нужно потребовать, чтобы x был близок к x0 и не равнялся x0. Утверждение (11.2) говорит, что если мы хотим, чтобы xn был близок к x0, то нужно выбрать достаточно большое значение n. Осталось соединить эти два утверждения.

Пусть мы хотим сделать так, чтобы f(xn) был ε-близок к b. Согласно (11.1), для этого нужно сделать так, чтобы xn был δ1(ε)-близок к x0. Согласно (11.2), для этого нужно сделать так, чтобы n был больше, чем N2(δ1(ε)). Иными словами, мы в утверждении (11.2) в качестве ε2 должны использовать значение δ1(ε).

Действительно, положим N(ε):=N2(δ1(ε)). Тогда согласно (11.2) для всех n>N(ε), выполняется неравенство

0<|xn−x0|<δ1(ε).

Согласно (11.1), для всех значений x, для которых верно неравенство 0<|x−x0|<δ1(ε), верно неравенство |f(x)−b|<ε.

Значит, для всех xn это неравенство также верно.

Итак, для всякого ε>0 мы построили такое N, что для всех n>N выполняется неравенство |f(xn)−b|<ε. Таким образом, f(xn)→b.

Это построение работает для любой последовательности {xn}, удовлетворяющей условиям xn→x0 и xn≠x0 для всех n. Значит, утверждение определения по Гейне доказано.

Из Гейне следует Коши. Будем доказывать от противного. Пусть есть такая функция f(x), что для неё выполняется утверждение limx→x0f(x)=b по Гейне, но не выполняется такое же утверждение по Коши.

Запишем формально, что значит «не выполняется такое же утверждение по Коши». Для этого нужно навесить отрицание на формулу (11.1). Получится такая штука:

∃ε1>0 ∀δ1>0 ∃x=x(δ1):(0<|x−x0|<δ1)∧|f(x)−b|≥ε1.

В этой формуле δ1>0 произвольна, а x зависит от этой δ1. Чтобы прийти к противоречию, мы построим последовательность {xn}, для которой утверждение в определении предела по Гейне будет нарушаться: а именно, xn будет стремиться к x0, но f(xn) не будет стремиться к b.

Для этого возьмём последовательность δn:=1n. (Как обычно в таких случаях, подойдёт любая последовательность положительных чисел, стремящаяся к нулю.) Положим также xn:=x(δn)=x(1n). Для всякого натурального n,

x0−1n<xn<x0+1n.

Левая и правая границы стремятся к x0, следовательно, по теореме о двух милиционерах, xn→x0. Дополнительно верно, что для всех n, xn≠x0. Таким образом, последовательность {xn} удовлетворяет условию в определении предела по Гейне.

Однако, |f(xn)−b|≥ε1>0. Это значит, что последовательность {f(xn)} отделена от b, и следовательно не может иметь b своим пределом (см. упражнение 1 из лекции 6).

Противоречие с определением предела по Гейне: мы построили последовательность {xn}, стремящуюся к x0 и не посещающую x0, для которой f(xn)↛b.

Это доказывает теорему.∎

11.3Применение предела по Гейне

Доказывать, что предел чему-то равен, пользуясь определением по Гейне, довольно тяжело — нужно рассмотреть все возможные последовательности. Зато с ним гораздо проще доказывать утверждение, что предел не существует или чему-то не равен — достаточно предъявить одну последовательность. Также с помощью предела по Гейне можно легко переносить результаты, доказанные для последовательностей, на функции. Например, докажем теорему о пределе суммы:

Утверждение 1. Пусть f(x)→a и g(x)→b при x→x0. Рассмотрим функцию h(x)=f(x)+g(x). Докажем, что h(x)→a+b при x→x0.

Доказательство. Докажем, что для функции h(x) выполняется опрделение предела по Гейне. Пусть {xn} произвольная последовательность, удовлетворяющая условиям xn→x0 и xn≠x0 для всех n. Тогда согласно определению предела по Гейне, примененному к функциям f(x) и g(x):

f(xn)→a,g(xn)→b.

По теореме о пределе суммы для последовательностей, отсюда следует, что

h(xn)=f(xn)+g(xn)→a+b.

Значит, условие определения по Гейне действительно выполняется: если xn→x0 и xn≠x0 для всех n, то h(xn)→a+b. Утверждение доказано.∎

Упражнение 1. Докажите аналогично теоремы о пределе произведения и частного.

Кстати, до сих пор мы не доказывали, что предел функции определён однозначно. Это несложно сделать явно (хорошее упражнение!), но теперь мы получим этот факт совсем бесплатно. У нас есть аналогичное утверждение для последовательностей (см. соответствующую теорему в лекции 4), и с помощью определения по Гейне он автоматически переносится на предел функции: в определении по Гейне требуется, чтобы предел f(xn) был одним и тем же для всех подходящих последовательностей {xn}, и значит если бы нашлось два разных числа b, удовлетворяющих определению по Гейне, мы бы пришли к противоречию с единственностью предела последовательности.

11.4Заключение

Мы показали, что определения по Коши и по Гейне эквивалентны друг другу, и теперь в случае необходимости будем пользоваться тем или другим. Как правило, если нам нужно доказать, что предел чему-то равен, мы будем пользоваться определением по Коши. Определение по Гейне удобно там, где нужно доказывать противоположное утверждение (что предел чему-то не равен, или вообще не существует), а также в некоторых теоретических построениях. Дополнительный бонус определения по Гейне — оно позволяет переносить на пределы функций ряд свойств, доказанных для пределов последовательностей, практически «бесплатно».

← Предыдущая глава Следующая глава →

Предел функции в точке

Сегодня рассмотрим подборку новых задач на нахождение предела в точке. Начнем с простых примеров на подстановку значения, чаще всего рассматривают в 11 классе школьной программы по математике.
Далее остановимся и проанализируем пределы с неопределенностями, методы раскрытия неопределенностей, применением первой и второй важных границ и их последствий.
Приведенные примеры полностью не охватят всей темы, но на многие вопросы внесут ясность.

Пример 46. Предел функции в точке определяем подстановкой

Так как знаменатель дроби не превращается в ноль то такую задача под силу решить каждому выпускнику школы.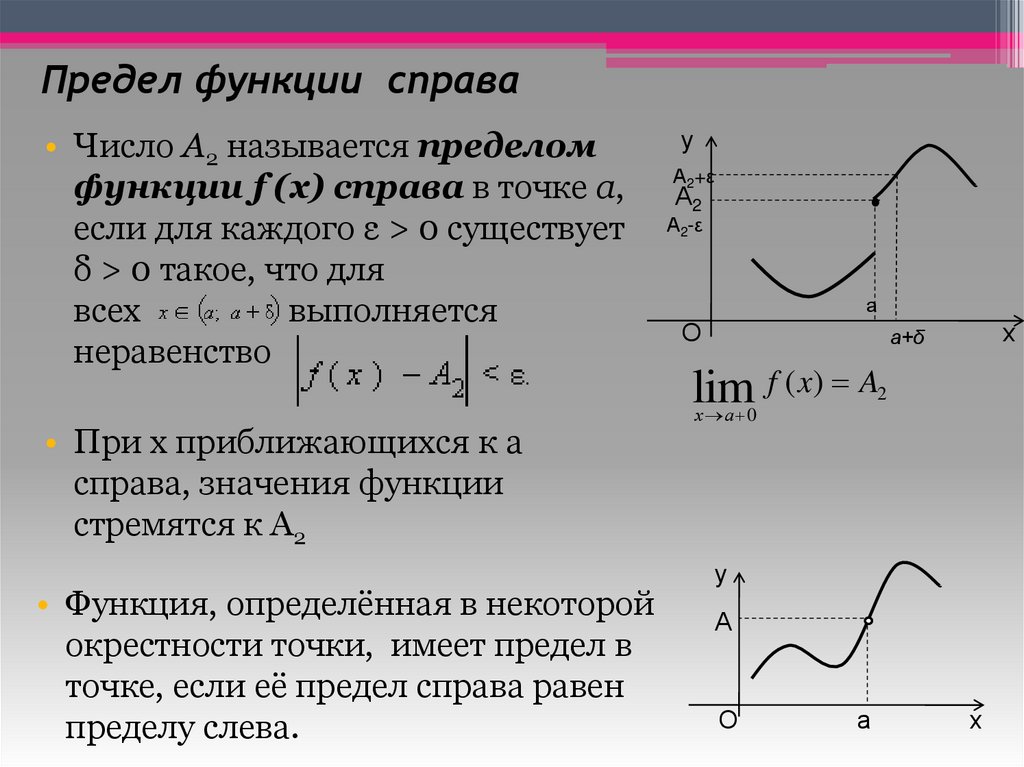

Пример 47. Имеем долю полиномов, кроме того знаменатель не содержит особенности (не равен нулю).
Еще одна задача, фактически за 11 класс.

Пример 48. Методом подстановки определяем предел функции
Из условия следует, что граница функции равна двум, если переменная стремится к бесконечности.

Пример 49.Прямая подстановка x=2 показывает, что граница в точке имеет особенность {0/0}. Это означает, что и числитель и знаменатель скрыто содержат (x-2).
Выполняем разложение полиномов на простые множители, а потом сокращаем дробь на указанный множитель (x-2).
Предел дроби, которая останется, находим методом подстановки.

Пример 50.Предел функции в точке имеет особенность типа {0/0}.
Избавляемся разницы корней методом умножения на сумму корней (сопряженное выражение), полином раскладываем.
Далее, упростив функцию, находим значение предела в единице.

Пример 51.Рассмотрим задачу на сложные пределы.
До сих пор от иррациональности избавлялись методом умножения на сопряженное выражение.
Здесь же, в знаменателе, имеем корень кубический, поэтому нужно использовать формулу разности кубов.
Все остальные преобразования повторяются от условия к условию.
Полином раскладываем на простые множители,
далее сокращаем на множитель, который вносит особенность (0)
и подстановкой x=-3 находим предел функции в точке

Пример 52.Особенность вида {0/0} раскрываем с помощью первого замечательного предела и его последствий.
Сначала разницу синусов распишем согласно тригонометрической формуле
sin(7x)-sin(3x)=2sin(2x)cos(5x).
Далее числитель и знаменатель дроби дополняем выражениями, которые необходимы для выделения важных пределов.
Переходим к произведению пределов и оцениваем вложение каждого множителя.

Здесь использовали первый замечательный предел:

и следствия из него

где a и b – произвольные числа.

Пример 53. Чтобы раскрыть неопределенность при переменной стремящейся к нулю, используем второй замечательный предел.
Чтобы выделить экспоненту, приводим показатель к 2-му замечательному пределу, а все остальное, что останется в предельном переходе, даст степень експоненты.

Здесь использовали следствие из второго замечатеьного предела:

Вычислить предел функции в точке:

Пример 54. Нужно найти предел функции в точке. Простая подстановка значения показывает, что имеем деление нулей.
Для ее раскрытия разложим на простые множители полиномы и выполним сокращение на множитель, который вносит особенность (х+2).
Однако числитель дальше содержит (x+2), а это значит, что при x=-2 граница равна нулю.

Пример 55.Имеем дробную функцию — в числителе разница корней, в знаменателе — поленом.
Прямая подстановка дает особенность вида {0/0}.
Переменная стремится к минус единице, а это значит, что следует искать и избавляться особенности вида (x+1).
Для этого избавляемся иррациональности умножением на сумму корней, а квадратичную функцию раскладываем на простые множители.
После всех сокращений методом подстановки определяем предел функции в точке

Пример 56.С виду подлимитной функции можно ошибочно заключить, что нужно применить первый предел, но вычисления показали, что все гораздо проще.
Сначала распишем сумму синусов в знаменателе sin(2x)+sin(6x)=2sin(4x)*cos(2x).
Далее расписываем tg(2x), и синус двойного угла sin(4x)=2sin(2x)cos (2x).
Синусы упрощаем и методом подстановки вычисляем предел дроби

Пример 57.Задача на умение использовать вторую замечательный предел:
суть заключается в том, что следует выделить ту часть, которая дает экспоненту.
Остальное, что останется в показателе в предельном переходе даст степень экспоненты.

На этом разбор задач на пределы функций и последовательностей не заканчивается.
В настоящее время подготовлено более 150 готовых ответов к пределам функций, поэтому изучайте и делитесь ссылками на материалы с однокласниками.

Ограничения функций | Brilliant Math & Science Wiki

Тадеуш Абий, Патрик Корн, Мэй Ли, и

способствовал

Содержимое

Формальное определение
Свойства пределов
Односторонние ограничения
Двусторонние ограничения
Бесконечные пределы
Пределы в бесконечности
Лимиты по факторингу
Ограничения по замене
Правило Лопиталя
Ограничения функций — решение проблем
Рекомендации

Основная статья: Определение предела эпсилон-дельта

Точное определение лимита обсуждается в wiki Epsilon-Delta Definition of a Limit.

Формальное определение предела функции:
Предел \(f(x)\) при приближении \(x\) к \(x_0\) равен \(L\), т.е.
\[\lim _{ х \к х_{0} }{f(x)} = L\]
, если для каждого \(\epsilon > 0 \) существует \(\delta >0 \) такое, что для всех \(x\)
\[ 0 <\влево| x - x_{0} \right |<\delta \textrm{ } \ подразумевает \textrm{ } \left |f(x) - L \right| <\эпсилон. \]

На практике это определение используется только в относительно необычных ситуациях. Для многих приложений проще использовать это определение, чтобы доказать некоторые основные свойства пределов и использовать эти свойства для ответа на простые вопросы, связанные с ограничениями.

Наиболее важными свойствами пределов являются алгебраические свойства, которые, по существу, говорят о том, что пределы учитывают алгебраические операции:

Предположим, что \( \lim\limits_{x\to a} f(x) = M\) и \(\lim\limits_{x\to a} g(x) = N.\) Тогда
\[ \начать{выравнивать} \lim\limits_{x\to a} \big(f(x)+g(x)\big) &= M+N \\\\ \lim\limits_{x\to a} \big(f(x)-g(x)\big) &= M-N \\\\ \lim\limits_{x\to a} \big(f(x)g(x)\big) &= MN \\\\ \lim\limits_{x\to a} \left(\frac{f(x)}{g(x)}\right) &= \frac MN \ \ \text{ (если } N\ne 0) \\ \\ \lim\limits_{x\to a} f(x)^k &= M^k \ \\text{ (если } M,k > 0). \end{выравнивание} \]

Все это можно доказать с помощью определения эпсилон-дельта. Обратите внимание, что результаты верны только в том случае, если существуют пределы отдельных функций: если \( \lim\limits_{x\to a} f(x) \) и \( \lim\limits_{x\to a} g( х)\) не существуют, предел их суммы (или разности, произведения или частного) тем не менее может существовать.

В сочетании с основными пределами \( \lim_{x\to a} c = c,\), где \( c\) — константа, а \( \lim_{x\to a} x = a,\) свойства можно использовать для вывода пределов, включающих рациональные функции:

Пусть \(f(x)\) и \(g(x)\) — полиномы, и предположим, что \(g(a) \ne 0.\) Тогда
\[ \lim_{x\to a} \frac{f(x)}{g(x)} = \frac{f(a)}{g(a)}. \]

Это пример непрерывности или того, что иногда называют ограничениями замещения.

Обратите внимание, что \(g(a)=0\) — более сложный случай; см. вики Indeterminate Forms для дальнейшего обсуждения.

Пусть \(m\) и \(n\) — натуральные числа. n-1}. \] 9+,\)» мы рассматриваем только значения больше \(a\). Односторонние пределы важны при оценке пределов, содержащих абсолютные значения \(|x|\), знак \(\text{sign}(x)\) , функции пола \(\lfloor x \rfloor\) и другие кусочные функции
На изображении выше показаны левосторонний и правосторонний пределы непрерывной функции \(f(x).\)
Найдите левый и правый пределы сигнум-функции \(\text{signum}(x)\) как \(x \to 0:\) 9-} \frac{|x-1|}{-|x — 1|} = -1 . \]
Таким образом, двусторонний предел \( \lim\limits_{x \to 1} \frac{|x — 1|}{x — 1}\) не существует. \(_\квадрат\)
Изображение ниже представляет собой график функции \(f(x)\). Как показано, он непрерывен для всех точек, кроме \(x = -1\) и \(x=2\), которые являются его асимптотами. Найдите все целые точки \(-4
изображение
Поскольку граф непрерывен во всех точках, кроме \(x=-1\) и \(x=2\), двусторонний предел существует в точках \(x=-3\), \(x=-2 \), \(х=0\), \(х=1,\) и \(х=3\). В точке \(x=2,\) нет конечного значения ни для одного из двусторонних пределов, поскольку функция неограниченно возрастает по мере приближения координаты \(x\) к \(2\) (но см. следующий раздел для дальнейшего обсуждения). Ситуация аналогична для \(x=-1.\). Таким образом, точки \(x=-3\), \(x=-2\), \(x=0\), \(x=1,\ ) и \(x=3\) — все целые числа, на которых определены двусторонние пределы. \(_\квадрат\)
Как было показано в предыдущем разделе, один из способов несуществования предела — это несоответствие односторонних пределов. Другой распространенный способ отсутствия предела в точке \(a\) состоит в том, что функция «взрывается» вблизи \(a,\), т. е. функция неограниченно возрастает. Это происходит в приведенном выше примере при \(x=2,\), где есть вертикальная асимптота. Эта общая ситуация приводит к следующему обозначению:
Учитывая функцию \(f(x)\) и действительное число \(a,\), мы говорим
\[\lim_{x\to a} f(x) = \infty.\]
Если функцию можно сделать произвольно большой, переместив \(x\) достаточно близко к \(a,\)
\[\text{для всех } N>0, \text{ существует } \delta>0 \text{ такое, что } 0<|x-a|<\delta \подразумевает f(x)>N. \]
Аналогичные определения существуют для односторонних пределов, а также пределов «приближающихся к \(-\infty\)».
Предупреждение: Если \(\lim\limits_{x\to a} f(x) = \infty,\), то заманчиво сказать, что предел в \(a\) существует и равен \(\infty .\) Это неверно. Если \(\lim\limits_{x\to a} f(x) = \infty,\) предел равен 9-} \frac{1}{x} = -\infty. \]
Чтобы доказать первое утверждение, для любого \(N>0\) в формальном определении можно взять \(\delta = \frac1N,\), и доказательство второго утверждения аналогично.
Таким образом, функция неограниченно возрастает с правой стороны и неограниченно убывает с левой стороны. Мы ничего не можем сказать о двустороннем пределе \(\lim\limits_{x\to a} \frac1{x} \ne \infty\) или \(-\infty.\). Сравните это со следующим примером. \(_\квадрат\)

9{n+l}},\]
где \(a_0 \neq 0, b_0 \neq 0,\) и \(m,n \in \mathbb N.\)
Тогда дано (A), (B ), (C) или (D), \(\displaystyle\lim_{x\rightarrow 0}f(x)\) равно какому из (1), (2), (3) и (4)?
Соответствие столбцам:
Столбец-I Столбец-II
(A), если \(m>n\) 90 244 (1) \(\infty\)
(B) если \(m=n\) (2) \(-\infty\)
(C) если \(m0\) \(\hspace{10mm}\) (3) \(\frac{a_0}{b_0}\)
(D) если \(m (4) \(0\)
Примечание: Например, если (A) правильно соответствует (1), (B ) с (2), (C) с (3) и (D) с (4), тогда ответьте как 1234. \(\infty\)», то есть при неограниченном увеличении \(x\).
Уравнение \( \lim\limits_{x\to\infty} f(x) = L\) означает, что значения \(f\) можно сделать сколь угодно близкими к \(L\), взяв \(x\ ) достаточно большой. То есть
\[\text{для всех } \epsilon > 0, \text{ существует } N>0 \text{ такое, что } x>N \ подразумевает |f(x)-L|<\epsilon.\]
Существуют аналогичные определения для \(\lim\limits_{x\to\infty} f(x) = L,\), а также \(\lim\limits_{x\to\infty} f(x ) = \infty,\) и так далее.
Графически \(\lim\limits_{x\to\a} f(x) = \infty\) соответствует вертикальной асимптоте в точке \(a,\), а \( \lim\limits_{x\to\infty } f(x) = L \) соответствует горизонтальной асимптоте в \(L.\)
Основная статья: Лимиты по факторингу
Пределы с помощью факторинга относится к методу оценки пределов, который требует нахождения и устранения общих факторов.
Основная статья: Ограничения по замене
Оценка пределов путем подстановки относится к идее, что при определенных обстоятельствах (а именно, если исследуемая функция непрерывна) мы можем оценить предел, просто вычислив функцию в интересующей нас точке. {11}} \справа) = \, ?\]
Александров, О. Разрыв . Получено 12 сентября 2005 г., от https://commons.wikimedia.org/wiki/Файл:Discontinuity_removable.eps.png
Процитировать как: Пределы функций. Brilliant.org . Извлекаются из https://brilliant.org/wiki/limits-of-functions/
Исчисление I — Предел
Показать мобильное уведомление Показать все примечания Скрыть все примечания
Уведомление для мобильных устройств
Похоже, вы используете устройство с «узкой» шириной экрана ( т. е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
Раздел 2.2: Предел
В предыдущем разделе мы рассмотрели пару задач, и в обеих задачах у нас была функция (наклон в случае касательной задачи и средняя скорость изменения в задаче о скорости изменения), и мы хотели чтобы узнать, как эта функция вела себя в какой-то момент \(x = a\). На данном этапе игры нас больше не волнует, откуда взялись функции, и нас больше не волнует, увидим ли мы их снова в будущем или нет. Все, что нам нужно знать или беспокоиться, это то, что у нас есть эти функции, и мы хотим что-то о них знать.
Чтобы ответить на вопросы в последнем разделе, мы выбираем значения \(x\), которые все ближе и ближе к \(x = a\), и подставляем их в функцию. Мы также убедились, что рассмотрели значения \(x\), которые были как слева, так и справа от \(x = a\). Сделав это, мы посмотрели на нашу таблицу значений функции и увидели, к чему приближаются значения функции по мере того, как \(x\) становилось все ближе и ближе к \(x = a\), и использовали это, чтобы угадать значение, которое нам нужно.
Этот процесс называется 92} + 25}}{{т — 5}} = 15\]
В этих обозначениях мы заметим, что мы всегда даем функцию, с которой работаем, а также значение \(x\) (или \(t\)), к которому мы движемся.
В этом разделе мы собираемся применить интуитивный подход к ограничениям и попытаться понять, что они из себя представляют и что они могут рассказать нам о функции. Имея в виду эту цель, мы пока не собираемся вдаваться в то, как мы на самом деле вычисляем лимиты. Вместо этого мы будем полагаться на то, что мы сделали в предыдущем разделе, а также на другой подход, чтобы угадать значение пределов.
Оба подхода, которые мы собираемся использовать в этом разделе, разработаны, чтобы помочь нам понять, что такое пределы. Как правило, мы обычно не используем методы, описанные в этом разделе, для вычисления лимитов, и во многих случаях их может быть очень сложно использовать даже для оценки значения лимита, и/или иногда мы будем давать неправильное значение. Мы рассмотрим фактические вычисления пределов в нескольких разделах.
Начнем со следующего «определения» лимита.
Определение
Мы говорим, что предел \(f(x)\) равен \(L\), когда \(x\) приближается к \(a\), и записываем это как
\[\ mathop {\lim}\limits_{x \to a} f\left(x \right) = L\]
при условии, что мы можем сделать \(f(x)\) настолько близким к \(L\), насколько мы хотим, для всех \(x\), достаточно близких к \(a\), с обеих сторон, фактически не позволяя \( х\) быть \(а\).
Это не совсем точное определение предела. Если вы хотите увидеть более точное и математическое определение лимита, вам следует обратиться к разделу «Определение лимита» в конце этой главы. Приведенное выше определение является скорее «рабочим». Это определение помогает нам понять, что такое пределы и что они могут рассказать нам о функциях.
Так что же означает это определение? Что ж, давайте предположим, что мы знаем, что предел действительно существует. В соответствии с нашим «рабочим» определением мы можем решить, насколько близко к \(L\) мы хотим сделать \(f(x)\). В качестве аргумента предположим, что мы хотим сделать \(f(x)\) не более чем на 0,001 от \(L\). Это означает, что нам нужен один из следующих
\[\ begin{array}{lcl}f\left(x\right) — L <0,001 & \hspace{0,25in} & {\mbox{if}}f\left(x\right){\mbox{ is больше, чем L}}\\ L - f\left( x \right) < 0,001& \hspace{0,25in} & {\mbox{if}}f\left( x \right){\mbox{ меньше L }}\конец{массив}\]
Теперь согласно «рабочему» определению это означает, что если мы получим \(x\) достаточно близко к \(a\), мы можем сделать одно из приведенных выше истинным. Однако на самом деле это говорит немного больше. В нем говорится, что где-то в мире есть значение \(x\), скажем, \(X\), так что для всех \(x\), которые ближе к \(a\), чем \(X \), то одно из приведенных выше утверждений будет верным.
Это довольно важная идея. В мире существует множество функций, которые мы можем сделать максимально близкими к \(L\) для конкретных значений \(x\), близких к \(a\), но будут и другие значения \(x \) ближе к \(a\), которые дают значения функций, далекие от \(L\). Чтобы предел существовал, как только мы получим \(f(x)\) настолько близко к \(L\), насколько мы хотим для некоторого \(x\), тогда он должен будет оставаться в этом близком к \(L\ ) (или приблизиться) для всех значений \(x\), которые ближе к \(a\). Мы увидим пример этого позже в этом разделе.
Проще говоря, определение говорит, что по мере того, как \(x\) становится все ближе и ближе к \(x=a\) (конечно, с обеих сторон…), тогда \(f(x)\) должно приближаться все ближе и ближе к \(L\). Или, когда мы движемся к \(x=a\), тогда \(f(x)\) должно двигаться к \(L\).
Важно еще раз отметить, что мы должны смотреть на значения \(x\), которые находятся по обе стороны от \(x=a\). Мы также должны отметить, что нам не разрешено использовать \(x=a\) в определении. Мы будем часто использовать информацию, которую дают нам ограничения, чтобы получить некоторую информацию о том, что происходит прямо в точке \(x=a\), но сам предел не связан с тем, что на самом деле происходит в точке \(x=a\). . Предел связан только с тем, что происходит вокруг точки \(x=a\). Это важное понятие об ограничениях, которые мы должны иметь в виду.
Альтернативное обозначение, которое мы иногда будем использовать для обозначения пределов, это
. \[f(x) \to L\hspace{0,25 дюйма}{\rm{as}}\hspace{0,25in}x \to a\]
Как мы можем использовать это определение, чтобы оценить пределы? Мы делаем именно то, что делали в предыдущем разделе. Мы берем \(x\) по обе стороны от \(x=a\), которые приближаются все ближе и ближе к \(a\), и подставляем их в нашу функцию. Затем мы смотрим, можем ли мы определить, к какому числу приближаются значения функции, и используем это как нашу оценку. 92} — 2x}}\]
Показать решение
Обратите внимание, что мы сказали оценить значение лимита. Опять же, в этом разделе мы не собираемся напрямую вычислять ограничения. Цель этого раздела — дать нам лучшее представление о том, как работают ограничения и что они могут рассказать нам о функции.
Итак, помня об этом, мы собираемся работать почти так же, как в предыдущем разделе. Мы выберем значения \(x\), которые все ближе и ближе к \(x=2\), и подставим эти значения в функцию. Это дает следующую таблицу значений.
\(х\) \(f(x)\) \(х\) \(f(x)\)
2,5 3,4 1,5 5,0
2. 1 3,857142857 1,9 4.157894737
2,01 3,985074627 1,99 4.015075377
2,001 3,998500750 1,999 4.001500750
2,0001 3,999850007 1,9999 4.000150008
2.00001 3,999985000 1,99999 4.000015000
Обратите внимание, что мы удостоверились и выбрали значения \(x\), которые были по обе стороны от \(x = 2\), и что мы подошли очень близко к \(x = 2\), чтобы убедиться, что любые тенденции, которые мы можем наблюдать, на самом деле верны. 92} — 2x}} = 4\]
Давайте еще немного подумаем о том, что здесь происходит. Построим график функции из последнего примера. Ниже показан график функции в интересующем диапазоне \(x\).
Во-первых, обратите внимание на довольно большую открытую точку \(x = 2\). Это должно напомнить нам, что функция (и, следовательно, график) не существует в точке \(x = 2\).
Поскольку мы подставляли значения \(x\) в функцию, мы в действительности двигаемся по графику к точке как \(x = 2\). Это показано на графике двумя стрелками на графике, которые движутся к точке.
Когда мы вычисляем пределы, вопрос, который мы на самом деле задаем, заключается в том, к какому значению \(y\) приближается наш график, когда мы приближаемся к \(x = a\) на нашем графике. Мы НЕ спрашиваем, какое значение \(y\) принимает график в рассматриваемой точке. Другими словами, мы спрашиваем, что делает график вокруг точки \(x = a\). В нашем случае мы можем видеть, что по мере того, как \(x\) приближается к 2 (с обеих сторон), функция приближается к \(y = 4\), хотя сама функция даже не существует в \(x = 2\). 2} — 2x}} & {\mbox{if} }x \ne 2\\ 6 & {\mbox{if}}x = 2\end{массив} \right.\]
Показать решение
Прежде всего следует отметить, что это точно такая же функция, как и в первом примере, за исключением того, что мы присвоили ей значение \(x = 2\). Итак, сначала отметим, что
\[г\влево( 2 \вправо) = 6\]
Что касается оценки значения этого лимита, то по сравнению с первым примером ничего не изменилось. Мы могли бы построить таблицу значений, как в первом примере, или быстро взглянуть на график функции. Любой метод даст нам значение предела.
Давайте сначала посмотрим на таблицу значений и посмотрим, что она нам говорит. Обратите внимание, что наличие значения функции в \(x = 2\) не изменит наш выбор для \(x\). Мы выбираем только те значения \(x\), которые приближаются к \(x = 2\), но никогда не берем \(x = 2\). Другими словами, таблица значений, которую мы использовали в первом примере, будет точно такой же таблицей, которую мы будем использовать здесь. Итак, поскольку мы уже сделали это один раз, нет причин переделывать это здесь.
Из этой таблицы снова видно, что ограничение равно
\[\ mathop {\lim}\limits_{x \to 2} g\left(x\right) = 4\]
Предел НЕ 6! Помните из обсуждения после первого примера, что пределы не заботятся о том, что на самом деле делает функция в рассматриваемый момент. Ограничения касаются только того, что происходит на вокруг точки. Поскольку единственное, что мы фактически изменили в функции, это ее поведение при \(x = 2\), это не изменит предел.
Давайте также взглянем на график этой функции, чтобы увидеть, говорит ли он о том же самом.
Опять же, мы можем видеть, что по мере того, как мы приближаемся к \(x = 2\) на нашем графике, функция все еще приближается к значению \(y\), равному 4. Помните, что мы только спрашиваем, что делает функция около \(x = 2\), и нам все равно, что на самом деле делает функция в \(x = 2\). Затем график также поддерживает вывод о том, что предел равен
. \[\ mathop {\lim}\limits_{x \to 2} g\left(x\right) = 4\]
Давайте еще раз остановимся на этом, просто чтобы убедиться, что мы его поняли. Пределы , а не связаны с тем, что происходит в точке \(x = a\). Пределы касаются только того, что происходит вокруг \(x = a\). Мы продолжаем говорить об этом, но это очень важная концепция ограничений, которую мы всегда должны помнить. Поэтому мы будем использовать любую возможность, чтобы напомнить себе об этой идее.
Поскольку пределы не связаны с тем, что на самом деле происходит в \(x = a\), мы будем иногда сталкиваться с ситуациями, подобными предыдущему примеру, когда предел в точке и значение функции в точке различны. Это не всегда будет происходить, конечно. Бывают случаи, когда значение функции и предел в точке совпадают, и мы в конечном итоге увидим несколько таких примеров. Однако важно не волноваться по поводу вещей, когда функция и предел не принимают одно и то же значение в какой-то точке. Это случается иногда, поэтому нам нужно будет иметь дело с такими случаями, когда они возникают.
Давайте рассмотрим еще один пример, чтобы попытаться воплотить эту идею в жизнь.
Пример 3. Оцените значение следующего предела. \[\ mathop {\lim}\limits_{\theta\to 0} \,\frac{{1 — \cos\left(\theta\right)}}{\theta}\]
Показать решение
Во-первых, не волнуйтесь о \(\theta\) в функции. Это просто буква, точно так же, как \(х\) — это буква! Это греческая буква, но это буква, и иногда вам будет предложено иметь дело с греческими буквами, поэтому неплохо начать привыкать к ним на этом этапе.
Теперь также обратите внимание, что если мы подставим \(\theta =0\), то получим деление на ноль, поэтому на данный момент функция не существует. На самом деле в этой точке мы получаем 0/0, но из-за деления на ноль эта функция не существует в точке \(\theta=0\).
Итак, как и в первом примере, давайте получим таблицу значений и посмотрим, что если мы сможем угадать, к какому значению движется функция.
\(\ тета \) \(f\влево(\тета\вправо)\) \(\тета\) \(f\влево(\тета\вправо)\)
1 0,45969769 -1 -0,45969769
0,1 0,04995835 -0,1 -0,04995835
0,01 0,00499996 -0,01 -0,00499996
0,001 0,00049999 -0,001 -0,00049999
Хорошо, похоже, что функция приближается к нулевому значению, когда \(\theta\) приближается к 0, конечно, с обеих сторон.
Следовательно, мы предполагаем, что предел имеет значение
\[\ mathop {\lim}\limits_{\theta\to 0} \,\frac{{1 — \cos\left(\theta\right)}}{\theta} = 0\]
Итак, еще раз, предел имел значение, несмотря на то, что функция не существовала в интересующей нас точке. что мы собираемся обсудить.
Пример 4. Оцените значение следующего предела. \[\ mathop {\lim}\limits_{t \to 0} \cos\left({\frac{\pi}}{t}} \right)\]
Показать решение
Давайте создадим таблицу значений и посмотрим, что происходит с нашей функцией в этом случае.
\(т\) \(ф(т)\) \(т\) \(ф(т)\)
1 -1 -1 -1
0,1 1 -0,1 1
0,01 1 -0,01 1
0,001 1 -0,001 1
Теперь, если бы нам нужно было угадать предел из этой таблицы, мы бы предположили, что предел равен 1. Однако, если бы мы сделали это предположение, мы бы ошиблись. Рассмотрим любую из следующих оценок функции.
\[f\left( {\frac{1}{{2001}}} \right) = — 1\hspace{0,55in}f\left({\frac{2}{{2001}}} \right) = 0 \ hspace {0,5 дюйма} f \ слева ( {\ гидроразрыва {4} {{4001}}} \ справа) = \ гидроразрыва {{\ sqrt 2}} {2} \]
Во всех трех вычислениях функции мы оценивали функцию по числу меньше 0,001 и получили три совершенно разных числа. Напомним, что определение предела, с которым мы работаем, требует, чтобы функция приближалась к единственному значению (нашему предположению) по мере того, как \(t\) становится все ближе и ближе к рассматриваемой точке. Это не говорит о том, что только некоторые значения функции должны приближаться к догадке. В нем говорится, что все значения функции должны быть все ближе и ближе к нашему предположению.
Чтобы увидеть, что здесь происходит, был бы удобен график функции.
Из этого графика видно, что по мере приближения к \(t = 0\) функция начинает сильно колебаться, и чем ближе к \(t = 0\), тем больше скорость колебаний. Напомним из нашего определения предела, что для того, чтобы предел существовал, функция должна стремиться к одному значению по мере того, как мы приближаемся к рассматриваемой точке.
Эта функция явно не подходит для одного номера, поэтому этот предел не существует !
Последний пример указывает на недостаток простого выбора значений переменной и использования таблицы значений функции для оценки значения предела. Значения переменной, которые мы выбрали в предыдущем примере, были действительными и фактически были значениями, которые выбрали бы многие. На самом деле, это были точно такие же значения, которые мы использовали в предыдущей задаче, и они работали в этой задаче!
При использовании таблицы значений всегда существует вероятность того, что мы выбираем неправильные значения и неправильно угадываем наш лимит. Это то, что мы всегда должны помнить, когда делаем это, чтобы угадать значение ограничений. На самом деле это такая проблема, что после этого раздела мы больше никогда не будем использовать таблицу значений, чтобы угадать значение лимита.
Этот последний пример также показал нам, что ограничения не обязательно должны существовать. До этого момента мы видели только существующие ограничения, но это не всегда так.
Давайте рассмотрим еще один пример в этом разделе.
Пример 5. Оцените значение следующего предела. \[\ mathop {\ lim } \ limit_ {t \ to 0} H \ left ( t \ right) \ hspace {0,25 дюйма} {\ mbox {где}} \ hspace {0,25 дюйма} H \ left ( t \ справа) = \left\{ \begin{array}{ll}0 & {\mbox{if}}t < 0\\ 1 & {\mbox{if}}t \ge 0\end{массив} \right. \]
Показать решение
Эту функцию часто называют функцией Heaviside или step . Мы могли бы использовать таблицу значений для оценки предела, но, вероятно, в этом случае будет так же быстро использовать график, так что давайте сделаем это. Ниже представлен график этой функции.
На графике видно, что если мы приближаемся к \(t = 0\) справа, функция приближается к значению \(y\), равному 1. На самом деле она просто остается на уровне 1, но в терминология, которую мы использовали в этом разделе, приближается к 1…
Кроме того, если мы движемся к \(t = 0\) слева, функция движется к значению \(y\), равному 0.
Согласно нашему определению предела, функция должна двигаться в к одному значению по мере продвижения к \(t = a\) (с обеих сторон). В данном случае этого не происходит, поэтому в этом примере мы также будем говорить, что предела не существует.
Обратите внимание, что предел в этом примере немного отличается от предыдущего примера. В предыдущем примере функция не остановилась на одном числе, когда мы приблизились к \(t = 0\). Однако в этом примере функция сводится к одному числу как \(t = 0\) с обеих сторон. Проблема в том, что число на каждой стороне \(t = 0\) разное. Это идея, которую мы рассмотрим более подробно в следующем разделе.
Давайте обобщим то, что мы (надеюсь) узнали в этом разделе. В первых трех примерах мы видели, что пределы не заботятся о том, что на самом деле делает функция в рассматриваемой точке. Их интересует только то, что происходит вокруг точки. На самом деле у нас могут быть пределы в \(x = a\), даже если самой функции в этой точке не существует. Точно так же, даже если функция существует в какой-то точке, нет оснований (на данный момент) думать, что предел будет иметь то же значение, что и функция в этой точке. Иногда предел и функция будут иметь одно и то же значение в точке, а иногда они не будут иметь одинакового значения.
Далее, в третьем и четвертом примерах мы увидели основную причину отказа от использования таблицы значений для угадывания значения лимита. В этих примерах мы использовали точно такой же набор значений, однако они работали только в одном из примеров. Использование таблиц значений для угадывания значений лимитов — просто не лучший способ получить значение лимита. Это единственный раздел, в котором мы будем это делать. Таблицы значений всегда должны быть вашим последним выбором при поиске значений пределов.
Последние два примера показали нам, что на самом деле существуют не все ограничения. Мы не должны зацикливаться на идее, что ограничения всегда будут существовать. В большинстве курсов по математическому анализу мы работаем с ограничениями, которые почти всегда существуют, поэтому легко начать думать, что ограничения существуют всегда. Ограничения не всегда существуют, поэтому не привыкайте предполагать, что они будут.
Наконец, в четвертом примере мы увидели, что единственный способ справиться с пределом — построить график функции. Иногда это единственный способ, однако этот пример также иллюстрирует недостатки использования графиков. Чтобы использовать график, чтобы угадать значение предела, вы должны иметь возможность набросать график. Для многих функций это не так просто сделать.
Есть еще один недостаток в использовании графиков. Даже если у вас есть график, он будет полезен только в том случае, если значение \(y\) приближается к целому числу. Если значение \(y\) приближается, скажем, к \(\frac{{ — 15}}{{123}}\), вы никак не сможете угадать это значение по графику, и мы обычно потребуются точные значения для наших пределов.
Таким образом, хотя графики функций иногда могут облегчить вашу жизнь при угадывании значений пределов, они опять же, вероятно, не лучший способ получить значения пределов. Они будут полезны только в том случае, если вы можете получить их в свои руки, а значение лимита является «хорошим» числом.
Тогда возникает естественный вопрос: почему мы вообще говорим об использовании таблиц и/или графиков для оценки пределов, если это не лучший способ? Было несколько причин.
Во-первых, они могут помочь нам лучше понять, что такое ограничения и что они могут нам сказать.
No related posts.