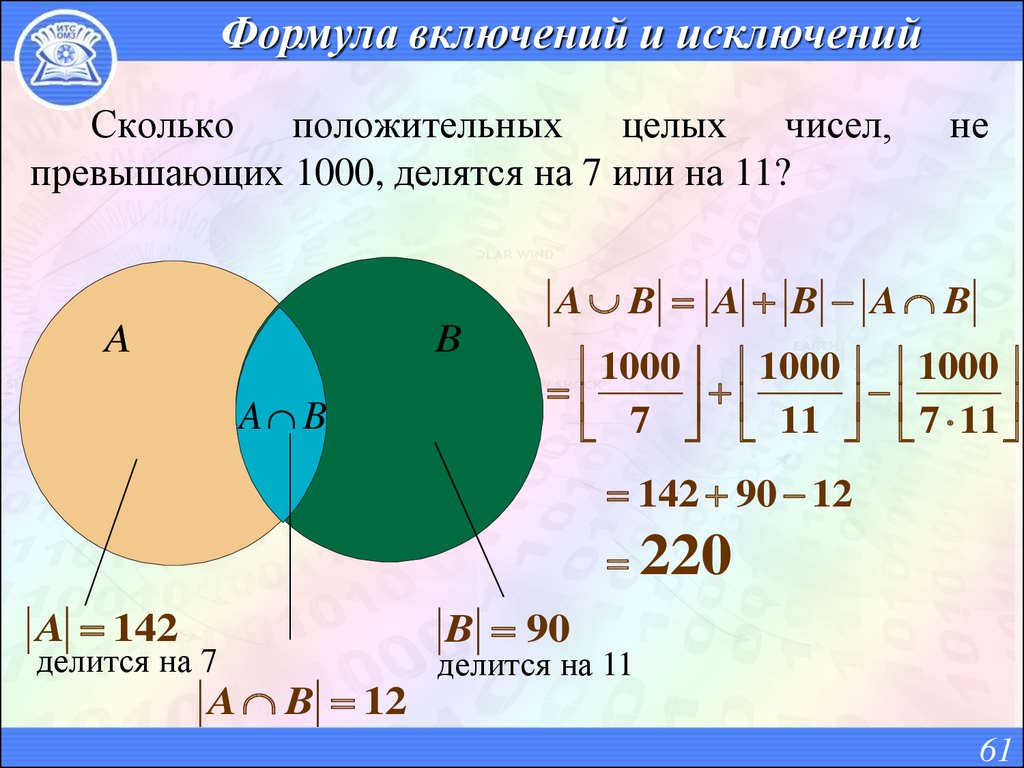
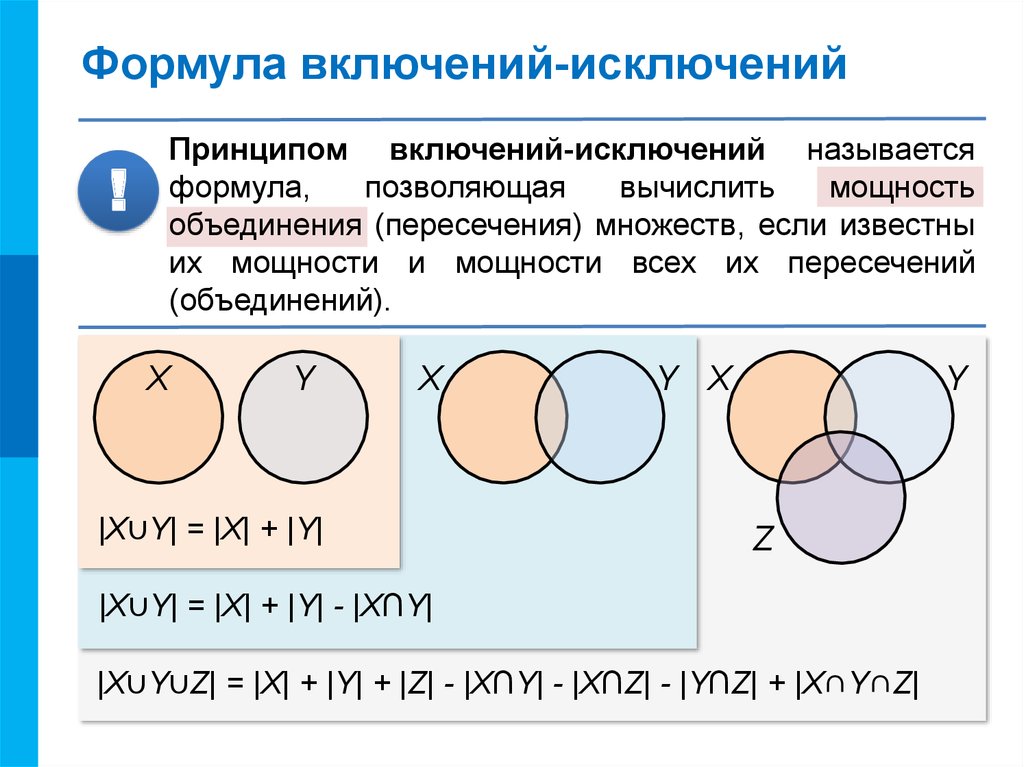
01. Формула включения и исключения
Основной задачей комбинаторики как раздела дискретной математики является определение числа элементов конечного множества, обладающих заданным набором свойств.
Теорема.1.1. (Формула включения и исключения).
Пусть даны конечных множеств , содержащих соответственно элементов. Тогда
Для решения комбинаторных задач используются частные случаи формулы включения и исключения.
Теорема.1.2. Для любых двух конечных множеств .
Пример. 9 студентов группы посещают лыжную и баскетбольную секции; 12 человек – баскетбольную и волейбольную, причём в баскетбольную секцию ходят 4 человека из группы. Сколько студентов данной группы занимаются спортом?
Решение. Обозначим символом множество студентов, посещающих лыжную и баскетбольную секции, по условию задачи . Обозначим символом множество студентов, посещающих баскетбольную и волейбольную секции, по условию задачи . Тогда множество есть множество студентов, посещающих баскетбольную секцию, множество есть множество студентов, занимающихся спортом.
Теорема 1.3. Для любых трёх конечных множеств
.
Доказательство.
Используются теорема 1.2, свойства ассоциативности объединения множеств, дистрибутивности объединения и пересечения множеств.
■
Пример. В группе второго курса 13 студентов. Каждый из них участвовал хотя бы в одной университетской олимпиаде. Десять студентов принимали участие в олимпиаде по математике, семеро – в олимпиаде по физике и шестеро – в олимпиаде по информатике. Пятеро студентов участвовали в олимпиадах по математике и физике, четверо – в олимпиадах по математике и информатике, трое –в олимпиадах по физике и информатике. Найдите число студентов, участвовавших во всех трех олимпиадах.
Решение. Введем обозначения: — множество студентов, принимавших участие в олимпиаде по математике; — множество студентов, принимавших участие в олимпиаде по физике, — множество студентов, принимавших участие в олимпиаде по информатике.
.□
Задачи и упражнения.
1.1. Среди студентов первого курса университета 30 человек посещают факультативные занятия по физике и математике. Известно, что углублённо изучают оба предмета 10 студентов, математику – 25 человек. Сколько студентов посещают факультативные занятия по физике?
1.2. В отчёте о языковой подготовке студентов первого курса сказано, что из 100 первокурсников английский язык в школе изучали 50 человек, немецкий – 23, французский – 30. С английским и французским языками знакомы 8 студентов, с французским и немецким – 10, с английским и немецким – 20. Все три языка изучали 5 первокурсников. Докажите, что в отчёте есть ошибка. Исправьте ошибку, если известно, что при обработке данных произошла потеря информации.
С английским и французским языками знакомы 8 студентов, с французским и немецким – 10, с английским и немецким – 20. Все три языка изучали 5 первокурсников. Докажите, что в отчёте есть ошибка. Исправьте ошибку, если известно, что при обработке данных произошла потеря информации.
1.3. Каждый студент группы занимается или спортом, или музыкой, или рисованием. Известно, что 23 студента увлечены спортом, 12 занимаются музыкой, 9 – занимаются рисованием. Семеро студентов совмещают занятия музыкой и увлечение спортом, трое студентов – занятия музыкой и рисованием, двое студентов – увлечение спортом и занятие рисованием. Один студент увлечен спортом, занимается музыкой и рисованием. Найдите число студентов в группе.
1.4. Из 30 студентов, участвовавших в экскурсионной поездке, все, кроме одного, рассказали сокурсникам о своих впечатлениях. О посещении музея с восторгом вспоминали 12 человек, о театральном спектакле — 10 человек, о джазовом концерте -13 человек. Пятеро студентов запомнили посещение музея и театра, трое студентов — посещение музея и концерта, четверо студентов — посещение театра и концерта. Шестеро студентов рассказали о посещении одновременно музея, театра и концерта. Сколько студентов участвовали в экскурсионной поездке?
Шестеро студентов рассказали о посещении одновременно музея, театра и концерта. Сколько студентов участвовали в экскурсионной поездке?
| Следующая > |
|---|
Формула включений-исключений | это… Что такое Формула включений-исключений?
Формула включений-исключений
Случай двух множеств
Например, в случае двух множеств формула включений-исключений имеет вид:
В сумме элементы пересечения учтены дважды, и чтобы компенсировать это мы вычитаем из правой части формулы. Справедливость этого рассуждения видна из диаграммы Эйлера-Венна для двух множеств, приведенной на рисунке справа.
Таким же образом и в случае множеств процесс нахождения количества элементов объединения состоит во включении всего, затем исключении лишнего, затем включении ошибочно исключенного и так далее, то есть в попеременном включении и исключении. Отсюда и происходит название формулы.
Отсюда и происходит название формулы.
Содержание
|
Формулировка
Формулу включений-исключений можно сформулировать в разных формах.
В терминах множеств
Пусть — конечные множества. Формула включений-исключений утверждает:
При получаем формулу для двух множеств, приведенную выше.
В терминах свойств
Принцип включений-исключений часто приводят в следующей альтернативной формулировке [4]. Пусть дано конечное множество , состоящее из элементов, и пусть имеется набор свойств . Каждый элемент множества может обладать или не обладать любым из этих свойств. Обозначим через количество элементов, обладающих свойствами (и, может быть, некоторыми другими).
Формулировка принципа включений-исключений в терминах множеств эквивалентна формулировке в терминах свойств. Действительно, если множества являются подмножествами некоторого множества , то в силу правил де Моргана (черта над множеством — дополнение в множестве ), и формулу включений-исключений можно переписать так:
Если теперь вместо «элемент принадлежит множеству » говорить «элемент обладает свойством », то мы получим формулировку принципа включений-исключений в терминах свойств, и наоборот.
Обозначим через количество элементов, обладающих в точности свойствами из набора .Тогда формулу включений-исключений можно переписать в следующей замкнутой форме (
Доказательство
Существует несколько доказательств формулы включений-исключений.
По индукции
Формулу включений-исключений можно доказать по индукции [1][5].
При формула включений-исключений тривиальна:
Пусть формула верна для , докажем ее для .
Пусть каждый элемент множества может обладать или не обладать любым из свойств . Применим формулу включений-исключений для свойств :
Теперь применим формулу для свойств к множеству объектов, для которых выполнено свойство :
Наконец, применим формулу для одного свойства к совокупности , объектов, которые не обладают свойствами :
Комбинируя выписанные три формулы, получим формулу включений-исключений для свойств . Что и требовалось доказать.
Комбинаторное доказательство
Рассмотрим произвольный элемент и подсчитаем, сколько раз он учитывается в правой части формулы включений-исключений [4].
Если элемент не обладает ни одним из свойств , то в правой части формулы он учитывается ровно 1 раз (в члене ).
Пусть элемент обладает в точности свойствами, скажем . Он дает по 1 в тех слагаемых суммы , для которых есть подмножество , и 0 для остальных. Число таких подмножеств по определению есть число сочетаний . Следовательно, вклад элемента в правую часть равен
Он дает по 1 в тех слагаемых суммы , для которых есть подмножество , и 0 для остальных. Число таких подмножеств по определению есть число сочетаний . Следовательно, вклад элемента в правую часть равен
При числа сочетаний равны нулю. Оставшаяся сумма в силу биномиальной теоремы равна
Таким образом, правая часть формулы включений-исключений учитывает каждый элемент, не имеющий указанных свойств точно по одному разу, а каждый элемент, обладающий хотя бы одним из свойств — нуль раз. Следовательно, она равна количеству элементов, не обладающих ни одним из свойств , то есть . Что и требовалось доказать.
Используя индикаторные функции
Пусть — произвольные (не обязательно конечные) множества, являющиеся подмножествами некоторого множества , и пусть — индикаторные функции (или, эквивалентно, свойств ).
Индикаторные функции их дополнений равны
а индикаторная функция пересечения дополнений:
Раскрывая скобки в правой части и еще раз используя тот факт, что индикаторная функция пересечения множеств равна произведению их индикаторных функций, получим
Это соотношение — одна из форм принципа включений-исключений. Оно выражает собой логическое тождество[1] и верно для произвольных множеств . В случае конечных множеств (и, соответственно, в предположении конечности множества ), просуммировав это соотношение по всем и воспользоваться тем, что для произвольного подмножества его мощность равна
Оно выражает собой логическое тождество[1] и верно для произвольных множеств . В случае конечных множеств (и, соответственно, в предположении конечности множества ), просуммировав это соотношение по всем и воспользоваться тем, что для произвольного подмножества его мощность равна
получим формулировку принципа включений-исключений в терминах мощностей множеств (или в терминах свойств).
Применение
Задача о беспорядках
Основная статья: Задача о беспорядках
Классический пример использования формулы включений-исключений — задача о беспорядках [4]. Требуется найти число перестановок множества таких что для всех . Такие перестановки называются беспорядками.
Пусть — множество всех перестановок и пусть свойство перестановки выражается равенством . Тогда число беспорядков есть . Легко видеть, что — число перестановок, оставляющих на месте элементы , и таким образом сумма содержит одинаковых слагаемых. Формула включений-исключений дает выражение для числа беспорядков:
Формула включений-исключений дает выражение для числа беспорядков:
Это соотношение можно преобразовать к виду
Нетрудно видеть, что выражение в скобках является частичной суммой ряда . Таким образом, с хорошей точностью число беспорядков составляет долю от общего числа перестановок:
Вычисление функции Эйлера
Основная статья: Функция Эйлера
Другой пример применения формулы включений-исключений — нахождение явного выражения для функции Эйлера [6].
Для целого положительного функция Эйлера дает количество чисел ряда , взаимно простых с . Найдем явное выражение для функции Эйлера.
Пусть каноническое разложение числа на простые множители имеет вид
Число взаимно просто с тогда и только тогда, когда ни один из простых делителей не делит . Если теперь свойство означает, что делит , то количество чисел взаимно простых с есть .
Количество чисел, обладающих свойствами равно , поскольку .
По формуле включений-исключений находим
Эта формула преобразуется к виду:
Вариации и обобщения
Принцип включения-исключения для вероятностей
Пусть — вероятностное пространство. Тогда для произвольных событий справедлива формула [1][5][7]
Эта формула выражает принцип включений-исключений для вероятностей. Ее можно получить из принципа включений-исключений в форме индикаторных функций:
Пусть — события вероятностного пространства , то есть . Возьмем математическое ожидание от обеих частей этого соотношения, и, воспользовавших линейностью математического ожидания и равенством для произвольного события , получим формулу включения-исключения для вероятностей.
Принцип включений-исключений в пространствах с мерой
Пусть — пространство с мерой. Тогда для произвольных измеримых множеств конечной меры имеет место формула включений-исключений:
Тогда для произвольных измеримых множеств конечной меры имеет место формула включений-исключений:
Очевидно, принцип включений-исключений для вероятностей и для мощностей конечных множеств являются частными случаями этой формулы. В первом случае мерой является, естественно, вероятностная мера в соответствующем вероятностном пространстве: . Во втором случае в качестве меры берется мощность множества: .
Вывести принцип включений-исключений для пространств с мерой можно также, как для указанных частных случаев, из тождества для индикаторных функций:
Пусть — измеримые множества пространства , то есть . Проинтегрируем обе части этого равенства по мере , воспользуемся линейностью интеграла и соотношением , и получим формулу включений-исключений для меры.
Тождество максимумов и минимумов
Основная статья: Тождество максимумов и минимумов
Формула включений-исключений может рассматриваться как частный случай тождества максимумов и минимумов:
Это соотношение справедливо для произвольных чисел . В частном случае, когда мы получаем одну из форм принципа включений-исключений. В самом деле, если положить , где — произвольный элемент из , то получим соотношение для индикаторных функций множеств:
В частном случае, когда мы получаем одну из форм принципа включений-исключений. В самом деле, если положить , где — произвольный элемент из , то получим соотношение для индикаторных функций множеств:
Обращение Мёбиуса
Основная статья: Обращение Мёбиуса
Пусть — конечное множество, и пусть — произвольная функция, определенная на совокупности подмножеств и принимающая действительные значения. Определим функцию следующим соотношением:
Тогда имеет место следующая формула обращения[8][9]:
Это утверждение является частным случаем общей формулы обращения Мёбиуса для алгебры инцидентности (англ.) совокупности всех подмножеств множества , частично упорядоченных по отношению включения .
Покажем, как из этой формулы следует принцип включения-исключения для конечных множеств. Пусть дано семейство подмножеств конечного множества , обозначим — множество индексов. Для каждого набора индексов определим как число элементов, входящих только в те множества , для которых . Математически это можно записать так:
Для каждого набора индексов определим как число элементов, входящих только в те множества , для которых . Математически это можно записать так:
Тогда функция , определенная формулой
дает количество элементов, каждый из которых входит во все множества , , и, быть может, еще в другие. То есть
Заметим далее, что — количество элементов, не обладающих ни одним из свойств:
С учетом сделанных замечаний запишем формулу обращения Мёбиуса:
Это есть в точности формула включений-исключений для конечных множеств, только в ней не сгруппированы слагаемые, относящиеся к одинаковым значениям .
См. также
- Формула Грассмана
- Неравенство Буля (англ.)
Примечания
- ↑ 1 2 3 4 5 Риордан Дж. Введение в комбинаторный анализ = An Introduction to Combinatorial Analysis.
 — М.: Изд-во иностранной литературы, 1963. — С. 63-66. — 289 с.
— М.: Изд-во иностранной литературы, 1963. — С. 63-66. — 289 с. - ↑ Weisstein, Eric W. Derangement (англ.) на сайте Wolfram MathWorld.
- ↑ Рыбников К. А. Введение в комбинаторный анализ. — 2-е изд. — М.: Изд-во МГУ, 1985. — С. 264. — 309 с.
- ↑ 1 2 3 Холл М. Комбинаторика = Combinatorial Theory. — М.: «Мир», 1970. — С. 18-20. — 424 с.
- ↑ 1 2 Рыбников К. А. Введение в комбинаторный анализ. — 2-е изд. — М.: Изд-во МГУ, 1985. — С. 69-73. — 309 с.
- ↑ Рыбников К. А. Введение в комбинаторный анализ. — 2-е изд. — М.: Изд-во МГУ, 1985. — С. 266. — 309 с.
- ↑ Боровков, А. А. Теория вероятностей. — 2-е изд. — М.: «Наука», 1986. — С. 24. — 431 с.
- ↑ Холл М. Комбинаторика = Combinatorial Theory. — М.: «Мир», 1970. — С. 30-31. — 424 с.
- ↑ Стенли Р.
 Перечислительная комбинаторика = Enumerative Combinatorics. — М.: «Мир», 1990. — С. 103-107. — 440 с.
Перечислительная комбинаторика = Enumerative Combinatorics. — М.: «Мир», 1990. — С. 103-107. — 440 с.
Ссылки
- Риордан Дж. Введение в комбинаторный анализ = An Introduction to Combinatorial Analysis. — М.: Изд-во иностранной литературы, 1963. — 289 с.
- Рыбников К. А. Введение в комбинаторный анализ. — 2-е изд. — М.: Изд-во МГУ, 1985. — 309 с.
- Стенли Р. Перечислительная комбинаторика = Enumerative Combinatorics. — М.: Мир, 1990. — 440 с.
- Холл М. Комбинаторика = Combinatorial Theory. — М.: Мир, 1970. — 424 с.
- И. Яглом Заплаты на кафтане // Квант. — 1974. — № 2. — С. 13—21.
- Weisstein, Eric W. Inclusion-Exclusion Principle (англ.) на сайте Wolfram MathWorld.
Принцип включения и исключения (PIE)
Эндрю Эллинор, Пи Хан Го, Бывший блестящий член, и
способствовал
Содержимое
- Два набора
- Три комплекта и больше
- расстройства
- Решение проблем
В случае разделения объектов на два (возможно, непересекающихся) множества принцип включения и исключения
\[ |A \cup B| = |А|+|В| — |A\cap B|,\]
, где \(|S|\) обозначает мощность или количество элементов множества \(S\) в системе обозначений.
Чтобы доказать это утверждение, мы покажем, что каждый элемент, принадлежащий одному из этих множеств, учитывается ровно один раз, а каждый элемент, не входящий в эти множества, учитывается ровно ноль раз.
Случай 1. Элемент не находится ни в \(A\), ни в \(B\).
Очевидно, что в LHS он считается ноль раз. Очевидно, что в RHS он считается ноль раз.Случай 2. Элемент находится в \(A\), а не в \(B\).
Будет засчитан один раз на LHS. В RHS он считается один раз в \( |A| \).Случай 3. Элемент находится не в \(A\), а в \(B\).
Будет засчитан один раз на LHS. В RHS он считается один раз в \( |B| \).Случай 4. Элемент находится в \(A\) и в \(B\).
Будет засчитан один раз на LHS. На правой стороне считается \(+1\) в \(|A|\), \(+1\) в \(|B|\) и \(-1\) в \(|A \cap Б|\). Следовательно, он считается ровно один раз.
Как диаграмму Венна, PIE для двух наборов можно легко изобразить:
Сколько целых чисел от 1 до 100 кратны 2 или 3?
Пусть \( A\) будет набором целых чисел от 1 до 100, кратных 2, тогда \(\lvert A \rvert = 50\).

Пусть \( B\) будет набором целых чисел от 1 до 100, кратных 3, тогда \(\lvert B \rvert = 33\).
Теперь \(A \cap B\) — это набор целых чисел от 1 до 100, кратных как 2, так и 3, а значит, кратных 6, что подразумевает \(\vert A \cap B \rvert = 16\ ).Следовательно, PIE, \[ | А\чашка Б| = |A|+|B|-|A\cap B| = 50 + 33 — 16 = 67. \_\квадрат\]
На экзаменах в старших классах средней школы 80% экзаменуемых сдали экзамены по английскому языку и 85% по математике, а 75% сдали экзамены по английскому языку и математике. Если 45 кандидатов не сдали экзамены по обоим предметам, найдите общее количество кандидатов. 9\text{й}\) клиент. Если в день открытия их посетило 1000 клиентов, сколько клиентов ушли с бесплатными подарками?
Мы уже рассмотрели корпус из 2 комплектов. Прежде чем мы углубимся в общий случай, давайте рассмотрим наличие 3 наборов.
При наличии трех наборов принцип включения и исключения гласит
\[ |A\cup B \cup C| = |А| + |Б| + |С| — |А\шапка Б| — |А\шапка С| — |В \заглушка С| + |A \cap B \cap C|. \]
\]
Мы можем сами убедиться в этих утверждениях, рассмотрев диаграмму событий Венна:
В школе есть ровно три типа учеников: гики, подражатели и спортсмены. Каждый студент относится по крайней мере к одной из этих категорий. А общее количество учеников в школе равно 1000. Предположим, что дано следующее:
- Всего студентов-гиков 310.
- Общее количество желающих стать учениками составляет 650 человек.
- Общее количество студентов-спортсменов составляет 440 человек.
- Общее количество студентов, которые одновременно являются фанатами и подражателями, составляет 170 человек.
- Общее количество студентов, которые одновременно являются компьютерщиками и спортсменами, составляет 150 человек.
- Общее количество студентов, которые одновременно являются подражателями и спортсменами, составляет 180 человек.
Каково общее количество студентов, подпадающих под все 3 категории?
Пусть \(G,W,A\) обозначает набор для гиков, подражателей и спортсменов соответственно.
Тогда по принципу включения и исключения имеем
\[n( G \cup W \cup A) = n(G) + n(W) + n(A) — n(W\cap G) — n(G\cap A) — n(W\cap A) + n(G\cap W \cap A),\]
, что дает нам \(1000 = 310 + 650 + 440 — 170 — 150 — 180 + n(G\cap W \cap A )=900 + n(G\cap W \cap A ) \).
Таким образом, общее количество учеников, попадающих во все 3 категории, равно 100. \(_\квадрат\)
Сколько положительных целых чисел, меньших или равных 60, делятся на 3, 4 или 5?
Доказательство отложим до общего случая. Если вам интересно, вы можете продублировать приведенное выше доказательство и проверить, что каждый элемент в \( A \cup B \cup C \) подсчитывается ровно один раз в RHS. 9{n-1} \left|A_1\cap\cdots\cap A_n\right|.\]
На пресс-конференции Зимней Олимпиады в Сочи присутствуют \(200\) иностранных журналистов. Из них
- \(175\) человек владеют немецким языком,
- \(150\) человек могут говорить по-французски,
- \(180\) человек могут говорить по-английски, а
- \(160\) человек говорят по-японски.

Какое минимальное количество иностранцев может говорить на всех четырех языках?
Основная статья: Психозы
На секретной вечеринке Санты восемь гостей. Каждый гость приносит подарок, и каждый получает еще один подарок взамен. Никому не позволено получить подарок, который они принесли. Сколько существует способов распределить подарки?
Пусть \( A\) обозначает множество способов раздачи подарков, при которых каждый получает подарок, возможно, свой. Пусть \( A_i\) обозначает множество способов раздачи подарков таким образом, что человек \( i\) получает свой собственный подарок. Тогда мы хотели бы найти
\[ |А| — |A_1 \чашка A_2 \чашка \cdots \чашка A_8|.\]
Поскольку \(A_i\) — это набор способов, которыми человек \(i\) может получить свой собственный подарок, существует 7 вариантов подарков для следующего человека, 6 вариантов подарков для следующего человека и т. д. . По правилу продукта,
\[ |A_i|=7\times 6 \times \cdots \times 2 \times 1 = 7!.
\]
Поскольку \( A_i \cap A_j\) представляет собой набор способов, которыми человек \(i\) и человек \(j\) получают свои подарки, существует 6 вариантов подарков для следующего человека, 5 вариантов подарков для следующего человека. следующий человек и так далее. Опять же по правилу произведения,
\[ |A_i \cap A_j| = 6 \times 5 \times \cdots \times 2 \times 1 = 6!.\]
Продолжая этот аргумент, если \( k\) люди получают свои собственные дары, то есть \( (8-k)!\) возможных способов. Применив PIE, получим
\[ |А| — |A_1 \чашка A_2 \чашка \cdots \чашка A_8| = 8! — {8 \выберите 1} \умножить на 7! + {8\выберите 2} \умножить на 6! — \cdots + {8 \выберите 8} \times 0! = 14833.\ _\квадрат\]
Примечание: расстройство \(n\) объектов — это такая перестановка объектов, при которой ни один из них не остается на одном и том же месте. Количество способов, которыми это можно сделать, обозначается \(D_n\), и этот расчет показывает \(D_8 = 14833\).
Чему равна сумма всех целых чисел от 1 до 100, кратных 2 или 3?
Хотя PIE часто используется для подсчета элементов множества, если убрать символы \( | \cdot |\), утверждение останется верным. Например, в двух переменных \( A \cup B = A + B — A \cap B \). То же самое доказательство с использованием диаграмм Венна работает, чтобы показать, что каждый элемент включен один раз. Таким образом, сумма элементов в \(A \cup B\) равна сумме элементов в \(A\) плюс сумма элементов в \(B\) минус сумма элементов в \(A\ крышка Б\). Пусть \(A\) будет множеством, кратным 2, а \(B\) будет множеством, кратным 3, тогда \(A \cap B\) будет множеством, кратным 6, и, следовательно, сумма \ (A \чашка B\) равно
\[ \frac {(2+100)\times 50}{2} + \frac {(3 +99)\times 33}{2} — \frac {(6+96)\times 16}{2} = 3417. \ _\квадрат \]
У нас есть 7 шаров разного цвета (красный, оранжевый, желтый, зеленый, синий, индиго, фиолетовый) и 3 коробки разной формы (тетраэдр, куб, додекаэдр).
7\). Пусть \(T\) — множество способов, при которых тетраэдр не имеет шаров, \(C\) — множество способов, при которых кубический ящик не имеет шаров, и \(D\) — множество способов, при которых коробка додекаэдра не имеет шаров. Мы хотим найти 97 — 0 = 1806. \ _\квадрат\]
Кэти преподает в классе из тридцати учеников, из которых четырнадцать девочек. Она знает, что есть двадцать два ученика-правши.
Какое минимальное количество девочек-правшей в этом классе?
35 45 55 65
На строительной площадке Хорхе отвечает за наем квалифицированных рабочих для проекта. Из 80 кандидатов, которых он проинтервьюировал, он обнаружил, что
- 45 маляров,
- 50 были электриками,
- 50 сантехников,
- 15 имели навыки во всех трех областях, а
- все они обладали навыками хотя бы в одной из этих областей.

Если он нанял всех, кто был квалифицирован ровно в двух областях, сколько кандидатов было нанято?
Цитировать как: Принцип включения и исключения (PIE). Brilliant.org . Извлекаются из https://brilliant.org/wiki/принцип-включения-и-исключения-пирога/
Включение-исключение и его различные приложения
В области комбинаторики это метод подсчета, используемый для вычисления мощности множества объединения. В соответствии с основным принципом включения-исключения :
- Для 2 конечных множеств и , которые являются подмножествами универсального множества, тогда и являются непересекающимися множествами.
- Отсюда можно сказать, что
. - Аналогично для 3 конечных множеств , и ,
Принцип:
Принцип включения-исключения гласит, что для любого числа конечных наборов объединение наборов определяется как = Сумма размеров всех отдельных наборов — Сумма всех пересечений двух наборов + Сумма всех пересечения 3-х наборов – сумма всех пересечений 4-х наборов . . + сумма всех пересечений i-го набора.
. + сумма всех пересечений i-го набора.
В целом можно сказать, что
Свойства :
- Вычисляет общее количество элементов, удовлетворяющих хотя бы одному из нескольких свойств.
- Предотвращает проблему двойного счета.
Пример 1:
Как показано на диаграмме, даны 3 конечных множества A, B и C с соответствующими значениями. Вычислить.
Решение:
0009 Нарушения
Чтобы определить количество нарушений (или перестановок) n объектов, при которых ни один объект не находится в исходном положении (например, задача проверки шляпы).
В качестве примера можно рассмотреть нарушения числа в следующих случаях:
При i = 1 общее количество нарушений равно 0.
При i = 2 общее количество нарушений равно 1. Это .
Для i = 3 общее количество нарушений равно 2. Это и 3 1 2.
Подход: – Принцип включения-исключения — это метод комбинаторного подсчета, который позволяет нам подсчитывать количество элементов в объединении нескольких наборов.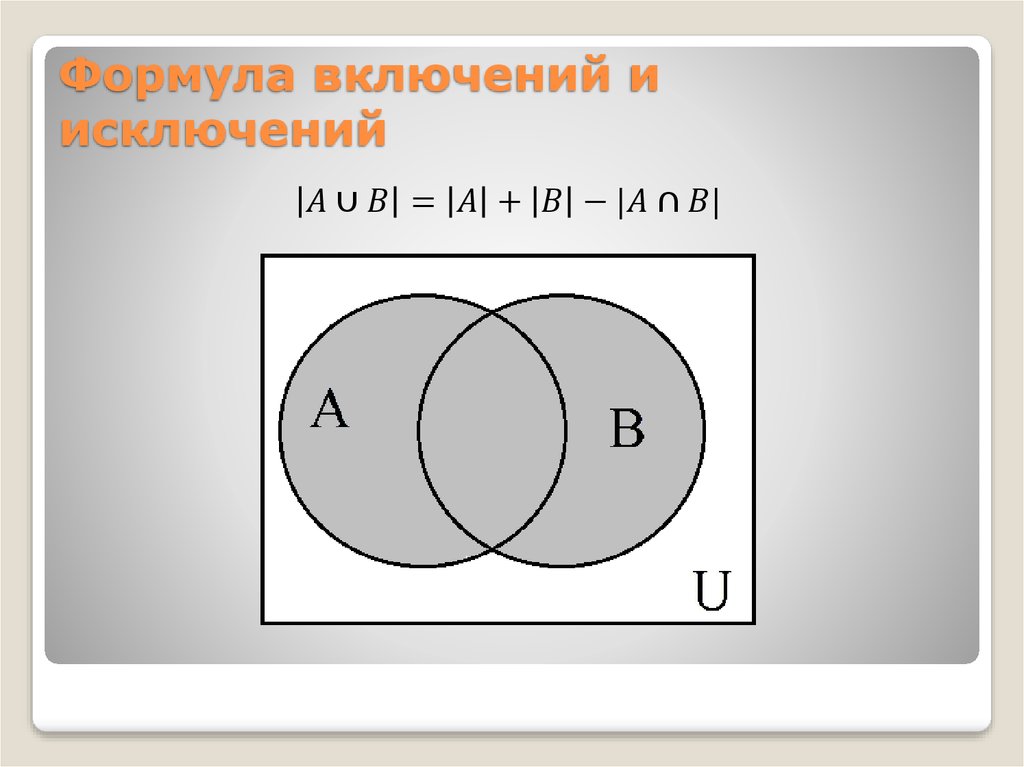 Принцип гласит, что размер объединения двух или более множеств равен сумме их размеров минус размер их пересечения, плюс размер пересечения их попарных пересечений и так далее.
Принцип гласит, что размер объединения двух или более множеств равен сумме их размеров минус размер их пересечения, плюс размер пересечения их попарных пересечений и так далее.
Вот пошаговый подход на C++ к реализации принципа включения-исключения:
Определите наборы, которые необходимо объединить.
Вычислите размер каждого набора.
Вычислить размер каждого пересечения двух наборов.
Вычислите размер каждого пересечения трех наборов.
Продолжайте вычислять размер каждого пересечения четырех, пяти и т. д. наборов, пока не дойдете до последнего пересечения.
Суммируйте размеры всех наборов.
Вычтите размер всех попарных пересечений.
Добавьте размеры всех трехсторонних перекрестков.
Продолжайте добавлять и вычитать пересечения увеличивающихся размеров, пока не достигнете конечного пересечения.
Вернуть окончательный счет.
Вот пример реализации принципа включения-исключения в C++ для нахождения количества положительных целых чисел меньше 100, которые делятся на 2, 3 или 5: iostream>
с использованием пространства имен стандартное;
int main() {
int n = 100;
int count = 0;
для ( INT I = 2; I I = 2; I+= 2) { I = 2;
}
для
для 0326 ( int i = 3; i < n; i += 3) { count++;
}
for ( int i = 5; i < n; i += 5) {
количество++;
}
для ( INT I = 6; I
2927 2 2927 2927 2927 2927 2927 2927 2927 2927 2927 2 2927 2927 2927 2 9036 2927 2 9036 2927 2927 2927 2927 2927 2927 2927 2 9036 2927 9036 2 9036 2927 2927 2927 2927 2927 2927 2927 2927 2927 9036 2 9036 2927 9.
}
for ( int i = 10; i < n; i += 10) {
считать--;
}
for ( int i = 15; i < n; i += 15) {
count --;
}
для ( для ( ( ( . 0327
0327
кол++;
}
COUT << ". 2, 3 или 5 — это " << count << "." << конец;
возврат 0;
}
Python3
|

 1 Задача о беспорядках
1 Задача о беспорядках — М.: Изд-во иностранной литературы, 1963. — С. 63-66. — 289 с.
— М.: Изд-во иностранной литературы, 1963. — С. 63-66. — 289 с.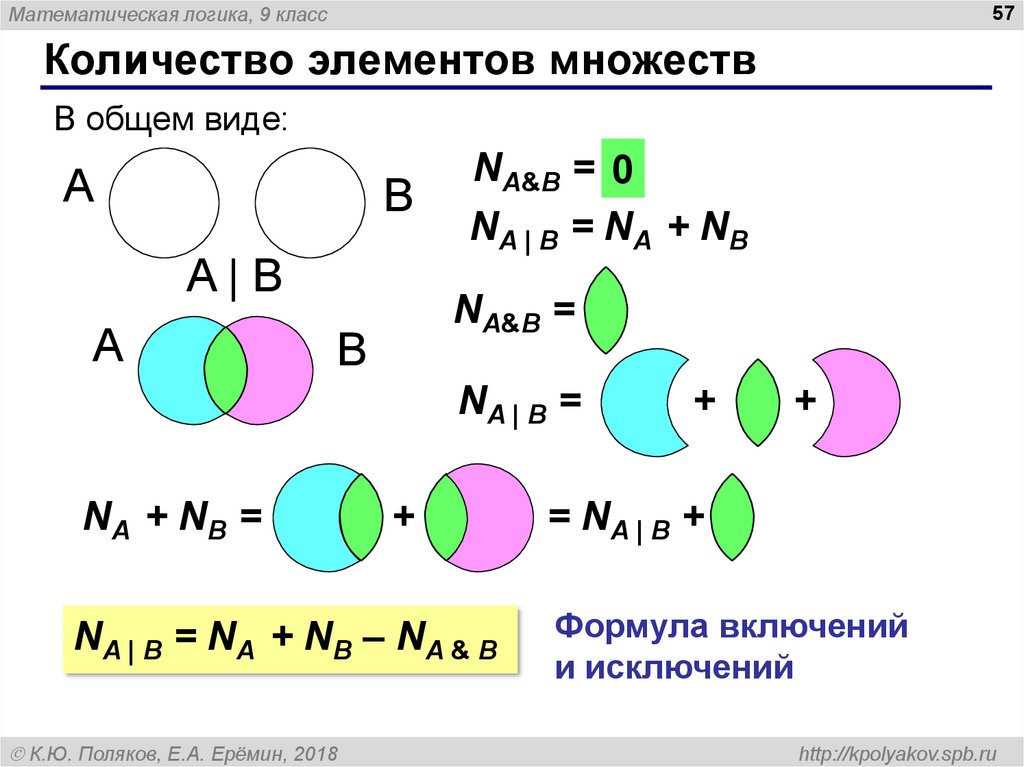 Перечислительная комбинаторика = Enumerative Combinatorics. — М.: «Мир», 1990. — С. 103-107. — 440 с.
Перечислительная комбинаторика = Enumerative Combinatorics. — М.: «Мир», 1990. — С. 103-107. — 440 с.
 Тогда по принципу включения и исключения имеем
Тогда по принципу включения и исключения имеем
 \]
\]
 7\). Пусть \(T\) — множество способов, при которых тетраэдр не имеет шаров, \(C\) — множество способов, при которых кубический ящик не имеет шаров, и \(D\) — множество способов, при которых коробка додекаэдра не имеет шаров. Мы хотим найти 97 — 0 = 1806. \ _\квадрат\]
7\). Пусть \(T\) — множество способов, при которых тетраэдр не имеет шаров, \(C\) — множество способов, при которых кубический ящик не имеет шаров, и \(D\) — множество способов, при которых коробка додекаэдра не имеет шаров. Мы хотим найти 97 — 0 = 1806. \ _\квадрат\]