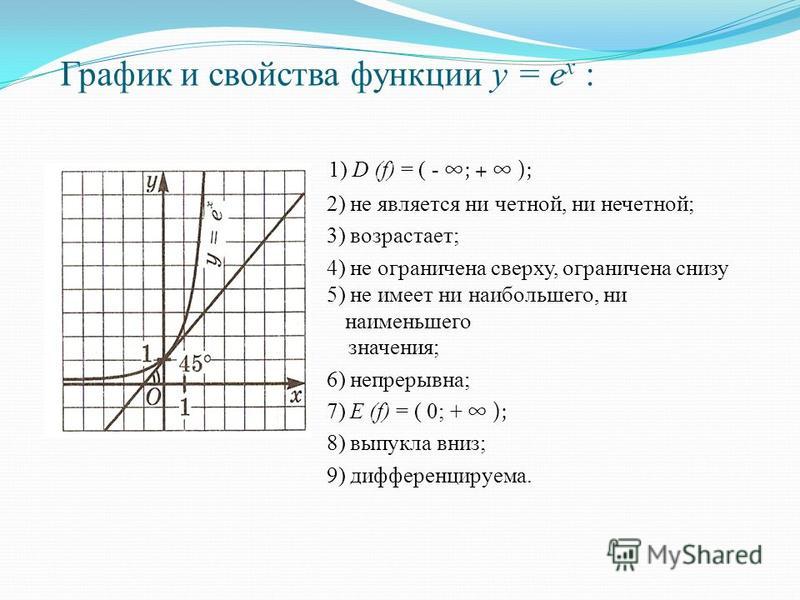
Функция е в степени х график: Число е. Функция у = е^x, её свойства, график, дифференцирование — урок. Алгебра, 11 класс.

x (серый)

Ветвь, для которой , называется , другая — .

Содержание

Постановка задачи

Задача. Научиться находить действительные корни уравнения следующего вида:

Как вы, наверное, уже догадались, для решения будем использовать W-функцию Ламберта. Итак, сначала возведем и левую, и правую часть в степень (это преобразование не является равносильным при четных целых , а при нечетных нужно будет расширять множество значений до всех действительных чисел, поэтому решаем задачу для указанных выше ограничений).

Теперь для того, чтобы воспользоваться основным Ламбертовым тождеством, нам нужно получить выражение с такое, как и в показателе степени экспоненты. Для этого поделим и левую, и правую часть на .

И теперь мы можем воспользоваться основным Ламбертовым тождеством:

Откуда и получаем уже итоговую формулу для .

Вычисление W-функции Ламберта

Заметим, что при функция Ламберта дает два действительных значения: по одному на каждой из ветвей и соответственно. В этом случае у изначального уравнения будет 2 корня.

Вычисление W₀. Будем использовать метод бинарного поиска по ответу. Мы можем так поступить, поскольку возрастает на .

Левая граница бинарного поиска понятна и равна. Теперь возникает вопрос, как выбрать правую границу. Первая идея, которая приходит на ум: положить ее равной , ибо верно неравенство , причем равенство достигается только в нуле.

Однако для достаточно больших это может быть не лучшим вариантом. Поэтому давайте посмотрим на другой: выберем правую границу равной .

Итого: при правой границей выбираем , а при берем .

Графики y = x (синий), y = W(x) (зеленый) и y = ln(x) (красный)

Ассимптотика: , prec — изначально выбранная точность (например, 10^-12)

Вычисление W_-1. Здесь будем использовать следующее бесконечное выражение для :

Чем глубже мы спускаемся, тем выше точность вычислений.

Реализация на Python

from math import *
def LambertW0(x):
    left = -1
    right = x if x <= e else log(x)
    prec = 10**-12 # точность
    # бинарный поиск
    while right - left > prec:
        mid = (right + left) / 2
        if mid * exp(mid) > x:
            right = mid
        else:
            left = mid
    return right
def LambertW_1(x, t): # t - показатель точности
    if t == 100:
      	return log(-x)
    else:
      	return log((-x)/(-LambertW_1(x, t + 1)))
def sol(p, q):
    s = q**(1/p) / p
    if s < -exp(-1):
        return "No real solutions"
    ans = "Solutions: " + str(p * LambertW0(s)) + " "
    if -exp(-1) < s and s < 0:
      	ans += str(p * LambertW_1(s, 0))
    return ans
    
p = float(input())
q = float(input())
print(sol(p, q))

Проверка

Уравнение 1.

{2}\) или \(y = \left| \frac{1}{x} \right|\). Чтобы построить такие графики, нужно соблюдать ряд правил преобразования функций. Каждая «сложная» функция состоит из набора таких преобразований.
ОТРИЦАТЕЛЬНЫЕ ЗНАЧЕНИЯ:
ИЗМЕНЕНИЕ АРГУМЕНТА
Если у мы знаем функцию f(x) и нам нужно построить функцию f(–x) (то есть заменить все иксы в функции на противоположные), тогда нужно отразить график симметрично относительно оси Оу, т.е. все ординаты останутся неизменными, а абсциссы поменяют знак.
Например:
Четная функция при таком изменении не изменяется, т.к. это следует из определения четной функции.
ИЗМЕНЕНИЕ ЗНАЧЕНИЯ ФУНКЦИИ
Если у мы знаем функцию f(x) и нам нужно построить функцию –f(x) (то есть заменить все значения функции на противоположные), тогда нужно отразить график симметрично относительно оси Ох, т.е. все абсциссы останутся неизменными, а ординаты поменяют знак.
{2}\) правее на 2 единичных отрезка:
ИЗМЕНЕНИЕ ЗНАЧЕНИЯ ФУНКЦИИ
Если мы знаем функцию \(f(x),\) а нам нужно построить функцию \(f(x)\ \pm \ a\ \)(то есть прибавить к получившимся значениям функции \(\pm\) a), тогда f(x) будет двигаться по оси Оу.
– Если нужно построить \(f(x)\ + \ a\), то функция поднимется на a единичных отрезков вверх.
– Если нужно построить \(f(x)\ –\ a\), то функция опуститься на a единичных отрезков вниз.
Например:
Функция \(y = \frac{1}{x} + 5\) будет выше функции \(y = \frac{1}{x}\) на 5 единичных отрезков, а функция \(\frac{1}{x}\ –\ 4\) ниже на 4 единичных отрезка:
ПРОИЗВЕДЕНИЕ:
ИЗМЕНЕНИЕ АРГУМЕНТА
Если мы знаем функцию \(f(x),\) а нам нужно построить функцию \(f(\text{ax})\ \)(то есть заменяем все иксы на выражение
ax), тогда функция \(f(x)\) будет «сжиматься» и «растягиваться» вдоль оси Ох. {2}\) растянута в 2 раза:
МОДУЛЬ:
ИЗМЕНЕНИЕ АРГУМЕНТА
Если мы знаем функцию \(f(x),\) а нам нужно построить график функции \(f(|x|)\) (то есть заменяем все иксы на модуль икс), тогда график в области с отрицательными абсциссами стирается, а график в области с положительными абсциссами отражается относительно оси Оу. Функция становится четной.
Например:
ИЗЕНЕНИЕ ЗНАЧЕНИЯ ФУНКЦИИ
Если мы знаем функцию \(f(x),\) а нам нужно построить график функции \(|f\left( x \right)|\) (то есть берем под модуль значение функции). Тогда график в области с отрицательными ординатами отражается относительно оси Ох.

Например:
3-8 9 Оценить квадратный корень из 12 10 Оценить квадратный корень из 20 11 Оценить квадратный корень из 50 94 18 Оценить квадратный корень из 45 19 Оценить квадратный корень из 32 20 Оценить квадратный корень из 18 92
Видео-урок: Графики экспоненциальных функций

Стенограмма видео
В этом видео мы научимся зарисовать и определить графические преобразования экспоненциальных функций. Экспоненциальная функция является одним из форма 𝑓 из 𝑥 равна 𝑏 в степени 𝑥. 𝑏 — положительное действительное число, не равно единице, а переменная 𝑥 выступает в качестве показателя степени. Эти функции чрезвычайно важны в математике, поскольку они имеют всевозможные приложения. Мы используем их для моделирования экспоненциального рост и распад. Например, мы могли бы использовать экспоненциальная функция для моделирования роста населения или количества денег в инвестиционный счет с учетом конкретных требований сложных процентов. Начнем с рассмотрения формы таких графиков.

Какой график демонстрирует экспоненциальный рост?
Во-первых, давайте вспомним, что мы подразумеваем под показательная функция. Это функция вида 𝑓 от 𝑥 равно 𝑏 в степени 𝑥, где 𝑏 — положительное действительное число, не равное единице и в котором переменная 𝑥 встречается как показатель степени.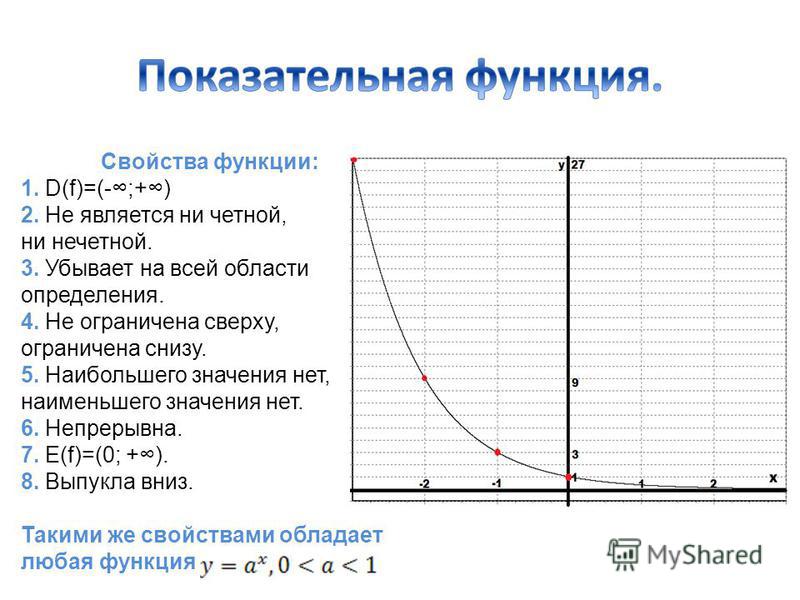 Давайте посмотрим, что произойдет, если мы попробуйте построить два типа этой функции. Мы построим функцию 𝑓 от 𝑥 равно двум в степени 𝑥. Другими словами, тот, где 𝑏 больше единицы, а функция 𝑔 от 𝑥 равна половине степени 𝑥. В данном случае мы рассматриваем поведение, где 𝑏 находится в открытом интервале от нуля до единицы.
Мы будем использовать таблицу для каждого. Когда 𝑥 отрицательно два, 𝑓 из 𝑥 равно двум в степени минус два. Это один на два в квадрате, что один на четыре или 0,25. Когда 𝑥 отрицательное, 𝑓 из 𝑥 это два в степени отрицательной единицы, что составляет половину или 0,5. Точно так же 𝑓 нуля равно единице, 𝑓 из одного — два, 𝑓 из двух — четыре, а 𝑓 из трех — два в кубе, т. е. восемь. Точно так же для 𝑔 из 𝑥 мы получаем 𝑔 отрицательных двух будет четыре, 𝑔 отрицательного один будет два, и так один. Давайте построим их на том же оси.

Когда мы строим функцию 𝑓 от 𝑥 и соединив его плавной кривой, мы увидим, что он увеличивается по всей своей области. Другими словами, он всегда наклонен. вверх. Принимая во внимание, что 𝑔 из 𝑥 уменьшается; он всегда наклонен вниз.
Фактически мы говорим, что функция форма 𝑓 из 𝑥 равна 𝑏 в степени 𝑥, где 𝑏 — действительная константа, большая чем единица, представляет собой экспоненциальный рост. Принимая во внимание, что когда 𝑏 больше, чем ноль и меньше единицы, функция представляет собой экспоненциальный спад. Итак, какой из наших графиков демонстрирует экспоненциальный рост? Другими словами, это выглядит немного немного похоже на функцию 𝑓 из 𝑥. Итак, мы видим, что эта функция 𝑏.

Теперь, по сути, мы можем сделать еще один вывод свойства этих функций из построенных нами графиков. Обратите внимание, как эти части линий кажутся все ближе и ближе к оси 𝑥.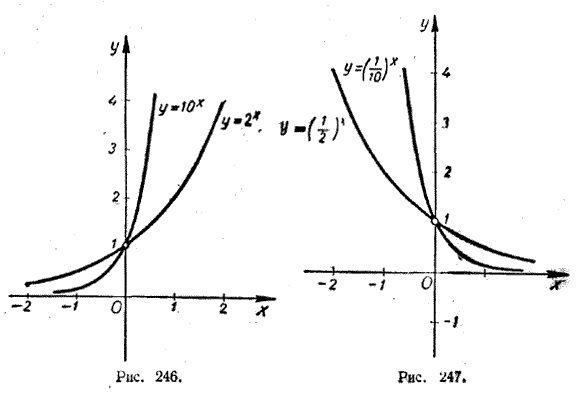 Они никогда не достигнут 𝑥-ось, однако. И это потому, что число получает дробно меньше каждый раз, так как мы вдвое уменьшаем значение функции. Но до нуля никогда не дойдет. Мы называем эту линию осью 𝑥 или линия 𝑦 равна нулю, горизонтальной асимптоте.

Таким образом, мы можем сказать, что следующий. Экспоненциальная функция является одним из форма 𝑓 от 𝑥 равна 𝑏 в степени 𝑥, где 𝑏 — положительное действительное число не равно единице. Если 𝑏 больше единицы, функция моделирует экспоненциальный рост. А если он больше нуля и меньше единицы, он моделирует экспоненциальный спад. Ось 𝑥 или линия 𝑦 равна ноль, является горизонтальной асимптотой таких функций. На самом деле есть еще один свойство, которое мы можем установить, поэтому давайте рассмотрим пример.
Определить точку, в которой график функции 𝑓 от 𝑥 равен шести в степени 𝑥 пересекает 𝑦-ось.

Напомним, что ось 𝑦 — это вертикальная линия, уравнение которой 𝑥, равна нулю. Таким образом, мы можем найти точку пересечение графика с осью 𝑦, приравняв 𝑥 к нулю и решив для 𝑦. Когда мы это делаем, когда мы устанавливаем 𝑥 равным нуля, мы получаем 𝑦 равно шести в степени нуля. Но, конечно, мы знаем, что что угодно в степени нуля равно единице. Это означает, что граф пересекает ось 𝑦 в точке 𝑦 равна единице. Теперь, когда, конечно, 𝑥 равен нулю. Итак, координата пересечения равен нулю, единице. В самом деле, если взять общий график функции 𝑓 от 𝑥 равен 𝑏 в степени 𝑥, где 𝑏 — вещественная константа больше нуля и не равна единице, мы знаем, что 𝑓 нуля равно 𝑏 сила нуля, которая также равна единице.
Помните, что независимо от стоимости 𝑏, пока это реальная константа, 𝑏 в степени нуля всегда будет единицей.
Поэтому мы можем сказать, что экспоненциальная функция вида 𝑓 от 𝑥 равна 𝑏 в степени 𝑥 пересекается 𝑦-ось в единице или точке с координатами ноль, единица.
В нашем следующем примере мы рассмотрим как мы можем определить правильный график экспоненциальной функции, используя функции мы установили и немного замены.
Какой из следующих графиков представляет уравнение 𝑦 равно трем в степени 𝑥?
Наше уравнение 𝑦 равно трем степень 𝑥 представляет показательное уравнение. Итак, давайте вспомним, что мы знаем о экспоненциальные функции. Во-первых, мы знаем, что экспоненциальная функция формы 𝑓 от 𝑥 равна 𝑏 в степени 𝑥, где 𝑏 равно положительная действительная постоянная, проходит через ноль через единицу. Другими словами, он проходит через 𝑦-ось на одном. Итак, давайте посмотрим, сможем ли мы устранить любой из наших графиков из нашего вопроса. График B проходит через ноль. График C не пересекается 𝑦-ось вообще. График E пересекается в отрицательной один. И это оставляет нас с графиком А и График D, которые пересекают ось 𝑦 в одной точке.
Есть два способа проверить какой из наших графиков правильный. Мы могли бы выбрать точку и проверить этот. Например, наш первый график проходит через точку с координатами один, три. Пусть 𝑥 равно единице, так как 𝑥-координата равна единице, и посмотрите, действительно ли 𝑦-координата равна трем. Если 𝑥 равно единице, 𝑦 равно к трем в степени одного, что действительно равно трем. Таким образом, мы можем сделать вывод, что график уравнения 𝑦, равного трем в степени 𝑥, должно проходить через точку один, три. Итак, наш график A.
Однако есть и другой способ можно было бы протестировать это. Мы знаем, что если 𝑏 больше, чем один, наш график представляет собой экспоненциальный рост. Другими словами, всегда увеличение. Принимая во внимание, что если 𝑏 находится между нулем и во-первых, он представляет собой экспоненциальный спад; она всегда уменьшается. Мы видим, что график D убывает во всей своей области. Он всегда наклонен вниз. Итак, значение 𝑏, основание, если вы будете, должно быть между нулем и единицей. Так что это может быть 𝑦 равно например, одну треть в степени 𝑥. Тогда правильный ответ здесь А.
Давайте посмотрим на другой пример.
Какой из следующих графиков представляет уравнение 𝑦 равно четверти степени 𝑥.
Полезно начать с определения что это показательное уравнение. Показательное уравнение является одним из форма 𝑦 равна 𝑏 в степени 𝑥, где 𝑏 — действительная положительная константа, не равен единице. Теперь мы знаем несколько вещей о графики показательных уравнений.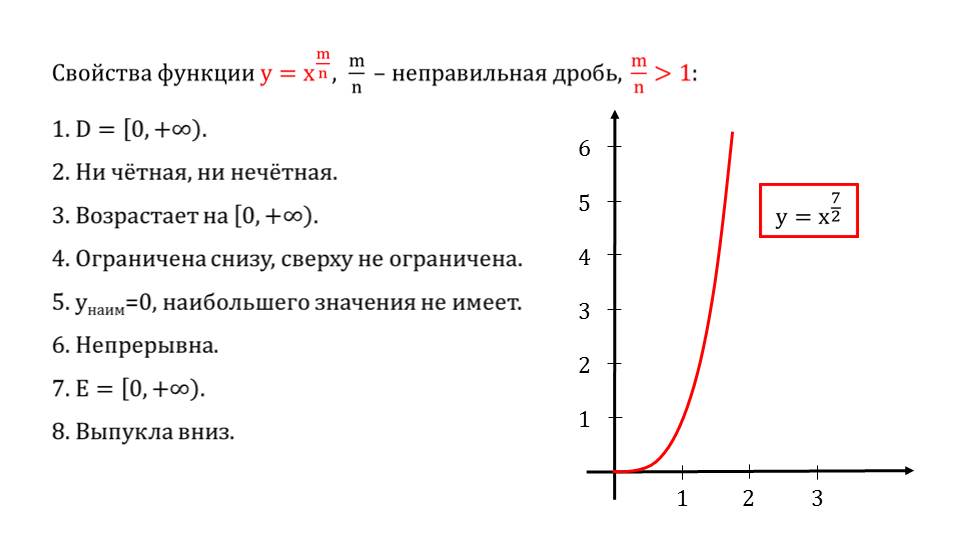 Мы знаем, что их 𝑦-перехваты для начала это одно. Они проходят через нулевую точку, один. И поэтому мы можем мгновенно устранить три наших графика. Мы можем исключить A, B и C. График A на самом деле пересекается в нуле. как и график C, тогда как график B вообще не пересекает 𝑦-ось.
Теперь мы также знаем кое-что о форму этих кривых. Если наше значение для 𝑏 больше, чем один, то мы представляем экспоненциальный рост. И график выглядит немного что-то вроде этого. Обратите внимание, что ось 𝑥 представляет горизонтальная асимптота нашего графика. Он становится все ближе и ближе, но никогда вполне умиляет. Теперь, если 𝑏 больше нуля и меньше единицы, имеем экспоненциальный спад. Наш график убывает по весь домен. 𝑥-ось по-прежнему является горизонтальной асимптота к нашему графику, но на этот раз она выглядит примерно так.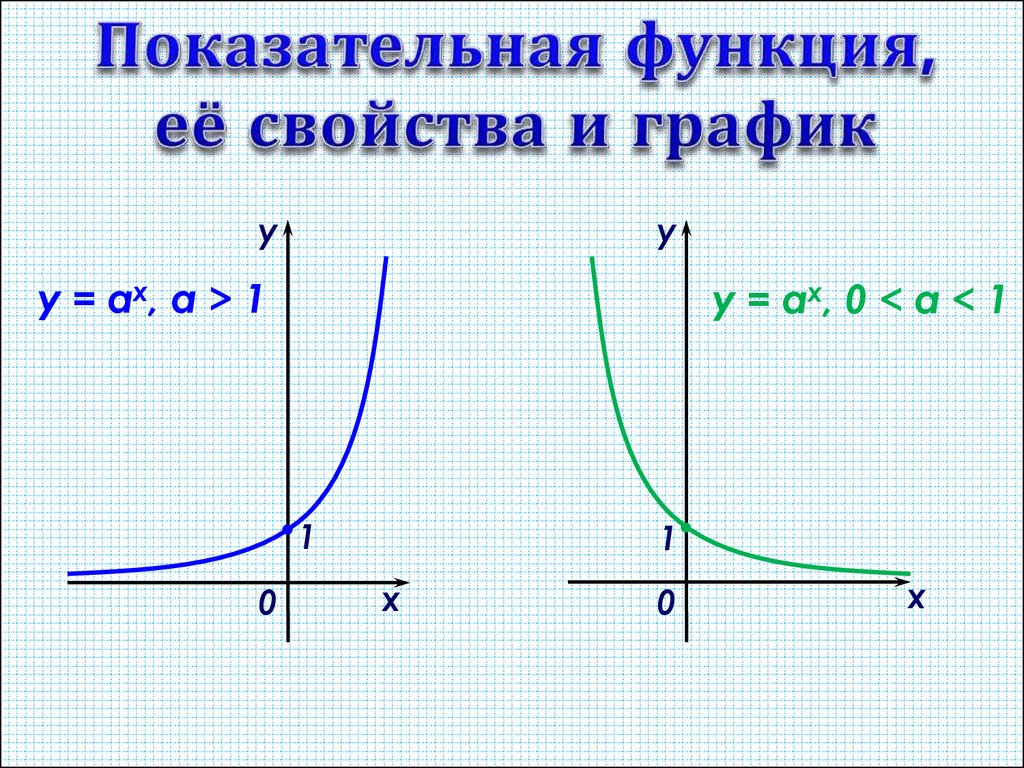
Итак, какова наша ценность 𝑏? Ну, уравнение 𝑦 равно четверть в степени 𝑥. Итак, 𝑏 равно четверти, которая больше нуля и меньше единицы. Это говорит нам о том, что наш график представляет собой экспоненциальный спад. Он будет уменьшаться в течение весь его домен. Мы видим, что это график D.
В нашем последнем примере мы рассмотрим как определить график более сложного показательного уравнения.
Какой из следующих графиков представляет собой уравнение 𝑦, равное дважды трем в степени 𝑥.
Теперь, хотя это может и не выглядеть Это пример показательного уравнения. По сути, это кратное его общая форма 𝑦 равна 𝑏 в степени 𝑥, где 𝑏 — положительная действительная постоянная не равно единице. На этот раз, правда, в форме 𝑎𝑏 в степени 𝑥. Помните, согласно распоряжению операции, мы применяем показатель степени перед умножением.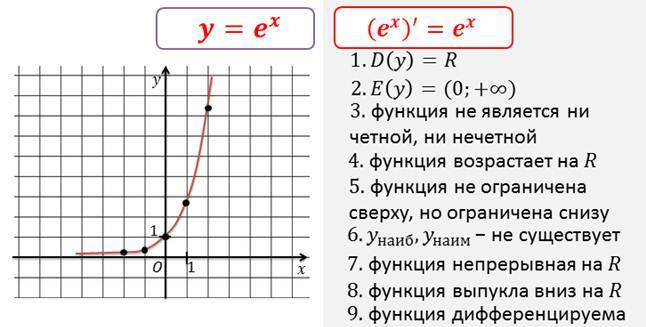 Итак, это три в степени 𝑥 раз два. А это значит, что нам понадобится вспомнить, что мы знаем о преобразованиях графов. Ну а для графика функции 𝑦 равно 𝑓 из 𝑥, 𝑦 равно 𝑓 из 𝑥 плюс некоторая константа 𝑎 является переводом ноль 𝑎. Он перемещает 𝑎 единиц вверх.
График 𝑦 равен 𝑓 из 𝑥 плюс 𝑏 — это перевод отрицательным 𝑏 нулем. На этот раз он перемещает 𝑏 единиц в левый. Теперь, если мы посмотрим на наше уравнение, мы видим, что мы вообще не добавили константу. Поэтому мы вспоминаем другие правила, которые мы знать. 𝑦 равно некоторой константе 𝑎 умножить на 𝑓 из 𝑥 — вертикальное растяжение или увеличение с масштабным коэффициентом 𝑎. Принимая во внимание, что 𝑦 равно 𝑓 из 𝑏𝑥 является горизонтальное растяжение с масштабным коэффициентом один больше 𝑏. Теперь, возвращаясь к нашему уравнению, мы есть три в степени 𝑥.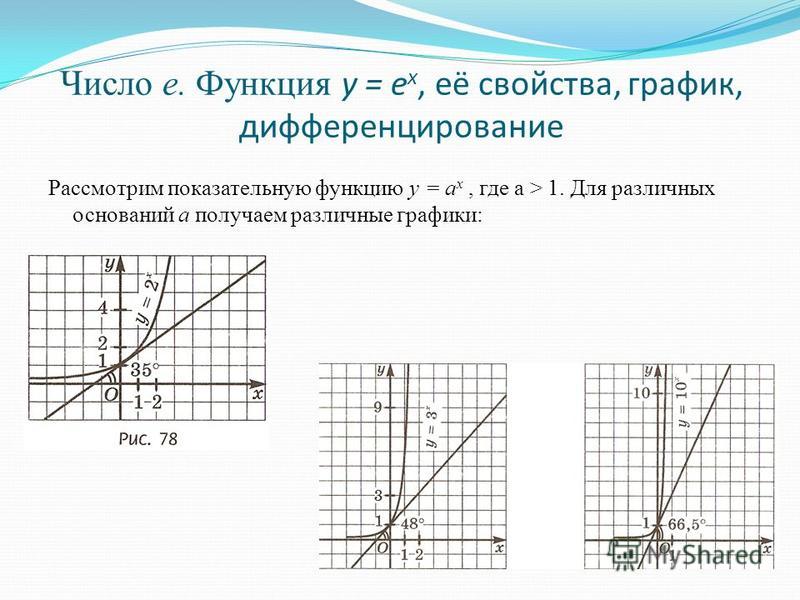 И мы измеряем время всего функционируют вдвоем. Итак, мы смотрим на вертикаль потягиваться. На самом деле, нам нужно выполнить вертикальное растяжение функции 𝑦 равно трем в степени 𝑥 по шкале коэффициент два.
Итак, чему равен график 𝑦 три в степени 𝑥 выглядят. Это экспоненциальная функция, и основание больше единицы. Это означает, что наша функция представляет экспоненциальный рост. Это означает, что мы можем исключить графы A и B. На самом деле они представляют собой экспоненциальные распад, так как они уменьшаются; они наклонены вниз. Итак, нам нужно выбрать из C, D и E. Итак, мы также помним, что функция 𝑦 равна 𝑏 в степени 𝑥 проходит через ось 𝑦 за единицу. Наша функция 𝑦 равна трем сила 𝑥 сделает то же самое. Он пройдет через ноль, один. Но растянуто по вертикали с масштабным коэффициентом два.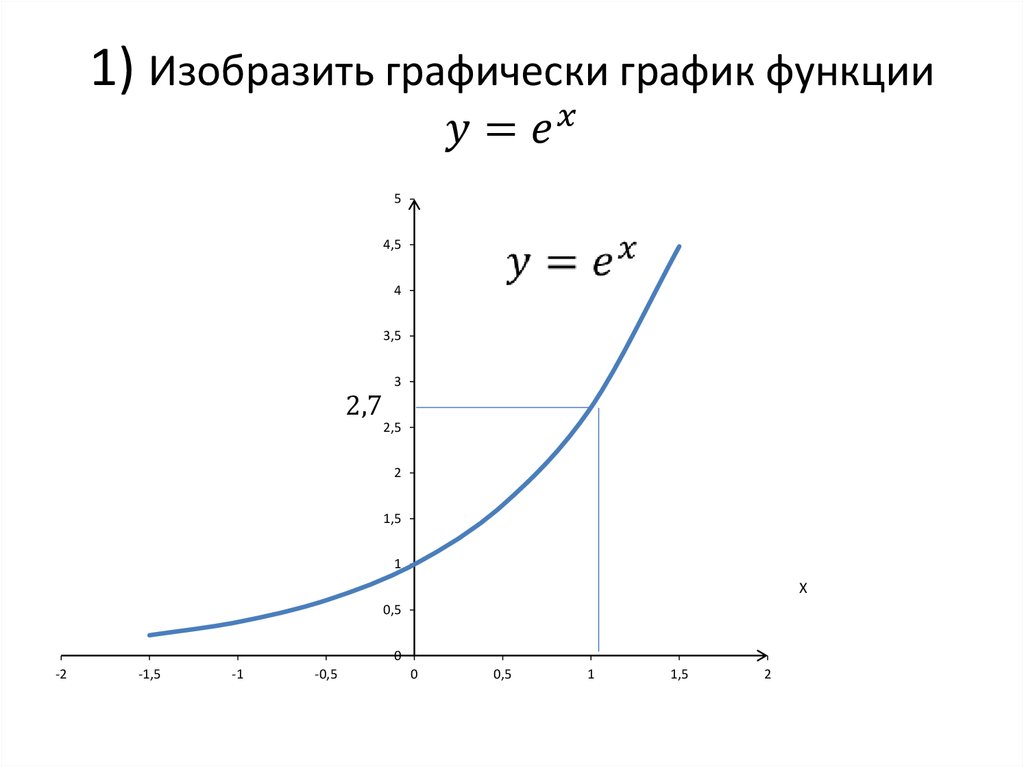 Это означает, что наша функция 𝑦 равна два раза по три в степени 𝑥 должны пройти через ноль, два.
Из C, D и E единственный Функция, которая делает это, есть E. C проходит через единицу, а D проходит в три. Итак, график, представляющий уравнение 𝑦 равно удвоенному трем в степени 𝑥 равно E.
В этом видео мы узнали, что экспоненциальная функция имеет вид 𝑓 от 𝑥 равно 𝑏 в степени 𝑥, где 𝑏 положительное действительное число, не равное единице. Мы видели, что для значений 𝑏 больше единицы наша функция моделирует экспоненциальный рост; он наклонен вверх. И что если ноль меньше 𝑏, меньше единицы функция моделирует экспоненциальный спад; он склоняется вниз. Обратите внимание, что причина, по которой мы проигнорировали 𝑏 равно единице, если 𝑏 равно единице, функция дает простую горизонтальную линию, что не является экспоненциальным ростом.
No related posts.