| |||||||
|
Получение схемы логического элемента по итоговым значениям логической функции с использованием СДНФ ИЛИ СКНФ
Похожие презентации:
Совершенные конъюнктивные и дизъюнктивные нормальные формы
Базовые логические функции.
Основные понятия алгебры логики
Серии логических элементов. Минимизация
Логические основы ЭВМ. Минимизация
Логические функции
Базовые логические операции и функции. Таблицы истинности. Контактные схемы
Логика и алгебра высказываний
Компьютерная дискретная математика. Нормальные формы
Основы теории логических преобразований
Основные понятия алгебры логики
1. Получение схемы логического элемента по итоговым значениям логической функции с использованием СДНФ ИЛИ СКНФ
2. Определения:
Конъюнкция – логическое умножение.Элементарной конъюнкцией называется конъюнкция
нескольких переменных, взятых с отрицанием или без отрицания,
причем среди переменных могут быть одинаковые:
¬C Λ C;
C Λ ¬A;
¬C Λ B Λ ¬A ;
Дизъюнкция –логическое сложение.
Элементарной дизъюнкцией называется дизъюнкция
нескольких переменных, взятых с отрицанием или без отрицания,
причем среди переменных могут быть одинаковые:
¬CVC;
CV¬A;
¬CVBV¬A ;
3.
ДНФ и КНФВсякую дизъюнкцию элементарныхконъюнкций назовем дизъюнктивной
нормальной формой (ДНФ):
(CΛCΛ¬B)V(¬CΛA)
Всякую конъюнкцию элементарных
дизъюнкций назовем
конъюнктивной нормальной формой
(КНФ): (CVCV¬ B)Λ(¬CVA)
4. СКНФ и СДНФ
Cовершенной ДНФ называется ДНФ, в которойнет одинаковых элементарных конъюнкций и все
конъюнкции состоят из одного и того же набора
переменных, в который каждая переменная
входит только один раз ( возможно с отрицанием)
(C Λ B Λ ¬A)V (C Λ B Λ A)
Cовершенной КНФ называется КНФ, в которой
нет одинаковых элементарных дизъюнкций и все
дизъюнкции состоят из одного и того же набора
переменных, в который каждая переменная
входит только один раз ( возможно с
отрицанием)
(¬ CVBVA) Λ(C V¬BVA)
5. Алгоритм получения СДНФ по таблице истинности:
F(А,В,С)1
0
1
0
1
0
0
0
Дана таблица итоговых значений логической функции
1.
Записываем исходные значения логических переменных.
2.
Применяем СДНФ (так как значений «1» меньше):
3.
Обрабатываем те строки ТИ, в последнем столбце которых
стоят «1»
4.
Выписываем для каждой отмеченной строки конъюнкцию все
переменных следующим образом: если значение логической
переменной в данной строке =1, то в конъюнкцию включают
саму эту переменную, если =0, то ее отрицание:
5.
Все полученные конъюнкции связать в дизъюнкцией (записат
произведение сумм):
6.
Упрощаем логическое выражение, применяя законы алгебры
логики
Склеивания
Распределительный
Поглощения
А
В
С
F(А,В,С)
0
0
0
0
0
1
1
0
0
0
1
1
0
1
1
0
1
1
1
1
0
0
1
1
0
1
0
1
1
0
0
0
1) Применяем закон склеивания к 1-му и 3-му
выражениям ( ̚ а Λ ̚в Λ ̚с) V( ̚ а Λ в Λ ̚с) V( а Λ ̚в Λ ̚с) =
2) Применяем распределительный закон
( ̚в Λ ̚с) V( ̚ а Λ в Λ ̚с) =
3) Применяем закон поглощения
̚с Λ ( ̚в V( ̚ а Λ в))= ̚с Λ( ̚в V( ̚ а))
4) Проставляем на полученной формуле порядок
выполнения логических операций согласно приоритета.
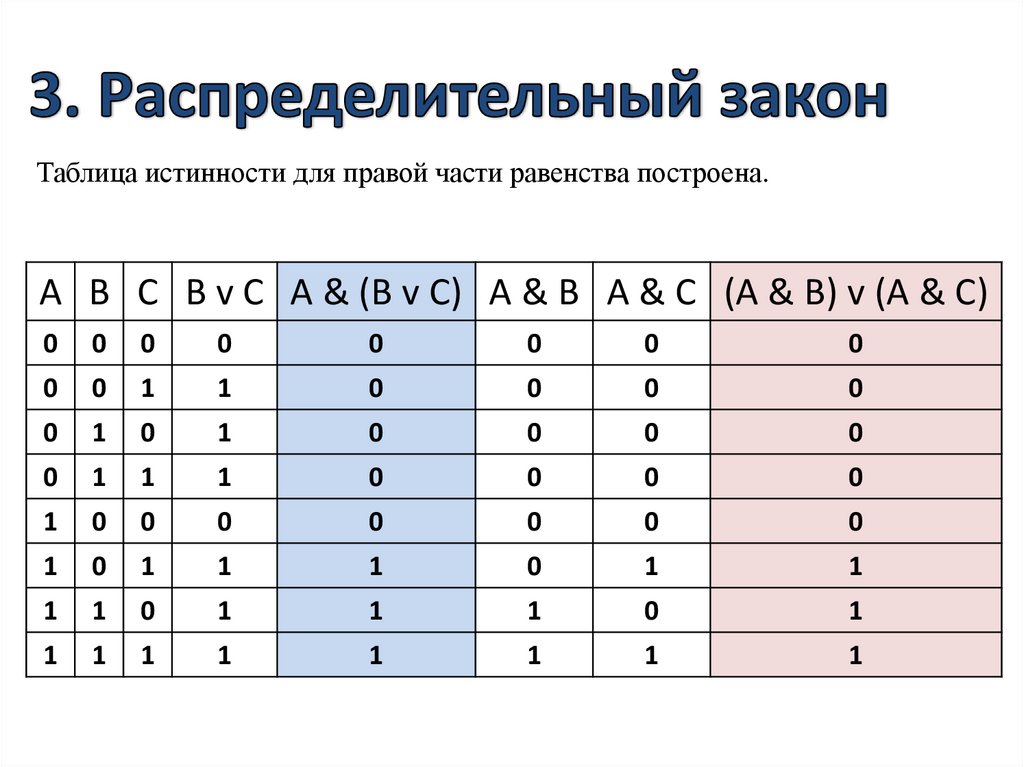
̚с Λ( ̚в V( ̚ а))
3
5 2
4
1
изображаем каждую операцию на схеме логического элемента
по порядку, заменяя операции соответствующим значком:
̚с Λ( ̚в V( ̚ а))
Инверсия ̚
А
1
&
Конъюнкция Λ
1
Дизъюнкция v
В
&
С
F(A,B,C)
9. Алгоритм получения СКНФ по таблице истинности:
(В случае если среди значений функции значений«0»меньше, применяют СКНФ)
Отметить те строки таблицы истинности, в последнем столбце
которых стоят 0:
Выписать для каждой отмеченной строки дизъюнкцию всех
переменных следующим образом: если значение некоторой
переменной в данной строке =0, то в дизъюнкцию включают саму
эту переменную, если =1, то ее отрицание:
Все полученные дизъюнкции связать в конъюнкцию(записать
сумму произведений):
Упростить логическое выражение, применив законы
Склеивания
Распределительный
Поглощения
(Предлагается выполнить самостоятельно)
10. Задания: построить схемы логических элементов, реализующих заданные логические функции
1 вариант2 вариант
3 вариант
4.
Вариант5. Вариант
6. Вариант
7. Вариант
F(А,В,С) F(А,В,С) F(А,В,С) F(А,В,С) F(А,В,С) F(А,В,С) F(А,В,С)
1
0
0
1
0
1
1
1
1
0
0
0
0
1
0
0
0
1
1
1
1
1
1
0
1
1
1
1
1
0
1
0
0
1
0
1
1
0
0
0
0
0
0
0
1
0
1
1
1
0
0
1
0
0
0
0
Логические операции
в порядке приоритета
Инверсия ̚
&
Конъюнкция
Λ
1
Дизъюнкция
v
12. Домашнее задание
Анализ и упрощение логической схемы:Нарисовать схему логического элемента с
тремя логическими входами (X,Y,Z),
содержащую не менее семи логических
операций.
Построить таблицу истинности к ней.
Применить СКНФ или СДНФ.
Упростить по приведенному в презентации
алгоритму.
Построить новую схему.
13. Ключ для проверки:
1.2.
3.
4.
5.
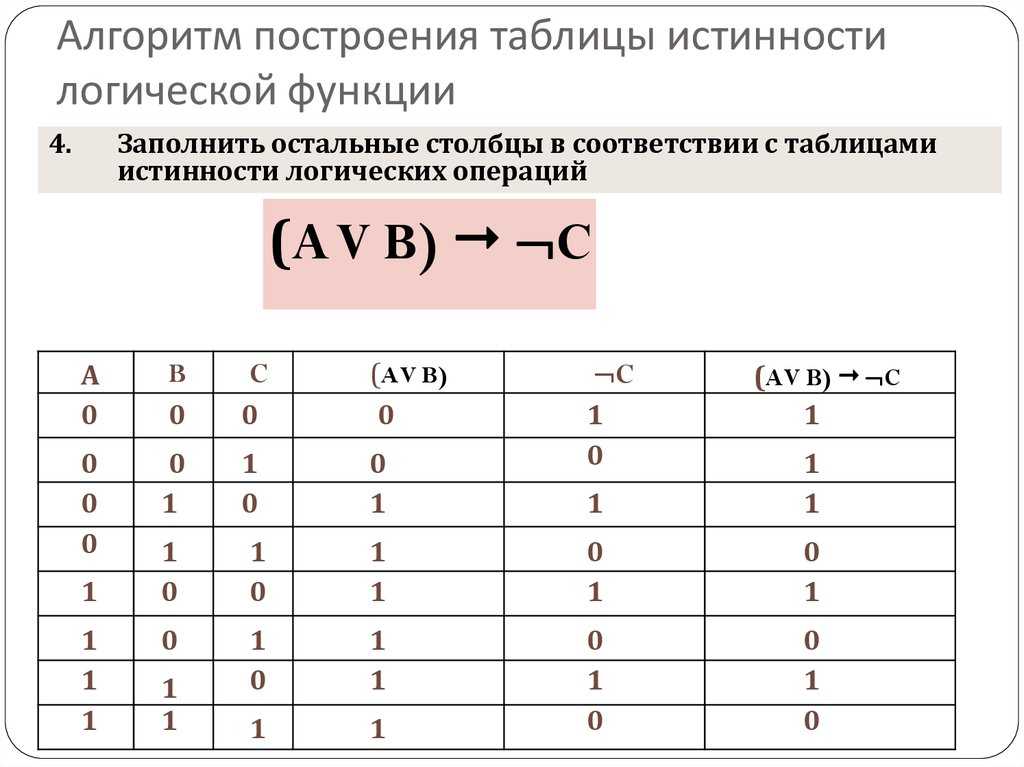
6.
7.
Сv(BΛ ̚ А)
СΛ ( ̚ Вv ̚ А)
̚ СΛ( ̚ Вv А)
̚ АΛ(Bv ̚ С)
̚ ВΛ(Сv ̚ А)
̚ Вv(СΛ ̚ А)
̚ Аv(BΛ ̚ С)
English Русский Правила
Таблицы истинности, логические выражения и схемы
спросил
Изменено 5 лет, 5 месяцев назад
Просмотрено 514 раз
Я создал свою таблицу истинности и вывел из нее логическое выражение (f = B’A’ + CA’ + DC’ + DB + D’CB’), которое затем попытался преобразовать в схему с помощью Quartus.
Я новичок в цифровой логике, и мне нужна помощь опытного человека, который может сказать мне, правильно ли выглядит то, что я пытался сделать.
Я не могу скомпилировать схему, так как у меня не установлена »поддержка устройств». Если бы кто-нибудь мог указать мне в правильном направлении, как это получить, это было бы очень признательно.
Это схема, которую я создал на основе логического выражения.
Это моя таблица истинности. Схема соответствует ф столбцу
- логическое выражение
- схема
- цифровая логика
- таблица истинности
1
Все, что находится слева от ваших ворот И , выглядит математически правильно (хотя и не очень эффективно). Вы можете значительно сократить количество используемых вентилей , а НЕ .
Вместо разделения сигналов до вентили НЕ и каждая отдельная ветвь имеет свои собственные НЕ вентилей, вы можете разделить сигналы после вентиля НЕ , тем самым уменьшив общее количество используемых вентилей НЕ .
В любом случае, основная причина того, что ваша схема недействительна, заключается в том, что она находится в самой правой части, здесь:
Вы закорачиваете выходы двух вентилей, что недопустимо.
Один узел не может одновременно иметь два отдельных напряжения.
Что вам нужно сделать, чтобы решить эту проблему, так это взять каждый отдельный вывод ваших 5 И вентилей и вывести их все на отдельный вход 5-входового вентиля ИЛИ .
Что-то вроде этого:
Если этот программный пакет, который вы используете, не поддерживает пять входов на вентиль, вы можете разделить его следующим образом:
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
9Архитектура процессора 0000 — Как определить, есть ли ошибка в таблице истинности?спросил
Изменено 2 года, 7 месяцев назад
Просмотрено 523 раза
На моем уроке цифрового дизайна и компьютерной архитектуры.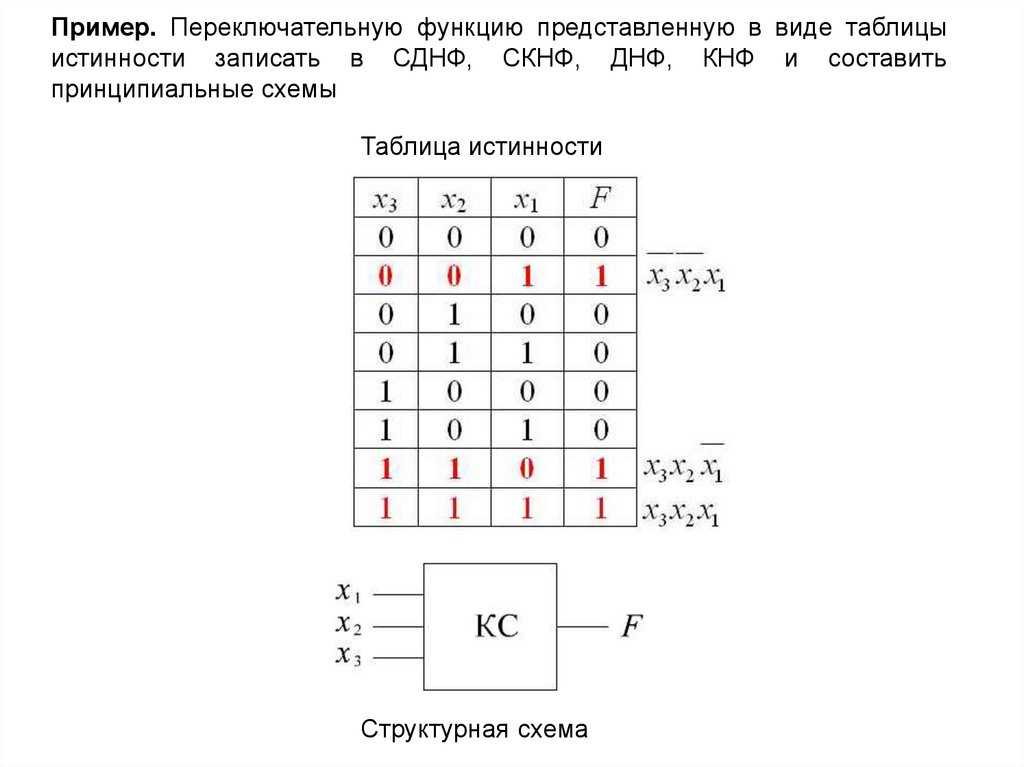
Наш учитель дал таблицу истинности, для которой мы должны были построить K-карту и минимизировать ее, чтобы найти логическое выражение
Но некоторые студенты быстро определили, что в таблице истинности есть ошибки, и начали указывать на ошибку. Как они это сделали? Есть ли способ выявить ошибки в таблице истинности? Что я упустил?
- архитектура процессора
- логическая логика
- логическое выражение
- таблица истинности
- логическая алгебра
4
В этой таблице истинности имеется четыре входа.
Это означает, что у вас будут все комбинации настроек для входов (a, b, c и d). Однако в этой таблице есть две записи для (0, 0, 0, 0) и нет записи для (0, 0, 0, 1)
Поскольку таблица не охватывает все входные данные, в таблице есть ошибка потому что в нем не указано, каким должен быть Y для (0, 0, 0, 1). Кроме того, есть два ответа для (0, 0, 0, 0), ответ (0) и ответ (1).