Резюме
- 1 Варианты
- 2 Графическое представление
- 3 Производная обратной функции
- 4 Примитивы обратной функции
- 5 Абстрактная обратная функция
- 6 См. Также
Вариации
Эта функция строго убывает на интервале ] -∞, 0 [ из реального строго отрицательна и строго убывает на интервале ] 0, + ∞ [ положительных вещественных, с 0 , как «запрещенной» значение (полюс). Но это не является строго убывающим на ℝ *, потому что, если a <0 < b , мы сохраняем неравенство 1 / a <0 <1 / b .
Обратная функция не компенсирует друг друга и не допускает максимум или минимум на ℝ *, даже на ] –∞, 0 [ или на ] 0, + ∞ [ .
Он имеет предел 0 в + ∞ и в –∞ . Таким образом, эта функция позволяет моделировать определенное количество моделей поведения, которые уменьшаются, но представляют « нижний предел » (функции не стремятся к –∞ ), например, гравитация и электростатическая сила, которые находятся в 1 /
В 0 его предел слева равен –∞, а справа + ∞ .
Графическое представление
Графическое представление обратной функции является гипербола .
Уравнение гипербола допускает две асимптоты : горизонтальную (ось x, с уравнением y = 0) и вертикальную (ось y, с уравнением x = 0). Поскольку эти две асимптоты (в ортонормированной системе координат ) перпендикулярны , гипербола называется равносторонней (ее эксцентриситет стоит ). yзнак равно1Икс{\ displaystyle y = {\ frac {1} {x}}}2{\ displaystyle {\ sqrt {2}}}
С другой стороны, мы замечаем, что центром симметрии этой гиперболы является точка (0, 0), которая транслирует тот факт, что обратная функция является нечетной функцией .
Наконец, мы замечаем, что эта гипербола (H) имеет ось симметрии : линию уравнения y = x . Действительно, точка ( x , y ) принадлежит (H) тогда и только тогда, когда точка ( y , x ) принадлежит (H) ( y = 1 / x эквивалентно x = 1 / y ).
{- 1}.}
Следовательно, обратное позволяет распространить на отрицательные целые показатели степени понятие мощности числа (или элемента группы), установив для любого положительного целого числа n : x –n = ( x n ) −1 .
Смотрите также
Элементарная математика | |
|---|---|
| Области математики | Классическая алгебра · Элементарная арифметика · Анализ · Реальный анализ · Цифровые наборы · Классическая геометрия · Логика · Вероятность · Статистика · Символы |
| Классическая алгебра | Добавление · Умножение · Отдел · Порядок операций · Добавление таблицы · Таблица умножения · Ассоциативность · Перестановочность · Дистрибутивность · транзитивность · пропорциональность · Процент · Правило трех · Доля · Первая степень уравнение · Второе уравнение степени · Система линейных уравнений |
| Классическая геометрия | Декартовы координаты · геометрия треугольника · Масштабирование · четырехугольник · Все уточняет · плоские вращения · Сходство · теорема Пифагора · Фалес теорема · теорема Фалеса (окружности) · окружности теорема · теорема Аль-Каши · Перевод |
| Арифметика | Многократное · Делитель · евклидово деление · Prime число · Согласованность на целых · НОД чисел · Наименьшее общее кратное · Критерий делимости · Доказательство девятью |
| Люксы и функции | Ссылка функция · Функция рафинирует · функция второй степени · Функция питание · Функция тригонометрических · Функции логарифм · Функция Экспоненциального · После арифметической · После геометрического · Концевой · обходного · Операция пределы · обычных срочного · производные транзакции · Список функций цифровой · элементарной функции |
| Логика | Аксиома · Демонстрация · Контрпример · Математическая сложность |
| Статистика и вероятности | Критерии положения · Критерии рассеяния · Двумерный статистический ряд · Дерево вероятностей · Элементарные случайные величины |
Полиномы | |||||
|---|---|---|---|---|---|
| Градусы |
| ||||
| Количество терминов |
| ||||
| Алгоритмы |
| ||||
<img src=»https://fr.
wikipedia.org/wiki/Special:CentralAutoLogin/start?type=1×1″ alt=»» title=»»>
Сложная и обратная функция | Образовательный портал. Решение задач по физике, математике, химии. Справочник физико-химических величин. Онлайн-учебники.
Сложная функция Обратная функция Взаимно обратные функции
Понятие сложной функции, или функции от функции, определяется следующим образом. Пусть $u = \phi(x)$ — некоторая функция от $x$; рассмотрим другую функцию $y = f(u)$ такую, чтобы ее область определения совпадала или хотя бы имела общую часть с областью значений функции $u = \phi(x)$. Тогда можно рассматривать $y = f(u) = f(\phi(x))$ как функцию от $x$: задание $x$ определяет $u = \phi(x)$, а значение $u$, если оно попадет в область определения функции $y = f(u)$, определит $y$. Таким образом, в конечном счете заданием $x$ определяется значение $y$, т.
т. е. представить ее как сложную функцию.
Обратная функция
рис.2
Рассмотрим функцию $y = f(x)$, областью определения которой служит, например, сегмент $[a, b]$ (рис.2), а областью изменения — сегмент $[c, d]$. Функция $y = f(x)$ ставит каждой точке сегмента $[a, b]$ в соответствие некоторую точку сегмента $[c, d]$. Для изображенной на рис. функции (благодаря тому, что она монотонна) можно установить и обратное соответствие: каждому значению $y_{0}$ из сегмента $[c, d]$ соответствует единственное значение $x_{0}$ из сегмента $[a, b]$ такое, что $y_{0} = f(x_{0})$. Тем самым $x$ можно рассматривать как функцию от $y$ с областью определения $[c, d]$ и областью изменения $[a, b]$. Функцию $x = g(y)$ назовем обратной по отношению к функции $y=f(x)$ (можно эти две функции назвать взаимно обратными).
При схематическом изображении взаимно обратные функции $f$ и $g$ представятся стрелками, как показано на рис. 3. При этом, однако, существенно, чтобы данному $y$ могло отвечать лишь одно значение $x$ такое, что $y = f(x)$, тогда мы и пишем: $x = g(y)$.
Записи $y = f(x)$ и $x = g(y)$ имеют здесь равнозначный смысл: $x = g(y)$ в том и только в том случае, если $y = f(x)$.
рис.3
Поэтому пары чисел $(x, y)$, определяемые любым из двух соотношений $y = f(x)$ и $x = g(y)$, будут одними и теми же. Это означает, что графики функций $y = f(x)$ и $x = g(y)$ совпадают. Первая из этих функций имеет своим аргументом переменную $x$, изменяющуюся на сегменте $[a,b]$, вторая — переменную $y$ с областью изменения аргумента $[c, d]$. Следует заметить, что во втором случае мы значения аргумента изображаем на оси ординат, а значения функции — на оси абсцисс. Такое изображение является непривычным и потому менее удобным. Представим себе, что произойдет, если теперь и для обратной функции $x = g(y)$ мы станем значения аргумента обозначать через $x$ и изображать на оси $Ox$, а значения функции будем обозначать через $y$ и изображать на оси ординат (напомним, что мы условились обозначать для разных функций разными буквами законы соответствия, символизируемые здесь буквами $f$ и $g$; зависимые же и независимые переменные для разных функций допустимо обозначать одинаково).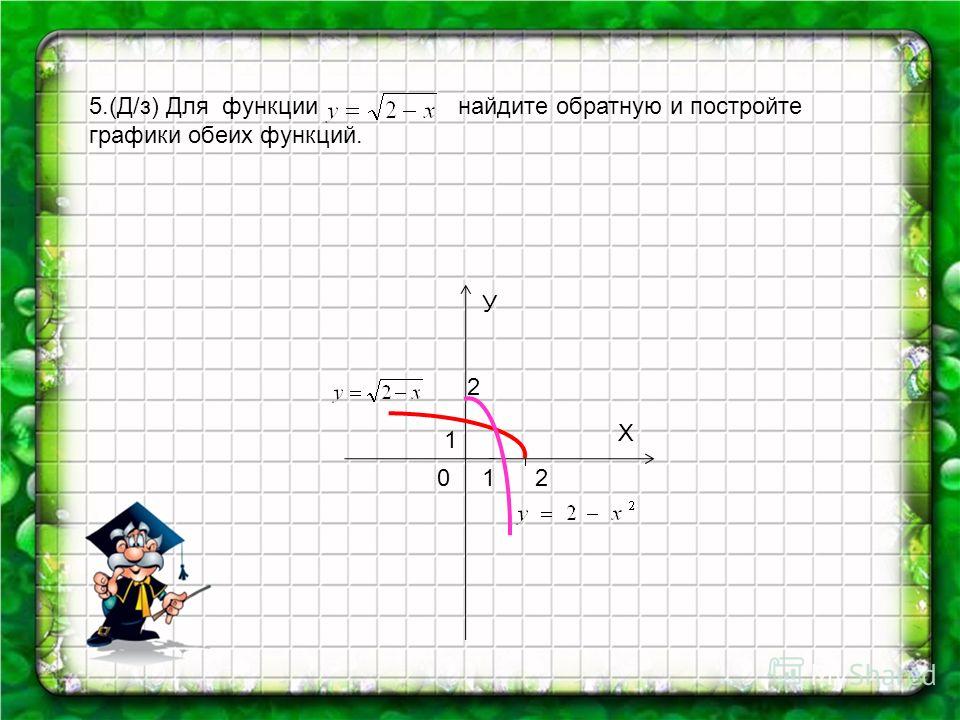
рис.4
Теперь график функции $y = g(x)$ будет получаться из графика $y = f(x)$ (или $x = g(y)$) с помощью преобразования зеркальной симметрии относительно биссектрисы первого — третьего координатных углов (рис. 4). В самом деле, пусть точка $(x_{0}, y_{0})$ лежит на графике данной функции; тогда точка $(y_{0}, x_{0})$ с переставленными координатами должна лежать на графике обратной функции. Но такие две точки расположены симметрично относительно указанной биссектрисы, а отсюда и следует наше утверждение: графики двух взаимно обратных функций расположены симметрично относительно биссектрисы I — III координатных углов.
Пример. Найти функцию, обратную по отношению к функции $y = 4 \sqrt[3]{x} – 1$.
Решение. Из равенства, определяющего данную функцию, выразим $x$ через $y$:
$4 \sqrt[3]{x} = y+1, \sqrt[3]{x} = \frac{y+1}{4}, x = \frac{(y+1)^{3}}{64}$.
{3}}{64}$
обратной по отношению к данной функции.
Внесем некоторые уточнения в понятие обратной функции. Мы начали рассматривать вопрос об обратной функции на примере функции, заданной графиком на рис. 2. Эта функция монотонна всюду в области определения. Именно этим обусловлен тот факт, что каждой точке $y_{0}$ из сегмента $[c, d]$ функция $x = g(y)$ ставит в соответствие только одну точку $x_{0}$ из сегмента $[a, b]$. Но для функции, не являющейся монотонной, это может не выполняться. В самом деле, на рис. 5 на сегменте $[a, b]$ показан график немонотонной функции $y = f(x)$. По этой причине имеются значения $y$, которым соответствует не единственная точка сегмента $[a, b]$; так, точке $y_{0}$ отвечают три точки $x_{0}, x_{1}, x_{2}$ такие, что $y_{0} = f(x_{0}), y_{0} = f(x_{1}), y_{0} = f(x_{2})$. В силу этого функция $y = f(x)$, рассматриваемая на сегменте $[a, b]$, не имеет обратной функции, если, конечно, не обобщать понятие функции, вводя «многозначные функции».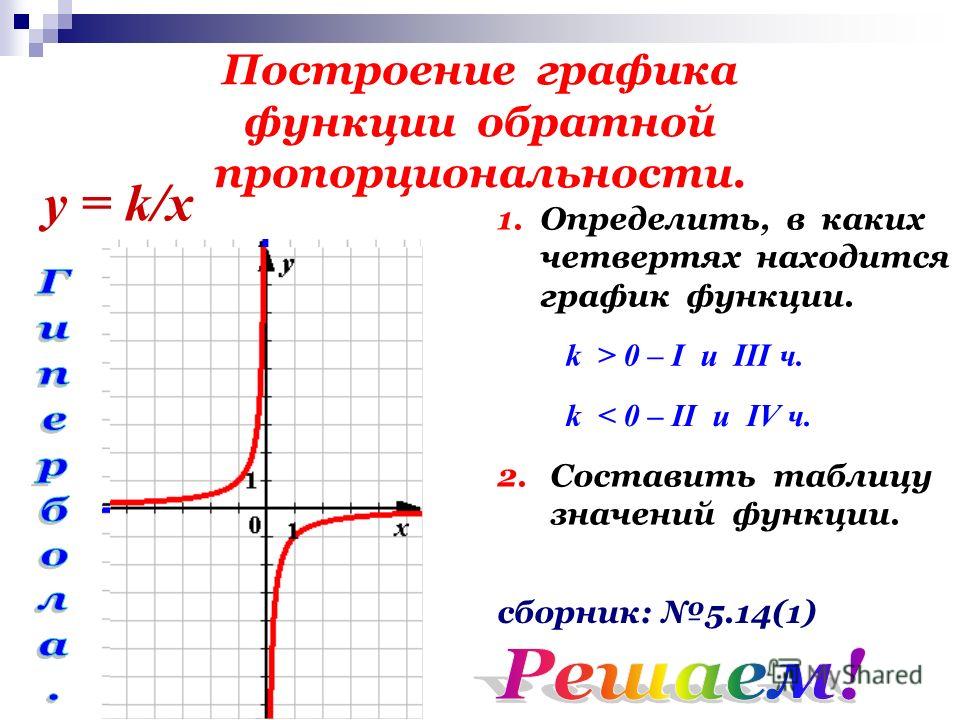
Если наряду с функцией $f(x)$, определенной на сегменте $[a, b]$, рассматривать функцию, определенную только на интервале монотонности функции $f(x)$ (например, $[a, c], [c, d]$ или $[d, b]$) и совпадающую с $f(x)$ на этом интервале, то у этой новой функции уже будет существовать обратная функция.
рис.5
Математическая сцена — Функции 2 — Урок 6
Математическая сцена — Функции 2 — Урок 6 — Обратные функции2009 Расмус Эф и Джанн Сак |
Урок 6
Обратный функции
г.
Мы
уже видели некоторые функции, которые являются обратными друг другу.
функции f(x) = x 2 и g(x) = √x
обратны друг другу, если мы ограничим значения x до
неотрицательные числа. Эти функции компенсируют друг друга в том смысле, что
если мы применим сначала одну функцию, а затем другую к числу, то это как если бы
ничего не произошло, номер тот же, что и был изначально. смотреть на
следующий пример:
f(x) = x 2 и g(x) =
f(2) = 2 2 = 4 и g(4) = √4 = 2
f(g(a)) = = a
г(ф(а)) = = а
Это не так Независимо от того, какую из двух функций f(x) или g(x) применить первой, результат то же самое. Диапазон одной функции становится областью действия другой.
Функция имеет обратную, только если она является взаимно-однозначной и на. В этом случае мы
ограничить наши значения x неотрицательными числами так, чтобы функция f(x) = x 2 удовлетворяет этому
условие.
Другими словами, функция имеет обратную, если она возрастает или убывает на
это домен. Функция g(x) = √x является возрастающей и может
взять неотрицательные числа, что снова означает, что f(x) = x 2 ограничено неотрицательными числами.
Уравнение обратной функции можно найти алгебраически, решив уравнение уравнение функции для x. Посмотрите на следующий пример:
г.
Пример 1
Найдите инверсию следующих функций:
а) f(x) = 2x + 4
у = 2х + 4 поставить y вместо f(x)
2x = 4 года
x = 2 + y Мы разделили на 2
Это уравнение, где x является функцией y. Имя переменной не материи, поэтому мы можем поменять местами x и y. Если мы вызовем эту функцию g, мы получим уравнение обратной функции f(x).
г.г (х) = у = х 2 .
Мы можем проверить наш результат, введя число.
f(1) = 21 + 4 = 6 и g(6) = 6 2 = 3 2 = 1
Если мы используем общее значение a, получаем
f(a) = 2a + 4 и g(2a+4) = (2a+4) 2 = а + 2 2 = а
б) f(x) = sin 2x, D f = [/4,/4 , f(x) возрастает на этом интервале и
поэтому имеет обратную функцию.
у = грех 2x
2x = грех 1 у
х = грех 1 у
Обратная функция: g(x) = sin 1 x.
В большинстве книг обратная функция записывается с использованием индекса 1 так что f(x) имеет обратную функцию ж 1 (х). Это не означает 1/f, это просто обозначение обратной функции.
В приведенном выше примере ф 1 (х) = грех 1 х.
Проверять.
е (/ 12) = грех 2/12 =
f 1 () = sin 1 = /6 = /12
г.в) f(x) = e 2x
у = е 2x
ln y = ln e 2x = 2x
х = пер у
Обратное поэтому функция f(x) равна f 1 (x) = пер х.
г) f(x) = x 2 1, Д ф = Р +
г.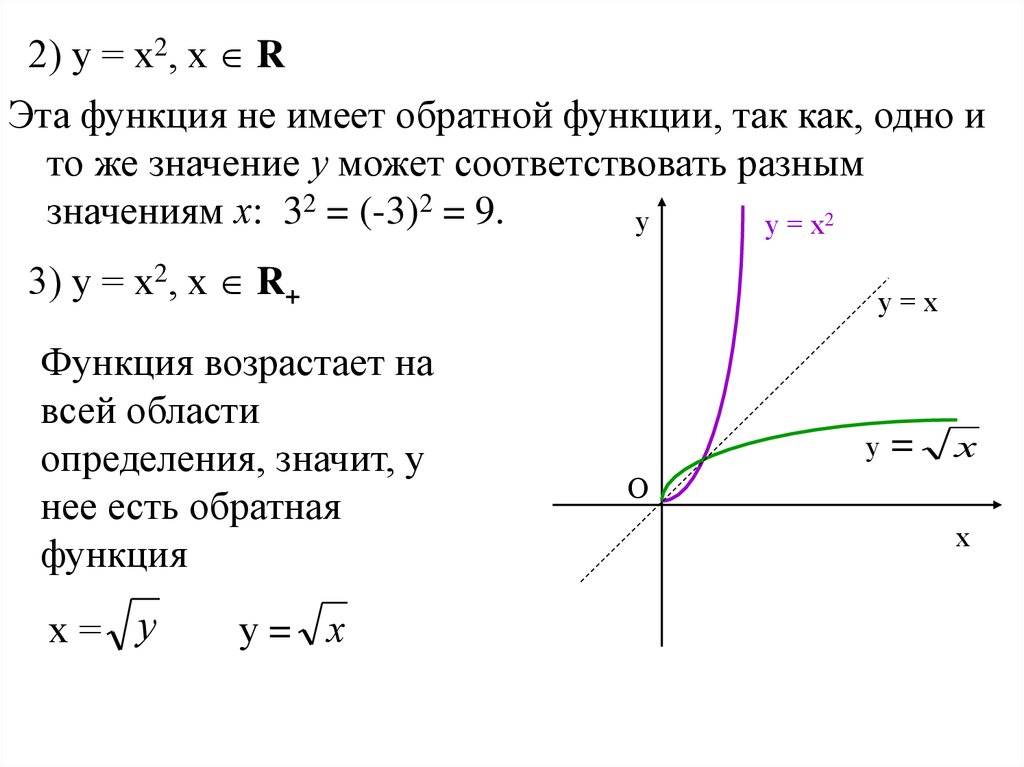
= х 2 1
х 2 = у + 1
| Обратная функция: |
д)
Выбираем D f = R+ и куб обеих частей уравнения Тогда извлеките квадратный корень |
Обратная функция равна
.
Если функция f(x) либо всегда возрастает, либо всегда убывает, то имеет обратную функцию f 1 (x). Диапазон f(x) становится доменом f 1 (х). г. Уравнение обратного находим по формуле решение уравнения y = f(x) относительно x. |
Пример 2
Как нам нужно ограничить область определения функции f(x) = sin x, чтобы она
имеет обратную функцию? Мы знаем, что непрерывная функция, которая всегда
увеличение (или уменьшение) имеет обратное.
Итак, мы смотрим на производная функции f(x) = sin x , f(x) = потому что х.
г.Используя единичный круг, мы можем видеть, что cos x положителен из /2 к /2 и отрицательный на остальной части круга.
Посмотрите на график f (х) = грех х.
Мы видим, что график возрастает на /2 < х < /2
так что f(x) = sin x имеет обратное значение, если мы ограничиваем область определения этим интервалом.
Мы могли бы выбрать другой интервал, например /2 < х < 3/2
где функция убывает, но обычно интервал /2
< х < /2
выбран.
Пример 3
Найдите интервал, на котором функция f(x) = x 2 4x + 3 возрастает, ограничьте область определения этим интервалом, а затем найдите формулу для обратная функция. Наконец, нарисуйте график для f(x) и f 1 (x) в той же системе координат.
Начнем с поиска вершины
параболы, дифференцируя и находя, где производная равна нулю.
(
Касательная к f(x) в вершине горизонтальна, поэтому производная равна
ноль)
f(x) = x 2 4x + 3
f(x) = 2x 4 = 0
2х = 4
х = 2
Вершина находится там, где x = 2, после чего функция возрастает. Поэтому мы выберите домен
| Д ф = | . |
Чтобы найти уравнение обратное, нужно решить уравнение у = х 2 4x + 3 вместо x.
у = х 2 4х + 3 у 3 = х 2 4х у 3 + 4 знак равно х 2 4х + 4 у + 1 = (х 2) 2 |
Мы выберите +, так как x находится на интервале
Вставить x вместо y
|
Теперь рисуем
график, предварительно составив таблицу значений.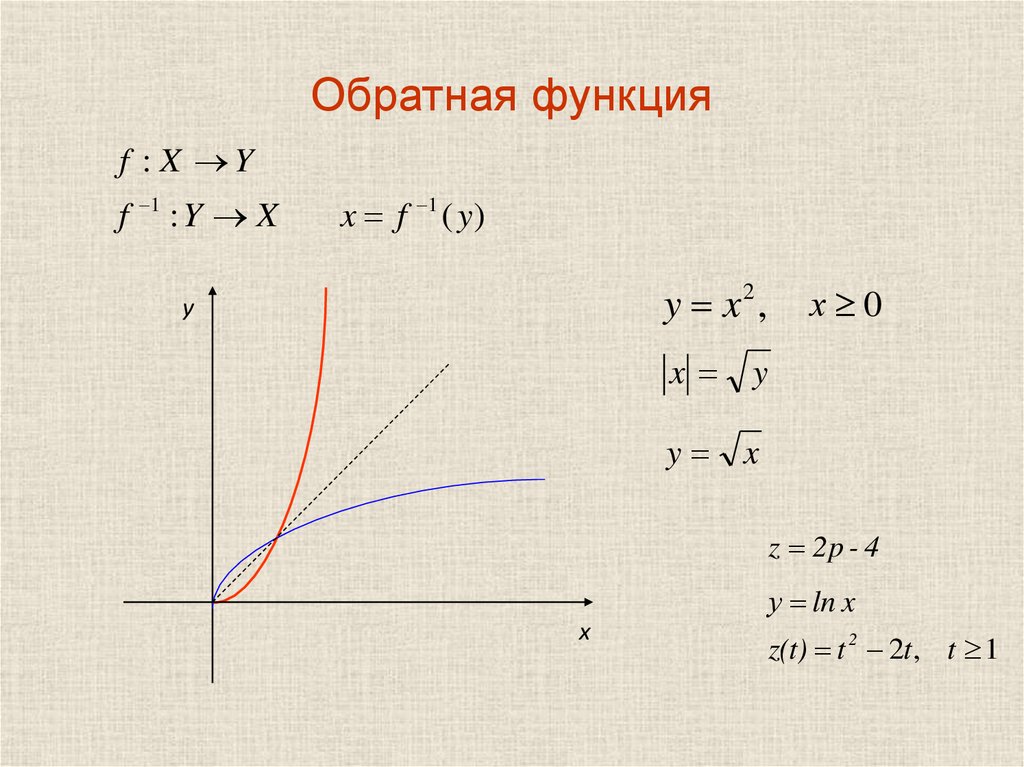
Расчет f(2) говорит нам что f(x) = y принимает значения от 1 и выше (функция возрастает). Поэтому нам нужно начать с нахождения f 1 (1).
Двое графики показаны ниже.
Заметим, что два графика являются зеркальным отображением друг друга в линии y = x. (
линия, которая делит пополам угол между осями x и y). Мы также можем видеть это из
таблица значений. Каждая точка на f(x) является зеркальным отображением точки на
г.
ф 1 (х). Например, (2, 1) находится на f(x) и (1, 2)
находится на ф 1 (х). (3, 0) находится на f(x) и (0, 3) на f 1 (x).
В общем случае, если (a, b) находится на одном графике, то (b, a)
находится на графике обратной функции.
График функции и функция, обратная ей, всегда зеркальны. изображения друг друга в линии y = x. |
Пример 4
Посмотрите на функцию f(x) = e x и ее обратную
функция г(х) =
х.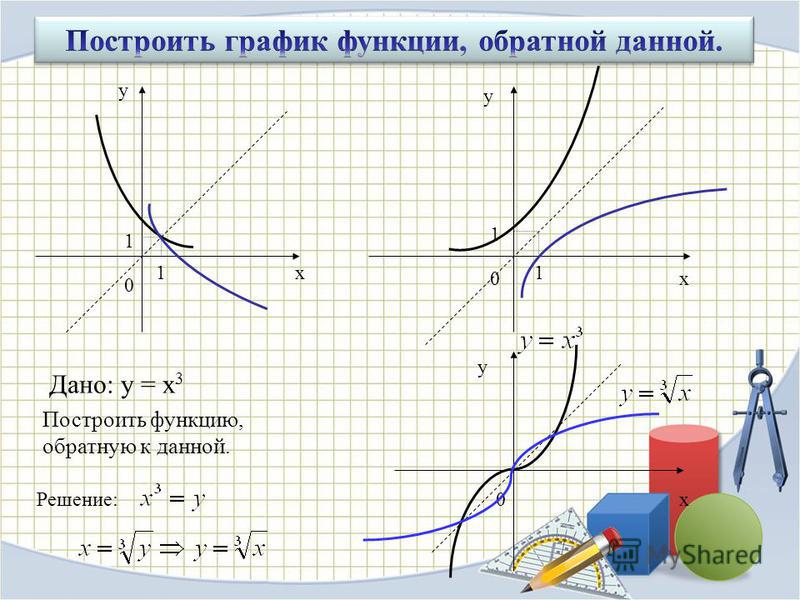
Функция f(x) = e x может принимать любое значение x, поэтому его область определения
все действительные числа Р.
Ценности, которые f(x) = e x всегда положительны, поэтому диапазон
интервал .
Функция g(x) = ln x может принимать только положительные значения x , поэтому
это домен .
г.
С другой стороны, функция g(x) = ln x дает все значения действительных чисел, поэтому
диапазон составляет
Диапазон функции то же, что и домен его обратного, а домен функции — это диапазон его обратного.
Графики двух функций показаны ниже. Обратите внимание, что они являются зеркальным отражением друг друга в линии y = x .
Пример 5
Найдите интервал, на котором функция растет. Выбрав этот интервал в качестве области определения, найдите уравнение его обратной функции затем начертите оба графика в одной системе координат.
г.Дифференцируйте, используя цепное правило, чтобы найти, где функция возрастает, а где убывает,
Знаменатель всегда
положительный, так что это x в числителе, который говорит нам, где функция
увеличивается или уменьшается.
Функция возрастает для неотрицательных значений x, поэтому мы выбираем область
| Д ф = |
Далее мы решаем x, чтобы найти обратный.
у = 1 + (х 2 + 1)
у 1 = (х 2 + 1)
(у 1) 2 = х 2 + 1
х 2 = (у 1) 2 1
= у 2 2 года + 1 1
= у 2 2у
(выбирая положительное значение для x ) |
Обратная функция |
Графики f(x), f 1 (x) и линия у = х выглядит так.
г.Пример 6
Найдите обратную функцию и нарисуй графики в одной системе координат.
График имеет вертикальную
асимптота x = 1 и горизонтальной асимптоты y = 2.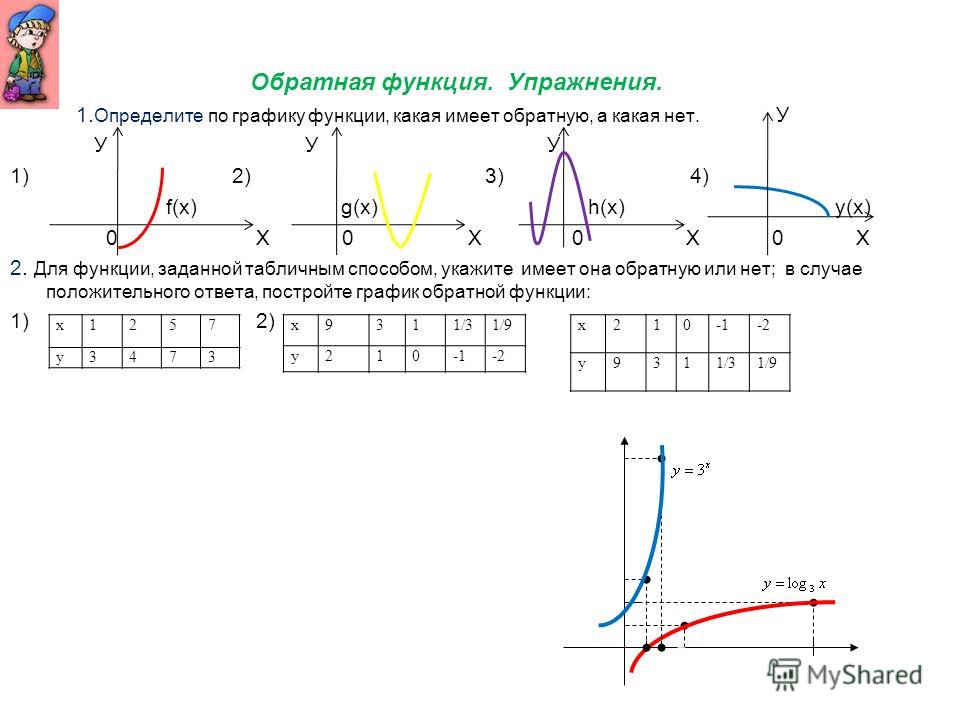
Область не содержит x = 1.
Продифференцируем, чтобы найти наклон графика.
Знаменатель всегда положительный, а числитель всегда отрицательный, что означает что наклон графика всегда отрицателен. Таким образом, функция убывает на все это домен.
г.Находим обратную функцию, решая x.
Обратное | Сначала избавься от затем дроби перемещают все члены со знаком x влево сторону уравнения. Теперь x можно разложить на множители. Мы видим, что у не может быть 2.
|
Эта функция имеет вертикальную асимптота в x = 2 и горизонтальная асимптота в y = 1. Это полная противоположность f(x), которая имеет вертикальную асимптоту по x = 1 и горизонтальную асимптоту по y = 2.
г.Посмотрите на два графика.
графики и их асимптоты являются зеркальным отображением друг друга в прямой y = x.
Практикуйте эти методы, а затем
пройти тест 6 в функциях 2.