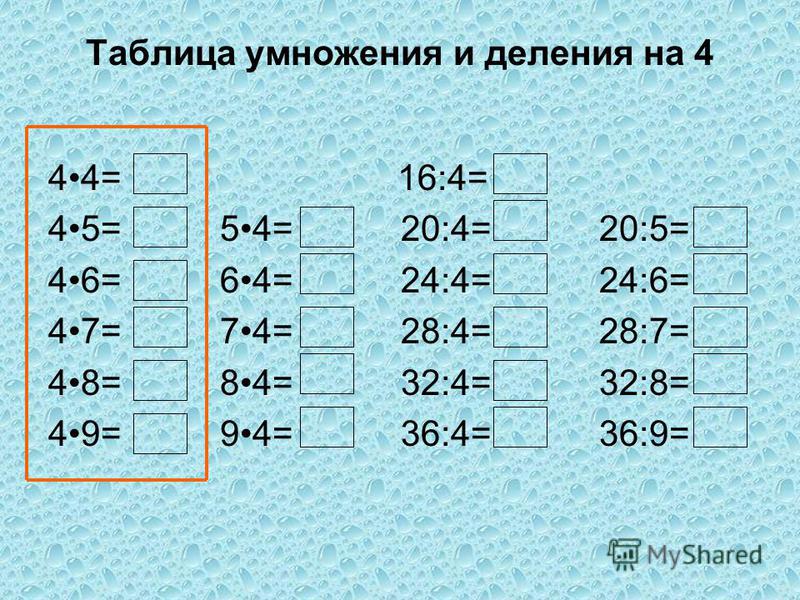
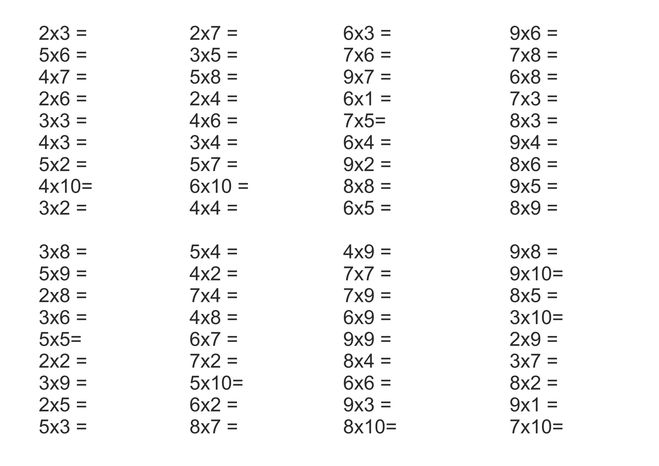Примеры на умножение. Математика 4 класс.
Примеры на умножение. Математика 4 класс. Задачи по математике 4 класс
MAT-ZADACHI.RU
Математика 4 класс
- Математические диктанты
- Тесты
- Нестандартные задачи
- Логические задачи
- Задачи с ответами
- Примеры
Контрольные работы
- Числа, которые больше 1000. Нумерация
- Итоговая контрольная работа за 1 четверть
- 1 четверть
- 2 четверть
- Итоговая контрольная работа 1
- 3 четверть
- Контрольная работа 1
- 4 четверть
- Деление на двузначное число
- Итоговые контрольные работы за курс начальной школы
- Контрольная работа 1
Математика 4 класс ->> Примеры
Чтобы увидеть решение, наведите на пример курсор мыши.
| 60 * 91 = 5460 | 108 * 63 = 6804 | 31 * 583 = 18073 | 590 * 30 = 17700 | 300 * 47 = 14100 |
| 110 * 49 = 5390 | 92 * 692 = 63664 | 250 * 5 = 1250 | 700 * 3 =2100 | 73 * 80 = 5840 |
| 988 * 99 = 97812 | 930 * 6 = 5580 | 81 * 415 = 33615 | 260 * 40 = 10400 | 690 * 30 = 20700 |
| 4800 * 80 = 384000 | 93 * 40 = 3720 | 0 * 937 = 0 | 150 * 80 = 12000 | 50 * 19 = 950 |
| 98 * 50 = 4900 | 2730 * 7 = 19110 | 14 * 616 = 8624 | 890 * 30 = 26700 | 894 * 70 = 62580 |
| 40 * 277 = 11080 | 2320 * 8 = 18560 | 8960 * 8 = 71680 | 82 * 20 = 1640 | 32 * 50 = 1600 |
| 89 * 80 = 7120 | 87 * 550 = 47850 | 350 * 30 = 10500 | 264 * 29 = 7656 | 4200 * 20 = 84000 |
| 350 * 6 = 2100 | 77 * 60 = 4620 | 130 * 2 = 260 | 710 * 2 = 1420 | 640 * 70 = 44800 |
| 780 * 8 = 6240 | 4300 * 5 = 21500 | 43 * 371 = 15953 | 360 * 5 = 1800 | 46 * 213 = 9798 |
| 950 * 2 = 1900 | 3 * 430 = 1290 | 9600 * 96 = 921600 | 44 * 44 = 1936 | 10 * 12 = 120 |
| 630 * 50 = 31500 | 282 * 73 = 20586 | 660 * 7 = 4620 | 330 * 7 = 2310 | 8500 * 80 = 680000 |
| 40 * 729 = 29160 | 35 * 56 = 1960 | 65 * 369 = 23985 | 32 * 40 = 1280 | 10 * 555 = 5550 |
| 22 * 90 = 1980 | 790 * 50 = 39500 | 40 * 60 = 2400 | 480 * 3 = 1440 | 71 * 30 = 2130 |
| 13 * 20 = 260 | 5100 * 80 = 408000 | 2800 * 50 = 140000 | 8300 * 90 = 747000 | 800 * 8 = 6400 |
| 740 * 9 = 6660 | 15 * 60 = 900 | 390 * 40 = 15600 | 570 * 60 = 34200 | 400 * 80 = 32000 |
| 80 * 14 = 1120 | 480 * 3 = 1440 | 260 * 60 = 15600 | 40 * 210 = 8400 | 46 * 50 = 2300 |
| 790 * 40 = 31600 | 910 * 4 = 3640 | 2200 * 70 = 154000 | 1700 * 50 = 85000 | 40 * 80 = 3200 |
| 42 * 80 = 3360 | 5000 * 30 = 150000 | 47 * 70 = 3290 | 8900 * 70 = 623000 | 580 * 80 = 46400 |
| 6300 * 40 = 252000 | 34 * 90 = 3060 | 9600 * 90 = 864000 | 4000 * 30 = 120000 | 90 * 832 = 74880 |
| 380 * 4 = 1520 | 310 * 8 = 2480 | 56 * 60 = 3360 | 337 * 0 = 0 | 87 * 810 = 70470 |
| 853 * 28 = 23884 | 140 * 3 = 420 | 590 * 60 = 35400 | 37 * 587 = 21719 | 1400 * 60 = 84000 |
| 17 * 184 = 3128 | 300 * 6 = 1800 | 290 * 2 = 580 | 929 * 41 = 38089 | 20 * 90 = 1800 |
| 980 * 60 = 58800 | 100 * 320 = 32000 | 100 * 64 = 6400 | 680 * 20 = 13600 | 42 * 50 = 2100 |
| 25 * 60 = 1500 | 8300 * 60 = 498000 | 550 * 7 = 3850 | 749 * 67 = 50183 | 9 * 20 = 11805 |
| 320 * 5 = 1600 | 140 * 40 = 5600 | 783 * 50 = 39150 | 50 * 500 = 25000 | 859 * 19 = 16321 |
| О * 870 = 0 | 290 * 2 = 580 | 700 * 50 = 35000 | 14 * 576 = 8064 | 68 * 30 = 2040 |
| 428 * 73 = 31244 | 120 * 6 = 720 | 640 * 70 = 44800 | 352 * 40 = 14080 | 11 * 531 = 5841 |
| 300 х 30 = 30030 | 802 * 7 = 5614 | 61 * 90 = 5490 | 750 * 9 = 6750 | 20 * 90 = 1800 |
| 980 * 80 = 78400 | 97 * 20 = 1940 | 500 * 8 = 4000 | 87 * 80 = 6960 | 60 * 67 = 4020 |
| 920 * 70 = 64400 | 7300 * 40 = 292000 | 86 * 70 = 6020 | 770 * 2 = 1540 | 500 * 70 = 35000 |
| ____________________ | ____________________ | ____________________ | ____________________ | ____________________ |
Простые задачи
- Простые задачи на движение
Составные задачи
- Задачи на встречное движение
- Задачи на движение в одном направлении
- Задачи на противоположное движение
- Задачи на нахождение неизвестного по двум разностям
- Задачи на нахождение числа по доле и доли по числу
- Задачи на нахождение площади
- Задачи на сложение и вычитание многозначных чисел
- Задачи на умножение и деление многозначных чисел
- Задачи на приведение к единице и пропорциональное деление
- Задачи на определение цены, количества, стоимости
Сайт vpr-klass.
 com — впр-класс.ком : гдз, решебник, гиа, егэ, решение задач, задания, варианты, подготовка к экзамену, тесты, презентации.
com — впр-класс.ком : гдз, решебник, гиа, егэ, решение задач, задания, варианты, подготовка к экзамену, тесты, презентации.Error in links file
Сайт vpr-klass.com — впр-класс.ком : гдз, решебник, гиа, егэ, решение задач, задания, варианты, подготовка к экзамену, тесты, презентации. У нас вы найдете много учебных материалов: решебники, ГДЗ, тестовые задания, видео уроки, генераторы задач, решения упражнений гиа и егэ.
| Расскажи друзьям vpr-klass или впр-класс Презентации Детские презентации Презентации по математике Презентации по астрономии Демо-варианты: Математика Русский язык Физика Обществознание Английский язык Информатика История Биология Химия Литература География Математика Русский язык |  com (впр-класс) com (впр-класс) Последние новости ГИА и ЕГЭ 2017. Другие школьные предметы. Сайт Vpr-klass.com — это учебный-образовательно-познавательный сайт для школьников! Приветствуем на уникальном сайте помощи всем ученикам 1-11 классов. На образовательном ресурсе полно полезной, учебной информации от способов решения заданий по математике до разных генераторов задач по алгебре и онлайн калькуляторов по геометрии, которые облегчат жизнь школьника. В частности, сделан больший уклон на решебники и ГДЗ, ведь правильная домашняя работа — это хорошие оценки и учеба в школе. | Интересно Много разных решений Тесты ГИА онлайн. Видео — ГИА 2013: геометрия Видео — ГИА 2012 Видео — Демо-вариант 2012. Решение Демо-варианта 2013 года (2014 года). Задача №1, Вычислить. Задача №2, Числа и прямая. Задача №3, Сравнение чисел. Задача №4, Уравнения. Задача №5, Графики и формулы. Задача №6, Прогрессии. Задача №7, Упростить выражение. Задача №8, Неравенства, системы неравенств. Задача №9, Задания по геометрии. Генератор вариантов ГИА 2014 Много разных решений. Онлайн тесты. Видео уроки ЕГЭ по математике. Генератор вариантов ЕГЭ 2014 Книги, справочники Решение демо варианта ЕГЭ по математике 2014 Задания B1, задача. Задания B2, диаграммы. Задания B5, уравнения. Задания B8, производная. Задания B10, вероятность. Видео уроки |
Copyright © 2017 vpr-klass.com | Если какой-либо из материалов нарушает ваши авторские права, просим немедленно связаться с Администрацией!!! Наш e-mail: [email protected] | Правообладателям |
sitemap. xml
xml
Тест по математике Умножение и деление (4 класс)
Последний раз тест пройден более 24 часов назад.
Для учителя
Материал подготовлен совместно с учителем высшей категории Харитоненко Натальей Владимировной.
Опыт работы учителем математики — более 33 лет.
Вопрос 1 из 10
Чему равен Х в уравнении: 240 : Х = 24?
1
10
100
Правильный ответ
Неправильный ответ
В вопросе ошибка?
Вопрос 2 из 10
Верно ли равенство: 75 х 3 = 235?
Да
Нет
Правильный ответ
Неправильный ответ
В вопросе ошибка?
Вопрос 3 из 10
Найдите правильный ответ: 250 х 6 =
1500
150
1200
Правильный ответ
Неправильный ответ
В вопросе ошибка?
Вопрос 4 из 10
В овощной магазин привезли 130 мешков картофеля по 80 кг в каждом.
 Сколько всего кг картофеля привезли в магазин?
Сколько всего кг картофеля привезли в магазин?14000
10400
9400
Правильный ответ
Неправильный ответ
В вопросе ошибка?
Вопрос 5 из 10
Найдите правильный ответ: 3425 : 5 =
715
605
685
Правильный ответ
Неправильный ответ
В вопросе ошибка?
Вопрос 6 из 10
Сколько кг в 68 ц?
680 кг
6800 кг
68000 кг
Правильный ответ
Неправильный ответ
В вопросе ошибка?
Вопрос 7 из 10
Найдите частное: 700 : 35 =
2
20
200
Правильный ответ
Неправильный ответ
В вопросе ошибка?
Вопрос 8 из 10
Сколько мм в 36 дм ?
36
360
3600
Правильный ответ
Неправильный ответ
В вопросе ошибка?
Вопрос 9 из 10
Чему равно произведение: 0 х 16?
0
16
160
Правильный ответ
Неправильный ответ
В вопросе ошибка?
Вопрос 10 из 10
Сравните выражение: 734 + 865 и 734 + 870
=
>
<
Правильный ответ
Неправильный ответ
В вопросе ошибка?
Доска почёта
Чтобы попасть сюда — пройдите тест.
Наталья Букарина
10/10
chashkova-tatyan чашкова
10/10
Константин Анисимов
10/10
Милана Петросян
10/10
Надежда Абрамова
10/10
Мубина Адхамова
8/10
Жмакина Ирина
10/10
Артём Мещеряков
8/10
Кристина Шаравьёва
10/10
Владислав Семьянинов
9/10
Тест «Умножение и деление» по математике рассчитан на учеников младшей школы. Он поможет закрепить знания по теме, выявить плохо усвоенный материал. Выполнение теста требует понимания самых простых математических действий, знания соответствующих таблиц и правил. Предлагаемые тесты разного уровня сложности, что позволяет объективно оценить знания ребенка. Задания можно проходить в онлайн режиме с любого доступного устройства.
Тест «Деление» (4 класс) с ответами позволяет самостоятельно или с помощью родителей повторить и систематизировать материал для успешного написания текущих и итоговых проверочных работ.
Рейтинг теста
4.1
Средняя оценка: 4.1
Всего получено оценок: 1187.
А какую оценку получите вы? Чтобы узнать — пройдите тест.
Умножение – Определение, Формула, Примеры
В математике умножение – это метод нахождения произведения двух или более чисел. Это основная арифметическая операция, которая довольно часто используется в реальной жизни. Умножение используется, когда нам нужно объединить группы одинакового размера. Давайте узнаем больше об умножении на этой странице.
| 1. | Что такое умножение? |
| 2. | Формула умножения |
| 3. | Как решать задачи на умножение? |
| 4. | Умножение с помощью числовой строки |
| 5. | Задачи на умножение слов |
| 6. | Часто задаваемые вопросы по умножению |
Что такое умножение?
Умножение — это операция, представляющая основную идею многократного сложения одного и того же числа. Числа, которые перемножаются, называются множителями, а результат, полученный после умножения двух или более чисел, известен как произведение этих чисел. Умножение используется для упрощения задачи многократного сложения одного и того же числа .
Числа, которые перемножаются, называются множителями, а результат, полученный после умножения двух или более чисел, известен как произведение этих чисел. Умножение используется для упрощения задачи многократного сложения одного и того же числа .
Пример: Если есть 6 коробок кексов и в каждой коробке 9 кексов, найдите общее количество кексов.
Решение: Мы можем решить этот вопрос сложением, но это займет больше времени, чтобы получить ответ. То есть 9+9+9+9+9+9=54 кекса. Другими словами, когда у нас есть большие числа для работы, полезно умножение.
Теперь давайте решим эту задачу с помощью умножения. Мы умножим количество коробок на количество кексов в каждой коробке. Если мы умножим 6 × 9, мы получим общее количество капкейков, а это 6 × 9 = 54 капкейка. Таким образом, мы видим, что получаем тот же результат за более короткий промежуток времени. Вот почему умножение также называют повторным сложением.
Символ умножения (×)
В математике используются разные символы. Символ умножения является одним из наиболее часто используемых математических символов. В примере, приведенном выше, мы узнали об умножении двух чисел 6 и 9. Если мы наблюдаем выражение умножения (6 × 9 = 54), то видим, что символ (× ) соединяет два числа и завершает данное выражение. Помимо символа креста (×), умножение также обозначается оператором точки срединной линии (⋅) и знаком звездочки ( *).
Символ умножения является одним из наиболее часто используемых математических символов. В примере, приведенном выше, мы узнали об умножении двух чисел 6 и 9. Если мы наблюдаем выражение умножения (6 × 9 = 54), то видим, что символ (× ) соединяет два числа и завершает данное выражение. Помимо символа креста (×), умножение также обозначается оператором точки срединной линии (⋅) и знаком звездочки ( *).
Формула умножения
Формула умножения выражается следующим образом: Множимое × Множитель = Произведение ; где:
- Множимое: первое число (множитель).
- Множитель: второе число (коэффициент).
- Продукт: Конечный результат после умножения множимого и множителя.
- Символ умножения: ‘×’ (соединяет все выражение)
Давайте поймем формулу умножения с помощью следующего выражения.
7(множимое) × 5 (множитель) = 35 (произведение)
Используя эту основную концепцию умножения, давайте научимся решать задачи на умножение.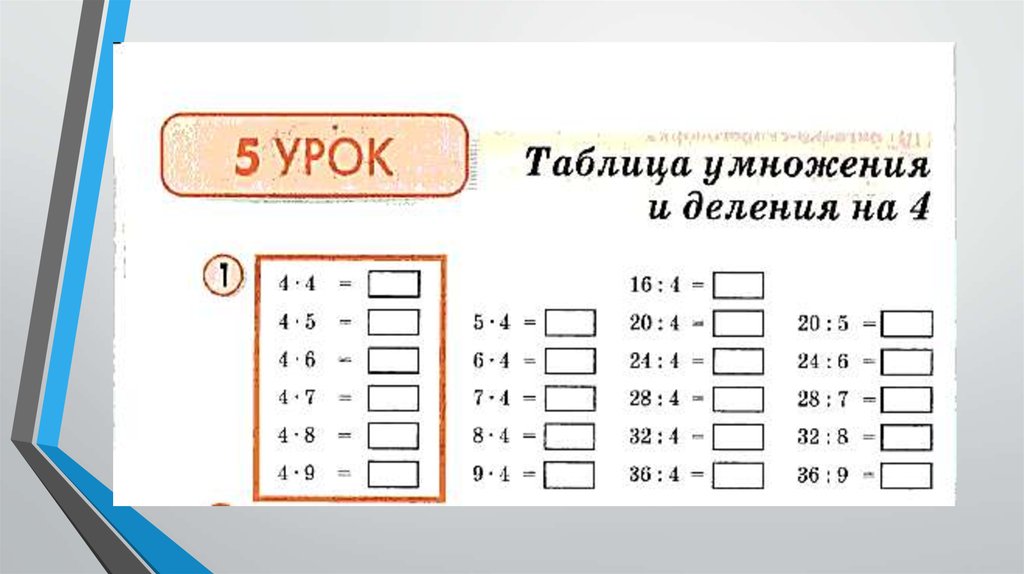
Как решать задачи на умножение?
При решении задач на умножение однозначные числа можно умножать простым способом с помощью таблиц умножения, но для больших чисел мы разбиваем числа на столбцы, используя соответствующие разрядные значения, такие как единицы, десятки, сотни, тысячи, и так далее. Есть два типа задач на умножение:
- Умножение без перегруппировки
- Умножение с перегруппировкой
Давайте разберем оба случая на примерах.
Умножение без перегруппировки
Умножение двух чисел без перегруппировки включает меньшие числа, когда нет необходимости выполнять перенос на следующее более высокое разрядное значение. Это базовый уровень, который может помочь учащемуся понять основы умножения, прежде чем перейти к более высокому уровню задач, включая перегруппировку. Давайте разберемся в этом с помощью примера, приведенного ниже.
Пример: умножьте 3014 на 2.
Решение:
- Шаг 1: Начните с разряда единиц.
 (2 × 4 = 8)
(2 × 4 = 8) - Шаг 2: Умножьте 2 на разряд десятков. (2 × 1 = 2)
- Шаг 3: Теперь умножьте 2 на цифру в сотнях. (2 × 0 = 0)
- Шаг 4: Теперь умножьте 2 на разряд тысяч. (2 × 3 = 6)
- Шаг 5: 3014 × 2 = 6028.
Чт Х Т О
3 0 1 4
× 2
6 0 2 8
Умножение с перегруппировкой
Умножение более двух чисел с перегруппировкой включает числа с двузначным произведением. В этом типе умножения нам нужно сделать перенос на следующее более высокое разрядное значение. Давайте разберемся в этом с помощью примера, приведенного ниже.
Пример: умножьте 2468 на 8
Решение: Давайте умножим 2468 × 8, используя приведенные ниже шаги, и попытаемся связать их с числом, приведенным после шагов.
- Шаг 1: Начните с разряда единиц, то есть 8 × 8 = 64 единицы, что означает 6 десятков 4 единицы.
 Теперь перенесите 6 десятков в столбец десятков.
Теперь перенесите 6 десятков в столбец десятков. - Шаг 2: Умножьте 8 на разряд десятков, то есть 8 × 6 = 48 десятков. Теперь мы добавим это к переносу. Это означает, что 48 + 6 (перенос из шага 1) = 54. Перенесите 5 в столбец сотен.
- Шаг 3: Умножьте 8 на цифру в разряде сотен, то есть 8 × 4 = 32 сотни. Теперь давайте добавим это к переносу с предыдущего шага. Это означает, что 32 + 5 (перенос из шага 2) = 37. Мы снова перенесем 3 в столбец тысяч.
- Шаг 4: Умножьте 8 на разряд тысяч, то есть 8 × 2 = 16 тысяч. Итак, давайте снова добавим это к переносу, то есть 16 + 3 (перенос с шага 3) = 19
- Шаг 5: Следовательно, произведение 2468 × 8 = 19744.
Умножение с использованием числовой строки
Умножение на числовую прямую означает применение операции умножения к заданному набору чисел через числовую прямую. Числовая линия — это визуальное представление чисел на прямой линии. Мы знаем, что умножение также известно как многократное сложение. Итак, чтобы выполнить умножение на числовой прямой, мы начинаем с нуля и двигаемся к правой стороне числовой строки заданное количество раз.
Мы знаем, что умножение также известно как многократное сложение. Итак, чтобы выполнить умножение на числовой прямой, мы начинаем с нуля и двигаемся к правой стороне числовой строки заданное количество раз.
Пример: Умножьте 3 × 5, используя числовую прямую.
Решение: Обратите внимание на следующую числовую линию, чтобы увидеть работу 3 × 5 = 15. Мы начнем с 0 и будем двигаться вправо от числовой линии. Мы сформируем 3 группы по 5 равных интервалов. Это приведет нас к 15.
Приведенная выше числовая строка показывает, что 3 умножить на 5 равно 15. Представление также можно записать как 5 + 5 + 5 = 15. Оператор умножения выражается как 3 × 5 = 15.
Задачи на умножение слов
Задачи на умножение слов можно легко решить, внимательно наблюдая за ситуацией и находя решение. Давайте разберемся в теории реальных задач на умножение слов с помощью интересного примера.
Пример: В коробке 245 фруктов. Найдите количество фруктов в 4 таких ящиках, используя формулу умножения.
Найдите количество фруктов в 4 таких ящиках, используя формулу умножения.
Решение: Чтобы решить такие задачи на умножение слов, проще всего записать заданные параметры, а затем решить.
Дано:
Общее количество фруктов в одном ящике = 245
Количество ящиков = 4
Общее количество фруктов в 4 таких ящиках = 245 × 4.
Шаг 1: Начните с разряда единиц. Умножьте 4 × 5 = 20. Теперь перенесите 2 в столбец десятков.
Шаг 2: Умножьте 4 на цифру десятков, то есть 4 × 4 = 16. Теперь прибавьте это к переносу с предыдущего шага. 16 + 2 (перенос из шага 1) = 18. Отсюда перенесите 1 в столбец сотен.
Шаг 3: Умножьте 4 на разряд сотен, 4 × 2 = 8 сотен. 8 + 1 (перенос из шага 2) = 9.
Шаг 4: Следовательно, произведение 245 × 4 = 980.
H T O
1 2
2 4 5
× 4
9 8 0
Следовательно, общее количество фруктов в 4 таких коробках = 245 × 4 = 980. несколько советов и приемов, которые можно использовать при выполнении умножения.
несколько советов и приемов, которые можно использовать при выполнении умножения.
- При умножении порядок чисел не имеет значения. Так что выбирайте тот порядок, в котором вам удобнее. При использовании таблицы умножения, по сравнению с 9 × 4, учащиеся могут легче запомнить 4 × 9.
- При умножении трех чисел выберите два числа, которые легко умножаются. Например, умножение 5 × 17 × 2 будет затруднено, если мы попытаемся сначала умножить 5 × 17. Вместо этого умножение 5 на 2 дает 10, которые можно легко умножить на 17, чтобы получить 170.
- При умножении двузначного числа на однозначное иногда помогает разбить двузначное число по разрядности. Затем умножьте каждую часть и сложите. Например, 37 × 4 можно решить в уме, разбив 37 как 30 + 7. Тогда 30 × 4 = 120 и 7 × 4 = 28. Таким образом, окончательный ответ будет 120 + 28 = 148. Хотя это может показаться более утомительным, когда записано, гораздо легче решить в уме.
- Даже если вы не помните факт умножения, его можно легко вычислить в уме.
 Например, 17 × 9трудно запомнить. Но это можно мысленно переформулировать как 17 × (10 — 1). Значит, ответ будет 170 — 17 = 153, .
Например, 17 × 9трудно запомнить. Но это можно мысленно переформулировать как 17 × (10 — 1). Значит, ответ будет 170 — 17 = 153, .
☛ Статьи по теме
- Длинное умножение
- Калькулятор умножения
- Таблица умножения
- Рабочие листы с задачами на умножение
- Длинные рабочие листы умножения
- Рабочие листы умножения
Примеры умножения
Пример 1. Используйте трюки с умножением, чтобы решить следующую задачу на умножение слов.
Цена книги 48 долларов. Найдите цену 500 таких книг.Решение:
Цена одной книги = 48
$ Цена 500 книг = 500 × 48H T O
5 0 0
× 4 8
4 0 0 0
+2 0 0 0 х
2 4 0 0 0 _Цена таких 500 книг $24000.
Другой способ решить этот вопрос — просто умножить 48 на 5 и присоединить два нуля к окончательному ответу.
 Итак, умножая 48 × 5, мы получаем 240. Но заданное значение равно 500, поэтому наш конечный продукт будет 24000 долларов.
Итак, умножая 48 × 5, мы получаем 240. Но заданное значение равно 500, поэтому наш конечный продукт будет 24000 долларов.Пример 2. Решите следующую задачу на умножение слов.
Сколько будет 784 умножить на 44?Решение:
Используя формулу умножения, 784 умножить на 44 = 784 × 44
Следовательно, 784 умножить на 44 равно 34496.
Пример 3: Укажите истинность или ложность следующих утверждений, используя факты умножения.
а.) Умножение представляет собой основную идею многократного вычитания.
b.) Формула умножения выражается как: Множитель × Множитель = Произведение
Решение:
а.) Неверно, умножение представляет собой основную идею повторного сложения одного и того же числа.
b.) Правда, формула умножения выражается как: Множимое × Множитель = Произведение
перейти к слайдуперейти к слайдуперейти к слайду
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Записаться на бесплатный пробный урок
Практические вопросы по умножению
перейти к слайдуперейти к слайду
Часто задаваемые вопросы по умножению
Что означает умножение?
Умножение — это операция, представляющая основную идею многократного сложения одного и того же числа. Числа, которые перемножаются, называются множителями, а результат, полученный после умножения двух или более чисел, известен как произведение этих чисел. Умножение используется для упрощения задачи многократного сложения одного и того же числа 9.0003 . Используется, когда нам нужно объединить группы одинакового размера. Например, если в 5 корзинах по 4 яблока, то чтобы найти общее количество яблок, мы можем использовать умножение и решить это как 5 × 4 = 20 яблок.
Какая формула используется для выполнения умножения?
Формула, которую мы используем для выполнения умножения: «Множное × Множитель = Произведение». Например, 9 (множимое) × 5 (множитель) = 45 (произведение)
Например, 9 (множимое) × 5 (множитель) = 45 (произведение)
Каковы свойства умножения?
Различные свойства умножения приведены ниже.
- Коммутативное свойство умножения : Произведение двух чисел не изменится, если мы изменим порядок чисел. Это свойство умножения известно как коммутативное свойство умножения, которое представлено как A × B = B × A. Например, 12 × 13 = 13 × 12 = 156,
- Ассоциативное свойство умножения : Произведение трех или более чисел не меняется при изменении группировки чисел. Это свойство умножения известно как ассоциативное свойство умножения, которое представлено как A × (B × C) = (A × B) × C = B × (A × C). Например, 12 × (13 × 5) = (12 × 13) × 5 = 13 × (12 × 5) = 780,
- Свойство идентичности умножения : Если любое число умножается на 1, произведением является само число. Например, 12 × 1 = 12. Здесь 1 — единица умножения.
- Нулевое свойство умножения : Если любое число умножается на 0, произведение всегда равно нулю.
 Это нулевое свойство умножения. Например, 12 × 0 = 0, .
Это нулевое свойство умножения. Например, 12 × 0 = 0, . - Распределительное свойство умножения : Согласно распределительному свойству умножения, когда мы умножаем число на сумму двух или более слагаемых, мы получаем результат, равный результату, полученному при умножении каждого слагаемого по отдельности на число. Это свойство также применимо к вычитанию и представляется как A × (B + C) = AB + AC или A × (B — C) = AB — AC. Например, 12 × (13 + 5) = (12 × 13) + (12 × 5) = 216,
Что такое символ умножения?
При выполнении умножения мы используем символ креста (×), который соединяет все выражение, этот символ (×) известен как символ умножения. Например, 7 умножить на 4 равно 28 можно представить как 7 × 4 = 28.
Какие части умножения?
Различные части умножения выражаются следующим образом. Разберем это на примере: 6 × 4 = 24.
- Множественное (множитель): множимое — это первое число. В этом случае 6 является множимым.

- Множитель (Коэффициент): Множитель — это второе число. В данном случае множитель 4.
- Продукт: Конечный результат после умножения множимого и множителя. В этом примере 24 — это произведение.
- Символ умножения: ‘×’ (соединяет все выражение)
Приведите пример предложения с умножением.
Чтобы решить задачу на умножение, нам нужно записать ее в виде предложения на умножение. Например, сколько будет 36 умножить на 9? Мы знаем, что 36 умножить на 9 записывается в форме предложения умножения как 36 × 9 = 324. Здесь 36 и 9 — множители, а 324 — произведение. Таким образом, 36 умножить на 9 равно 324.
Как умножение связано со сложением?
Умножение представляет собой основную идею многократного сложения одного и того же числа. Это упрощает задачу повторного добавления. Например, если есть 3 пачки карандашей и в каждой пачке по 6 карандашей, найдем общее количество карандашей. Мы можем решить этот вопрос сложением, то есть 6 + 6 + 6 = 18 карандашей. Однако когда нам приходится иметь дело с большими числами, умножение полезно. Теперь, если мы используем умножение для решения этой задачи, нам нужно умножить количество пачек на количество карандашей в каждой пачке. Это означает, что 3 × 6 = 18 карандашей. Таким образом, мы легко получаем тот же результат. Следовательно, умножение также называется повторным сложением.
Однако когда нам приходится иметь дело с большими числами, умножение полезно. Теперь, если мы используем умножение для решения этой задачи, нам нужно умножить количество пачек на количество карандашей в каждой пачке. Это означает, что 3 × 6 = 18 карандашей. Таким образом, мы легко получаем тот же результат. Следовательно, умножение также называется повторным сложением.
В чем разница между умножением и делением?
При умножении мы объединяем группы одинакового размера, а при делении делим или разделяем заданное число на равные группы. Умножение — это произведение двух или более чисел, где умножаемые числа являются множителями, а результат называется произведением. При делении число, на которое делится делимое, называется делимым, число, на которое делится делимое, называется делителем, а результат — частным.
Как умножение используется в повседневной жизни?
Умножение широко используется в нашей повседневной жизни. Например, мы можем рассчитать цену предметов в соответствии со ставкой за количество, мы можем найти правильное количество ингредиентов, которые будут использоваться в приготовлении пищи, мы можем рассчитать стоимость нескольких предметов, когда известна стоимость 1 предмета, и так далее.
Каковы стратегии умножения?
Стратегии умножения — это различные способы изучения умножения. Например, умножение с помощью числовой прямой, умножение с помощью таблицы стоимостных значений, разделение десятков и единиц и их умножение по отдельности и т. д. Эти стратегии помогают учащимся понять концепцию умножения в более широкой перспективе.
Пошаговое обучение стандартному алгоритму умножения
Стандартный алгоритм умножения может быть очень трудным для обучения в 5-м и 6-м классах, это знает любой, кто раньше преподавал в старших классах начальной школы.
Несмотря на самые лучшие намерения, всегда найдется несколько учеников, которые либо не уверены в методах, которые они использовали для многозначного умножения раньше, либо не уверены в своих фактах умножения.
Если в этом учебном году вы будете впервые обучать стандартному алгоритму умножения, вас ждет все это с нетерпением, но не отчаивайтесь – это случается каждый год.
Прежде чем вы изучите стандартный алгоритм умножения, вы, как правило, понимаете умножение многозначных чисел по частям и сложение частичных произведений в конце. В стандартном алгоритме это скорее сокращенный способ умножения по частям, при этом часть сложения выполняется одновременно с умножением. Его часто называют многоразрядным умножением, и этот метод рекомендуется использовать при умножении больших чисел.
Прежде чем приступить к стандартному алгоритму, учащиеся в идеале должны быть уверены в фактах умножения и понимать ключевые термины, такие как множимое и множитель.
- Множитель — это число, с которого вы начинаете умножение
- Множитель — это количество таких групп, которые вам нужны; сколько раз вы собираетесь умножать множимое.
Учащихся 4-х классов можно познакомить с многозначным умножением путем умножения трехзначных чисел на однозначное число и перемножения двух двузначных чисел. Они будут делать это с помощью таких методов, как площадные модели и частичные продукты. По мере развития способностей учащихся учащиеся 5-6 классов будут умножать многозначные целые числа по стандартному алгоритму.
Они будут делать это с помощью таких методов, как площадные модели и частичные продукты. По мере развития способностей учащихся учащиеся 5-6 классов будут умножать многозначные целые числа по стандартному алгоритму.
Крайне важно, чтобы учащиеся свободно владели этим методом, чтобы иметь доступ к более сложной математике по мере перехода в среднюю школу и выше. В средней школе учащиеся будут развивать этот навык и умножать многозначные десятичные числа. Когда я говорю свободно, я имею в виду:
«Свободное владение речью — это процесс извлечения информации из долговременной памяти без использования нашей рабочей памяти, высвобождающий ценное пространство в нашей рабочей памяти, чтобы уделить внимание другим вещам». Рассуждение и решение проблем
Каков стандартный алгоритм?Формальный стандартный алгоритм представляет собой пошаговый метод, помогающий детям понять концептуально и практически, как умножать многозначные числа, и обычно вводится, когда учащиеся начинают умножать большие числа.
Стандартный алгоритм шаг за шагомВот стандартный алгоритм в разбивке по шагам:
Как выполнить стандартный алгоритм шаг за шагом Пример: 124 x 26 8 9 0 вопрос по вертикалиНе забудьте начать процесс умножения справа с разряда единиц Умножить 6 на 4 Запишите ответ правильно, включая любые несущие Умножить 6 на 2 Прибавь все, что осталось от предыдущего умножения. Умножить 6 на 1 Добавьте все, что вы перенесли из предыдущего умножения, и правильно запишите ответ Начните следующую неполную линейку произведений, поставив 0 в разряде единиц, так как теперь мы умножаем в разряде десятков Умножь 2 на 4 Запиши ответ правильно Умножь 2 на 2 Запиши ответ Умножить 2 на 1 Напишите ответ правильно Правильно сложите два ответа Это в общей сложности 16 шагов, которые дети должны освоить, изучая этот новый процесс, чтобы получить окончательный ответ.
Принимая во внимание ограничения нашей рабочей памяти, это очень много, и можно довольно легко перегрузить и предотвратить кодирование этой информации.
Итак ответ на вопрос: Как сделать по стандартному алгоритму? это просто следовать инструкциям!
Но здесь отсутствует важнейший этап обучения — переход от процедурного к концептуальному пониманию того, что происходит.
В оставшейся части этой статьи объясняется, как научить стандартный алгоритм оказывать наибольшее влияние на ваш класс. Он включает ссылки на стандартные рабочие листы алгоритмов, чтобы дать вам много практики.
Как когнитивная наука повлияла на мое преподавание стандартного алгоритмаДва урока когнитивной науки сильно изменили мой подход к преподаванию стандартного алгоритма.
1. Долговременная и кратковременная памятьПервым было понимание того, что у нас есть долговременная память, которая почти безгранична в отношении информации, которую она может хранить; и рабочая память, где мы делаем наши сознательные мысли.
Важно отметить, что пространство в нашей рабочей памяти ограничено, многие исследователи оценивают его между 4 или 7 элементами. Oliver Caviglioli любезно нарисовал замечательный плакат, демонстрирующий этот процесс.
Из https://www.olicav.com/#/diagrams/Из модели видно, что человек использует свое внимание, чтобы перенести вещи из окружающей среды в рабочую память. Затем мы пытаемся закодировать эту информацию в нашу долговременную память, но некоторая информация может быть забыта по множеству причин.
Когда эта информация находится в нашей долговременной памяти, мы можем вернуть ее на передний план нашей рабочей памяти, чтобы использовать ее. Однако, если эти воспоминания остаются бездействующими слишком долго (то есть мы не вспоминаем эти воспоминания в течение длительного периода времени), они тоже могут быть забыты.
Подробнее: Обучение и память в классе
2. Теория когнитивной нагрузкиДругим уроком когнитивной науки, который повлиял на мое преподавание, является теория когнитивной нагрузки.
Теория когнитивной нагрузки пытается объяснить, почему мы не можем закодировать новую информацию из нашей рабочей памяти в нашу долговременную память.
Это может быть вызвано многими причинами, такими как: слишком сложная работа; слишком быстро покрываются; слишком много отвлекающих факторов в окружающей среде; отсутствие предварительных знаний по теме (мы вернемся к этому позже) и т. д.
Как это поможет нам обучить стандартный алгоритм? Ну, давайте сначала проясним кое-что.
Моим результатом первого или двух уроков будет придание моим ученикам уверенности в изучении метода. Только после этого переходим к остальным.
Как обучать стандартному алгоритму Базовые знания по умножениюПрежде чем мы начнем работу над стандартным алгоритмом, я всегда проверяю, кто из моих учеников уже испытывал трудности с умножением в младших классах.
Если ребенок не уверен в своих знаниях об умножении, вам необходимо организовать вмешательство, чтобы научить его быстрому обучению.
возраста, в старших классах начальной школы очень трудно найти время.
Вам также могут понравиться: 35 игр на умножение, подходящих для дома и школы — выбирайте одну или две каждую неделю для домашнего обучения, если вашим ученикам все еще нужно выработать последовательность.
Как упростить стандартный алгоритмПо моему опыту, те ученики, которые знают, что они свободно умножают 3 или 4 цифры на 1 цифру, легче работают с большими числами.
Это имеет смысл, поскольку, если они бегло владеют этими областями, они фактически сокращают то, на что должна обращать внимание их рабочая память. Если предположить, что они свободно владеют этими двумя вещами, то количество предметов, которые им нужно выучить, сокращается с 16 до 4-6 вещей.
Ребенок, который не уверен в умножении, скорее всего, использует так много своей рабочей памяти для решения части задачи, связанной с умножением, что все остальные шаги, как мы видели в предыдущей модели, забываются.
Это важный момент, который учителя должны признать: дело не в том, что у одного ребенка есть врожденная способность выполнять стандартный алгоритм, а у другого нет. Дело в том, что один ребенок просто сохранил важные знания, необходимые для достижения успеха, и, следовательно, может установить связь с предыдущими знаниями, чтобы резко сократить то, что им нужно для активной работы.
Как сказал Осубел: «Самый важный фактор, влияющий на обучение, — это то, что учащийся уже знает. Выясните это и научите их соответствующим образом».
Стандартный метод алгоритма: Урок 1Независимо от того, с чего начинают учащиеся, есть вещи, которые мы можем сделать в классе, чтобы помочь им всем разобраться с процедурой обучения. стандартный алгоритм. Как я упоминал ранее, моя цель на первых двух уроках — укрепить уверенность в методе.
Для этого я гарантирую, что наш первый множитель равен 11. Делая второй множитель равным 11, все, что здесь требуется, это умножить на единицу.
Я еще не встречал ребенка, который может бороться со своим умножением, который не знает фактов умножения своих единиц.
Это значительно снижает когнитивную нагрузку на учащихся и помогает высвободить всю их рабочую память для изучения процедуры стандартного алгоритма. Конечно, этим учащимся все равно придется выучить свои факты умножения, но это просто поможет сломать эти барьеры и поможет им добиться успеха.
Теперь вдруг процедура выглядит так:
Пошаговый процесс решения проблемы такой же, как в примере выше, но мы значительно сократили нагрузку на рабочую память.
Это повышает вероятность того, что процедура запомнится, поскольку учащиеся могут сосредоточить все свое внимание на понимании процедуры, а не на умножении. Опять же, я хотел бы подчеркнуть, что цель этого состоит в том, чтобы студенты могли справиться с процедурой, чтобы ее можно было усвоить.
Этап 1. Закрепление предварительных знаний об умноженииВ начале урока у меня на доске было бы несколько вопросов 4 на 1, чтобы класс мог самостоятельно решить их, убедившись, что я доберусь до всех учащихся, которые Я думаю, что они могут бороться с этим и выяснять, с чем они борются — с умножением или с процедурой? Если бы это было первое, я бы помог им с их таблицей умножения, а если бы это было второе, я бы рассмотрел с ними пример.
Пример серии вопросов на умножение цифр 4×1 из онлайн-класса Third Space Learning.По прошествии достаточного количества времени я просматривал вопросы на доске, чтобы проверить понимание ими процедуры и их знание «умножения»:
- Что такое множимое и множитель? (т. е. «верхнее число» и «нижнее число»)
- Чему равно ___, умноженное на ____?
- Что произойдет, если произведение больше одной цифры?
- С какого разряда начинать умножение?
Ответы учащихся на эти вопросы помогут спланировать будущие вмешательства. По моему опыту, я не встречал многих студентов, чье предварительное достижение означает, что они не могут правильно изложить метод умножения в столбик.
Если вам нужно вернуться в прошлое, чтобы создать более прочную базу в умножении, то есть учебный курс по умножению или более подробное руководство по обучению умножению в разных классах начальной школы. Если родители хотят помочь своим детям в умножении, то в этой статье дается простое резюме: каков стандартный алгоритм?
Шаг 2.Знакомство с новыми задачами на многозначное умножение
В следующей части урока я покажу пример типа вопроса, на который они должны будут ответить к концу модуля – в данном случае это будет умножение 4 на 2 цифры с любой цифрой с использованием стандартного алгоритма.
Я бы очень быстро попросил их потратить 30 секунд на обсуждение друг с другом, чтобы увидеть, чем этот вопрос отличается от того, который они задавали в начале урока.
Как только они поймут, что в качестве множителя используется двузначное число, я решу это молча в обычном темпе — причина этого в том, чтобы показать, насколько легко это может быть, и дать им уверенность в том, что это то, с чем им не нужно бороться.
Затем я покажу им другой пример, на этот раз с 11 в качестве множителя — он будет на том же слайде, что и предыдущий пример.
Тогда я спрашивал: «Большой палец вверх — да, большой палец вниз — нет». Изменился ли способ, которым я поставил задачу, когда множитель состоит из двух цифр?»
Тогда я надеялся бы увидеть все большие пальцы вниз.
Шаг 3 – Настройка стандартного алгоритмаЕсли ребенок поднимает большой палец вверх, я вступаю в диалог со всем классом, чтобы понять, почему это так, и ссылаюсь на пример, написанный на доске.
Мой следующий шаг – записать задачу для стандартного алгоритма.
Следующей моей инструкцией классу будет: «Для начала мы рассмотрели примеры, в которых множитель был однозначным числом. Это число будет в разряде единиц. Таким образом, с числом, которое находится в «единицах» в этом двузначном числе, мы поступаем точно так же».
Чтобы убедиться, что все участвуют, я бы попросил их показать мне с помощью пальцев или мини-доски ответы на вопросы по умножению – не потому, что я думаю, что они этого не знают, а для того, чтобы твердо держать свою рабочую память на математике под рукой. .
На доске теперь у меня есть:
Теперь мы подошли к новой части информации, которую мы хотим, чтобы учащиеся усвоили, поэтому я хотел бы замедлиться и объяснить, что здесь происходит, снова используя этот момент, чтобы усилить значение места.
«Пока все, что было раньше, для нас не ново. Теперь у нас есть совершенно новый шаг. Чтобы понять, что происходит, нам нужно активировать наше знание о значении места. Первая цифра множителя находится в единицах и равна единице.
Вторая цифра стоит в разряде десятков, поэтому она равна 10. Это означает, что у нас есть 10, умноженное на 3. Чтобы показать, что мы умножаем на 10, мы можем поставить ноль в разряде единиц, чтобы действовать как заполнитель . ”
Тогда я бы поставил ноль на нужное место.
«Тогда мы можем умножать числа в множимом, как если бы мы умножали их на 1».
Затем я призываю всех учеников решить задачу умножения, снова показывая мне на пальцы, чтобы обеспечить участие.
Наконец, я прошу учащихся посмотреть на другой рабочий пример на доске и сказать своему партнеру, каким будет последний шаг — добавление двух продуктов. Класс делал это вместе со мной, показывая ответы пальцами/мини-доской.
Это оставит нас с готовым продуктом:
Шаг 4 – Повторные примеры стандартного алгоритмаПовторите описанный выше процесс еще с двумя примерами.
По мере изучения каждого примера учащиеся должны больше объяснять, особенно когда речь идет об отбрасывании нуля и напоминании друг другу о сложении двух произведений. Если вы обнаружите, что дети борются с трудностями, остановитесь и прорепетируйте это, чтобы убедиться, что используется правильный язык.
Требуйте правильных ответов полными предложениями и правильного языка. Когда учащиеся не могут этого сделать, я прошу добровольца, которого я выбрал, который может сделать это, дать примерный ответ, а затем прошу первоначальных учеников, которые сначала не смогли ответить, повторить то, что было сказано.
Шаг 5. Очередь студентов со стандартным алгоритмомЗатем я предлагаю два стандартных вопроса по алгоритму, которые я прошу студентов выполнить самостоятельно. В течение этого времени я буду наблюдать и поддерживать по мере необходимости.
В предыдущих блогах я упомянул о том, что лучше учиться, чем работать, и это ничем не отличается.
Несмотря на то, что я слышал, как ученики действительно четко отвечали на шаге 2 или правильно отвечали на оба вопроса на шаге 3, я все же прекрасно осознаю, что, хотя эти ученики показывают хорошие результаты, в их долговременной памяти ничего не изменилось, поскольку они просто повторяют то, что уже было сказано. показано им.
В зависимости от результата шага 3 мне нужно будет либо: просмотреть другие примеры и изменить свои объяснения, либо перейти к шагу 4.
Шаг 6. Повторное применение учащимися стандартного алгоритмаРад, что учащиеся могут воспроизвести процесс и понять его, теперь я предлагаю им заполнить лист стандартного алгоритма.
Нет необходимости различать рабочий лист; каждый ребенок будет иметь равный доступ к работе.
Дифференциация рабочего листа приведет только к увеличению разрыва в успеваемости. Дифференциация будет исходить из дополнительных инструкций, которые я могу дать в это время.
Рабочий лист, который я бы дал, не будет состоять из 20 вопросов на одну и ту же тему.
Здесь я бы использовал переплетение. 10 вопросов о том, чему я учил, будут на листе в случайном порядке, остальные 10 вопросов будут составлены из ранее изученного материала.
Подробнее: 8 стратегий дифференциации для вашего класса для преодоления разрыва в успеваемости ранее изученный контент. Это непрерывное переключение помогает процессу кодирования.
По возможности делайте содержание связанным с тем, чему вас учили; например, поскольку я преподавал умножение, у меня были некоторые вопросы о делении из целей предыдущего года, чтобы подчеркнуть, что деление является обратным умножению.
Чередование связанного содержимого, например. разделение может быть отличным способом внедрения обучения. Этот обучающий слайд «Третье пространство обучения один на один» показывает, как вы можете чередовать знание формы с делением.Последний вопрос на умножение также будет иметь множитель, отличный от 11, чтобы увидеть, смогут ли учащиеся применить процесс, когда требования к рабочей памяти выше.
Когда это произойдет, я буду ходить по комнате, чтобы оценить, как учащиеся справляются не только с вопросами этого урока, но и с предыдущим содержанием. Студенты могут пропускать вопросы, в которых они не уверены.
Этап 7 – Совместное оцениваниеНа этом этапе учащимся будет предложено дать ответы, и весь класс сможет поставить отметку, услышав ответ. Если кто-то из них не согласен с ответом, мы можем обсудить его всем классом, пока не будет найден правильный ответ.
Шаг 8. Диагностические вопросыДиагностические вопросы и диагностическое оценивание в целом — невероятно эффективный способ оценить понимание учащимися концепции. Они работают, задавая вопрос и давая 4 возможных ответа.
В то время как один ответ правильный, остальные три отвлекающих фактора будут тщательно спланированы, чтобы показать конкретное заблуждение.
Ниже приведен пример того, что я буду использовать в этом уроке.
Стандартный алгоритм диагностики пример проблемыКакой стандартный вопрос алгоритма показывает правильный ответ?
В этом примере каждый неправильный ответ показывает неверное представление в игре.
- A правильный но вы можете видеть, что каждый другой ответ может быть ошибкой, которую может сделать ребенок:
- В B они опустили ноль при умножении на единицы.
- В C забыли отбросить ноль при умножении на столбец десятков
- В D забыли прибавить единицу, которая была перенесена при прибавлении 8 к 6.
Именно выбор неправильных ответов делает диагностические вопросы такими мощными; они четко определяют, о чем думает учащийся, и могут предоставить вам немедленную обратную связь об успеваемости, которую вы можете исправить на основе данного ответа.
Делая это на уроках, я присваиваю каждой букве число, например, A=1, B=2 и т. д., что соответствует количеству пальцев, которые я хочу, чтобы они держали.
Затем я даю команду «думать». Учащиеся думают над правильным ответом.
Затем я скажу «спрячься», и они закроют пальцы, которые хотят показать, на одной руке другой. Наконец, я говорю «покажи», и ученики показывают мне соответствующий палец, и я могу быстро оглядеть класс, чтобы увидеть ответы, которые они дали.
Другим преимуществом диагностических вопросов является возможность обсудить неправильные ответы и понять, почему они неверны. Это создает фантастические темы для обсуждения и действительно заставляет класс думать и искать ошибки.
Если вы хотите попробовать другие диагностические вопросы, вы можете загрузить бесплатный набор математических диагностических тестов для 4-го и 5-го класса.
Заключение вашего первого стандартного урока алгоритма!Надеемся, что постепенная прогрессивная структура урока — или их может быть два или три, в зависимости от вашего класса — показывает, как можно уверенно преподавать стандартный алгоритм.
Стоит еще раз повторить, что основная цель первого урока – укрепить уверенность учащихся и приступить к изучению этого метода умножения.
По мере роста их уверенности и дальнейшего внедрения процесса можно изменить множитель, а также ввести логические вопросы и вопросы для решения проблем, на которые можно будет отвечать с большей независимостью.
Примеры стандартных алгоритмовНиже приведены два примера стандартных алгоритмов.
Пример 1: 6321 x 15 = 94 815
Пример 2: 6321 x 25 = 158 025
Вопросы стандартного алгоритмаHere are a few standard algorithm questions and answers to get you started:
- 1543 x 11 = 16,973
- 2,374 x 13 = 30,862
- 4,537 x 27 = 122,499
- 8,983 x 37 = 332 371
- 9 452 x 48 = 453 696
Есть ли у вас ученики, которым нужна дополнительная помощь по математике?
Предоставьте учащимся четвертого и пятого классов больше возможностей для закрепления навыков обучения и практики с помощью персонализированного обучения элементарной математике с их собственным онлайн-репетитором по математике.Каждый учащийся получает дифференцированное обучение, предназначенное для устранения индивидуальных пробелов в обучении, а организованное обучение гарантирует, что каждый учащийся учится в нужном темпе. Уроки соответствуют стандартам и оценкам вашего штата, плюс вы будете получать регулярные отчеты о каждом шаге.
Программы доступны для четвертого и пятого классов, и вы можете попробовать 6 уроков абсолютно бесплатно.
Содержание этой статьи было первоначально написано ведущим учителем начальных классов Нилом Алмондом, а затем было отредактировано и адаптировано для школ США учителем математики начальных классов Жаклин Вассел.
Умножение: целые числа
Умножение можно рассматривать как повторное добавление. Итак, если вы умножаете число а по другому номеру б , это то же самое, что добавить число а снова и снова б раз. (Или добавление б снова и снова а раз).
Например:
3 × 5 знак равно 5 + 5 + 5 знак равно 15 3 × 5 знак равно 3 + 3 + 3 + 3 + 3 знак равно 15
Другой способ думать об умножении целых чисел а × б состоит в том, чтобы визуализировать объекты, расположенные в виде прямоугольника, с а ряды и б столбцы.
3 × 5
Обратите внимание, что есть 15 точки на рисунке.
Стандартный алгоритм
Чтобы умножить многозначное число на однозначное с помощью стандартного алгоритма, напишите два числа друг над другом так, чтобы единицы были выровнены по вертикали, а многозначное число — сверху.
127 × 3 _
Умножьте цифру единиц верхнего числа на нижнее число. Запишите разряд единиц результата. Если результат больше 10 , несите цифру десятков, как при сложении.
Здесь, 7 × 3 знак равно 21 , так
1 2 2 7 × 3 _ 1
Теперь умножьте разряд десятков верхнего числа на нижнее число и прибавьте полученную цифру к результату.
Здесь, 2 × 3 знак равно 6 , а потом добавляем 2 получить 8 . С 8 меньше чем 10 , мы не должны нести на этот раз.
1 2 2 7 × 3 _ 8 1
Наконец, умножьте разряд сотен верхнего числа на нижнее число. Здесь, 3 × 1 знак равно 3 .
1 2 2 7 × 3 _ 3 8 1
Так, 127 × 3 знак равно 381 .
Чтобы умножить два многозначных числа , напишите число с большим количеством цифр сверху. Например, чтобы умножить 29 по 543 , мы пишем
543 × 29 _
Сначала умножьте верхнее число на разряд единиц нижнего числа, как описано выше. 3 × 9 знак равно 27 , так что запишите 7 и нести 2 :
5 4 2 3 × 2 9_ 7
4 × 9 36, плюс 2 является 38 , поэтому запишите 8 и несите 3 :
5 3 4 2 3 × 2 9_ 8 7
5 × 9 является 45 , плюс 3 является 48 .
Больше нет цифр для переноса, так что записывайте 48 .
5 2 4 2 3 × 2 9_ 4 8 8 7
Далее нам нужно умножить верхнее число на разряд десятков нижнего номера. Поскольку мы на самом деле умножаем на 20 , не по 2 , мы записываем 0 в качестве заполнителя.
5 4 3 × 29_ 4887 0
3 × 2 является 6 , поэтому запишите 6 .
5 4 3 × 2 9_ 4887 6 0
4 × 2 является 8 , поэтому запишите 8 .
5 4 3 × 2 9_ 4887 8 6 0
5 × 2 является 10 , и больше нет цифр для переноса, поэтому запишите 10 .
5 4 3 × 2 9_ 4887 10 860
Последним шагом является добавление двух результатов.
5 4 3 × 29_ 4887 + 10 860 _ 13947
Так, 543 × 29знак равно 13947 .

 Также имеется достаточно материалов, которые пригодятся к экзаменам в 9-ых и 11-ых классах. Есть много готовых решенных задач ЕГЭ (ГИА, ОГЭ) и упражнений для отличной самоподготовки к экзаменам. Имеются демонстрационные варианты разных лет и онлайн тесты на основе КИМов для качественной самопроверки знаний. Также есть уникальные генераторы заданий, которые помогут учителям создать карточки для учеников. Есть разделы посвещенные контрольным и самостоятельным и проверочным работам для 3-4-ых и 5-6 классов. Помимо прочего имеются полезные презентации для учителей по разным школьным предметам — биология, обж, информатика, кубановедение, химия и другие. Кроме того есть обучающие видео уроки по математике (ЕГЭ, ГИА, КДР) и информатике (ОГЭ), которые принесут огромную пользу старшеклассникам в подготовке к экзаменам 2018 учебного года.
Также имеется достаточно материалов, которые пригодятся к экзаменам в 9-ых и 11-ых классах. Есть много готовых решенных задач ЕГЭ (ГИА, ОГЭ) и упражнений для отличной самоподготовки к экзаменам. Имеются демонстрационные варианты разных лет и онлайн тесты на основе КИМов для качественной самопроверки знаний. Также есть уникальные генераторы заданий, которые помогут учителям создать карточки для учеников. Есть разделы посвещенные контрольным и самостоятельным и проверочным работам для 3-4-ых и 5-6 классов. Помимо прочего имеются полезные презентации для учителей по разным школьным предметам — биология, обж, информатика, кубановедение, химия и другие. Кроме того есть обучающие видео уроки по математике (ЕГЭ, ГИА, КДР) и информатике (ОГЭ), которые принесут огромную пользу старшеклассникам в подготовке к экзаменам 2018 учебного года. 

 Сколько всего кг картофеля привезли в магазин?
Сколько всего кг картофеля привезли в магазин? (2 × 4 = 8)
(2 × 4 = 8) Теперь перенесите 6 десятков в столбец десятков.
Теперь перенесите 6 десятков в столбец десятков. Например, 17 × 9трудно запомнить. Но это можно мысленно переформулировать как 17 × (10 — 1). Значит, ответ будет 170 — 17 = 153,
Например, 17 × 9трудно запомнить. Но это можно мысленно переформулировать как 17 × (10 — 1). Значит, ответ будет 170 — 17 = 153, Итак, умножая 48 × 5, мы получаем 240. Но заданное значение равно 500, поэтому наш конечный продукт будет 24000 долларов.
Итак, умножая 48 × 5, мы получаем 240. Но заданное значение равно 500, поэтому наш конечный продукт будет 24000 долларов.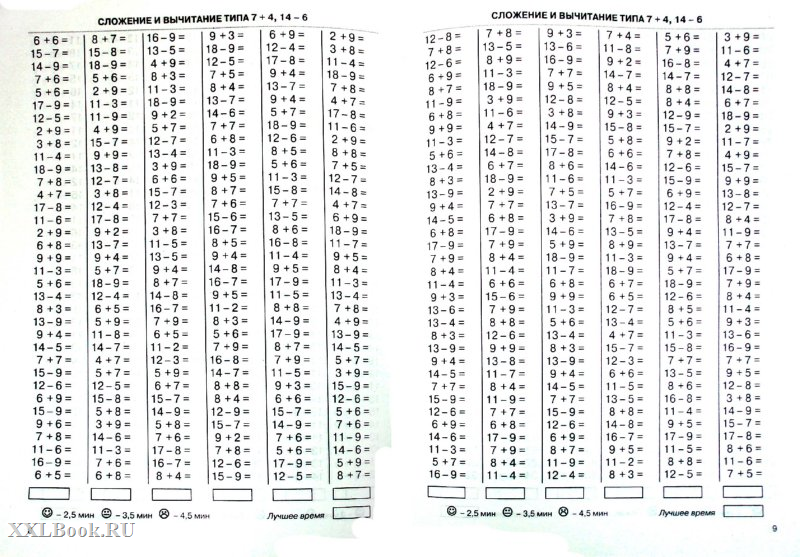 Это нулевое свойство умножения. Например, 12 × 0 = 0,
Это нулевое свойство умножения. Например, 12 × 0 = 0,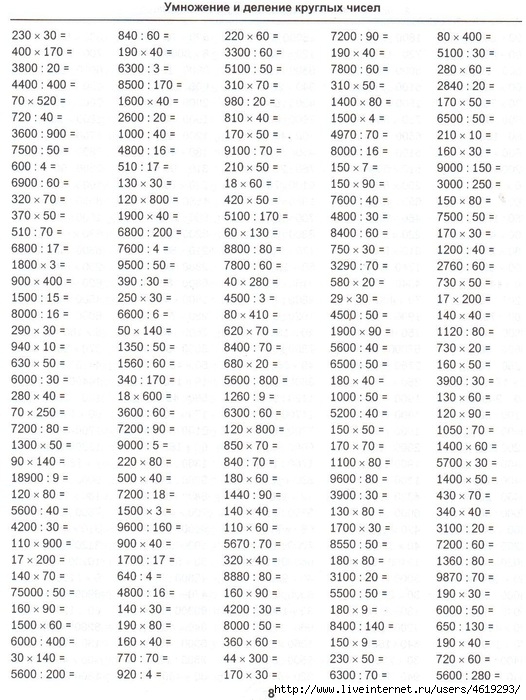

 Принимая во внимание ограничения нашей рабочей памяти, это очень много, и можно довольно легко перегрузить и предотвратить кодирование этой информации.
Принимая во внимание ограничения нашей рабочей памяти, это очень много, и можно довольно легко перегрузить и предотвратить кодирование этой информации.
 Теория когнитивной нагрузки пытается объяснить, почему мы не можем закодировать новую информацию из нашей рабочей памяти в нашу долговременную память.
Теория когнитивной нагрузки пытается объяснить, почему мы не можем закодировать новую информацию из нашей рабочей памяти в нашу долговременную память. возраста, в старших классах начальной школы очень трудно найти время.
возраста, в старших классах начальной школы очень трудно найти время.
 Я еще не встречал ребенка, который может бороться со своим умножением, который не знает фактов умножения своих единиц.
Я еще не встречал ребенка, который может бороться со своим умножением, который не знает фактов умножения своих единиц.
 Знакомство с новыми задачами на многозначное умножение
Знакомство с новыми задачами на многозначное умножение  Если ребенок поднимает большой палец вверх, я вступаю в диалог со всем классом, чтобы понять, почему это так, и ссылаюсь на пример, написанный на доске.
Если ребенок поднимает большой палец вверх, я вступаю в диалог со всем классом, чтобы понять, почему это так, и ссылаюсь на пример, написанный на доске.

 Несмотря на то, что я слышал, как ученики действительно четко отвечали на шаге 2 или правильно отвечали на оба вопроса на шаге 3, я все же прекрасно осознаю, что, хотя эти ученики показывают хорошие результаты, в их долговременной памяти ничего не изменилось, поскольку они просто повторяют то, что уже было сказано. показано им.
Несмотря на то, что я слышал, как ученики действительно четко отвечали на шаге 2 или правильно отвечали на оба вопроса на шаге 3, я все же прекрасно осознаю, что, хотя эти ученики показывают хорошие результаты, в их долговременной памяти ничего не изменилось, поскольку они просто повторяют то, что уже было сказано. показано им.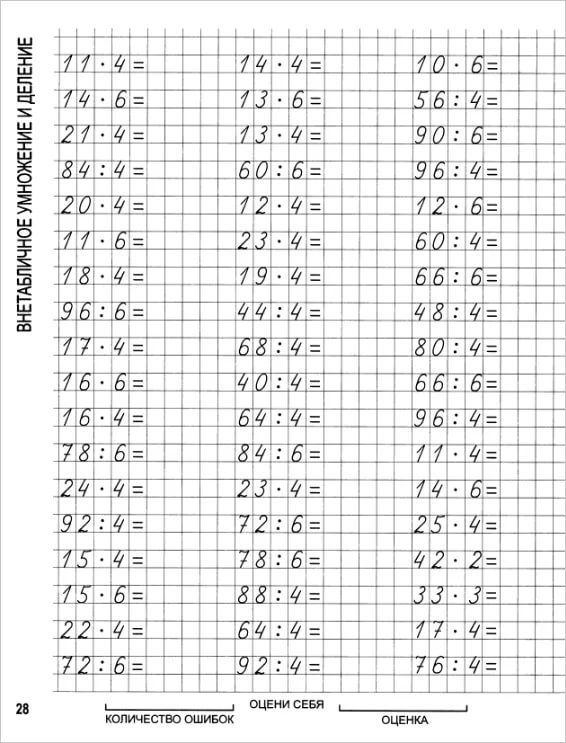 Здесь я бы использовал переплетение. 10 вопросов о том, чему я учил, будут на листе в случайном порядке, остальные 10 вопросов будут составлены из ранее изученного материала.
Здесь я бы использовал переплетение. 10 вопросов о том, чему я учил, будут на листе в случайном порядке, остальные 10 вопросов будут составлены из ранее изученного материала.
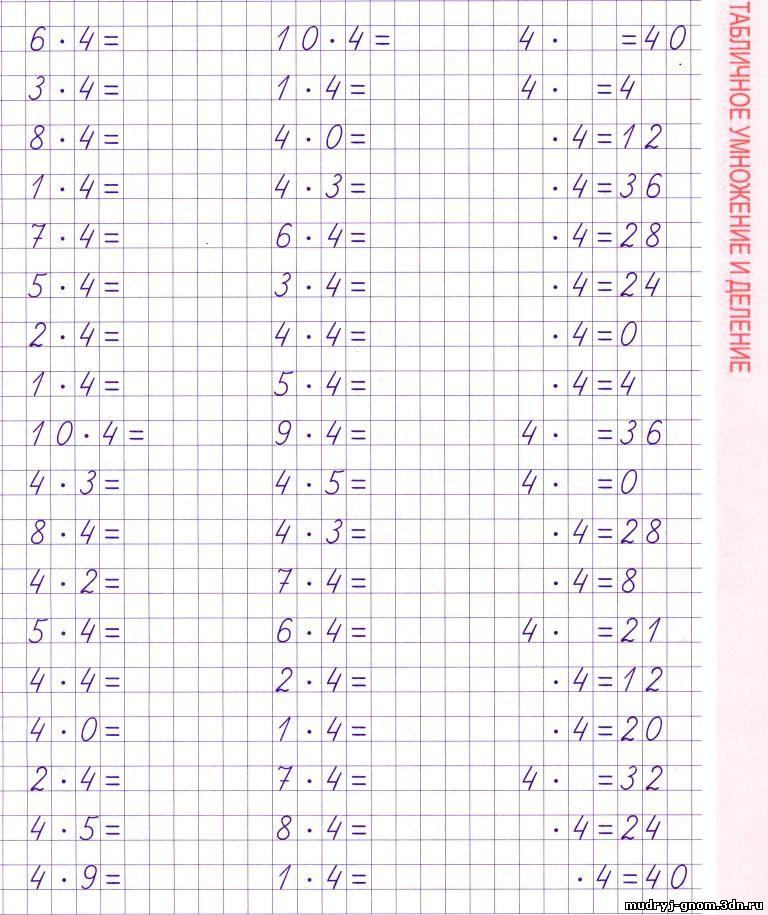
 Затем я даю команду «думать». Учащиеся думают над правильным ответом.
Затем я даю команду «думать». Учащиеся думают над правильным ответом.
 Например:
Например:
 Здесь,
2
×
3
знак равно
6
, а потом добавляем
2
получить
8
. С
8
меньше чем
10
, мы не должны нести на этот раз.
Здесь,
2
×
3
знак равно
6
, а потом добавляем
2
получить
8
. С
8
меньше чем
10
, мы не должны нести на этот раз.
 Больше нет цифр для переноса, так что записывайте
48
.
Больше нет цифр для переноса, так что записывайте
48
.