Просмотр темы — округление до 5 значащих цифр — Онлайн-этап олимпиад «Физтех» 2022 года
Просмотр темы — округление до 5 значащих цифр — Онлайн-этап олимпиад «Физтех» 2022 годаНазад в раздел
-
Игорь Костышин
Участник
16 января 2018 г.
Здравствуйте. Внизу каждой задачи мелким шрифтом написано «при необходимости округлите до 5 значащих цифр». Это означает округлить до 5 цифр после запятой? Т.е., если при решении получаем 5,4444444444444444444, то пишем 5,44444?
Здравствуйте. Внизу каждой задачи мелким шрифтом написано «при необходимости округлите до 5 значащих цифр». Это означает округлить до 5 цифр после запятой? Т.е., если при решении получаем 5,4444444444444444444, то пишем 5,44444?
-
Егор Батарин
Участник
18 января 2018 г.

В данном случае у вас 6 значащих цифр. Значащие цифры — это не то же самое, что цифры после запятой. Так что пишите 5.4444.
В данном случае у вас 6 значащих цифр. Значащие цифры — это не то же самое, что цифры после запятой. Так что пишите 5.4444.
-
Иван Насонов
Участник
21 января 2018 г.
Здравтсвуйте! Тоже вопрос по поводу округления ответов. Если получается ответ 0,2994174, можно ли его записать как 0,3 или же нужно записывать по правилам округления, то есть 0,29942? Буду благодарен за ответ.
Здравтсвуйте! Тоже вопрос по поводу округления ответов. Если получается ответ 0,2994174, можно ли его записать как 0,3 или же нужно записывать по правилам округления, то есть 0,29942? Буду благодарен за ответ.
-
Алёна Рытова
Участник
27 января 2018 г.

Здравствуйте!
1) округление до 5 значащих цифр — это что?
а) оставить ровно 5 цифр в ответе;
б) оставить столько значащих цифр, сколько разумно из условия (например, в условии всё дано с 2-3 значащими цифрами, значит, в ответе оставляем не 5 цифр (которые бессмысленны так как являются ошибкой), а 2 или 3)?
2) имеет ли правильное округление одного и того же ответа значение при засчитывании балла за задание?Здравствуйте!
1) округление до 5 значащих цифр — это что?
а) оставить ровно 5 цифр в ответе;
б) оставить столько значащих цифр, сколько разумно из условия (например, в условии всё дано с 2-3 значащими цифрами, значит, в ответе оставляем не 5 цифр (которые бессмысленны так как являются ошибкой), а 2 или 3)? -
Руслан Тюстин
Участник
28 января 2018 г.
 (-4))
(-4)) -
Данила Липатов
Участник
3 февраля 2018 г.
здравстуйте, хотел узнать, у меня ли одного такая ошибка, что вводишь число с дробным значением(запятой), а оно ‘некоректно’?
здравстуйте, хотел узнать, у меня ли одного такая ошибка, что вводишь число с дробным значением(запятой), а оно ‘некоректно’?
-
Айтал Местников
Участник
3 февраля 2018 г.
Значащей цифрой десятичной дроби называют ее первую (слева направо) отлиичную от нуля цифру, а также все следующие за ней цифры.
Значащей цифрой десятичной дроби называют ее первую (слева направо) отлиичную от нуля цифру, а также все следующие за ней цифры.
-
Николай Ужинский
Участник
4 февраля 2018 г.

Данила Липатов сказал:
здравстуйте, хотел узнать, у меня ли одного такая ошибка, что вводишь число с дробным значением(запятой), а оно ‘некоректно’?
Нужна точка, а не запятая
Данила Липатов сказал:
здравстуйте, хотел узнать, у меня ли одного такая ошибка, что вводишь число с дробным значением(запятой), а оно ‘некоректно’?
Нужна точка, а не запятая
-
Илья Симанчев
Участник
4 февраля 2018 г.
Здравствуйте! Если в ответе получается например 25,24649446, то надо записывать 25,24649 или 25,2465?
Здравствуйте! Если в ответе получается например 25,24649446, то надо записывать 25,24649 или 25,2465?
-
Татьяна Якобовская
Участник
4 февраля 2018 г.

25,246
25,246
-
Екатерина Зайченкова
Участник
4 февраля 2018 г.
Здравствуйте! Если ответ 3,862953 ,то его округлять до 3,8630 (4 значащие цифры), 3,86295 (6 значащих цифр) или оставить 3,8629 — не по правилам округления?
Здравствуйте! Если ответ 3,862953 ,то его округлять до 3,8630 (4 значащие цифры), 3,86295 (6 значащих цифр) или оставить 3,8629 — не по правилам округления?
-
Светлана Суракина
Участник
4 февраля 2018 г.
Данила Липатов сказал:
здравстуйте, хотел узнать, у меня ли одного такая ошибка, что вводишь число с дробным значением(запятой), а оно ‘некоректно’?
Переведи на английский, в русском запятая не ставится
Данила Липатов сказал:
здравстуйте, хотел узнать, у меня ли одного такая ошибка, что вводишь число с дробным значением(запятой), а оно ‘некоректно’?
Переведи на английский, в русском запятая не ставится
-
Кирилл Порозов
Участник
4 февраля 2018 г.

А если 4,23 можно так и оставить? Или обязательно округлить?
А если 4,23 можно так и оставить? Или обязательно округлить?
-
Ренат Акчурин
Участник
5 февраля 2018 г.
Здравствуйте, так как в низу было написано «округлять до 5 значащих, то в одной из задач я так и сделал. Верным ответом оказался 0,652, тогда как я написал 0,6522 и получил 0 баллов
Здравствуйте, так как в низу было написано «округлять до 5 значащих, то в одной из задач я так и сделал. Верным ответом оказался 0,652, тогда как я написал 0,6522 и получил 0 баллов
-
Алена Кирюхина
Участник
5 февраля 2018 г.
Почему не засчитано?
Почему не засчитано?
-
Иван Фролов
Участник
5 февраля 2018 г.

Алёна, потому что неправильно. Даже до 5 цифр: 0.20000А, а никак не 0.157
Не надоело спамить во все темы?
Алёна, потому что неправильно. Даже до 5 цифр: 0.20000А, а никак не 0.157
Не надоело спамить во все темы?
-
Абубакр Абдуллоев
Участник
5 февраля 2018 г.
У меня тоже такая ситуация
Я написал в ответе 0.1547 но зказано округлить до 5 значных цифр
Но в ответе 0.2
Как это понять.
Если округлит то получается 0.2
У меня тоже такая ситуация
Я написал в ответе 0.1547 но зказано округлить до 5 значных цифр
Но в ответе 0.2
Как это понять.
Если округлит то получается 0.2
-
Абубакр Абдуллоев
Участник
5 февраля 2018 г.

У меня тоже такая ситуация
Я написал в ответе 0.1547 но зказано округлить до 5 значных цифр
Но в ответе 0.2
Как это понять.
Если округлит то получается 0.2
У меня тоже такая ситуация
Я написал в ответе 0.1547 но зказано округлить до 5 значных цифр
Но в ответе 0.2
Как это понять.
Если округлит то получается 0.2
-
Анастасия Кочеткова
Участник
5 февраля 2018 г.
Идентичная ситуация.В задании сказано: округлите до десятых, я поставила — 2.4. В ответе- 2
Идентичная ситуация.В задании сказано: округлите до десятых, я поставила — 2.4. В ответе- 2
Назад в раздел
Округлить до целых онлайн. Округление
Образование
В математике округлением называют операцию, которая позволяет уменьшить в числе количество знаков при помощи их замены, учитывая определенные правила.
- Статистический — используют при уточнении численности жителей города. Говоря о количестве граждан, называют лишь приближенное значение, а не точную цифру.
- Половинный — округление половины происходит до ближайшего четного числа.
- Округление до меньшего числа (округление к нулю) — это самое легкое округление, при котором происходит отбрасывание всех «лишних» цифр.
- Округление до большего числа — если знаки, которые хотят округлить, не равны нулю, то число округляют в большую сторону. Такой способ используют провайдеры или операторы сотовой связи.
- Ненулевое округление — числа округляются по всем правилам, но когда результатом должен стать 0, то округление совершается «от нуля».
- Чередующееся округление — когда N+1 равняется 5-ти, число поочередно округляют то в меньшую, то в большую сторону.

К примеру, вам нужно округлить число 21,837 до сотых. После округления вашим правильным ответом должно стать 21,84. Объясним, почему. Цифра 8 входит в разряд десятых, следовательно, 3 в разряд сотых, а 7 — тысячных. 7 больше 5-ти, поэтому мы увеличиваем 3-ку на 1, то есть до 4-х. Это совсем несложно, если знать несколько правил:
1. Последняя сохраняемая цифра увеличивается на один в том случае, если первая отбрасываемая перед ней — больше чем 5. Если же эта цифра равняется 5-ти и за ней имеются еще какие-либо другие цифры, то предыдущая также увеличивается на 1.
Например, нам нужно округлить до десятых: 54,69=54,7, или 7,357=7,4.
Если вам задали вопрос о том, как округлить число до сотых, действуйте аналогично представленному выше варианту.
2. Последняя сохраняемая цифра остается неизменной, если первая из отбрасываемых, которая стоит перед ней меньше чем 5.
Пример: 96,71=96,7.
3. Последняя из сохраняемых цифр остается неизменной при условии, что она четная, и если первая из отбрасываемых — это число 5, и за ним нет больше никаких цифр. Если же оставляемая цифра — нечетная, то она увеличивается на 1.
Если же оставляемая цифра — нечетная, то она увеличивается на 1.
Примеры: 84,45=84,4 или 63,75=63,8.
Примечание. Во многих школах ученикам дают упрощенную версию правил округления, так что стоит иметь это в виду. В них все цифры остаются неизменными, если после них идут числа от 0 до 4 и увеличиваются на 1 при условии, что после стоит число от 5 до 9. Грамотно решать задачи с округлением по строгим правилам, но если в школе заведен упрощенный вариант, то во избежание недоразумений стоит придерживаться его. Надеемся, вы поняли, как округлить число до сотых.
Округление в жизни необходимо для удобства работы с числами и указания точности измерений. В настоящее время появилось такое определение, как анти-округление. Например, при подсчете голосов какого-либо исследования круглые числа считаются дурным тоном. Магазины тоже используют анти-округление для создания у покупателей впечатления более выгодной цены (к примеру, пишут 199, а не 200). Надеемся, что на вопрос о том, как округлить число до сотых или десятых, теперь вы сможете ответить и сами.
Посмотрим на примерах, как округлить до десятых числа, используя правила округления.
Правило округления числа до десятых.
Чтобы округлить десятичную дробь до десятых, надо оставить после запятой только одну цифру, а все остальные следующие за ней цифры отбросить.
Если первая из отброшенных цифр 0, 1, 2, 3 или 4, то предыдущую цифру не изменяем.
Если первая из отброшенных цифр 5, 6, 7, 8 или 9, то предыдущую цифру увеличиваем на единицу.
Примеры .
Округлить до десятых числа:
Чтобы округлить число до десятых, оставляем после запятой первую цифру, а остальное отбрасываем. Так как первая отброшенная цифра 5, то предыдущую цифру увеличиваем на единицу. Читают: «Двадцать три целых семьдесят пять сотых приближенно равно двадцать три целых восемь десятых».
Чтобы округлить до десятых данное число, оставляем после запятой лишь первую цифру, остальное — отбрасываем. Первая отброшенная цифра 1, поэтому предыдущую цифру не изменяем. Читают: «Триста сорок восемь целых тридцать одна сотая приближенно равно триста сорок одна целая три десятых».
Округляя до десятых, оставляем после запятой одну цифру, а остальные — отбрасываем. Первая из отброшенных цифр — 6, значит, предыдущую увеличиваем на единицу. Читают: «Сорок девять целых, девятьсот шестьдесят две тысячных приближенно равно пятьдесят целых, нуль десятых».
Округляем до десятых, поэтому после запятой оставляем только первую из цифр, остальные — отбрасываем. Первая из отброшенных цифр — 4, значит предыдущую цифру оставляем без изменений. Читают: «Семь целых двадцать восемь тысячных приближенно равно семь целых нуль десятых».
Чтобы округлить до десятых данное число, после запятой оставляет одну цифру, а все следующие за ней — отбрасываем. Так как первая отброшенная цифра — 7, следовательно, к предыдущей прибавляем единицу. Читают: «Пятьдесят шесть целых восемь тысяч семьсот шесть десятитысячных приближенно равно пятьдесят шесть целых, девять десятых».
И еще пара примеров на округление до десятых:
Числа, с которыми нам приходится иметь дело в реальной жизни, бывают двух типов. Одни в точности передают истинную величину, другие — только приблизительную. Первые называют точными , вторые — приближёнными .
Одни в точности передают истинную величину, другие — только приблизительную. Первые называют точными , вторые — приближёнными .
В реальной жизни чаще всего пользуются приближёнными числами вместо точных, так как последние обычно не требуются. Например, приближённые значения используются при указании таких величин как длина или вес. Во многих же случаях точное число найти невозможно.
Правила округления
Для получения приближённого значения, полученное в результате каких-либо действий число нужно округлить, то есть заменить его ближайшим круглым числом.
Числа всегда округляют до определённого разряда. Натуральные числа округляются до десятков, сотен, тысяч и т. д. При округлении чисел до десятков, их заменяют круглыми числами, состоящими только из целых десятков, у таких чисел в разряде единиц стоят нули. При округлении до сотен, числа заменяются на более круглые, состоящие только из целых сотен, то есть нули стоят уже и в разряде единиц, и в разряде десятков. И так далее.
И так далее.
Десятичные дроби можно округлять так же как и натуральные числа, то есть до десятков, сотен и т. д. Но также их можно округлять и до десятых, сотых, тысячных частей и т. д. При округлении десятичных знаков разряды не заполняются нулями, а просто отбрасываются. В обоих случаях округление производится по определённому правилу:
Если отбрасываемая цифра больше или равна 5, то предыдущую нужно увеличить на единицу, а если меньше 5, то предыдущая цифра не меняется.
Рассмотрим несколько примеров округления чисел:
- Округлить 43152 до тысяч. Здесь надо отбросить 152 единицы, так как справа от разряда тысяч стоит цифра 1, то предыдущую цифру отставляем без изменений. Приближённое значение числа 43152, округлённое до тысяч будет равно 43000.
- Округлить 43152 до сотен. Первая из отбрасываемых чисел 5, значит предыдущую цифру увеличиваем на единицу: 43152 ≈ 43200.
- Округлить 43152 до десятков: 43152 ≈ 43150.
- Округлить 17,7438 до единиц: 17,7438 ≈ 18.

- Округлить 17,7438 до десятых: 17,7438 ≈ 17,7.
- Округлить 17,7438 до сотых: 17,7438 ≈ 17,74.
- Округлить 17,7438 до тысячных: 17,7438 ≈ 17,744.
Знак ≈ называют знаком приближённого равенства, он читается — «приближённо равно».
Если при округлении числа результат получился больше начального значения, то полученное значение называется приближённым значением с избытком , если меньше — приближённым значением с недостатком :
7928 ≈ 8000, число 8000 — приближённое значением с избытком
5102 ≈ 5000, число 5000 — приближённое значением с недостатком
Это быстрый способ отображаются в виде числа округляется изменения его числа десятичных разрядов. Выберите соответствующий пункт номер необходимо округлить и откройте вкладку Главная > Уменьшить разрядность .
Число в ячейке будет казаться округленным, но фактическое значение не изменится — при ссылке на ячейку будет использоваться полное значение.
Округление чисел с помощью функций
Для округления фактических значений в ячейках, можно использовать ОКРУГЛЕНИЯ , ОКРУГЛВВЕРХ , ОКРУГЛВНИЗ и ОКРУГЛТ функции, как показано в следующих примерах.
Округление числа до ближайшего значения
В этом примере показано, как с помощью функции ОКРУГЛЕНИЯ округления чисел до ближайшего числа.
При округлении числа формат ячейки может переопределять отображаемый результат. Например, если во втором аргументе указано 4 десятичных разряда, но в формате ячейки задано отображение 2 чисел после запятой, будет применяться формат ячейки.
Округление числа до ближайшего дробного значения
В этом примере показано, как округлить число до ближайшего дробного значения с помощью функции ОКРУГЛЕНИЯ .
Округление числа вверх
функцию ОКРУГЛВВЕРХ .
Можно также использовать функции ЧЕТНЫЕ и НЕЧЕТНЫЕ для округления числа до ближайшего четного или нечетного целого числа. Эти функции имеют ограниченный использует и важно помнить, что они всегда выполнять округление вверх «и» только до целого числа.
Округление числа вниз
В этом примере показано, как используется Функция ОКРУГЛВНИЗ .
Округление числа до указанного количества значимых разрядов
В этом примере показано, как округлить число до определенного количества значимых разрядов. Значимые разряды — это разряды, которые влияют на точность числа.
Значимые разряды — это разряды, которые влияют на точность числа.
В списке ниже приведены общие правила, которые необходимо учитывать при округлении чисел до указанного количества значимых разрядов. Вы можете поэкспериментировать с функциями округления и подставить собственные числа и параметры, чтобы получить значение с нужным количеством разрядов.
При использовании функции ОКРУГЛ число округляется вверх, если его дробная часть равна 0,5 или больше этого значения. Если она меньше, число округляется вниз. Целые числа также округляются вверх или вниз согласно аналогичному правилу (при этом проверяется, не меньше ли 5 последняя цифра числа).
Как правило когда округление целое число, вычитание длины от количество значащих цифр, к которым нужно округлить. Например для округления 2345678 вниз до 3 значащих цифр, ОКРУГЛВНИЗ использовать с параметром – 4. Например = ROUNDDOWN(2345678,-4) Округление числа вниз 2340000 «234» части как значащих цифр.
Для округления отрицательное число, то же число сначала преобразуется в его абсолютное значение — значением без знак «минус». По завершении округления повторно применяется знак «минус». Например при использовании ОКРУГЛВНИЗ для округления -889 для двух результатов значащих цифр в -880 -889 преобразуется в 889 и округляется вниз до 880 . Знак «минус» затем повторно для конечный результат -880 .
По завершении округления повторно применяется знак «минус». Например при использовании ОКРУГЛВНИЗ для округления -889 для двух результатов значащих цифр в -880 -889 преобразуется в 889 и округляется вниз до 880 . Знак «минус» затем повторно для конечный результат -880 .
Округление числа до заданного кратного
Иногда бывает нужно округлить число до кратного. Например, если ваша компания поставляет товары в ящиках по 18 единиц, вам может потребоваться узнать, сколько ящиков нужно для поставки 204 единиц. Функция ОКРУГЛТ делит число на нужное кратное, а затем округляет результат. В данном случае ответом является 12, так как при делении 204 на 18 получается значение 11,333, которое округляется до 12 из-за наличия остатка. В 12-м ящике будет только 6 единиц товара.
В этом примере показано, как использовать функцию ОКРУГЛТ для округления числа до заданного кратного.
Округление мы часто используем в повседневной жизни. Если расстояние от дома до школы будет 503 метра. Мы можем сказать, округлив значение, что расстояние от дома до школы 500 метров. То есть мы приблизили число 503 к более легко воспринимающемуся числу 500. Например, булка хлеба весит 498 грамм, то можно сказать округлив результат, что булка хлеба весит 500 грамм.
Если расстояние от дома до школы будет 503 метра. Мы можем сказать, округлив значение, что расстояние от дома до школы 500 метров. То есть мы приблизили число 503 к более легко воспринимающемуся числу 500. Например, булка хлеба весит 498 грамм, то можно сказать округлив результат, что булка хлеба весит 500 грамм.
Округление – это приближение числа к более “легкому” числу для восприятия человека.
В итоге округления получается приближенное число. Округление обозначается символом ≈, такой символ читается “приближённо равно”.
Можно записать 503≈500 или 498≈500.
Читается такая запись, как “пятьсот три приближенно равно пятистам” или “четыреста девяносто восемь приближенно равно пятистам”.
Разберем еще пример:
44 71≈4000 45 71≈5000
43 71≈4000 46 71≈5000
42 71≈4000 47 71≈5000
41 71≈4000 48 71≈5000
40 71≈4000 49 71≈5000
В данном примере было произведено округление чисел до разряда тысяч. Если посмотреть закономерность округления, то увидим, что в одном случае числа округляются в меньшую сторону, а в другом – в большую. После округления все остальные числа после разряда тысяч заменили на нули.
После округления все остальные числа после разряда тысяч заменили на нули.
Правила округления чисел:
1) Если округляемая цифра равна 0, 1, 2, 3, 4, то цифра разряда до которого идет округление не меняется, а остальные числа заменяются нулями.
2) Если округляемая цифра равна 5, 6, 7, 8, 9, то цифра разряда до которого идет округление становиться на 1 больше, а остальные числа заменяются нулями.
Например:
1) Выполните округление до разряда десятков числа 364.
Разряд десятков в данном примере это число 6. После шестерки стоит число 4. По правилу округления цифра 4 разряд десятков не меняет. Записываем вместо 4 нуль. Получаем:
36 4 ≈360
2) Выполните округление до разряда сотен числа 4 781.
Разряд сотен в данном примере это число 7. После семерки стоит цифра 8, которая влияет на то измениться ли разряд сотен или нет. По правилу округления цифра 8 увеличивает разряд сотен на 1, а остальные цифры заменяем нулями. Получаем:
47 8 1≈48 00
3) Выполните округление до разряда тысяч числа 215 936.
Разряд тысяч в данном примере это число 5. После пятерки стоит цифра 9, которая влияет на то измениться ли разряд тысяч или нет. По правилу округления цифра 9 увеличивает разряд тысяч на 1, а остальные цифры заменяются нулями. Получаем:
215 9 36≈216 000
4) Выполните округление до разряда десятков тысяч числа 1 302 894.
Разряд тысяч в данном примере это число 0. После нуля стоит цифра 2, которая влияет на то измениться ли разряд десятков тысяч или нет. По правилу округления цифра 2 разряд десятков тысяч не меняет, заменяем на нуль этот разряд и все разряды младшие разряды. Получаем:
130 2 894≈130 0000
Если точное значение числа неважно, то значение числа округляют и можно выполнять вычислительные операции с приближенными значениями . Результат вычисления называют прикидкой результата действий .
Например: 598⋅23≈600⋅20≈12000 сравним с 598⋅23=13754
Прикидкой результата действий пользуются для того, чтобы быстро посчитать ответ.
Примеры на задания по теме округление:
Пример №1:
Определите до какого разряда сделано округление:
а) 3457987≈3500000 б)4573426≈4573000 в)16784≈17000
Вспомним какие бывают разряды на числе 3457987.
7 – разряд единиц,
8 – разряд десятков,
9 – разряд сотен,
7 – разряд тысяч,
5 – разряд десятков тысяч,
4
– разряд сотен тысяч,
3 – разряд миллионов.
Ответ: а) 3 4
57 987≈3 5
00 000 разряд сотен тысяч б) 4 573
426≈4 573
000 разряд тысяч в)16
7 841≈17
0 000 разряд десятков тысяч.
Пример №2:
Округлите число до разрядов 5 999 994: а) десятков б) сотен в) миллионов.
Ответ: а) 5 999 994
≈5 999 990 б) 5 999 99
4≈6 000 000 (т.к. разряды сотен, тысяч, десятков тысяч, сотен тысяч цифра 9, каждый разряд увеличился на 1) 5 9
99 994≈6 000 000.
Онлайн округление чисел. Как округлить до десятых
Сегодня мы рассмотрим довольно скучную тему, без понимания которой двигаться дальше не представляется возможным.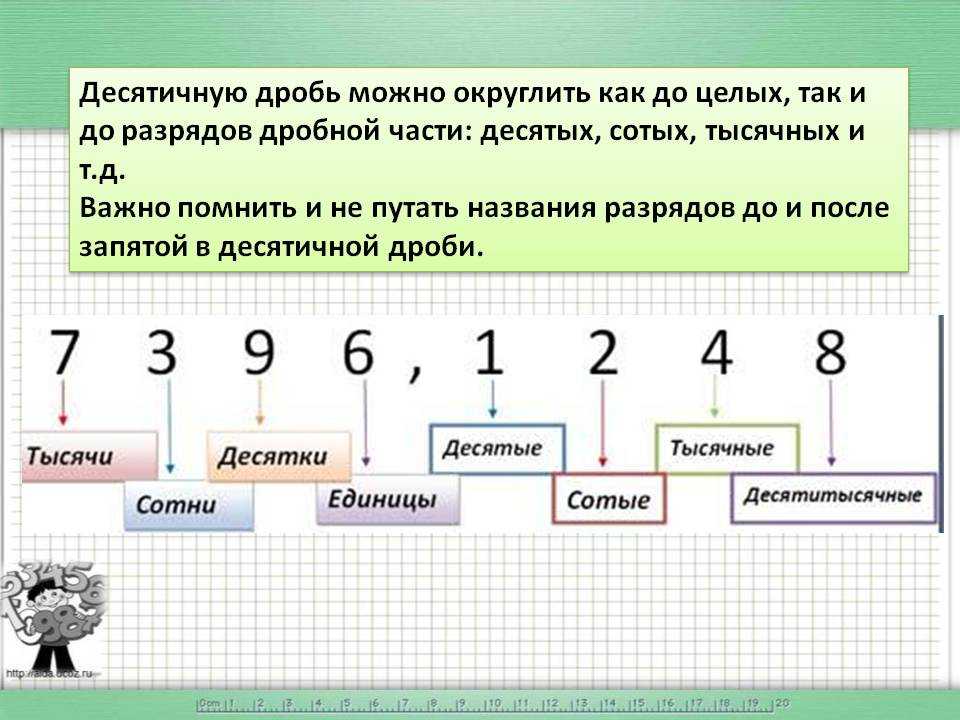 Эта тема называется «округление чисел» или по-другому «приближённые значения чисел».
Эта тема называется «округление чисел» или по-другому «приближённые значения чисел».
Содержание урока
Приближённые значения
Приближённые (или приблизительные) значения применяются тогда, когда точное значение чего-либо найти невозможно, или же это значение не важно для исследуемого предмета.
Например, на словах можно сказать, что в городе проживает полмиллиона человек, но это высказывание не будет истинным, поскольку количество человек в городе меняется — люди приезжают и уезжают, рождаются и умирают. Поэтому правильнее будет сказать, что в городе проживает приблизительно полмиллиона человек.
Ещё пример. В девять утра начинаются занятия. Мы вышли из дома в 8:30. Через некоторое время по дороге мы встретили своего товарища, который спросил у нас сколько сейчас времени. Когда мы выходили из дома было 8:30, на дорогу мы потратили какое-то неизвестное время. Мы не знаем сколько сейчас времени, поэтому отвечаем товарищу: «сейчас приблизительно около девяти часов».
В математике приближенные значения указываются с помощью специального знака. Выглядит он следующим образом:
Читается как «приблизительно равно».
Чтобы указать приблизительное значение чего-либо, прибегают к такой операции, как округление чисел.
Округление чисел
Для нахождения приближенного значения применяется такая операция, как округление чисел .
Слово «округление» говорит само за себя. Округлить число значит сделать его круглым. Круглым называется число, которое оканчивается нулем. Например, следующие числа являются круглыми,
10, 20, 30, 100, 300, 700, 1000
Любое число можно сделать круглым. Процедуру, при которой число делают круглым, называют округлением числа .
Мы уже занимались «округлением» чисел, когда делили большие числа. Напомним, что для этого мы оставляли без изменения цифру, образующую старший разряд, а остальные цифры заменяли нулями. Но это были лишь наброски, которые мы делали для облегчения деления. Своего рода лайфхак . По факту, это даже не являлось округлением чисел. Именно поэтому в начале данного абзаца мы взяли слово округление в кавычки.
Своего рода лайфхак . По факту, это даже не являлось округлением чисел. Именно поэтому в начале данного абзаца мы взяли слово округление в кавычки.
На самом деле, суть округления заключается в том, чтобы найти ближайшее значение от исходного. При этом, число может быть округлено до определённого разряда — до разряда десятков, разряда сотен, разряда тысяч.
Рассмотрим простой пример на округление. Дано число 17. Требуется округлить его до разряда десятков.
Не забегая вперёд попробуем понять, что означает «округлить до разряда десятков». Когда говорят округлить число 17, от нас требуют найти ближайшее круглое число для числа 17. При этом, в ходе этого поиска возможно изменения коснутся и цифры, которая находится в разряде десятков в числе 17 (т.е единицы).
Представим, что все числа от 10 до 20 лежат на прямой линии:
На рисунке видно, что для числа 17 ближайшее круглое число это 20. Значит ответ к задаче таким и будет: 17 приблизительно равно 20
17 ≈ 20
Мы нашли приближённое значение для 17, то есть округлили его до разряда десятков. Видно, что после округления в разряде десятков появилась новая цифра 2.
Видно, что после округления в разряде десятков появилась новая цифра 2.
Попробуем найти приближённое число для числа 12. Для этого снова представим, что все числа от 10 до 20 лежат на прямой линии:
На рисунке видно, что ближайшее круглое число для 12 это число 10. Значит ответ к задаче таким и будет: 12 приблизительно равно 10
12 ≈ 10
Мы нашли приближённое значение для 12, то есть округлили его до разряда десятков. В этот раз цифра 1, которая стояла в разряде десятков в числе 12, не пострадала от округления. Почему так случилось мы рассмотрим позже.
Попробуем найти ближайшее число для числа 15. Снова представим, что все числа от 10 до 20 лежат на прямой линии:
На рисунке видно, что число 15 одинаково удалено от круглых чисел 10 и 20. Возникает вопрос: которое из этих круглых чисел будет приближённым значением для числа 15? Для таких случаев условились принимать большее число за приближённое. 20 больше чем 10, поэтому приближённое значение для 15 будет число 20
15 ≈ 20
Округлять можно и большие числа. Естественно, для них рисовать прямую линию и изображать числа не представляется возможным. Для них существует свой способ. Например, округлим число 1456 до разряда десятков.
Естественно, для них рисовать прямую линию и изображать числа не представляется возможным. Для них существует свой способ. Например, округлим число 1456 до разряда десятков.
Мы должны округлить 1456 до разряда десятков. Разряд десятков начинается на пятёрке:
Теперь о существовании первых цифр 1 и 4 временно забываем. Остается число 56
Теперь смотрим, какое круглое число находится ближе к числу 56. Очевидно, что ближайшее круглое число для 56 это число 60. Значит заменяем число 56 на число 60
Значит при округлении числа 1456 до разряда десятков получим 1460
1456 ≈ 1460
Видно, что после округления числа 1456 до разряда десятков, изменения коснулись и самого разряда десятков. В новом полученном числе в разряде десятков теперь располагается цифра 6, а не 5.
Округлять числа можно не только до разряда десятков. Округлять можно также до разряда сотен, тысяч, десятков тысяч.
После того, как становится понятно, что округление это ни что иное, как поиск ближайшего числа, можно применять готовые правила, которые значительно облегчают округление чисел.
Первое правило округления
Из предыдущих примеров стало ясно, что округляя число до определенного разряда, младшие разряды заменяются нулями. Цифры, которые заменяются нулями, называют отбрасываемыми цифрами .
Первое правило округления выглядит следующим образом:
Если при округлении чисел первая из отбрасываемых цифр 0, 1, 2, 3 или 4, то сохраняемая цифра остаётся без изменений.
Например, округлим число 123 до разряда десятков.
В первую очередь находим сохраняемую цифру. Для этого надо прочитать само задание. В разряде, о котором говорится в задании и находится сохраняемая цифра. В задании сказано: округлить число 123 до разряда десятков.
Видим, что в разряде десятков находится двойка. Значит сохраняемой цифрой является цифра 2
Теперь находим первую из отбрасываемых цифр. Первой из отбрасываемых цифр является та цифра, которая следует после сохраняемой цифрой. Видим, что первая цифра после двойки это цифра 3. Значит цифра 3 является первой отбрасываемой цифрой .
Теперь применяем правило округления. Оно говорит, что если при округлении чисел первая из отбрасываемых цифр 0, 1, 2, 3 или 4, то сохраняемая цифра остаётся без изменений.
Так и делаем. Оставляем без изменения сохраняемую цифру, а все младшие разряды заменяем нулями. Другими словами, всё что следует после цифры 2 заменяем нулями (точнее нулём):
123 ≈ 120
Значит при округлении числа 123 до разряда десятков, получаем приближённое ему число 120.
Теперь попробуем округлить то же самое число 123, но уже до разряда сотен .
Нам требуется округлить число 123 до разряда сотен. Снова ищем сохраняемую цифру. В этот раз сохраняемой цифрой является 1, поскольку мы округляем число до разряда сотен.
Теперь находим первую из отбрасываемых цифр. Первой из отбрасываемых цифр является та цифра, которая следует после сохраняемой цифрой. Видим, что первая цифра после единицы это цифра 2. Значит цифра 2 является первой отбрасываемой цифрой:
Теперь применим правило. Оно говорит, что если при округлении чисел первая из отбрасываемых цифр 0, 1, 2, 3 или 4, то сохраняемая цифра остаётся без изменений.
Оно говорит, что если при округлении чисел первая из отбрасываемых цифр 0, 1, 2, 3 или 4, то сохраняемая цифра остаётся без изменений.
Так и делаем. Оставляем без изменения сохраняемую цифру, а все младшие разряды заменяем нулями. Другими словами, всё что следует после цифры 1 заменяем нулями:
123 ≈ 100
Значит при округлении числа 123 до разряда сотен, получаем приближённое ему число 100.
Пример 3. Округлить число 1234 до разряда десятков.
Здесь сохраняемая цифра это 3. А первая отбрасываемая цифра это 4.
Значит оставляем сохраняемую цифру 3 без изменений, а всё что располагается после неё заменяем нулём:
1234 ≈ 1230
Пример 4. Округлить число 1234 до разряда сотен.
Здесь сохраняемая цифра это 2. А первая отбрасываемая цифра это 3. Согласно правилу, если при округлении чисел первая из отбрасываемых цифр 0, 1, 2, 3 или 4, то сохраняемая цифра остаётся без изменений.
Значит оставляем сохраняемую цифру 2 без изменений, а всё что располагается после неё заменяем нулями:
1234 ≈ 1200
Пример 3. Округлить число 1234 до разряда тысяч.
Округлить число 1234 до разряда тысяч.
Здесь сохраняемая цифра это 1. А первая отбрасываемая цифра это 2. Согласно правилу, если при округлении чисел первая из отбрасываемых цифр 0, 1, 2, 3 или 4, то сохраняемая цифра остаётся без изменений.
Значит оставляем сохраняемую цифру 1 без изменений, а всё что располагается после неё заменяем нулями:
1234 ≈ 1000
Второе правило округления
Второе правило округления выглядит следующим образом:
Если при округлении чисел первая из отбрасываемых цифр 5, 6, 7, 8 или 9, то сохраняемая цифра увеличивается на единицу.
Например, округлим число 675 до разряда десятков.
В первую очередь находим сохраняемую цифру. Для этого надо прочитать само задание. В разряде, о котором говорится в задании и находится сохраняемая цифра. В задании сказано: округлить число 675 до разряда десятков.
Видим, что в разряде десятков находится семёрка. Значит сохраняемой цифрой является цифра 7
Теперь находим первую из отбрасываемых цифр. Первой из отбрасываемых цифр является та цифра, которая следует после сохраняемой цифрой. Видим, что первая цифра после семёрки это цифра 5. Значит цифра 5 является первой отбрасываемой цифрой .
Первой из отбрасываемых цифр является та цифра, которая следует после сохраняемой цифрой. Видим, что первая цифра после семёрки это цифра 5. Значит цифра 5 является первой отбрасываемой цифрой .
У нас первая из отбрасываемых цифр это 5. Значит мы должны увеличить на единицу сохраняемую цифру 7, а всё что следует после неё заменить нулём:
675 ≈ 680
Значит при округлении числа 675 до разряда десятков, получаем приближённое ему число 680.
Теперь попробуем округлить то же самое число 675, но уже до разряда сотен .
Нам требуется округлить число 675 до разряда сотен. Снова ищем сохраняемую цифру. В этот раз сохраняемой цифрой является 6, поскольку мы округляем число до разряда сотен:
Теперь находим первую из отбрасываемых цифр. Первой из отбрасываемых цифр является та цифра, которая следует после сохраняемой цифрой. Видим, что первая цифра после шестёрки это цифра 7. Значит цифра 7 является первой отбрасываемой цифрой:
Теперь применяем второе правило округления. Оно говорит, что если при округлении чисел первая из отбрасываемых цифр 5, 6, 7, 8 или 9, то сохраняемая цифра увеличивается на единицу.
Оно говорит, что если при округлении чисел первая из отбрасываемых цифр 5, 6, 7, 8 или 9, то сохраняемая цифра увеличивается на единицу.
У нас первая из отбрасываемых цифр это 7. Значит мы должны увеличить на единицу сохраняемую цифру 6, а всё что следует после неё заменить нулями:
675 ≈ 700
Значит при округлении числа 675 до разряда сотен, получаем приближённое ему число 700.
Пример 3. Округлить число 9876 до разряда десятков.
Здесь сохраняемая цифра это 7. А первая отбрасываемая цифра это 6.
Значит увеличиваем на единицу сохраняемую цифру 7, а всё что располагается после неё заменяем нулём:
9876 ≈ 9880
Пример 4. Округлить число 9876 до разряда сотен.
Здесь сохраняемая цифра это 8. А первая отбрасываемая цифра это 7. Согласно правилу, если при округлении чисел первая из отбрасываемых цифр 5, 6, 7, 8 или 9, то сохраняемая цифра увеличивается на единицу.
Значит увеличиваем на единицу сохраняемую цифру 8, а всё что располагается после неё заменяем нулями:
9876 ≈ 9900
Пример 5. Округлить число 9876 до разряда тысяч.
Округлить число 9876 до разряда тысяч.
Здесь сохраняемая цифра это 9. А первая отбрасываемая цифра это 8. Согласно правилу, если при округлении чисел первая из отбрасываемых цифр 5, 6, 7, 8 или 9, то сохраняемая цифра увеличивается на единицу.
Значит увеличиваем на единицу сохраняемую цифру 9, а всё что располагается после неё заменяем нулями:
9876 ≈ 10000
Пример 6. Округлить число 2971 до сотен.
При округлении этого числа до сотен следует быть внимательным, поскольку сохраняемая цифра здесь 9, а первая отбрасываемая цифра это 7. Значит цифра 9 должна увеличиться на единицу. Но дело в том, что после увеличения девятки на единицу получится 10, а это цифра не вместится в разряд сотен нового числа.
В этом случае, в разряде сотен нового числа надо записать 0, а единицу перенести на следующий разряд и сложить с цифрой, которая там находится. Далее заменить все цифры после сохраняемой нулями:
2971 ≈ 3000
Округление десятичных дробей
При округлении десятичных дробей следует быть особенно внимательным, поскольку десятичная дробь состоит из целой и дробной части. И каждая из этих двух частей имеет свои разряды:
И каждая из этих двух частей имеет свои разряды:
Разряды целой части:
- разряд единиц
- разряд десятков
- разряд сотен
- разряд тысяч
Разряды дробной части:
- разряд десятых
- разряд сотых
- разряд тысячных
Рассмотрим десятичную дробь 123,456 — сто двадцать три целых четыреста пятьдесят шесть тысячных. Здесь целая часть это 123, а дробная часть 456. При этом у каждой из этих частей есть свои разряды. Очень важно не путать их:
Для целой части применяются те же правила округления, что и для обычных чисел. Отличие в том, что после округления целой части и замены нулями всех цифр после сохраняемой цифры, дробная часть полностью отбрасывается.
Например, округлим дробь 123,456 до разряда десятков. Именно до разряда десятков , а не разряда десятых . Очень важно не перепутать эти разряды. Разряд десятков располагается в целой части, а разряд десятых в дробной.
Мы должны округлить 123,456 до разряда десятков. Сохраняемая цифра здесь это 2, а первая из отбрасываемых цифр это 3
Согласно правилу, если при округлении чисел первая из отбрасываемых цифр 0, 1, 2, 3 или 4, то сохраняемая цифра остаётся без изменений.
Значит сохраняемая цифра останется без изменений, а всё остальное заменится нулём. А что делать с дробной частью? Её просто отбрасывают (убирают):
123,456 ≈ 120
Теперь попробуем округлить ту же самую дробь 123,456 до разряда единиц . Сохраняемая цифра здесь будет 3, а первая из отбрасываемых цифр это 4, которая находится в дробной части:
Согласно правилу, если при округлении чисел первая из отбрасываемых цифр 0, 1, 2, 3 или 4, то сохраняемая цифра остаётся без изменений.
Значит сохраняемая цифра останется без изменений, а всё остальное заменится нулём. Оставшаяся дробная часть будет отброшена:
123,456 ≈ 123,0
Ноль, который остался после запятой тоже можно отбросить. Значит окончательный ответ будет выглядеть следующим образом:
Значит окончательный ответ будет выглядеть следующим образом:
123,456 ≈ 123,0 ≈ 123
Теперь займёмся округлением дробных частей. Для округления дробных частей справедливы те же правила, что и для округления целых частей. Попробуем округлить дробь 123,456 до разряда десятых. В разряде десятых располагается цифра 4, значит она является сохраняемой цифрой, а первая отбрасываемая цифра это 5, которая находится в разряде сотых:
Согласно правилу, если при округлении чисел первая из отбрасываемых цифр 5, 6, 7, 8 или 9, то сохраняемая цифра увеличивается на единицу.
Значит сохраняемая цифра 4 увеличится на единицу, а остальная часть заменится нулями
123,456 ≈ 123,500
Попробуем округлить ту же самую дробь 123,456 до разряда сотых. Сохраняемая цифра здесь это 5, а первая из отбрасываемых цифр это 6, которая находится в разряде тысячных:
Согласно правилу, если при округлении чисел первая из отбрасываемых цифр 5, 6, 7, 8 или 9, то сохраняемая цифра увеличивается на единицу.
Значит сохраняемая цифра 5 увеличится на единицу, а остальная часть заменится нулями
123,456 ≈ 123,460
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Посмотрим на примерах, как округлить до десятых числа, используя правила округления.
Правило округления числа до десятых.
Чтобы округлить десятичную дробь до десятых, надо оставить после запятой только одну цифру, а все остальные следующие за ней цифры отбросить.
Если первая из отброшенных цифр 0, 1, 2, 3 или 4, то предыдущую цифру не изменяем.
Если первая из отброшенных цифр 5, 6, 7, 8 или 9, то предыдущую цифру увеличиваем на единицу.
Примеры .
Округлить до десятых числа:
Чтобы округлить число до десятых, оставляем после запятой первую цифру, а остальное отбрасываем. Так как первая отброшенная цифра 5, то предыдущую цифру увеличиваем на единицу. Читают: «Двадцать три целых семьдесят пять сотых приближенно равно двадцать три целых восемь десятых».
Чтобы округлить до десятых данное число, оставляем после запятой лишь первую цифру, остальное — отбрасываем. Первая отброшенная цифра 1, поэтому предыдущую цифру не изменяем. Читают: «Триста сорок восемь целых тридцать одна сотая приближенно равно триста сорок одна целая три десятых».
Округляя до десятых, оставляем после запятой одну цифру, а остальные — отбрасываем. Первая из отброшенных цифр — 6, значит, предыдущую увеличиваем на единицу. Читают: «Сорок девять целых, девятьсот шестьдесят две тысячных приближенно равно пятьдесят целых, нуль десятых».
Округляем до десятых, поэтому после запятой оставляем только первую из цифр, остальные — отбрасываем. Первая из отброшенных цифр — 4, значит предыдущую цифру оставляем без изменений. Читают: «Семь целых двадцать восемь тысячных приближенно равно семь целых нуль десятых».
Чтобы округлить до десятых данное число, после запятой оставляет одну цифру, а все следующие за ней — отбрасываем. Так как первая отброшенная цифра — 7, следовательно, к предыдущей прибавляем единицу. Читают: «Пятьдесят шесть целых восемь тысяч семьсот шесть десятитысячных приближенно равно пятьдесят шесть целых, девять десятых».
Читают: «Пятьдесят шесть целых восемь тысяч семьсот шесть десятитысячных приближенно равно пятьдесят шесть целых, девять десятых».
И еще пара примеров на округление до десятых:
§ 4. Округление результатов
Обработка результатов измерений в лабораториях проводятся на калькуляторах и ПК, и просто удивительно, как магически действует на многих студентов длинных ряд цифр после запятой. «Так точнее» считают они. Однако легко видеть, например, что запись a = 2.8674523 ± 0.076 бессмысленна. При ошибке 0.076 последние пять цифр числа не означает ровно ничего.
Если мы допускаем ошибку в сотых долях, то тысячным, тем более десятитысячным долям веры нет. Грамотная запись результата была бы 2.87 ± 0.08. Всегда нужно производить необходимые округления, чтобы не было ложного впечатления о большей, чем это есть на самом деле, точности результатов.
Правила округления
- Погрешность измерения округляют до первой значащей цифры, всегда увеличивая ее на единицу.

Примеры:8.27 ≈ 9 0.237 ≈ 0.3 0.0862 ≈ 0.09 0.00035 ≈ 0.0004 857.3 ≈ 900 43.5 ≈ 50 - Результаты измерения округляют с точностью «до погрешности», т.е. последняя значащая цифра в результате должна находиться в том же разряде, что и в погрешности.
Примеры:243.871 ± 0.026 ≈ 243.87 ± 0.03;
243.871 ± 2.6 ≈ 244 ± 3;
1053 ± 47 ≈ 1050 ± 50. - Округление результата измерения достигается простым отбрасыванием цифр, если первая из отбрасываемых
цифр меньше 5.
Примеры:8.337 (округлить до десятых) ≈ 8.3;
833.438 (округлить до целых) ≈ 833;
0.27375 (округлить до сотых) ≈ 0.27. - Если первая из отбрасываемых цифр больше или равна 5 , (а за ней одна или несколько цифр отличны от нуля), то
последняя из остающихся цифр увеличивается на единицу.
Примеры:8.3351 (округлить дл сотых) ≈ 8.34;
0. 2510 (округлитьь до десятых) ≈ 0.3;
2510 (округлитьь до десятых) ≈ 0.3;
271.515 (округлить до целых) ≈ 272. - Если отбрасываемая цифра равна 5 , а за ней нет значащих цифр (или стоят одни нули), то последнюю оставляемую цифру увеличивают на единицу, когда она нечетная, и оставляют неизменной, когда она четная.
Примеры:0.875 (округлить до сотых) ≈ 0.88;
0.5450 (округлить до сотых) ≈ 0.54;
275.500 (округлить до целых) ≈ 276;
276.500 (округлить до целых) ≈ 276.
Примечание.
- Значащими называют верные цифры числа, кроме нулей, стоящих впереди числа. Например, 0,00807 в этом
числе имеется три значащих цифры: 8, ноль между 8 и 7 и 7 ; первые три нуля незначащие.
8.12 · 10 3 в этом числе 3 значащих цифры. - Записи 15,2 и 15,200 различны. Запись 15,200 означает, что верны сотые и тысячные доли. В записи 15,2 верны целые и десятые доли.
- Результаты физических экспериментов записывают только значащими цифрами. Запятую ставят сразу после отличной от нуля цифры, а число умножают на десять в соответствующей степени.
 Нули, стоящие в начале или
конце числа, как правило, не записывают. Например, числа 0,00435 и 234000 записывают так: 4,35·10 -3
и 2,34·10 5 . Подобная запись упрощает вычисления, особенно в случае формул, удобных для
логарифмирования.
Нули, стоящие в начале или
конце числа, как правило, не записывают. Например, числа 0,00435 и 234000 записывают так: 4,35·10 -3
и 2,34·10 5 . Подобная запись упрощает вычисления, особенно в случае формул, удобных для
логарифмирования.
Введение………………………………………………………………………………………………. | |
ЗАДАЧА № 1. Ряды предпочтительных чисел……………………………………….. | |
ЗАДАЧА № 2. Округление результатов измерений………………………………… | |
ЗАДАЧА № 3. Обработка результатов измерений………………………………….. | |
ЗАДАЧА № 4. Допуски и посадки гладких цилиндрических соединений… | |
ЗАДАЧА
№ 5. | |
ЗАДАЧА № 6. Шероховатость поверхности…………………………………………. | |
ЗАДАЧА № 7. Размерные цепи……………………………………………………………… | |
Список литературы……………………………………………………………………………….. |
При выполнении измерений важно соблюдать определенные правила округления и записи их результатов в технической документации, так как при несоблюдении этих правил возможны существенные ошибки в интерпретации результатов измерений.
Правила записи чисел
1. Значащие цифры данного числа — все цифры от первой слева, не равной нулю, до последней справа. При этом нули, следующие из множителя 10, не учитывают.
Примеры.
а) Число 12,0 имеет три значащие цифры.
б) Число 30 имеет две значащие цифры.
в) Число 12010 8 имеет три значащие цифры.
г) 0,51410 -3 имеет три значащие цифры.
д) 0,0056 имеет две значащие цифры.
2. Если необходимо указать, что число является точным, после числа указывают слово «точно» или последнюю значащую цифру печатают жирным шрифтом. Например: 1 кВт / ч = 3600 Дж (точно) или 1 кВт / ч = 3600 Дж.
3.
Различают записи приближенных чисел
по количеству значащих цифр. Например,
различают числа 2,4 и 2,40. Запись 2,4 означает,
что верны только целые и десятые доли,
истинное значение числа может быть,
например, 2,43 и 2,38. Запись 2,40 означает,
что верны и сотые доли: истинное значение
числа может быть 2,403 и 2,398, но не 2,41 и не
2,382. Запись 382 означает, что все цифры
верны: если за последнюю цифру ручаться
нельзя, то число должно быть записано
3,810 2 . Если в
числе 4720 верны лишь две первые цифры,
оно должно быть записано в виде: 4710 2 или 4,710 3 .
4. Число, для которого указывают допустимое отклонение, должно иметь последнюю значащую цифру того же разряда, как и последняя значащая цифра отклонения.
Примеры.
а) Правильно: 17,0 + 0,2. Неправильно: 17 + 0,2 или 17,00 + 0,2.
б) Правильно: 12,13+ 0,17. Неправильно: 12,13+ 0,2.
в) Правильно: 46,40+ 0,15. Неправильно: 46,4+ 0,15 или 46,402+ 0,15.
5. Числовые значения величины и её погрешности (отклонения) целесообразно записывать с указанием одной и той же единицы величины. Например: (80,555 + 0,002) кг.
6. Интервалы между числовыми значениями величин иногда целесообразно записывать в текстовом виде, тогда предлог «от» означает «», предлог «до»– «», предлог «свыше» – «>», предлог «менее» – «
«d принимает значения от 60 до 100″ означает «60d 100″,
«d принимает значения свыше 120 менее 150″ означает «120 d
«d принимает значения свыше 30 до 50″
означает «30 d
50».
Правила округления чисел
1. Округление числа представляет собой отбрасывание значащих цифр справа до определенного разряда с возможным изменением цифры этого разряда.
2. В случае если первая из отбрасываемых цифр (считая слева направо) менее 5, то последнюю сохраняемую цифру не меняют.
Пример: Округление числа 12,23 до трех значащих цифр дает 12,2.
3. В случае если первая из отбрасываемых цифр (считая слева направо) равна 5, то последнюю сохраняемую цифру увеличивают на единицу.
Пример: Округление числа 0,145 до двух цифр дает 0,15.
Примечание . В тех случаях, когда следует учитывать результаты предыдущих округлений, поступают следующим образом.
4. Если отбрасываемая
цифра получена в результате округления
в меньшую сторону, то последнюю оставшуюся
цифру увеличивают на единицу (с переходом
при необходимости в следующие разряды)
, иначе – наоборот. Это
касается и дробных и целых чисел.
Пример: Округление числа 0,25 (полученного в результате предыдущего округления числа 0,252) дает 0,3.
4. В случае если первая из отбрасываемых цифр (считая слева направо) более 5, то последнюю сохраняемую цифру увеличивают на единицу.
Пример: Округление числа 0,156 до двух значащих цифр дает 0,16.
5. Округление выполняют сразу до желаемого количества значащих цифр, а не по этапам.
Пример: Округление числа 565,46 до трех значащих цифр дает 565.
6. Целые числа округляют по тем же правилам, что и дробные.
Пример: Округление числа 23456 до двух значащих цифр дает 2310 3
Числовое значение результата измерения должно оканчиваться цифрой того же разряда, что и значение погрешности.
Пример: Число 235,732 + 0,15 должно быть округлено до 235,73 + 0,15, но не до 235,7 + 0,15.
7. Если первая из
отбрасываемых цифр (считая слева направо)
меньше пяти, то остающиеся цифры не
меняются.
Если первая из
отбрасываемых цифр (считая слева направо)
меньше пяти, то остающиеся цифры не
меняются.
Пример: 442,749+ 0,4 округляется до 442,7+ 0,4.
8. Если первая из отбрасываемых цифр больше или равна пяти, то последняя сохраняемая цифра увеличивается на единицу.
Пример: 37,268 + 0,5 округляется до 37,3 + 0,5; 37,253 + 0,5 должно быть округлено до 37,3 + 0,5.
9. Округление следует выполнять сразу до желаемого числа значащих цифр, поэтапное округление может привести к ошибкам.
Пример: Поэтапное округление результата измерения 220,46+ 4 дает на первом этапе 220,5+ 4 и на втором 221+ 4, в то время как правильный результат округления 220+ 4.
10.
Если погрешность средств измерения
указывается всего с
одной или двумя значащими цифрами, а
рассчетное значение погрешности
получают с большим числом знаков, в
окончательном значении рассчитанной
погрешности должны быть оставлены
соответственно только первые одна или
две значащие цифры. При этом, если
полученное число начинается с цифр 1
или 2, то отбрасывание второго знака
приводит к очень большой ошибке (до
3050
%), что недопустимо. Если же полученное
число начинается с цифры 3 и более,
например, с цифры 9, то сохранение второго
знака, т.е. указание погрешности, например,
0,94 вместо 0,9, является дезинформацией,
так как исходные данные не обеспечивают
такой точности.
При этом, если
полученное число начинается с цифр 1
или 2, то отбрасывание второго знака
приводит к очень большой ошибке (до
3050
%), что недопустимо. Если же полученное
число начинается с цифры 3 и более,
например, с цифры 9, то сохранение второго
знака, т.е. указание погрешности, например,
0,94 вместо 0,9, является дезинформацией,
так как исходные данные не обеспечивают
такой точности.
Исходя из этого на практике установилось такое правило: если полученное число начинается со значащей цифры, равной или большей 3, то в нем сохраняется лишь она одна; если же оно начинается со значащих цифр, меньших 3, т.е. с цифр 1 и 2, то в нем сохраняют две значащих цифры. В соответствии с этим правилом установлены и нормируемые значения погрешностей средств измерений: в числах 1,5 и 2,5 % указываются две значащих цифры, но в числах 0,5; 4; 6 % указывается лишь одна значащая цифра.
Пример: На
вольтметре класса точности 2,5 с пределом измерений х К = 300 В
был получен отсчет измеряемого напряжения
х = 267,5 В. В каком виде должен быть записан
результат измерения в отчете?
В каком виде должен быть записан
результат измерения в отчете?
Расчет погрешности удобнее вести в следующем порядке: вначале необходимо найти абсолютную погрешность, а затем – относительную. Абсолютная погрешность х = 0 х К /100, для приведенной погрешности вольтметра 0 = 2,5 % и пределов измерения (диапазона измерения) прибора х К = 300 В: х = 2,5300/100 = 7,5 В ~ 8 В; относительная погрешность = х 100/х = 7,5100/267,5 = 2,81 % ~ 2,8 % .
Так
как первая значащая цифра значения
абсолютной погрешности (7,5 В) больше
трех, то это значение должно быть
округлено по обычным правилам округления
до 8 В, но в значении относительной
погрешности (2,81 %) первая значащая цифра
меньше 3, поэтому здесь должны быть
сохранены в ответе два десятичных
разряда и указано
= 2,8 %. Полученное значение х = 267,5 В
должно быть округлено до того же
десятичного разряда, которым оканчивается
округленное значение абсолютной
погрешности, т. е. до целых единиц вольт.
е. до целых единиц вольт.
Таким образом, в окончательном ответе должно быть сообщено: «Измерение произведено с относительной погрешностью = 2,8 % . Измеренное напряжениеХ = (268+ 8) В».
При этом более наглядно указать пределы интервала неопределенности измеренной величины в виде Х = (260276) В или 260 ВX276 В.
Программа Microsoft Excel работает, в том числе, и с числовыми данными. При выполнении деления или работе с дробными числами, программа производит округление. Это связано, прежде всего, с тем, что абсолютно точные дробные числа редко когда бывают нужны, но оперировать громоздким выражением с несколькими знаками после запятой не очень удобно. Кроме того, существуют числа, которые в принципе точно не округляются. Но, в то же время, недостаточно точное округление может привести к грубым ошибкам в ситуациях, где требуется именно точность. К счастью, в программе Microsoft Excel имеется возможность самим пользователям устанавливать, как будут округляться числа.
Все числа, с которыми работает программа Microsoft Excel, делятся на точные и приближенные. В памяти хранятся числа до 15 разряда, а отображаются до того разряда, который укажет сам пользователь. Но, при этом, все расчеты выполняются согласно хранимых в памяти, а не отображаемых на мониторе данным.
С помощью операции округления, Microsoft Excel отбрасывает некоторое количество знаков после запятой. В Excel применяется общепринятый способ округления, когда число меньше 5 округляется в меньшую сторону, а больше или равно 5 – в большую сторону.
Округление с помощью кнопок на ленте
Самым простым способом изменить округление числа — это выделить ячейку или группу ячеек, и находясь во вкладке «Главная», нажать на ленте на кнопку «Увеличить разрядность» или «Уменьшить разрядность». Обе кнопки располагаются в блоке инструментов «Число». При этом, будет округляться только отображаемое число, но для вычислений, при необходимости будут задействованы до 15 разрядов чисел.
При нажатии на кнопку «Увеличить разрядность», количество внесенных знаков после запятой увеличивается на один.
При нажатии на кнопку «Уменьшить разрядность» количество цифр после запятой уменьшается на одну.
Округление через формат ячеек
Также можно выставить округление с помощью настроек формата ячеек. Для этого, нужно выделить диапазон ячеек на листе, кликнуть правой кнопкой мыши, и в появившемся меню выбрать пункт «Формат ячеек».
В открывшемся окне настроек формата ячеек нужно перейти во вкладку «Число». Если формат данных указан не числовой, то нужно выбрать именно числовой формат, иначе вы не сможете регулировать округление. В центральной части окна около надписи «Число десятичных знаков» просто указываем цифрой то число знаков, которое желаем видеть при округлении. После этого, выполняем клик по кнопке «OK».
Установка точности расчетов
Если в предыдущих случаях, устанавливаемые параметры влияли только на внешнее отображения данных, а при расчетах использовались более точные показатели (до 15 знака), то сейчас мы расскажем, как изменить саму точность расчетов.
Открывается окно параметров Excel. В этом окне переходим в подраздел «Дополнительно». Ищем блок настроек под названием «При пересчете этой книги». Настройки в данном бока применяются ни к одному листу, а ко всей книги в целом, то есть ко всему файлу. Ставим галочку напротив параметра «Задать точность как на экране». Жмем на кнопку «OK», расположенную в нижнем левом углу окна.
Теперь при расчете данных будет учитываться отображаемая величина числа на экране, а не та, которая хранится в памяти Excel. Настройку же отображаемого числа можно провести любым из двух способов, о которых мы говорили выше.
Применение функций
Если же вы хотите изменить величину округления при расчете относительно одной или нескольких ячеек, но не хотите понижать точность расчетов в целом для документа, то в этом случае, лучше всего воспользоваться возможностями, которые предоставляет функция «ОКРУГЛ», и различные её вариации, а также некоторые другие функции.
Среди основных функций, которые регулируют округление, следует выделить такие:
- ОКРУГЛ – округляет до указанного числа десятичных знаков, согласно общепринятым правилам округления;
- ОКРУГЛВВЕРХ – округляет до ближайшего числа вверх по модулю;
- ОКРУГЛВНИЗ – округляет до ближайшего числа вниз по модулю;
- ОКРУГЛТ – округляет число с заданной точностью;
- ОКРВВЕРХ – округляет число с заданной точность вверх по модулю;
- ОКРВНИЗ – округляет число вниз по модулю с заданной точностью;
- ОТБР – округляет данные до целого числа;
- ЧЕТН – округляет данные до ближайшего четного числа;
- НЕЧЕТН – округляет данные до ближайшего нечетного числа.

Для функций ОКРУГЛ, ОКРУГЛВВЕРХ и ОКРУГЛВНИЗ следующий формат ввода: «Наименование функции (число;число_разрядов). То есть, если вы, например, хотите округлить число 2,56896 до трех разрядов, то применяете функцию ОКРУГЛ(2,56896;3). На выходе получается число 2,569.
Для функций ОКРУГЛТ, ОКРВВЕРХ и ОКРВНИЗ применяется такая формула округления: «Наименование функции(число;точность)». Например, чтобы округлить число 11 до ближайшего числа кратного 2, вводим функцию ОКРУГЛТ(11;2). На выходе получается число 12.
Функции ОТБР, ЧЕТН и НЕЧЕТ используют следующий формат: «Наименование функции(число)». Для того, чтобы округлить число 17 до ближайшего четного применяем функцию ЧЕТН(17). Получаем число 18.
Функцию можно вводить, как в ячейку, так и в строку функций, предварительно выделив ту ячейку, в которой она будет находиться. Перед каждой функцией нужно ставить знак «=».
Существует и несколько другой способ введения функций округления. Его особенно удобно использовать, когда есть таблица со значениями, которые нужно преобразовать в округленные числа в отдельном столбике.
Его особенно удобно использовать, когда есть таблица со значениями, которые нужно преобразовать в округленные числа в отдельном столбике.
Для этого, переходим во вкладку «Формулы». Кликаем по копке «Математические». Далее, в открывшемся списке выбираем нужную функцию, например ОКРУГЛ.
После этого, открывается окно аргументов функции. В поле «Число» можно ввести число вручную, но если мы хотим автоматически округлить данные всей таблицы, тогда кликаем по кнопке справа от окна введения данных.
Окно аргументов функции сворачивается. Теперь нужно кликнуть по самой верхней ячейке столбца, данные которого мы собираемся округлить. После того, как значение занесено в окно, кликаем по кнопке справа от этого значения.
Опять открывается окно аргументов функции. В поле «Число разрядов» записываем разрядность, до которой нам нужно сокращать дроби. После этого, жмем на кнопку «OK».
Как видим, число округлилось. Для того, чтобы таким же образом округлить и все другие данные нужного столбца, наводим курсор на нижний правый угол ячейки с округленным значением, жмем на левую кнопку мыши, и протягиваем её вниз до конца таблицы.
После этого, все значения в нужном столбце будут округлены.
Как видим, существуют два основных способа округлить видимое отображение числа: с помощью кнопки на ленте, и путем изменения параметров формата ячеек. Кроме того, можно изменить и округление реально рассчитываемых данных. Это также можно сделать двумя способами: изменением настроек книги в целом, или путем применения специальных функций. Выбор конкретного способа зависит от того, собираетесь ли вы применять подобный вид округления для всех данных в файле, или только для определенного диапазона ячеек.
рабочих листов и онлайн-упражнений по округлению чисел
| Округление и сравнение целых чисел Класс/уровень: 3 класс по Sir_DEN | Округлить 1000 Ранг/уровень: 3 по Кьяти Тукрал | Округление чисел до ближайших десятков Класс/уровень: 1,2 по NNTM14021997 |
| Округлить 100 Класс/уровень: 3 по Кьяти Тукрал | Округление целых чисел Класс/уровень: 5 от СамантаКупс | Округлить до сотен Класс/уровень: 3 по Кьяти Тукрал |
| Округлить 100 Класс/уровень: 3 по Кьяти Тукрал | Округление до 1000 Класс/уровень: элементарный Синтиасмит | Округление до ближайших 10 Класс/уровень: 2-й по Майерлис16 |
| Округление до ближайших 10, 100, 1000 Класс/уровень: 5 класс от МсЗахра | Округление чисел Ранг/уровень: Уровень 3 от sudishna_ganesh | Y2 — Округлить до ближайшей сотни Ранг/уровень: 2 по мирабасри6677 |
| Округление целых чисел 5 класс Класс/уровень: элементарный Синтиасмит | Округление целых чисел Класс/уровень: 4-6 по MsJ242 | 4 класс Округление недели 3 Класс/уровень: 4 по jem45 |
| Округление и оценка Класс/уровень: 3 Учитель третьего класса | Округлить числа от 0 до 1000 до ближайших 10 Класс/уровень: 4 класс от flavia_anderson5 | Округление числа до 100 Класс/уровень: 4-5 классы по Аршиямарьям |
| Округлить 1000 Класс/уровень: 3 по Кьяти Тукрал | Практика округления Класс/уровень: 7 по ххай | Округлить 1000 Класс/уровень: 3 по Кьяти Тукрал |
| Округление Класс/уровень: 5-6 от Diane_Telle | Числовые строки для округления двузначных чисел до ближайших 10 Класс/уровень: 3 по Зайнаб Саттар | Округление до ближайших десятков и сотен Класс/уровень: 4 класс by Еноты |
| Округление целых чисел 6 9 класс0005 Класс/уровень: элементарный Синтиасмит | Номера до 100 000 Класс/уровень: 4 класс по jhoyce04 | Округление до ближайшей сотни Класс/уровень: Второй класс по хальварадо |
| Округлить Класс/уровень: 4 по Экаосария | Оценка и округление слова Задача Класс/уровень: 4 класс от flavia_anderson5 | Округление Класс/уровень: 4 класс по молотковr |
| Округление десятков Класс/уровень: 4 класс от mikepparker621 | G4 — круглые целые числа Класс/уровень: 4 от Galaxy191197 | Важные цифры Класс/уровень: 9-10 от Mrs_Godet |
| Округление до десятка Класс/уровень: 2 класс по хальварадо | Округлить до ближайших 10 и 100 -1 Класс/уровень: элементарный Синтиасмит | Округление до ближайших 10 Класс/уровень: 3 по Гершевский |
| Округление Класс/уровень: 4 от Колено | Округление целых чисел Класс/уровень: элементарный Синтиасмит | Округление до целых чисел, 1 знак после запятой, 2 знака после запятой Класс/уровень: 4, 5, 6 от Исилин |
| Рабочая тетрадь 4 класс 1-4 Класс/уровень: 4 по эвиск | Округление и значащие цифры Класс/уровень: 8 по sisG8and7 | Округление до ближайших 10 Класс/уровень: 1 класс от Monique_20 |
| Следующий доллар выше Ранг/уровень: Жизненные навыки по mfoley4 | Округление Класс/уровень: 4 по sisG8and7 | Округлить вверх или вниз Класс/уровень: 4 по NessaC |
| Округление чисел Класс/уровень: 4 по лоригребнер | Округление целых чисел Класс/уровень: 4 класс по remongonzales | Урок 1. 2 3 класс 2 3 класс Класс/уровень: 3 по Мариссаенсинас |
Бесплатная онлайн-игра для детей с округлением чисел
Добавить игру в избранное
Это математическая игра на тему футбола, в которой вы округляете числа до ближайших десяти, сотен, тысяч или десятичных знаков. Каждый правильный ответ приносит вам очки и мяч для броска.
- Выберите уровень сложности.
- Округлите числа до ближайшего указанного приращения, чтобы заработать шары.
- Забейте как можно больше пенальти. Как высоко вы можете набрать.
Комбинезон
Дизайн
Сложность
Воспроизвести
Играть в футбольную математическую игру с округлением онлайн
Дети и родители могут играть в эту игру с округлением чисел, щелкнув в окне ниже.
В качестве альтернативы дети и взрослые могут играть в эту футбольную видеоигру с округлением чисел бесплатно в виде веб-приложения здесь.
Математическая футбольная игра для детей Инструкции по игре
- Начало игры
- Нажмите кнопку воспроизведения, чтобы открыть экран приветствия.
- На экране приветствия выберите перейти кнопку под названием игры, чтобы начать.
- Управление игрой
- Рабочий стол
- Используйте цифры на клавиатуре над клавишами с буквами, чтобы указать ответ.
- Нажмите клавишу ввода, чтобы проверить свой ответ.
- Щелкните левой кнопкой мыши, чтобы зафиксировать координаты вашего футбольного удара.
- Устройства с сенсорным экраном
- Хотя эта игра могла загружаться на устройствах с сенсорным экраном, ее элементы управления были оптимизированы для настольных компьютеров с клавиатурой.
- Рабочий стол
- Игра
- Выбор уровня
- Выберите один из 3 уровней сложности, определяемых значениями мест, которые необходимо округлить.

- Уровень 1: округление до ближайших десятков и сотен
- Уровень 2 Округление до ближайших десятков, сотен и тысяч.
- Уровень 3: округление до ближайших десятков, сотен, тысяч и десятичных знаков.
- Выберите аватар игрока из 4 представленных фигурок.
- Выберите один из 3 уровней сложности, определяемых значениями мест, которые необходимо округлить.
- Основная игра
- Введите число, округленное до ближайшего указанного разряда.
- Числа от 5 и выше округляются на один разряд в большую сторону.
- например, 165, округленное до ближайшего десятка, будет 170.
- Числа 4 и ниже округляются до одного разряда.
- например, 1144, округленное до ближайшей сотни, равно 1100.
- Числа от 5 и выше округляются на один разряд в большую сторону.
- Отвечая на вопрос о десятичных дробях, помните, что каждая десятичная дробь представляет дробь, знаменатель которой равен 10.
- Таким образом, первое число после запятой — это десятая (x/10)
- Второе число после запятой — это сотая (x/100), третье — тысячная (x/1000) и так далее.

- Ответьте правильно на столько вопросов, чтобы заработать 5 штрафных футбольных мячей.
- Введите число, округленное до ближайшего указанного разряда.
- Игра с ударами
- В нижней левой части экрана находится система наведения в форме креста.
- Мяч движется как по горизонтали, так и по вертикали.
- Остановив мяч у красного круга в центре, вы гарантируете, что он достигнет цели
- Чтобы нанести удар, щелкните левой кнопкой мыши по кнопке под системой прицеливания в нужное время.
- Продолжайте играть, пока не израсходуете все выигранные мячи.
- В нижней левой части экрана находится система наведения в форме креста.
- Подсчет очков
- За каждый правильный ответ вы получаете 10 баллов.
- Каждый неправильный ответ стоит -10 баллов.
- За каждый выстрел вы получаете 10 очков.
- Если вы правильно ответите на все вопросы и не пропустите ни одного выстрела, вы сможете заработать максимум 100 очков в первом раунде.
- Вы теряете мячи каждый раз, когда неправильно отвечаете.
 Если вы правильно ответили на все свои вопросы в первые 4 раза и ответили неправильно в последний раз, вы получаете 30 очков и ни одного мяча.
Если вы правильно ответили на все свои вопросы в первые 4 раза и ответили неправильно в последний раз, вы получаете 30 очков и ни одного мяча. - Вы можете повторить этот процесс несколько раз, чтобы заработать более высокий балл по 30 очков за раз, даже не переходя к игре с ударами.
- Вы теряете мячи каждый раз, когда неправильно отвечаете.
- Ваши очки суммируются и переносятся на следующий раунд.
- За каждый правильный ответ вы получаете 10 баллов.
- Выбор уровня
- Целевая аудитория
- Игра подходит для детей, изучающих округление чисел, которые любят учиться в процессе игры.
- В игре нет контента для взрослых.
Нравится эта игра? Просмотрите эту игру с округлением чисел для девочек и мальчиков
Математика в футболе Округление чисел: игра с округлением чисел
В целом3,9
Дизайн3,9
Что люди говорят… Оставьте свой рейтинг
Заказ: Самые свежиеЛучшие баллыСамые полезныеХудшие баллы
length < 1″> Будьте первым, кто оставит отзыв.{{{ обзор.rating_title }}}
Показать больше
Оставьте свой рейтинг
- В целом
- Дизайн
- Развлечения
- Оригинальность
- Воспроизводимость
Бесплатная онлайн-игра для детей и взрослых.0636
Эта игра создана в формате HTML5, удобном для мобильных устройств, поэтому ее можно использовать на разных устройствах. Вы можете играть в нее на мобильных устройствах, таких как Apple iPhone, мобильных телефонах на базе Google Android от таких производителей, как Samsung, планшетах, таких как iPad или Kindle Fire, ноутбуках и настольных компьютерах на базе Windows. Все игровые файлы хранятся локально в кеше вашего веб-браузера. Эта игра работает в Apple Safari, Google Chrome, Microsoft Edge, Mozilla Firefox, Opera и других современных веб-браузерах.
Plays.org опубликовал этот Math Soccer 12 октября 2021 г. / 2 комментариев
/ 2 комментариев
Округлите любое число до ближайших 10, 100 или 1000
Связанные рабочие листы
Доступность игры:
- Онлайн в формате HTML5
Перестрелка с округлением ?
Интерактивная викторина, которая проверяет ваше понимание всех задач «Число и место» в учебной программе 4-го класса. Выберите одну цель или несколько целей. Вы можете сохранить или распечатать результаты теста в формате PDF в конце теста. Идеально подходит для формативного или суммативного оценивания.
В качестве альтернативы вы можете использовать интерактивную викторину по математике, которая включает цели из всех разделов учебной программы 4-го класса.
В этом тесте проверяются следующие задачи:
Доступность игры:
- Онлайн в формате HTML5
Y4 – Число — Число и разрядность — Интерактивная викторина ?
Правильно округляйте числа, чтобы съесть противника и украсть его очки.
 Играйте в одиночном режиме или в режиме двух игроков. Вам нужно будет заблокировать планшет в портретном режиме, чтобы играть в режиме двух игроков.
Играйте в одиночном режиме или в режиме двух игроков. Вам нужно будет заблокировать планшет в портретном режиме, чтобы играть в режиме двух игроков.Выберите один из следующих уровней:
1. Округление чисел до 100 до ближайших 10 (Y2)
2. Округление чисел до 1000 до ближайших 10 (Y3)
3. Округление чисел до 10 000 до ближайшие 10, 100 или 1000 (Y4)
4. Округление десятичных знаков с одним десятичным знаком до ближайшего целого числа (Y4)
5. Округление десятичных знаков с двумя десятичными знаками до ближайшего целого числа и до одного десятичного знака (Y5 )
Доступность игры:
- Онлайн в формате HTML5
Maths Maze Monsters — Округление чисел ?
Доступность игры:
- Онлайн в формате HTML5
Maths Road Hopper — округление чисел ?
Ответьте на вопросы по математике, а затем посмотрите, сколько противников вы сможете победить в битве снежками.

Доступность игры:
- Онлайн в формате HTML5
Удар снежком ?
Точно округлите числа для стабильного замаха и попытайтесь попасть в дыру в одном из них. Играйте в одиночку или против партнера. Кто может набрать наибольшее количество баллов в вашем классе?
Выберите один из следующих уровней:
1. Округление чисел до 100 до ближайших 10 (Y2)
2. Округление чисел до 1000 до ближайших 10 (Y3)
3. Округление чисел до 10 000 до ближайшие 10, 100 или 1000 (Y4)
4. Округление десятичных знаков с одним десятичным знаком до ближайшего целого числа (Y4)
5. Округление десятичных знаков с двумя десятичными знаками до ближайшего целого числа и до одного десятичного знака (Y5 )
6.Округление десятичных знаков до трех знаков после запятой до ближайшего целого, одного десятичного знака или двух знаков после запятой (Y6)
Доступность игры:
- Онлайн в формате HTML5
Округление — мини-гольф по математике ?
Переместите блок так, чтобы он соответствовал стене.
 Чем быстрее и точнее вы ответите на математические вопросы, тем медленнее будет двигаться стена.
Чем быстрее и точнее вы ответите на математические вопросы, тем медленнее будет двигаться стена.Сотни математических навыков для тренировки.
Доступность игры:
- Онлайн в формате HTML5
Match the Wall — Математическая игра ?
Отвечайте на вопросы быстро и точно, чтобы получить больше штрафов.
Сотни математических навыков на выбор с уровнями, включающими умножение, деление, сложение, вычитание, чтение чисел, округление чисел, чтение римских цифр, дроби чисел, упрощение дробей и преобразование между дробями, десятичными знаками и процентами.
Доступность игры:
- Онлайн в формате HTML5
Серия пенальти по математике ?
Доступность игры:
- Онлайн в формате HTML5
Суперматематический боулинг — округление чисел ?
Ответьте на вопросы по математике, а затем рассортируйте животных как можно быстрее.

Доступность игры:
- Онлайн в формате HTML5
Сортировка животных — Математическая игра ?
Выберите один из следующих уровней:
1. Округлите числа до 100 до ближайших 10 (Y2)
2. Округление чисел до 1000 до ближайших 10 (Y3)
3. Округление чисел до 10 000 до ближайших 10, 100 или 1000 (Y4)
4. Округление десятичных знаков с одним десятичным знаком до ближайшего целого число (Y4)
5. Округление десятичных знаков с двумя знаками после запятой до ближайшего целого числа и до одного знака после запятой (Y5)
Доступность игры:
- Онлайн в формате HTML5
Математика парковки — округление чисел ?
Ответьте на вопросы по математике и запустите космические корабли соответствующего цвета.
Доступность игры:
- Онлайн в формате HTML5
Подбор цветов по математике ?
Округляйте числа как можно быстрее, и у вас будет больше времени, чтобы нацелить стрелу.
 Играйте в одиночку или против партнера. Кто может набрать наибольшее количество баллов в вашем классе?
Играйте в одиночку или против партнера. Кто может набрать наибольшее количество баллов в вашем классе?Выберите один из следующих уровней:
1. Округление чисел до 100 до ближайших 10 (Y2)
2. Округление чисел до 1000 до ближайших 10 (Y3)
3. Округление чисел до 10 000 до ближайшие 10, 100 или 1000 (Y4)
4. Округление десятичных знаков с одним десятичным знаком до ближайшего целого числа (Y4)
5. Округление десятичных знаков с двумя десятичными знаками до ближайшего целого числа и до одного десятичного знака (Y5 )
6.Округление десятичных знаков до трех знаков после запятой до ближайшего целого, одного десятичного знака или двух знаков после запятой (Y6)
Доступность игры:
- Онлайн в формате HTML5
Арифметика стрельбы из лука — округление чисел ?
Округлите числа до заданной степени точности. Эта игра будет работать на любом устройстве.

Доступность игры:
- Онлайн в формате HTML5
Путь Томми — округление чисел ?
Округление чисел до ближайших 10, 100 или 1000 или округление десятичных до ближайшего целого, 1 или 2 знаков после запятой.
Доступность игры:
- Онлайн в формате HTML5
Математическая гонка — округление чисел ?
Марлон должен сражаться со зверями, используя свое понимание округления чисел.
Выберите один из следующих уровней:
1. Округление чисел до 100 до ближайших 10 (Y2)
2. Округление чисел до 1000 до ближайших 10 (Y3)
3. Округление чисел до 10 000 до ближайшие 10, 100 или 1000 (Y4)
4. Округление десятичных знаков с одним десятичным знаком до ближайшего целого числа (Y4)
5. Округление десятичных знаков с двумя десятичными знаками до ближайшего целого числа и до одного десятичного знака (Y5 )
6.
 Округление десятичных знаков до трех знаков после запятой до ближайшего целого, одного или двух знаков после запятой (Y6)
Округление десятичных знаков до трех знаков после запятой до ближайшего целого, одного или двух знаков после запятой (Y6)Доступность игры:
- Онлайн в формате HTML5
Волшебная математическая миссия Марлона — округление чисел ?
Округление чисел до заданной степени точности.
Доступность игры:
- Онлайн в формате HTML5
Башня математики — округление ?
Округление трехзначных или четырехзначных чисел до ближайших 10 или 100. Округление десятичных дробей до ближайшего целого числа или до 1 десятичного знака. Версия HTML5 (будет работать на планшетах).
Доступность игры:
- Онлайн в формате HTML5
Округление — версия для планшета ?
Поймай рыбу, а затем ответь на округляющие вопросы, прежде чем они уйдут.
 Эта игра подходит для планшетов и будет работать на любом устройстве.
Эта игра подходит для планшетов и будет работать на любом устройстве.Имеет следующие уровни (взято из новой программы по математике):
1. Округление чисел до 100 до ближайших 10 (Y2)
2. Округление чисел до 1000 до ближайших 10 (Y3)
3. Округление чисел до 10 000 до ближайших 10, 100 или 1000 (Y4)
4. Округление десятичных знаков с одним десятичным знаком до ближайшего целого числа (Y4)
5. Округление десятичных знаков с двумя десятичными знаками до ближайшего целого числа ближайшее целое число с точностью до одного десятичного знака (Y5)
6.Округление десятичных знаков до трех знаков после запятой до ближайшего целого, одного десятичного знака или двух знаков после запятой (Y6)
Доступность игры:
- Онлайн в формате HTML5
Математическая рыбалка — округление ?
Бросьте кирку в нужный кристалл. Эта игра имеет следующие уровни (взято из новой программы по математике):
1.
 Округление чисел до 100 до ближайших 10 (Y2)
Округление чисел до 100 до ближайших 10 (Y2)2. Округление чисел до 1000 до ближайших 10 (Y3)
3 , Округление чисел до 10 000 до ближайших 10, 100 или 1000 (Y4)
4. Округление десятичных знаков с одним десятичным знаком до ближайшего целого числа (Y4)
5. Округление десятичных знаков с двумя десятичными знаками до ближайшего целого числа и до одного десятичного знака (Y5)
6.Округление десятичных знаков с точностью до три знака после запятой до ближайшего целого, один знак после запятой или два знака после запятой (Y6)
Эта игра, как и все другие игры о кристальных крашах, доступна в виде отдельного приложения для iPad или Android.
Доступность игры:
- Онлайн в формате HTML5
Округление — Хрустальный крах ?
Стреляйте в НЛО правильным ответом и уклоняйтесь от входящего огня. Увлекательная игра для тренировки широкого спектра ключевых математических навыков.

Существует более сотни тщательно дифференцированных уровней, связанных с задачами из новой учебной программы по математике. Игра может быть использована для обучения: умножению, сложению, чтению чисел, вычитанию, дробям чисел, римским цифрам, округлению чисел, делению, преобразованию дробей в десятичные числа, преобразованию дробей в проценты, определению времени словами, распознаванию кратных, множителей, Простые, квадратные и кубические числа и упрощение дробей. Полный список уровней ниже.
Доступность игры:
- Онлайн в формате HTML5
Математика НЛО ?
Используйте калькулятор, чтобы ответить на вопрос, а затем округлите ответ до ближайших 10, 100, целого числа или до 1, 2 или 3 знаков после запятой. Затем правильный ответ отображается в числовой строке. Играйте на время, чтобы увидеть, сколько очков вы можете набрать.
Доступность игры:
- Онлайн в формате HTML5
Округление ответов ?
** Новая версия для планшетов добавлена 14 февраля 2018 г.
 Пожалуйста, дайте мне знать, если у вас возникнут проблемы — [email protected]
Пожалуйста, дайте мне знать, если у вас возникнут проблемы — [email protected]Стреляйте в космический корабль с правильным ответом и уклоняйтесь от входящего огня. Увлекательная игра для тренировки широкого спектра ключевых математических навыков.
Существует более сотни тщательно дифференцированных уровней, связанных с задачами новой учебной программы по математике. Игра может быть использована для обучения: умножению, сложению, чтению чисел, вычитанию, дробям чисел, римским цифрам, округлению чисел, делению, преобразованию дробей в десятичные числа, преобразованию дробей в проценты, определению времени словами, распознаванию кратных, множителей, Простые, квадратные и кубические числа и упрощение дробей. Полный список уровней ниже. Эта игра также доступна в виде приложения для iOS и Android.
Доступность игры:
- Онлайн в формате HTML5
KS2 Математические захватчики ?
Используйте клавиши со стрелками на компьютере или проведите пальцем по планшету, чтобы направить змею к правильным ответам.

В игре более 100 различных уровней. Полный список уровней смотрите ниже.
Доступность игры:
- Онлайн в формате HTML5
Змейка — Математическая игра KS2 ?
Быстро и точно отвечайте на вопросы по математике, чтобы заработать баскетбольные мячи, а затем посмотрите, сколько очков вы сможете набрать.
Сотни математических навыков на выбор с уровнями, включающими умножение, деление, сложение, вычитание, чтение чисел, округление чисел, чтение римских цифр, дроби чисел, упрощение дробей и преобразование между дробями, десятичными знаками и процентами.
Доступность игры:
- Онлайн в формате HTML5
Баскетбольная математика ?
Доступность игры:
- Онлайн в формате HTML5
Прыжок с белкой по математике ?
Ответьте на вопросы по математике, а затем посмотрите, сколько выстрелов вы сможете сэкономить.



 (-4))
(-4))







 2510 (округлитьь до десятых) ≈ 0.3;
2510 (округлитьь до десятых) ≈ 0.3;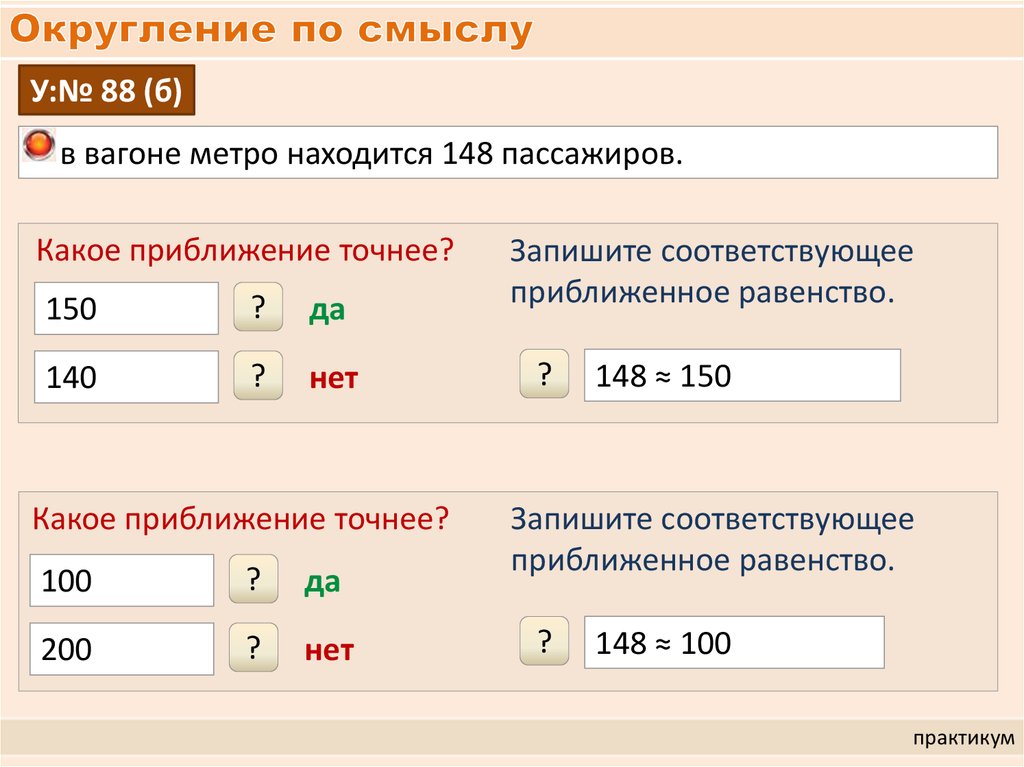 Нули, стоящие в начале или
конце числа, как правило, не записывают. Например, числа 0,00435 и 234000 записывают так: 4,35·10 -3
и 2,34·10 5 . Подобная запись упрощает вычисления, особенно в случае формул, удобных для
логарифмирования.
Нули, стоящие в начале или
конце числа, как правило, не записывают. Например, числа 0,00435 и 234000 записывают так: 4,35·10 -3
и 2,34·10 5 . Подобная запись упрощает вычисления, особенно в случае формул, удобных для
логарифмирования. Допуски формы и
расположения…………………………………….
Допуски формы и
расположения…………………………………….


 Если вы правильно ответили на все свои вопросы в первые 4 раза и ответили неправильно в последний раз, вы получаете 30 очков и ни одного мяча.
Если вы правильно ответили на все свои вопросы в первые 4 раза и ответили неправильно в последний раз, вы получаете 30 очков и ни одного мяча. Играйте в одиночном режиме или в режиме двух игроков. Вам нужно будет заблокировать планшет в портретном режиме, чтобы играть в режиме двух игроков.
Играйте в одиночном режиме или в режиме двух игроков. Вам нужно будет заблокировать планшет в портретном режиме, чтобы играть в режиме двух игроков.
 Чем быстрее и точнее вы ответите на математические вопросы, тем медленнее будет двигаться стена.
Чем быстрее и точнее вы ответите на математические вопросы, тем медленнее будет двигаться стена.
 Играйте в одиночку или против партнера. Кто может набрать наибольшее количество баллов в вашем классе?
Играйте в одиночку или против партнера. Кто может набрать наибольшее количество баллов в вашем классе?
 Округление десятичных знаков до трех знаков после запятой до ближайшего целого, одного или двух знаков после запятой (Y6)
Округление десятичных знаков до трех знаков после запятой до ближайшего целого, одного или двух знаков после запятой (Y6) Эта игра подходит для планшетов и будет работать на любом устройстве.
Эта игра подходит для планшетов и будет работать на любом устройстве. Округление чисел до 100 до ближайших 10 (Y2)
Округление чисел до 100 до ближайших 10 (Y2)
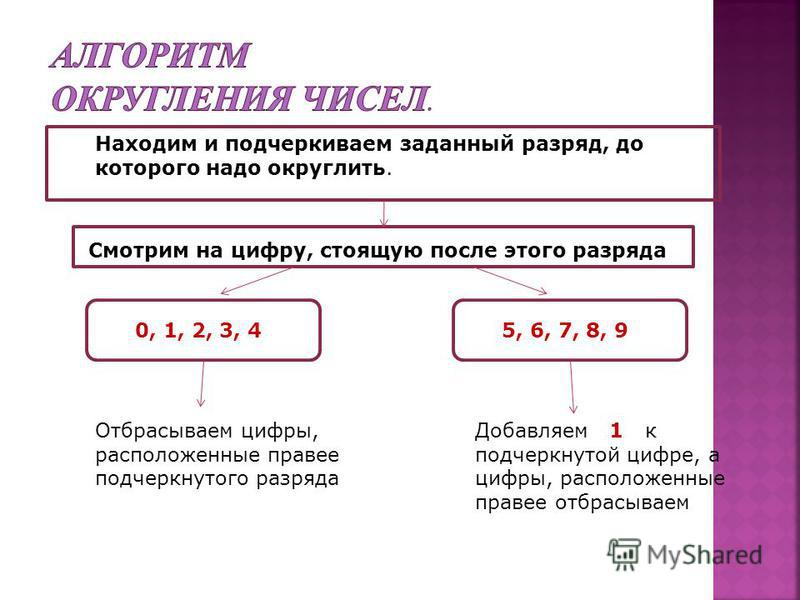 Пожалуйста, дайте мне знать, если у вас возникнут проблемы —
Пожалуйста, дайте мне знать, если у вас возникнут проблемы — 
