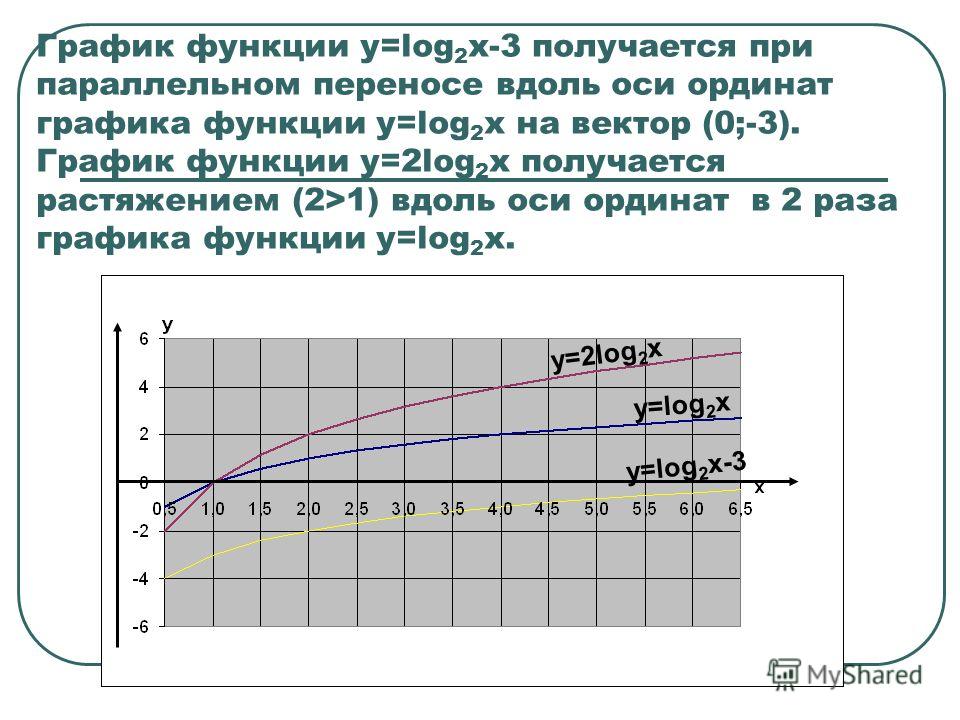
| 1 | Оценить с использованием заданного значения | квадратный корень из 50 | |
| 2 | Оценить с использованием заданного значения | квадратный корень из 45 | |
| 3 | Вычислить | 5+5 | |
| 4 | Вычислить | 7*7 | |
| 5 | Разложить на простые множители | 24 | |
| 6 | Преобразовать в смешанную дробь | 52/6 | |
| 7 | Преобразовать в смешанную дробь | 93/8 | |
| 8 | Преобразовать в смешанную дробь | 34/5 | |
| 9 | График | y=x+1 | |
| 10 | Оценить с использованием заданного значения | квадратный корень из 128 | |
| 11 | Найти площадь поверхности | сфера (3) | |
| 12 | Вычислить | 54-6÷2+6 | |
| 13 | График | y=-2x | |
| 14 | Вычислить | 8*8 | |
| 15 | Преобразовать в десятичную форму | 5/9 | |
| 16 | Оценить с использованием заданного значения | квадратный корень из 180 | |
| 17 | График | y=2 | |
| 18 | Преобразовать в смешанную дробь | 7/8 | |
| 19 | Вычислить | 9*9 | |
| 20 | Risolvere per C | C=5/9*(F-32) | |
| 21 | Упростить | 1/3+1 1/12 | |
| 22 | График | y=x+4 | |
| 23 | График | y=-3 | |
| 24 | График | x+y=3 | |
| 25 | График | x=5 | |
| 26 | Вычислить | 6*6 | |
| 27 | Вычислить | 2*2 | |
| 28 | Вычислить | 4*4 | |
| 29 | Вычислить | 1/2+(2/3)÷(3/4)-(4/5*5/6) | |
| 30 | Вычислить | 1/3+13/12 | |
| 31 | Вычислить | 5*5 | |
| 32 | Risolvere per d | 2d=5v(o)-vr | |
| 33 | Преобразовать в смешанную дробь | 3/7 | |
| 34 | График | y=-2 | |
| 35 | Определить наклон | y=6 | |
| 36 | Перевести в процентное соотношение | 9 | |
| 37 | График | y=2x+2 | |
| 38 | График | ||
| 39 | График | x=-3 | |
| 40 | Решить, используя свойство квадратного корня | x^2+5x+6=0 | |
| 41 | Преобразовать в смешанную дробь | 1/6 | |
| 42 | Преобразовать в десятичную форму | 9% | |
| 43 | Risolvere per n | 12n-24=14n+28 | |
| 44 | Вычислить | 16*4 | |
| 45 | Упростить | кубический корень из 125 | |
| 46 | Преобразовать в упрощенную дробь | 43% | |
| 47 | График | x=1 | |
| 48 | График | y=6 | |
| 49 | График | y=-7 | |
| 50 | График | y=4x+2 | |
| 51 | Определить наклон | y=7 | |
| 52 | График | y=3x+4 | |
| 53 | График | y=x+5 | |
| 54 | График | 3x+2y=6 | |
| 55 | Решить, используя свойство квадратного корня | x^2-5x+6=0 | |
| 56 | Решить, используя свойство квадратного корня | x^2-6x+5=0 | |
| 57 | Решить, используя свойство квадратного корня | x^2-9=0 | |
| 58 | Оценить с использованием заданного значения | квадратный корень из 192 | |
| 59 | Оценить с использованием заданного значения | квадратный корень из 25/36 | |
| 60 | Разложить на простые множители | 14 | |
| 61 | Преобразовать в смешанную дробь | 7/10 | |
| 62 | Risolvere per a | (-5a)/2=75 | |
| 63 | Упростить | x | |
| 64 | Вычислить | 6*4 | |
| 65 | Вычислить | 6+6 | |
| 66 | Вычислить | -3-5 | |
| 67 | Вычислить | -2-2 | |
| 68 | Упростить | квадратный корень из 1 | |
| 69 | Упростить | квадратный корень из 4 | |
| 70 | Найти обратную величину | 1/3 | |
| 71 | Преобразовать в смешанную дробь | 11/20 | |
| 72 | Преобразовать в смешанную дробь | 7/9 | |
| 73 | Найти НОК | 11 , 13 , 5 , 15 , 14 | , , , , |
| 74 | Решить, используя свойство квадратного корня | x^2-3x-10=0 | |
| 75 | Решить, используя свойство квадратного корня | x^2+2x-8=0 | |
| 76 | График | 3x+4y=12 | |
| 77 | График | 3x-2y=6 | |
| 78 | График | y=-x-2 | |
| 79 | График | y=3x+7 | |
| 80 | Определить, является ли полиномом | 2x+2 | |
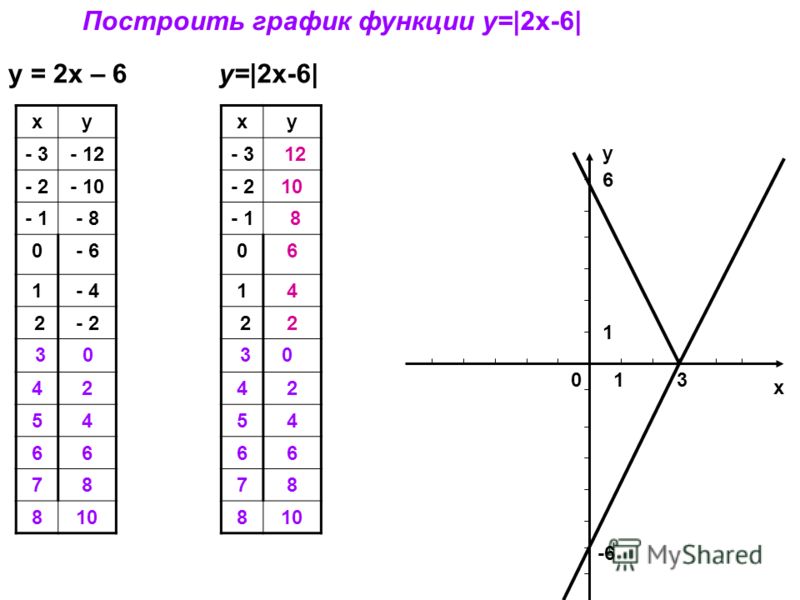
| 81 | График | y=2x-6 | |
| 82 | График | y=2x-7 | |
| 83 | График | y=2x-2 | |
| 84 | График | y=-2x+1 | |
| 85 | График | y=-3x+4 | |
| 86 | График | y=-3x+2 | |
| 87 | График | y=x-4 | |
| 88 | Вычислить | (4/3)÷(7/2) | |
| 89 | График | 2x-3y=6 | |
| 90 | График | x+2y=4 | |
| 91 | График | x=7 | |
| 92 | График | x-y=5 | |
| 93 | Решить, используя свойство квадратного корня | x^2+3x-10=0 | |
| 94 | Решить, используя свойство квадратного корня | x^2-2x-3=0 | |
| 95 | Найти площадь поверхности | конус (12)(9) | |
| 96 | Преобразовать в смешанную дробь | 3/10 | |
| 97 | Преобразовать в смешанную дробь | 7/20 | |
| 98 | Преобразовать в смешанную дробь | 2/8 | |
| 99 | Risolvere per w | V=lwh | |
| 100 | Упростить | 6/(5m)+3/(7m^2) |
Ответы | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука
| Похожие вопросы |
В треугольнике ABC известно, что AC=6, BC=8, угол C равен 90°. Найдите радиус описанной около этого треугольника окружность.
На пишите пожалуйста решение
Найдите радиус описанной около этого треугольника окружность.
На пишите пожалуйста решение
Решено
Площадь треугольника ABC равна 31, DE — средняя линия, параллельная стороне AB. Найдите площадь трапеции ABED.
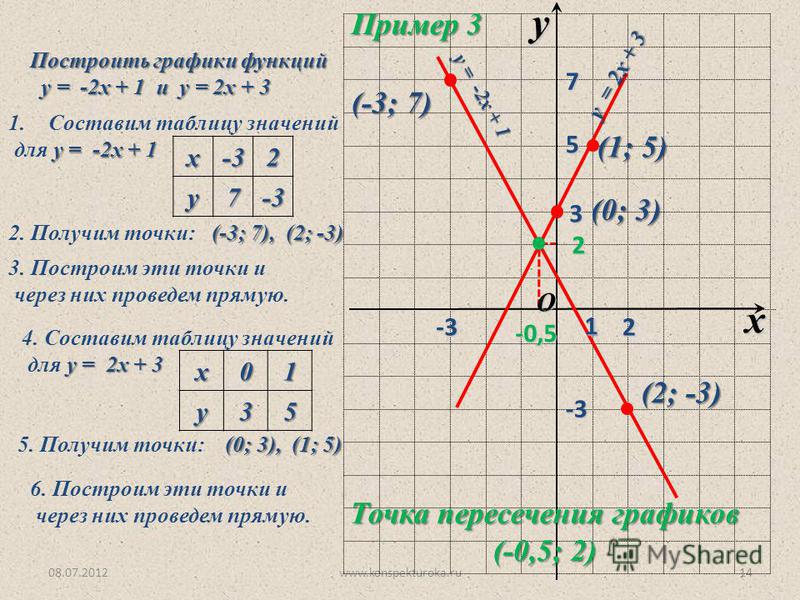
Построить график функции y=2x-2 и определить проходит ли график через точку:A(10;-20)
На экзамене 20 билетов, Андрей не выучил 1 из них. Найдите вероятность того, что ему попадется выученный билет
Решено
Последовательность задана условиями b1=-6,bn+1=-3×1/bn.найдите b3.
Пользуйтесь нашим приложением
Смещение графика квадратичной функции y = (x
- Дедерер Светлана Александровна, учитель математики
Презентация к уроку
Загрузить презентацию (806 кБ)
Цели урока:
Образовательная: исследовать смещение графика квадратичной функции, определить положение графика в зависимости от значений коэффициентов b, c.
Воспитательная: умение работать в группе, организованности.
Развивающая: навыки исследовательской работы, умение выдвигать гипотезы, анализировать полученные результаты, систематизировать полученные данные.
Структура урока
- Организационный момент – 3 минуты.
- Исследовательская работа – 20 минут.
- Закрепление изученного материала – 15 минут.
- Рефлексия – 2 минут.
- Итог урока – 3 минуты.
- Домашнее задание – 2 минуты.

Ход урока
1. Организационный момент.
Цель урока провести исследовательскую работу. Объектом исследования будут квадратичные функции разного вида. Вам предстоит определить, как влияют коэффициенты b, cна график функций вида y=x2+с, y=(x-b)2, y=(x-b)2+c.
Для выполнения задания необходимо разделиться на группы (4 группы по 5 человек, одна группа “эксперты” наиболее подготовленные ученики).
Каждая группа получает план исследования <Приложение>, лист формата А3 для оформления результатов.
2. Исследовательская работа
.
Две группы (уровень А) исследуют функции вида y= x2+с,
одна группа (уровень В) исследует функцию вида
y=(x-b)2, одна группа (уровень С) исследует
функцию y=(x-b)2+c.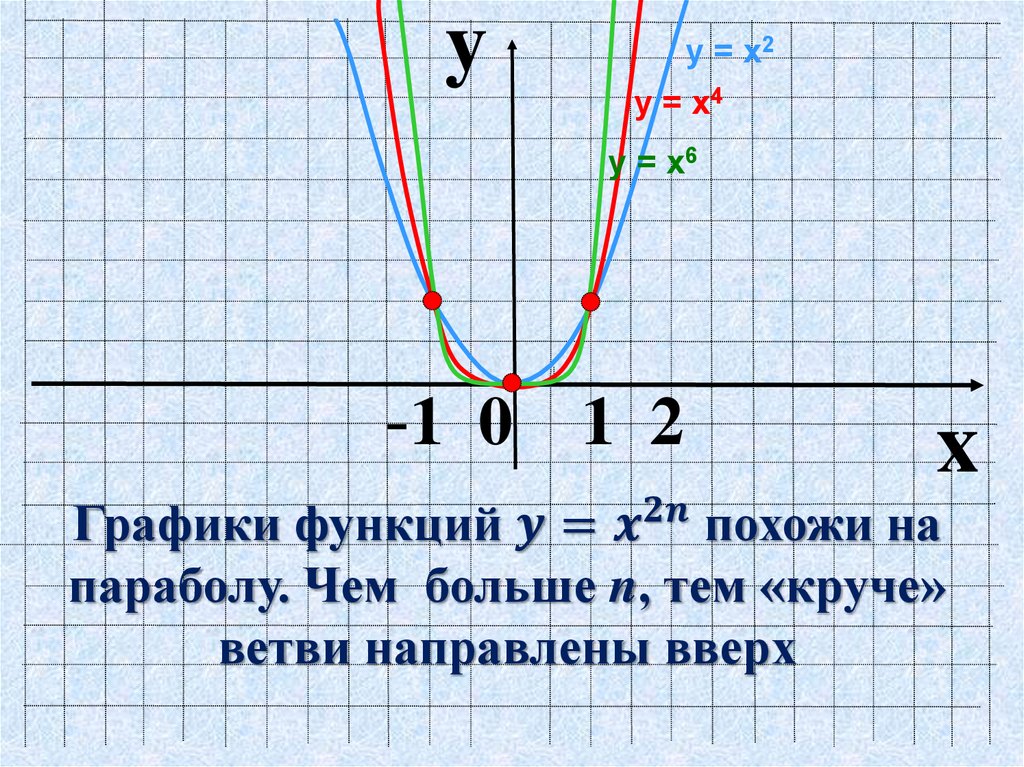 Группа “Экспертов”
исследует все функции.
Группа “Экспертов”
исследует все функции.
| Функция | Результат | ||
| 1 группа | у=x2+3; | <Рисунок 10> | |
| 2 группа | у=x2-5; | ||
| 3 группа | у=(х-4)2; | <Рисунок 12> | |
| 4 группа | у=(х-2)2+3. | <Рисунок 13> |
План работы
- Для того чтобы выдвинуть гипотезу сделайте
предположение, как может выглядеть ваша функция.

- Постройте график исследуемых функций (определите вершину параболы (х0, y0), задайте таблицей 4 точки).
- Сравните получившийся график с контрольным образцом y=x2.
- Сделайте вывод (как изменилось положение графика вашей функции относительно контрольного образца).
- Результаты оформите на листе формата А3 и представьте “экспертной” группе.
“Экспертная” группа сверяет результаты свои с результатами остальных групп, систематизирует и обобщает результаты, выступает с выводами. В случае неточностей или ошибок учитель вносит коррекционные замечания.
Сверка полученных результатов со слайдами №2-5.
Любую квадратичную функцию y=ax2+bx+c, можно
записать в виде y=a(x-x0)2+y0, где x0
и y0 выражаются через коэффициенты a, b, c. Таким образом, ваши коэффициенты b=x0, c=y0
являются координатами вершины параболы.
Таким образом, ваши коэффициенты b=x0, c=y0
являются координатами вершины параболы.
3. Закрепление изученного материала.
Фронтальная работа с классом.
1. Найти ошибку в графиках функций (Слайды№6-9).
y=(х+6)2 |
у=х2-2 |
Коэффициент b |
Нет ошибки |
Рисунок 1 |
Рисунок 2 |
| у=(х+5)2-1 | у=(х-2)2+2 |
| Коэффициент b и с | Коэффициент b |
| Рисунок 3 | Рисунок 4 |
Результаты
<Рисунок 7>
<Рисунок 2>
<Рисунок 8>
<Рисунок 9>
Какой коэффициент вам помог найти ошибку?
2.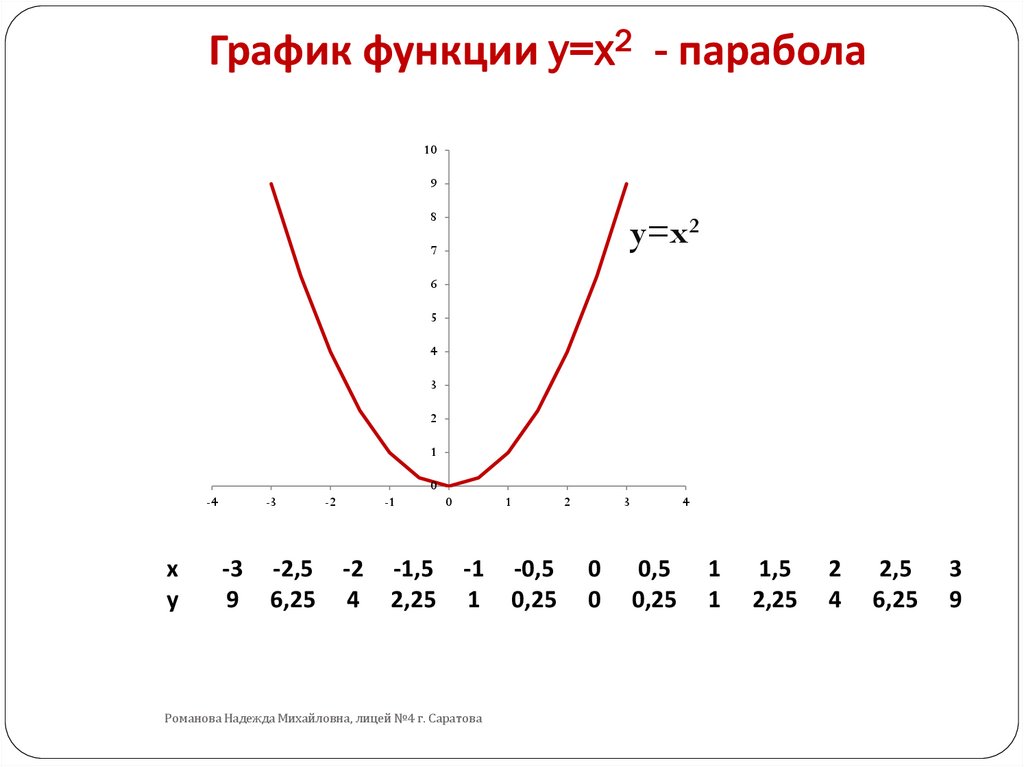 Соотнесите графики функций согласно цветам (слайд
№10).
Соотнесите графики функций согласно цветам (слайд
№10).
Рисунок 5
| y=(х-4)2-2 | синий |
| y=-x2+5 | красный |
| y=(x+1)2+3 | зеленый |
| y=(x-3)2 | фиолетовый |
4. Рефлексия.
Группа “Экспертов” отвечают на вопросы:
– Какие ошибки допустили группы?
– Достигнута ли цель занятия?
– Соответствуют ли полученные результаты исследования поставленной гипотезе?
5. Итог урока (слайд №11)
:
На положение графика функции y=(x-b)2+c влияют коэффициенты b и c,
“+b” парабола сдвинута вправо по оси абсцисс на b единичных отрезков,
“–b” парабола сдвинута влево по оси абсцисс на b единичных отрезков,
“+с” парабола сдвинута вверх по оси ординат на с единичных отрезков,
“-с” парабола сдвинута вниз по оси ординат на с
единичных отрезков.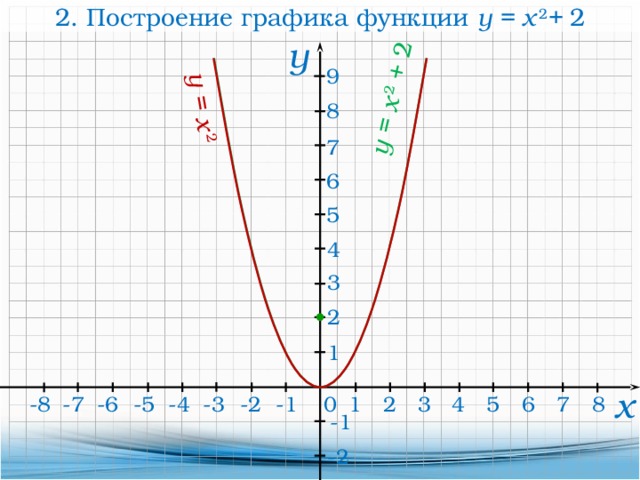
6. Домашнее задание
- Построить график квадратичной функции, имеющую вершину в точке А(1;-2), коэффициент a=1.
- Подумайте, в какой области можно использовать знания по данной теме (практическое применение).
Приложение
Постройте график функции y 2×2
Компьютеры admin 0 комментариев
Содержание
- 1 Введите график функции
- 1.1 Примеры
- 2 Исследование графика функции
- 2.0.1 Правила ввода выражений и функций
Здравствуйте!
Постройте график функции y = 2x – 2, пожалуйста.
Спасибо!
Задание.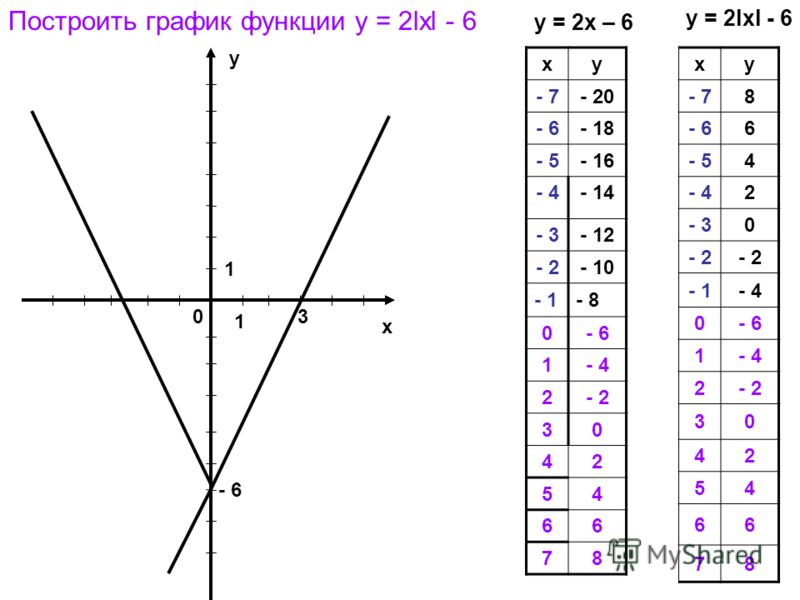
Постройте график функции y = 2x — 2
Решение.
Функция представлена в виде , следовательно, она линейная.
Начнем с вычисления области определения функции. Поскольку функция является линейной, то она имеет область определения всю числовую прямую.
Такой же вывод можно сделать и об области значений функции.
В таком случае для графика никаких ограничений не будет.
Проверим функцию, является ли она четной или нечетной. С этой целью подставим вместо переменной х переменную —х:
В результате получили, что данная функция является ни четной, ни нечетной.
Как упоминалось выше, функция — линейная. Тогда будет достаточно двух точек, чтобы построить ее график. С этой целью вычислим точки пересечения с координатными осями:
При пересечении оси Ох переменная х = 0. Подставим это значение в функцию:
При пересечении оси Оу переменная у = 0. Решим уравнение:
Итак, получили две точки пересечения с координатами:
(0; —2) и (1; 0).
Поскольку для линейной функции не существует точек минимума или максимума, то производную находить не будет.
Как уже упоминалось, достаточно двух точек, чтобы построить линейную функцию.
Здравствуйте!
Постройте график функции y = –2x + 2, пожалуйста.
Спасибо!
Задание.
Построить график функции y = —2x + 2
Решение.
Функции подобного вида строятся очень просто, так как они являются линейными. А как известно линию можно провести всего через две точки. Поэтому все решение сводится к тому, что нужно определить две точки, которые принадлежат этой функции, нанести их на координатную плоскость и провести через них линию. Это и будет графиком заданной функции.
Проведем небольшой анализ данной функции.
Поскольку функция представлена в виде , то, как уже упоминалось выше, она называется линейной. Как известно, линия бесконечна, поэтому и область определения функции, и область ее значений будет вся числовая прямая.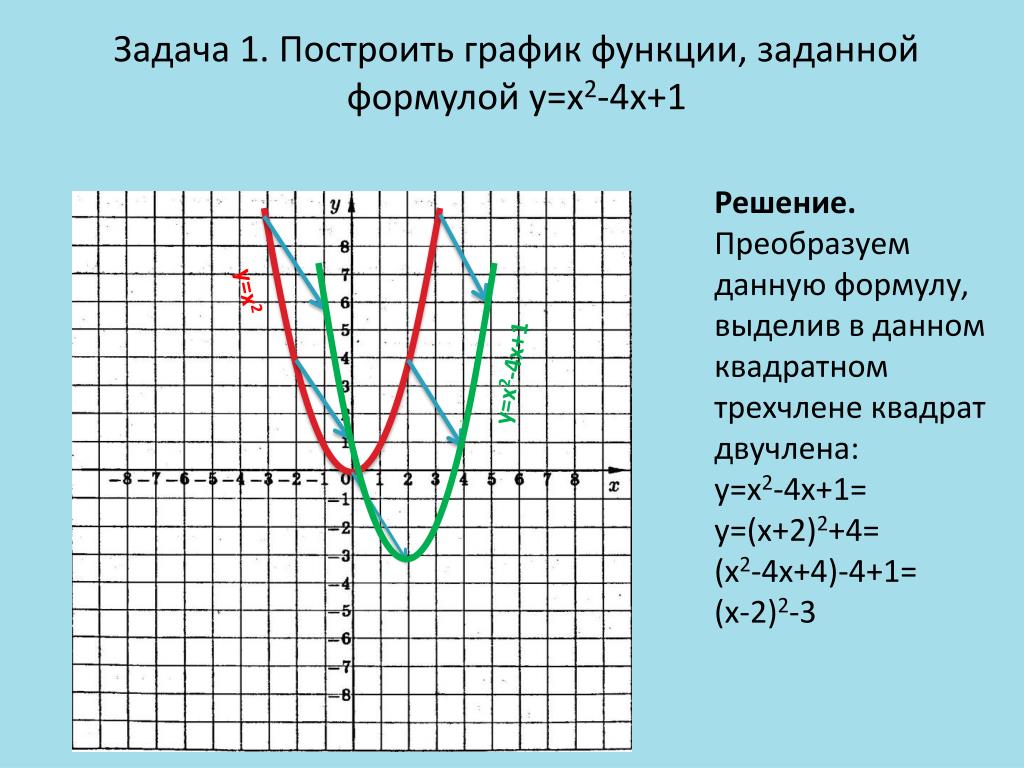
Функция может быть четной, нечетной или ни той, ни другой. Определим это с помощью несложных вычислений:
Получили, что функция является ни той, ни другой.
Для получения точек линейной прямой, через которые можно будет построить график заданной функции, найдем точки пересечения этой прямой с координатными осями.
Сначала найдем точку пересечения с координатной осью Оу. Для этого подставим значение х = 0 в функцию:
Точка пересечения с осью Оу будет иметь координаты (0; 2).
Теперь найдем точку пересечения с координатной осью Ох. Для этого подставим значение у = 0 в функцию и решим полученное простое уравнение:
Точка пересечения с осью Оx будет иметь координаты (1; 0).
Отметим на координатной плоскости полученные точки и проведем через них прямую.
Заданная функция построена.
Введите график функции
Построим (исследуем) график функции y=f(x), для этого задайте функцию f(x)
Важно: a должно быть меньше b, иначе график не сможет построиться.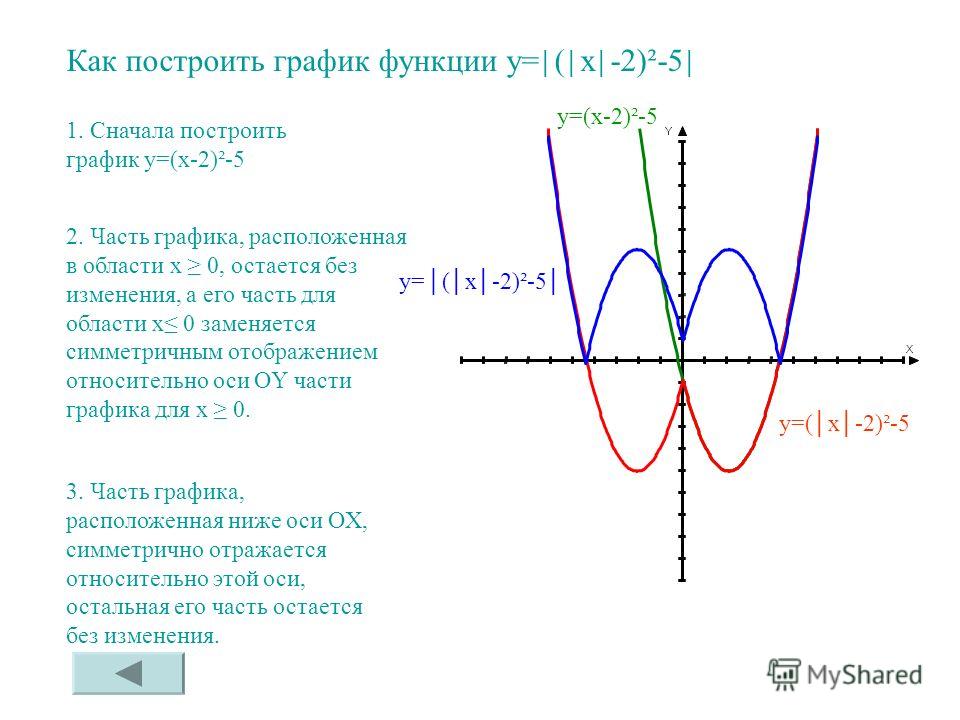 Cледите за масштабом — если графика на рисунке нету, значит стоит поварьировать значения a и b
Cледите за масштабом — если графика на рисунке нету, значит стоит поварьировать значения a и b
Примеры
С применением степени
(квадрат и куб) и дроби
С применением синуса и косинуса
Гиберболические синус и косинус
Гиберболические тангенс и котангенс
Гиберболические арксинус и арккосинус
Гиберболические арктангенс и арккотангенс
Исследование графика функции
Для периодических функций идет исследование графика функции только на промежутке периода
Наш калькулятор позволяет исследовать график функции. Но пока что нет возможности находить область определения функции
Что умеет находить этот калькулятор:
- Область определения функции: Да. Умеет определять только точки, в которых знаменатель функции обращается в нуль, но в остальных случаях:
- Умеет определять точки пересечения графика функции с осями координат: Да
- Экстремумы функции: интервалы (отрезки) возрастания и убывания функции: Да
- Точки перегибов графика функции: перегибы: интервалы выпуклости, вогнутости (впуклости): Да
- Вертикальные асимптоты : Да (это завязано с областью определения функции, на точки, где знаменатель функции обращается в нуль)
- Горизонтальные асимптоты графика функции: Да
- Наклонные асимптоты графика функции: Да
- Четность и нечетность функции: Да
Правила ввода выражений и функций
© Контрольная работа РУ — калькуляторы онлайн
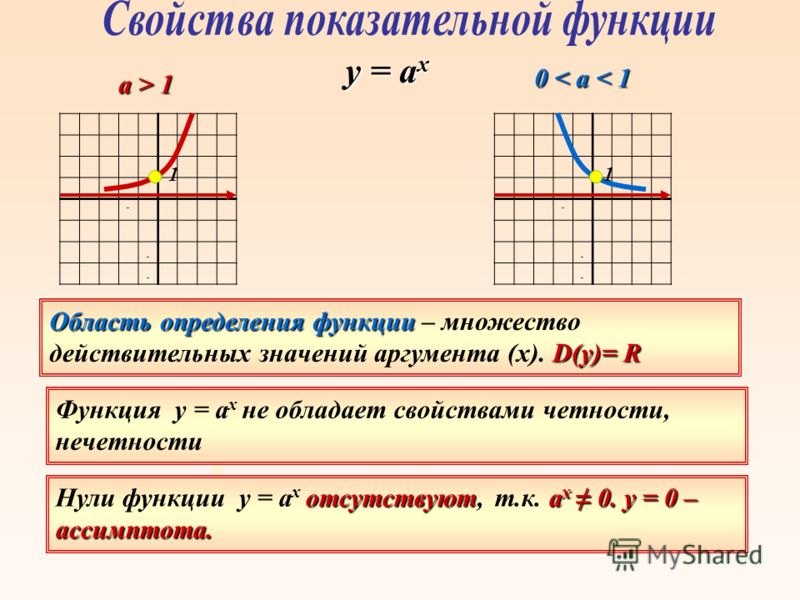
Алгебра Функция y= аx2, её график и свойства
youtube.com/embed/CrQlh2yZBuw» frameborder=»0″ allowfullscreen=»»>Материалы к уроку
5. Функция игрек равно а икс квадрат, ее график и свойства.doc
224 KBСкачать5. Функция y= аx2, её график и свойства.ppt
2.87 MBСкачать
Конспект урока
Одной из важных функций является квадратичная функция.
Квадратичной функцией называется функция вида игрек равно а икс квадрат плюс бэ икс плюс цэ, где икс – независимая переменная, а, бэ и цэ – некоторые числа, причем а не равно нулю.
Областью определения квадратичной функции является множество всех чисел.
Примером квадратичной функции является зависимость пути от времени при равноускоренном движении. Если тело движется с ускорением а и к началу отсчета времени тэ прошло путь эс нулевое, имея в этот момент скорость вэ нулевое, то зависимость пройденного пути эс от времени тэ выражается формулой эс равно а тэ квадрат деленное на два плюс вэ нулевое тэ.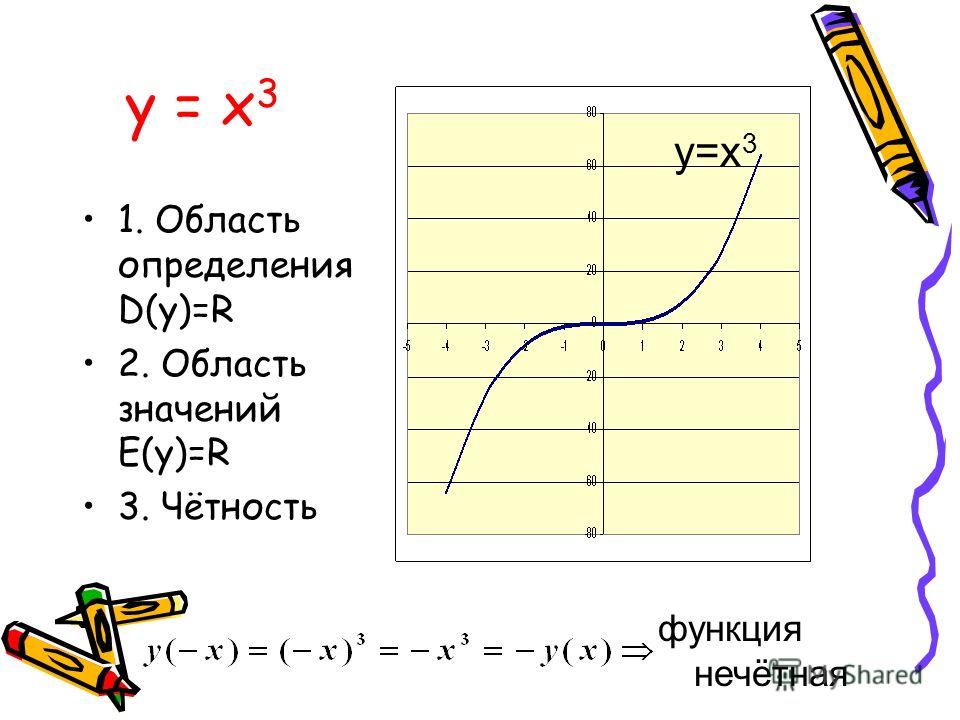 . плюс эс нулевое.
. плюс эс нулевое.
Если, например, а равно восьми, вэ нулевое равно трем, эс нулевое равно восемнадцати, то эс равно четыре тэ квадрат плюс три тэ плюс восемнадцать.
Изучение квадратичной функции начнем с частного случая – функции игрек равно а икс квадрат.
При а равном единице формула игрек равно а икс квадрат принимает вид игрек равно икс квадрат. Ее графиком является парабола.
Построим график функции игрек равно три икс квадрат. Составим таблицу значений этой функции. Отметим данные точки, соединим их плавной линией и получим график функции игрек равно три икс квадрат.
При любом икс не равном нулю значение функции игрек равно три икс квадрат больше соответствующего значения функции игрек равно икс квадрат в три раза. Если переместить каждую точку графика функции игрек равно икс квадрат вверх так, чтобы расстояние от этой точки до оси иксов увеличилось в три раза, то она перейдет в точку графика функции игрек равно три икс квадрат.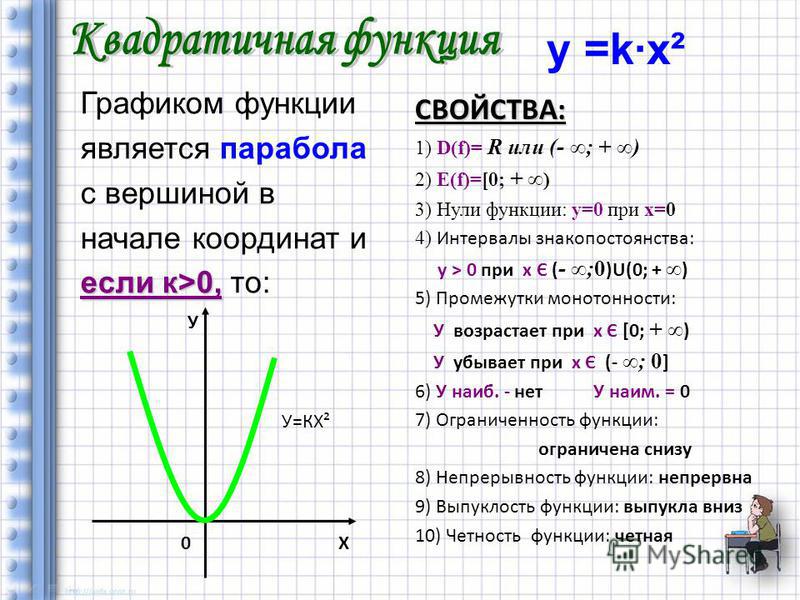 Таким образом, график функции игрек равно три икс квадрат можно получить из графика функции игрек равно икс квадрат растяжением от оси икс в три раза.
Таким образом, график функции игрек равно три икс квадрат можно получить из графика функции игрек равно икс квадрат растяжением от оси икс в три раза.
Построим теперь график функции игрек равно одна третья икс квадрат. Для этого составим таблицу ее значений. Отметив точки по данным координатам и соединив их плавной линией, получим график функции игрек равно одна третья икс квадрат.
При любом значении икс не равном нулю значение функции игрек равно одна третья икс квадрат меньше соответствующего значения функции игрек равно икс квадрат.. в три раза. Если переместить каждую точку графика функции игрек равно икс квадрат вниз так, чтобы расстояние от этой точки до оси икс уменьшилось в три раза, то она перейдет в точку графика функции игрек равно одна третья икс квадрат. Таким образом, график функции игрек равно одна третья икс квадрат можно получить из параболы игрек равно икс квадрат сжатием к оси икс в три раза.
Вообще график функции игрек равно а икс квадрат можно получить из параболы игрек равно икс квадрат растяжением от оси икс в а раз, если а больше единицы, и сжатием к оси икс в единица деленная на а раз, если а больше нуля и меньше единицы.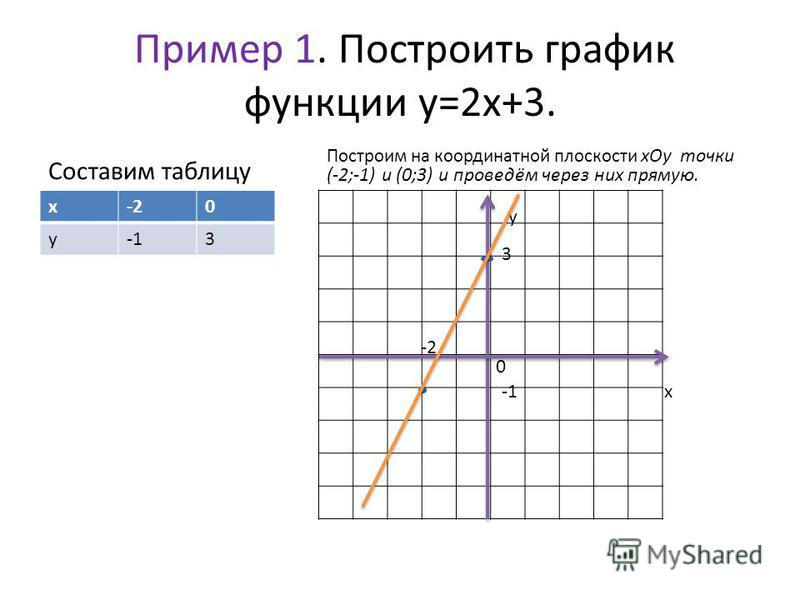
Рассмотрим теперь функцию игрек равно а икс квадрат, когда а меньше нуля.
Построим график функции игрек равно минус одна третья икс квадрат. Составим таблицу значений для этого графика и построим график функции.
Сравним графики функций минус одна третья икс квадрат и одна третья икс квадрат. При любом икс значения этих функций являются противоположными числами. Значит, соответствующие точки графиков симметричны относительно оси икс.
Таким образом, графики функций игрек равно а икс квадрат и минус а икс квадрат при а не равном нулю симметричны относительно оси икс.
График функции игрек равно а икс квадрат, где а не равно нулю называется параболой.
Сформулируем свойства функции игрек равно а икс квадрат при а большем нуля.
- Если икс равен нулю, то игрек равен нулю. График функции проходит через начало координат.
- Если икс не равен нулю, то игрек больше нуля. График функции расположен в верхней полуплоскости.
- Противоположным значениям аргумента соответствуют равные значения функции.
 График функции симметричен относительно оси игрек.
График функции симметричен относительно оси игрек. - Функция убывает в промежутке от минус бесконечности до нуля включительно и возрастает в промежутке от нуля до плюс бесконечности, включая ноль.
- Наименьшее значение, равное нулю, функция принимает при икс равном нулю, наибольшего значения функция не имеет. Областью значений функции является промежуток от нуля до плюс бесконечности, включая ноль.
Теперь сформулируем свойства функции игрек равно а икс квадрат при а меньшем нуля.
- Если икс равен нулю, то игрек равен нулю. График функции проходит через начало координат.
- Если икс не равен нулю, то игрек меньше нуля. График функции расположен в нижней полуплоскости.
- Противоположным значениям аргумента соответствуют равные значения функции. График функции симметричен относительно оси игрек.
- Функция возрастает в промежутке от минус бесконечности до нуля, включая ноль и убывает в промежутке от нуля до плюс бесконечности, включая ноль.

- Наибольшее значение, равное нулю, функция принимает при икс равном нулю, наименьшего значения функция не имеет. Областью значений функции является промежуток от минус бесконечности до нуля, включая ноль.
Из перечисленных свойств следует, что при а большем нуля ветви параболы направлены вверх, при а меньшем нуля – вниз. Ось игрек является осью симметрии параболы. Точку пересечения параболы с ее осью симметрии называют вершиной параболы. Вершиной параболы игрек равно а икс квадрат является начало координат.
К преобразованиям графика функции игрек равно а икс квадрат относят построение графика, симметричного данному относительно оси икс, растяжение графика от оси икс или сжатие графика к оси икс.
Таким образом, график функции игрек равно минус эф от икс можно получить из графика функции игрек равно эф от икс с помощью симметрии относительно оси икс. График функции игрек равно а эф от икс можно получить из графика функции игрек равно эф от икс с помощью растяжения от оси икс в а раз, если а больше единицы,. . и с помощью сжатия к оси х в единица деленная на а раз, если а больше нуля и меньше единицы.
. и с помощью сжатия к оси х в единица деленная на а раз, если а больше нуля и меньше единицы.
Остались вопросы по теме? Наши репетиторы готовы помочь!
Подготовим к ЕГЭ, ОГЭ и другим экзаменам
Найдём слабые места по предмету и разберём ошибки
Повысим успеваемость по школьным предметам
Поможем подготовиться к поступлению в любой ВУЗ
Выбрать репетитора
3-8Графики смещения, отражения и растяжения
1. 5 — Графики смещения, отражения и растяжения
5 — Графики смещения, отражения и растяженияОпределения
- Абсцисса
- Координата x
- Ординат
- Координата Y
- Смена
- Перевод, при котором размер и форма графика функции не изменяются, но расположение графика.
- Весы
- Перевод, в котором изменены размер и форма графика функции.
- Отражение
- Перевод, при котором график функции зеркально отражается относительно оси.
Общие функции
Частью красоты математики является то, что почти все строится на чем-то еще, и если вы можете понять основы, тогда вы можете применять новые элементы к старым. Именно эта способность что делает возможным понимание математики. Если бы вы запоминали каждую часть представленная вам математика без установления связи с другими частями, вы 1) станете разочарован в математике и 2) не очень понимаю математику.
г. Есть несколько простых графиков, которые мы уже видели.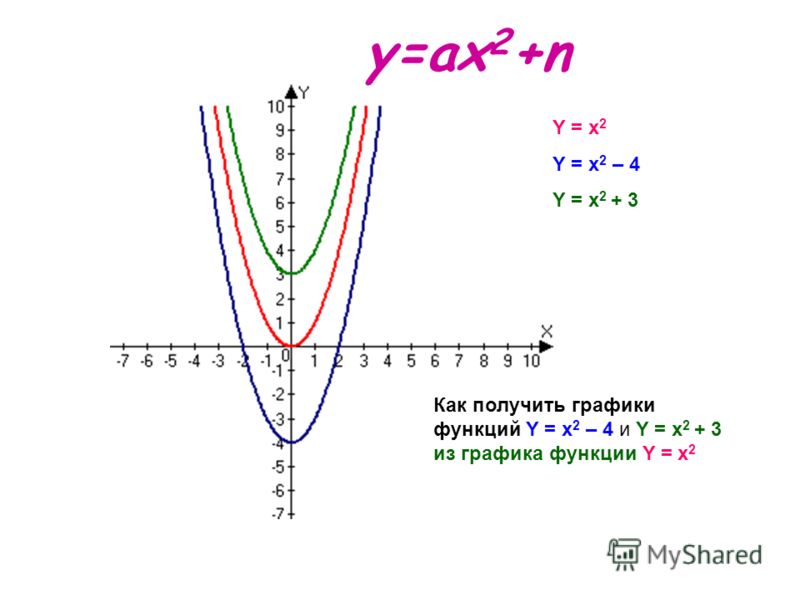 Применяя переводы к этим основным
графы, мы можем получить новые графы, которые сохраняют все свойства старых. По
понимание основных графиков и того, как к ним применяется перевод, мы узнаем каждый
новый график как небольшая вариация старого, а не как совершенно другой график, который у нас есть
никогда не видел раньше. Понимание этих переводов позволит нам быстро распознавать и
нарисуйте новую функцию, не прибегая к построению точек.
Применяя переводы к этим основным
графы, мы можем получить новые графы, которые сохраняют все свойства старых. По
понимание основных графиков и того, как к ним применяется перевод, мы узнаем каждый
новый график как небольшая вариация старого, а не как совершенно другой график, который у нас есть
никогда не видел раньше. Понимание этих переводов позволит нам быстро распознавать и
нарисуйте новую функцию, не прибегая к построению точек.
Вот общие функции, графики которых вы должны знать в настоящее время:
- Постоянная Функция: y = c
- Линейная функция: у = х
- Квадратичная функция: у = х 2
- Кубическая функция: у = х 3
- Функция абсолютного значения: y = |x|
- Функция извлечения квадратного корня: y = sqrt(x)
- Функция наибольшего целого числа: y = int(x) обсуждалась в предыдущем разделе.
Постоянная функция | Линейная функция | Квадратичная функция |
Кубическая функция | Функция абсолютного значения | Функция извлечения квадратного корня |
В вашем тексте линейная функция называется функцией тождества, а квадратичная функция — возведением в квадрат.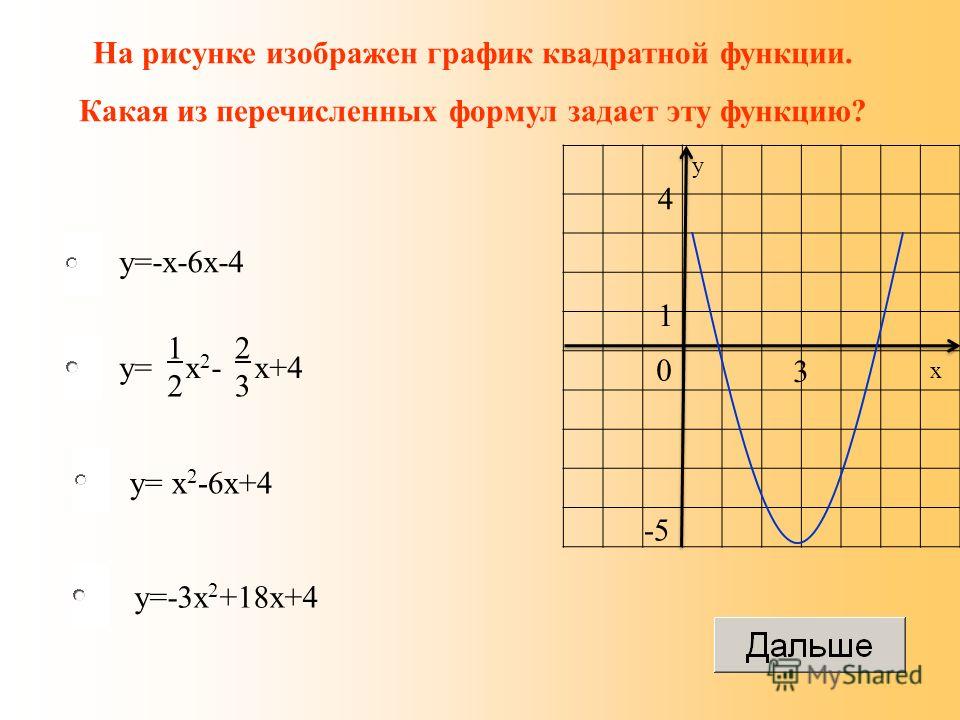 функция.
функция.
переводов
Есть два вида переводов, которые мы можем сделать с графиком функции. Они смещаются и масштабирование. Если считать отражения, их три, но отражения — это всего лишь частный случай второй перевод.
Смены
Сдвиг является жестким переносом в том смысле, что он не изменяет форму или размер графика функция. Все, что сделает сдвиг, — это изменит расположение графика. Вертикальный сдвиг добавляет/вычитает константу к/из каждой координаты y, оставляя координату x неизменной. Горизонтальный сдвиг добавляет/вычитает константу к/от каждой координаты x, оставляя координату y неизменной. Вертикальные и горизонтальные сдвиги могут быть объединены в одно выражение.
г.Сдвиги добавляются/вычитаются из компонентов x или f(x). Если константа сгруппирована с x, то это сдвиг по горизонтали, иначе сдвиг по вертикали.
Весы (растяжение/сжатие)
Масштаб представляет собой нежесткое преобразование в том смысле, что он изменяет форму и размер графика
функция.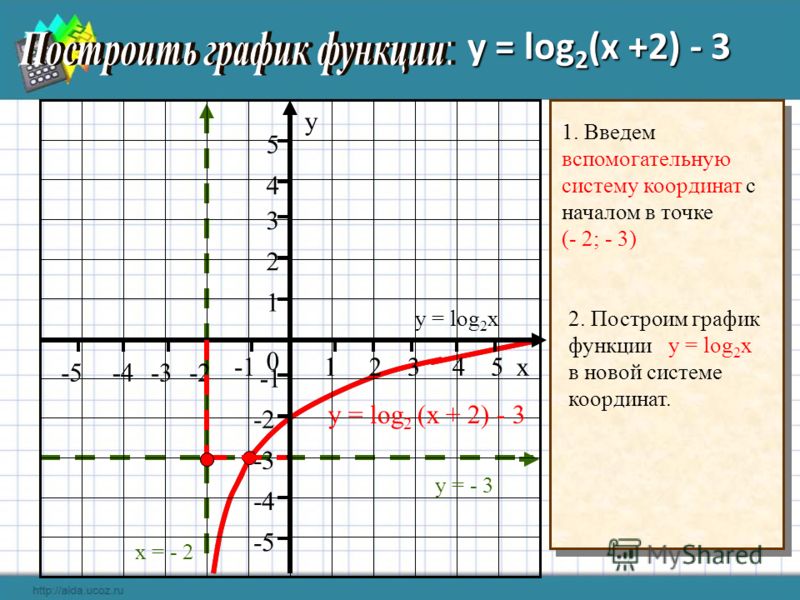 Масштаб будет умножать/разделять координаты, и это изменит внешний вид, а также
Местоположение. Вертикальное масштабирование умножает/делит каждую координату y на константу, оставляя
координата x не изменилась. Горизонтальное масштабирование умножает/делит каждую координату x на
постоянным, оставляя координату y неизменной. Вертикальное и горизонтальное масштабирование может быть
объединены в одно выражение.
Масштаб будет умножать/разделять координаты, и это изменит внешний вид, а также
Местоположение. Вертикальное масштабирование умножает/делит каждую координату y на константу, оставляя
координата x не изменилась. Горизонтальное масштабирование умножает/делит каждую координату x на
постоянным, оставляя координату y неизменной. Вертикальное и горизонтальное масштабирование может быть
объединены в одно выражение.
Коэффициенты масштабирования умножаются/делятся на компоненты x или f(x). Если константа сгруппирована с x, то это горизонтальное масштабирование, иначе это вертикальное масштабирование.
Отражения
Функция может быть отражена относительно оси путем умножения на отрицательную единицу. Чтобы отразить ось Y, умножьте каждый x на -1, чтобы получить -x. Чтобы отразить ось x, умножьте f(x) на -1, чтобы получить -f(x).
Собираем все вместе
Рассмотрим основной график функции: y = f(x)
г.Все переводы могут быть выражены в виде:
у = а * е [b (х-с)] + d
| Вертикальный | Горизонтальный | |
|---|---|---|
| Шкала | и | б |
| Смена | д | с |
| действует нормально | действует обратно |
Отступление
Понимание представленных здесь концепций имеет основополагающее значение для понимания полиномиальных и рациональных
функций (гл.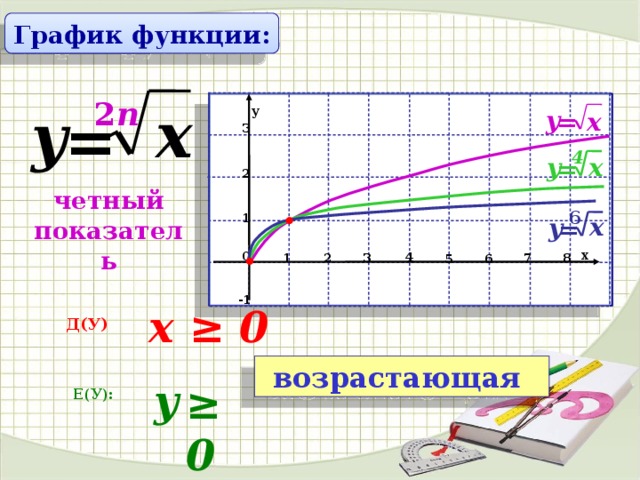 3) и особенно конических сечений (гл. 8). Это также сыграет очень большую роль в
Тригонометрия (математика 117) и исчисление (математика 121, 122, 221 или 19).0).
3) и особенно конических сечений (гл. 8). Это также сыграет очень большую роль в
Тригонометрия (математика 117) и исчисление (математика 121, 122, 221 или 19).0).
Ранее в тексте (раздел 1.2, задачи 61-64) был ряд задач, которые написали уравнение линии как:
х/а + у/б = 1
Где a — точка пересечения по оси x, а b — точка пересечения с линией y. «а» может действительно быть думал о том, как далеко идти в направлении х (масштабирование по оси х) и «b» может думать о том, как далеко идти в направлении «у» (у-масштабирование). Итак, «а» и «б» есть на самом деле множители (хотя они и появляются внизу). Что они умножение это 1 который находится с правой стороны. x+y=1 будет иметь точку пересечения x и y 1.
г.Хорошо. Рассмотрим уравнение: y = f(x)
Это самый простой график функции. Но преобразования могут применяться и к нему. Его можно записать в формате, показанном ниже.
В этом формате «а» — это множитель по вертикали, а «b» — по горизонтали.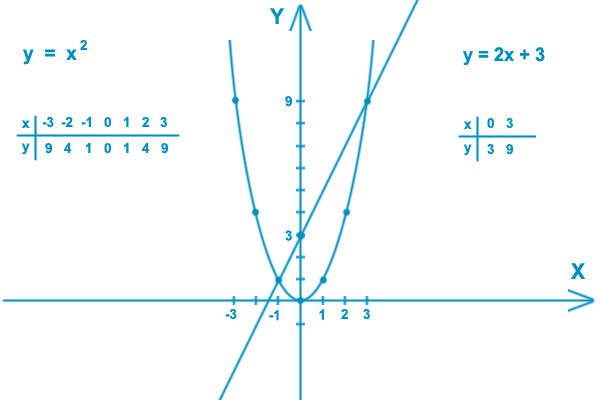 множитель. Мы знаем, что «а» влияет на у, потому что она сгруппирована с
y и «b» влияет на
x, потому что он сгруппирован с x.
множитель. Мы знаем, что «а» влияет на у, потому что она сгруппирована с
y и «b» влияет на
x, потому что он сгруппирован с x.
«d» и «c» вертикальные и горизонтальные смены соответственно. Мы знаем, что это сдвиги, потому что они вычитаются от переменной скорее чем разделить на переменную, что сделало бы их весами.
г.В этом формате все изменения кажутся противоположными ожидаемым. Если у вас есть выражение (y-2)/3, это сдвиг по вертикали на 2 вправо (хотя там написано y минус 2) и это вертикальное растяжение на 3 (хотя там написано y разделить на 3). Важно понимать, что в этом формат, когда константы сгруппированы с переменной, на которую они влияют, перевод противоположное (обратное) тому, что большинство людей думает, что это должно быть.
г. Однако этот формат не подходит для рисования с помощью технологии,
потому что нам нравится, когда функции записываются как y =, а не (y-c)/d =.
Итак, если вы возьмете обозначение выше и решите его для y, вы получите обозначение ниже, которое
похожее, но не совсем наше базовое состояние формы выше.
у = а * е ((х-с) / б) + д
Обратите внимание, что для определения y вам пришлось инвертировать обе константы «a» и «d». Вместо деления на «а» вы теперь умножаете на «а». Ну, раньше быть, что ты все равно пришлось применить обратную константу. Когда было сказано «разделить на а», ты знал это Это имел в виду «умножить каждый y на a». Когда он сказал «вычесть d», вы знали, что вам действительно нужно «добавить д». У вас есть уже применил обратное, так что не делайте этого снова! С константами, влияющими у, так как они были перемещены на другую сторону, примите их за чистую монету. Если написано умножить на 2, делай, не надо разделить на 2.
г. Однако константы, влияющие на x, не изменились. Они по-прежнему противоположны
какими, по вашему мнению, они должны быть. И, что еще хуже, «x разделить b», что на самом деле означает
умножение каждой координаты x на «b» было перевернуто и записано как «b умножить на x», так что это действительно
означает разделить каждый x на «b».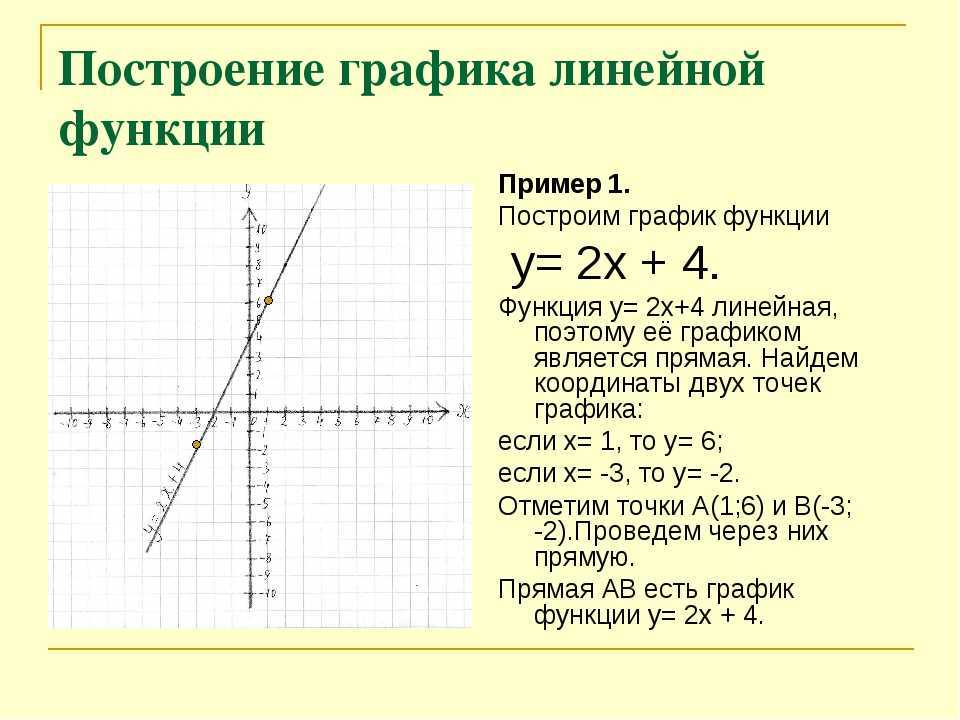 «x минус c» на самом деле означает добавление c к каждой координате x.
«x минус c» на самом деле означает добавление c к каждой координате x.
Итак, окончательная форма (для технологии) такая, как указано выше:
у = а * е [b (х-с)] + d
Хорошо, конец отступления.
Нормальное и обратное поведение
Вы заметите, что на диаграмме указано, что вертикальное перемещение является нормальным, а горизонтальное переводы обратные. Чтобы понять, почему, читайте отступление выше. концепции в действительно имеют фундаментальное значение для понимания многих графиков.
Примеры
- у=f(х)
- Без перевода
- у=е(х+2)
- +2 сгруппировано с x, поэтому это горизонтальный перевод. Так как он добавлен
к х, а не умножается на х, это сдвиг, а не масштаб. Так как там написано плюс а горизонтальные изменения обратные, фактическое перемещение заключается в перемещении всего
график на две единицы влево или «вычесть два из каждой координаты x», оставив
только y-координаты.

- у=f(х)+2
- +2 не сгруппирован с x, поэтому это вертикальный перевод. Поскольку он добавлен, а не умножение, это сдвиг, а не масштаб. Так как он говорит плюс и вертикальный изменения действуют так, как они выглядят, фактический перевод состоит в том, чтобы переместить весь график на два единицы вверх или «добавьте два к каждой координате y», оставив только координаты x. г.
- у=f(x-3)+5
- На этот раз сдвиг по горизонтали на три вправо и сдвиг по вертикали на пять вверх. Так перевод будет состоять в том, чтобы переместить весь график вправо на три и вверх на пять или «добавить три на каждую координату x и пять на каждую координату y»
- у=3f(х)
- 3 умножается, так что это масштабирование, а не смещение. 3 не сгруппирован с
x, так что это вертикальное масштабирование. Вертикальные изменения влияют так, как вы думаете
должно быть, поэтому результатом будет «умножить каждую координату y на три», оставив только координаты x.
 г.
г. - у=-f(х)
- Y нужно умножить на -1. Это делает перевод «отражающим по оси x», оставляя координаты x в покое.
- у=е(2х)
- 2 умножается, а не добавляется, так что это масштабирование, а не смещение. 2 это сгруппированы с x, так что это горизонтальное масштабирование. Горизонтальные изменения обратны то, чем они кажутся, вместо того, чтобы умножать каждую координату x на два, перевод состоит в том, чтобы «делить каждую координату x на два», оставляя координаты y без изменений. г.
- у=е(-х)
- x нужно умножить на -1. Это делает перевод «отражающим ось Y», оставляя координаты Y в покое.
- у=1/2 е(х/3)
- Перевод здесь будет «умножить каждую координату y на 1/2 и умножить каждую координату x на 3».
- у=2f(х)+5
- Здесь может быть некоторая двусмысленность. Вы «добавляете пять к каждой координате y, а затем
умножить на два» или вы «умножаете каждую координату y на два, а затем добавляете пять»?
Вот здесь-то и вступает в силу мой предыдущий комментарий о том, что математика строится на самой себе.
 играть в. Существует порядок действий, в котором говорится, что умножение и деление
выполняется перед сложением и вычитанием. Если вы помните это, то решение
легкий. Правильное преобразование состоит в том, чтобы «умножить каждую координату y на два, а затем
добавьте пять дюймов, оставив координаты x в покое. г.
играть в. Существует порядок действий, в котором говорится, что умножение и деление
выполняется перед сложением и вычитанием. Если вы помните это, то решение
легкий. Правильное преобразование состоит в том, чтобы «умножить каждую координату y на два, а затем
добавьте пять дюймов, оставив координаты x в покое. г. - у=е(2х-3)
- Теперь, когда порядок операций четко определен, двусмысленность здесь, о которой должно быть сделано в первую очередь удаляется. Ответ не в том, чтобы «делить каждую координату x на два». и прибавьте три», как и следовало ожидать. Причина в том, что проблема , а не , написанная на стандартная форма. Стандартная форма: y=f[b(x-c)]. При записи в стандартной форме это проблема становится y=f[2(x-3/2)]. Это означает, что правильный перевод должен быть «разделить каждую координату x на два и добавить три половины», оставив координаты y без изменений. г.
- у=3f(х-2)
- Перевод здесь «умножить каждую координату y на три и добавить два к каждой координате x».
 Кроме того, вы можете изменить порядок. Изменения в x или y
можно сделать независимо друг от друга, но если есть масштабы и сдвиги к одному и тому же
переменная, важно сначала выполнить масштабирование, а затем смещение.
Кроме того, вы можете изменить порядок. Изменения в x или y
можно сделать независимо друг от друга, но если есть масштабы и сдвиги к одному и тому же
переменная, важно сначала выполнить масштабирование, а затем смещение.
Переводы и влияние на домен и диапазон
Любое горизонтальное перемещение повлияет на домен и оставит диапазон без изменений. Любая вертикаль перевод повлияет на диапазон и оставит домен без изменений.
г.Примените к домену или диапазону то же преобразование, что и к координатам x или y. Это работает, потому что область может быть записана в виде интервала как интервал между двумя координатами x. Аналогично для диапазона как интервала между двумя координатами y.
Помните, что в следующей таблице домен и диапазон указаны в виде интервалов. Если ты
не знакомы с записью интервалов, пожалуйста, ознакомьтесь с главой о предварительных требованиях. Первая строка это
оператор определения и должен использоваться для определения остальных ответов.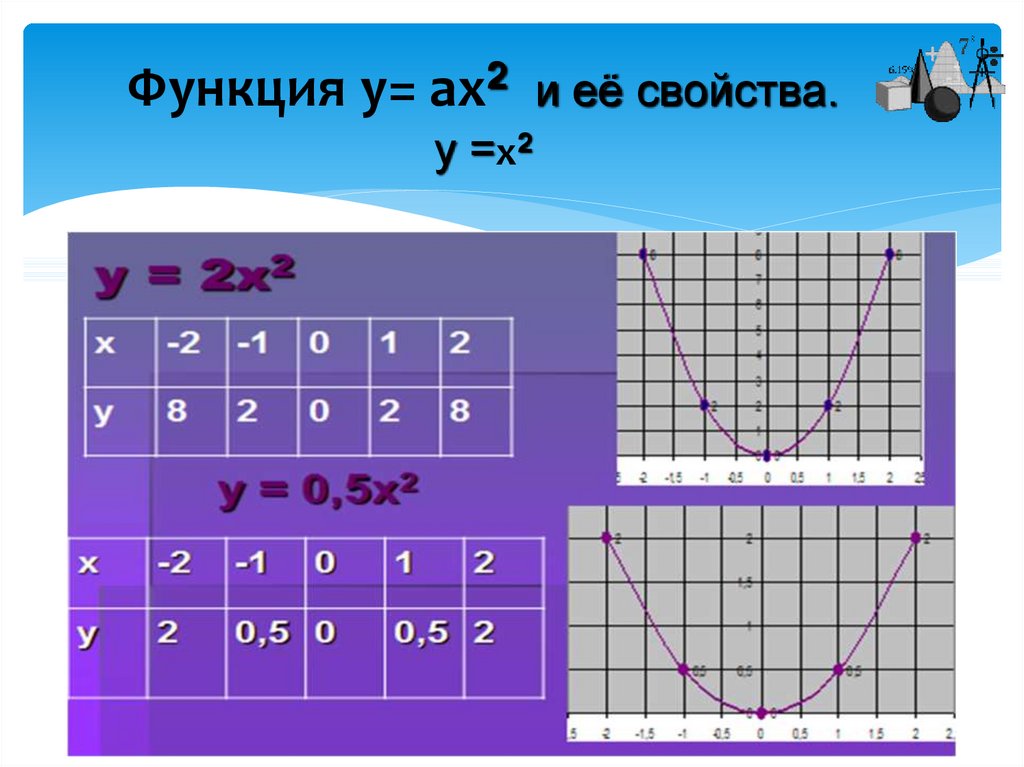
| График | Перевод | Домен | Диапазон |
|---|---|---|---|
| у=f(х) | нет | (-2,5) | [4,8] |
| у=f(х-2) | справа 2 | (0,7) | [4,8] |
| y=f(x)-2 | вниз 2 | (-2,5) | [2,6] |
| у=3f(х) | умножить каждый y на 3 | (-2,5) | [12,24] |
| у=f(3x) | разделить каждый х на 3 | (-2/3,5/3) | [4,8] |
| y=2f(x-3)-5 | умножьте каждый y на 2 и вычтите 5; прибавить 3 к каждому x | (1,8) | [3,11] |
| у=-f(x) | отражение относительно оси x | (-2,5) | [-8,-4] |
| y=1/f(x) | взять обратное значение каждого y | (-2,5) | [1/8,1/4] |
Обратите внимание на последние два, что порядок в диапазоне изменился. Это потому, что в интервале
обозначение, меньшее число всегда идет первым.
Это потому, что в интервале
обозначение, меньшее число всегда идет первым.
Действительно хорошие вещи
Понимание переводов также может помочь при поиске домена и диапазона функции. Допустим, ваша проблема состоит в том, чтобы найти домен и диапазон функции y=2-sqrt(x-3).
Начните с того, что вы знаете. Вы знаете, что основная функция — это sqrt(x), и вы знаете домен и диапазон sqrt (x) оба [0, + бесконечность). Ты знаешь это, потому что знаешь этих шестерых общие функции на обложке вашего текста, которые будут использоваться в качестве строительных блоков для других функций.
г.| Функция | Перевод | Домен | Диапазон | |
|---|---|---|---|---|
| Начните с чего ты знаешь | у=кв(х) | Нет | [0,+бесконечность) | [0,+бесконечность) |
| Применить переводы | г=-кв. (х) (х) | Отражение вокруг оси x | [0,+бесконечность) | (-бесконечность,0] |
| y=2-sqrt(x) | Прибавить 2 к каждой ординате | [0,+бесконечность) | (-бесконечность,2] | |
| у=2-кв.(х-3) | Прибавить 3 к каждой оси абсцисс | [3,+бесконечность) | (-бесконечность,2] |
Итак, для функции y=2-sqrt(x-3) область определения равна x≥3, а диапазон равен y≤2.
И лучшая часть в том, что вы это поняли! Вы не только поняли это, но и Это можно сделать без построения графика на калькуляторе.
Нет ничего плохого в том, чтобы построить график, чтобы увидеть, что происходит, но вы должны быть в состоянии
понять, что происходит без графика, потому что мы узнали, что график
калькулятор не всегда точно показывает, что происходит.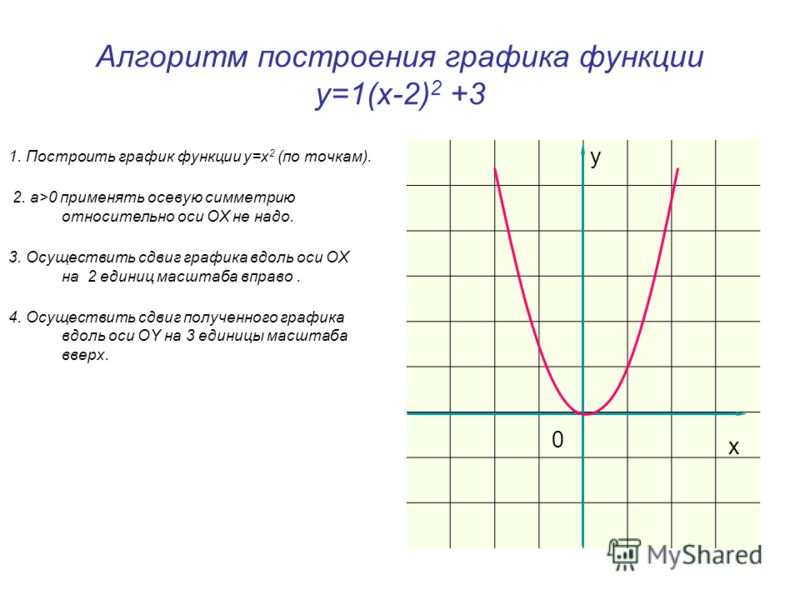 Это инструмент, помогающий вашему пониманию
и понимание, а не инструмент, чтобы заменить его.
Это инструмент, помогающий вашему пониманию
и понимание, а не инструмент, чтобы заменить его.
Именно эту связность математики я хочу, чтобы вы все «усвоили». Все подходит вместе так красиво.
Графики квадратных уравнений с использованием оси симметрии
Горячая математикаКвадратное уравнение это многочлен уравнение степень 2 . Стандартная форма квадратного уравнения:
0 знак равно а Икс 2 + б Икс + с
куда а , б а также с все действительные числа и а ≠ 0 .
Если мы заменим 0 с у , то мы получаем квадратичная функция
у знак равно а Икс 2 + б Икс + с
график которого будет
парабола
.
Осью симметрии этой параболы будет линия Икс знак равно − б 2 а . Ось симметрии проходит через вершину, поэтому Икс -координата вершины − б 2 а . Заменять Икс знак равно − б 2 а в уравнении найти у -координата вершины. Замените еще несколько Икс -значения в уравнении, чтобы получить соответствующие у -значения и построить точки. Соедините их и удлините параболу.
Пример 1:
График параболы у знак равно Икс 2 − 7 Икс + 2 .
Сравните уравнение с
у
знак равно
а
Икс
2
+
б
Икс
+
с
чтобы найти значения
а
,
б
, а также
с
.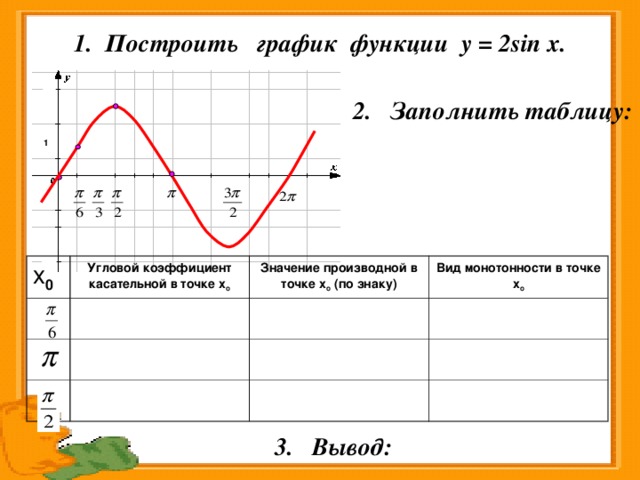
г. Здесь, а знак равно 1 , б знак равно − 7 а также с знак равно 2 .
Используя значения коэффициентов, напишите уравнение ось симметрии .
График квадратного уравнения в виде у знак равно а Икс 2 + б Икс + с имеет своей осью симметрии линию Икс знак равно − б 2 а . Итак, уравнение оси симметрии данной параболы имеет вид Икс знак равно − ( − 7 ) 2 ( 1 ) или же Икс знак равно 7 2 .
Заменять
Икс
знак равно
7
2
в уравнении найти
у
-координата вершины.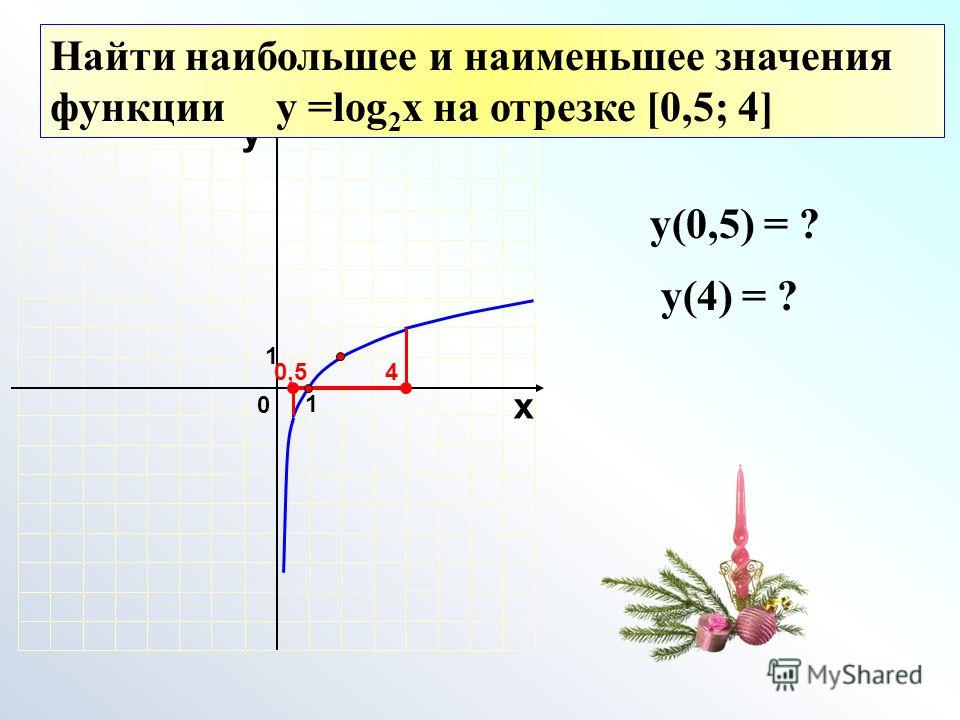
у знак равно ( 7 2 ) 2 − 7 ( 7 2 ) + 2 знак равно 494 − 49 2 + 2 знак равно 49 − 98 + 8 4 знак равно − 41 4
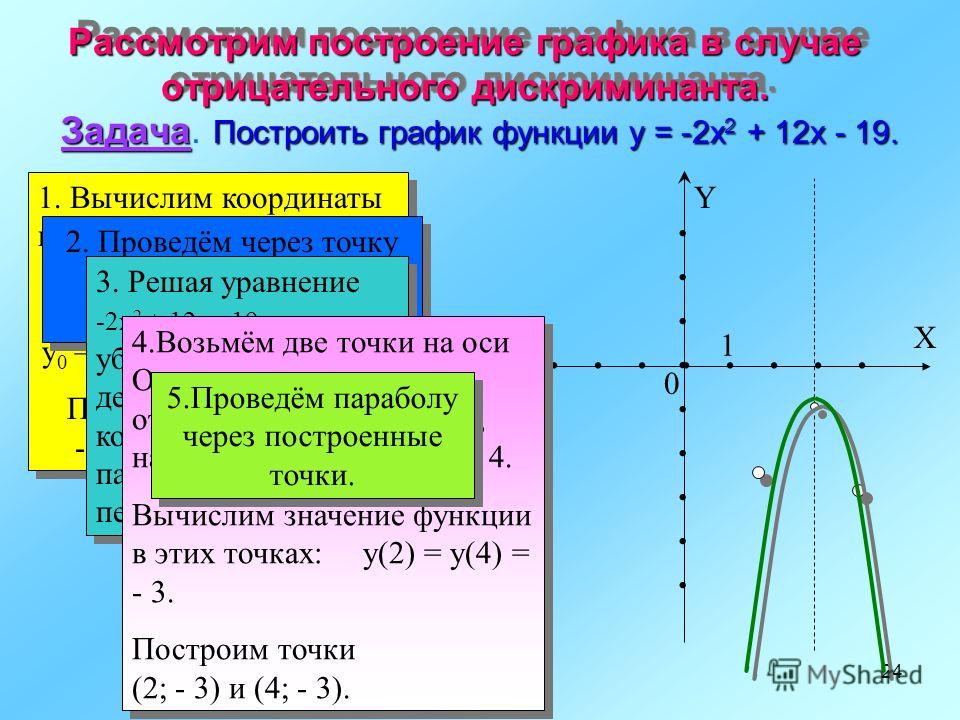
Следовательно, координаты вершины равны
(
7
2
,
−
41
4
)
.
Теперь замените еще несколько Икс -значения в уравнении, чтобы получить соответствующие у -ценности.
| Икс | у знак равно Икс 2 − 7 Икс + 2 |
| 0 | 2 |
| 1 | − 4 |
| 2 | − 8 |
| 3 | − 10 |
| 5 | − 8 |
| 7 | 2 |
Нанесите точки и соедините их, чтобы получить параболу.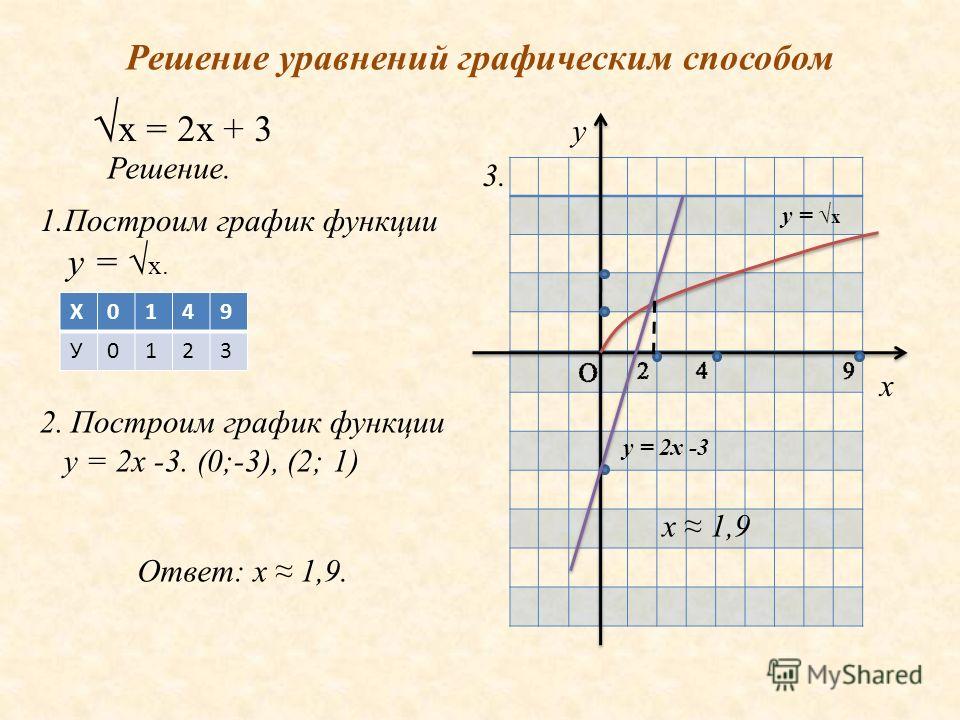
Пример 2:
График параболы у знак равно − 2 Икс 2 + 5 Икс − 1 .
Сравните уравнение с у знак равно а Икс 2 + б Икс + с чтобы найти значения а , б , а также с .
Здесь, а знак равно − 2 , б знак равно 5 а также с знак равно − 1 .
Используя значения коэффициентов, напишите уравнение оси симметрии.
График квадратного уравнения в виде
у
знак равно
а
Икс
2
+
б
Икс
+
с
имеет своей осью симметрии линию
Икс
знак равно
−
б
2
а
. Итак, уравнение оси симметрии данной параболы имеет вид
Икс
знак равно
−
(
5
)
2
(
−
2
)
или же
Икс
знак равно
5
4
.
Итак, уравнение оси симметрии данной параболы имеет вид
Икс
знак равно
−
(
5
)
2
(
−
2
)
или же
Икс
знак равно
5
4
.
Заменять Икс знак равно 5 4 в уравнении найти у -координата вершины.
у знак равно − 2 ( 5 4 ) 2 + 5 ( 5 4 ) − 1 знак равно − 50 16 + 25 4 − 1 знак равно − 50 + 100 − 16 16 знак равно 34 16 знак равно 17 8
Следовательно, координаты вершины равны
(
5
4
,
17
8
)
.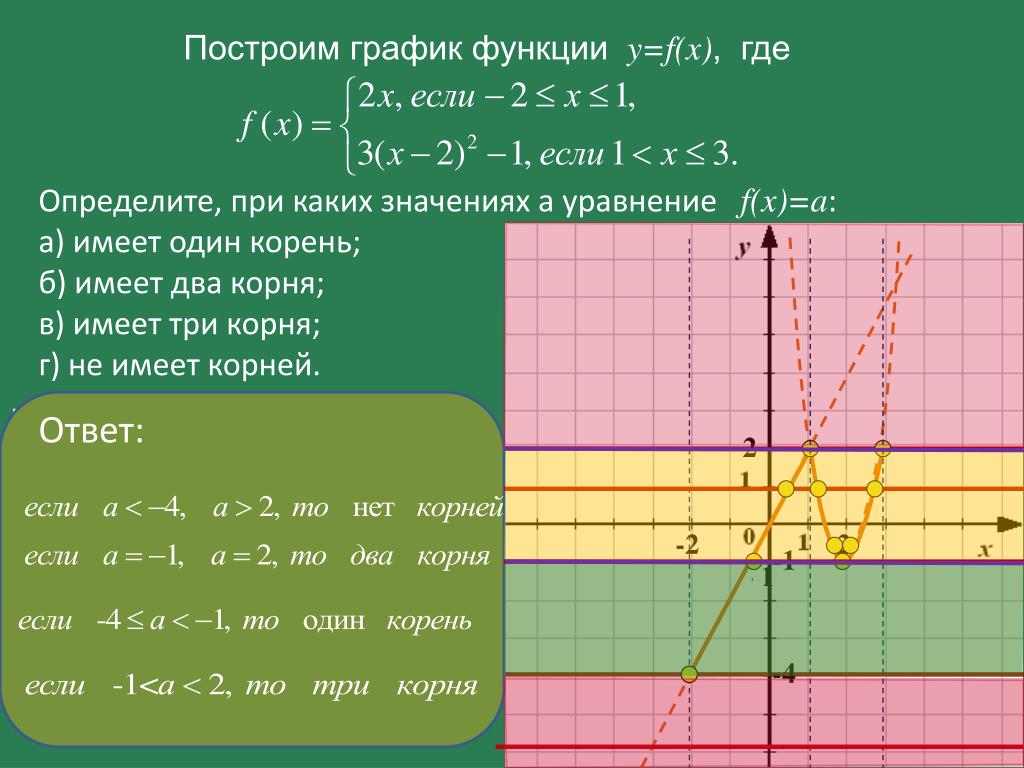
Теперь замените еще несколько Икс -значения в уравнении, чтобы получить соответствующие у -ценности.
| Икс | у знак равно − 2 Икс 2 + 5 Икс − 1 |
| − 1 | − 8 |
| 0 | − 1 |
| 1 | 2 |
| 2 | 1 |
| 3 | − 4 |
Нанесите точки и соедините их, чтобы получить параболу.
Пример 3:
График параболы Икс знак равно у 2 + 4 у + 2 .
Здесь, Икс является функцией у . Парабола открывается «вбок» и ось симметрии параболы горизонтальна. Стандартная форма уравнения горизонтальной параболы: Икс знак равно а у 2 + б у + с куда а , б , а также с все действительные числа и а ≠ 0 а уравнение оси симметрии имеет вид у знак равно − б 2 а .
Сравните уравнение с
Икс
знак равно
а
у
2
+
б
у
+
с
чтобы найти значения
а
,
б
, а также
с
.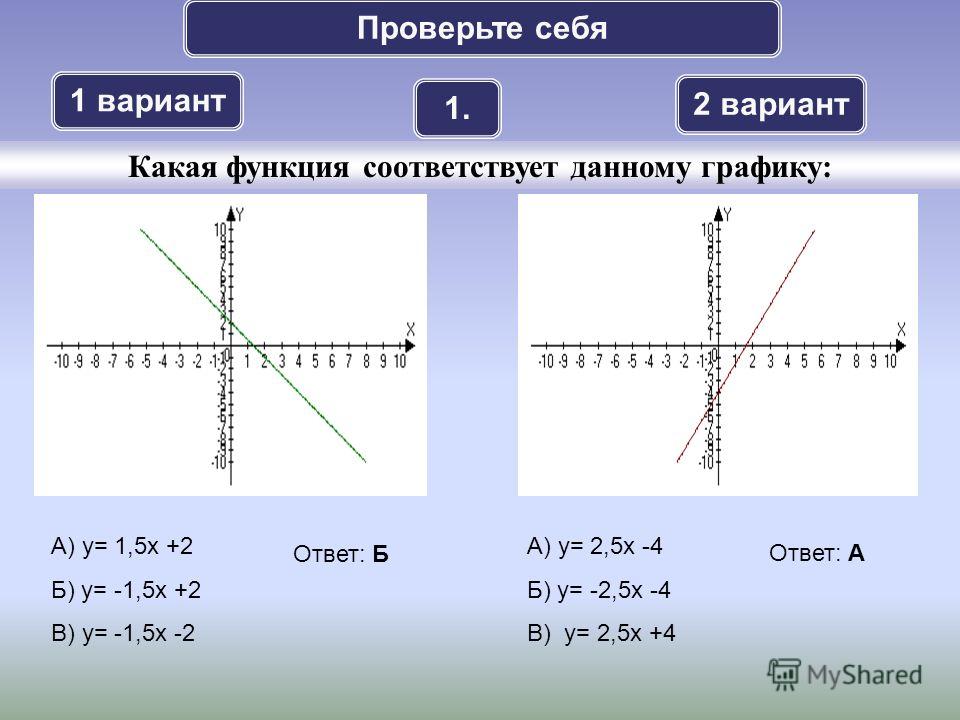
Здесь, а знак равно 1 , б знак равно 4 а также с знак равно 2 .
Используя значения коэффициентов, напишите уравнение оси симметрии.
График квадратного уравнения в виде Икс знак равно а у 2 + б у + с имеет своей осью симметрии линию у знак равно − б 2 а . Итак, уравнение оси симметрии данной параболы имеет вид у знак равно − 4 2 ( 1 ) или же у знак равно − 2 .
Заменять
у
знак равно
−
2
в уравнении найти
Икс
-координата вершины.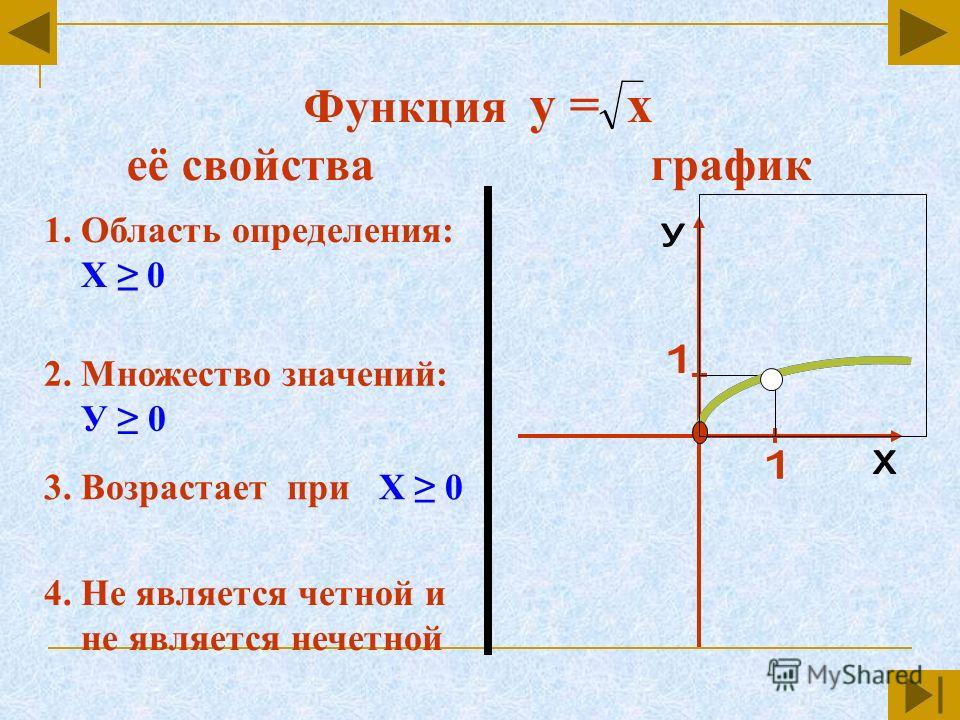
Икс знак равно ( − 2 ) 2 + 4 ( − 2 ) + 2 знак равно 4 − 8 + 2 знак равно − 2
Следовательно, координаты вершины равны ( − 2 , − 2 ) .
Теперь замените еще несколько у -значения в уравнении, чтобы получить соответствующие Икс -ценности.
| у | Икс знак равно у 2 + 4 у + 2 |
| − 5 | 7 |
| − 4 | 2 |
| − 3 | − 1 |
| − 1 | − 1 |
| 0 | 2 |
| 1 | 7 |
Нанесите точки и соедините их, чтобы получить параболу.
ППЛАТО | Базовая математика | Квадратичные функции и их графики
Общий квадратичный имеет вид:
г = ах 2 + бх + в
где a , b и c — константы, а a ≠ 0. Простейшее из них:
у = х 2
— когда a = 1, b = c = 0.
По поводу этого простейшего случая можно сделать следующие замечания:
- Поскольку возведение любого числа в квадрат дает положительное число, все значения y положительны, за исключением случая, когда x = 0, и в этом случае y = 0.
- По мере увеличения размера x увеличивается и x 2 ,
но увеличение значения «быстрее», чем увеличение x.

- График y = x 2 симметричен относительно оси y. ( х = 0). Например, если x = 3, соответствующее значение y равно 3 2 = 9. Если x = −3, то значение y равно (−3) 2 = 9. Два значения x равны равноудаленный от оси y, одно влево и одно вправо, но два значения y имеют одинаковую высоту над осью x.
Этого достаточно, чтобы набросать функцию.
На графике y = x 2 :
- Линия x = 0 (, т.е. по оси Y) будет называться линией симметрии для этого квадратичного уравнения.
- Линия y = 0 (, т.е. — ось x) будет называться ортогональной осью для этого квадратичного уравнения.
Если уравнение, скажем, y = 2 x 2 , то график будет похож на график y = x 2 , но будет лежать над ним.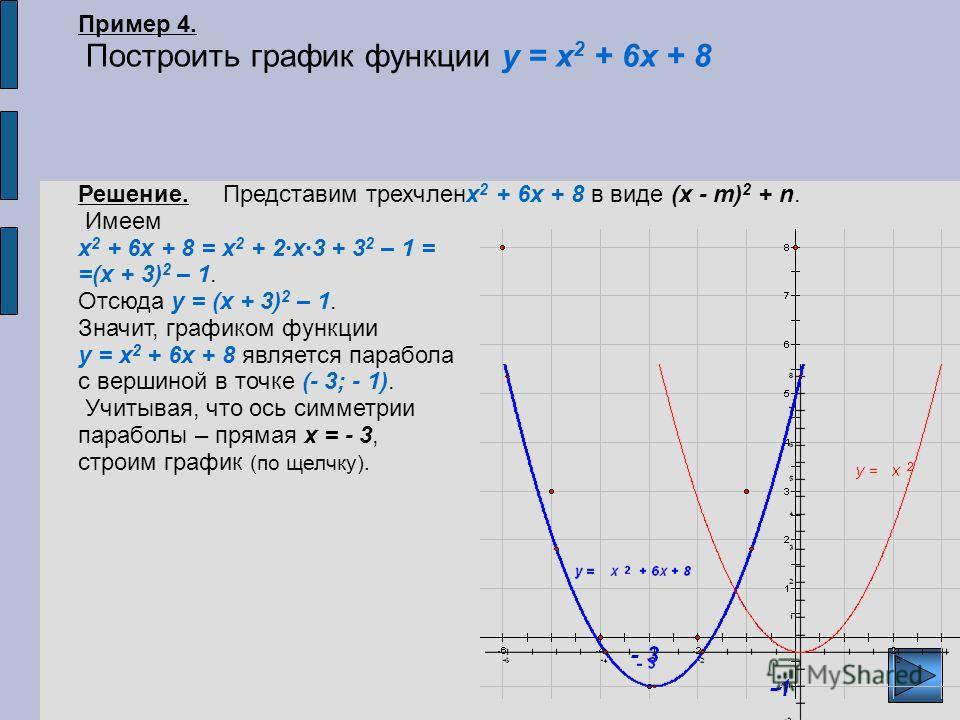 Например, когда x = 1, значение x 2 равно 1, значение 2 x 2 равно 2.
Значение y для y = 2 x 2 выше, чем для y = x 2 . Аналогично, для уравнения y = x 2 ⁄ 2 график выглядит аналогично y = x 2 , но теперь лежит под ним. Это показано на рисунке ниже.
Например, когда x = 1, значение x 2 равно 1, значение 2 x 2 равно 2.
Значение y для y = 2 x 2 выше, чем для y = x 2 . Аналогично, для уравнения y = x 2 ⁄ 2 график выглядит аналогично y = x 2 , но теперь лежит под ним. Это показано на рисунке ниже.
Следующий возможный выбор: a = −1, с уравнением y = − x 2 . В этом случае график уравнения будет иметь ту же форму, но теперь вместо того, чтобы быть над осью x, это ниже. Когда x = 1, соответствующее значение y равно −1. Аналогичным образом, для различных отрицательных значений и графики расположены ниже оси x.
Тест 1: На рисунке ниже показан эскиз трех квадратичных уравнений. Что можно определить относительно a , b и c ?
(a) a > c и c > 0 Неверно — попробуйте еще раз!
(b) b > c и a > 0 Неверно — попробуйте еще раз!
(c) c > b > a Неверно — попробуйте еще раз!
(г) б > в > а Правильно — молодец!
Объяснение: Кривые для y = bx 2 и y = cx 2 обе расположены над осью x и первая из них
выше последнего, поэтому b > c .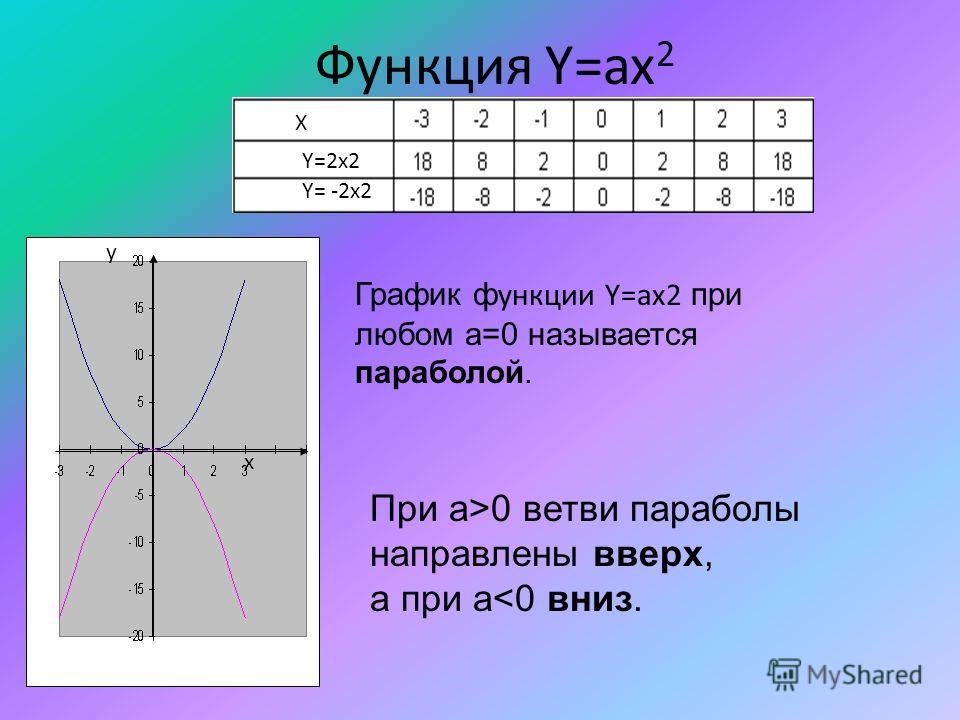 Кривая для y = x 2 находится ниже оси x, поэтому a < 0. Поскольку каждое положительное число больше любого отрицательного
число, то следует, что б > с > а .
Кривая для y = x 2 находится ниже оси x, поэтому a < 0. Поскольку каждое положительное число больше любого отрицательного
число, то следует, что б > с > а .
Этот тип квадратичного подобен основным в разделе «Введение», но с добавленной константой, , т.е. , с общей формой:
у = ах 2 + с
В качестве простого примера возьмем случай y = x 2 + 2. Сравнивая это с функцией y = x 2 , разница только в добавлении 2 шт. Как таковой:
- Когда х = 1, х 2 = 1, но х 2 + 2 = 1 + 2 = 3.
- Когда х = 2, х 2 = 4, но х 2 + 2 = 4 + 2 = 6.
- Эти пункты были подняты на 2 единицы.

- Это происходит для всех x , поэтому форма графика не изменилась, но поднялась вверх на 2 единицы.
Точно так же график y = x 2 − 2 опустится на 2 единицы.
В примерах, рассмотренных до сих пор, осью симметрии является ось y, , т. е. , линия x = 0. Следующая возможность — квадратичная, ось симметрии которой находится не на оси y. Примером этого является:
у = ( х — 3) 2
который имеет ту же форму и ту же ортогональную ось, что и y = x 2 , но с осью линии симметрии х = 3.
- Точки х = 0 и х = 6 равноудалены от 3.
- Когда x = 0, значение y равно (0 − 3) 2 = 9
- г.
Когда x = 6, значение y равно (6 − 3) 2 = 9.

- Обе точки на кривой при этих значениях находятся на 9 единиц выше оси x.
- Это верно для всех чисел, равноудаленных от 3.
График y = ( x − 3) показан ниже:
До сих пор обсуждались два отдельных случая: во-первых, у стандартного квадратичного уравнения его ортогональная ось смещена вверх или вниз; и во-вторых, стандартная квадратичная имеет ось симметрии, смещенную влево или вправо. Следующим шагом является рассмотрение квадратичных уравнений, включающих оба сдвига.
Пример 1: Квадратичная y = x 2 сдвинута так, что ее ось симметрии равна x = 3, а ее ортогональная ось находится в точке y = 2.
(a) Запишите уравнение новой кривой.
Решение: Новая кривая симметрична относительно x = 3 и смещена вверх на 2 единицы, поэтому ее уравнение имеет вид y = ( x − 3) 2 + 2.
(b) Найдите координаты точки пересечения оси Y.
Решение: Кривая пересекает ось Y, когда x = 0 . Внесение этого в уравнение y = x 2 + 2, соответствующее значение y равно y = (0 − 3) 2 + 2 = 11, поэтому кривая пересекает ось y в точке y = 11.
(c) Нарисуйте кривую.
Решение:
Упражнение 1: Кривая y = −2 x 2 сдвинута так, что ее ось симметрии совпадает с линия x = -2, а ее ортогональная ось равна x = 8.
(a) Запишите уравнение новой кривой.
Решение: Уравнение:
у = -2( х + 2) 2 + 8
(b) Найдите координаты точек, где эта новая кривая пересекает оси x и y.
Решение: Кривая пересекает ось Y, когда x = 0.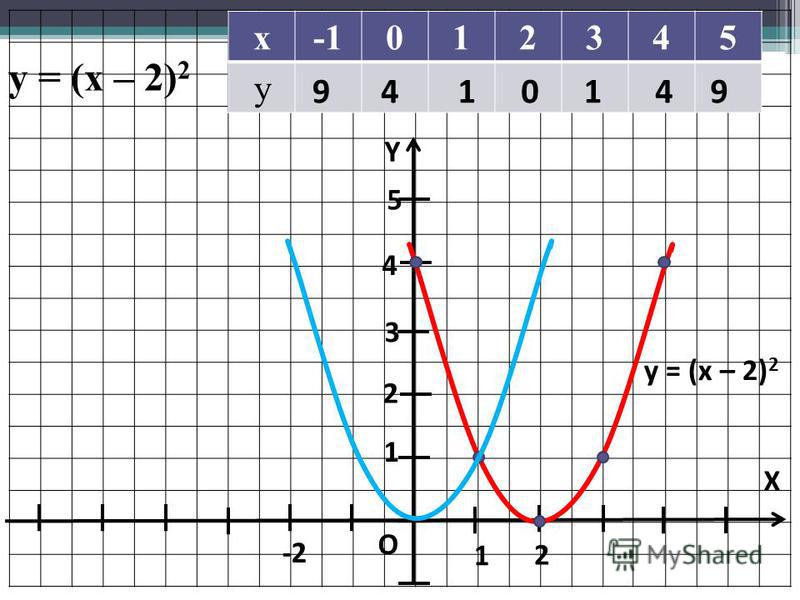 Подставляя x = 0 в уравнение y = −2 ( x + 2) 2 + 8,
соответствующее значение y равно:
Подставляя x = 0 в уравнение y = −2 ( x + 2) 2 + 8,
соответствующее значение y равно:
−2 (0 + 2) 2 + 8 = −2 (2) 2 + 8 = − 8 + 8 = 0, , т. е. y = 0.
Кривая пересекает ось x, когда y = 0. В этом случае подстановка значения y = 0 в уравнение y = −2( x + 2) 2 + 8 приводит к:
| −2 ( x + 2) 2 + 8 | = | 0 |
| 8 | = | 2 ( x + 2) 2 |
| ( x + 2) 2 | = | 4 |
| ( х + 2) | = | ±2 |
| х | = | −2 ± 2 |
поэтому есть два решения, x = -4 и х = 0.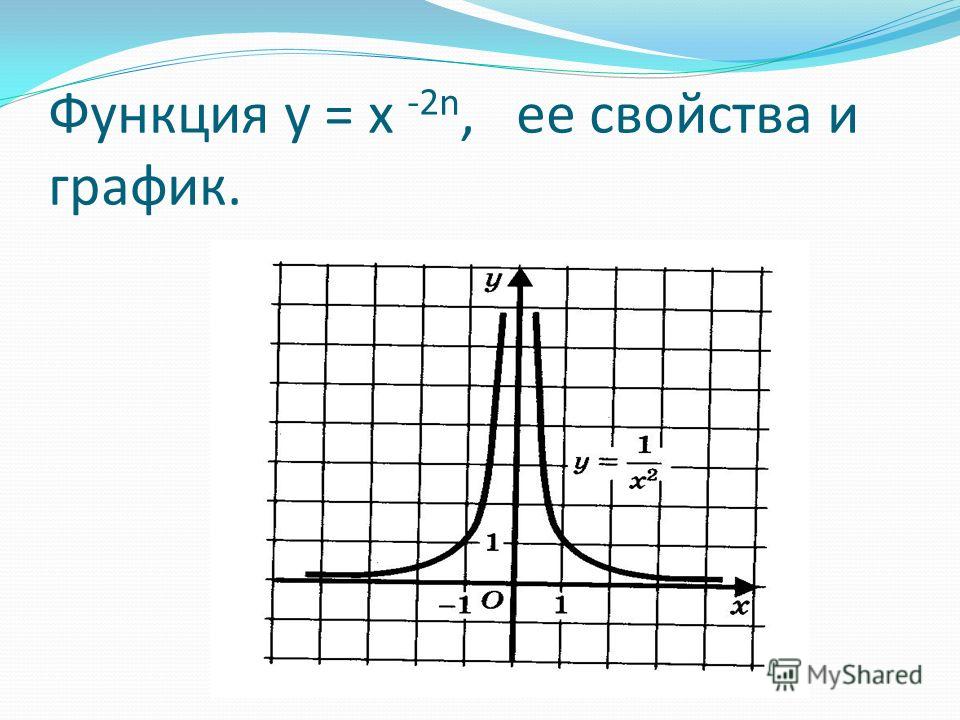
Подводя итог: график пересекает координатные оси в двух точках с координатами (−4, 0) и (0, 0).
(c) Нарисуйте кривую.
Решение: Кривая изображена ниже:
Нажмите на вопросы, чтобы узнать их решения
Упражнение 2: Для следующих кривых запишите уравнение каждой кривой, найдите координаты точек, где кривая пересекает x — и y — оси и нарисуйте кривую.
(a) Кривая y = x 2 сместилась так, что ее осью симметрии является линия x = 7, а ее ортогональная ось y = 6.
Решение: Уравнение сдвинутой кривой имеет вид
y = ( x −7) 2 + 6
г. Это пересечет ось Y, когда x = 0, т.е. когда:
y = (0 − 7) 2 + 6 = (−7) 2 + 6 = 55
Он не пересекает ось x, так как его нижняя точка находится на ортогональной оси, то есть y = 6. Эскиз графика показан ниже:
Эскиз графика показан ниже:
(b) Кривая y = x 2 , сдвинутая так, что ее осью симметрии является линия x = 7, а его ортогональная ось равна y = -9.
Решение: Эта кривая будет иметь ту же форму, что и кривая в части (а), но теперь она сдвинута вниз, а не вверх. Уравнение кривой:
у = ( х — 7) 2 — 9
Это пересечет ось y, когда x = 0 и y = (0 − 7) 2 − 9 = 49 − 9 = 40. Он пересечет ось x, когда y = 0. Подстановка этого в уравнение дает:
| ( x −7) 2 − 9 | = | 0 |
| ( x −7) 2 | = | 9 |
| х − 7 | = | ±3 |
| х | = | 7 ± 3 |
т. е. . кривая пересекает ось x в точках 4 и 10.
е. . кривая пересекает ось x в точках 4 и 10.
Подводя итог, самая нижняя точка находится на ортогональной оси в точке x = 7, y = -9, она пересекает ось y в точке y = 40 и пересекает ось x в точке x = 4. , x = 10. Кривая изображена ниже:
(в) Кривая y = − x 2 сдвинут так, что его ось симметрии совпадает с линией x = 7, а его ортогональная ось равна y = 9,
Решение: Уравнение для этой кривой:
у = -( х — 7) 2 + 9
Это пересечет ось Y, когда x = 0, , то есть при y = -(0 — 7) 2 + 9 = -49 + 9 = -40. Он пересекает ось x, когда г = 0, т.е.
| −( x − 7) 2 + 9 | = | 0 |
| 9 | = | ( х — 7) 2 |
| х − 7 | = | ±3 |
| х | = | 7 ± 3 |
что дает х = 4 и х = 10.
Подводя итог, кривая имеет самую высокую точку, когда x = 7 и y = 9, которая является ортогональной осью, она пересекает ось y в точке y = -40 и пересекает ось x в точке x = 4 и x = 10. Эскиз кривой показан ниже:
Нажмите на вопросы, чтобы узнать их решения
Этот раздел посвящен рисованию общих квадратичных функций, то есть функций вида
топор 2 + бх + в
Алгебраическое выражение необходимо изменить так, чтобы можно было определить линию симметрии и ортогональную ось. Требуемая процедура — заполнить квадрат (см. модуль «Квадратика»).
Пример 2: Квадратичная функция задается как −2 92 477 x 92 478 91 848 2 91 849 + 4 92 477 x 92 478 + 16.
(a) Заполните квадрат этой функции.
Решение: Завершение квадрата:
| y = −2 x 2 + 4 x + 16 | = | −2 ( х 2 − 2 х ) + 16 |
| = | −2 [( x − 1) 2 − 1] + 16 | |
| т. е. у | = | −2 ( x − 1) 2 + 18 |
(b) Используйте это, чтобы определить ось симметрии и ортогональную ось кривой.
Решение: Это функция y = −2 x 2 переместился так, что его ось симметрии равна x = 1, а его ортогональная ось равна y = 18
(c) Найдите точки на осях x и y, где кривая их пересекает.
Решение: Функция имеет вид y = −2( x − 1) 2 + 18. Это пересечет ось x, когда y = 0, , т. е. , когда:
Это пересечет ось x, когда y = 0, , т. е. , когда:
| −2 ( x −1) 2 + 18 | = | 0 |
| 18 | = | 2 ( x − 1) 2 |
| 9 | = | ( х — 1) 2 |
| извлечение квадратного корня, x − 1 | = | ±3 |
| х | = | 1 ± 3 |
| = | 4 или −2 |
Подставляя x = 0 в исходную форму функции y = −2 x 2 + 4 x + 16, получаем y = 16, , т. е. пересекает ось . в х = 16.
е. пересекает ось . в х = 16.
(d) Нарисуйте кривую.
Решение:
Вот несколько упражнений для практики:
Упражнение 3: Используя метод, показанный в примере 2, нарисуйте каждое из следующих квадратных уравнений:
(а) у = х 2 + 2 х + 1
Решение: Уравнение можно переписать как y = ( х + 1) 2 . Набросок функции показан ниже:
(б) у = 6 − х 2
Решение: Функция y = 6 − x 2 уже является полным квадратом и показана ниже:
(в) у = х 2 − 6 х + 5
Решение: При построении квадрата исходная функция y = x 2 — 6 x + 5 становится y = ( x — 3) 2 — 4.
(г) у = 4 х − х 2
Решение: После завершения квадрата функция принимает вид y = −( x − 2) 2 + 4. График показан ниже:
(д) г = х 2 + 2 х + 5
Решение: После завершения квадрата функция становится равной y = ( x + 1) 2 + 4. График показан ниже:
(е) y = 3 − 2 x − x 2
Решение: После завершения квадрата эта функция становится равной y = −( x + 1) 2 + 4. Это набросано ниже:
Нажмите на вопросы, чтобы узнать их решения
Этот раздел заканчивается небольшой викториной:
Тест 2: Какая из следующих пар прямых является соответственно осью симметрии и ортогональной осью квадратичной функции y = − 2 x 2 − 8 x ?
(a) x = 2, y = 8 Неверно — попробуйте еще раз!
(b) x = 2, y = −8 Неверно — попробуйте еще раз!
(c) x = −2, y = 8 Правильно — молодец!
(d) x = −2, y = −8 Неверно — попробуйте еще раз!
Объяснение: Завершение квадрата на y = −2 x 2 − 8 x дает функцию
y = −2 ( x + 2) 2 + 8
, т. е. , ортогональная ось равна y = 8, а ось симметрии равна x = −2. Это именно та функция, которая рассматривалась в упражнении 1, где можно найти все детали и схему.
е. , ортогональная ось равна y = 8, а ось симметрии равна x = −2. Это именно та функция, которая рассматривалась в упражнении 1, где можно найти все детали и схему.
Каждый из следующих вопросов относится к квадратичной функции y = − x 2 + 6 x + 7.
1. В какой из следующих двух точек он пересекает ось x?
(а) х = -1, 7
(б) х = 1, -7
(в) х = 1, 7
(г) — х 192, −7
2. В каком из следующих случаев он пересекает ось y?
(A) Y = 7
(B) Y = 8
(C) Y = 5
(D) Y = 6
(D) Y = 6
(D) Y = 6
(D) Y = 6
(D) Y = 6
(D) Y = 6
(D) Y = 6
(D) . ось симметрии?
(а) х = 2
(б) х = −2
(c) x = −3
(d) x = 3
4. Какая из следующих осей является ортогональной?
Какая из следующих осей является ортогональной?
(a) y = 14
(b) y = 15
(c) y = 16
(d) y = 13
1.3 Functions
Функция $y=f(x)$ есть правило для определения $y$, когда нам дано значение $x$. Например, правило $y=f(x)=2x+1$ — функция. Любая линия $y=mx+b$ называется линейная функция . График функции выглядит как кривая выше (или ниже) оси $x$, где для любого значения $x$ правило $y=f(x)$ говорит нам, как далеко можно подняться выше (или ниже) Ось $x$, чтобы достичь кривой.
Функции могут быть определены различными способами: алгебраической формулой или несколькими алгебраические формулы, графиком или экспериментально установленной таблицей значений. (В последнем случае таблица дает набор точек на плоскости, которые мы могли бы затем интерполируйте плавной кривой, если это имеет смысл.) 92$
Рисунок 1. 3.1. Некоторые графики.
3.1. Некоторые графики.
Например, функция квадратного корня $y=f(x)=\sqrt{x}$ является правилом в котором говорится, что для заданного значения $x$ нужно взять неотрицательное число, квадрат равен $x$. Это правило имеет смысл только в том случае, если $x$ положительно или равно нулю. Мы говорим, что область определения этой функции равна $x\ge 0$, или, более формально, $\{x\in\R\mid x\ge 0\}$. Поочередно, мы можно использовать интервальную нотацию и написать, что домен равен $[0,\infty)$. (В записи интервала квадратные скобки означают, что конечная точка включены, а скобки означают, что конечная точка не включена.) Тот факт, что областью определения $y=\sqrt{x}$ является $[0,\infty)$, означает, что в график этой функции (см. рис. 1.3.1) у нас есть точки $(x,y)$ только над $x$-значениями в правой части $x$-ось.
Другой пример функции, областью определения которой является не вся ось $x$.
есть: $y=f(x)=1/x$, обратная функция. Мы не можем заменить $x=0$
в этой формуле. Однако функция имеет смысл для любого ненулевого
$x$, поэтому мы берем домен следующим образом: $\{x\in\R\mid x\ne 0\}$. 2$ — это все
$\R$. Но в контексте задачи-рассказа о нахождении площадей квадратов
мы ограничиваем область определения положительными значениями $x$, потому что квадрат
с отрицательной или нулевой стороной не имеет смысла.
93$.
Кроме того, могут использоваться буквы, отличные от $f$. Например, если $y$ равно
скорость чего-либо в момент времени $t$, мы можем написать $y=v(t)$ с
буква $v$ (вместо $f$), обозначающая функцию скорости (и
$t$ играет роль $x$).
2$ — это все
$\R$. Но в контексте задачи-рассказа о нахождении площадей квадратов
мы ограничиваем область определения положительными значениями $x$, потому что квадрат
с отрицательной или нулевой стороной не имеет смысла.
93$.
Кроме того, могут использоваться буквы, отличные от $f$. Например, если $y$ равно
скорость чего-либо в момент времени $t$, мы можем написать $y=v(t)$ с
буква $v$ (вместо $f$), обозначающая функцию скорости (и
$t$ играет роль $x$).
Буква, играющая роль $x$, называется независимым переменная , а буква, играющая роль $y$, называется зависимая переменная (потому что ее значение «зависит от» значения независимого переменная). В задачах истории, когда один должен перевести с английского языка на математический, решающим шагом является определить, какие буквы обозначают переменные. Если только слова и нет буквы даны, то мы должны решить, какие буквы использовать. Немного буквы традиционные. Например, почти всегда $t$ означает время.
Пример 1. 3.1. Ящик с открытым верхом сделан из $a\times b$ прямоугольного куска
картона, вырезав квадрат со стороной $x$ из каждого из четырех
углы, а затем загибаем стороны вверх и герметизируем их воздуховодом
лента. Найдите формулу зависимости объема $V$ ящика от
$x$ и найти область определения этой функции.
3.1. Ящик с открытым верхом сделан из $a\times b$ прямоугольного куска
картона, вырезав квадрат со стороной $x$ из каждого из четырех
углы, а затем загибаем стороны вверх и герметизируем их воздуховодом
лента. Найдите формулу зависимости объема $V$ ящика от
$x$ и найти область определения этой функции.
Получившийся ящик будет иметь высоту $x$ и прямоугольное основание размеры $a-2x$ на $b-2x$. Таким образом, $$ V=f(x)=x(a-2x)(b-2x). $$ Здесь $a$ и $b$ — константы, а $V$ — переменная, зависящая от на $x$, т. е. $V$ играет роль $y$. 92
Функция не всегда должна быть задана одной формулой, поскольку мы
уже видели (в проблеме подоходного налога, например).
Предположим, что $y=v(t)$ — функция скорости автомобиля
который выходит из состояния покоя (нулевой скорости) в момент времени $t=0$; тогда
неуклонно увеличивает скорость до 20 м/с, на это требуется 10 секунд.
это; затем движется с постоянной скоростью 20 м/сек в течение 15 секунд; а также
наконец, применяет тормоза, чтобы неуклонно снижать скорость до 0, что занимает 5
секунды, чтобы сделать это. Формула для $y=v(t)$ различна в каждом из
три временных интервала: сначала $y=2x$, затем $y=20$, затем $y=-4x+120$.
График этой функции показан на рисунке 1.3.3.
Формула для $y=v(t)$ различна в каждом из
три временных интервала: сначала $y=2x$, затем $y=20$, затем $y=-4x+120$.
График этой функции показан на рисунке 1.3.3.
Рисунок 1.3.3. Функция скорости.
Вообще не все функции задаются формулами. Функция может быть определяется экспериментально установленной таблицей значений или описание, отличное от формулы. Например, население $y$ США является функцией времени $t$: мы можем написать $y=f(t)$. Этот — совершенно хорошая функция — мы могли бы изобразить ее (с точностью до присутствует), если бы у нас были данные для различных $t$ — но мы не можем найти алгебраическая формула для него.
Найдите область определения каждой из следующих функций: 92-9)/(x-3)& $x\neq 3$\cr 6& если $x=3$.\cr}$ (отвечать)
Пример 1.3.13 Предположим, что $f(x) = 3x-9$ и $\ds g(x) = \sqrt{x}$. Что это область композиции $(g\circ f)(x)$? (Напомним, что состав определяется как $(g\circ f)(x) = g(f(x))$.) Что такое домен $(f\circ g)(x)$? (отвечать)
Пример 1.

 ..
.. 05.17
05.17

 График функции симметричен относительно оси игрек.
График функции симметричен относительно оси игрек.

 играть в. Существует порядок действий, в котором говорится, что умножение и деление
выполняется перед сложением и вычитанием. Если вы помните это, то решение
легкий. Правильное преобразование состоит в том, чтобы «умножить каждую координату y на два, а затем
добавьте пять дюймов, оставив координаты x в покое.
играть в. Существует порядок действий, в котором говорится, что умножение и деление
выполняется перед сложением и вычитанием. Если вы помните это, то решение
легкий. Правильное преобразование состоит в том, чтобы «умножить каждую координату y на два, а затем
добавьте пять дюймов, оставив координаты x в покое. Кроме того, вы можете изменить порядок. Изменения в x или y
можно сделать независимо друг от друга, но если есть масштабы и сдвиги к одному и тому же
переменная, важно сначала выполнить масштабирование, а затем смещение.
Кроме того, вы можете изменить порядок. Изменения в x или y
можно сделать независимо друг от друга, но если есть масштабы и сдвиги к одному и тому же
переменная, важно сначала выполнить масштабирование, а затем смещение.