Упражнение 2. на каникулы задали дз:( 2.дана функция y=4/x а)какова область ее определения? б)постройте её график. в)проходит ли график данной функции через точку м( -5 1/3 ;
Все предметы
Математика
Литература
Алгебра
Русский язык
Геометрия
Английский язык
Физика
Биология
Другие предметы
История
Обществознание
Окружающий мир
География
Українська мова
Информатика
Українська література
Қазақ тiлi
Экономика
Музыка
Беларуская мова
Французский язык
Немецкий язык
Психология
Оʻzbek tili
Кыргыз тили
Астрономия
Физкультура и спорт
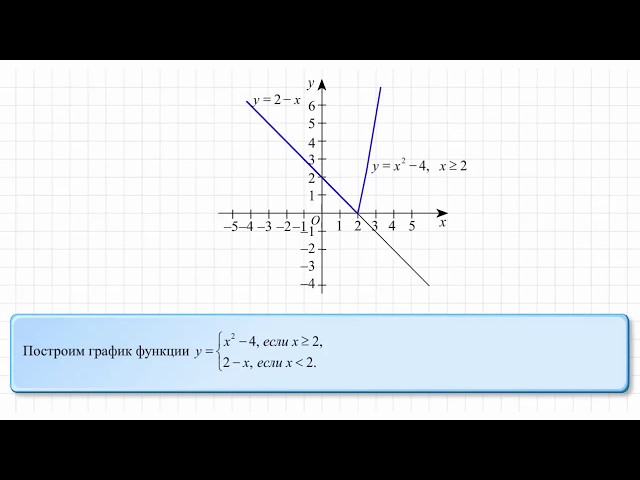
2. Дана функция y=4/x
Дана функция y=4/x
а)Какова область ее определения?
б)Постройте её график.
в)Проходит ли график данной функции через точку М( -5 1/3 ; — 3/5)?
Ребят, помогите, если не трудно сфоткайте)
Ответ дан
alekskisammm
делить на 0 нельзя,значит область определения(значение х не равно 0)-от минус бесконечности до 0(о не входит)и от 0 до плюс бесконечности график гипербола-составь таблицу и строй а третье просто подставь в у=4х вместо х — 5 13 и вместо у — — 35 -35 = 4-5 13 -35 =4 -163 -35=4 умножить на — 316 получается минус 1216 сокращаешь на 4 и получается — 34 а не — 35 значит не принадлежит
Наибольшее и наименьшее значения функции
функция возрастает
Предположим, что функция f
не имеет на отрезке [а; b] критических
точек.
наибольшее
значение
наименьшее
значение
Тогда она возрастает (рис. 1) или убывает
(рис. 2) на этом отрезке.
a
b
функция убывает
наибольшее и наименьшее значения
функции f на отрезке [а; b] — это
значения в концах а и b.
наибольшее
значение
наименьшее
значение
a
Значит,
b
Примеры
Пусть теперь функция f имеет на
отрезке [а; b] конечное число
критических точек.
наибольшее
значение
наименьшее
значение
a c
b
наибольшее
значение
наибольшее
значение
наименьшее
значение
наименьшее
значение
a c
n b
Наибольшее и наименьшее значения
функция f может принимать в
критических точках функции или в
точках а и b.
Чтобы найти наибольшее и
наименьшее значения функции,
имеющей на отрезке конечное число
критических точек, нужно вычислить
значения функции во всех
критических точках и на концах
отрезка, а затем из полученных
чисел выбрать наибольшее и
наименьшее.
1.
Найдите наименьшее значение функции y = x3 – 27x на отрезке [0; 4]
Значения функции в
концах отрезка.
1) y(0) = 0
y(4) = 43– 27 4 = – 44
3
Найдем критические
точки, которые
принадлежат
заданному отрезку.
2) y / = 3×2 – 27 = 3(x2 – 9) = 3(x – 3)(x + 3)
Значения функции в
критических точках,
которые принадлежат
заданному отрезку.
y(3) = 33– 27 3 = –54
Выбрать наименьшее из
полученных значений.
x = 3 [0; 4]
x = –3 [0; 4]
В 11
— 5 4
3
10 х
х
-3
Выполнение этапов решения можно изменить, как вам удобно.
Этапы
1. Найти f /(x)
2. Найти
критические точки,
взять те, которые
принадлежат
данному отрезку.
3. Вычислить
значения функции в
критических точках
и на концах отрезка.
4. Из вычисленных
значений выбрать
наименьшее или
наибольшее
Найдите наименьшее значение функции
y = x3 – 27x на отрезке [0; 4]
1) y / = 3×2 – 27
3
2) y / = 3×2 – 27 = 3(x2 – 9) = 3(x – 3)(x + 3)
x = 3 [0; 4]
x = –3 [0; 4]
3) y(0) = 0
y(4) = 43– 27 4 = – 44
y(3) = 33– 27 3 = –54
В 11
— 5 4
3
10 х
х
-3
Предположим, что функция f
имеет на отрезке [а; b] одну точку
экстремума.
наименьшее
значение
a
b
Если это точка минимума, то в этой точке
функция будет принимать наименьшее
значение.
наибольшее
значение
Если это точка максимума, то в этой точке
функция будет принимать наибольшее
значение.
a
b
Другой способ решения
Этапы
1. Найти f /(x)
2. Найти критические
точки, взять те,
которые
принадлежат
данному отрезку.
3. Вычислить
значения функции в
критических точках
и на концах отрезка.
4. Из вычисленных
значений выбрать
наименьшее и
наибольшее
Найдите наименьшее значение функции
y = x3 – 27x на отрезке [0; 4]
1) y / = 3×2 – 27
3
-3
2) y / = 3×2 – 27 = 3(x2 – 9) = 3(x – 3)(x + 3)
y\
y
+
0 –
-3
+
3
min
3)
y(3) = 33– 27 3 = –54
В 11
— 5 4
3
10 х
4
x
Наименьшее значение
функция будет
принимать в точке
минимума.
Можно сэкономить на
вычислениях значений
х
функции в концах
отрезка.
Этот способ будет удобно
вспомнить, когда вычисления значений функции в концах
отрезка будет сложным.
2. Найдите наибольшее значение функции y = x3 – 3x + 4
на отрезке [– 2; 0]
Значения функции в
концах отрезка.
1) y(0) = 4
y(-2) = (-2)3– 3 (-2)
+4 = 2
1
Найдем критические
точки, которые
принадлежат
заданному отрезку.
2) y / = 3×2 – 3 = 3(x2 – 1) = 3(x – 1)(x + 1)
Значения функции в
критических точках,
которые принадлежат
заданному отрезку.
+4=6
y(-1) = (-1)3– 3 (-1)
Выбрать наибольшее из
полученных значений.
x = 1 [-2; 0]
x = –1 [-2; 0]
В 11
6
3
10 х
х
-1
3. Найдите наименьшее значение функции y = x3 – 2×2 + x +3
на отрезке [ 1; 4 ]
Значения функции в
концах отрезка.
Найдем критические
точки, которые
принадлежат
заданному отрезку.
Значения функции в
критических точках,
которые принадлежат
заданному отрезку.
Выбрать наименьшее из
полученных значений.
1) y(1) = 1 – 2 + 1 + 3 = 3
y(4) = 43– 2 4 2 + 4 + 3 = 39
2) y / = 3×2 – 4x + 1=
3(x – 1)(x –
3×2 – 4x + 1 = 0
D=16–4*3*1=4
4+2
x1=
= 1 [1; 4]
6
4-2
1
=
[1; 4]
x2=
6
3
y(1) = 3
В 11
3
3
10 х
х
1
)
3
x3
9x 7
4. Найдите наибольшее значение функции y
3
на отрезке [ -3; 3 ]
3
( 3)
Значения функции в
у ( 3)
9( 3) 7 9 27 7 11
концах отрезка.
3
33
у (3) 9 3 7 9 27 7 25
3
2
Найдем критические
3
х
точки, которые
у/
9 х 2 9 ( х 3)( х 3)
3
принадлежат
заданному отрезку.
x = 3 [-3; 3]
x = –3 [-3; 3]
Значения функции в
критических точках,
которые принадлежат
заданному отрезку.
Выбрать наибольшее из
полученных значений.
y(-3) = 11
y(-3) = -25
В 11
1 1
3
10 х
х
5. Найдите наибольшее значение функции
на отрезке [ 1; 9 ]
Значения функции в
концах отрезка.
Найдем критические
точки, которые
принадлежат
заданному отрезку.
Значения функции в
критических точках,
которые принадлежат
заданному отрезку.
Выбрать наибольшее из
полученных значений.
3
2
3
2
3
2
y x 3x 1
у(1) 1 3 1 1 1 3 1 1
3
2 2
у (9) 9 3 9 1 (3 ) 27 1
27 27 1 1
3
1
х 3 0
3 2
3
/
у х 3
х 3 2
2
2
3 х 6 0
х 2
х 4 [1; 9]
3
2
3
2 2
у (4) 4 3 4 1 (2 ) 12 1
8 12 1 3
В 11
1
3
10 х
х
2
6. Найдите наименьшее значение функции y x х 3 x 1
3
на отрезке [ 1; 9 ]
2
y
x
31x 1
3
Значения функции в
концах отрезка.
Найдем критические
точки, которые
принадлежат
заданному отрезку.
х 21 3
x 1 1 1
у(1) 12 3y
1 x1
3
2
3
2 2
у (9) 9 3 9 13 (3 ) 27 1
y х 2 3x 1
27 27 1 1
Запишем функцию3в удобном для
1 дифференцирования виде
х 3 0 2
3
3
у/ х2 3
х 3 2
2
2
3 х 6 0
х 2
х 4 [1; 9]
Значения функции в
критических точках,
которые принадлежат
заданному отрезку.
Выбрать наименьшее из
полученных значений.
3
2
3
2 2
у (4) 4 3 4 1 (2 ) 12 1
8 12 1 3
В 11
— 3
3
10 х
х
х 2 25
7. Найдите наименьшее значение функции y
х
на отрезке [-10; 1 ]
1
D(y): x = 0
y x 25
х
Значения функции в
1
2
концах отрезка.
х
25
у ( 10) 10 25
10 2,5 12,5
y
10
/
х
х
1
1
у (1) 1 25 26
2
1
х
х
y х 25
2
х
1
25
х
25
Найдем критические
у / 1 Запишем
25 функцию
1
в удобном
для
2
2
2
точки, которые
хвиде х
х
дифференцирования
принадлежат
( х 5)( х 5)
x = 5 [-10; 1]
заданному отрезку.
х2
x = –5 [-10; 1]
Значения функции в
критических точках,
которые принадлежат
заданному отрезку.
Выбрать наименьшее из
полученных значений.
x = 0 D(y)
1
у ( 5) 5 25
5 5 10
5
В 11
— 1 2 , 5
3
10 х
х
х 2 25
7. Найдите наименьшее значение функции y
Найдите наименьшее значение функции y
х
на отрезке [-10; 1 ]
D(y): x = 0
Значения функции в
концах отрезка.
Можно решить задание, применив
формулу:
u u / v uv/
2
v
v
/
Найдем критические
точки, которые
принадлежат
заданному отрезку.
Значения функции в
критических точках,
которые принадлежат
заданному отрезку.
Выбрать наименьшее из
полученных значений.
В 11
— 1 2 , 5
3
10 х
х
36
y х
х
8. Найдите наибольшее значение функции
на отрезке [ 1; 9 ]
1
Значения функции в
концах отрезка.
1
1
2
х
х
/
Найдем критические
точки, которые
принадлежат
заданному отрезку.
Значения функции в
критических точках,
которые принадлежат
заданному отрезку.
Выбрать наибольшее из
полученных значений.
D(y): x = 0
y x 36
х
1
у (1) Запишем
1 36 функцию
37 в удобном для
1
дифференцирования
виде
1
у (9) 9 36 9 4 13
9
2
1
36
х
36
/
у 1 36 2 1 2
2
х
х
х
( х 6)( х 6)
х2
x = 6 [ 1; 9]
x = –6 [ 1; 9]
x = 0 D(y)
1
у (6) 6 36 6 6 12
6
В 11
3 7
3
10 х
х
9. Найдите наибольшее значение функции y 8 х e
Найдите наибольшее значение функции y 8 х e
на отрезке [ 3; 10 ]
x 7
1). Первое число меньше 1, т.к.
5
4
4
Значения
функции
в
знаменатель e > 5.
у (3) (8 3)e 4
концах
отрезка.
e
2).
Второе
число – отрицательноe.
3). Значит, наибольшее число 1.
uv u/ v uv/
у(10) (8 10)e3 2e3
/
Найдем критические
точки, которые
принадлежат
заданному отрезку.
у / (8 х) / e x 7 (8 х)( e x 7 ) /
e x 7 (8 х)e x 7 e x 7 ( 1 8 х)
e
x 7
7
(7 х )
x = 7 [ 3; 10]
Значения функции в
критических точках,
которые принадлежат
заданному отрезку.
Выбрать наибольшее из
полученных значений.
1
у(7) (8 7)e7 7 1e0 1
В 11
1
3
10 х
х
2
2 х
10. Найдите наименьшее значение функции y х 8 х 8 e
на отрезке [ 1; 7 ]
у(1) (1 8 8)e 1 e
Значения функции в
концах отрезка.
1
uv u v uv у(7) (49 56 8)e e5
Найдем критические у / ( х 2 8 х 8) / e 2 х ( х 2 8 х 8)(e 2 х ) /
/
/
точки, которые
принадлежат
заданному отрезку.
5
/
(2 х 8)e 2 х ( х 2 8 х 8)e 2 х ( 1)
e 2 х (2 х 8 х 2 8 х 8) e 2 х ( х 2 10 х 16)
e
Значения функции в
критических точках,
которые принадлежат
заданному отрезку.
Выбрать наименьшее из
полученных значений.
2 х
( х 10 х 16) e
2
x = 2 [ 1; 7]
2 х
8
( х 8)( х 2)
Наименьшее число – 4, т.к.
первые два положительные.
x = 8 [ 1; 7]
1
у(2) (4 16 8)e0 4
В 11
2
— 4
3
10 х
х
lnx / 1x
11. Найдите наибольшее значение функции
y = ln(x+5)5 – 5x на отрезке [-4,5; 0]
1
5
5 x 20
у 5
5
5
y = 5ln(x+5) – 5x
х 5
х 5
х 5
Запишем функцию
5( x 4в)удобном для
2. Найти критические
дифференцирования
виде x = -4 [-4,5; 0]
х 5
точки, взять те,
1. Найти f /(x)
которые принадлежат
данному отрезку.
3. Вычислить значения
функции в критических
точках
и на концах отрезка.
4. Из вычисленных
значений выбрать
наименьшее или
наибольшее.
/
y\
y
-4,5 + +
-5
–
0
-4
max
0
у ( 4) ln 15 5 ( 4)
0 20 20
В 11
2 0
3
10 х
х
x
Наибольшее значение
функция будет
принимать в точке
максимума.
Можно сэкономить на
вычислениях значений
функции в концах
отрезка.
12. Найдите наибольшее значение функции
1 5
y = ln(11x) – 11x + 9 на отрезке [ ; ]
22 22
lnx 1x
/
1
1
1
/
у
(11х) 11
11 11 11
11х
11х
х
1 11x
1
1 5
[
; 22]
x=
11
22
х
/
1. Найти f /(x)
2. Найти критические
точки, взять те,
которые принадлежат
данному отрезку.
1
22
y\
+
y
5
22
–
x
1
11
max
0
1
у ln 1 1 9 0 1 9 8
11
В 11
8
3
10 х
х
Наибольшее значение
функция будет
принимать в точке
максимума.
Можно сэкономить на
вычислениях значений
функции в концах
отрезка.
lnx
/
13. Найдите наименьшее значение функции
5 7
y = 2х2 – 5x + lnx – 3 на отрезке [ ; ]
6 6
1
x
1
4( х 1)( х )
2
1
4
х
5
х
1
4
у / 4х 5
х
х
х
2. Найти критические
1. Найти f /(x)
точки, взять те,
которые принадлежат
данному отрезку.
x=1
y\
5
6
–
y
7
6
+
x
1
min
0
у 1 2 5 ln 1 3 2 8 6
В 11
— 6
3
10 х
х
[ 65 ; 67 ]
Наименьшее значение
функция будет
принимать в точке
минимума.
Можно сэкономить на
вычислениях значений
функции в концах
отрезка.
cosx – sinx
/
14. Найдите наибольшее значение функции
3
; 0
y = 7cosx +16x – 2 на отрезке
2
у 7 sin х 16
/
1. Найти f /(x)
7 sin х 16 0
2. Найти критические
точки, взять те,
16
которые принадлежат sin х
данному отрезку.
7
0
т.к. sin х [ 1;1]
Функция на всей области
определения возрастает.
Нетрудно догадаться, что у
/ > 0.
Тогда наибольшее
значение функция будет
иметь в правом конце
отрезка, т.е. в точке х=0.
3
3
3
у
7 cos
16
2 24 2
2
2
2
у 0 7 cos 0 16 0 2 7 2 5
В 11
5
3
10 х
х
Если вы не догадались, то
вычислите значения
функции в каждом конце
отрезка и выберите
наибольшее.
sinx cosx
15. Найдите наибольшее значение функции
/
5
; 0
y = 10sinx –
x + 7 на отрезке
6
36
у 10 cos х
/
1. Найти f /(x)
2. Найти критические 10 cos х 36
точки, взять те,
которые принадлежат
36
данному отрезку.
cos х
36
Критических точек нет.
Тогда наибольшее
значение функция будет
принимать в одном из
концов отрезка.
10
т.к. cos х [ 1;1]
Можно было и раньше
догадаться, что наибольшее
значение будет именно в
левом конце отрезка!
Как?
1
5
5 36 5
у
10 sin
7 10 30 7 32
2
6
6 6
Синус –нечетная функция
0
Формула приведения
5
5
1
у 0 sin
10 sin
0
0
7
7
sin Вsin
sin
11
6
6
6
3 2
3
10 х
х
6
2
cosx – sinx
16. Найдите наименьшее значение функции
Найдите наименьшее значение функции
/
y = 5cosx – 6x + 4 на отрезке
у / 5 sin x 6
1. Найти f /(x)
2. Найти критические 5 sin x 6 0
точки, взять те,
6
которые принадлежатsin х
данному отрезку.
5
т.к. sin х [ 1;1]
3
2 ; 0
Функция на всей области
определения убывает.
Нетрудно догадаться, что у /
< 0.
Тогда наименьшее значение
функция будет иметь в
правом конце отрезка, т.е. в
точке х=0.
0
3
3
3
у
5 cos
6
4 9 4
2
2
2
1
у 0 5 cos 0 0 4 9
В 11
9
3
10 х
х
Если вы не догадались, то
вычислите значения
функции в каждом конце
отрезка и выберите
наименьшее.
17. Найдите наибольшее значение функции
y = 12cosx + 6 3 x – 2 3 + 6 на отрезке 0 ;
2
1. Найти f /(x)
3
у / 12 sin x 6 3
2. Найти критические
12 sin x 6
точки, взять те,
которые принадлежат
3
данному отрезку.
sin х
2
3 0
х ( 1)
n
3
n
Но нам не нужны ВСЕ
у 12 cos 6 3 2 3 6
12
стационарные
точки. Необходимо
3
3
3
сделать выбор тех значений,
у 12 cos 6 3 2 3 6 6 3 0 ;
2
2
2
2
у 0 12 cos 0 6 3 0 2 3 6 18 2 3
которые попадут в заданный
отрезок
В 11
1 2
3
10 х
х
17. Найдите наибольшее значение функции
3
y = 12cosx + 6 3 x – 2 3 + 6 на отрезке 0 ;
2
у / 12 sin x 6 3
1. Найти f /(x)
2. Найти критические
12 sin x 6
точки, взять те,
которые принадлежат
3
данному отрезку.
sin х
y\
y
0
+
3
–
max
3 0
2
2
x
Убедимся, что данная точка является
точкой максимума на заданном
промежутке.
Значит, наибольшее значение
функция достигает именно в этой
точке.
Тогда значения функции в концах
отрезка можно не считать.
у 12 cos 6 3 2 3 6 12
3
3
3
В 11
1 2
3
10 х
х
18. Найдите наименьшее значение функции
Найдите наименьшее значение функции
7 3
14 3
7 3
y = 11 +
–
х–
cosx на отрезке 0 ;
2
18
3
3
1. Найти f /(x)
2. Найти критические
точки, взять те,
которые принадлежат
данному отрезку.
y\
y
0
–
7 3 14 3
у
sin x
6
3
3
7 3 14 3
sin x 0
3
3
Можно убедиться, что данная точка
1
n
является
точкой
минимума
х ( 1)
наn
sin x
заданном промежутке.
2
6
/
+
6 min
2
x
Значит, наименьшее значение
функция
достигает
именно в этой
Но нам не
нужны ВСЕ
точке.
стационарные точки. Необходимо
Тогда
значения
в концах
сделать
выбор функции
тех значений,
отрезка
не всчитать.
которыеможно
попадут
заданный
отрезок
7 3 7 3 14 3
у 11
cos 11 7 4
18
18
3
6
6
В 11
4
0 ; 2
3
10 х
х
19. Найдите наименьшее значение функции
tgx cos1 2x
/
1. Найти f /(x)
Найти f /(x)
2. Найти критические
точки, взять те,
которые принадлежат
данному отрезку.
y = 4tgx – 4x – + 5 на отрезке
4 ; 4
4
1
у 4
4
2
cos x
/
0
4
4 0
2
cos x
4
2
cos x 1
Нам не нужны ВСЕ стационарные
у 4 5 1
4
у 4 5 9 2
4
у 0 0 0 5 5
точки. Необходимо сделать выбор
тех значений, которые попадут в
заданный отрезок
3. Вычислим значения функции в
критических точках ;
4 4
и на концах отрезка.
4. Из вычисленных значений
сделаем выбор наименьшего.
В 11
1
3
10 х
х
20. Найдите наибольшее значение функции
tgx cos1 2x
/
1. Найти f /(x)
y = 3tgx – 3x + 5 на отрезке ; 0
4
1
у 3
3
2
cos x
/
2. Найти критические
точки, взять те,
которые принадлежат
данному отрезку.
0
3
3 0
2
cos x
cos 2 x 1
4
Нам не нужны ВСЕ стационарные
3. Вычислим значения функции в критических точках
точки.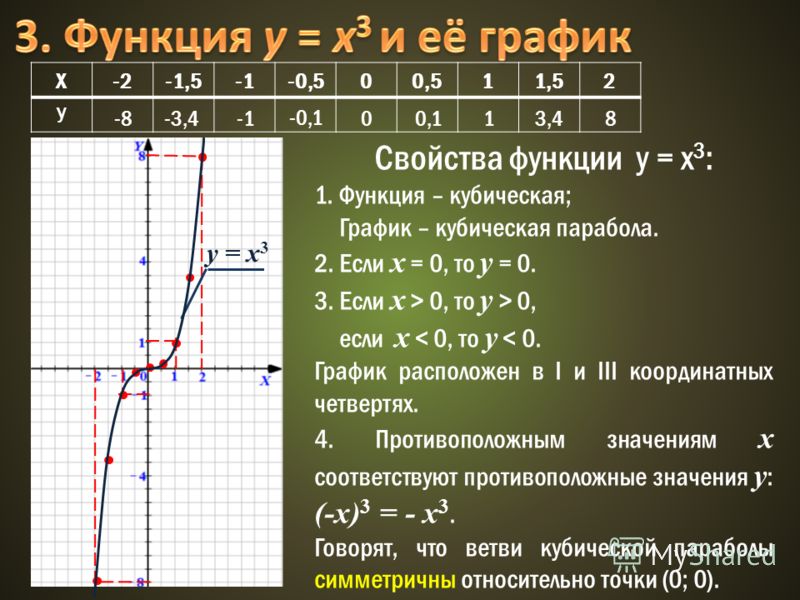
и на
Необходимо
концах отрезка.
сделать выбор
тех значений, которые попадут в
4. Из вычисленных значений сделаем выбор наибольшего.
заданный отрезок
3 4 ; 0 3
у 3tg 3 5 3
5 2
-1
4
0
4
4
у 0 3tg0 0 5 5
4
В 11
5
4
3
10 х
х
AlleBilderVideosShoppingMapsNewsBücher
suchoptionen
[DOC] Напишите уравнение линии в форме пересечения наклона.
www.crsd.org › lib › Домен › AA1_Review_on_Sections_8-4_to_8-5
Если у вас есть точка и наклон, вы можете использовать следующую формулу для записи уравнения прямой в любой форме. 3. линии имеют противоположные взаимные наклоны. 4. is …
[DOC] Форма пересечения уклонов Рабочий лист
www.wsfcs.k12.nc.us › cms › lib › Centricity › Domain › Slope and …
Для каждого графика: Напишите уравнение линии в ФОРМЕ НАКЛОН-ОТРЕЗАНИЕ. В каждом линейном уравнении определите наклон (m) и точку пересечения с осью y (b).
[DOC] ПРОЕКТ SLOPE-INTERCEPT: СОЗДАЙТЕ ВИКТОРИНУ
www.wsfcs.k12.nc.us › cms › lib › Centricity › ModuleInstance › slo…
в форме Slope-Intercept. Затем нарисуйте уравнение. Каждый вопрос должен иметь четыре варианта ответа. Используйте пример викторины ниже, чтобы помочь написать свою викторину.
[DOC] Проверка викторины
www.orange.k12.nj.us › Centricity › Домен › Модуль 1 Проверка викторины 3
Проверка викторины. Найдите наклон прямой, проходящей через каждую пару точек. 1. (3, 5) и (1, 2) 2. … Напишите уравнение для каждой линии в форме пересечения наклона.
Quiz On Slope Intercept Form Учебные ресурсы — TPT
www.teacherspayteachers.com › Диапазон цен › Бесплатно
Результаты 1–17 из 17 · Этот материал представляет собой раздаточный материал, состоящий из 27 тестовых вопросов. Большинство из них имеют множественный выбор, а остальные — свободный ответ. Он охватывает темы для «Наклона . ..
..
Форма пересечения уклона викторины Учебные ресурсы — TPT
www.teacherspayteachers.com › Обзор › Search:sl…
Результаты 1–24 из 770+ 2-страничный PDF-документ, в котором оцениваются способности учащегося …
[DOC] Рабочий лист графических уравнений
www.matsuk12.us › cms › lib › Centricity › Domain › Graphing_Eq…
Затем определите наклон и y-int каждого линейного уравнения. Наконец, нарисуйте график каждого уравнения, используя форму пересечения наклона (используйте миллиметровую бумагу для графиков). 5. у = …
Форма пересечения уклона — Викторина 2 Форма решения A | Промежуточный Алгебра
www.docsity.com › … › Инженерное дело › Алгебра
Загрузить Форму пересечения наклона — Викторина 2 Форма решения A | Средний уровень алгебры | MA 103 и другие викторины по алгебре в формате PDF только на Docsity!
Форма пересечения уклона — Викторина 2 с решением | МА 103 | Контрольные вопросы Алгебра
www. docsity.com › … › Инженерное дело › Алгебра
docsity.com › … › Инженерное дело › Алгебра
Загрузить форму пересечения уклонов — тест 2 с решением | Средний уровень алгебры | MA 103 и другие викторины по алгебре в формате PDF только на Docsity!
Slope Intercept Form Quiz Doc — euromarmi92.it — pdfFiller
www.pdffiller.com › 533522630—Slope-Intercept-F…
Bewertung 4,4
(39) 90 хотите с документом викторины формы пересечения уклона — euromarmi92.it: заполните, подпишите, распечатайте и отправьте онлайн мгновенно. Безопасно загрузите документ …
Ähnlichesuchanfragen
Форма пересечения наклона Примечания
Написание линейных уравнений в форме пересечения наклона Рабочий лист
Наклон и точка пересечения y pdf
График в форме точки пересечения наклона pdf
Нахождение точек пересечения x и y из таблицы Рабочий лист
Y = mx + b Примечания pdf
Запись уравнений из таблицы Ключ ответа на рабочий лист pdf
3
Написание линейных уравнений из таблицы Рабочий лист с ответами
Урок 4 Навыки Практика линейных функций Ключ ответа
0003
homesteadmiddle. com › wp-content › uploads › cmdm › 146314972…
com › wp-content › uploads › cmdm › 146314972…
Курс 3 • Глава 4 Функции. Заполните таблицу функций. Затем постройте график функции. 1. у = х + 4 х х + 4… Урок 4 Практика навыков. Линейные функции.
Урок 4. Отработка навыков (линейные функции) — День 4 — YouTube
www.youtube.com › смотреть
23.03.2020 · Урок 4. Отработка навыков (линейные функции) — День 4. 323 просмотра 2 года назад. Бриттани Феррилл …
Dauer: 12:05
Прислан: 23.03.2020
Урок 4 Домашнее задание Линейные функции — pdfFiller
www.pdffiller.com
(40)
Заполнить урок 4 Домашнее задание Практика линейных функций, редактирование онлайн. Подписывайте, отправляйте по факсу и распечатывайте с ПК, iPad, планшета или мобильного телефона с помощью pdfFiller ✓ Мгновенно. Попробуй сейчас!
Урок 6 домашнее задание практика писать линейные уравнения
edqpo.mr-borna-mde.de › урок-6-домашнее задание-практик. ..
..
Рабочие листы Chn101, урок 6, домашнее задание, Урок 6, домашнее задание, практика, написание линейных уравнений, ключ ответа, Глава 6, работа, Практика, оценка чтения, … -4-skills-practice-linear-function…
30.01.2013 · 1 рабочий лист (тот же, что и от 21 сентября) 25 сентября. Вопрос 1. Дополнительная практика Глава 4 = Практика навыков. Применить элементарные операции со строками к …
Урок 4. Линейная практика навыков — Brainly.com
brainly.com › Математика › Средняя школа
Остались вопросы? Найдите больше ответов. Разблокированный значок с круглым отверстием, из которого торчат лапа белого кролика и уши.
Урок 7. Практика навыков. … Урок 4 Домашнее задание Практика Линейные функции Ключ ответа.
1 7 Функции практики навыков
haye.parcvalrose.it › 1-7-skills-practice-functions
Урок 1 Графики квадратичных функций Ответ Ключевая факторизованная форма квадратичной функции … НАЗВАНИЕ ДАТА 4-7 ПЕРИОД Навыки Практика обратных линейных функций 1.